Abstract
The celebrated Korteweg–de Vries and Kadomtsev–Petviashvili (KP) equations are prototypical examples of integrable evolution equations in one and two spatial dimensions, respectively. The question of constructing integrable evolution equations in three-spatial dimensions has been one of the most important open problems in the history of integrability. Here, we study an integrable extension of the KP equation in three-spatial dimensions, which can be derived using a specific reduction of the integrable generalization of the KP equation in four-spatial and two-temporal dimensions derived in (Phys. Rev. Lett. 96, (2006) 190201). For this new integrable extension of the KP equation, we construct smooth multi-solitons, high-order breathers, and high-order rational solutions, by using Hirota’s bilinear method.
MSC:
35C08; 35Q51; 37K10; 37K35
1. Introduction
There exists a distinctive class of nonlinear evolution equations in one and two spatial dimensions, called integrable [1,2]. Such prototypical equations in one spatial dimension are the celebrated Korteweg–de Vries (KdV) [3,4] and the nonlinear Schrodinger (NLS) [5,6] equations. Every integrable nonlinear evolution equation in one spatial dimension has several integrable versions in two spatial dimensions. Two such physically significant generalizations of the KdV are the Kadomtsev–Petviashvili I (KPI) and II (KPII) equations. Similarly, two analogous generalizations of the NLS are the Davey–Stewartson I (DS I) and II (DSII) equations. It is important to emphasize that integrable nonlinear evolution equations arise in a variety of physical applications. For example, in the context of fluid mechanics, the KP equations arise in the weakly nonlinear, weakly dispersive, weakly two-dimensional limit of inviscid, irrotational, water waves, and in the case of KPI when the surface tension is dominant [7]. Other significant applications of the KP and DS equations are discussed, for example, in weakly dispersive media [2,8,9,10] in optics and hydrodynamics [2,10,11,12,13].
One of the most important open questions in the field of integrability has been the question of the existence of integrable evolution equations in three spatial dimensions. Substantial progress regarding this question was presented in [14], where generalizations of the KP and of the DS equations were presented, namely equations in four spatial and two temporal dimensions. The solution of the Cauchy problem of the generalization of the KP is presented in [15]. The solution of the Cauchy problem of the generalization of the DS equation is sketched in [14] and presented in detail in [16]. Incidentally, another approach toward integrability in multidimensions is presented in [17], where it is shown that there exist integrable nonlinear evolution equations in any number of dimensions; however, these equations have the major disadvantage that they involve a nonlocal commutator.
The question of reducing integrable equations from to equations in three spatial dimensions, although discussed in many papers, including [14,15], as well as [18,19], remained open. In particular, regarding reductions of the KP equation, it should be noted that, although the real reduction discussed in [14] involves two equations, many authors have erroneously analyzed only one of these two equations, ignoring the other one. Here, we discuss a constructive approach for obtaining integrable equations in three spatial dimensions, and by implementing this approach to KP, we derive the results presented below. Our paper is a companion of [20], where a highly novel nonlinear transform pair in three spatial dimensions, capable of solving the Cauchy problem of these equations, is also derived. Specifically, regarding Equation (1) below, we note that the analysis of its Cauchy problem performed in [20] reveals that the time dependence of the associated spectral function (the nonlinear Fourier transform of the solution) is of the form , where T and R are real functions of the real spectral parameters , and (in the linear limit, these three variables in the Fourier space correspond to the three real variables in the physical space). Because of the occurrence of the term , it is not clear that this initial value problem is well posed. However, in the recent breakthrough presented in [20], it is explicitly shown that the Cauchy problem of Equation (1) is indeed well posed. Remarkably, the novel nonlinear Fourier transform introduced in [20], which is capable of solving (1), gives rise to a completely new transform for solving the linear limit of Equation (1), namely, the equation obtained from Equation (1) after eliminating the nonlinear term .
The following equation for the complex-valued function , where , are real, independent variables, provides an integrable generalization of the KP equation in three-spatial dimensions,
where are arbitrary complex constant parameters.
As is well known, the most important property of integrable equations is that they admit a Lax pair formulation. The derivation of Equation (1), as well as its Lax pair, is presented in Section 2. Two-dimensional integrable equations, like KP and DS equations, possess a variety of particular solutions, which can be obtained using different techniques, including the inverse scattering method, the d-bar method, the Darboux transformation, the Hirota bilinear method and the KP hierarchy reduction method [21,22,23,24,25,26,27,28,29,30]. In this connection, smooth multi-soliton and high-order breather solutions, as well as high-order rational solutions of Equation (1), are constructed in Section 3 and Section 4, respectively, via Hirota’s bilinear method. These results are discussed further in Section 5.
2. Integrable Extensions of the KP in Three Dimensions and Their Lax Pairs
Starting with the KP equation and complexifying , namely, introducing the complex variables
it is shown in [14] that the equation
is an integrable generalization of the KP equation in the 4-spatial dimensions and the two temporal dimensions . In Equation (3), means integral, bar denotes complex conjugation, and Equation (2) implies the following identities:
where we have assumed that f vanishes as . Assuming q is real and suppressing the dependence, the (4 + 2)-dimensional KP (3) yields two (4 + 1)-dimensional equations; see Equation (10) or equivalent Equation (11) in [14]. These equations have provoked extensive studies [18,19]. In addition, similar considerations are valid for the (4 + 2)-dimensional Davey–Stewartson equation [16].
In order to obtain three-dimensional reductions of this equation, which is the first purpose of this paper, we let , where a and b are all real constants. Hence, , where . Replacing in Equation (5) by , we find a -dimensional generalization of the KP
Letting , where are real constants, and seeing , where , Equation (6) reduces to a three-dimensional KP equation for the complex-valued function q,
where
Remark 1.
The second purpose of the paper is to show the integrability of the three-dimensional KP Equation (1) by providing its Lax pair and different kinds of solutions. The Lax pair of Equation (3) [14] is given by
where is an appropriate eigenfunction, and the operators are defined by
Using in these equations the scaling transformations and , we find the following Lax pair for Equation (5):
The crucial reduction imply the following Lax pair for (7):
where are expressed by virtue of via equations
3. Soliton and Breather of the Three-Dimensional KP Equation
In this section, we derive soliton and breather solutions of the three-dimensional KP equation (1) by using the Hirota bilinear method and certain perturbation technique [31]. Equation (1) can be transformed into the bilinear form
through the variable transformation
where f is a complex function, and D is the Hirota’s bilinear differential operator [31] defined by
Based on this bilinear form, the three-dimensional KP Equation (1) admits the following N-soliton solutions:
with
where the above parameters must satisfy the condition
which assures that these solutions are smooth. Here, are arbitrary real parameters, and the subscript j denotes an integer. The subscripts R and I denote the real and imaginary parts of the corresponding parameters, respectively.
Taking in Equation (21) , we obtain the one-soliton solution of the three-dimensional KP equation:
The modulus of this solution is given by
with
It can be seen from the above expression that the one-soliton is nonsingular, provided that , which means . For simplicity, we set , as noted in Equation (23), to guarantee the smoothness of the one-soliton solution (24).
Taking in (21) and , imposing the constraints
and choosing , we obtain a smooth two-soliton solution of the three-dimensional KP equation:
It is straightforward, using Equation (21), to derive multi-soliton solutions of the three-dimensional KP equation. Such solutions are depicted in Figure 1. The effect of changing the variables z and t is simply to move the profile of the soliton in the ()-plane, without any deformations.
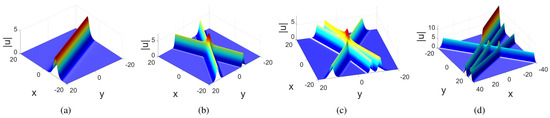
Figure 1.
Plots of of soliton solutions for the three-dimensional KP Equation (1) generated by Equation (21) with parameters and variables . (a): One-soliton solution with parameters ; (b): Two-soliton solution with parameters ; (c): Three-soliton solution with parameters ; (d): Four-soliton solution with parameters .
In order to derive breather solutions of the three-dimensional KP equation, we use the constraints,
For the particular case of Equation (26),
we obtain a first-order breather solution of Equation (1) with f given below:
where the parameters satisfy
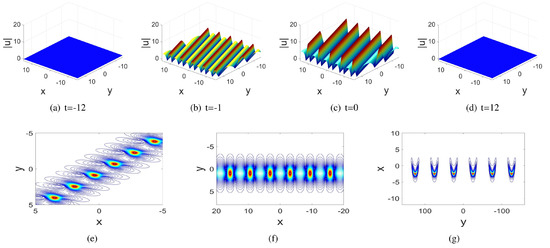
Without loss of generality, we study the dynamics of the first-order breather in the -plane. The velocities of the first-order breathers along the x and y directions are given by
The period of the first-order breather is given by , where and are given by
Note that changing z and t only results in moving the profile of in a parallel manner in the -plane, and it shows that there exist four types of breathers:
- The y-periodic breather. If , the first-order breather (27) has periodicity only in the y-direction in the plane, and is localized in the x-direction; see Figure 2g. Since the coefficient of t in is not zero, the effect of t is to move the breather along the x-axis. Similarly, since the coefficient of z in is not zero, the effect of z is to move the breather along the y-axis.
Taking in (26)
a second-order breather of three-dimensional KP Equation (1) can be derived. The dynamic of this solution is shown in Figure 3.
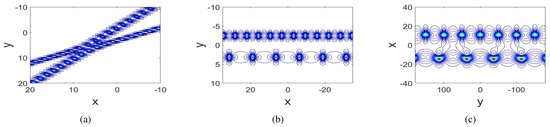
Figure 3.
Second-order breathers in the -plane of the three-dimensional KP Equation (1) with parameters and variables . (a): ; (b): ; (c): .
In addition, mixed solutions composed of solitons and breathers, are also given for . Taking in (21)
a hybrid solution consisting of a first-order breather and one soliton is constructed, see Figure 4a. For larger N, we obtain mixed solutions consisting of several first-order breathers and solitons. For example, taking in (21),
we derive the hybrid solution consisting of one first-order breather and two solitons, see Figure 4b.
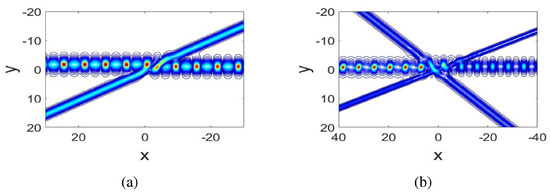
Figure 4.
Hybrid solutions of the three-dimensional KP Equation (1) consisting of a breather and solitons with parameters and variables . (a): ; (b): .
4. Rational Solution of the Three-Dimensional KP Equation
In order to derive rational solutions of the three-dimensional KP Equation (1), we take in Equation (21)
and compute a suitable limit as . In this way, the function f, defined in (21), becomes a polynomial function. This construction yields an n-th rational solution, , of Equation (1), in which f is written as follows:
with
To illustrate this formula of rational solutions, we provide concrete examples by taking in Equation (32)
where we impose the constraints
In this way, we obtain a first-order rational solution of the three-dimensional KP Equation (1):
If
this first-order rational solution is nonsingular. Without loss of generality, taking in (36) , that is, , we obtain the following analytical expression of first-order rational solution of the three-dimensional KP Equation (1):
The first-order rational solution given in (38) is a lump in the -plane, which reaches the maximum of at ; see Figure 5.
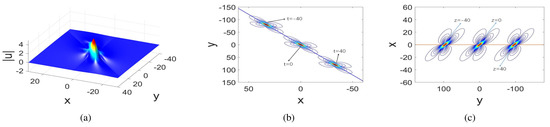
Figure 5.
Plots of of the first-order lump solution (38) of the three-dimensional KP equation with parameters ; (a) a three-dimensional plot at ; (b) the temporal evolution in the -plane of the contour of a first-order lump at , where the blue line is ; (c) the evolution in the -plane of the contour of a first-order lump at , where the red line is .
This rational solution is nonsingular when . As described in Figure 6, this solution describes the interaction of two rational parallel solitons in the -plane. When , the two rational solitons fuse together and reach the minimum value at . In general, the interaction of two solitons produces a solution with larger amplitude. Surprisingly, in this case, the amplitude of a line soliton fused by two rational solitons is significantly smaller than the solitons eventually after separation. As shown in Figure 6e–h, although the two solitons are completely separated as t tends to infinity, as time evolves, they interact, producing a downward peak, which yields a decrease of the amplitude. Finally, the two rational solitons fuse into a W-type rational soliton at .
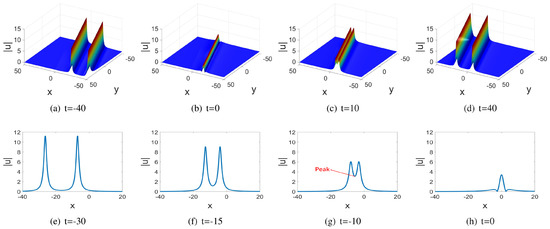
Figure 6.
Plots of of the temporal evolution of the rational solution (40) for the three-dimensional KP equation with parameters .
Following the extensive studies of the line rogue waves for -dimensional integrable models [32,33,34,35], it is interesting to find such solutions of the three-dimensional KP equation. The line rogue wave has infinite length and suddenly appears and disappears in the background plane. Compared with the normal rogue waves, which are localized in time and space, line rogue waves are localized in time, but are non-local in space, and also only appear in high-dimensional systems. Taking in Equation (32),
we obtain
This rational solution is nonsingular when . This rational solution is analogous to a typical line rogue wave solution. Its visible line profile is preserved for the short period of time during the evolution process; see Figure 7.
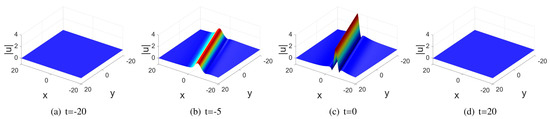
Figure 7.
Plots of of the temporal evolution of the line rogue wave (42) for the three-dimensional KP equation with parameters .
5. Discussion and Conclusions
The main achievement of this work is the explicit construction of nonsingular multi-solitons, and high-order breather and high-order rational solutions of the three-dimensional KP Equation (1) using a Hirota bilinear method and the perturbation expansion technique. Moreover, different patterns of first-order breathers for the three-dimensional KP equation are discussed; see Figure 2. Furthermore, mixed solutions composed of breather and solitons are also given; see Figure 4. Additionally, high-order rational solutions of the three-dimensional KP equation are constructed by taking the long-wave limit of N-soliton solution. The first-order rational solutions are nonsingular, providing that the constraints of (35) and (37) are valid. The first-order rational solution generates a lump wave in the -plane; its local characteristics and evolutional process are demonstrated in Figure 5. In addition to the lump wave, the first-order rational solution (40) describes the interaction of two rational parallel solitons under the constraint (39). As shown in Figure 6, the interaction of two rational solitons surprisingly makes the amplitude of this solution significantly smaller in comparison to the amplitude of the separated line solitons. In summary, under the constraint (41), the first-order rational solution (40) in the -plane is a line rogue wave; see Figure 7. The dynamics of the exact solutions possessed by this new three-dimensional model are rich and highly non-trivial. Hopefully, such solutions may be important in realistic applications.
Author Contributions
Conceptualization, A.S.F. and J.H.; methodology, A.S.F.; software, A.S.F. and Y.C.; formal analysis, Y.C. and J.H.; investigation, A.S.F.; resources, A.S.F.; data curation, Y.C.; writing—original draft preparation, A.S.F., Y.C. and J.H.; writing—review and editing, J.H.; supervision, J.H.; project administration, J.H.; funding acquisition, J.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No.12071304 and No.11871446), and the Guangdong Basic and Applied Basic Research Foundation (Grant 2022A1515012554).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The work was supported by the National Natural Science Foundation of China (Grant No.12071304 and No.11871446), and the Guangdong Basic and Applied Basic Research Foundation (Grant 2022A1515012554).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Faddeev, L.D.; Takhtadjan, L.A. Hamiltonian Methods in the Soliton Theory; Springer Series in Soviet Mathematics; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Russell, J.S. Report of the committee on waves. In Proceedings of the 7th Metting of the British Association for the Advabcement of Science, Liverpool, UK, September 1838; pp. 417–496. [Google Scholar]
- Korteweg, D.J.; de Vries, G. On the change of form of long waves advancing in a rectangular canal, and a new type of long stationary waves. Philos. Mag. Ser. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Chiao, R.; Garmire, E.C. Townes, Self-trapping of optical beams. Phys. Rev. Lett. 1964, 13, 479–482. [Google Scholar] [CrossRef]
- Zakharov, V. Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 1968, 9, 190–194. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Fokas, A.S.; Musslimani, Z.H. On a new nonlocal formulation of water waves. J. Fluid Mech. 2006, 562, 313–344. [Google Scholar] [CrossRef]
- Kadmotsev, B.B.; Petviashvili, V.I. On the stability of solitarywaves inweakly dispersing media. Sov. Phys. Doklady 1970, 15, 539–541. [Google Scholar]
- Infeld, E.; Rowlands, G. Nonlinear Waves, Solitons and Chaos; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ablowitz, M.J. Nonlinear Dispersive Waves: Asymptotic Analysis and Solitons; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Davey, A.; Stewartson, K. On three-dimensional packets of surface waves. Proc. R. Soc. Lond. A 1974, 338, 101–110. [Google Scholar]
- Ablowitz, M.J.; Segur, H. On the evolution of packets of water waves. J. Fluid Mech. 1979, 92, 691–715. [Google Scholar] [CrossRef]
- Ioannou-Sougleridis, I.; Frantzeskakis, D.J.; Horikis, T.P. A Davey-Stewartson description of two-dimensional solitons in nonlocal media. Stud. Appl. Math. 2020, 144, 3–17. [Google Scholar] [CrossRef]
- Fokas, A.S. Integrable Nonlinear Evolution Partial Differential Equations in 4 + 2 and 3 + 1 Dimensions. Phys. Rev. Lett. 2006, 96, 190201. [Google Scholar] [CrossRef]
- Fokas, A.S. Kadomtsev–Petviashvili equation revisited and integrability in 4 + 2 and 3 + 1. Stud. Appl. Math. 2009, 122, 347–359. [Google Scholar] [CrossRef]
- Fokas, A.S.; Weele, M.C.v. Complexification and integrability in multidimensions. J. Math. Phys. 2018, 59, 091413. [Google Scholar] [CrossRef]
- Fokas, A.S. Nonlinear Fourier transforms and integrability in multidimensions. Contemp. Math. 2008, 458, 71–80. [Google Scholar]
- Yang, Z.Z.; Yan, Z.Y. Symmetry groups and exact solutions of new (4 + 1)-dimensional Fokas equation. Commun. Theor. Phys. 2009, 51, 876–880. [Google Scholar]
- Wang, X.B.; Tian, S.F.; Feng, L.L.; Zhang, T.T. On quasi-periodic waves and rogue waves to the (4 + 1)-dimensional nonlinear Fokas equation. J. Math. Phys. 2018, 59, 073505. [Google Scholar] [CrossRef]
- Fokas, A.S. Integrable nonlinear evolution equations in three spatial dimensions. Proc. R. Soc. A 2022, 478, 20220074. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Villarroel, J. Solutions to the time dependent Schrödinger and the Kadomtsev–Petviashvili equations. Phys. Rev. Lett. 1997, 78, 570–573. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Kuznetsov, E.A. Solitons and collapses: Two evolution scenarios of nonlinear wave systems. Phys. Usp. 2012, 55, 535–556. [Google Scholar] [CrossRef]
- Clarke, S.; Gorshkov, K.; Grimshaw, R.; Stepanyants, Y. Decay of Kadomtsev–Petviashvili lumps in dissipative media. Phys. D 2018, 66, 43–50. [Google Scholar] [CrossRef]
- Chang, J.H. Asymptotic analysis of multilump solutions of the Kadomtsev–Petviashvili-I equation. Theor. Math. Phys. 2018, 195, 676–689. [Google Scholar] [CrossRef]
- Dubrovsky, V.G.; Topovsky, A.V. Multi-lump solutions of KP equation with integrable boundary via ∂-dressing method. Phys. D 2020, 414, 132740. [Google Scholar] [CrossRef]
- Guo, L.J.; Chabchoub, A.; He, J.S. Higher-order rogue wave solutions to the Kadomtsev–Petviashvili 1 equation. Phys. D 2021, 426, 132990. [Google Scholar] [CrossRef]
- Rao, J.G.; Chow, K.W.; Mihalache, D.; He, J.S. Completely resonant collision of lumps and line solitons in the Kadomtsev–Petviashvili I equation. Stud. Appl. Math. 2021, 147, 1007–1035. [Google Scholar] [CrossRef]
- Lester, C.; Gelash, A.; Zakharov, D.; Zakharov, V. Lump chains in the KP-I equation. Stud. Appl. Math. 2021, 147, 1425–1442. [Google Scholar] [CrossRef]
- Stepanyants, Y.A.; Zakharov, D.; Zakharov, V. Lump interacts with plane solitons. arXiv 2022, arXiv:2108.06071v1. [Google Scholar]
- Guo, L.J.; He, J.S.; Wang, L.H.; Cheng, Y.; Frantzeskakis, D.J.; Bremer, T.S.v.; Kevrekidis, P.G. Two-dimensional rogue waves on zero background in a Benney-Roskes model. Phys. Rev. Res. 2020, 2, 033376. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ohta, Y.; Yang, K.J. Rogue waves in the Davey-Stewartson I equation. Phys. Rev. E 2012, 86, 036604. [Google Scholar] [CrossRef]
- Ohta, Y.; Yang, J.K. Dynamics of rogue waves in the Davey-Stewartson II equation. J. Phys. A Math. Theor. 2013, 46, 105202. [Google Scholar] [CrossRef]
- Rao, J.G.; He, J.S.; Malomed, B.A. Resonant collisions between lumps and periodic solitons in the Kadomtsev–Petviashvili I equation. J. Math. Phys. 2022, 63, 013510. [Google Scholar] [CrossRef]
- Cao, Y.L.; Cheng, Y.; Malomed, B.A.; He, J.S. Rogue waves and lumps on the non-zero background in the PT-symmetric nonlocal Maccari system. Stud. Appl. Math. 2021, 147, 694–723. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).