New Discussion on Approximate Controllability for Semilinear Fractional Evolution Systems with Finite Delay Effects in Banach Spaces via Differentiable Resolvent Operators

Abstract

This manuscript mainly discusses the approximate controllability for certain fractional delay evolution equations in Banach spaces. We introduce a suitable complete space to deal with the disturbance due to the time delay. Compared with many related papers on this issue, the major tool we use is a set of differentiable properties based on resolvent operators, rather than the theory of $C_0$-semigroup and the properties of some associated characteristic solution operators. By implementing an iterative method, some new controllability results of the considered system are derived. In addition, the system with non-local conditions and a parameter is also discussed as an extension of the original system. An instance is proposed to support the theoretical results.

1. Introduction

This manuscript mainly investigates the sufficient conditions of the approximate controllability of some fractional control systems as below:

$$\left\{\begin{array}{c}{}^C{D}^{\beta }x\left(t\right)=Ax\left(t\right)+f(t,x_t)+Bu\left(t\right),t\in I:=[0,a],\hfill \\ x\left(t\right)=\varphi \left(t\right),t\in [-b,0],\hfill \end{array}\right.$$

(1)

and

$$\left\{\begin{array}{c}{}^C{D}^{\beta }x\left(t\right)=Ax\left(t\right)+f(t,x_t)+Bu\left(t\right),t\in I:=[0,a],\hfill \\ x\left(t\right)+\lambda g_t\left(x\right)=\varphi \left(t\right),t\in [-b,0],\hfill \end{array}\right.$$

(2)

where ${}^C{D}^{\beta }$ means the Caputo derivative with order ${\displaystyle \frac{1}{2}<\beta \le 1.}$ X and U are Banach spaces. Linear operator $A:\mathcal{D}\subset X\to X$ is unbounded with dense domain $\mathcal{D}$. The delay term $x_t$ is explained in Equation (5). The control u takes values in $L^2(I;U)$. For any $t\in [-b,0]$, the non-local term $g_t:C([-b,a];X)\to X$ satisfies some given conditions. $\lambda$ is a parameter. Let $\varphi \in L^1([-b,0];X).$ $B:L^2(I;U)\to L^2(I;\mathcal{D})$ is a bounded linear operator. f is a non-linearity that will be specified later.

Fractional differential systems and evolution systems have been studied extensively owing to its widespread backgrounds of some scientific and engineering realms, such as signal processing, finance, anomalous diffusion phenomena, heat conduction, etc. We refer readers to [1,2,3,4] for further detailed information. On the other side, controllability has gained a lot of importance and interest, and it plays a significant role in the description of various dynamical problems [5,6,7,8]. It is known to all that the fractional evolution system is closely related to time. In this regard, it has something in common with the controllability problem. Therefore, the controllability of some kinds of fractional evolution systems has become an important research hotspot. For example, exact controllability and approximate controllability are two mainstream research directions and they have important differences from the viewpoint of mathematics. Exact controllability can steer the control system to any given final time point. The control operator is usually assumed to be reversible. Then, the controllability problem is transformed into a fixed point problem [9,10,11,12,13]. Furthermore, an induced inverse of the control operator is not necessarily true in infinite-dimensional space. In consideration of these strong assumptions, more and more scholars begin to study the approximate controllability in various abstract spaces, which means that it can steer the control system to an any small neighborhood of final time point [14,15,16,17,18,19,20]. In addition, controllability of fractional evolution systems also has important applications in the research areas of logical control networks or Boolean networks.

For instance, S. Ji [16] and F. Ge et al. [17] studied the approximate controllability of fractional semi-linear non-local evolution systems and fractional differential systems with impulsive conditions via approximating method under the assumption that A generated a $C_0$-semigroup, respectively. Moreover, the approximate controllability of some other fractional systems, such as stochastic equations, neutral equations, etc., have also been deeply investigated (one can see [18,19,20] for more details). However, approximate controllability of the linear systems correspondence to the considered systems is necessary in this method. Therefore, some other approaches, such as the iterative method, are used to solve the approximate controllability problems for some evolution systems. For example, H. Zhou [21] obtained a sufficient condition of the approximate controllability for certain first-order evolution equations by utilizing iterative approach and the theory of strongly continuous semigroup. Authors in [22] dealt with the approximate controllability of some evolution systems with fractional order without delay by using iterative method. The properties of $C_0$-semigroup are also included. By applying the same method, [23] also derived some appropriate controllability conclusions for some fractional differential equations with no delay effects.

It is noted that the results of approximate controllability discussed above are based on the $C_0$-semigroup together with some associated characteristic solution operators [24]. However, in many cases, infinitesimal generator A may not be able to generate a $C_0$-semigroup, but it can generate a resolvent operator instead [25]. On the other side, a resolvent operator can degenerate into a $C_0$-semigroup when the integral kernel is equal to 1, that is, a resolvent operator covers a $C_0$-semigroup as a special case. Of course, this can also be explained by the subordinate principle [26].

In comparision with results in [27] considering the influence of delay, we shall study the approximate controllability for some fractional control systems on the supposition that A is an infinitesimal generator of a differentiable resolvent operator rather than a $C_0$-semigroup; we shall consider a control problem with variable delay, not fixed delay by contrast; the function $\varphi \left(t\right)$ is supposed to be integrable rather than continuous. Under these generalized conditions, the difficulty mainly lies in how to overcome the obstacles caused by the variable delay and how to make use of the differentiability of resolvent operators. We solve this problem by means of a new special complete space we introduced and the theory of differentiable resolvent operator developed in [25].

Motivated by the aforementioned discussions, we shall establish a set of new approximate controllability results for systems (1) and (2) by using iterative method. As far as we know, the approximate controllability for the fractional evolution equations with finite variable delay and with non-local conditions and a parameter under the hypothesis that A generate a differentiable resolvent operator is still an untreated topic in the existing literature. Therefore, it is necessary to make further investigations to fill the gap in this regard.

Summarily, different from the above discussed papers, some highlights of the manuscript are presented as follows. (i) The approximate controllability of considered systems is studied on the supposition that the resolvent operator is differentiable, rather than utilizing the theory of $C_0$-semigroup together with the properties of associated characteristic solution operators; (ii) The delay-induced-difficulty is overcome by introducing a special complete integrable space since we generalize the delay term from continuity to integrability compared with some other papers; (iii) The system (2) discussed in this manuscript is provided with some more generalized nonlocal conditions compared with many related papers [5,9,11,16,17] $(\lambda =1,t=0)$.

This manuscript is arranged as below. In the next part, we include some necessary preparations for the main controllability results. InSection 3, some existence results of the mild solution of the considered systems are obtained. In Section 4, we investigate the approximate controllability for the fractional delay control systems, and the case with non-local conditions and a parameter is discussed in Section 5. An instance is proposed in Section 6 to illustrate our abstract conclusions.

2. Preparations

Let X be a Banach space with norm $\parallel x\parallel$, $x\in X$. The linear operator $A:\mathcal{D}\subset X\to X$ is closed and unbounded, in which $\mathcal{D}$ means the domain of A equipped with graph norm ${\parallel x\parallel }_{\mathcal{D}}=\parallel x\parallel +\parallel Ax\parallel$. $C(I;X)$ stands for the space with all the continuous functions mapping I into X equipped with the sup-norm ${\parallel x\parallel }_C$, $L^2(I;X)$ stands for the space of all Bochner integrable functions mapping I into X equipped with the norm ${\parallel x\parallel }_{L^2(I;X)}={\left({\displaystyle {\int }_0^a{\parallel x\left(t\right)\parallel }^{2}dt}\right)}^{1/2}$, and $C^{\beta }(I;X)$ denotes the space of all the $\beta$-Hölder continuous functions mapping I into X provided with the norm ${\parallel x\parallel }_{C^{\beta }(I;X)}={\parallel x\parallel }_{C(I;X)}+{\left[\right|x\left|\right]}_{C^{\beta }(I;X)}$, where

$${\displaystyle {\left[\right|x\left|\right]}_{C^{\beta }(I;X)}=\underset{t,s\in I,t\ne s}{sup}\frac{\parallel x\left(t\right)-x\left(s\right)\parallel }{{(t-s)}^{\beta }}.}$$

In the next discussion, the following equation

$$x\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t\frac{Ax\left(s\right)}{{(t-s)}^{1-\beta }}ds,t\ge 0,$$

(3)

is assumed to possess an resolvent operator ${\left\{\mathfrak{R}\left(t\right)\right\}}_{t\ge 0}$ on X.

Definition 1

([28]). The fractional integral of order $\beta >0$ with the lower limit zero is written as

$${\displaystyle I_{0^{+}}^{\beta }x\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}x\left(s\right)ds,t>0,}$$

where Γ denotes the Gamma function.

Definition 2

([28]). The fractional derivative of the function $x\in C\left(\right(0,+\infty );\mathbb{R})$ in the Caputo sense can be defined by

$${\displaystyle {}^C{D}_{0^{+}}^{\beta }x\left(t\right)=\frac{1}{\mathrm{\Gamma }(n-\beta )}{\int }_0^t\frac{x^{\left(n\right)}\left(s\right)}{{(t-s)}^{\beta -n+1}}ds,t>0,}$$

where $n=\left[\beta \right]+1,\left[\beta \right]$ represents the integer part of the positive constant β.

Definition 3

([25]). Suppose a set of operators ${\left\{\mathfrak{R}\left(t\right)\right\}}_{t\ge 0}$ to be bounded and linear on space X. If it fulfills hypotheses as below:

(i) $\mathfrak{R}\left(t\right)$ is strongly continuous on ${\mathbb{R}}_{+}$ and $\mathfrak{R}\left(0\right)=\mathcal{I}$;

(ii) $\mathfrak{R}\left(t\right)\mathcal{D}\subset \mathcal{D};$ for each $x\in \mathcal{D},t\ge 0,$ it satisfies $A\mathfrak{R}\left(t\right)x=\mathfrak{R}\left(t\right)Ax$;

(iii) The following equality can be established

$$\mathfrak{R}\left(t\right)x=x+\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t\frac{Ax\left(s\right)}{{(t-s)}^{1-\beta }}ds,$$

then we define it as a resolvent operator of Equation (3).

Definition 4

([25]). A resolvent operator $\mathfrak{R}\left(t\right)$ of Equation (3) is known as differentiable, if it satisfies $\mathfrak{R}(·)x\in W_{loc}^{1,1}({\mathbb{R}}_{+};X)$, $\forall x\in \mathcal{D}$. In addition, for $\forall x\in \mathcal{D}$, there exists a function $\omega \in L_{loc}^1\left({\mathbb{R}}_{+}\right)$ satisfying

$$\parallel \dot{\mathfrak{R}}{\left(t\right)x\parallel \le \omega \left(t\right)\parallel x\parallel }_{\mathcal{D}}a.e.on{\mathbb{R}}_{+}.$$

Consider the following equality

$$x\left(t\right)=w\left(t\right)+\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t\frac{Ax\left(s\right)}{{(t-s)}^{1-\beta }}ds,t\in I,$$

(4)

where $w\in L^1(I;X).$

Definition 5

([25]). A function $x\in C(I;X)$ is said to be a mild solution of equality Equation (4) if it satisfies ${\displaystyle {\int }_0^t\frac{x\left(s\right)}{{(t-s)}^{1-\beta }}ds\in \mathcal{D}}$ and

$$x\left(t\right)=w\left(t\right)+\frac{1}{\mathrm{\Gamma }\left(\beta \right)}A{\int }_0^t\frac{x\left(s\right)}{{(t-s)}^{1-\beta }}ds,\forall t\in I.$$

The following result provides another equivalent form of mild solution for Equation (4).

Lemma 1

([25]). If the resolvent operator $\mathfrak{R}\left(t\right)$ of Equation (4) is differentiable, then for $w\in C(I;\mathcal{D})$, the following function

$$x\left(t\right)={\int }_0^t\dot{\mathfrak{R}}(t-s)w\left(s\right)ds+w\left(t\right),t\in I,$$

is called a mild solution of Equation (4).

To end this section, the set $L^1([-b,0];X)$ is proposed which stands for a space of all the integrable functions mapping $[-b,0]$ into X equipped with norm ${\displaystyle {\parallel ·\parallel }_{L^1[-b,0]}={\int }_{-b}^0\parallel ·\left(t\right)\parallel dt}$. Obviously, it is complete. Considering Equation (1), for any $x\in C(I;X)$, $t\in I$, let

$$x_t\left(\theta \right)=\left\{\begin{array}{cc}x(t+\theta ),\hfill & t+\theta \ge 0,\hfill \\ \varphi (t+\theta ),\hfill & t+\theta \le 0,\hfill \end{array}\right.$$

(5)

for any $\theta \in [-b,0]$, where $\varphi \left(t\right)$ denotes the function mentioned in Equation (1). Obviously, we can check that $x_t\in L^1([-b,0];X).$

On the basis of Equation (5), we give the following result.

Lemma 2.

Assume that $x_n\to x_0$$(n\to +\infty )$ for $x_n,x_0\in C(I;X)$. Then, for any $t\in I$, one can derive that ${\left(x_n\right)}_t\to {\left(x_0\right)}_t$$(n\to +\infty )$ for ${\left(x_n\right)}_t,{\left(x_0\right)}_t\in L^1([-b,0];X)$.

Proof. 

In view of (5), we can easily derive

$$\parallel {\left(x_n\right)}_t-{\left(x_0\right)}_t{\parallel }_{L^1[-b,0]}=\left\{{\displaystyle \begin{array}{cc}{\displaystyle {\int }_0^t\parallel x_n\left(s\right)-x_0\left(s\right)\parallel ds,}\hfill & t\le b,\hfill \\ {\displaystyle {\int }_{t-b}^t\parallel x_n\left(s\right)-x_0\left(s\right)\parallel ds,}\hfill & t\ge b,\hfill \end{array}}\right.$$

which indicates that

$$\parallel {\left(x_n\right)}_t-{\left(x_0\right)}_t{\parallel }_{L^1[-b,0]}\le b{\parallel x_n-x_0\parallel }_C,$$

(6)

for any $t\in I$.

3. Existence Results

This part establishes the existence results of mild solution of Equation (1). Now, assume resolvent operator ${\left\{\mathfrak{R}\left(t\right)\right\}}_{t\ge 0}$ to be differentiable. Let ${\omega }_A$ be the function mentioned in Definition 4.

From Definition 1 and Definition 5, we can obtain

Definition 6.

For any $u\in L^2(I;U),$ a function $x\in C(I;X)$ is called a mild solution of Equation (1) on I, provided that

$$x\left(t\right)=\varphi \left(0\right)+\frac{1}{\mathrm{\Gamma }\left(\beta \right)}A{\int }_0^t\frac{x\left(s\right)}{{(t-s)}^{1-\beta }}ds+\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t\frac{f(s,x_s)}{{(t-s)}^{1-\beta }}ds+\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t\frac{Bu\left(s\right)}{{(t-s)}^{1-\beta }}ds,$$

where ${\displaystyle {\int }_0^t\frac{x\left(s\right)}{{(t-s)}^{1-\beta }}ds\in \mathcal{D}}$, $\forall t\in I,$ and $x_s$ is defined by Equation (5).

In the next content, we will need the following assumptions.

Hypothesis 1 (H1).

f is a continuous function from $I\times L^1([-b,0];X)$ into $\mathcal{D}$ and $\varphi \left(0\right)\in \mathcal{D}$. There is a real number ${\beta }_1\in (0,\beta )$ and a function $m\in L^{\frac{1}{{\beta }_1}}(I;{\mathbb{R}}_{+})$ satisfying ${\parallel f(t,x)\parallel }_{\mathcal{D}}\le m\left(t\right)$ for any $t\in I$ and $x\in L^1([-b,0];X)$.

Hypothesis 2 (H2).

For any $x,y\in L^1([-b,0];X),$ there exists a constant $L>0$ satisfying

$${\parallel f(t,x)-f(t,y)\parallel }_{\mathcal{D}}\le L{\parallel x-y\parallel }_{L^1[-b,0]}.$$

For simplicity, we denote

$${\displaystyle {\mathfrak{F}}_x\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t\frac{f(s,x_s)}{{(t-s)}^{1-\beta }}ds,{\mathfrak{B}}_u\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t\frac{Bu\left(s\right)}{{(t-s)}^{1-\beta }}ds,\vartheta =\frac{\beta -1}{1-{\beta }_1}.}$$

From Lemma 1 and Definition 6, we can derive the mild solution of Equation (1) on I of another expression as follows.

Definition 7.

For any $u\in L^2(I;U),$ a function $x\in C(I;X)$ is called a mild solution of Equation (1) on I, provided that

$${\displaystyle x\left(t\right)=\varphi \left(0\right)+{\mathfrak{F}}_x\left(t\right)+{\mathfrak{B}}_u\left(t\right)+{\int }_0^t\dot{\mathfrak{R}}(t-s)\left(\varphi \left(0\right)+{\mathfrak{F}}_x\left(s\right)+{\mathfrak{B}}_u\left(s\right)\right)ds.}$$

Remark 1.

It follows from Definition 1 that the classical solution of system Equation (1) is a convolution equation. Hence, it is natural to apply Laplace transform on it to express an appropriate formula for the mild solution representation of the considered system. For this purpose, we suppose that resolvent operator $\mathfrak{R}\left(t\right)$ is exponentially bounded. By utilizing the theory of the Laplace transform and inverse Laplace transform, the mild solution of Equation (1) could be defined by

$$x\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \mathfrak{R}\left(t\right)\varphi \left(0\right)+{\int }_0^t{\mathcal{K}}_{\odot }(t-s)f(s,x_s)ds+{\int }_0^t{\mathcal{K}}_{\odot }(t-s)Bu\left(s\right)ds,}\hfill & t\in I=[0,a],\hfill \\ \varphi \left(t\right),t\in [-b,0],\hfill \end{array}\right.$$

where ${\displaystyle {\mathcal{K}}_{\odot }\left(t\right)=\frac{d}{dt}\left(I_{0^{+}}^{\beta }\mathfrak{R}\left(t\right)\right)}$ and $x_s$ is defined by Equation (5).

Lemma  3.

(i) If hypothesis (H1) holds, then for arbitrarily given $x\in C(I;X)$, we have ${\mathfrak{F}}_x\in C^{\beta -{\beta }_1}(I;\mathcal{D}),$ and

$$\left[\right|{\mathfrak{F}}_x{\left|\right]}_{C^{\beta -{\beta }_1}(I;\mathcal{D})}\le \frac{{2\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}{\mathrm{\Gamma }\left(\beta \right){(1+\vartheta )}^{1-{\beta }_1}}.$$

(ii) For any $u\in L^2(I;U),$ we have ${\mathfrak{B}}_u\in C^{\beta -\frac{1}{2}}(I;\mathcal{D}),$ and

$$\left[\right|{\mathfrak{B}}_u{\left|\right]}_{C^{\beta -\frac{1}{2}}(I;\mathcal{D})}\le \frac{{2\parallel Bu\parallel }_{L^2(I;\mathcal{D})}}{\mathrm{\Gamma }\left(\beta \right){(2\beta -1)}^{\frac{1}{2}}}.$$

Proof. 

(i) For arbitrarily given $x\in C(I;X)$, $\forall t\in [0,a)$, $\forall h>0$ satisfying $t+h\in [0,a]$, by using Hölder inequality, one can derive

$$\begin{array}{ccc}& & \parallel {\mathfrak{F}}_x(t+h)-{\mathfrak{F}}_x{\left(t\right)\parallel }_{\mathcal{D}}\hfill \\ & \le \hfill & {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t[{(t-s)}^{\beta -1}-{(t+h-s)}^{\beta -1}]{\parallel f(s,x_s)\parallel }_{\mathcal{D}}ds}\hfill \\ & & {\displaystyle +\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_t^{t+h}{(t+h-s)}^{\beta -1}{\parallel f(s,x_s)\parallel }_{\mathcal{D}}ds}\hfill \\ & \le \hfill & {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\left({\int }_0^t{\left[{(t-s)}^{\beta -1}-{(t+h-s)}^{\beta -1}\right]}^{\frac{1}{1-{\beta }_1}}ds\right)}^{1-{\beta }_1}{\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}\hfill \\ & & {\displaystyle +\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\left({\int }_t^{t+h}{\left[{(t+h-s)}^{\beta -1}\right]}^{\frac{1}{1-{\beta }_1}}ds\right)}^{1-{\beta }_1}{\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}\hfill \\ & \le \hfill & {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\left({\int }_0^t\left[{(t-s)}^{\vartheta }-{(t+h-s)}^{\vartheta }\right]ds\right)}^{1-{\beta }_1}{\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}\hfill \\ & & {\displaystyle +\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\left({\int }_t^{t+h}{(t+h-s)}^{\vartheta }ds\right)}^{1-{\beta }_1}{\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}\hfill \\ & \le \hfill & {\displaystyle \frac{{\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}{\mathrm{\Gamma }\left(\beta \right){(1+\vartheta )}^{1-{\beta }_1}}{(t^{1+\vartheta }-{(t+h)}^{1+\vartheta }+h^{1+\vartheta })}^{1-{\beta }_1}+\frac{{\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}{\mathrm{\Gamma }\left(\beta \right){(1+\vartheta )}^{1-{\beta }_1}}{h}^{(1+\vartheta )(1-{\beta }_1)}}\hfill \\ & \le \hfill & {\displaystyle \frac{{2\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}{\mathrm{\Gamma }\left(\beta \right){(1+\vartheta )}^{1-{\beta }_1}}{h}^{(1+\vartheta )(1-{\beta }_1)}}\hfill \\ & =\hfill & {\displaystyle \frac{{2\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}{\mathrm{\Gamma }\left(\beta \right){(1+\vartheta )}^{1-{\beta }_1}}{h}^{\beta -{\beta }_1},}\hfill \end{array}$$

which indicates that ${\displaystyle \left[\right|{\mathfrak{F}}_x{\left|\right]}_{C^{\beta -{\beta }_1}(I;\mathcal{D})}\le \frac{{2\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}{\mathrm{\Gamma }\left(\beta \right){(1+\vartheta )}^{1-{\beta }_1}}}$ and ${\mathfrak{F}}_x\in C^{\beta -{\beta }_1}(I;\mathcal{D})$.

(ii) In the light of the proof for (i), it can be obtained similarly. □

Lemma 4.

(i) If Hypotheses (H1) and (H2) hold, then for $\forall x,y\in C(I;X)$,

$${\displaystyle \parallel {\mathfrak{F}}_x\left(t\right)-{\mathfrak{F}}_y{\left(t\right)\parallel }_{\mathcal{D}}\le \frac{L{a}^{\beta }b}{\mathrm{\Gamma }(\beta +1)}{\parallel x-y\parallel }_C,\forall t\in I,}$$

and

$${\displaystyle \parallel {\mathfrak{F}}_x{\left(t\right)\parallel }_{\mathcal{D}}\le \frac{a^{\beta -{\beta }_1}{\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}{\mathrm{\Gamma }\left(\beta \right){(1+\vartheta )}^{1-{\beta }_1}},\forall t\in I.}$$

(ii) For any $u,v\in L^2(I;U)$,

$${\displaystyle \parallel {\mathfrak{B}}_u\left(t\right)-{\mathfrak{B}}_v{\left(t\right)\parallel }_{\mathcal{D}}\le \frac{1}{\mathrm{\Gamma }\left(\beta \right)}\sqrt{\frac{a^{2\beta -1}}{2\beta -1}}{\parallel Bu-Bv\parallel }_{L^2(I;\mathcal{D})},\forall t\in I,}$$

and

$${\displaystyle \parallel {\mathfrak{B}}_u{\left(t\right)\parallel }_{\mathcal{D}}\le \frac{1}{\mathrm{\Gamma }\left(\beta \right)}\sqrt{\frac{a^{2\beta -1}}{2\beta -1}}{\parallel Bu\parallel }_{L^2(I;\mathcal{D})},\forall t\in I.}$$

Proof. 

(i) In view of Lemma 2, we can obtain

$$\begin{array}{ccc}\parallel {\mathfrak{F}}_x\left(t\right)-{\mathfrak{F}}_y{\left(t\right)\parallel }_{\mathcal{D}}\hfill & \le \hfill & {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}{\parallel f(s,x_s)-f(s,y_s)\parallel }_{\mathcal{D}}ds}\hfill \\ & \le \hfill & {\displaystyle \frac{L}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}{\parallel x_s-y_s\parallel }_{L[-b,0]}ds}\hfill \\ & \le \hfill & {\displaystyle \frac{Lb}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}{\parallel x-y\parallel }_{C}ds}\hfill \\ & =\hfill & {\displaystyle \frac{L{a}^{\beta }b}{\mathrm{\Gamma }(\beta +1)}{\parallel x-y\parallel }_C,\forall t\in I.}\hfill \end{array}$$

In addition,

$$\begin{array}{ccc}\parallel {\mathfrak{F}}_x{\left(t\right)\parallel }_{\mathcal{D}}\hfill & \le \hfill & {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}{\parallel f(s,x_s)\parallel }_{\mathcal{D}}ds}\hfill \\ & \le \hfill & {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\left({\int }_0^t{\left[{(t-s)}^{\beta -1}\right]}^{\frac{1}{1-{\beta }_1}}ds\right)}^{1-{\beta }_1}{\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}\hfill \\ & \le \hfill & {\displaystyle \frac{t^{(1+\vartheta )(1-{\beta }_1)}}{\mathrm{\Gamma }\left(\beta \right){(1+\vartheta )}^{1-{\beta }_1}}{\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}\hfill \\ & \le \hfill & {\displaystyle \frac{a^{\beta -{\beta }_1}{\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}{\mathrm{\Gamma }\left(\beta \right){(1+\vartheta )}^{1-{\beta }_1}},\forall t\in I.}\hfill \end{array}$$

(ii) Obviously, we can obtain that

$$\begin{array}{ccc}\parallel {\mathfrak{B}}_u\left(t\right)-{\mathfrak{B}}_v{\left(t\right)\parallel }_{\mathcal{D}}\hfill & \le \hfill & {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}{\parallel Bu\left(s\right)-Bv\left(s\right)\parallel }_{\mathcal{D}}ds}\hfill \\ & \le \hfill & {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\left({\int }_0^t{\left[{(t-s)}^{\beta -1}\right]}^{2}ds\right)}^{\frac{1}{2}}{\parallel {\mathfrak{B}}_u-{\mathfrak{B}}_v\parallel }_{L^2(I;\mathcal{D})}}\hfill \\ & =\hfill & {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\beta \right)}\sqrt{\frac{a^{2\beta -1}}{2\beta -1}}{\parallel {\mathfrak{B}}_u-{\mathfrak{B}}_v\parallel }_{L^2(I;\mathcal{D})},\forall t\in I.}\hfill \end{array}$$

Similarly, we can obtain

$${\displaystyle \parallel {\mathfrak{B}}_u{\left(t\right)\parallel }_{\mathcal{D}}\le \frac{1}{\mathrm{\Gamma }\left(\beta \right)}\sqrt{\frac{a^{2\beta -1}}{2\beta -1}}{\parallel Bu\parallel }_{L^2(I;\mathcal{D})},\forall t\in I.}$$

□

Theorem 1.

If the Hypotheses (H1) and (H2) hold, then for any given control $u\in L^2(I;U),$ fractional evolution system Equation (1) has an unique mild solution on I, provided that

$${\displaystyle \frac{L{a}^{\beta }b(1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)})}{\mathrm{\Gamma }(\beta +1)}<1.}$$

(7)

Proof. 

In view of Definition 7, for any $t\in I$, define an operator $\mathrm{\Psi }:C(I;X)\to C(I;X)$ as below

$${\displaystyle \left(\mathrm{\Psi }x\right)\left(t\right)=\varphi \left(0\right)+{\mathfrak{F}}_x\left(t\right)+{\mathfrak{B}}_u\left(t\right)+{\int }_0^t\dot{\mathfrak{R}}(t-s)\left(\varphi \left(0\right)+{\mathfrak{F}}_x\left(s\right)+{\mathfrak{B}}_u\left(s\right)\right)ds.}$$

(8)

Evidently, we only need to consider the fixed point of $\mathrm{\Psi }$.

Step 1. $\mathrm{\Psi }$ maps $C(I;X)$ into $C(I;X)$.

For every $x\in C(I;X),0<t<t+h\le a$, we have

$$\begin{array}{ccc}\left(\mathrm{\Psi }x\right)(t+h)-\left(\mathrm{\Psi }x\right)\left(t\right)\hfill & =\hfill & {\mathfrak{F}}_x(t+h)-{\mathfrak{F}}_x\left(t\right)+{\mathfrak{B}}_u(t+h)-{\mathfrak{B}}_u\left(t\right)\hfill \\ & & {\displaystyle +{\int }_0^{t+h}\dot{\mathfrak{R}}(t+h-s)\varphi \left(0\right)ds-{\int }_0^t\dot{\mathfrak{R}}(t-s)\varphi \left(0\right)ds}\hfill \\ & & {\displaystyle +{\int }_0^{t+h}\dot{\mathfrak{R}}(t+h-s){\mathfrak{F}}_x\left(s\right)ds-{\int }_0^t\dot{\mathfrak{R}}(t-s){\mathfrak{F}}_x\left(s\right)ds}\hfill \\ & & {\displaystyle +{\int }_0^{t+h}\dot{\mathfrak{R}}(t+h-s){\mathfrak{B}}_u\left(s\right)ds-{\int }_0^t\dot{\mathfrak{R}}(t-s){\mathfrak{B}}_u\left(s\right)ds}\hfill \\ & =\hfill & {\displaystyle \sum _{i=1}^5{\mathsf{{\rm Y}}}_i,}\hfill \end{array}$$

where

${\mathsf{{\rm Y}}}_1={\mathfrak{F}}_x(t+h)-{\mathfrak{F}}_x\left(t\right),$

${\mathsf{{\rm Y}}}_2={\mathfrak{B}}_u(t+h)-{\mathfrak{B}}_u\left(t\right),$

${\displaystyle {\mathsf{{\rm Y}}}_3={\int }_0^{t+h}\dot{\mathfrak{R}}(t+h-s)\varphi \left(0\right)ds-{\int }_0^t\dot{\mathfrak{R}}(t-s)\varphi \left(0\right)ds,}$

${\displaystyle {\mathsf{{\rm Y}}}_4={\int }_0^{t+h}\dot{\mathfrak{R}}(t+h-s){\mathfrak{F}}_x\left(s\right)ds-{\int }_0^t\dot{\mathfrak{R}}(t-s){\mathfrak{F}}_x\left(s\right)ds,}$

${\displaystyle {\mathsf{{\rm Y}}}_5={\int }_0^{t+h}\dot{\mathfrak{R}}(t+h-s){\mathfrak{B}}_u\left(s\right)ds-{\int }_0^t\dot{\mathfrak{R}}(t-s){\mathfrak{B}}_u\left(s\right)ds.}$

By Lemma 3, we can obtain

$$\begin{array}{ccc}\parallel {\mathsf{{\rm Y}}}_1\parallel \hfill & \le \hfill & {\displaystyle \frac{{2\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}{\mathrm{\Gamma }\left(\beta \right){(1+\vartheta )}^{1-{\beta }_1}}{h}^{\beta -{\beta }_1}\to 0,ash\to 0,}\hfill \end{array}$$

and

$$\begin{array}{ccc}\parallel {\mathsf{{\rm Y}}}_2\parallel \hfill & \le \hfill & {\displaystyle \frac{{2\parallel Bu\parallel }_{L^2(I;\mathcal{D})}}{\mathrm{\Gamma }\left(\beta \right){(2\beta -1)}^{\frac{1}{2}}}{h}^{\beta -\frac{1}{2}}\to 0,ash\to 0.}\hfill \end{array}$$

Notice that

$$\begin{array}{ccc}{\mathsf{{\rm Y}}}_3\hfill & =\hfill & {\displaystyle {\int }_0^h\dot{\mathfrak{R}}(t+h-s)\varphi \left(0\right)ds+{\int }_h^{t+h}\dot{\mathfrak{R}}(t+h-s)\varphi \left(0\right)ds-{\int }_0^t\dot{\mathfrak{R}}(t-s)\varphi \left(0\right)ds}\hfill \\ & =\hfill & {\displaystyle {\int }_0^h\dot{\mathfrak{R}}(t+h-s)\varphi \left(0\right)ds.}\hfill \end{array}$$

Then, we have

$${\displaystyle \parallel {\mathsf{{\rm Y}}}_3{\parallel \le \parallel \varphi \left(0\right)\parallel }_{\mathcal{D}}{\int }_0^h{\omega }_A(t+h-s)ds\to 0,ash\to 0.}$$

In addition, since

$$\begin{array}{ccc}{\mathsf{{\rm Y}}}_4\hfill & =\hfill & {\displaystyle {\int }_0^h\dot{\mathfrak{R}}(t+h-s){\mathfrak{F}}_x\left(s\right)ds+{\int }_h^{t+h}\dot{\mathfrak{R}}(t+h-s){\mathfrak{F}}_x\left(s\right)ds-{\int }_0^t\dot{\mathfrak{R}}(t-s){\mathfrak{F}}_x\left(s\right)ds}\hfill \\ & =\hfill & {\displaystyle {\int }_0^h\dot{\mathfrak{R}}(t+h-s){\mathfrak{F}}_x\left(s\right)ds+{\int }_0^t\dot{\mathfrak{R}}\left(s\right){\mathfrak{F}}_x(t+h-s)ds-{\int }_0^t\dot{\mathfrak{R}}\left(s\right){\mathfrak{F}}_x(t-s)ds,}\hfill \end{array}$$

we thus can derive from Definition 4, Lemma 3 and Lemma 4 that

$$\begin{array}{ccc}\parallel {\mathsf{{\rm Y}}}_4\parallel \hfill & \le \hfill & {\displaystyle {\int }_0^h\parallel \dot{\mathfrak{R}}(t+h-s){\mathfrak{F}}_x\left(s\right)\parallel ds+{\int }_0^t\parallel \dot{\mathfrak{R}}\left(s\right)({\mathfrak{F}}_x(t-s+h)-{\mathfrak{F}}_x(t-s))\parallel ds}\hfill \\ & \le \hfill & {\displaystyle {\int }_0^h{\omega }_A(t+h-s)\parallel {\mathfrak{F}}_x{\left(s\right)\parallel }_{\mathcal{D}}ds+{\int }_0^t{\omega }_A\left(s\right)\left[\right|{\mathfrak{F}}_x{\left|\right]}_{C^{\beta -{\beta }_1}(I;\mathcal{D})}{h}^{\beta -{\beta }_1}ds}\hfill \\ & \le \hfill & {\displaystyle \frac{a^{\beta -{\beta }_1}{\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}{\mathrm{\Gamma }\left(\beta \right){(1+\vartheta )}^{1-{\beta }_1}}{\int }_0^h{\omega }_A(t+h-s)ds+\frac{{2\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}{h}^{\beta -{\beta }_1}}{\mathrm{\Gamma }\left(\beta \right){(1+\vartheta )}^{1-{\beta }_1}}{\int }_0^t{\omega }_A\left(s\right)ds}\hfill \\ & \le \hfill & {\displaystyle \frac{{\parallel m\parallel }_{L^{\frac{1}{{\beta }_1}}}}{\mathrm{\Gamma }\left(\beta \right){(1+\vartheta )}^{1-{\beta }_1}}\left(a^{\beta -{\beta }_1}{\int }_0^h{\omega }_A(t+h-s)ds+2h^{\beta -{\beta }_1}{\parallel {\omega }_A\parallel }_{L^1\left(I\right)}\right)}\hfill \\ \\ & & \to 0,ash\to 0.\hfill \end{array}$$

It is not difficult to have

$$\begin{array}{ccc}{\mathsf{{\rm Y}}}_5\hfill & =\hfill & {\displaystyle {\int }_0^h\dot{\mathfrak{R}}(t+h-s){\mathfrak{B}}_u\left(s\right)ds+{\int }_h^{t+h}\dot{\mathfrak{R}}(t+h-s){\mathfrak{B}}_u\left(s\right)ds-{\int }_0^t\dot{\mathfrak{R}}(t-s){\mathfrak{B}}_u\left(s\right)ds}\hfill \\ & =\hfill & {\displaystyle {\int }_0^h\dot{\mathfrak{R}}(t+h-s){\mathfrak{B}}_u\left(s\right)ds+{\int }_0^t\dot{\mathfrak{R}}\left(s\right){\mathfrak{B}}_u(t+h-s)ds-{\int }_0^t\dot{\mathfrak{R}}\left(s\right){\mathfrak{B}}_u(t-s)ds,}\hfill \end{array}$$

which together with Lemma 3 and Lemma 4 implies

$$\begin{array}{ccc}\parallel {\mathsf{{\rm Y}}}_5\parallel \hfill & \le \hfill & {\displaystyle {\int }_0^h\parallel \dot{\mathfrak{R}}(t+h-s){\mathfrak{B}}_u\left(s\right)\parallel ds+{\int }_0^t\parallel \dot{\mathfrak{R}}\left(s\right)({\mathfrak{B}}_u(t-s+h)-{\mathfrak{B}}_u(t-s))\parallel ds}\hfill \\ & \le \hfill & {\displaystyle {\int }_0^h{\omega }_A(t+h-s)\parallel {\mathfrak{B}}_u{\left(s\right)\parallel }_{\mathcal{D}}ds+{\int }_0^t{\omega }_A\left(s\right)\left[\right|{\mathfrak{B}}_u{\left|\right]}_{C^{\beta -\frac{1}{2}}(I;\mathcal{D})}{h}^{\beta -\frac{1}{2}}ds}\hfill \\ & \le \hfill & {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\beta \right)}\sqrt{\frac{a^{2\beta -1}}{2\beta -1}}{\parallel Bu\parallel }_{L^2(I;\mathcal{D})}{\int }_0^h{\omega }_A(t+h-s)ds}\hfill \\ & & {\displaystyle +\frac{{2\parallel Bu\parallel }_{L^2(I;\mathcal{D})}{h}^{\beta -\frac{1}{2}}}{\mathrm{\Gamma }\left(\beta \right){(2\beta -1)}^{\frac{1}{2}}}{\int }_0^t{\omega }_A\left(s\right)ds}\hfill \\ & \le \hfill & {\displaystyle \frac{{\parallel Bu\parallel }_{L^2(I;\mathcal{D})}}{\mathrm{\Gamma }\left(\beta \right){(2\beta -1)}^{\frac{1}{2}}}\left(a^{\beta -\frac{1}{2}}{\int }_0^h{\omega }_A(t+h-s)ds+2h^{\beta -\frac{1}{2}}{\parallel {\omega }_A\parallel }_{L^1\left(I\right)}\right)}\hfill \\ \\ & & \to 0,ash\to 0.\hfill \end{array}$$

Hence, $\parallel \left(\mathrm{\Psi }x\right)(t+h)-\left(\mathrm{\Psi }x\right)\left(t\right)\parallel \to 0$, $h\to 0,$ which indicates that $\mathrm{\Psi }x\in C(I;X),$$\forall x\in C(I;X)$.

Step 2.$\mathrm{\Psi }$ is contractive on $C(I;X).$

In fact, Lemma 2 indicates that

$$\begin{array}{ccc}\parallel \left(\mathrm{\Psi }x\right)\left(t\right)-\left(\mathrm{\Psi }y\right)\left(t\right)\parallel \hfill & \le \hfill & {\displaystyle \parallel {\mathfrak{F}}_x\left(t\right)-{\mathfrak{F}}_y{\left(t\right)\parallel }_{\mathcal{D}}+{\int }_0^t{\omega }_A(t-s){\parallel {\mathfrak{F}}_x\left(s\right)-{\mathfrak{F}}_y\left(s\right)\parallel }_{\mathcal{D}}ds}\hfill \\ & \le \hfill & {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}{\parallel f(s,x_s)-f(s,y_s)\parallel }_{\mathcal{D}}ds}\hfill \\ & & {\displaystyle +\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t{\omega }_A(t-s)\left({\int }_0^s{(s-\tau )}^{\beta -1}{\parallel f(\tau ,x_{\tau })-f(\tau ,y_{\tau })\parallel }_{\mathcal{D}}d\tau \right)ds}\hfill \\ & \le \hfill & {\displaystyle \frac{L}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}{\parallel x_s-y_s\parallel }_{L^1[-b,0]}ds}\hfill \\ & & {\displaystyle +\frac{L}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t{\omega }_A(t-s)\left({\int }_0^s{(s-\tau )}^{\beta -1}{\parallel x_{\tau }-y_{\tau }\parallel }_{L^1[-b,0]}d\tau \right)ds}\hfill \\ & \le \hfill & {\displaystyle \frac{L{a}^{\beta }b}{\mathrm{\Gamma }(\beta +1)}{\parallel x-y\parallel }_C+\frac{L{a}^{\beta }b{\parallel {\omega }_A\parallel }_{L^1\left(I\right)}}{\mathrm{\Gamma }(\beta +1)}{\parallel x-y\parallel }_C}\hfill \\ & =\hfill & {\displaystyle \frac{L{a}^{\beta }b(1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)})}{\mathrm{\Gamma }(\beta +1)}{\parallel x-y\parallel }_C,\forall t\in I,}\hfill \end{array}$$

which shows that

$${\displaystyle {\parallel \mathrm{\Psi }x-\mathrm{\Psi }y\parallel }_C\le \frac{L{a}^{\beta }b(1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)})}{\mathrm{\Gamma }(\beta +1)}{\parallel x-y\parallel }_C.}$$

Hence, $\mathrm{\Psi }$ is contractive on $C(I;X)$ due to the Hypothesis (1). By utilizing the Banach’s fixed point theorem, we find that $\mathrm{\Psi }$ has a unique fixed point on $C(I;X).$ □

4. Main Results

This part gives the results of approximate controllability of Equation (1). Let us show the next definitions which is critical to our work.

Definition 8.

The set $K(a,f)=\{x(a;u):u\in L^2(I;U)\}$ is said to be the reachable set of Equation (1) at final point a, where $x(t;u)$ is the state value of Equation (1) at time point t corresponding to control $u\in L^2(I;U).$ If $\overline{K(a,f)}=X,$ we call that Equation (1) is approximately controllable on I, where $\overline{K(a,f)}$ stands for the closure of $K(a,f)$.

Denote Nemytskii operator $\mathcal{F}:C(I;X)\to L^2(I;\mathcal{D})$ corresponding to the non-linearity f by

$$\mathcal{F}x\left(t\right)=f(t,x_t),t\in I,$$

and define the continuous operator $\mathcal{P}:L^2(I;\mathcal{D})\to X$ by

$${\displaystyle \mathcal{P}y=\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^a\frac{y\left(t\right)}{{(a-t)}^{1-\beta }}dt+\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^a\dot{\mathfrak{R}}(a-t)\left({\displaystyle {\int }_0^t\frac{y\left(s\right)}{{(t-s)}^{1-\beta }}ds}\right)dt,y\in L^2(I;\mathcal{D}).}$$

(9)

It is not difficult to see that the approximate controllability of Equation (1) on I is equivalent to that the set $K(a,f)$ is dense on X. That is to say, we can obtain an equivalent definition as below.

Definition 9.

System (1) is said to be approximately controllable on I, provided that for any $\epsilon >0$ and any final value $\xi \in X$, there exists a control term $u_{\epsilon }\in L^2(I;U)$ satisfying

$$\parallel \xi -\mathfrak{R}\left(a\right)\varphi \left(0\right)-\mathcal{P}\left(\mathcal{F}{x}_{\epsilon }\right)-\mathcal{P}\left(B{u}_{\epsilon }\right)\parallel <\epsilon ,$$

where$x_{\epsilon }\left(t\right)=x(t;u_{\epsilon })$is a mild solution of Equation (1) corresponding to$u_{\epsilon }\in L^2(I;U)$.

In addition, following hypotheses to obtain our approximate controllability results are presented.

Hypothesis 3 (H3).

For arbitrarily given $\epsilon >0$ and $\psi \in L^2(I;\mathcal{D})$, there is a function $u\in L^2(I;U)$ satisfying

$$\parallel \mathcal{P}\psi -\mathcal{P}\left(Bu\right)\parallel <\epsilon ,$$

and

$${\parallel Bu\parallel }_{L^2(I;\mathcal{D})}<\mu {\parallel \psi \parallel }_{L^2(I;\mathcal{D})},$$

where $\mu >0$ is a real number independent of ψ.

Hypothesis 4 (H4).

Under Equation (7), the following inequality holds

$$\mu L{a}^{\frac{1}{2}}b{\left({\displaystyle 1-\frac{L{a}^{\beta }b(1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)})}{\mathrm{\Gamma }(\beta +1)}}\right)}^{-1}\frac{1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)}}{\mathrm{\Gamma }\left(\beta \right)}\sqrt{\frac{a^{2\beta -1}}{2\beta -1}}<1.$$

Next, to demonstrate our main result, we still need a lemma as below.

Lemma 5.

If the Hypotheses (H1) and (H2) hold, then for any mild solutions of Equation (1), the following result holds

$$\parallel x_1-x_2{\parallel }_C\le {\left({\displaystyle 1-\frac{L{a}^{\beta }b(1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)})}{\mathrm{\Gamma }(\beta +1)}}\right)}^{-1}\frac{1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)}}{\mathrm{\Gamma }\left(\beta \right)}\sqrt{\frac{a^{2\beta -1}}{2\beta -1}}{\parallel B{u}_1-B{u}_2\parallel }_{L^2(I;\mathcal{D})},$$

for any $u_1,u_2\in L^2(I;U)$.

Proof. 

The mild solution $x_i\left(t\right)=x(t;u_i)(i=1,2)$ of system (1) corresponding to $u_i(i=1,2)$ satisfy

$${\displaystyle x_i\left(t\right)=\varphi \left(0\right)+{\mathfrak{F}}_{x_i}\left(t\right)+{\mathfrak{B}}_{u_i}\left(t\right)+{\int }_0^t\dot{\mathfrak{R}}(t-s)\left(\varphi \left(0\right)+{\mathfrak{F}}_{x_i}\left(s\right)+{\mathfrak{B}}_{u_i}\left(s\right)\right)ds,\forall t\in I.}$$

From Lemma 4, one can obtain

$$\begin{array}{ccc}& & \parallel x_1\left(t\right)-x_2\left(t\right)\parallel \hfill \\ & \le \hfill & \parallel {\mathfrak{F}}_{x_1}\left(t\right)-{\mathfrak{F}}_{x_2}\left(t\right)\parallel +\parallel {\mathfrak{B}}_{u_1}\left(t\right)-{\mathfrak{B}}_{u_2}\left(t\right)\parallel \hfill \\ & & {\displaystyle +{\int }_0^t\parallel \dot{\mathfrak{R}}(t-s)({\mathfrak{F}}_{x_1}\left(s\right)-{\mathfrak{F}}_{x_2}\left(s\right))\parallel ds+{\int }_0^t\parallel \dot{\mathfrak{R}}(t-s)({\mathfrak{B}}_{u_1}\left(t\right)-{\mathfrak{B}}_{u_2}\left(t\right))\parallel ds}\hfill \\ & \le \hfill & \parallel {\mathfrak{F}}_{x_1}\left(t\right)-{\mathfrak{F}}_{x_2}{\left(t\right)\parallel }_{\mathcal{D}}+{\parallel {\mathfrak{B}}_{u_1}\left(t\right)-{\mathfrak{B}}_{u_2}\left(t\right)\parallel }_{\mathcal{D}}\hfill \\ & & {\displaystyle +{\int }_0^t{\omega }_A(t-s)\parallel {\mathfrak{F}}_{x_1}\left(s\right)-{\mathfrak{F}}_{x_2}{\left(s\right)\parallel }_{\mathcal{D}}ds+{\int }_0^t{\omega }_A(t-s){\parallel {\mathfrak{B}}_{u_1}\left(s\right)-{\mathfrak{B}}_{u_2}\left(s\right)\parallel }_{\mathcal{D}}ds}\hfill \\ & \le \hfill & {\displaystyle \frac{L{a}^{\beta }b(1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)})}{\mathrm{\Gamma }(\beta +1)}\parallel x_1-x_2{\parallel }_C+\frac{1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)}}{\mathrm{\Gamma }\left(\beta \right)}\sqrt{\frac{a^{2\beta -1}}{2\beta -1}}{\parallel B{u}_1-B{u}_2\parallel }_{L^2(I;\mathcal{D})},\forall t\in I,}\hfill \end{array}$$

which implies that

$$\parallel x_1-x_2{\parallel }_C\le {\left({\displaystyle 1-\frac{L{a}^{\beta }b(1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)})}{\mathrm{\Gamma }(\beta +1)}}\right)}^{-1}\frac{1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)}}{\mathrm{\Gamma }\left(\beta \right)}\sqrt{\frac{a^{2\beta -1}}{2\beta -1}}{\parallel B{u}_1-B{u}_2\parallel }_{L^2(I;\mathcal{D})}.$$

□

Theorem 2.

If the Hypotheses (H1)–(H4) hold, then system (1) is approximately controllable on $I.$

Proof. 

It is only needed to prove that $\mathcal{D}\subset \overline{K(a,f)}$ due to the fact that $\mathcal{D}$ is dense, i.e., for $\forall \epsilon >0$ and $\xi \in \mathcal{D}$, there is a control term $u_{\epsilon }\in L^2(I;U)$ satisfying

$$\parallel \xi -\mathfrak{R}\left(a\right)\varphi \left(0\right)-\mathcal{P}\left(\mathcal{F}{x}_{\epsilon }\right)-\mathcal{P}\left(B{u}_{\epsilon }\right)\parallel <\epsilon .$$

(10)

It follows from the Definition 3 that $\mathfrak{R}\left(a\right)\varphi \left(0\right)\in \mathcal{D}$ for $\varphi \left(0\right)\in \mathcal{D}$, which indicates that $\xi -\mathfrak{R}\left(a\right)\varphi \left(0\right)\in \mathcal{D}.$ Then, it can be see that there exists some $\psi \in L^2(I;\mathcal{D})$, such that $\mathcal{P}\psi =\xi -\mathfrak{R}\left(a\right)\varphi \left(0\right).$ Next, we are to show that there is a control $u_{\epsilon }\in L^2(I;U)$ satisfying (4.2). Actually, for $\forall \epsilon >0$ and $u_1\in L^2(I;U)$, in view of (H3), we can find a function $u_2\in L^2(I;U)$, such that

$$\parallel \xi -\mathfrak{R}\left(a\right)\varphi \left(0\right)-\mathcal{P}\left(\mathcal{F}{x}_1\right)-\mathcal{P}\left(B{u}_2\right)\parallel <\frac{\epsilon }{2^2},$$

where $x_1\left(t\right)=x(t;u_1),t\in I.$ Further, for $u_2\in L^2(I;U)$, we can find a function $v_2\in L^2(I;U)$ by (H3) again, such that

$$\parallel \mathcal{P}(\mathcal{F}{x}_2-\mathcal{F}{x}_1)-\mathcal{P}\left(B{v}_2\right)\parallel <\frac{\epsilon }{2^3},$$

where $x_2\left(t\right)=x(t;u_2),t\in I.$ Then, from Lemma 5, we derive

$$\begin{array}{ccc}& & \parallel B{v}_2{\parallel }_{L^2(I;\mathcal{D})}\hfill \\ & \le \hfill & \mu \parallel \mathcal{F}{x}_2-\mathcal{F}{x}_1{\parallel }_{L^2(I;\mathcal{D})}\hfill \\ & \le \hfill & \mu L{a}^{\frac{1}{2}}b{\parallel x_2-x_1\parallel }_C\hfill \\ & \le \hfill & {\displaystyle \mu L{a}^{\frac{1}{2}}b{\left({\displaystyle 1-\frac{L{a}^{\beta }b(1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)})}{\mathrm{\Gamma }(\beta +1)}}\right)}^{-1}\frac{1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)}}{\mathrm{\Gamma }\left(\beta \right)}\sqrt{\frac{a^{2\beta -1}}{2\beta -1}}{\parallel B{u}_1-B{u}_2\parallel }_{L^2(I;\mathcal{D})}.}\hfill \end{array}$$

Next, define $u_3=u_2-v_2\in L^2(I;U),$ and, thus, it has

$$\begin{array}{ccc}& & \parallel \xi -\mathfrak{R}\left(a\right)\varphi \left(0\right)-\mathcal{P}\left(\mathcal{F}{x}_2\right)-\mathcal{P}\left(B{u}_3\right)\parallel \hfill \\ & \le \hfill & \parallel \xi -\mathfrak{R}\left(a\right)\varphi \left(0\right)-\mathcal{P}\left(\mathcal{F}{x}_1\right)-\mathcal{P}\left(B{u}_2\right)\parallel +\parallel \mathcal{P}\left(B{v}_2\right)-\mathcal{P}(\mathcal{F}{x}_2-\mathcal{F}{x}_1)\parallel \hfill \\ & \le \hfill & \left({\displaystyle \frac{1}{2^2}+\frac{1}{2^3}}\right)\epsilon .\hfill \end{array}$$

Utilizing induction, it is not hard to find a sequence $\{u_n:n\ge 1\}\subset L^2(I;U)$ satisfying

$$\parallel \xi -\mathfrak{R}\left(a\right)\varphi \left(0\right)-\mathcal{P}\left(\mathcal{F}{x}_n\right)-\mathcal{P}\left(B{u}_{n+1}\right)\parallel <\left({\displaystyle \frac{1}{2^2}+\frac{1}{2^3}+···+\frac{1}{2^{n+1}}}\right)\epsilon ,$$

(11)

where $x_n\left(t\right)=x(t;u_n),t\in I,$ and

$$\begin{array}{ccc}& & \parallel B{u}_{n+1}-B{u}_n{\parallel }_{L^2(I;\mathcal{D})}\hfill \\ & \le \hfill & {\displaystyle \mu L{a}^{\frac{1}{2}}b{\left({\displaystyle 1-\frac{L{a}^{\beta }b(1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)})}{\mathrm{\Gamma }(\beta +1)}}\right)}^{-1}\frac{1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)}}{\mathrm{\Gamma }\left(\beta \right)}\sqrt{\frac{a^{2\beta -1}}{2\beta -1}}{\parallel B{u}_n-B{u}_{n-1}\parallel }_{L^2(I;\mathcal{D})}.}\hfill \end{array}$$

From Hypothesis (H4), we know that $\{B{u}_n:n\ge 1\}$ is a Cauchy sequence on $L^2(I;\mathcal{D})$, and, thus, there exists a function $u^{*}\in L^2(I;\mathcal{D})$ satisfying

$$\underset{n\to \infty }{lim}B{u}_n=u^{*}in{L}^2(I;\mathcal{D}).$$

Hence, for every $\epsilon >0,$ we can obtain a number $N>0$ satisfying

$$\parallel \mathcal{P}\left(B{u}_{N+1}\right)-\mathcal{P}\left(B{u}_N\right)\parallel <\frac{\epsilon }{2}.$$

(12)

Then, from Equations (11) and (12), it is easy to deduce

$$\begin{array}{ccc}& & \parallel \xi -\mathfrak{R}\left(a\right)\varphi \left(0\right)-\mathcal{P}\left(\mathcal{F}{x}_N\right)-\mathcal{P}\left(B{u}_N\right)\parallel \hfill \\ & \le \hfill & \parallel \xi -\mathfrak{R}\left(a\right)\varphi \left(0\right)-\mathcal{P}\left(\mathcal{F}{x}_N\right)-\mathcal{P}\left(B{u}_{N+1}\right)\parallel +\parallel \mathcal{P}\left(B{u}_{N+1}\right)-\mathcal{P}\left(B{u}_N\right)\parallel \hfill \\ & \le \hfill & {\displaystyle \left({\displaystyle \frac{1}{2^2}+\frac{1}{2^3}+···+\frac{1}{2^{N+1}}}\right)\epsilon +\frac{\epsilon }{2}<\epsilon ,}\hfill \end{array}$$

where $x_N\left(t\right)=x(t;u_N),t\in I.$ Consequently, the fractional evolution system (1) is approximately controllable on $I.$ □

5. Non-Local Conditions

The practical usefulness and significance of non-local conditions in the field of technology and mechanical engineering have been demonstrated [5,9,11]. It has been proved that the non-local initial condition can provide more accurate descriptions than the classical initial conditions. Therefore, we concern the following system involving non-local conditions and a parameter as below:

$$\left\{\begin{array}{c}{}^C{D}^{\beta }x\left(t\right)=Ax\left(t\right)+f(t,x_t)+Bu\left(t\right),t\in I:=[0,a],\hfill \\ x\left(t\right)+\lambda g_t\left(x\right)=\varphi \left(t\right),t\in [-b,0].\hfill \end{array}\right.$$

Firstly, we present the following hypothesis about the non-local conditions.

Hypothesis 5 (H5).

$g_t:C([-b,a];X)\to \mathcal{D}$, for any $t\in [-b,0]$;

(i) For $\forall x,y\in C(I;X)$, there has a number $l>0$ satisfying

$$\parallel g_t\left(x\right)-g_t{\left(y\right)\parallel }_{\mathcal{D}}\le l{\parallel x-y\parallel }_C;$$

(ii) The non-local term $g_t\left(x\right)$ is continuous in $t\in [-b,0]$ for all $x\in C\left(\right[-b,a];X)$, and there has a constant $C>0$ satisfying $\parallel g_t{\left(x\right)\parallel }_{\mathcal{D}}\le C.$

Next, for $\forall x\in C(I;X)$ and $t\in I$, let

$$x_t\left(\theta \right)=\left\{\begin{array}{cc}x(t+\theta ),\hfill & t+\theta \ge 0,\hfill \\ \varphi (t+\theta )-\lambda g_{t+\theta }\left(x\right),\hfill & t+\theta \le 0,\hfill \end{array}\right.$$

(13)

for $\forall \theta \in [-b,0]$. Obviously, we can check that $x_t\in L^1([-b,0];X).$ On the basis of Equation (13) and (H5), we have the following result similar to Lemma 2.

Lemma 6.

Assume that $x_n\to x_0$$(n\to +\infty )$ for $x_n,x_0\in C(I;X)$. Then, for any $t\in I$, one can derive that ${\left(x_n\right)}_t\to {\left(x_0\right)}_t$$(n\to +\infty )$ for ${\left(x_n\right)}_t,{\left(x_0\right)}_t\in L^1([-b,0];X)$, and satisfies

$$\parallel {\left(x_n\right)}_t-{\left(x_0\right)}_t{\parallel }_{L^1[-b,0]}\le \left(\right|\lambda |l+1)b\parallel x_n-x_0{\parallel }_C,t\in I.$$

Proof. 

In accordance with Equation (13) and condition (H5), we can draw the inequalities as below:

$$\begin{array}{ccc}\parallel {\left(x_n\right)}_t-{\left(x_0\right)}_t{\parallel }_{L^1[-b,0]}\hfill & =\hfill & {\displaystyle {\int }_{-b}^0\parallel {\left(x_n\right)}_t\left(\theta \right)-{\left(x_0\right)}_t\left(\theta \right)\parallel d\theta }\hfill \\ & =\hfill & {\displaystyle {\int }_{t-b}^0\left|\lambda \right|\parallel g_s\left(x_n\right)-g_s\left(x_0\right)\parallel ds+{\int }_0^t\parallel x_n\left(s\right)-x_0\left(s\right)\parallel ds}\hfill \\ & \le \hfill & \left|\lambda \right|lb\parallel x_n-x_0{\parallel }_C+b{\parallel x_n-x_0\parallel }_C\hfill \\ & =\hfill & \left(\right|\lambda |l+1)b\parallel x_n-x_0{\parallel }_C,t\le b,\hfill \end{array}$$

and

$$\begin{array}{ccc}\parallel {\left(x_n\right)}_t-{\left(x_0\right)}_t{\parallel }_{L^1[-b,0]}\hfill & =\hfill & {\displaystyle {\int }_{-b}^0\parallel {\left(x_n\right)}_t\left(\theta \right)-{\left(x_0\right)}_t\left(\theta \right)\parallel d\theta }\hfill \\ & =\hfill & {\displaystyle {\int }_{t-b}^t\parallel x_n\left(s\right)-x_0\left(s\right)\parallel ds}\hfill \\ & \le \hfill & b\parallel x_n-x_0{\parallel }_C,t\ge b,\hfill \end{array}$$

which imply that

$$\parallel {\left(x_n\right)}_t-{\left(x_0\right)}_t{\parallel }_{L^1[-b,0]}\le \left(\right|\lambda |l+1)b\parallel x_n-x_0{\parallel }_C,$$

for any $t\in I.$ □

Definition 10.

(i) For any $u\in L^2(I;U),$ a function $x\in C(I;X)$ is called a mild solution of Equation (2) on I, provided that

$${\displaystyle x\left(t\right)=\varphi \left(0\right)-\lambda g_0\left(x\right)+{\mathfrak{F}}_x\left(t\right)+{\mathfrak{B}}_u\left(t\right)+{\int }_0^t\dot{\mathfrak{R}}(t-s)\left(\varphi \left(0\right)-\lambda g_0\left(x\right)+{\mathfrak{F}}_x\left(s\right)+{\mathfrak{B}}_u\left(s\right)\right)ds,t\in I.}$$

(ii) System (2) is said to be approximately controllable on I, provided that for any $\epsilon >0$ and any final value $\xi \in X$, there exists a control term $u_{\epsilon }\in L^2(I;U)$ satisfying

$$\parallel \xi -\mathfrak{R}\left(a\right)(\varphi \left(0\right)-\lambda g_0\left(x_{\epsilon }\right))-\mathcal{P}\left(\mathcal{F}{x}_{\epsilon }\right)-\mathcal{P}\left(B{u}_{\epsilon }\right)\parallel <\epsilon ,$$

where $x_{\epsilon }\left(t\right)=x(t;u_{\epsilon })$ is a mild solution of Equation (2) corresponding to $u_{\epsilon }\in L^2(I;U)$.

Theorem 3.

In accordance with the proof steps of Theorem 1, one finds that if the Hypotheses (H1)–(H2) hold, then for any given control $u\in L^2(I;U),$ system (2) has an unique mild solution on I, provided that

$$(1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)})\left(\left|\lambda \right|l+\frac{L{a}^{\beta }\left(\right|\lambda |l+1)b}{\mathrm{\Gamma }(\beta +1)}\right)<1.$$

(14)

Under the condition Equation (14), we further suppose the following hypothesis:

Hypothesis 6 (H6).

The following inequality holds

$$\mu L{a}^{\frac{1}{2}}\left(\right|\lambda |l+1)b{\left(1-(1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)})\left({\displaystyle \left|\lambda \right|l+\frac{L{a}^{\beta }\left(\right|\lambda |l+1)b}{\mathrm{\Gamma }(\beta +1)}}\right)\right)}^{-1}\frac{1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)}}{\mathrm{\Gamma }\left(\beta \right)}\sqrt{\frac{a^{2\beta -1}}{2\beta -1}}<1.$$

In addition, to obtain the non-local results, we still need a lemma as below.

Lemma 7.

If the hypotheses (H1)–(H2) hold, then for any mild solutions of system (2), the following result holds

$$\parallel x_1-x_2{\parallel }_C\le {\left(1-(1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)})\left({\displaystyle \left|\lambda \right|l+\frac{L{a}^{\beta }\left(\right|\lambda |l+1)b}{\mathrm{\Gamma }(\beta +1)}}\right)\right)}^{-1}\frac{1+\parallel {\omega }_A{\parallel }_{L^1\left(I\right)}}{\mathrm{\Gamma }\left(\beta \right)}\sqrt{\frac{a^{2\beta -1}}{2\beta -1}}{\parallel B{u}_1-B{u}_2\parallel }_{L^2(I;\mathcal{D})},$$

for any $u_1,u_2\in L^2(I;U)$.

By means of iterative method utilized in Theorem 2 similarly, we now can obtain the main controllability result of the non-local case:

Theorem 4.

If the Hypotheses (H1)–(H3) and (H5) hold, then system (2) is approximately controllable on $I.$

Remark 2.

Usually, the non-local condition can be given as follows

$${\displaystyle \lambda g_t\left(x\right)=\lambda \sum _{i=1}^q{l}_{i}x(t+{\iota }_i),t\in [-b,0],}$$

where $l_i(i=1,···,q)$ are some real numbers; $0<{\iota }_1<{\iota }_2<···<{\iota }_q\le a.$ When $\lambda =1$ and at time $t=0$, it is evident that

$${\displaystyle g_0\left(x\right)=g\left(x\right)=\sum _{i=1}^q{l}_{i}x\left({\iota }_i\right),}$$

which is exactly the case in [5,9,11,16,17].

6. Applications

Evolutionary fractional behavior has widespread backgrounds of some practical fields of science and engineering. For example, in an electrical circuit, the voltage produced by some non-linear device can be expressed by the non-linear term f in the evolution systems; some related resistances can be represented by A; and linear operator B can denote some inductances. On the other hand, non-local conditions are more extensive in practical applications because they usually includes many other conditions, such as conditions of initial value, multipoint average, and periodic, etc. In this part, we consider the following fractional non-local delayed evolution systems

$$\left\{\begin{array}{c}{\displaystyle \frac{{\partial }^{\frac{3}{4}}}{\partial t^{\frac{3}{4}}}x(t,\xi )=\frac{{\partial }^2}{\partial {\xi }^2}x(t,\xi )+\frac{\varpi \left(t\right)e^{-t}}{1+e^{2t}}{\int }_{t-b}^t\varrho (t-s)sin\left(x(s,\xi )\right)ds+Bu(t,\xi ),(t,\xi )\in [0,a]\times (0,\pi ),}\hfill \\ x(t,0)=x(t,\pi )=0,t\in [0,a],\hfill \\ {\displaystyle x(t,\xi )+\lambda \sum _{j=1}^m{k}_{j}sin\left(x({\varsigma }_j+t,\xi )\right)=\varphi (t,\xi ),(t,\xi )\in [-b,0]\times [0,\pi ],{\varsigma }_j\in [0,a],}\hfill \end{array}\right.$$

(15)

where $\varpi \in C\left(\right[0,a];\mathbb{R})$, $\varrho \in L_{loc}^1\left({\mathbb{R}}_{+}\right)$, and $\varphi \in C^{2,1}([-b,0]\times [0,\pi ];\mathbb{R})$. $\varphi (t,0)=\varphi (t,\pi )=0,$$\forall t\in [-b,0]$.

Let $X=U=L^2\left([0,\pi ]\right),$$Ax=x^{″}$ for $x\in \mathcal{D},$ where

$$\mathcal{D}=\{x\in X:x,x^{\prime }areabsolutelycontinuous,x^{\prime \prime }\in X,x\left(0\right)=x\left(\pi \right)=0\}.$$

Evidently, A is an infinitesimal generator of a semigroup ${\left\{T\left(t\right)\right\}}_{t\ge 0}$ satisfying

$$T\left(t\right)x=\sum _{n=1}^{\infty }{e}^{-n^{2}t}⟨x,{\delta }_n⟩{\delta }_n,x\in X.$$

In view of subordinate principle (Chapter 3, [26]), we know that A is also an infinitesimal generator of a continuous differentiable bounded linear operators family ${\left\{\mathfrak{R}\left(t\right)\right\}}_{t\ge 0}$ satisfying $\mathfrak{R}\left(0\right)=\mathcal{I}$, and

$$\mathfrak{R}\left(t\right)={\int }_0^{\infty }{\eta }_{t,\beta }\left(s\right)T\left(s\right)ds,t>0,$$

where ${\eta }_{t,\beta }\left(s\right)=t^{-\beta }{\Phi }_{\beta }\left(s{t}^{-\beta }\right),$ and

$${\Phi }_{\beta }\left(y\right)=\sum _{n=0}^{\infty }\frac{{(-y)}^n}{n!\mathrm{\Gamma }(-\beta n+1-\beta )}=\frac{1}{2\pi i}{\int }_{\mathcal{H}}{\zeta }^{\beta -1}exp(\zeta -y{\zeta }^{\beta })d\zeta ,0<\beta <1,$$

where $\mathcal{H}$ is a contour which encircles the origin once counterclockwise.

For each $u\in L^2([0,a];U),$ one has

$$u\left(t\right)=\sum _{n=0}^{\infty }{u}_n\left(t\right){\delta }_n,u_n\left(t\right)=⟨u\left(t\right),{\delta }_n⟩.$$

Then, an operator B can be defined by

$$Bu=\sum _{n=1}^{\infty }{\overline{u}}_n{\delta }_n,$$

where

$${\overline{u}}_n\left(t\right)=\left\{\begin{array}{cc}0,\hfill & 0\le t<a-\frac{a}{n^2},\hfill \\ u_n\left(t\right),\hfill & a-\frac{a}{n^2}\le t\le a,\hfill \end{array}\right.$$

for every $n=1,2,···.$ This ensures that B is a bounded linear operator. In addition, the operator $\mathcal{P}$ in Equation (9) is exactly the case of the operator in [29] when $B=\mathcal{I}$ and $t=a.$ Furthermore, denote by

${\displaystyle \beta =\frac{3}{4}\in (\frac{1}{2},1]}$,

${\displaystyle {}^C{D}^{\frac{3}{4}}x\left(t\right)\left(\xi \right)=\frac{{\partial }^{\frac{3}{4}}}{\partial t^{\frac{3}{4}}}x(t,\xi ),}$

$x\left(t\right)\left(\xi \right)=x(t,\xi ),$

$Bu\left(t\right)\left(\xi \right)=Bu(t,\xi ),$

$\varphi \left(t\right)\left(\xi \right)=\varphi (t,\xi ),$

${\displaystyle g_t\left(x\right)\left(\xi \right)=\sum _{j=1}^m{k}_{j}sin\left(x({\varsigma }_j+t,\xi )\right),}$

${\displaystyle f(t,x_t)\left(\xi \right)=\frac{\varpi \left(t\right)e^{-t}}{1+e^{2t}}{\int }_{t-b}^t\varrho (t-s)sin\left(x(s,\xi )\right)ds.}$

Hence, Equation (15) can be regarded as

$$\left\{\begin{array}{c}{}^C{D}^{\beta }x\left(t\right)=Ax\left(t\right)+f(t,x_t)+Bu\left(t\right),t\in [0,a],\hfill \\ x\left(t\right)+\lambda g_t\left(x\right)=\varphi \left(t\right),t\in [-b,0],\hfill \end{array}\right.$$

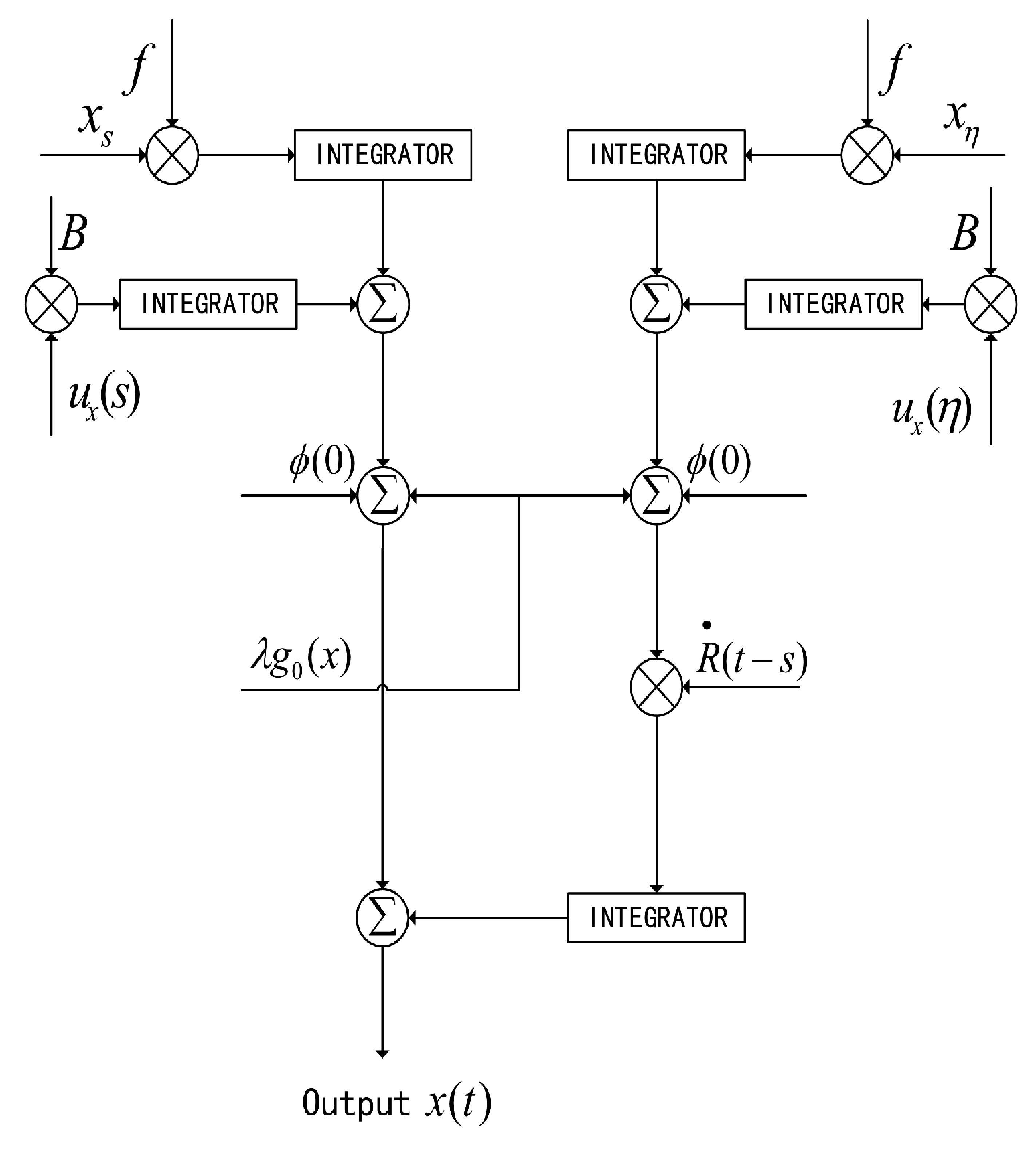
In addition, it can be checked that $f,B,g_t,\varphi$ satisfy all assumptions in Theorem 4. Therefore, system (15) is approximately controllable on $[0,a].$ In addition, it is well known to all that the prospect of digital signal processing (DSP) is widespread and developmental, and digital filters play a significant role in it. Therefore, in this part, we also present the filter pattern of the system we studied which is given in Figure 1.

Figure 1. Filter system.

For any time t, the resultant values of samples $x_t$ and $f\left(t\right)$ are produced and transferred to the integrators $I_1$ and $I_2$, where the signals are integrated over time 0 to t. The signals of resultant values of B and $u_x\left(t\right)$ are integrated in integrators $I_3$ and $I_4$. Integrators $I_1$ and $I_3$ are entered into summer network-1; Integrators $I_2$ and $I_4$ are entered into summer network-2. Inputs $\varphi \left(t\right)$ and $\lambda g_t\left(x\right)$ at time $t=0$ are added up in the summer network-3 and summer network-4. The integral for the product of $\dot{\mathfrak{R}}(t-s)$ and the signals in summer network-4 over time 0 to t is performed in integrators $I_5$. At last, move the above outputs and integrators $I_5$ to summer network-5, and, thus, the final outputs $x\left(t\right)$ is derived, which is bounded and approximately controllable.

7. Conclusions

In this manuscript, some approximate controllability results of fractional delay systems with non-local conditions and a parameter are derived by using an iterative method. We substitute for the theory of $C_0$-semigroup and its associated characteristic solution operators by utilizing differentiability properties about resolvent operator. A special complete space is used to assist in solving the disturbance due to delay effects. Then, the current results seem to be more general and generalize some recent analogous outcomes, e.g., [21,22,23,27].

By means of iterative method, some further new study can be devoted to the approximate controllability of fractional impulsive systems as below:

$$\left\{\begin{array}{c}{}^C{D}^{\beta }x\left(t\right)=Ax\left(t\right)+f(t,x_t,Q_x\left(t\right))+Bu\left(t\right),a.e.t\in I=[0,a],\hfill \\ \Delta x\left(t_i\right)=x\left(t_i^{+}\right)-x\left(t_i^{-}\right)=I_i\left(x\left(t_i^{-}\right)\right),i=1,2,···,m,\hfill \\ x\left(t\right)+\lambda g_t\left(x\right)=\varphi \left(t\right),t\in [-b,0],\hfill \end{array}\right.$$

where ${\displaystyle Q_x\left(t\right)={\int }_0^{t}q(t,s,x_s)ds,}$$q:\mathsf{\Lambda }\times L\left(\right[-b,0];X)\to X$ and $\mathsf{\Lambda }=\left\{\right(t,s)\in I\times I:s\le t\}.$ The impulsive items $I_i(i=1,2,···,m)$ are given functions that satisfy some appropriate hypotheses. $\varphi \in L^1([-b,0];X).$ The main tools we are about to use here can be the theory of differentiable resolvent operators or analytic resolvent operators [25,30,31]. Furthermore, evolutionary fractional behavior is more accurately captured by variable-order fractional calculus. To this end, extending the present results to the more generalized variable-order fractional system will be an interesting problem.