Modelling of Electron and Thermal Transport in Quasi-Fractal Carbon Nitride Nanoribbons
Abstract
:1. Introduction
2. Electronic Properties of Quasi-Fractal Carbon Nitride Monolayers
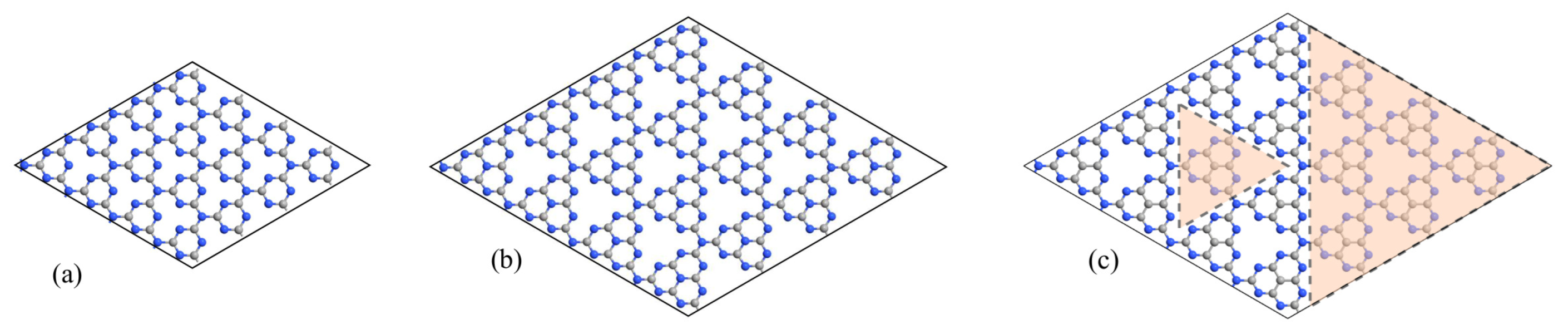
2.1. Materials and Methods
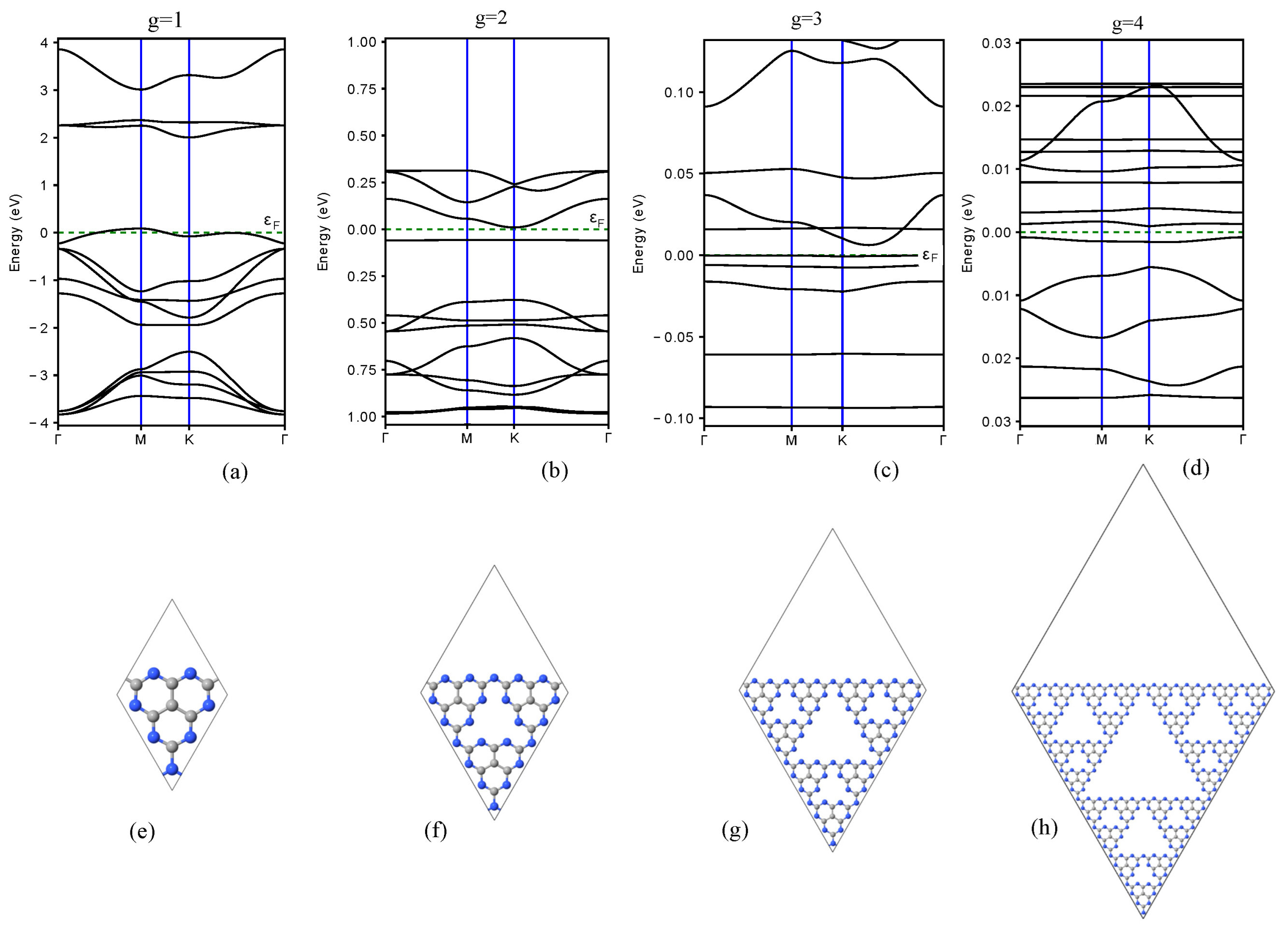
2.2. Band Structures
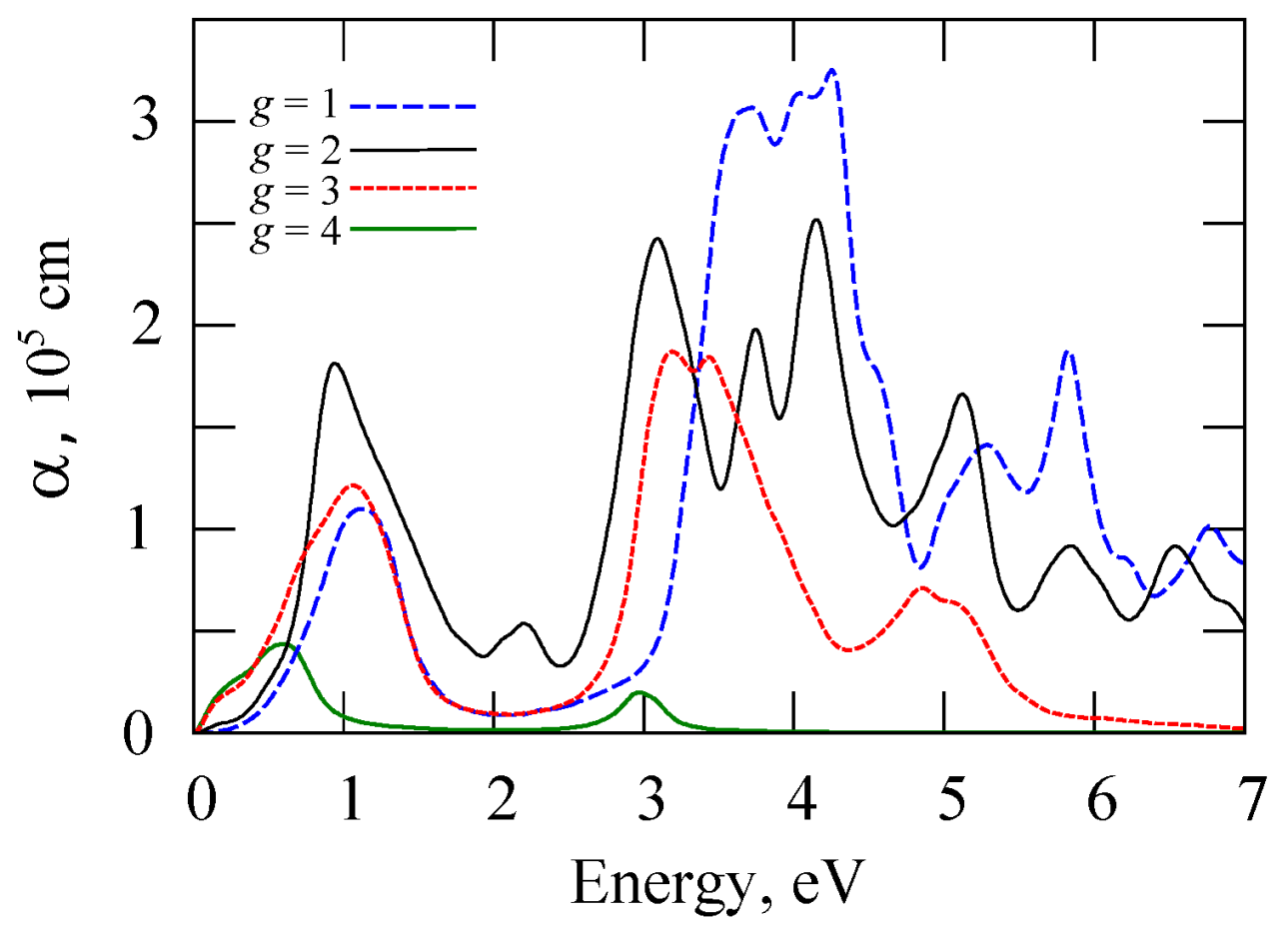
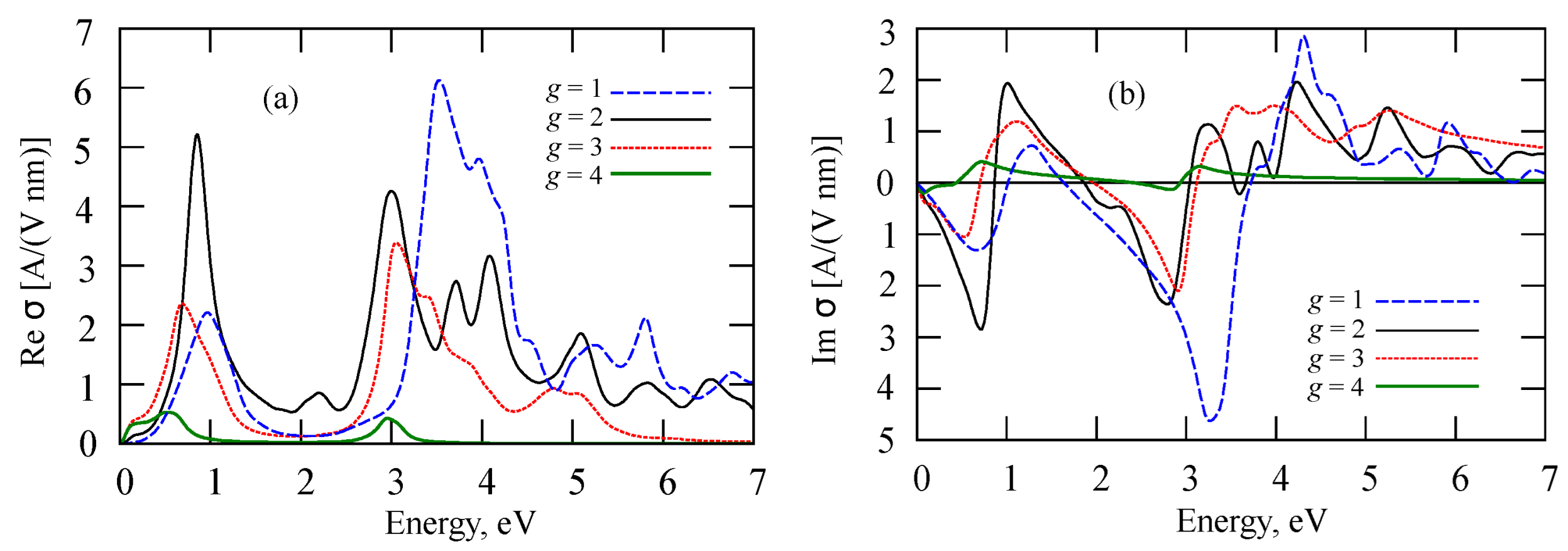
2.3. Absorption Spectra and Optical Conductivity
3. Electron Transmission of Quasi-Fractal Nanoribbons
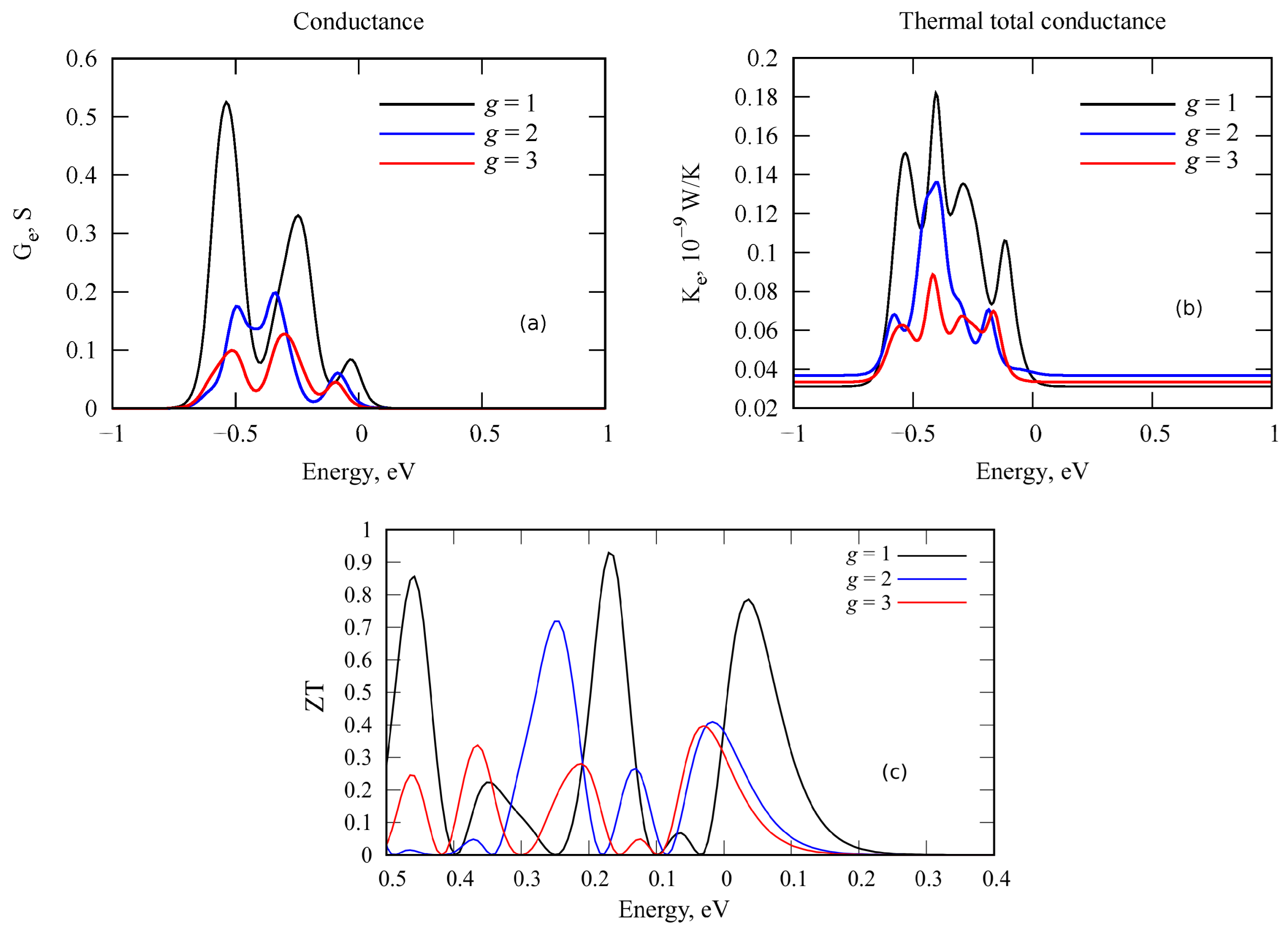
4. Thermoelectric Properties
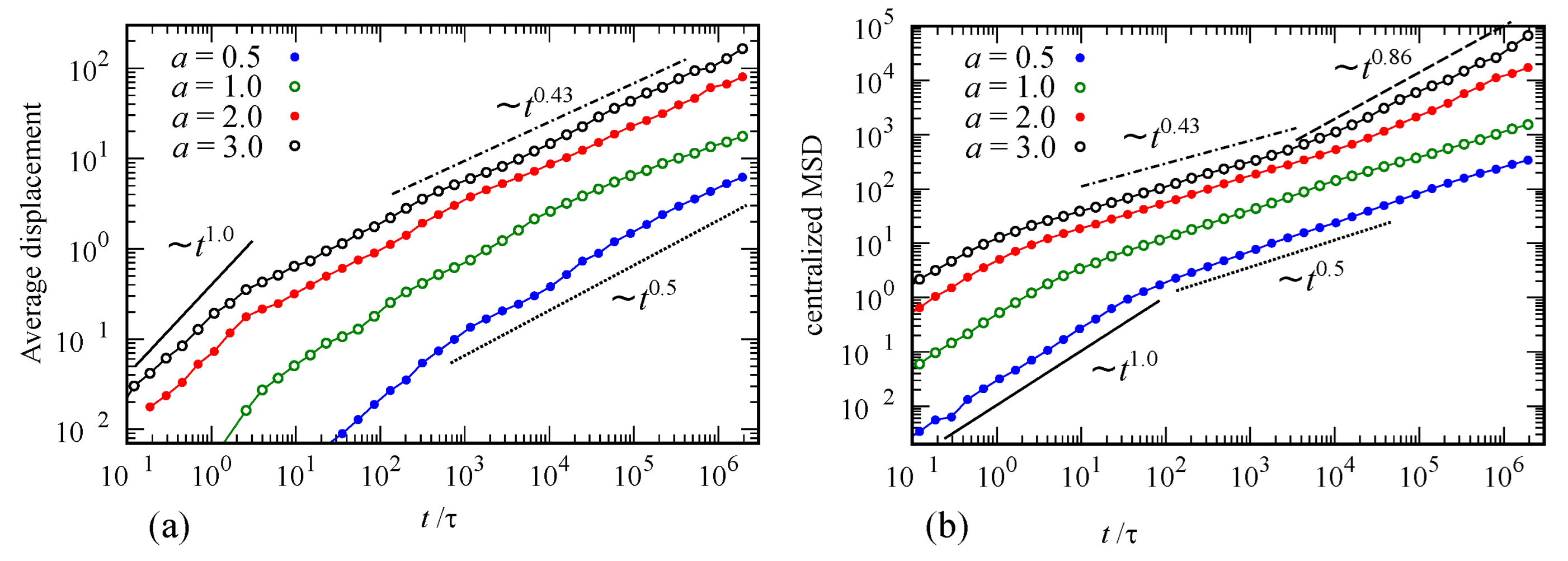
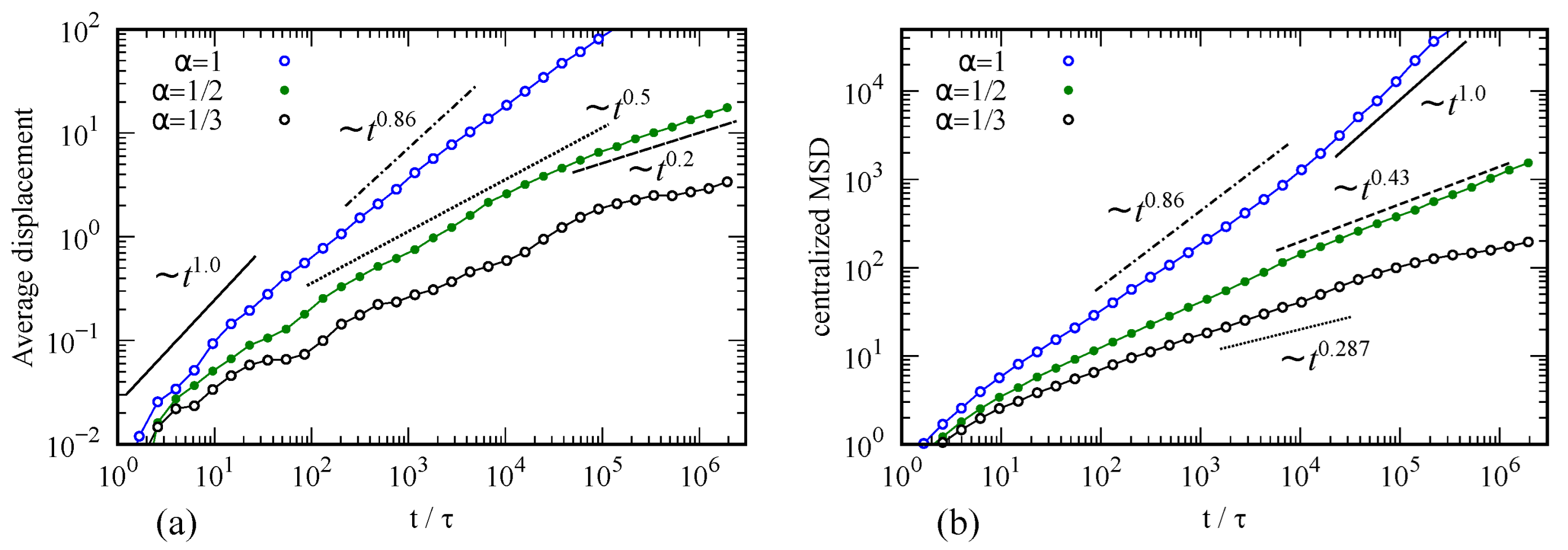
5. Hopping in Quasi-Fractal Nanoribbons with Energetic Disorder
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Haldane, F.D.M. ‘Luttinger liquid theory’ of one-dimensional quantum fluids. I. Properties of the Luttinger model and their extension to the general 1D interacting spinless Fermi gas. J. Phys. C Solid State Phys. 1981, 14, 2585. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan-Wen, T.; Horst L, S.; Kim, P. Experimental observation of the quantum hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kempkes, S.; Slot, M.; Freeney, S.; Zevenhuizen, S.; Vanmaekelbergh, D.; Swart, I.; Smith, M. Design and characterization of electrons in a fractal geometry. Nat. Phys. 2019, 15, 127–131. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Gu, G.; Zhang, X.; Song, D.; Zhang, Y.; Teo, B.K.; Peng, L.; Hou, S.; Wang, Y. Packing fractal Sierpiński triangles into one-dimensional crystals via a templating method. Chem. Commun. 2017, 53, 3469–3472. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Zhang, X.; Li, N.; Wang, Y.; Yang, J.; Gu, G.; Zhang, Y.; Hou, S.; Peng, L.; Wu, K.; et al. Construction of Sierpinski triangles up to the fifth order. J. Am. Chem. Soc. 2017, 139, 13749–13753. [Google Scholar] [CrossRef]
- Ghadiyali, M.; Chacko, S. Confinement of wave-function in fractal geometry, a detection using DFT. arXiv 2019, arXiv:1904.11862. [Google Scholar]
- Westerhout, T.; van Veen, E.; Katsnelson, M.I.; Yuan, S. Plasmon confinement in fractal quantum systems. Phys. Rev. B 2018, 97, 205434. [Google Scholar] [CrossRef] [Green Version]
- Pedersen, T.G. Graphene fractals: Energy gap and spin polarization. Phys. Rev. B 2020, 101, 235427. [Google Scholar] [CrossRef]
- Khalili Golmankhaneh, A.; Kamal Ali, A. Fractal Kronig-Penney model involving fractal comb potential. J. Math. Model. 2021, 9, 331–345. [Google Scholar]
- Xu, X.Y.; Wang, X.W.; Chen, D.Y.; Smith, S.M.; Jin, X.M. Quantum transport in fractal networks. Nat. Photonics 2021, 15, 703–710. [Google Scholar] [CrossRef]
- Zosimov, V.V.; Lyamshev, L.M. Fractals in wave processes. Physics-Uspekhi 1995, 38, 347. [Google Scholar] [CrossRef]
- Wang, K.J.; Li, G.; Liu, J.H.; Wang, G.D. Solitary waves of the fractal regularized long-wave equation traveling along an unsmooth boundary. Fractals 2021, 2021, 2250008. [Google Scholar] [CrossRef]
- Pook, W.; Janßen, M. Multifractality and scaling in disordered mesoscopic systems. Z. Phys. B Condens. Matter 1991, 82, 295–298. [Google Scholar] [CrossRef]
- Hegger, H.; Huckestein, B.; Hecker, K.; Janssen, M.; Freimuth, A.; Reckziegel, G.; Tuzinski, R. Fractal conductance fluctuations in gold nanowires. Phys. Rev. Lett. 1996, 77, 3885. [Google Scholar] [CrossRef] [Green Version]
- Barthelemy, P.; Bertolotti, J.; Wiersma, D.S. A Lévy flight for light. Nature 2008, 453, 495. [Google Scholar] [CrossRef]
- Kohno, H.; Yoshida, H. Multiscaling in semiconductor nanowire growth. Phys. Rev. E 2004, 70, 062601. [Google Scholar] [CrossRef]
- Kohno, H. Self-organized nanowire formation of Si-based materials. In One-Dimensional Nanostructures; Springer: Berlin/Heidelberg, Germany, 2008; pp. 61–78. [Google Scholar]
- Raboutou, A.; Peyral, P.; Lebeau, C.; Rosenblatt, J.; Burin, J.P.; Fouad, Y. Fractal vortices in disordered superconductors. Phys. A Stat. Mech. Its Appl. 1994, 207, 271–279. [Google Scholar] [CrossRef]
- Miller, T.S.; Jorge, A.B.; Suter, T.M.; Sella, A.; Corà, F.; McMillan, P.F. Carbon nitrides: Synthesis and characterization of a new class of functional materials. Phys. Chem. Chem. Phys. 2007, 19, 15613–15638. [Google Scholar] [CrossRef] [Green Version]
- Bafekry, A.; Shayesteh, S.F.; Peeters, F.M. Two-dimensional carbon nitride (2d-CN) nanosheets: Tuning of novel electronic and magnetic properties by hydrogenation, atom substitution and defect engineering. J. Appl. Phys. 2019, 126, 215104. [Google Scholar] [CrossRef]
- Bafekry, A.; Faraji, M.; Karbasizadeh, S.; Hieu, N.N.; Ang, Y.S.; Sarsari, I.A.; Ghergherehchi, M. Two-dimensional dirac half-metal in porous carbon nitride C6N7 monolayer via atomic doping. Nanotechnology 2021, 33, 075707. [Google Scholar] [CrossRef]
- Smidstrup, S.; Markussen, T.; Vancraeyveld, P.; Wellendorff, J.; Schneider, J.; Gunst, T.; Verstichel, B.; Stradi, D.; Khomyakov, P.A.; Vej-Hansen, U.G.; et al. QuantumATK: An integrated platform of electronic and atomic-scale modelling tools. J. Phys. Condens. Matter 2019, 32, 015901. [Google Scholar] [CrossRef] [PubMed]
- Van Setten, M.J.; Giantomassi, M.; Bousquet, E.; Verstraete, M.J.; Hamann, D.R.; Gonze, X.; Rignanese, G.M. The PseudoDojo: Training and grading a 85 element optimized norm-conserving pseudopotential table. Comput. Phys. Commun. 2018, 226, 39–54. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Levy, Y.E.; Souillard, B. Superlocalization of electrons and waves in fractal media. EPL (Europhys. Lett.) 1987, 4, 233. [Google Scholar] [CrossRef]
- Choukiker, Y.K.; Behera, S.K. Modified Sierpinski square fractal antenna covering ultra-wide band application with band notch characteristics. IET Microwaves Antennas Propag. 2014, 8, 506–512. [Google Scholar] [CrossRef]
- Darimireddy, N.K.; Reddy, R.R.; Prasad, A.M. A miniaturized hexagonal-triangular fractal antenna for wide-band applications. IEEE Antennas Propag. Mag. 2018, 60, 104–110. [Google Scholar] [CrossRef]
- Ouyang, Y.; Guo, J. A theoretical study on thermoelectric properties of graphene nanoribbons. Appl. Phys. Lett. 2009, 94, 263107. [Google Scholar] [CrossRef]
- Kodama, T.; Ohnishi, M.; Park, W.; Shiga, T.; Park, J.; Shimada, T.; Shinohara, H.; Shiomi, J.; Goodson, K.E. Modulation of thermal and thermoelectric transport in individual carbon nanotubes by fullerene encapsulation. Nat. Mater. 2017, 16, 892–897. [Google Scholar] [CrossRef]
- Pai, S.J.; Yeo, B.C.; Han, S.S. Development of the reaxff cbn reactive force field for the improved design of liquid CBN hydrogen storage materials. Phys. Chem. Chem. Phys. 2016, 18, 1818–1827. [Google Scholar] [CrossRef]
- Markussen, T.; Jauho, A.P.; Brandbyge, M. Electron and phonon transport in silicon nanowires: Atomistic approach to thermoelectric properties. Phys. Rev. B 2009, 79, 035415. [Google Scholar] [CrossRef] [Green Version]
- Meftakhutdinov, R.M.; Sibatov, R.T.; Kochaev, A.I. Graphenylene nanoribbons: Electronic, optical and thermoelectric properties from first-principles calculations. J. Phys. Condens. Matter 2020, 32, 345301. [Google Scholar] [CrossRef] [PubMed]
- Kochaev, A.I.; Meftakhutdinov, R.M.; Sibatov, R.T.; Timkaeva, D.A. Optical and thermoelectric properties of graphenylene and octagraphene nanotubes from first-principles calculations. Comput. Mater. Sci. 2021, 186, 109999. [Google Scholar] [CrossRef]
- Gómez-Navarro, C.; Weitz, R.T.; Bittner, A.M.; Scolari, M.; Mews, A.; Burghard, M.; Kern, K. Electronic transport properties of individual chemically reduced graphene oxide sheets. Nano Lett. 2007, 7, 3499–3503. [Google Scholar] [CrossRef]
- Joung, D.; Zhai, L.; Khondaker, S.I. Coulomb blockade and hopping conduction in graphene quantum dots array. Phys. Rev. B 2011, 83, 115323. [Google Scholar] [CrossRef] [Green Version]
- Pfister, G.; Scher, H. Dispersive (non-Gaussian) transient transport in disordered solids. Adv. Phys. 1978, 27, 747–798. [Google Scholar] [CrossRef]
- Bässler, H. Charge transport in disordered organic photoconductors. A Monte Carlo simulation study. Phys. Status Solidi (Basic Res.) 1993, 175, 15–56. [Google Scholar] [CrossRef]
- Blumen, A.; Klafter, J.; White, B.S.; Zumofen, G. Continuous-time random walks on fractals. Phys. Rev. Lett. 1984, 53, 1301. [Google Scholar] [CrossRef]
- White, S.R.; Barma, M. Field-induced drift and trapping in percolation networks. J. Phys. A Math. Gen. 1984, 17, 2995–3008. [Google Scholar] [CrossRef]
- Weiss, G.H.; Havlin, S. Some properties of a random walk on a comb structure. Phys. A Stat. Mech. Appl. 1986, 134, 474–482. [Google Scholar] [CrossRef]
- Arkhincheev, V.E.; Baskin, E.M. Anomalous diffusion and drift in a comb model of percolation clusters. Sov. Phys. JETP 1991, 73, 161–165. [Google Scholar]
- Baskin, E.; Iomin, A. Superdiffusion on a comb structure. Phys. Rev. Lett. 2004, 93, 120603. [Google Scholar] [CrossRef]
- Lubashevskii, I.A.; Zemlyanov, A.A. Continuum description of anomalous diffusion on a comb structure. J. Exp. Theor. Phys. 1998, 87, 700–713. [Google Scholar] [CrossRef]
- Iomin, A. Subdiffusion on a fractal comb. Phys. Rev. E 2011, 83, 052106. [Google Scholar] [CrossRef] [Green Version]
- Sibatov, R.T.; Morozova, E.V. Multiple trapping on a comb structure as a model of electron transport in disordered nanostructured semiconductors. J. Exp. Theor. Phys. 2015, 120, 860–870. [Google Scholar] [CrossRef]
- Sandev, T.; Iomin, A.; Méndez, V. Lévy processes on a generalized fractal comb. J. Phys. A Math. Theo. 2016, 49, 355001. [Google Scholar] [CrossRef] [Green Version]
- Sandev, T.; Iomin, A.; Kantz, H.; Metzler, R.; Chechkin, A. Comb model with slow and ultraslow diffusion. Math. Model. Nat. Phenom. 2016, 11, 18–33. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Sokolov, I.M. Models of anomalous diffusion in crowded environments. Soft Matter 2012, 8, 9043–9052. [Google Scholar] [CrossRef]
- Zahran, M.A.; Abulwafa, E.M.; Elwakil, S.A. The fractional Fokker-Planck equation on comb-like model. Phys. A Stat. Mech. Appl. 2003, 323, 237–248. [Google Scholar] [CrossRef]
- Arkhincheev, V.E. Unified continuum description for sub-diffusion random walks on multi-dimensional comb model. Phys. A Stat. Mech. Appl. 2010, 389, 1–6. [Google Scholar] [CrossRef]
- Meroz, Y.; Sokolov, I.M.; Klafter, J. Subdiffusion of mixed origins: When ergodicity and nonergodicity coexist. Phys. Rev. E 2010, 81, 010101. [Google Scholar] [CrossRef]
- Hou, R.; Cherstvy, A.G.; Metzler, R.; Akimoto, T. Biased continuous-time random walks for ordinary and equilibrium cases: Facilitation of diffusion, ergodicity breaking and ageing. Phys. Chem. Chem. Phys. 2018, 20, 20827–20848. [Google Scholar] [CrossRef]
- Wang, W.; Barkai, E. Fractional advection-diffusion-asymmetry equation. Phys. Rev. Lett. 2020, 125, 240606. [Google Scholar] [CrossRef]
- Ben-Avraham, D.; Havlin, S. Diffusion and Reactions in Fractals and Disordered Systems; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]


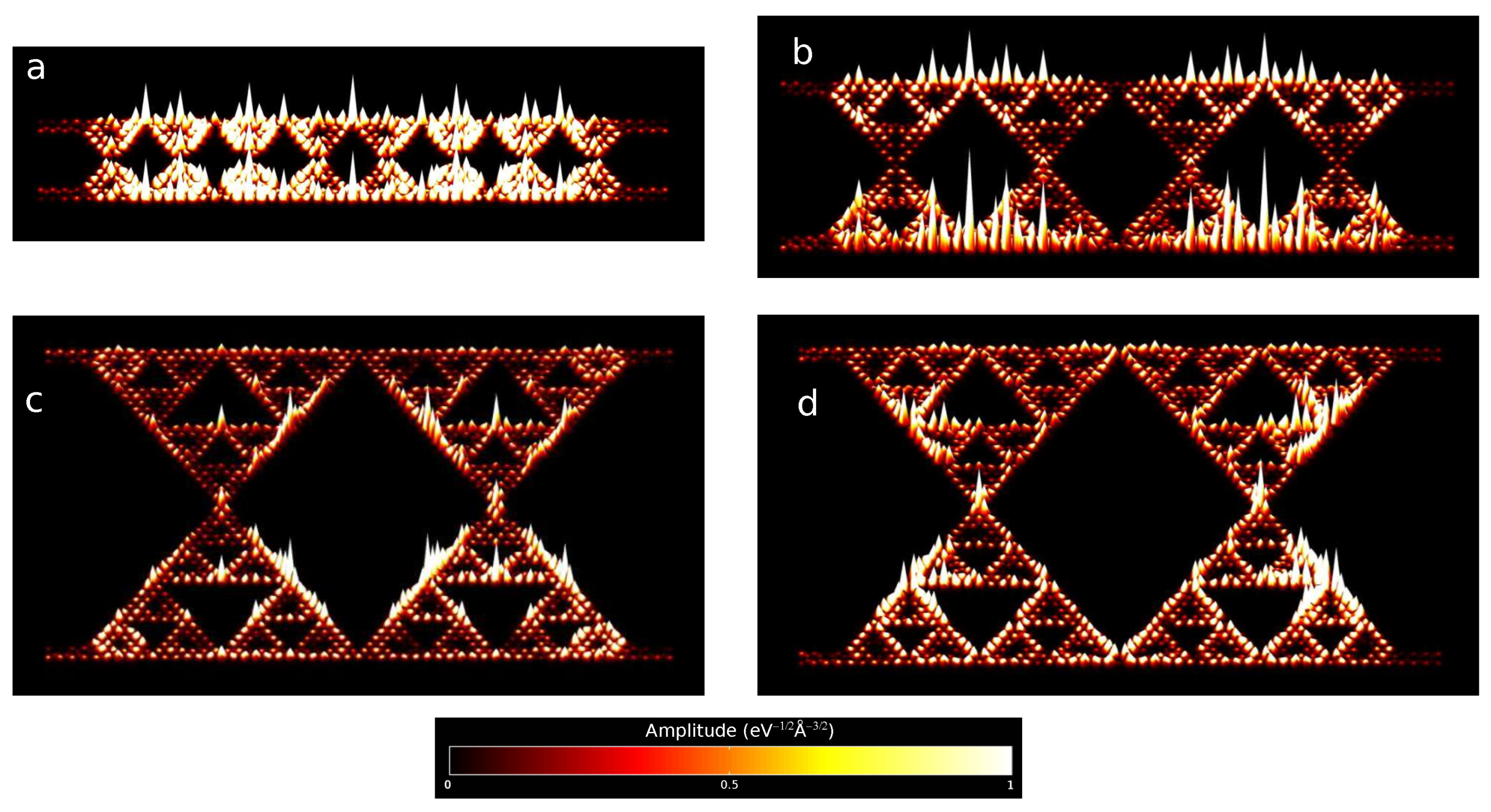

| Generation | a, Å | Direct BG, meV | Indirect BG, meV | , % |
|---|---|---|---|---|
| 7.1316 | 0 | 0 | 0 | |
| 13.9941 | 66.5 | 66.5 | ||
| 27.9662 | 6.70 | 6.34 | ||
| 55.9194 | 2.12 | 1.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sibatov, R.T.; Golmankhaneh, A.K.; Meftakhutdinov, R.M.; Morozova, E.V.; Timkaeva, D.A. Modelling of Electron and Thermal Transport in Quasi-Fractal Carbon Nitride Nanoribbons. Fractal Fract. 2022, 6, 115. https://doi.org/10.3390/fractalfract6020115
Sibatov RT, Golmankhaneh AK, Meftakhutdinov RM, Morozova EV, Timkaeva DA. Modelling of Electron and Thermal Transport in Quasi-Fractal Carbon Nitride Nanoribbons. Fractal and Fractional. 2022; 6(2):115. https://doi.org/10.3390/fractalfract6020115
Chicago/Turabian StyleSibatov, Renat T., Alireza Khalili Golmankhaneh, Ruslan M. Meftakhutdinov, Ekaterina V. Morozova, and Diana A. Timkaeva. 2022. "Modelling of Electron and Thermal Transport in Quasi-Fractal Carbon Nitride Nanoribbons" Fractal and Fractional 6, no. 2: 115. https://doi.org/10.3390/fractalfract6020115
APA StyleSibatov, R. T., Golmankhaneh, A. K., Meftakhutdinov, R. M., Morozova, E. V., & Timkaeva, D. A. (2022). Modelling of Electron and Thermal Transport in Quasi-Fractal Carbon Nitride Nanoribbons. Fractal and Fractional, 6(2), 115. https://doi.org/10.3390/fractalfract6020115







