Asymmetric Lévy Flights Are More Efficient in Random Search
Abstract
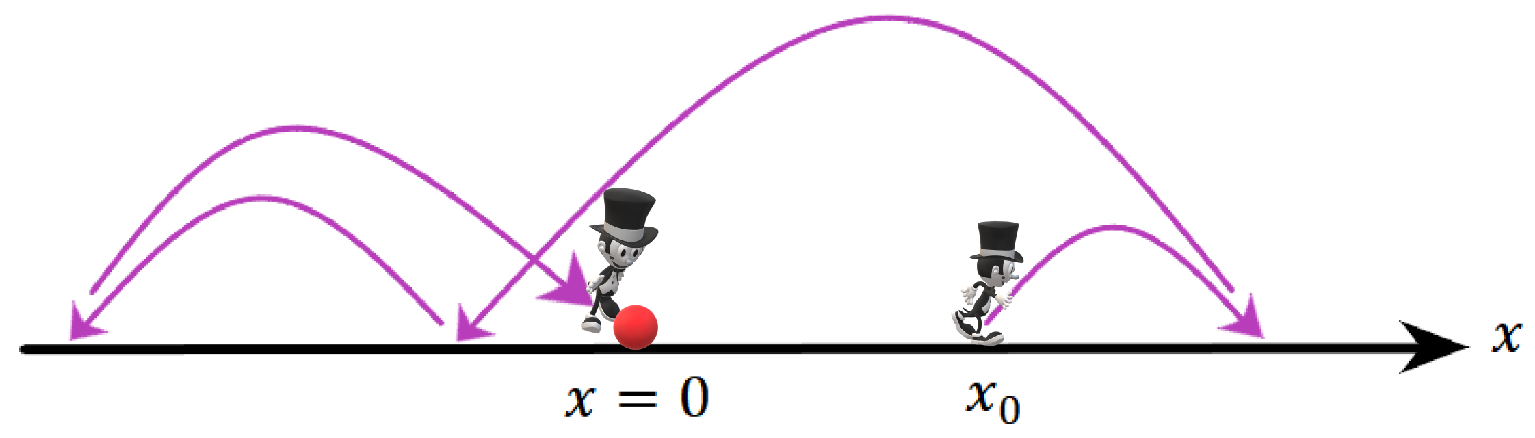
1. Introduction
2. Formulation of the Problem and Solution
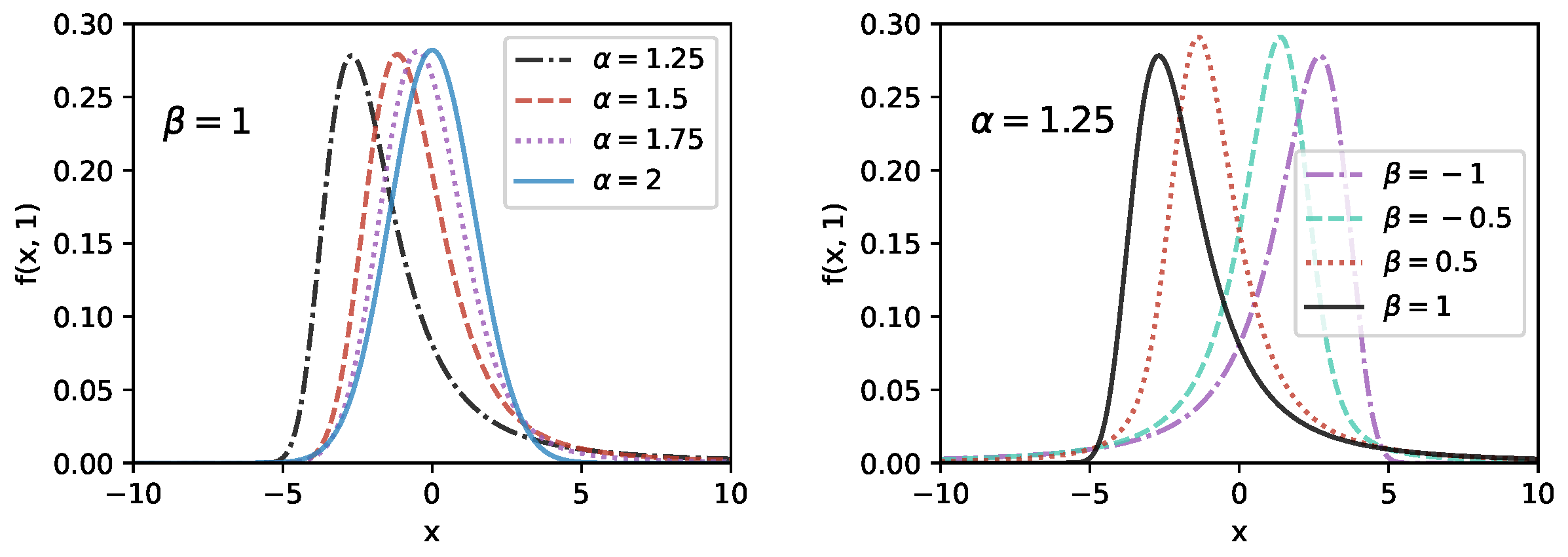
2.1. Diffusion Equation for Asymmetric Lévy Flights
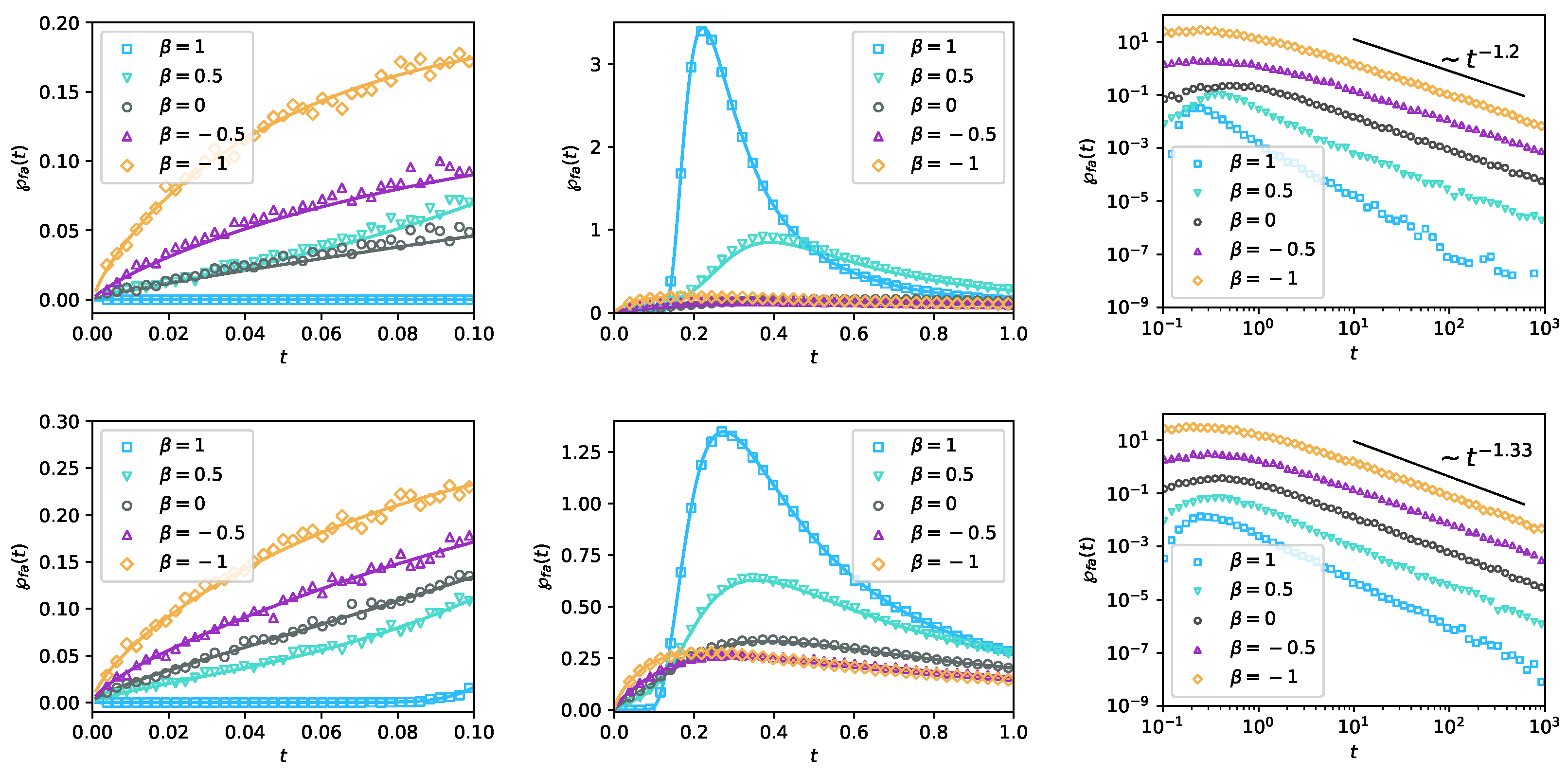
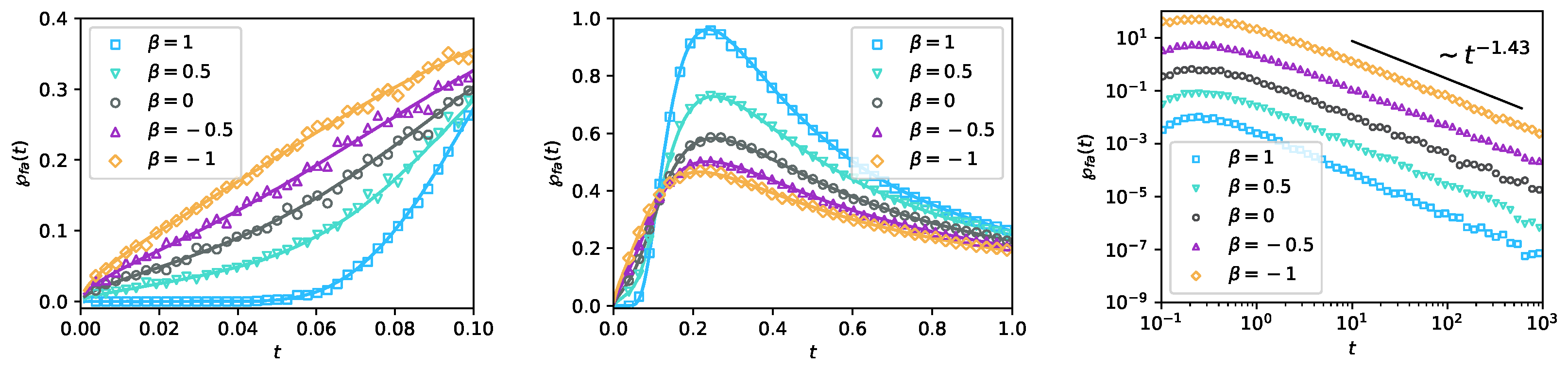
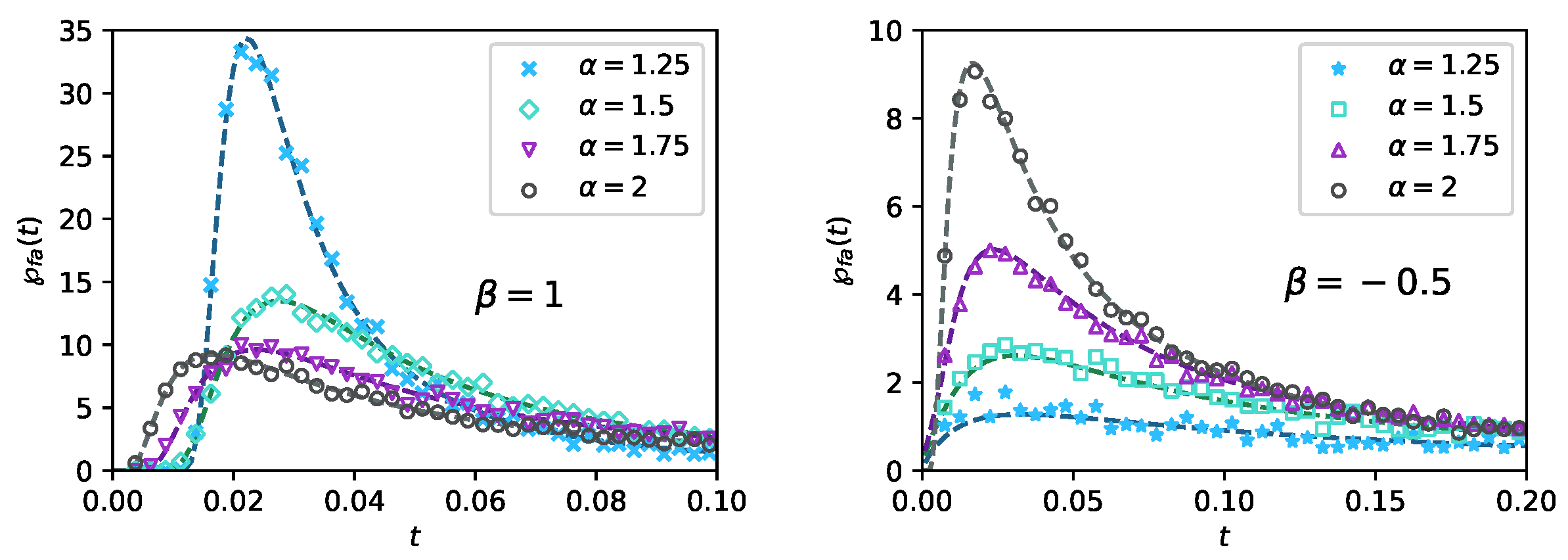
2.2. Presence of the -Sink and Calculation of the First-Arrival Density
3. Langevin Equation Approach
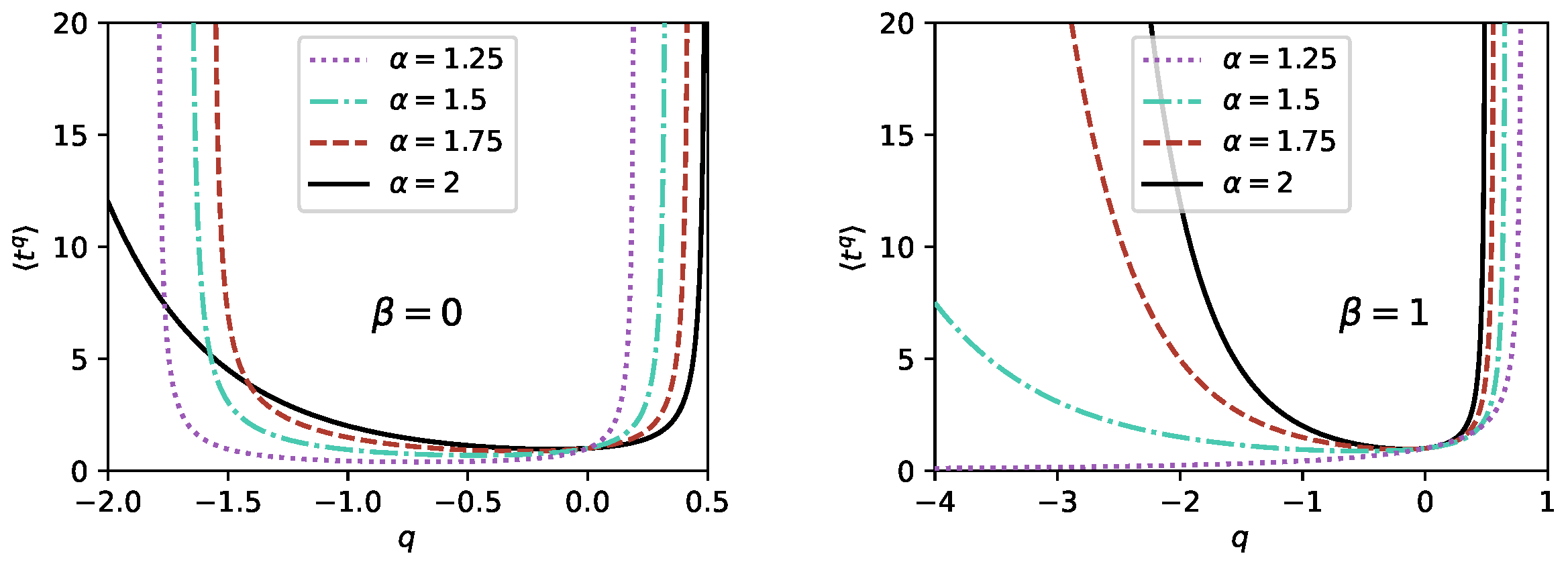
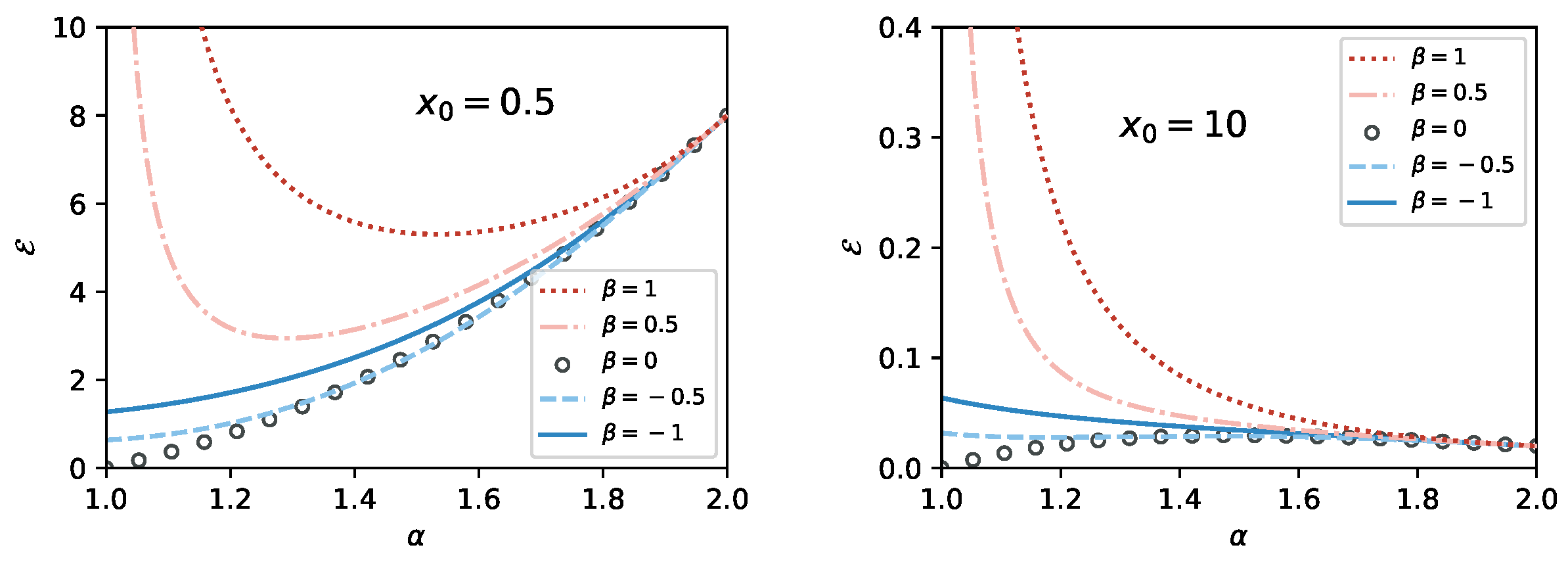
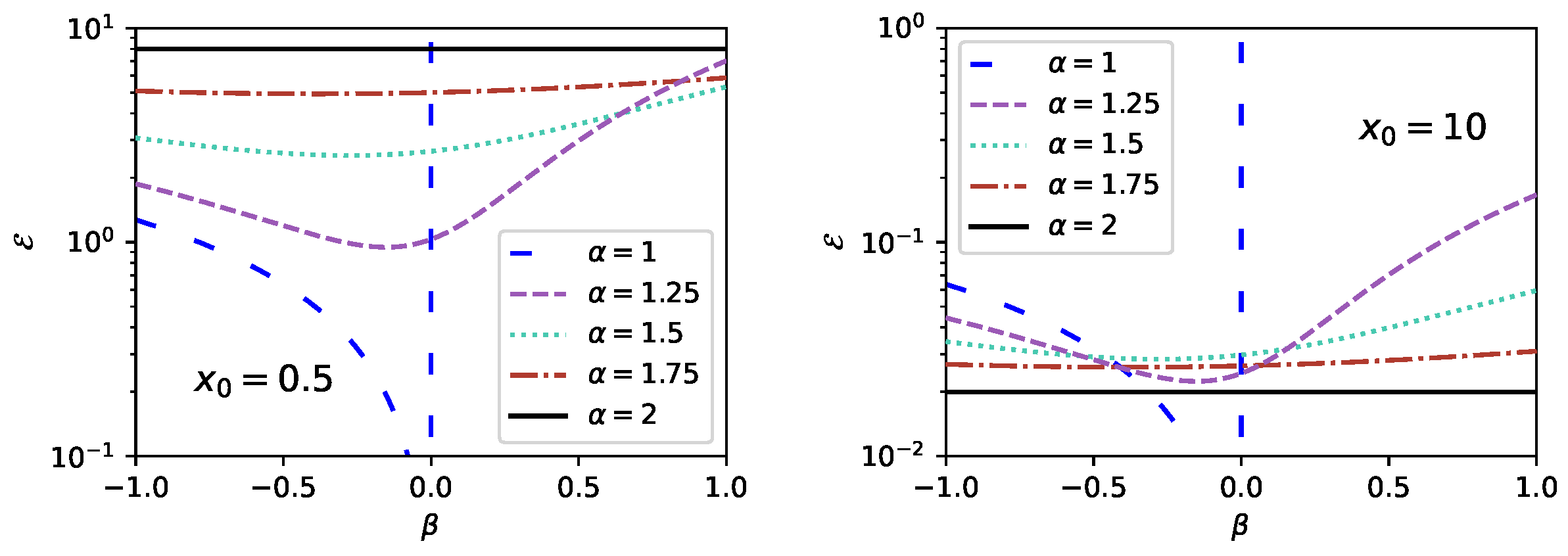
4. Calculation of the Search Efficiency
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Probability density function |
Appendix A. Characteristic Functions of α-Stable Processes
Appendix B. Mittag–Leffler and Fox H-Functions
Appendix C. Derivation of the Lévy α-Stable PDF
Appendix D. On the Positivity of the q-Order Moments
Appendix E. Some Details of the Derivation of the First-Arrival Density of Asymmetric Lévy Flights
Appendix F. Derivation of the Short-Time and Long-Time Limit of the First-Arrival Density of Asymmetric Lévy Flights
Appendix G. On the Calculation of the Efficiency for the Limit α→1 with β≠0
References
- Viswanathan, G.M.; Buldyrev, S.V.; Havlin, S.; Da Luz, M.G.E.; Raposo, E.P.; Stanley, H.E. Optimizing the success of random searches. Nature 1999, 401, 911–914. [Google Scholar] [CrossRef] [PubMed]
- Shlesinger, M.F. Search research. Nature 2005, 443, 281–282. [Google Scholar] [CrossRef] [PubMed]
- Bressloff, P.C.; Newby, J.M. Stochastic models of intracellular transport. Rev. Mod. Phys. 2013, 85, 135. [Google Scholar] [CrossRef]
- Luby, M.; Sinclair, A.; Zuckerman, D. Optimal speedup of Las Vegas algorithms. Inf. Process. Lett. 1993, 47, 173–180. [Google Scholar] [CrossRef]
- Gomes, C.P.; Selman, B.; Kautz, H. Boosting combinatorial search through randomization. In Proceedings of the Fifteenth National Conference on Artificial Intelligence (AAAI, 1998), Madison, WI, USA, 26–30 July 1998; Volume 98, p. 431. [Google Scholar] [CrossRef]
- Champagne, L.; Carl, R.G.; Hill, R. Search theory, agent-based simulation, and u-boats in the Bay of Biscay. In Proceedings of the 2003 Winter Simulation Conference, Orleans, LA, USA, 7–10 December 2003; p. 991. [Google Scholar] [CrossRef]
- Shlesinger, M.F. Random searching. J. Phys. A Math. Theor. 2009, 42, 434001. [Google Scholar] [CrossRef]
- Anderson, J.P.; Stephens, D.W.; Dunbar, S.R. Saltatory search: A theoretical analysis. Behav. Ecol. 1997, 8, 307–317. [Google Scholar] [CrossRef]
- Palyulin, V.V.; Chechkin, A.V.; Metzler, R. Lévy flights do not always optimize random blind search for sparse targets. Proc. Natl. Acad. Sci. USA 2014, 111, 2931. [Google Scholar] [CrossRef]
- James, A.; Pitchford, J.W.; Plank, M.J. Efficient or inaccurate? Analytical and numerical modelling of random search strategies. Bull. Math. Biol. 2010, 72, 896–913. [Google Scholar] [CrossRef]
- Magnello, M.E. Karl Pearson and the establishment of mathematical statistics. Int. Stat. Rev. 2009, 77, 3. [Google Scholar] [CrossRef]
- Shlesinger, M.F.; Klafter, J. Lévy Walks Versus Lévy Flights. In On Growth and Form; Stanley, H.E., Ostrowsky, N., Eds.; NATO ASI Series (Series E: Applied Sciences); Springer: Dordrecht, The Netherlands, 1986; Volume 100, pp. 279–283. [Google Scholar] [CrossRef]
- Viswanathan, G.M.; Afanasyev, V.; Buldyrev, S.V.; Murphey, E.J.; Prince, P.A.; Stanley, H.E. Lévy flight search patterns of wandering albatrosses. Nature 1996, 381, 413–415. [Google Scholar] [CrossRef]
- Viswanathan, G.M.; Da Luz, M.G.; Raposo, E.P.; Stanley, H.E. The Physics of Foraging: An Introduction to Random Searches and Biological Encounters; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Ramos-Fernández, G.; Mateos, J.L.; Miramontes, O.; Cocho, G.; Larralde, H.; Ayala-Orozco, B. Lévy walk patterns in the foraging movements of spider monkeys (Ateles geoffroyi). Behav. Ecol. Sociobiol. 2004, 55, 223–230. [Google Scholar] [CrossRef]
- Levandowsky, M.; White, B.S.; Schuster, F.L. Random movements of soil amebas. Acta Protozool. 1997, 36, 237. [Google Scholar]
- Mandelbrot, B.B. The Variation of Certain Speculative Prices. J. Bus. 1963, 36, 394–419. Available online: https://www.jstor.org/stable/2350970 (accessed on 10 March 2022). [CrossRef]
- Mandelbrot, B.B. Forecasts of Future Prices, Unbiased Markets and “Martingale” Models. J. Bus. 1966, 39, 242–255. Available online: https://www.jstor.org/stable/2351745 (accessed on 10 March 2022). [CrossRef]
- Carati, A.; Galgani, L.; Pozzi, B. Lévy flights in the Landau-Teller model of molecular collisions. Phys. Rev. Lett. 2003, 90, 010601. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Gonchar, V.Y.; Szydlowsky, M. Fractional kinetics for relaxation and superdiffusion in magnetic field. Phys. Plasma 2002, 9, 78. [Google Scholar] [CrossRef]
- Del-Castillo-Negrete, D. Truncation effects in superdiffusive front propagation with Lévy flights. Phys. Rev. E 2009, 79, 031120. [Google Scholar] [CrossRef]
- Del-Castillo-Negrete, D.; Carreras, B.A.; Lynch, V.E. Fractional diffusion in plasma turbulence. Phys. Plasmas 2004, 11, 3854. [Google Scholar] [CrossRef]
- Tribel, O.; Boon, J.P. Lévy Laws for Lattice Gas Automata. In Pattern Formation and Lattice Gas Automata; Lawniczak, A., Kapral, R., Eds.; Fields Institute of Mathematics (Toronto): Toronto, ON, Canada, 1994; Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.31.5159&rep=rep1&type=pdf (accessed on 10 March 2022).
- Betello, G.; Succi, S. Lévy-flight cellular automata on the IBM RISC-6000 workstation. In Proceedings of the [1991] Proceedings, Advanced Computer Technology, Reliable Systems and Applications, Bologna, Italy, 13–16 May 1991; pp. 695–700. [Google Scholar] [CrossRef]
- Levernier, N.; Textor, J.; Bénichou, O.; Voituriez, R. Inverse Square Lévy Walks are not Optimal Search Strategies for d≥2. Phys. Rev. Lett. 2020, 124, 080601. [Google Scholar] [CrossRef]
- Lomholt, M.A.; Koren, T.; Metzler, R.; Klafter, J. Lévy strategies in intermittent search processes are advantageous. Proc. Natl. Acad. Sci. USA 2008, 105, 11055–11059. [Google Scholar] [CrossRef]
- Palyulin, V.V.; Chechkin, A.V.; Metzler, R. Space-fractional Fokker-Planck equation and optimization of random search processes in the presence of an external bias. J. Stat. Mech. 2014, 2014, P11031. [Google Scholar] [CrossRef]
- Bénichou, O.; Coppey, M.; Moreau, M.; Suet, P.H.; Voiturierz, R. Optimal search strategies for hidden targets. Phys. Rev. Lett. 2005, 94, 198101. [Google Scholar] [CrossRef] [PubMed]
- Loverdo, C.; Bénichou, O.; Moreau, M.; Voiturierz, R. Enhanced reaction kinetics in biological cells. Nat. Phys. 2008, 4, 134–137. [Google Scholar] [CrossRef]
- Bartumeus, F.; Levin, S.A. Fractal reorientation clocks: Linking animal behavior to statistical patterns of search. Proc. Natl. Acad. Sci. USA 2008, 105, 19072–19077. [Google Scholar] [CrossRef]
- Bénichou, O.; Loverdo, C.; Moreau, M.; Voituriez, R. Intermittent search strategies. Rev. Mod. Phys. 2011, 83, 81. [Google Scholar] [CrossRef]
- Bartumeus, F.; Peters, F.; Pueyo, S.; Marrasé, C.; Catalan, J. Helical Lévy walks: Adjusting searching statistics to resource availability in microzooplankton. Proc. Natl. Acad. Sci. USA 2003, 100, 12771–12775. [Google Scholar] [CrossRef]
- Pacheco-Cobos, L.; Winterhalder, B.; Cuatianquiz-Lima, C.; Rosetti, M.F.; Hudson, R.; Ross, C.T. Nahua mushroom gatherers use area-restricted search strategies that conform to marginal value theorem predictions. Proc. Natl. Acad. Sci. USA 2019, 116, 10339–10347. [Google Scholar] [CrossRef]
- Knell, A.S.; Codling, E.A. Classifying area-restricted search (ars) using a partial sum approach. Theor. Ecol. 2012, 5, 325–339. [Google Scholar] [CrossRef]
- Mooney, B.L.; Corrales, L.R.; Clark, A.E. MoleculaRnetworks: An integrated graph theoretic and data mining tool to explore solvent organization in molecular simulation. J. Comput. Chem. 2012, 33, 853–860. [Google Scholar] [CrossRef]
- Tejedor, V.; Bénichou, O.; Voituriez, R. Global mean first-passage times of random walks on complex networks. Phys. Rev. E 2009, 80, 065104(R). [Google Scholar] [CrossRef] [PubMed]
- Perra, N.; Baronchelli, A.; Mocanu, D.; Gonçalves, B.; Pastor-Satorras, R.; Vespignani, A. Random walks and search in time-varying networks. Phys. Rev. Lett. 2012, 109, 238701. [Google Scholar] [CrossRef] [PubMed]
- Lomholt, M.A.; Ambjörnsson, T.; Metzler, R. Optimal target search on a fast-folding polymer chain with volume exchange. Phys. Rev. Lett. 2005, 85, 260603. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, A.M. Optimal random Lévy-loop searching: New insights into the searching behaviours of central-place foragers. Europhys. Lett. 2008, 82, 20001. [Google Scholar] [CrossRef]
- Blumenthal, R.M.; Getoor, R.K.; Ray, D.B. On the distribution of first hits for the symmetric stable processes. Trans. Amer. Math. Soc. 1961, 99, 540–554. [Google Scholar] [CrossRef]
- Port, S.C. Hitting times and potentials for recurrent stable processes. J. Anal. Math. 1967, 20, 371–395. [Google Scholar] [CrossRef]
- Port, S.C. The first hitting distribution of a sphere for symmetric stable processes. Trans. Amer. Math. Soc. 1969, 135, 115–125. [Google Scholar] [CrossRef]
- Doney, R.A. Hitting probabilities for spectrally positive Lévy processes. J. Lond. Math. Soc. 1991, 44, 566–576. [Google Scholar] [CrossRef]
- Cordero, F. On the Excursion Theory for the Symmetric Stable Lévy Processes with Index α∈(1,2] and Some Applications. Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 2010. Available online: http://dml.mathdoc.fr/item/tel-00521136 (accessed on 10 March 2022).
- Yano, K.; Yano, Y.; Yor, M. On the Laws of First Hitting Times of Points for One-Dimensional Symmetric Stable Lévy Processes; Séminaire de Probabilités XLII, 187, Lecture Notes in Math, 1979; Springer: Berlin, Germany, 2009. [Google Scholar] [CrossRef]
- Kwaśnicki, M. Spectral theory for symmetric one-dimensional Lévy processes killed upon hitting the origin. Electron. J. Probab. 2012, 17, 1–29. [Google Scholar] [CrossRef]
- Juszczyszyn, T.; Kwaśsnicki, M. Hitting times of points for symmetric Lévy processes with completely monotone jumps. Electron. J. Probab. 2015, 20, 1–24. [Google Scholar] [CrossRef]
- Grzywny, T.; Ryznar, M. Hitting times of points and intervals for symmetric Lévy processes. Potential Anal. 2017, 46, 739–777. [Google Scholar] [CrossRef][Green Version]
- Peskir, G. The law of the hitting times to points by a stable Lévy process with no negative jumps. Electron. Commun. Probab. 2008, 13, 653–659. [Google Scholar] [CrossRef]
- Simon, T. Hitting densities for spectrally positive stable processes. Stochastics 2011, 83, 203–214. [Google Scholar] [CrossRef]
- Kuznetsov, A.; Kyprianou, A.; Pardo, J.C.; Watson, A. The hitting time of zero for a stable process. Electron. J. Probab. 2014, 19, 1–26. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Metzler, R.; Gonchar, V.Y.; Klafter, J.; Tanatarov, L.V. First passage and arrival time densities for Lévy flights and the failure of the method of images. J. Phys. A Math. Gen. 2003, 36, L537. [Google Scholar] [CrossRef]
- Palyulin, V.V.; Blackburn, G.; Lomholt, M.A.; Watkins, N.W.; Metzler, R.; Klages, R.; Chechkin, A.V. First passage and first hitting times of Lévy flights and Lévy walks. New J. Phys. 2019, 21, 103028. [Google Scholar] [CrossRef]
- Palyulin, V.V.; Chechkin, A.V.; Klages, R.; Metzler, R. Search reliability and search efficiency of combined Lévy-Brownian motion: Long relocations mingled with thorough local exploration. J. Phys. A Math. Theor. 2016, 49, 394002. [Google Scholar] [CrossRef]
- Dybiec, B.; Gudowaska-Nowak, E.; Chechkin, A.V. To hit or to pass it over-remarkable transient behaviour of first arrivals and passages for Lévy flights in finite domains. J. Phys. A Math. Theor. 2016, 49, 504001. [Google Scholar] [CrossRef]
- Dybiec, B.; Gudowska-Nowak, E.; Barkai, E.; Dubkov, A.A. Lévy flights versus Lévy walks in bounded domains. Phys. Rev. E 2017, 95, 052102. [Google Scholar] [CrossRef]
- Szu, H.; Hartley, R. Fast simulated annealing. Phys. Lett. A 1987, 122, 157–162. [Google Scholar] [CrossRef]
- Pavlyukevich, I. Lévy flights, non-local search and simulated annealing. J. Comput. Phys. 2007, 226, 1830–1844. [Google Scholar] [CrossRef]
- Pavlyukevich, I. Simulated annealing for Lévy-driven jump-diffusions. Stochast. Process. Appl. 2008, 118, 1071–1105. [Google Scholar] [CrossRef]
- Koren, T.; Chechkin, A.V.; Klafter, J. On the first passage time and leapover properties of Lévy motions. Phys. A Stat. Mech. Appl. 2007, 379, 10–22. [Google Scholar] [CrossRef]
- Koren, T.; Lomholt, M.A.; Chechkin, A.V.; Klafter, J.; Metzler, R. Leapover lengths and first passage time statistics for Lévy flights. Phys. Rev. Lett. 2007, 99, 160602. [Google Scholar] [CrossRef] [PubMed]
- Padash, A.; Chechkin, A.V.; Dybiec, B.; Pavlyukevich, I.; Shokri, B.; Metzler, R. First-passage properties of asymmetric Lévy flights. J. Phys. A Math. Theor. 2019, 52, 454004. [Google Scholar] [CrossRef]
- Padash, A.; Chechkin, A.V.; Dybiec, B.; Magdziarz, M.; Shokri, B.; Metzler, R. First passage time moments of asymmetric Lévy flights. J. Phys. A Math. Theor. 2020, 53, 275002. [Google Scholar] [CrossRef]
- Ditlevsen, P.D. Anomalous jumping in a double-well potential. Phys. Rev. E 1999, 60, 172. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Gonchar, V.Y.; Klafter, J.; Metzler, R. Barrier crossing of a Lévy flight. Europhys. Lett. 2005, 72, 348. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Sliusarenko, O.Y.; Klafter, J.; Metzler, R. Barrier crossing driven by Lévy noise: Universality and the Role of Noise Intensity. Phys. Rev. E. 2007, 75, 041101. [Google Scholar] [CrossRef]
- Imkeller, P.; Pavlyukevich, I. Lévy flights: Transitions and meta-stability. J. Phys. A Math. Gen. 2006, 39, L237. [Google Scholar] [CrossRef]
- Imkeller, P.; Pavlyukevich, I. First Exit Times of SDEs Driven by Stable Lévy Processes. Stoch. Proc. Appl. 2006, 116, 611–642. Available online: https://www.sciencedirect.com/science/article/pii/S0304414905001614 (accessed on 10 March 2022). [CrossRef]
- Dubkov, A.A.; La Cognata, A.; Spagnolo, B. The problem of analytical calculation of barrier crossing characteristics for Lévy flights. J Stat. Mech. Theory Exp. 2009, 2009, P01002. [Google Scholar] [CrossRef]
- Dubkov, A.A.; Kharcheva, A.A. Features of barrier crossing event for Lévy flights. EPL (Europhys. Lett.) 2016, 113, 30009. [Google Scholar] [CrossRef]
- Zolotarev, V.M. One-Dimensional Stable Distributions; American Mathematical Society: Providence, RI, USA, 1986. [Google Scholar] [CrossRef]
- Mainardi, F.; Pagnini, G.; Saxena, R.K. Fox H-functions in fractional diffusion. J. Comput. Appl. Math. 2005, 178, 321–331. [Google Scholar] [CrossRef]
- Mainardi, F.; Pagnini, G.; Gorenflo, R. Mellin Transform and Subodination Laws in Fractional Diffusion Processes. Fract. Calc. Appl. Anal. 2003, 6, 441–459. Available online: http://www.diogenes.bg/fcaa/volume6/fcaa64/amapago.pdf (accessed on 10 March 2022).
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Further solutions of fractional reaction-diffusion equations in terms of the H-function. J. Comput. Appl. Math. 2011, 235, 1311–1316. [Google Scholar] [CrossRef]
- Paradisi, P.; Cesari, R.; Mainardi, F.; Maurizi, A.; Tampieri, F. A generalized Fick’s law to describe non-local transport effects. Phys. Chem. Earth Part B Hydrol. Oceans Atmos. 2001, 26, 275. [Google Scholar] [CrossRef]
- Paradisi, P.; Cesari, R.; Mainardi, F.; Tampieri, F. The fractional Fick’s law for non-local transport processes. Physica A 2001, 293, 130. [Google Scholar] [CrossRef]
- Seshadri, V.; West, B.J. Fractal dimensionality of Lévy processes. Proc. Natl. Acad. Sci. USA 1982, 79, 4501–4505. [Google Scholar] [CrossRef]
- West, B.J.; Seshadri, V. Linear systems with Lévy fluctuations. Phys. A Stat. Mech. Appl. 1982, 113, 203–216. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Gonchar, V.Y. Linear relaxation processes governed by fractional symmetric kinetic equations. J. Exp. Theor. Phys. 2000, 91, 635–651. [Google Scholar] [CrossRef]
- Feller, W. An Introduction to Probability Theory and Its Applications, 2nd ed.; Wiley: New York, NY, USA, 1991; Volume 2, Available online: https://www.amazon.de/-/en/William-Feller/dp/0471257095/ref=pd_lpo_1?pd_rd_i=0471257095&psc=1 (accessed on 10 March 2022).
- Chambers, J.M.; Mallows, C.L.; Stuck, B.W. A Method for Simulating Stable Random Variables. J. Am. Stat. Assoc. 1976, 71, 340–344. [Google Scholar] [CrossRef]
- Palyulin, V.V.; Mantsevich, V.N.; Klages, R.; Metzler, R.; Chechkin, A.V. Comparison of pure and combined search strategies for single and multiple targets. Eur. Phys. J. B 2017, 90, 170. [Google Scholar] [CrossRef]
- Samorodnitsky, G.; Taqqu, M.S. Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance; Chapman and Hall: New York, NY, USA, 1994. [Google Scholar] [CrossRef]
- Prabhakar, T.R. A singular integral equation with a generalized Mittag-Leffler function in the kernel. Yokohama Math. J. 1971, 19, 7–15. [Google Scholar]
- Mathai, A.M.; Saxena, R.K.; Haubold, H.J. The H-Function: Theory and Applications; Springer: New York, NY, USA; Dordrecht, The Netherlands; Heidelberg, Germany; London, UK, 2010. [Google Scholar] [CrossRef]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series; Gordon and Breach: New York, NY, USA, 1990. [Google Scholar]
- Klafter, J.; Sokolov, I.M. First Steps in Random Walks; Oxford University Press: Oxford, UK, 2011. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Padash, A.; Sandev, T.; Kantz, H.; Metzler, R.; Chechkin, A.V. Asymmetric Lévy Flights Are More Efficient in Random Search. Fractal Fract. 2022, 6, 260. https://doi.org/10.3390/fractalfract6050260
Padash A, Sandev T, Kantz H, Metzler R, Chechkin AV. Asymmetric Lévy Flights Are More Efficient in Random Search. Fractal and Fractional. 2022; 6(5):260. https://doi.org/10.3390/fractalfract6050260
Chicago/Turabian StylePadash, Amin, Trifce Sandev, Holger Kantz, Ralf Metzler, and Aleksei V. Chechkin. 2022. "Asymmetric Lévy Flights Are More Efficient in Random Search" Fractal and Fractional 6, no. 5: 260. https://doi.org/10.3390/fractalfract6050260
APA StylePadash, A., Sandev, T., Kantz, H., Metzler, R., & Chechkin, A. V. (2022). Asymmetric Lévy Flights Are More Efficient in Random Search. Fractal and Fractional, 6(5), 260. https://doi.org/10.3390/fractalfract6050260







