Fractional Order Fuzzy Dispersion Entropy and Its Application in Bearing Fault Diagnosis
Abstract
1. Introduction
2. Fractional Order Fuzzy Dispersion Entropy
2.1.
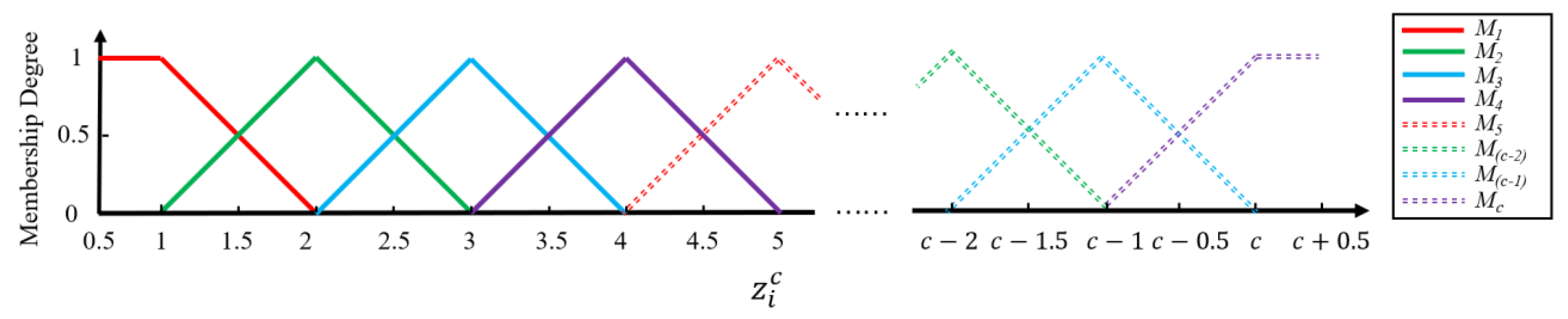
2.2. Parameter Selection
3. Experiments on Simulated Signals
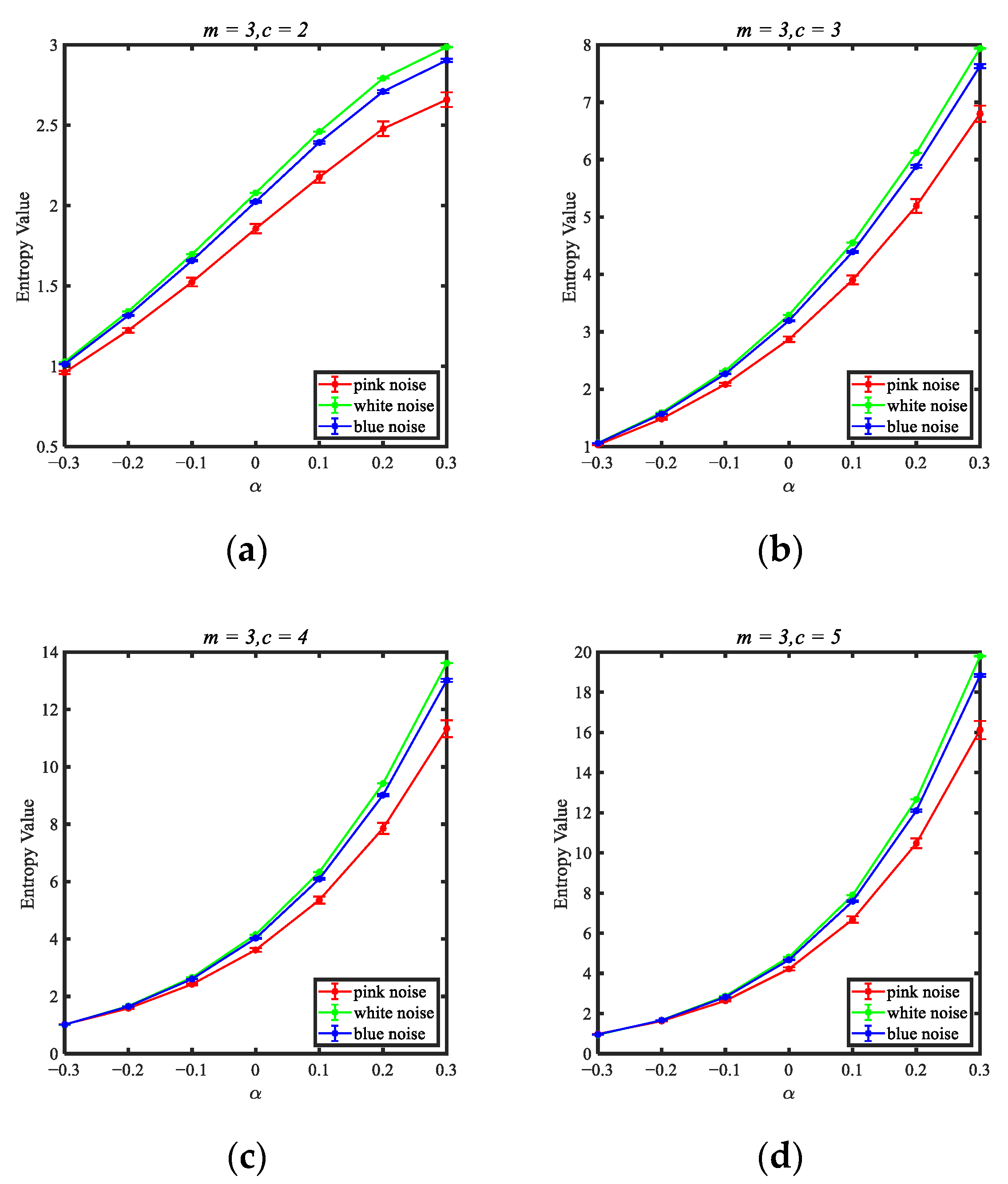
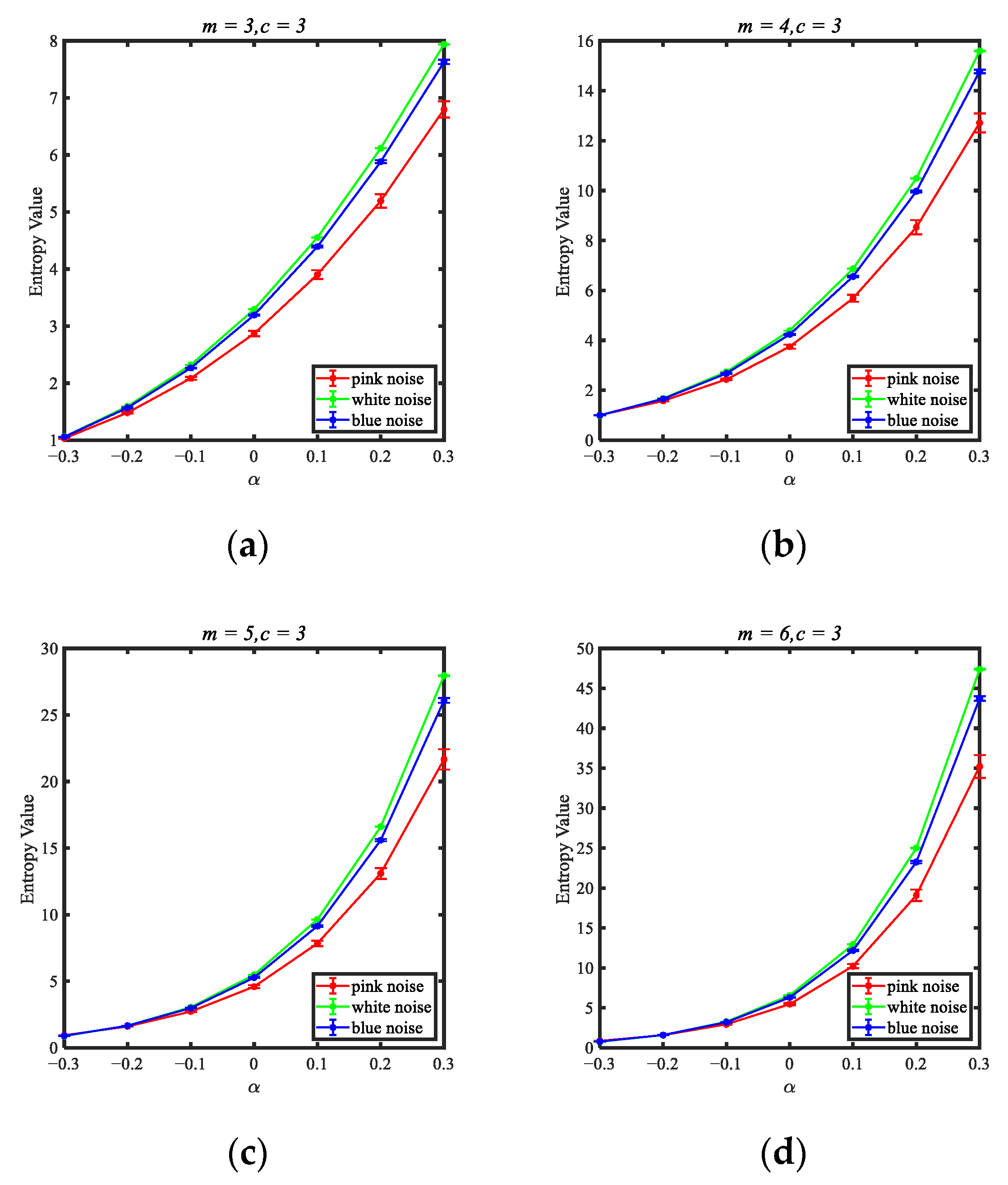
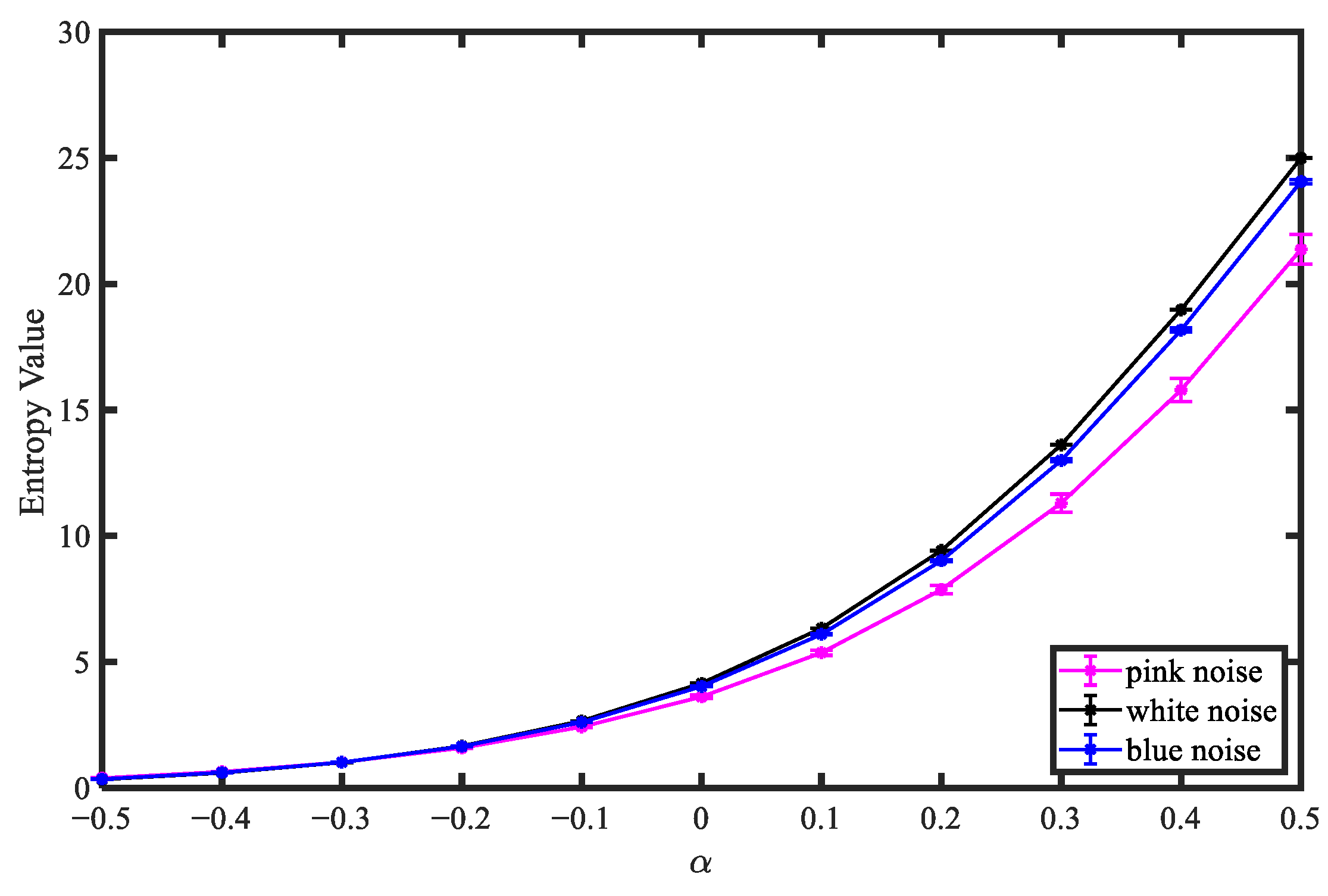
3.1. Noise Signals Experiment
3.2. Chirp Signal Experiment
3.3. MIX Signal Experiment
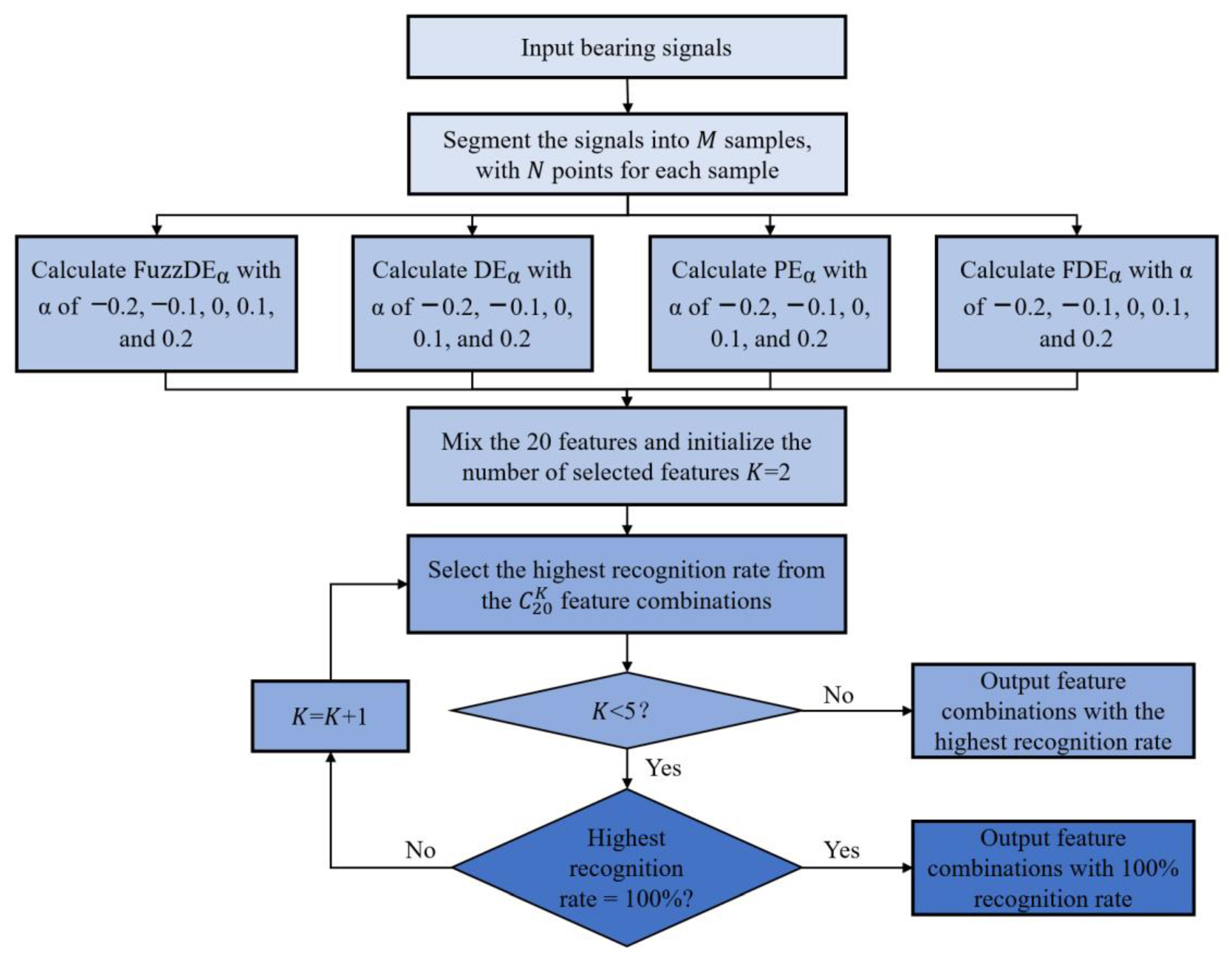
4. Experiments on Bearing Fault Diagnosis
4.1. Analysis of Experiment Data
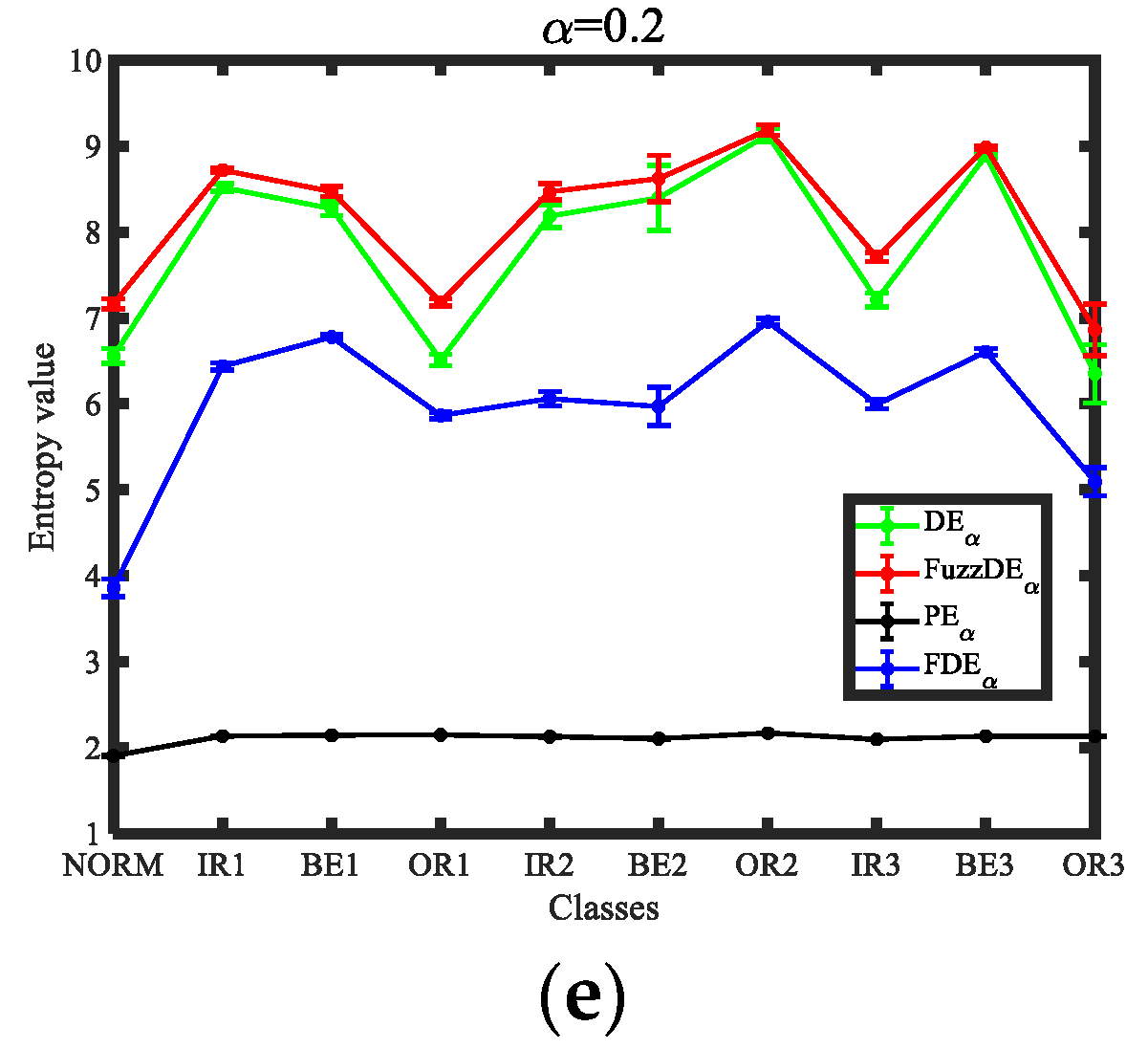
4.2. Single Feature Extraction and Classification
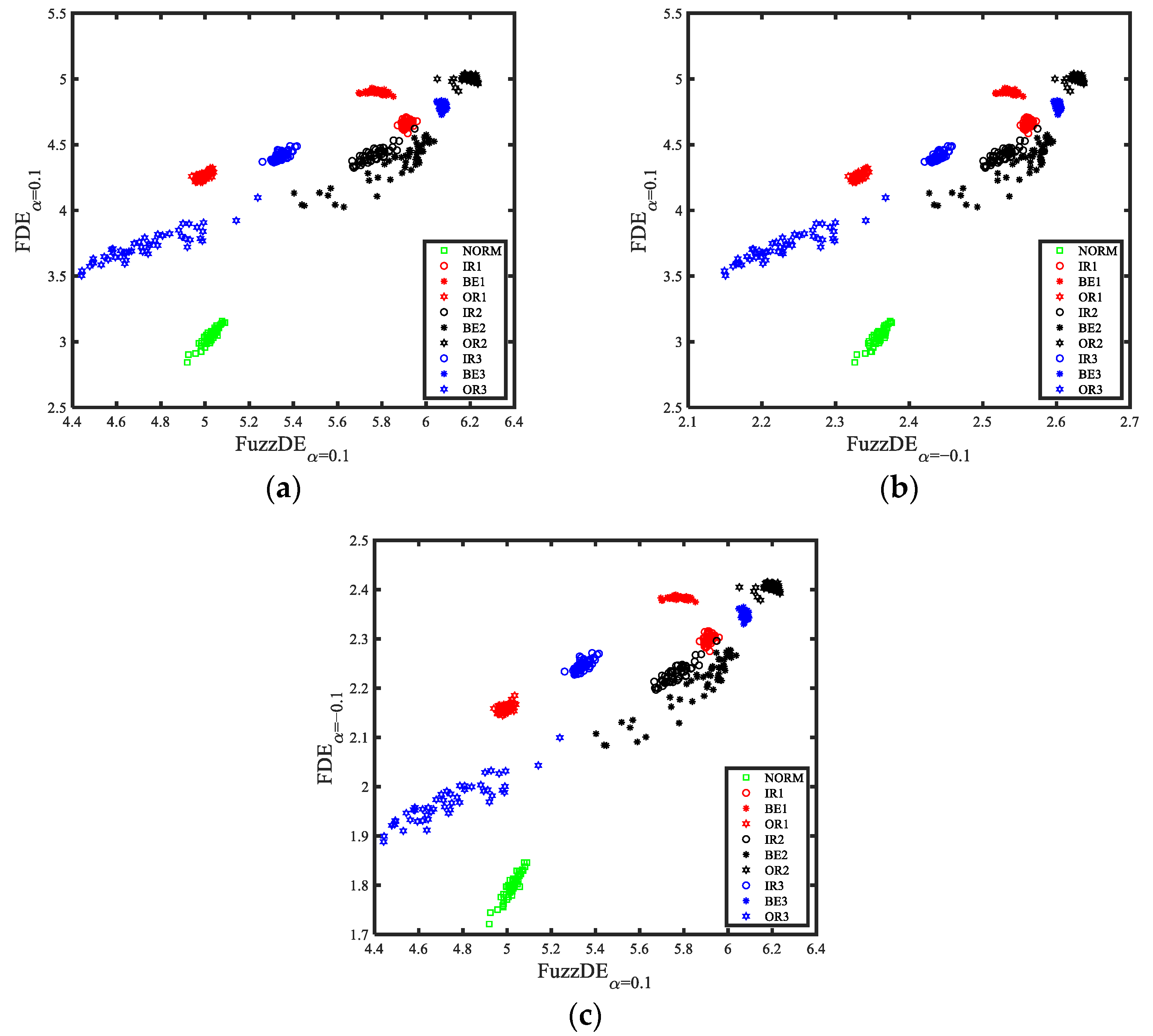
4.3. Double Features Extraction and Classification
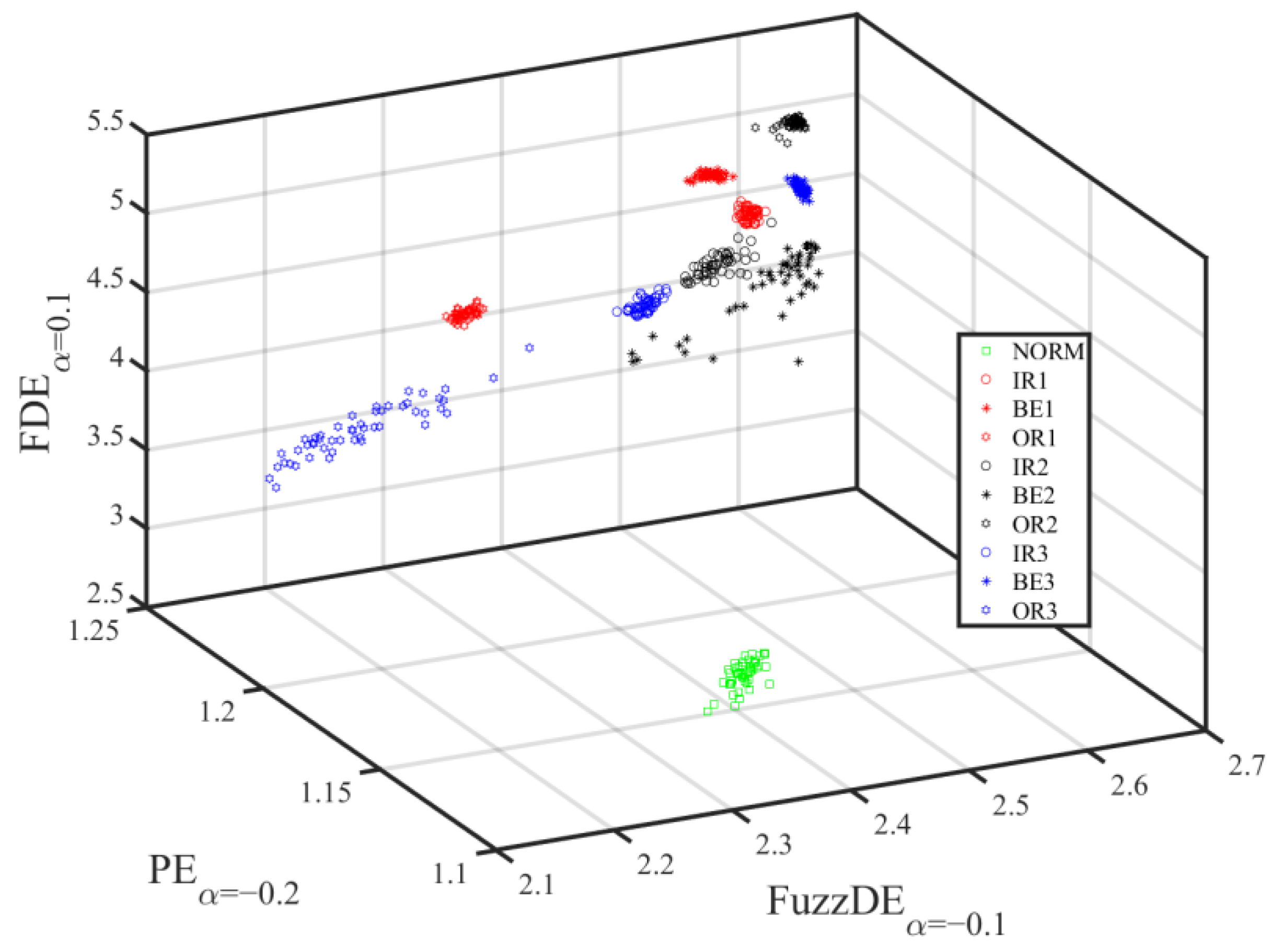
4.4. Triple Features Extraction and Classification
5. Conclusions
- Fractional order calculation is introduced on the basis of fuzzy dispersion entropy (FuzzDE), and a new entropy called fractional order FDE () is proposed. Simulated experiments have shown that compared with , can provide more features of greater sensitivity to changes in the dynamics of the time series.
- is combined with , as well as to present a mixed features extraction method. For ten classes of bearing signals, the proposed mixed features fault diagnosis method achieves 100% recognition rate at only triple features.
- Regardless of how many features are selected, the proposed in this paper is the most effective in fault diagnosis compared to the other three fractional order entropies, where appears a total of 11 times in the combination of the triple features with the recognition rate of 100%
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| FuzzDE | Fuzzy Dispersion Entropy |
| Fractional order fuzzy dispersion entropy | |
| PE | Permutation entropy |
| Fractional order permutation entropy | |
| DE | Dispersion entropy |
| Fractional order dispersion entropy | |
| FDE | Fluctuation-based dispersion entropy |
| Fractional order fluctuation-based dispersion entropy | |
| NCDF | Normal cumulative distribution function |
| SE | Sample entropy |
| FRDE | Fluctuation-based reverse dispersion entropy |
| RDE | Reverse dispersion entropy |
| FuzzEn | Fuzzy entropy |
| RCMDE | Refined composite multiscale dispersion entropy |
| Generalized refined composite multiscale fluctuation-based fractional dispersion entropy | |
| LM | Linear mapping |
| TANSIG | Tangent sigmoid |
| LOGSIG | Logarithm sigmoid |
| SORT | Sorting method |
References
- Berger, A.L.; Della Pietra, V.J.; Della Pietra, S.A. A maximum entropy approach to natural language processing. Comput. Linguist. 1996, 22, 39–71. [Google Scholar]
- Martyushev, L.M.; Seleznevb, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Rostaghi, M.; Khatibi, M.M.; Ashory, M.R.; Azami, H. Bearing Fault Diagnosis Using Refined Composite Generalized Multiscale Dispersion Entropy-Based Skewness and Variance and Multiclass FCM-ANFIS. Entropy 2021, 23, 1510. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Liang, Y.; Zhou, J.; Zang, Y. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM. Measurement 2015, 69, 164–179. [Google Scholar] [CrossRef]
- Yan, R.; Liu, Y.; Gao, R. Permutation entropy: A nonlinear statistical measure for status characterization of rotary machines. Mech. Syst. Signal Process. 2012, 29, 474–484. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Ren, M.; He, M.; Jin, L. Rolling Bearing Fault Diagnosis Based on Multiscale Permutation Entropy and SOA-SVM. Machines 2022, 10, 485. [Google Scholar] [CrossRef]
- Ying, W.; Tong, J.; Dong, Z.; Pan, H.; Liu, Q.; Zheng, J. Composite Multivariate Multi-Scale Permutation Entropy and Laplacian Score Based Fault Diagnosis of Rolling Bearing. Entropy 2022, 24, 160. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion Entropy: A Measure for Time Series Analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Gu, C.; Qiao, X.; Li, H. Misfire Fault Diagnosis Method for Diesel Engine Based on MEMD and Dispersion Entropy. Shock Vib. 2021, 5, 1–14. [Google Scholar] [CrossRef]
- Azami, H.; Fernandez, A.; Escudero, J. Multivariate Multiscale Dispersion Entropy of Biomedical Times Series. Entropy 2017, 21, 913. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Amplitude- and Fluctuation-Based Dispersion Entropy. Entropy 2018, 20, 210. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Gao, X.; Wang, L. Reverse Dispersion Entropy: A New Complexity Measure for Sensor Signal. Sensors 2019, 19, 5203. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Jiao, S.; Gao, X. A novel signal feature extraction technology based on empirical wavelet transform and reverse dispersion entropy. Def. Technol. 2021, 17, 1625–1635. [Google Scholar] [CrossRef]
- Jiao, S.; Geng, B.; Li, Y. Fluctuation-based reverse dispersion entropy and its applications to signal classification. Appl. Acoust. 2021, 175, 107857. [Google Scholar] [CrossRef]
- Rostaghi, M.; Khatibi, M.M.; Ashory, M.R.; Azami, H. Fuzzy Dispersion Entropy: A Nonlinear Measure for Signal Analysis. IEEE Trans. Fuzzy Syst. 2022, 30, 3785–3796. [Google Scholar] [CrossRef]
- Ali, K. Fractional order entropy: New perspectives. Opt.-Int. J. Light Electron Opt. 2016, 127, 9172–9177. [Google Scholar]
- Ingo, C.; Magin, R.L.; Parrish, T.B. New Insights into the Fractional Order Diffusion Equation Using Entropy and Kurtosis. Entropy 2014, 16, 5838–5852. [Google Scholar] [CrossRef] [PubMed]
- Zunino, L.; Pérez, D.G.; Martín, M.T. Permutation entropy of fractional Brownian motion and fractional Gaussian noise. Phys. Lett. A 2008, 372, 4768–4774. [Google Scholar] [CrossRef]
- He, S.; Sun, K. Fractional fuzzy entropy algorithm and the complexity analysis for nonlinear time series. Eur. Phys. J. Spec. Top. 2018, 227, 943–957. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H. Use of generalized refined composite multiscale fractional dispersion entropy to diagnose the faults of rolling bearing. Nonlinear Dyn. 2021, 101, 1417–1440. [Google Scholar] [CrossRef]
- Li, Y.; Mu, L. Particle Swarm Optimization Fractional Slope Entropy: A New Time Series Complexity Indicator for Bearing Fault Diagnosis. Fractal Fract. 2022, 6, 345. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Improved multiscale permutation entropy for biomedical signal analysis: Interpretation and application to electroencephalogram recordings. Biomed. Signal Process. Control 2016, 23, 28–41. [Google Scholar] [CrossRef]
- Azami, H.; Fernandez, A.; Escudero, J. Refined Multiscale Fuzzy Entropy based on Standard Deviation for Biomedical Signal Analysis. Med. Biol. Eng. Comput. 2017, 55, 2037–2052. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Baleanu, D. Chaos synchronization of the discrete fractional logistic map. Signal Process. 2014, 102, 96–99. [Google Scholar] [CrossRef]
- Li, Y.; Liu, F.; Wang, S. Multi-scale Symbolic Lempel-Ziv: An Effective Feature Extraction Approach for Fault Diagnosis of Railway Vehicle Systems. IEEE Trans. Ind. Inform. 2021, 17, 199–208. [Google Scholar] [CrossRef]
- Case Western Reserve University. Available online: http://csegroups.case.edu/bearingdatacenter/pages/download-data-file (accessed on 1 July 2022).



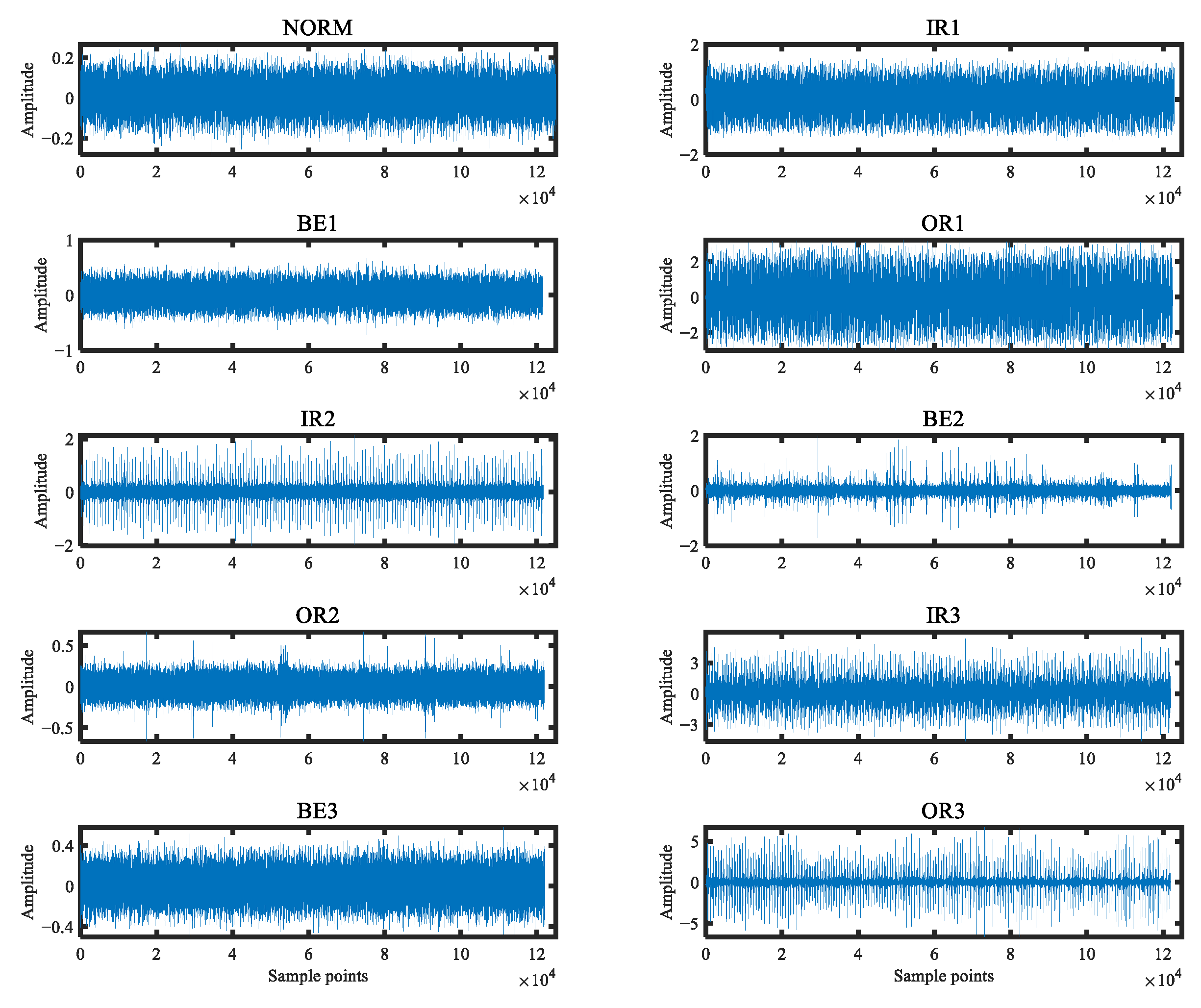

| Class | Label | Fault Size (mm) | Selected Data |
|---|---|---|---|
| Normal | NORM | 0 | 100_normal_3 |
| Inner race fault | IR1 | 0.1778 | 108_IR007_3 |
| Balling element fault | BE1 | 0.1778 | 121_B007_3 |
| Outer race fault | OR1 | 0.1778 | 133_OR007@6_3 |
| Inner race fault | IR2 | 0.3556 | 172_IR014_3 |
| Balling element fault | BE2 | 0.3556 | 188_B014_3 |
| Outer race fault | OR2 | 0.3556 | 200_OR014@6_3 |
| Inner race fault | IR3 | 0.5334 | 212_IR021_3 |
| Balling element fault | BE3 | 0.5334 | 225_B021_3 |
| Outer race fault | OR3 | 0.5334 | 237_OR021@6_3 |
| Entropy | Recognition Rates (%) | ||||
|---|---|---|---|---|---|
| 82.8 | 81.6 | 74 | 68.4 | 67.6 | |
| 76.4 | 79.6 | 76.4 | 71.2 | 66.0 | |
| 59.6 | 56.8 | 58.4 | 56.8 | 54.0 | |
| 79.2 | 82.8 | 78.4 | 77.6 | 80.4 | |
| Feature Extraction Methods | Combinations | Recognition Rate (%) |
|---|---|---|
| -based | 91.6 | |
| -based | 88.4 | |
| -based | 58.4 | |
| -based | 90.0 | |
| Proposed method | & (1 of 3) | 99.6 |
| Feature Extraction Methods | Combinations | Recognition Rate (%) |
|---|---|---|
| -based | 92 | |
| -based | 92 | |
| -based | 58 | |
| -based | 91.6 | |
| Proposed method | (1 of 15) | 100 |
| Feature | Appear Times |
|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Tang, B.; Geng, B.; Jiao, S. Fractional Order Fuzzy Dispersion Entropy and Its Application in Bearing Fault Diagnosis. Fractal Fract. 2022, 6, 544. https://doi.org/10.3390/fractalfract6100544
Li Y, Tang B, Geng B, Jiao S. Fractional Order Fuzzy Dispersion Entropy and Its Application in Bearing Fault Diagnosis. Fractal and Fractional. 2022; 6(10):544. https://doi.org/10.3390/fractalfract6100544
Chicago/Turabian StyleLi, Yuxing, Bingzhao Tang, Bo Geng, and Shangbin Jiao. 2022. "Fractional Order Fuzzy Dispersion Entropy and Its Application in Bearing Fault Diagnosis" Fractal and Fractional 6, no. 10: 544. https://doi.org/10.3390/fractalfract6100544
APA StyleLi, Y., Tang, B., Geng, B., & Jiao, S. (2022). Fractional Order Fuzzy Dispersion Entropy and Its Application in Bearing Fault Diagnosis. Fractal and Fractional, 6(10), 544. https://doi.org/10.3390/fractalfract6100544








