1. Introduction
Fractal theory has been established to interpret the characteristics of self-similar or self-affine features [
1,
2,
3]. For such features, when the measurement scale (
L) is lowered, finer structures can be observed. In order to quantify the complexity of fractal objects, the concept of fractal dimension (
D) was proposed by Mandelbrot [
4] and widely used [
5,
6]. In the field of mathematics, there are strictly self-similar Cantor discrete point sets, Koch curve sets and so on. In the research on natural objects, it is also believed that fractal geometry could be applied, such as machining signals [
7,
8,
9], micro-structure of new materials [
10,
11,
12], surfaces topography [
13,
14,
15], etc.
However, not all objects have perfect fractal characteristics [
16,
17]. Once they exceed a certain range, they will show non-fractal characteristics. In the region that has fractal characteristics, the root-mean-squared roughness (
, also known as RMS) usually shows scaling characteristics, which is called the scaling region.
D is then calculated using the scaling region. In order to accurately calculate the value of
D, the scaling region needs to be extracted. Yokoya et al. [
18] proposed an empirical formula to calculate the upper and lower limits of the scaling region, but due to the lack of objective standards, this method had poor general applicability. In addition, other fitting methods, including three-line segment fitting [
19], curve-line-curve fitting [
20] and S-shaped curve fitting [
21], were used to extract the scaling region. Due to the error between the fitted curve and the actual
-
L curve, the calculation result of
D was inaccurate. Chen et al. [
22] used the K-means method to intercept the scaling region, while the clustering algorithm might lead to the local optimal solution. Zhou et al. [
23] proposed a density peak clustering algorithm based on machine learning to identify the scaling region, which was relatively complex and difficult to implement.
There are many algorithms for calculating the
D value, and the Weierstrass-Mandelbrot (W-M) function, which has played a significant role in the research literature, such as simulation of signals or surfaces, is often used to verify the validity of the algorithm. In the study by Zuo et al. [
24], ideal fractal sequences were constructed to investigate the scaling characteristics of the root-mean-squared roughness (
, also known as RMS) in order to select the appropriate sampling length for the
D calculation. In the study by Wang et al. [
25], fractal sequences constructed by using the W-M function were analyzed with traditional
D calculation methods such as Higuchi [
26] and Katz [
27]. In the study by Zhang et al. [
28], the performances of the box-counting method [
29] and power spectral density method [
30] were also analyzed through the ideal sequences constructed by using the W-M function. Similarly, in the fractal analysis of surface topography, the two-dimensional W-M function was also widely used to simulate artificial surfaces [
31,
32,
33].
When using the W-M function, its parameters need to meet the upper and lower critical conditions [
34,
35,
36]. Theoretically, the W-M function is a geometric progression of cosine functions, and its frequency spectrum ranges from
to infinity, where
and
are parameters defined in
Section 2 below. However, in the practical simulation by using the W-M function, infinity is not applicable; thus, the lower and upper cut-off frequencies will be with the practical W-M function. Generally, when a sufficiently large number is used to replace infinity, the influence of upper cut-off frequency, which is also called the upper critical condition, could be neglected. However, there is a lack of research on the impact of lower critical conditions and the value of fundamental frequency
on simulations when using the W-M function.
In our previous study, a roughness scaling extraction (RSE) algorithm, whose accuracy in
D calculation is much superior to the traditional algorithms, was proposed [
37] based on the scaling characteristics of
[
38,
39]. The reason why the RSE algorithm performs well is the robust property of
[
40], which could be feasible to calculate
D based on a single morphological image or a single profile, and the capability of the RSE algorithm to quantify the complexity of both fractal and non-fractal features, which could not be achieved by the traditional algorithms for
D calculation [
41,
42]. Such advantages might be attributed to the flattening procedure, which enables a higher efficiency of data utilization compared with the conventional roughness method without flattening [
37]. Because our previous studies revealed that the
-
L curves could not be of scaling property entirely and merely the data within the scaling region could be reliable to carry out a rigorous fractal analysis, a scaling region interception method was applied to extract the scaling region. However, the influencing factors of scaling region length are still unclear, and it would be necessary to use an RSE algorithm with a scaling region interception method to conduct an investigation into this.
Although the W-M function is widely used and the scaling region can be effectively extracted, there is still a lack of relevant research on the influencing factors of the lower critical condition of the W-M function and the factors that affect the scaling region length. In this study, the properties and applications of the W-M function and the length of scaling regions were studied. The RSE algorithm was used to analyze the fractal profiles generated by the W-M function. The performance of -L curves of the W-M function was studied, and a scaling region interception method was applied to obtain the scaling region. In addition, a method is given to improve the ideality of the W-M function, and a modified approach is proposed for signal simulation. The main factors influencing the scaling region and the mechanism of both the ideal improvement of the W-M function and modified approach for signal simulation are discussed.
2. Methods
2.1. Generation of Fractal Profiles
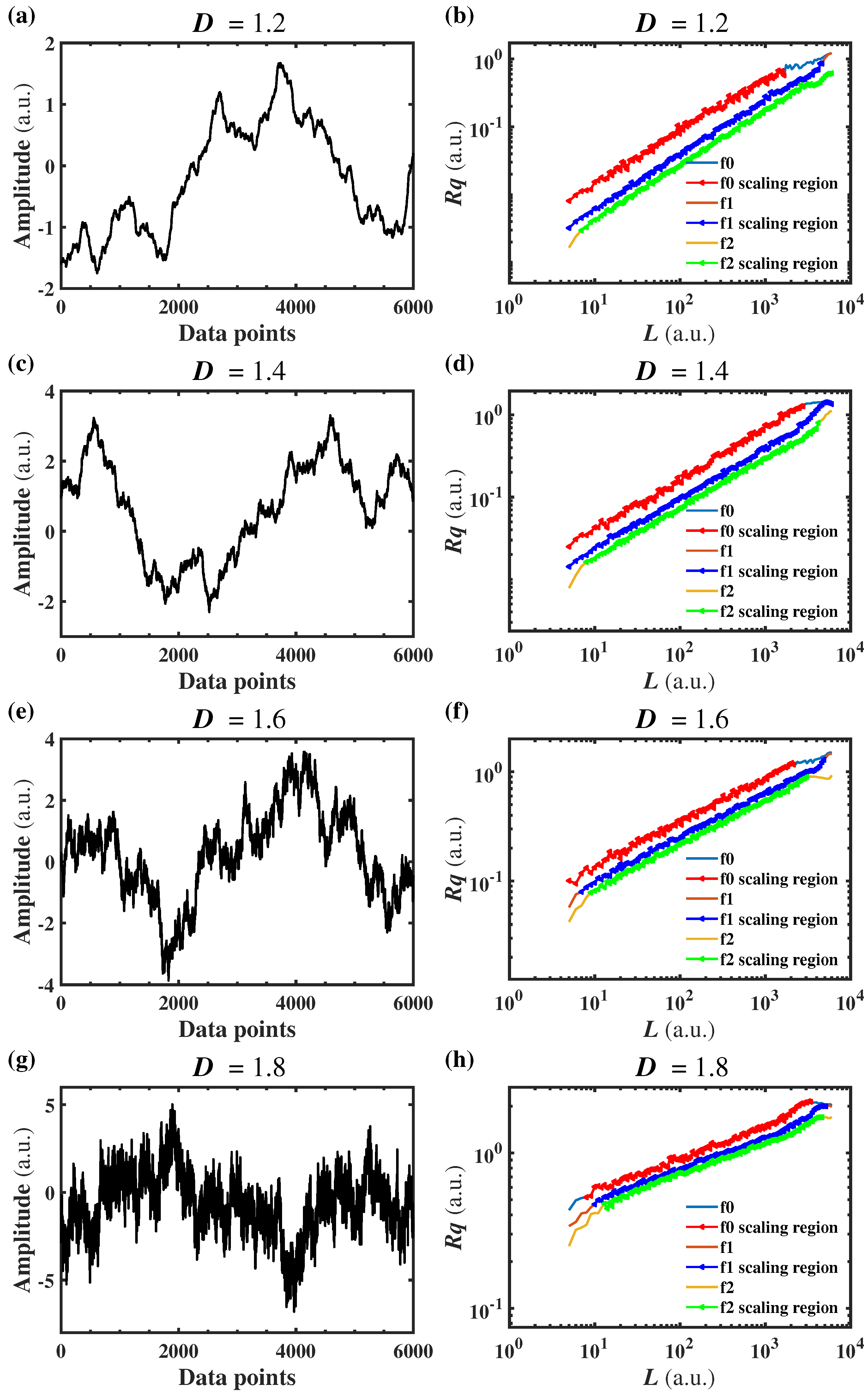
As for generating artificially fractal profiles, a series of fractal profiles were generated by using the one-dimensional W-M function with random phase, whose specific mathematical expression is as follows [
25,
35,
36]:
where
D represents the ideal fractal dimension.
is a parameter determining the frequency density, which is set as 1.5.
n is the number of items accumulated by the series and its maximum value is
M (
).
represents the random phase, which could help to avoid the coincidence of different frequencies at any position of the fractal profile [
35,
43].
In this section, a series of fractal profiles were generated to simulate time series signals with a fixed duration
T = 20 s. Equation (
1), where
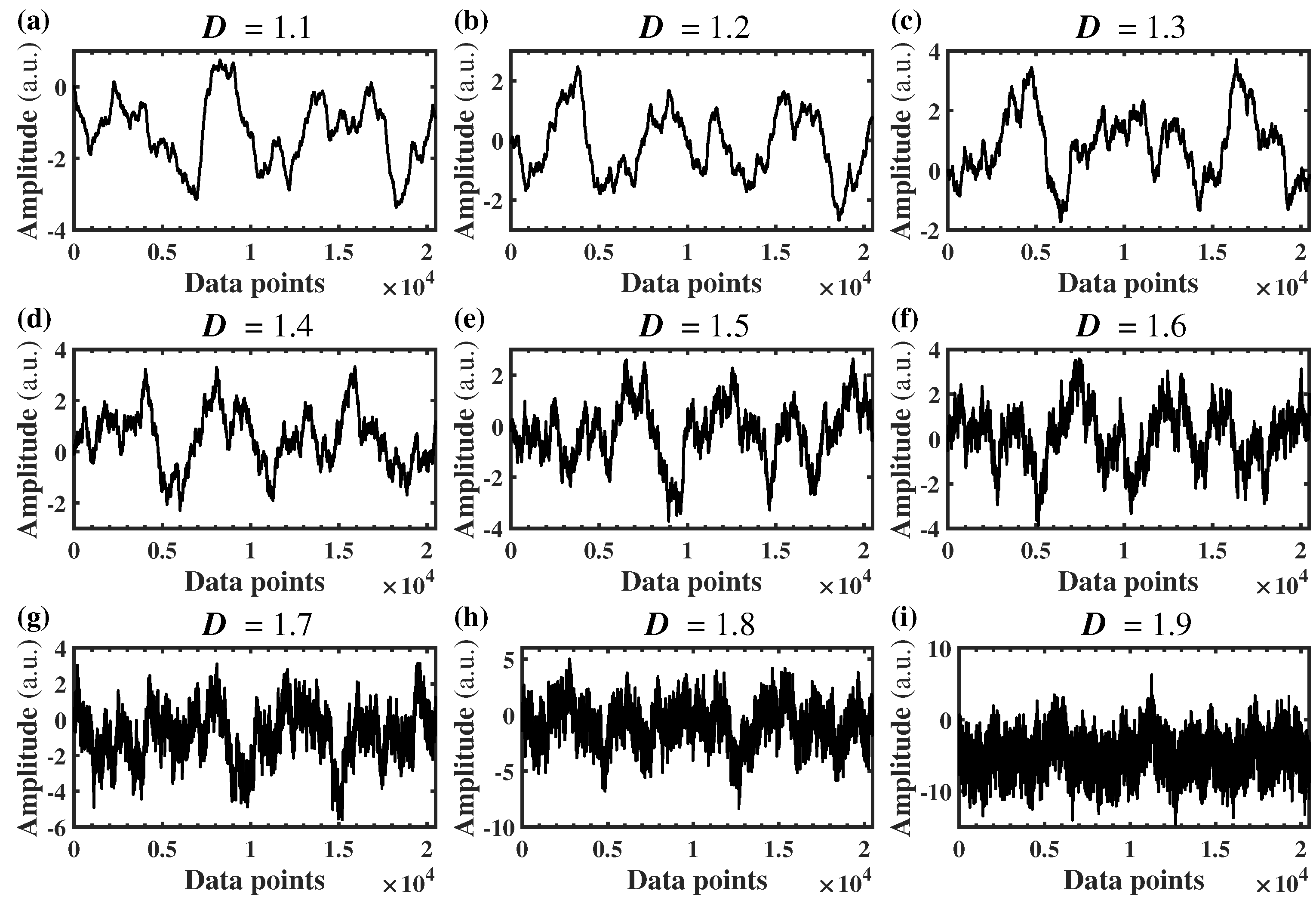
, was used to generate the profiles with ideal
D values from 1.1 to 1.9 (with an interval of 0.1). In the meantime, 30 original sequences were randomly generated for each
D value to reduce the calculation error. To consider both the efficiency and accuracy of calculation, the sampling frequency was 1024.
In order to study the performance of the RSE algorithm under different sampling lengths, 21 different sampling lengths were selected, which were 500, 1000, 2000, …, 20,000 (when the sampling length exceeded 1000, the interval was 1000), respectively, and the 30 original sequences for each D were randomly truncated to obtain 30 sampling sequences with target sampling length. The RSE algorithm was applied for the 30 sampling sequences to calculate D, and then these values were averaged as the measured D.
2.2. Operation of RSE Algorithm
The datum of a generated fractal profile is a one-dimensional sequence
,
, where
indicates the position of
i-th data-point constituting the sequence and
represents the amplitude of the
i-th data-point. In order to apply the RSE algorithm to analyze these sequences,
is first defined as below:
For each original sequence with
N data points,
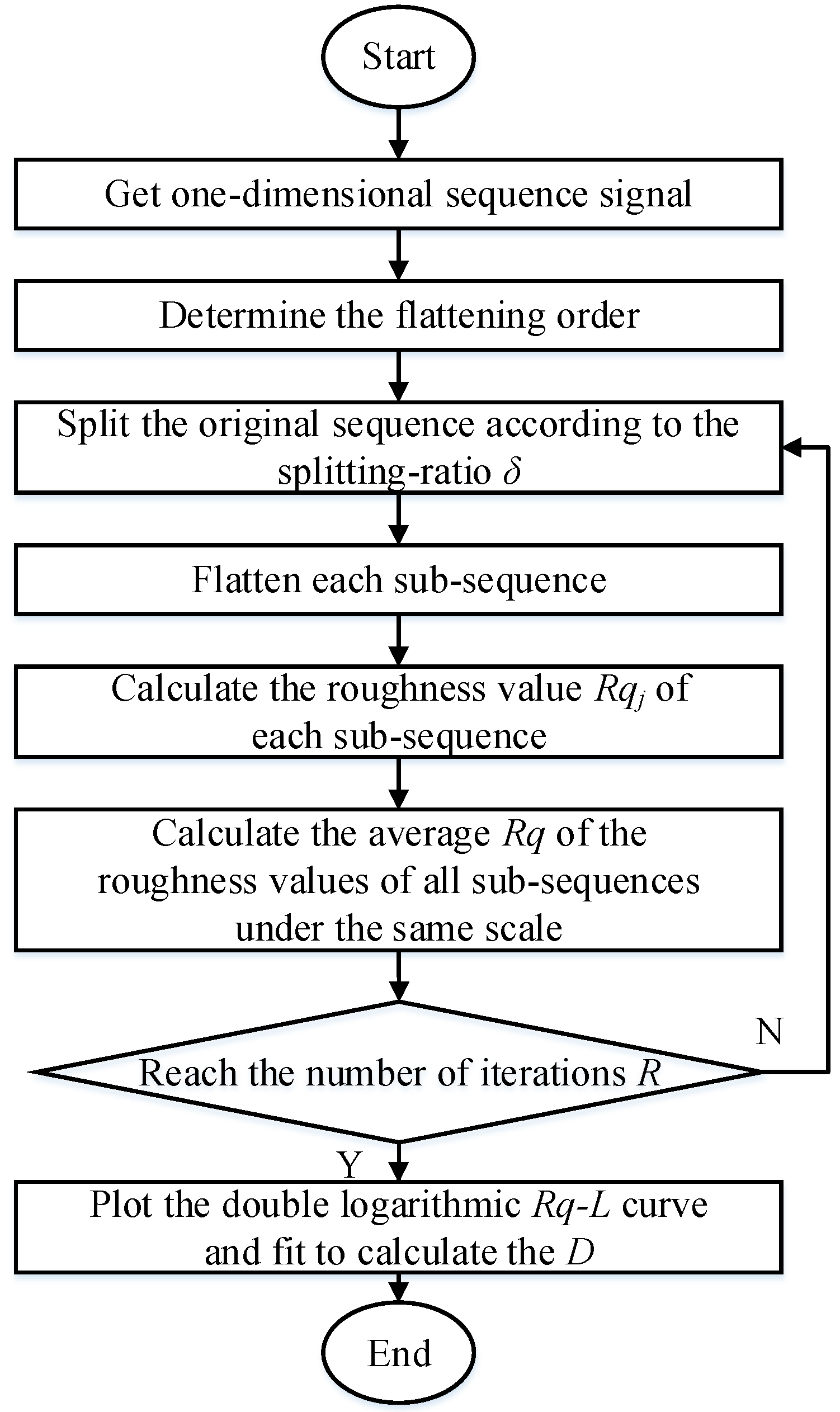
value pairs are calculated as follows, and the flowchart of the RSE algorithm is shown in
Figure 1.
First, the lengths of sub-sequence are defined as , where , , , i = 2, 3, …, p. The value of represents the reduction ratio of the sub-sequence length, which is 0.95 in this study. denoted the maximum integer value of the number in the brackets.
Second, the data pairs are obtained. A starting point in the original sequence is randomly determined, where means a random number, . Then the sub-sequence with length is extracted out of the original sequence from the starting point, and thus the sub-sequence is composed of , , …, .
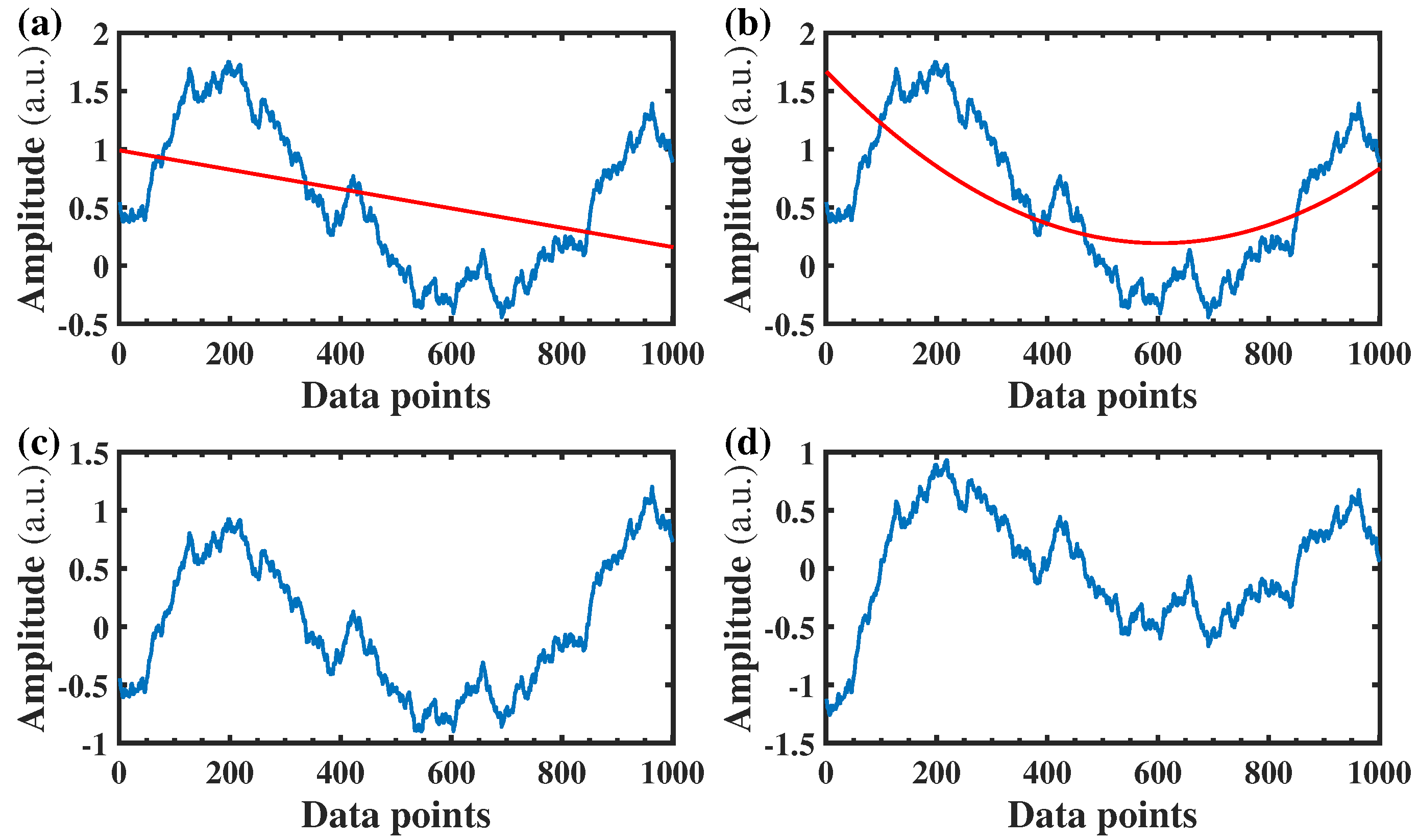
Third, the sub-sequences need to be flattened [
25,
37]. As shown in
Figure 2, a polynomial fitting with a certain order (1 or 2 in this study) is performed on the sub-sequence, and the fitted polynomial is subtracted to obtain the flattened sub-sequence, which is used to calculate
through Equation (
2). The condition with flattening would be denoted as f0, and the flattening processes with 1-order and 2-orders would be denoted as f1 and f2, respectively.
Fourth, the above operation is repeated for
R times (
in this study) and the average values of
of these sub-sequences are calculated as
. Therefore, a series of
pairs could be obtained. If the original sequence has a fractal characteristic, the
pairs would follow the power-law relationship shown in Equation (
3) [
39]. Meanwhile, the power-law relationship could enable a linear property under double-logarithm coordinates because of Equation (
4), which could be fitted to obtain the value of
D for a concerned profile.
2.3. Scaling Region Interception
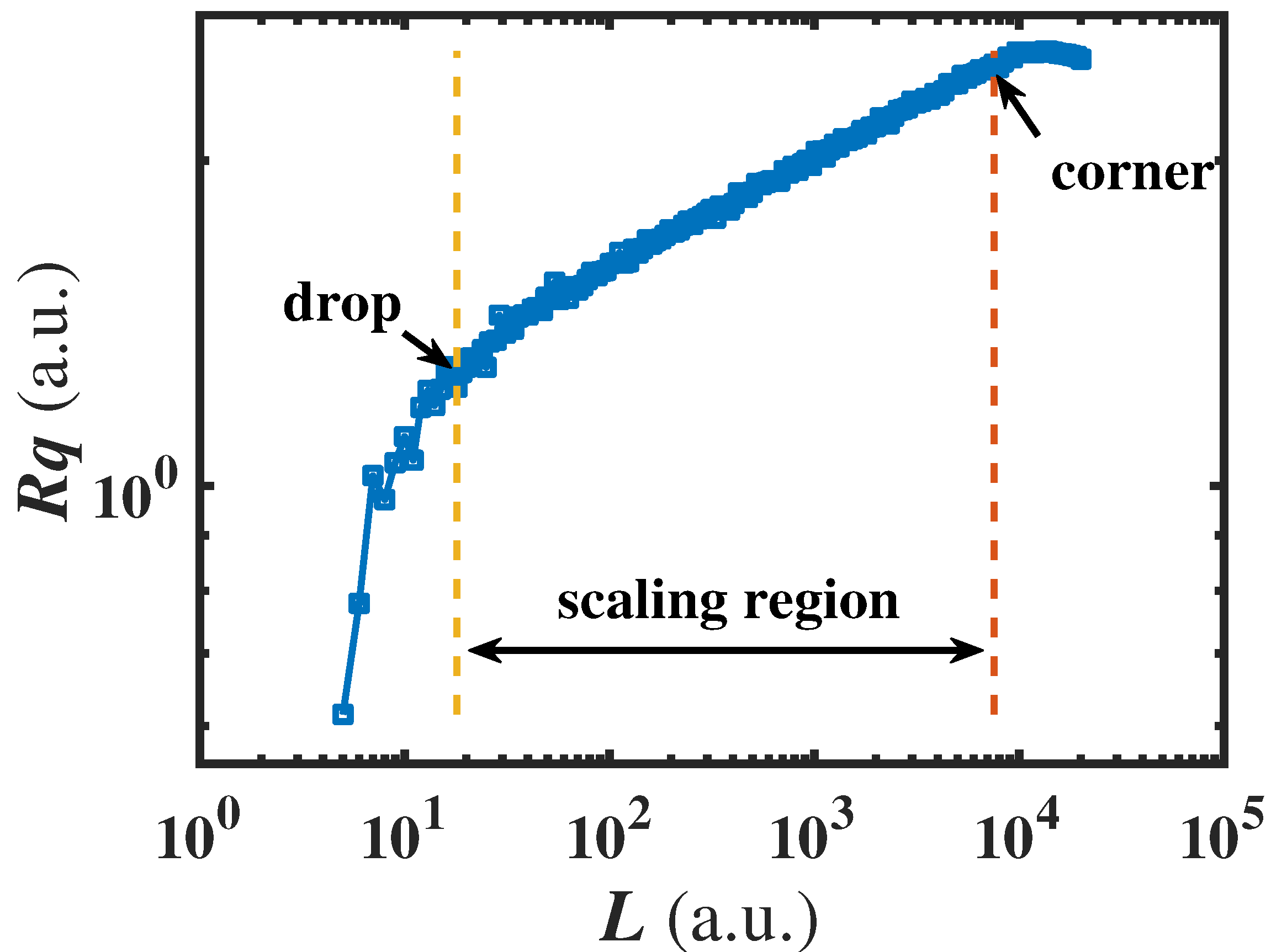
According to
Figure 1, a typical
-
L curve obtained by the RSE operation with a 2-order flattening processing is illustrated in
Figure 3. The deviation on the right (at larger
L) would be named corner phenomenon, while that on the left (at smaller
L), drop phenomenon. The location where the corner or drop began is defined as
or
. The linear part of the
-
L curve between
and
is the scaling region.
Due to the existence of corner and drop, the data fitting on the scaling region of -L curve is appropriate to acquire D rather than the global fitting on the entire curve. In our previous studies where the RSE algorithm was utilized, the data points which deviated from the scaling region were manually removed to carry out the fitting. However, the manual intervention might result in inaccuracy and inefficiency; thus, a scaling region interception method was used in this study.
This method was based on the characteristics of a scaling region in the
-
L curve, and the flowchart is shown in
Figure 4. First, a polynomial
is used to fit the entire
-
L curve. Second, the first and second derivatives (
and
) of the polynomial
are obtained. Due to the linearity of the scaling region, the corresponding
should be a constant in the region, while
should be close to 0. Therefore, the scaling region is determined according to the first criterion of
. The series of
x values in the region are marked as
, then the corresponding
values are calculated and averaged to obtain
, which could be considered as the slope of the region. Since there are always fluctuations in the actual curves, the second criterion
should also be met, and the obtained series of
x values are
, which should be a continuous segment corresponding to the targeted scaling region in the
-
L curve. In this study,
and
were used to determine
and
, thus identifying the scaling regions as shown in
Figure 5.
2.4. Ideality Improvement of W-M Function
For the purpose of improving the ideality of the W-M function, a method that reduces the value of fundamental frequency
was proposed to achieve this goal. According to Equation (
1),
was set as 1.2 in this section. Because
was a fixed value, decreasing the first item of
n could have a positive effect on the ideality of the W-M function, thus taking the first item of
n from 0 to −10, respectively, with an interval of −1. The position of drop and corner was calculated for different fractal dimensions
D from 1.1 to 1.9 using the RSE algorithm, which was based on the scaling region interception method with 1-order flattening.
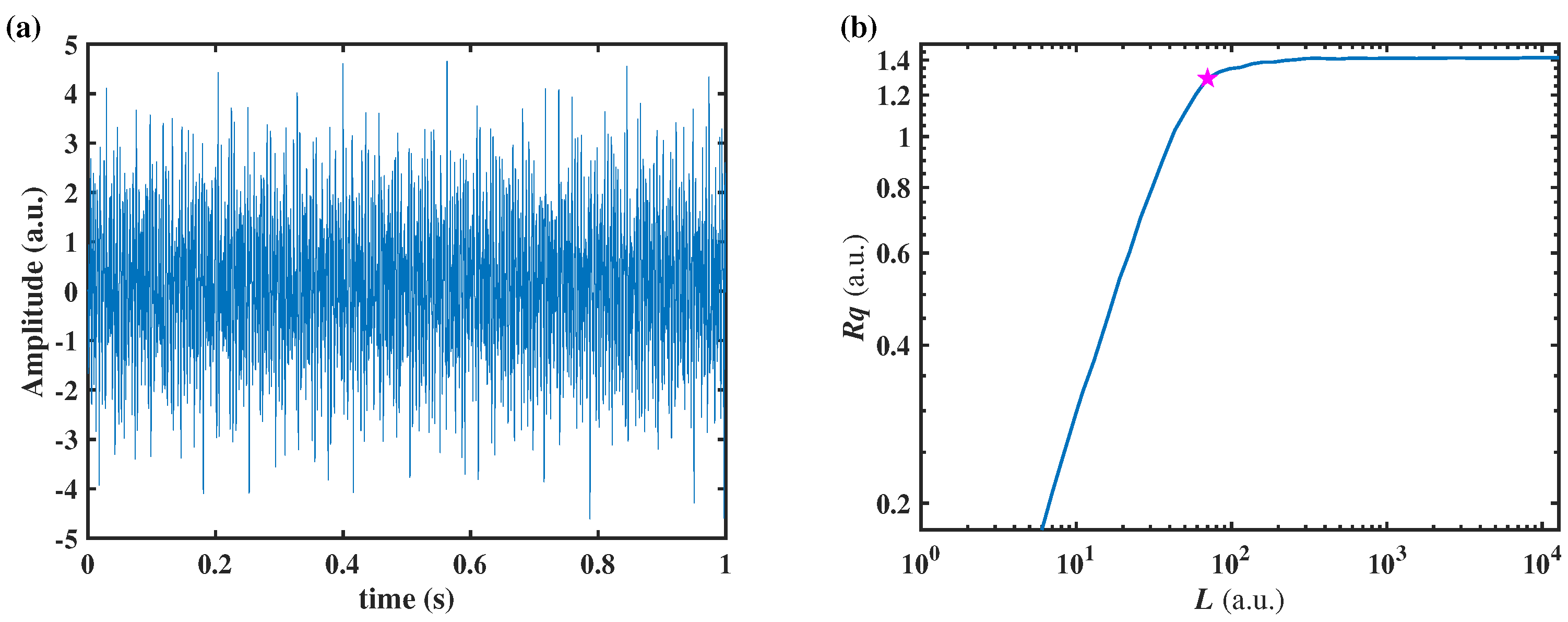
2.5. Modified Approach for Signal Simulation
In order to effectively simulate the acceleration signal of stable milling, the W-M function was modified. Equation (
5) is the improved form of the W-M function. Where
was also set as 1.2 in this section and the correction coefficient
A of the W-M function is determined according to the value of the real signal
-
L curve on the right side of the corner. Let
A = 1 and calculate the corresponding
-
L curve, then the value of
on the right side of corner position is
. Equation (
6) shows that correction coefficient
A is the quotient of the
, which is the value of the right of the corner position of the actual signal, and
, which is the value of the right of the corner position of the simulated signal. Furthermore, the value of
D is the fractal dimension calculated by the real signal. Moreover, the maximum value of
n is
M (
), and the initial value of
n is the position corresponding to the corner of the
-
L curve of the real signal, which is calculated by Equation (
7), where
is the sampling frequency, and
is the position of the corner.
4. Discussion
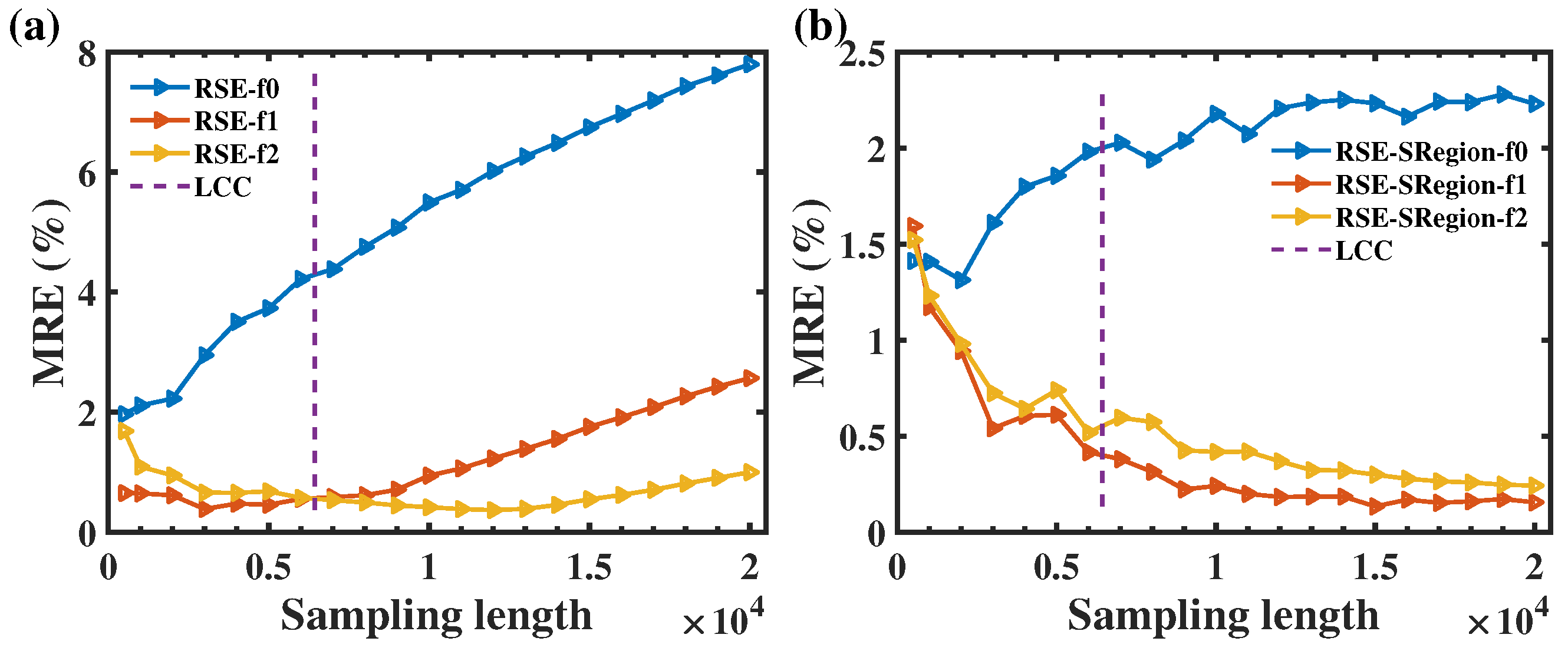
The application of the RSE algorithm with the scaling region interception method in the study of W-M function properties and scaling region length is of great significance. On the one hand, compared with our previous study [
33,
37], the results in
Section 3.3 showed that the mean relative error between the fractal dimension calculated by the scaling region interception method and the ideal fractal dimension could be as low as 0.13%. Therefore, the calculation accuracy can be effectively improved. On the other hand, the RSE algorithm with the scaling region interception method is helpful in understanding the scaling regions of various forms and their properties. According to our latest paper [
42], this method can be used for non-fractal research and is expected to have a deeper understanding of various nonlinear problems in nature.
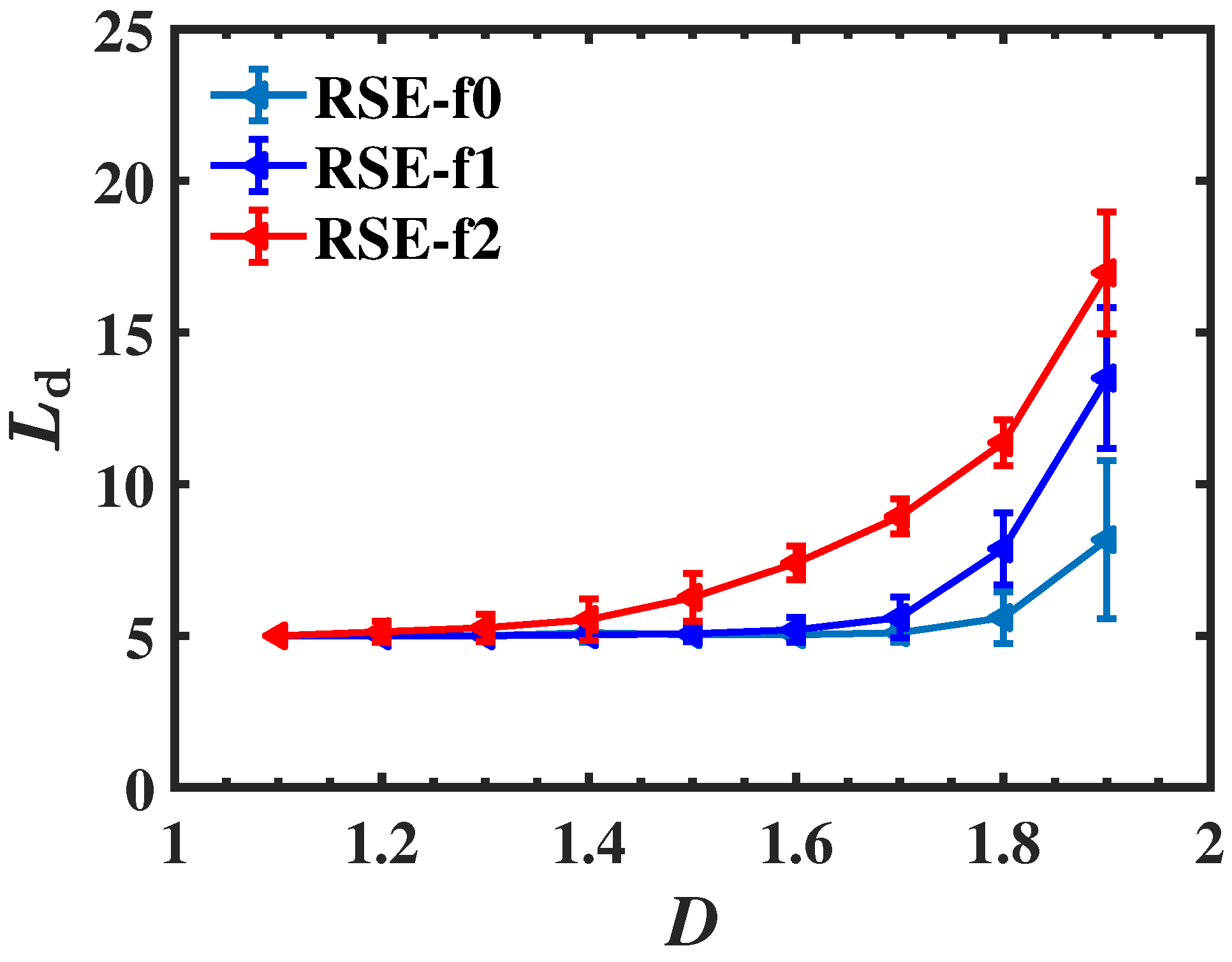
Theoretically, the scaling region should be closely correlated to the lower critical condition because of the structure of the W-M function. As shown in Equation (
1), a W-M function was superimposed by summing a series of cosine function terms, which enabled the scaling characteristics of the generated profile within a large scope of scale. However, the index of the first term could not be
in the practical application of the W-M function; thus, its scaling characteristics could be compromised by the first cosine function with the lowest frequency, which determined the lower critical condition.
The first term in
Section 2.1 was indexed as
, and the term expression was
, whose wavelength is equal to
. If the concerned scope to analyze the property of the W-M function was defined as
T, the surpassing
would lead to a repetition of the lowest-frequency information of
in the scope beyond
. If there was no item with a lower frequency, the fractal nature of the function could not be maintained. Therefore, to lead to more lowest-frequency information in the scope beyond the wavelength, reducing the first term could achieve this goal so that the ideality of the W-M function could be improved.
Such an approach to the lower critical condition could be reflected in the
-
L curves by the behavior of
shown in
Figure 8. Because
, the length of the scaling region (
-
) is mainly determined by
. Therefore, the relationship between lower critical condition and corner phenomenon should be analyzed. When the sampling length increased,
was first raised and then stabilized; thus, the sampling length, which could stabilize
was a critical parameter found in this study.
However, the sampling lengths that could stabilize
are not equal to the length corresponding to the lower critical condition (LCC = 6434). Moreover, the flattening order has a significant influence, as shown in
Table 1, where the average folds relative to LCC of the sampling lengths which could stabilize
were 0.81, 1.28 and 1.64, respectively. When 0-order flattening was used, the stabilization of
could occur if the sampling length was near LCC. While 1-order or 2-order flattening was used, the stabilization occurred after the sampling length surpassed LCC.
The above influence of the flattening order could enable an improvement in the accuracy of the RSE algorithm, as shown in
Figure 11, because the sampling length that could stabilize
could be enlarged by using the higher flattening order, which indicates a higher efficiency of sampling length. Moreover, there is another important reason for the accuracy improvement, which could be observed in the slope difference of the curves within the scope of small sampling lengths in
Figure 10. The slopes are listed in
Table 2, which could be summarized as the percentages of data points in the scaling region under flattening with 0-order, 1-order, and 2-order were 50%, 62% and 75%, respectively. Therefore, the efficiency of the sampling length is also significantly enhanced by increasing the flattening order, which improves the accuracy of data fitting to calculate
D.
As for signal simulation, the key to the modified W-M function is to determine the index of the first term. According to Equation (
7), the value of
n corresponding to a point on the
-
L curve is inversely proportional to the abscissa of this point. Therefore, since the corner is a point to distinguish the fractal region and non-fractal region, the initial value of
n of the simulated signal is determined by the value of
n corresponding to the corner of a real signal, and then the lowest frequency is determined so that the
-
L curve of the simulated signal has the same corner position as the real signal. In addition, since the
D value in Equation (
5) was the
D value of the real signal, the
-
L curve of the simulated signal and the real signal had the same slope on the left side of the corner. Moreover, the value of the correction coefficient
A was adjusted so that the value of the right side of the corner of the
-
L curve for the simulated signal was the same as the real signal.