Dynamic Analysis of a Novel 3D Chaotic System with Hidden and Coexisting Attractors: Offset Boosting, Synchronization, and Circuit Realization
Abstract
:1. Introduction
2. Mathematical Model and Its Properties
3. Dynamics of Novel Double-Wing Chaotic System
3.1. Bifurcation Diagram and Lyapunov Exponents
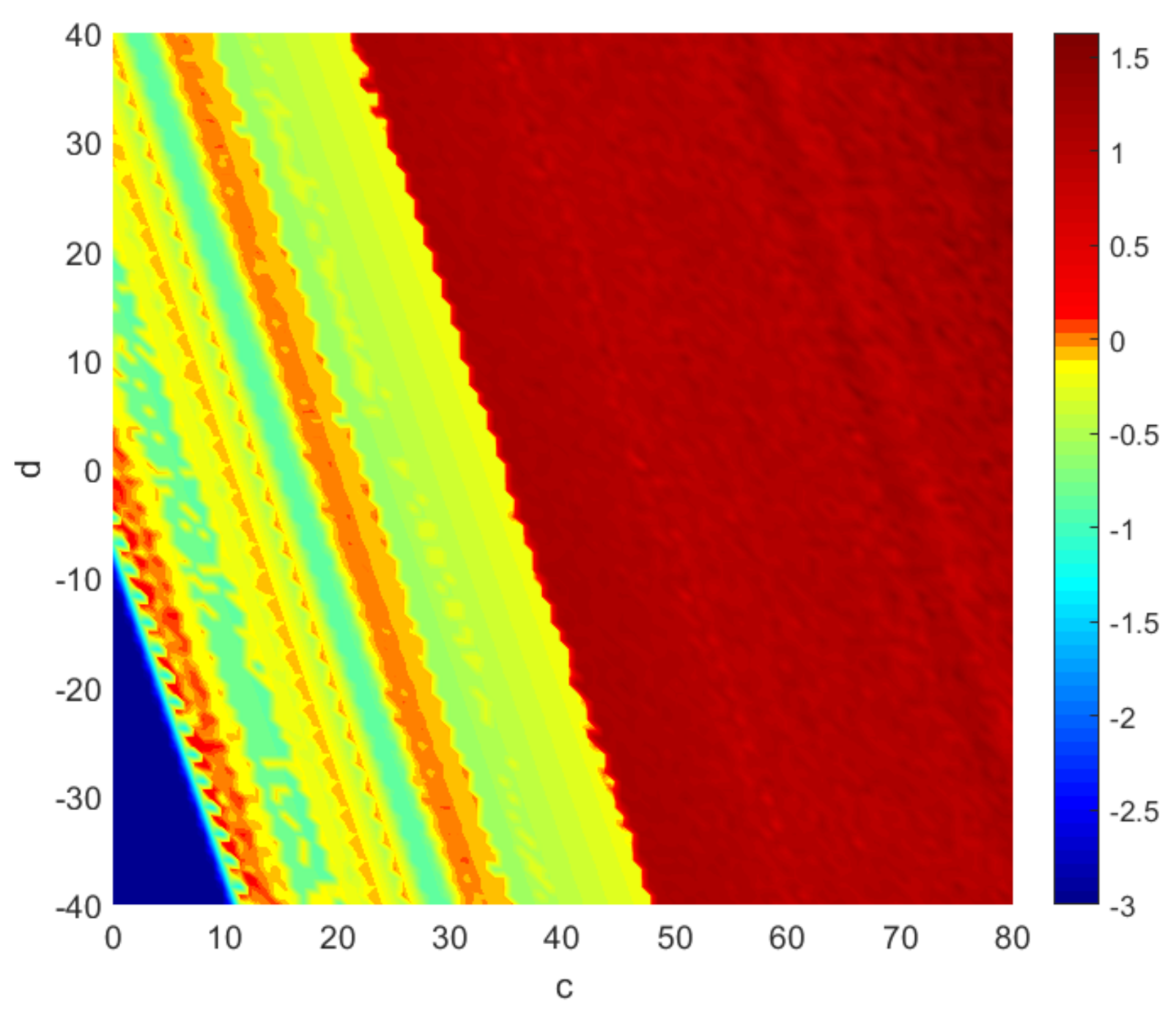
3.2. Two-Parameter Lyapunov Exponents Analysis
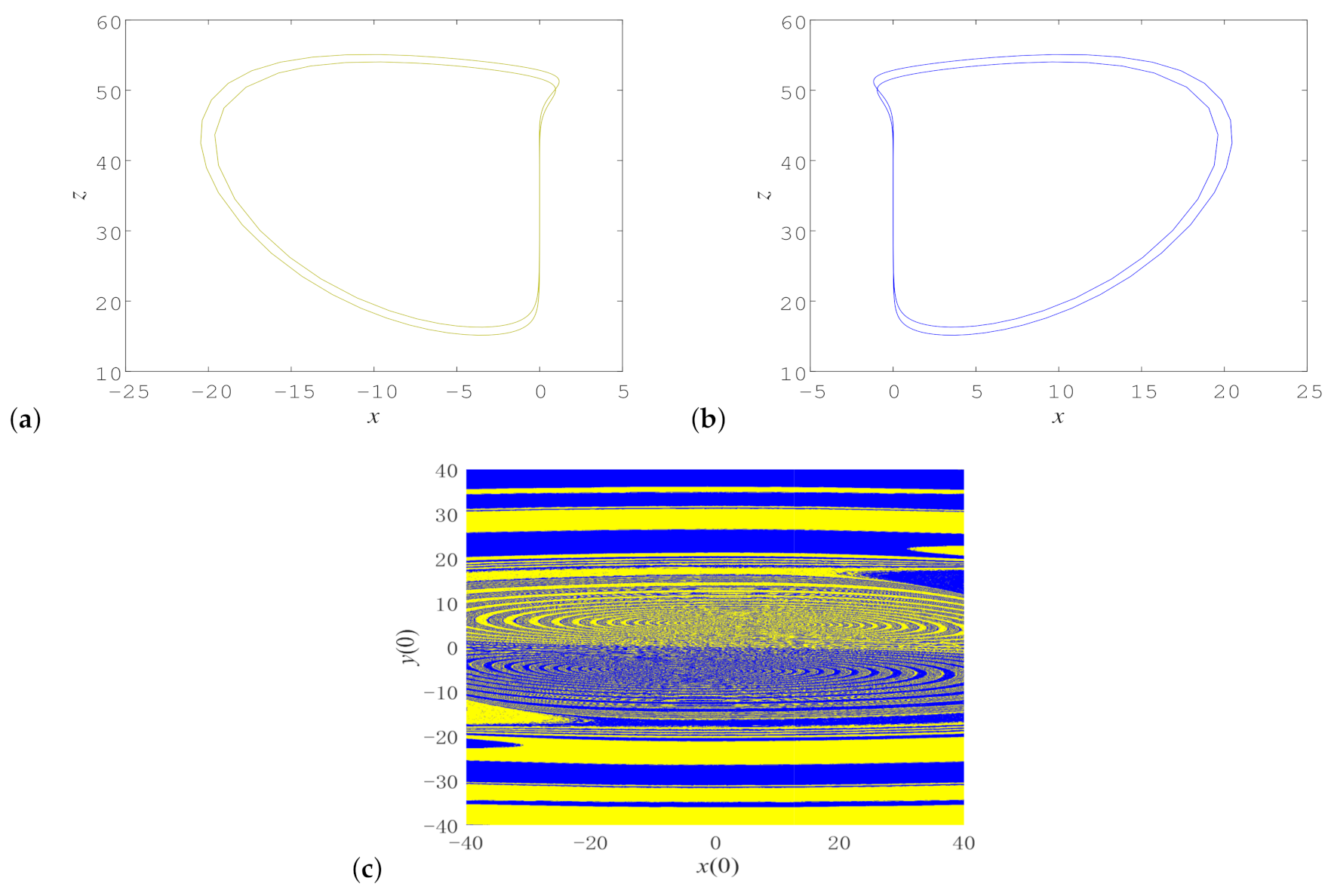
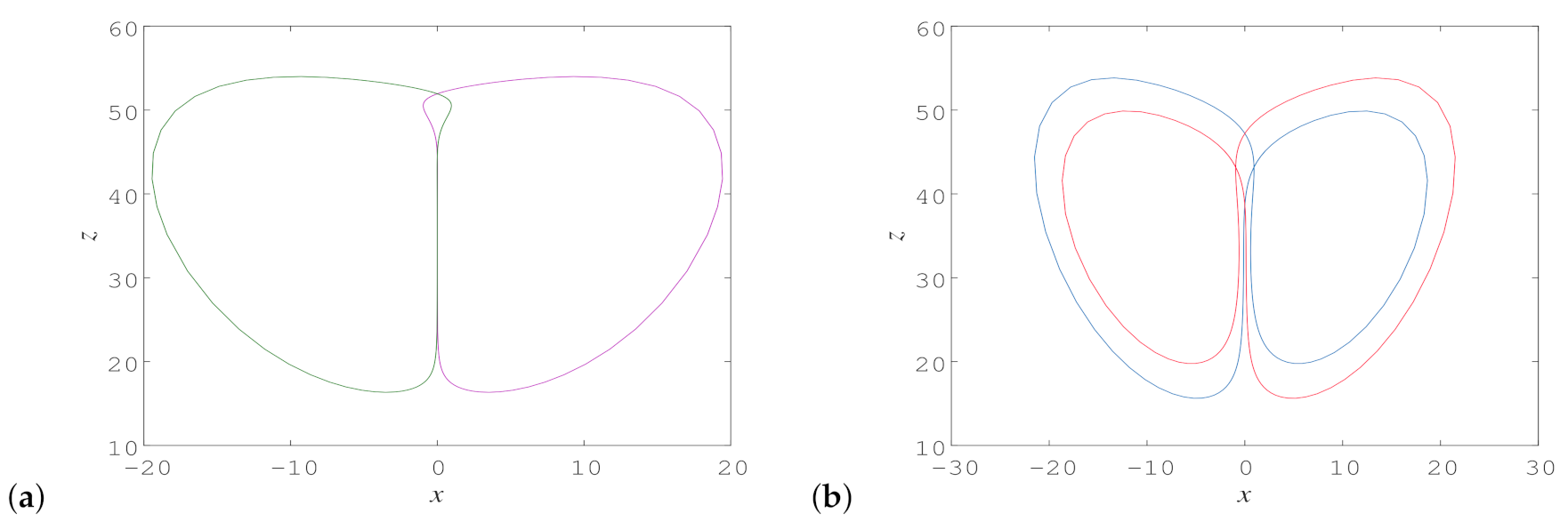
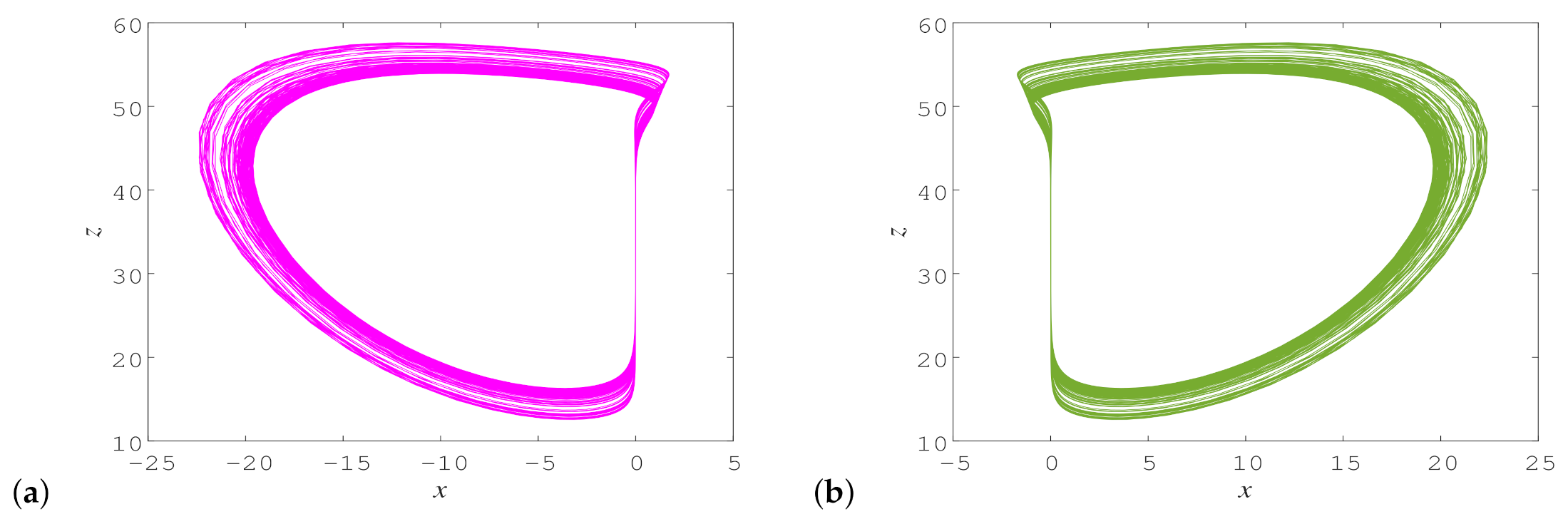
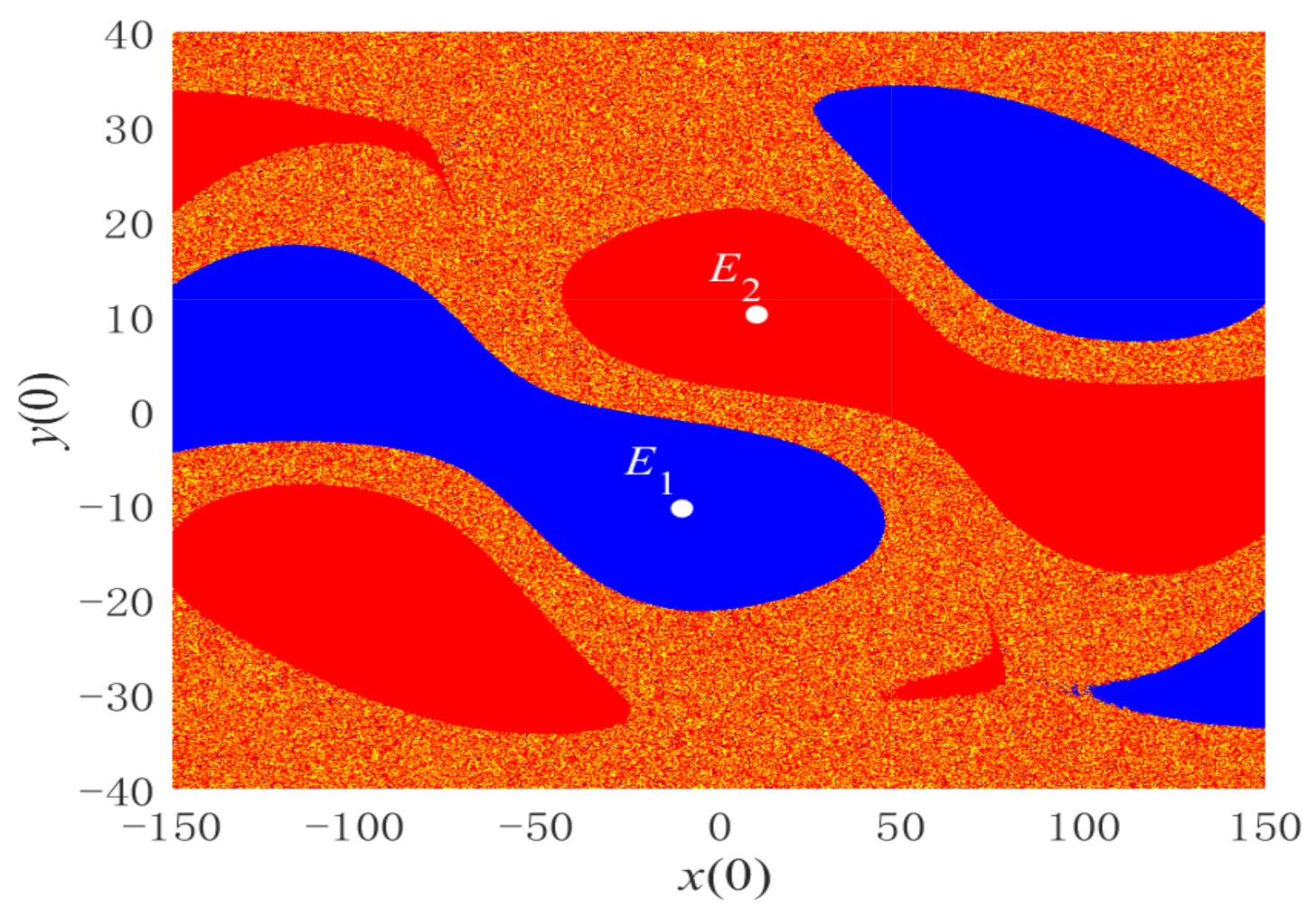
3.3. Coexisting Attractors and Basins of Attraction
3.4. Impact of Constant Term d
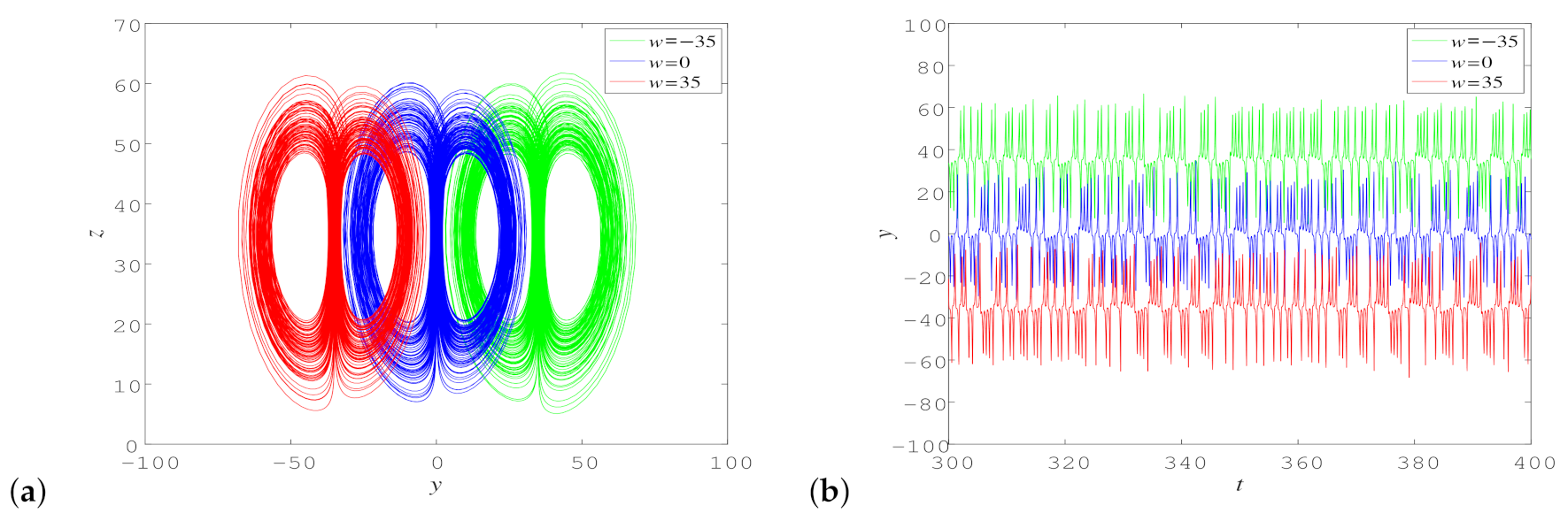
3.5. Offset Boosting Control
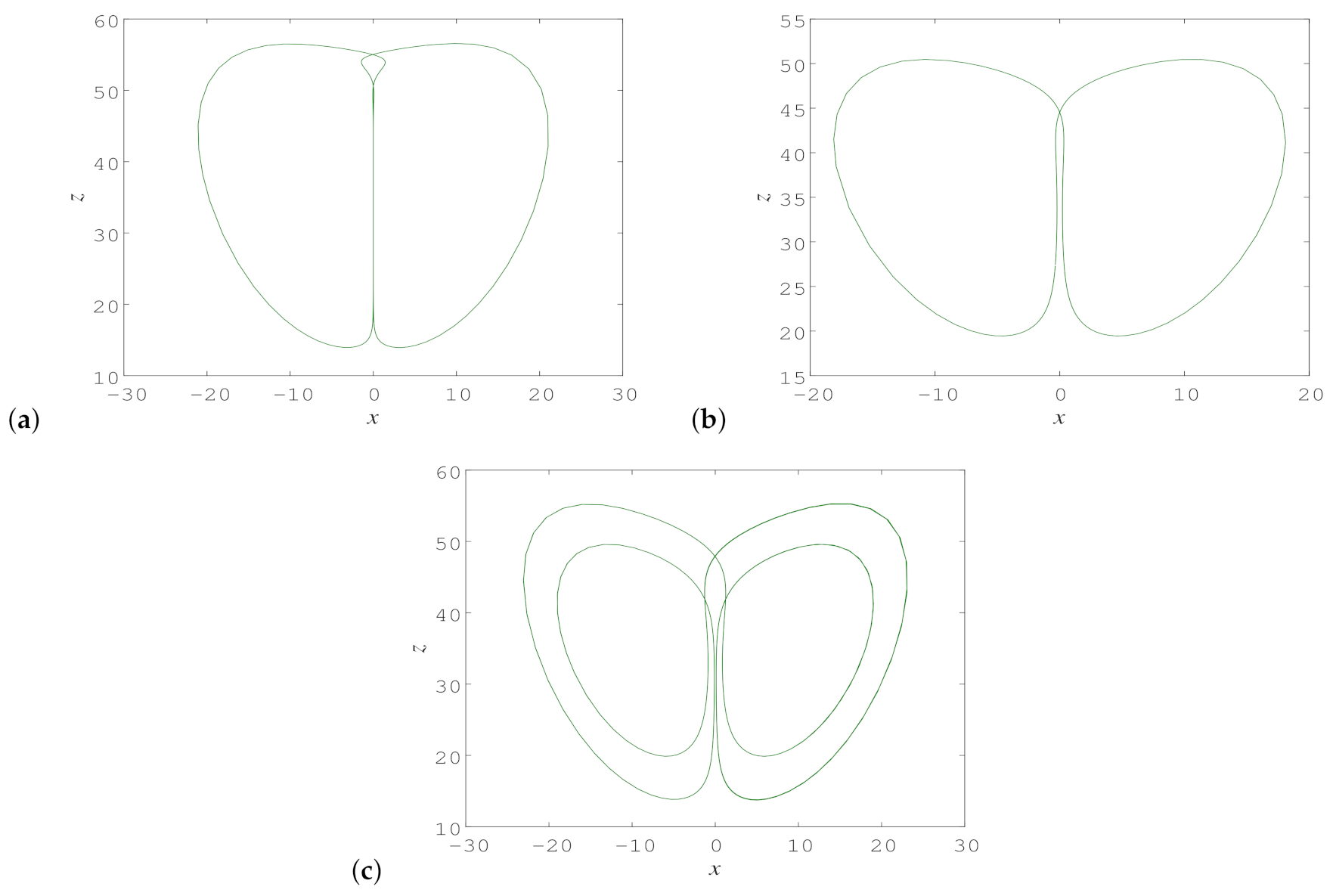
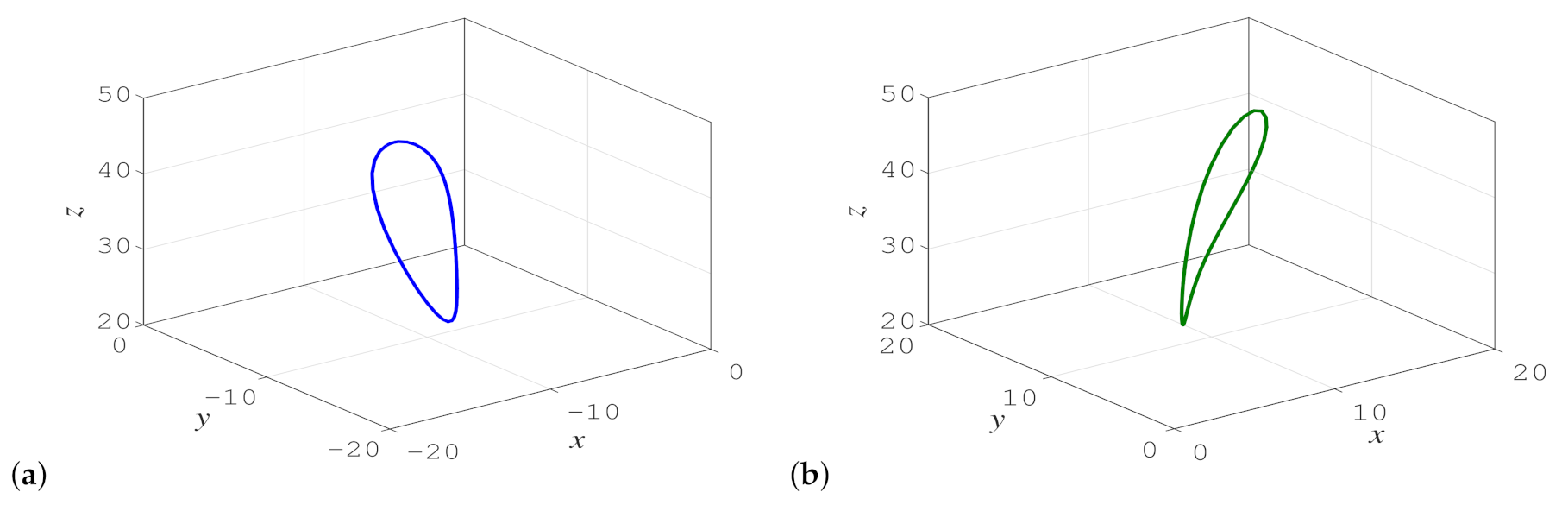
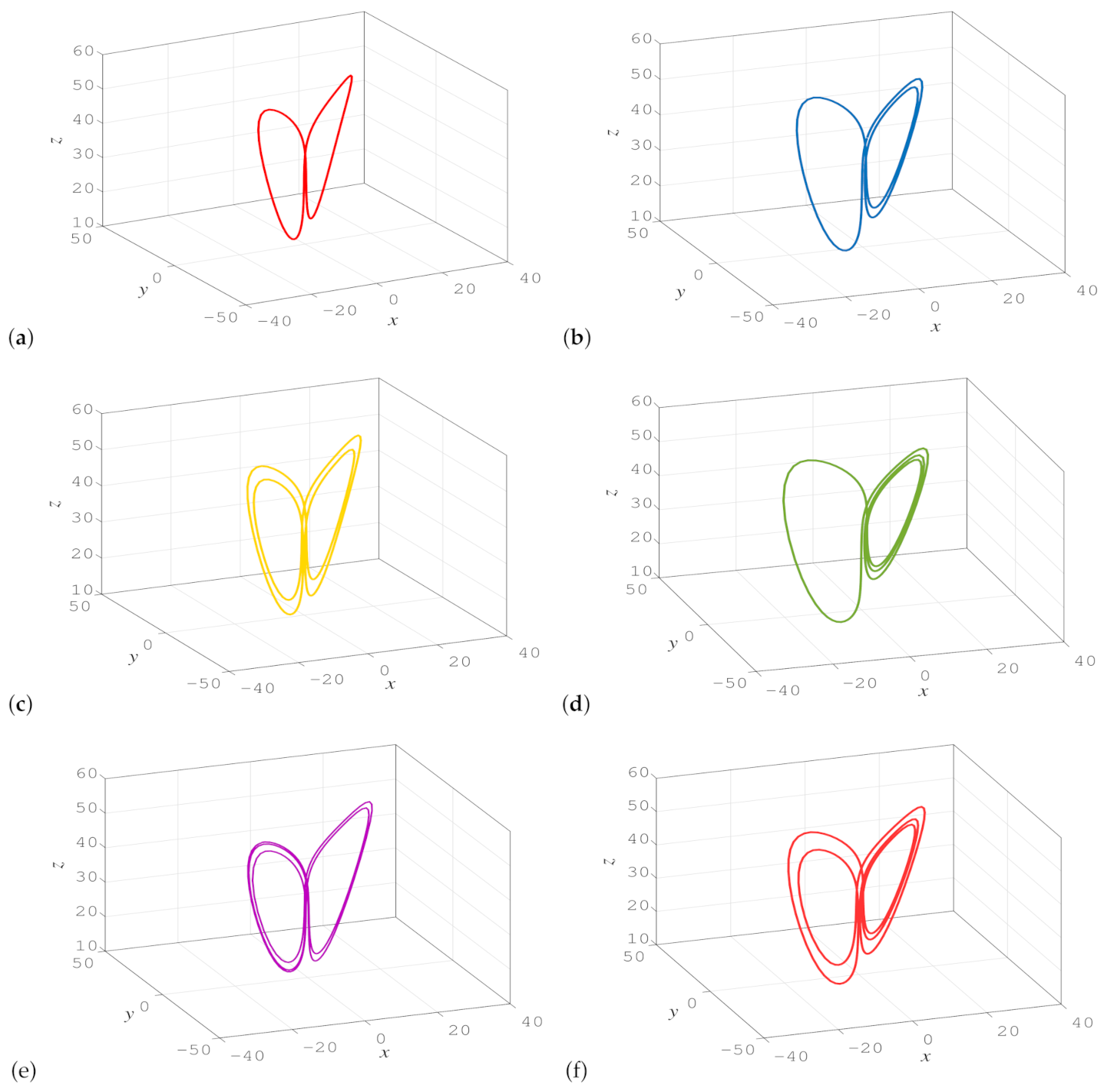
4. One-Dimensional Symbolic Dynamics for Unstable Cycles Embedded in Hidden Chaotic Attractor
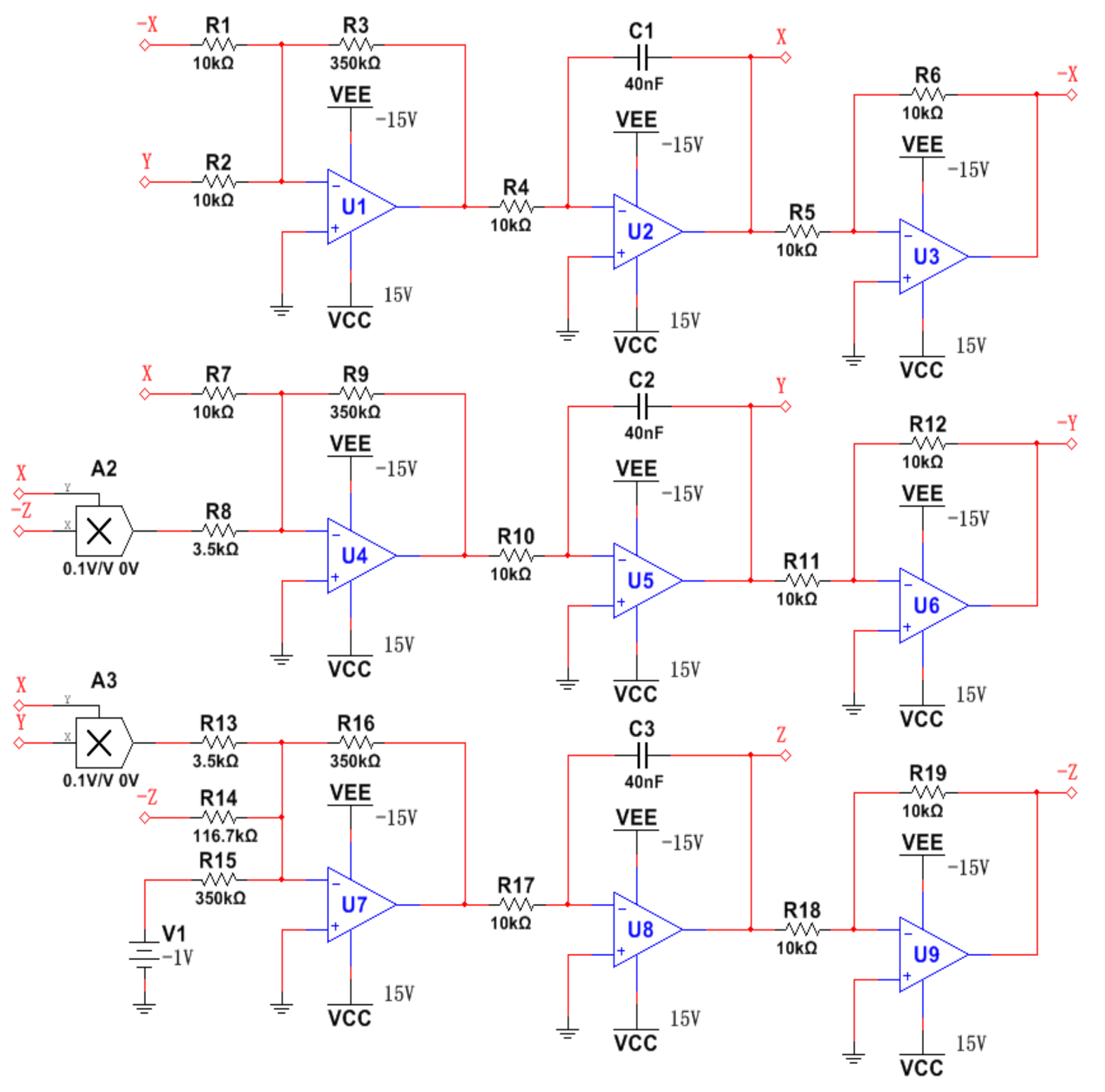
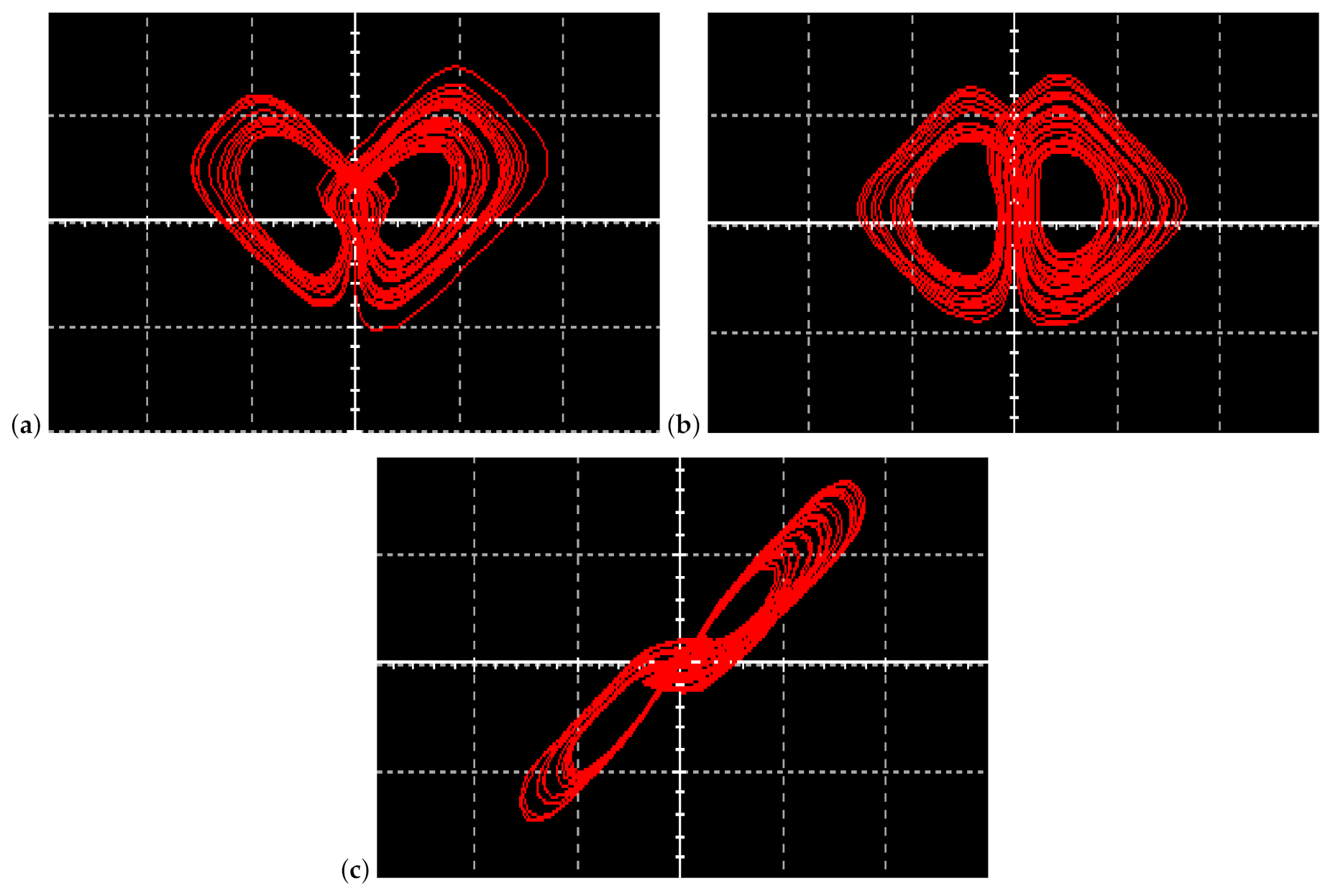
5. Circuit Implementation
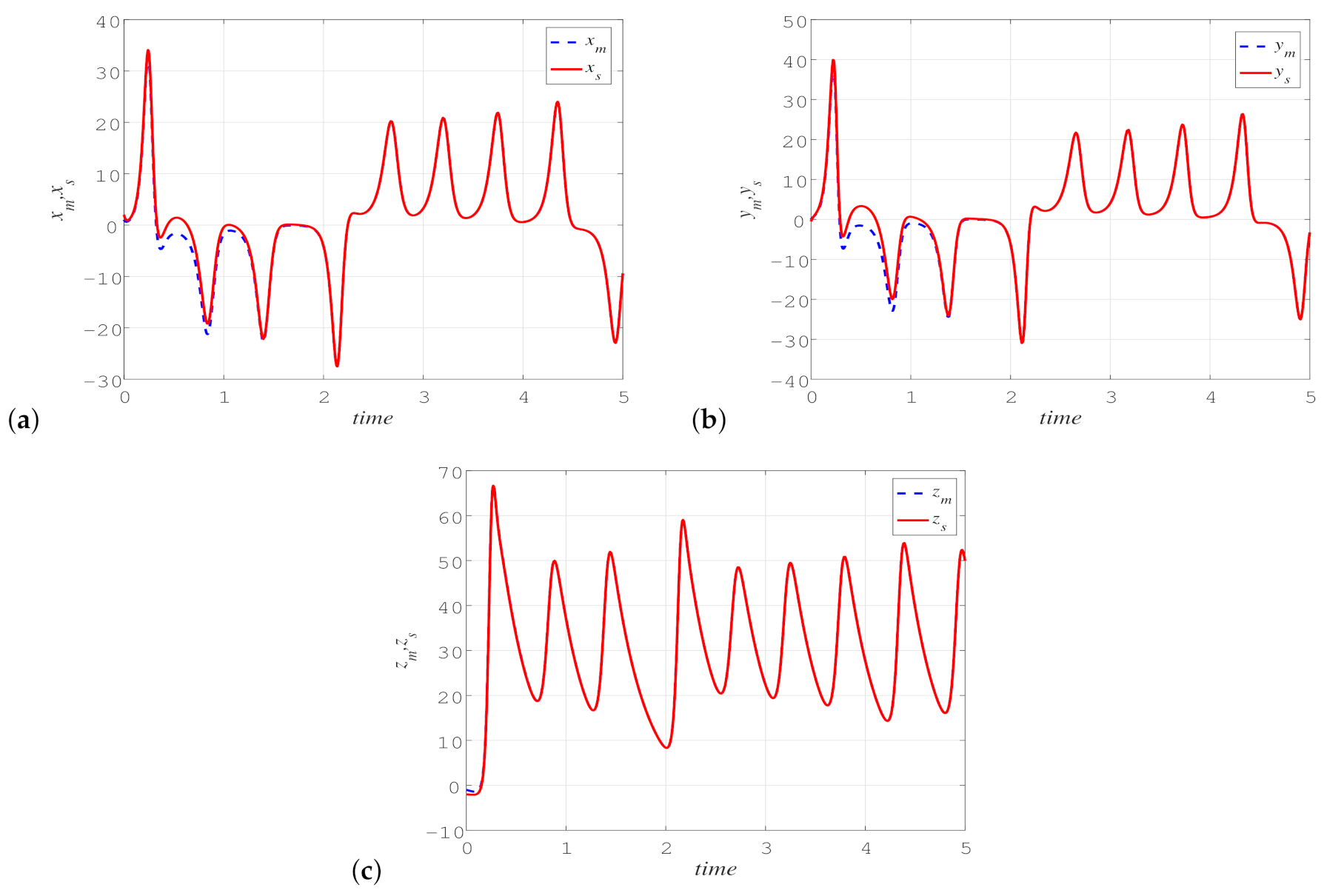
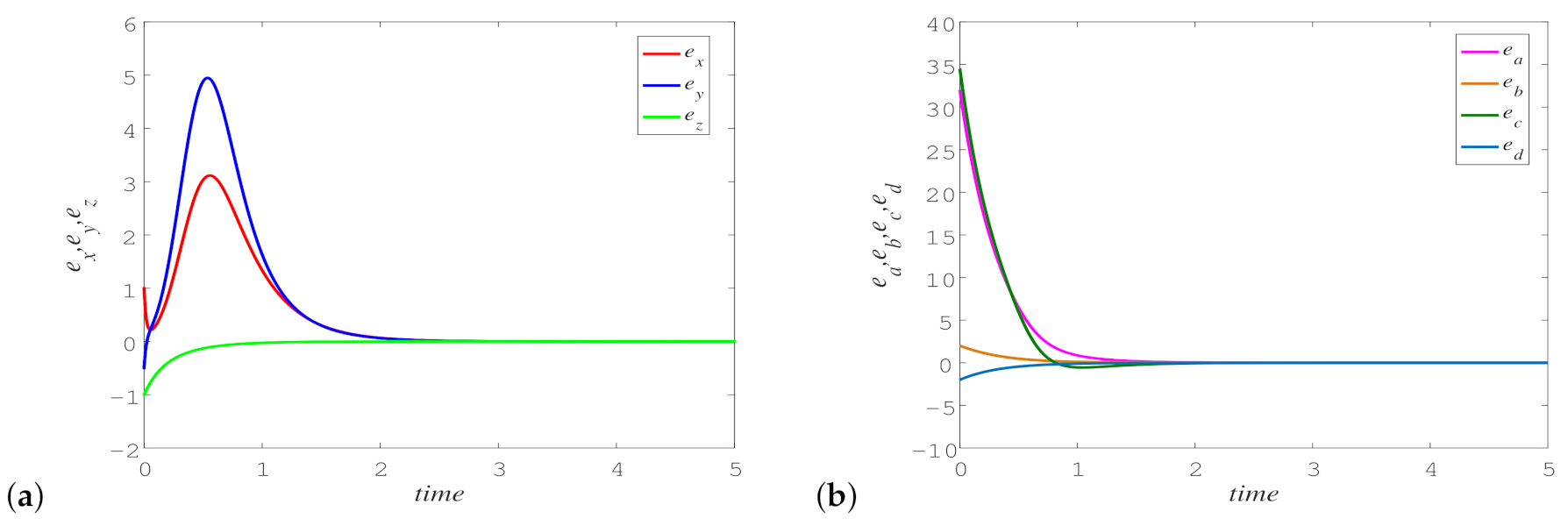
6. Adaptive Synchronization of Novel Three-Dimensional Chaotic System
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Chua, L.O.; Itoh, M.; Kocarev, L.; Eckert, K. Chaos synchronization in Chua’s circuit. Int. J. Bifurcat. Chaos 1993, 3, 93–108. [Google Scholar]
- Sprott, J.C. Some simple chaotic flows. Phys. Rev. E 1994, 50, 647–650. [Google Scholar] [CrossRef] [PubMed]
- Kuate, P.D.K.; Lai, Q.; Fotsin, H. Dynamics, synchronization and electronic implementations of a new Lorenz-like chaotic system with nonhyperbolic equilibria. Int. J. Bifurcat. Chaos 2019, 29, 1950197. [Google Scholar] [CrossRef]
- Negou, A.N.; Kengne, J. Dynamic analysis of a unique jerk system with a smoothly adjustable symmetry and nonlinearity: Reversals of period doubling, offset boosting and coexisting bifurcations. Int. J. Electron. Commun. 2018, 90, 1–19. [Google Scholar] [CrossRef]
- Ma, C.; Mou, J.; Xiong, L.; Banerjee, S.; Liu, T.; Han, X. Dynamical analysis of a new chaotic system: Asymmetric multistability, offset boosting control and circuit realization. Nonlinear Dyn. 2021, 103, 2867–2880. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Perseus Books: Reading, MA, USA, 1994. [Google Scholar]
- Wang, X.; Kuznetsov, N.V.; Chen, G. (Eds.) Chaotic Systems with Multistability and Hidden Attractors; Emergence, Complexity and Computation; Springer: Cham, Switzerland, 2021; Volume 40, p. 9. [Google Scholar]
- Deng, Q.; Wang, C.; Wu, Y.; Lin, H. Hidden multiwing chaotic attractors with multiple stable equilibrium points. Circuit World 2022. ahead-of-print. [Google Scholar] [CrossRef]
- Dong, C. Dynamics, periodic orbit analysis, and circuit implementation of a new chaotic system with hidden attractor. Fractal Fract. 2022, 6, 190. [Google Scholar] [CrossRef]
- Yang, Q.; Wei, Z.; Chen, G. An unusual 3d autonomous quadratic chaotic system with two stable node-foci. Int. J. Bifurcat. Chaos 2010, 20, 1061–1083. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C. Simple chaotic flows with a line equilibrium. Chaos Soliton. Fract. 2013, 57, 79–84. [Google Scholar] [CrossRef]
- Ma, J.; Chen, Z.; Wang, Z.; Zhang, Q. A four-wing hyper-chaotic attractor generated from a 4-D memristive system with a line equilibrium. Nonlinear Dyn. 2015, 81, 1275–1288. [Google Scholar] [CrossRef]
- Kingni, S.T.; Pham, V.T.; Jafari, S.; Woafo, P. A chaotic system with an infinite number of equilibrium points located on a line and on a hyperbola and its fractional-order form. Chaos Soliton. Fract. 2017, 99, 209–218. [Google Scholar] [CrossRef]
- Pham, V.T.; Jafari, S.; Volos, C.; Kapitaniak, T. A gallery of chaotic systems with an infinite number of equilibrium points. Chaos Soliton. Fract. 2016, 93, 58–63. [Google Scholar] [CrossRef]
- Huynh, V.V.; Khalaf, A.J.M.; Alsaedi, A.; Hayat, T.; Abdolmohammadi, H.R. A new memristive chaotic flow with a line of equilibria. Eur. Phys. J. Spec. Top. 2019, 228, 2339–2349. [Google Scholar] [CrossRef]
- Nazarimehr, F.; Sprott, J.C. Investigating chaotic attractor of the simplest chaotic system with a line of equilibria. Eur. Phys. J. Spec. Top. 2020, 229, 1289–1297. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Pham, V.T.; Volos, C.K. A 5-D hyperchaotic Rikitake dynamo system with hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1575–1592. [Google Scholar] [CrossRef]
- Chowdhury, S.N.; Ghosh, D. Hidden attractors: A new chaotic system without equilibria. Eur. Phys. J. Spec. Top. 2020, 229, 1299–1308. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, G.; Kuznetsov, N.V.; Li, H. Generating grid chaotic sea from system without equilibrium point. Commun. Nonlinear Sci. Numer. Simul. 2022, 107, 106194. [Google Scholar] [CrossRef]
- Dong, C.; Wang, J. Hidden and coexisting attractors in a novel 4D hyperchaotic system with no equilibrium point. Fractal Fract. 2022, 6, 306. [Google Scholar] [CrossRef]
- Almatroud, A.O.; Matouk, A.E.; Mohammed, W.W.; Iqbal, N.; Alshammari, S. Self-excited and hidden chaotic attractors in Matouks’s hyperchaotic systems. Discrete Dyn. Nat. Soc. 2022, 2022, 6458027. [Google Scholar] [CrossRef]
- Yan, H.; Jiang, J.; Hong, L. The birth of a hidden attractor through boundary crisi. Int. J. Bifurcat. Chaos 2022, 32, 2230005. [Google Scholar] [CrossRef]
- Pham, V.T.; Jafari, S.; Volos, C.; Fortuna, L. Simulation and experimental implementation of a line–equilibrium system without linear term. Chaos Soliton. Fract. 2019, 120, 213–221. [Google Scholar] [CrossRef]
- Tapche, R.W.; Njitacke, Z.T.; Kengne, J.; Pelap, F.B. Complex dynamics of a novel 3D autonomous system without linear terms having line of equilibria: Coexisting bifurcations and circuit design. Analog Integr. Circ. Sig. Process. 2020, 103, 57–71. [Google Scholar] [CrossRef]
- Tan, Q.; Zeng, Y.; Li, Z. A simple inductor-free memristive circuit with three line equilibria. Nonlinear Dyn. 2018, 94, 1585–1602. [Google Scholar] [CrossRef]
- Tian, H.; Wang, Z.; Zhang, H.; Cao, Z.; Zhang, P. Dynamical analysis and fixed-time synchronization of a chaotic system with hidden attractor and a line equilibrium. Eur. Phys. J. Spec. Top. 2022, 231, 2455–2466. [Google Scholar] [CrossRef]
- Zeng, D.; Li, Z.; Ma, M.; Wang, M. Generating self-excited and hidden attractors with complex dynamics in a memristor-based Jerk system. Indian J. Phys. 2022, 1–15. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C. Multiscroll hyperchaotic system with hidden attractors and its circuit implementation. Int. J. Bifurcat. Chaos 2019, 29, 1950117. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C. Multistability in the Lorenz system: A broken butterfly. Int. J. Bifurcat. Chaos 2014, 24, 1450131. [Google Scholar] [CrossRef]
- Doubla, I.S.; Ramakrishnan, B.; Tabekoueng, Z.N.; Kengne, J.; Rajagopal, K. Infinitely many coexisting hidden attractors in a new hyperbolic-type memristor-based HNN. Eur. Phys. J. Spec. Top. 2022, 231, 2371–2385. [Google Scholar] [CrossRef]
- Lai, Q.; Wang, Z. Dynamical analysis, FPGA implementation and synchronization for secure communication of new chaotic system with hidden and coexisting attractors. Mod. Phys. Lett. B 2022, 36, 2150538. [Google Scholar] [CrossRef]
- Ahmadi, A.; Rajagopal, K.; Alsaadi, F.E.; Pham, V.T.; Alsaadi, F.E.; Jafari, S. A Novel 5D chaotic system with extreme multi-stability and a line of equilibrium and its engineering applications: Circuit design and FPGA implementation. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 59–67. [Google Scholar] [CrossRef]
- Bao, J.; Chen, D. Coexisting hidden attractors in a 4D segmented disc dynamo with one stable equilibrium or a line equilibrium. Chin. Phys. B 2017, 26, 080201. [Google Scholar] [CrossRef]
- Dang, X.Y.; Li, C.B.; Bao, B.C.; Wu, H.G. Complex transient dynamics of hidden attractors in a simple 4D system. Chin. Phys. B 2015, 24, 050503. [Google Scholar] [CrossRef]
- Bayani, A.; Rajagopal, K.; Khalaf, A.J.M.; Jafari, S.; Leutcho, G.D.; Kengne, J. Dynamical analysis of a new multistable chaotic system with hidden attractor: Antimonotonicity, coexisting multiple attractors, and offset boosting. Phys. Lett. A 2019, 383, 1450–1456. [Google Scholar] [CrossRef]
- Wen, J.; Feng, Y.; Tao, X.; Cao, Y. Dynamical analysis of a new chaotic system: Hidden attractor, coexisting-attractors, offset boosting, and DSP realization. IEEE Access 2021, 9, 167920–167927. [Google Scholar] [CrossRef]
- Pham, V.T.; Volos, C.; Jafari, S.; Kapitaniak, T. Coexistence of hidden chaotic attractors in a novel no-equilibrium system. Nonlinear Dyn. 2017, 87, 2001–2010. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, G. A chaotic system with one saddle and two stable node-foci. Int. J. Bifurcat. Chaos 2008, 18, 1393–1414. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Hislop, P.D.; Sigal, I.M. The general theory of spectral stability. In Introduction to Spectral Theory; Applied Mathematical Sciences; Springer: New York, NY, USA, 1996; Volume 113. [Google Scholar]
- Zhou, L.; You, Z.; Tang, Y. A new chaotic system with nested coexisting multiple attractors and riddled basins. Chaos Soliton. Fract. 2021, 148, 111057. [Google Scholar] [CrossRef]
- Sambas, A.; Vaidyanathan, S.; Zhang, S.; Zeng, Y.; Mohamed, M.A.; Mamat, M. A new double-wing chaotic system with coexisting attractors and line equilibrium: Bifurcation analysis and electronic circuit simulation. IEEE Access 2019, 7, 115454–115462. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, L.; Liu, J.; Guo, Q.; Du, X. A new method of constructing cyclic symmetric conservative chaotic systems and improved offset boosting control. Chaos Soliton. Fract. 2022, 158, 112103. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C.; Liu, Y.; Gu, Z.; Zhang, J. Offset boosting for breeding conditional symmetry. Int. J. Bifurcat. Chaos 2018, 28, 1850163. [Google Scholar] [CrossRef]
- Liu, X.C.; Tu, Q. Coexisting and hidden attractors of memristive chaotic systems with and without equilibria. Eur. Phys. J. Plus 2022, 137, 516. [Google Scholar] [CrossRef]
- Hao, B.L.; Zheng, W.M. Applied Symbolic Dynamics and Chaos; World Scientic: Singapore, 1998; pp. 11–13. [Google Scholar]
- Lan, Y.; Cvitanović, P. Variational method for finding periodic orbits in a general flow. Phys. Rev. E 2004, 69, 016217. [Google Scholar] [CrossRef]
- Dong, C.; Lan, Y. Organization of spatially periodic solutions of the steady Kuramoto–Sivashinsky equation. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2140–2153. [Google Scholar] [CrossRef]
- Dong, C. Topological classification of periodic orbits in the Kuramoto–Sivashinsky equation. Mod. Phys. Lett. B 2018, 32, 1850155. [Google Scholar] [CrossRef]
- Dong, C. Periodic orbits of diffusionless Lorenz system. Acta Phys. Sin. 2018, 67, 240501. [Google Scholar] [CrossRef]
- Dong, C.; Liu, H.; Li, H. Unstable periodic orbits analysis in the generalized Lorenz–type system. J. Stat. Mech. 2020, 2020, 073211. [Google Scholar] [CrossRef]
- Dong, C.; Jia, L.; Jie, Q.; Li, H. Symbolic encoding of periodic orbits and chaos in the Rucklidge system. Complexity 2021, 2021, 4465151. [Google Scholar] [CrossRef]
- Dong, C.; Liu, H.; Jie, Q.; Li, H. Topological classification of periodic orbits in the generalized Lorenz-type system with diverse symbolic dynamics. Chaos Soliton. Fract. 2022, 154, 111686. [Google Scholar] [CrossRef]
- Sene, N. On the modeling and numerical discretizations of a chaotic system via fractional operators with and without singular kernels. Math. Sci. 2022, 1–21. [Google Scholar] [CrossRef]
- Hammouch, Z.; Yavuz, M.; Ödemir, N. Numerical solutions and synchronization of a variable-order fractional chaotic system. Math. Model. Numer. Simul. Appl. 2021, 1, 11–23. [Google Scholar] [CrossRef]
- Gao, X.J.; Cheng, M.F.; Hu, H.P. Adaptive impulsive synchronization of uncertain delayed chaotic system with full unknown parameters via discrete-time drive signals. Complexity 2016, 21, 43–51. [Google Scholar] [CrossRef]
- Azar, A.T.; Volos, C.; Gerodimos, N.A.; Tombras, G.S.; Pham, V.T.; Radwan, A.G.; Vaidyanathan, S.; Ouannas, A.; Munoz-Pacheco, J.M. A novel chaotic system without equilibrium: Dynamics, synchronization, and circuit realization. Complexity 2017, 2017, 7871467. [Google Scholar] [CrossRef]
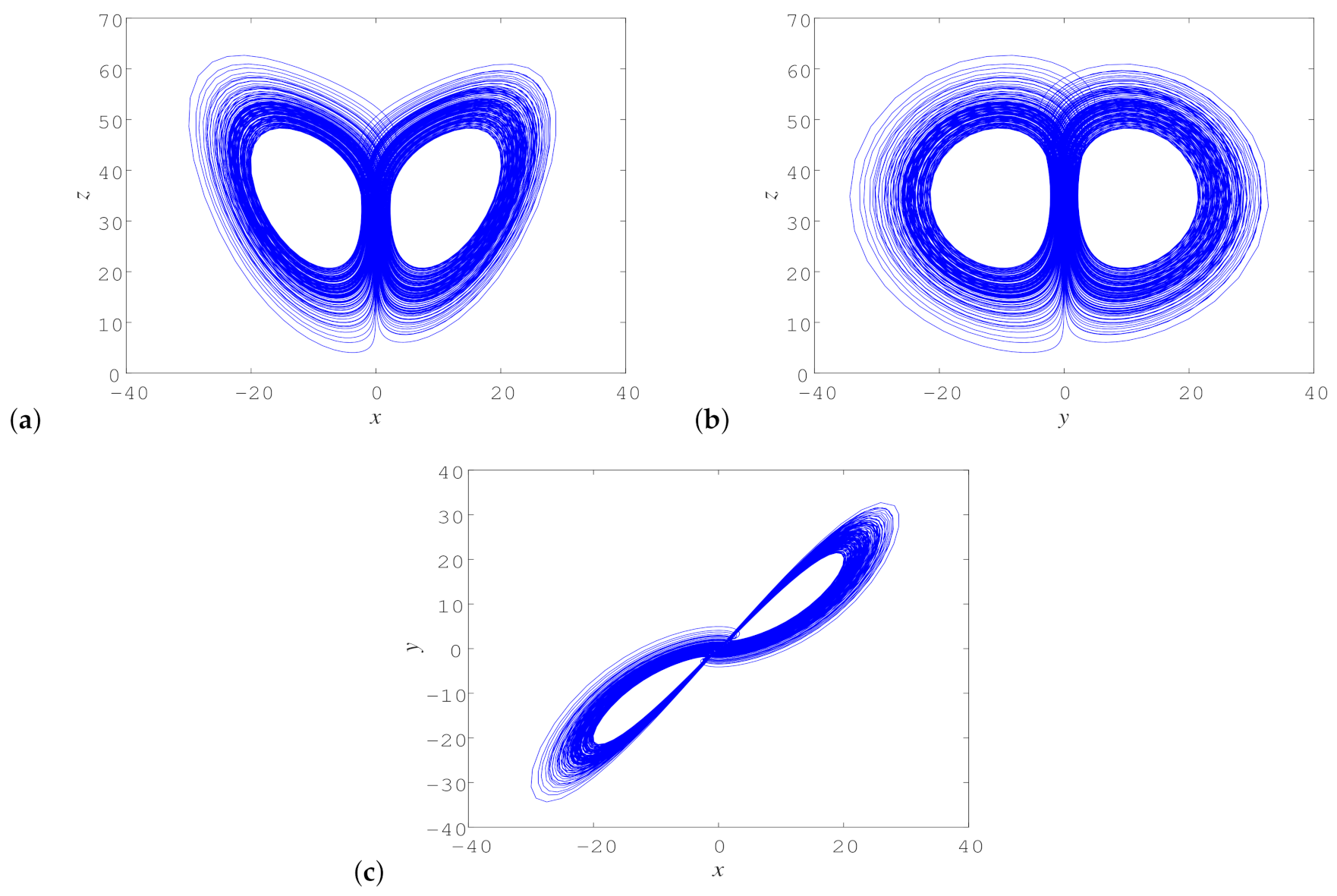




| Systems | Equations | Parameters | Equilibria | Eigenvalues | Lyapunov Exponents | Fractional Dimensions | Attractor Type |
|---|---|---|---|---|---|---|---|
| This work | Hidden | ||||||
| 0 | |||||||
| Dong [10] | Hidden | ||||||
| Self-excited | |||||||
| This Work | Dong [10] | |
|---|---|---|
| Establishment of mathematical model | Adding a simple constant term to Yang-Chen system | Adding a nonlinear term of cross-product to generalized Lorenz-type system |
| Dynamics | Yes | Yes |
| Coexisting attractors | Yes | No |
| Offset boosting control | Yes | No |
| Symbolic dynamics of unstable cycles | Two letters | Four letters for hidden attractor |
| Six letters for self-excited attractor | ||
| Circuit implementation | Yes | Yes |
| Synchronization | Yes | No |
| Length | Itineraries | Periods | x | y | z |
|---|---|---|---|---|---|
| 1 | 0 | 0.468918 | −10.393417 | −7.216587 | 43.634264 |
| 1 | 0.468918 | 10.393417 | 7.216587 | 43.634264 | |
| 2 | 01 | 1.190901 | −15.856545 | −21.285817 | 21.799902 |
| 3 | 001 | 1.768396 | −1.142202 | 0.192829 | 40.538631 |
| 011 | 1.768396 | 1.142202 | −0.192829 | 40.538631 | |
| 4 | 0001 | 2.338366 | −5.390366 | −2.042326 | 44.498047 |
| 0011 | 2.364638 | 8.016602 | 2.946163 | 47.893544 | |
| 0111 | 2.338366 | 5.390366 | 2.042326 | 44.498047 | |
| 5 | 00001 | 2.975663 | −0.259779 | 0.021441 | 36.277845 |
| 00011 | 2.939762 | −2.797000 | −3.617918 | 20.432365 | |
| 00101 | 2.962243 | −15.163685 | −7.655255 | 52.919827 | |
| 00111 | 2.939762 | 2.797000 | 3.617918 | 20.432365 | |
| 01011 | 2.962243 | 15.163685 | 7.655255 | 52.919827 | |
| 01111 | 2.975663 | 0.259779 | −0.021441 | 36.277845 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, C. Dynamic Analysis of a Novel 3D Chaotic System with Hidden and Coexisting Attractors: Offset Boosting, Synchronization, and Circuit Realization. Fractal Fract. 2022, 6, 547. https://doi.org/10.3390/fractalfract6100547
Dong C. Dynamic Analysis of a Novel 3D Chaotic System with Hidden and Coexisting Attractors: Offset Boosting, Synchronization, and Circuit Realization. Fractal and Fractional. 2022; 6(10):547. https://doi.org/10.3390/fractalfract6100547
Chicago/Turabian StyleDong, Chengwei. 2022. "Dynamic Analysis of a Novel 3D Chaotic System with Hidden and Coexisting Attractors: Offset Boosting, Synchronization, and Circuit Realization" Fractal and Fractional 6, no. 10: 547. https://doi.org/10.3390/fractalfract6100547
APA StyleDong, C. (2022). Dynamic Analysis of a Novel 3D Chaotic System with Hidden and Coexisting Attractors: Offset Boosting, Synchronization, and Circuit Realization. Fractal and Fractional, 6(10), 547. https://doi.org/10.3390/fractalfract6100547






