State of Charge Estimation of Lithium-Ion Batteries Based on Fuzzy Fractional-Order Unscented Kalman Filter
Abstract
:1. Introduction
2. Theory and Method Research
2.1. Fractional-Order Calculus
2.2. Fractional-Order Model
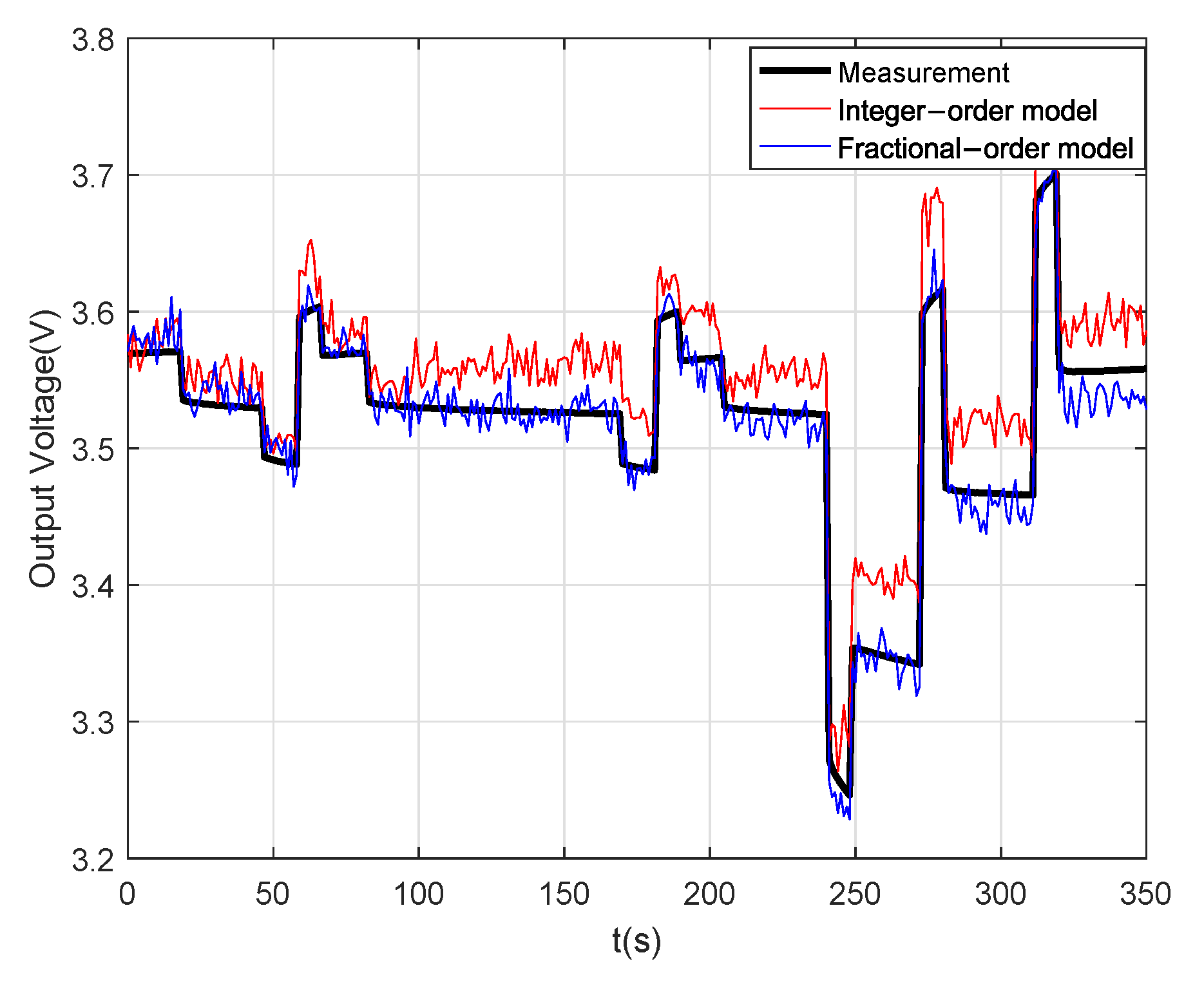
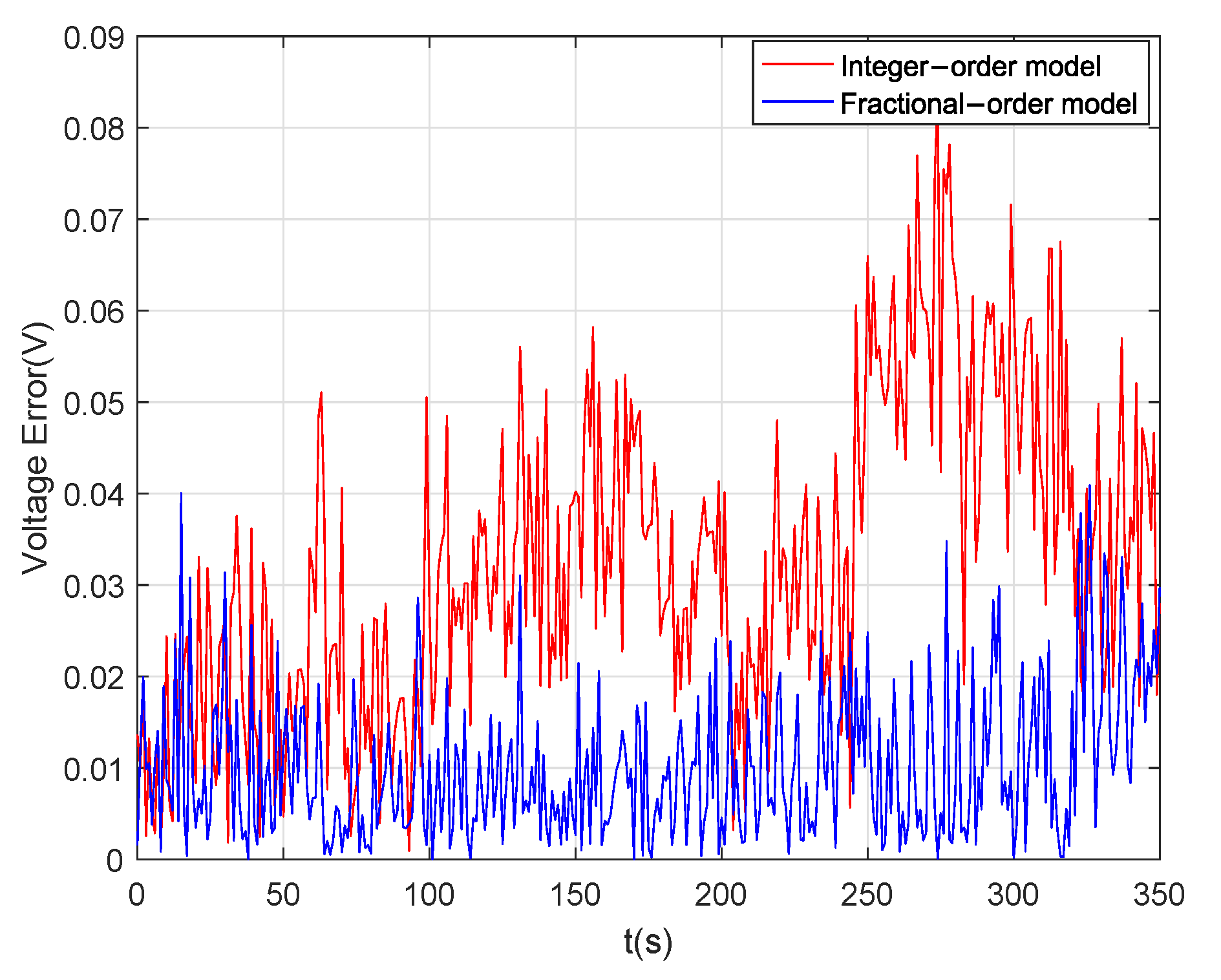
2.3. Model Parameter Identification and Validation
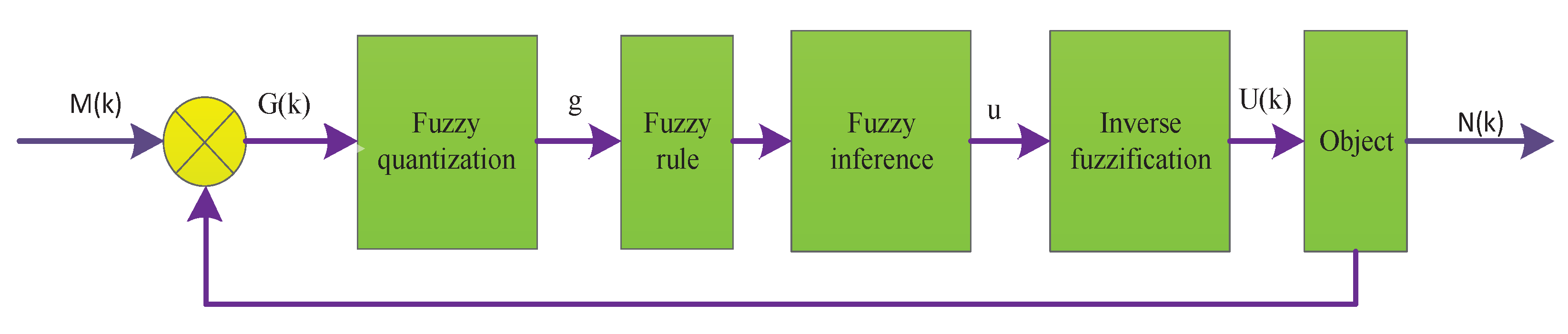
3. Fuzzy Controller
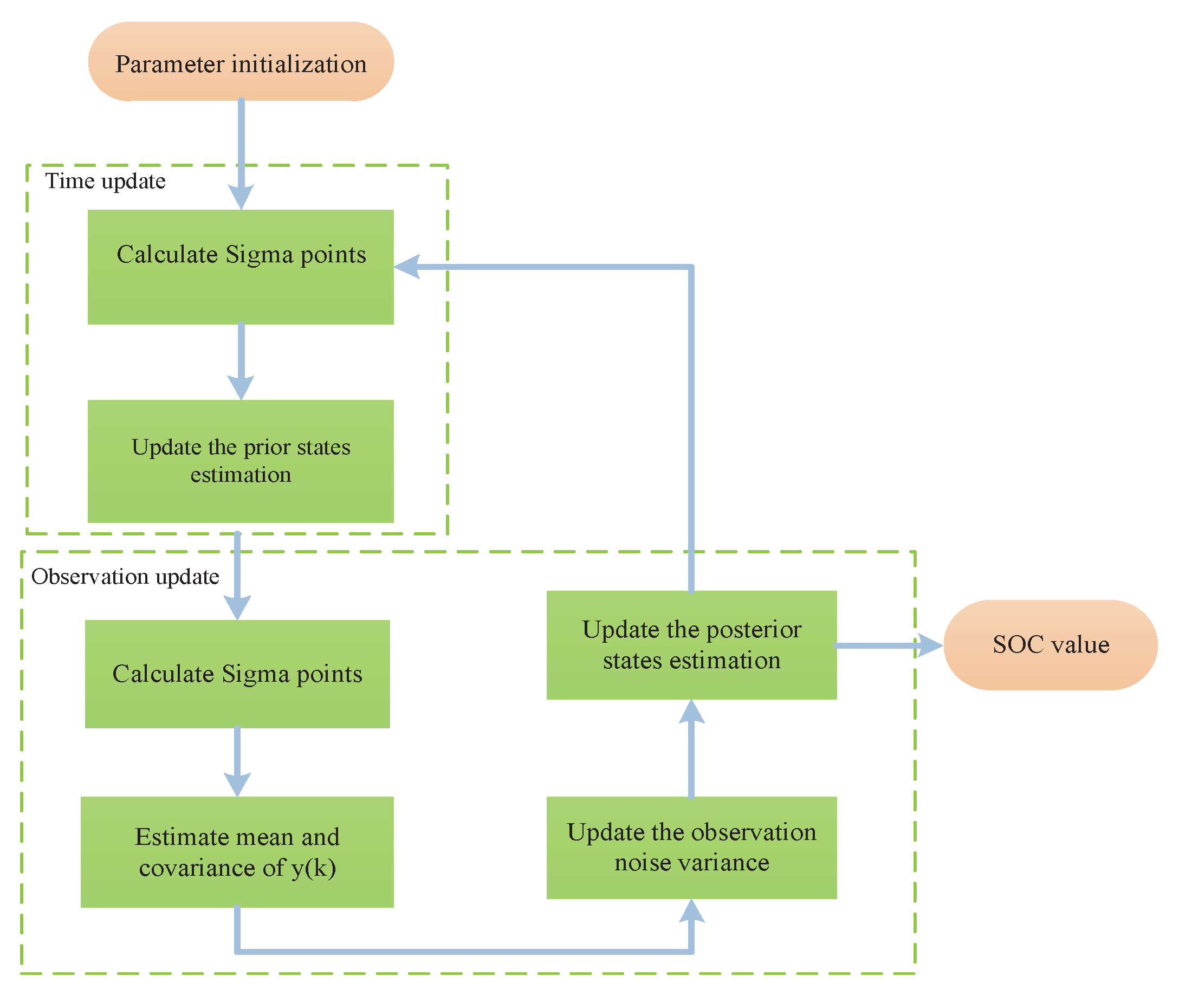
4. SOC Estimation
- 1
- Initialization
- (1)
- Give the initial state , Q, R and state error covariance P.
- 2
- Time updating
- (1)
- Calculate sigma points using the singular value decomposition:where is a scale coefficient that we can set equal to 1. The symbols and are the ith eigenvalue and eigenvector of and . The weight of sigma points can be calculated by the formula:where denotes , and k represent scaling and tuning parameters, respectively, n is the dimension of the state vector x, and is a parameter related to the noise type.
- (2)
- Transform the sigma sampling points using the nonlinear function :
- (3)
- Update the prior states estimation. The mean and covariance of and can be calculated by:
- 3
- Observation updating
- (1)
- Calculate sigma points using the singular value decomposition. The weight of the sigma points is obtained using (20):
- (2)
- Transform the sigma sampling points using the nonlinear function :
- (3)
- Estimate the observation-error covariance matrix:
- (4)
- Calculate the theoretical and actual covariances:
- (5)
- Update the observation noise variance:where is the input value of the fuzzy controller and is the output value as an adjusted factor through the fuzzy inference system. We can then obtain the new .
- (6)
- Update the posterior states estimation:where is the Kalman filter gain. With the update of , we can get the updated Kalman filter gain and the state error covariance matrix .
5. Numerical Verification and Discussion
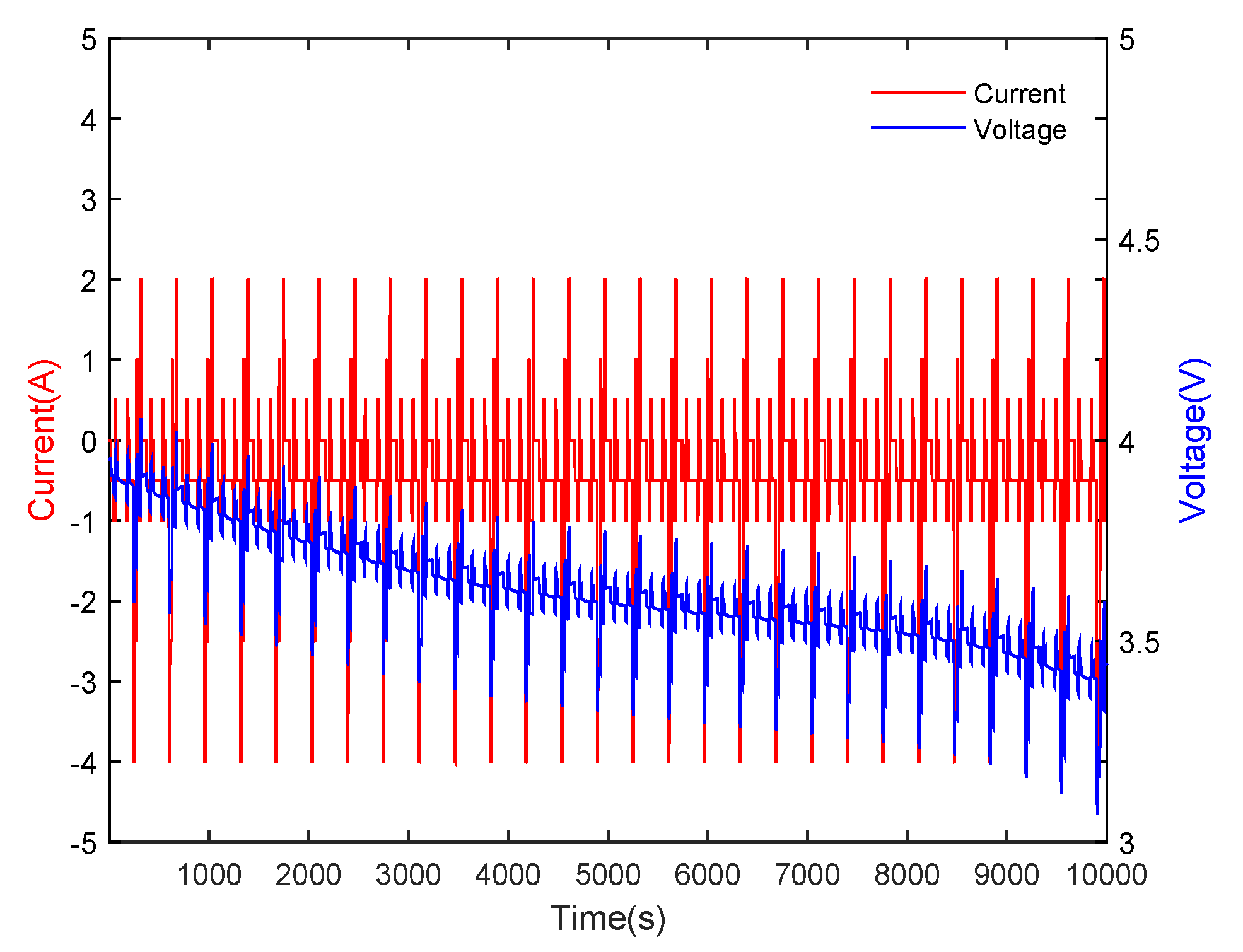
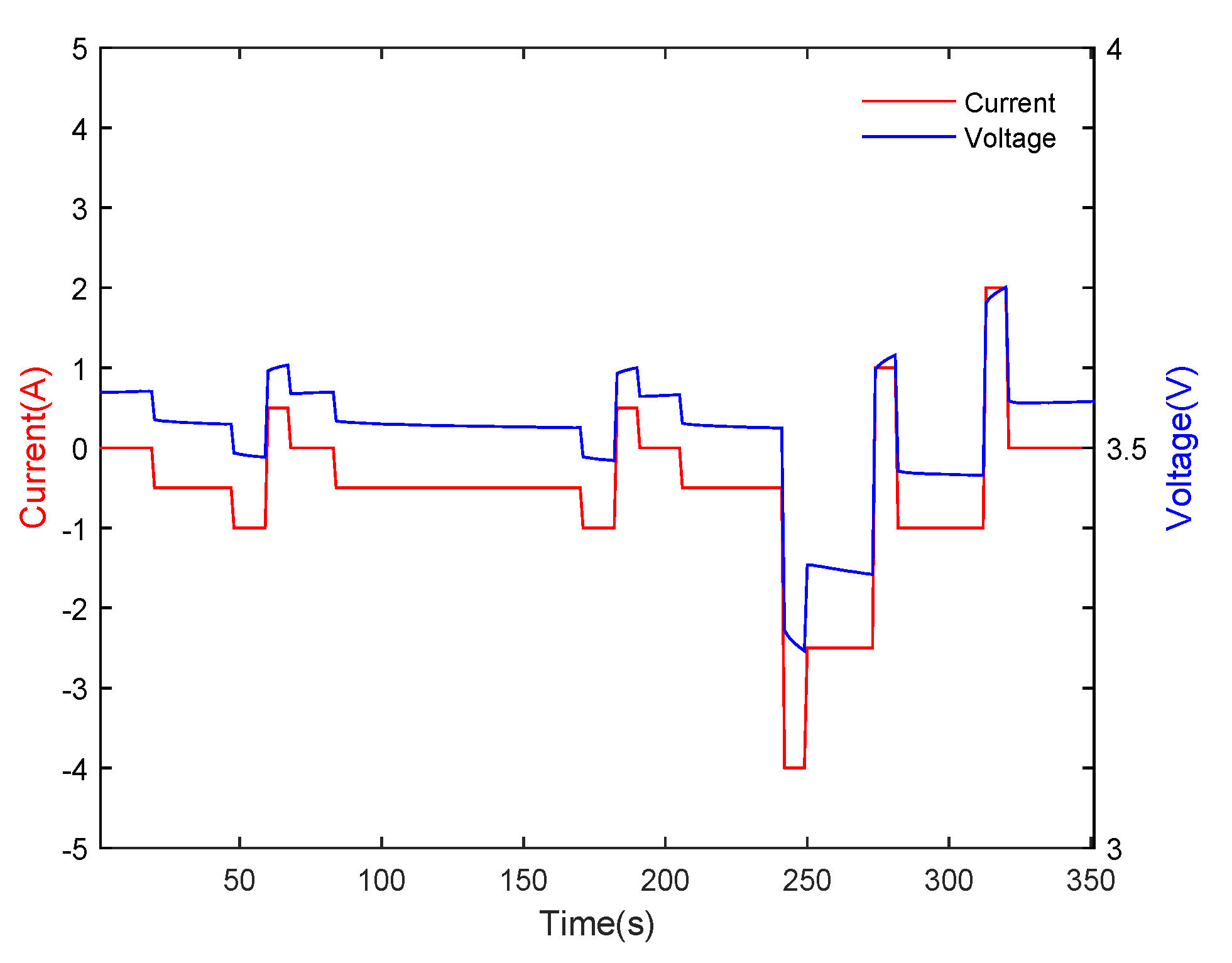
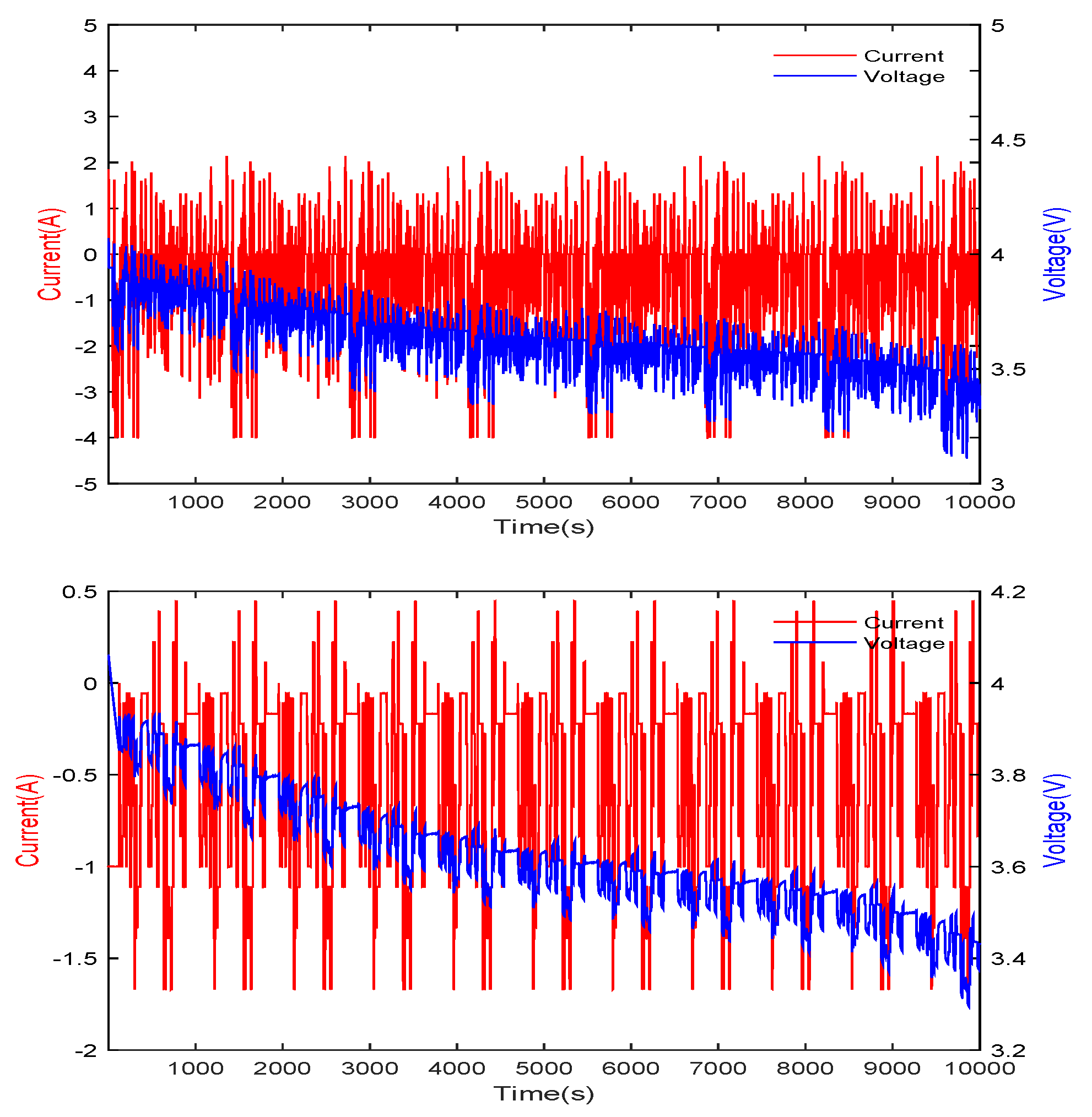
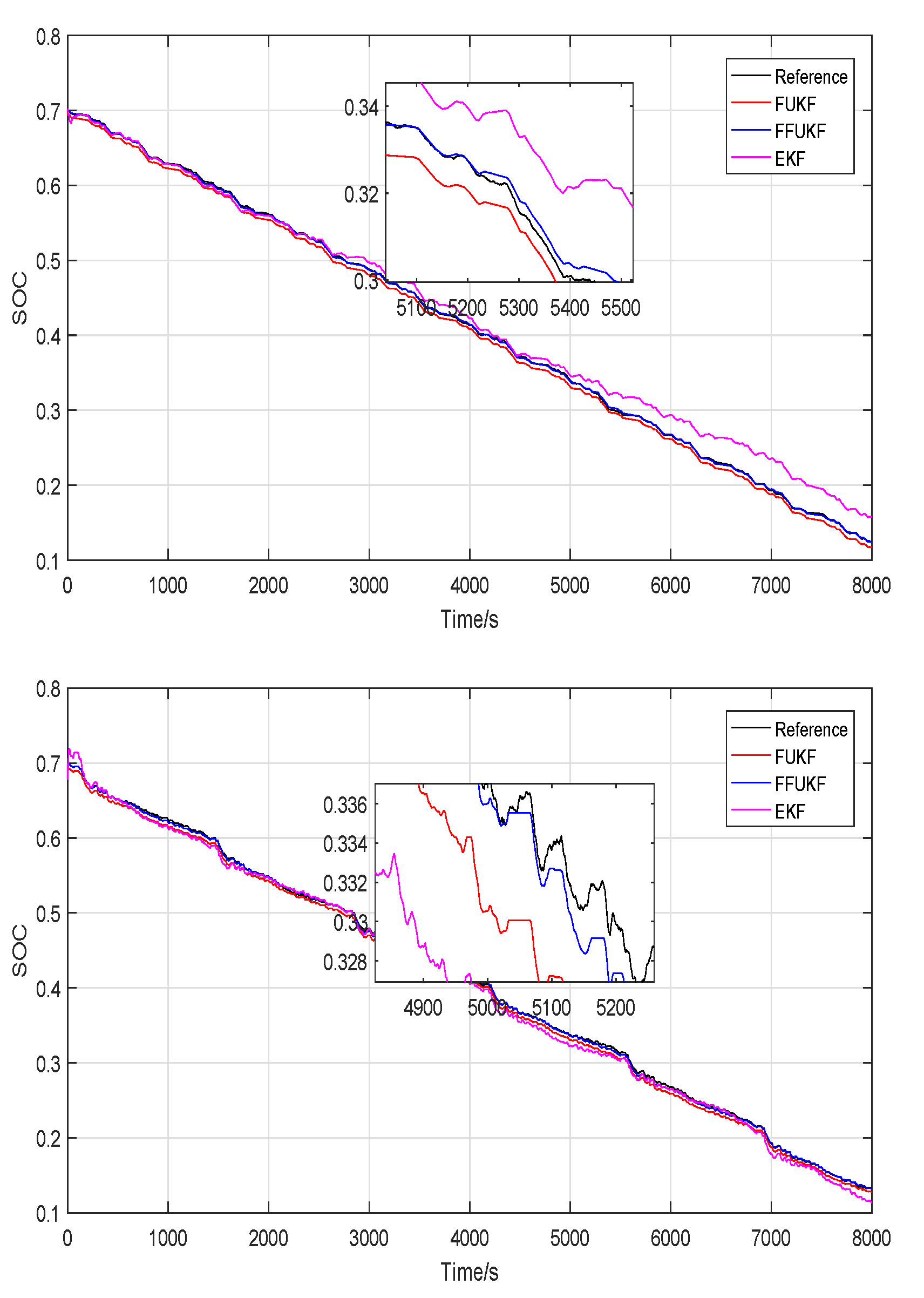
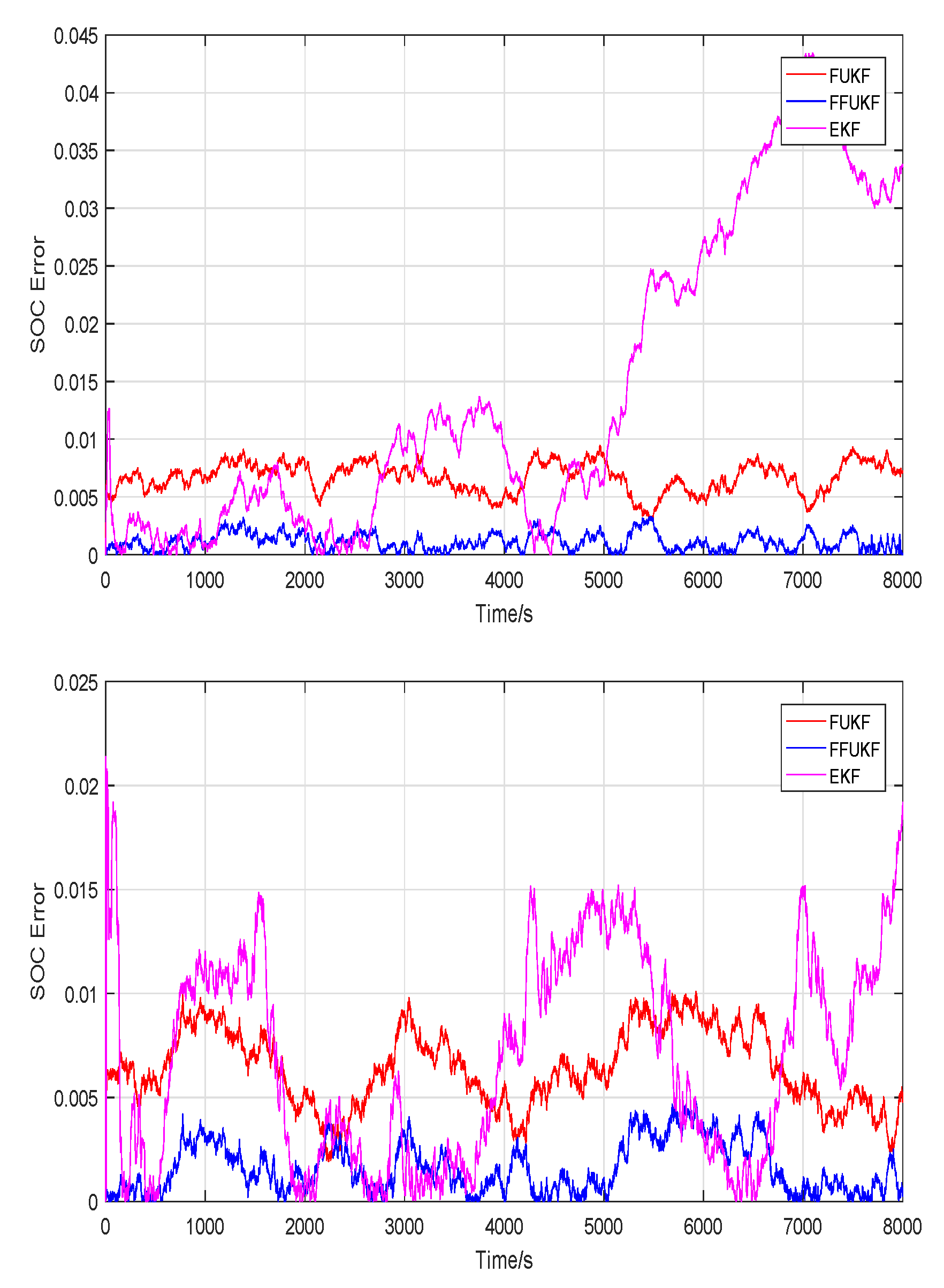
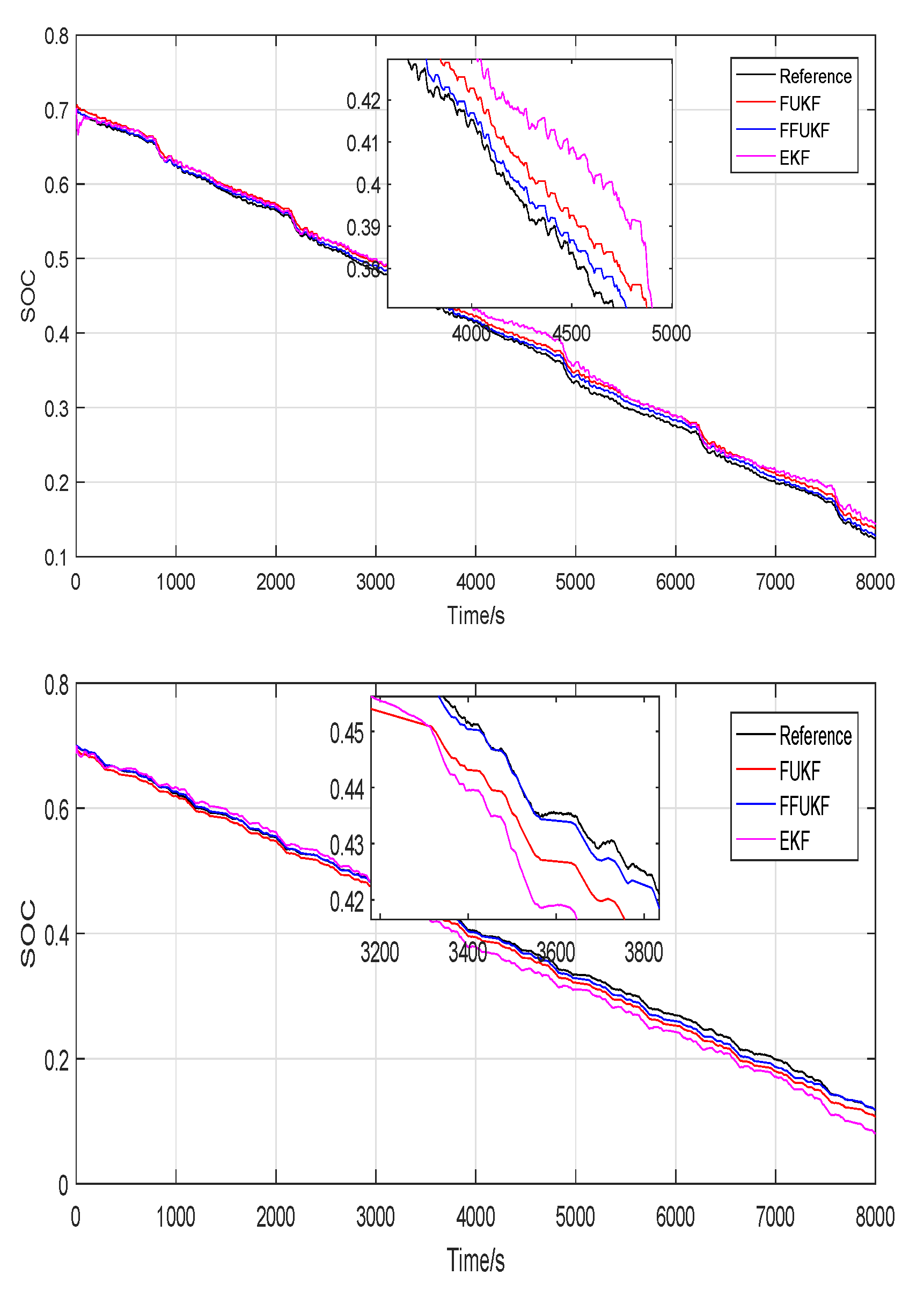
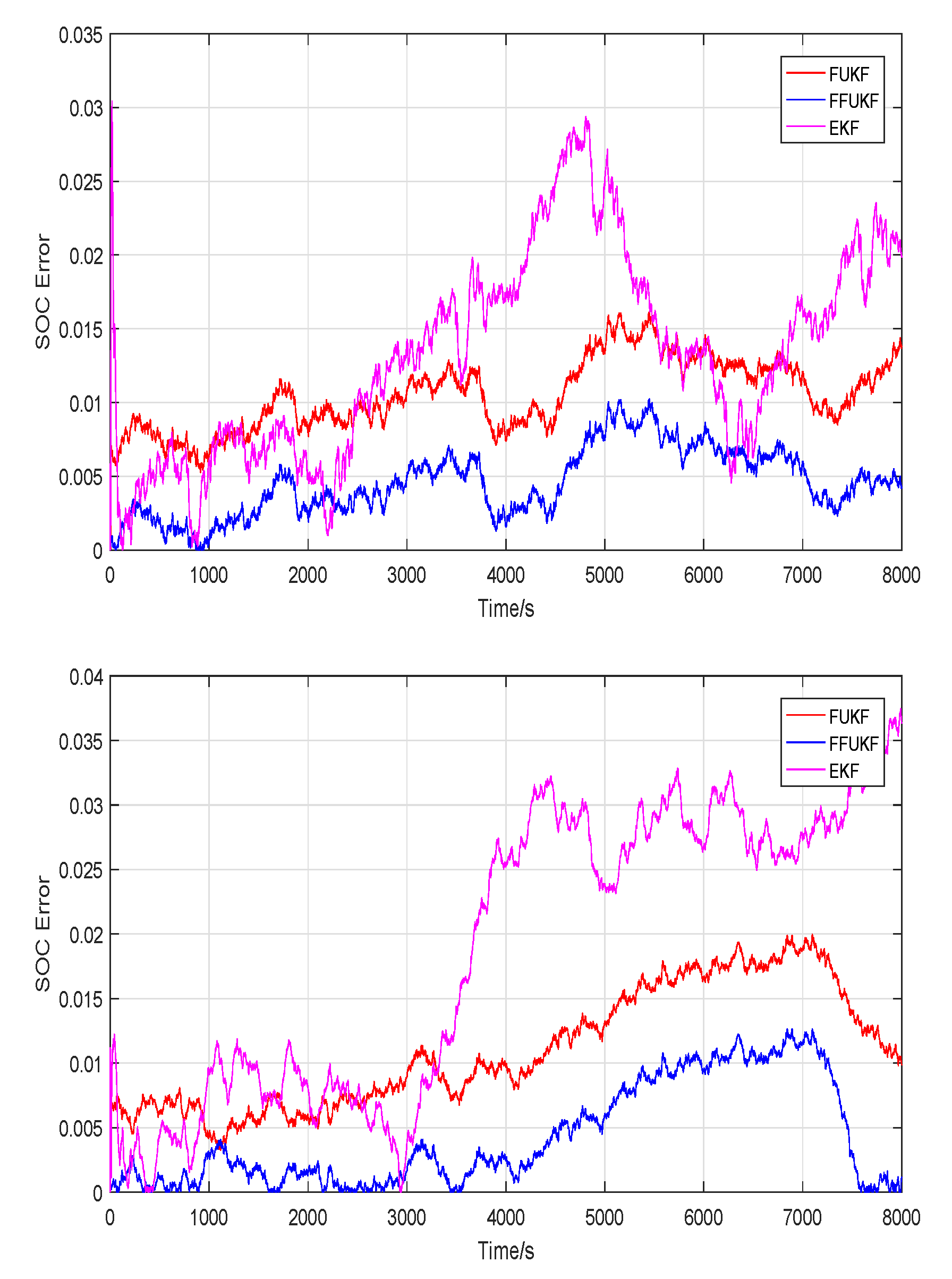
5.1. Experimental Results at 25 °C
5.2. Experimental Results at 0 °C
5.3. Experimental Results at 45 °C
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fernández, R.Á. A more realistic approach to electric vehicle contribution to greenhouse gas emissions in the city. J. Clean. Prod. 2018, 172, 949–959. [Google Scholar] [CrossRef]
- Larcher, D.; Tarascon, J.M. Towards greener and more sustainable batteries for electrical energy storage. Nat. Chem. 2015, 7, 19–29. [Google Scholar] [CrossRef] [PubMed]
- Cheng, K.W.E.; Divakar, B.; Wu, H.; Ding, K.; Ho, H.F. Battery-management system (BMS) and SOC development for electrical vehicles. IEEE Trans. Veh. Technol. 2010, 60, 76–88. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Y.; Shang, Y.; Duan, B.; Cui, N.; Zhang, C. A fractional-order kinetic battery model of lithium-ion batteries considering a nonlinear capacity. Electronics 2019, 8, 394. [Google Scholar] [CrossRef] [Green Version]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison study on the battery models used for the energy management of batteries in electric vehicles. Energy Convers. Manag. 2012, 64, 113–121. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, G.; Liu, X.; He, Z. A time-efficient and accurate open circuit voltage estimation method for lithium-ion batteries. Energies 2019, 12, 1803. [Google Scholar] [CrossRef] [Green Version]
- Aylor, J.H.; Thieme, A.; Johnso, B. A battery state-of-charge indicator for electric wheelchairs. IEEE Trans. Ind. Electron. 1992, 39, 398–409. [Google Scholar] [CrossRef]
- Feng, F.; Lu, R.; Zhu, C. A combined state of charge estimation method for lithium-ion batteries used in a wide ambient temperature range. Energies 2014, 7, 3004–3032. [Google Scholar] [CrossRef] [Green Version]
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles. J. Power Sources 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Shen, W.; Lu, J. State-of-charge estimation of LiFePO4 batteries in electric vehicles: A deep-learning enabled approach. Appl. Energy 2021, 291, 116812. [Google Scholar] [CrossRef]
- Belhani, A.; M’Sirdi, N.K.; Naamane, A. Adaptive sliding mode observer for estimation of state of charge. Energy Procedia 2013, 377–386. [Google Scholar] [CrossRef] [Green Version]
- Nath, A.; Gupta, R.; Mehta, R.; Bahga, S.S.; Gupta, A.; Bhasin, S. Attractive ellipsoid sliding mode observer design for state of charge estimation of lithium-ion cells. IEEE Trans. Veh. Technol. 2020, 69, 14701–14712. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, J.; Zhou, F.; Xu, S. State-of-charge estimation of lithium-ion batteries based on improved H infinity filter algorithm and its novel equalization method. J. Clean. Prod. 2021, 290, 125180. [Google Scholar] [CrossRef]
- Li, L.; Hu, M.; Xu, Y.; Fu, C.; Jin, G.; Li, Z. State of charge estimation for lithium-ion power battery based on H-infinity filter Algorithm. Appl. Sci. 2020, 10, 6371. [Google Scholar] [CrossRef]
- Tao, J.; Zhu, D.; Sun, C.; Chu, D.; Ma, Y.; Li, H.; Li, Y.; Xu, T. A novel method of SOC estimation for electric vehicle based on adaptive particle filter. Autom. Control. Comput. Sci. 2020, 54, 412–422. [Google Scholar]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Xiao, R.; Shen, J.; Li, X.; Yan, W.; Pan, E.; Chen, Z. Comparisons of modeling and state of charge estimation for lithium-ion battery based on fractional order and integral order methods. Energies 2016, 9, 184. [Google Scholar] [CrossRef]
- Yang, S.; Zhou, S.; Hua, Y.; Zhou, X.; Liu, X.; Pan, Y.; Ling, H.; Wu, B. A parameter adaptive method for state of charge estimation of lithium-ion batteries with an improved extended Kalman filter. Sci. Rep. 2021, 11, 1–15. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Guo, X.; Zhang, X. An improved adaptive unscented kalman filtering for state of charge online estimation of lithium-ion battery. J. Energy Storage 2020, 32, 101980. [Google Scholar] [CrossRef]
- Han, J.; Kim, D.; Sunwoo, M. State-of-charge estimation of lead-acid batteries using an adaptive extended Kalman filter. J. Power Sources 2009, 188, 606–612. [Google Scholar] [CrossRef]
- Sun, F.; Hu, X.; Zou, Y.; Li, S. Adaptive unscented Kalman filtering for state of charge estimation of a lithium-ion battery for electric vehicles. Energy 2011, 36, 3531–3540. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, L.; Zhang, L.; Huang, C. State-of-charge estimation of lithium-ion battery pack by using an adaptive extended Kalman filter for electric vehicles. J. Energy Storage 2021, 37, 102457. [Google Scholar] [CrossRef]
- Zeng, M.; Zhang, P.; Yang, Y.; Xie, C.; Shi, Y. SOC and SOH joint estimation of the power batteries based on fuzzy unscented Kalman filtering algorithm. Energies 2019, 12, 3122. [Google Scholar] [CrossRef] [Green Version]
- Lai, X.; Qiao, D.; Zheng, Y.; Zhou, L. A fuzzy state-of-charge estimation algorithm combining ampere-hour and an extended Kalman filter for Li-ion batteries based on multi-model global identification. Appl. Sci. 2018, 8, 2028. [Google Scholar] [CrossRef] [Green Version]
- Victor, S.; Malti, R.; Garnier, H.; Oustaloup, A. Parameter and differentiation order estimation in fractional models. Automatica 2013, 49, 926–935. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, D.; Zhu, Q.; Liu, W.; Liu, C.; Xiong, N. A new state of charge estimation algorithm for lithium-ion batteries based on the fractional unscented Kalman filter. Energies 2017, 10, 1313. [Google Scholar] [CrossRef]
- Xiong, R.; Tian, J.; Shen, W.; Sun, F. A novel fractional order model for state of charge estimation in lithium ion batteries. IEEE Trans. Veh. Technol. 2018, 68, 4130–4139. [Google Scholar] [CrossRef]
- Sabatier, J.; Cugnet, M.; Laruelle, S.; Grugeon, S.; Sahut, B.; Oustaloup, A.; Tarascon, J. A fractional order model for lead-acid battery crankability estimation. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1308–1317. [Google Scholar] [CrossRef]
- Liu, C.; Liu, W.; Wang, L.; Hu, G.; Ma, L.; Ren, B. A new method of modeling and state of charge estimation of the battery. J. Power Sources 2016, 320, 1–12. [Google Scholar] [CrossRef]
- Xu, J.; Mi, C.C.; Cao, B.; Cao, J. A new method to estimate the state of charge of lithium-ion batteries based on the battery impedance model. J. Power Sources 2013, 233, 277–284. [Google Scholar] [CrossRef]
- Wei, Z.; Zou, C.; Leng, F.; Soong, B.H.; Tseng, K.J. Online model identification and state-of-charge estimate for lithium-ion battery with a recursive total least squares-based observer. IEEE Trans. Ind. Electron. 2017, 65, 1336–1346. [Google Scholar] [CrossRef]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z.; Li, S.E.; Moura, S.J.; Peng, H. State-of-Charge estimation for lithium-ion batteries based on a nonlinear fractional model. IEEE Trans. Control Syst. Technol. 2017, 25, 3–11. [Google Scholar] [CrossRef]
- Hu, X.; Yuan, H.; Zou, C.; Li, Z.; Zhang, L. Co-estimation of state of charge and state of health for lithium-ion batteries based on fractional-order calculus. IEEE Trans. Veh. Technol. 2018, 67, 10319–10329. [Google Scholar] [CrossRef]
- Aggab, T.; Avila, M.; Vrignat, P.; Kratz, F. Unifying model-based prognosis with learning-based time-series prediction methods: Application to Li-Ion battery. IEEE Syst. J. 2021. [Google Scholar] [CrossRef]
- Coronel-Escamilla, A.; Gómez-Aguilar, J.; Torres-Jiménez, J.; Mousa, A.; Elagan, S. Fractional synchronization involving fractional derivatives with nonsingular kernels: Application to chaotic systems. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Zheng, F.; Xing, Y.; Jiang, J.; Sun, B.; Kim, J.; Pecht, M. Influence of different open circuit voltage tests on state of charge online estimation for lithium-ion batteries. Applied Energy 2016, 183, 513–525. [Google Scholar] [CrossRef]
- Tavakoli, M.; Tabatabaei, M. Controllability and observability analysis of continuous-time multi-order fractional systems. Multidimens. Syst. Signal Process. 2017, 28, 427–450. [Google Scholar] [CrossRef]




| 0.5975 | 264.25 | 1.2679 | 448.54 | 0.4325 | 0.4380 |
| Input fuzziness | NB | NS | Z | PS | PB |
| Output fuzziness | NB | NS | Z | PS | PB |
| RMSE | EKF | FUKF | FFUKF |
|---|---|---|---|
| FUDS | 0.87% | 0.67% | 0.20% |
| BJDST | 1.95% | 0.68% | 0.13% |
| RMSE | EKF | FUKF | FFUKF |
|---|---|---|---|
| FUDS | 0.88% | 0.85% | 0.20% |
| BJDST | 1.49% | 1.04% | 0.32% |
| RMSE | EKF | FUKF | FFUKF |
|---|---|---|---|
| FUDS | 1.49% | 1.08% | 0.51% |
| BJDST | 2.18% | 1.20% | 0.58% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Chen, Y.; Lopes, A.M.; Kong, H.; Wu, R. State of Charge Estimation of Lithium-Ion Batteries Based on Fuzzy Fractional-Order Unscented Kalman Filter. Fractal Fract. 2021, 5, 91. https://doi.org/10.3390/fractalfract5030091
Chen L, Chen Y, Lopes AM, Kong H, Wu R. State of Charge Estimation of Lithium-Ion Batteries Based on Fuzzy Fractional-Order Unscented Kalman Filter. Fractal and Fractional. 2021; 5(3):91. https://doi.org/10.3390/fractalfract5030091
Chicago/Turabian StyleChen, Liping, Yu Chen, António M. Lopes, Huifang Kong, and Ranchao Wu. 2021. "State of Charge Estimation of Lithium-Ion Batteries Based on Fuzzy Fractional-Order Unscented Kalman Filter" Fractal and Fractional 5, no. 3: 91. https://doi.org/10.3390/fractalfract5030091
APA StyleChen, L., Chen, Y., Lopes, A. M., Kong, H., & Wu, R. (2021). State of Charge Estimation of Lithium-Ion Batteries Based on Fuzzy Fractional-Order Unscented Kalman Filter. Fractal and Fractional, 5(3), 91. https://doi.org/10.3390/fractalfract5030091








