Design of Fractional-Order Lead Compensator for a Car Suspension System Based on Curve-Fitting Approximation
Abstract
1. Introduction
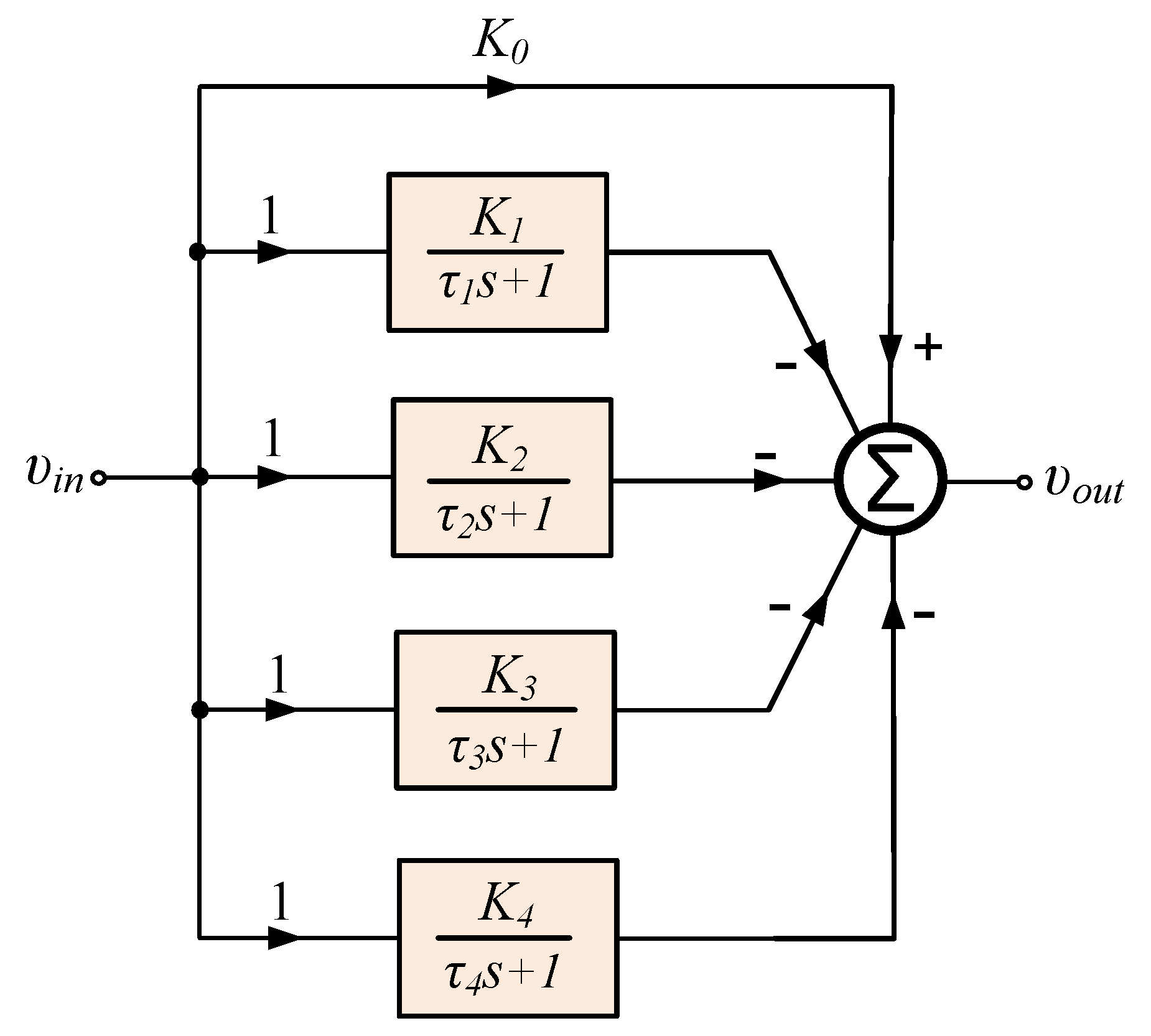
2. Curve-Fitting-Based Approximation of the Compensator Transfer Function
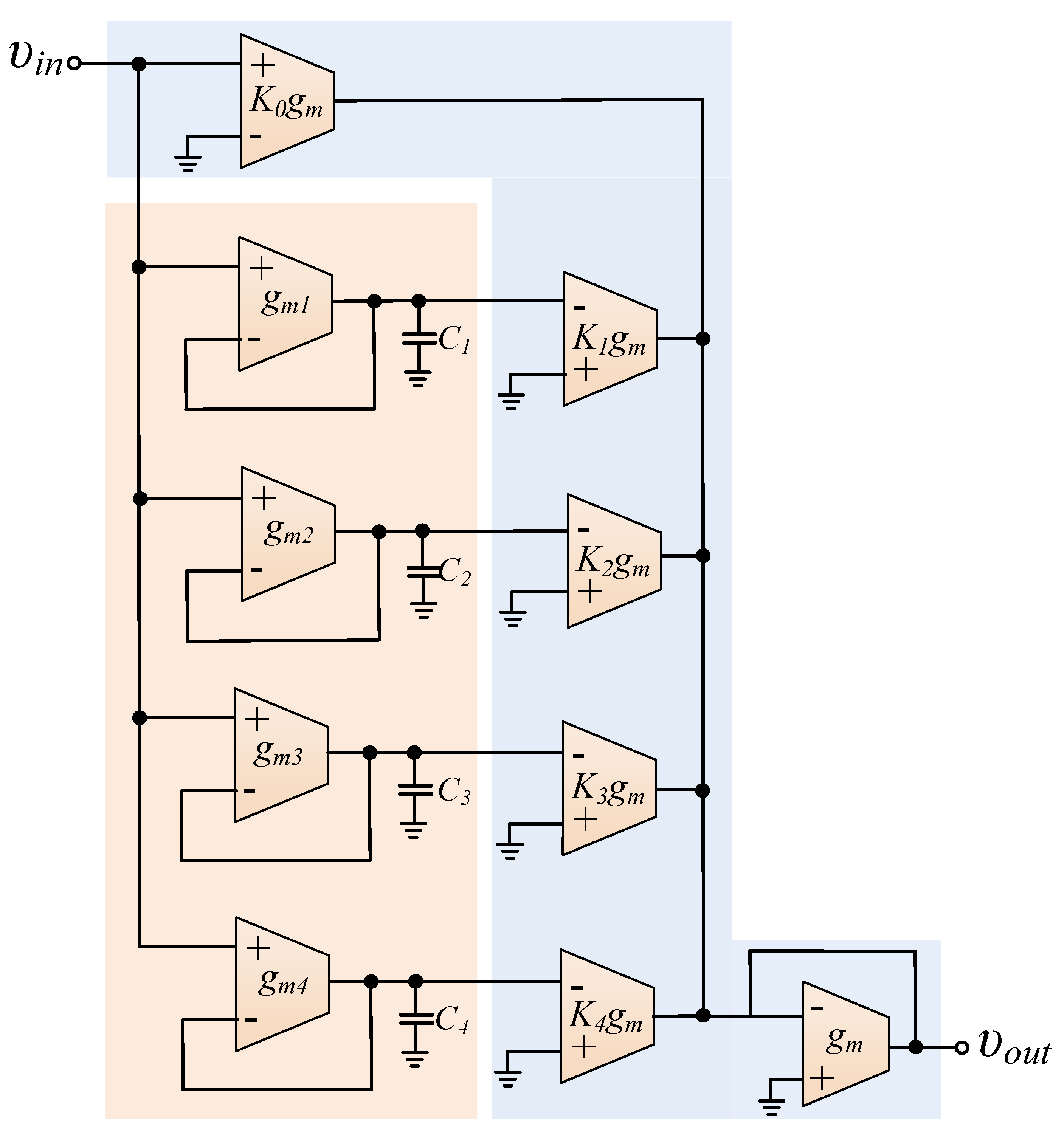
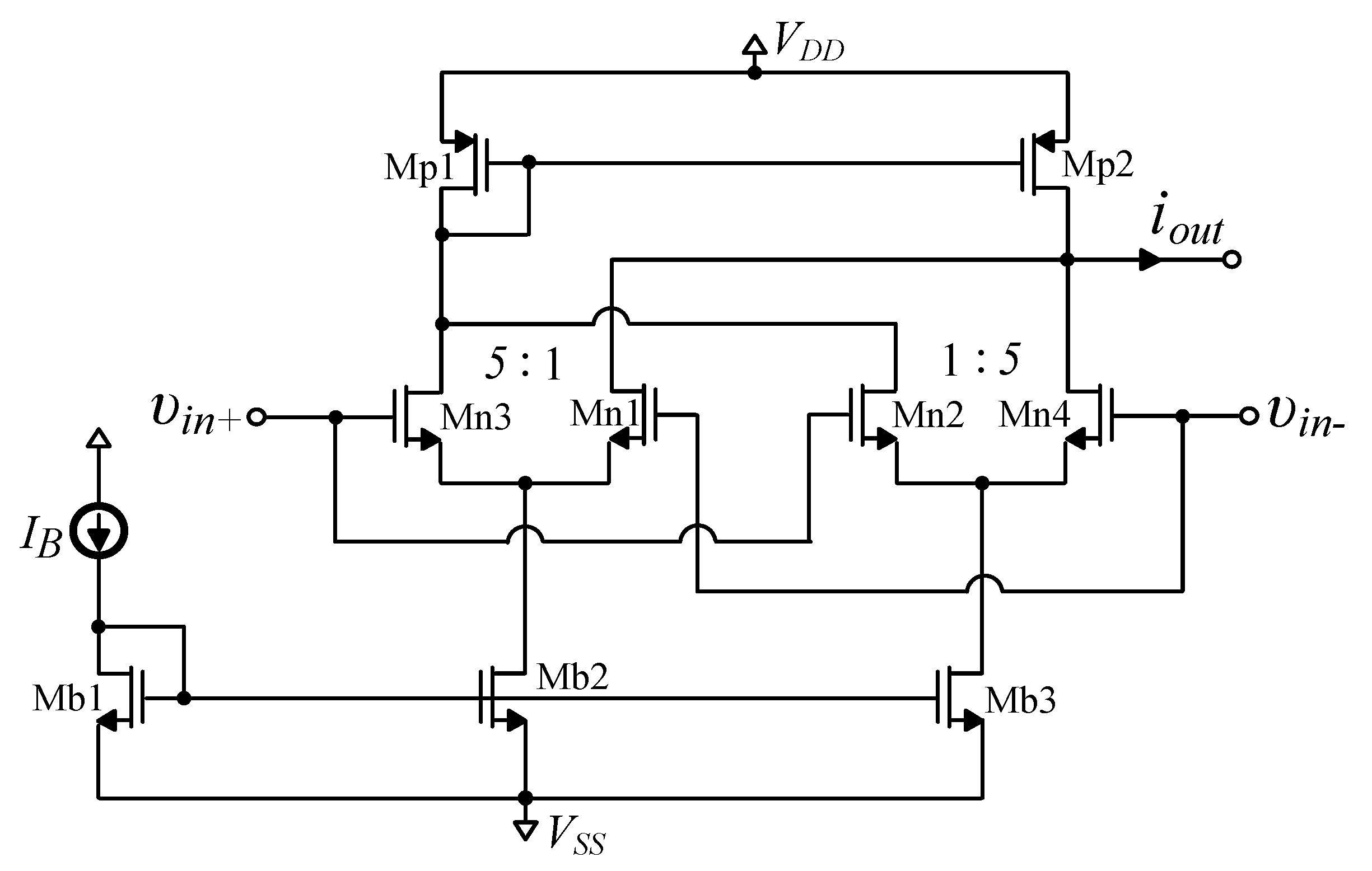
3. Implementation of the Approximated Compensator
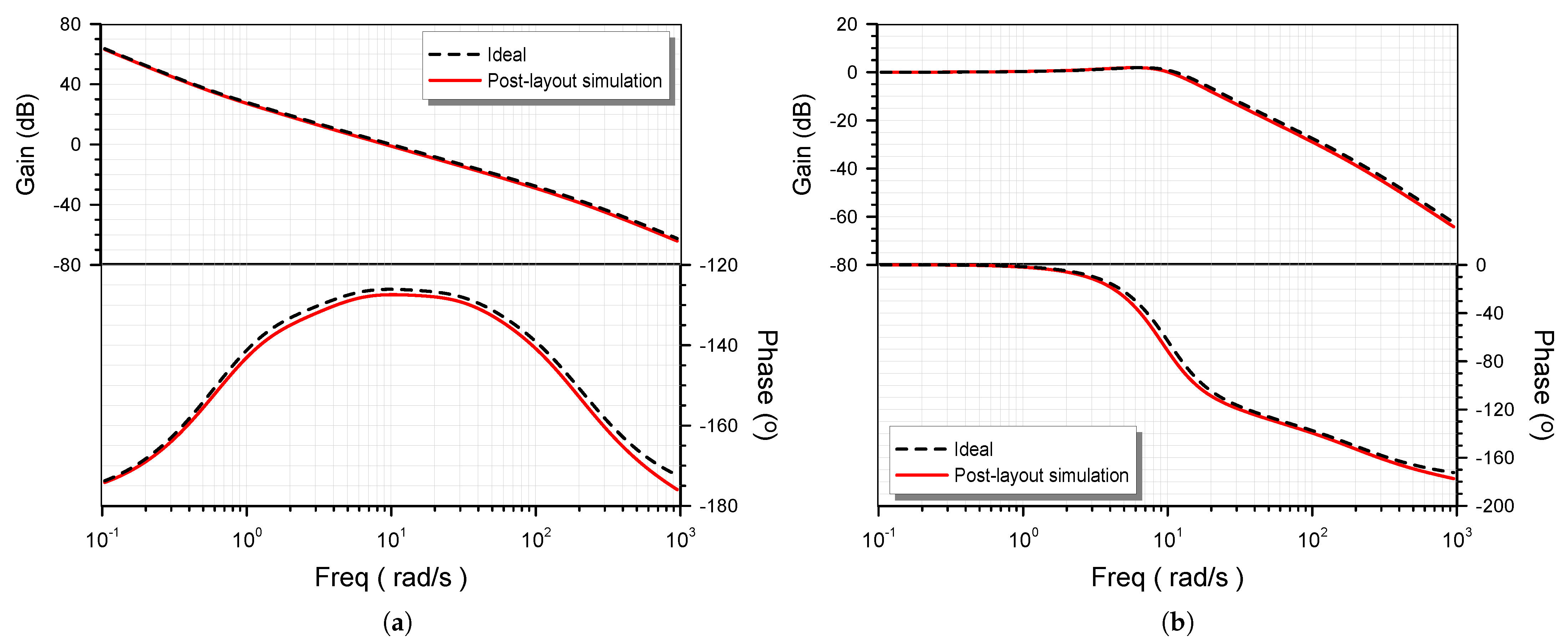
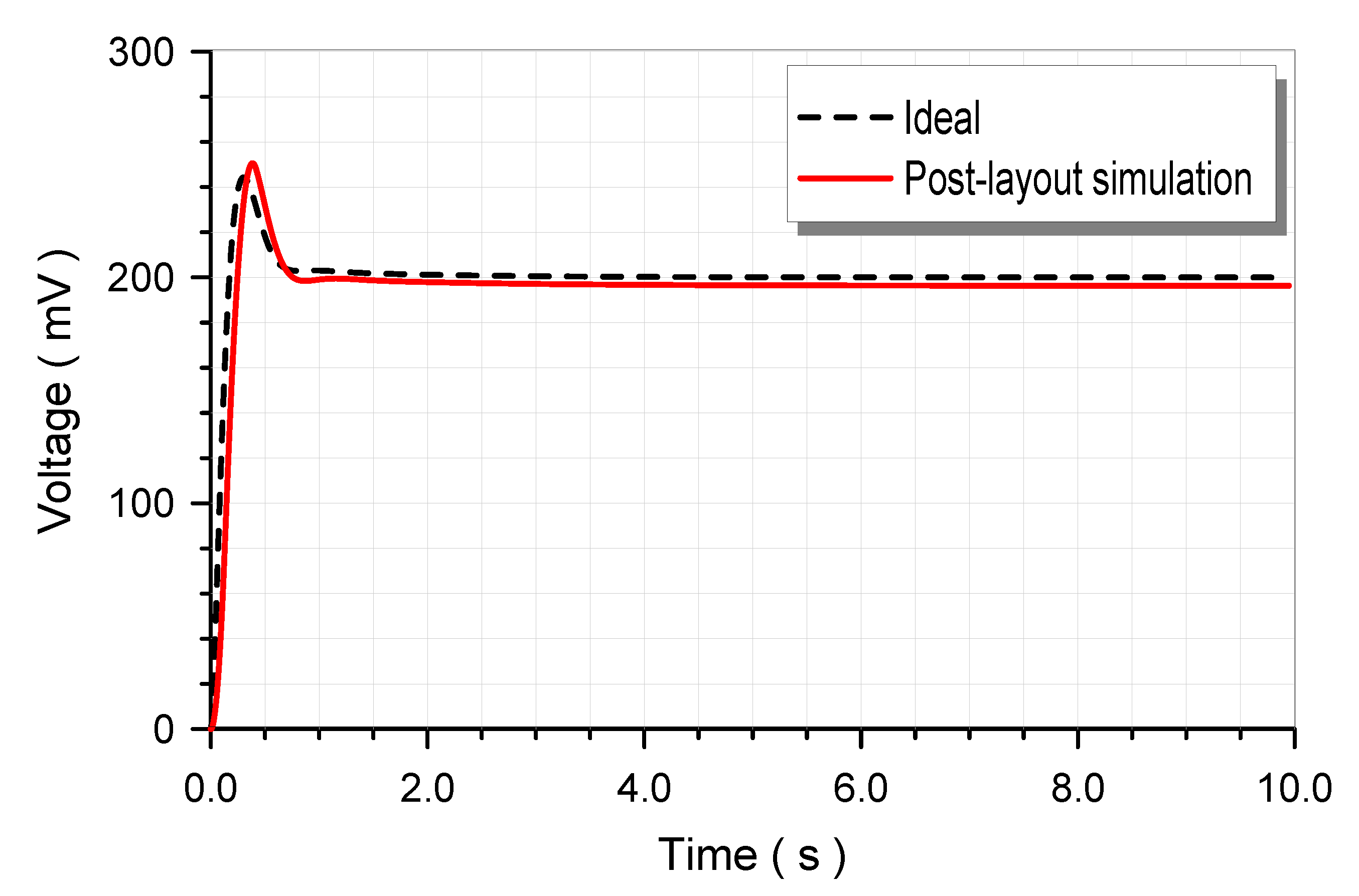
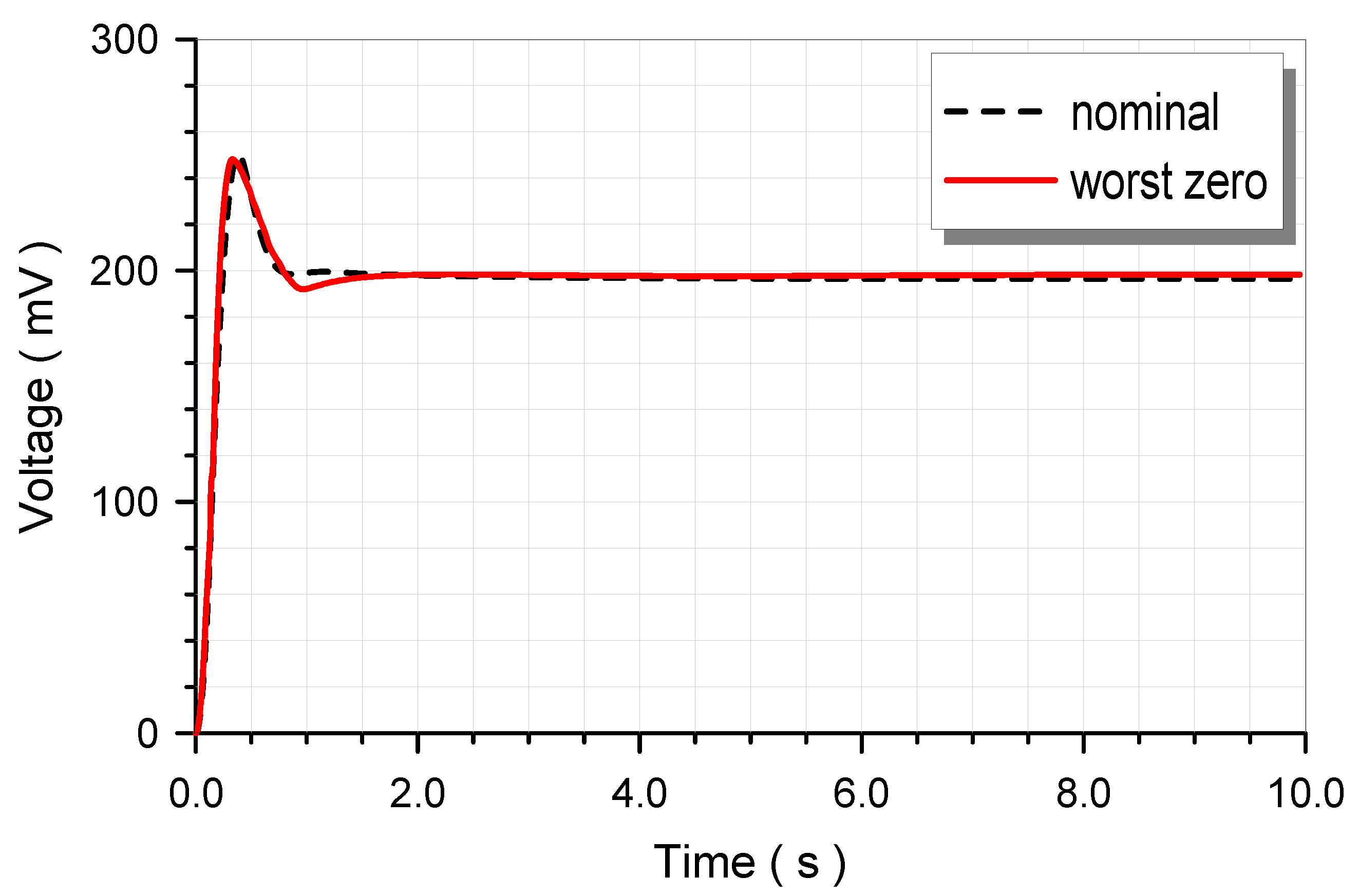
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMS | Austria Mikro Systeme |
| CMOS | Complementary metal oxide semiconductor |
| CCII | Second generation current conveyor |
| FO | Fractional-order |
| FBD | Functional block diagram |
| IC | Integrated circuit |
| IO | Integer-order |
| MOS | Metal oxide semiconductor |
| OTA | Operational transconductance amplifier |
| PFE | Partial fraction expansion |
References
- Oustaloup, A.; Moreau, X.; Nouillant, M. The CRONE suspension. Control Eng. Pract. 1996, 4, 1101–1108. [Google Scholar] [CrossRef]
- Aldair, A.A.; Wang, W.J. Design of fractional order controller based on evolutionary algorithm for a full vehicle nonlinear active suspension systems. Int. J. Control Autom. 2010, 3, 33–46. [Google Scholar]
- Taksale, A.S. Modeling, Analysis and Control of Passive and Active Suspension System for a Quarter Car. Int. J. Appl. Eng. Res. 2013, 8, 1405–1414. [Google Scholar]
- Dong, X.; Zhao, D.; Yang, B.; Han, C. Fractional-order control of active suspension actuator based on parallel adaptive clonal selection algorithm. J. Mech. Sci. Technol. 2016, 30, 2769–2781. [Google Scholar] [CrossRef]
- Baig, W.M.; Hou, Z.; Ijaz, S. Fractional order controller design for a semi-active suspension system using Nelder-Mead optimization. In Proceedings of the 2017 29th Chinese Control And Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 2808–2813. [Google Scholar] [CrossRef]
- Chen, Y.D. Study on Active Suspension with Variable Structure Control Based on the Fractional Order Exponential Reaching Law. In Applied Mechanics and Materials; Trans Tech Publ: Baech, Switzerland, 2017; Volume 872, pp. 337–345. [Google Scholar]
- Kumar, V.; Rana, K.; Kumar, J.; Mishra, P. Self-tuned robust fractional order fuzzy PD controller for uncertain and nonlinear active suspension system. Neural Comput. Appl. 2018, 30, 1827–1843. [Google Scholar] [CrossRef]
- You, H.; Shen, Y.; Xing, H.; Yang, S. Optimal control and parameters design for the fractional-order vehicle suspension system. J. Low Freq. Noise Vib. Act. Control 2018, 37, 456–467. [Google Scholar] [CrossRef]
- Swethamarai, P.; Lakshmi, P. Adaptive-Fuzzy Fractional Order PID Controller-Based Active Suspension for Vibration Control. IETE J. Res. 2020, 2020, 1–16. [Google Scholar] [CrossRef]
- Nguyen, S.D.; Lam, B.D.; Choi, S.B. Smart dampers-based vibration control–Part 2: Fractional-order sliding control for vehicle suspension system. Mech. Syst. Signal Process. 2021, 148, 107145. [Google Scholar] [CrossRef]
- Monje, C.A.; Calderon, A.J.; Vinagre, B.M.; Feliu, V. The fractional order lead compensator. In Proceedings of the Second IEEE International Conference on Computational Cybernetics, 2004. ICCC 2004, Vienna, Austria, 30 August–1 September 2004; pp. 347–352. [Google Scholar]
- Tavazoei, M.S.; Tavakoli-Kakhki, M. Compensation by fractional-order phase-lead/lag compensators. IET Control Theory Appl. 2014, 8, 319–329. [Google Scholar] [CrossRef]
- Vinagre, B.M.; Monje, C.A.; Calderón, A.J.; Suárez, J.I. Fractional PID controllers for industry application. A brief introduction. J. Vib. Control 2007, 13, 1419–1429. [Google Scholar] [CrossRef]
- Jadhav, S.P.; Hamde, S.T. A simple method to design robust fractional-order lead compensator. Int. J. Control Autom. Syst. 2017, 15, 1236–1248. [Google Scholar] [CrossRef]
- Dastjerdi, A.A.; Vinagre, B.M.; Chen, Y.; HosseinNia, S.H. Linear fractional order controllers; A survey in the frequency domain. Annu. Rev. Control 2019, 47, 51–70. [Google Scholar] [CrossRef]
- Monje, C.A.; Vinagre, B.M.; Calderon, A.J.; Feliu, V.; Chen, Y. Auto-tuning of fractional lead-lag compensators. IFAC Proc. Vol. 2005, 38, 319–324. [Google Scholar] [CrossRef]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-band complex noninteger differentiator: Characterization and synthesis. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 25–39. [Google Scholar] [CrossRef]
- Lanusse, P.; Sabatier, J.; Gruel, D.N.; Oustaloup, A. Second and third generation crone control-system design. In Fractional Order Differentiation and Robust Control Design; Springer: Berlin/Heidelberg, Germany, 2015; pp. 107–192. [Google Scholar]
- Ozdemir, A.A.; Gumussoy, S. Transfer function estimation in system identification toolbox via vector fitting. IFAC Pap. 2017, 50, 6232–6237. [Google Scholar] [CrossRef]
- Bingi, K.; Ibrahim, R.; Karsiti, M.N.; Hassam, S.M.; Harindran, V.R. Frequency response based curve fitting approximation of fractional–order PID controllers. Int. J. Appl. Math. Comput. Sci. 2019, 29, 311–326. [Google Scholar] [CrossRef]
- Bingi, K.; Ibrahim, R.; Karsiti, M.N.; Hassan, S.M.; Harindran, V.R. Fractional-order Systems and PID Controllers; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Maione, G. Design of Cascaded and Shifted Fractional-Order Lead Compensators for Plants with Monotonically Increasing Lags. Fractal Fract. 2020, 4, 37. [Google Scholar] [CrossRef]
- Kapoulea, S.; Psychalinos, C.; Elwakil, A.S. Power law filters: A new class of fractional-order filters without a fractional-order Laplacian operator. AEU Int. J. Electron. Commun. 2021, 129, 153537. [Google Scholar] [CrossRef]
- Raynaud, H.F.; Zergaınoh, A. State-space representation for fractional order controllers. Automatica 2000, 36, 1017–1021. [Google Scholar] [CrossRef]
- Dimeas, I.; Petras, I.; Psychalinos, C. New analog implementation technique for fractional-order controller: A DC motor control. AEU Int. J. Electron. Commun. 2017, 78, 192–200. [Google Scholar] [CrossRef]
- Bertsias, P.; Psychalinos, C.; Maundy, B.J.; Elwakil, A.S.; Radwan, A.G. Partial fraction expansion–based realizations of fractional-order differentiators and integrators using active filters. Int. J. Circuit Theory Appl. 2019, 47, 513–531. [Google Scholar] [CrossRef]
- Corbishley, P.; Rodriguez-Villegas, E. A nanopower bandpass filter for detection of an acoustic signal in a wearable breathing detector. IEEE Trans. Biomed. Circuits Syst. 2007, 1, 163–171. [Google Scholar] [CrossRef] [PubMed]
- Tsirimokou, G.; Psychalinos, C.; Elwakil, A. Design of CMOS Analog Integrated Fractional-Order Circuits: Applications in Medicine and Biology; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Mohan, P.A. VLSI Analog Filters: Active RC, OTA-C, and SC; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Gonzalez, E.; Dorčák, L.; Monje, C.; Valsa, J.; Caluyo, F.; Petráš, I. Conceptual design of a selectable fractional-order differentiator for industrial applications. Fract. Calc. Appl. Anal. 2014, 17, 697–716. [Google Scholar] [CrossRef]
- Muñiz-Montero, C.; García-Jiménez, L.V.; Sánchez-Gaspariano, L.A.; Sánchez-López, C.; González-Díaz, V.R.; Tlelo-Cuautle, E. New alternatives for analog implementation of fractional-order integrators, differentiators and PID controllers based on integer-order integrators. Nonlinear Dyn. 2017, 90, 241–256. [Google Scholar] [CrossRef]
- Psychalinos, C. Development of fractional-order analog integrated controllers–application examples. Appl. Control 2019, 6, 357. [Google Scholar] [CrossRef]
- Silva-Juárez, A.; Tlelo-Cuautle, E.; de la Fraga, L.G.; Li, R. FPAA-based implementation of fractional-order chaotic oscillators using first-order active filter blocks. J. Adv. Res. 2020, 25, 77–85. [Google Scholar] [CrossRef]

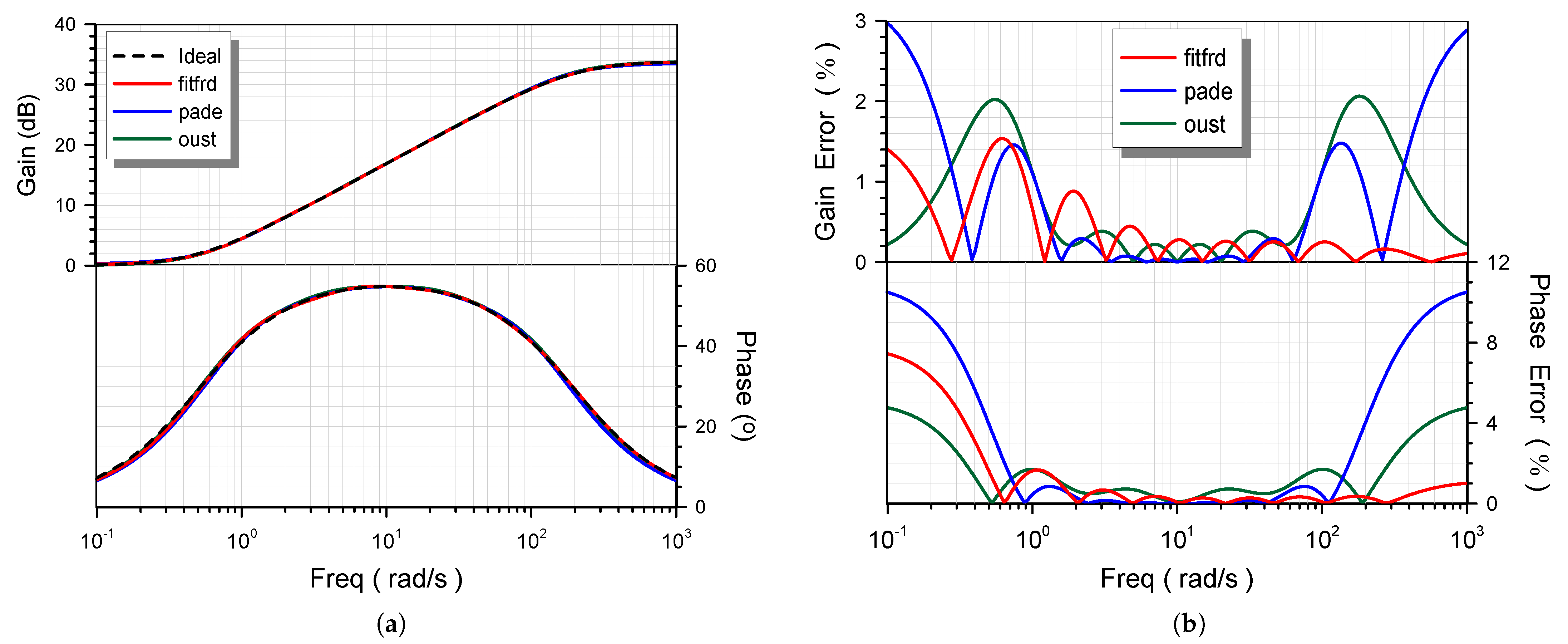

| Scaling Factors | Time Constants | ||
|---|---|---|---|
| Variable | Value | Variable | Value |
| 49.044 | |||
| 33.780 | (ms) | 5.9 | |
| 9.840 | (ms) | 20.1 | |
| 3.328 | (ms) | 91 | |
| 1.074 | (ms) | 480.9 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Memlikai, E.; Kapoulea, S.; Psychalinos, C.; Baranowski, J.; Bauer, W.; Tutaj, A.; Piątek, P. Design of Fractional-Order Lead Compensator for a Car Suspension System Based on Curve-Fitting Approximation. Fractal Fract. 2021, 5, 46. https://doi.org/10.3390/fractalfract5020046
Memlikai E, Kapoulea S, Psychalinos C, Baranowski J, Bauer W, Tutaj A, Piątek P. Design of Fractional-Order Lead Compensator for a Car Suspension System Based on Curve-Fitting Approximation. Fractal and Fractional. 2021; 5(2):46. https://doi.org/10.3390/fractalfract5020046
Chicago/Turabian StyleMemlikai, Evisa, Stavroula Kapoulea, Costas Psychalinos, Jerzy Baranowski, Waldemar Bauer, Andrzej Tutaj, and Paweł Piątek. 2021. "Design of Fractional-Order Lead Compensator for a Car Suspension System Based on Curve-Fitting Approximation" Fractal and Fractional 5, no. 2: 46. https://doi.org/10.3390/fractalfract5020046
APA StyleMemlikai, E., Kapoulea, S., Psychalinos, C., Baranowski, J., Bauer, W., Tutaj, A., & Piątek, P. (2021). Design of Fractional-Order Lead Compensator for a Car Suspension System Based on Curve-Fitting Approximation. Fractal and Fractional, 5(2), 46. https://doi.org/10.3390/fractalfract5020046












