Physics of the Unsteady Response of Turbine Cascade to Pulsed Flow Conditions †
Abstract
1. Introduction
2. Methodology
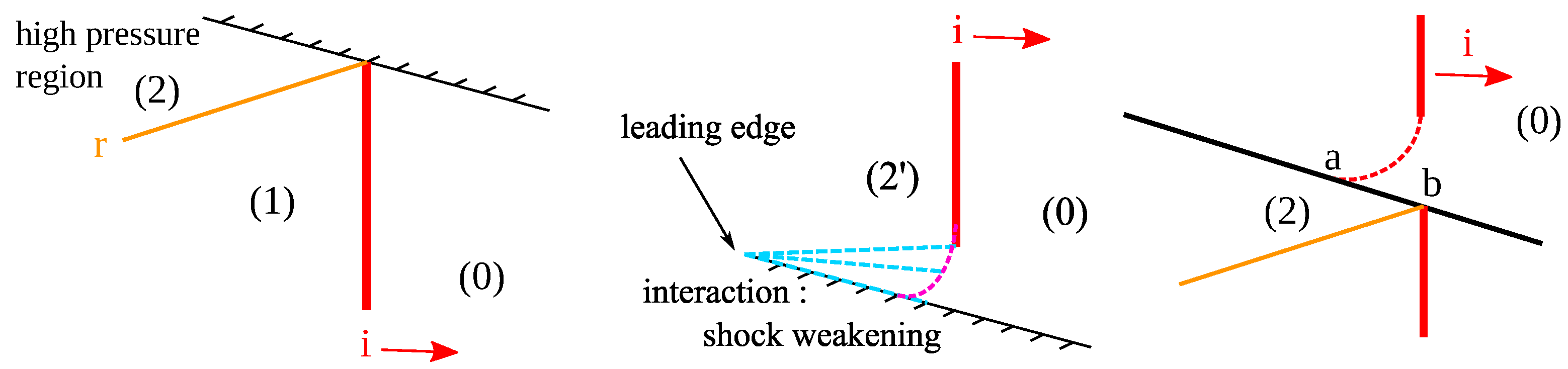
2.1. Physical Origin of the Overloading
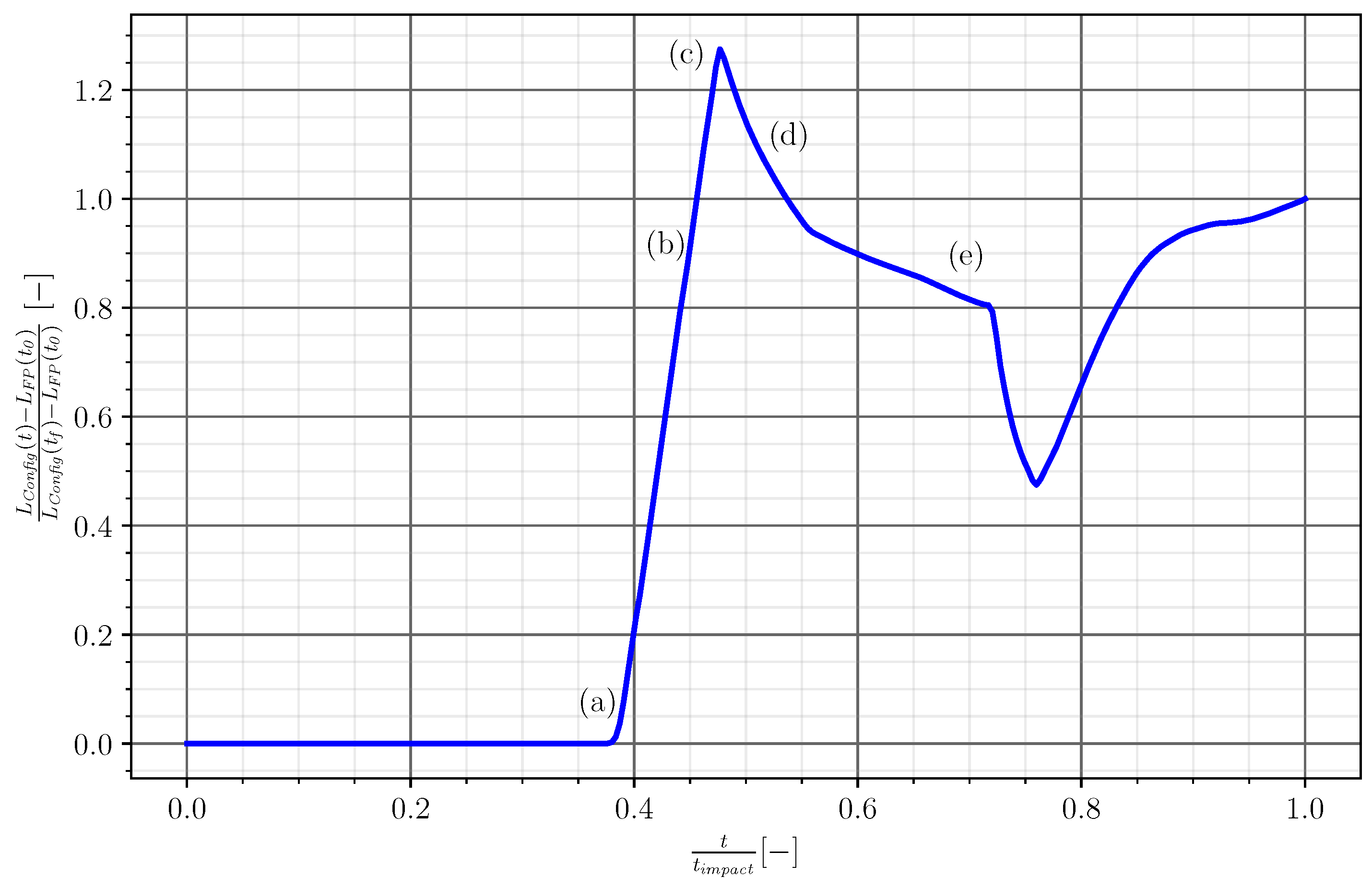
- A portion of the flat plate, the length [a,b] in Figure 1 (right), is submitted to a strong difference of pressure during the propagation of the shock-wave.
2.2. Numerical Method
2.2.1. Geometries Investigated
2.2.2. Solver
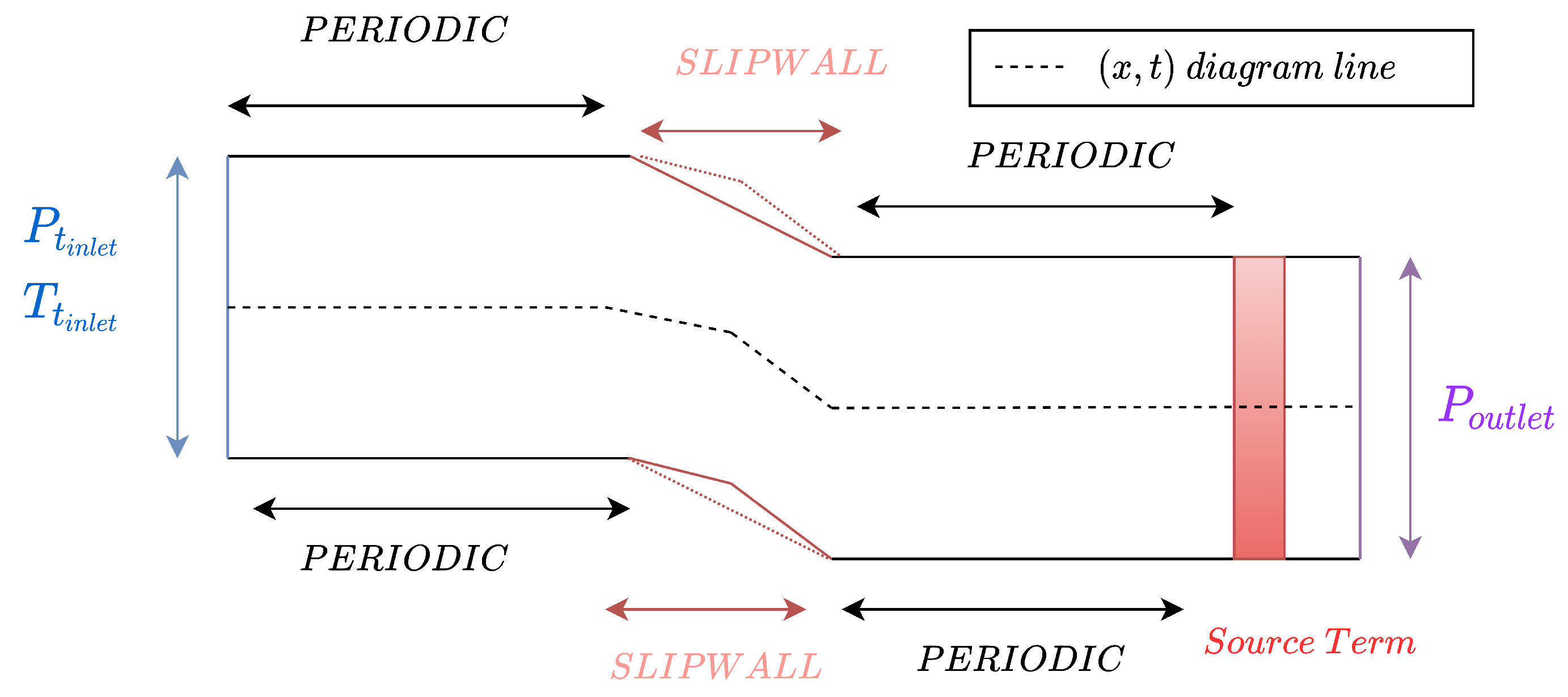
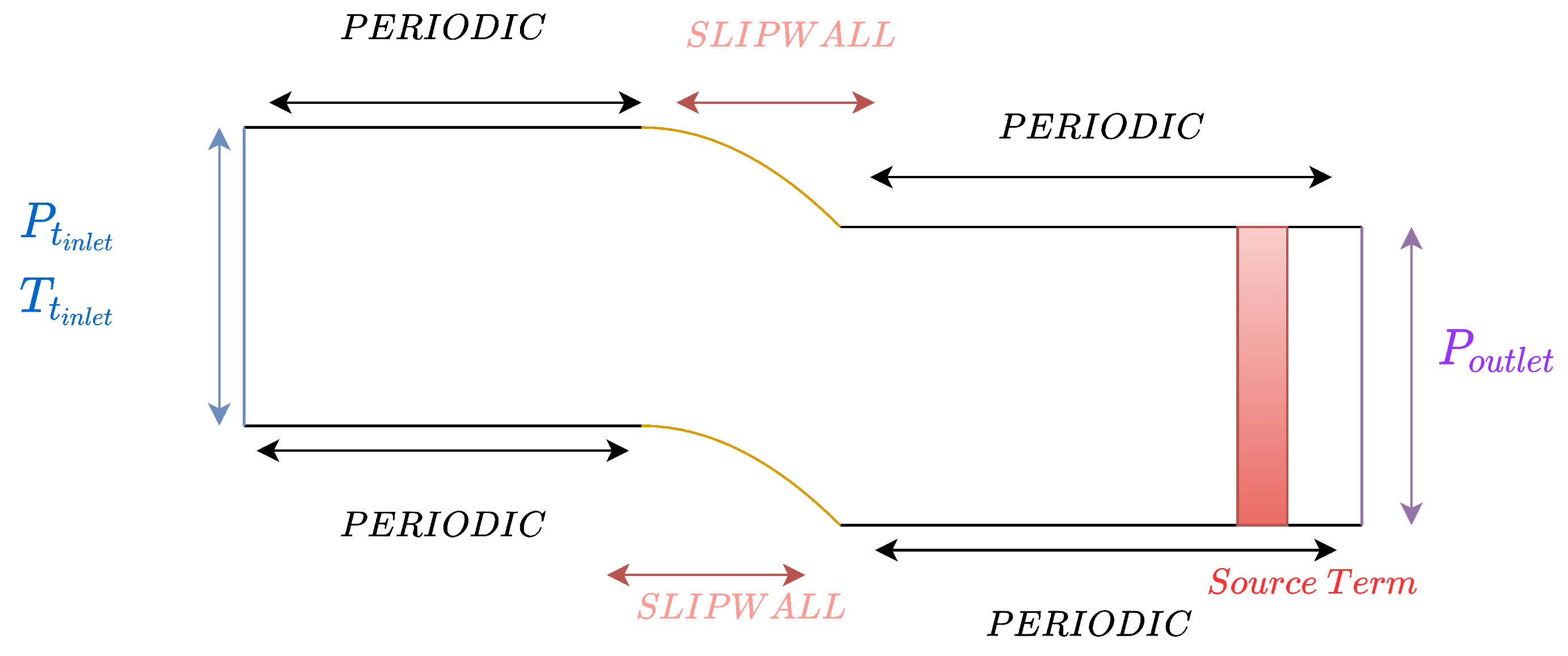
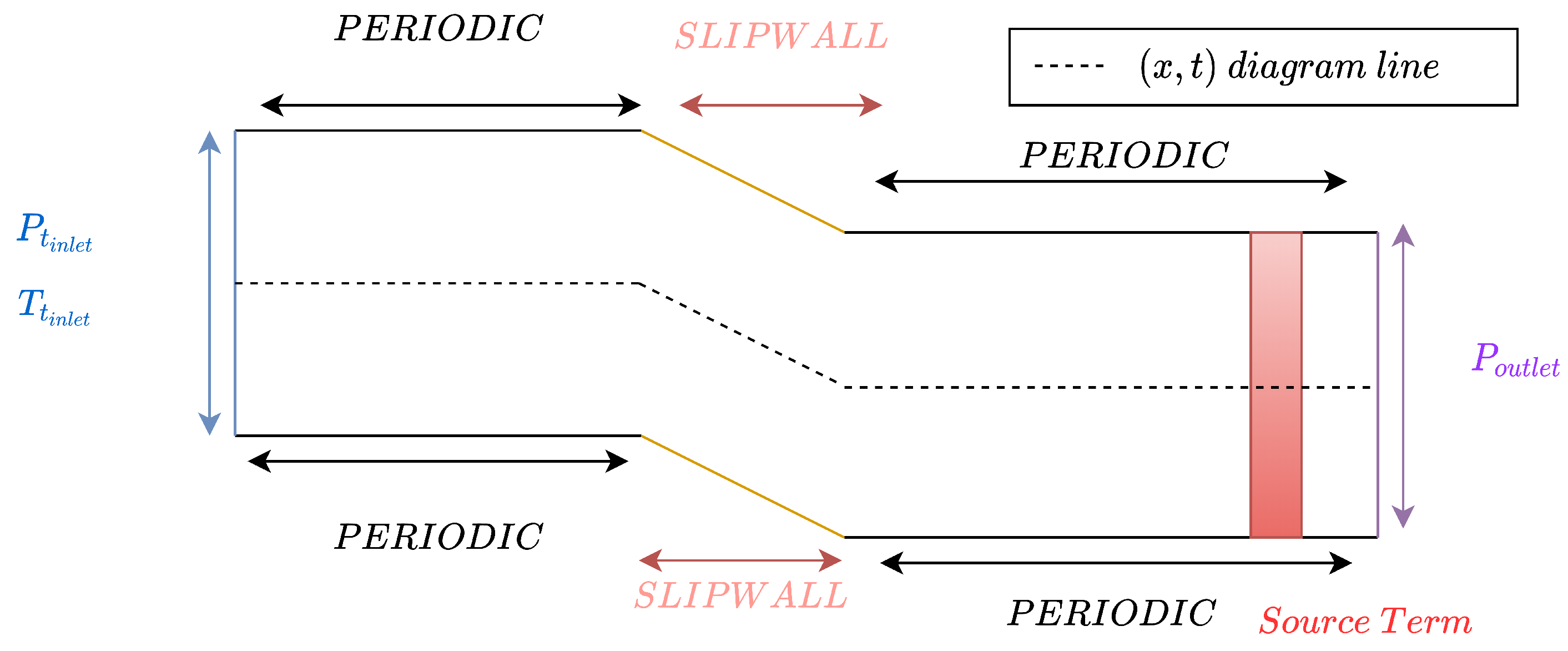
2.2.3. Numerical Domain
2.2.4. Source Term to Model a Converging/Diverging Geometry
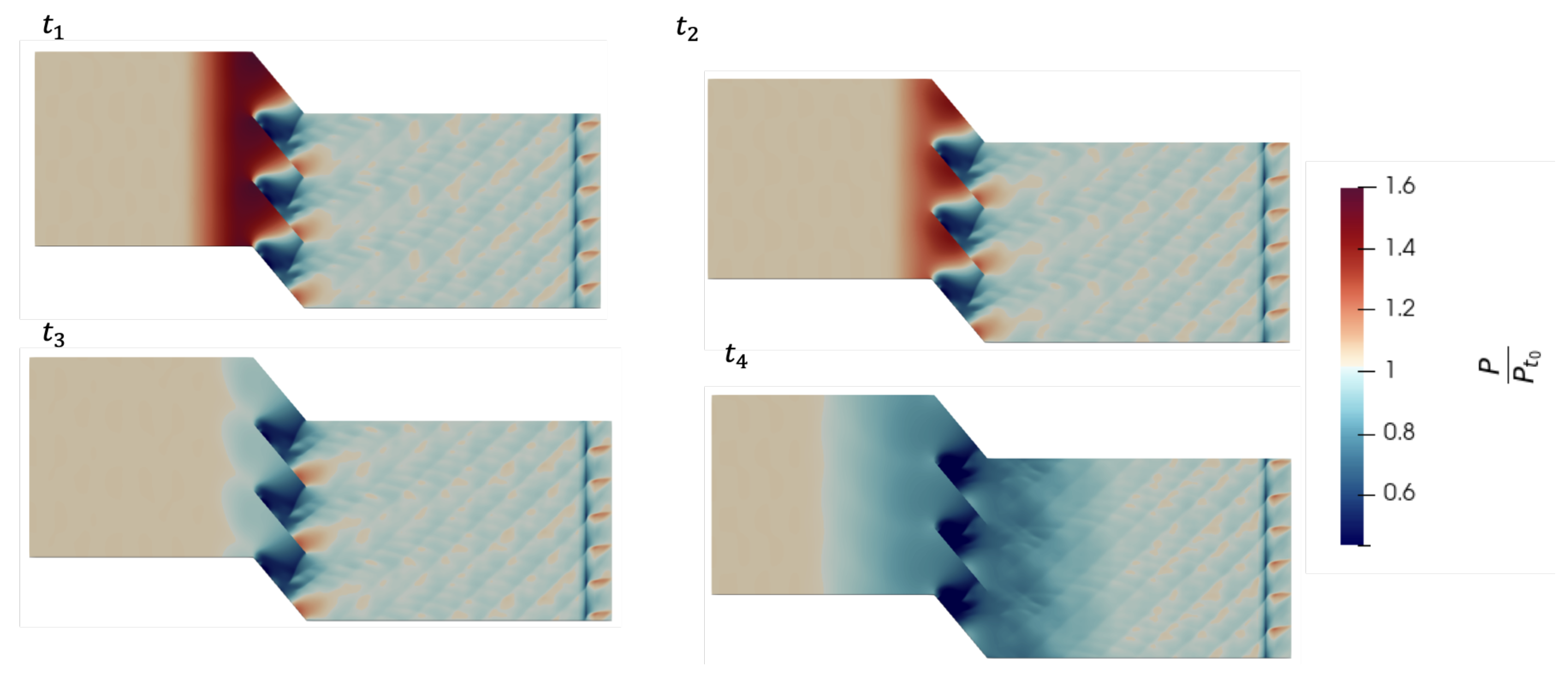
3. Results
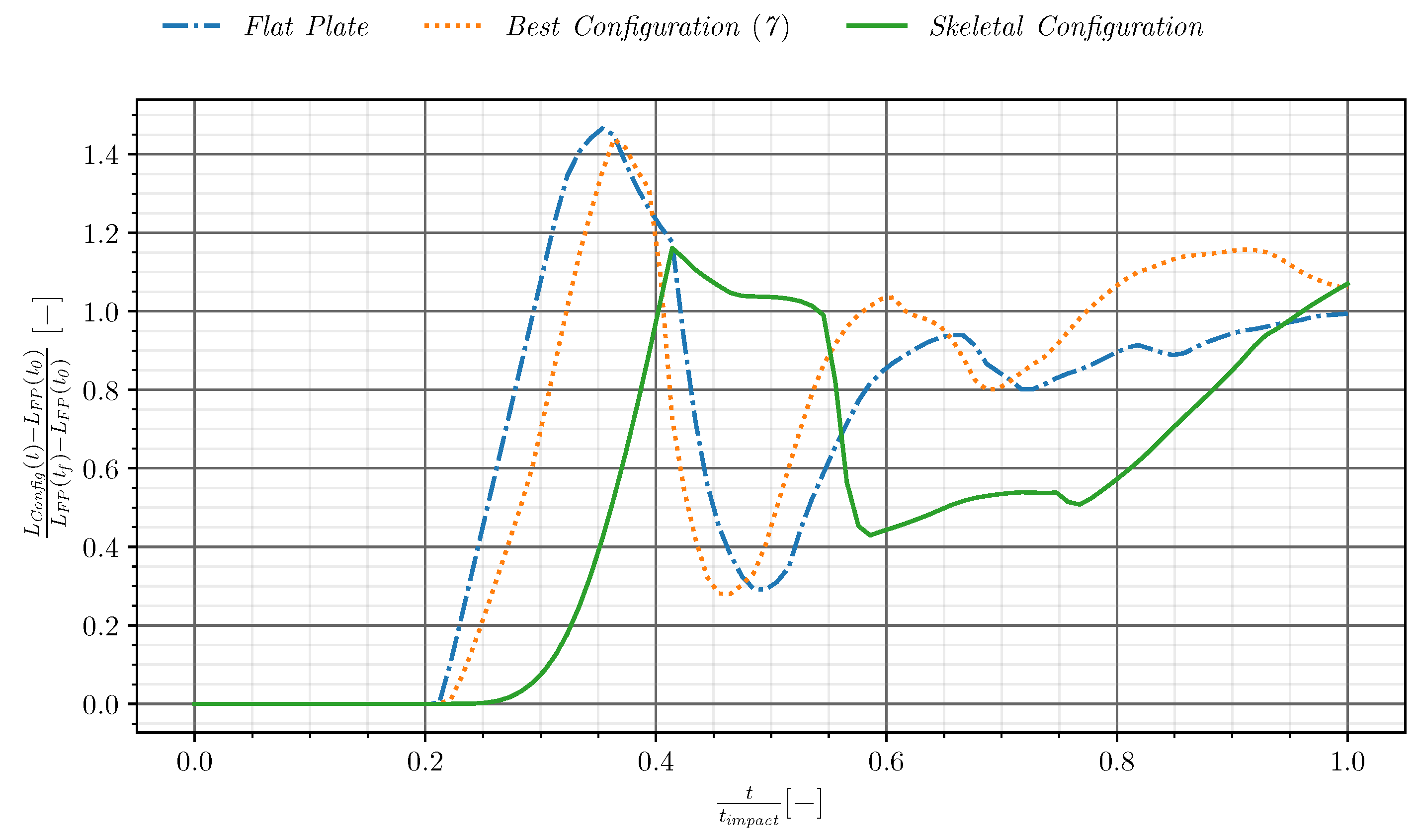
3.1. Results for an Isolated Flat Plate
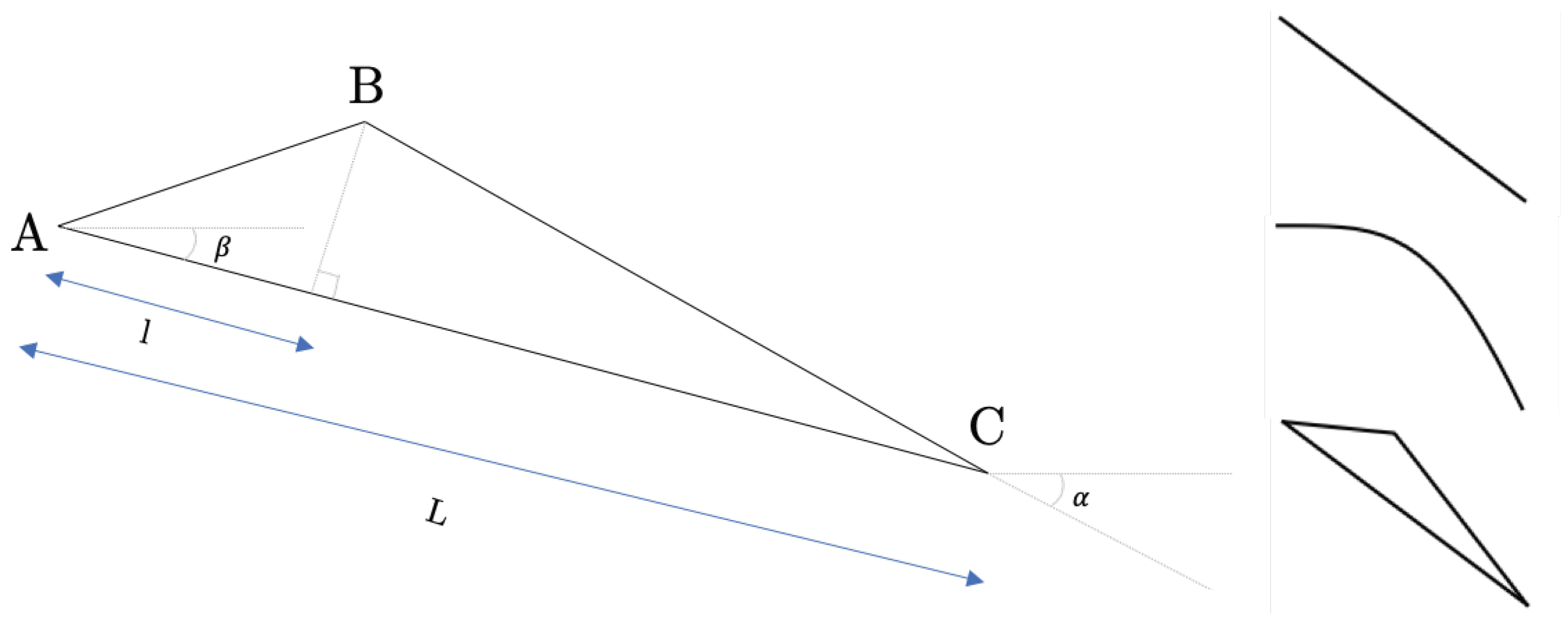
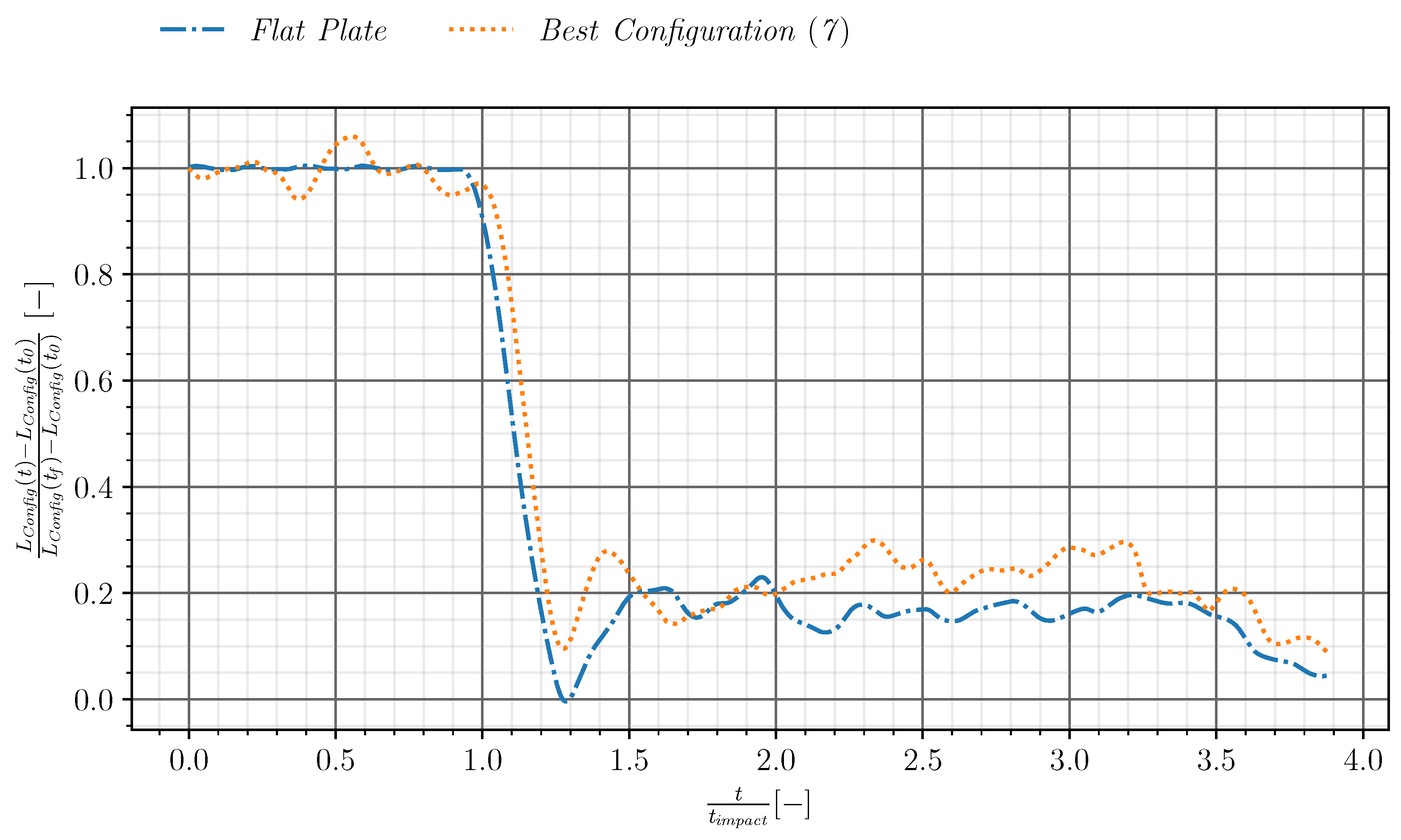
3.2. Parametric Study of the Triangle-Shaped Profile
3.2.1. Design of Experiment Configuration
- The chordwise position of B on the pressure surface;
- The trailing edge angle ;
- The angle .
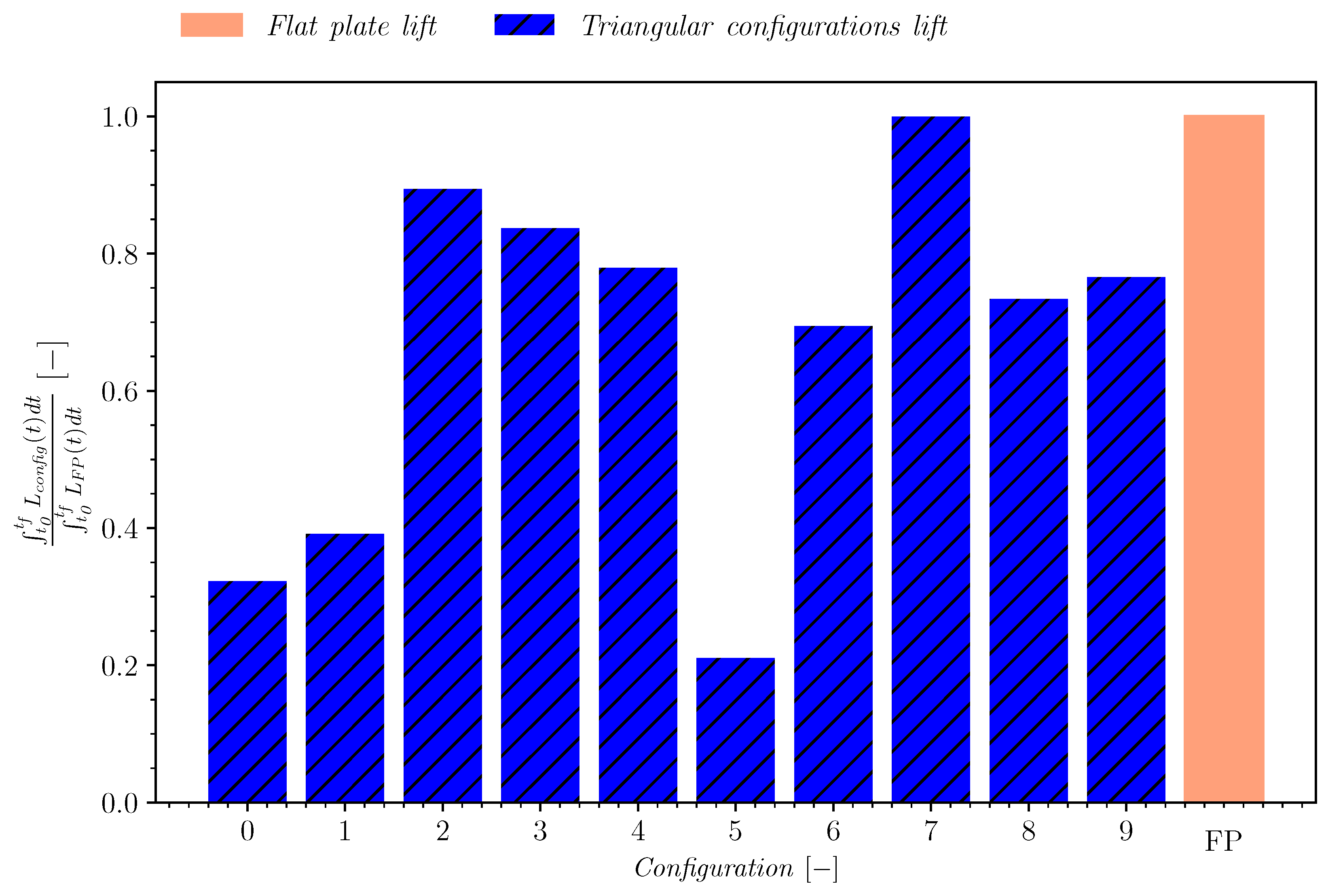
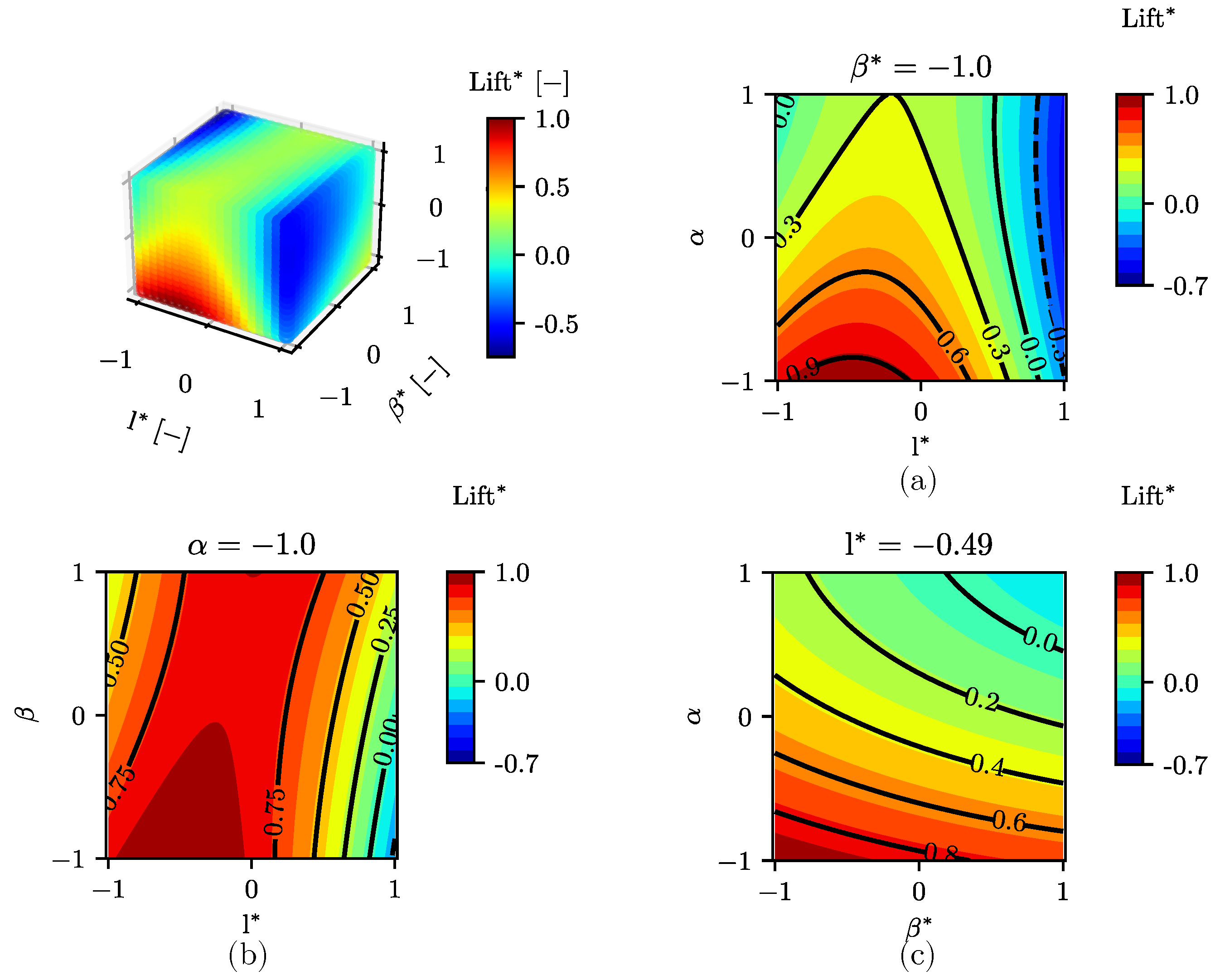
3.2.2. Results of the Design of Experiments
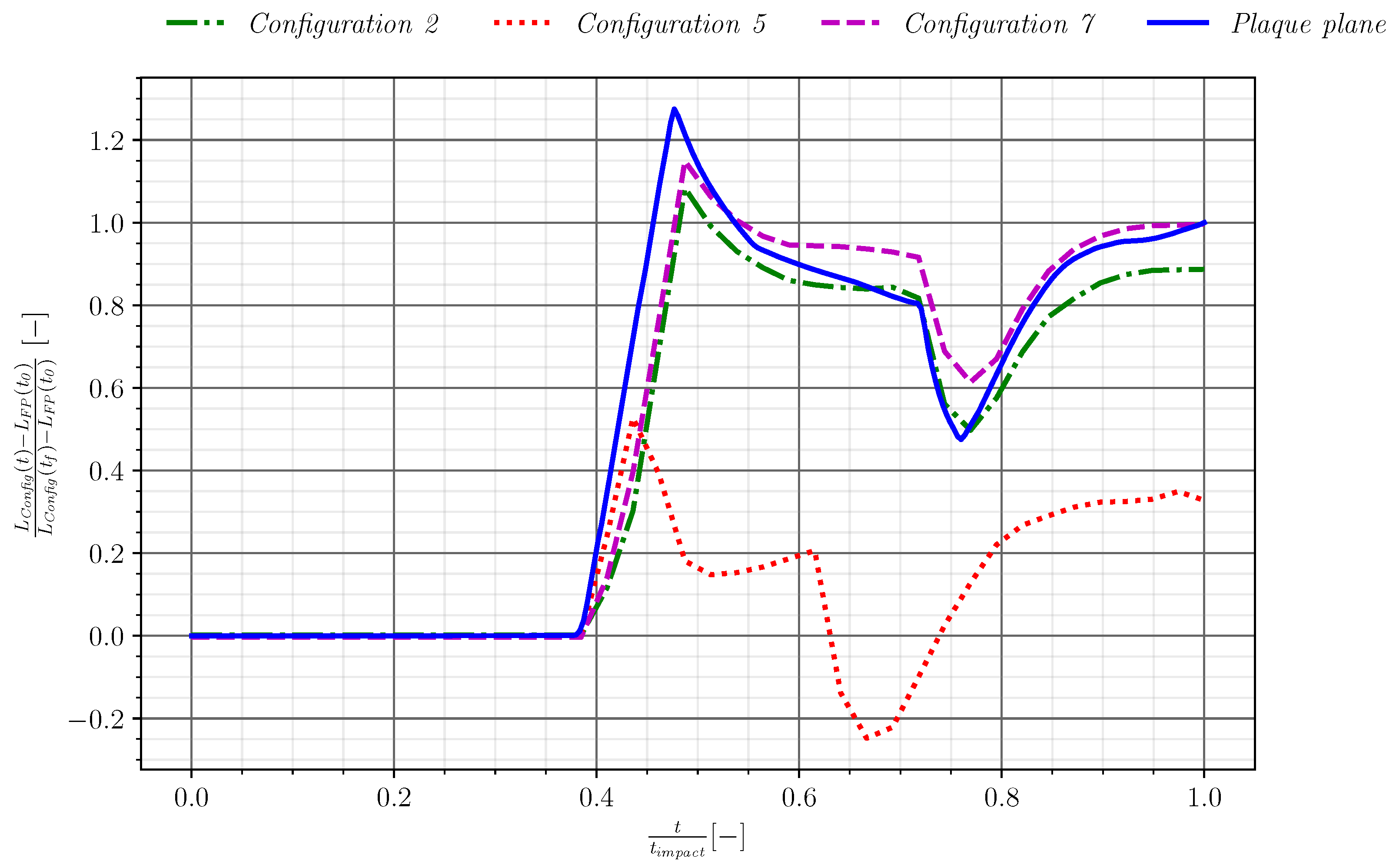
3.2.3. Influence of Solidity
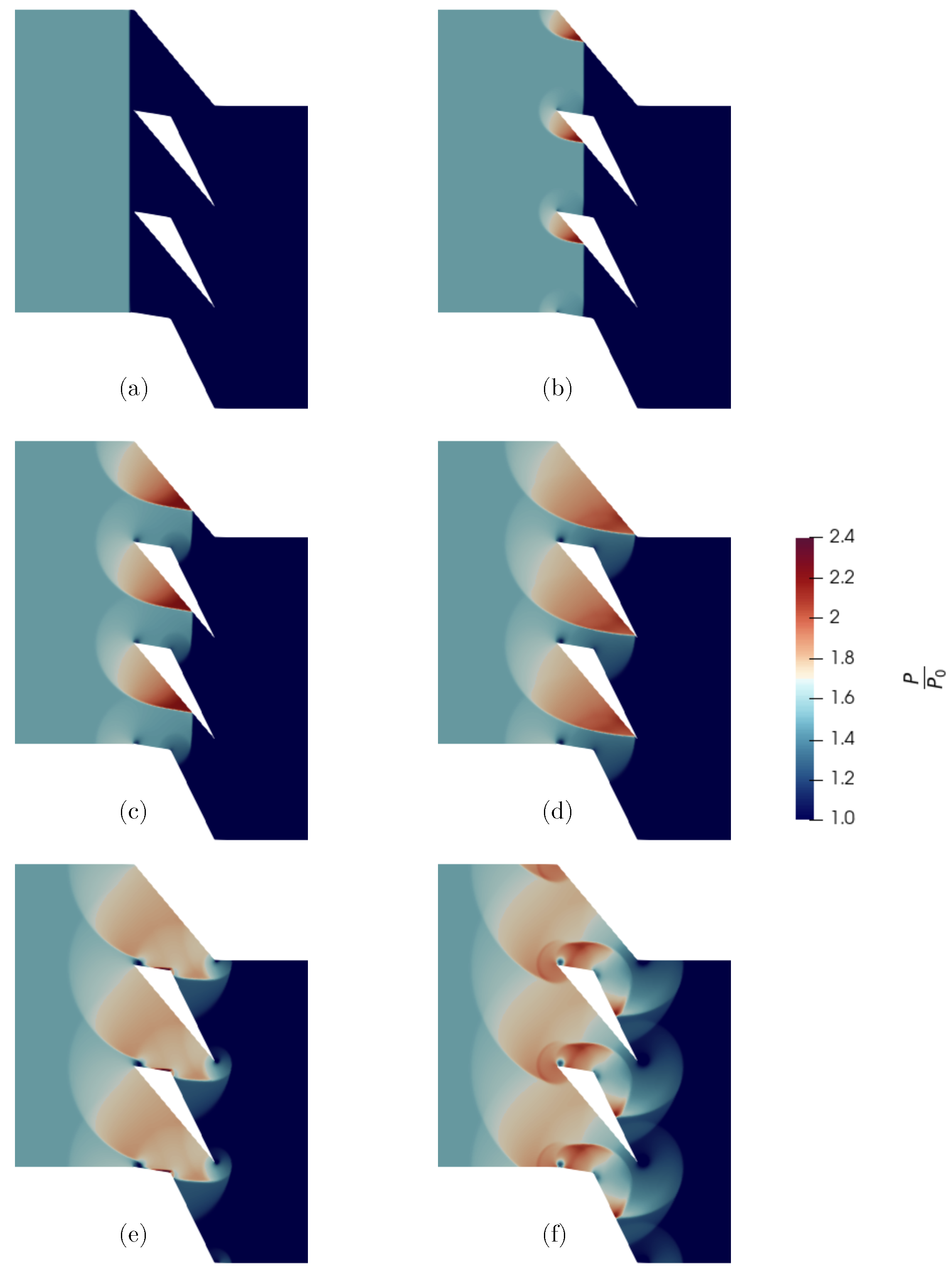
3.3. Complete Stage Configuration
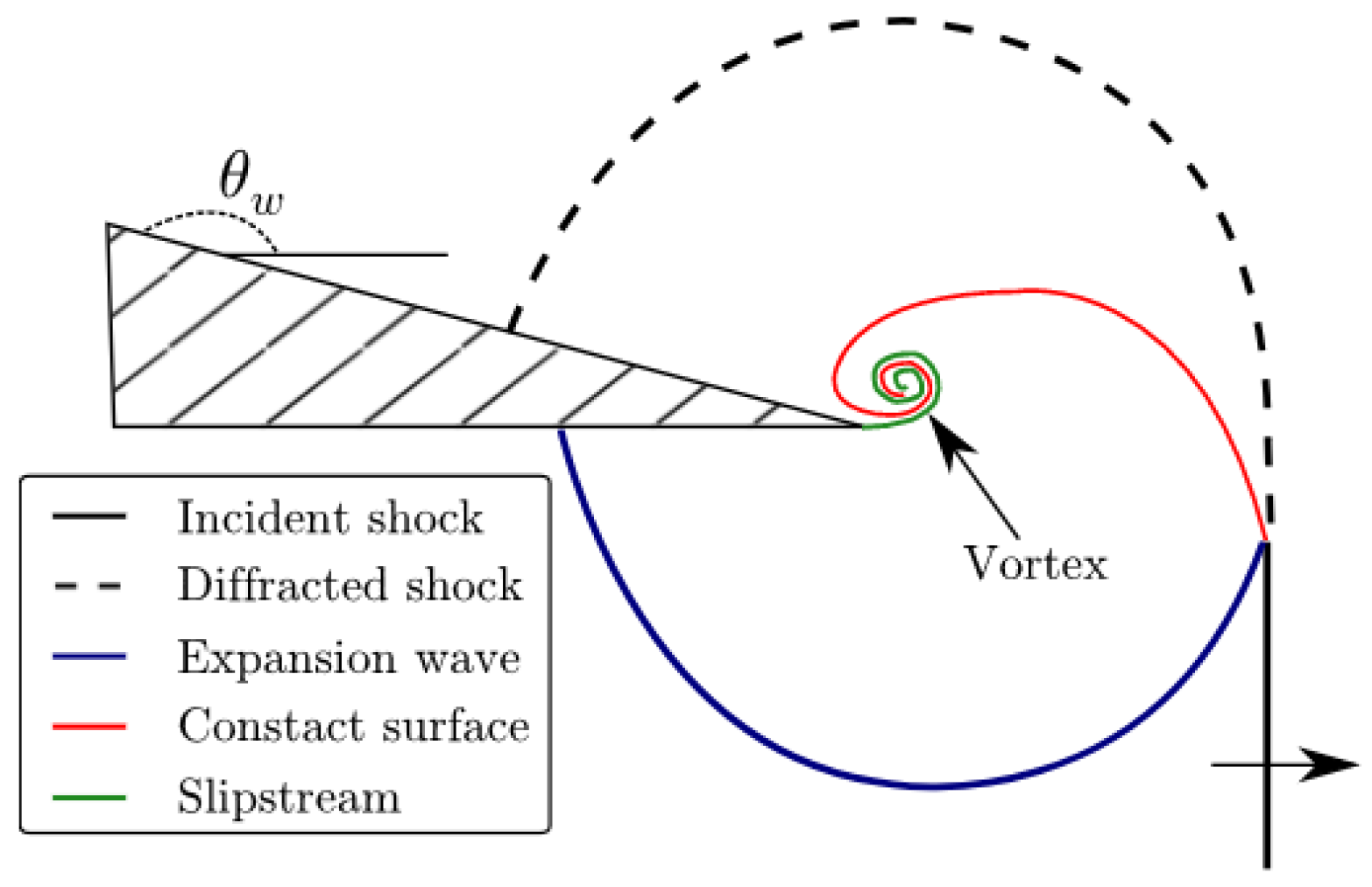
3.4. Expansion Wave Propagation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Chord [m] | |
| a | Speed of sound [] |
| U | Translation Speed of the blade [] |
| S | Source term |
| A | Section |
| Flat Plate | |
| L | Lift force [N] |
| Total Pressure [] | |
| Total Temperature [K] | |
| Initial time [s] | |
| Time when the first wave impacts outlet boundary condition [s] | |
| Pressure ratio [-] | |
| Length parameter of the triangle [] | |
| First angle parameter of the triangle [°] | |
| Second angle parameter of the triangle [°] | |
| Normalized length parameter of the triangle [-] | |
| Normalized lift [-] | |
| / [-] | |
| Subscripts | |
| Inlet | |
| Outlet | |
| x | Axial coordinate |
| i | Incident shockwave |
| r | Reflected shockwave |
References
- Anand, V.; George, A.; Knight, E.; Gutmark, E. Investigation of pulse detonation combustors–Axial turbine system. Aerosp. Sci. Technol. 2019, 93, 105350. [Google Scholar] [CrossRef]
- Naples, A.; Hoke, J.; Battelle, R.; Schauer, F. T63 Turbine response to rotating detonation combustor exhaust flow. J. Eng. Gas Turbines Power 2019, 141, 021029. [Google Scholar] [CrossRef]
- Sousa, J.; Paniagua, G.; Morata, E.C. Thermodynamic analysis of a gas turbine engine with a rotating detonation combustor. Appl. Energy 2017, 195, 247–256. [Google Scholar] [CrossRef]
- Yokoo, R.; Goto, K.; Kasahara, J.; Athmanathan, V.; Braun, J.; Paniagua, G.; Meyer, T.R.; Kawasaki, A.; Matsuoka, K.; Matsuo, A.; et al. Experimental study of internal flow structures in cylindrical rotating detonation engines. Proc. Combust. Inst. 2021, 38, 3759–3768. [Google Scholar] [CrossRef]
- George, A.; Driscoll, R.; Gutmark, E.; Munday, D. Experimental Comparison of Axial Turbine Performance Under Steady and Pulsating Flows. J. Turbomach. 2014, 136, 111005. [Google Scholar] [CrossRef]
- Hermet, F. Simulation des Transitoires Violents et des Ecoulements Pulses Dans les Turbines. Ph.D. Thesis, ISAE-SUPAERO, Toulouse, France, 2021. Available online: http://www.theses.fr/2021ESAE0005/document (accessed on 8 November 2023).
- Binder, N.; Bousquet, Y.; Hermet, F. Physics and Instantaneous Performance of Radial Turbines in Unsteady Flows: Validity of the Quasi-Steady Assumption for the Rotor. J. Turbomach. 2022, 144, 281–287. [Google Scholar] [CrossRef]
- Ben-Dor, G. Shock Wave Reflection Phenomena, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Raphael, L.; Jeremie, G.; Gilles, G. High-Order Compact Limiter Based on Spatially Weighted Projections for the Spectral Volume and the Spectral Differences Method. J. Sci. Comput. 2016, 67, 375–403. [Google Scholar] [CrossRef]
- Saez-Mischlich, G. High Order Numerical Methods for Unstructured Grids and Sliding Mesh. Ph.D. Thesis, ISAE-SUPAERO, Toulouse, France, 2021. Available online: http://www.theses.fr/2021ESAE0024/document (accessed on 8 November 2023).
- Hermet, F.; Binder, N.; Gressier, J.; Sáez-Mischlich, G. Pulsed Flow Turbine Design Recommendations. Int. J. Turbomach. Propuls. Power 2021, 6, 24. [Google Scholar] [CrossRef]
- Hermet, F.; Binder, N.; Gressier, J. Shock motion inside a varying cross-section channel and consequences on the downstream flow. Phys. Rev. Fluids 2021, 6, 044802. [Google Scholar] [CrossRef]
- Grebert, A. Simulations of shock wave/turbulent boundary layer interaction with upstream micro vortex generators. Int. J. Heat Fluid Flow 2018, 72, 73–85. [Google Scholar] [CrossRef]
- Richardson, L.F. Perspective: The Deferred Approach to the Limit. Philos. Trans. R. Soc. Lond. 1994. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: A Method for Uniform Reporting of Grid Refinement Studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Goupy, J. Ntroduction aux Plans d’Experiences, 2nd ed.; Dunod: Malakoff, France, 2001. [Google Scholar]
- Hermet, F.; Binder, N.; Gressier, J. Transient flow in infinitely thin airfoil cascade. In Proceedings of the 13 th European Conference on Turbomachinery Fluid dynamics & Thermodynamics, Lausanne, Switzerland, 8–12 April 2019. [Google Scholar] [CrossRef]
- Bertojo, P.; Binder, N.; Gressier, J. Effect of thickness on the unsteady response of turbine submitted to pulsed flow conditions. In Proceedings of the 15th European Turbomachinery Conference, Paper n. ETC2023-247, Budapest, Hungary, 24–28 April 2023; Available online: https://www.euroturbo.eu/publications/proceedings-papers/etc2023-247 (accessed on 8 November 2023).





| Code Number | |||
|---|---|---|---|
| −1 | 0.3 | 50 | 0.75 |
| 0 | 0.5 | 60 | 1.0 |
| 1 | 0.7 | 70 | 1.25 |
| Simulation Number | |||
|---|---|---|---|
| 0 | 0 | 1 | −1 |
| 1 | 0 | 0 | 0 |
| 2 | 1 | −1 | −1 |
| 3 | 1 | 0 | 1 |
| 4 | −1 | 1 | 1 |
| 5 | 1 | 1 | 0 |
| 6 | −1 | −1 | 0 |
| 7 | −1 | 0 | −1 |
| 8 | 0 | −1 | 1 |
| 9 | −1 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Bertojo, P.; Binder, N.; Gressier, J. Physics of the Unsteady Response of Turbine Cascade to Pulsed Flow Conditions. Int. J. Turbomach. Propuls. Power 2024, 9, 19. https://doi.org/10.3390/ijtpp9020019
Bertojo P, Binder N, Gressier J. Physics of the Unsteady Response of Turbine Cascade to Pulsed Flow Conditions. International Journal of Turbomachinery, Propulsion and Power. 2024; 9(2):19. https://doi.org/10.3390/ijtpp9020019
Chicago/Turabian StyleBertojo, Pierre, Nicolas Binder, and Jeremie Gressier. 2024. "Physics of the Unsteady Response of Turbine Cascade to Pulsed Flow Conditions" International Journal of Turbomachinery, Propulsion and Power 9, no. 2: 19. https://doi.org/10.3390/ijtpp9020019
APA StyleBertojo, P., Binder, N., & Gressier, J. (2024). Physics of the Unsteady Response of Turbine Cascade to Pulsed Flow Conditions. International Journal of Turbomachinery, Propulsion and Power, 9(2), 19. https://doi.org/10.3390/ijtpp9020019






