Next Article in Journal
Sci: An Inclusive, Multidisciplinary Scientific Journal
Next Article in Special Issue
σ-Hole Bonds and the VSEPR Model—From the Tetrahedral Structure to the Trigonal Bipyramid
Previous Article in Journal
Neisseria mucosa Does Not Inhibit the Growth of Neisseria gonorrhoeae
Previous Article in Special Issue
Malonaldehyde-like Systems: BeF2 Clusters—A Subtle Balance between Hydrogen Bonds, Beryllium Bonds, and Resonance
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sci
Volume 4
Issue 1
10.3390/sci4010009
sci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Halogen-Bonded Driven Tetra-Substituted Benzene Dimers and Trimers: Potential Hosts for Metal Ions

by
Rubén D. Parra
Department of Chemistry and Biochemistry, DePaul University, Chicago, IL 60614, USA
Sci 2022, 4(1), 9; https://doi.org/10.3390/sci4010009
Submission received: 29 November 2021 / Revised: 28 January 2022 / Accepted: 22 February 2022 / Published: 25 February 2022
(This article belongs to the Special Issue Define What Is Not Defined: In Chemistry and Beyond)
Browse Figures
Versions Notes

Abstract

:
Cyclic dimers and trimers of tetra-substituted benzenes, ((HOOC)2-C6H2-(NHI)2), are selected as convenient model systems for investigating NI…O=C halogen bond strength and cooperativity. The four substituents in benzene are chosen so that two of them act as halogen bond acceptors (COOH) and two act as halogen bond donors (NHI), as shown in the graphical abstract below. The potential for metal ion binding by each of the halogen-bonded aggregates is also investigated using the monoatomic sodium ion, Na+. Density functional theory calculations performed using the wB97XD functional and the DGDZVP basis set confirmed the ability of halogen bonding to drive the formation of the cyclic dimers and trimers of the model system chosen for this study. Evidence of halogen bond cooperativity is seen, for example, in a 9% shortening of each NI…O=C halogen bond distance with a corresponding 53% increase in the respective critical point density value, ρNI…O=C. Cooperativity also results in a 36% increase in the magnitude of the complexation energy per halogen-bond of the trimer relative to that of the dimer. The results of this study confirm the potential for binding a single Na+ ion by either the dimer or the trimer through their respective halogen-bond networks. Binding of two metal ions was shown to be possible by the dimer. Likewise, the trimer was also found to bind three metal ions. Lastly, the overall structure of the halogen-bonded dimer or trimer endured after complexation of the Na+ ions.

1. Introduction

The ability of individual molecules to interact with one another through noncovalent interactions opens up a world of molecular assemblies with practically boundless structure–function possibilities. Indeed, an entire field, supramolecular chemistry, specializes in the creative use of the entire intermolecular interaction toolkit for the judicious design of novel molecular assemblies or supramolecules [1,2,3,4,5,6]. Supramolecular scientists tend to use van der Waals, dipole–dipole, ion–dipole, ion–ion, π-bonding, and hydrogen-bonding interactions to bring together molecules into assemblies with desired functionalities. Because of their directional and tunable character, hydrogen bonds appear among the most commonly utilized noncovalent interactions. More recently, other interactions have been realized and added to the noncovalent interaction toolkit. Such interactions include the tetrel, pnicogen, chalcogen, and halogen bonds [7,8,9,10,11,12,13]. With these additional interactions, there is even more versatility in the intermolecular interaction toolbox, substantially expanding the horizons of what can be achieved in the field of supramolecular chemistry.
One function an assembly of molecules can be, and often is, designed for is to host a neutral or electrically charged guest. To achieve this goal, a fundamental two-folded challenge needs to be considered. On the one hand, the host must possess properly situated binding sites for the guest. On the other hand, the assembly of molecules making up the host must also be strategically designed with strong-enough intermolecular forces to prevent the falling apart of the supramolecular host structure upon binding of the guest. The intermolecular interaction toolkit provides the necessary building blocks to meet successfully this two-folded challenge. Certainly, the more versatile the toolkit is and the deeper our understanding of noncovalent interactions is, the better equipped we become to develop highly effective supramolecular structures tailored to specific functions.
Over the last two decades, halogen bonds have attracted considerable attention for the design and synthesis of molecular assemblies, including self-assembling towards nanostructured polymeric materials [14,15,16,17,18,19,20]. One distinctive feature of the halogen atoms participating in halogen bonding is their amphoteric character that enables them to act as a Lewis base in the direction perpendicular to the halogen bond itself [21,22]. The size and polarizability of the halogen atoms themselves provide additional flexibility for fine-tuning the halogen bond interactions, as well as their Lewis base capabilities. Recent studies have demonstrated the ability of carefully designed cyclic halogen-bonded aggregates to develop a sufficiently electron-rich cavity to host a metal ion of suitable size [23,24]. Although still in its infancy, the potential of the halogen-bonded networks to recognize and bind cations clearly complement their known ability for anion recognition and coordination [25,26]. In the work presented here, the ability of halogen bonds to drive the self-assembly of molecular aggregates into cyclic structures with well-defined interior cavities is further investigated computationally within the framework of density functional theory. Additionally, the ability of the cyclic halogen-bonded structures to bind metal ions via the halogen-bonded network is also investigated. The motivation to investigate ion-complexes stems from their importance in deepening our understanding of the distinctive features of ion recognition, which would then help in the effective design and development of metal ion receptors, for example. Indeed, the study of metal ion-receptor binding affinity has proven valuable in the understanding of such processes as ion-transfer, enzyme catalysis, and inhibition [27,28,29]. Among metal ions, sodium ion is one of the most abundant in biological systems, and it has been shown to play a chief role in several processes such as the stabilization of protein structures and the promotion of protein function and enzyme activity [30,31,32]. It is then of fundamental importance to investigate the sodium binding affinity by a potential receptor. The work presented here provides insight on the ability of a halogen-bonded network to bind a sodium ion, in particular the coordination sites and the combination of noncovalent interactions that can support the binding of the metal ion. A convenient model system chosen here is based on the structure of 4,6-diamino isophthalic acid, ((HOOC)2-C6H2-(NHI)2), replacing one of the NH2 hydrogens of each amino group with a halogen atom, specifically, with an iodine atom. Among all the halogen atoms, and under similar environments, the iodine atom is known to produce the strongest halogen bonds, given its large size and polarizability. The relatively large electronegativity of the nitrogen atom makes the halogen atom even better suited for halogen bonding. Moreover, the potential for intramolecular, O-H…NHI hydrogen bonding can be used to enhance a halogen bond interaction involving the NHI unit, such as that with the carbonyl oxygen atom of one of the COOH groups in another molecule.

2. Methodology

Geometry optimizations, frequency calculations, interaction energy calculations, and molecular electrostatic potentials were carried out using the GAUSSIAN 16 program [33]. Calculations were performed with the wB97XD implementation of density functional theory and the DGDZVP basis set. Frequency calculations were used to determine the nature (minimum or saddle point) of the optimized geometries reported in this study. Interaction energies were all corrected for basis set superposition error (BSSE) using the Boys–Bernardi counterpoise procedure [34]. The theory of atoms in molecules (AIM) of Bader [35,36,37] was employed to examine the electron density at selected intermolecular bond critical points using the AIMALL software package [38].
It is worth noting that the wB97X-D functional has been developed with the capability of capturing both short-range and long-range interactions. Benchmarking studies have shown that wB97X-D performs with satisfactory accuracy, particularly for noncovalent interactions, including halogen bonding [39,40]. The use of the all-electron, double-zeta valence polarized basis set, DGDZVP, for iodine-containing compounds, including halogen bonding, has shown to give reliable results at a much lower computational cost than those using pseudopotential such as the aug-cc-pVTZ-PP basis set [41,42]. Thus, both the relatively small size of DGDZVP and the quality of results it gives for iodine bonding make this basis set a sound choice to investigate halogen bond strengths on large complexes, such as the ones reported in this work.

3. Results and Discussion

3.1. N-I…O=C Halogen Bond

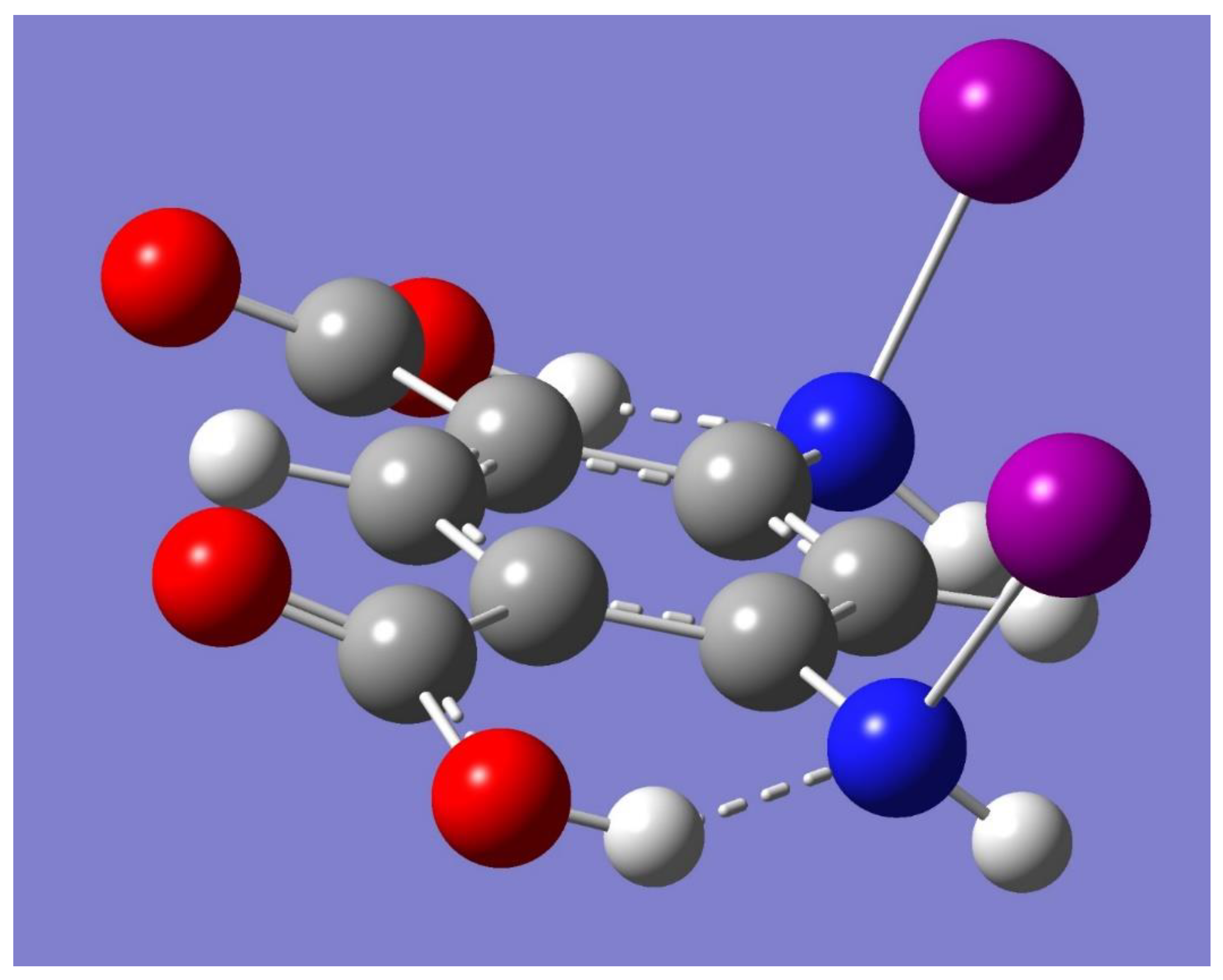
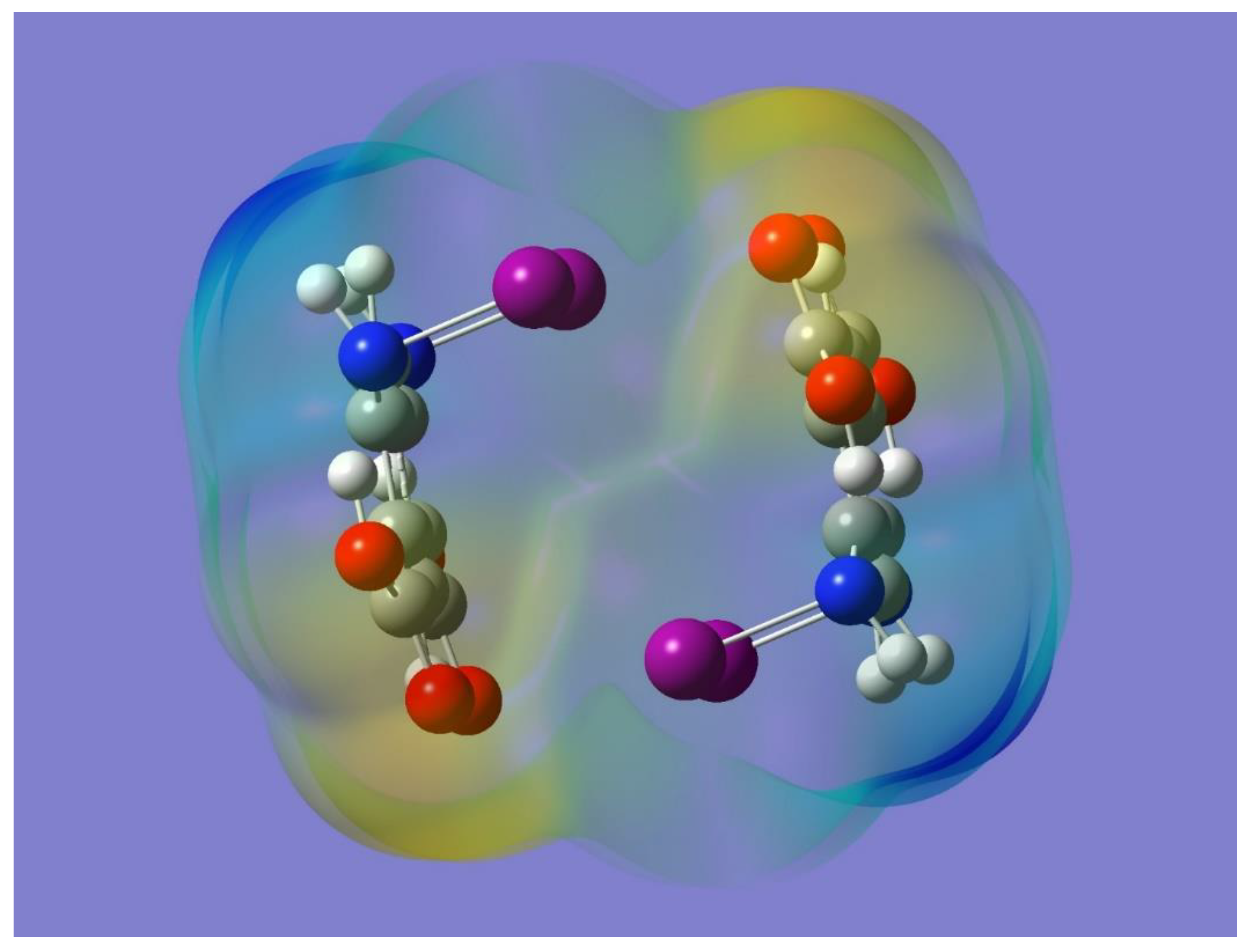
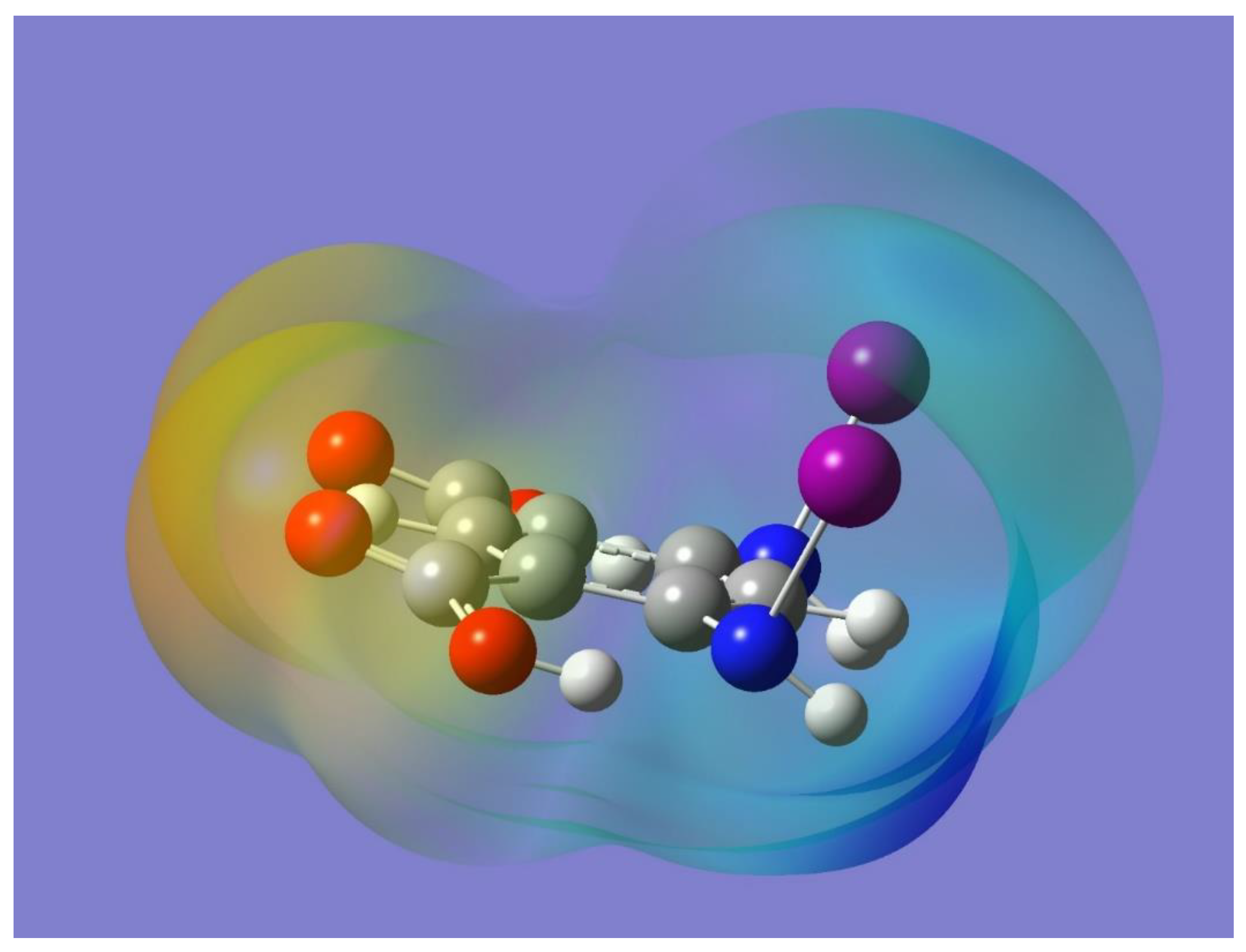
The potential for halogen bonding was first examined by optimizing the monomer and then by considering its electrostatic potential. The optimized geometry of the monomer is displayed in Figure 1. Incidentally, a monomer with the halogen atoms facing in opposite directions with respect to the organic framework was also optimized and found to be a stable minimum with no imaginary frequencies. The two optimized monomers were essentially isoenergetic, although the one used in this work is the one that allows for the intermolecular halogen bonding. The orientation of each O-H bond is conveniently chosen trans to the C=O group in the pertinent carboxy group to allow for intramolecular O-H…N hydrogen bonding with the nitrogen atom of the adjacent NHI group. The intramolecular hydrogen bonding should polarize the corresponding N-I bond, which would then enhance a potential intermolecular N-I…O=C halogen bond interaction. Frequency calculations resulted in no imaginary frequencies, and hence demonstrated that the selected optimized monomer is indeed a minimum on the potential energy surface of the molecule. It has been shown that a halogen atom covalently bonded to a more electronegative element tends to exhibit an asymmetric distribution of electron density with less electron density on the region opposite to the covalent bond than on the region orthogonal to it. The former region has been termed the halogen σ-hole and it usually has a positive electrostatic potential [43]. The presence of the σ-hole on each of the N-I bonds in the optimized monomer can be appreciated in Figure 2 as a light blue region that indicates a corresponding positive electrostatic potential. Also apparent in Figure 2 is the negative electrostatic potential around the oxygen atoms (yellow-red region). It is worth noting that the presence and relative locations of the complementary (positive and negative) electrostatic potentials in the monomer can indeed facilitate the formation of halogen bonding, N-I…O=C, via intermolecular interactions of two or more monomers.
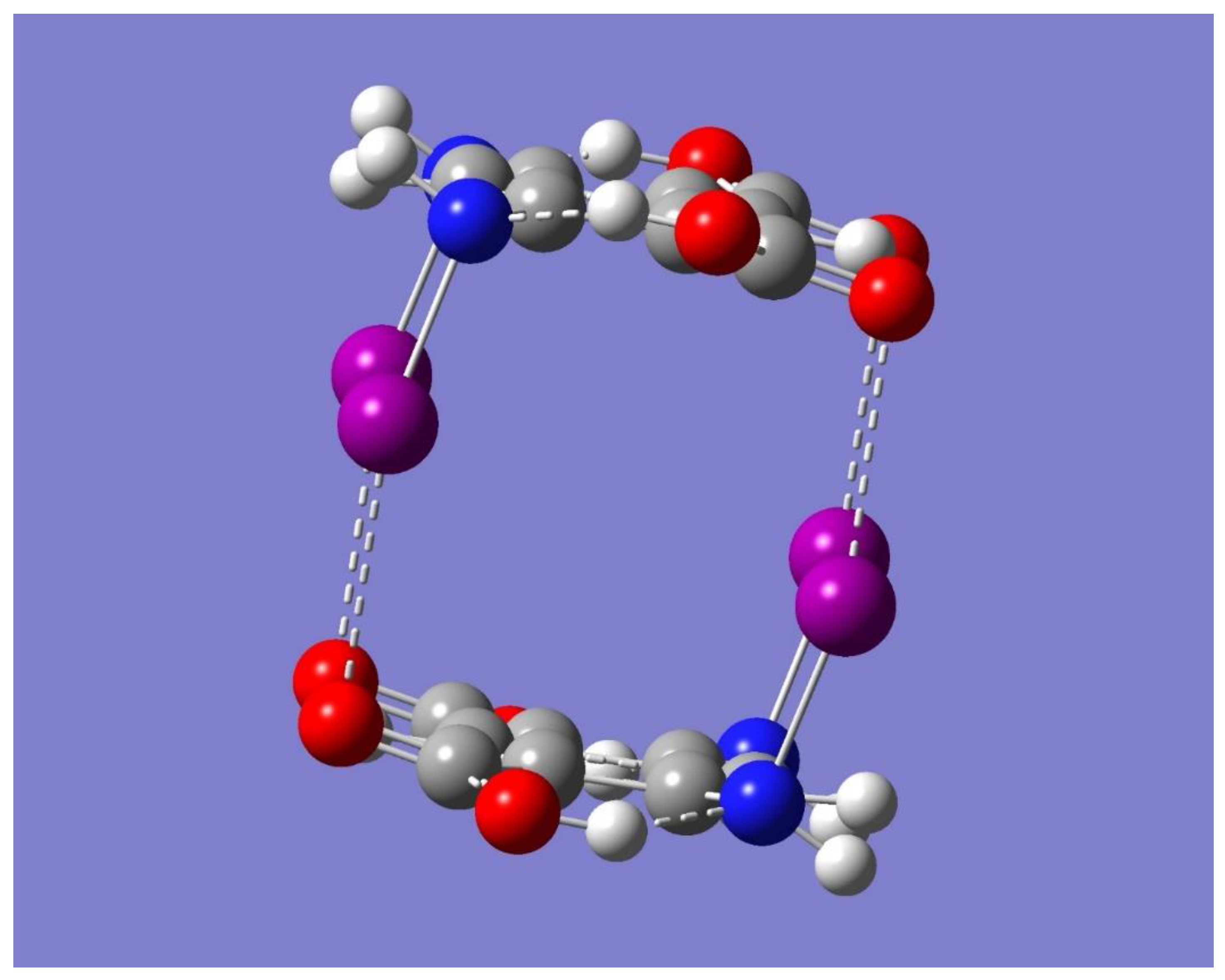
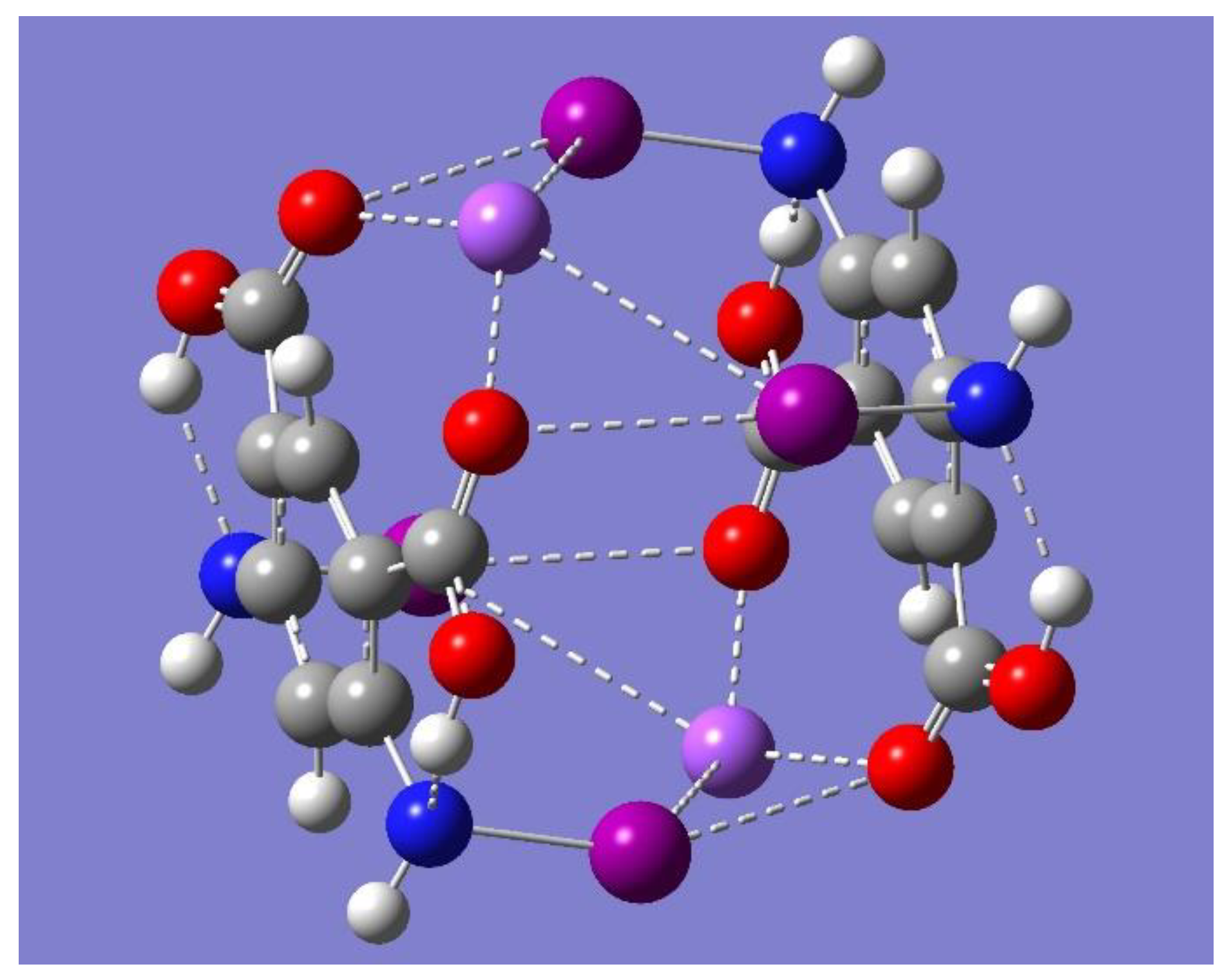
A halogen-bonded driven cyclic dimer can be built by conveniently placing two monomers facing each other with the N-I bonds in one monomer interacting with the carbonyl oxygen atoms in the other monomer. The resulting optimized geometry has C2h symmetry, and it is displayed in Figure 3. Frequency calculations show, however, a small imaginary frequency (−9 cm−1). A new initial guess for geometry optimization was created by perturbing the small negative frequency. The newly optimized geometry is very similar to the C2h dimer, but with a reduced Ci symmetry instead, and with no imaginary frequencies. 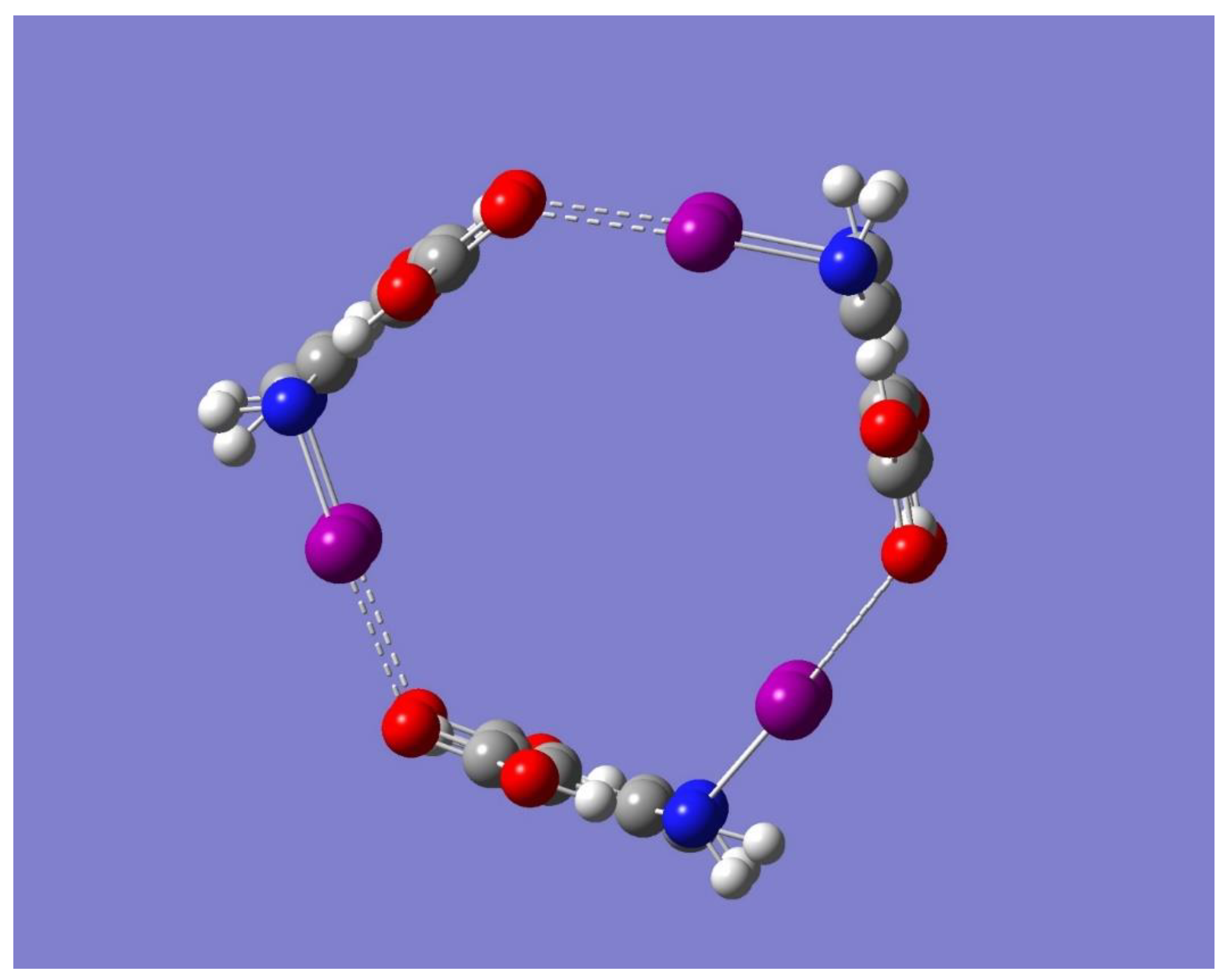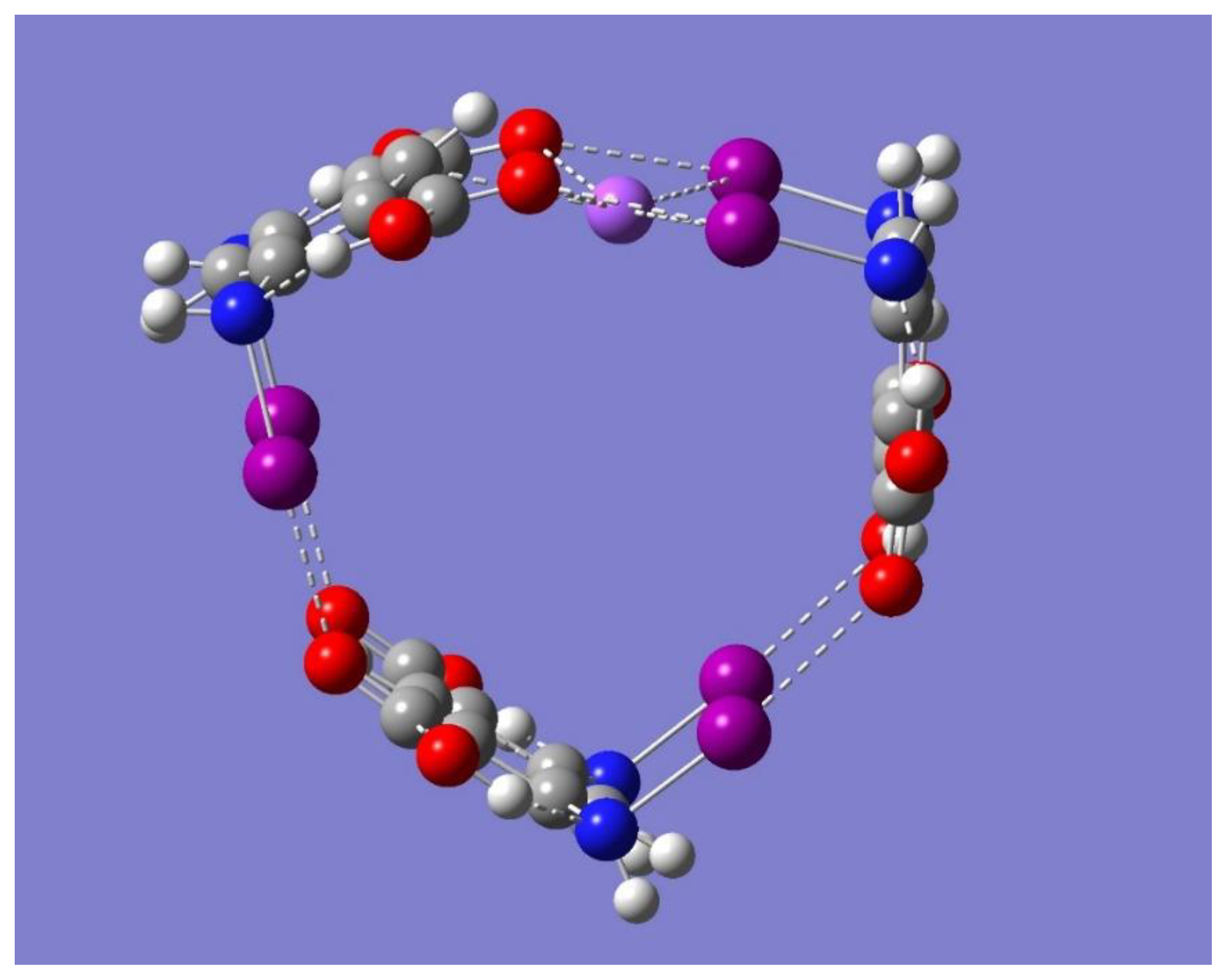Moreover, the Ci monomer has virtually the same electronic energy as its C2h counterpart. A halogen-bonded driven trimer was built in a manner similar to the cyclic dimer. The resulting optimized geometry has C3h symmetry, and it is displayed in Figure 4. Frequency calculations confirm that the optimized geometry is a minimum on the corresponding potential energy surface, with no imaginary frequencies.
Some key geometrical parameters for the optimized monomer, dimer, and trimer systems are listed in Table 1. It should be noted that the parameters listed in Table 1 for the dimer of Ci symmetry represent average values, and these average values are very close to the corresponding geometrical values of the C2h dimer. More specifically, in the dimer of Ci symmetry, there are two distinct pairs of N-I…O=C halogen bond interactions, with NI…O=C distances of 2.962 Å and of 3.080 Å, respectively. The NI…O=C angles are 162.2° and 154.7° for the former and latter halogen bonds, respectively. Similarly, two distinct pairs of COH…N hydrogen bond interactions are present, with COH…N distances of 1.771 Å and of 1.775 Å, respectively. The CO-H…N angles are 147.2° and 146.9° for the former and latter hydrogen bonds, respectively. Lastly, two sets of covalent N-I (2.130 and 2.128 Å) and C=O (1.218 and 1.216 Å) bonds are found in the Ci dimer.
An inspection of Table 1 reveals that dimer formation brings about an elongation, relative to the monomer, of the two covalent bonds N-I and C=O. These changes are consistent with attractive N-I…O=C interactions that can be considered halogen bonded interactions, given that the interaction distances are smaller than the sum (3.50 Å) of the van der Waals radii of the iodine (1.98 Å) and oxygen (1.52 Å) atoms [44]. The directional character of the halogen bond in a cyclic dimer is seen in the relatively large interaction angle of about 158°. Dimer formation strengthens the intramolecular hydrogen bonds, as seen in the sizeable shortening of the intramolecular COH…N hydrogen bond distances. The enhanced hydrogen bond interactions may be traced back to a concerted resonance-assisted cooperativity involving the halogen and the hydrogen bonds. Indeed, a cyclic network of alternating halogen and hydrogen bonds can be observed on either side of the dimer: [NI…O=C-OH…NI…O=C-OH…NI]. This sequence of interactions results in resonance-assisted cooperativity, reflected in an increase in the O-H bond length and a decrease in the C-O bond length, in addition to the shortening of the COH…N distances (Table 1).
Table 1 also shows that, upon trimer formation, cooperativity brings about an enhancement of the NI…O=C halogen bonds in addition to further strengthening the COH…N hydrogen bonds. Particularly striking is the sizeable decrease in the halogen bond distance (about 9% reduction) and widening of the corresponding angle (about 7% wider) relative to the dimer.
In addition to geometrical parameters, interaction energies provide a direct measure of both the strength and the cooperativity of the intermolecular interactions holding the dimer and trimer systems together. Table 2 lists the interaction energies corrected for basis set superposition error, BSSE. An inspection of Table 2 shows that the interaction energies for both dimers (Ci and C2h) are virtually the same. Cooperativity is made apparent in an important increase in the interaction energy in the trimer relative to the dimer. More specifically, and on a per-halogen bond interaction basis, the magnitude of the interaction energy increases more than 36% from the dimer to the trimer. Also shown in Table 2 are the intermolecular halogen bond distances and the corresponding bond critical point electron densities, ρNI…O=C, calculated within the framework of the quantum theory of atoms in molecules, QTAIM [35,36,37]. In particular, the existence of a bond critical point (that is, the point where the gradient of the density is zero) provides evidence of the existence of a bond, whereas its absence indicates the lack of bonding. Moreover, the magnitude of the electron density at the bond critical point directly correlates with the strength of the bond. The more than 50% increase in ρNI…O=C in the trimer compared with the dimer confirms the significant cooperative strengthening of the N-I…O=C interaction already evinced by the changes in both geometrical parameters and interaction energies.

3.2. Na+ Binding by Dimer

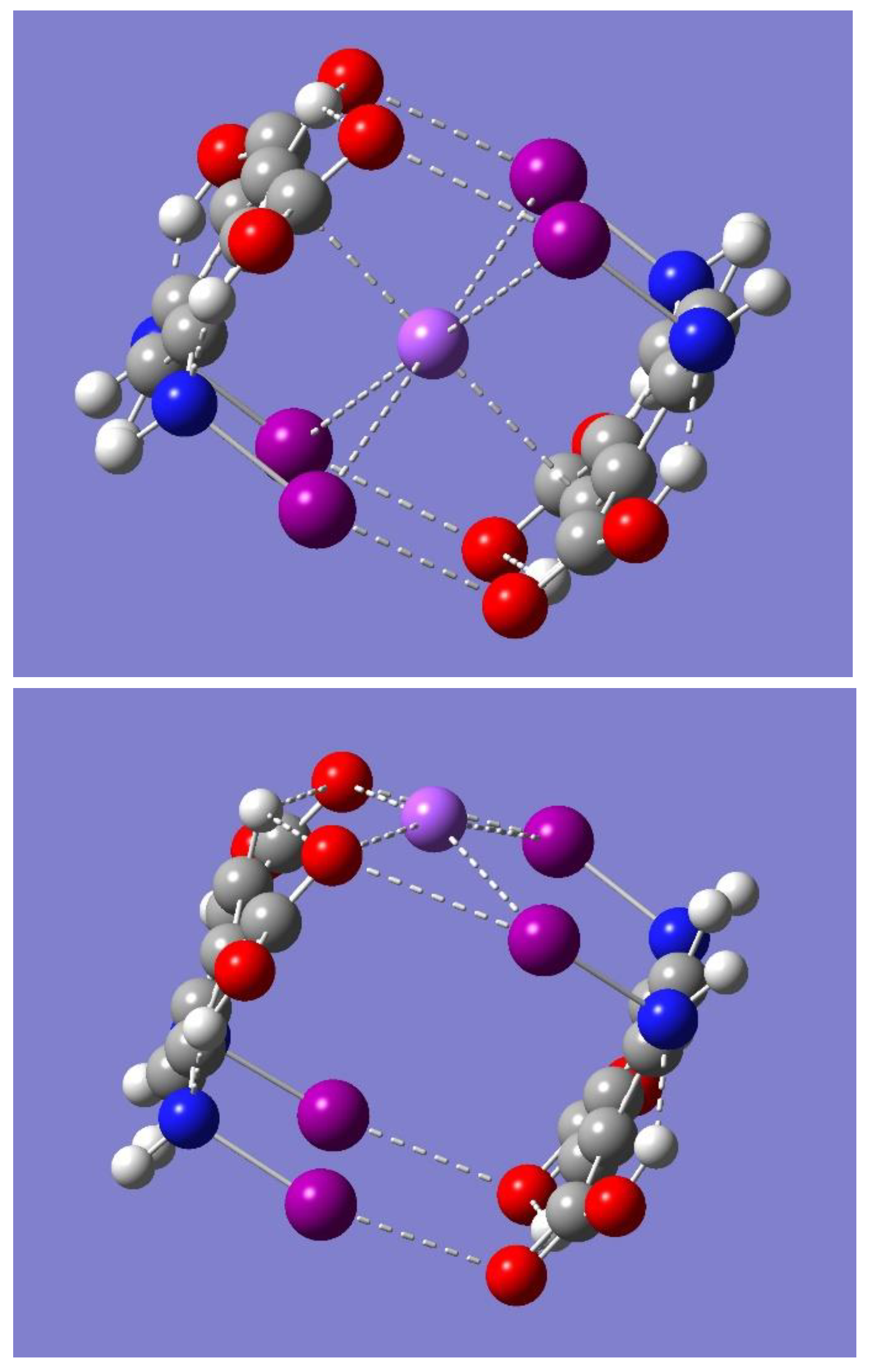
The potential for Na+ binding by the dimer was examined by considering the electrostatic potential of the dimer using the optimized dimer of symmetry C2h. Inspection of Figure 5 reveals a couple of regions of negative electrostatic potential. One region can be identified as the yellow-red color, mostly near the oxygen atoms, while the other as the light purple color around the iodine atoms, mostly perpendicular to the respective N-I…O=C interaction lines. These regions are located on the sides of the dimer and to some extent in the cavity of the cyclic structure. Accordingly, the dimer should be able to bind a Na+ on either side of the dimer or in the middle of the dimer cavity. To test these hypotheses, a full geometry optimization was first performed starting with the metal ion on the center of the dimer cavity. The result was the binding of Na+ in a complex geometry of C2h symmetry. It is worth noting that the same complex geometry occurred regardless of the neutral dimer (Ci or C2h symmetry) used as the host. Next, a full geometry optimization with a Na+ on each side of the dimer (that is, two Na+ ions) resulted in a minimum energy structure of C2h symmetry, confirming the ability of the dimer to bind a metal ion on the sides based on their corresponding negative electrostatic potentials. Lastly, a geometry optimization using the optimized dimer with the two Na+ ions was carried after removing one of the Na+. The successful geometry optimization resulted in a complex geometry of Cs symmetry. Frequency calculations demonstrated that all of the metal-complexed optimized geometries are indeed minimum energy structures with no imaginary frequencies. The optimized geometries for the Dimer-Na+ and Dimer-2Na+ complexes are displayed in Figure 6, while Table 3 lists some relevant geometrical parameters.
Inspection of both Table 3 and Figure 6 suggests that the binding of a single Na+ within the cavity of the cyclic dimer is driven primarily by the attractive interactions of the metal ion with the four iodine atoms and with both aromatic rings. The electron-rich region, resulting from the halogen atom lone pairs not involved in the halogen bonds around the center of symmetry of the dimer, helps stabilize and therefore bind electron-deficient species such as Na+. The aromatic rings also provide electron-rich regions to help bind the metal ion. Specifically, the smallest separation between Na+ and one of the CH groups in a benzene ring is readily visible in Figure 6, while the corresponding distance, HC…Na+, is listed in Table 3. It is important to note that the halogen bonds were strengthened rather than weakened following the complexation of Na+ at the center of symmetry of the dimer. Supporting evidence to this effect is found in a decrease in the halogen bond distances (3.007 Å to 2.836 Å) and a slight widening of the angles (158.9° to 162.5°).
When the binding of Na+ occurs on the side of the dimer, the metal ion sits on top of the plane formed by the iodine and oxygen atoms participating in one of the halogen-bonding networks. Here, the Na+ binding is driven mostly by the attractive interactions of the metal ion with the two carbonyl oxygen atoms, the two iodine atoms, and one of the aromatic rings. The enhanced contribution of the carbonyl oxygen atoms to bind Na+, with respect to the binding inside the dimer cavity, is seen in a substantial decrease (35% reduction) in the Na+…O=C distances. Moreover, the dihedral angle between the planes formed by the metal ion and the halogen-bonded network, Na+…I…I…O, changes from -73.8° (Na+ inside) to 13.1° (Na+ outside), which is consistent with the larger role played by the carbonyl oxygen atoms in binding the metal ion. Although in this complex the metal ion interacts with only one of the aromatic rings and just two iodine atoms, these interactions appear somewhat stronger, as suggested by a reduction of 5% and 2% in the HC…Na+ and NI…Na+ distances, respectively. When compared with the free C2h dimer, the halogen bond network that interacts with the metal ion is weakened upon Na+ complexation, as seen in an increase in the halogen bond distances (3.007 Å to 3.157 Å) and a narrowing of the angles (158.9° to 147.2°). In contrast, the halogen bond network that is farther away from Na+ becomes somewhat stronger, as indicated by shorter halogen bond distances, 2.847 Å, and wider angles, 164.4°.
The binding of two metal ions by the cyclic dimer involves both halogen-bonded networks, each binding one Na+ respectively. Both Na+ ions are symmetrically equivalent within an overall C2h symmetry. As in the binding of a single Na+ on the outer side of the dimer, each metal ion sits on top of the plane formed by the iodine and oxygen atoms participating in the appropriate halogen-bonded network, as seen in Figure 6. Similarly, each Na+ binding is driven mostly by the attractive interactions of the Na+ with two carbonyl oxygen atoms, an aromatic ring, and two iodine atoms. Inspection of Table 3 reveals, however, that the interactions with the ring and the iodine atoms are weaker compared with the binding of a single Na+ counterpart. For example, both the NI…Na+ and the HC…Na+ distances are, respectively, 0.098 Å and 0.133 Å longer than those found in the binding of a single Na+ on the complex side. Additionally, the larger value of the dihedral angle (an increase of 9.8°), Na+…I…I…O, demonstrates a larger displacement of Na+ from the pertinent halogen-bond plane which results in the longer NI…Na+ and HC…Na+ separations. The moving away of each Na+ from its respective halogen-bond plane is a manifestation of the moving away of the two Na+ ions from each other to reach an equilibrium distance, Na+…Na+, of 6.748 Å, in response to their repulsive electrostatic interactions.
One direct measure of the strength of a metal ion binding is provided by the corresponding binding energy, calculated as the negative of the complex interaction energy, with the metal ion taken as one unit in the complex and the dimer as the other unit in the complex. The BSSE-corrected binding energies listed in Table 4 demonstrate that the binding of a single Na+ is energetically favorable. The binding is even more favorable when Na+ is found on the outside rather than in the interior of the halogen-bonded dimer. The bond critical point electron densities shown also in Table 4 serve to reveal more specifically the role of the aromatic rings, the iodine atoms, and the carbonyl oxygen atoms in the binding of Na+. In particular, a critical point is found along each of the four NI…Na+ bond paths in the Dimer-Na+ complex of C2h symmetry. Additionally, the interaction of Na+ with each aromatic ring is demonstrated with the presence of a related critical point along the line connecting Na+ with the closest CH group in the aromatic ring. No critical points are found, however, between Na+ and any other regions on either aromatic ring. Likewise, no critical points are found in any of the C=O…Na+ interaction lines, which indicate that the binding of Na+ is driven mainly by the two aromatic rings and the four iodine atoms. In contrast, the Dimer-Na+ complex of Cs symmetry exhibits a critical point along each C=O…Na+ interaction line, which demonstrates the important role of the carbonyl oxygen atoms to bind the metal ion in this complex. Additionally, a critical point is also found along each of the two NI…Na+ interaction lines, and one critical point with the closer aromatic ring. The corresponding electron density values ρNI…Na+ and ρHC…Na+ appear larger in this complex than in that of C2h symmetry. Overall, the combined effect of all these stabilization factors, especially the important contribution of the carbonyl oxygen atoms, as shown in their ρC=O…Na+ values, helps explain the larger binding energy in the Dimer-Na+ complex of Cs symmetry.
As shown in Table 4, bringing together the two monomers and the two Na+ ions upon formation of the Dimer-2Na+ system is energetically favorable, and results in a binding energy comparable to those in the Dimer-Na+ systems. This result is particularly important given the repulsive interaction between the two positively charged metal ions. Indeed, the calculated repulsive interaction for the two isolated Na+ ions, at the distance they have in the Dimer-2Na+ complex, is 49.12 kcal/mol. Table 4 shows also that the electron densities on the bond critical points along the C=O…Na+ and the HC…Na+ interaction lines are comparable to those in the system with only one Na+. However, the importance of the Na+ interaction with the halogen atoms in stabilizing the complex appears diminished to the point that no critical point is actually found along any of the NI…Na+ interaction lines.
The impact on the relative strength of the NI…O=C halogen bonds upon Na+ binding can be seen in the changes in the corresponding critical point electron densities, ρNI…O=C. For example, the halogen bond in the Dimer-Na+ of C2h symmetry exhibits a significant 34% increase in ρNI…O=C relative, for example, to the optimized dimer of C2h symmetry in the absence of the metal ion. In contrast, binding two Na+, as in the Dimer-2Na+, weakens each of the halogen bond, as seen in a respective 11% decrease in ρNI…O=C. The two sets of halogen bonds in the Dimer-Na+ of Cs symmetry are impacted differently by the presence of Na+. Accordingly, the two halogen bonds closer to the metal ion are weakened (15% decrease in ρNI…O=C) while the two halogen bonds farther from the metal ion, each with a ρNI…O=C value of 0.0189 a.u., are actually strengthened (29% increase in ρNI…O=C).

3.3. Na+ Binding by Trimer

The electrostatic potential of the optimized cyclic trimer of symmetry C3h shown in Figure 7 shows the potential of this trimer to bind an electron-deficient species such as Na+ mostly on the sides or edges of the trimer. One striking result from Figure 7 is, however, the lack of any negative electrostatic potential that can attract Na+ in the central cavity of the molecule. In fact, a full geometry optimization, followed by frequency calculations performed with the metal ion on the point of symmetry of the trimer, resulted in a structure with three imaginary frequencies. On the other hand, a geometry optimization with Na+ on one side of the cyclic trimer was confirmed to be a minimum energy structure, with frequency calculations showing no imaginary frequencies. Similarly, a geometry optimization with one Na+ on each side of the trimer also resulted in a minimum energy structure with no imaginary frequencies. The symmetry of the optimized Trimer-Na+ complex is Cs, while the optimized Trimer-3Na+ complex retains the symmetry of the trimer, C3h. It is worth noting that a geometry optimization of a Trimer-2Na+ complex, using the optimized Trimer-3Na+ geometry as an initial guess but removing one of the Na+, resulted in a geometry that retains the overall shape of the complex. However, this optimized Trimer-2Na+ complex was shown to be a saddle point of first order (frequency calculations resulted in one imaginary frequency). Thus, the focus of the discussion is on the two minimum energy structures shown in Figure 8 which have no imaginary frequencies, Trimer-Na+ and Trimer-3Na+, and whose relevant geometrical parameters are listed in Table 5.
Figure 6 and Figure 8 show that the binding in Trimer-Na+ can be conveniently compared with the corresponding binding in Dimer-Na+ of symmetry Cs, given that, in each case, the binding of Na+ occurs primarily with one of the halogen-bonded networks. One interesting difference is that the metal ion in the Trimer-Na+ complex is found toward the interior of the complex, in contrast to the corresponding Dimer-Na+ complex, where the metal ion is found toward the outside of the complex. This difference is further confirmed by the opposite signs of the dihedral angle, Na+…I…I…O: 13.1° and −14.4° for the Dimer-Na+ and Trimer-Na+, respectively (Table 3 and Table 5). Moreover, geometrical parameters suggest an enhanced role of the NI…Na+ interactions for Na+ binding by the trimer. For example, an inspection of Table 3 and Table 5 shows, relative to the Dimer-Na+, a sizeable decrease in the NI…Na+ distances concomitant with respectively minor increases in the C=O… Na+ and HC…Na+ distances. Compared with the free C3h trimer, the halogen bond network that interacts with the metal ion is weakened upon Na+ complexation, as indicated by longer halogen bond distances (2.746 Å to 2.919 Å) and smaller angles (169.5° to 156.0°). The impact of Na+ complexation on the other two halogen-bonded networks can be conveniently described by considering the monomer that is farthest away from Na+ in its dual role as the halogen-bond donor or as the halogen-bond acceptor. In the former case, it is found that the associated NI…Na+ distances are longer (2.823 Å), while the opposite is true in the latter case (2.655 Å). These results indicate an enhanced halogen-bond donor ability of the monomer that interacts with Na+ through the carbonyl oxygen atoms, C=O. The increase in the halogen-bond strength with the farthest (from Na+) monomer is offset, on the other hand, by a concurrent reduced halogen-bond acceptor ability of the monomer that interacts with Na+ through the iodine atoms.
The binding of three metal ions by the cyclic trimer involves all three halogen-bonded networks, each binding one Na+. The three Na+ ions are equivalent within an overall C3h symmetry. Unlike the binding of a single Na+, which occurs towards the inner side of the trimer, each of the three metal ions sits now on top of the plane formed by the iodine and oxygen atoms participating in the pertinent halogen-bonding network, as displayed in Figure 8. The sign change in Na+…I…I…O, (from −14.4° to 14.1°), results in relatively large Na+…Na+ separations of 7.327 Å, which help minimize the repulsive electrostatic interactions among the three metal ions. As with the binding of a single Na+, the binding of each Na+ in the Trimer-3Na+ complex is driven mostly by the attractive interactions of the Na+ with the corresponding halogen-bonded network through two carbonyl oxygen atoms, an aromatic ring, and two iodine atoms. Inspection of Table 5 shows, however, that the interactions with the ring and the iodine atoms appear weaker (longer distances) compared with the binding of a single Na+ counterpart, while the C=O…Na+ interactions appear stronger (shorter distances).
The BSSE-corrected metal ion binding energies listed in Table 6 demonstrate that the binding of a single Na+ by the trimer is energetically favorable. Moreover, the binding energy is actually larger than that in either dimer (Cs or C2h symmetry, Table 4). The bond critical point electron densities also shown in Table 6 help to better appreciate the role of the aromatic rings, the iodine atoms, and the carbonyl oxygen atoms in the binding of Na+. In particular, a critical point is found along each of the associated NI…Na+ and C=O…Na+ interaction lines in the Trimer-Na+ complex. Additionally, the interaction of Na+ with the closest aromatic ring is demonstrated with the presence of a related critical point along the line connecting Na+ with the closest carbon atom of the aromatic ring. The values of the critical point electron densities, ρC=O…Na+ and ρC…Na+, in the Trimer-Na+ complex are comparable to those in the Dimer-Na+ complex of symmetry Cs. However, the ρNI…Na+ values are much larger in the Trimer-Na+ complex. It should be noted that the changes in the critical point electron density values consistently mirror the interrelated changes in the geometrical parameters, namely a sizeable decrease in the NI…Na+ distances concomitant with respectively minor changes in the C=O…Na+ and HC…Na+ distances.
As shown in Table 6, bringing together the three monomers and the three Na+ ions upon formation of the Trimer-3Na+ system is still an energetically favorable process. Compared with Trimer-Na+, the binding energy in Trimer-3Na+ is, nonetheless, substantially smaller. This result is not surprising, given the large repulsive electrostatic interaction among the three positively charged metal ions. Indeed, the calculated molar repulsive energy for the three Na+ ions is 135.92 kcal/mol. An inspection of Table 6 shows that the electron densities on the bond critical points ρHC…Na+ and ρNI…Na+ are reduced, while those for ρC=O…Na+ are increased relative to the Trimer-Na+ complex.
The critical point electron density values in Table 6 and Table 4 indicate that the HC…Na+ interactions are enhanced, while the C=O…Na+ interactions weakened in the Trimer-3Na+ complex relative to the Dimer-2Na+ complex. One interaction that appears heightened in the Trimer–3Na+ is the NI…Na+ interaction, as the existence of a corresponding bond critical point demonstrates. The presence of bond critical points along each of the NI…Na+ interactions denotes the enhanced role of these interactions in the binding of each Na+ in the Trimer-3Na+ complex. In contrast, no such critical points were found the Dimer-2Na+ complex.
The impact on the relative strength of the NI…O=C halogen bonds upon Na+ binding by the trimer can be appreciated in the changes of the corresponding critical point electron densities, ρNI…O=C. For example, an inspection of Table 2 and Table 6 shows that each of the halogen bonds interacting with Na+ in the Trimer-Na+ exhibits a significant 23% decrease in ρNI…O=C relative to the trimer optimized in the absence of the metal ion. The two sets of halogen bonds in the Trimer-Na+ not directly involved in binding the metal ion are impacted differently by the presence of Na+. One set of halogen bonds has ρNI…O=C values of 0.0188 a.u. (16% decrease in ρNI…O=C), while the other set has ρNI…O=C values of 0.0263 a.u. (18% increase in ρNI…O=C). Each of the halogen bonds in the Trimer-3Na+ complex exhibits a substantial 40% decrease in ρNI…O=C. As expected, the changes in the critical point electron density values are in accordance with the interrelated changes in the relevant geometrical parameters.

4. Concluding Remarks

The results of this study demonstrate the ability of halogen bonding to drive the formation of cyclic dimers and trimers of a model tetra-substituted benzene, ((HOOC)2-C6H2-(NHI)2). A 36% increase in the magnitude of the complexation energy of the trimer relative to the dimer shows a sizeable cooperative strengthening of the halogen bonds. Further evidence of cooperativity is seen in a 9% shortening of each NI…O=C halogen bond distance, with a corresponding 53% increase in the critical point density value, ρNI…O=C. The results of this study also confirm the potential for binding a single Na+ ion by either the dimer or the trimer. Specifically, complexation of the metal ion by the dimer, Dimer-Na+, is shown to occur either at the center of symmetry of the molecule (C2h symmetry) or on the side of the molecule (Cs symmetry). The binding energy of the latter is about 23% larger than that of the former. Complexation of the metal ion by the trimer, Trimer-Na+, is shown to occur on the side of the molecule with a binding energy that is about 4% larger than that of the Dimer-Na+ of Cs symmetry. Binding of two metal ions was shown to be also possible by the dimer, Dimer-2Na+. Likewise, the trimer was also found to bind three metal ions, Trimer-3Na+. The overall structure of the halogen-bonded networks of either the dimer or the trimer remained after complexation of the Na+ ions.
The generality of the results presented in this work should be evaluated by conducting further studies on other appropriate tetra-substituted benzene unit molecules. For example, the effect of acceptor and donor group abilities of the substituents can be systematically investigated using different halogen bond acceptors, A, and donors, D, ((A)2-C6H2-(D)2). Ongoing research in the author’s group includes, for example, using the formyl group as the acceptor, A, and -CH2I as the donor, D. The effect of using chlorine or bromine rather than iodine for halogen bonding is also being explored. Lastly, the ability of the cyclic dimers and trimers to bind other metal ions of varying size and charge, such as Li+, K+, Be2+ and Ca2+, is currently under investigation, and the results will be published elsewhere.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The author is grateful to the Department of Chemistry and Biochemistry at DePaul University for its continuous support.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Williams, G.T.; Haynes, C.J.E.; Fares, M.; Caltagirone, C.; Hiscock, J.R.; Gale, P.A. Advances in applied supramolecular technologies. Chem. Soc. Rev. 2021, 50, 2737–2763. [Google Scholar] [CrossRef]
  2. Menger, F.M. Supramolecular chemistry and self-assembly. Proc. Natl. Acad. Sci. USA 2002, 99, 4818–4822. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  3. Savyasachi, A.J.; Kotova, O.; Shanmugaraju, S.; Bradberry, S.J.; O’Máille, G.M.; Gunnlaugsson, T. Supramolecular Chemistry: A Toolkit for Soft Functional Materials and Organic Particles. Chem 2017, 3, 764–811. [Google Scholar] [CrossRef]
  4. Bhalla, V. Supramolecular Chemistry. Reson 2018, 23, 277–290. [Google Scholar] [CrossRef]
  5. Cragg, P.G. A Practical Guide to Supramolecular Chemistry; John Wiley & Sons: Chichester, UK, 2005. [Google Scholar]
  6. Steed, J.W.; Atwood, J.L. Supramolecular Chemistry; John Wiley & Sons: Chichester, UK, 2000. [Google Scholar]
  7. Dong, W.; Li, Q.; Scheiner, S. Comparative Strengths of Tetrel, Pnicogen, Chalcogen, and Halogen Bonds and Contributing Factors. Molecules 2018, 23, 1681. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  8. Scheiner, S. Detailed comparison of the pnicogen bond with chalcogen, halogen, and hydrogen bonds. Int. J. Quantum Chem. 2012, 113, 1609–1620. [Google Scholar] [CrossRef] [Green Version]
  9. Mahmudov, K.T.; Gurbanov, A.V.; Aliyeva, V.A.; Resnati, G.; Pombeiro, A.J.L. Pnictogen bonding in coordination chemistry. Coord. Chem. Rev. 2020, 418, 213381. [Google Scholar] [CrossRef]
  10. de Silva, V.; Averkiev, B.B.; Sinha, A.S.; Aakeröy, C.B. The Balance between Hydrogen Bonds, Halogen Bonds, and Chalcogen Bonds in the Crystal Structures of a Series of 1,3,4-Chalcogenadiazoles. Molecules 2021, 26, 4125. [Google Scholar] [CrossRef]
  11. Biot, N.; Bonifazi, D. Chalcogen-bond driven molecular recognition at work. Coord. Chem. Rev. 2020, 413, 213243. [Google Scholar] [CrossRef]
  12. Bauzá, A.; Seth, S.K.; Frontera, A. Tetrel bonding interactions at work: Impact on tin and lead coordination compounds. Coord. Chem. Rev. 2019, 384, 107–125. [Google Scholar] [CrossRef]
  13. Akorta, I.; Legon, A.C. Nucleophilicities of Lewis Bases B and Electrophilicities of Lewis Acids A Determined from the Dissociation Energies of Complexes B⋯A Involving Hydrogen Bonds, Tetrel Bonds, Pnictogen Bonds, Chalcogen Bonds and Halogen Bonds. Molecules 2017, 10, 1786. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Metrangolo, P.; Meyer, F.; Pilati, T.; Resnati, G.; Terraneo, G. Halogen Bonding in Supramolecular Chemistry. Angew. Chem. Int. Ed. 2008, 47, 6114–6127. [Google Scholar] [CrossRef] [PubMed]
  15. Metrangolo, P.; Resnati, G. Halogen Bonding: A Paradigm in Supramolecular Chemistry. Chem. Eur. J. 2001, 7, 2511–2519. [Google Scholar] [CrossRef]
  16. Turunen, L.; Hansen, J.H.; Erdélyi, M. Halogen Bonding: An Odd Chemistry. Chem. Rec. 2021, 21, 1252–1257. [Google Scholar] [CrossRef] [PubMed]
  17. Meazza, L.; Foster, J.A.; Fucke, K.; Metrangolo, P.; Resnati, G.; Steed, J.W. Halogen-bonding-triggered supramolecular gel formation. Nat. Chem. 2013, 5, 42–47. [Google Scholar] [CrossRef] [PubMed]
  18. Metrangolo, P.; Neukirch, H.; Pilati, T.; Resnati, G. Halogen Bonding Based Recognition Processes: A World Parallel to Hydrogen Bonding. Acc. Chem. Res. 2005, 38, 386–395. [Google Scholar] [CrossRef]
  19. Meyer, F.; Dubois, P. Halogen bonding at work: Recent applications in synthetic chemistry and materials science. CrystEngComm 2013, 15, 3058–3071. [Google Scholar] [CrossRef]
  20. Berger, G.; Soubhyea, J.; Meyer, F. Halogen bonding in polymer science: From crystal engineering to functional supramolecular polymers and materials. Polym. Chem. 2015, 6, 3559–3580. [Google Scholar] [CrossRef]
  21. Nelyubina, Y.V.; Antipin, M.Y.; Dunin, D.S.; Kotov, V.Y.; Lyssenko, K.A. Unexpected “amphoteric” character of the halogen bond: The charge density study of the co-crystal of N- methylpyrazine iodide with I2. Chem. Commun. 2010, 46, 5325–5327. [Google Scholar] [CrossRef]
  22. Parra, R.D. Concerted halogen bonding and orthogonal metal-halogen interactions in dimers of lithium formamidinate and halogenated formamidines: An ab Initio study. Molecules 2014, 19, 1069–1084. [Google Scholar] [CrossRef] [Green Version]
  23. Parra, R.D. Metal-ion binding by cyclic halogen-bonded structures: A theoretical study using M-(BrZ)4 clusters (Z = F or NH2; M = Li+, Na+, or Mg2+). Chem. Phys. Lett. 2015, 637, 177–181. [Google Scholar] [CrossRef]
  24. Parra, R.D.; Castillo, A. Cyclic networks of halogen-bonding interactions in molecular self-assemblies: A theoretical N-X···N versus C-X···N investigation. Acta Cryst. B 2017, 73, 179–187. [Google Scholar] [CrossRef] [PubMed]
  25. Tepper, R.; Schulze, B.; Jager, M.; Friebe, C.; Scharf, D.H.; Görls, H.; Schubert, U.S. Anion Receptors Based on Halogen Bonding with Halo-1,2,3- triazoliums. J. Org. Chem. 2015, 80, 3139–3150. [Google Scholar] [CrossRef] [PubMed]
  26. Turner, G.; Docker, A.; Beer, P.D. Anion recognition by halogen bonding and hydrogen bonding bis(triazole)-imidazolium [2] rotaxanes. Dalton Trans. 2021, 50, 12800–12805. [Google Scholar] [CrossRef] [PubMed]
  27. Singh, N.J.; Olleta, A.C.; Kumar, A.; Park, M.; Yi, H.-B.; Bandyopadhyay, I.; Lee, H.M.; Tarakeshwar, P.; Kim, K.S. Study of interactions of various ionic species with solvents toward the design of receptors. Theor. Chem. Acc. 2006, 115, 127–135. [Google Scholar] [CrossRef]
  28. Choi, H.S.; Suh, S.B.; Cho, S.J.; Kim, K.S. Ionophores and receptors using cation-π interactions: Collarene. Proc. Natl. Acad. Sci. USA 1998, 95, 12094–12099. [Google Scholar] [CrossRef] [Green Version]
  29. Domaille, D.W.; Que, E.L.; Chang, C.J. Synthetic fluorescent sensors for studying the cell biology of metals. Nat. Chem. Biol. 2008, 4, 168–175. [Google Scholar] [CrossRef]
  30. Page, M.J.; Cera, E.D. Role of Na+ and K+ in enzyme function. Physiol. Rev. 2006, 86, 1049–1092. [Google Scholar] [CrossRef] [Green Version]
  31. Einholm, A.P.; Nielsen, H.N.; Holm, R.; Toustrup-Jensen, M.S.; Vilsen, B. Importance of a potential protein kinase a phosphorylation site of Na+,K+-ATPase and its interaction network for Na+ binding. J. Biol. Chem. 2016, 291, 10934–10947. [Google Scholar] [CrossRef] [Green Version]
  32. Cerda, B.; Hoyau, S.; Ohanessian, G.; Wesdemiotis, C. Na+ Binding to cyclic and linear dipeptides. Bond energies, entropies of Na+ complexation, and attachment sites from the dissociation of Na+-bound heterodimers and ab Initio calculations. J. Am. Chem. Soc. 1998, 120, 2437–2448. [Google Scholar] [CrossRef]
  33. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  34. Boys, S.F.; Bernardi, F. Calculation of small molecular interactions by differences of separate total energies—Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
  35. Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
  36. Grabowski, S.J. QTAIM characteristics of halogen bond and related interactions. J. Phys. Chem. A 2012, 116, 1838–1845. [Google Scholar] [CrossRef] [PubMed]
  37. Zou, J.-W.; Lu, Y.-X.; Yu, Q.-S.; Zhang, H.-X.; Jiang, Y.-J. Halogen bonding: An AIM analysis of the weak interactions. Chin. J. Chem. 2006, 24, 1709–1715. [Google Scholar] [CrossRef]
  38. Biegler-König, F.; Schönbohm, J.; Bayles, D. AIM2000—A program to analyze and visualize atoms in molecules. J. Comput. Chem. 2001, 22, 545–554. [Google Scholar]
  39. Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  40. Siiskonen, A.; Priimagi, A. Benchmarking DFT methods with small basis sets for the calculation of halogen-bond strengths. J. Mol. Model. 2017, 23, 1–9. [Google Scholar] [CrossRef] [PubMed]
  41. Yurieva, A.G.; Poleshchuk, O.K.; Filimonov, V.D. Filimonov, Comparative analysis of a full-electron basis set and pseudopotential for the iodine atom in DFT quantum-chemical calculations of iodine-containing compounds. J. Struct. Chem. 2008, 49, 548–552. [Google Scholar] [CrossRef]
  42. Kozuch, S.; Martin, J.M. Halogen bonds: Benchmarks and theoretical analysis. J. Chem. Theory Comput. 2013, 9, 1918–1931. [Google Scholar] [CrossRef]
  43. Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The σ-hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef]
  44. Bondi, J. Van der Waals volumes and radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
Sci 04 00009 g001 550
Figure 1. Optimized geometry of the molecular model system, ((HOOC)2-C6H2-(NHI)2). Intramolecular OH…N hydrogen bonding indicated with dashed lines. Individual atoms can be distinguished by color: C (grey), H (white), N (blue), O (red), and I (purple).
Figure 1. Optimized geometry of the molecular model system, ((HOOC)2-C6H2-(NHI)2). Intramolecular OH…N hydrogen bonding indicated with dashed lines. Individual atoms can be distinguished by color: C (grey), H (white), N (blue), O (red), and I (purple).
Sci 04 00009 g001
Sci 04 00009 g002 550
Figure 2. Electrostatic potential on the 0.001-au molecular surface of the optimized model system, ((HOOC)2-C6H2-(NHI)2). Yellow-red represents the most negative electrostatic potential and blue the most positive.
Figure 2. Electrostatic potential on the 0.001-au molecular surface of the optimized model system, ((HOOC)2-C6H2-(NHI)2). Yellow-red represents the most negative electrostatic potential and blue the most positive.
Sci 04 00009 g002
Sci 04 00009 g003 550
Figure 3. Optimized geometry of the ((HOOC)2-C6H2-(NHI)2) dimer. Intramolecular OH…N hydrogen bonding and intermolecular NI…O=C halogen bonding indicated with respective dashed lines. Individual atoms can be distinguished by color: C (grey), H (white), N (blue), O (red), and I (purple).
Figure 3. Optimized geometry of the ((HOOC)2-C6H2-(NHI)2) dimer. Intramolecular OH…N hydrogen bonding and intermolecular NI…O=C halogen bonding indicated with respective dashed lines. Individual atoms can be distinguished by color: C (grey), H (white), N (blue), O (red), and I (purple).
Sci 04 00009 g003
Sci 04 00009 g004 550
Figure 4. Optimized geometry of the ((HOOC)2-C6H2-(NHI)2) trimer. Intramolecular OH…N hydrogen bonding and intermolecular NI…O=C halogen bonding indicated with respective dashed lines. Individual atoms can be distinguished by color: C (grey), H (white), N (blue), O (red), and I (purple).
Figure 4. Optimized geometry of the ((HOOC)2-C6H2-(NHI)2) trimer. Intramolecular OH…N hydrogen bonding and intermolecular NI…O=C halogen bonding indicated with respective dashed lines. Individual atoms can be distinguished by color: C (grey), H (white), N (blue), O (red), and I (purple).
Sci 04 00009 g004
Sci 04 00009 g005 550
Figure 5. Electrostatic potential on the 0.001-au molecular surface of the optimized dimer system. Yellow-red represents the most negative electrostatic potential and blue the most positive.
Figure 5. Electrostatic potential on the 0.001-au molecular surface of the optimized dimer system. Yellow-red represents the most negative electrostatic potential and blue the most positive.
Sci 04 00009 g005
Sci 04 00009 g006a 550Sci 04 00009 g006b 550
Figure 6. Optimized geometry of the Dimer-Na+ complex of C2h symmetry (top), the Dimer-Na+ complex of Cs symmetry (middle), and the Dimer-2Na+ complex of C2h symmetry (bottom). Intramolecular OH…N hydrogen bonding interactions, and intermolecular HC…Na+ and NI…O=C interactions indicated with respective dashed lines. Individual atoms can be distinguished by color: C (grey), H (white), N (blue), O (red), and I (purple).
Figure 6. Optimized geometry of the Dimer-Na+ complex of C2h symmetry (top), the Dimer-Na+ complex of Cs symmetry (middle), and the Dimer-2Na+ complex of C2h symmetry (bottom). Intramolecular OH…N hydrogen bonding interactions, and intermolecular HC…Na+ and NI…O=C interactions indicated with respective dashed lines. Individual atoms can be distinguished by color: C (grey), H (white), N (blue), O (red), and I (purple).
Sci 04 00009 g006aSci 04 00009 g006b
Sci 04 00009 g007 550
Figure 7. Electrostatic potential on the 0.001-au molecular surface of the optimized trimer system. Yellow-red represents the most negative electrostatic potential and blue the most positive.
Figure 7. Electrostatic potential on the 0.001-au molecular surface of the optimized trimer system. Yellow-red represents the most negative electrostatic potential and blue the most positive.
Sci 04 00009 g007
Sci 04 00009 g008a 550Sci 04 00009 g008b 550
Figure 8. Optimized geometry of the Trimer-Na+ complex (top) and the Trimer-3Na+ complex (bottom). Intramolecular OH…N hydrogen bonding interactions and intermolecular HC…Na+ and NI…O=C interactions are indicated with respective dashed lines. Individual atoms can be distinguished by color: C (grey), H (white), N (blue), O (red), and I (purple).
Figure 8. Optimized geometry of the Trimer-Na+ complex (top) and the Trimer-3Na+ complex (bottom). Intramolecular OH…N hydrogen bonding interactions and intermolecular HC…Na+ and NI…O=C interactions are indicated with respective dashed lines. Individual atoms can be distinguished by color: C (grey), H (white), N (blue), O (red), and I (purple).
Sci 04 00009 g008aSci 04 00009 g008b
Table
Table 1. Relevant geometrical parameters for the model system, ((HOOC)2-C6H2-(NHI)2), and its cyclic dimer and trimer complexes. Bond lengths or distances, R, in angstroms, and angles, A, in degrees.
Table 1. Relevant geometrical parameters for the model system, ((HOOC)2-C6H2-(NHI)2), and its cyclic dimer and trimer complexes. Bond lengths or distances, R, in angstroms, and angles, A, in degrees.
SystemSymmetryRN-IRC=ORC-ORCO-HRCOH…NACO-H…NRNI…O=CAN-I…O=C
MonomerCs2.1171.2061.3360.9821.829145.7N/AN/A
Dimer *Ci2.1291.2171.3270.9901.773147.13.021158.4
DimerC2h2.1301.2171.3260.9901.772147.13.007158.9
TrimerC3h2.1371.2211.3190.9981.715150.62.746169.5
* average values. See text for details.
Table
Table 2. Complexation energy, ΔE (kcal/mol), average complexation energy, <ΔE> (kcal/mol), and electron density at bond critical point, ρ (a.u.), for cyclic dimers and trimer of the model system, ((HOOC)2-C6H2-(NHI)2).
Table 2. Complexation energy, ΔE (kcal/mol), average complexation energy, <ΔE> (kcal/mol), and electron density at bond critical point, ρ (a.u.), for cyclic dimers and trimer of the model system, ((HOOC)2-C6H2-(NHI)2).
SystemSymmetryρNI…O=CΔE<ΔE> *
DimerCi0.0144−25.66−6.42
DimerC2h0.0146−25.89−6.47
TrimerC3h0.0223−52.67−8.78
* Complexation energy per halogen bond.
Table
Table 3. Relevant geometrical parameters for Na+ binding by the cyclic dimer of the model system, ((HOOC)2-C6H2-(NHI)2). Bond distances, R, in angstroms, bond angle, A, and dihedral, D, in degrees.
Table 3. Relevant geometrical parameters for Na+ binding by the cyclic dimer of the model system, ((HOOC)2-C6H2-(NHI)2). Bond distances, R, in angstroms, bond angle, A, and dihedral, D, in degrees.
SystemSymmetryRNI…O=CAN-I…O=CRHC…Na+RNI…Na+RC=O…Na+DNa+…I…I…O
Dimer-Na+C2h2.836162.52.9163.5763.938−73.8
Dimer-Na+Cs3.157147.22.7583.5072.56713.1
Dimer-2Na+C2h3.105153.62.8913.6052.54722.9
Table
Table 4. Metal ion binding energy, BE (kcal/mol), and electron density at bond critical points, ρ (a.u), for Na+ binding by the cyclic dimer of the model system, ((HOOC)2-C6H2-(NHI)2).
Table 4. Metal ion binding energy, BE (kcal/mol), and electron density at bond critical points, ρ (a.u), for Na+ binding by the cyclic dimer of the model system, ((HOOC)2-C6H2-(NHI)2).
SystemSymmetryρNI…O=CρHC…Na+ρNI…Na+ρC=O…Na+BE
Dimer-Na+C2h0.01960.00700.0046N/A41.26
Dimer-Na+Cs0.01240.00960.00500.011650.91
Dimer-2Na+C2h0.01300.0081N/A0.011948.25
Table
Table 5. Relevant geometrical parameters for Na+ binding by the cyclic trimer of the model system, ((HOOC)2-C6H2-(NHI)2). Bond distances, R, in angstroms, bond angle, A, and dihedral, D, in degrees.
Table 5. Relevant geometrical parameters for Na+ binding by the cyclic trimer of the model system, ((HOOC)2-C6H2-(NHI)2). Bond distances, R, in angstroms, bond angle, A, and dihedral, D, in degrees.
SystemSymmetryRNI…O=CAN-I…O=CRHC…Na+RNI…Na+RC=O…Na+DNa+…I…I…O
Trimer-Na+Cs2.919156.02.7963.2852.602−14.4
Trimer-3Na+C3h3.052157.42.9663.3232.56714.1
Table
Table 6. Complexation energy, ΔE (kcal/mol), and electron density at bond critical points, ρ (a.u), for Na+ binding by the cyclic trimer of the model system, ((HOOC)2-C6H2-(NHI)2).
Table 6. Complexation energy, ΔE (kcal/mol), and electron density at bond critical points, ρ (a.u), for Na+ binding by the cyclic trimer of the model system, ((HOOC)2-C6H2-(NHI)2).
SystemSymmetryρNI…O=CρHC…Na+ρNI…Na+ρC=O…Na+ΔE
Trimer-Na+Cs0.01720.00980.00790.010853.20
Trimer-3Na+C3h0.01340.00870.00730.011321.73
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Parra, R.D. Halogen-Bonded Driven Tetra-Substituted Benzene Dimers and Trimers: Potential Hosts for Metal Ions. Sci 2022, 4, 9. https://doi.org/10.3390/sci4010009

AMA Style

Parra RD. Halogen-Bonded Driven Tetra-Substituted Benzene Dimers and Trimers: Potential Hosts for Metal Ions. Sci. 2022; 4(1):9. https://doi.org/10.3390/sci4010009

Chicago/Turabian Style

Parra, Rubén D. 2022. "Halogen-Bonded Driven Tetra-Substituted Benzene Dimers and Trimers: Potential Hosts for Metal Ions" Sci 4, no. 1: 9. https://doi.org/10.3390/sci4010009

APA Style

Parra, R. D. (2022). Halogen-Bonded Driven Tetra-Substituted Benzene Dimers and Trimers: Potential Hosts for Metal Ions. Sci, 4(1), 9. https://doi.org/10.3390/sci4010009

Article Metrics

Back to TopTop