Next Article in Journal
Reliability of Historical Car Data for Operating Speed Analysis along Road Networks
Next Article in Special Issue
Aromaticity Concepts Derived from Experiments
Previous Article in Journal
Mathematics and Poetry · Yang–Baxter Equations, Boolean Algebras, and BCK-Algebras
Previous Article in Special Issue
Halogen-Bonded Driven Tetra-Substituted Benzene Dimers and Trimers: Potential Hosts for Metal Ions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sci
Volume 4
Issue 2
10.3390/sci4020017
sci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

σ-Hole Bonds and the VSEPR Model—From the Tetrahedral Structure to the Trigonal Bipyramid

by
Sławomir J. Grabowski
1,2
1
Polimero eta Material Aurreratuak: Fisika, Kimika eta Teknologia, Kimika Fakultatea, Euskal Herriko Unibertsitatea UPV/EHU & Donostia International Physics Center (DIPC) PK 1072, 20080 Donostia, Spain
2
IKERBASQUE, Basque Foundation for Science, 48011 Bilbao, Spain
Sci 2022, 4(2), 17; https://doi.org/10.3390/sci4020017
Submission received: 9 March 2022 / Revised: 29 March 2022 / Accepted: 7 April 2022 / Published: 19 April 2022
(This article belongs to the Special Issue Define What Is Not Defined: In Chemistry and Beyond)
Browse Figures
Versions Notes

Abstract

:
Complexes linked by various interactions are analysed in this study. They are characterized by the tetrahedral configuration of the Lewis acid centre. Interactions, being a subject of this study, are classified as σ-hole bonds, such as the halogen, chalcogen, pnicogen, and tetrel bonds. In the case of strong interactions, the tetrahedral configuration of the Lewis acid centre changes into the trigonal bipyramid configuration. This change is in line with the Valence-Shell Electron-Pair Repulsion model, VSEPR, and this is supported here by the results of high-level ab initio calculations. The theoretical results concerning the geometries are supported mainly by the Natural Bond Orbital, NBO, method.

1. Introduction

There are numerous phenomena in chemistry categorized by various terms. Some of these terms are ambiguous and, consequently, they are difficult to define. However, these terms are indispensable in descriptions and discussions of various reactions and processes. One can mention such terms as aromaticity, hydrogen bond, stabilization energy, electronegativity, and so on [1,2,3,4,5,6]. Even such a term as a chemical bond, which is commonly used in various studies, dissertations, and monographs, is a subject of numerous debates and polemics [7,8,9]. One can mention the definition recommended by the IUPAC, which states: “Chemical bond—when forces acting between two atoms or groups of atoms lead to the formation of a stable independent molecular entity, a chemical bond is considered to exist between these atoms or groups. The principal characteristic of a bond in a molecule is the existence of a region between the nuclei of constant potential contours that allows the potential energy to improve substantially by atomic contraction at the expense of only a small increase in kinetic energy. Not only directed covalent bonds characteristic of organic compounds, but also bonds such as those existing between sodium cations and chloride anions in a crystal of sodium chloride or the bonds binding aluminium to six molecules of water in its environment, and even weak bonds that link two molecules of O2 into O4, are to be attributed to chemical bonds” [10]. This definition makes reference to the Pauling monograph [11] and to other studies [12,13].
However, one can also refer to early Lewis concepts, where arrangements of electrons in molecular structures are taken into account [14]. Hence, so-called Lewis structures may be considered that are commonly presented in various academic books and monographs. Lewis stated that “Two electrons thus coupled together, when lying between two atomic centres, and held jointly in the shells of the two atoms, I have considered to be the chemical bond” [14]. In other words, the chemical bond is related to the occurrence of the electron pair situated between two atomic centres; this pair may be less or more moved to one of the atomic centres, which is related to the bond polarization and that determines the degree of the ionic character of the bond [15].
On the other hand, numerous inter- and intramolecular interactions are very strong and possess various characteristics of covalent bonds. As a consequence, there is no sharp border between bonds and intermolecular as well as intramolecular contacts. The hydrogen bond is an example, since it is often very strong; the covalency of this interaction was analysed in different studies [16]. Other interactions, not only hydrogen bonds, may possess numerous characteristics of covalent bonds [17]. One can mention the σ-hole and π-hole bonds, which may be often treated as counterparts of the hydrogen bond [18,19,20,21]. However, it is also very important that interactions may be treated as the preliminary stages of chemical reactions [22] and that, if they are strong enough, they change the configurations of reactants [23]. The interrelation between interactions and the Valence-Shell Electron-Pair Repulsion, VSEPR, model [24] was discussed, and it was justified that the classification of interactions may be based on the changes in the configurations of interacting centres [23]. There are other numerous studies where various kinds of interactions are analysed and compared between themselves [25,26,27,28]; in particular, those interactions that are related to the σ-hole and π-hole concepts are widely discussed in recent studies [29,30,31,32]. On the other hand, the studies related to the changes in the configurations of interacting centres are rather rare [33]. One of the studies on very strong chalcogen bonds may be mentioned here [34], which found clear trigonal bipyramid structures for the analysed chalcogen bonded complexes.
This is why two topics are analysed here: very strong interactions possessing the characteristics of covalent bonds and changes in the configurations resulting from such interactions. The following interactions classified as the σ-hole bonds are analysed in this study: tetrel, pnicogen, chalcogen, and halogen bonds. For the latter interactions, the elements of the 14th, 15th, 16th, and 17th groups, respectively, act as the Lewis acid centres. The tetrahedral systems that interact with chloride anions are discussed here, since such charge-assisted interactions possess numerous characteristics of covalent bonds. These complexes were discussed earlier [17]; however, not in terms of the VSEPR model or in terms of the changes in the configurations of interacting units. In other words, neither the relationships concerning the structures discussed here nor their characteristics that are also presented were analysed before.

2. Computational Details

The complexes connected by halogen, chalcogen, pnicogen, and tetrel bonds, where the Cl− anion acts as the Lewis base, are analysed. The FCl and FBr electron acceptors form complexes with the latter anion by the halogen bond; the SFH and SeFH species form complexes through the chalcogen bond; similarly, the pnicogen bond links the chloride anion with the PFH2 and AsFH2 moieties, while the tetrel bond connects the SiFH3 and GeFH3 species with the Cl− anion. In the complexes analysed here, the Z centre (Z = Cl, Br, S, Se, As, P, Si, or Ge) of the Lewis acid unit is connected to the chloride anion through the σ-hole. The latter is situated approximately at the Z-centre, in the extension of the F–Z bond. There are also σ-holes located in elongations of the H–Z bonds; however, the contacts with them are not analysed here. The above-mentioned σ-holes are characterized by the depletion of the electron charge and the positive electrostatic potential (EP); four σ-holes are observed for the Ge and Si centres, three for As and P, two for S and Se, and one for Br and Cl. Figure 1 shows two examples of EP mapped at the molecular surfaces of the AsFH2 and FBr moieties; the σ-holes are shown there. The species containing fluorine substituents were chosen as the Lewis acid units, since the fluorine, as the electron-withdrawing substituent, enhances the σ-hole (positive EP increases) at the Z-centre in the extension of the F–Z bond. In the case of the FBr species, there is one σ-hole at the bromine centre located in the elongation of the F–Br bond, while, for the AsFH2 moiety, there are three σ-holes at the arsenic centre; the strongest one is characterised by the greatest positive EP in the extension of the F–As bond and two in extensions of the H–As bonds (only one of them is visible in Figure 1).
The chloride anion was chosen here as an electron donor; the fluoride anion could be a better choice, since it is a stronger Lewis base [35]. However, the F-substituent is connected to the Z-centre of the Lewis acid unit to enhance the σ-hole. The interactions of such units with fluoride anions lead to the symmetrical ZHxF2 units (x = 0, 1, 2, or 3) with two equivalent Z∙∙∙F contacts. Such systems may be the subject of another study.
Figure 2 presents the 2D maps of the Laplacian of electron density, ∇2ρ, for the FCl species and for the FCl∙∙∙Cl− complex. One can see here the positive ∇2ρ value in the extension of the F–Cl bond for the isolated FCl unit that corresponds to the σ-hole. The complexation is connected to the electron charge shifts from the chloride anion to the FCl unit that leads to the accumulation of the electron charge between the Cl centres; both chlorine centres in the complex are surrounded by areas of negative ∇2ρ values.
Such “closure” of the valence shell is possible, since the great electron charge shift from the chloride anion to the F–Cl Lewis acid moiety is observed (see further discussion). However, in the case of weaker interactions in the FCl∙∙∙C2H2 and FCl∙∙∙NH3 complexes, lower charge shifts are observed and the valence shell of the Cl centre is not closed [36]. Another topic is related to the heavier halogen centres. For example, in the case of the F3CBr species, the σ-hole is observed at the Br centre in the elongation of the C–Br bond; the large depletion of the electron charge is observed here due to the influence of F substituents [36]. The valence electron shell of the bromine centre is open, but the ring of the negative Laplacian is around its nucleus due to the inner electron shells. However, the positive total electrostatic potential, EP, at the σ-hole area is very important here; it is the sum of the electron EP and of the nucleus EP contributions. For example, at the σ-hole areas of the chlorine and bromine centres of the F3CCl and F3CBr moieties, the total EP is equal to +0.034 au and +0.040 au, respectively (MP2/aug-cc-pVTZ results). The valence shell for the bromine centre is not closed in the F3C-Br∙∙∙NH3 and F3C-Br∙∙∙OH− complexes; however, the closed rings of inner electrons are still observed here. A similar situation is observed for the isolated F–Br species and for this species involved in the halogen bond interaction in the F–Br∙∙∙NH3 complex [37], where, in both cases, the valence electron charge ring is open and the closed inner shell rings are observed.
For the complexes analysed in this study, the second-order Møller–Plesset perturbation theory (MP2) [38] calculations were performed with the use of Gaussian16 [39]; the Dunning-style aug-cc-pVTZ basis set was applied [40]. Frequency calculations performed at the same computational level have shown that the optimized structures correspond to energetic minima. For the systems containing the Ge, As, Se, and Br atoms, additional calculations were carried out to check the significance of the relativistic effects; the Stuttgart/Cologne group ECP10MDF pseudopotentials were applied for these centres [41], with the corresponding Peterson AVTZ (11s12p10d2f)/[6s5p4d2f] basis sets [42]. These results that partly take into account relativistic effects are presented in this study; however, they do not differ significantly from the MP2/aug-cc-pVTZ results, where such effects are not included. For example, the interaction energy differences between both approaches, relativistic and non-relativistic, do not exceed 0.2 kcal/mol; only slight and negligible differences are observed for other parameters, with geometrical ones between them.
The interaction energy for the complexes analysed, Eint, was calculated as the difference between the energy of the complex and the sum of the energies of monomers, where the energies of monomers correspond to their geometries in the complex [43]. The basis set superposition error (BSSE) [44] correction was also calculated; thus, the BSSE-corrected Eint values are discussed hereafter. The Natural Bond Orbital (NBO) method [45,46] was also applied to analyse the electron charge shifts resulting from complexations. For the NBO calculations, the NBO 5.0 program [47] implemented in the GAMESS codes [48] was used. Additionally, the AIMAll program [49] was used to calculate the delocalization indices.

3. Results and Discussion

3.1. σ-Hole Bonds Analysed in This Study

It was pointed out in previous studies that various interactions may be treated as preliminary stages of chemical reactions [22]. For example, the hydrogen bond may initiate the proton transfer process [50,51] while the tetrel bond may lead to the SN2 reaction [52]. It was shown also that interactions, if they are strong enough, lead to a change in the configurations of reaction centres. For example, the tetrel centre, characterized by the tetrahedral configuration, may act as the electron acceptor interacting with the Lewis base unit through the σ-hole bond. The latter interaction may lead to the change of the tetrahedral configuration of the tetrel centre into the trigonal bipyramid configuration. Scheme 1 presents an example of the SiFH3 species that interacts strongly with the chloride anion, since the interaction energy, Eint, is equal to −32.6 kcal/mol (Table 1). The angle presented in Scheme 1, designated later here as the α angle, may be treated as a degree of the change of one configuration (tetrahedral) into another (trigonal bipyramid). This angle is equal to 109.5° for the “pure” tetrahedral structure characterized by the same substituents (as for methane with the same H-atoms attached to the carbon centre). In the case of various substituents, this angle is different to 109.5°, more or less. For the “pure” trigonal bipyramid configuration, the α angle is equal to 90°. Scheme 1 shows the change in this angle that is smaller, i.e., 95.7°, for the SiFH3∙∙∙Cl− system than that for the isolated SiFH3 unit, i.e., 108.2°. It is worth mentioning that, for the SN2 reactions of the tetrel centres, the transition states are characterized by the α angle being equal to 90° or nearly so.
The above mentioned changes in configurations from the tetrahedral into the trigonal bipyramid were analysed in another study for the tetrel and pnicogen centres if they interacted with the electron-donating species through the σ-hole bonds, through the tetrel bond, or the charge-assisted pnicogen bond [33]. It was found that the reduction of the α angle occurs if the Lewis acid unit interacts with the electron donor; this reduction is greater with the greater electron charge transfer from the Lewis base unit to the Lewis acid unit.
Various changes in configurations that result from interactions are observed. For example, the triel trigonal centres interact with the Lewis base units, causing a change into tetrahedral configurations in the case of strong interactions [54]. However, it is worth mentioning that the configuration in the complex is usually intermediate between that which corresponds to the isolated Lewis acid moiety and that corresponding to the very strong and covalent-in-nature link between interacting units. The aim of this study is to analyse the changes in the tetrel, pnicogen, chalcogen, and halogen centres that interact with the strong Lewis base unit, chloride anion. The following centres are considered here: tetrel ones that possess four covalent bonds, pnicogen centres possessing three bonds and one electron pair, two bonds and two electron pairs occurring in the chalcogen centres, and, for the halogen centres, one bond and three electron pairs were observed (see Scheme 2). It was assumed that all of these centres were characterized by a tetrahedral structure and sp3 hybridization, at least approximately. However, this was not always true. For example, the water structure was characterized by two covalent O–H bonds and two lone electron pairs. However, in contrast to numerous monographs and scholarly books, these pairs are not equivalent and they do not fit into sp3 hybridization [55]. Similarly, the latter hybridization does not occur in the case of halogen centres. However, the reaction paths are often in agreement with this rough assumption [23]. The oxygen of the water molecule in crystal structures is often characterized by the coordination four corresponding to the sp3 hybridization; the HF dimer possesses the structure that also corresponds to this hybridization for the fluorine centre [24].
Scheme 2 presents the changes in the configurations of the above centres if they interact strongly with the Lewis base units. The tetrel centre linked by very strong interactions with the Lewis base centre is characterized by the trigonal bipyramid configuration; one can observe three equatorial and two axial neighbours of this centre here. In the case of the remaining interactions—pnicogen, chalcogen, and halogen bonds—the lone electron pairs in complexes possessing trigonal bipyramid configuration are always situated in equatorial positions, while the axial positions are reserved for covalent bonds (Scheme 2). This may be explained by the occurrence of three-centre–four-electron (3c/4e) hypervalent bonds [9] that are observed for the linear systems and axial positions in complexes analysed here. These axial bonds are more polarized and characterized by lower orders than those occurring in the equatorial positions. The latter bond orbitals are usually characterized by high occupancy, close to two, similar to the lone electron pairs located in equatorial positions. The existence of weaker axial bonds than equatorial ones guarantees that the octet rule is obeyed, at least approximately.

3.2. Geometries and Energies

The Quantum Theory of Atoms in Molecules [56,57], QTAIM, is applied here to indicate the interactions between centres in the species analysed in this study. Figure 3 and Figure 4 present molecular graphs of the species that act as the Lewis acid units and the molecular graphs of their corresponding complexes with the chloride anion. There are links between the Z-centre (halogen, chalcogen, pnicogen, or tetrel) and the chloride anion in these systems. The bond paths with bond critical points (BCPs), which are presented in the figures, correspond to the above-mentioned links; this is evidence of the stabilizing interactions in complexes analysed here [58,59]. The Z-centre is linked to the chlorine one through its σ-hole located in the elongation of the F–Z bond. The links through the σ-holes located in the extension of the H–Z bonds are not considered, since the EP positive values are lower here than those for the corresponding F–Z σ-holes. The aim of this study is to discuss the very strong interactions, and the links through the σ-holes enhanced by the F-substituent guarantee them. The molecular graphs in Figure 3 and Figure 4 correspond to Scheme 2. They also present the changes in the tetrahedral configurations of the Z-centres into trigonal bipyramid ones. These figures do not show the localizations of lone electron pairs, however. This is why, only in the case of the tetrel bonded complexes, SiFH3∙∙∙Cl− and GeFH3∙∙∙Cl−, the trigonal bipyramid structures are expressed clearly by the molecular graphs; there are no lone electron pairs in tetrel centres here.
It is worth mentioning, however, that the chalcogen bonded systems with the chalcogen centre possessing the trigonal bipyramid structure were analysed [34], and the ELF approach [60,61,62,63] was applied to localize lone electron pairs.
Table 1 presents selected parameters of the analysed complexes; the interaction energies, Eints, are included. Large |Eint| values, usually exceeding 30 kcal/mol, may indicate the covalent character of interactions with the chloride anion. Only for the pnicogen-bonded complexes, PFH2∙∙∙Cl− and AsFH2∙∙∙Cl−, lower |Eint| values, but still high, are observed, which are 23.6 kcal/mol and 29.4 kcal/mol, respectively. It was found in a former study [17] that all interactions with the chloride anion, which are analysed here, possess numerous characteristics of covalent bonds. Several various parameters indicate the latter characteristics, such as the total electron energy density at the Z∙∙∙Cl BCP, HBCP, which is negative, the important contribution to the total interaction of the interaction related to electron charge shifts, or the Heitler–London term of the energy of interaction that is positive. Other parameters that express the covalency of interactions, being a subject of this study, are discussed further here.
Table 1 also presents a few geometrical parameters. One can see that the α angle discussed earlier (Scheme 1), which is included in this table, was greater for the isolated Lewis acid units (α*) than for these species involved in interactions in complexes (α). In other words, this angle is closer to the tetrahedral configurations for the former species, while, for the latter ones, it is closer to the trigonal bipyramid. However, only in a few cases is the agreement with the parameters of ideal configurations observed; for the isolated tetrel centres, this angle is close to 109.5°, and for the pnicogen and chalcogen-bonded complexes, an angle close to 90° occurs. However, the above differences in the α angle between isolated units and complexes show that the σ-hole interactions lead to the change of configurations (Scheme 2), or at least one can observe the disruption of geometries towards other configurations—from tetrahedral to trigonal bipyramid for the species discussed in this study.
The F–Z∙∙∙Cl σ-hole interactions analysed here correspond to the linear, or nearly so, arrangements. In particular, the F–Z∙∙∙Cl angles are equal to or are very close to 180° for the systems linked by tetrel and halogen bonds. This may be explained in the following way. For the former interactions, the σ-hole characterized by the positive electrostatic potential is situated exactly in the extension of the F–Z bond, since the ZFH3 Lewis acid unit possesses the C3v symmetry; in the case of FZ (Z is a halogen centre) species, the same location of the σ-hole is observed—in the extension of the F–Z bond. The “belt” of the negative EP around the Z-centre resulting from the lone electron pairs was also observed for such FZ species [15] (see FBr species in Figure 1). In the case of ZFH2 and ZFH, which are pnicogen and chalcogen species, respectively, the occurrence of lone electron pairs disturbs the location of the σ-holes from the extension of the F–Z bond. This is why the F–Z∙∙∙Cl angle was slightly different from 180° here.
The F–Z bond lengths are also presented in Table 1 for the isolated Lewis acid units and for the corresponding complexes with the chloride anion. One can see that, for almost all species, the complexation leads to the elongation of the F–Z bond by about 0.1–0.2 Å or even more; only for the SiFH3∙∙∙Cl− complex, this elongation is slightly lower than 0.1 Å. The similar elongation of the A–H bond that results from the formation of the A–H∙∙∙B hydrogen bond is observed for the majority of the hydrogen-bonded complexes [3,4]. The shortening of the A–H bond being the effect of hydrogen bond formation is not so usual [64,65].
Table 1 shows the Z∙∙∙Cl distances corresponding to the local intermolecular atom–atom contacts. Distances between 2.28 Å and 2.61 Å are observed. They are shorter than the corresponding sums of the van der Waals radii. Referring to these radii, the following values for those were proposed by Bondi [53]; Cl—1.75 Å, Br—1.85 Å, S—1.80 Å, Se—1.90 Å, P—1.80 Å, As—1.85 Å, and Si—2.10 Å (the Bondi value for Ge is not given, but it should be greater than or close to that one of the Si centre). One can see that, for the majority of the Z∙∙∙Cl contacts, the corresponding sum of van der Waals radii amounted to ~3.6 Å; this was much greater than the distances in complexes by about 0.95–1.37 Å (Table 1).

3.3. Nature of σ-Hole Bonds

Table 2 shows the NBO [9,45,46] atomic charges for the centres directly involved in the F–Z∙∙∙Cl σ-hole bond. The Cl centre was characterized by a lower charge (less negative) in the complex than that observed for the free chloride anion (−1 au). This indicates that the complexation leads to the outflow of the electron charge from the anion into the Lewis acid species. Outflow between −0.18 au and −0.44 au is observed for the complexes analysed here. This outflow results in charge changes at the F and Z centres directly involved in the σ-hole bond; a lower positive charge of the Z-centre and a greater negative charge of fluorine are observed. Both changes oscillate around a value of 0.1 au. However, they are the greatest for the halogen-bonded complexes. For the FCl∙∙∙Cl− interaction, a decrease in the positive charge of Z by 0.15 au and an increase in the negative charge of the F-centre by 0.30 au are observed; in the case of the FBr∙∙∙Cl− complex, these changes amount to 0.14 au and 0.24 au, respectively.
One can see that the above changes differ from those that occur in hydrogen-bonded systems. For the A–H∙∙∙B hydrogen bond, complexation led to the outflow of the electron charge from the B Lewis base unit, an increase in the negative charge of the A-centre, and an increase in the positive charge of the H-centre [9]. In the case of the σ-hole bonds analysed here, the positive charge of the Z-centre being in contact with the chloride anion decreased.
Table 3 shows the other NBO parameters—the polarizations of bonds involved in interactions in complexes. For the F–Z bonds (in complexes and in isolated species designated by a star), such polarization is understood as the percentage of the F–Z σ bond orbital electron density at the Z-centre. In complexes, these polarizations were lower than those in the isolated Lewis acid units. This means that the complexation leads to the greater outflow of the electron charge from the Z-centre to the more electronegative F-substituent than that observed for isolated Lewis acid units. However, in complexes, the transfer of the electron charge from the chloride anion to the Z-centre is also observed (Table 2); thus, the positive charge of Z decreased, as discussed earlier. It is worth mentioning that the meanings of the F–Z σ-bonds’ polarizations discussed here and presented in Table 3 are not the same as those related to the polarization interaction energies resulting from the decomposition schemes [66]. For example, the hybrid variation–perturbation theory (HVPT) [67,68,69] was applied to perform the decomposition of the energy of the interactions for complexes linked by various σ-hole bonds [17]. It was found that the significance of the delocalization energy term and, consequently, the ratio between the delocalization and electrostatic terms increases with the increase in the strength of the interaction. For the complexes of the chloride anion, the latter ratio is situated between approximately 0.6 and 1.1. The delocalization interaction energy in the HVPT approach is related to the electron charge shift phenomena and it containes the polarization and charge transfer interaction energy terms, which are not separated here. However, they are separated in some other decomposition schemes.
One can see (Table 3) that the polarizations of Z-Cl links are also presented; this is because the NBO approach shows the Z-Cl bond orbitals for very strong interactions discussed here. In two cases of halogen-bonded complexes, the hypervalent 3c/4e (three centre—four electrons) bonds are formed. These F:-Cl(Br)–:Cl hyperbonds are characterized by the following equilibrium: F–Cl(Br): Cl ↔ F:Cl(Br)–Cl. For the F:–Cl–:Cl system, the percentage of the configuration with the Cl–Cl bond amounted to 62.1%, while, for the F:–Br–:Cl system, the percentage of the configuration with the Br–Cl bond amounted to 60.8%. This is why, according to the NBO approach, complexation led to the disappearance of F–Cl(Br) bonds.
Table 4 presents the delocalization indices for the F–Z, δ(F,Z) and Z–Cl, δ(Z,Cl) contacts in the F–Z∙∙∙Cl σ-hole bonds. For the former index, the values for the complex, δ(F,Z), and for the isolated Lewis acid unit, δ(F,Z)* are given. This parameter may be treated as that which expresses the covalent characteristics of the interaction [70,71] (Equation (1)).
δ(A,B) = −2 ∫A∫B (2Γ(r1,r2) − ρ(r1)ρ(r2))dr1dr2
where ρ(r) and Γ(r1,r2) are the one- and two-electron densities, respectively; the integrations are performed here through two atomic basins. Hence, the delocalization index δ(A,B) corresponds to the number of electrons delocalized between two atoms (A and B). Thus, it expresses the degree of covalency and indicates the number of shared electrons.
One can see that the δ(F,Z) value was lower than the corresponding δ(F,Z)* value. This is connected to the elongation of the F–Z bond resulting from the complexation discussed earlier. Such elongation is connected to the decrease in the bond order (bond number) [72,73] and thus with the decrease in the covalent character of the interacting F–Z pair of atoms. The latter decrease is compensated by the additional Z∙∙∙Cl interaction in the complex. Table 4 shows the δ(Z,Cl) values for the complexes analysed here. The greatest δ(Z,Cl) indices are observed for the FCl∙∙∙Cl− and FBr∙∙∙Cl− complexes, 0.749 and 0.728, respectively. These values correspond to the greatest decreases of the δ(F,Z)* values from the isolated species to the δ(F,Z) values in complexes. They also correspond to the strongest interactions (Table 1); the greatest |Eint| values are observed here, which are 45.0 kcal/mol and 46.3 kcal/mol.

4. σ-Hole Bonds and VSEPR Model—Discussion and Summary

The σ-hole bonds discussed in this study, similar to numerous other interactions, are in line with the Valence-Shell Electron-Pair Repulsion, VSEPR, model. There are the following main assumptions of this model [24,74,75]:
The location of covalent bonds with the centre considered depends on the number of electron pairs in the valence shell; these pairs are attributed to bonds and to nonbonding pairs, such as lone electron pairs.
The valence electron pairs of the centre analysed are located in such a way as to maximize their distances apart.
It is assumed in the VSEPR model that the non-valence inner electrons with the nucleus (this means the core) are characterized by spherical symmetry; in particular, such symmetry is observed for the main groups’ elements.
There are the following structures, according to the VSEPR approach, for the increase in the number of electron pairs from two to six: linear (L), trigonal (Tr), tetrahedral (Td), trigonal bipyramid (TBP), and octahedral (Oc); the Tr, Td, TBP, and Oc abbreviations of structures were proposed by Martin [76]. Other designations of structures may be mentioned that indicate the numbers of bonds and lone electron pairs, such as AXnEm, (ref. 24) where A indicates the central atom, n is the number of X atoms (not necessarily the same atoms) linked by single bonds with the A centre, and m is the number of nonbonding or lone electron pairs (marked by E). Thus, there are n+m electron pairs in the valence shell of the central atom.
If one refers to the designations mentioned above here, the following changes for the σ-hole bonds analysed in this study can be observed for halogen, chalcogen, pnicogen, and tetrel bonds: AXE3 → AX2E3, AX2E2 → AX3E2, AX3E → AX4E and AX4 → AX5, respectively.
Another way to mark various interactions was proposed recently [23]. This is because marks related to changes in configurations are much more informative than those often applied in various studies so far. For example, for halogen bonds that occur in the complexes analysed here, there are the following marks: (AXE3 → AX2E3) Cl∙∙∙Cl, (AXE3 → AX2E3) Br∙∙∙Cl; for chalcogen bonds, (AX2E2 → AX3E2) S∙∙∙Cl and (AX2E2 → AX3E2) Se∙∙∙Cl; for pnicogen bonds, (AX3E → AX4E) P∙∙∙Cl and (AX3E → AX4E) As∙∙∙Cl; and for tetrel bonds, (AX4 → AX5) Si∙∙∙Cl and (AX4 → AX5) Ge∙∙∙Cl. These designations inform of the changes in the configurations and the centres being in contact; the Lewis acid and the Lewis base centres at the left and right sites, respectively. For all interactions analysed here, a change of the tetrahedral structure towards the trigonal bipyramid occurs (see Scheme 2 as well as Figure 3 and Figure 4).
There were interrelations between the positions of bonds and lone electron pairs for the trigonal bipyramid structure, TBP. The positions of vertices for TBP are not equivalent. The non-equivalency may be interpreted in relation to the positions of lone electron pairs and bonds [24]. However, one can refer also to the ω 3c/4e hypervalent bonds discussed by Weinhold and Landis [9] that correctly explains the locations of lone electron pairs in TBP structures. These pairs are characterized by electron occupancies equal to or very close to two. On the other hand, the bonds often have occupancies much lower than two, especially in the case of significant bonds´ polarizations. Hence, for TBP structures, the lone pairs occupy the positions in the triangle and they are not directed to the axial vertices. The axial XAX arrangement may be considered as the ω 3c/4e hypervalent bond, where a shift of the electron charge to the X centres is observed. In the case of such arrangements where lone electron pairs may occupy only triangle positions, the eight-electron valence shell of the A-centre is exceeded only slightly (if at all) and the octet rule is obeyed, at least approximately.
The details of the new designations of interactions were discussed in the previous study [23]. Only selected types of interactions (see Scheme 2) are discussed here. It is shown here that they are at least partly covalent in nature; three-centre–four-electron, 3c/4e, bonds found for the halogen-bonded systems. The most important is that, for all interactions discussed here—halogen, chalcogen, pnicogen, and tetrel bonds—if one refers to the designations often applied in various studies, they possess similar characteristics. The common feature is that they are related to the change in the tetrahedral structure towards the trigonal bipyramid. This is connected certainly to the electron charge shifts from the chloride anion to the Lewis acid unit.

Funding

This research was funded by the Spanish Government MINECO/FEDER, grant number PID2019-109555GB-I00, and Eusko Jaurlaritza, grant number IT-1254-19.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable, new results are presented here.

Acknowledgments

Technical and human support provided by Informatikako Zerbitzu Orokora—Servicio General de Informática de la Universidad del País Vasco (SGI/IZO-SGIker UPV/EHU), the European Social Fund (ESF) is gratefully acknowledged.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Szatyłowicz, H.; Krygowski, T.M.; Zachara-Horeglad, J.E. Long-Distance Structural Consequences of H-Bonding. How H-Bonding Affects Aromaticity of the Ring in Variously Substituted Aniline/Anilinium/Anilide Complexes with Bases and Acids. J. Chem. Inf. Model. 2007, 47, 875–886. [Google Scholar] [CrossRef] [PubMed]
  2. Krygowski, T.M.; Szatyłowicz, H.; Zachara, J.E. How H-Bonding Affects Aromaticity of the Ring in Variously Substituted Phenol Complexes with Bases. 4. Molecular Geometry as a Source of Chemical Information. J. Chem. Inf. Comp. Sci. 2004, 44, 2077–2082. [Google Scholar] [CrossRef]
  3. Jeffrey, G.A.; Saenger, W. Hydrogen Bonding in Biological Structures; Springer: Berlin, Germany, 1991. [Google Scholar]
  4. Jeffrey, G.A. An Introduction to Hydrogen Bonding; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
  5. Kaplan, I.G. Intermolecular Interactions: Physical Picture, Computational Methods and Model Potentials; John Wiley & Sons, Ltd.: Chichester, UK, 2006. [Google Scholar]
  6. Cotton, F.A.; Wilkinson, G. Advanced Inorganic Chemistry, 4th ed.; John Wiley & Sons: New York, NY, USA; Chichester, UK; Brisbane, Australia; Toronto, ON, Canada, 1980. [Google Scholar]
  7. The Chemical Bond: Fundamental Aspects of Chemical Bonding; Frenking, G.; Shaik, S. (Eds.) Wiley-VCH: Weinheim, Germany, 2014. [Google Scholar]
  8. Kutzelnigg, W. Chemical Bonding in Higher Main Group Elements. Angew. Chem. Int. Ed. 1984, 23, 272–295. [Google Scholar] [CrossRef]
  9. Weinhold, F.; Landis, C. Valency and Bonding, a Natural Bond Orbital Donor—Acceptor Perspective; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
  10. Minkin, V.I. Glossary of Terms Used in Theoretical Organic Chemistry. Pure Appl. Chem. 1999, 71, 1919–1981. [Google Scholar] [CrossRef] [Green Version]
  11. Pauling, L. The Nature of the Chemical Bond; Cornell University Press: Ithaca, NY, USA, 1960. [Google Scholar]
  12. Ruedenberg, K. The Physical Nature of the Chemical Bond. Rev. Mod. Phys. 1962, 34, 326–376. [Google Scholar] [CrossRef]
  13. Sutcliffe, B.T. The chemical bond and molecular structure. J. Mol. Struct. 1992, 259, 29–59. [Google Scholar] [CrossRef]
  14. Lewis, G.N. Valence and the Structure of Atoms and Molecules; American Chemical Society Monograph Series; The Chemical Catalog Company, Inc.: New York, NY, USA, 1923; pp. 81–82. [Google Scholar]
  15. Gillespie, R.J.; Popelier, P.L.A. Chemical Bonding and Molecular Geometry; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
  16. Grabowski, S.J. What is the Covalency of Hydrogen Bonding? Chem. Rev. 2011, 11, 2597–2625. [Google Scholar] [CrossRef]
  17. Grabowski, S.J.; Sokalski, W.A. Are Various σ-Hole Bonds Steered by the Same Mechanisms? ChemPhysChem 2017, 18, 1569–1577. [Google Scholar] [CrossRef]
  18. Politzer, P.; Riley, K.E.; Bulat, F.A.; Murray, J.S. Perspectives on halogen bonding and other σ-hole interactions: Lex parsimoniae (Occam’s Razor). Comput. Theor. Chem. 2012, 998, 2–8. [Google Scholar] [CrossRef]
  19. Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding: An electrostatically-driven highly directional noncovalent interaction. Phys. Chem. Chem. Phys. 2010, 12, 7748–7758. [Google Scholar] [CrossRef]
  20. Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other σ-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef]
  21. Politzer, P.; Murray, J.S.; Clark, T. The π-hole revisited. Phys. Chem. Chem. Phys. 2021, 23, 16458–16468. [Google Scholar] [CrossRef] [PubMed]
  22. Grabowski, S.J. Hydrogen Bond and Other Lewis Acid–Lewis Base Interactions as Preliminary Stages of Chemical Reactions. Molecules 2020, 25, 4668. [Google Scholar] [CrossRef] [PubMed]
  23. Grabowski, S.J. Classification of So-Called Non-Covalent Interactions Based on VSEPR Model. Molecules 2021, 26, 4939. [Google Scholar] [CrossRef]
  24. Gillespie, R.J.; Hargittai, I. The VSEPR Model of Molecular Geometry; Allyn & Bacon: Boston, MA, USA, 1991; reprinted: Gillespie, R.J.; Hargittai, I. The VSEPR Model of Molecular Geometry; Dover Publications, Inc.: New York, NY, USA, 2012. [Google Scholar]
  25. Wang, W.; Ji, B.; Zhang, Y. Chalcogen bond: A sister noncovalent bond to halogen bond. J. Phys. Chem. A 2009, 113, 8132–8135. [Google Scholar] [CrossRef]
  26. Scheiner, S. Detailed Comparison of the Pnicogen Bond with Chalcogen, Halogen, and Hydrogen Bonds. Int. J. Quantum Chem. 2013, 113, 1609–1620. [Google Scholar] [CrossRef] [Green Version]
  27. Scheiner, S. The Pnicogen Bond: Its Relation to Hydrogen, Halogen, and Other Noncovalent Bonds. Acc. Chem. Res. 2013, 46, 280–288. [Google Scholar] [CrossRef]
  28. Crabtree, R.H. Hypervalency, secondary bonding and hydrogen bonding: Siblings under the skin. Chem. Soc. Rev. 2017, 46, 1720–1729. [Google Scholar] [CrossRef]
  29. Scilabra, P.; Terraneo, G.; Resnati, G. The chalcogen bond in crystalline solids: A world parallel to halogen bond. Acc. Chem. Res. 2019, 52, 1313–1324. [Google Scholar] [CrossRef]
  30. Bundhun, A.; Ramasami, P.; Murray, J.S.; Politzer, P. Trends in σ-hole Strengths and Interactions of F3MX Molecules (M = C, Si, Ge and X = F, Cl, Br, I). J. Mol. Model. 2013, 19, 2739–2746. [Google Scholar] [CrossRef] [PubMed]
  31. Angarov, V.; Kozuch, S. On the σ, π and δ hole interactions: A molecular orbital overview. New J. Chem. 2018, 42, 1413–1422. [Google Scholar] [CrossRef]
  32. Alkorta, I.; Elguero, J.; Frontera, A. Not Only Hydrogen Bonds: Other Noncovalent Interactions. Crystals 2020, 10, 180. [Google Scholar] [CrossRef] [Green Version]
  33. Grabowski, S.J. Pnicogen and tetrel bonds-tetrahedral Lewis acid centres. Struct. Chem. 2019, 30, 1141–1152. [Google Scholar] [CrossRef]
  34. Alikhani, E.; Fuster, F.; Madebene, B.; Grabowski, S.J. Topological reaction sites–very strong chalcogen bonds. Phys. Chem. Chem. Phys. 2014, 16, 2430–2442. [Google Scholar] [CrossRef] [PubMed]
  35. Van Zeist, W.-J.; Yi, R.; Bickelhaupt, F.M. Halogen versus halide electronic structure. Sci. China Chem. 2010, 53, 210–215. [Google Scholar] [CrossRef]
  36. Grabowski, S.J. Hydrogen Bonds and Halogen Bonds—A Comparative Study. In Intermolecular Interactions in Crystals: Fundamentals of Crystal Engineering; Novoa, J.J., Ed.; The Royal Society of Chemistry: London, UK, 2018. [Google Scholar]
  37. Amezaga, N.J.M.; Pamies, S.C.; Peruchena, N.M.; Sosa, G.L. Halogen Bonding: A Study based on the Electronic Charge Density. J. Phys. Chem. A 2010, 114, 552–562. [Google Scholar] [CrossRef]
  38. Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef] [Green Version]
  39. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  40. Woon, D.E.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef] [Green Version]
  41. Metz, B.; Stoll, H.; Dolg, M. Small-core multiconfiguration-Dirac–Hartree–Fock-adjusted pseudopotentials for post-d main group elements: Application to PbH and PbO. J. Chem. Phys. 2000, 113, 2563–2569. [Google Scholar] [CrossRef]
  42. Peterson, K.A. Systematically convergent basis sets with relativistic pseudopotentials. I. Correlation consistent basis sets for the post-d group 13–15 elements. J. Chem. Phys. 2003, 119, 11099–11112. [Google Scholar] [CrossRef] [Green Version]
  43. Piela, L. Ideas of Quantum Chemistry; Elsevier Science Publishers: Amsterdam, The Netherlands, 2007; pp. 684–691. [Google Scholar]
  44. Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–561. [Google Scholar] [CrossRef]
  45. Reed, E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  46. Alabugin, I.V.; Manoharan, M.; Peabody, S.; Weinhold, F. Electronic Basis of Improper Hydrogen Bonding: A Subtle Balance of Hyperconjugation and Rehybridization. J. Am. Chem. Soc. 2003, 125, 5973–5987. [Google Scholar] [CrossRef] [PubMed]
  47. Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Weinhold, F. NBO 5.0; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 2001. [Google Scholar]
  48. Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.J.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
  49. Todd, A.; Keith, T.K. AIMAll (Version 11.08.23), Gristmill Software; Todd A. Keith: Overland Park, KS, USA, 2011. Available online: aim.tkgristmill.com (accessed on 8 March 2022).
  50. Scheiner, S. Hydrogen Bonding; A Theoretical Perspective; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
  51. Zundel, G. Series of Ten Lectures On: Proton Polarizability of Hydrogen Bonds and Proton Transfer Processes, Their Role in Electrochemistry and Biology; Institut für Physikalische Chemie der Universität München: München, Germany, 1997. [Google Scholar]
  52. Grabowski, S.J. Tetrel bond-σ-hole bond as a preliminary stage of the SN2 reaction. Phys. Chem. Chem. Phys. 2014, 16, 1824–1834. [Google Scholar] [CrossRef]
  53. Bondi, J. Van der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
  54. Grabowski, S.J. Triel bond and coordination of triel centres–Comparison with hydrogen bond interaction. Coord. Chem. Rev. 2020, 407, 213171. [Google Scholar] [CrossRef]
  55. Clauss, A.D.; Nelsen, S.F.; Ayoub, M.; Moore, J.W.; Landis, C.R.; Weinhold, F. Rabbit-ears hybrids, VSEPR sterics, and other orbital anachronisms. Chem. Educ. Res. Pract. 2014, 15, 417–434. [Google Scholar] [CrossRef]
  56. Bader, R.F.W. Atoms in Molecules, A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
  57. Matta, C.; Boyd, R.J. (Eds.) Quantum Theory of Atoms in Molecules: Recent Progress in Theory and Application; Wiley-VCH: Weinheim, Germany, 2007. [Google Scholar]
  58. Bader, R.F.W. A bond path: A universal indicator of bonded interactions. J. Phys. Chem. A 1998, 102, 7314–7323. [Google Scholar] [CrossRef]
  59. Bader, R.F.W. Bond paths are not chemical bonds. J. Phys. Chem. A 2009, 113, 10391–10396. [Google Scholar] [CrossRef] [Green Version]
  60. Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
  61. Savin, A.; Becke, A.D.; Flad, J.; Nesper, R.; Preuss, H.; von Schnering, H.G. A new look at electron localization. Angew. Chem. Int. Ed. 1991, 30, 409–412. [Google Scholar] [CrossRef]
  62. Savin, A.; Silvi, B.; Colonna, F. Topological analysis of the electron localization function applied to delocalized bonds. Can. J. Chem. 1996, 74, 1088–1096. [Google Scholar] [CrossRef]
  63. Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
  64. Hobza, P.; Havlas, Z. Blue-Shifting Hydrogen Bonds. Chem. Rev. 2000, 100, 4253–4264. [Google Scholar] [CrossRef]
  65. Kryachko, E.S. Neutral Blue-Shifting and Blue-Shifted Hydrogen Bonds, pages 293–336, Chapter 8 in the book Hydrogen Bonding—New Insights; Grabowski, S.J., Ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
  66. Jeziorski, B.; Moszyński, R.; Szalewicz, K. Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
  67. Sokalski, W.A.; Roszak, S.; Pecul, K. An efficient procedure for decomposition of the SCF interaction energy into components with reduced basis set dependence. Chem. Phys. Lett. 1988, 153, 153–159. [Google Scholar] [CrossRef]
  68. Sokalski, W.A.; Roszak, S. Efficient Techniques for the Decomposition of Intermolecular Interaction Energy at SCF Level and Beyond. J. Mol. Struct. 1991, 234, 387–400. [Google Scholar] [CrossRef]
  69. Gora, R.W.; Sokalski, W.A.; Leszczynski, J.; Pett, W.B. The Nature of Interactions in the Ionic Crystal of 3-Pentenenitrile, 2-Nitro-5-oxo, Ion(−1), Sodium. J. Phys. Chem. B 2005, 109, 2027–2033. [Google Scholar] [CrossRef]
  70. Fradera, X.; Austen, M.A.; Bader, R.F.W. The Lewis Model and Beyond. J. Phys. Chem. A 1999, 103, 304–314. [Google Scholar] [CrossRef]
  71. Fradera, X.; Poater, J.; Simon, S.; Duran, M.; Solà, M. The calculation of electron localization and delocalization índices at the Hartree–Fock, density functional and post-Hartree–Fock levels of theory. Theor. Chem. Acc. 2002, 107, 362–371. [Google Scholar]
  72. Brown, I.D. Bond valences—A simple structural model for inorganic chemistry. Chem. Soc. Rev. 1978, 7, 359–376. [Google Scholar] [CrossRef]
  73. Pauling, L. Atomic radii and interatomic distances in metals. J. Am. Chem. Soc. 1947, 69, 542–553. [Google Scholar] [CrossRef]
  74. Gillespie, R.J.; Silvi, B. The octet rule and hypervalence: Two misunderstood concepts. Coord. Chem. Rev. 2002, 233–234, 53–62. [Google Scholar] [CrossRef]
  75. Noury, S.; Silvi, B.; Gillespie, R.J. Chemical Bonding in Hypervalent Molecules:  Is the Octet Rule Relevant? Inorg. Chem. 2002, 41, 2164–2172. [Google Scholar] [CrossRef] [PubMed]
  76. Martin, J.C. “Frozen” Transition States: Pentavalent Carbon et al. Science 1983, 221, 509–514. [Google Scholar] [CrossRef] [PubMed]
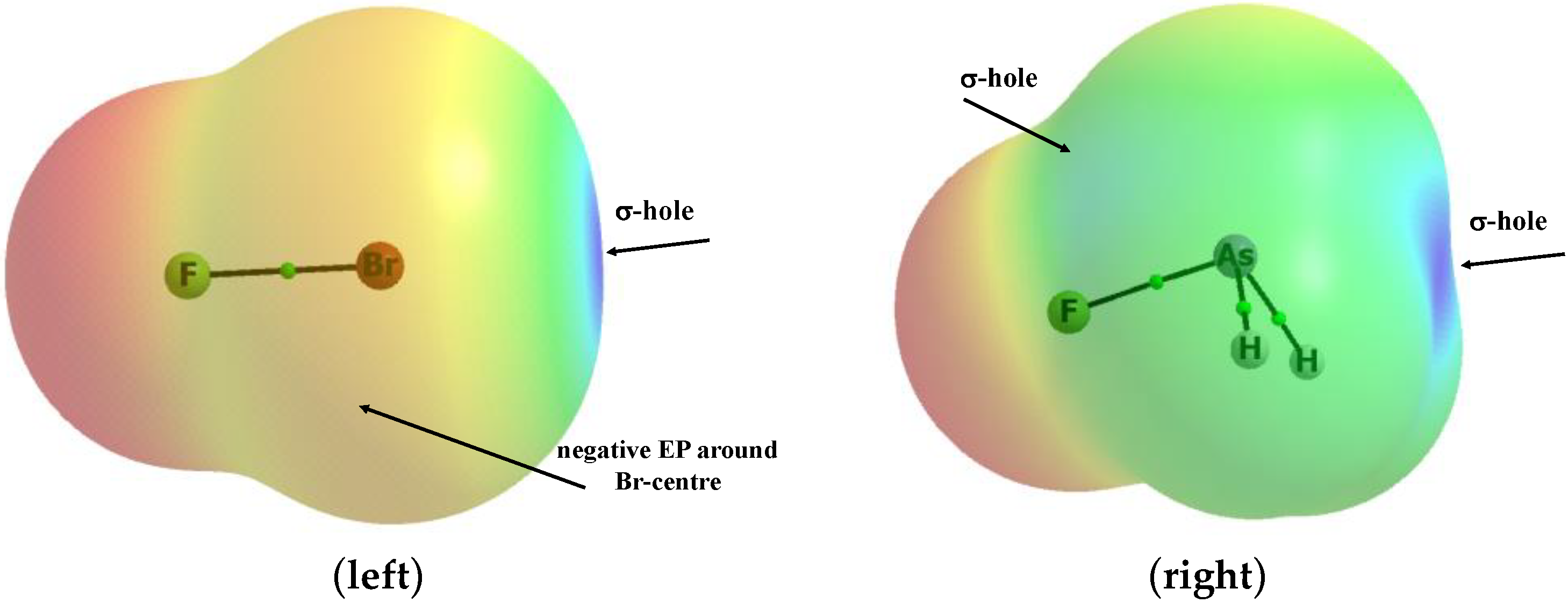
Sci 04 00017 g001 550
Figure 1. Electrostatic potential maps of the FBr (left) and AsFH2 (right) species for the surfaces characterized by an electron density of 0.001 au.
Figure 1. Electrostatic potential maps of the FBr (left) and AsFH2 (right) species for the surfaces characterized by an electron density of 0.001 au.
Sci 04 00017 g001
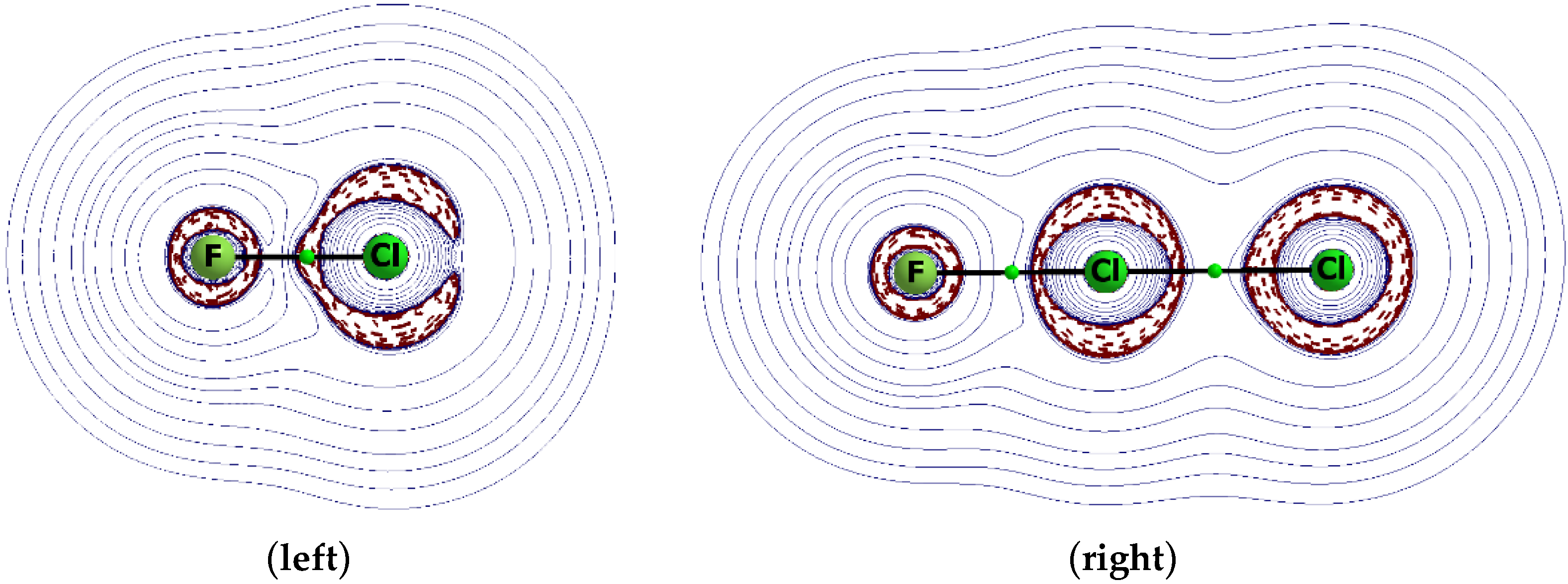
Sci 04 00017 g002 550
Figure 2. Maps of the Laplacian of the electron density for the F–Cl species (left) and for its complex, FCl∙∙∙Cl− (right). The areas of negative Laplacian values are designated by the broken brown lines.
Figure 2. Maps of the Laplacian of the electron density for the F–Cl species (left) and for its complex, FCl∙∙∙Cl− (right). The areas of negative Laplacian values are designated by the broken brown lines.
Sci 04 00017 g002
Sci 04 00017 sch001 550
Scheme 1. Definition of the α* and α angles for the isolated Lewis acid unit and for the complex; examples of the SiFH3 unit and of the SiFH3∙∙∙Cl− complex are presented.
Scheme 1. Definition of the α* and α angles for the isolated Lewis acid unit and for the complex; examples of the SiFH3 unit and of the SiFH3∙∙∙Cl− complex are presented.
Sci 04 00017 sch001
Sci 04 00017 sch002 550
Scheme 2. Changes in the tetrahedral configuration into the trigonal bipyramid resulting from the formation of tetrel, pnicogen, chalcogen, and halogen bonds. Red lines correspond schematically to covalent bonds (or strong interactions), while blue ellipsoids correspond to lone electron pairs.
Scheme 2. Changes in the tetrahedral configuration into the trigonal bipyramid resulting from the formation of tetrel, pnicogen, chalcogen, and halogen bonds. Red lines correspond schematically to covalent bonds (or strong interactions), while blue ellipsoids correspond to lone electron pairs.
Sci 04 00017 sch002
Sci 04 00017 g003 550
Figure 3. Molecular graphs of the Lewis acid units and the corresponding complexes (Z centre is of the third row of the periodic system). The big circles correspond to attractors (related to the atoms’ positions) and the small green circles to bond critical points; attractors are connected by bond paths.
Figure 3. Molecular graphs of the Lewis acid units and the corresponding complexes (Z centre is of the third row of the periodic system). The big circles correspond to attractors (related to the atoms’ positions) and the small green circles to bond critical points; attractors are connected by bond paths.
Sci 04 00017 g003
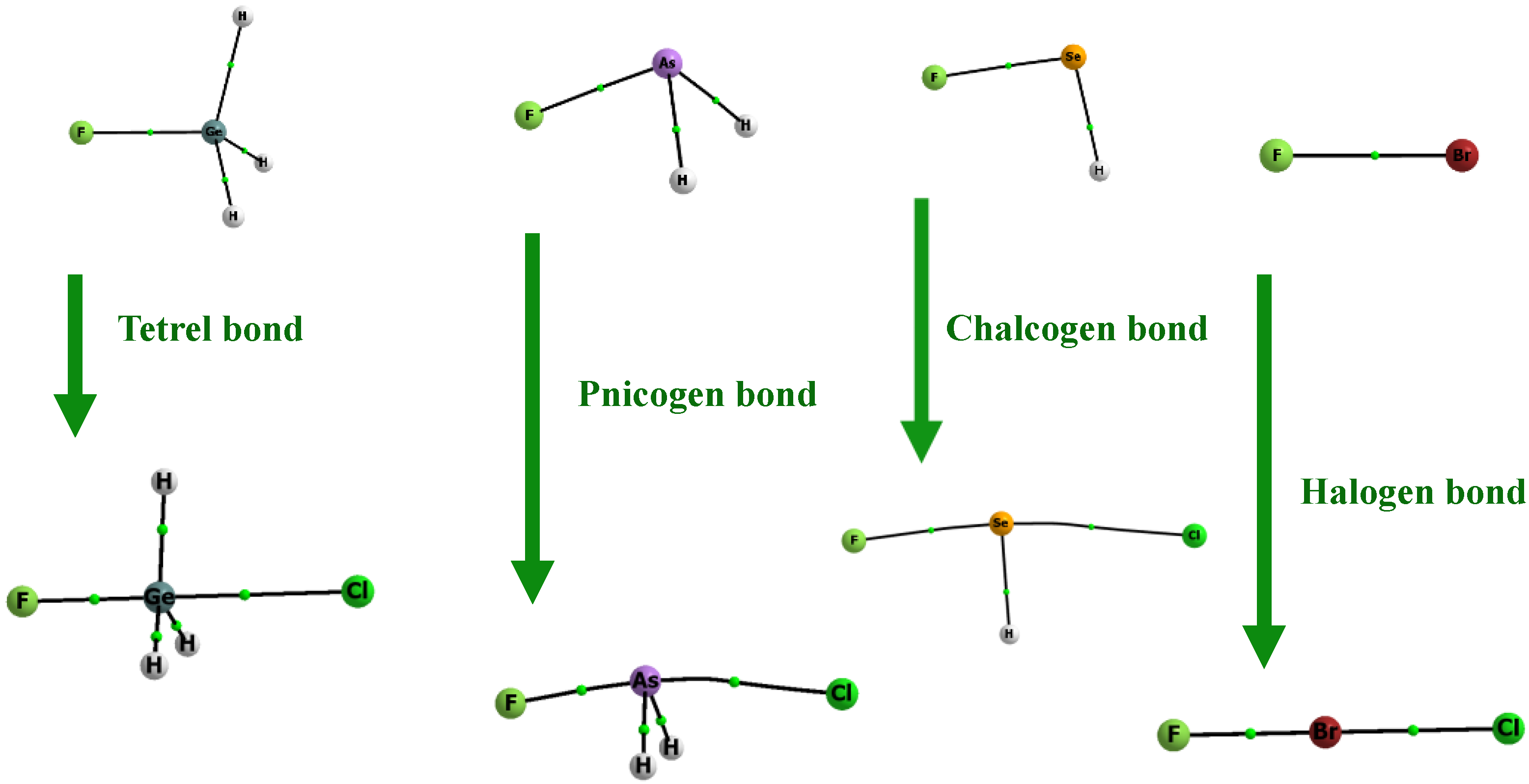
Sci 04 00017 g004 550
Figure 4. Molecular graphs of the Lewis acid units and the corresponding complexes (Z centre is of the fourth row of the periodic system). The big circles correspond to attractors (related to the atoms’ positions) and the small green circles to bond critical points; attractors are connected by bond paths.
Figure 4. Molecular graphs of the Lewis acid units and the corresponding complexes (Z centre is of the fourth row of the periodic system). The big circles correspond to attractors (related to the atoms’ positions) and the small green circles to bond critical points; attractors are connected by bond paths.
Sci 04 00017 g004
Table
Table 1. Interaction energy (in kcal/mol) and the geometrical parameters (in Å, lengths, and degrees, angles) of the complexes analysed here. The α* and α angles are defined in Scheme 1; the F–Z∙∙∙Cl angle concerns the intermolecular contact. Z∙∙∙Cl is the intermolecular distance, the difference between the sum of the corresponding van der Waals radii (the Bondi radii, ref. [53], were applied here), and this Z∙∙∙Cl distance is given in parentheses. The F–Z bond length and its corresponding length of the isolated Lewis acid unit, F–Z*, are also given. Z∙∙∙Cl distances and Eint energies were also presented earlier in another study (ref.17).
Table 1. Interaction energy (in kcal/mol) and the geometrical parameters (in Å, lengths, and degrees, angles) of the complexes analysed here. The α* and α angles are defined in Scheme 1; the F–Z∙∙∙Cl angle concerns the intermolecular contact. Z∙∙∙Cl is the intermolecular distance, the difference between the sum of the corresponding van der Waals radii (the Bondi radii, ref. [53], were applied here), and this Z∙∙∙Cl distance is given in parentheses. The F–Z bond length and its corresponding length of the isolated Lewis acid unit, F–Z*, are also given. Z∙∙∙Cl distances and Eint energies were also presented earlier in another study (ref.17).
ComplexF–Z*F–ZZ∙∙∙ClF–Z∙∙∙Clα*αEint
SiFH3∙∙∙Cl−1.6151.7072.485 (1.37)180.0108.295.7−32.6
PFH2∙∙∙Cl−1.6221.7332.598 (0.95)167.797.792.2−23.6
SFH∙∙∙Cl−1.6341.8022.432 (1.12)170.095.788.9−31.3
FCl∙∙∙Cl−1.6391.8842.276 (1.22)180.0--−45.0
GeFH3∙∙∙Cl−1.7381.8432.587 (>1.26)180.0106.595.0−32.6
AsFH2∙∙∙Cl−1.7511.8772.614 (0.99)167.095.589.7−29.4
SeFH∙∙∙Cl−1.7551.9142.500 (1.15)169.794.287.5−36.7
FBr∙∙∙Cl−1.7581.8292.293 (1.31)179.9--−46.3
Table
Table 2. NBO charges (in au) of the centres of the complexes analysed in this study. qClc is the charge of the chloride anion involved in the interaction in the complex (for a free anion, this charge is equal to −1 au). qFc and qZc are the charges of the F and Z centres in the complex, while qFm and qZm are these charges in the isolated Lewis acid units.
Table 2. NBO charges (in au) of the centres of the complexes analysed in this study. qClc is the charge of the chloride anion involved in the interaction in the complex (for a free anion, this charge is equal to −1 au). qFc and qZc are the charges of the F and Z centres in the complex, while qFm and qZm are these charges in the isolated Lewis acid units.
ComplexqFmqZmqFcqZcqClc
SiFH3∙∙∙Cl−−0.6831.500−0.7511.387−0.772
PFH2∙∙∙Cl−−0.6280.898−0.7160.797−0.822
SFH∙∙∙Cl−−0.5240.468−0.6840.352−0.730
FCl∙∙∙Cl−−0.3870.387−0.6820.238−0.556
GeFH3∙∙∙Cl−−0.6931.401−0.7751.318−0.800
AsFH2∙∙∙Cl−−0.6600.978−0.7610.880−0.804
SeFH∙∙∙Cl−−0.5840.590−0.7370.470−0.727
FBr∙∙∙Cl−−0.4820.482−0.7180.340−0.622
Table
Table 3. Polarizations of the F–Z and Cl–Z bonds; F–Z* is the polarization in the isolated Lewis acid unit. Polarizations express the percentage of the bond orbital electron charge density at the Z-centre. The 3c/4e hyperbonds in halogen-bonded systems are presented; the percentages of the configurations with the Cl–Cl bond and the Cl–Br bonds are given in parentheses.
Table 3. Polarizations of the F–Z and Cl–Z bonds; F–Z* is the polarization in the isolated Lewis acid unit. Polarizations express the percentage of the bond orbital electron charge density at the Z-centre. The 3c/4e hyperbonds in halogen-bonded systems are presented; the percentages of the configurations with the Cl–Cl bond and the Cl–Br bonds are given in parentheses.
ComplexPol F–Z*Pol F–ZPol Cl–Z3c/4e Hyperbond
SiFH3∙∙∙Cl−12.48.89.0-
PFH2∙∙∙Cl−16.510.57.1-
SFH∙∙∙Cl−22.912.210.7-
FCl∙∙∙Cl−30.3-25.6Cl-Cl-F (62.1)
GeFH3∙∙∙Cl−13.18.07.4-
AsFH2∙∙∙Cl−15.58.57.4-
SeFH∙∙∙Cl−20.19.810.4-
FBr∙∙∙Cl−25.8-21.5Cl-Br-F (60.8)
Table
Table 4. Delocalization indices for the F–Z and Z–Cl bonds, δ(F,Z) and δ(Z,Cl), respectively. δ(F,Z)* is the delocalization index for the F–Z bond of the isolated Lewis acid unit.
Table 4. Delocalization indices for the F–Z and Z–Cl bonds, δ(F,Z) and δ(Z,Cl), respectively. δ(F,Z)* is the delocalization index for the F–Z bond of the isolated Lewis acid unit.
Complexδ(F,Z)*δ(F,Z)δ(Z,Cl)
SiFH3∙∙∙Cl−0.3220.2560.169
PFH2∙∙∙Cl−0.5720.5060.336
SFH∙∙∙Cl−0.8620.6920.585
FCl∙∙∙Cl−0.9960.6620.749
GeFH3∙∙∙Cl−0.5440.4290.286
AsFH2∙∙∙Cl−0.6640.5430.403
SeFH∙∙∙Cl−0.8250.6390.588
FBr∙∙∙Cl−0.9420.6690.728
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Grabowski, S.J. σ-Hole Bonds and the VSEPR Model—From the Tetrahedral Structure to the Trigonal Bipyramid. Sci 2022, 4, 17. https://doi.org/10.3390/sci4020017

AMA Style

Grabowski SJ. σ-Hole Bonds and the VSEPR Model—From the Tetrahedral Structure to the Trigonal Bipyramid. Sci. 2022; 4(2):17. https://doi.org/10.3390/sci4020017

Chicago/Turabian Style

Grabowski, Sławomir J. 2022. "σ-Hole Bonds and the VSEPR Model—From the Tetrahedral Structure to the Trigonal Bipyramid" Sci 4, no. 2: 17. https://doi.org/10.3390/sci4020017

APA Style

Grabowski, S. J. (2022). σ-Hole Bonds and the VSEPR Model—From the Tetrahedral Structure to the Trigonal Bipyramid. Sci, 4(2), 17. https://doi.org/10.3390/sci4020017

Article Metrics

Back to TopTop