Abstract
We have investigated the ultrasonically induced birefringence traces of aqueous solutions of dexamethasone disodium phosphate, a derivative of hydrocortisone (cortisol). The stationary birefringence and the transient built-up and decay relaxation processes were studied as a function of solution concentration, ultrasound frequency and intensity, as well as a function of temperature. The results were analyzed in view of structural peculiarities of the system in an effort to gain further insights into the molecular relaxation dynamics and the proposed self-association process occurring in the system. The detected ultrasonically induced birefringence relaxation is motivated by the rotational diffusion of dexamethasone disodium phosphate aggregates due to self-association depending on the solution concentration. The observed relaxation mechanism is directly linked to the hydrodynamic size of the acoustic field-induced self-assembly. The systematic analysis of the transient birefringence signals caused by the applied ultrasonic field allowed us to evaluate the interplay between permanent and induced dipoles with changing concentration, temperature, and ultrasound properties. The birefringence traces are adequately fitted with a stretched exponential law indicating the polydispersive nature of the self-aggregated molecular structures. The obtained results are described in the light of recent studies performed on this system.
1. Introduction
The optical birefringence growth driven by an electric [1,2] or magnetic [3,4,5] field in liquids has been extensively studied in the past. On the other hand, much less attention has been paid to the acousto-optic effect, which is referred to as the generation of birefringence. The application of an ultrasonic field to the, initially, isotropic liquid induces anisotropy in the refractive index that is reflected macroscopically as birefringence. Molecules in neat liquid or in solutions adopt a random orientation due to thermal agitation, even though the molecules may be intrinsically anisotropic. The applied acoustic field forces ordering of the molecules or particles in the direction of the ultrasound propagation. An analogous effect is observed when the applied field is electric (Kerr effect) or magnetic (Hall effect). Nevertheless, electrically or magnetically induced birefringence can be achieved only when the molecules already exhibit electric or magnetic properties, respectively. Thus, this requirement poses a significant limitation in their application [6,7]. The ultrasonically induced birefringence provides information concerning the orientational motion of molecules without any specific property, thus allowing the investigation of the molecular motion of all anisotropic molecules including polymers, colloids, liquid crystals, and pharmaceutical molecules, such as the dexamethasone disodium phosphate (DSP) studied in this work. In the context of the ultrasonically induced birefringence method, the longitudinal ultrasonic wave propagates in the liquid or in solution, inducing diffraction due to the compression and refraction of the acoustic wave generating pressure and density variations in the liquid. Therefore, the interaction between the ultrasonic and electromagnetic field yields different phenomena—namely the Bragg reflection, the Raman-Nath diffraction, and the anisotropy in the refractive index (birefringence) [6] and references therein.
We have chosen to study the structural and dynamical properties of dexamethasone disodium phosphate (DSP) due to its attractive applications, mainly in medicine. It is widely used in cancer therapy and epicondylitis, while it also has anti-inflammatory ability [8,9]. Furthermore, dexamethasone, a member of the corticosteroids, is a derivative of hydrocortisone (cortisol) and is applied in the treatment of rheumatic problems and several lung and brain diseases [10]. Another interesting use of dexamethasone is in the improvement of the outcomes in the baby after a preterm labor [11]. Nowadays, dexamethasone is used in patients with COVID-19 who need mechanical ventilation or supplemental oxygen without ventilation [12]. From the structural point of view, dexamethasone disodium phosphate reveals several functional groups including fused aromatic rings, the phosphate group, and others, such as −OH, −F, and C=O. This characteristic structure of DPS may exhibit conformational changes, proton-transfer, and molecular self-aggregation. Recently, an ultrasonic relaxation spectroscopic study of the aqueous DSP solutions was reported in the MHz frequency range [13]. The results revealed that, above 2.82 mM, the dominating process behind the detected relaxation is the self-association mechanism. The aggregation number was determined experimentally equal to 2 [13].
In the present work, we evaluated the transient and stationary birefringence signal in aqueous DSP solutions in a wide range of concentration, temperature, and ultrasound characteristics including frequency and intensity. The transient birefringence traces were estimated and analyzed in terms of collective motions of DPS molecules with interesting pharmaceutical properties. The degree of DSP molecules’ orientation depends strongly on the energy associated with the interaction between permanent and induced dipoles and the strength of the acoustic field.
2. Materials and Methods
2.1. Solution Preparation
The aqueous solutions of dexamethasone disodium phosphate (DSP) were prepared by weighing the desired amount of the crystalline solid and triply distilled water under ambient conditions. Dexamethasone disodium phosphate, corresponding to molecular formula C22H28FNa2O8P, was purchased from Alfa Aesar with a purity of 98.0%. The so-obtained solutions were colorless and homogeneous. The concentrations of the solutions in mM and the corresponding mole fractions are presented in Table 1. All birefringence measurements were carried out in fresh solutions.

Table 1.
Concentrations and mole fractions of the DSP aqueous solutions.
2.2. Ultrasonically Induced Optical Birefringence Measurements
The optical ultrasonically induced birefringence measurements were carried out by means of a laboratory-made setup, which is described in detail previously [14,15,16]. In brief, the ultrasonically induced birefringence signals were measured after completely loading the acoustic cell with the solution, eliminating possible directional flow or liquid sharing. The acoustic cell was cylindrical in shape and temperature-controlled with an accuracy of ±0.1 °C. The two parallel faces of the cell correspond to a fixed distance (optical path-length) of 1 cm. The acoustic cell was subjected to two different fields in crossed directions. An He–Ne laser working at λ = 632.8 nm in a linear polarization was directed through the solution and served as the probe for the birefringence measurements. The power of the laser-line was fixed at 5 mW to avoid overheating of the liquid. In a perpendicular direction relative to the laser-line, a square ultrasonic pulse was applied utilizing a wide-band piezoelectric element. The central (fundamental) frequency of the transducer was 1 MHz. The ultrasonic pulses had low repetition rate, a condition that is necessary to avoid heating and streaming. The acoustic field was applied uniformly to the entire volume of the liquid for accurate birefringence measurements.
The optical cell was inserted between a polarizer and an analyzer. The light intensity was detected by means of a fast photodiode and monitored in a digital oscilloscope. When the acoustic field is off and the polarizer–analyzer set is settled in crossed polarization, then no optical transmission (light intensity, I) is detected in the photodiode. After applying the ultrasonic field, an optical retardation δ is observed since the anisotropic molecules tend to orient and the system becomes birefringent. The phase retardation is related to the light intensity detected by a photodiode, through the equation:
where I0 is the intensity with acoustic field off and the polarizer–analyzer set in parallel configuration. Furthermore, the optical retardation is related to the ultrasonically induced birefringence as:
with d and λ corresponding to the optical path-length and the laser wavelength, respectively. The resolution limit for the birefringence measurements was estimated lower than 10−8 [14].
sin(δ/2) = (I/I0)0.5
Δn = λδ/(2πd)
3. Results and Discussion
Figure 1 presents the applied ultrasonic squared pulse (a) and the system’s response/birefringence signal (b) measured at 24 °C from a DSP solution with a concentration of 3.18 mM. The frequency of the ultrasonic wave used was fixed at 770 KHz. When the acoustic field is on, the corresponding rise in birefringence trace is assigned to the orientation mechanism, while the decay of the birefringence signal is attributed to the disorientation–randomization process. In the transient birefringence region, the observed different profiles for the rise (field on) and decay (field off) relaxation mechanisms with distinct relaxation times indicate that the mechanisms underlying both processes are not necessarily the same. Indeed, the orientation relaxation is a process that is forced by the applied acoustic field, while the disorientation relaxation is a spontaneous rotational diffusion process. During the orientation process, the radiation pressure, caused by the ultrasonic wave, induces a turning torque in the molecules that are forced to reorient along the ultrasound propagation direction. The birefringence signal saturates when all the molecules are fully aligned, and this region defines the stationary birefringence region with an almost constant value of Δn. The orientation process, the stationary birefringence region, and the randomization processes are shown in Figure 1b.
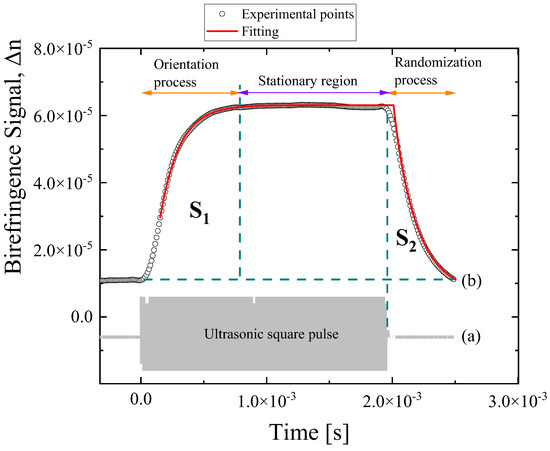
Figure 1.
(a) The applied ultrasonic squared pulse. (b) Representative birefringence signal for DSP solution corresponding to a concentration of 3.18 mM at 24 °C. The frequency of the ultrasound was 770 kHz. Circles and solid line represent experimental birefringence signal and fitting curves, respectively. See text for details concerning the fitting procedure.
The rise of the birefringence signal can be fitted by a stretched exponential function [15,16,17]:
While, in the field off region, the birefringence signal decays according to the equation:
In the above equations, Δnmax and τ are the maximum steady-state birefringence value and the relaxation time of the rise and decay regions, respectively. Parameter β is the polydispersity factor and reveals the width of the relaxation time distribution. A simple exponential function is obtained for β = 1, and the birefringence signal in this case is characteristic of fully monodispersed samples. In Figure 1b, open circles and solid line represent experimental birefringence data and fitting curves according to Equations (3) and (4) for the field on and field off regions, respectively.
The characteristic relaxation time τ of the decay trace is related to the average rotational diffusion coefficient Dr of the particles through the equation [4,5]:
In general, the diffusion coefficient is directly linked to the particle size and can be used to estimate the dimensions of the shape of the particles.
The birefringence signal may provide information concerning the charge distribution, the particle’s size and shape, as well as the presence of permanent and/or induced dipoles. The ratio of the contribution of permanent to induced dipole moments in the orientation process of the DSP molecules can be estimated as [5]:
where S1 and S2 are the areas under the birefringence rise and decay, respectively. In the limiting case where S1/S2 = 1, the permanent-to-induced ratio of dipole moments equals zero (R = 0). This means that the studied molecules have no permanent dipole moments, or these are negligible compared to the induced dipole moments. The second limiting case is S1/S2 = 4. In this case, R becomes infinity (R→∞), which means that the permanent dipoles take over the orientation mechanism.
The rotational diffusion coefficient Dr in rad2/s or Hz is related to the effective hydrodynamic radius r of the molecule through the Stokes–Einstein–Debye relationship:
where kB is the Boltzmann constant, T is the absolute temperature, and ηs is the shear (dynamic) viscosity of the solvent. The denominator in Equation (7) corresponds to the friction.
3.1. Concentration Dependent Birefringence
By analyzing the transient region of the birefringence signal, one is able to gain important information concerning the dynamical behavior of the studied system. In Figure 2a, we present the concentration effect on the polydispersity parameter β. It seems that the organization and disorganization process is characterized by a constant and rather narrow distribution of the relaxation times with a value close to one. Analogous behavior is exhibited by the rotational diffusion coefficient Dr presented in Figure 2b. The observed behavior of the polydispersity parameter and the rotation diffusion coefficient with mole fraction is more or less as expected since the concentration variation is limited in the highly diluted region below 4 mM. On the other hand, the ratio of the contribution of permanent to induced dipole moments in the orientation process for the aqueous DSP solutions reveals a completely different behavior with increasing solution concentration. From Figure 2c, it seems that the ratio R decreases monotonically with increasing mole fraction. Furthermore, it reveals a sudden change at a specific mole fraction signifying a cross-over of two different regions that are related to the self-association (dimerization) mechanism exhibited by the DSP molecules for concentrations above 2.82 mM [13].
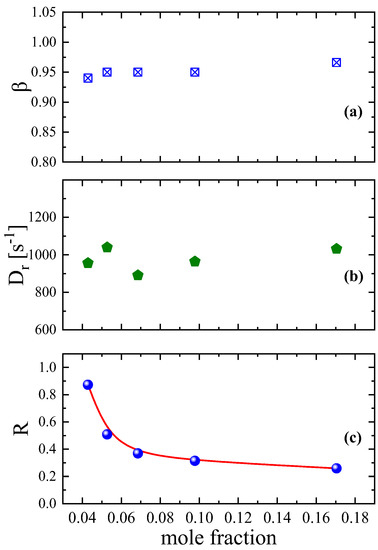
Figure 2.
Concentration dependence of the parameter β (a) related to the width of the relaxation time distribution, the rotational diffusion coefficient Dr (b), and the ratio (c) of the contribution of permanent to induced dipole moments in the orientation process for the aqueous DSP solutions. All measurements correspond to 24 °C, 770 kHz, and ultrasonic intensity 0.242 W/cm2.
3.2. Frequency Effect on Birefringence Signals
The maximum value of the birefringence signal, the so-called static birefringence, as a function of ultrasonic frequency is presented in Figure 3 for a DSP aqueous solution with concentration 2.55 mM at 20 °C.
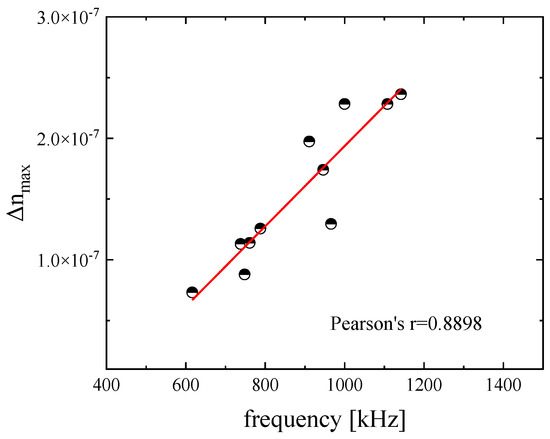
Figure 3.
Maximum (static) birefringence signal as a function of ultrasonic frequency for the DSP aqueous solution with a concentration of 2.55 mM at 20 °C. The value of Pearson’s r = 0.8898 implies a rather linear dependency between induced birefringence and ultrasonic frequency. The intensity of the ultrasound applied to the solution was 0.242 W/cm2.
The results seem to follow a nearly linear dependency with a Pearson’s coefficient equal to r = 0.8898.
The root mean square of the acoustically induced birefringence, Δnrms, that is induced by the applied ultrasonic field is given by [18,19]:
where Δε is the anisotropy in the dielectric constant in the case where all molecules are oriented in one direction, ρ is the solution density, A is the quadratic expansion coefficient of free energy, and c0 is the ultrasound speed measured in the low-frequency limit. In the above equation are also involved the ultrasonic intensity Wu, the angular frequency ω = 2πf of the ultrasound wave, and the translation–reorientation coupling parameter Rc estimated as [20]:
In Equation (9), parameters μ and ν are the so-called viscosity constant parameters and ηs represents the dynamic or shear viscosity. The linear birefringence observed in Figure 3 is justified based on Equation (8), where the ultrasonically induced birefringence is proportional to the frequency of the ultrasound.
In Figure 4a, we present the polydispersity parameter β variation with frequency. The results reveal that the parameter increases slightly with frequency reaching the limiting value of β = 1 in the high ultrasonic frequency limit. The rotational diffusion coefficient, shown in Figure 4b, exhibits the opposite behavior with frequency. This coefficient is related to rotational mobility and is the characteristic value of the Brownian rotation of a particle. Thus, this quantity is important in studies of the alignment of non-spherical particles that are subjected to an external field, such as the acoustic field in our case. From Figure 4b, it seems that faster ultrasonic pulses induce a lower rotational diffusion coefficient.
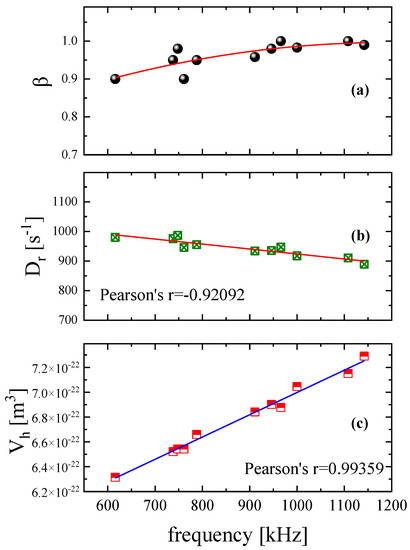
Figure 4.
Frequency dependence of the width of the relaxation time distribution β (a), the rotational diffusion coefficient Dr (b), and the hydrodynamic volume Vh (c) for the aqueous DSP solution with a concentration of 2.55 mM. All measurements correspond to 20 °C and 0.242 W/cm2 ultrasonic intensity. Except for parameter β, the rotational diffusion coefficient and hydrodynamic volume seem to follow a rather linear dependency.
It is also interesting to note that the rotational diffusion is linearly correlated to ultrasonic frequency as is evidenced by the Pearson’s coefficient (r = −0.92092). An analogous linear behavior, although with positive slope, exhibits the estimated hydrodynamic volume presented in Figure 4c. In general, the hydrodynamic volume of a particle in solution is the sum of the time-average of the particle’s volume and the volume of the solvent molecules that are associated with this one. Since the spectral features of the birefringence signal are strongly related to the size and the shape of the particles dissolved in solution, the hydrodynamic volume can be easily estimated based on Equation (7). With the term particle, we refer to single- or macro-molecules, aggregate systems, and colloidal systems of any type. The hydrodynamic volume is linearly correlated with the ultrasonic frequency and faster acoustic pulses induce larger hydrodynamic volumes. Initially, we performed a linear fitting of the experimental data, and we examined the calculated Pearson’s r value. When the absolute value of the Pearson’s parameter was estimated below 0.75, a linear function is inadequate to fit the experimental values and the linear correlation is questionable. Subsequently, we performed a second-order polynomial fitting of the data.
When a longitudinal ultrasonic field is applied to a solution composed of molecules with ellipsoidal shape, then the rotational diffusion coefficient and the ultrasonically induced birefringence are related through the equation [21,22]:
where Ν0 is the number density of the ellipsoids and is the mean refractive index. The two parameters, a1 and a2, are the polarizabilities of the ellipsoid that are parallel and perpendicular to the principal axis. The rest of the symbols in Equation (10) have their usual meanings. We already have seen that the static birefringence is linearly dependent on the ultrasonic frequency (Figure 3) and, from Equation (10), it seems that birefringence is inversely analogous to the rotational diffusion coefficient. Thus, the linear variation of the rotational diffusion coefficient with a negative slope is fully justified.
3.3. Ultrasonic Intensity Effect on Birefringence Signals
The variation of the ultrasonically induced birefringence signal with the acoustic field intensity is presented in Figure 5a for several peak-to-peak voltage values applied to the piezoelectric element. The power of the ultrasonic field was limited to below 0.5 W/cm2 in order to establish the absence of any absorption and scattering of the acoustic waves in the modulation that would require a high-powered and focused ultrasonic field. Furthermore, the frequency of the ultrasonic wave was in the MHz and not in the low-kHz region required to trigger sonochemistry effects. The influence of the power of the laser at the sample, which is below 5 mW, is also negligible. The application of higher voltage leads to a higher ultrasonic field with higher intensity, since the following relation holds [23]:
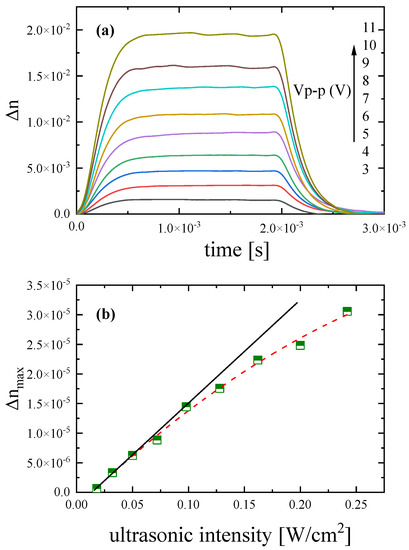
Figure 5.
(a) Ultrasonically induced birefringence traces corresponding to various peak-to-peak voltage values applied to the liquid sample. (b) Maximum birefringence values Δnmax as a function of ultrasonic intensity. These values correspond to the plateau (maximum) of the birefringence signal in the stationary region. See text for more details. The concentration of the DSP solution was 2.55 mM and all measurements were performed at 20 °C and 770 kHz.
It seems from Equation (10) that the birefringence trace is proportional to the square root of the ultrasonic intensity or equivalently proportional to the ultrasonic amplitude. In addition, the ultrasonic amplitude is proportional to the voltage applied to the transducer, and, thus:
It is interesting to note that the birefringence signals presented in Figure 5a all start from zero for t = 0 and all decay to zero without presenting a kind of anisotropy hysteresis or any other anomalous birefringence behavior. Initially, the solution is completely isotropic. The application of the external acoustic field forces the molecule to align along the direction of the ultrasonic wave propagation. The birefringence saturates when all particles are completely aligned. After shutting down the field, the oriented particles are completely randomized leading to a fully isotropic liquid, indicating that the effect of the acoustic pressure on the system is reversible and reproducible.
The maximum birefringence values Δnmax as a function of ultrasonic intensity are presented in Figure 5b. The Δnmax values correspond to the constant maximum value of the birefringence signal (plateau) in the stationary region or, equivalently, the birefringence at the equilibrium state after complete alignment of the particles (orientation process). At low ultrasonic fields, a linear relationship is observed between Δnmax values and ultrasonic intensity Wu while, for higher fields, birefringence tends to saturate following a Langevin behavior. The experimental results were fitted adequately with the relation [24]:
where L2(ξ) is the first-order or usual Langevin function and ξ is a Langevin parameter related to the dipole moments of the particles. For the low acoustic field for the Langevin parameter, the relation ξ << 1 holds.
In Figure 6a, the polydispersity parameter β variation is presented as a function of ultrasonic intensity. The results reveal that the width of the relaxation time distribution β decreases from the limiting value of β = 1 with increasing the intensity of the acoustic field. The variation of the exponent β of the stretched exponential functions (Equations (3) and (4)) was found to be slightly dependent on the ultrasonic field intensity considering that the value β = 0.95 is reached at the highest ultrasonic intensity. The rotational diffusion coefficient, presented in Figure 6b, increases, exhibiting the exact opposite behavior. From Figure 6b, it seems that stronger ultrasonic fields induce a higher rotational diffusion coefficient. This behavior is explained considering that the Dr coefficient is related to rotational mobility, which is enhanced at higher fields. An increasing trend is also observed in Figure 6c for the ratio R of the contribution of permanent to induced dipole moments in the orientation process for the aqueous DSP solution with a concentration of 2.55 mM.
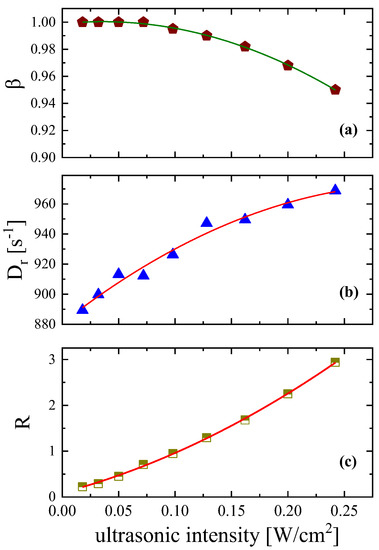
Figure 6.
Ultrasonic intensity dependence of the width of the relaxation time distribution β (a), the rotational diffusion coefficient Dr (b), and the ratio (c) of the contribution of permanent to induced dipole moments in the orientation process for the aqueous DSP solution with a concentration of 2.55 mM. All measurements were performed at 20 °C and ultrasonic frequency set at 770 kHz. Lines are drawn as guides to the eye.
Figure 7 shows the variation of the characteristic relaxation times with ultrasonic intensity for the orientation and disorientation processes that correspond to the rise and decay regions of the birefringence traces for a DSP solution with a concentration of 2.55 mM under isobaric and isothermal conditions. The relaxation times were estimated by fitting the birefringence signals with Equations (3) and (4) for the field on and field off regions, respectively. Both sets of relaxation times follow an almost perfect linear dependency with Pearson’s coefficient equal to r = −0.99448 for the orientation process and r = −0.98965 for the disorientation process.
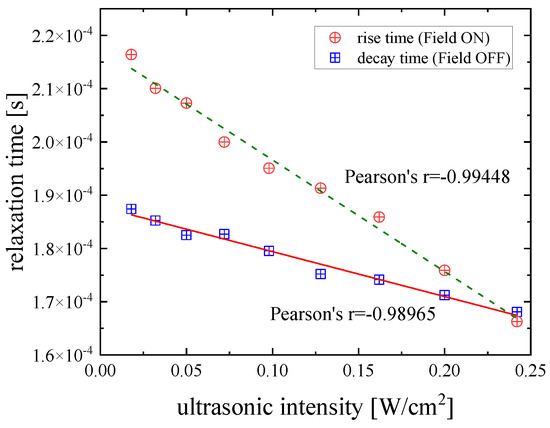
Figure 7.
Characteristic relaxation times as a function of ultrasonic intensity corresponding to orientation/rise (circles) and disorientation/decay (squares) processes for DSP solution with a concentration of 2.55 mM at 20 °C. Both sets of relaxation times follow an almost perfect linear dependency. Solid lines correspond to linear fitting curves.
A stronger acoustic field triggers a more intense driving force in the particles and, thus, the system exhibits higher birefringence. Furthermore, the time that is required for the system to reach the equilibrium state is shorter. The fact that the decay and rise relaxation times are different implies that the processes in the field on and off regimes are attributed to completely different mechanisms. It seems that the rise times are slower compared to the decay times, indicating that the orientation process in the field on regions is slower than the randomization process occurring in the field off regions. The relatively slow relaxation time values presented in Figure 7 for both orientation and disorientation processes are indicative of a collective molecular motion over a long range, since the reorientational relaxation time of an isolated molecule is in the order of 10−8 to 10−9 s.
3.4. Temperature Dependent Birefringence
The study of the maximum (static) birefringence signal static birefringence as a function temperature may progress on the comprehensive understanding of the fast molecular orientation dynamics induced by the external acoustic field. In Figure 8, we present the temperature dependence of Δnmax for the DSP aqueous solution with a concentration of 2.55 mM under isobaric conditions. The results reveal a monotonous decreasing trend with increasing temperature and it tends to saturate at the higher temperature. As seen from Equation (8), birefringence is, among others, a function of shear viscosity, density, refractive index, and sound velocity. All these physical properties are temperature dependent and, thus, the maximum birefringence values are also temperature dependent.
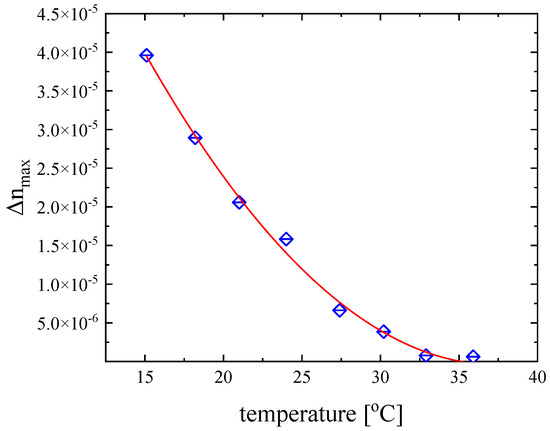
Figure 8.
Temperature dependence of the maximum (static) birefringence signal for a DSP solution with a concentration of 2.55 mM under isobaric conditions. The ultrasonic frequency was set at 846 kHz. Line is drawn as a guide to the eye.
The polydispersity parameter β is also found to be temperature dependent as seen in Figure 9a, and seems to follow a decreasing trend from the limiting value of β = 1 to lower values with increasing temperature, which means that, at higher temperatures, the size of the rotating particles follows a wider distribution. The variation of the exponent β of the stretched exponential functions (Equations (3) and (4)) was found to be almost linearly dependent on temperature as is evidenced by the Pearson’s parameter value equal to r = −0.9557. The rotational diffusion coefficient, presented in Figure 9b, also in this case, exhibits the exact opposite behavior. It seems that the rotational diffusion coefficient increases linearly with temperature with Pearson’s r = 0.91378. This behavior is more or less expected since the Dr coefficient is related to rotational mobility, which is enhanced with increasing temperature. The ratio R of the contribution of permanent to induced dipole moments, presented in Figure 9c, for the aqueous DSP solution with a concentration of 2.55 mM decreases monotonically, with increasing temperature revealing that the number of induced dipoles is enhanced at higher temperatures.
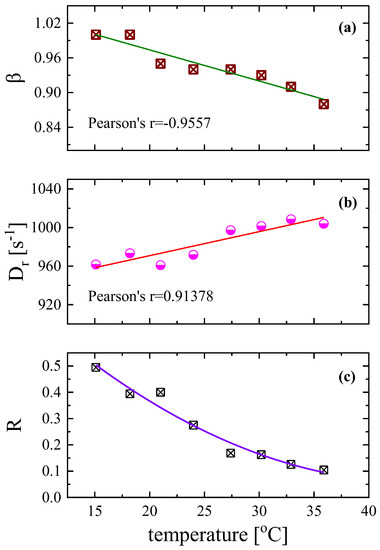
Figure 9.
Temperature dependence of the width of the relaxation time distribution β (a), the rotational diffusion coefficient Dr (b), and the ratio (c) of the contribution of permanent to induced dipole moments in the orientation process for the aqueous DSP solution with a concentration of 2.55 mM. All measurements correspond 846 kHz and ultrasonic intensity 0.242 W/cm2.
As is observed in Figure 10, the characteristic relaxation times for both orientation and randomization regions were found to be linearly dependent on reciprocal temperature, and the corresponding Pearson’s parameters were estimated equal to r = 0.99588 and r = 0.99823. Furthermore, the relatively slow relaxation times for both orientation and disorientation processes are indicative of a collective molecular motion over a long range.
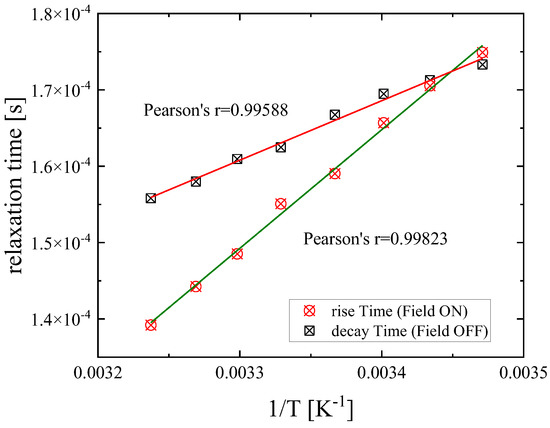
Figure 10.
Characteristic relaxation times as a function of reciprocal temperature corresponding to orientation/rise (circles) and disorientation/decay (squares) processes for DSP solution with a concentration of 2.55 mM. Both sets of relaxation times follow an almost perfect linear dependency. Solid lines correspond to linear fitting curves.
The hydrodynamic volume Vh of the particle is related to the relaxation time of the disorientation regions through the following equation [1,25,26,27,28]:
The so-obtained values of the hydrodynamic volume as a function of temperature are presented in Figure 11, where a clear linear increasing trend is observed as Equation (14) predicts. The theoretical molar volume of the DSP monomer is Vm = 5.27 × 10−28 m3. The calculation of the theoretical molar volume was performed on the optimized structure of the DSP molecule. The optimized structure was estimated in a vacuum environment at the B3LYP level of theory combined with the 6-311++G(d,p) basis set and tight optimization convergence criteria. The origin of the difference between molecular and hydrodynamic volume is yielded on the further self-assembling of the DSP molecules into larger super-molecular aggregates that become acoustically susceptible and birefringent. The inherent intermolecular interaction among the DSP molecules through hydrogen bonding or neat proton transfer results in a molecular pair that appears intrinsically anisotropic. This behavior of the DSP system, which involves the mutual interaction of all molecules, indicates a system structurally and dynamically perplexed. The system studied in this work cannot be considered as a simple ensemble of individual and spatially dispersed anisotropic units in a uniform solvent matrix. On the contrary, the organization of the DSP molecules can be considered as a percolated structure of the DSP molecules through dipole–dipole and dipole-induced dipole interactions. The mobility of aggregates in a medium is a fundamental property that can be readily measured and depends on several interweaving factors. Mobility strongly affects the aggregate transport, dispersal, and the kinetics of their continued growth via aggregation. The size of the aggregate as measured by the hydrodynamic volume provides a measure for the number of primary particles or monomers that make up the aggregate. As the monomer number falls to one, the aggregate is no longer fractal. Another significant factor is the flow regions, which is determined largely by the aggregate’s linear size in comparison to the molecular mean free path of the molecules of the medium in which it is moving. The aggregates are clusters of DSP molecules with a self-similar structure over a finite range of length scales.
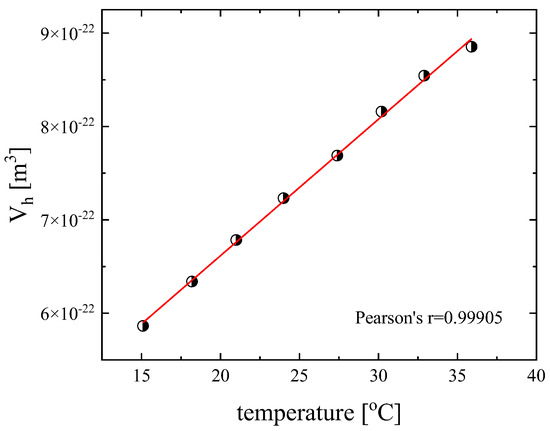
Figure 11.
Variation of the hydrodynamic volume with temperature for a concentration of 2.55 mM. Solid line corresponds to linear filling curve with Pearson’s r = 0.99905 signifying an almost perfect linear dependency.
4. Conclusions
The application of an acoustic field can induce substantial optical anisotropy and, thus, birefringence signals in aqueous DSP solutions. The characteristic relaxation times of the forced orientation and the spontaneous disorientation processes arise in a timescale different than that of reorientations of isolated molecules that occur in the ns to ps timescale. This behavior arises from the orientation of supra-molecular structures due to the action of the external acoustic field. This means that the system can be described as containing acoustically deformable soft molecules-based nanostructures. The results reveal that the structures built during the ordering action of the applied acoustic field are more stable due to electrostatic interaction, hydrogen bonding, and potential steric constraints. The hydrodynamic volume is linearly dependent on temperature, as expected, and is higher than the molecular volume since the acoustically induced birefringence is attributed to self-aggregated molecular structures. It seems that, at higher temperatures, the self-aggregated molecular structures are extended. The variation of the birefringence signals in the static and transient regions as a function of mole fraction, frequency, field intensity, and temperature have been investigated. The results are consistent and indicate that the process is reversible and reproducible, while, after shutting down of the acoustic field, the induced anisotropy is eliminated completely and the particles are randomly disoriented through thermal agitation. On the other hand, the width of the relaxation time distribution β increases smoothly with frequency and decreases with increasing ultrasonic intensity. It appears insensitive to solution concentration indicating that, in the relatively dense region, the polydispersity of the system remains unaffected. On the other hand, temperature variation seems to significantly alter the polydispersity of the system.
The rotational diffusion coefficient Dr remains unaffected in the diluted region of concentrations. It exhibits a weak linear decrease with frequency, a weak increase with ultrasonic intensity, while it tends to saturate at higher values of Wu. Furthermore, the diffusion coefficient was found to increase linearly with temperature. Both ultrasonic intensity and temperature enhance rotational mobility, which is reflected in the behavior of the rotational diffusion coefficient. The ratio R of the contribution of permanent to induced dipole moments in the orientation process decreases monotonically with increasing mole fraction, revealing an inflection point at a specific mole fraction signifying a cross-over of two different regions related to the self-association mechanism exhibited by the DSP molecules. An increase of ultrasonic intensity diminishes the population of the dipole moments, while temperature has the opposite effect. The rotational diffusion coefficient and the polydispersion parameter β demonstrate the exact opposite behavior with increasing frequency, ultrasonic intensity, and temperature. The maximum (static) value of the ultrasonically induced birefringence increases with ultrasonic intensity and tends to saturate at high intensities, as is predicted theoretically.
In fact, all the above findings can be practically attributed to interactions between large aggregates providing progress on the understanding of nano-architectonics at the molecular level.
Author Contributions
Conceptualization, A.G.K.; methodology, A.G.K.; validation, A.G.K. and C.K.; formal analysis, A.G.K. and C.K.; investigation, C.K. and A.G.K.; resources, A.G.K.; data curation, C.K. and A.G.K.; writing—original draft preparation, A.G.K.; writing—review and editing, A.G.K. and C.K.; supervision, A.G.K.; project administration, A.G.K.; funding acquisition, A.G.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are available upon request from the corresponding author.
Acknowledgments
This work was carried out in fulfilment of the requirements for the Ph.D thesis of C. Kouderis according to the curriculum of the Department of Chemistry, University of Ioannina, under the supervision of A. G. Kalampounias.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pochylski, M.; Lombardo, D.; Calandra, P. Optical Birefringence Growth Driven by Magnetic Field in Liquids: The Case of Dibutyl Phosphate/Propylamine System. Appl. Sci. 2020, 10, 164. [Google Scholar] [CrossRef]
- Koralewski, M.; Pochylski, M.; Mitroova, Z.; Melnikova, L.; Kovac, J.; Timko, M.; Kopcansky, P. Magnetic Birefringence Study of the Magnetic Core Structure of Ferritin. Acta Phys. Pol. A 2012, 121, 1237–1239. [Google Scholar] [CrossRef]
- Wilhelm, C.; Gazeau, F.; Roger, J.; Pons, J.N.; Salis, M.F.; Perzynski, R.; Bacri, J.C. Binding of biological effectors on magnetic nanoparticles measured by a magnetically induced transient birefringence experiment. Phys. Rev. E 2002, 65, 031404. [Google Scholar] [CrossRef] [PubMed]
- Ritacco, H.; Fernadez-Leyes, M.; Dominguez, C.; Langevin, D. Electric Birefringence of Aqueous Solutions of a Rigid Polyelectrolyte. Polarization Mechanism and Anomalous Birefringence Signals. Macromolecules 2016, 49, 5618–5629. [Google Scholar] [CrossRef]
- Ritacco, H.A. Electro-optic Kerr effect in the study of mixtures of oppositely charged colloids. The case of polymer-surfactant mixtures in aqueous solutions. Adv. Colloid Interface Sci. 2017, 247, 234–257. [Google Scholar] [CrossRef] [PubMed]
- Kalampounias, A.G.; Kastrissios, D.T.; Yannopoulos, S.N. Structure and vibrational modes of sulfur around the λ-transition and the glass-transition. J. Non-Cryst. Solids. 2003, 326–327, 115–119. [Google Scholar] [CrossRef]
- Yasuda, K.; Matsuoka, T.; Koda, S.; Nomura, H. Dynamics of Entanglement Networks of Rodlike Micelles Studied by Measurements of Ultrasonically Induced Birefringence. J. Phys. Chem. B 1997, 101, 1138–1141. [Google Scholar] [CrossRef]
- Grunwald, H.W.; Rosner, F. Dexamethasone as an antiemetic during cancer chemotherapy. Ann. Intern. Med. 1984, 101, 398. [Google Scholar] [CrossRef]
- Cassileth, P.A.; Lusk, E.J.; Torri, S.; DiNubile, N.; Gerson, S.L. Antiemetic efficacy of dexamethasone therapy in patients receiving cancer chemotherapy. Arch. Intern. Med. 1983, 143, 1347–1349. [Google Scholar] [CrossRef]
- Cohen, S.P.; Bicket, M.C.; Jamison, D.; Wilkinson, I.; Rathmell, J.P. Epidural steroids: A comprehensive, evidence-based review. Reg. Anesth. Pain Med. 2013, 38, 175–200. [Google Scholar] [CrossRef]
- National Institutes of Health; National Heart, Lung, and Blood Institute. Global Initiative for Asthma: Global Strategy for Asthma Management and Prevention NHLBI/WHO Workshop Report; National Institutes of Health: Bethesda, MD, USA, 1995.
- Sterne, J.A.; Murthy, S.; Diaz, J.V.; Slutsky, A.S.; Villar, J.; Angus, D.C. Association between administration of systemic corticosteroids and mortality among critically Ill patients with COVID-19A meta-analysis. JAMA 2020, 324, 1330–1341. [Google Scholar] [PubMed]
- Kouderis, C.; Siafarika, P.; Kalampounias, A.G. Molecular relaxation dynamics and self-association of dexamethasone sodium phosphate solutions. Chem. Pap. 2021, 75, 6115–6125. [Google Scholar] [CrossRef]
- Stogiannidis, G.; Tsigoias, S.; Kaziannis, S.; Kalampounias, A.G. Stationary and transient acoustically induced birefringence of methyl acetate molecules dissolved in ethanol. Chem. Pap. 2020, 74, 2059–2067. [Google Scholar] [CrossRef]
- Kouderis, C.; Tsigoias, S.; Siafarika, P.; Kalampounias, A.G. Acoustically induced birefringence in polymer aqueous solutions: The case of polyvinyl alcohol. Phys. B 2022, 643, 414189. [Google Scholar] [CrossRef]
- Meretoudi, A.; Banti, C.N.; Siafarika, P.; Kalampounias, A.G.; Hadjikakou, S.K. Tetracycline Water Soluble Formulations with Enhanced Antimicrobial Activity. Antibiotics 2020, 9, 845. [Google Scholar] [CrossRef] [PubMed]
- Arenas-Guerrero, P.; Iglesias, G.R.; Delgado, Á.V.; Jiménez, M.L. Electric birefringence spectroscopy of montmorillonite particles. Soft Matter 2016, 12, 4923–4931. [Google Scholar] [CrossRef] [PubMed]
- Nomura, H.; Matsuoka, T.; Koda, S. Translational-orientational coupling motion of molecules in liquids and solutions. J. Mol. Liq. 2002, 96–97, 135–151. [Google Scholar] [CrossRef]
- Nomura, H.; Matsuoka, T.; Koda, S. Ultrasonically induced birefringence in liquids and solutions. In Novel Approaches to the Structure and Dynamics of Liquids: Experiments, Theories and Simulations; Samios, J., Durov, V.A., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004; pp. 167–192. [Google Scholar]
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystals; Claredron: Oxford, UK, 1993. [Google Scholar]
- Peterlin, A. La biréfringence acoustique des liquides purs. J. Phys. Radium 1950, 11, 45–48. [Google Scholar] [CrossRef]
- Hilyard, N.C.; Jerrard, H.G. Theories of Birefringence Induced in Liquids by Ultrasonic Waves. J. Appl. Phys. 1962, 33, 3470–3479. [Google Scholar] [CrossRef]
- Koda, S.; Koyama, T.; Enamoto, Y.; Nomura, H. Study on orientational motion of liquid crystals by acoustically induced birefringence. Jpn. J. Appl. Phys. 1992, 31, 51–53. [Google Scholar] [CrossRef]
- Neitzel, U.; Barner, K. Optical measurements on ferromagnetic colloids. Phys. Lett. A 1977, 63, 327–329. [Google Scholar] [CrossRef]
- Degiorgio, V.; Piazza, R.; Mantegazza, F.; Bellini, T. Stretched-exponential relaxation of electric birefringence in complex liquids. J. Phys. Condens. Matter 1990, 2, SA69. [Google Scholar] [CrossRef]
- Benoit, H. Study of the Kerr effect by dilute solutions of rigid macromolecules. Ann. Phys. 1951, 12, 6. [Google Scholar]
- Siafarika, P.; Papanikolaou, M.G.; Kabanos, T.A.; Kalampounias, A.G. Probing the equilibrium between mono- and di-nuclear nickel(II)-diamidate {[NiII(DQPD)]x, x = 1, 2} complexes in chloroform solutions by combining acoustic and vibrational spectroscopies and molecular orbital calculations. Chem. Phys. 2021, 549, 111279. [Google Scholar] [CrossRef]
- Yasuda, K.; Matsuoka, T.; Koda, S.; Nomura, H. Frequency dependence of ultrasonically induced birefringence of rodlike particles. J. Phys. Chem. 1996, 100, 5892–58974. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).