Abstract
Under the JST-ERATO project in progress to develop X-ray and neutron phase-imaging methods together, recent achievements have been selected and reviewed after describing the merit and the principle of the phase imaging method. For X-ray phase imaging, recent developments of four-dimensional phase tomography and phase microscopy at SPring-8, Japan are mainly presented. For neutron phase imaging, an approach in combination with the time-of-flight method developed at J-PARC, Japan is described with the description of new Gd grating fabrication.
Keywords:
phase imaging; phase tomography; grating; interferometry; synchrotron radiation; neutron; X-ray; microscopy; radiography 1. Introduction
High-energy beams of quanta (such as photons, neutrons, electrons, and so forth) that penetrate materials can be used to visualize inner structures non-destructively. In radiography and microscopy, various imaging systems have been developed and widely used for many purposes. The most primitive imaging signal is attenuation of the penetrating beam intensity by absorption in addition to nominal decrease in intensity due to scattering. However, when materials of high transmittance (in other words, transparent materials) are observed, one is faced with a problem of insufficient contrast in the resultant images. For high-energy photons (X-rays), materials consisting of low-Z elements, such as biological soft tissues and polymers, cause this problem; as shown in Figure 1, the absorption cross sections decrease significantly for elements with a lower atomic number (Z) [1]. While neutron absorption cross-sections do not depend on an atomic number as simple as those for X-rays, Figure 1 shows that neutron absorption contrasts are high for materials consisting of specific elements [2]. These properties limit the scope of X-ray and neutron radiography.
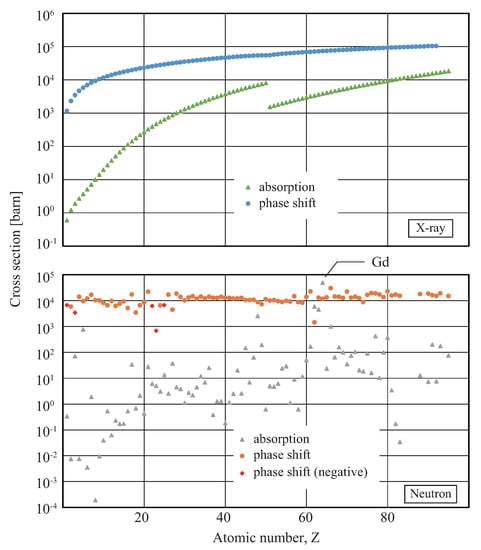
Figure 1.
Interaction cross sections per atom of absorption and phase shift for X-rays (30 keV) and neutrons (25 meV).
By using the wave nature of quanta, phase contrast can overcome this problem. The interaction of quanta with matter is described in terms of complex refractive index, complex permittivity, complex susceptibility, or complex scattering length. The imaginary parts of these quantities describe absorption, and the real parts cause the phase shift in the wave of quanta. The real parts are generally much larger than the imaginary parts; Figure 1 shows that the interaction cross sections of the phase shift of X-rays (30 keV) and neutrons (25 meV) per atom are much larger than those of absorption. Using this fact, one can visualize inner structures of even almost transparent materials by exploring phase-contrast techniques.
The interaction cross section of the X-ray phase shift is given by , where is the classical electron radius (or Thomson scattering length), is the real part of the anomalous scattering factor, and is the X-ray wavelength. The interaction cross section of the neutron phase shift is given by , where and are the coherent scattering length and the de Broglie wavelength of neutrons, respectively. Macroscopic phase shifts are calculated by taking into account the constitution and density.
The phase information is normally lost by measuring the intensity of wave simply, and specific optical techniques should be used to generate phase contrast, which were mainly developed in optical microscopy after the first pioneering work by Zernike in 1934 [3]. However, the development of phase-contrast techniques for X-rays and neutrons appeared nearly half a century later [4,5,6,7]. This is because the magnitudes of interaction of X-rays and neutrons with matter are not high compared with that of visible light and therefore optical elements, such as lenses and mirrors, available for X-rays and neutrons are extremely limited unlike the field of visible light. Another reason is that the wavelengths of X-rays and de Broglie wave of neutrons used for radiography (cold and thermal neutrons) are much shorter than the wavelengths of visible light, and therefore extremely high mechanical stability in optical alignment is required. As a result, controlling X-rays and neutrons is not a straightforward process. Moreover, as some degree of spatial coherency is required to generate phase contrast, the performance of X-ray and neutron sources is indicated as a key factor to realize phase-contrast techniques.
After many years’ efforts, the development of fabrication technologies of X-ray optical elements and synchrotron radiation facilities has activated the progress of X-ray phase-contrast techniques especially since the 1990s. With regard to neutrons, accelerator-based neutron facilities have recently been put into operation in addition to reactor-based types, and the phase-contrast techniques developed for X-rays are extending to neutron radiography. In addition, as described later, the development of digital X-ray and neutron image detectors has played an important role.
Among phase-contrast techniques, the grating-based approach is now widely used because of its flexibility. We have been conducting a collaboration program (JST-ERATO) to expand the frontiers of phase-imaging methods with the beams of high-energy photons (X-rays) and neutrons, and our recent activities are introduced in this review.
2. Grating-Based Phase Imaging Method
2.1. Methods to Generate Phase Contrast
There are several techniques to generate X-ray phase contrast, as shown in Figure 2. Before describing the grating-based phase imaging method in detail, an overview of other techniques is provided.
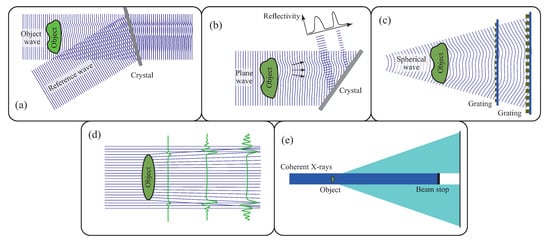
Figure 2.
Techniques developed to generate X-ray phase contrast: (a) Two-beam interferometry, (b) diffraction-enhanced imaging, (c) grating interferometry, (d) propagation-based method, (e) coherent diffraction imaging.
The most direct approach is to use a two-beam interferometer, where an object beam through a sample and a coherent reference beam are generated and mixed (Figure 2a). Interference fringes corresponding to contours of the phase shift caused by the sample are observed. Since the wavelengths of X-rays are extremely shorter than those of visible light, it is difficult to construct a two-beam interferometer so stable that the fluctuation in the optical path difference is much less than one wavelength. Nevertheless, a crystal interferometer monolithically cut out from an ingot of Si single crystal is used [8]. X-ray phase imaging and phase tomography described later was first demonstrated with this device [9], and its excellent sensitivity to cancerous tissues was reported [10]. Neutron interferometry was also realized by this device [11], although to the best of our knowledge, neutron phase imaging has not yet been reported with this approach.
The approach shown in Figure 2b uses an analyzer crystal, which diffracts X-rays partially through Bragg diffraction [12,13,14]. Since the angular width of Bragg diffraction by a single crystal (dynamical diffraction) is the order of a 10 rad or smaller and the angle of the X-ray deflection induced by refraction at a sample is in the same order, contrast depending on the X-ray refraction caused by a sample is generated by an analyzer crystal placed behind the sample.
When crystals are used through Bragg diffraction, however, monochromatic and plane wave must be used, and the flux density available for imaging is extremely reduced. Therefore, these approaches (Figure 2a,b) are feasible with synchrotron radiation. Since it is not easy to ensure a neutron flux sufficient for radiography through crystal optics, no reports have been published for neutron phase imaging with these approaches.
Figure 2c shows that grating interferometry, which is the main subject in this review, uses a transmission grating as an analyzer [15]. Since all phenomena in this system occur under the paraxial approximation, polychromatic and spherical wave is available. As a result, even laboratory-based X-ray sources and neutron sources are available for imaging applications, as described later.
Another approach attracting attention is the propagation-based method (Figure 2d), which generates contrast due to Fresnel diffraction [16,17,18,19]. In radiography, an image detector is placed just behind a sample to avoid image blurring (penumbra). However, under coherent illumination, one observes the Fresnel diffraction phenomena behind a sample even with X-rays and neutrons by setting a certain space between a sample and an image detector. The visibility of Fresnel diffraction fringes reduces when the degree of spatial coherence of the illumination is not high. However, the contrast consisting of a pair of black (dark) and white (bright) lines remains and outlines structural boundaries in a sample. This method is easily implemented because no optics are used except that illumination with partial spatial coherence is ensured. This effect is observed routinely at third-generation synchrotron radiation facilities and by using a micro-focus X-ray tube in a laboratory. This approach was also demonstrated with neutrons [20].
In the far field (Fraunhofer regime), a diffraction pattern corresponding to the Fourier transform of the electron density of a sample is observed (in the case of X-rays). Strictly speaking, the amplitude of the Fourier transform is detected, but the phase factor is lost. Therefore, one cannot reconstruct the electron density from the diffraction pattern via inverse Fourier transform (the so-called phase problem). However, after the development of iterative phase retrieval approaches with a boundary condition whereby a sample is isolated in the field of view, the phase problem can be solved (coherent diffraction imaging, Figure 2e) [21]. Recently, this technique has been combined with a scanning scheme to observe extended samples (X-ray ptychography) [22]. This development has been attracting increased attention combined with the construction of ultimate storage rings for synchrotron radiation [23] and X-ray free electron lasers [24,25,26]. More details are described in excellent reviews [27,28]
X-ray phase imaging is also introduced into X-ray microscopy. Following the developments with Zernike’s approach, various different approaches were also demonstrated [29]. One of them is by grating interferometry, more details of which are described below.
2.2. Principle of Talbot Interferometry and Phase Imaging
Phase imaging is used in this review to emphasize that it is realized by combining the optical technique of phase-contrast generation with the digital technique of phase measurement. The former is the grating-based system, such as the Talbot interferometer [15] or Talbot–Lau interferometer [30], which consists of transmission gratings. The latter is typically the phase-stepping (in other words, fringe-scanning) technique [31], which acquires multiple phase-contrast pictures by displacing one of the gratings [15]. When a phase-contrast picture is recorded, absorption contrast is normally mixed. Furthermore, contrast due to the imperfection in optical elements and their alignment is added. As a result, the feature in the picture is occasionally too complicated to understand the structures of samples. The phase measurement technique can generate images of the phase shift and absorption separately and quantitatively from such phase-contrast pictures recorded by a digital image detector. In addition, an image of scattering by a sample is also generated through the reduction of the visibility of interference fringes [32]. The images generated by phase imaging are thus effective in understanding sample structures.
The configuration of a Talbot interferometer is shown in Figure 3a. Two transmission gratings (G1 and G2) are aligned along the optical axis. G1, for which a phase grating is normally used, generates a self-imaging (fractional Talbot) effect [33,34] when it is illuminated by a spatially coherent wave. Behind the grating, diffractions (0th, ±1st, ±2nd, ⋯) occur and a specific interference field (Talbot carpet) is formed. The self-imaging effect is maximized in the Talbot carpet at specific distances
where and are the period of G1 and the wavelength of the wave, and p is a half integer when the grating is a type of phase shift and an odd multiple of 1/8 when a type of phase shift. R is the distance between the source and G1.
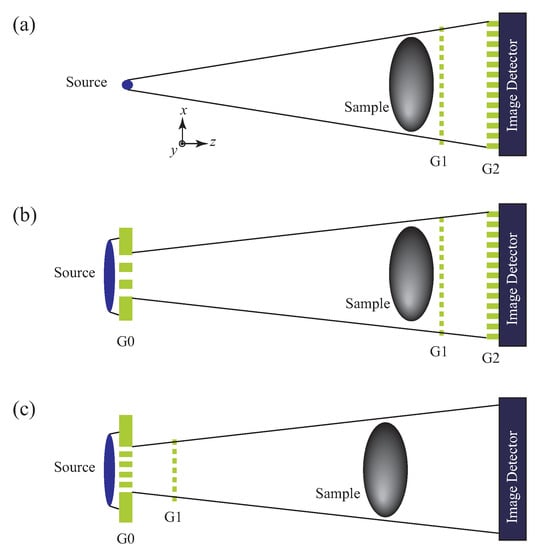
Figure 3.
Configuration of grating interferometry for phase imaging: (a) Talbot interferometer, (b) Talbot–Lau interferometer, (c) Lau interferometer.
A sample is normally placed in front of G1, but the position between G1 and G2 is selected occasionally. Then, the Talbot carpet is deformed due to the refraction by the sample. By analyzing the deformation, the structures in the sample can be visualized even if no clear absorption contrast is shown.
The self-imaging effect cannot be observed unless the spatial coherence length of the incident wave is larger than the period of the gratings. The spatial coherence length at G1 is given by , where s is the size of the source, and the typical spatial coherence length achieved for X-rays is about 10 m. Therefore, the gratings whose periods are several microns are normally fabricated and utilized. The period of the self-image appearing in the Talbot carpet is also several microns. While it is possible to analyze the self-image by employing a high-resolution X-ray image detector, the field of view (FOV) is normally limited.
To ensure a larger FOV, Talbot interferometry employs a second grating (G2), which is an absorption grating that transmit X-rays partially and is placed at the position of self-imaging. The period of G2 () should be almost the same as that of the self-image; that is, . Behind G2, a moiré pattern is generated by the superposition of the self-image and the transmission function of G2. The feature of the moiré pattern corresponds to the deformation of the self-image. The moiré pattern is resolved easily with a normal X-ray image detector with a large FOV even if the self-image is not resolved. This is the concept of the phase-contrast generation.
Here, it is assumed that the grating has a linear pattern of a periodicity in the x direction. Then, the moiré pattern is given with three independent parameters , , and approximately by
where, using the phase shift caused by the sample,
Theterm is added to express the effects of the imperfection in grating fabrication and grating alignment. When a phase grating is used, interference between neighboring diffraction orders causes the self-imaging with a period of , and . When a phase grating is used, the period of the self image is half of , and therefore . This is because interference between the 1st and −1st order diffraction waves is dominant (the 0th order diffraction is suppressed). Strictly speaking, by considering all possible interferences, higher-order terms should be added in Equation (2) [35]. However, because the phase-stepping technique described below deals with the fundamental sinusoidal component and the higher-order component is negligible in many experiments, using the form of Equation (2) is reasonable.
is not used as it is for imaging applications. Absorption contrast and phase contrast coexist in , and furthermore moiré fringes are added (when the fringe period is larger than FOV, this effect is observed as a gentle gradient in intensity). The phase-stepping (in other words, fringe scanning) technique generates images of and separately and quantitatively. The effect of is eliminated by repeating the measurements with and without a sample. In addition, the extraction of , which relates to the scattering property of a sample, is feasible, as discussed later.
To perform the measurements for the phase-stepping technique, one of the gratings is displaced in the x direction by a step of the fraction of (or ) and the measurement of the moiré pattern is repeated. The measured moiré patterns are
where M is an integer (). When disregarding the effect of higher orders in obtaining Equation (2) is a concern, selecting a larger integer for M is effective to remove the effect [36]. At every pixel position, , the detected intensity follows a sinusoidal curve (so-called, phase-stepping curve) correspondingly with Equation (2). The average, shift, and amplitude of the curve correspond to , , and , respectively (Figure 4a). Moiré patterns are acquired at discrete points along the phase-stepping curve, and they are calculated by
where implies the extraction of the argument, and

Figure 4.
(a) Phase-stepping curve expressed by , , and . Images of (b) absorption, (c) differential phase, and (d) visibility obtained with X-rays for a grape.
In Equation (7), the term can be determined by using the measurement data with out a sample. The visibility , where and are the maximum and minimum values in the phase-stepping curve, is used rather than in forming an image. Figure 4b–d show an example of phase-stepping measurement of a grape. Images of absorption, differential phase, and visibility calculated from five moiré patterns measured by displacing G2 with a step of are presented.
The formalization of the phase-stepping technique assumes that the grating displacement is ideal and the beam flux is constant during the measurement. However, in practical use of the phase-stepping technique, problems of mechanical thermal drift, mechanical vibration, and/or instability in the beam intensity occur occasionally and cause artifacts in the calculations by Equations (5)–(7). Therefore, we developed a new algorithm that estimates stepping errors of the grating and/or flux fluctuation and generates images as close as those in the ideal condition [37]. This algorithm was used in the techniques described in the next section.
2.3. Visibility Reduction Induced by Scattering
The physical senses of and are trivial; that is, absorption and refraction, respectively. With the linear absorption coefficient ,
where is the intensity of the incident beam. For the latter, introducing the relation
to Equation (3), is written as
where is the refractive index decrement from unity.
How is the visibility reduction by a sample , where is the visibility with out a sample, translated to material property? From an optical viewpoint, the visibility reduction implies the decrease in the spatial coherence. A part of the beam scattered by a sample that no longer contributes to forming a moiré pattern is considered to be responsible for the visibility reduction, and this signal is often referred to as the dark-field signal [32]. The wavefront deformed by a sample has various components of spatial frequency depending on the structures in the sample. Since the wave propagates in the direction perpendicular to the wavefront in a free space, lower-frequency components tend to go forward and higher-frequency components are deflected further. Considering the threshold between these frequency regions to be the spatial resolution, the former can be observed in . The latter corresponds to (ultra) small-angle scattering and is depicted not in , but in .
The auto-correlation function of the wavefront plays an important role [38,39,40]. When a sample is placed upstream of G1 and use of plane wave is assumed, the frequency component corresponding to the auto-correlation length given by reduces visibility significantly, where is the distance between G1 and G2. It is considered that structures (scatterers) with sizes around the auto-correlation length mainly cause the visibility reduction. When a sample is placed behind G1 with a distance to G2, the frequency component corresponding to the auto-correlation length given by reduces visibility. Therefore, the sensitivity to scatterers is tuned depending on their size by changing the position of the sample.
2.4. Phase Tomography
X-ray computed tomography (CT) is a technique to visualize inner structures three-dimensionally with out cutting a sample [41]. Conventional X-ray CT measures the transmittance , which has the following relation with the linear absorption coefficient :
By repeating measurements of transmittance from multiple projection directions surrounding a sample, can be reconstructed. When the phase shift is measured quantitatively, Equation (10) is found as the relation corresponding to Equation (12). Then, a three-dimensional map of the refractive index (or ) is reconstructed by using the same reconstruction scheme as that for conventional X-ray CT (phase tomography [9]).
In the phase imaging by grating interferometry, a similar relation is found in Equation (11) except that the derivative is in the integral. By using a Hilbert kernel in the filtered back-projection method [42], phase tomography that reconstructs is attained.
With regard to the visibility (dark-field) signal, can be used for tomographic input data, expressing it approximately using a quantity ,
In terms of linear diffusion coefficient [43] or generalized scattering parameter [44], the physical sense of is discussed. However, bridging this quantity to structural properties is not so straightforward as in the case of absorption (conventional) tomography or phase tomography. Structural boundaries (and surfaces) also generate the strong dark-field signal, and the reconstruction results show features outlining boundaries apart from the distribution of scatterers [45]. Furthermore, when polychromatic X-rays are used, a beam-hardening effect caused by a sample generates pseudo contrast because the visibility also decreases when the X-ray spectrum changes [46]. Further studies on how to acquire structural information from the dark-field signals are now in progress.
2.5. Grating Fabrication for X-ray Talbot Interferometer
G2 must be an absorption type that blocks a part of X-rays efficiently. Gold is used for the grating material because its absorption coefficient is high and electroplating is applicable. However, while the grating period should be in the order of microns, the pattern height (thickness in the direction of X-rays) should be several tens of microns or more even if gold is used. Thus, a high aspect-ratio structure must be fabricated. Furthermore, the area of the grating pattern should be as large as possible, because it defines the FOV. As a solution to this demand, an approach by combining X-ray lithography and gold electroplating was successfully developed [47,48] and is now commercialized. Gratings with a pattern 10 cm × 10 cm and ca 200 m high are currently available. Recently tiling approaches have been used to extend FOV [49,50].
2.6. Extension from Talbot Interferometry
Talbot interferometers should be operated under spatial coherent illumination so that the spatial coherence length is comparable to or larger than the grating period. It is comparatively easy to meet this demand for X-ray experiments by using synchrotron radiation or micro-focus X-ray tubes. However, for neutron radiography, it is tough to prepare spatially coherent beams especially with a sufficient flux. One of remarkable properties of Talbot interferometry is that the concept can be extended to a form available with an incoherent beam; that is, Talbot–Lau interferometry shown in Figure 3b.
A Talbot–Lau interferometer is built by adding a source grating (G0) to the configuration of a Talbot interferometer (G1 and G2). The function of G0 is creating an array of point sources. Strictly speaking, the source array (grating pattern) is extended in the y direction, which is independent of the interferometer function, and therefore an array of line sources would be a more correct expression. However, point source is used in the following explanation for the sake of comprehensiveness. Each source functions as a point source (like a micro-focus X-ray tube) for the Talbot interferometer downstream. The period of G0 is designed so that the self-images formed at G2 by two neighboring point sources are shifted by one period and as a result all self-images are overlaid constructively. Then, a radiation source with a large size and a high power, which provides only incoherent illumination, is available for phase imaging. This advance enabled us to construct X-ray phase imaging systems for (pre-)clinical purposes [51,52,53,54,55] and industrial non-destructive testing [50] with a conventional X-ray tube. Neutron beams for radiography are in general incoherent, and neutron phase imaging was realized by using Talbot–Lau interferometry [56].
Figure 3c shows another form of grating interferometry for using an incoherent beam. The merit of this configuration is that G2 is not used, which is remarkable when higher energy X-rays are used to observe thicker objects. Absorption gratings for higher X-ray energy require a much higher aspect-ratio structures because the X-ray absorption coefficient is inversely proportional roughly to the third power of the photon energy. Fabricating such a grating is not straightforward especially with the approach described in Section 2.5.
In designing a Talbot–Lau interferometer, there are two solutions in optical alignment for a given total length. Regarding Figure 3b, inverse geometry [57] is also a solution; that is, G2, G1, and G0 are aligned in this order from the source side. In Figure 3c, G0 corresponds to G2 in Figure 3b and the position of G1 is shifted near to the source. Since the distance from G1 to the detector is large, the self-image of G1 is magnified and can be resolved directly with out using G2. This configuration is called a Lau interferometer [58]. In addition to the potential for high-energy X-ray phase imaging, the Lau interferometer was also utilized for the development of X-ray microscope described in Section 3.2 later.
3. Development for X-ray Phase Imaging
3.1. Four-Dimensional X-ray Phase Tomography
Most X-ray phase tomography activities were demonstrated for static objects. Even if the structures are revealed, the functions in the objects are not always understood. Dynamics must be observed to overcome this limitation, and therefore we have been developing four-dimensional X-ray phase tomography.
A remarkable characteristic of Talbot interferometry is that polychromatic X-rays are available, since the interferometer functions in the paraxial region. Therefore, we took advantage of the extremely high flux of white synchrotron radiation to perform high-speed phase imaging [59] and four-dimensional phase tomography [60]. The aforementioned phase-stepping technique with a step-by-step grating displacement would not be compatible for these purposes because such mechanical motions should generate vibration by speeding up and adversely affect the interferometer. Therefore, the Fourier-transform method [61] with the introduction of carrier fringes (rotation moiré fringes) by inclining one of the gratings (but with out any grating movement) was employed. Temporal resolutions of millisecond order in 2D and second order in 3D were attained. However, the spatial resolution limited by the carrier-fringe spacing was not satisfactory for further applications. Moreover, serious radiation damage to samples remained as a problem, especially when living organisms were observed.
The visibility attained by a Talbot interferometer with X-rays of a bandwidth () about 10% is almost comparable to that with monochromatic X-rays [36,62]. Under white synchrotron radiation from a bending section of a storage ring (bandwidth ∼1), a part of the spectrum components cannot contribute to contrast formation but is harmful for samples because of radiation damage. Therefore, we have installed a band-pass filter multilayer mirror at BL28B2 of SPring-8, Japan, which is dedicated for various user experiments with white synchrotron radiation. As shown in Figure 5, white synchrotron radiation is reflected on a depth-graded W/Si multilayer with a glancing angle of 5.11 mrad, and a pink beam of a 25-keV central energy and a 10% bandwidth is formed slightly downward. The maximum beam section is 50 mm wide and 5 mm high and the photon flux density is 10 photons/s/mm.
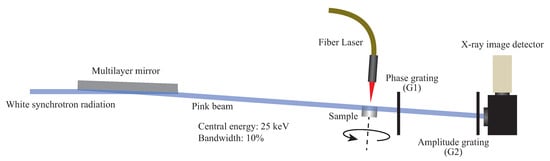
Figure 5.
Experimental setup (side view) of pink-beam 4D phase computed tomography (CT) for observing a sample under laser irradiation.
A Talbot interferometer optimal for 25-keV X-rays was set on the axis of the pink beam, and a video of moiré pattern was recorded by a CMOS camera combined with a YAlO:Ce scintillator (20 m in thickness) via a coupling lens. The effective pixel size was set to 10 m for the experiments described below.
This system was applied to the observation of polymer samples under infrared laser irradiation [63]. The motivation was to visualize the dynamics of the interaction of polymers against laser, emulating the situation of laser processing. Figure 6 shows the result obtained for a polypropylene sample in the form of a thick disk (9.8 mm in diameter and 2 mm in thickness). For a CT scan, the sample was rotated about the center axis of the disk. An infrared CW fiber laser beam (Nd:YAG, 50 W) was introduced along the center axis with a spot size of 35 m. The sample was rotated by 450/s, and CT measurement was continued for 56 s. In this study, instead of the Fourier-transform method, we employed the continuous fringe-scanning method [64], which was developed to seek a compatibility with four-dimensional phase tomography by rotating a sample and displacing a grating with constant speeds unidirectionally. The spatial resolution and image quality is much better than those by the Fourier-transform method although the temporal resolution was compromised by a factor of 10.
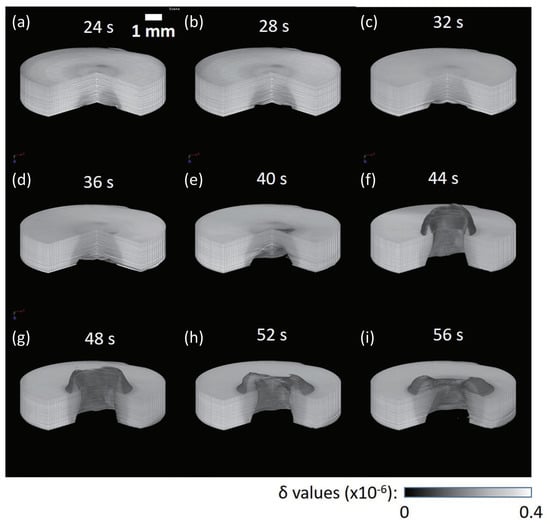
Figure 6.
Three-dimenstional rendering views of the 4D phase tomograms obtained for the polypropylene sample at different laser irradiation times [63]: (a) 24 s, (b) 28 s, (c) 32 s, (d) 36 s, (e) 40 s, (f) 44 s, (g) 48 s, (h) 52 s, and (i) 56 s.
In this result, the laser transmitted the sample and hit the Al support beneath the sample, and melting was observed from the opposite side to the laser irradiation. Thanks to the phase-imaging sensitivity, solid and melt sample regions were differentiated (darker for the melted region), as shown in Figure 6. The speed of the expansion of the melting frontier was evaluated to be ca 78 m/s.
Another application result for a carbon fiber reinforced polymer (CFRP), where tomographic reconstruction by the visibility reduction (dark-field signal) was effective, is shown in Figure 7 [65]. A semi-fusiform region from the laser impact grew, showing visibility reduction more clearly at the frontier of the semi-fusiform region. While the laser spot size was about 35 m, the diameter of the region exceeded 1 mm in a few seconds.

Figure 7.
Tomographic reconstruction from visibility reduction for a carbon fiber reinforced polymer (CFRP) sample [65]: (a) Sagittal section views at different times after starting laser irradiation, and axial section views at (b) 1 s and (c) 17.5 s on the position indicated by the yellow arrow in (a).
3.2. X-ray Phase Microscopy and Tomography
The spatial resolution achievable with a Talbot interferometer is limited by the grating period (several microns), according to its contrast generation mechanism. However, considering the recent progress in materials science and life science, this spatial resolution is unsatisfied occasionally. Fabricating gratings of a sub-micron period [66] would be a direct solution to achieve better spatial resolutions. However, microscopic phase-imaging has not been reported by using such gratings, except for a unique approach of grating interferometry demonstrated by using only three sub-micron phase gratings [67,68].
We have been developing an approach where an X-ray imaging microscope is combined with a Talbot interferometer [69,70], as shown in Figure 8a. In the X-ray region, a Fresnel zone plate (FZP) is employed as a lens element. By placing a sample in front of the FZP and an X-ray image detector far downstream (several meters or more), a magnified image of the sample is observed. Under synchrotron radiation illumination, a focus is formed at the focal plane of the FZP and considered as a point source for the Talbot interferometer (G1 and G2) aligned in front of the image detector. The wavefront modulation by the sample causes the change in the intensity profile on the focal plane and corresponding differential phase contrast is obtained on the detector plane through the interferometer. Thanks to the magnification of the microscope, a spatial resolution beyond the grating periods of G1 and G2 is achieved (200 nm in 2D and 600 nm in 3D [71]). This microscope was applied to mouse bone imaging [70,71,72,73] (Figure 9), which was conducted to study postnatal bone formation utilizing the advantage that the degree of bone mineralization and soft tissues (bone cells and blood vessels) are depicted together.
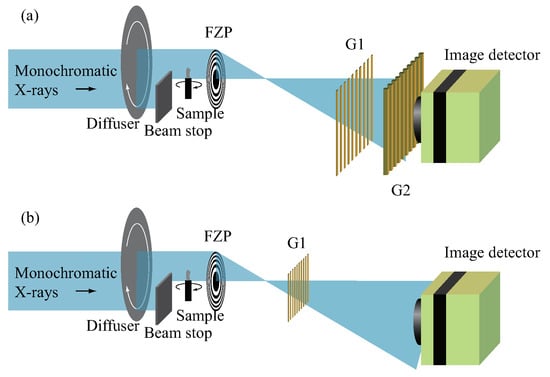
Figure 8.
Configurations of X-ray phase microscopy by the combination of a Fresnel zone plate (FZP) and gratings: Approaches by (a) Talbot interferometry and (b) single phase grating.
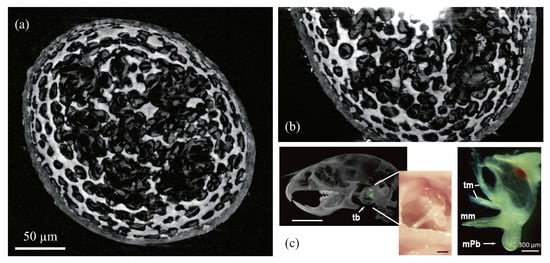
Figure 9.
Phase tomogram of a removed malleal processus brevis (mPb) from a mouse nine days after birth [71]: (a) Axial view, (b) meridian view, (c) location of the sample in a body (X-ray and optical pictures) [72].
Figure 8b shows another configuration for microscopic phase imaging, which has a potential for better image quality. The differential phase contrast in combination with microscopy has a drawback of sensitivity reduction due to the magnification. This is because the wavefront is expanded laterally while the phase shift is constant through the microscope. As a result, the signal (differential phase) is decreased inversely in proportion to the magnification. Figure 8b corresponds to the inverse geometry of the Talbot interferometer. Then, the self-image is directly resolved by an image detector because of the long distance between the G1 and detector, and therefore G2 is omitted. Through a phase-stepping measurement, a twin phase image :
which consists of a positive phase image and a negative phase image overlaid with a shear distance r, is obtained [74]. Because of the magnification, r was much larger than the system spatial resolution and the twin feature appears, while r is smaller than the spatial resolution in normal conditions, resulting in a differential phase image.
When an incoherent X-ray source, such as a rotating anode source, is used, by placing a G0 grating upstream of a sample, the same concept is implemented in a laboratory-based X-ray microscope [75]. Recently, this configuration has been realized with a commercially available X-ray microscope (ZEISS Xradia 800 Ultra, Carl Zeiss X-ray Microscopy, Inc.; CA, USA). The superiority of this approach to the Zernike phase contrast [76] and an iterative deconvolution method to obtain single phase images from the twin phase images [77] were reported. Figure 10a shows its optical configuration; the image of G0 (not shown) is formed by the FZP in front of G1 and functions as the G0 of Figure 3c. The twin phase image and its deconvolution results obtained for a larval Ciona robusta are presented in Figure 10b–d. Phase tomography based on this microscope is also in progress [78].
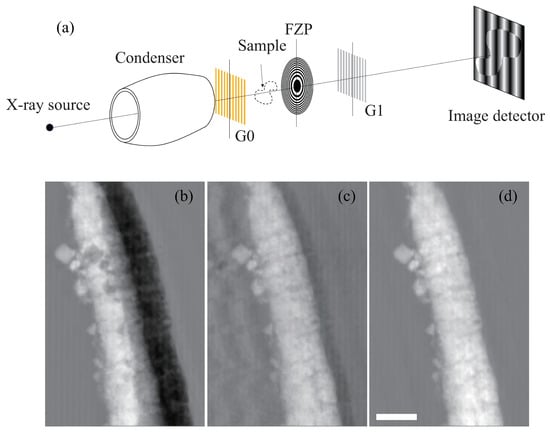
Figure 10.
Optical configuration of the X-ray phase microscope (a) and the images of a larval Ciona robusta [77]: (b) Twin phase image, (c) phase image by simple deconvolution, and (d) phase image by iterative deconvolution algorithm. Scale bar: 10 m.
4. Development for Neutron Phase Imaging
4.1. Neutron-Grating Fabrication
As shown in Figure 1b, the neutron absorption coefficient of Au is not high, and the gold X-ray grating is not used for neutron imaging. The absorption coefficient of Gd is exceptionally high, and therefore fabrication of Gd gratings is a key issue. However, Gd electroplating is not commonly performed and other approaches should be sought to fabricate neutron absorption gratings.
Grünzweig et al. started grating-based neutron phase imaging by realizing a Gd absorption grating with the inclined evaporation method [79]. A Si linear grating was first fabricated by photo lithography, reactive ion etching, and KOH wet etching, and then Gd was evaporated on the side and shoulder of Si lamellae, resulting in a Gd pattern with a 4 m period and a height of 11 m, which was available for cold neutrons. A Talbot–Lau interferometer was constructed at the Swiss Spallation Neutron Source (SINQ). A technique of Gd-powder filling to a Si grating was adopted to fabricate G0 because its period was large (1.08 mm). G1 was a Si phase grating fabricated in the same manner as the base of G2. This interferometer produced various pioneering results of neutron phase imaging/tomography, showing that the dark-field signal (visibility reduction) is useful for depicting bulk magnetic domain structures [80,81,82] and superconductors [83]. Recently, its application has been extended to the visualization of magnetic fields by polarized neutron grating interferometry [84].
At BL22 RADEN [85] in J-PARC MLF, Japan, we have developed a Talbot–Lau interferometer to study energy resolved neutron phase imaging by the time-of-flight (TOF) method [86]. To fabricate high-aspect ratio Gd gratings for G2, we studied two approaches: Metallic-glass imprinting [87] and improved inclined Gd evaporation [88,89].
4.1.1. Gd-Based Metallic-Glass Imprinting
Metallic glass [90] has an amorphous form and superior thermoplastic-forming ability in the supercooled liquid region. Moreover, it is possible to explore constitutions with a high percentage of Gd atoms. Therefore, we studied the possibility of fabricating Gd gratings by imprinting on a Si grating. Since Si is almost transparent to neutrons, the structure of Gd-based metallic glass formed between Si lamellae functions as a neutron absorption grating. While isothermal conditions for the impinging procedure were not successful in filling the metallic glass into the Si grating fully because of the collapse of the Si grating pattern, isochronal conditions via the crystal phase were found to be effective. As a result, gratings of GdCuAl and GdCuAlB with a depth of ca 30 m and a period of 9 m were fabricated [87]. The Talbot–Lau interferometer with the Gd-based metallic-glass grating functioned at J-PARC [91]. However, the FOV was limited by the size of the grating (1 cm × 1 cm). At present, expanding the size has not been attained because imprinting with a higher pressure under a rapid and uniform heating treatment is not straightforward.
4.1.2. Improved Inclined Gd Evaporation
The size of gratings that define imaging FOV should be as large as possible especially for neutron applications because a typical spatial resolution of neutron image detectors is 100 m or larger and it is characteristic of neutron radiography that thick and large objects can be imaged. Inclined Gd evaporation is attractive for attaining a large FOV, although dumpling-like Gd deposits tend to be formed [79]. In our study, the form of Gd deposits could be controlled to some extent by repeating deposition on a sliding Si grating [88]. It was demonstrated that a Talbot–Lau interferometer functions with the grating at J-PARC [92], and refinement of the process has been in progress, resulting in a 64 mm × 64 mm grating size and a 24 m pattern height (9 m period), as shown in Figure 11 [89].

Figure 11.
Gd absorption grating fabricated by inclined evaporation [89]: (a) Illustration of Gd deposition by repleting evaporation at every step of Si grating shift. The geometrical direction of the Gd source changes by the shifts. (b) Photograph of a Gd grating with an area of 64 mm × 64 mm. (c) Image of scanning electron microscopy obtained for a section of Gd grating made by a focused ion beam.
4.2. Neutron Phase Imaging at J-PARC
Using the pulse nature of the neutron beam at J-PARC, we combined Talbot–Lau interferometry and the TOF method with the time-resolved counting-type neutron imaging detector NID [93]. As mentioned, a Talbot–Lau interferometer functions with a polychromatic wave. However, the refractive index is a function of the neutron energy, and the resultant differential phase image is obtained as a mixture of those at various spectrum components. In an X-ray study [94], the effective energy was defined to deal with resultant images in the same manner as those by monochromatic X-rays. However, the reduction in the contrast by using polychromatic illumination was not overcome. Due to the availability of the TOF method with pulsed neutrons, assuming the spectrum dependence of , the differential phase image at every energy bin can be converted to that at the design energy optimal for the interferometer. Then, by summing up the converted images, a clearer image with statistics better than that by a monochromatic beam only can be generated [86].
Figure 12 demonstrates this concept with rod samples of Ti and Al of a diameter of 5 mm. The design wavelength optimal for the Talbot–Lau interferometer was 5 Å, and TOF measurements were performed in the range of 1.5–8.5 Å. Figure 12a is the image obtained from the data at 5 Å only. The rods produced opposite differential phase contrasts, showing that Ti causes a negative phase shift. However, the statistics of the image were not satisfactory because the number of neutrons was limited. Figure 12b shows the wavelength dependence of the differential phase revealed by the TOF measurement. The longer the wavelength, the stronger the differential phase contrast (i.e., refraction). Assuming , the differential phase image at each energy bin was converted to that at 5 Å, and Figure 12c was obtained by summing them all up. In contrast, the differential phase image produced in the normal way with out resolving energy showed a weaker contrast (Figure 12d).
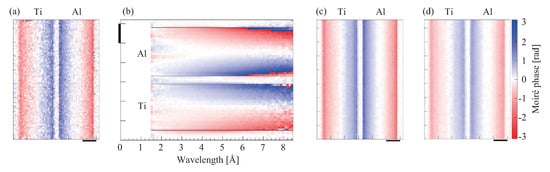
Figure 12.
Results (differential phase images) obtained for rod samples of Ti and Al by a neutron Talbot–Lau interferometer with the time-of-flight (TOF) method: (a) Image obtained from the data of 5 Å only, (b) wavelength dependence of the differential phase, (c) image calculated assuming , and (d) image produced in the normal way with out resolving energy (wavelength). The color implies the moiré phase, which corresponds to . Scale bar: 2 mm.
5. Summary
Recent achievements of X-ray and neutron phase imaging under our collaboration program supported by JST-ERATO were introduced. Developments for high-end grating-based phase imaging are in progress at quantum beam facilities. Pink-beam four-dimensional X-ray phase tomography and X-ray phase microscopy/tomography were representatively described. We are also developing super-resolution X-ray phase imaging, stroboscopic X-ray phase imaging, sensitivity-enhanced X-ray phase imaging, and so forth in this program, the details of which will be reported in the near future [95,96,97]. Moreover, at neutron facilities, further studies for energy-resolved phase imaging, spin-polarized phase imaging, and so forth, will be performed.
X-ray grating interferometry started with synchrotron radiation first and has recently attracted attention from medicine and industry fields because conventional X-ray generators are also available, and implementation in hospitals, laboratories, factories, and inspection sites is expected. Thus, its expansion from huge facilities to compact systems should be highlighted. Even for neutron grating interferometry, the combination with a compact neutron source [98] is within our scope, following the progress of X-ray grating interferometry.
In addition to the development of methods and apparatuses, applications of phase imaging should be promoted. While the use of the X-ray phase microscopy for studying bone samples was only introduced, a variety of interdisciplinary collaborations are expected to be initiated further by the progress in phase imaging. Under the cooperation between X-ray phase imaging and neutron phase imaging, interesting applications may emerge by utilizing them both together because different responses to an object are expected between X-rays and neutrons. Furthermore, we consider that collaboration with information science is an important and attractive subject. In dealing with digital images for phase imaging/tomography, introducing state-of-the-art progress in image reconstruction algorithms will be effective especially when the radiation dose should be reduced, the number of projections should be decreased, and/or a sample larger than the FOV is scanned.
In this review, introduction to the entire progress in this field was not possible. For other important subjects, such as vector radiography and tensor tomography based on the dark-field signal, combination with energy-resolvable photon-counting image detector, speckle-based approach, coded aperture approach, and so forth, we recommend readers to check the references [99,100,101,102,103,104,105,106]. Finally, we expect that this description of the contents of both X-ray and neutron developments together will be suggestive and stimulating for further progress and application promotion of phase imaging.
Funding
This work was supported by JST ERATO Grant No. JPMJER1403, Japan.
Acknowledgments
The synchrotron radiation experiments introduced in Figure 6, Figure 7 and Figure 9 were approved by SPring-8 committee, 2016B1147, 2017A1041, 2017A1288, 2017B1361, and 2017B1445. For grating fabrication, this work was supported by ”Nanotechnology Platform” of the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan, at the Center for Integrated Nanotechnology Support, Tohoku University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- X-ray Interactions with Matter. Available online: http://henke.lbl.gov/optical_constnts/ (accessed ona 10 February 2020).
- Sears, V.F. Neutron scattering lengths and cross sections. Neutron News 1992, 3, 26–37. [Google Scholar] [CrossRef]
- Zernike, F. Inflection theory of the cutting method and its improved form, the phase contrast method. Physica 1934, 1, 689–704. [Google Scholar] [CrossRef]
- Momose, A. Recent advances in X-ray phase imaging. Jpn. J. Appl. Phys. 2005, 44, 6355–6367. [Google Scholar] [CrossRef]
- Nugent, K. Coherent methods in the X-ray sciences. Adv. Phys. 2010, 59, 1–99. [Google Scholar] [CrossRef]
- Bravin, A.; Coan, P.; Suortti, P. X-ray phase-contrast imaging: From pre-clinical applications towards clinics. Phys. Med. Biol. 2013, 58, R1–R35. [Google Scholar] [CrossRef] [PubMed]
- Strobl, M.; Manke, I.; Kardjilov, N.; Hilger, A.; Dawson, M.; Banhart, J. Advances in neutron radiography and tomography. J. Phys. D Appl. Phys. 2009, 42, 243001. [Google Scholar] [CrossRef]
- Bonse, U.; Hart, M. An X-ray interferometer. Appl. Phys. Lett. 1965, 6, 155–156. [Google Scholar] [CrossRef]
- Momose, A. Demonstration of phase-contrast X-ray computed tomography using an X-ray interferometer. Nucl. Instrum. Methods A 1995, 352, 622–628. [Google Scholar] [CrossRef]
- Momose, A.; Takeda, T.; Itai, Y.; Hirano, K. Phase-contrast X-ray computed tomography for observing biological soft tissues. Nat. Med. 1996, 2, 473–475. [Google Scholar] [CrossRef]
- Rauch, H.; Treimer, W.; Bonse, U. Test of a single-crystal neutron interferometer. Phys. Lett. A 1974, 47, 369–371. [Google Scholar] [CrossRef]
- Davis, T.J.; Gao, D.; Gureyev, T.E.; Stevenson, A.W.; Wilkins, S.W. Phase-contrast imaging of weakly absorbing materials using hard X-rays. Nature 1995, 373, 595–598. [Google Scholar] [CrossRef]
- Ingal, V.N.; Beliaevskaya, E.A. X-ray phase-wave topography observation of the phase-contrast from a noncrystalline object. J. Phys. D Appl. Phys. 1995, 28, 2314–2317. [Google Scholar] [CrossRef]
- Chapman, D.; Thomlinson, W.; Johnston, R.E.; Washburn, D.; Pisano, E.; Gmür, N.; Zhong, Z.; Menk, R.; Arfelli, F.; Sayers, D. Diffraction enhanced X-ray imaging. Phys. Med. Biol. 1997, 42, 2015–2025. [Google Scholar] [CrossRef] [PubMed]
- Momose, A.; Kawamoto, S.; Koyama, I.; Hamaishi, Y.; Takai, K.; Suzuki, Y. Demonstration of X-ray Talbot interferometry. Jpn. J. Appl. Phys. 2003, 42, L866–L868. [Google Scholar] [CrossRef]
- Snigirev, A.; Snigireva, I.; Kohn, V.; Kuznetsov, S.; Schelokov, I. On the possibilities of X-ray phase contrast microimaging by coherent high-energy synchrotron radiation. Rev. Sci. Instrum. 1995, 66, 5486–5492. [Google Scholar] [CrossRef]
- Nugent, K.A.; Gureyev, T.E.; Cookson, D.F.; Paganin, D.; Barnea, Z. Quantitative phase imaging using hard X-rays. Phys. Rev. Lett. 1996, 77, 2961–2964. [Google Scholar] [CrossRef]
- Cloetens, P.; Barret, R.; Baruchel, J.; Guigay, J.P.; Schlenker, M. Phase objects in synchrotron radiation hard X-ray imaging. J. Appl. Phys. D Appl. Phys. 1996, 29, 133–146. [Google Scholar] [CrossRef]
- Wilkins, S.W.; Gureyev, T.E.; Gao, D.; Pogany, A.; Stevenson, A.W. Phase-contrast imaging using polychromatic hard X-rays. Nature 1996, 384, 335–338. [Google Scholar] [CrossRef]
- Allman, B.E.; McMahon, P.J.; Nugent, K.A.; Paganin, D.; Jacobson, D.L.; Arif, M.; Werner, S.A. Phase radiography with neutrons. Nature 2000, 408, 158–159. [Google Scholar] [CrossRef]
- Miao, J.; Charalambous, P.; Kirz, J.; Sayre, D. Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens. Nature 1999, 400, 342–344. [Google Scholar] [CrossRef]
- Thibault, P.; Dierolf, M.; Menze, A.; Bunk, O.; David, C. High-resolution scanning X-ray diffraction microscopy. Science 2008, 321, 379–382. [Google Scholar] [CrossRef] [PubMed]
- Bei, M.; Borland, M.; Cai, Y.; Elleaume, P.; Gerig, R.; Harkay, K.; Emery, L.; Hutton, A.; Hettel, R.; Nagaoka, R.; et al. The potential of an ultimate storage ring for future light sources. Nucl. Instrum. Methods A 2010, 622, 518–535. [Google Scholar] [CrossRef]
- Emma, P.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bozek, J.; Brachmann, A.; Bucksbaum, P.; Coffee, R.; Decker, F.J.; et al. First lasing and operation of an angstrom-wavelength free-electron laser. Nat. Photon. 2010, 4, 641–647. [Google Scholar] [CrossRef]
- Yabashi, M.; Tanaka, H.; Ishikawa, T. Overview of the SACLA facility. J. Synchrotron Rad. 2015, 22, 477–484. [Google Scholar] [CrossRef]
- Altarelli, M. The European X-ray free-electron laser facility in Hamburg. Nucl. Instrum. Methods B 2011, 269, 2845–2849. [Google Scholar] [CrossRef]
- Chapman, H.; Nugent, K.A. Coherent lensless X-ray imaging. Nat. Photon. 2010, 4, 833–839. [Google Scholar] [CrossRef]
- Pfeiffer, F. X-ray ptychography. Nat. Photon. 2018, 12, 9–17. [Google Scholar] [CrossRef]
- Momose, A. Development toward high-resolution X-ray phase imaging. Microscopy 2017, 66, 155–166. [Google Scholar] [CrossRef]
- Pfeiffer, F.; Weitkamp, T.; Bunk, O.; David, C. Phase retrieval and differential phase-contrast imaging with low-brilliance X-ray sources. Nat. Phys. 2006, 2, 258–261. [Google Scholar] [CrossRef]
- Bruning, J.H.; Herriott, D.R.; Gallagher, J.E.; Rosenfeld, D.P.; White, A.D.; Brangaccio, D.J. Digital wavefront measuring interferometer for testing optical surfaces and lenses. Appl. Opt. 1974, 13, 2693–2703. [Google Scholar] [CrossRef]
- Pfeiffer, F.; Bech, M.; Bunk, O.; Kraft, P.; Eikenberry, E.F.; Brönnimann, C.H.; Grünzweig, C.; David, C. Hard-X-ray dark-field imaging using a grating interferometer. Nat. Mat. 2008, 7, 134–137. [Google Scholar] [CrossRef] [PubMed]
- Talbot, H.F. Facts relating to optical science. Phlos. Mag. 1836, 9, 401–407. [Google Scholar]
- Guigay, J.P. On Fresnel diffraction by one-dimensional periodic object, with application to structure determination of phase objects. Opt. Acta 1971, 18, 677–682. [Google Scholar] [CrossRef]
- Momose, A.; Yashiro, W.; Takeda, Y. X-ray phase imaging with Talbot interferometry. In Biomedical Mathematics: Promising Directions in Imaging, Therapy Planning, and Inverse Problems; Censor, Y., Jiang, M., Wang, G., Eds.; Medical Physics Publishing: Madison, WI, USA, 2009; pp. 281–320. [Google Scholar]
- Momose, A.; Yasihro, W.; Takeda, Y.; Suzuki, Y.; Hattori, T. Phase tomography by X-ray Talbot interferometry for biological imaging. Jpn. J. Appl. Phys. 2006, 45, 5254–5262. [Google Scholar] [CrossRef]
- Hashimoto, K.; Takano, H.; Momose, A. Improved reconstruction method for phase stepping data with stepping errors and dose fluctuations. submitted. [CrossRef]
- Yashiro, W.; Terui, Y.; Kawabata, K.; Momose, A. On the origin of visibility contrast in X-ray Talbot interferometry. Opt. Express 2010, 18, 16890–16901. [Google Scholar] [CrossRef]
- Lynch, S.K.; Pai, V.; Auxier, J.; Stein, A.F.; Bennett, E.E.; Kemble, C.K.; Xiao, X.; Lee, W.K.; Morgan, N.Y.; Wen, H.H. Interpretation of dark-field contrast and particle-size selectivity in grating interferometers. Appl. Opt. 2011, 50, 4310–4319. [Google Scholar] [CrossRef] [PubMed]
- Strobl, M. General solution for quantitative dark-field contrast imaging with grating interferometers. Sci. Rep. 2014, 4, 7243. [Google Scholar] [CrossRef] [PubMed]
- Grangeat, P. (Ed.) Tomography; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Faris, G.W.; Byer, R.L. Three-dimensional beam-deflection optical tomography of a supersonic jet. Appl. Opt. 1988, 27, 5202–5212. [Google Scholar] [CrossRef] [PubMed]
- Bech, M.; Bunk, O.; Donath, T.; Feidenhans’l, R.; David, C.; Pfeiffer, F. Quantitative X-ray dark-field computed tomography. Phys. Med. Biol. 2010, 55, 5529–5539. [Google Scholar] [CrossRef]
- Strobl, M.; Grünzweig, C.; Hilger, A.; Manke, I.; Kardjilov, N.; David, C.; Pfeiffer, F. Neutron dark-field tomography. Phys. Rev. Lett. 2008, 101, 123902. [Google Scholar] [CrossRef] [PubMed]
- Yashiro, W.; Momose, A. Effects of unresolvable edges in grating-based X-ray differential phase imaging. Opt. Express 2015, 23, 9233–9251. [Google Scholar] [CrossRef] [PubMed]
- Yashiro, W.; Vagovic, P.; Momose, A. Effect of beam hardening on a visibility-contrast image obtained by X-ray grating interferometry. Opt. Express 2015, 23, 23462–23471. [Google Scholar] [CrossRef]
- Matsumoto, M.; Takiguchi, K.; Tanaka, M.; Hunabiki, Y.; Takeda, H.; Momose, A.; Utsumi, Y.; Hattori, T. Fabrication of diffraction grating for X-ray Talbot interferometer. Microsys. Technol. 2007, 13, 543–546. [Google Scholar] [CrossRef]
- Mohr, J.; Grund, T.; Kunka, D.; Kenntner, J.; Leuthold, J.; Meiser, J.; Schulz, J.; Walter, M. High aspect ratio gratings for X-ray phase contrast imaging. AIP Conf. Proc. 2012, 1466, 41–50. [Google Scholar]
- Schröter, T.J.; Koch, F.J.; Mayer, P.; Kunka, D.; Meiser, J.; Willer, K.; Gromann, L.; De Marco, F.; Herzen, J.; Noel, P.; et al. Large field-of view tiled grating structures for X-ray phase-contrast imaging. Rev. Sci. Instrum. 2017, 88, 015104. [Google Scholar] [CrossRef] [PubMed]
- Kageyama, M.; Okajima, K.; Maesawa, M.; Nonoguchi, M.; Koike, T.; Noguchi, M.; Yamada, A.; Morita, E.; Kawase, S.; Kuribayashi, M.; et al. X-ray phase-imaging scanner with tiled bent gratings for large-field-of-view nondestructive testing. NDT E Int. 2019, 105, 19–24. [Google Scholar] [CrossRef]
- Tapfer, A.; Bech, M.; Velroyen, A.; Meiser, J.; Mohr, J.; Walter, M.; Schulz, J.; Pauwels, B.; Bruyndonckx, P.; Liu, X.; et al. Experimental results from a preclinical X-ray phase-contrast CT scanner. Proc. Natl. Acad. Sci. USA 2012, 109, 15691–15696. [Google Scholar] [CrossRef]
- Momose, A.; Yashiro, W.; Kido, K.; Kiyohara, J.; Makifuchi, C.; Ito, T.; Nagatsuka, S.; Honda, C.; Noda, D.; Hattori, T.; et al. X-ray phase imaging: From synchrotron to hospital. Phil. Trans. R. Soc. A 2014, 372, 20130023. [Google Scholar] [CrossRef][Green Version]
- Koehler, T.; Daerr, H.; Martens, G.; Kuhn, N.; Loescher, S.; van Stevendaal, U.; Roessl, E. Slit-scanning differential X-ray phase-contrast mammography: Proof-of-concept experimental studies. Med. Phys. 2015, 42, 1959–1965. [Google Scholar] [CrossRef]
- Hauke, C.; Bartl, P.; Leghissa, M.; Ritschl, L.; Sutter, S.M.; Weber, T.; Zeidler, J.; Freudenberger, J.; Mertelmeier, T.; Tadicke, M.; et al. A preclinical Talbot–Lau prototype for x-ray dark-field imaging of human-sized objects. Med. Phys. 2018, 45, 2565–2571. [Google Scholar] [CrossRef] [PubMed]
- Willer, K.; Fingerle, A.A.; Gromann, L.B.; De Marco, F.; Herzen, J.; Achterhold, K.; Gleich, B.; Muenzel, D.; Scherer, K.; Renz, M.; et al. X-ray dark-field imaging of the human lung—A feasibility study on a deceased body. PLoS ONE 2018, 13, e0204565. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, F.; Grünzweig, C.; Bunk, O.; Frei, G.; Lehmann, E.; David, C. Neutron phase imaging and tomography. Phys. Rev. Lett. 2006, 96, 215505. [Google Scholar] [CrossRef] [PubMed]
- Donath, T.; Chabior, M.; Pfeiffer, F.; Bunk., O.; Reznikova, E.; Mohr, J.; Hempel, E.; Popescu, S.; Hoheisel, M.; Schuster, M.; et al. Inverse geometry for grating-based x-ray phase-contrast imaging. J. Appl. Phys. 2009, 106, 054703. [Google Scholar] [CrossRef]
- Momose, A.; Kuwabara, H.; Yasihro, W. X-ray phase imaging using Lau effect. Appl. Phys. Express 2011, 4, 066603. [Google Scholar] [CrossRef]
- Momose, A.; Yashiro, W.; Maikusa, H.; Takeda, Y. High-speed X-ray phase imaging and X-ray phase tomography with Talbot interferometer and white synchrotron radiation. Opt. Express 2009, 17, 12540–12545. [Google Scholar] [CrossRef]
- Momose, A.; Yashiro, W.; Harasse, S.; Kuwabara, H. Four-dimensional X-ray phase tomography with Talbot interferometry and white synchrotron radiation: Dynamic observation of a living worm. Opt. Express 2011, 19, 8423–8432. [Google Scholar] [CrossRef]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- Weitkamp, T.; Diaz, A.; David, C.; Pfeiffer, F.; Stampanoni, M.; Cloetens, P.; Ziegler, E. X-ray phase imaging with a grating interferometer. Opt. Express 2005, 13, 6296–6304. [Google Scholar] [CrossRef]
- Vegso, K.; Wu, Y.; Takano, H.; Hoshino, M.; Momose, A. Development of pink-beam 4D phase CT for -Situ Obs. Polym. Infrared Laser Irradiation. Sci. Rep. 2019, 9, 7404. [Google Scholar] [CrossRef]
- Kibayashi, S.; Harasse, S.; Yashiro, W.; Momose, A. High-speed X-ray phase tomography with Talbot interferometer and fringe-scanning method. AIP Conf. Proc. 2012, 1466, 261–265. [Google Scholar]
- Momose, A.; Vegso, K.; Takano, H.; Wu, Y.; Hashimoto, K.; Hoshino, M. Four-dimensional pink-beam X-ray phase tomography for studying laser processing. SPIE Proc. 2019, 11113, 111130I. [Google Scholar]
- Miao, H.; Gomella, A.A.; Chedid, N.; Chen, L.; Wen, H. Fabrication of 200 nm period hard X-ray phase gratings. Nano Lett. 2014, 14, 3453–3458. [Google Scholar] [CrossRef] [PubMed]
- Miao, H.; Gomella, A.A.; Harmon, K.J.; Bennett, E.E.; Chedid, N.; Znati, S.; Panna, A.; Foster, B.A.; Bhandarkar, P.; Wen, H. Enhancing tabletop X-ray phase contrast imaging with nano-fabrication. Sci. Rep. 2015, 5, 13581. [Google Scholar] [CrossRef] [PubMed]
- Miao, H.; Panna, A.; Gomella, A.A.; Bennett, E.E.; Znati, S.; Chen, L.; Wen, H. A universal moiré effect and application in X-ray phase-contrast imaging. Nat. Commun. 2016, 12, 830–834. [Google Scholar] [CrossRef] [PubMed]
- Takeda, Y.; Yashiro, W.; Hattori, T.; Takeuchi, A.; Suzuki, Y.; Momose, A. Differential phase X-ray imaging microscopy with X-ray Talbot interferometer. Appl. Phys. Express 2008, 1, 117002. [Google Scholar] [CrossRef]
- Nango, N.; Kubota, S.; Takeuchi, A.; Suzuki, Y.; Yashiro, W.; Momose, A.; Matsuo, K. Talbot-defocus multiscan tomography using the synchrotron X-ray microscope to study the lacuno-canalicular network in mouse bone. Biomed. Opt. Express 2013, 4, 917–923. [Google Scholar] [CrossRef]
- Momose, A.; Takano, H.; Hoshino, M.; Wu, Y.; Vegso, K. Recent advance in grating-based X-ray phase tomography. SPIE Proc. 2017, 103910, 103910Y. [Google Scholar]
- Matsuo, K.; Kuroda, Y.; Nango, N.; Shimoda, K.; Kubota, Y.; Ema, M.; Bakiri, L.; Wagner, E.F.; Takeda, Y.; Yashiro, W.; et al. Osteogenic capillaries orchestrate growth plate-independent ossification of the malleus. Development 2015, 142, 3912–3920. [Google Scholar] [CrossRef]
- Nango, N.; Kubota, S.; Hasegawa, T.; Yashiro, W.; Momose, A.; Matsuo, K. Osteocyte-directed bone demineralization along canaliculi. Bone 2016, 84, 279–288. [Google Scholar] [CrossRef]
- Yashiro, W.; Takeda, Y.; Takeuchi, A.; Suzuki, Y.; Momose, A. Hard-X-ray phase-difference microscopy using a Fresnel zone plate and a transmission grating. Phys. Rev. Lett. 2009, 103, 180801. [Google Scholar] [CrossRef] [PubMed]
- Kuwabara, H.; Yashiro, W.; Harasse, S.; Mizutani, H.; Momose, A. Hard-X-ray phase-difference microscopy with a low-brilliance laboratory X-ray source. Appl. Phys. Express 2011, 4, 062502. [Google Scholar] [CrossRef]
- Takano, H.; Wu, Y.; Irwin, J.; Maderych, S.; Leibowitz, M.; Tkachuk, A.; Kumer, A.; Hornberger, B.; Momose, A. Comparison of image properties in full-field phase X-ray microscopes based on grating interferometry and Zernike’s phase contrast optics. Appl. Phys. Lett. 2018, 113, 063105. [Google Scholar] [CrossRef]
- Takano, H.; Hashimoto, K.; Nagatani, Y.; Irwin, J.; Omlor, L.; Kumar, A.; Tkachuk, A.; Wu, Y.; Momose, A. Improvement in quantitative phase mapping by a hard x-ray microscope equipped with a Lau interferometer. Optica 2019, 6, 1012–1015. [Google Scholar] [CrossRef]
- Takano, H.; Hashimoto, K.; Nagatani, Y.; Wu, Y.; Momose, A. Development of laboratory-based x-ray phase tomographic microscope. SPIE Proc. 2019, 11113, 111130J. [Google Scholar]
- Grünzweig, C.; Pfeiffer, F.; Bunk, O.; Donath, T.; Kuhne, G.; Frei, G.; Dierolf, M.; David, C. Design, fabrication, and characterization of diffraction gratings for neutron phase contrast imaging. Rev. Sci. Instrum. 2008, 79, 053703. [Google Scholar] [CrossRef]
- Grünzweig, C.; David, C.; Bunk, O.; Dierolf, M.; Frei, G.; Kühne, G.; Kohlbrecher, J.; Schafer, R.; Lejcek, P.; Rønnow, H.M.R.; et al. Neutron decoherence imaging for visualizing bulk magnetic domain structures. Phys. Rev. Lett. 2008, 101, 025504. [Google Scholar] [CrossRef]
- Grünzweig, C.; David, C.; Bunk., O.; Dierolf, M.; Frei, G.; Kühne, G.; Schäfer, R.; Pofahl, S.; Rønnow, H.M.R.; Pfeiffer, F. Bulk magnetic domain structures visualized by neutron dark-field imaging. Appl. Phys. Lett. 2008, 93, 112504. [Google Scholar]
- Manke, I.; Kardjilov, N.; Schäfer, R.; Hilger, A.; Strobl, M.; Dawson, M.; Grünzweig, C.; Behr, G.; Hentschel, M.; David, C.; et al. Three-dimensional imaging of magnetic domains. Nat. Commun. 2010, 1, 125. [Google Scholar] [CrossRef]
- Reimann, T.; Mühlbauer, S.; Schulz, M.; Betz, B.; Kaestner, A.; Pipich, V.; Böni, P.; Grünzweig, C. Visualizing the morphology of vortex lattice domains in a bulk type-II superconductor. Nat. Commun. 2015, 6, 8813. [Google Scholar] [CrossRef]
- Valsecchi, J.; Harti, R.P.; Raventós, M.; Siegwart, M.D.; Morgano, M.; Boillat, P.; Strobl, M.; Hautle, P.; Holitzner, L.; Filges, U.; et al. Visualization and quantification of inhomogeneous and anisotropic magnetic fields by polarized neutron grating interferometry. Nat. Commun. 2019, 10, 3788. [Google Scholar] [CrossRef] [PubMed]
- Shinohara, T.; Kai, T.; Oikawa, K.; Segawa, M.; Harada, M.; Nakatani, M.; Ooi, M.; Aizawa, K.; Sato, H.; Kamiyama, T.; et al. Final design of the energy-resolved neutron imaging system “RADEN” at J-PARC. J. Phys. Conf. Ser. 2016, 746, 012007. [Google Scholar] [CrossRef]
- Seki, Y.; Shinohara, T.; Parker, J.D.; Ueno, W.; Samoto, T.; Yashiro, W.; Momose, A.; Otake, Y.; Kiyanagi, Y. Efficient phase imaging using wavelength-resolved neutron Talbot–Lau interferometry with TOF method. EPL 2018, 123, 12002. [Google Scholar] [CrossRef]
- Sadeghilaridjani, M.; Kato, K.; Shinohara, T.; Yashiro, W.; Momose, A.; Kato, H. High aspect ratio grating by isochronal imprinting of less viscous workable Gd-based metallic glass for neutron phase imaging. Intermetallics 2016, 78, 55–63. [Google Scholar] [CrossRef]
- Samoto, T.; Takano, H.; Momose, A. Evaluation of obliquely evaporated gadolinium gratings for neutron interferometry by X-ray microtomography. Mater. Sci. Semicond. Process. 2019, 92, 91–95. [Google Scholar] [CrossRef]
- Samoto, T.; Takano, H.; Momose, A. Gadolinium oblique evaporation approach to make large scale neutron absorption gratings for phase imaging. Jpn. J. Appl. Phys. 2019, 58, SDDF12. [Google Scholar] [CrossRef]
- Wang, W.H.; Dong, C.; Shek, C.H. Bulk metallic glasses. Mater. Sci. Eng. R 2004, 44, 45–89. [Google Scholar] [CrossRef]
- Seki, Y.; Shinohara, T.; Parker, J.D.; Yashiro, W.; Momose, A.; Kato, K.; Kato, H.; Sadeghilaridjani, M.; Otake, Y.; Kiyanagi, Y. Development of multi-colored neutron Talbot–Lau interferometer with absorption grating fabricated by imprinting method of metallic glass. J. Phys. Soc. Jpn. 2017, 86, 044001. [Google Scholar] [CrossRef]
- Seki, Y.; Shinohara, T.; Ueno, W.; Parker, J.D.; Samoto, T.; Yashiro, W.; Momose, A. Experimental evaluation of neutron absorption grating fabricated by oblique evaporation of gadolinium for phase imaging. Phys. Procedia 2017, 88, 217–223. [Google Scholar] [CrossRef]
- Parker, J.D.; Harada, M.; Hattori, K.; Iwaki, S.; Kabuki, S.; Kishimoto, Y.; Kubo, H.; Kurosawa, S.; Matsuoka, Y.; Miuchi, K.; et al. Spatial resolution of a mu PIC-based neutron imaging detector. Nucl. Instrum. Methods A 2013, 726, 155–161. [Google Scholar] [CrossRef]
- Sarapata, A.; Chabior, M.; Cozzini, C.; Sperl, J.I.; Bequé, D.; Langner, O.; Coman, J.; Zanette, I.; Ruiz-Yaniz, M.; Pfeiffer, F. Quantitative electron density characterization of soft tissue substitute plastic materials using grating-based X-ray phase-contrast imaging. Rev. Sci. Instrum. 2014, 85, 103708. [Google Scholar] [CrossRef] [PubMed]
- Ikematsu, K.; Takano, H.; Wu, Y.; Kimura, K.; Mamyrbayev, T.; Opolka, A.; Ershov, A.; Gutekunst, J.; Meyer, P.; Last, A.; et al. Super-resolution X-ray phase imaging with two dimensional biconcave parabolic multi lens array. in preparation.
- Wu, Y.; Takano, H.; Momose, A. Observation of structural degradation using grating-interferometer-based X-ray stroboscopic tomography. 2020; in preparation. [Google Scholar]
- Momose, A.; Ikematsu, K.; Wu, Y.; Kimura, K.; Takano, H. Sensitivity enhancement in X-ray Talbot interferometry by using parabolic gratings. 2020; in preparation. [Google Scholar]
- Yamagata, Y.; Hirota, K.; Ju, J.; Wang, S.; Morita, S.; Kato, J.; Otake, Y.; Taketani, A.; Seki, Y.; Yamada, M.; et al. Development of a neutron generating target for compact neutron sources using low energy proton beams. J. Radioanal. Nucl. Chem. 2015, 305, 787–794. [Google Scholar] [CrossRef]
- Jensen, T.H.; Bech, M.; Bunk, O.; Donath, T.; David, C.; Feidenhans’l, R.; Pfeiffer, F. Directional x-ray dark-field imaging. Phys. Med. Biol. 2010, 55, 3317–3323. [Google Scholar] [CrossRef]
- Malecki, A.; Potdevin, G.; Biernath, T.; Eggl, E.; Willer, K.; Lasser, T.; Maisenbacher, J.; Gibmeier, J.; Wanner, A.; Pfeiffer, F. X-ray tensor tomography. Europhys. Lett. 2014, 105, 38002. [Google Scholar] [CrossRef]
- Kagias, M.; Wang, Z.; Villanueva-Perez, P.; Jefimovs, K.; Stampanoni, M. 2D-Omnidirectional hard-X-ray scattering sensitivity in a single shot. Phys. Rev. Lett. 2016, 116, 093902. [Google Scholar] [CrossRef]
- Kagias, M.; Wang, Z.; Birkback, M.E.; Lauridsen, E.; Abis, M.; Lovric, G.; Jefimovs, K.; Stampanoni, M. Diffractive small angle X-ray scattering imaging for anisotropic structures. Nat. Commun. 2019, 10, 5130. [Google Scholar] [CrossRef]
- Thuering, T.; Barber, W.C.; Seo, Y.; Alhassen, F.; Iwanczyk, J.S.; Stampanoni, M. Energy resolved X-ray grating interferometry. Appl. Phys. Lett. 2013, 102, 191113. [Google Scholar] [CrossRef]
- Berujon, S.; Wang, H.; Sawhney, K. X-ray multimodal imaging using a random-phase object. Phys. Rev. A 2012, 86, 063813. [Google Scholar] [CrossRef]
- Morgan, K.S.; Paganin, D.M.; Siu, K.K.W. X-ray phase imaging with a paper analyzer. Appl. Phys. Lett. 2012, 100, 124102. [Google Scholar] [CrossRef]
- Olivo, A.; Speller, R. A coded-aperture technique allowing X-ray phase contrast imaging with conventional sources. Appl. Phys. Lett. 2007, 91, 074106. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).