High Resolution Mapping of Orientation and Strain Gradients in Metals by Synchrotron 3D X-ray Laue Microdiffraction
Abstract
1. Introduction
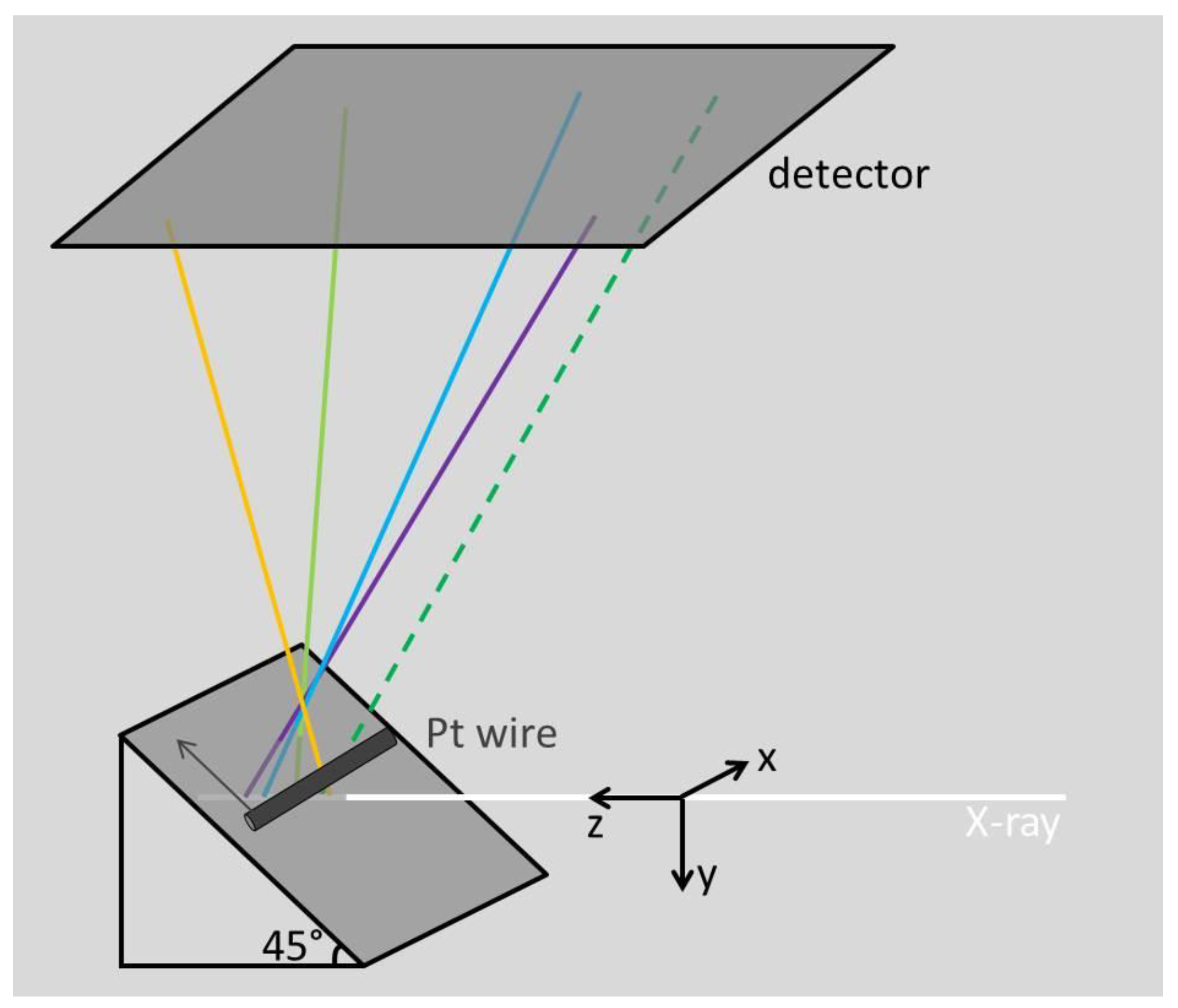
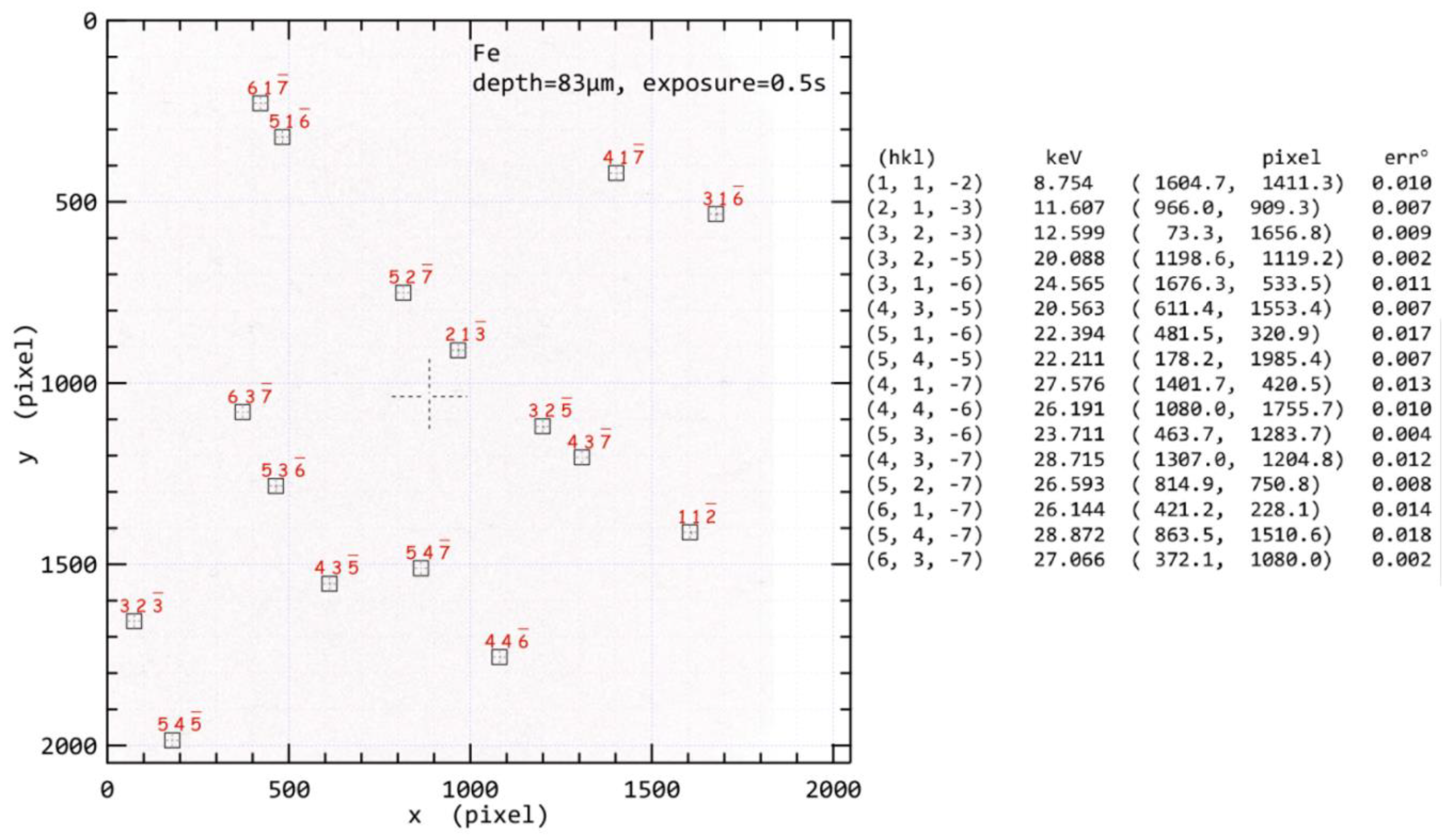
2. Differential Aperture X-ray Microscopy
3. Quantification of Plastic Strain and Geometrically Necessary Dislocation Density Based on Orientation Maps
4. Local Thermal Residual Stress in Metal Composite
4.1. Microstructure of Ductile Cast Iron
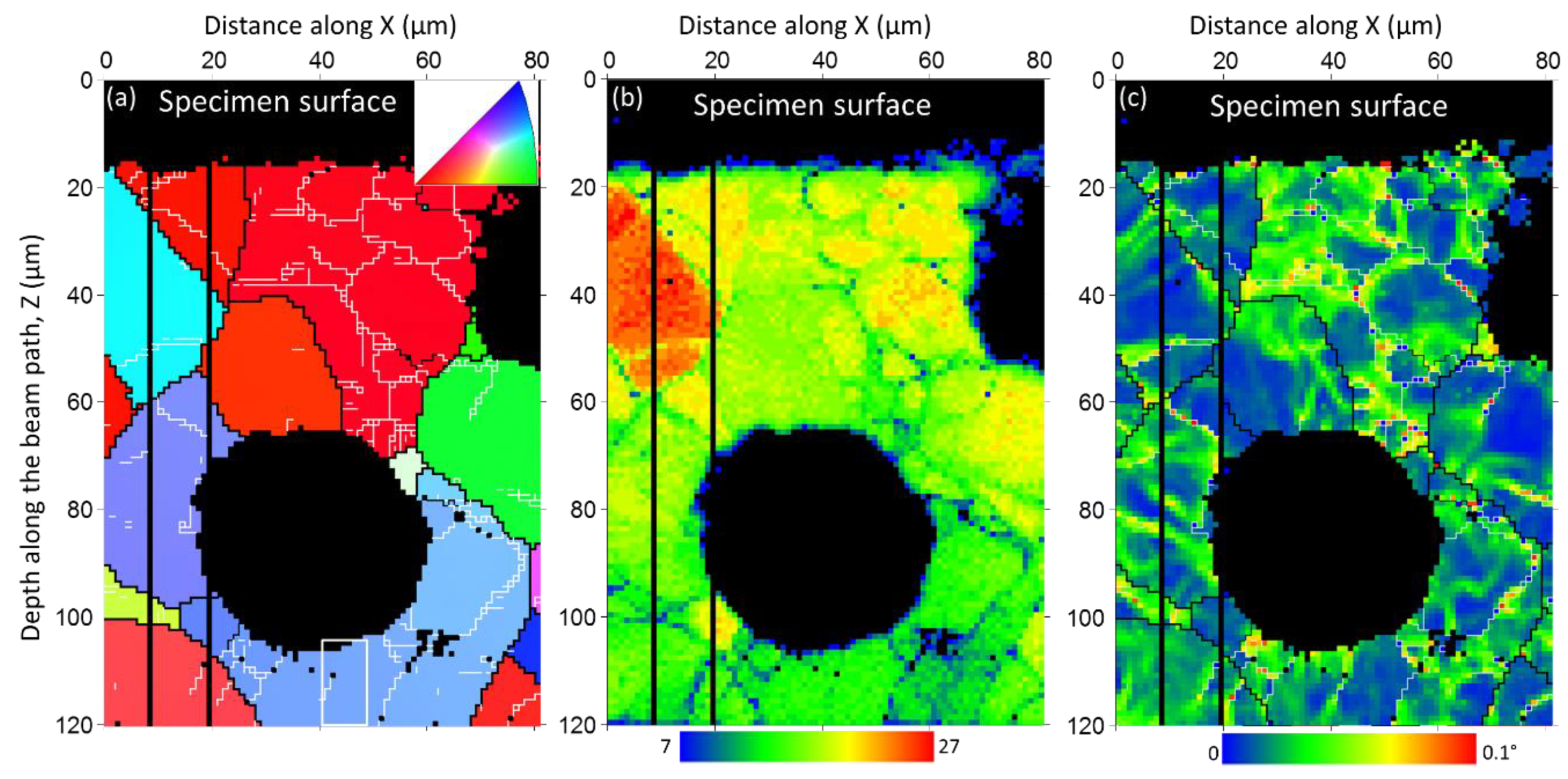
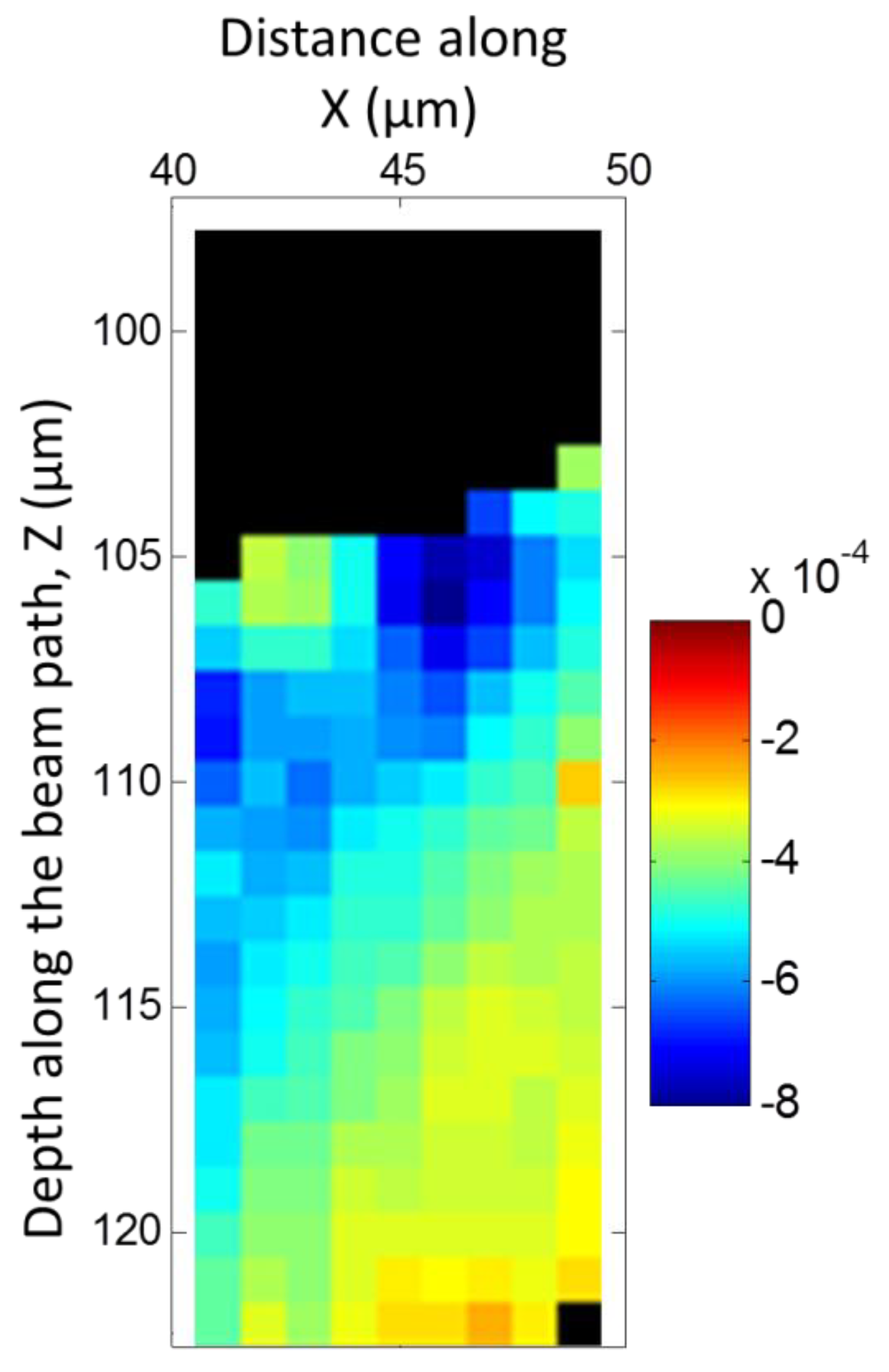
4.2. Elastic Strain Distribution
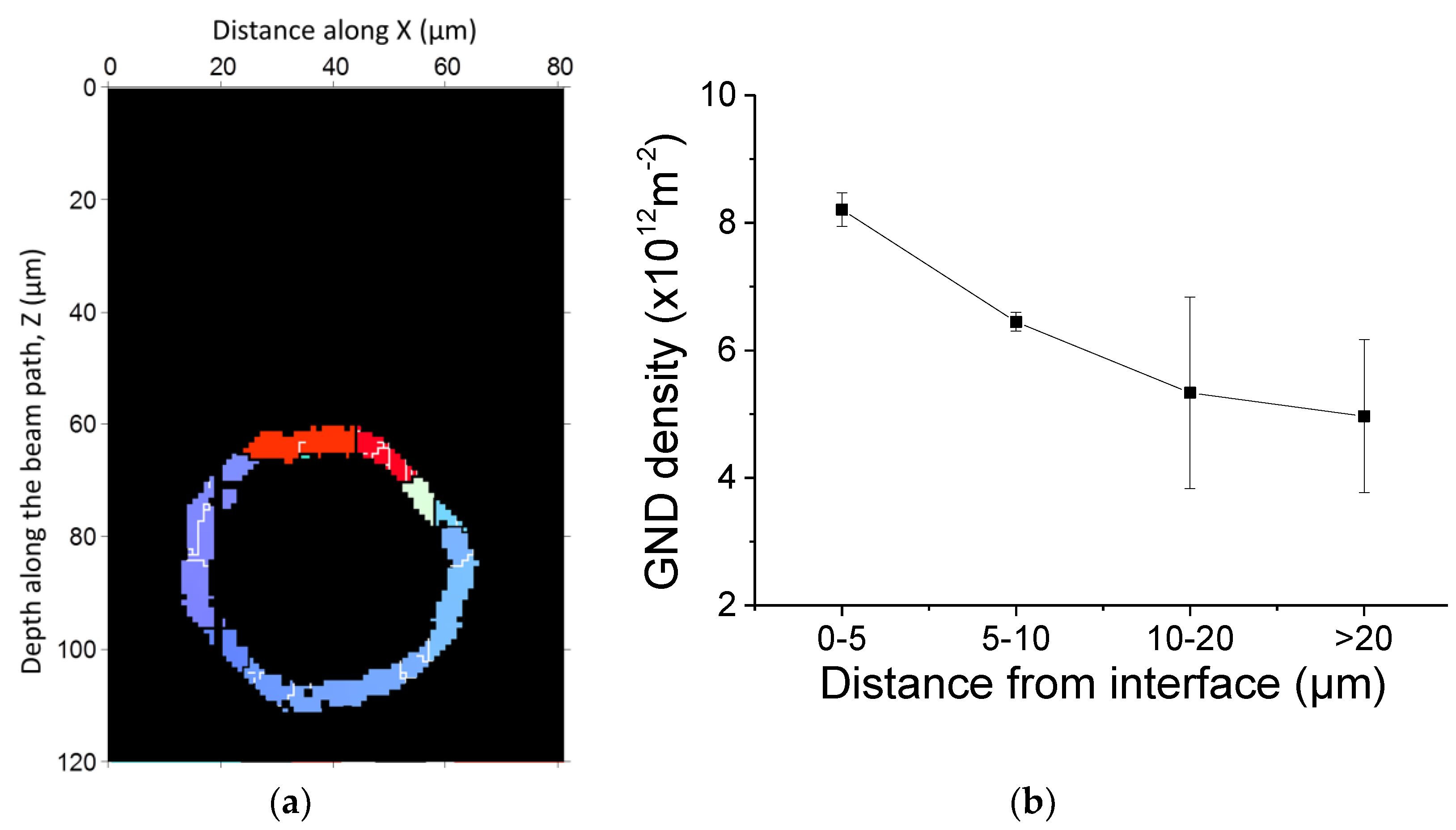
4.3. Quantification of Geometrically Necessary Dislocation Density
4.4. Discussion
5. Local Residual Stress in Single Phase Metals
5.1. Microstrucure of Partially Recrystallized Ni Processed by Accumulative Roll Bonding
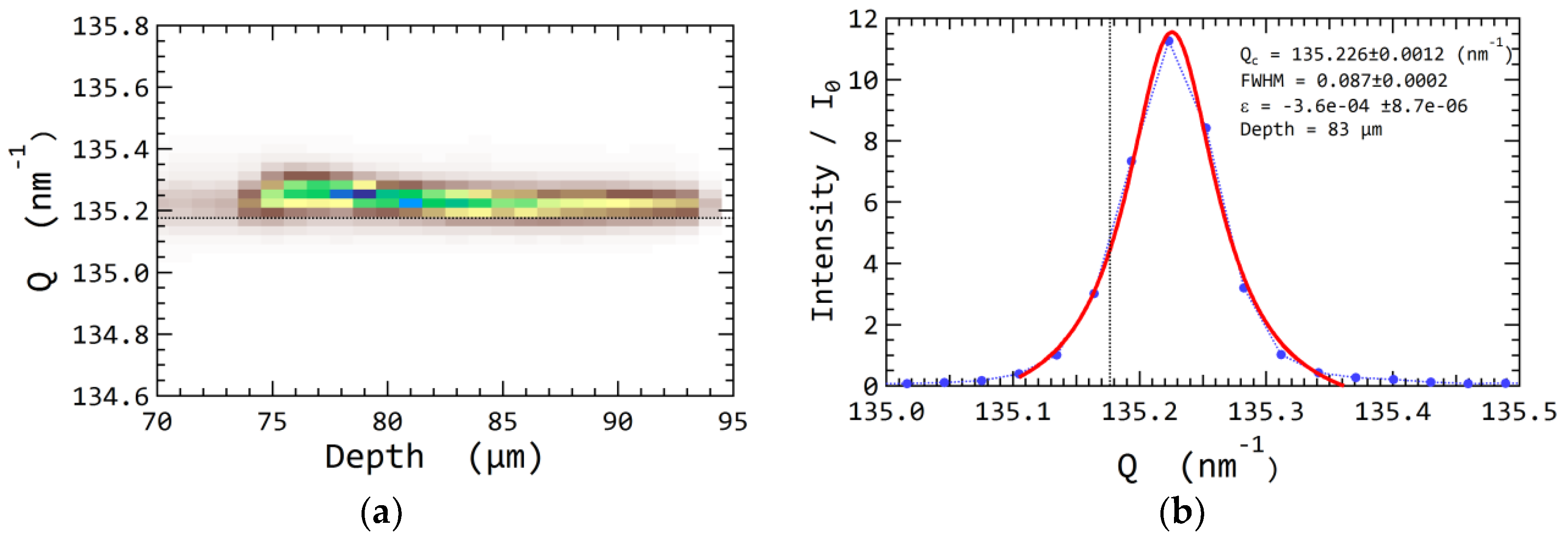
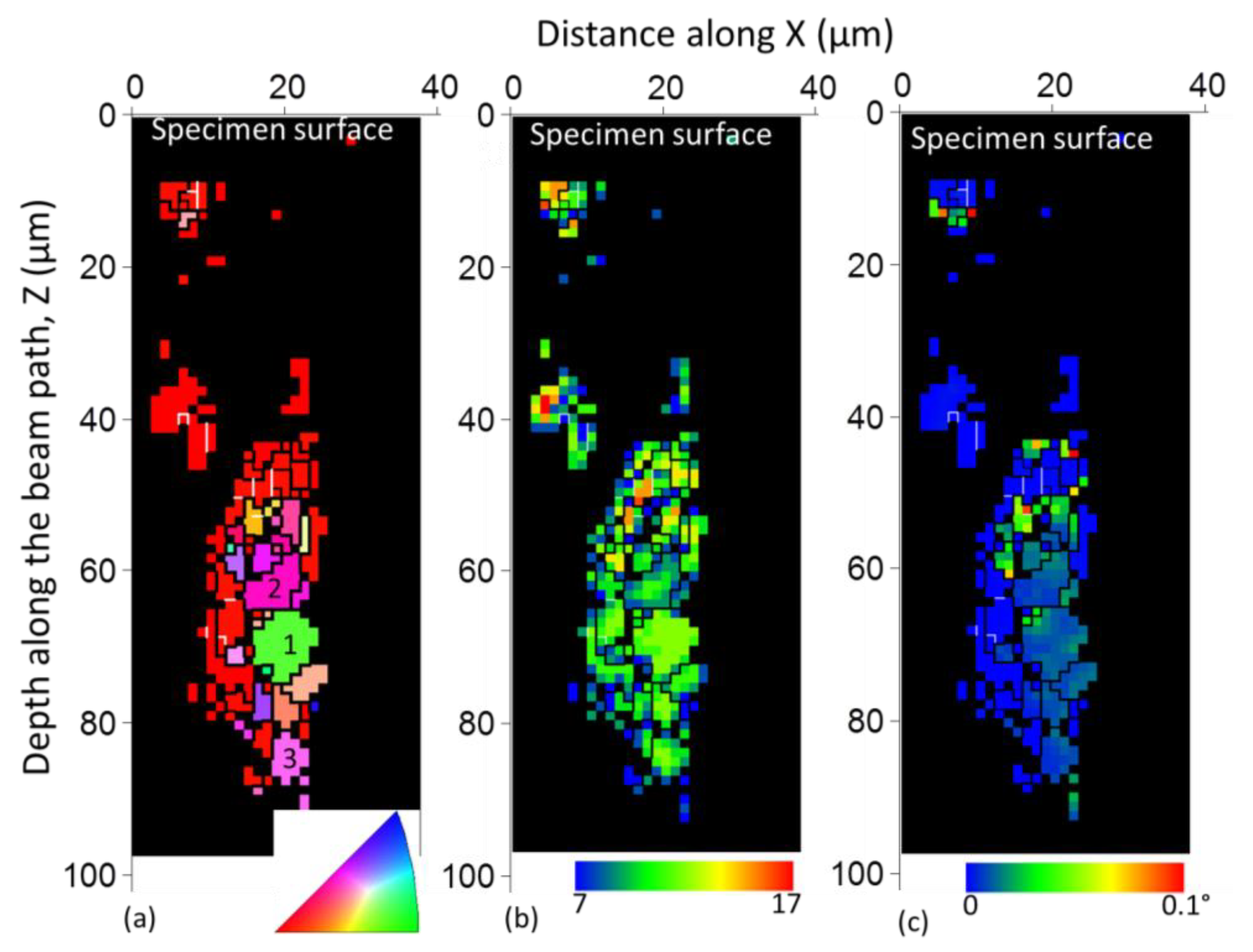
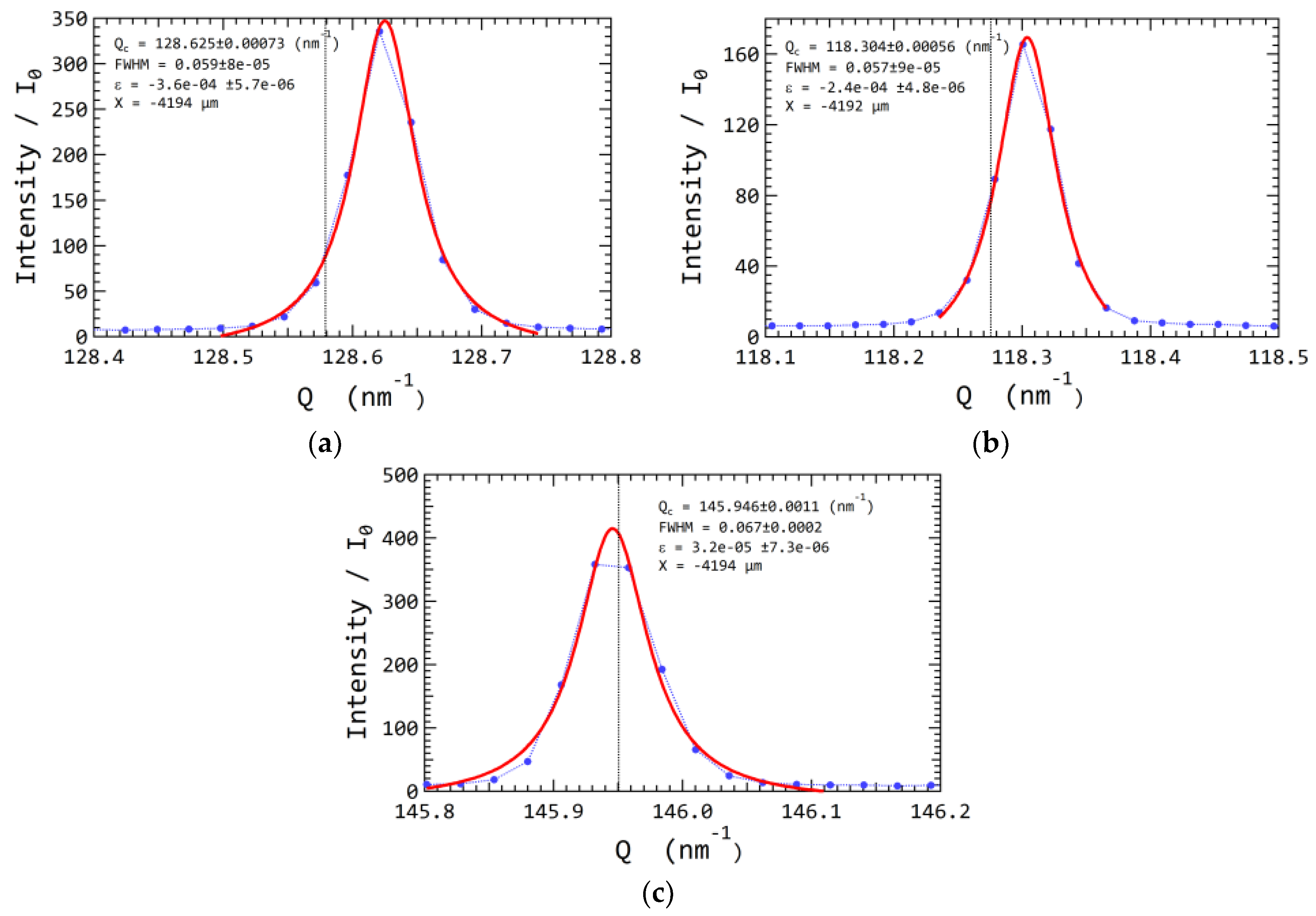
5.2. Elastic Strain
5.3. Discussion
6. Conclusions and Outlook
- (i)
- Local thermal stress has developed at graphite nodules during cooling of DCI and led to plastic deformation of the ferrite matrix, which in turn relaxes part of the stress. Compressive elastic strains along specimen normal direction are observed. Both plastic and elastic strains exhibit gradients, with maximum at or near the interface and decrease into the matrix.
- (ii)
- Local elastic strain variation of 3.6 × 10−4 was observed within recrystallized grains in partially recrystallized nickel. Similar to previous studies, the recrystallized grains contain dislocations of about 1012 m−2. The presence of dislocations and the variations of local elastic strains are important for understanding the recrystallization process.
Funding
Acknowledgments
Conflicts of Interest
References
- Withers, P.J.; Bhadeshia, H.K.D.H. Residual stress. Part 2—Nature and origins. Mater. Sci. Technol. 2001, 17, 366–375. [Google Scholar] [CrossRef]
- Withers, P.J.; Bhadeshia, H.K.D.H. Residual stress Part 1—Measurement techniques. Mater. Sci. Technol. 2001, 17, 355–365. [Google Scholar]
- Ho, S.; Lavernia, E.J. Thermal residual stresses in metal matrix composites: A review. Appl. Compos. Mater. 1995, 2, 1–30. [Google Scholar] [CrossRef]
- Withers, P.J. Residual stress and its role in failure. Rep. Prog. Phys. 2007, 70, 2211–2264. [Google Scholar] [CrossRef]
- Poulsen, H.F. Three-Dimensional X-ray Microscopy: Mapping Polycrystals and Their Dynamics; Springer: New York, NY, USA, 2004; ISBN 9783540444831. [Google Scholar]
- Oddershede, J.; Schmidt, S.; Poulsen, H.F.; Sørensen, H.O.; Wright, J.; Reimers, W. Determining grain resolved stresses in polycrystalline materials using three-dimensional X-ray diffraction. J. Appl. Crystallogr. 2010, 43, 539–549. [Google Scholar] [CrossRef]
- Poulsen, H.F. An introduction to three-dimensional X-ray diffraction microscopy. J. Appl. Crystallogr. 2012, 45, 1084–1097. [Google Scholar] [CrossRef]
- Pantleon, W.; Wejdemann, C.; Jakobsen, B.; Lienert, U.; Poulsen, H.F. Advances in characterization of deformation structures by high resolution reciprocal space mapping. In Proceedings of the 31st Risø International Symposium on Materials Science, Roskilde, Denmark, 6–10 September 2010; pp. 79–100. [Google Scholar]
- Jakobsen, B.; Poulsen, H.F.; Lienert, U.; Almer, J.; Shastri, S.D.; Sørensen, H.O.; Gundlach, C.; Pantleon, W. Formation and subdivision of deformation structures during plastic deformation. Science 2006, 312, 889–892. [Google Scholar] [CrossRef] [PubMed]
- Lienert, U.; Li, S.F.; Hefferan, C.M.; Lind, J.; Suter, R.M.; Bernier, J.V.; Barton, N.R.; Brandes, M.C.; Mills, M.J.; Miller, M.P.; et al. High-energy diffraction microscopy at the advanced photon source. JOM 2011, 63, 70–77. [Google Scholar] [CrossRef]
- Li, S.F.; Suter, R.M. Adaptive reconstruction method for three-dimensional orientation imaging. J. Appl. Crystallogr. 2013, 46, 512–524. [Google Scholar]
- Ludwig, W.; Schmidt, S.; Lauridsen, E.M.; Poulsen, H.F. X-ray diffraction contrast tomography: A novel technique for three-dimensional grain mapping of polycrystals. I. Direct beam case. J. Appl. Crystallogr. 2008, 41, 302–309. [Google Scholar]
- Reischig, P.; King, A.; Nervo, L.; Viganó, N.; Guilhem, Y.; Palenstijn, W.J.; Batenburg, K.J.; Preuss, M.; Ludwig, W. Advances in X-ray diffraction contrast tomography: Flexibility in the setup geometry and application to multiphase materials. J. Appl. Crystallogr. 2013, 46, 297–311. [Google Scholar] [CrossRef]
- Simons, H.; King, A.; Ludwig, W.; Detlefs, C.; Pantleon, W.; Schmidt, S.; Snigireva, I.; Snigirev, A.; Poulsen, H.F. Dark-field X-ray microscopy for multiscale structural characterization. Nat. Commun. 2015, 6, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Yau, A.; Cha, W.; Kanan, M.W.; Matthew, W.; Stephenson, G.B.; Ulvestad, A. Bragg coherent diffractive imaging of single-grain defect dynamics in polycrystalline films. Science 2017, 356, 739–742. [Google Scholar] [CrossRef] [PubMed]
- Robinson, I.; Harder, R. Coherent X-ray diffraction imaging of strain at the nanoscale. Nat. Mater. 2009, 8, 291. [Google Scholar] [CrossRef] [PubMed]
- Cornelius, T.; Thomas, O. Progress of in situ synchrotron X-ray diffraction studies on the mechanical behavior of materials at small scales. Prog. Mater. Sci. 2018, 94, 384–434. [Google Scholar] [CrossRef]
- Larson, B.; Yang, W.; Ice, G.; Budai, J.; Tischler, J. Three-dimensional X-ray structural microscopy with submicrometre resolution. Nature 2002, 415, 887–890. [Google Scholar] [CrossRef] [PubMed]
- Levine, L.E.; Larson, B.C.; Yang, W.; Kassner, M.E.; Tischler, J.Z.; Delos-Reyes, M.A.; Fields, R.J.; Liu, W. X-ray microbeam measurements of individual dislocation cell elastic strains in deformed single-crystal copper. Nat. Mater. 2006, 5, 619–622. [Google Scholar] [CrossRef] [PubMed]
- Ice, G.E.; Budai, J.D.; Pang, J.W.L. The race to X-ray microbeam and nanobeam science. Science 2011, 334, 1234–1239. [Google Scholar] [CrossRef] [PubMed]
- Larson, B.C.; Levine, L.E. Submicrometre-resolution polychromatic three-dimensional X-ray microscopy. J. Appl. Crystallogr. 2013, 46, 153–164. [Google Scholar] [CrossRef]
- Ice, G.E.; Pang, J.W.L.; Barabash, R.I.; Puzyrev, Y. Characterization of three-dimensional crystallographic distributions using polychromatic X-ray microdiffraction. Scr. Mater. 2006, 55, 57–62. [Google Scholar] [CrossRef]
- Ice, G.E.; Pang, J.W.L. Tutorial on X-ray microLaue diffraction. Mater. Charact. 2009, 60, 1191–1201. [Google Scholar] [CrossRef]
- Ohashi, T.; Barabash, R.I.; Pang, J.W.L.; Ice, G.E.; Barabash, O.M. X-ray microdiffraction and strain gradient crystal plasticity studies of geometrically necessary dislocations near a Ni bicrystal grain boundary. Int. J. Plast. 2009, 25, 920–941. [Google Scholar] [CrossRef]
- Levine, L.E.; Geantil, P.; Larson, B.C.; Tischler, J.Z.; Kassner, M.E.; Liu, W.; Stoudt, M.R.; Tavazza, F. Disordered long-range internal stresses in deformed copper and the mechanisms underlying plastic deformation. Acta Mater. 2011, 59, 5803–5811. [Google Scholar] [CrossRef]
- Levine, L.E.; Geantil, P.; Larson, B.C.; Tischler, J.Z.; Kassner, M.E.; Liu, W. Validating classical line profile analyses using microbeam diffraction from individual dislocation cell walls and cell interiors. J. Appl. Crystallogr. 2012, 45, 157–165. [Google Scholar] [CrossRef]
- Kassner, M.E.; Geantil, P.; Levine, L.E. Long range internal stresses in single-phase crystalline materials. Int. J. Plast. 2013, 45, 44–60. [Google Scholar] [CrossRef]
- Barabash, R.I.; Gao, Y.F.; Ice, G.E.; Barabash, O.M.; Chung, J.S.; Liu, W.; Kroger, R.; Lohmeyer, H.; Sebald, K.; Gutowski, J.; et al. Mapping strain gradients in the FIB-structured InGaN/GaN multilayered films with 3D X-ray microbeam. Mater. Sci. Eng. A 2010, 528, 52–57. [Google Scholar] [CrossRef]
- Barabash, R.I.; Liu, W.; Tischler, J.Z.; Bei, H.; Budai, J.D. Phase-specific elastic/plastic interface interactions in layered NiAl-Cr(Mo) structures. Acta Mater. 2012, 60, 3279–3286. [Google Scholar] [CrossRef]
- Barabash, R.I.; Barabash, O.M.; Ojima, M.; Yu, Z.; Inoue, J.; Nambu, S.; Koseki, T.; Xu, R.; Feng, Z. Interphase strain gradients in multilayered steel composite from microdiffraction. Metall. Mater. Trans. A 2014, 45, 98–108. [Google Scholar] [CrossRef]
- Barabash, R.I.; Ice, G.E.; Liu, W.; Einfeldt, S.; Hommel, D.; Roskowski, A.M.; Davis, R.F. White X-ray microbeam analysis of strain and crystallographic tilt in GaN layers grown by maskless pendeoepitaxy. Phys. Status Solidi Appl. Mater. Sci. 2005, 202, 732–738. [Google Scholar] [CrossRef]
- Barabash, R.I.; Roder, C.; Ice, G.E.; Einfeldt, S.; Budai, J.D.; Barabash, O.M.; Figge, S.; Hommel, D. Spatially resolved distribution of dislocations and crystallographic tilts in GaN layers grown on Si(111) substrates by maskless cantilever epitaxy. J. Appl. Phys. 2006, 100, 1–11. [Google Scholar] [CrossRef]
- Bei, H.; Barabash, R.I.; Ice, G.E.; Liu, W.; Tischler, J.; George, E.P. Spatially resolved strain measurements in Mo-alloy micropillars by differential aperture X-ray microscopy. Appl. Phys. Lett. 2008, 93, 3–5. [Google Scholar] [CrossRef]
- Barabash, R.I.; Bei, H.; Gao, Y.F.; Ice, G.E. Interface strength in NiAl-Mo composites from 3-D X-ray microdiffraction. Scr. Mater. 2011, 64, 900–903. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Budai, J.D.; Tischler, J.Z.; Liu, W.; Xu, R.; Homer, E.R.; Godfrey, A.; Juul Jensen, D. Boundary migration in a 3D deformed microstructure inside an opaque sample. Sci. Rep. 2017, 7, 04087. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Zhang, Y.; Godfrey, A.; Wu, G.; Liu, W.; Tischler, J.Z.; Juul Jensen, D. Direct observation of nucleation in the bulk of an opaque sample. Sci. Rep. 2017, 7, 42508. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.F.; Larson, B.C.; Lee, J.H.; Nicola, L.; Tischler, J.Z.; Pharr, G.M. Lattice Rotation Patterns and Strain Gradient Effects in Face-Centered-Cubic Single Crystals Under Spherical Indentation. J. Appl. Mech. 2015, 82, 061007. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Andriollo, T.; Fæster, S.; Liu, W.; Hattel, J.; Barabash, R.I. Three-dimensional local residual stress and orientation gradients near graphite nodules in ductile cast iron. Acta Mater. 2016, 121, 173–180. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Andriollo, T.; Fæster, S.; Liu, W.; Sturlason, A.; Barabash, R.I. Synchrotron measurements of local microstructure and residual strains in ductile cast iron. IOP Conf. Ser. Mater. Sci. Eng. 2017, 219, 012054. [Google Scholar] [CrossRef]
- Ice, G.E.; Larson, B.C.; Yang, W.; Budai, J.D.; Tischler, J.Z.; Pang, J.W.L.; Barabash, R.I.; Liu, W. Polychromatic X-ray microdiffraction studies of mesoscale structure and dynamics. J. Synchrotron Radiat. 2005, 12, 155–162. [Google Scholar] [CrossRef] [PubMed]
- Barabash, R.I.; Ice, G.E.; Larson, B.C.; Yang, W. Application of white X-ray microbeams for the analysis of dislocation structures. Rev. Sci. Instrum. 2002, 73, 1652–1654. [Google Scholar] [CrossRef]
- Ice, G.E.; Barabash, R.I. White Beam Microdiffraction and Dislocations Gradients. In Dislocations Solids; Hirth, J.P., Nabarro, F.R.N., Eds.; Elsevier: Amsterdam, Netherlands, 2007; Volume 13, pp. 499–601. [Google Scholar]
- Liu, W.; Zschack, P.; Tischler, J.; Ice, G.E.; Larson, B. X-ray laue diffraction microscopy in 3D at the advanced photon source. AIP Conf. Proc. 2010, 1365, 108–111. [Google Scholar]
- Tischler, J.Z. Reconstructing 2D and 3D X-ray Orientation Maps from White-Beam Laue. In Strain Dislocation Gradients from Diffraction; Barabash, R.I., Ice, G.E., Eds.; World Scientific: London, UK, 2014; pp. 358–375. [Google Scholar]
- Kubin, L.P.; Mortensen, A. Geometrically necessary dislocations and strain-gradient plasticity: A few critical issues. Scr. Mater. 2003, 48, 119–125. [Google Scholar] [CrossRef]
- Gao, H.; Hang, Y.; Nix, W.D.; Hutchinson, J.W. Mechanism-based strain gradient plasticity—I. Theory. J. Mech. Phys. Solids 1999, 47, 1239–1263. [Google Scholar] [CrossRef]
- Calcagnotto, M.; Ponge, D.; Demir, E.; Raabe, D. Orientation gradients and geometrically necessary dislocations in ultrafine grained dual-phase steels studied by 2D and 3D EBSD. Mater. Sci. Eng. A 2010, 527, 2738–2746. [Google Scholar] [CrossRef]
- Labrecque, C.; Gagne, M. Review ductile iron: Fifty years of continuous development. Can. Metall. Q. 1998, 37, 343–378. [Google Scholar] [CrossRef]
- Hütter, G.; Zybell, L.; Kuna, M. Micromechanisms of fracture in nodular cast iron: From experimental findings towards modeling strategies—A review. Eng. Fract. Mech. 2015, 144, 118–141. [Google Scholar] [CrossRef]
- Andriollo, T.; Thorborg, J.; Tiedje, N.; Hattel, J. A micro-mechanical analysis of thermo-elastic properties and local residual stresses in ductile iron based on a new anisotropic model for the graphite nodules. Model. Simul. Mater. Sci. Eng. 2016, 24, 055012. [Google Scholar] [CrossRef]
- Mukherjee, K.; Fæster, S.; Hansen, N.; Dahl, A.B.; Gundlach, C.; Frandsen, J.O.; Sturlason, A. Graphite nodules in fatigue-tested cast iron characterized in 2D and 3D. Mater. Charact. 2017, 129, 169–178. [Google Scholar] [CrossRef]
- Andriollo, T.; Hellström, K.; Sonne, M.R.; Thorborg, J.; Tiedje, N.; Hattel, J. Uncovering the local inelastic interactions during manufacture of ductile cast iron: How the substructure of the graphite particles can induce residual stress concentrations in the matrix. J. Mech. Phys. Solids 2018, 111, 333–357. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S.A. Variational approach to the theory of the elastic behaviour of polycrystals. J. Mech. Phys. Solids 1962, 10, 343–352. [Google Scholar] [CrossRef]
- Bonora, N.; Ruggiero, A. Micromechanical modeling of ductile cast iron incorporating damage. Part I: Ferritic ductile cast iron. Int. J. Solids Struct. 2005, 42, 1401–1424. [Google Scholar] [CrossRef]
- Górny, M.; Stefanescu, D.M. Thin-wall ductile iron castings. In ASM Handbook, Cast Iron Science and Technology; Stefanescu, D.M., Ed.; ASM International: Metals Park, OH, USA, 2017; pp. 617–628. [Google Scholar]
- Górny, M.; Tyrała, E. Effect of cooling rate on microstructure and mechanical properties of thin-walled ductile iron castings. J. Mater. Eng. Perform. 2013, 22, 300–305. [Google Scholar] [CrossRef]
- Humphreys, F.J.; Hatherly, M. Recrystallization and Related Annealing Phenomena; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Lin, F.; Zhang, Y.; Tao, N.; Pantleon, W.; Juul Jensen, D. Effects of heterogeneity on recrystallization kinetics of nanocrystalline copper prepared by dynamic plastic deformation. Acta Mater. 2014, 72, 252–261. [Google Scholar] [CrossRef]
- Wu, X.; Yang, M.; Yuan, F.; Wu, G.; Wei, Y.; Huang, X.; Zhu, Y. Heterogeneous lamella structure unites ultrafine-grain strength with coarse-grain ductility. Proc. Natl. Acad. Sci. USA 2015, 112, 14501–14505. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Chen, Z.; Wang, Y.; Ma, G.; Huang, T.; Wu, G.; Huang, X.; Juul Jensen, D. Fabricating interstitial-free steel with simultaneous high strength and good ductility with homogeneous layer and lamella structure. Scr. Mater. 2017, 141, 111–114. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Mishin, O.V.; Kamikawa, N.; Godfrey, A.; Liu, W.; Liu, Q. Microstructure and mechanical properties of nickel processed by accumulative roll bonding. Mater. Sci. Eng. A 2013, 576, 160–166. [Google Scholar] [CrossRef]
- Mishin, O.V.; Zhang, Y.B.; Godfrey, A. The influence of multiscale heterogeneity on recrystallization in nickel processed by accumulative roll bonding. J. Mater. Sci. 2017, 52, 2730–2745. [Google Scholar] [CrossRef]
- Ahl, S.R.; Simons, H.; Zhang, Y.B.; Detlefs, C.; Stöhr, F.; Jakobsen, A.C.; Juul Jensen, D.; Poulsen, H.F. Ultra-low-angle boundary networks within recrystallizing grains. Scr. Mater. 2017, 139, 87–91. [Google Scholar] [CrossRef]
- Dhar, S.; Zhang, Y.; Xu, R.; Danielsen, H.K.; Juul Jensen, D. Synchrotron X-ray measurement of residual strain within the nose of a worn manganese steel railway crossing. IOP Conf. Ser. Mater. Sci. Eng. 2017, 219, 012016. [Google Scholar] [CrossRef]
- Okoro, C.; Levine, L.E.; Xu, R.; Hummler, K.; Obeng, Y. Synchrotron-based measurement of the impact of thermal cycling on the evolution of stresses in Cu through-silicon vias. J. Appl. Phys. 2014, 115, 243509. [Google Scholar] [CrossRef]
- Phan, T.Q.; Levine, L.E.; Lee, I.F.; Xu, R.; Tischler, J.Z.; Huang, Y.; Langdon, T.G.; Kasssner, M.E. Synchrotron X-ray microbeam diffraction measurements of full elastic long range internal strain and stress tensors in commercial-purity aluminum processed by multiple passes of equal-channel angular pressing. Acta Mater. 2016, 112, 231–241. [Google Scholar] [CrossRef]
- Levine, L.E.; Okoro, C.; Xu, R. Full elastic strain and stress tensor measurements from individual dislocation cells in copper through-Si vias. IUCrJ 2015, 2, 635–642. [Google Scholar] [CrossRef] [PubMed]
- Castelvecchi, D. X-ray science gets an upgrade. Nature 2015, 525, 15–16. [Google Scholar] [CrossRef] [PubMed]
- ESRF Upgrade Programme Phase II (2015–2019) White Paper; ESRF: Grenoble, France, 2015.
- Haeffner, R. APS-U Beamline Update; APS: St. Paul, MN, USA, 2017. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Barabash, R.I. High Resolution Mapping of Orientation and Strain Gradients in Metals by Synchrotron 3D X-ray Laue Microdiffraction. Quantum Beam Sci. 2019, 3, 6. https://doi.org/10.3390/qubs3010006
Zhang Y, Barabash RI. High Resolution Mapping of Orientation and Strain Gradients in Metals by Synchrotron 3D X-ray Laue Microdiffraction. Quantum Beam Science. 2019; 3(1):6. https://doi.org/10.3390/qubs3010006
Chicago/Turabian StyleZhang, Yubin, and Rozaliya I. Barabash. 2019. "High Resolution Mapping of Orientation and Strain Gradients in Metals by Synchrotron 3D X-ray Laue Microdiffraction" Quantum Beam Science 3, no. 1: 6. https://doi.org/10.3390/qubs3010006
APA StyleZhang, Y., & Barabash, R. I. (2019). High Resolution Mapping of Orientation and Strain Gradients in Metals by Synchrotron 3D X-ray Laue Microdiffraction. Quantum Beam Science, 3(1), 6. https://doi.org/10.3390/qubs3010006





