EMuS Muon Facility and Its Application in the Study of Magnetism
Abstract
1. Introduction
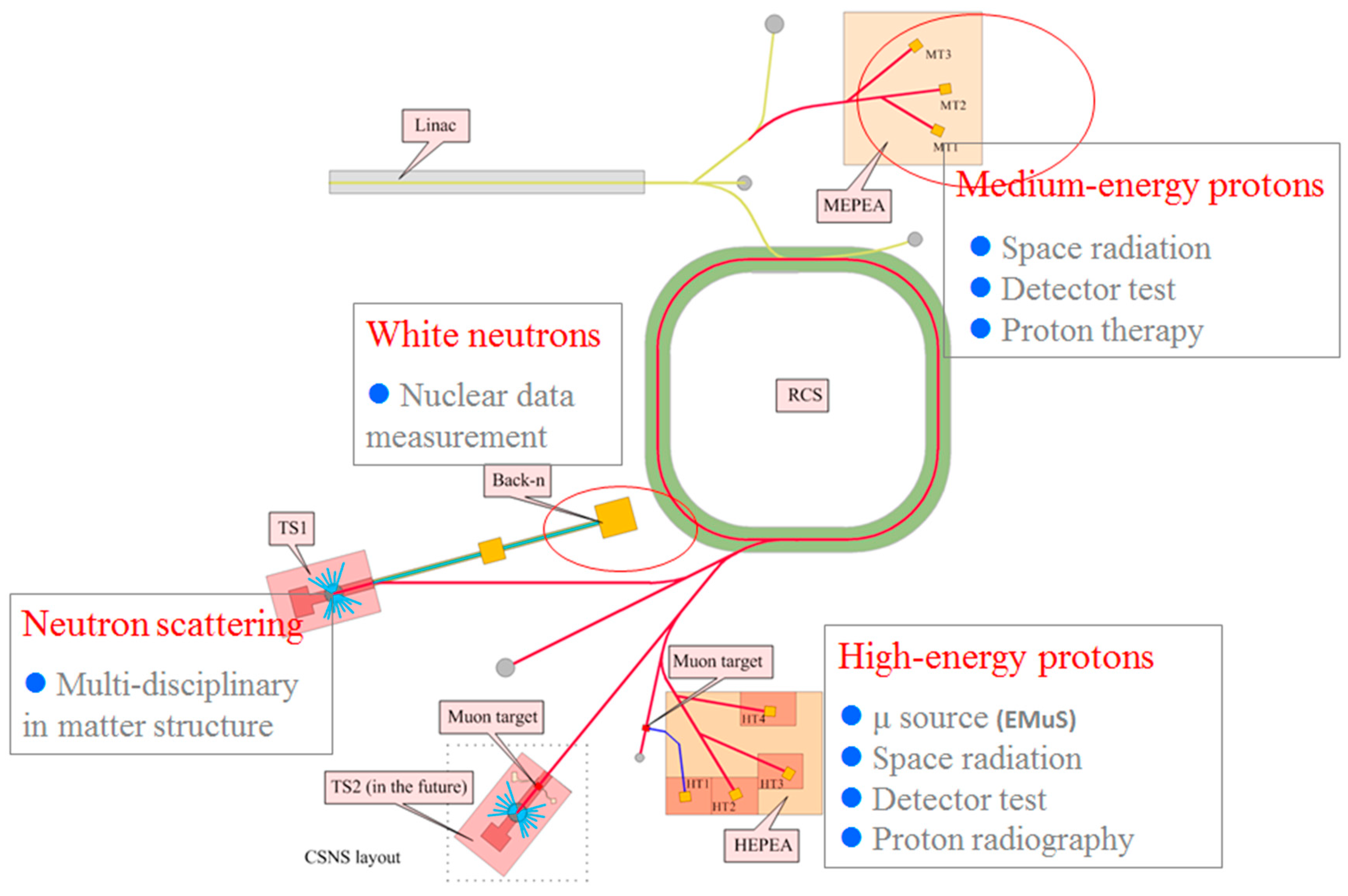
2. EMuS Muon Beam Facility
2.1. General Design
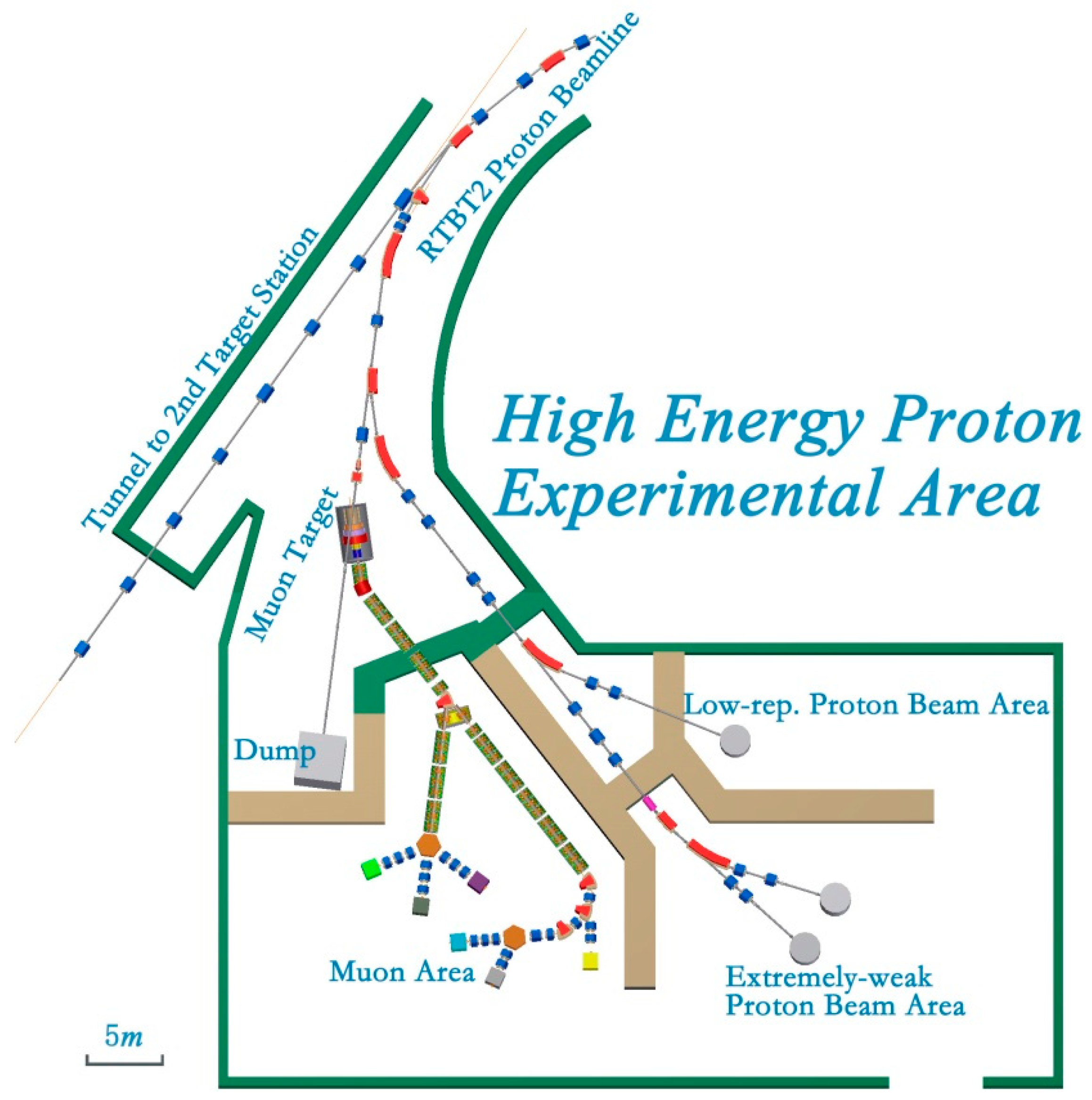
2.2. Proton Beamline and Beam Dump
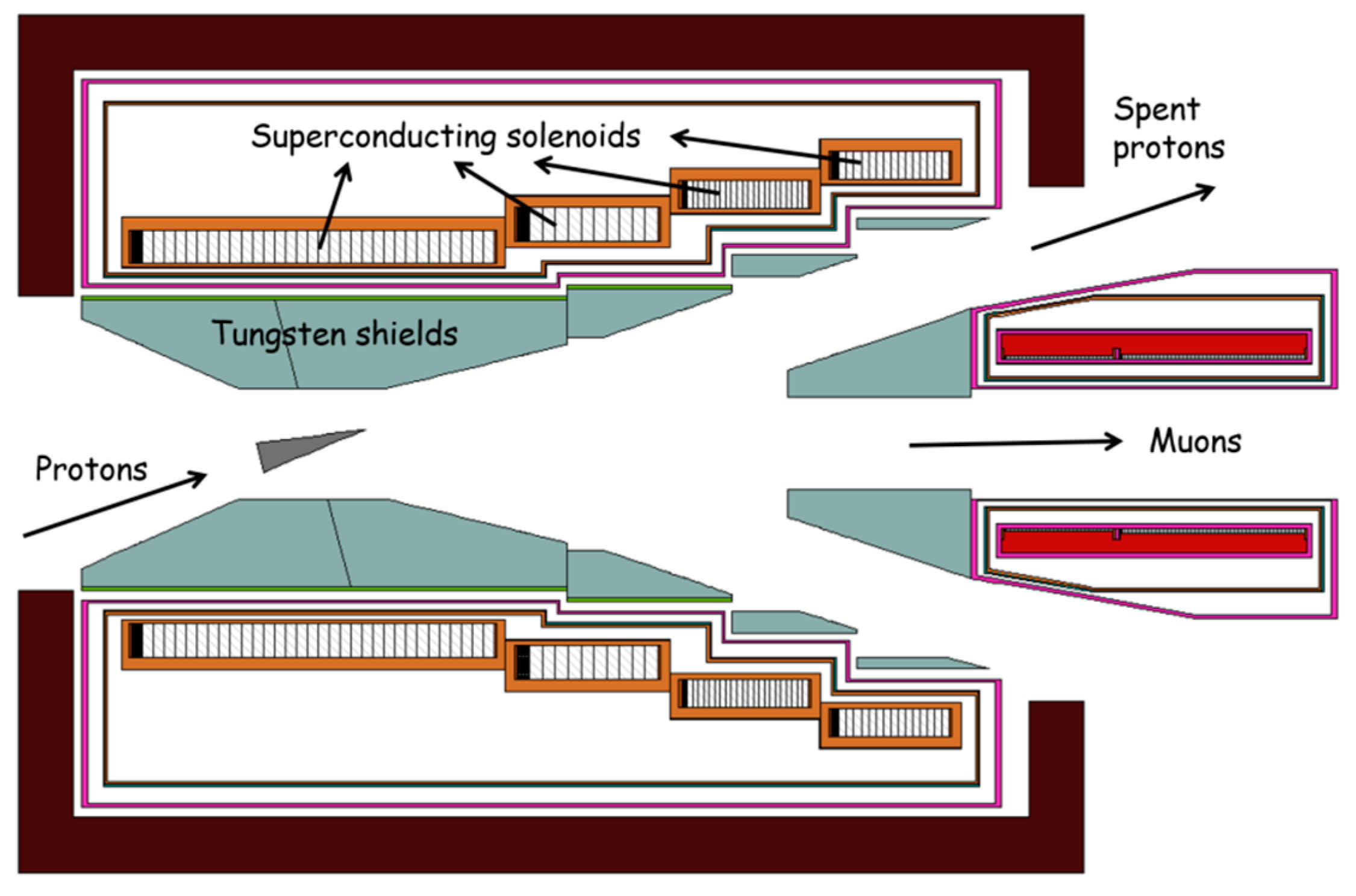
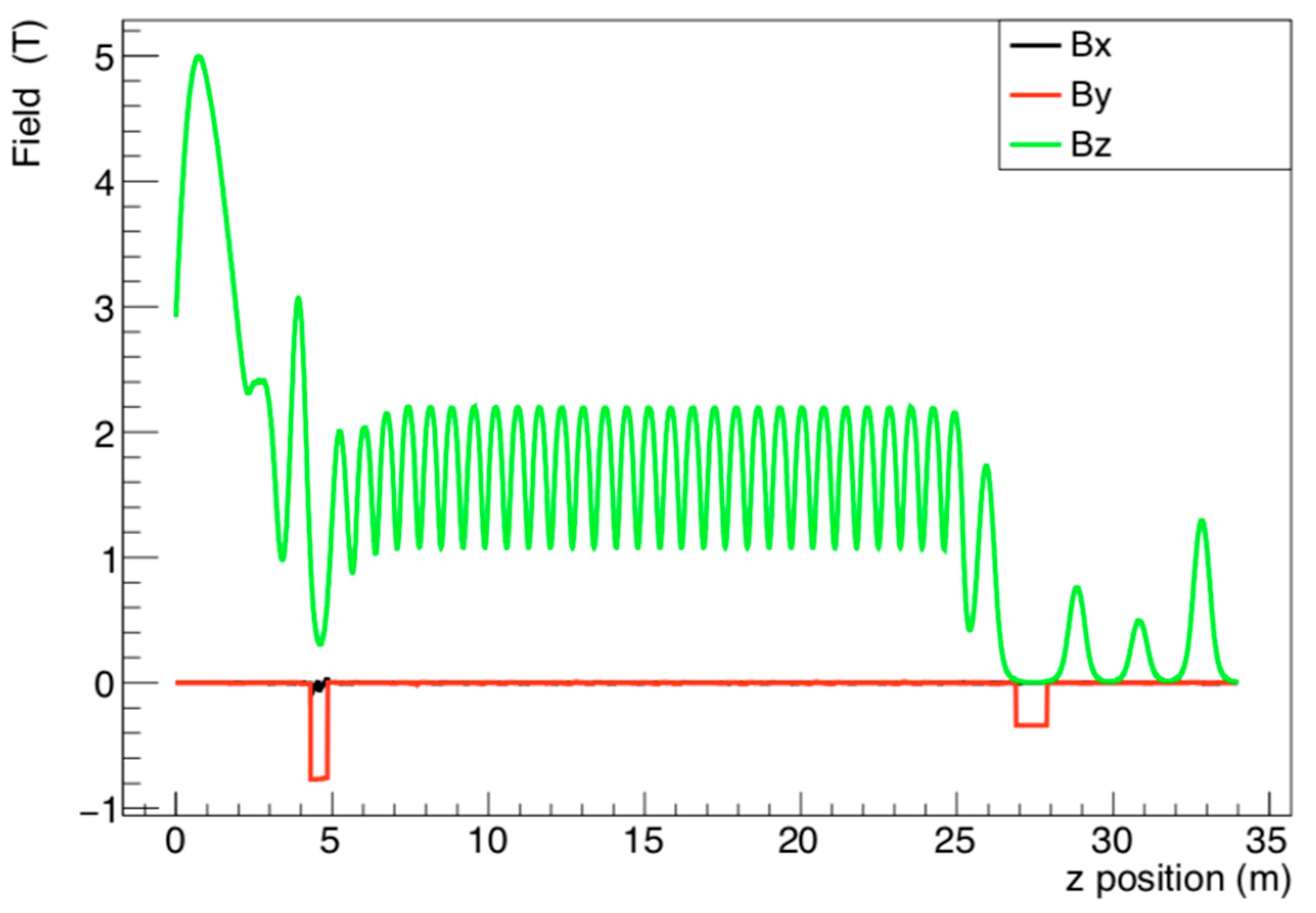
2.3. Muon Target Station
2.4. Muon Transport Beamlines
3. μSR Spectrometers
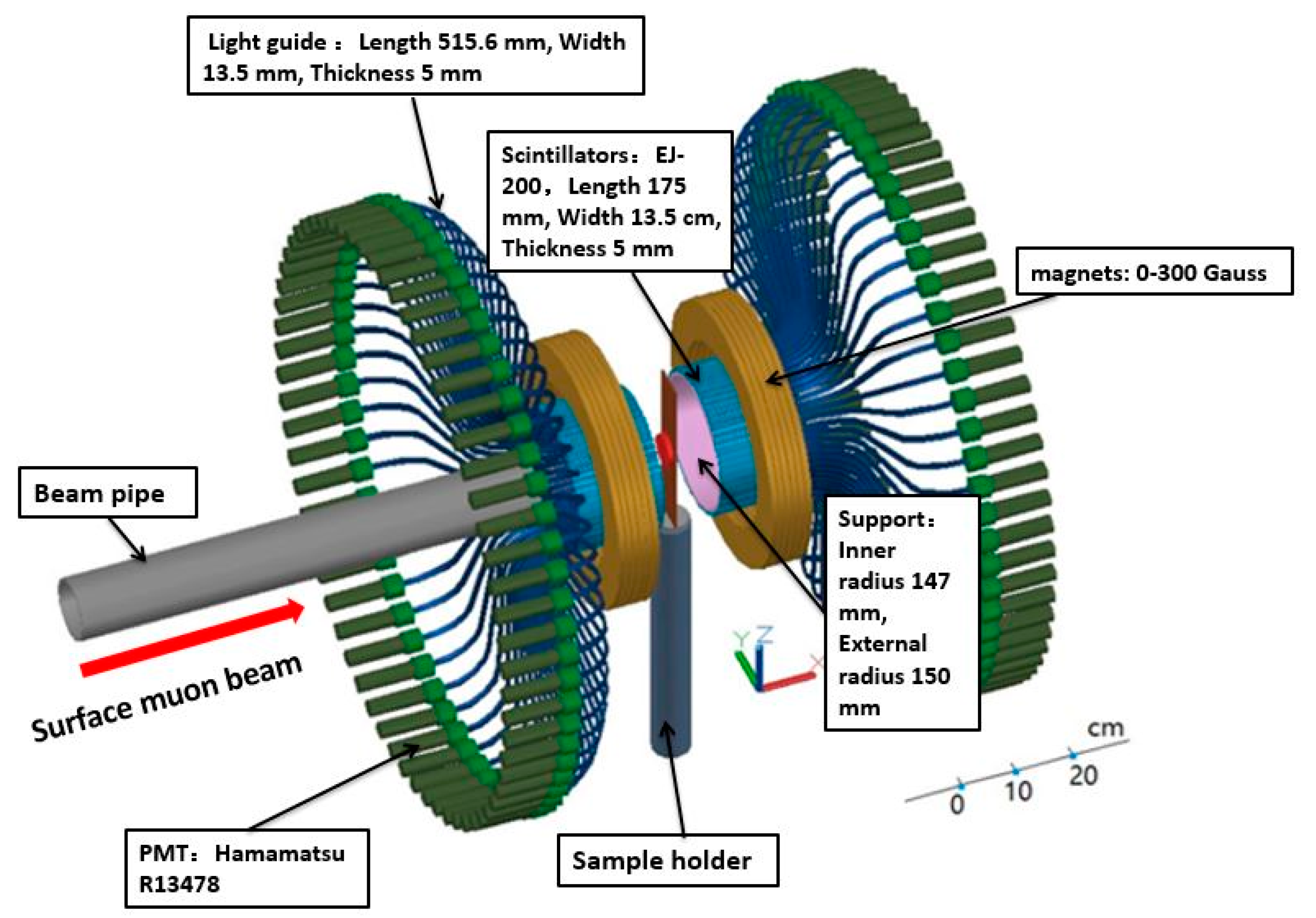
3.1. μSR Spectrometer Prototype for EMuS
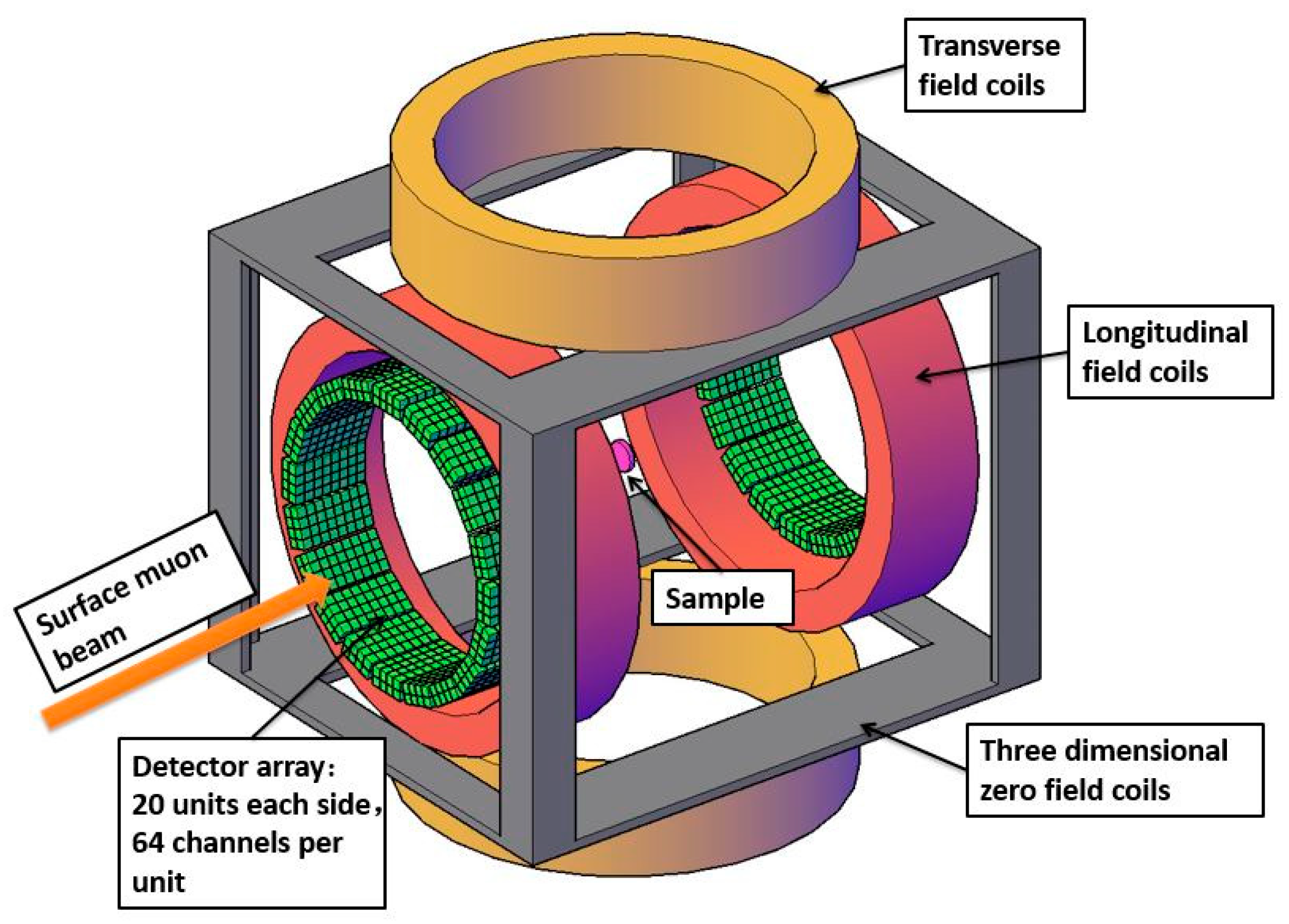
3.2. Design of a Super-μSR Spectrometer
4. Prospects in Magnetism Study at EMuS
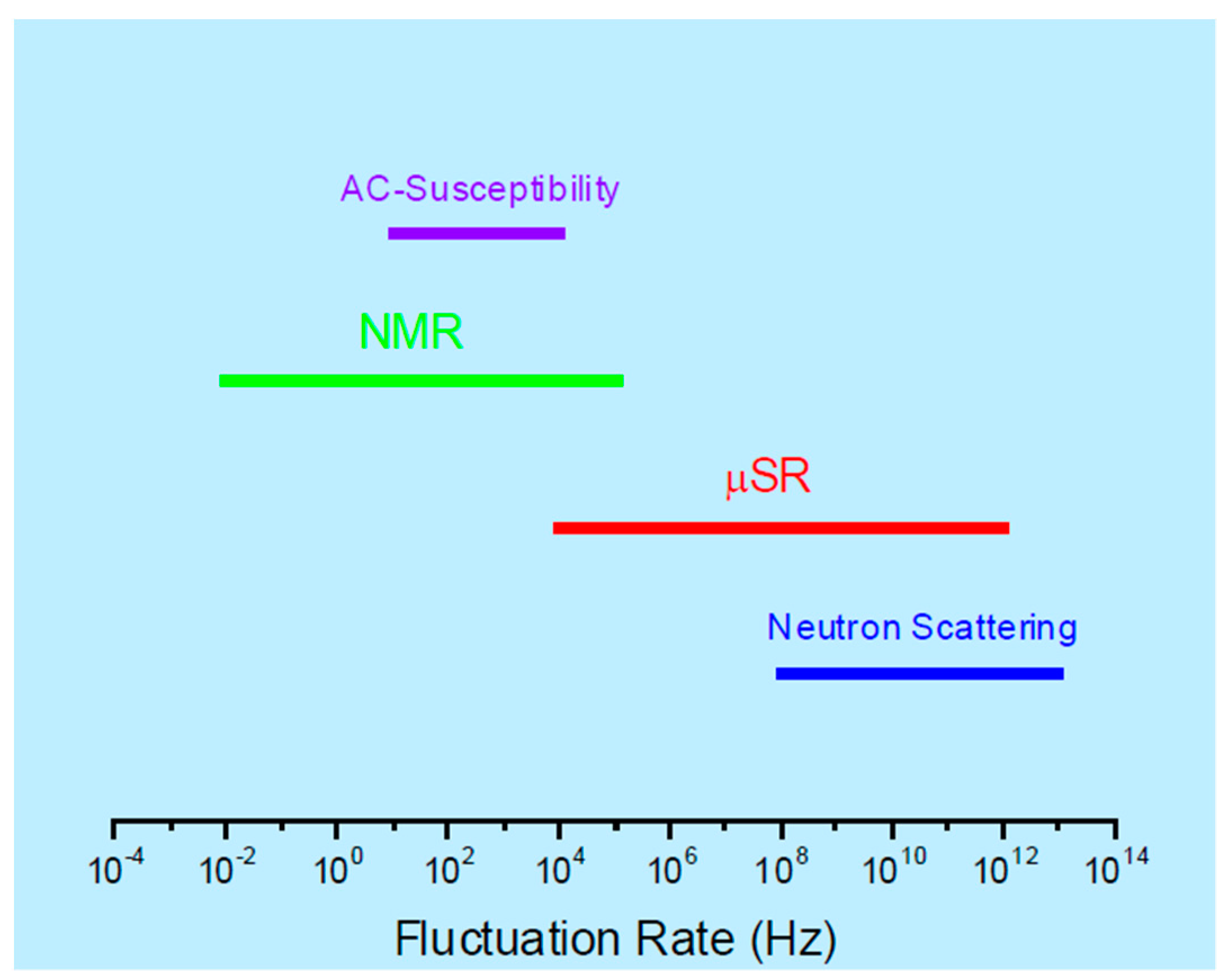
4.1. Comparison between μSR and Other Probes for Magnetism
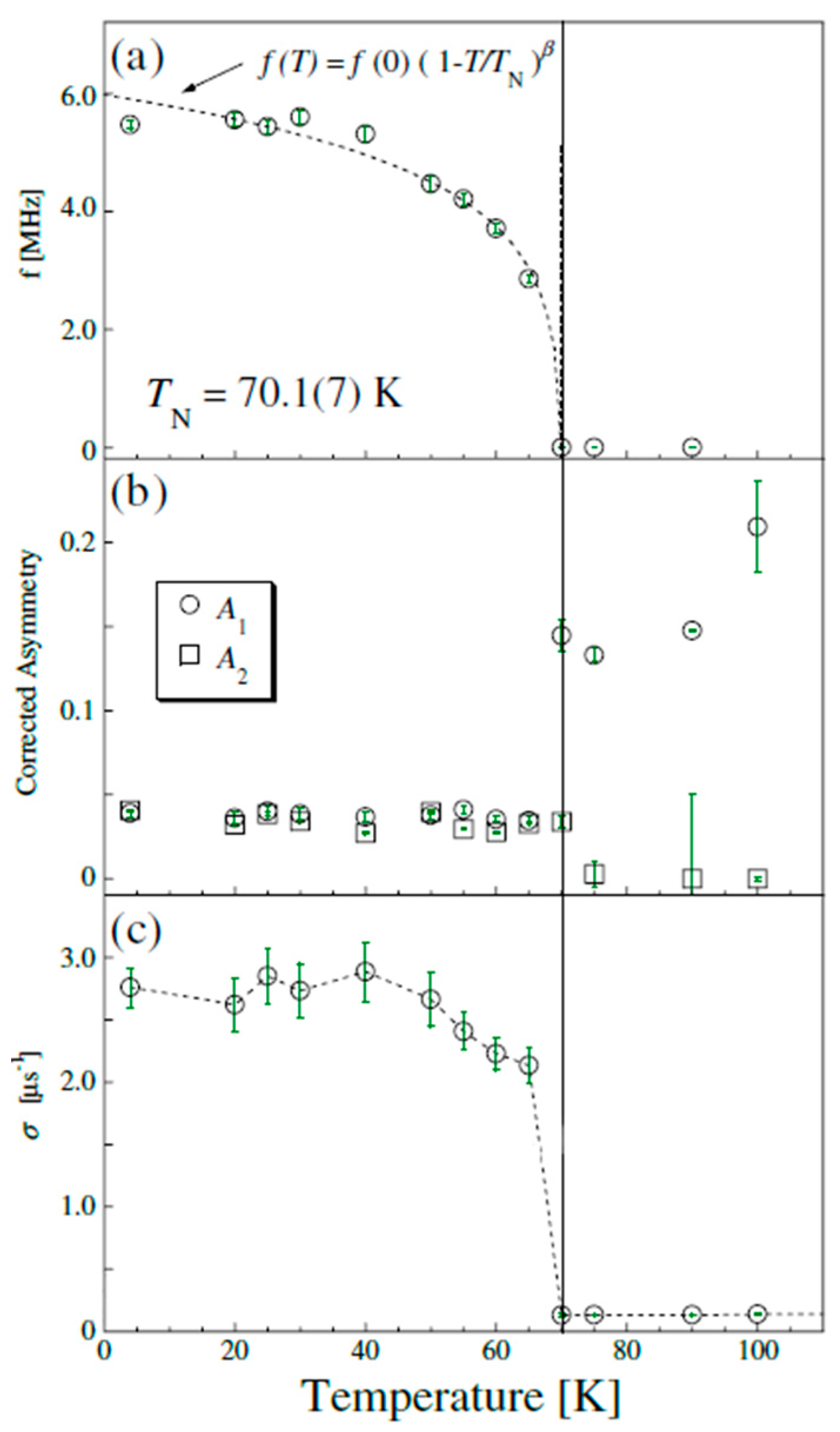
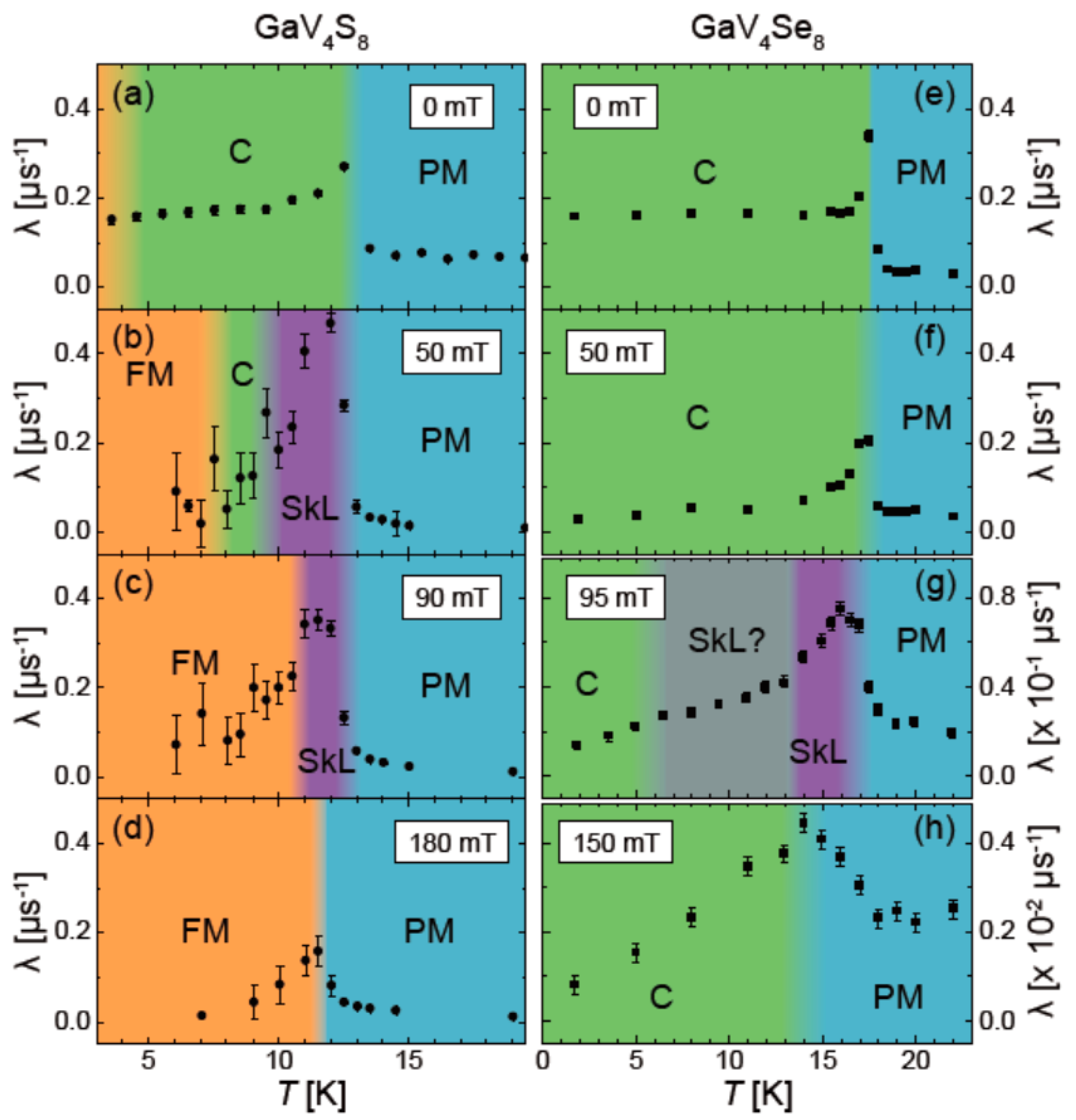
4.2. μSR Study on Magnetically Ordered Materials
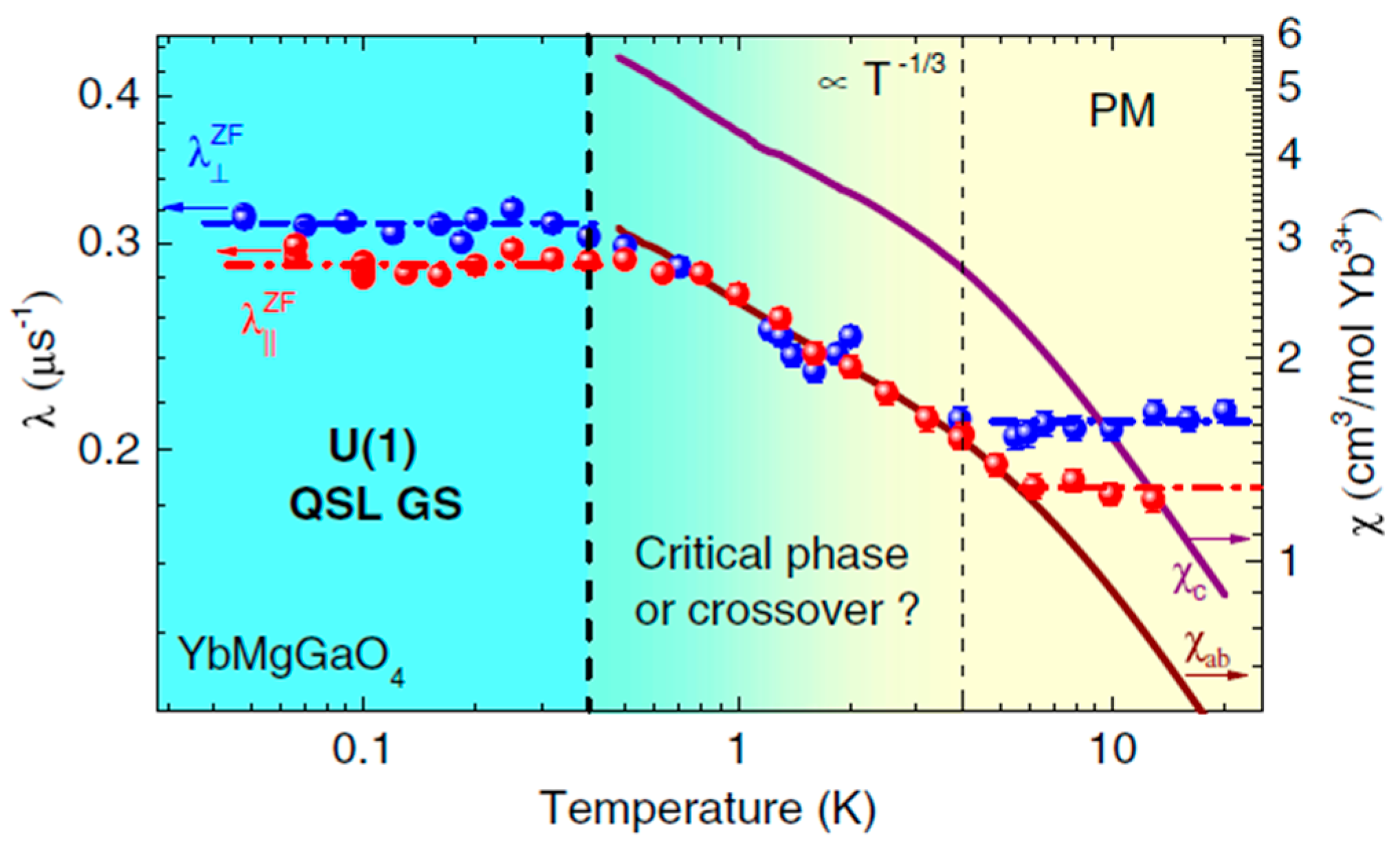
4.3. μSR Study on Quantum Spin Liquid Materials
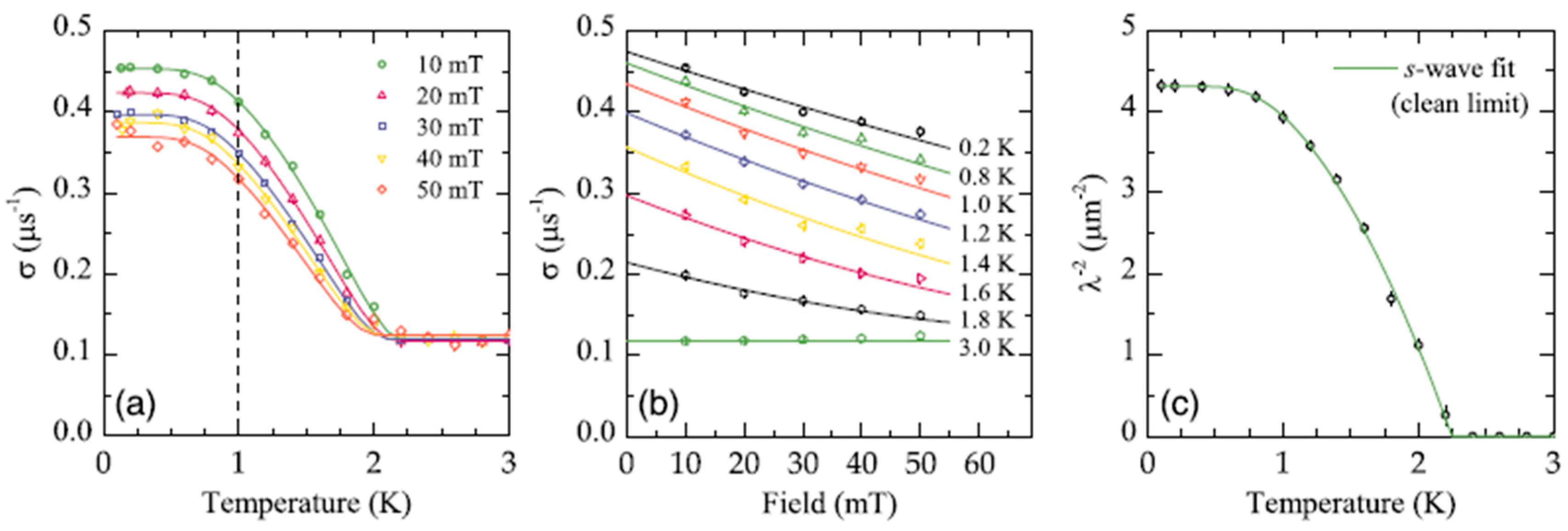
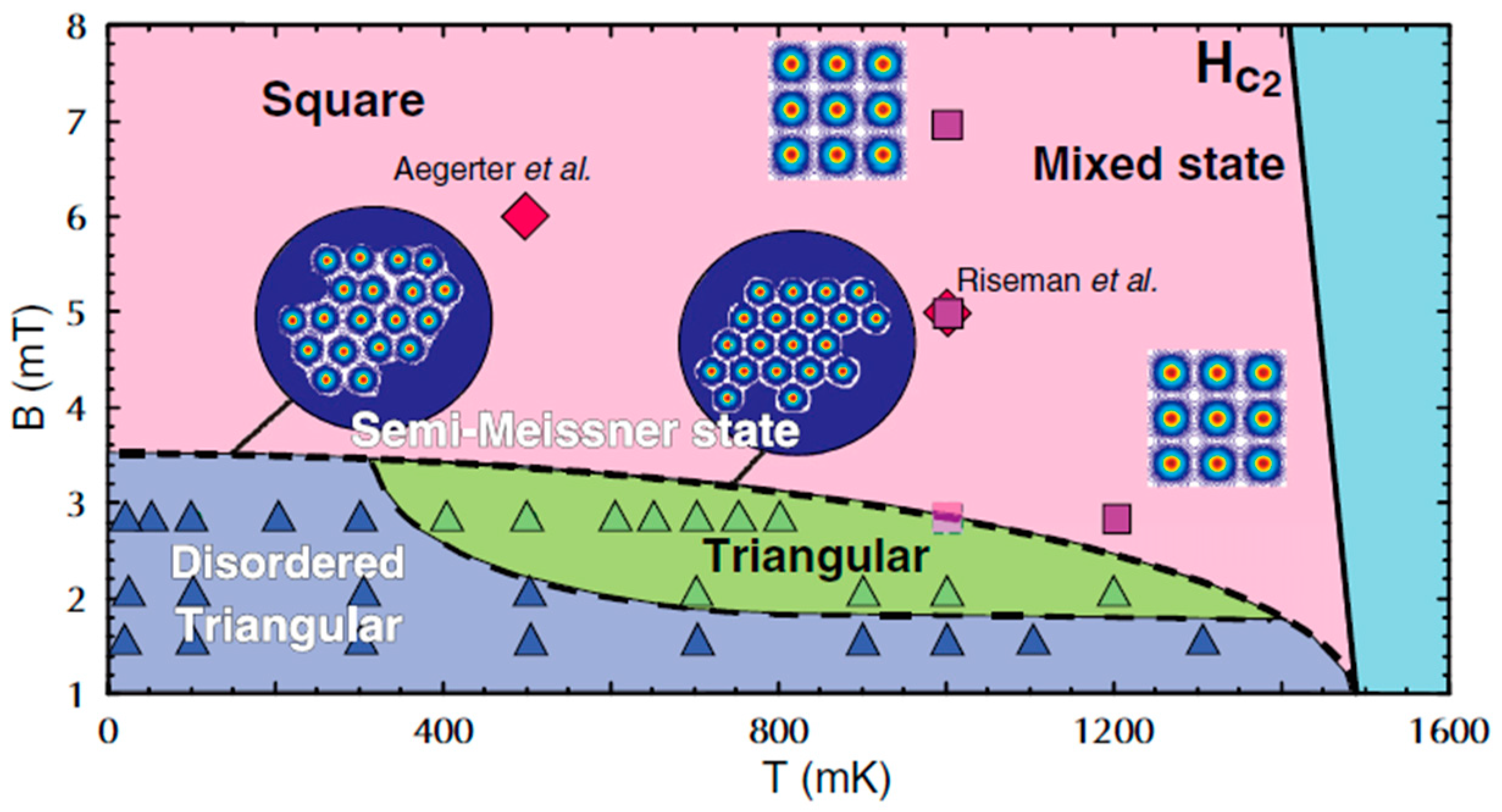
4.4. μSR Studies on Superconducting Materials
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schenck, A. Muon Spin Rotation Spectroscopy; Adam Hilger: Bristol, UK, 1985. [Google Scholar]
- Yaouanc, A.; Dalmas de Réotier, P. Muon Spin Rotation, Relaxation and Resonance: Applications to Condensed Matter; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- de Réotier, P.D.; Yaouanc, A. Muon spin rotation and relaxation in magnetic materials. J. Phys. Condens. Matter 1997, 9, 9113–9166. [Google Scholar] [CrossRef]
- PSI-LMU: Laboratory for Muon Spin Spectroscopy. Available online: https://www.psi.ch/lmu/ (accessed on 1 November 2018).
- TIUMF Centre for Molecular and Materials Science. Available online: http://cmms.triumf.ca/ (accessed on 1 November 2018).
- ISIS Muons. Available online: https://www.isis.stfc.ac.uk/Pages/Muons.aspx (accessed on 1 November 2018).
- J-PARC/MUSE. Available online: http://www.j-parc.jp/MatLife/en/index.html (accessed on 1 November 2018).
- RCNP-MuSIC. Available online: http://www.rcnp.osaka-u.ac.jp/RCNPhome/music/ (accessed on 1 November 2018).
- Tang, J.Y.; Fu, S.N.; Wei, J. Characteristics and potential applications of the proton beams at the CSNS. J. Korean Phys. Soc. 2008, 52, 710–713. [Google Scholar] [CrossRef]
- Jing, H.T.; Meng, C.; Tang, J.Y.; Ye, B.J.; Sun, J.L. Production target and muon collection studies for an experimental muon source at CSNS. Nucl. Instrum. Meth. A 2012, 684, 109–116. [Google Scholar] [CrossRef]
- Xiao, R.; Liu, Y.-F.; Xu, W.-Z.; Ni, X.-J.; Pan, Z.-W.; Ye, B.-J. A new muon-pion collection and transport system design using superconducting solenoids based on CSNS. Chin. Phys. C 2016, 40, 057004. [Google Scholar] [CrossRef]
- Won, E. A proposal muon facility in RAON/Korea. In Proceedings of the International Symposium Science Explored by Ultra Slow Muon (USM2013), Matsue, Japan, 9–12 August 2013; p. 010110. [Google Scholar]
- Akhmetshin, R.; Akuma, K.; Aoki, M.; Appleby, R.B.; Arimoto, Y.; Begaturia, Y.; Bertsche, W.; Bondar, A.; Bryman, D.; Chiladze, B.; et al. COMET Phase-1 Technical Design Report; KEK Report 2015-1. 2015. Available online: http://comet.kek.jp/Documents.html (accessed on 1 November 2018).
- Stoykov, A.; Scheuermann, R.; Sedlak, K.; Shiroka, T.; Zhuk, V. First experience with G-APDs in instrumentation. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2009, 610, 374–377. [Google Scholar] [CrossRef]
- Higemoto, W.; Kadono, R.; Kawamura, N.; Koda, A.; Kojima, K.M.; Makimura, S.; Matoba, S.; Miyake, Y.; Shimomura, K.; Strasser, P. Materials and life science experimental facility at the Japan proton accelerator research complex IV: The Muon facility. Quantum Beam Sci. 2017, 1, 11. [Google Scholar] [CrossRef]
- Salman, Z.; Baker, P.J.; Blundell, S.J.; Cottrell, S.P.; Giblin, S.R.; Hillier, A.D.; Holsman, B.H.; King, P.J.C.; Lancaster, T.; Lord, J.S.; et al. HiFi-A new high field muon spectrometer at ISIS. Phys. B Condens. Matter 2009, 404, 978–981. [Google Scholar] [CrossRef]
- Blundell, S.J. Spin-polarized muons in condensed matter physics. Contemp. Phys. 1999, 40, 175–192. [Google Scholar] [CrossRef]
- Kawashima, K.; Okabe, H.; Suzuki, K.; Kuroiwa, S.; Akimitsu, J.; Sato, K.H.; Koda, A.; Kadono, R. Antiferromagnetic ordering in Cu2OCl2 studied by the muon spin rotation/relaxation technique. J. Phys. Condens. Matter 2007, 19, 145275. [Google Scholar] [CrossRef]
- Major, J.; Mundy, J.; Schmolz, M.; Seeger, A.; Doring, K.P. Zero-field muon spin rotation in monocrystalline chromium. Hyp. Int. 1986, 31, 259. [Google Scholar] [CrossRef]
- Amato, A. Heavy-fermion systems studied by μSR technique. Rev. Mod. Phys. 1997, 69, 1119–1179. [Google Scholar] [CrossRef]
- Müller, H.; Kockelmann, W.; Johrendt, D. The magnetic structure and electronic ground states of mott insulators GeV4S8 and GaV4S8. Chem. Matter 2006, 18, 2174–2180. [Google Scholar] [CrossRef]
- Lancaster, T.; Williams, R.C.; Thomas, I.O.; Xiao, F.L.; Pratt, F.L.; Blundell, S.J.; Loudon, J.C.; Hesjedal, T.; Clarck, S.J.; Hatton, P.D.; et al. Transverse field muon-spin rotation signature of the skyrmion-lattice phase in Cu2OSeO3. Phys. Rev. B 2015, 91, 224408. [Google Scholar] [CrossRef]
- Ogielski, A.T. Dynamics of three-dimensional Ising spin glasses in thermal equilibrium. Phys. Rev. B 1985, 32, 7384. [Google Scholar] [CrossRef]
- Brown, P.; Smith, G.N.; Hernández, E.P.; James, C.; Eastoe, J.; Nunes, W.C.; Settens, C.M.; Hatton, T.A.; Baker, P.J. Magnetic surfactants as molecular based-magnets with spin glass-like properties. J. Phys. Condens. Matter 2016, 28, 176002. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Adroja, D.; Biswas, P.K.; Baker, P.J.; Zhang, Q.; Liu, J.; Tsirlin, A.A.; Gegenwart, P.; Zhang, Q. Muon spin relaxation evidence for the U(1) quantum spin-liquid ground state in the triangular antiferromagnet YbMgGaO4. Phys. Rev. Lett. 2016, 117, 097201. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Feng, Z.; Lohstroh, W.; Dela Cruz, C.; Yi, F.; Ding, Z.F.; Zhang, J.; Tan, C.; Shu, L.; Wang, Y.-C.; et al. Evidence for a Z2 topological ordered quantum spin liquid in a kagome-lattice antiferromagnet. arXiv, 2017; arXiv:1710.02991. [Google Scholar]
- Quilliam, J.A.; Bert, F.; Manseau, C.; Darie, C.; Guillot/Deudon, C.; Payen, C.; Baines, C.; Amato, A.; Mendels, P. Gapless quantum spin liquid ground state in the spin-1 antiferromagnet 6HB-Ba3NiSb2O9. Phys. Rev. B 2016, 93, 214432. [Google Scholar] [CrossRef]
- Sibille, R.; Lhotel, E.; Pomjakushin, V.; Baines, C.; Fennell, T.; Kenzelmann, M. Candidate quantum spin liquid in the Ce3+ pyrochlore stannate Ce2Sn2O7. Phys. Rev. Lett. 2015, 115, 097202. [Google Scholar] [CrossRef] [PubMed]
- Khasanov, R.; Guguchia, Z. Probing the multi gap behavior within ‘11’ and ‘122’ families of iron based superconductors: The muon-spin rotation studies. Supercond. Sci. Technol. 2015, 28, 034003. [Google Scholar] [CrossRef]
- Fesenko, V.I.; Gorbunov, V.N.; Smilga, V.P. Analytical properties of muon polarization spectra in type-II superconductors and experimental data interpretation for mono- and polycrystalline HTSCs. Phys. C Supercond. 1991, 176, 551–558. [Google Scholar] [CrossRef]
- Brandt, E.H. Flux distribution and penetration depth measured by muon spin rotation in high-Tc superconductors. Phys. Rev. B 1988, 37, 2349–2352. [Google Scholar] [CrossRef]
- Zimmermann, P.; Keller, H.; Lee, S.L.; Savić, I.M.; Warden, M.; Zech, D.; Cubitt, R.; Forgan, E.M.; Kaldis, E.; Karpinski, J.; et al. Muon-spin-rotation studies of the temperature dependence of the magnetic penetration depth in the YBa2Cu3Ox family and related compounds. Phys. Rev. B 1995, 52, 541–552. [Google Scholar] [CrossRef]
- Khasanov, R.; Conder, K.; Pomjakushina, E.; Amato, A.; Baines, C.; Bukowski, Z.; Karpinski, J.; Katrych, S.; Klauss, H.-H.; Luetkens, H.; et al. Evidence of nodeless superconductivity in FeSe0.85 from a muon-spin-rotation study of the in-plane magnetic penetration depth. Phys. Rev. B 2008, 78, 220510. [Google Scholar] [CrossRef]
- Barker, J.A.T.; Singh, D.; Thamizhavel, A.; Hiller, A.D.; Lees, M.R.; Balakrishnan, G.; Paul, D.M.; Singh, R.P. Unconventional superconductivity in La7Ir3 revealed by muon spin relaxation: Introducing a new family of noncentrosymmetric superconductor that breaks time-reversal symmetry. Phys. Rev. Lett. 2015, 115, 267001. [Google Scholar] [CrossRef] [PubMed]
- Ray, S.J.; Gibbs, A.S.; Bending, S.J.; Curran, P.J.; Babaev, E.; Baines, C.; Mackenzie, A.P.; Lee, S.L. Muon-spin rotation measurements of the vortex state in Sr2RuO4: Type-1.5 superconductivity, vortex clustering, and a crossover from a triangular to a square vortex lattice. Phys. Rev. B 2014, 89, 094504. [Google Scholar] [CrossRef]
| Surface Muon | Decay Muon (High Polarization) | Decay Muon (High Momentum) | |
|---|---|---|---|
| Momentum (MeV/c) | 28 | 130 | 450 |
| Intensity (1 × 106/s) | 43 | 100 | 50 |
| Polarization (%) | −77 | 68 | −30 |
| Δp/p (±%) | 12 | 9 | 10 |
| Emittance (πmm-rad) | 30 | 30 | 30 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Ni, X.; Ma, X.; Luo, H.; Bao, Y.; Yuan, Y.; Chen, Y.; Chen, Y.; Deng, F.; Dong, J.; et al. EMuS Muon Facility and Its Application in the Study of Magnetism. Quantum Beam Sci. 2018, 2, 23. https://doi.org/10.3390/qubs2040023
Tang J, Ni X, Ma X, Luo H, Bao Y, Yuan Y, Chen Y, Chen Y, Deng F, Dong J, et al. EMuS Muon Facility and Its Application in the Study of Magnetism. Quantum Beam Science. 2018; 2(4):23. https://doi.org/10.3390/qubs2040023
Chicago/Turabian StyleTang, Jingyu, Xiaojie Ni, Xiaoyan Ma, Huiqian Luo, Yu Bao, Ye Yuan, Yuan Chen, Yukai Chen, Fanshui Deng, Jingyu Dong, and et al. 2018. "EMuS Muon Facility and Its Application in the Study of Magnetism" Quantum Beam Science 2, no. 4: 23. https://doi.org/10.3390/qubs2040023
APA StyleTang, J., Ni, X., Ma, X., Luo, H., Bao, Y., Yuan, Y., Chen, Y., Chen, Y., Deng, F., Dong, J., Hou, Z., Hu, C., Jing, H., Liang, H., Mu, Q., Ning, C., Pan, Z., Song, Y., Tang, J., ... Zhuang, M. (2018). EMuS Muon Facility and Its Application in the Study of Magnetism. Quantum Beam Science, 2(4), 23. https://doi.org/10.3390/qubs2040023





