Design of an Energy Pile Based on CPT Data Using Soft Computing Techniques
Abstract
1. Introduction
2. Data Analysis
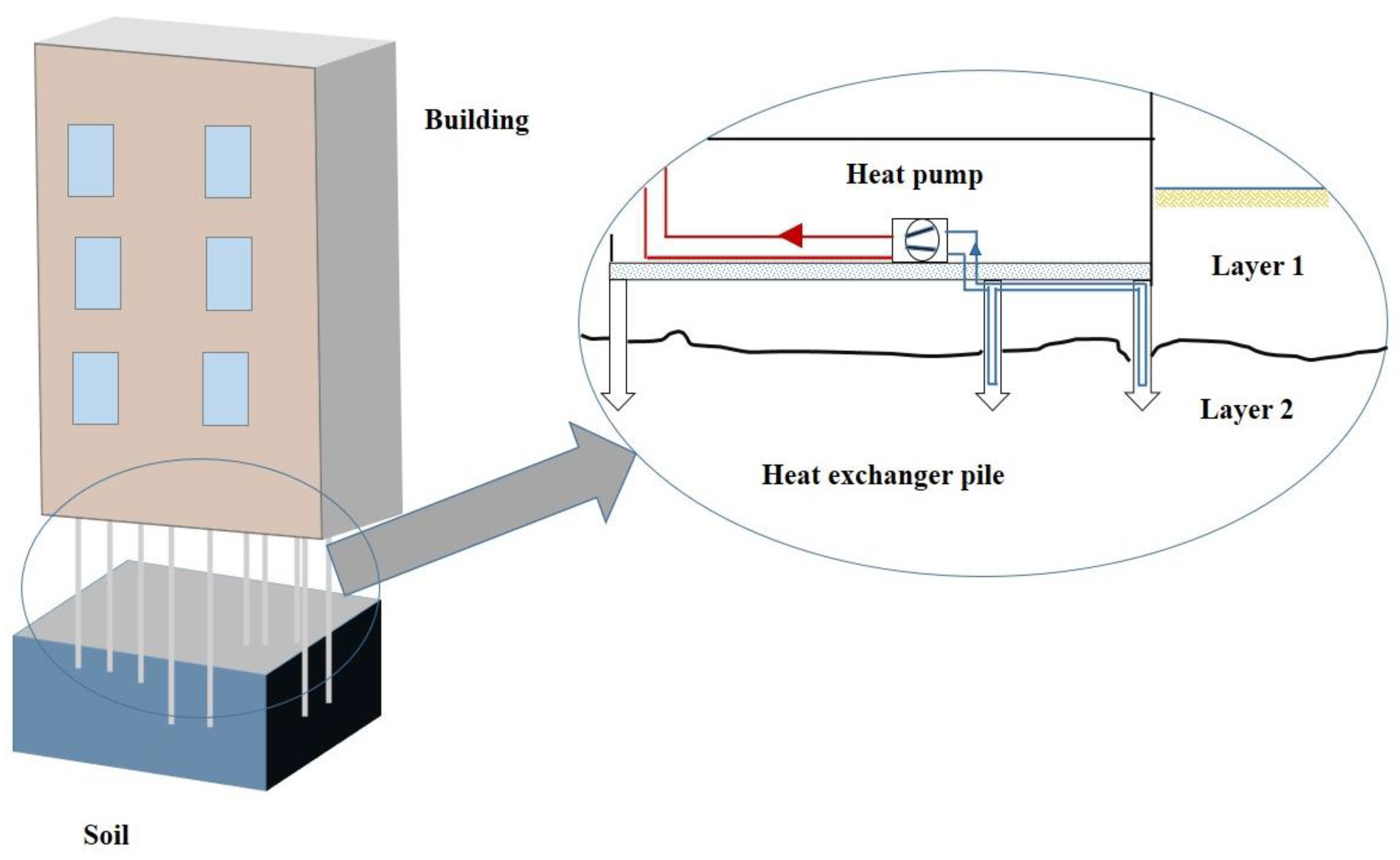
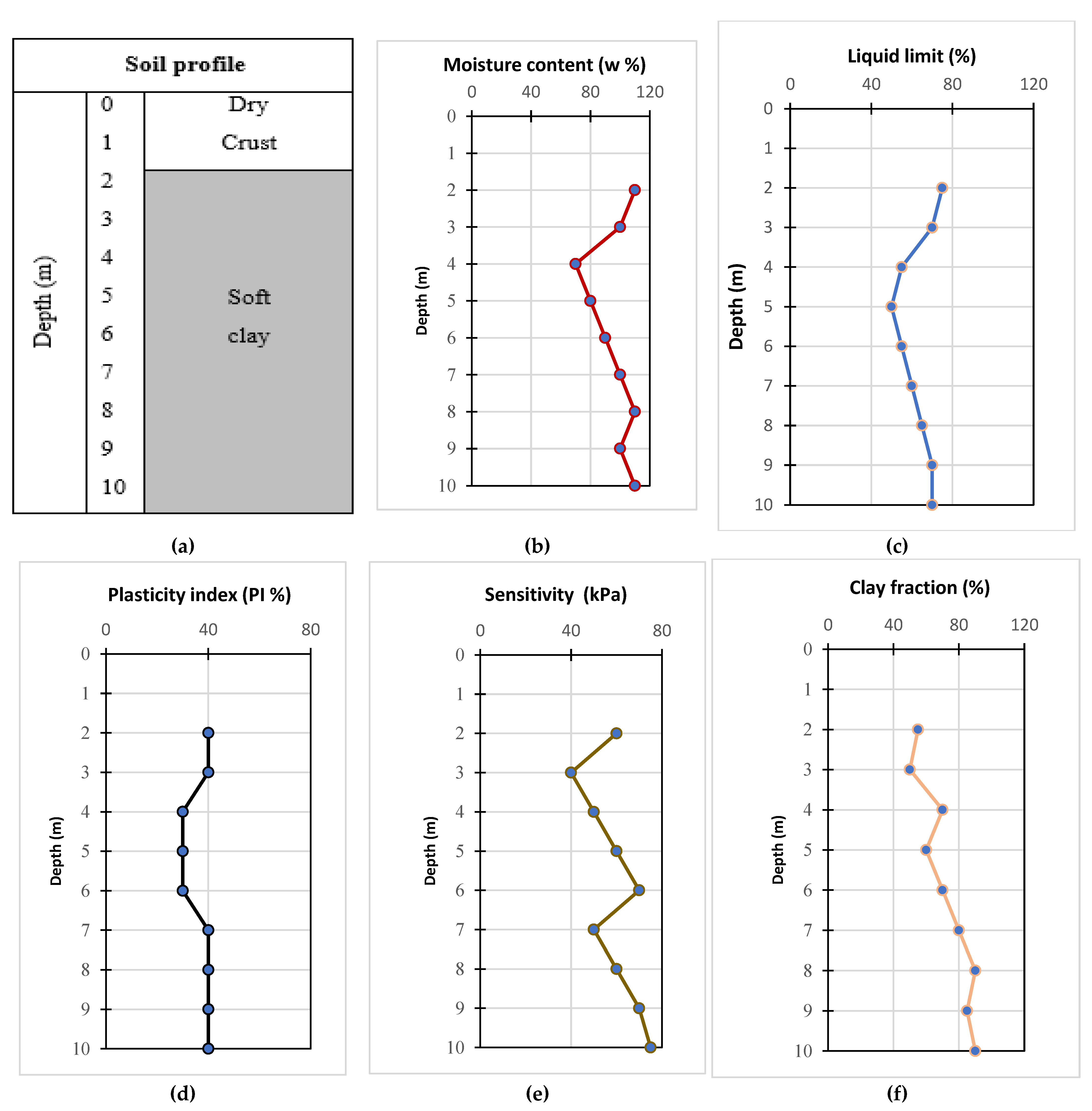
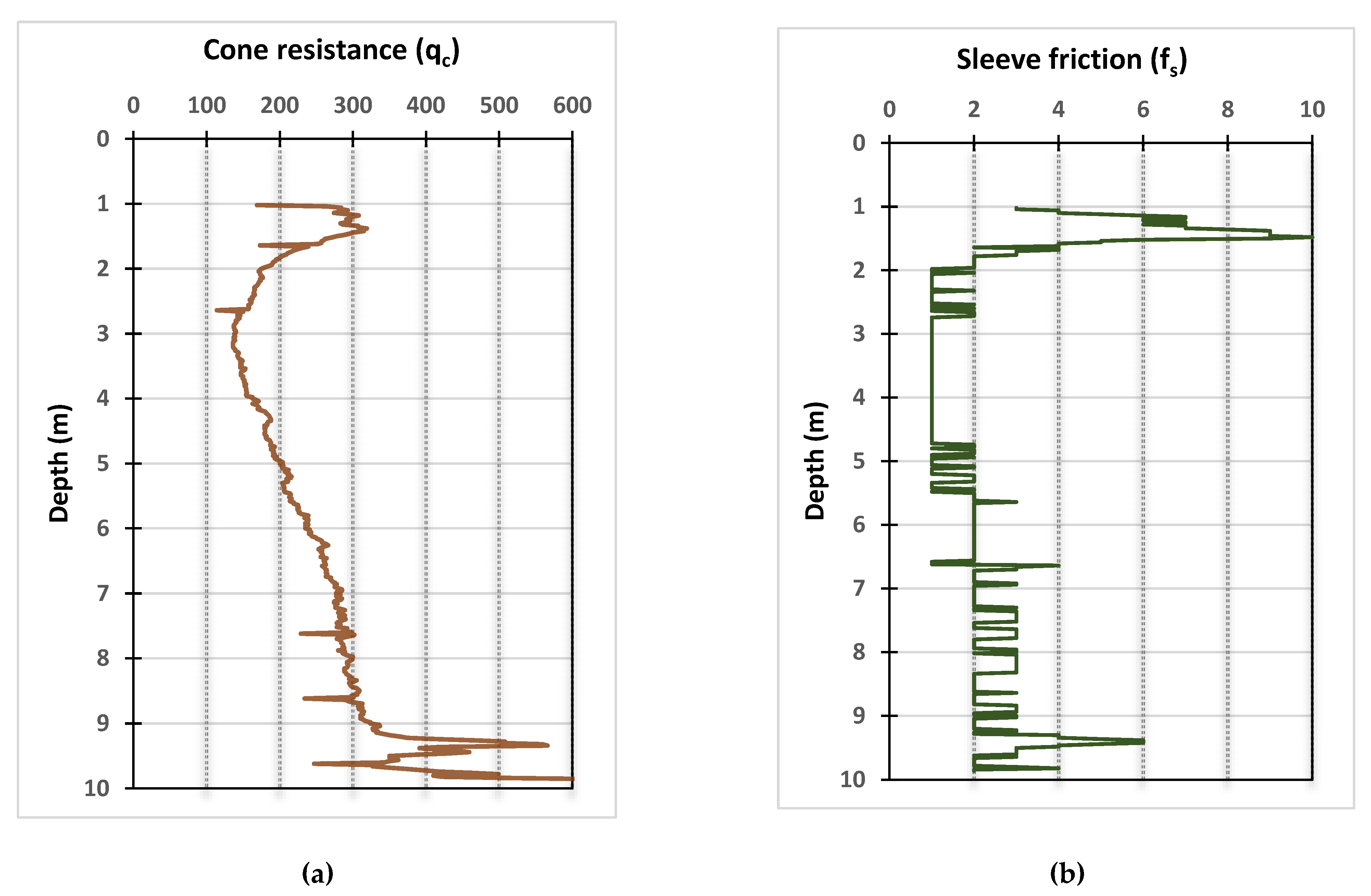
2.1. Database and Soil Characteristics
2.2. Energy Pile Characteristics
2.3. Thermal Characteristics
3. Methodology
3.1. Pile-Load-Capacity Determination
Indian Standard (Code of Practice for Design and Construction Pile Foundations), Part 1: Concrete Piles, Section 1: Driven Cast In-Situ Concrete Piles [20]
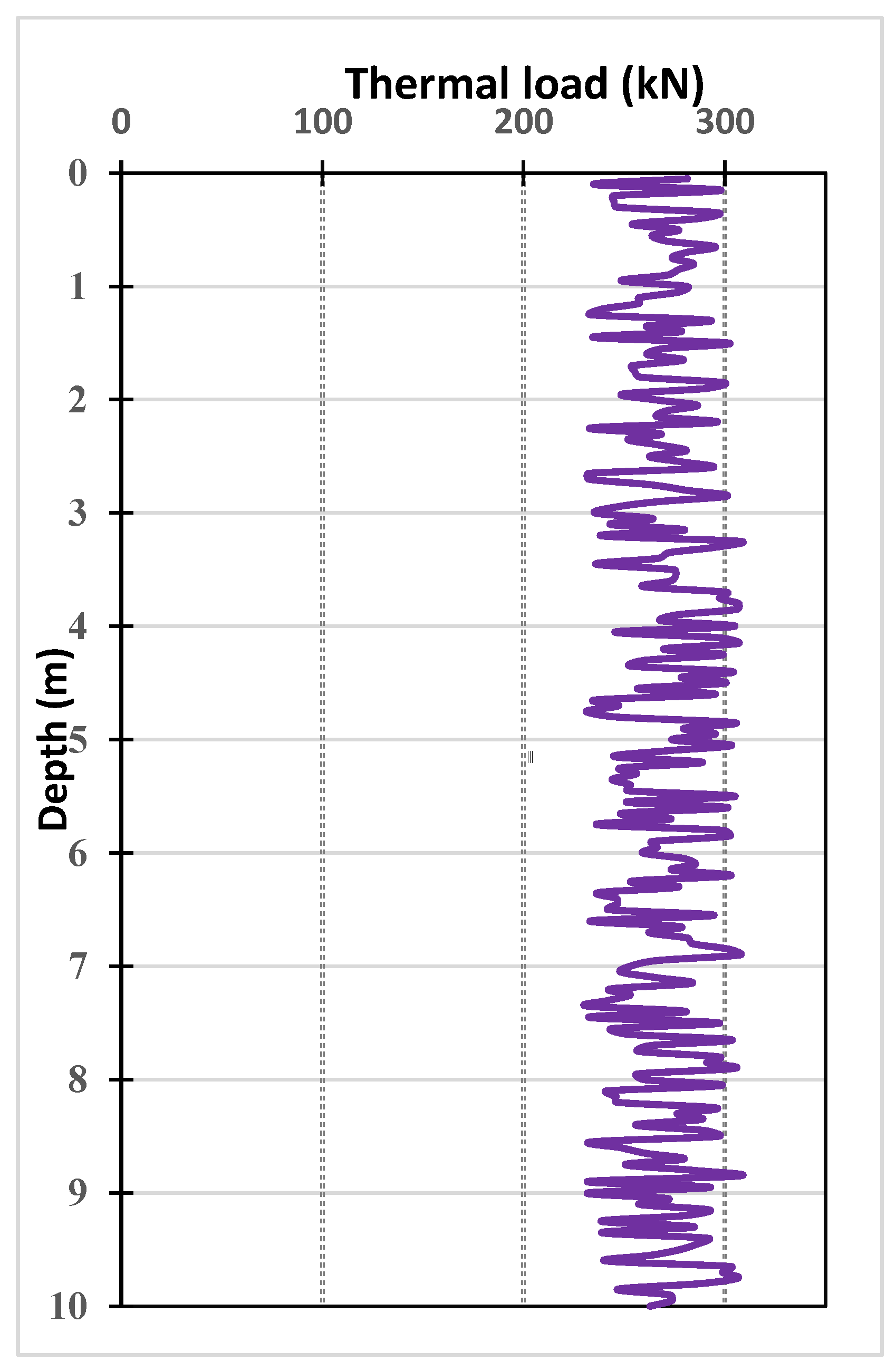
3.2. Thermal Load Determination
3.3. Group Capacity of Pile
3.4. Allowable Load on Piles
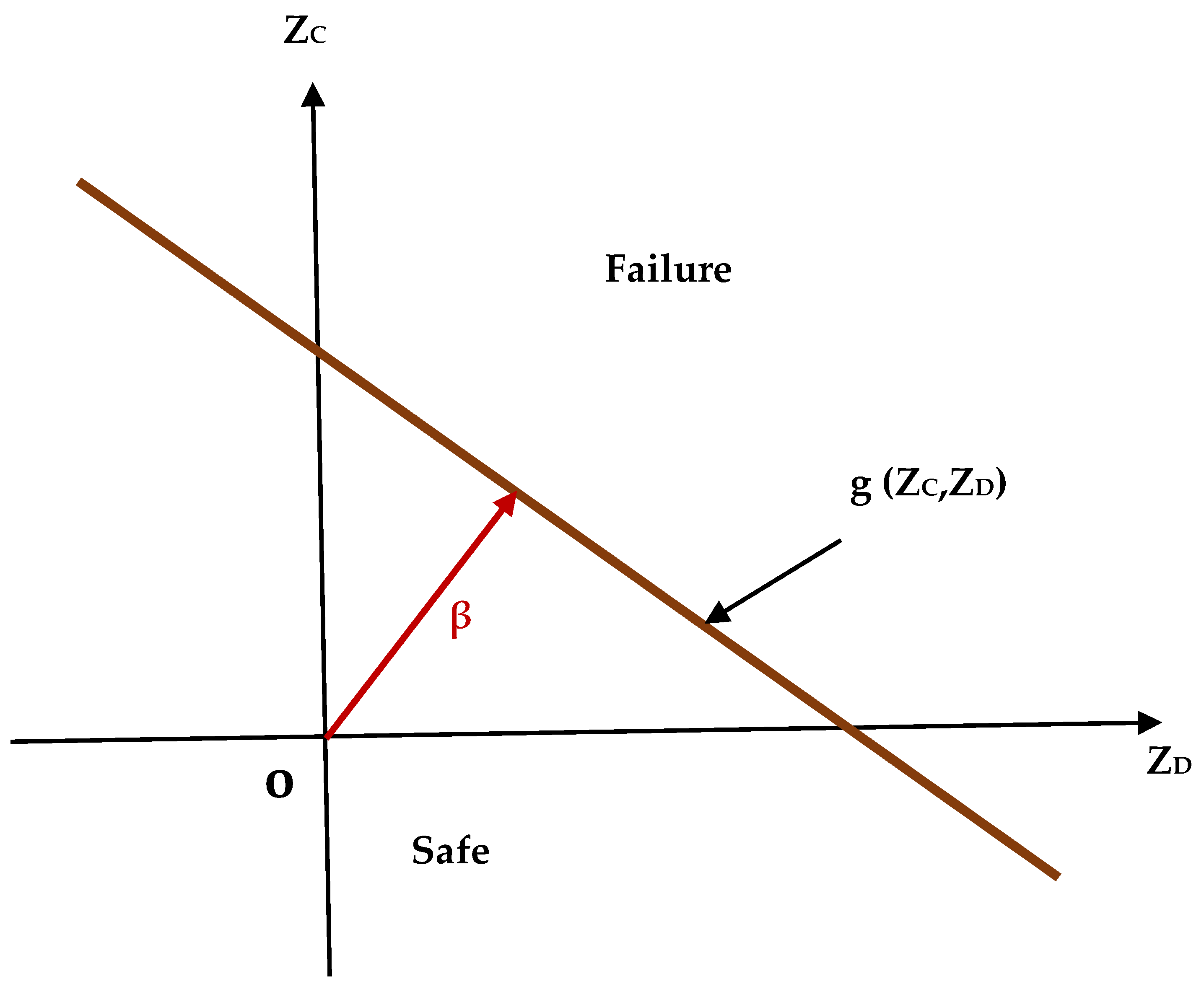
3.5. Reliability Analysis
3.6. Soft Computing Algorithms
3.6.1. Random Forest (RF) Algorithms
3.6.2. Support Vector Machine (SVM) Algorithms

3.6.3. Gradient Boosting Machine (GBM) Algorithms
3.6.4. Extreme Gradient Boosting (XGB) Algorithms
3.7. Performance Assessment
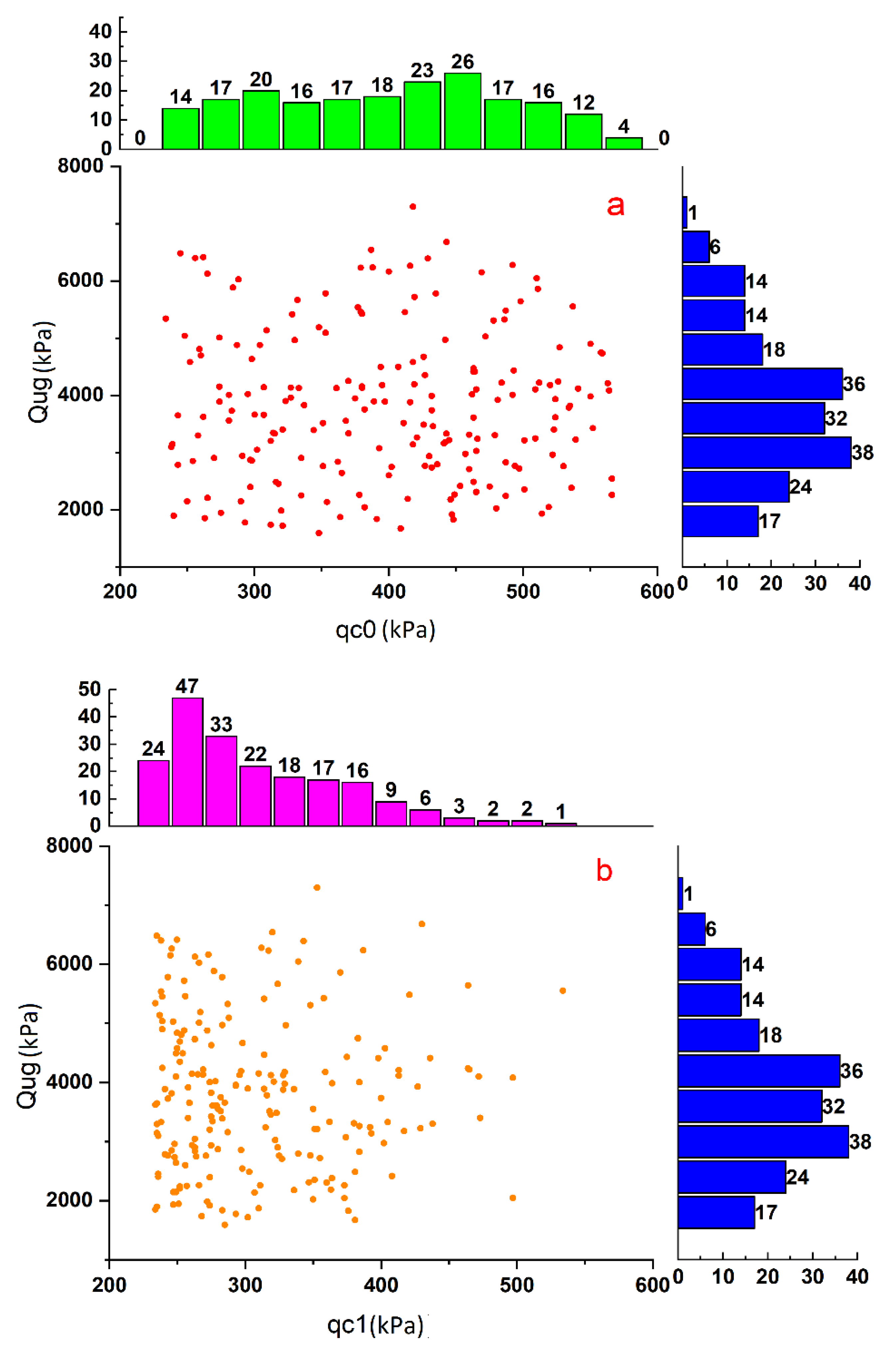
4. Data Preparation and Statistics
Statistical Plotting of the Variables
5. Data Preprocessing
6. Results and Discussion
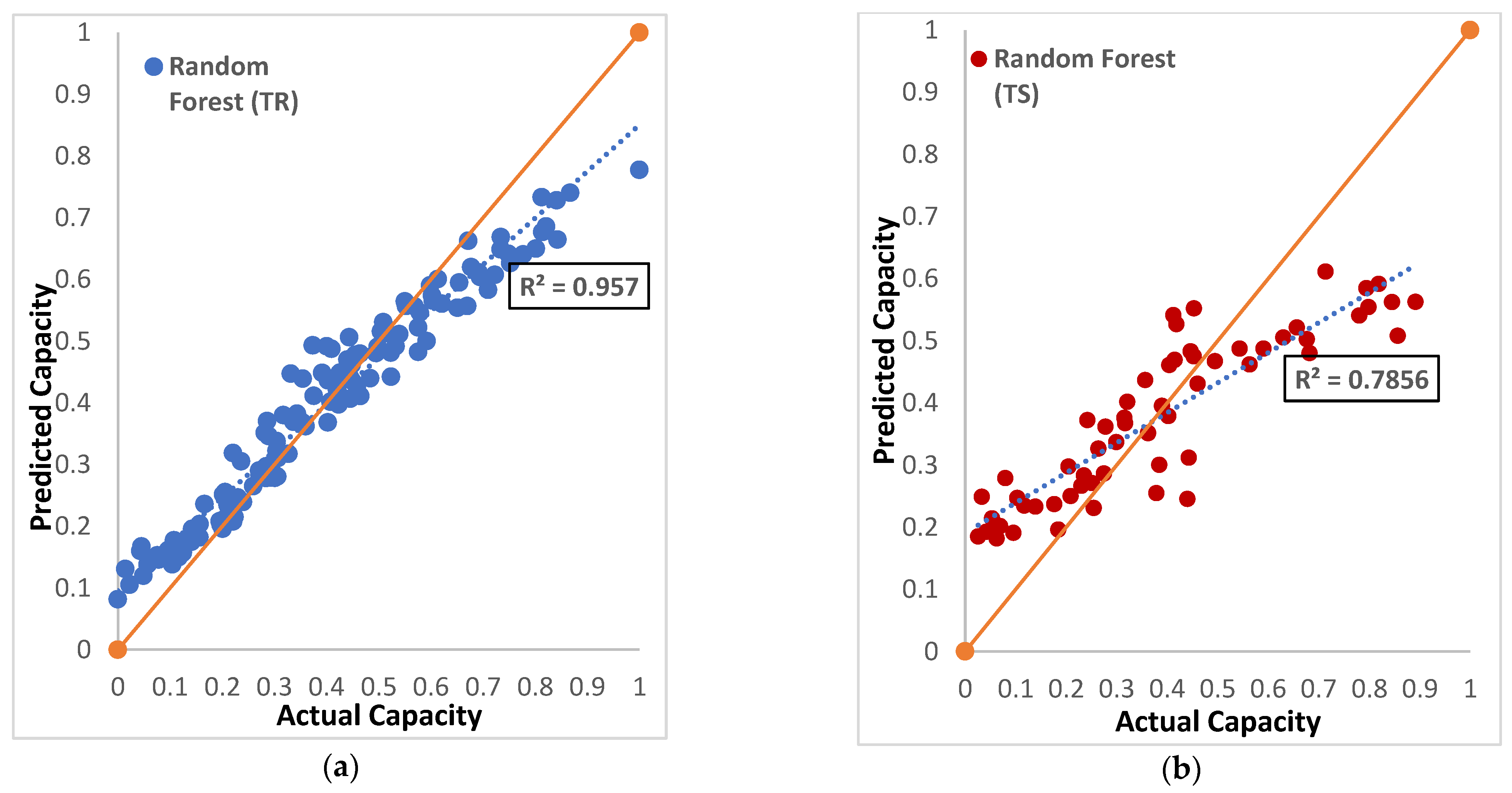
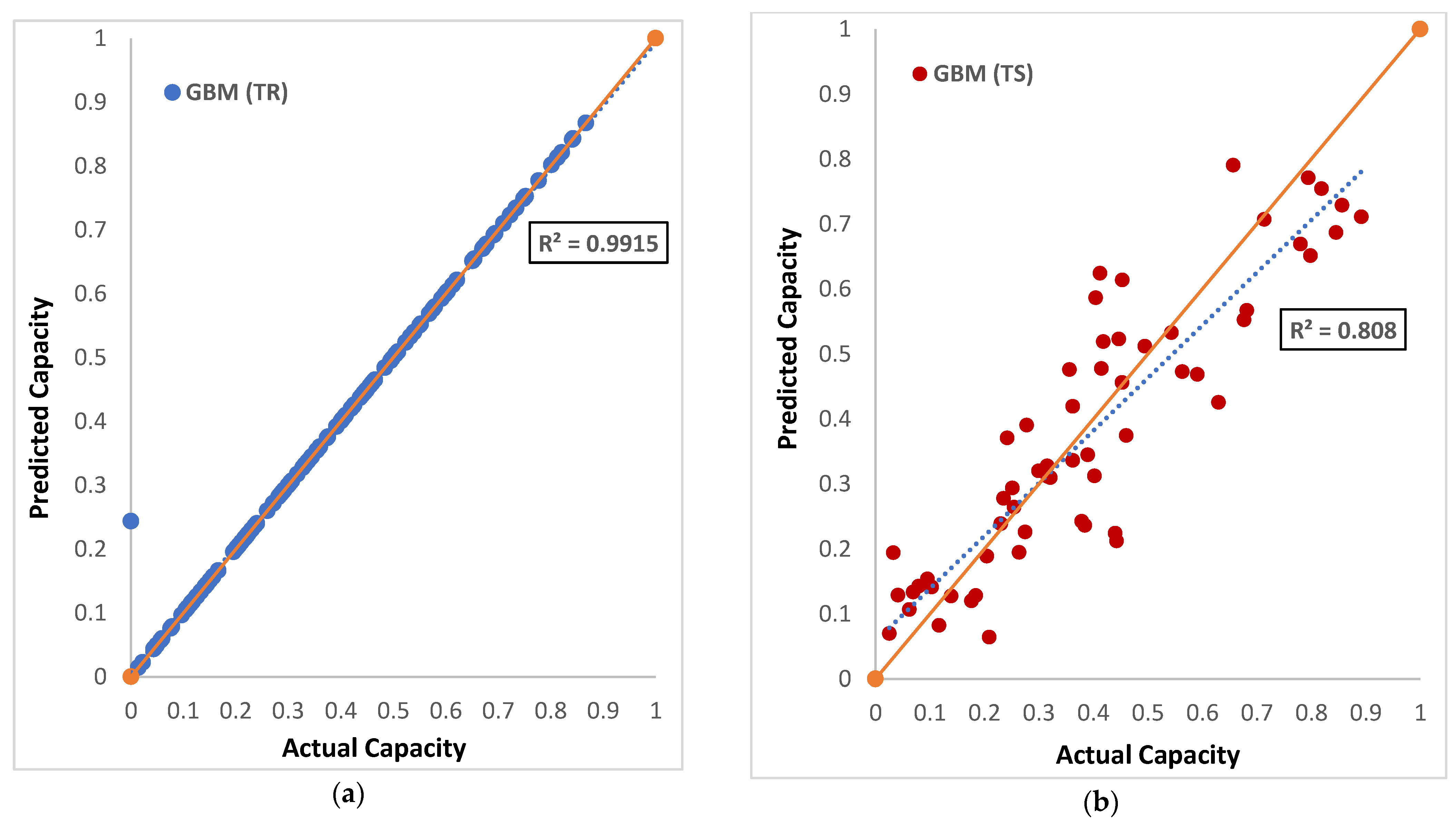
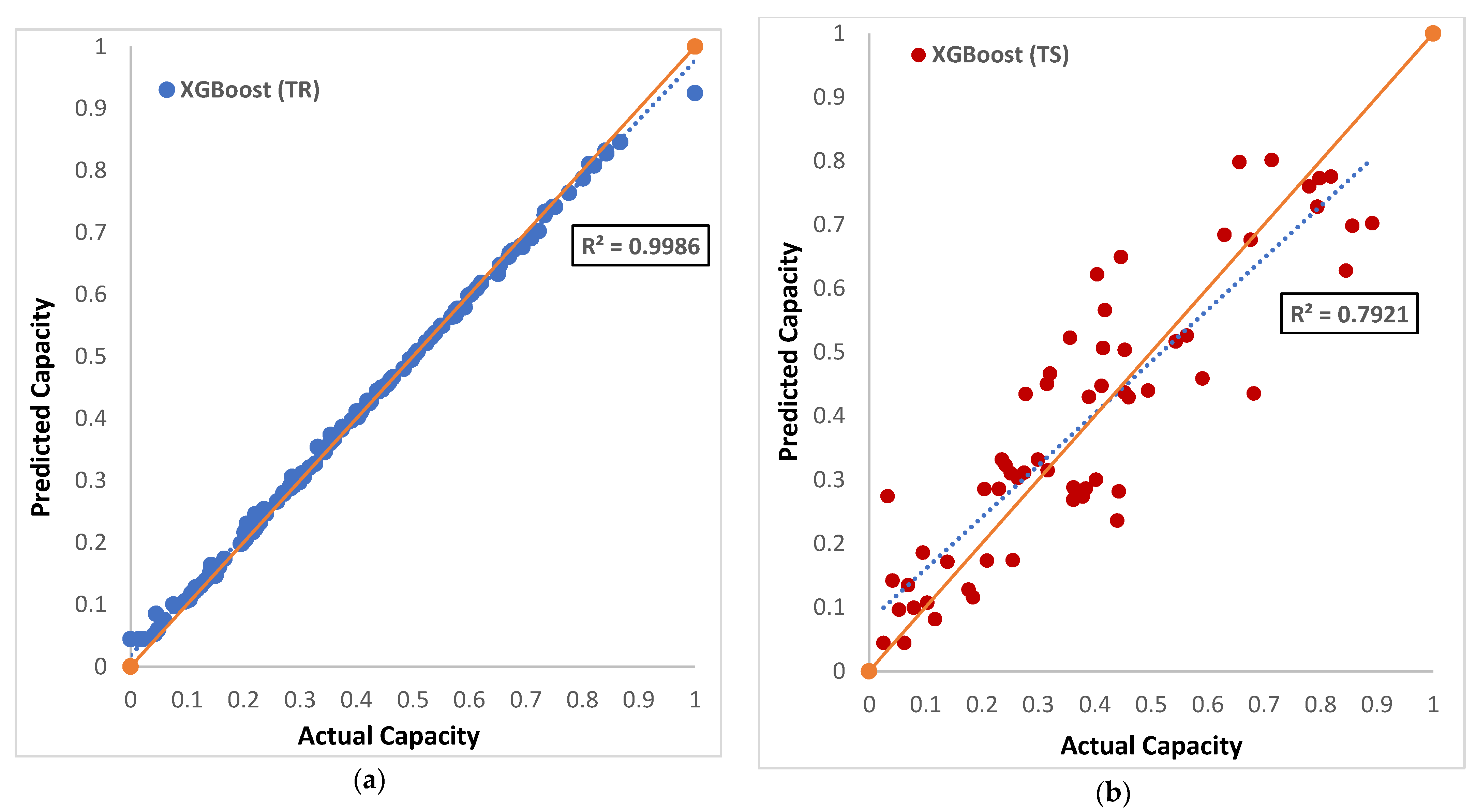
6.1. Models Regression Plot
6.2. Rank Analysis for Different Soft Computing Models
6.3. Error Matrix for Different Soft Computing Models
6.4. Taylor’s Diagram
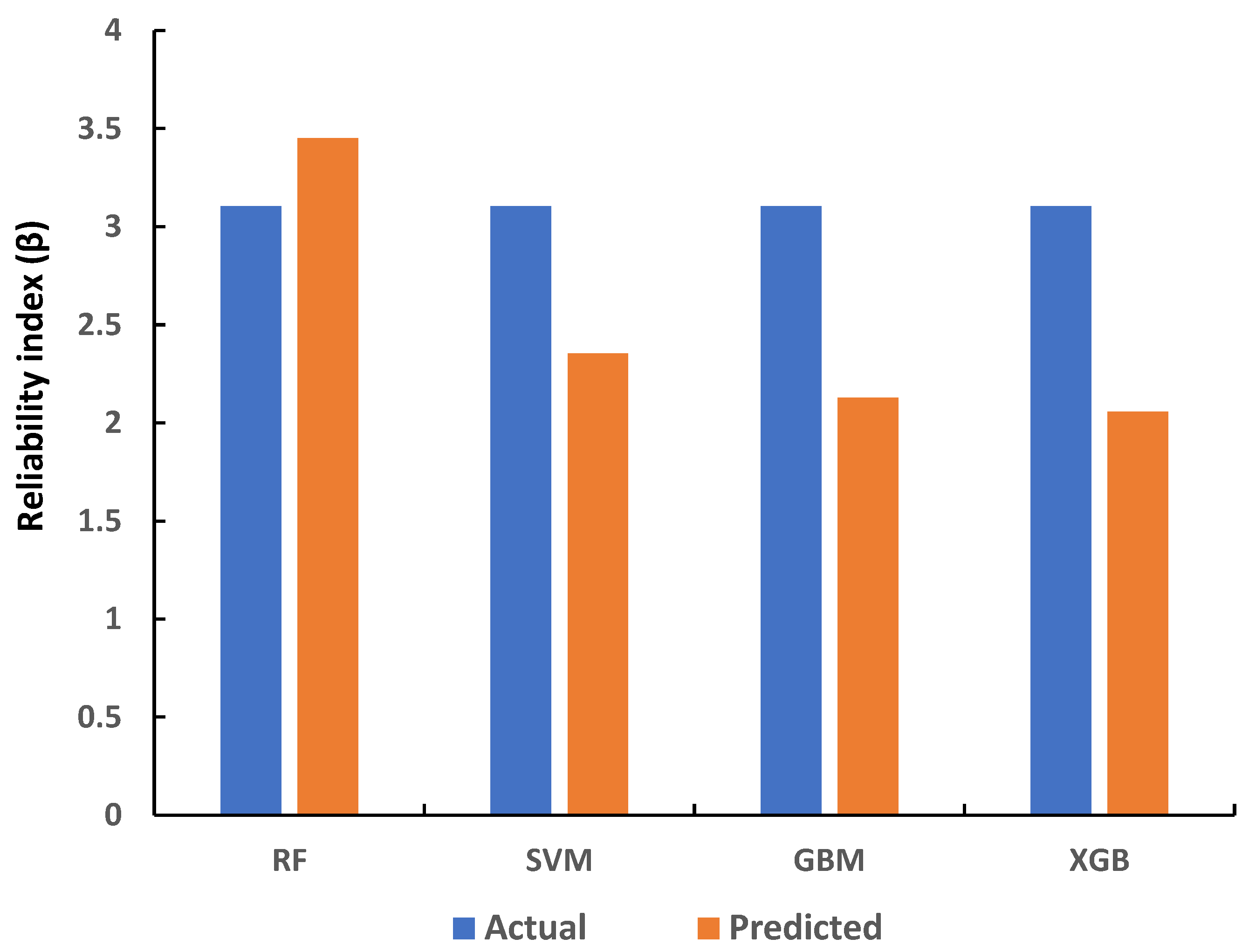
6.5. Reliability Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| CPT | Cone Penetration Test |
| RF | Random Forest |
| SVM | Support Vector Machine |
| GBM | Gradient Boosting Machine |
| XGB | Extreme Gradient Boosting |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
| MBE | Mean Biased Error |
| MAD | Median Absolute Deviation |
| WMAPE | Weighted Mean Absolute Percentage Error |
| GPI | Global Performance Indicator |
| TIC | Theil’s Inequality Index |
| IA | Index of Agreement |
| GSHP | Ground-Source Heat Pump |
| GHE | Ground-Heat Exchanger |
| HDPE | High-Density Polyethylene |
| COP | Coefficient of Performance |
| ML | Machine Learning |
| MLR | Multiple Linear Regression |
| ANN | Artificial Neural Networks |
| MARS | Multivariate Adaptive Regression Splines |
| HCF | Heat Carrier Fluid |
| GEP | Geothermal Energy Pile |
| TRT | Thermal Response Test |
| CART | Classification and Regression Trees |
| SRM | Structural Risk Minimization |
| ERM | Empirical Risk Minimization |
| DOF | Degree-of-Freedom |
| RI | Rank Index |
| FOS | Factor of Safety |
References
- Ahmed, A.A.; Assadi, M.; Kalantar, A.; Sliwa, T.; Sapińska-Śliwa, A. A Critical Review on the Use of Shallow Geothermal Energy Systems for Heating and Cooling Purposes. Energies 2022, 15, 4281. [Google Scholar] [CrossRef]
- Anongphouth, A. Investigating the Performance of Geothermal Energy Piles Using Coupled Thermo-Hydro-Mechanical Finite Element Analyses. Master’s Thesis, University of Manitoba, Winnipeg, MB, Canada, 2019. [Google Scholar]
- Kalogirou, S.A.; Florides, G.A. Measurements of Ground Temperature at Various Depths. In Proceedings of the 3rd International Conference on Sustainable Energy Technologies, Nottingham, UK, 28–30 June 2004. [Google Scholar]
- Çuhac, C.; Mäkiranta, A.; Välisuo, P.; Hiltunen, E.; Elmusrati, M. Temperature Measurements on a Solar and Low Enthalpy Geothermal Open-Air Asphalt Surface Platform in a Cold Climate Region. Energies 2020, 13, 979. [Google Scholar] [CrossRef]
- Amatya, B.L.; Soga, K.; Bourne-Webb, P.J.; Amis, T.; Laloui, L. Thermo-Mechanical Behaviour of Energy Piles. Géotechnique 2012, 62, 503–519. [Google Scholar] [CrossRef]
- Knellwolf, C.; Peron, H.; Laloui, L. Geotechnical Analysis of Heat Exchanger Piles. J. Geotech. Geoenviron. Eng. 2011, 137, 890–902. [Google Scholar] [CrossRef]
- Preene, M.; Powrie, W. Ground Energy Systems: From Analysis to Geotechnical Design. Géotechnique 2009, 59, 261–271. [Google Scholar] [CrossRef]
- Johnston, I.W.; Narsilio, G.A.; Colls, S. Emerging Geothermal Energy Technologies. KSCE J. Civ. Eng. 2011, 15, 643–653. [Google Scholar] [CrossRef]
- Narsilio, G.A.; Johnston, I.W.; Bidarmaghz, A.; Colls, S.; Mikhaylovaa, O.; Kivi, A.; Aditya, R. Geothermal Energy: Introducing an Emerging Technology. In Proceedings of the International Conference on Advances in Civil Engineering for Sustainable Development, Nakhon Ratchasima, Thailand, 27–29 August 2014. [Google Scholar]
- Lund, J.W.; Boyd, T.L. Direct Utilization of Geothermal Energy 2015 Worldwide Review. Geothermics 2016, 60, 66–93. [Google Scholar] [CrossRef]
- Bayer, P.; de Paly, M.; Beck, M. Strategic Optimization of Borehole Heat Exchanger Field for Seasonal Geothermal Heating and Cooling. Appl. Energy 2014, 136, 445–453. [Google Scholar] [CrossRef]
- Retkowski, W.; Thöming, J. Thermoeconomic Optimization of Vertical Ground-Source Heat Pump Systems through Nonlinear Integer Programming. Appl. Energy 2014, 114, 492–503. [Google Scholar] [CrossRef]
- Bidarmaghz, A. 3D Numerical Modelling of Vertical Ground Heat Exchangers. Ph.D. Thesis, University of Melbourne, Melbourne, Australia, 2014. [Google Scholar]
- Huang, S.; Ma, Z.; Wang, F. A Multi-Objective Design Optimization Strategy for Vertical Ground Heat Exchangers. Energy Build. 2015, 87, 233–242. [Google Scholar] [CrossRef]
- Sivasakthivel, T.; Murugesan, K.; Thomas, H.R. Optimization of Operating Parameters of Ground Source Heat Pump System for Space Heating and Cooling by Taguchi Method and Utility Concept. Appl. Energy 2014, 116, 76–85. [Google Scholar] [CrossRef]
- Moreni, M.; Vulliet, L.; Laloui, L. Behavior of a Dual-Purpose Pile as Foundation and Heat Exchanger [Comportement d’un Pieu Bi-Fonction, Fondation et Échangeur de Chaleur]. Can. Geotech. J. 2003, 40, 388–402. [Google Scholar]
- Brandl, H. Energy Foundations and Other Thermo-Active Ground Structures. Géotechnique 2006, 56, 81–122. [Google Scholar] [CrossRef]
- Laloui, L.; Nuth, M.; Vulliet, L. Experimental and Numerical Investigations of the Behaviour of a Heat Exchanger Pile. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 763–781. [Google Scholar] [CrossRef]
- Elsamee, W.N.A. New Method for Prediction Pile Capacity Executed by Continuous Flight Auger (CFA). Engineering 2013, 5, 344–354. [Google Scholar] [CrossRef][Green Version]
- ISO 2911-1-1. B.I.S. Bureau of I. Design and Construction of Pile Foundations-Code of Practice. ISO: Geneva, Switzerland, 2010.
- Kordjazi, A.; Nejad, F.P.; Jaksa, M.B. Prediction of Ultimate Axial Load-Carrying Capacity of Piles Using a Support Vector Machine Based on CPT Data. Comput. Geotech. 2014, 55, 91–102. [Google Scholar] [CrossRef]
- Abu-Farsakh, M.Y.; Titi, H.H. Assessment of Direct Cone Penetration Test Methods for Predicting the Ultimate Capacity of Friction Driven Piles. J. Geotech. Geoenviron. Eng. 2004, 130, 935–944. [Google Scholar] [CrossRef]
- Gao, W.; Alsarraf, J.; Moayedi, H.; Shahsavar, A.; Nguyen, H. Comprehensive Preference Learning and Feature Validity for Designing Energy-Efficient Residential Buildings Using Machine Learning Paradigms. Appl. Soft Comput. 2019, 84, 105748. [Google Scholar] [CrossRef]
- Dogan, T.; Reinhart, C. Shoeboxer: An Algorithm for Abstracted Rapid Multi-Zone Urban Building Energy Model Generation and Simulation. Energy Build. 2017, 140, 140–153. [Google Scholar] [CrossRef]
- Egan, J.; Finn, D.; Soares, P.H.D.; Baumann, V.A.R.; Aghamolaei, R.; Beagon, P.; Neu, O.; Pallonetto, F.; O’Donnell, J. Definition of a Useful Minimal-Set of Accurately-Specified Input Data for Building Energy Performance Simulation. Energy Build. 2018, 165, 172–183. [Google Scholar] [CrossRef]
- Zhao, H.; Magoulès, F. A Review on the Prediction of Building Energy Consumption. Renew. Sustain. Energy Rev. 2012, 16, 3586–3592. [Google Scholar] [CrossRef]
- Yezioro, A.; Dong, B.; Leite, F. An Applied Artificial Intelligence Approach towards Assessing Building Performance Simulation Tools. Energy Build. 2008, 40, 612–620. [Google Scholar] [CrossRef]
- Catalina, T.; Virgone, J.; Blanco, E. Development and Validation of Regression Models to Predict Monthly Heating Demand for Residential Buildings. Energy Build. 2008, 40, 1825–1832. [Google Scholar] [CrossRef]
- Shahin, M.A. Intelligent Computing for Modeling Axial Capacity of Pile Foundations. Can. Geotech. J. 2010, 47, 230–243. [Google Scholar] [CrossRef]
- Lee, I.-M.; Lee, J.-H. Prediction of Pile Bearing Capacity Using Artificial Neural Networks. Comput. Geotech. 1996, 18, 189–200. [Google Scholar] [CrossRef]
- Dibike, Y.B.; Velickov, S.; Solomatine, D.; Abbott, M.B. Model Induction with Support Vector Machines: Introduction and Applications. J. Comput. Civ. Eng. 2001, 15, 208–216. [Google Scholar] [CrossRef]
- Shahin, M.A.; Maier, H.R.; Jaksa, M.B. Predicting Settlement of Shallow Foundations Using Neural Networks. J. Geotech. Geoenviron. Eng. 2002, 128, 785–793. [Google Scholar] [CrossRef]
- Nejad, F.P.; Jaksa, M.B.; Kakhi, M.; McCabe, B.A. Prediction of Pile Settlement Using Artificial Neural Networks Based on Standard Penetration Test Data. Comput. Geotech. 2009, 36, 1125–1133. [Google Scholar] [CrossRef]
- Makasis, N.; Narsilio, G.A.; Bidarmaghz, A. A Machine Learning Approach to Energy Pile Design. Comput. Geotech. 2018, 97, 189–203. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Goh, S.H. Support Vector Machines: Their Use in Geotechnical Engineering as Illustrated Using Seismic Liquefaction Data. Comput. Geotech. 2007, 34, 410–421. [Google Scholar] [CrossRef]
- Samui, P. Support Vector Machine Applied to Settlement of Shallow Foundations on Cohesionless Soils. Comput. Geotech. 2008, 35, 419–427. [Google Scholar] [CrossRef]
- Samui, P.; Sitharam, T.G.; Kurup, P.U. OCR Prediction Using Support Vector Machine Based on Piezocone Data. J. Geotech. Geoenviron. Eng. 2008, 134, 894–898. [Google Scholar] [CrossRef]
- Pal, M.; Deswal, S. Modelling Pile Capacity Using Gaussian Process Regression. Comput. Geotech. 2010, 37, 942–947. [Google Scholar] [CrossRef]
- Adarsh, S.; Dhanya, R.; Krishna, G.; Merlin, R.; Tina, J. Prediction of Ultimate Bearing Capacity of Cohesionless Soils Using Soft Computing Techniques. Int. Sch. Res. Not. 2012, 2012, 628496. [Google Scholar] [CrossRef]
- Pal, M.; Deswal, S. Modeling Pile Capacity Using Support Vector Machines and Generalized Regression Neural Network. J. Geotech. Geoenviron. Eng. 2008, 134, 1021–1024. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, C.; Li, Y.; Wang, L.; Samui, P. Assessment of Pile Drivability Using Random Forest Regression and Multivariate Adaptive Regression Splines. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2021, 15, 27–40. [Google Scholar] [CrossRef]
- Zhao, Z.; Duan, W.; Cai, G.; Wu, M.; Liu, S. CPT-Based Fully Probabilistic Seismic Liquefaction Potential Assessment to Reduce Uncertainty: Integrating XGBoost Algorithm with Bayesian Theorem. Comput. Geotech. 2022, 149, 104868. [Google Scholar] [CrossRef]
- Huat, C.Y.; Moosavi, S.M.H.; Mohammed, A.S.; Armaghani, D.J.; Ulrikh, D.V.; Monjezi, M.; Hin Lai, S. Factors Influencing Pile Friction Bearing Capacity: Proposing a Novel Procedure Based on Gradient Boosted Tree Technique. Sustainability 2021, 13, 11862. [Google Scholar] [CrossRef]
- ISO/TS 17892-4. Geotechnical Investigation and Testing–Laboratory Testing of Soil—Part 4: Determination of Particle Size Distribution. ISO: Geneva, Switzerland, 2004.
- ISO E.N. 22476-1. Geotechnical Investigation and Testing—Field Testing—Part 1: Electrical Cone and Piezocone Penetration Test. ISO: Geneva, Switzerland, 2012.
- Di Buo, B. Evaluation of the Preconsolidation Stress and Deformation Characteristics of Finnish Clays Based on Piezocone Testing. Ph.D. Thesis, Tampere University, Tampere, Finland, 2020. [Google Scholar]
- Bhattacharya, S.; Carrington, T.M.; Aldridge, T.R. Buckling Considerations in Pile Design. In Proceedings of the International Symposium on Frontiers in Offshore Geotechnics, Perth, Australia, 19–21 September 2005; pp. 815–821. [Google Scholar]
- Gao, J.; Zhang, X.; Liu, J.; Li, K.; Yang, J. Numerical and Experimental Assessment of Thermal Performance of Vertical Energy Piles: An Application. Appl. Energy 2008, 85, 901–910. [Google Scholar] [CrossRef]
- Sani, A.K.; Singh, R.M.; Amis, T.; Cavarretta, I. A Review on the Performance of Geothermal Energy Pile Foundation, Its Design Process and Applications. Renew. Sustain. Energy Rev. 2019, 106, 54–78. [Google Scholar] [CrossRef]
- Gashti, E.H.N.; Uotinen, V.-M.; Kujala, K. Numerical Modelling of Thermal Regimes in Steel Energy Pile Foundations: A Case Study. Energy Build. 2014, 69, 165–174. [Google Scholar] [CrossRef]
- Gashti, E.H.N.; Malaska, M.; Kujala, K. Evaluation of Thermo-Mechanical Behaviour of Composite Energy Piles during Heating/Cooling Operations. Eng. Struct. 2014, 75, 363–373. [Google Scholar] [CrossRef]
- Kukkonen, I.T. Geothermal Energy in Finland. In Proceedings of the World Geothermal Congress 2000, Kyushu-Tohoku, Japan, 28 May–10 June 2000; pp. 277–282. [Google Scholar]
- Laloui, L. Thermo-Mechanical Behaviour of Soils. Rev. Fr. Génie Civ. 2001, 5, 809–843. [Google Scholar] [CrossRef]
- Murthy, V.N.S. Geotechnical Engineering: Principles and Practices of Soil Mechanics and Foundation Engineering; CRC Press: Boca Raton, FL, USA, 2002; ISBN 0824708733. [Google Scholar]
- Schmertmann, J.H. Guidelines for Cone Penetration Test: Performance and Design; Federal Highway Administration: Washington, DC, USA, 1978. [Google Scholar]
- 4-I.S. 2911-Part 1. Section Design and Construction of Pile Foundations–Code of Practice. ISO: Geneva, Switzerland, 2010.
- Xue, J.-F.; Gavin, K. Simultaneous Determination of Critical Slip Surface and Reliability Index for Slopes. J. Geotech. Geoenviron. Eng. 2007, 133, 878–886. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; Taylor & Francis: Abingdon, UK, 1984. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Cham, Switzerland, 1999; ISBN 0387987800. [Google Scholar]
- Smola, A.J. Regression Estimation with Support Vector Learning Machines. Master’s Thesis, Technische Universität München, Munich, Germany, 1996. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A Tutorial on Support Vector Regression; Rep. No; NC2-TR-1998-030. NeuroCOLT2 Technical Report Series; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000; ISBN 0521780195. [Google Scholar]
- Samui, P.; Dixon, B. Application of Support Vector Machine and Relevance Vector Machine to Determine Evaporative Losses in Reservoirs. Hydrol. Process. 2012, 26, 1361–1369. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K. Xgboost: Extreme Gradient Boosting; R Package Version 0.4-2; R Foundation for Statistical Computing: Vienna, Austria, 2015; Volume 1, pp. 1–4. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Chen, X.; Huang, L.; Xie, D.; Zhao, Q. EGBMMDA: Extreme Gradient Boosting Machine for MiRNA-Disease Association Prediction. Cell Death Dis. 2018, 9, 1–16. [Google Scholar] [CrossRef]
- Kardani, N.; Zhou, A.; Nazem, M.; Shen, S.-L. Estimation of Bearing Capacity of Piles in Cohesionless Soil Using Optimised Machine Learning Approaches. Geotech. Geol. Eng. 2020, 38, 2271–2291. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root Mean Square Error (RMSE) or Mean Absolute Error (MAE)?–Arguments against Avoiding RMSE in the Literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Behar, O.; Khellaf, A.; Mohammedi, K. Comparison of Solar Radiation Models and Their Validation under Algerian Climate–The Case of Direct Irradiance. Energy Convers. Manag. 2015, 98, 236–251. [Google Scholar] [CrossRef]
- Despotovic, M.; Nedic, V.; Despotovic, D.; Cvetanovic, S. Review and Statistical Analysis of Different Global Solar Radiation Sunshine Models. Renew. Sustain. Energy Rev. 2015, 52, 1869–1880. [Google Scholar] [CrossRef]
- Zhao, E.; Sun, S.; Wang, S. New Developments in Wind Energy Forecasting with Artificial Intelligence and Big Data: A Scientometric Insight. Data Sci. Manag. 2022, 5, 84–95. [Google Scholar] [CrossRef]
- Nejad, F.P.; Jaksa, M.B. Prediction of Pile Behavior Using Artificial Neural Networks Based on Standard Penetration Test Data. In Proceedings of the 13th International Conference of the IACMAG, Melbourne, Australia, 9–11 May 2011; pp. 564–569. [Google Scholar]
- Rotta Loria, A.F. Performance-Based Design of Energy Pile Foundations. DFI J. J. Deep Found. Inst. 2018, 12, 94–107. [Google Scholar] [CrossRef]
- Kumar, D.R.; Samui, P.; Burman, A. Prediction of Probability of Liquefaction Using Soft Computing Techniques. J. Inst. Eng. India Ser. A 2022, 103, 1195–1208. [Google Scholar] [CrossRef]






| L (m) | D (mm) | Flow Rate of Water (m3/h) | Heat Carrier Fluid Inlet Velocity (m/s) | Collector Type (mm) |
|---|---|---|---|---|
| 8 | 700 | 0.325 | 0.182 | U-tube 40 |
| Materials | Density (kg/m3) | Thermal Conductivity (W/m K) | Heat Capacity (J/kg K) |
|---|---|---|---|
| HDPE | 950 | 0.42 | 2250 |
| Clay | 1812 | 1.1 | 1845 |
| Steel | 7850 | 44.5 | 475 |
| Concrete | 2400 | 1.8 | 880 |
| Clay | Steel | Concrete | ||
|---|---|---|---|---|
| Young’s modulus (MPa) | E | 15 | 200 × 103 | 32 × 103 |
| Shear modulus (MPa) | G | 5.62 | 75 × 103 | 12 × 103 |
| Coefficient of thermal expansion (°C−1) | αc | 0.5 × 10−5 | 1.23 × 10−5 | 1 × 10−5 |
| Poisson ratio | ν | 0.33 | 0.33 | 0.33 |
| Soil Type | (kPa) |
|---|---|
| Clays and peat | |
| Clays | |
| Silty clays and silty sands | |
| Sands | |
| Coarse sands and gravels |
| S.No | qc0 (kPa) | qc1 (kPa) | qc2 (kPa) | qc (kPa) | E (kPa) | Qug (kN) |
|---|---|---|---|---|---|---|
| 1 | 348 | 285 | 246 | 120 | 36,559,730 | 1589 |
| 2 | 487 | 421 | 138 | 454 | 30,512,281 | 5483 |
| 3 | 453 | 408 | 205 | 141 | 38,723,679 | 2416 |
| 4 | 400 | 273 | 237 | 476 | 31,791,913 | 6166 |
| 5 | 312 | 274 | 296 | 313 | 31,823,050 | 3198 |
| 6 | 480 | 350 | 151 | 170 | 31,997,539 | 2022 |
| 7 | 419 | 255 | 223 | 463 | 38,513,073 | 5718 |
| 8 | 391 | 283 | 293 | 118 | 37,369,266 | 1837 |
| 9 | 535 | 246 | 137 | 357 | 33,011,764 | 3815 |
| 10 | 463 | 436 | 189 | 452 | 35,985,785 | 4415 |
| 11 | 421 | 384 | 135 | 273 | 34,280,458 | 3260 |
| 12 | 265 | 263 | 284 | 523 | 35,216,679 | 6127 |
| 13 | 541 | 413 | 244 | 276 | 38,355,105 | 4116 |
| 14 | 519 | 497 | 162 | 134 | 36,511,371 | 2042 |
| 15 | 566 | 311 | 186 | 133 | 35,571,078 | 2256 |
| . | . | . | . | . | . | . |
| . | . | . | . | . | . | . |
| . | . | . | . | . | . | . |
| . | . | . | . | . | . | . |
| . | . | . | . | . | . | . |
| 189 | 291 | 261 | 239 | 364 | 37,193,735 | 2940 |
| 190 | 297 | 274 | 245 | 219 | 36,076,104 | 2394 |
| 191 | 472 | 247 | 124 | 542 | 34,210,352 | 5029 |
| 192 | 397 | 336 | 300 | 300 | 31,309,579 | 3889 |
| 193 | 432 | 364 | 240 | 415 | 39,380,051 | 3987 |
| 194 | 457 | 402 | 288 | 307 | 38,824,246 | 2971 |
| 195 | 344 | 283 | 124 | 319 | 39,835,672 | 3389 |
| 196 | 512 | 269 | 121 | 404 | 37,392,469 | 4217 |
| 197 | 510 | 339 | 254 | 481 | 32,045,184 | 6045 |
| 198 | 377 | 238 | 229 | 453 | 35,433,571 | 5539 |
| 199 | 302 | 263 | 207 | 226 | 35,553,756 | 3043 |
| 200 | 536 | 364 | 164 | 178 | 34,147,133 | 2382 |
| Proposed Models | R2 | RMSE | MAE | MBE | MAD | WMAPE | U95 | GPI | TIC | IA |
|---|---|---|---|---|---|---|---|---|---|---|
| RF | 0.957 | 0.065 | 0.049 | 0.000 | 0.038 | 0.127 | 0.180 | 3.09 × 10−8 | 0.074 | 0.973 |
| SVM | 0.829 | 0.092 | 0.064 | −0.003 | 0.029 | 0.164 | 0.257 | −4.0 × 10−6 | 0.106 | 0.948 |
| GBM | 0.991 | 0.020 | 0.001 | 0.001 | 0.000 | 0.000 | 0.057 | 1.72 × 10−8 | 0.014 | 1.000 |
| XGB | 0.998 | 0.124 | 0.008 | 0.002 | 0.005 | 0.020 | 0.034 | 3.85 × 10−9 | 0.023 | 0.998 |
| Proposed Models | R2 | RMSE | MAE | MBE | MAD | WMAPE | U95 | GPI | TIC | IA |
|---|---|---|---|---|---|---|---|---|---|---|
| RF | 0.785 | 0.135 | 0.109 | −0.008 | 0.097 | 0.279 | 0.376 | −4.9 × 10−8 | 0.159 | 0.855 |
| SVM | 0.734 | 0.122 | 0.018 | −0.012 | 0.067 | 0.247 | 0.340 | −1.0 × 10−4 | 0.140 | 0.910 |
| GBM | 0.808 | 0.104 | 0.084 | −0.015 | 0.066 | 0.217 | 0.288 | −1.0 × 10−4 | 0.119 | 0.941 |
| XGB | 0.792 | 0.107 | 0.086 | 0.006 | 0.067 | 0.216 | 0.298 | 1.88 × 10−5 | 0.118 | 0.944 |
| Performance Parameters | RF | SVM | GBM | XGB | ||||
|---|---|---|---|---|---|---|---|---|
| TR | TS | TR | TS | TR | TS | TR | TS | |
| R2 | 3 | 3 | 4 | 4 | 2 | 1 | 1 | 2 |
| RMSE | 2 | 4 | 3 | 3 | 1 | 1 | 4 | 2 |
| MAE | 3 | 4 | 4 | 1 | 1 | 2 | 2 | 3 |
| MBE | 1 | 2 | 4 | 3 | 2 | 4 | 3 | 1 |
| MAD | 4 | 3 | 3 | 2 | 1 | 1 | 2 | 2 |
| WMAPE | 3 | 4 | 4 | 3 | 1 | 1 | 2 | 2 |
| U95 | 3 | 4 | 4 | 3 | 2 | 1 | 1 | 2 |
| GPI | 1 | 4 | 4 | 2 | 2 | 2 | 3 | 1 |
| TIC | 3 | 4 | 4 | 3 | 1 | 2 | 2 | 1 |
| IA | 3 | 4 | 4 | 3 | 1 | 2 | 2 | 1 |
| Sub total | 26 | 36 | 38 | 27 | 14 | 17 | 22 | 17 |
| Total score | 62 | 65 | 31 | 39 | ||||
| Overall rank | 3 | 4 | 1 | 2 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, P.; Samui, P. Design of an Energy Pile Based on CPT Data Using Soft Computing Techniques. Infrastructures 2022, 7, 169. https://doi.org/10.3390/infrastructures7120169
Kumar P, Samui P. Design of an Energy Pile Based on CPT Data Using Soft Computing Techniques. Infrastructures. 2022; 7(12):169. https://doi.org/10.3390/infrastructures7120169
Chicago/Turabian StyleKumar, Pramod, and Pijush Samui. 2022. "Design of an Energy Pile Based on CPT Data Using Soft Computing Techniques" Infrastructures 7, no. 12: 169. https://doi.org/10.3390/infrastructures7120169
APA StyleKumar, P., & Samui, P. (2022). Design of an Energy Pile Based on CPT Data Using Soft Computing Techniques. Infrastructures, 7(12), 169. https://doi.org/10.3390/infrastructures7120169






