ANN-Based Assessment of Soft Surface Soil Layers’ Impact on Fault Rupture Propagation and Kinematic Distress of Gas Pipelines
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Simulations
2.2. Artifical Neural Networks
3. Results
4. Discussion
5. Conclusions
- -
- The overlying soil stratum may have a critical impact on the fault rupture propagation paths, leading to fully-developed failure patterns up to the ground surface. In addition, the presence of the soil layer may affect the structural performance of buried gas pipelines in a beneficial or even a detrimental manner, compared to the case where the pipeline is directly laid on bedrock.
- -
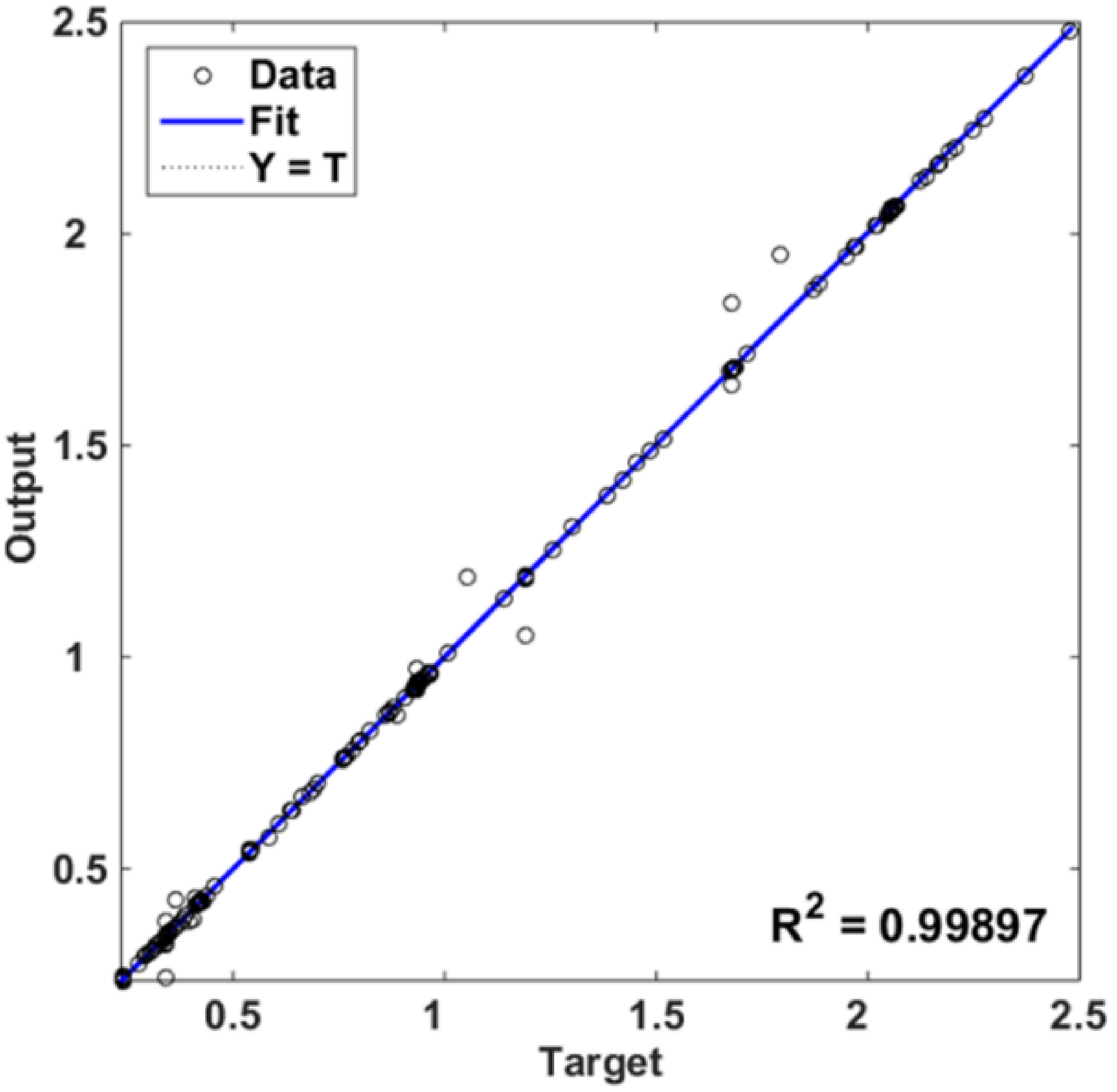
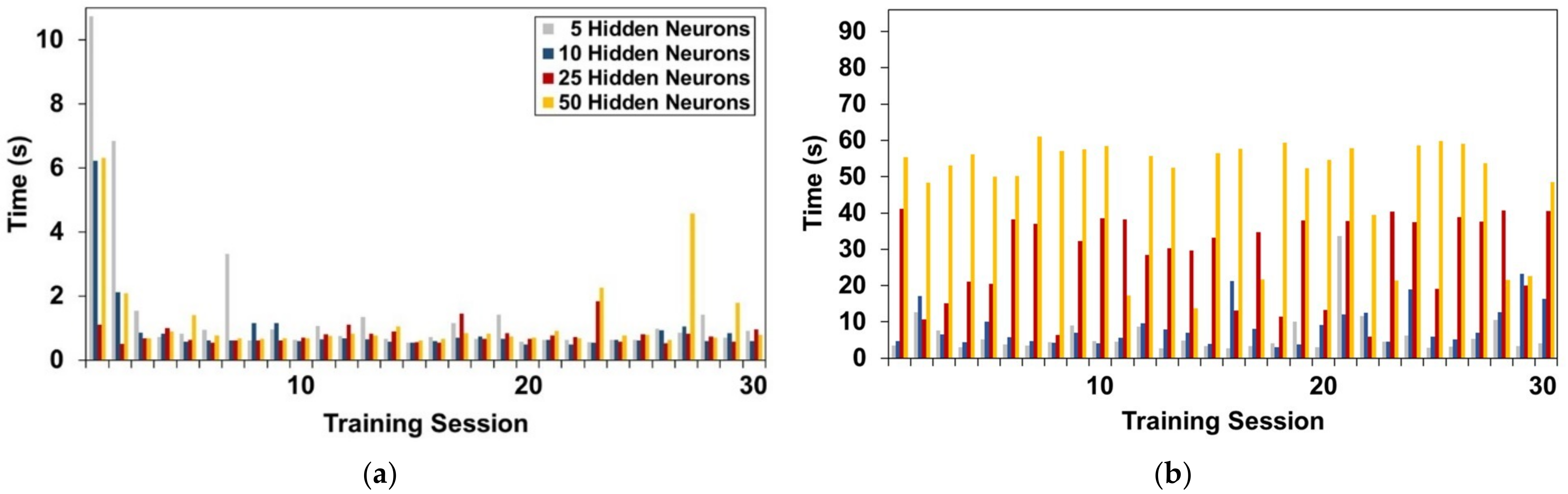
- The developed geotechnical FFNN (FFNN1), which focuses on surface PGDs due to seismic fault rupture, has produced satisfactory predictions, since RMSE and R2 are close to 0 and 1, respectively, for all the examined architectures and training algorithms. BR-trained FFNN1 exhibits a better overall performance compared to LM-trained. A marginal impact on the training duration has been reported from the increase of hidden neurons in LM, whereas increasing the number of hidden neurons has led to slightly better results, but significantly longer training duration for BR-trained networks.
- -
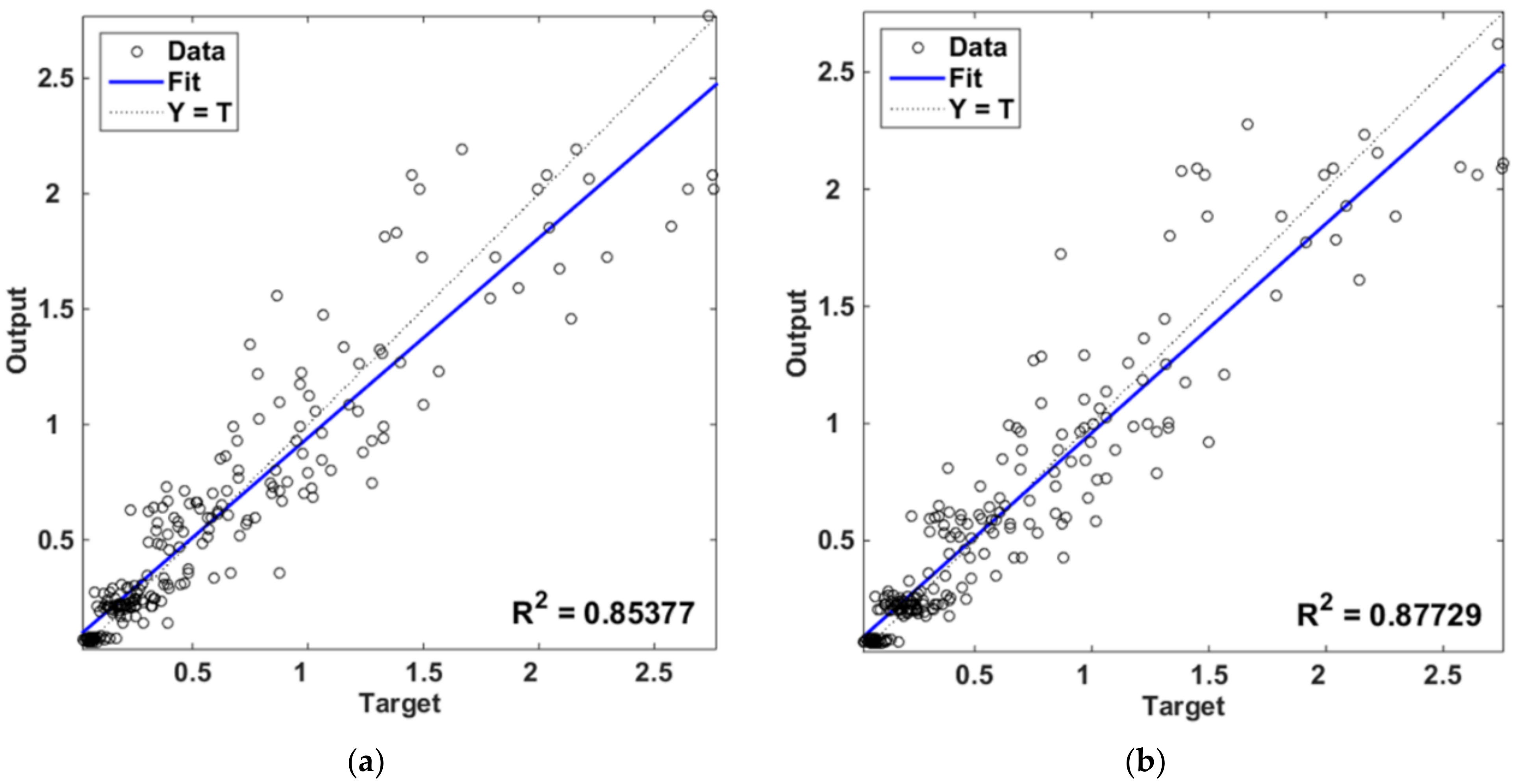
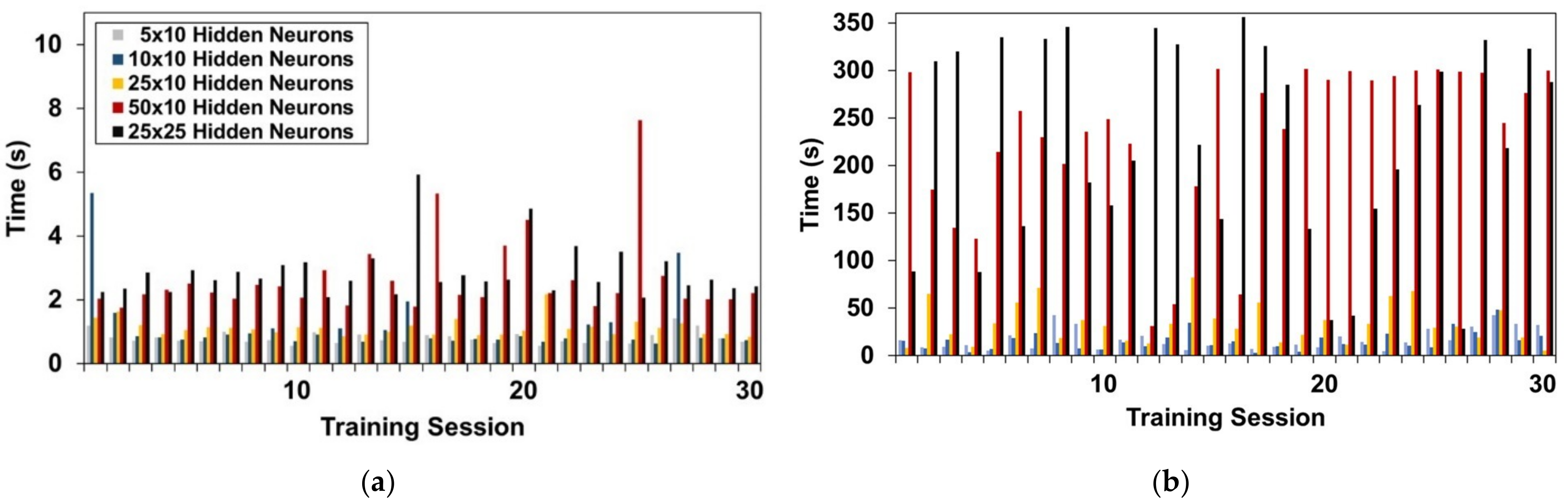
- The developed structural metamodel (FFNN2) exhibits worse performance metrics than FFNN1. The BR-trained single hidden layer network consisting of 50 neurons outperforms the other schemes. Similarly to FFNN1, the increase on the number of hidden neurons has affected only the training duration and performance of the BR-trained network. Increasing the number of hidden layers of FFNN2 has not improved much the performance metrics, regardless of training algorithm and number of neurons per hidden layer.
- -
- Regarding the cross-validation with new data, FFNN1 is characterized by exceptional predictive performance for independent data, leading to 0.71% and 0.09% prediction errors for dx and dy, respectively. Conversely, FFNN2 has generally resulted in prediction errors greater than 10%. However, the LM-trained FFNN2 with a single hidden layer having 50 neurons resulted in errors slightly lower than 6% and 2% for εt and εc, respectively. Although the use of two hidden layers in FFNN2 has not led to a notable reduction of the prediction errors, the LM-trained network consisting of 50 × 10 hidden neurons has resulted in acceptable prediction errors, i.e., 1.6% and 1.1% for εt and εc, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nair, G.S.; Dash, S.R.; Mondal, G. Review of Pipeline Performance during Earthquakes since 1906. J. Perform. Constr. Facil. 2018, 32, 04018083. [Google Scholar] [CrossRef]
- Newmark, N.M.; Hall, W.J. Pipeline Design to Resist Large Fault Displacement. In Proceedings of US National Conference on Earthquake Engineering; Earthquake Engineering Research Institute: Oakland, CA, USA, 1975. [Google Scholar]
- Kennedy, R.P.; Chow, A.M.; Williamson, R.A. Fault Movement Effects on Burried Oil Pipeline. ASCE Transp. Eng. J. 1977, 103, 617–633. [Google Scholar] [CrossRef]
- Wang, L.R.; Yeh, Y.-H. A Refined Seismic Analysis and Design of Buried Pipeline for Fault Movement. Earthq. Eng. Struct. Dyn. 1985, 13, 75–96. [Google Scholar] [CrossRef]
- Jalali, H.H.; Rofooei, F.R.; Khajeh, A.A.N. Performance of Buried Gas Distribution Pipelines Subjected to Reverse Fault Movement. J. Earthq. Eng. 2018, 22, 1068–1091. [Google Scholar] [CrossRef]
- Tsatsis, A.; Loli, M.; Gazetas, G. Pipeline in Dense Sand Subjected to Tectonic Deformation from Normal or Reverse Faulting. Soil Dyn. Earthq. Eng. 2019, 127, 105780. [Google Scholar] [CrossRef]
- Fadaee, M.; Farzaneganpour, F.; Anastasopoulos, I. Response of Buried Pipeline Subjected to Reverse Faulting. Soil Dyn. Earthq. Eng. 2020, 132, 106090. [Google Scholar] [CrossRef]
- Dey, S.; Chakraborty, S.; Tesfamariam, S. Structural Performance of Buried Pipeline Undergoing Strike-Slip Fault Rupture in 3D Using a Non-Linear Sand Model. Soil Dyn. Earthq. Eng. 2020, 135, 106180. [Google Scholar] [CrossRef]
- Joshi, S.; Prashant, A.; Deb, A.; Jain, S.K. Analysis of Buried Pipelines Subjected to Reverse Fault Motion. Soil Dyn. Earthq. Eng. 2011, 31, 930–940. [Google Scholar] [CrossRef]
- Uckan, E.; Akbas, B.; Shen, J.; Rou, W.; Paolacci, F.; O’Rourke, M. A Simplified Analysis Model for Determining the Seismic Response of Buried Steel Pipes at Strike-Slip Fault Crossings. Soil Dyn. Earthq. Eng. 2015, 75, 55–65. [Google Scholar] [CrossRef]
- Chatzidakis, D.; Tsompanakis, Y.; Psarropoulos, P.N. Kinematic Distress of Pipelines Subjected to Secondary Seismic Fault Rupture. Soil Dyn. Earthq. Eng. 2022, 152, 107065. [Google Scholar] [CrossRef]
- Makrakis, N.; Psarropoulos, P.N.; Sextos, A.; Tsompanakis, Y. Quantifying the Impact of Soft Surface Soil Layers on Fault Rupture Propagation and Kinematic Distress of Offshore and Onshore Pipelines. In Proceedings of the 17th International Pipeline Technology Conference (PTC), Berlin, Germany, 7–10 March 2022. [Google Scholar]
- Karamitros, D.K.; Bouckovalas, G.D.; Kouretzis, G.P. Stress Analysis of Buried Steel Pipelines at Strike-Slip Fault Crossings. Soil Dyn. Earthq. Eng. 2007, 27, 200–211. [Google Scholar] [CrossRef]
- Trifonov, O.V.; Cherniy, V.P. Elastoplastic Stress-Strain Analysis of Buried Steel Pipelines Subjected to Fault Displacements with Account for Service Loads. Soil Dyn. Earthq. Eng. 2012, 33, 54–62. [Google Scholar] [CrossRef]
- Sarvanis, G.C.; Karamanos, S.A. Analytical Model for the Strain Analysis of Continuous Buried Pipelines in Geohazard Areas. Eng. Struct. 2017, 152, 57–69. [Google Scholar] [CrossRef]
- Sarvanis, G.C.; Karamanos, S.A.; Vazouras, P.; Mecozzi, E.; Lucci, A.; Dakoulas, P. Permanent Earthquake-Induced Actions in Buried Pipelines: Numerical Modeling and Experimental Verification. Earthq. Eng. Struct. Dyn. 2018, 47, 966–987. [Google Scholar] [CrossRef]
- Psyrras, N.; Sextos, A.; Crewe, A.; Dietz, M.; Mylonakis, G. Physical Modeling of the Seismic Response of Gas Pipelines in Laterally Inhomogeneous Soil. J. Geotech. Geoenvironmental Eng. 2020, 146, 04020031. [Google Scholar] [CrossRef]
- Demirci, H.E.; Bhattacharya, S.; Karamitros, D.; Alexander, N. Experimental and Numerical Modelling of Buried Pipelines Crossing Reverse Faults. Soil Dyn. Earthq. Eng. 2018, 114, 198–214. [Google Scholar] [CrossRef]
- Rojhani, M.; Moradi, M.; Galandarzadeh, A.; Takada, S. Centrifuge Modeling of Buried Continuous Pipelines Subjected to Reverse Faulting. Can. Geotech. J. 2012, 49, 659–670. [Google Scholar] [CrossRef]
- Saiyar, M.; Ni, P.; Take, W.A.; Moore, I.D. Response of Pipelines of Differing Flexural Stiffness to Normal Faulting. Geotechnique 2016, 66, 275–286. [Google Scholar] [CrossRef]
- American Society of Civil Engineers (ASCE); Committee on Gas and Liquid Fuel Lifelines. Guidelines for the Seismic Design of Oil and Gas Pipeline Systems; American Society of Civil Engineers: New York, NY, USA, 1984; ISBN 978-0-87262-428-3. [Google Scholar]
- American Lifelines Alliance. Guidelines for the Design of Buried Steel Pipe; American Society of Civil Engineers: Reston, VA, USA, 2001. [Google Scholar]
- EN 1998-4:2006; European Commitee for Standardization (CEN)—Eurocode 8: Design of Structures for Earthquake Resistance—Part 4: Silos, Tanks and Pipelines. European Commitee for Standardization: Brussels, Belgium, 2006.
- Makrakis, N.; Psarropoulos, P.N.; Sextos, A.; Tsompanakis, Y. New Empirical Relationships for the Assessment of Soft Surface Soil Layers Impact on Fault-Rupture Propagation. 2022; to be sumbitted. [Google Scholar]
- Makrakis, N.; Psarropoulos, P.N.; Sextos, A.; Tsompanakis, Y. Quantifying the Impact of Soft Soil Layers on the Kinematic Distress of Onshore High-Pressure Gas Pipelines. Bull. Earthq. Eng. 2022. under review. [Google Scholar]
- Lagaros, N.D.; Tsompanakis, Y. Intelligent Computational Paradigms in Earthquake Engineering; Lagaros, N.D., Tsompanakis, Y., Eds.; Idea Group Publishing, Inc.: Hershey, PA, USA, 2007; ISBN 9781599040998. [Google Scholar]
- Das, S.K.; Kumar, A.; Das, B.; Burnwal, B. On Soft Computing Techniques in Various Areas. Comput. Sci. Inf. Technol. 2013, 3, 59–68. [Google Scholar] [CrossRef]
- Sobhani, J.; Ramezanianpour, A.A. Service Life of the Reinforced Concrete Bridge Deck in Corrosive Environments: A Soft Computing System. Appl. Soft Comput. J. 2011, 11, 3333–3346. [Google Scholar] [CrossRef]
- Chandwani, V.; Agrawal, V.; Nagar, R. Applications of Soft Computing in Civil Engineering: A Review. Int. J. Comput. Appl. 2013, 81, 00975–08887. [Google Scholar] [CrossRef]
- Fister, I.; Gandomi, A.H.; Fister, I., Jr.; Mousavi, M.; Farhadi, A. Soft Computing in Earthquake Engineering: A Short Overview. Int. J. Earthq. Eng. Hazard Mitig. 2014, 2, 42–48. [Google Scholar]
- Tsompanakis, Y.; Lagaros, N.D.; Stavroulakis, G.E. Soft Computing Techniques in Parameter Identification and Probabilistic Seismic Analysis of Structures. Adv. Eng. Softw. 2008, 39, 612–624. [Google Scholar] [CrossRef]
- Salehi, H.; Burgueño, R. Emerging Artificial Intelligence Methods in Structural Engineering. Eng. Struct. 2018, 171, 170–189. [Google Scholar] [CrossRef]
- Das, S.K.; Samui, P.; Sabat, A.K. Application of Artificial Intelligence to Maximum Dry Density and Unconfined Compressive Strength of Cement Stabilized Soil. Geotech. Geol. Eng. 2011, 29, 329–342. [Google Scholar] [CrossRef]
- Kim, S.; Hwang, Y.; Seo, H.; Kim, B. Ground Motion Amplification Models for Japan Using Machine Learning Techniques. Soil Dyn. Earthq. Eng. 2020, 132, 106095. [Google Scholar] [CrossRef]
- Gajan, S. Application of Machine Learning Algorithms to Performance Prediction of Rocking Shallow Foundations during Earthquake Loading. Soil Dyn. Earthq. Eng. 2021, 151, 106965. [Google Scholar] [CrossRef]
- Zhang, Y.; Ge, T.; Tian, W.; Liou, Y.A. Debris Flow Susceptibility Mapping Using Machine-Learning Techniques in Shigatse Area, China. Remote Sens. 2019, 11, 2801. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Tiede, D.; Aryal, J. Evaluation of Different Machine Learning Methods and Deep-Learning Convolutional Neural Networks for Landslide Detection. Remote Sens. 2019, 11, 196. [Google Scholar] [CrossRef]
- Rahmati, O.; Falah, F.; Dayal, K.S.; Deo, R.C.; Mohammadi, F.; Biggs, T.; Moghaddam, D.D.; Naghibi, S.A.; Bui, D.T. Machine Learning Approaches for Spatial Modeling of Agricultural Droughts in the South-East Region of Queensland Australia. Sci. Total Environ. 2020, 699, 134230. [Google Scholar] [CrossRef]
- Wagenaar, D.; Curran, A.; Balbi, M.; Bhardwaj, A.; Soden, R.; Hartato, E.; Mestav, S.G.; Ruangpan, L.; Molinario, G.; Lallemant, D. Invited Perspectives: How Machine Learning Will Change Flood Risk and Impact Assessment. Nat. Hazards Earth Syst. Sci. 2020, 20, 1149–1161. [Google Scholar] [CrossRef]
- Ma, Z.; Mei, G. Deep Learning for Geological Hazards Analysis: Data, Models, Applications, and Opportunities. Earth-Sci. Rev. 2021, 223, 103858. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A Logical Calculus of the Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5, 115–143. [Google Scholar] [CrossRef]
- Nedic, V.; Despotovic, D.; Cvetanovic, S.; Despotovic, M.; Babic, S. Comparison of Classical Statistical Methods and Artificial Neural Network in Traffic Noise Prediction. Environ. Impact Assess. Rev. 2014, 49, 24–30. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Pearson Prentice Hall: Noida, India, 2003; ISBN 8120323734. [Google Scholar]
- Papadrakakis, M.; Lagaros, N.D.; Tsompanakis, Y. Structural Optimization Using Evolution Strategies and Neural Networks. Comput. Methods Appl. Mech. Eng. 1998, 156, 309–333. [Google Scholar] [CrossRef]
- Hurtado, J.E.; Alvarez, D.A. Neural-Network-Based Reliability Analysis: A Comparative Study. Comput. Methods Appl. Mech. Eng. 2001, 191, 113–132. [Google Scholar] [CrossRef]
- Naderpour, H.; Kheyroddin, A.; Amiri, G.G. Prediction of FRP-Confined Compressive Strength of Concrete Using Artificial Neural Networks. Compos. Struct. 2010, 92, 2817–2829. [Google Scholar] [CrossRef]
- Dhanya, J.; Raghukanth, S.T.G. Ground Motion Prediction Model Using Artificial Neural Network. Pure Appl. Geophys. 2018, 175, 1035–1064. [Google Scholar] [CrossRef]
- Lagaros, N.D.; Papadrakakis, M.; Fragiadakis, M.; Stefanou, G.; Tsompanakis, Y. Neural Network Aided Stochastic Computations and Earthquake Engineering. Comput. Assist. Mech. Eng. Sci. 2007, 14, 251–275. [Google Scholar]
- Khosravikia, F.; Zeinali, Y.; Nagy, Z.; Clayton, P.; Rathje, E.M. Neural Network-Based Equations for Predicting PGA and PGV in Texas, Oklahoma, and Kansas. arXiv 2018, arXiv:1806.01052. [Google Scholar]
- Syifa, M.; Kadavi, P.R.; Lee, C.W. An Artificial Intelligence Application for Post-Earthquake Damage Mapping in Palu, Central Sulawesi, Indonesia. Sensors 2019, 19, 542. [Google Scholar] [CrossRef]
- Tsompanakis, Y.; Lagaros, N.D.; Psarropoulos, P.N.; Georgopoulos, E.C. Simulating the Seismic Response of Embankments via Artificial Neural Networks. Adv. Eng. Softw. 2009, 40, 640–651. [Google Scholar] [CrossRef]
- Arslan, M.H. An Evaluation of Effective Design Parameters on Earthquake Performance of RC Buildings Using Neural Networks. Eng. Struct. 2010, 32, 1888–1898. [Google Scholar] [CrossRef]
- Sakellariou, M.G.; Ferentinou, M.D. A Study of Slope Stability Prediction Using Neural Networks. Geotech. Geol. Eng. 2005, 23, 419–445. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Landslide Risk Analysis Using Artificial Neural Network Model Focussing on Different Training Sites. Int. J. Phys. Sci. 2009, 4, 001–015. [Google Scholar]
- Pradhan, B.; Lee, S. Regional Landslide Susceptibility Analysis Using Back-Propagation Neural Network Model at Cameron Highland, Malaysia. Landslides 2010, 7, 13–30. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought Modeling—A Review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Yang, B.; Yin, K.; Lacasse, S.; Liu, Z. Time Series Analysis and Long Short-Term Memory Neural Network to Predict Landslide Displacement. Landslides 2019, 16, 677–694. [Google Scholar] [CrossRef]
- Cho, Y.; Khosravikia, F.; Rathje, E.M. A Comparison of Artificial Neural Network and Classical Regression Models for Earthquake-Induced Slope Displacements. Soil Dyn. Earthq. Eng. 2022, 152, 107024. [Google Scholar] [CrossRef]
- Chakraborty, A.; Goswami, D.D. Slope Stability Prediction Using Artificial Neural Network (ANN). Int. J. Eng. Comput. Sci. 2017, 6, 21845–21848. [Google Scholar] [CrossRef]
- Shokri, M.; Tavakoli, K. A Review on the Artificial Neural Network Approach to Analysis and Prediction of Seismic Damage in Infrastructure. Int. J. Hydromechatronics 2019, 2, 178–196. [Google Scholar] [CrossRef]
- Rachedi, M.; Matallah, M.; Kotronis, P. Seismic Behavior & Risk Assessment of an Existing Bridge Considering Soil-Structure Interaction Using Artificial Neural Networks. Eng. Struct. 2021, 232, 111800. [Google Scholar] [CrossRef]
- Portillo Juan, N.; Negro Valdecantos, V. Review of the Application of Artificial Neural Networks in Ocean Engineering. Ocean Eng. 2022, 259, 111947. [Google Scholar] [CrossRef]
- Liu, Z.; Sextos, A.; Guo, A.; Zhao, W. ANN-Based Rapid Seismic Fragility Analysis for Multi-Span Concrete Bridges. Structures 2022, 41, 804–817. [Google Scholar] [CrossRef]
- Wells, D.L.; Coppersmith, K.J. New Empirical Relationships among Magnitude, Rupture Length, Rupture Width, Rupture Area, and Surface Displacement. Bull.-Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar]
- Dassault Systèmes Simulia Abaqus 6.14. Abaqus 6.14 Anal. User’s Guide; Dassault Systèmes: Shangai, China, 2014. [Google Scholar]
- Ni, P.; Moore, I.D.; Take, W.A. Numerical Modeling of Normal Fault-Pipeline Interaction and Comparison with Centrifuge Tests. Soil Dyn. Earthq. Eng. 2018, 105, 127–138. [Google Scholar] [CrossRef]
- Bray, J.D. The Effects of Tectonic Movements on Stresses and Deformations in Earth Embankments; University of California: Berkley, CA, USA, 1990. [Google Scholar]
- Anastasopoulos, I.; Gazetas, G.; Bransby, M.F.; Davies, M.C.R.; El Nahas, A. Fault Rupture Propagation through Sand: Finite-Element Analysis and Validation through Centrifuge Experiments. J. Geotech. Geoenvironmental Eng. 2007, 133, 943–958. [Google Scholar] [CrossRef]
- Rokonuzzaman, M.; Nahas, A.E.; Sakai, T. Experimental Validation of a Numerical Model for the Interaction of Dip-Slip Normal Fault Ruptures, Sand Deposits, and Raft Foundations. Int. J. Geotech. Eng. 2015, 9, 239–250. [Google Scholar] [CrossRef]
- Thebian, L.; Najjar, S.; Sadek, S.; Mabsout, M. Numerical Investigation of Dip-Slip Fault Propagation Effects on Offshore Seabed Sediments. Eng. Geol. 2018, 237, 149–167. [Google Scholar] [CrossRef]
- Rosso, M.M.; Aloisio, A.; Cucuzza, R.; Pasca, D.P.; Cirrincione, G.; Marano, G.C. Structural Health Monitoring with Artificial Neural Network and Subspace-Based Damage Indicators. In Proceedings of the Trends on Construction in the Digital Era. ISIC 2022. Lecture Notes in Civil Engineering; Gomes Correia, A., Azenha, M., Cruz, P.J.S., Novais, P., Pereira, P., Eds.; Springer: Cham, Switzerland, 2022; Volume 306, pp. 524–537. [Google Scholar]
- Teslyuk, V.; Kazarian, A.; Kryvinska, N.; Tsmots, I. Optimal Artificial Neural Network Type Selection Method for Usage in Smart House Systems. Sensors 2021, 21, 47. [Google Scholar] [CrossRef] [PubMed]
- Demuth, H.; Beale, M.; Hagan, M. Neural Network Toolbox 5 User’s Guide; The MathWorks, Inc.: Portola Valley, CA, USA, 2005. [Google Scholar]
- Dietterich, T. Overfitting and Undercomputing in Machine Learning. ACM Comput. Surv. 1995, 27, 251–260. [Google Scholar] [CrossRef]
- Lawrence, S.; Giles, C.L.; Tsoi, A.C. Lessons in Neural Network Training: Overfitting May Be Harder than Expected. In Proceedings of the Fourteenth National Conference on Artificial Intelligence and Ninth Conference on Innovative Applications of Artificial Intelligence, AAAI-97; AAAI Press: Washington, DC, USA, 1997; pp. 540–545. [Google Scholar]
- Jena, R.; Pradhan, B.; Beydoun, G.; Nizamuddin; Ardiansyah; Sofyan, H.; Affan, M. Integrated Model for Earthquake Risk Assessment Using Neural Network and Analytic Hierarchy Process: Aceh Province, Indonesia. Geosci. Front. 2020, 11, 613–634. [Google Scholar] [CrossRef]
- Rosso, M.M.; Marasco, G.; Aiello, S.; Aloisio, A.; Chiaia, B.; Marano, G.C. Convolutional Networks and Transformers for Intelligent Road Tunnel Investigations. Comput. Struct. 2023, 275, 106918. [Google Scholar] [CrossRef]
- Mandal, S.; Prabaharan, N. Ocean Wave Forecasting Using Recurrent Neural Networks. Ocean Eng. 2006, 33, 1401–1410. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M.B. Training Feedforward Networks with the Marquardt Algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H.; De Jesus, O. Neural Network Design, 2nd ed.; Martin Hagan: Stillwater, OK, USA, 2014; ISBN 0971732116. [Google Scholar]
- Alarifi, A.S.N.; Alarifi, N.S.N.; Al-Humidan, S. Earthquakes Magnitude Predication Using Artificial Neural Network in Northern Red Sea Area. J. King Saud Univ.-Sci. 2012, 24, 301–313. [Google Scholar] [CrossRef]
- Kwag, S.; Hahm, D.; Kim, M.; Eem, S. Development of a Probabilistic Seismic Performance Assessment Model of Slope Using Machine Learning Methods. Sustainability 2020, 12, 3269. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Cai, Q.P.; Hu, P. Centrifuge and Numerical Modeling of Normal Fault-Rupture Propagation in Clay with and without a Preexisting Fracture. J. Geotech. Geoenvironmental Eng. 2012, 138, 1492–1502. [Google Scholar] [CrossRef]
- Ahmadi, M.; Moosavi, M.; Jafari, M.K. Experimental Investigation of Reverse Fault Rupture Propagation through Wet Granular Soil. Eng. Geol. 2018, 239, 229–240. [Google Scholar] [CrossRef]
- Lee, J.W.; Hamada, M. An Experimental Study on Earthquake Fault Rupture Propagation through a Sandy Soil Deposit. Struct. Eng. Eng. 2005, 22, 1s–13s. [Google Scholar] [CrossRef]
- Loukidis, D.; Bouckovalas, G.D.; Papadimitriou, A.G. Analysis of Fault Rupture Propagation through Uniform Soil Cover. Soil Dyn. Earthq. Eng. 2009, 29, 1389–1404. [Google Scholar] [CrossRef]
- Hazeghian, M.; Soroush, A. Numerical Modeling of Dip-Slip Faulting through Granular Soils Using DEM. Soil Dyn. Earthq. Eng. 2017, 97, 155–171. [Google Scholar] [CrossRef]
- Özcebe, A.G.; Paolucci, R.; Mariani, S. Numerical Modeling of the Interaction of Pressurized Large Diameter Gas Buried Pipelines with Normal Fault Ruptures. Soil Dyn. Earthq. Eng. 2017, 101, 105–115. [Google Scholar] [CrossRef]
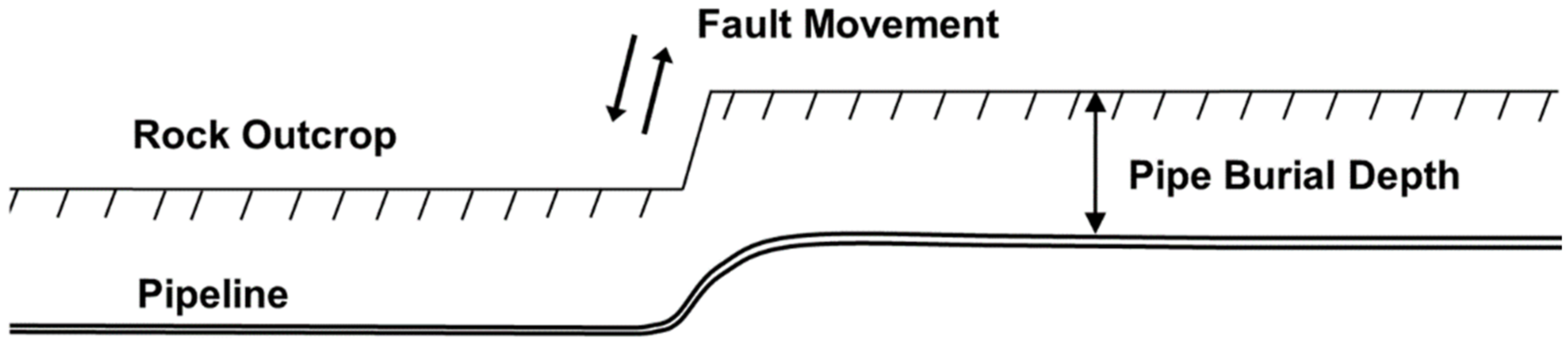
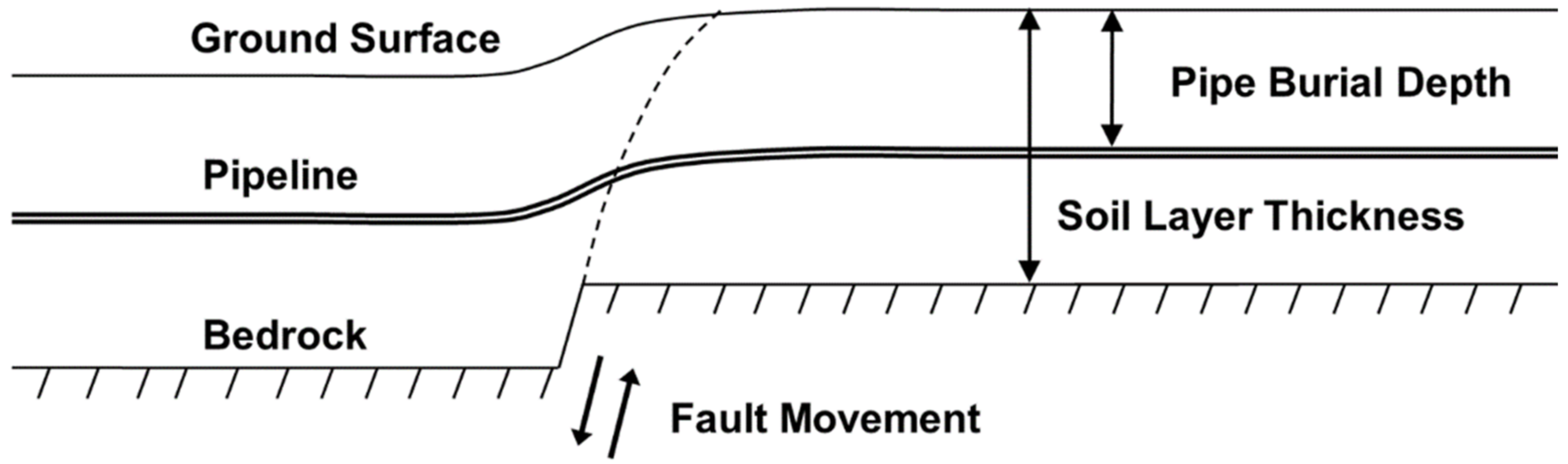





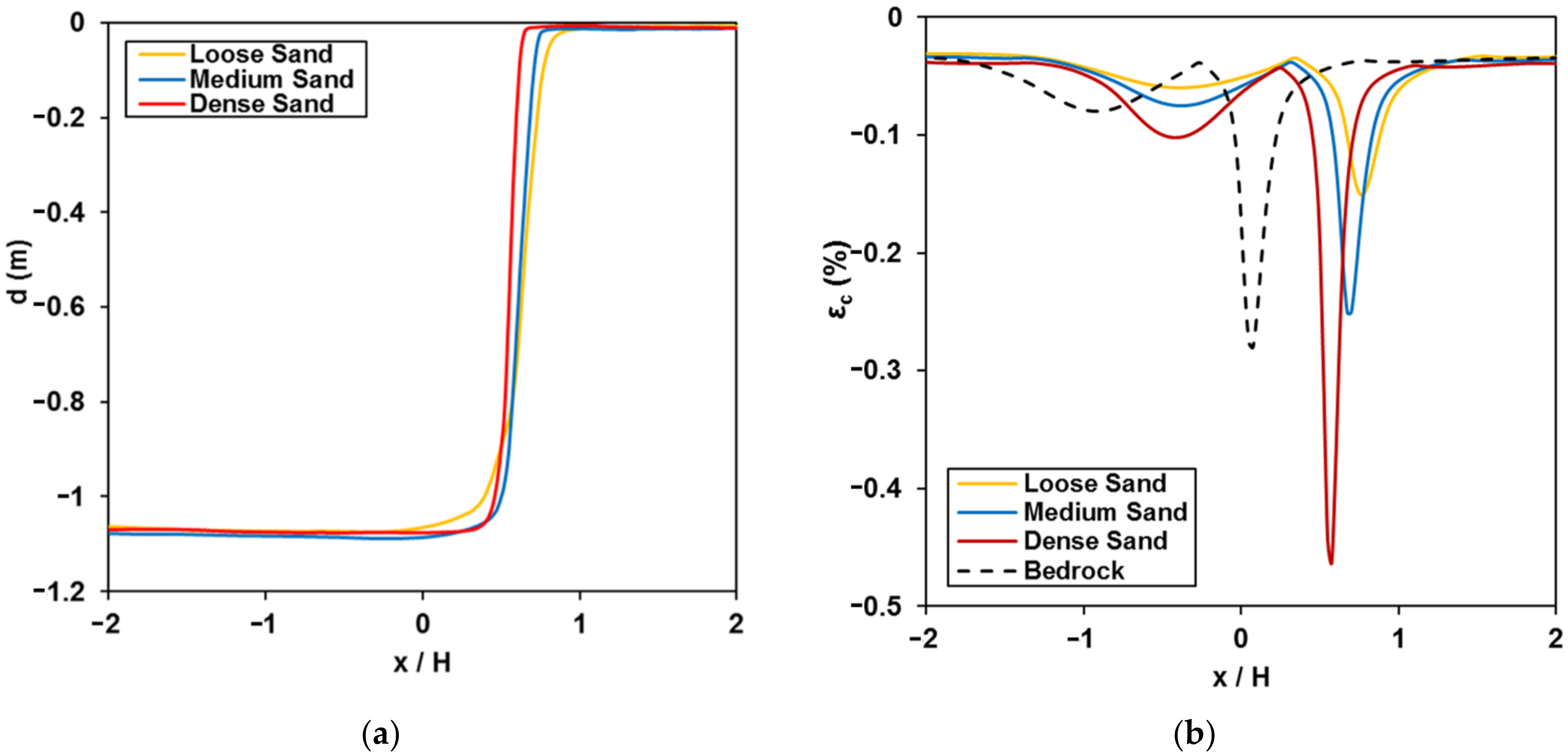



| Sand Type | Soil Density (t/m3) | Elastic Modulus 1 (MPa) | Friction Angle φp–φres (o) | Dilation Angle ψp–ψres (o) |
|---|---|---|---|---|
| Loose | 1.6 | 5 + 0.75 ∙ z | 30 | 0 |
| Medium | 1.8 | 10 + 1.5 ∙ z | 34–30 | 6–0 |
| Dense | 2.0 | 20 + 3 ∙ z | 39–30 | 11–0 |
| FFNN1 (Geotechnical) | FFNN2 (Structural) | |
|---|---|---|
| Input parameters | H, α, Sand type, M | max dx, max dy |
| Target parameters | max dx, max dy | max εt, max εc |
| Architecture | Statistical Variables | RMSE | R2 |
|---|---|---|---|
| LM—10 Hidden Neurons | Median | 0.03698 | 0.99695 |
| Standard Deviation | 0.02278 | 0.00539 | |
| Max | 0.09797 | 0.99876 | |
| Min | 0.02324 | 0.97904 | |
| BR—10 Hidden Neurons | Median | 0.02262 | 0.99885 |
| Standard Deviation | 0.00204 | 0.00020 | |
| Max | 0.02784 | 0.99916 | |
| Min | 0.01905 | 0.99831 | |
| LM—25 Hidden Neurons | Median | 0.04153 | 0.99610 |
| Standard Deviation | 0.02235 | 0.00569 | |
| Max | 0.10206 | 0.99855 | |
| Min | 0.02463 | 0.97917 | |
| BR—25 Hidden Neurons | Median | 0.02334 | 0.99885 |
| Standard Deviation | 0.00688 | 0.00081 | |
| Max | 0.04677 | 0.99962 | |
| Min | 0.01297 | 0.99542 | |
| LM—50 Hidden Neurons | Median | 0.15587 | 0.95146 |
| Standard Deviation | 0.04422 | 0.03045 | |
| Max | 0.28601 | 0.98646 | |
| Min | 0.07902 | 0.84409 | |
| BR—50 Hidden Neurons | Median | 0.02205 | 0.99897 |
| Standard Deviation | 0.00646 | 0.00067 | |
| Max | 0.03853 | 0.99979 | |
| Min | 0.00969 | 0.99696 |
| Architecture | Statistical Variables | RMSE | R2 |
|---|---|---|---|
| LM—5 Hidden Neurons | Median | 0.27155 | 0.78168 |
| Standard Deviation | 0.04859 | 0.04432 | |
| Max | 0.45701 | 0.85027 | |
| Min | 0.21981 | 0.68250 | |
| BR—5 Hidden Neurons | Median | 0.29566 | 0.72811 |
| Standard Deviation | 0.00278 | 0.00511 | |
| Max | 0.29879 | 0.75549 | |
| Min | 0.28145 | 0.72533 | |
| LM—10 Hidden Neurons | Median | 0.23587 | 0.83134 |
| Standard Deviation | 0.04046 | 0.05297 | |
| Max | 0.35286 | 0.87156 | |
| Min | 0.20347 | 0.64175 | |
| BR—10 Hidden Neurons | Median | 0.29587 | 0.72799 |
| Standard Deviation | 0.01386 | 0.02695 | |
| Max | 0.29916 | 0.83781 | |
| Min | 0.22979 | 0.72135 | |
| LM—25 Hidden Neurons | Median | 0.24025 | 0.83521 |
| Standard Deviation | 0.05237 | 0.08218 | |
| Max | 0.40672 | 0.86591 | |
| Min | 0.20778 | 0.52519 | |
| BR—25 Hidden Neurons | Median | 0.22004 | 0.85013 |
| Standard Deviation | 0.02441 | 0.03798 | |
| Max | 0.30105 | 0.85634 | |
| Min | 0.21514 | 0.72450 | |
| LM—50 Hidden Neurons | Median | 0.24151 | 0.81832 |
| Standard Deviation | 0.05512 | 0.06510 | |
| Max | 0.38717 | 0.90133 | |
| Min | 0.17772 | 0.63919 | |
| BR—50 Hidden Neurons | Median | 0.21655 | 0.85377 |
| Standard Deviation | 0.00999 | 0.01015 | |
| Max | 0.25247 | 0.86430 | |
| Min | 0.20890 | 0.82439 |
| Architecture | Statistical Variables | RMSE | R2 |
|---|---|---|---|
| LM—5 × 10 Hidden Neurons | Median | 0.26565 | 0.82506 |
| Standard Deviation | 0.05739 | 0.04323 | |
| Max | 0.47187 | 0.88050 | |
| Min | 0.21242 | 0.72356 | |
| BR—5 × 10 Hidden Neurons | Median | 0.29571 | 0.76856 |
| Standard Deviation | 0.02252 | 0.03180 | |
| Max | 0.29722 | 0.88047 | |
| Min | 0.21246 | 0.76587 | |
| LM—10 × 5 Hidden Neurons | Median | 0.23103 | 0.86412 |
| Standard Deviation | 0.03109 | 0.04338 | |
| Max | 0.34773 | 0.90018 | |
| Min | 0.19409 | 0.68232 | |
| BR—10 × 5 Hidden Neurons | Median | 0.29513 | 0.76904 |
| Standard Deviation | 0.03057 | 0.03993 | |
| Max | 0.30058 | 0.90850 | |
| Min | 0.18706 | 0.76318 | |
| LM—10 × 10 Hidden Neurons | Median | 0.25370 | 0.83276 |
| Standard Deviation | 0.05271 | 0.04883 | |
| Max | 0.42663 | 0.93434 | |
| Min | 0.15752 | 0.71802 | |
| BR—10 × 10 Hidden Neurons | Median | 0.29577 | 0.76843 |
| Standard Deviation | 0.00151 | 0.00172 | |
| Max | 0.30071 | 0.76963 | |
| Min | 0.29467 | 0.76257 | |
| LM—10 × 25 Hidden Neurons | Median | 0.23298 | 0.86119 |
| Standard Deviation | 0.06378 | 0.06466 | |
| Max | 0.43960 | 0.94042 | |
| Min | 0.14983 | 0.65386 | |
| BR—10 × 25 Hidden Neurons | Median | 0.29586 | 0.76807 |
| Standard Deviation | 0.02948 | 0.03941 | |
| Max | 0.37691 | 0.87892 | |
| Min | 0.21367 | 0.66373 | |
| LM—25 × 10 Hidden Neurons | Median | 0.24362 | 0.84878 |
| Standard Deviation | 0.10106 | 0.06233 | |
| Max | 0.75498 | 0.90155 | |
| Min | 0.19536 | 0.63703 | |
| BR—25 × 10 Hidden Neurons | Median | 0.29542 | 0.76880 |
| Standard Deviation | 0.00126 | 0.00159 | |
| Max | 0.29925 | 0.76983 | |
| Min | 0.29438 | 0.76335 | |
| LM—25 × 25 Hidden Neurons | Median | 0.24299 | 0.85201 |
| Standard Deviation | 0.09679 | 0.10996 | |
| Max | 0.55564 | 0.89903 | |
| Min | 0.19498 | 0.32879 | |
| BR—25 × 25 Hidden Neurons | Median | 0.29525 | 0.76875 |
| Standard Deviation | 0.02397 | 0.03263 | |
| Max | 0.29890 | 0.87516 | |
| Min | 0.21697 | 0.76328 | |
| LM—50 × 10 Hidden Neurons | Median | 0.23846 | 0.86035 |
| Standard Deviation | 0.06901 | 0.09167 | |
| Max | 0.46603 | 0.92467 | |
| Min | 0.17090 | 0.47852 | |
| BR—50 × 10 Hidden Neurons | Median | 0.21545 | 0.87729 |
| Standard Deviation | 0.03271 | 0.04266 | |
| Max | 0.30066 | 0.93083 | |
| Min | 0.16150 | 0.75999 | |
| LM—10 × 50 Hidden Neurons | Median | 0.23592 | 0.85442 |
| Standard Deviation | 0.07041 | 0.07959 | |
| Max | 0.49993 | 0.90093 | |
| Min | 0.19422 | 0.57819 | |
| BR—10 × 50 Hidden Neurons | Median | 0.29554 | 0.76844 |
| Standard Deviation | 0.01753 | 0.02313 | |
| Max | 0.29964 | 0.89289 | |
| Min | 0.20085 | 0.76273 |
| Hidden Neurons | Training Algorithm | Abaqus dx/dy | FFNN dx/dy | Error (%) dx/dy |
|---|---|---|---|---|
| 10 | LM | 1.52/2.25 | 1.55/2.19 | 2.15/2.71 |
| BR | 1.58/2.21 | 3.91/1.73 | ||
| 25 | LM | 1.53/2.23 | 0.93/0.89 | |
| BR | 1.54/2.22 | 1.61/1.63 | ||
| 50 | LM | 1.51/2.26 | 0.71/0.09 | |
| BR | 1.54/2.26 | 1.47/0.41 |
| Hidden Neurons | Training Algorithm | Abaqus εt/εc | FFNN εt/εc | Error (%) εt/εc |
|---|---|---|---|---|
| 5 | LM | 2.14/1.02 | 1.83/0.85 | 14.57/16.51 |
| BR | 1.71/0.80 | 20.30/21.56 | ||
| 10 | LM | 1.83/0.87 | 14.67/14.35 | |
| BR | 1.71/0.80 | 20.02/21.27 | ||
| 25 | LM | 2.05/0.90 | 4.13/11.81 | |
| BR | 1.83/0.87 | 14.47/14.68 | ||
| 50 | LM | 2.26/1.00 | 5.87/1.93 | |
| BR | 1.86/0.88 | 13.07/14.17 |
| Hidden Neurons | Training Algorithm | Abaqus εt/εc | FFNN εt/εc | Error (%) εt/εc |
|---|---|---|---|---|
| 5 × 10 | LM | 2.14/1.02 | 1.80/0.87 | 15.62/14.58 |
| BR | 1.70/0.80 | 20.37/21.59 | ||
| 10 × 5 | LM | 1.87/0.90 | 12.59/12.09 | |
| BR | 1.71/0.81 | 19.91/21.12 | ||
| 10 × 10 | LM | 1.95/0.87 | 9.00/14.66 | |
| BR | 1.71/0.80 | 20.11/21.36 | ||
| 10 × 25 | LM | 2.00/0.87 | 6.72/14.73 | |
| BR | 1.71/0.80 | 20.04/21.32 | ||
| 25 × 10 | LM | 2.07/0.87 | 3.39/14.47 | |
| BR | 1.70/0.80 | 20.49/21.71 | ||
| 25 × 25 | LM | 2.09/0.97 | 2.32/5.46 | |
| BR | 1.71/0.80 | 20.15/21.22 | ||
| 50 × 10 | LM | 2.17/1.01 | 1.56/1.10 | |
| BR | 1.87/0.88 | 12.62/13.40 | ||
| 10 × 50 | LM | 1.96/0.80 | 8.23/22.04 | |
| BR | 1.71/0.81 | 20.00/21.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makrakis, N.; Psarropoulos, P.N.; Tsompanakis, Y. ANN-Based Assessment of Soft Surface Soil Layers’ Impact on Fault Rupture Propagation and Kinematic Distress of Gas Pipelines. Infrastructures 2023, 8, 6. https://doi.org/10.3390/infrastructures8010006
Makrakis N, Psarropoulos PN, Tsompanakis Y. ANN-Based Assessment of Soft Surface Soil Layers’ Impact on Fault Rupture Propagation and Kinematic Distress of Gas Pipelines. Infrastructures. 2023; 8(1):6. https://doi.org/10.3390/infrastructures8010006
Chicago/Turabian StyleMakrakis, Nikolaos, Prodromos N. Psarropoulos, and Yiannis Tsompanakis. 2023. "ANN-Based Assessment of Soft Surface Soil Layers’ Impact on Fault Rupture Propagation and Kinematic Distress of Gas Pipelines" Infrastructures 8, no. 1: 6. https://doi.org/10.3390/infrastructures8010006
APA StyleMakrakis, N., Psarropoulos, P. N., & Tsompanakis, Y. (2023). ANN-Based Assessment of Soft Surface Soil Layers’ Impact on Fault Rupture Propagation and Kinematic Distress of Gas Pipelines. Infrastructures, 8(1), 6. https://doi.org/10.3390/infrastructures8010006








