Arbitrarily Oriented Phase Randomization of Design Ground Motions by Continuous Wavelets
Abstract
:1. Introduction
2. Stochastic Method
2.1. Conventional Fourier Analysis
2.2. Modification Using DWT
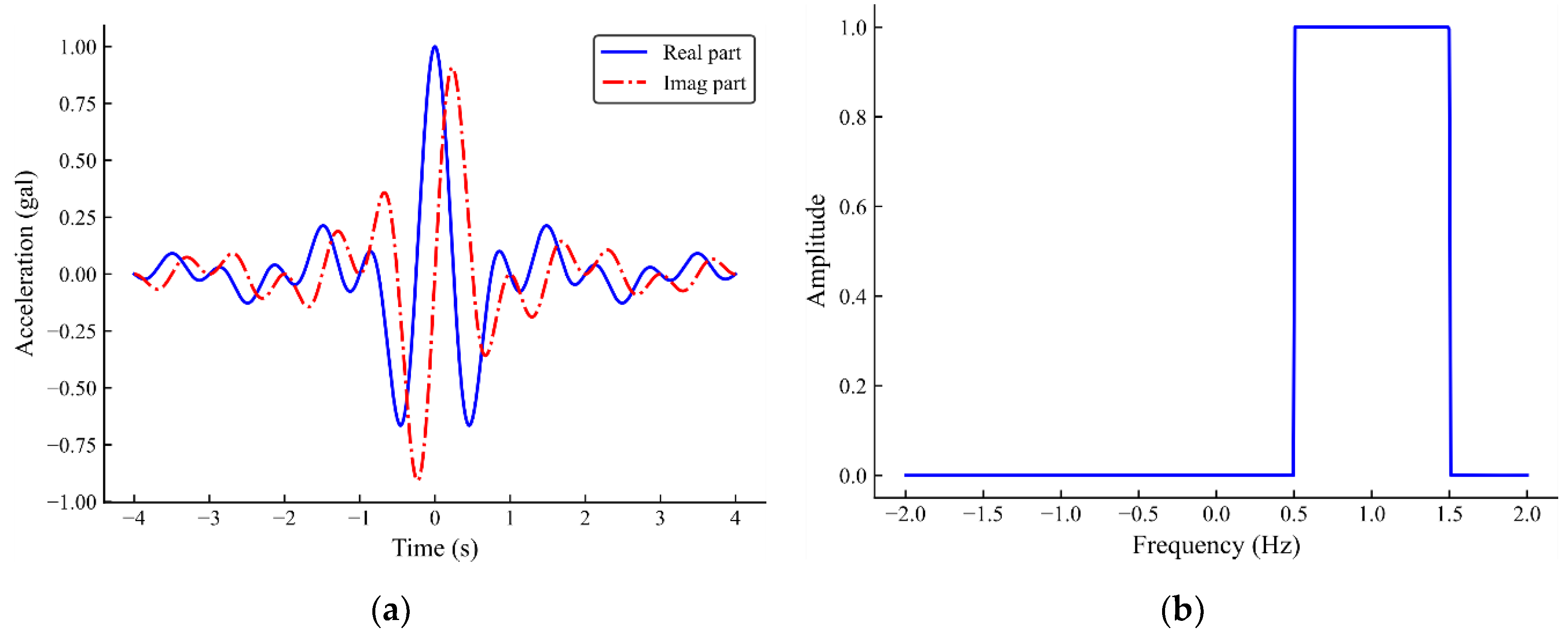
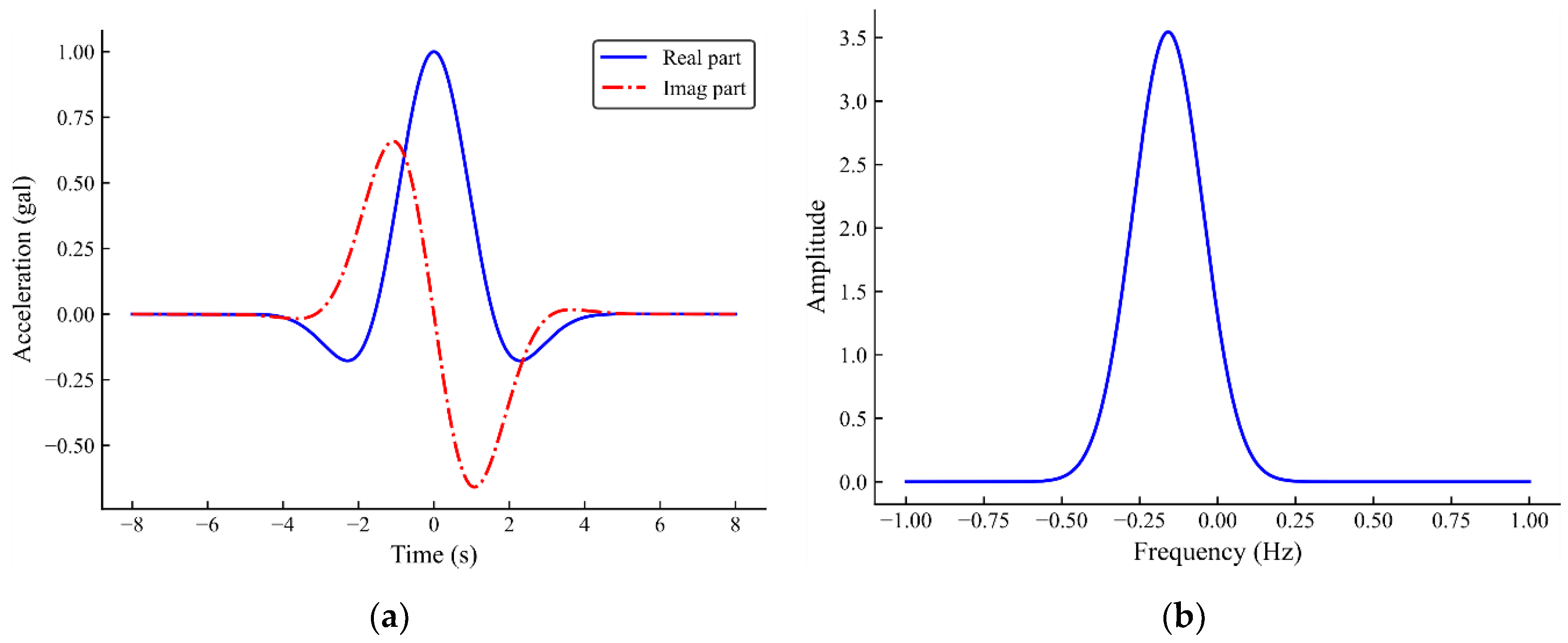
3. Modified Inverse CWT
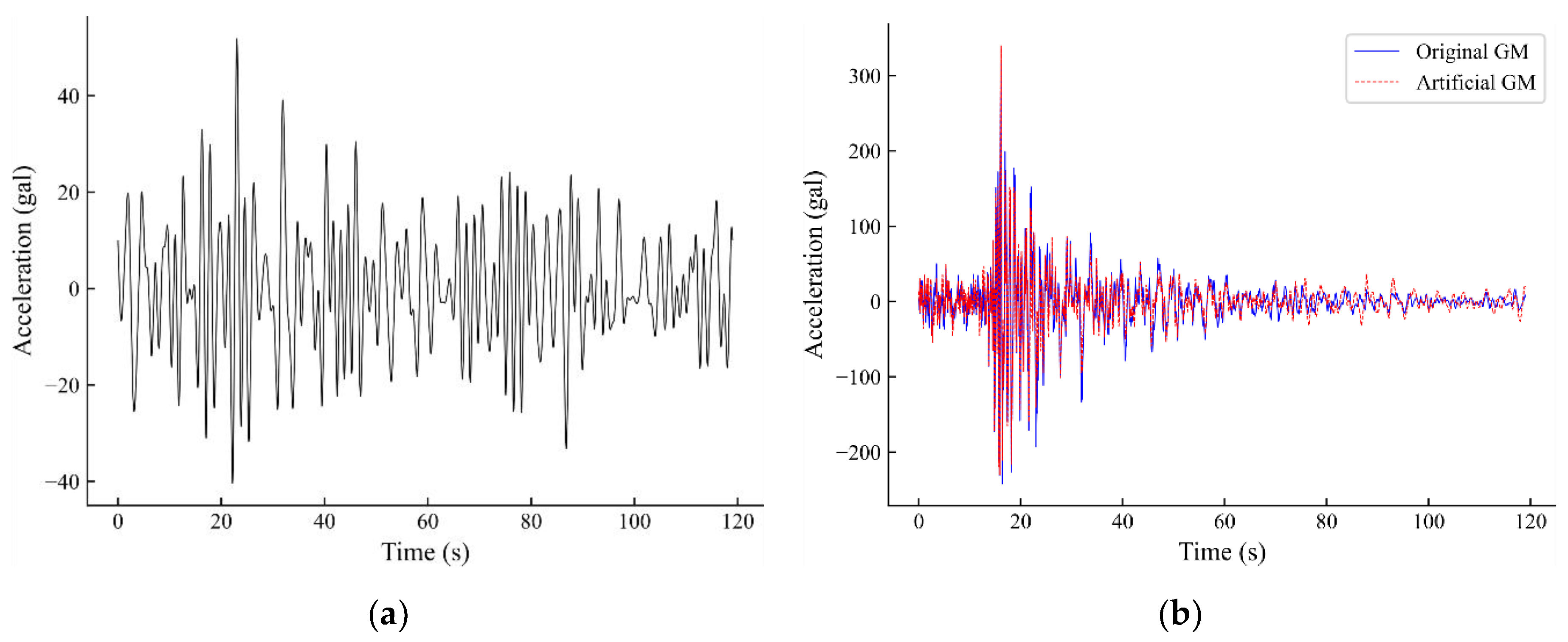
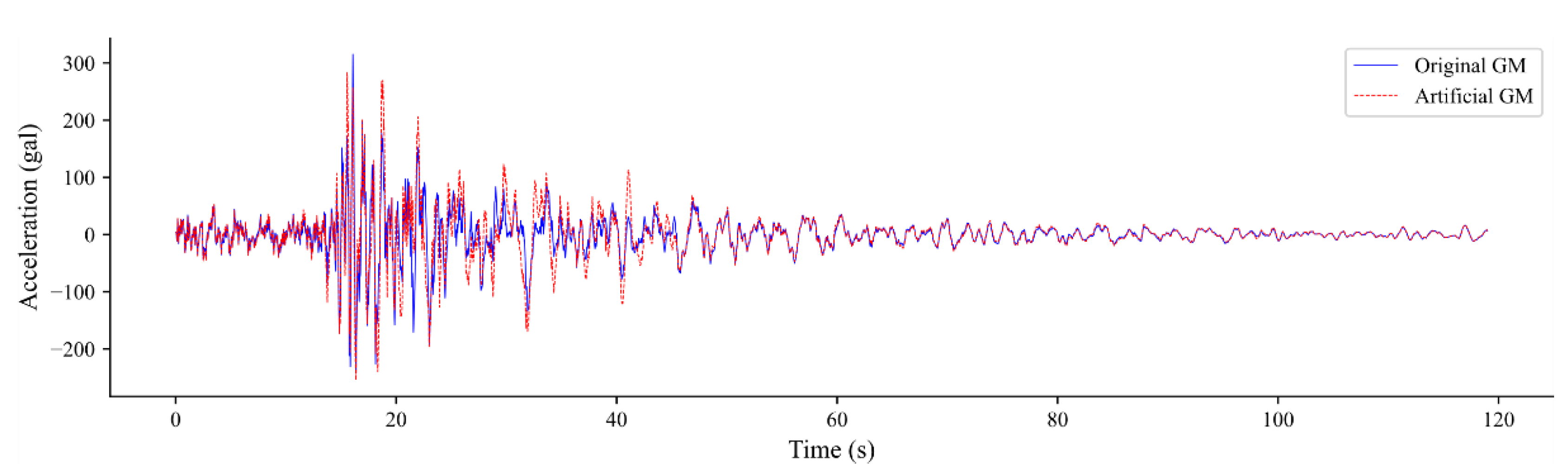
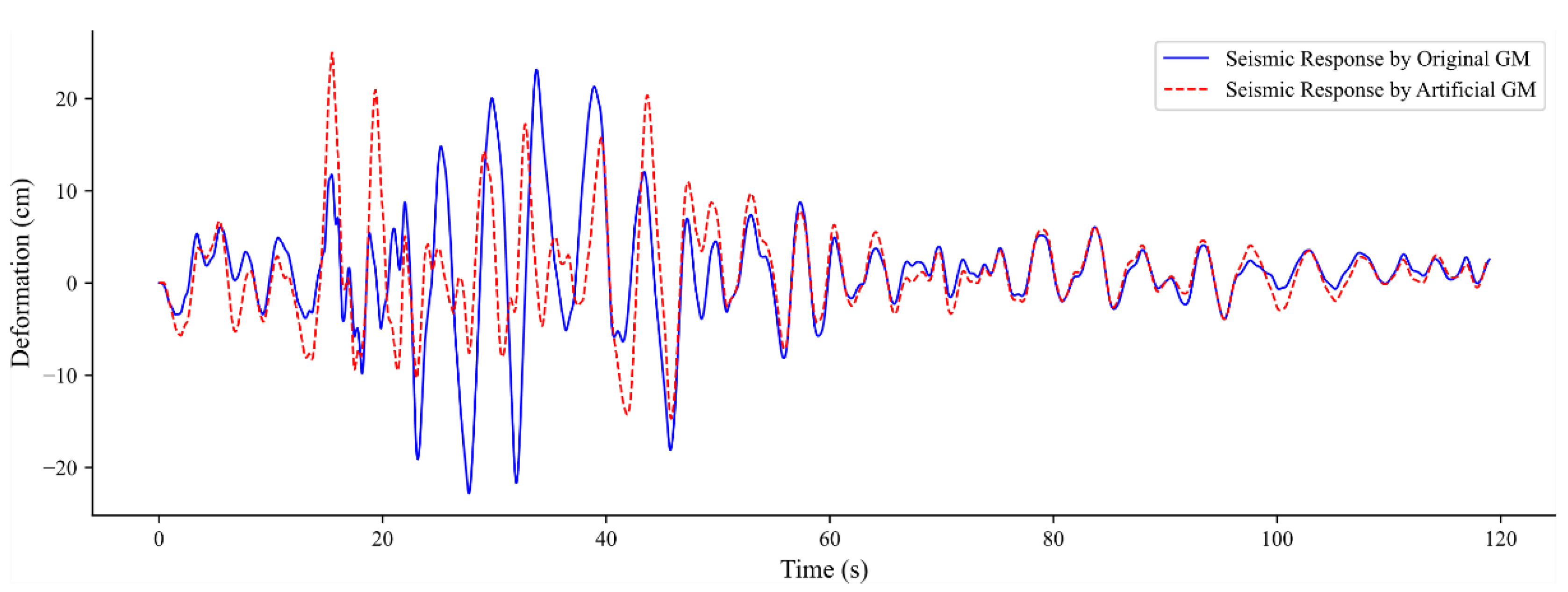
4. Numerical Simulation
4.1. Spectral Analysis
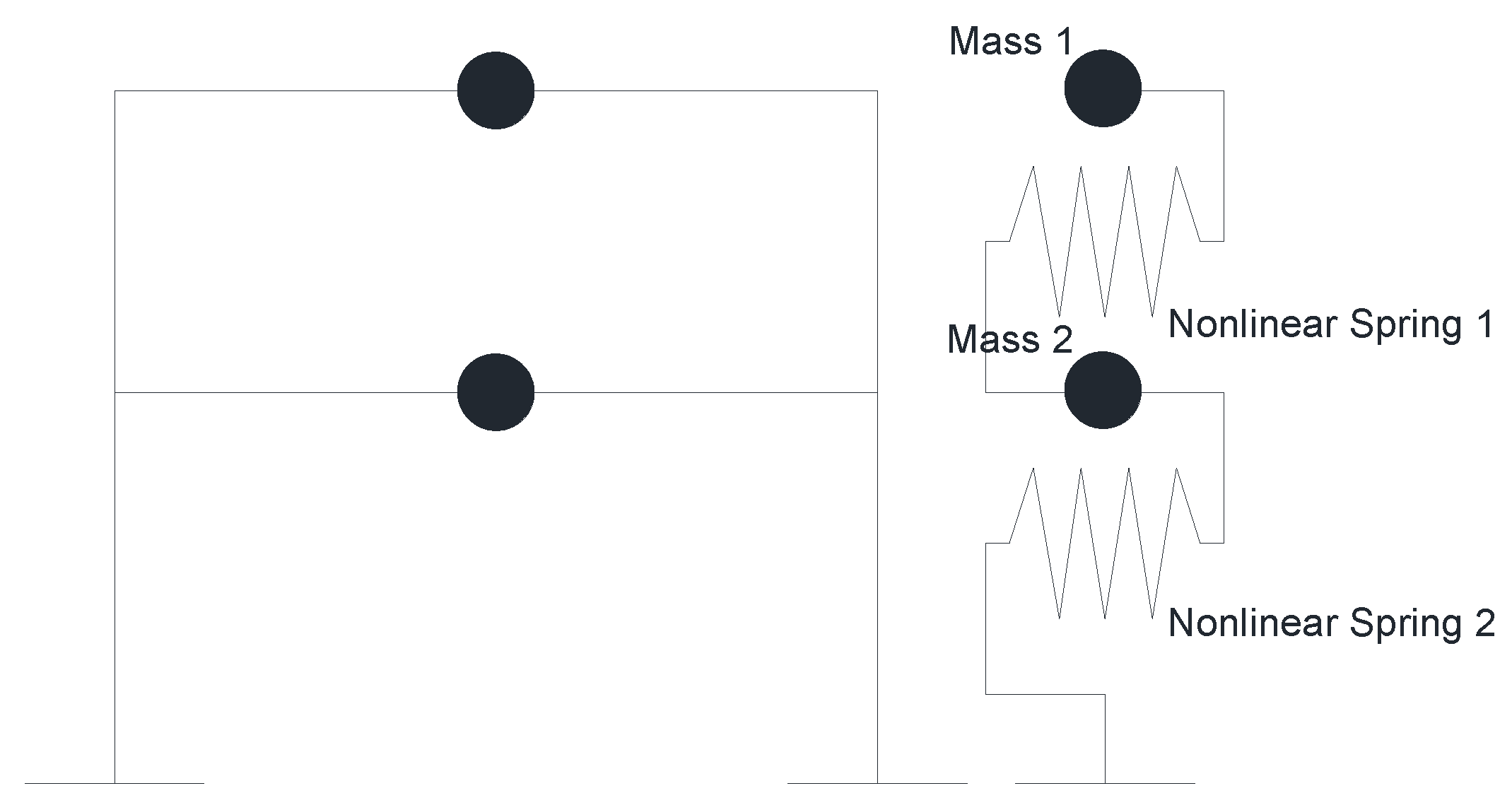
4.2. Dynamic Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, H.; Zhuo, W.; Lavorato, D.; Nuti, C.; Fiorentino, G.; Marano, G.C.; Greco, R.; Briseghella, B. Probabilistic seismic response and uncertainty analysis of continuous bridges under near-fault ground motions. Front. Struct. Civ. Eng. 2019, 13, 1510–1519. [Google Scholar] [CrossRef]
- Honda, R. Study for implementation of anti-catastrophe-oriented seismic design. J. Jpn. Assoc. Earthq. Eng. 2018, 37, 1077–1086. (In Japanese) [Google Scholar] [CrossRef]
- Jeong, K.H.; Lee, H.S. Ground-motion prediction equation for South Korea based on recent earthquake records. Earthq. Struct. 2018, 15, 29–44. [Google Scholar]
- Atkinson, G.M. The interface between empirical and simulation-based ground-motion models. Pure Appl. Geophys. 2018, 177, 2069–2081. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Atkinson, G.M.; Bommer, J.; Abrahamson, N. Alternative approaches to modeling epistemic uncertainty in ground motions in probabilistic seismic hazard analysis. Seismol. Res. Lett. 2014, 85, 1141–1144. [Google Scholar] [CrossRef]
- Hikita, T.; Koketsu, K.; Miyake, H. Variability of ground motion simulation due to aleatory uncertainty of source parameters. J. Jpn. Assoc. Earthq. Eng. 2020, 20, 21–34. [Google Scholar] [CrossRef]
- Yang, L.; Xie, W.; Xu, W.; Ly, B.L. Generating drift-free, consistent, and perfectly spectrum-compatible time histories. Bull. Seismol. Soc. Am. 2019, 109, 1674–1690. [Google Scholar] [CrossRef]
- Jayaram, N.; Lin, T.; Baker, J.W. A computationally efficient ground-motion selection algorithm for matching a target response spectrum mean and variance. Earthq. Spectra 2011, 27, 797–815. [Google Scholar] [CrossRef]
- Cecini, D.; Palmeri, A. Spectrum-compatible accelerograms with harmonic wavelets. Comput. Struct. 2015, 147, 26–35. [Google Scholar] [CrossRef] [Green Version]
- Zacchei, E.; Molina, J.L. Application of artificial accelerograms to estimating damage to dams using failure criteria. Int. J. Sci. Technol. 2020, 27, 2740–2751. [Google Scholar]
- Boore, D.M. Simulation of ground motion using the Stochastic Method. Pure Appl. Geophys. 2003, 160, 635–676. [Google Scholar] [CrossRef] [Green Version]
- Honda, R.; Ahmed, T. Design input motion synthesis considering the effect of uncertainty in structural and seismic parameters by feature indexes. J. Struct. Eng. 2011, 137, 391–400. [Google Scholar] [CrossRef]
- Honda, R.; Khatri, P.P. Discrete analytic signal wavelet decomposition for phase localized in time-frequency domain for generation of stochastic signal with phase uncertainty. In Proceedings of the 15th Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets; Rutgers University and AT&T Bell Laboratories: Murray Hill, NJ, USA, 1992. [Google Scholar]
- Fugal, D.L. Conceptual Wavelets in Digital Signal Processing; Space & Signals Technologies LLC: Spring Valley, CA, USA, 2009. [Google Scholar]
- Kiban Kyoshin Net (KIK-NET). Available online: http://www.kik.bosai.go.jp (accessed on 14 September 2021).
- Architectural Institute of Japan. Seismic Response Analysis and Design of Buildings Considering Dynamic Soil-Structure Interaction; Architectural Institute of Japan: Tokyo, Japan, 2006. (In Japanese) [Google Scholar]
- The Open System for Earthquake Engineering Simulation. Available online: http://opensees.berkeley.edu (accessed on 14 September 2021).




| Frequency (Hz) | Period (s) | |
|---|---|---|
| 1st Mode | 0.39 | 2.57 |
| 2nd Mode | 0.78 | 1.29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, H.; Honda, R. Arbitrarily Oriented Phase Randomization of Design Ground Motions by Continuous Wavelets. Infrastructures 2021, 6, 144. https://doi.org/10.3390/infrastructures6100144
Xie H, Honda R. Arbitrarily Oriented Phase Randomization of Design Ground Motions by Continuous Wavelets. Infrastructures. 2021; 6(10):144. https://doi.org/10.3390/infrastructures6100144
Chicago/Turabian StyleXie, Haoyu, and Riki Honda. 2021. "Arbitrarily Oriented Phase Randomization of Design Ground Motions by Continuous Wavelets" Infrastructures 6, no. 10: 144. https://doi.org/10.3390/infrastructures6100144
APA StyleXie, H., & Honda, R. (2021). Arbitrarily Oriented Phase Randomization of Design Ground Motions by Continuous Wavelets. Infrastructures, 6(10), 144. https://doi.org/10.3390/infrastructures6100144





