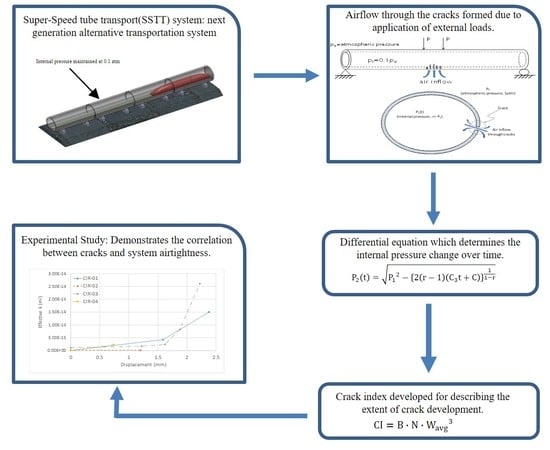
Analytical Model for Air Flow into Cracked Concrete Structures for Super-Speed Tube Transport Systems
Abstract
:1. Introduction
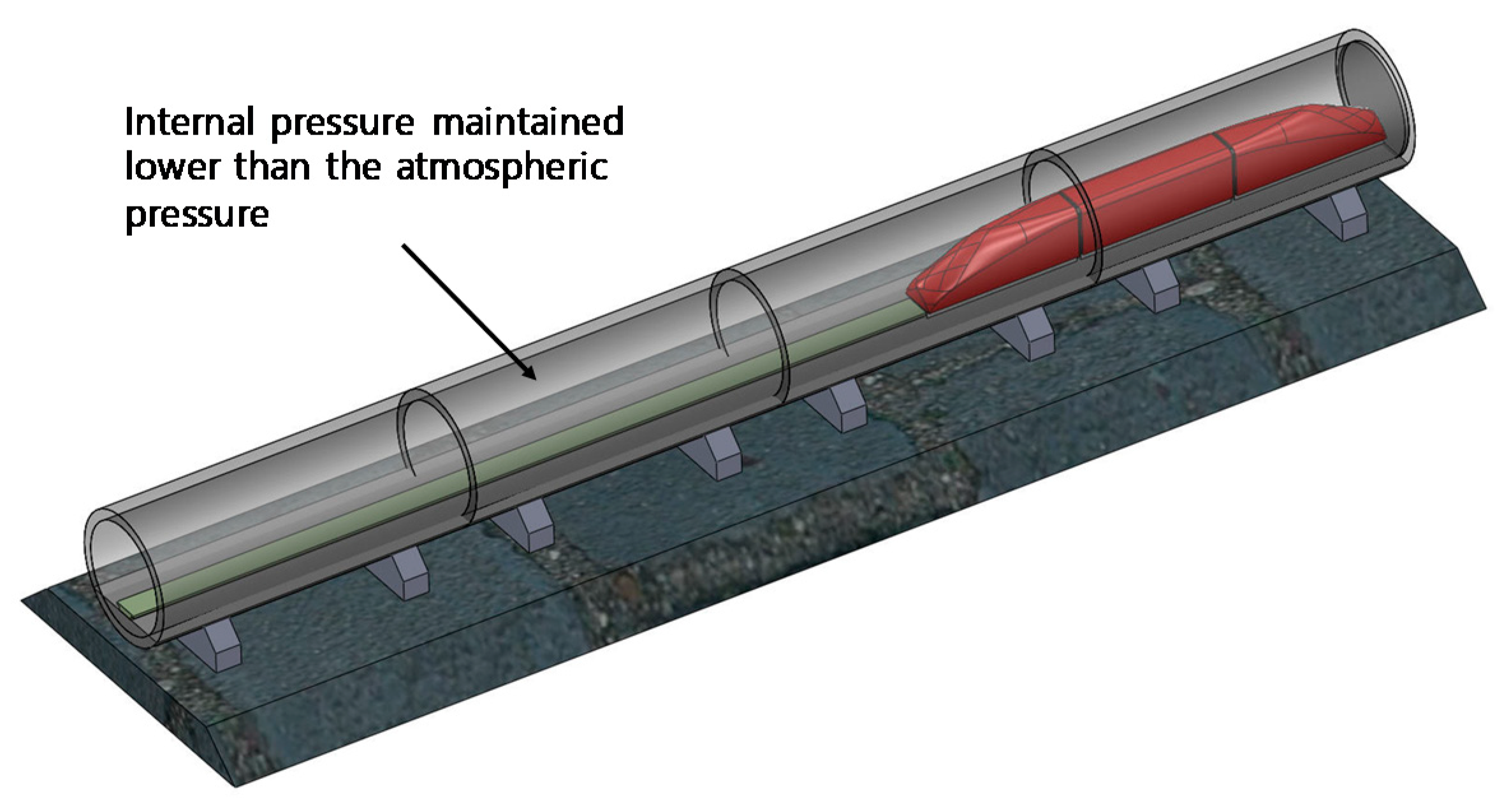
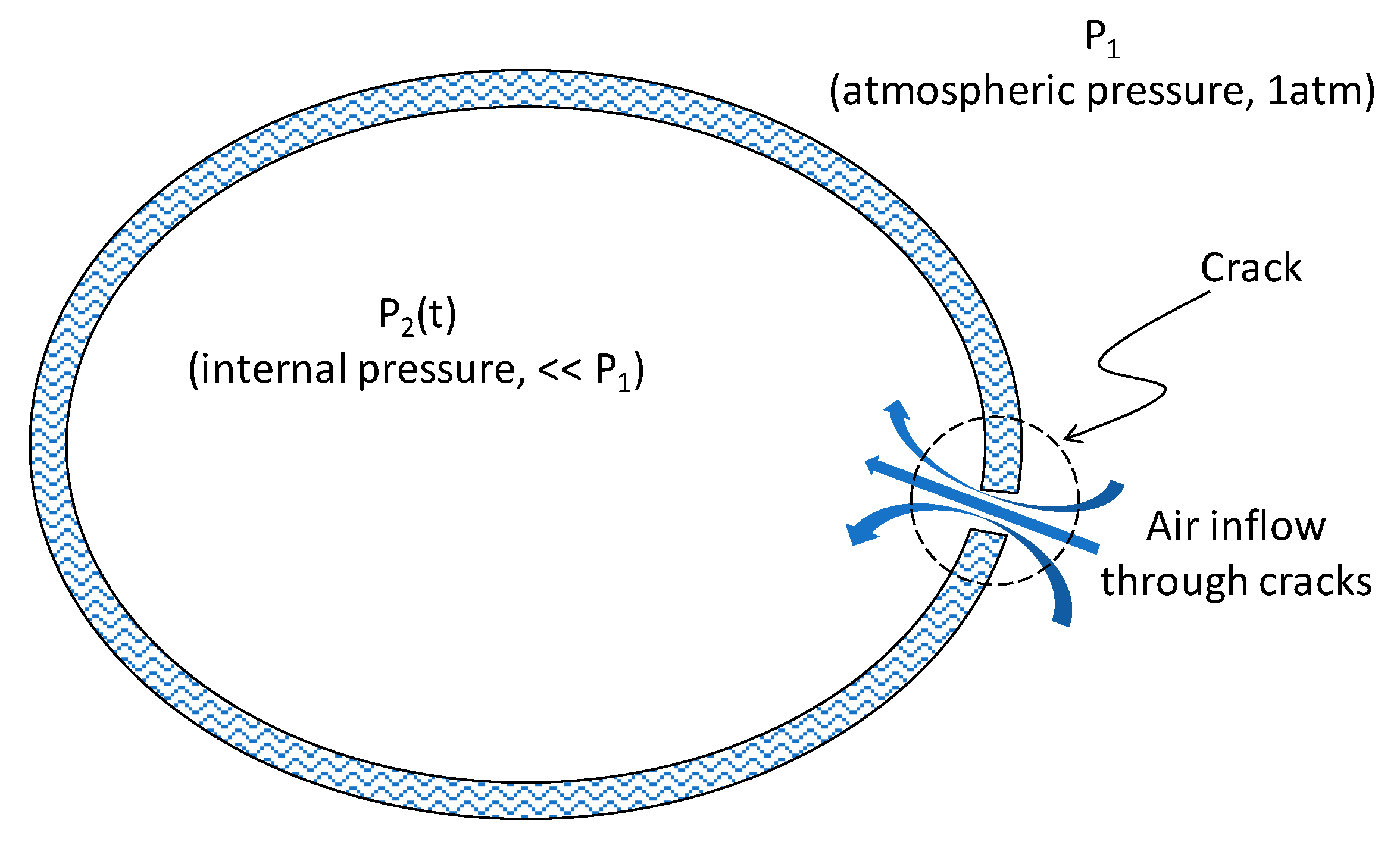
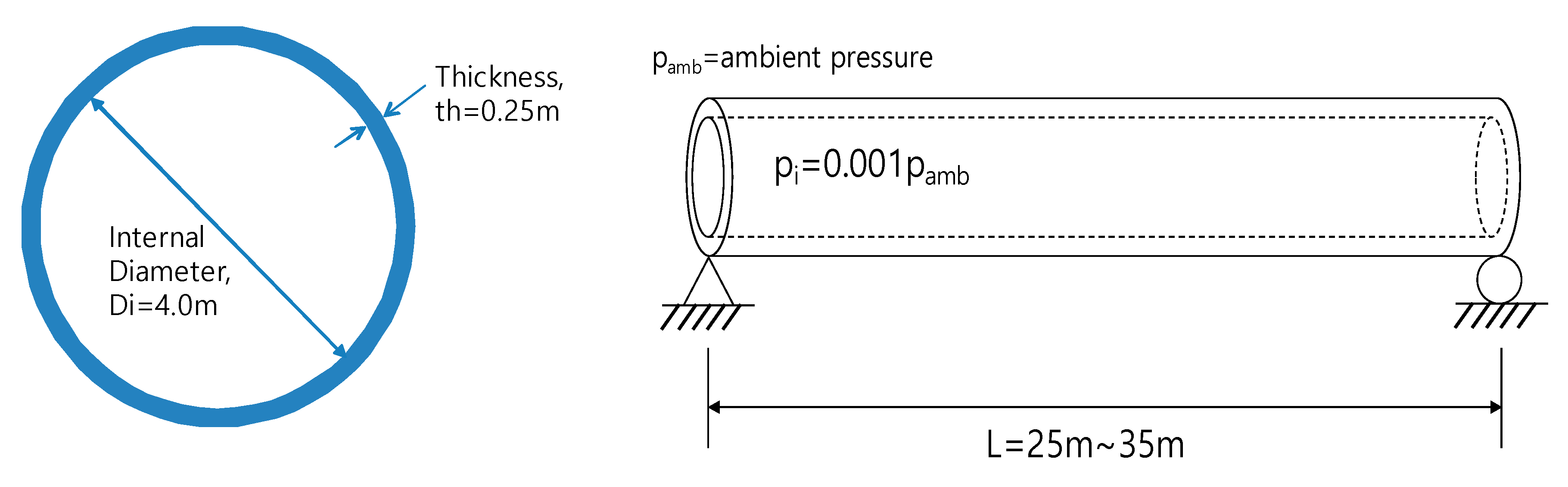
2. Development of Analytical Model for Air Inflow through Cracks
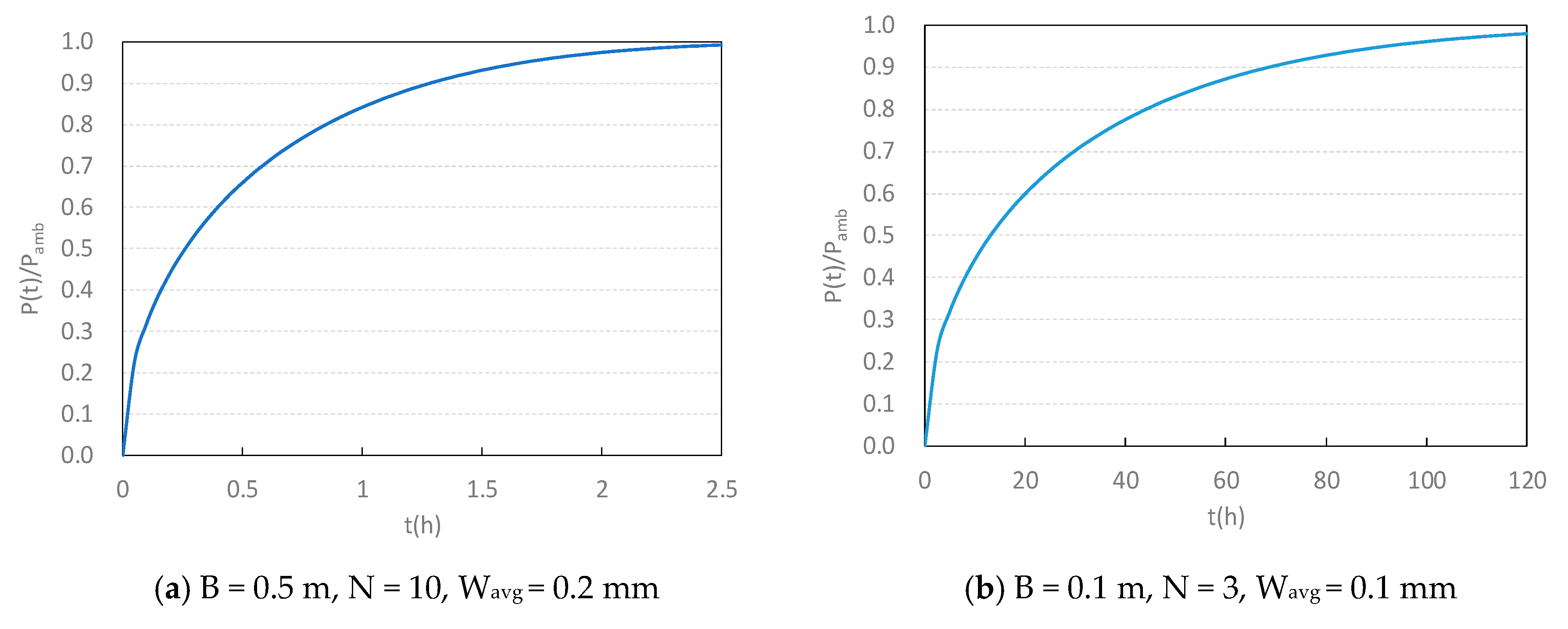
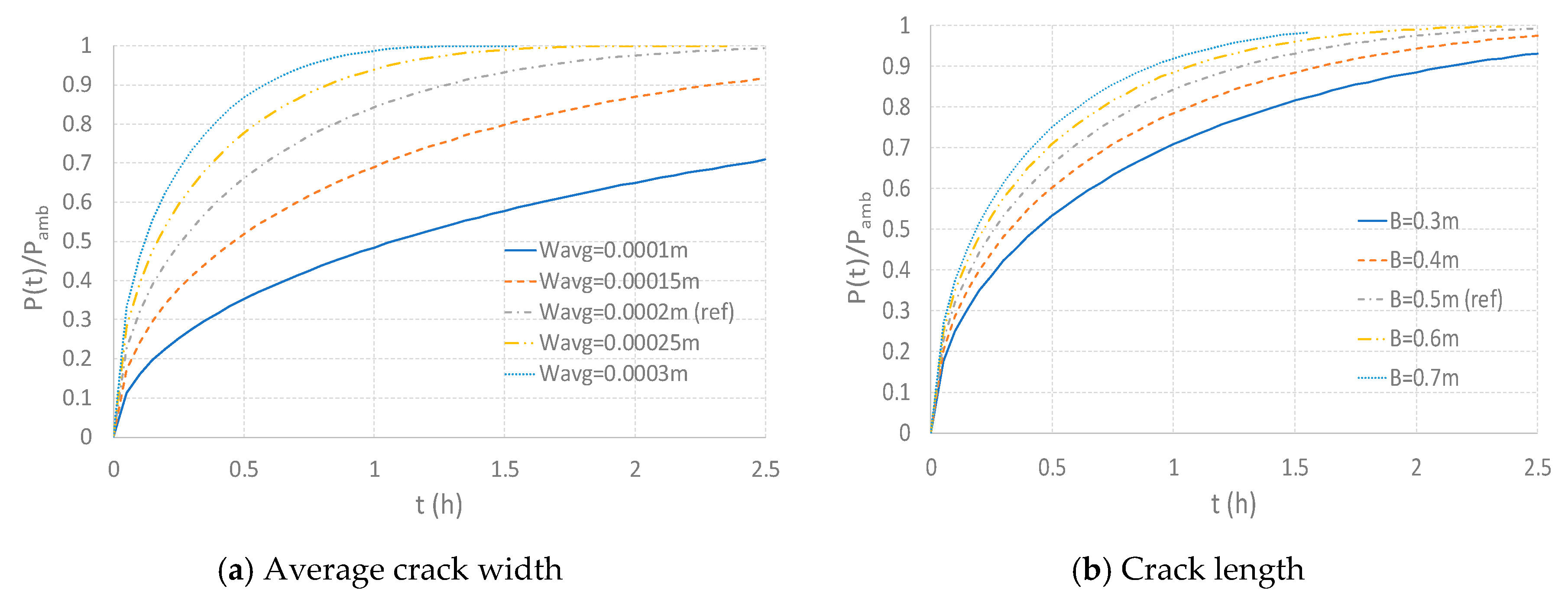
3. Investigation of Crack Effect on the Air Inflow
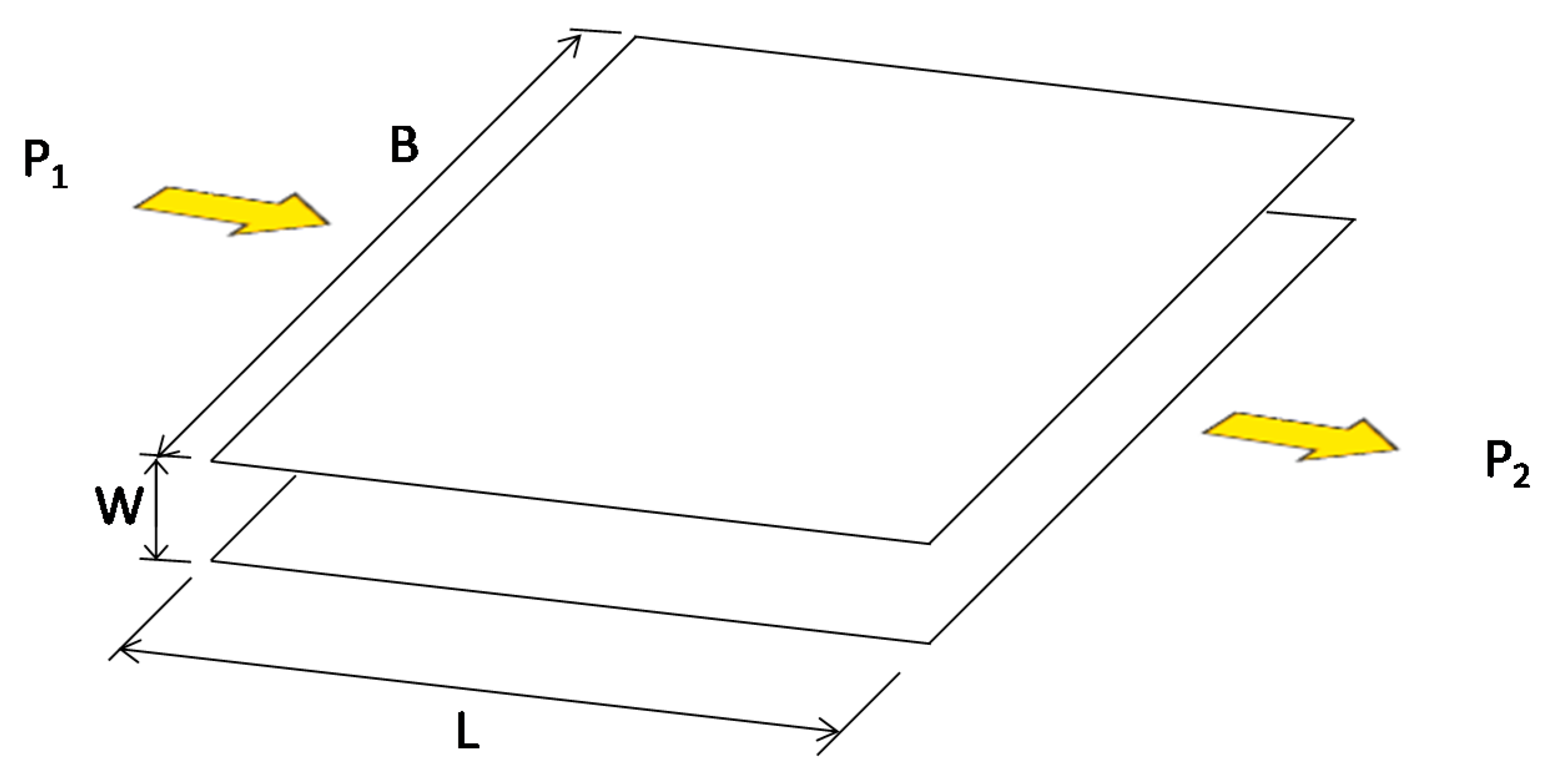
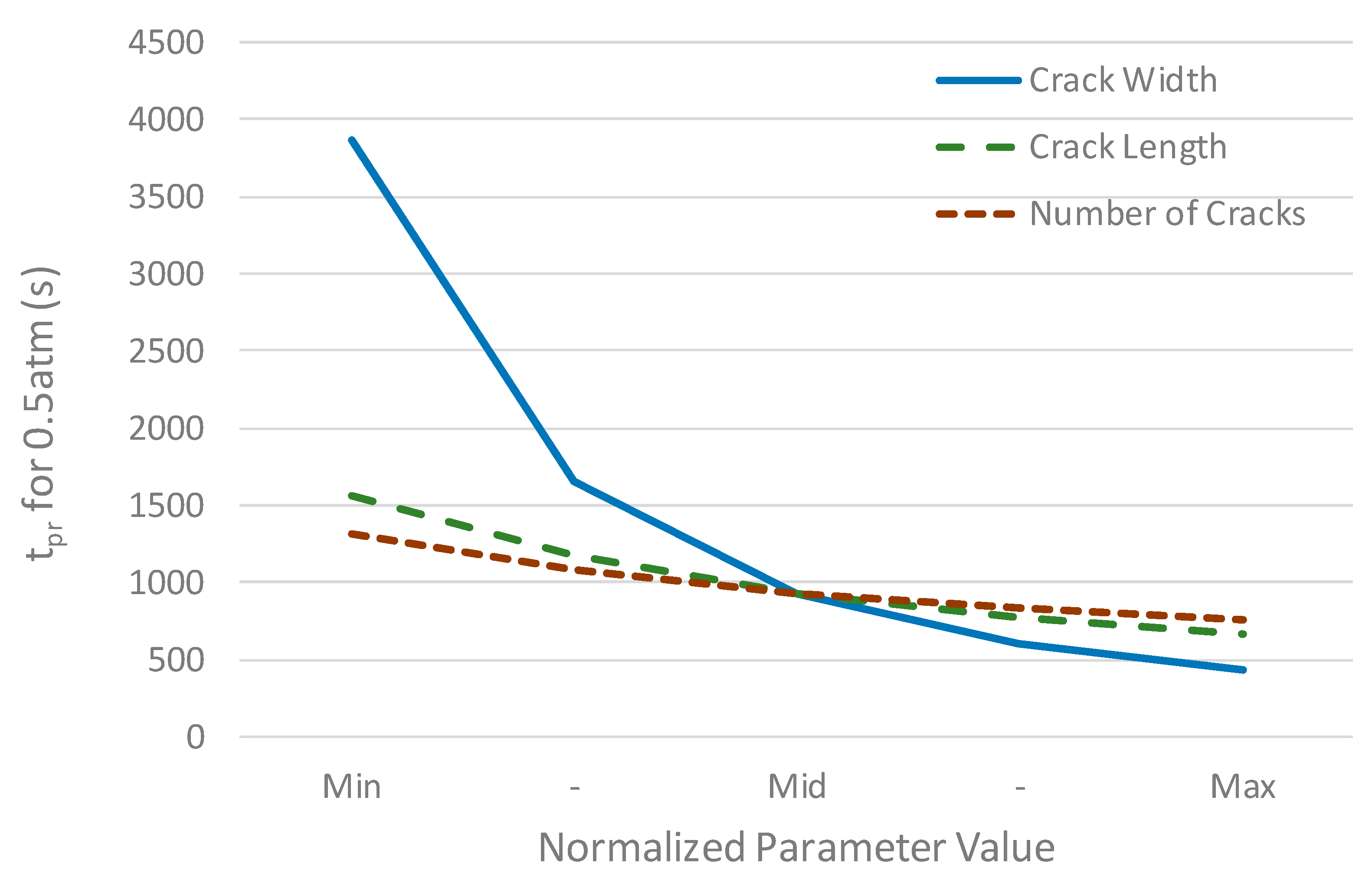
4. Definition of Crack Index for Air-Tightness of Tube Structures
5. Correlation between Cracks and Airtightness: Experimental Demonstration
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cassat, A.; Bourquin, V.; Mossi, M.; Badoux, M.; Vernez, D.; Jufer, M.; Macabrey, N.; Rossel, P. SWISSMETRO—0Project Development Status. In Proceedings of the International Symposium on Speed-up Service Technology for Railway and Maglev Systems (STECH’03), Tokyo, Japan, 19–22 August 2003; pp. 453–460. [Google Scholar]
- Park, J.; Kim, L.H.; Nam, S.W.; Yeo, I. Performance evaluation of airtightness in concrete tube structures for super-speed train systems. Mag. Concr. Res. 2013, 65, 535–545. [Google Scholar] [CrossRef]
- Park, C.H.; Cheon, D.S.; Park, J. Analytical model of fluid flow through closed structures for vacuum tube systems. Math. Probl. Eng. 2015, 2015, 210727. [Google Scholar] [CrossRef] [Green Version]
- Park, C.H.; Synn, J.H.; Park, J. Probabilistic performance assessment of airtightness in concrete tube structures. KSCE J. Civ. Eng. 2016, 20, 1443–1451. [Google Scholar] [CrossRef]
- Mehta, P.; Monteiro, P. Concrete: Microstructure, Properties, and Materials; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- KCI. Concrete Structure Standard; Ministry of Land, Transport and Maritime Affairs: Gyeonggi-do, Seoul, Korea, 2012.
- Park, J.; Cho, J.; Park, H.J. Probabilistic estimation of air-tightness of performance of concrete vacuum tube structures. In Proceedings of the 10th International Symposium on High Performance Concrete—Innovation & Utilization, Beijing, China, 16–18 September 2014. [Google Scholar]
- Soppe, T.E.; Hutchinson, T.C. Assessment of Gas Leakage Rates through Damaged Reinforced-Concrete Walls. J. Mater. Civ. Eng. 2012, 24, 560–567. [Google Scholar] [CrossRef]
- Rizkalla, S.H.; Lau, B.L.; Simmonds, S.H. Air leakage characteristics in reinforced concrete. J. Struct. Eng. 1984, 110, 1149–1162. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, T.; Takiguchi, K.; Hotta, H. Leakage of gas through cracked concrete cracks. Nucl. Eng. Des. 1992, 133, 121–130. [Google Scholar] [CrossRef] [Green Version]
- Nagano, T.; Kowada, A.; Matumura, T.; Inada, Y.; Yajima, K. Experimental study of leakage through residual shear cracks on R/C walls. In Proceedings of the Structural Mechanics in Reactor Technology, Raleigh, NC, USA, 14–18 August 1989; pp. 139–144. [Google Scholar]
- Greiner, U.; Ramm, W. Air leakage characteristics in cracked concrete. Nucl. Eng. Des. 1995, 156, 167–172. [Google Scholar] [CrossRef] [Green Version]
- RPS Structure. Structural Requirements and Basic Design of Next Generation of Ultra-High Speed Transportation Tube System; Project Report; KICT: Ilsan, Korea, 2016. [Google Scholar]
- Ziari, A.; Kianoush, M.R. Investigation of flexural cracking and leakage in RC liquid containing structures. Eng. Struct. 2009, 31, 1056–1067. [Google Scholar] [CrossRef]
- Frosch, R.J. Another look at cracking and crack control in reinforced concrete. ACI Struct. J. 1999, 96, 437–442. [Google Scholar]

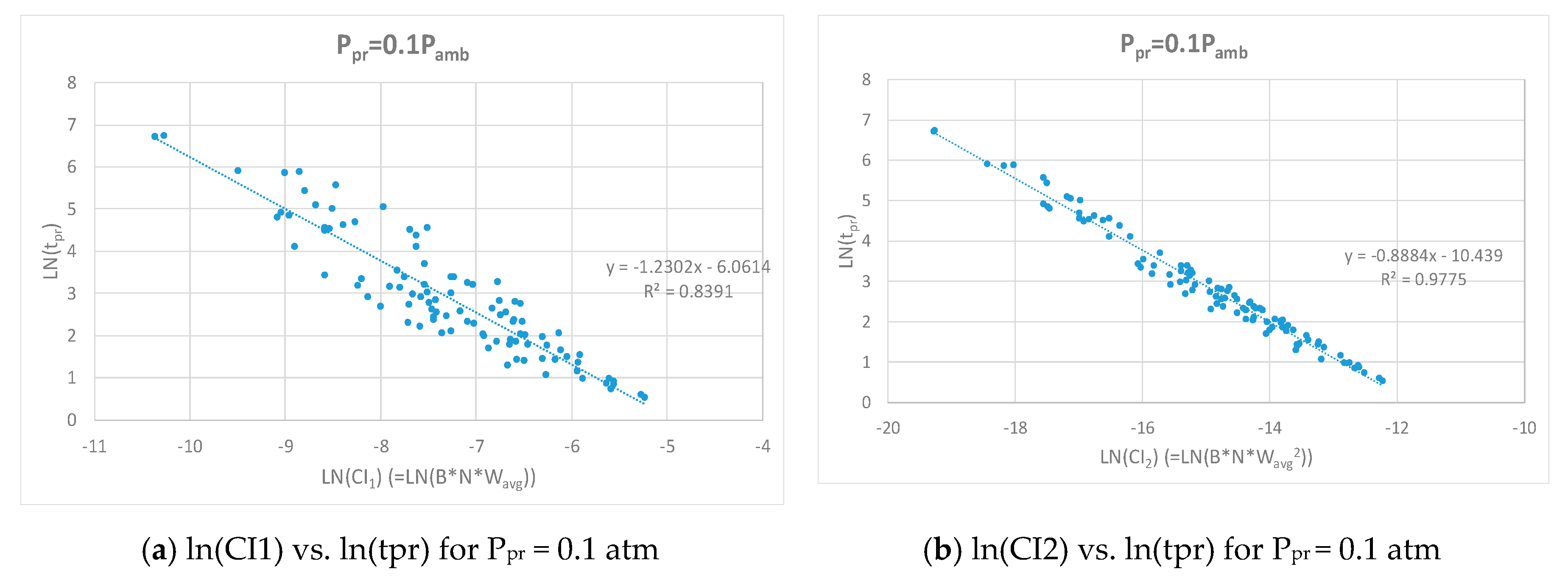
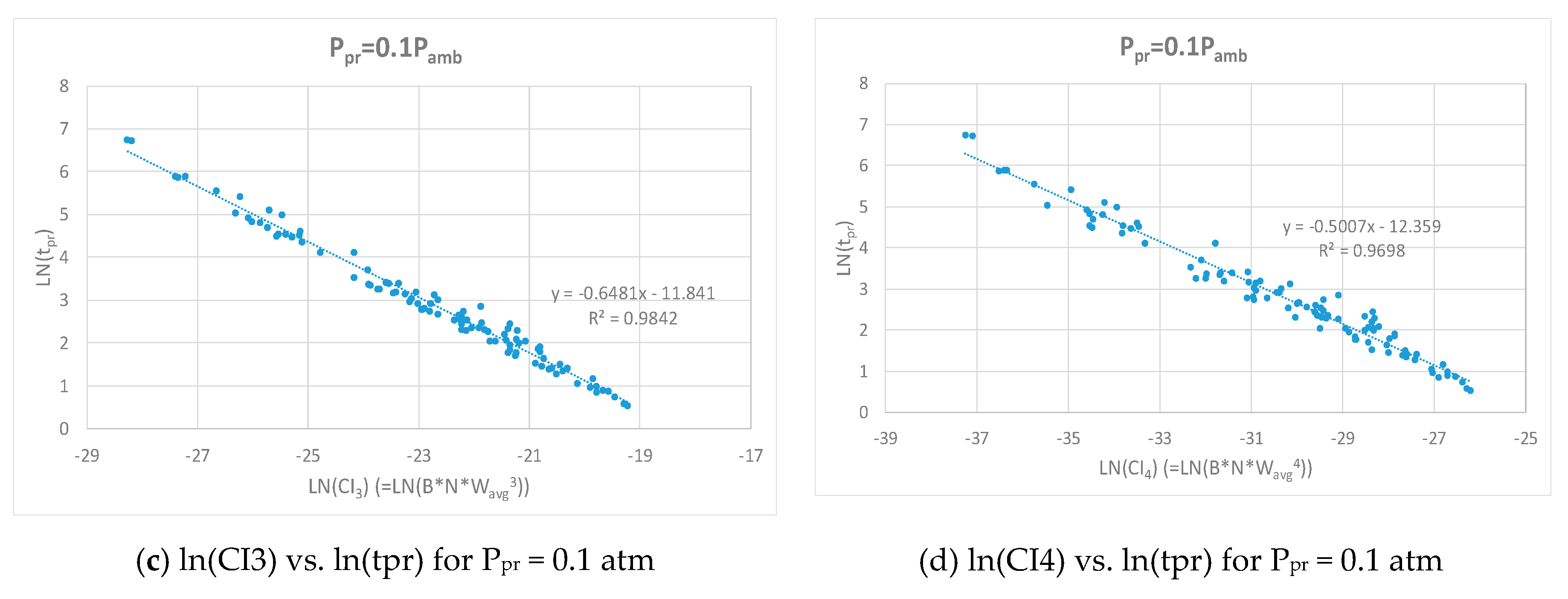
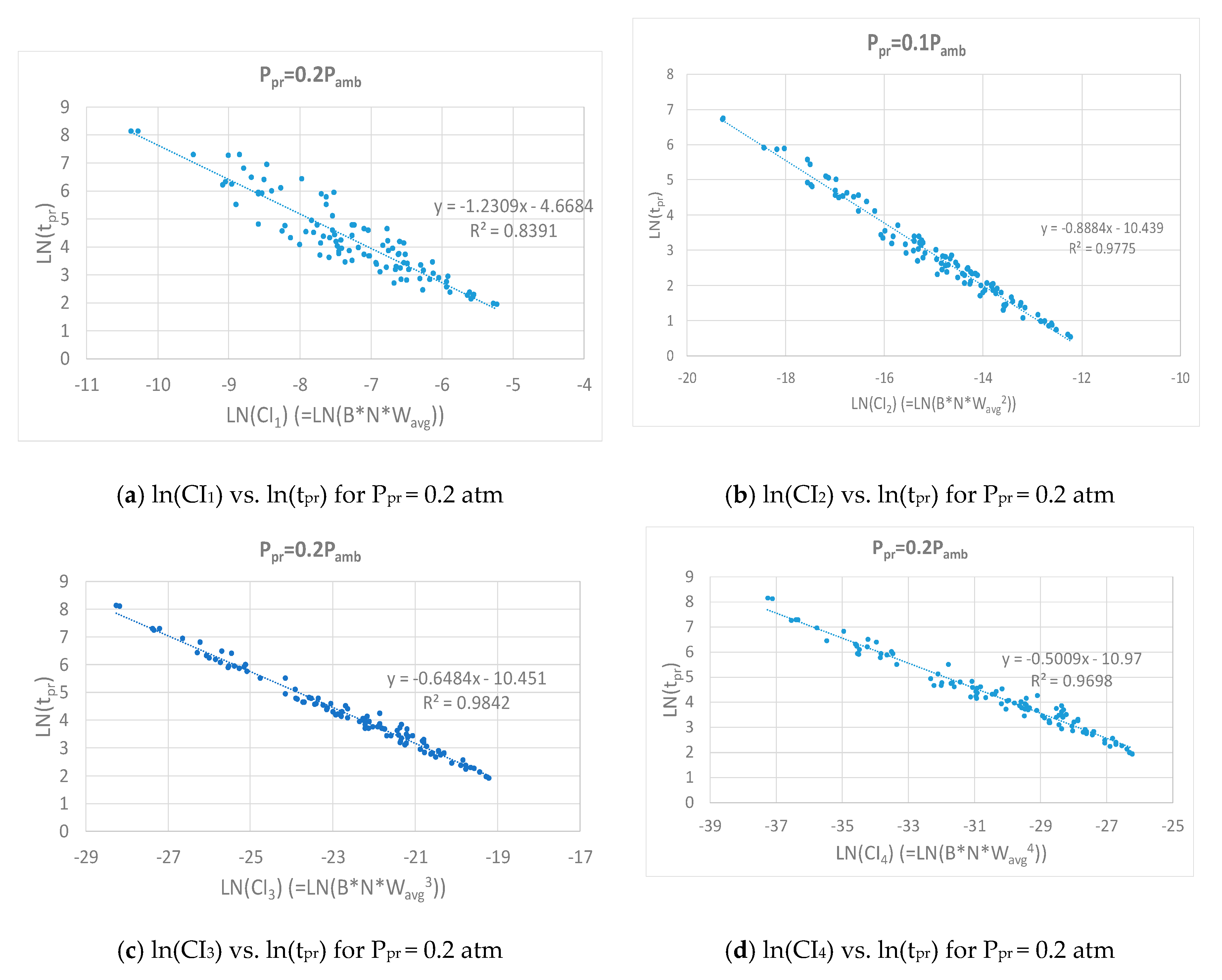
| Control Variable | Minimum Value | Maximum Value |
|---|---|---|
| B (m) | 0.1 | 0.7 |
| N | 1 | 10 |
| Wavg (m) | 0.0001 | 0.001 |
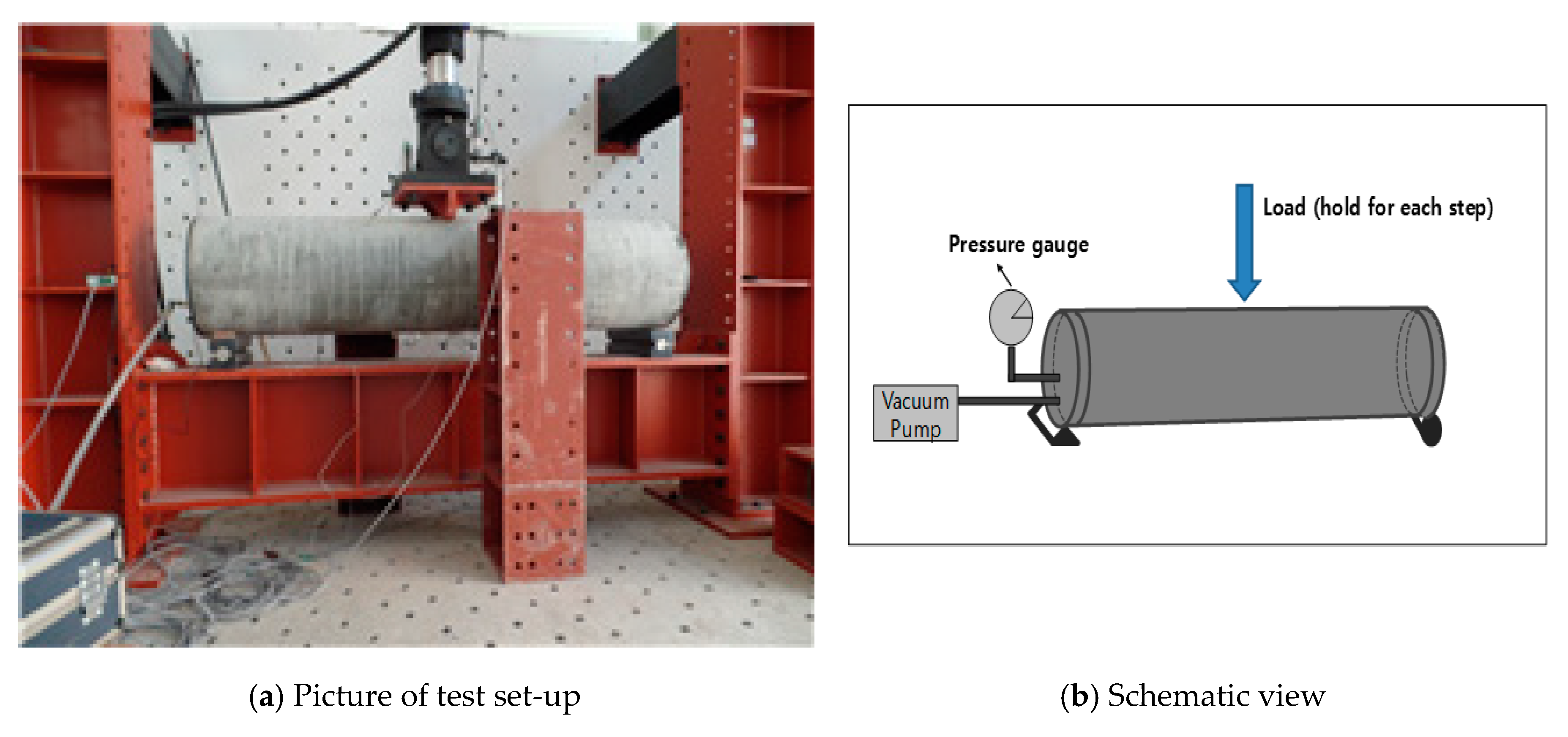
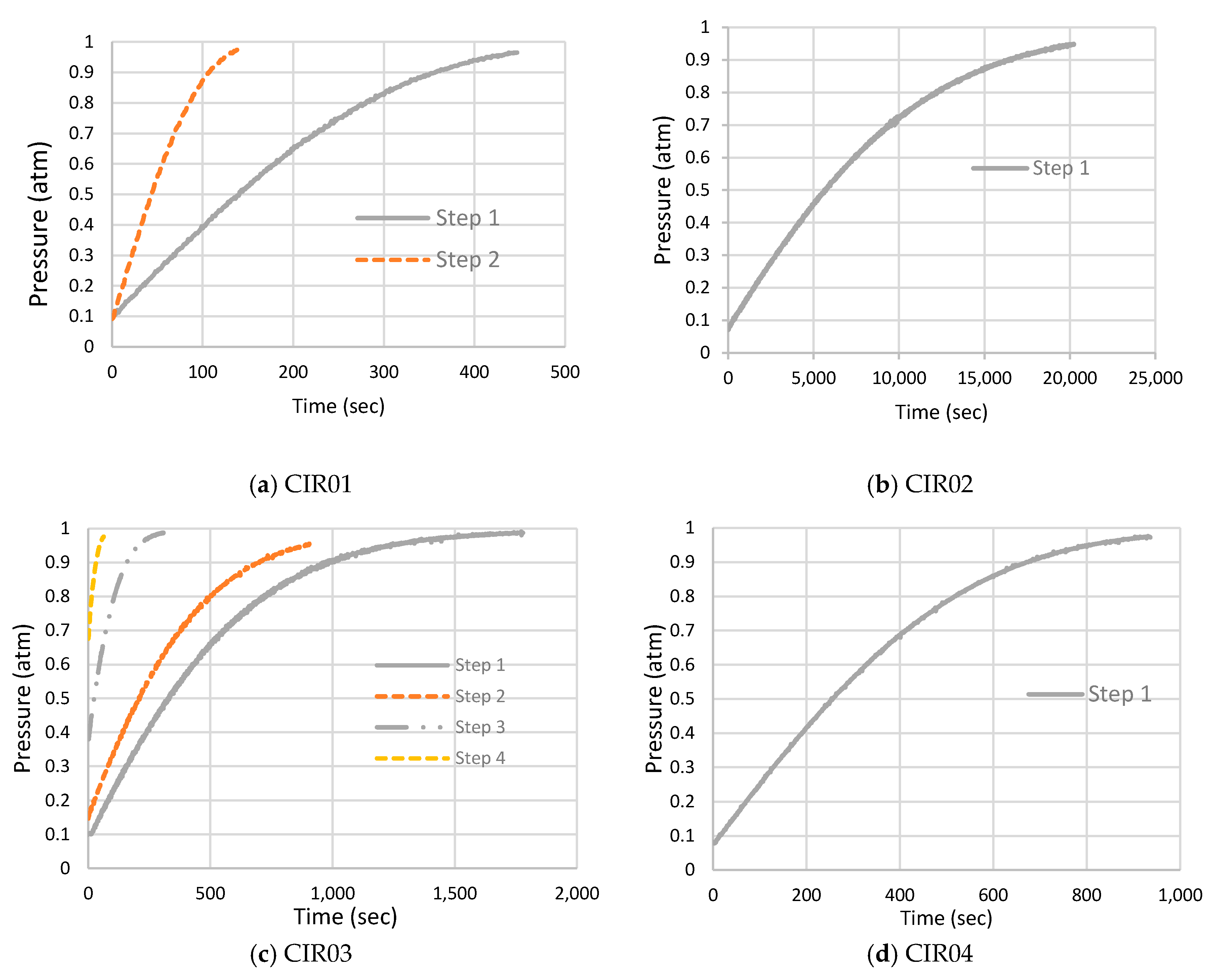
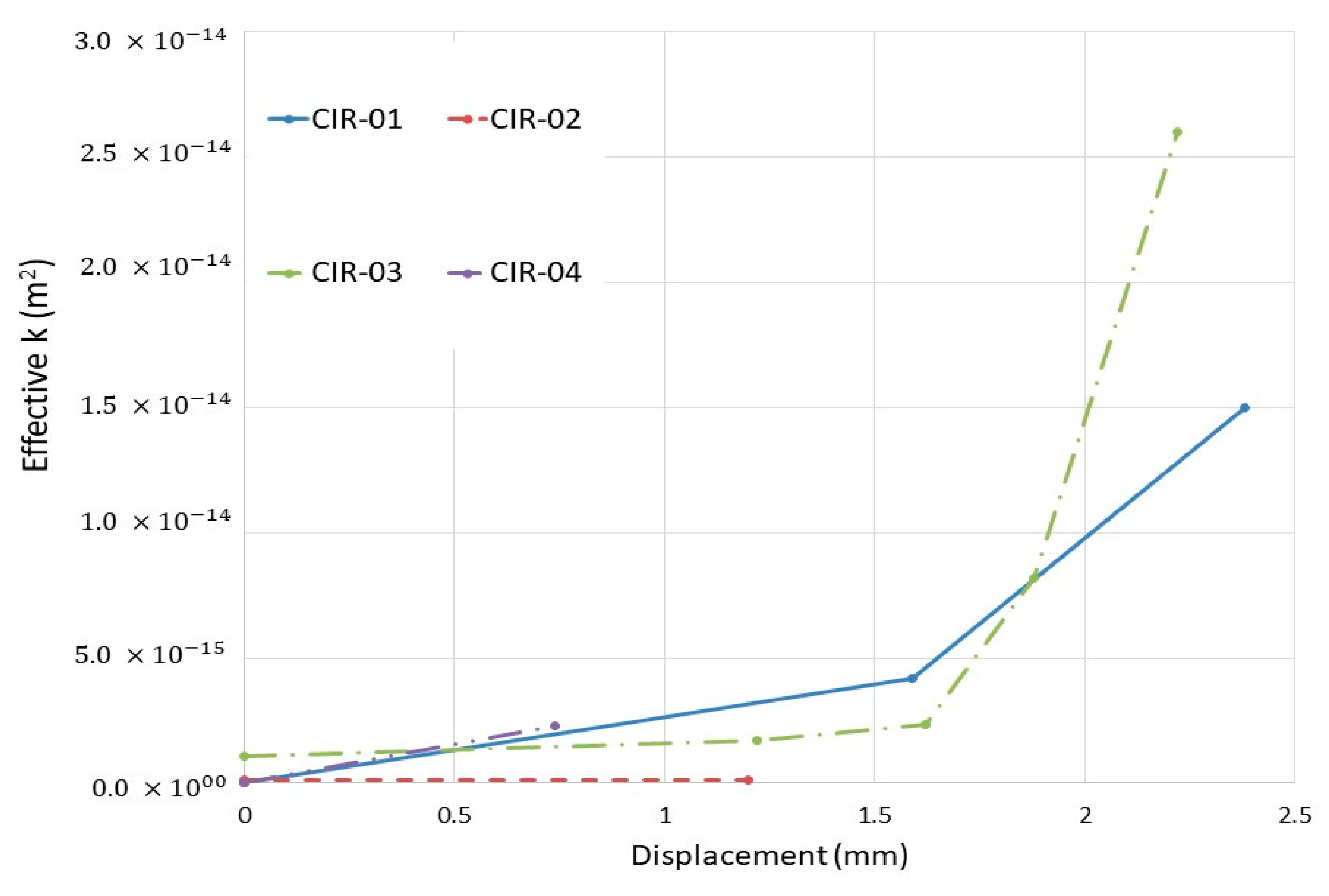
| Test Structure | Load Step | Displacement (mm) (Measured at Top of Tube Center) | Effective k (m2) |
|---|---|---|---|
| CIR-01 | Step 1 | 1.59 | 4.20 × |
| Step 2 | 2.38 | 1.50 × | |
| CIR-02 | Step 1 | 1.20 | 1.05 × |
| CIR-03 | Step 1 | 1.22 | 1.70 × |
| Step 2 | 1.62 | 2.34 × | |
| Step 3 | 1.88 | 8.20 × | |
| Step 4 | 2.22 | 2.60 × | |
| CIR-04 | Step 1 | 0.74 | 2.30 × |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Devkota, P.; Park, J. Analytical Model for Air Flow into Cracked Concrete Structures for Super-Speed Tube Transport Systems. Infrastructures 2019, 4, 76. https://doi.org/10.3390/infrastructures4040076
Devkota P, Park J. Analytical Model for Air Flow into Cracked Concrete Structures for Super-Speed Tube Transport Systems. Infrastructures. 2019; 4(4):76. https://doi.org/10.3390/infrastructures4040076
Chicago/Turabian StyleDevkota, Prakash, and Joonam Park. 2019. "Analytical Model for Air Flow into Cracked Concrete Structures for Super-Speed Tube Transport Systems" Infrastructures 4, no. 4: 76. https://doi.org/10.3390/infrastructures4040076
APA StyleDevkota, P., & Park, J. (2019). Analytical Model for Air Flow into Cracked Concrete Structures for Super-Speed Tube Transport Systems. Infrastructures, 4(4), 76. https://doi.org/10.3390/infrastructures4040076