Abstract
In this paper, ensemble empirical mode decomposition (EEMD) and empirical mode decomposition (EMD) methods are used for the effective identification of bridge natural frequencies from drive-by measurements. A vehicle bridge interaction (VBI) model is created using the finite element (FE) method in Matlab. The EMD is employed to decompose the signals measured on the vehicle to their main components. It is shown that the bridge component of the response measured on the vehicle can be extracted using the EMD method. The influence of some factors, such as the road roughness profile and measurement noise, on the results are investigated. The results suggest that the EMD shows good performance under those conditions, but the accuracy of the results may still need to be improved. It is shown that in some cases, the EMD may not be able to decompose the signal effectively and includes mode mixing. This results in inaccuracies in the identification of bridge frequencies. The use of the ensemble empirical mode decomposition (EEMD) method is proposed to overcome the mode mixing problem. The influence of factors such as road profile, measurement noise and vehicle velocity are investigated. It is numerically demonstrated that employing the EEMD improves the results compared to the EMD.
1. Introduction
Bridges play an important role in connectivity and serviceability of modern transportation systems. It is important to keep bridges healthy and practical. Environmental conditions, vehicle strike and increasing bridge traffic loading can cause small damages to the bridge structure. In order to prevent happening of more severe bridge damages, the first step is to detect small damages at right timing. To do so, more effective and economical bridge structural health monitoring systems are needed. The use of structural vibration data for non-destructive damage assessment tends to be an increasing popular approach. These methods usually monitor dynamic properties, e.g., natural frequencies and mode shapes of bridges using dynamic responses. These methods are generally categorized into two main groups based on the instrumentation: Direct and indirect methods. In direct methods, the bridge damage is usually identified using the measurements from the sensors directly installed on the bridge [1]. However, the inconvenience, the cost of installing the equipment on the bridge and even the potential dangers drive researchers to work on indirect measurements, which is the method that does not require equipment installation on the bridge.
Yang et al. [2] proposed an idea that dynamic properties of bridges can be found using the response of a vehicle passing over the bridge. In this approach, only a vehicle instrumented with sensors is needed rather than installing several pieces of equipment over a bridge. The vehicle itself is the exciter and receiver in this process. Over the past decade, many researchers have been developing indirect bridge monitoring methods. A comprehensive review of the most recent methods proposed for indirect bridge monitoring can be found in the works of Malekjafarian et al. [3] and Yang and Yang [4]. Figure 1 shows an overview of the state-of-the-art in this field.
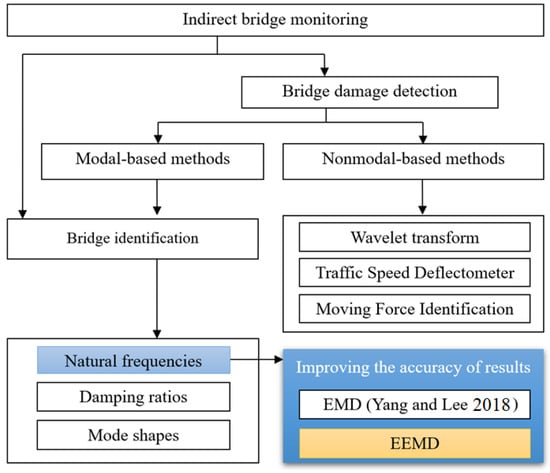
Figure 1.
The contribution of this study to the state of the art (EMD: empirical mode decomposition, EEMD: ensemble empirical mode decomposition).
Bu et al. [5] propose an indirect approach for damage assessment of a bridge deck. Oshima et al. [6] suggest using a heavy vehicle, which incorporates an excitation machine to apply a constant vibration on the bridge and it shows that using this machine has a positive effect on the extraction of low-order bridge frequencies. There are key parameters for the more successful identification of bridge natural frequencies, such as acceleration amplitude ratio, vehicle speed parameter and bridge frequency to vehicle frequency ratio [7]. González et al. [8] set up a laboratory experiment with a scaled bridge and moving vehicles. They concluded that the accurate determination of bridge frequency is feasible only when the vehicle velocity is low and the dynamic excitation of the bridge vibration is sufficiently high. In addition to bridge frequencies, researchers also have investigated the estimation of bridge damping ratios [8] and mode shapes [9]. Malekjafarian and OBrien [10] use instantaneous amplitude of the signal measured on a passing vehicle for the estimation of bridge mode shapes. Yang and Lee [11] use empirical mode decomposition (EMD) method to study the effect of vehicle damping on indirect identification of bridge frequency. They find that higher vehicle damping tends to suppress the vehicle frequency and make the bridge frequency more visible. They decompose the signal using the EMD, which in some cases encounters mode mixing. In these cases, two or more components of the decomposed signal include the bridge frequency components. OBrien et al. [12] propose a bridge damage detection using the EMD of the responses measured on a passing vehicle. They show that the bridge damage can be detected from some components of the response measured on a passing vehicle. They ignore the bridge natural frequency component of the signal and find the damage from the pseudo frequency component. However, separating the response components is still an important challenge in their work. Dhakal and Malla [13] employ indirect measurements for the estimation of natural frequencies of a steel railroad bridge in an experimental case study. They compare their results with a finite element (FE) model of the bridge to confirm them. Kong et al. [14] develop a specialized test vehicle consisting of a tractor and two following trailers for finding the bridge modal properties. They subtract the time-shifted responses measured on the two following trailers. They show that the bridge natural frequencies can be estimated from the fast Fourier transformation (FFT) of the residual response. They present a field test data of an existing bridge to verify the proposed methodology. However, subtraction of signals from two following axles requires the employment of identical axles. Despite all of the progress that has been made on the estimation of bridge natural frequencies from indirect measurements, it is still required to improve the accuracy of frequency identification. Particularly, when it comes to practical application of indirect methods, the current trend is towards cloud measurements using multiple vehicles [15,16]. In this case, not only is the FFT peak important, but also the accuracy of the whole spectrum, particularly in a range close to the bridge natural frequency, is important. The main focus of this paper is to improve the accuracy of frequency identification using indirect measurements.
In this paper, a vehicle bridge interaction (VBI) model is created using the finite element (FE) method in Matlab. The EMD and the ensemble empirical mode decomposition (EEMD) methods are implemented to decompose the vehicle acceleration response into intrinsic mode functions (IMFs). The EEMD is a more advanced version of the EMD method. The ability of EEMD method to remove high frequency components from other frequency components makes it possible to mitigate the influence from measurement noise. It is shown in the literature that the EEMD can solve the mode mixing problem of the EMD method [17]. The main purpose of the current study is to improve the accuracy of the indirect identification of bridge natural frequencies, particularly indifferent vehicle speeds. The effectiveness of both methods is evaluated in presence of noise, road roughness and various vehicle speeds. It is shown that in some cases the EMD fails in accurate identification bridge frequencies, where the EEMD provides the bridge natural frequency with acceptable accuracy. The contribution of this study to state-of-the-art indirect bridge monitoring is shown in Figure 1.
2. Theoretical Background
2.1. Empirical Mode Decomposition (EMD) Method
The EMD method is first proposed by Huang et al. [18]. It is a signal processing method which decomposes a signal into several intrinsic mode functions (IMFs). In this procedure, all the maxima and minima in the original time signal are identified. Then, upper and lower envelopes are created by connecting all the maxima and minima with cubic splines. Finally, the mean value of the two envelopes is calculated and subtracted from the original signal. The procedure is as follows:
- (a)
- Obtain the original signal;
- (b)
- Identify the positive peaks and negative peaks of the original signal; the upper envelope and the lower envelope can be obtained as connecting maxima and minima of the original signal with the cubic spline separately. Then, the mean value of upper envelop and the lower envelop can be calculated;
- (c)
- Subtract the mean from the original signal to obtain the first intrinsic mode function (IMF1);
- (d)
- The first residual component is calculated by subtracting IMF1 from the original signal. This residual component is treated as a new data and subjected to the same process described above to calculate the next IMF.
2.2. Ensemble Empirical Mode Decomposition (EEMD) Method
The EEMD method is first introduced by Wu and Huang [19] to address the mode mixing problem of the EMD. Figure 2 shows the EEMD procedure. The IMF component from the EEMD is defined as the mean of an ensemble number of trials that white noise is added to the signal. Adding noise will uniformly distribute in the whole time-frequency space with the components of different scales separated by the filter. By repeating the same procedure as that of EMD, the added noise can be cancelled out in the ensemble mean by using an optimum number of trials. This number can be defined using the recommendations in the literature [19]. As the number of trials increases, the only persistent part would be the original signal. The noise amplitude is a key parameter affecting the performance of the EEMD method on the mode separation. Too low of a noise amplitude would not cause enough changes of the decomposed signal and too high of one would create redundant IMFs [17].
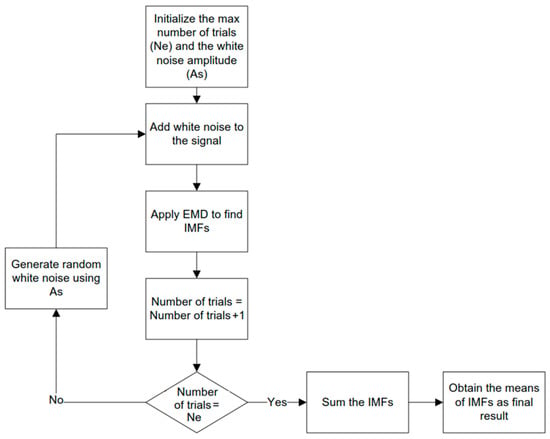
Figure 2.
The EEMD procedure (IMF: intrinsic mode functions).
3. Numerical Modelling of Vehicle Bridge Interaction
In a two-dimensional VBI system, a moving quarter car is modelled to pass over a bridge (Figure 3) and the dynamic response of the VBI system is processed by the Wilson-θ method. The quarter-car model which represents the behavior of the vehicle is modelled using a body mass and an axle mass supported by a spring with a constant stiffness of and a dashpot with suspension viscous damping coefficient of . The vehicle is modelled as a two degree-of-freedom (DOF) system. The tyre is modelled as a spring with a constant stiffness of . The gross vehicle mass is 1500 kg and the axle mass is 300 kg. The axle part of the vehicle is small in this study since the axle mass is much lighter than body mass. The vehicle frequencies are 1.80 and 12.74 Hz, respectively.
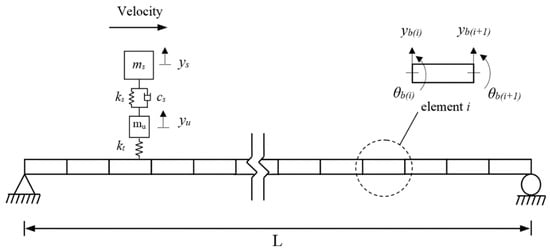
Figure 3.
The vehicle–bridge interaction model.
The bridge is represented by a simply supported FE beam model of length . It is modelled by 40 beam elements with four DOFs for each element, one DOF for the transverse displacement and one DOF for rotation at each node. The bridge’s Young’s modulus is E = 27.5 GPa and it has a mass per unit length of and a second moment of inertia of . The first and second bridge natural frequencies are calculated from FE analysis as 3.83 Hz and 15.32 Hz, respectively. The equations of motion for the vehicle and bridge are respectively given as [9]:
where , and represent the mass, damping and stiffness matrices of the vehicle. , and represent vectors of vehicle acceleration, velocity and displacement. is the dynamic interaction force vector applied to the vehicle degrees of freedom. , and represent mass, damping and stiffness matrices of the beam. , and represent vectors of nodal bridge acceleration, velocity and displacement.
The coupled motion equation can be obtained by combining Equations (1) and (2):
where and are the system mass and damping matrices, respectively. is the system stiffness matrix and is the system force vector. , and represent vectors of vehicle acceleration, velocity and displacement.
In this study, the contact force is the main excitation to the bridge. However, other excitation sources e.g., wind and other traffic have been shown [9] to be beneficial for indirect bridge frequency identification. The road surface is not perfectly smooth in practice. To consider a more realistic and practical condition, a high-level road surface roughness profile which is numerically generated in the VBI model is adopted in this study. The road roughness profile normally excites vehicle frequencies which makes the bridge monitoring more complicated. It is generated using the power spectral density (PSD) curve presented in ISO 8608 [20]. The vehicle and the bridge are coupled at the tyre contact points via the interaction force vector. The Wilson-θ integration scheme [21] is used to solve the equations for the coupled system, with the optimal value of the parameter being θ = 1.420815 for unconditional stability in the integration scheme. The initial condition of the solution is considered to be zero vertical translation, velocity and acceleration in all simulations.
4. Estimation of the Bridge Frequency Using the EMD Method
The vehicle is simulated to pass over the bridge with a smooth road profile and the velocity of the vehicle is set as 15 m/s. The vehicle’s acceleration response which is measured with a sampling frequency of 1000 Hz is shown in Figure 4a. The fast Fourier transform (FFT) of the acceleration is shown in Figure 4b. It can be seen from the FFT that the vehicle response is mainly dominated by the bridge natural frequencies. The first peak indicates the first natural frequency of the bridge and the second peak is the bridge’s second natural frequency.
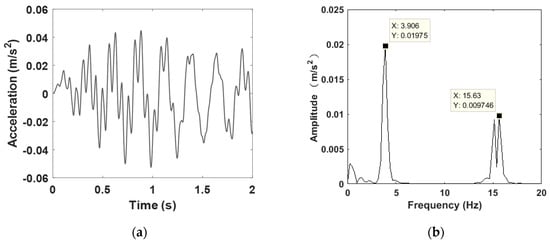
Figure 4.
(a) The acceleration response measured on the vehicle and (b) the fast Fourier transformation (FFT) of the acceleration response.
The EMD method is applied to the acceleration response measured on the vehicle. The IMFs obtained from the EMD and their FFT spectra are shown in Figure 5a,b, respectively. IMF1 and IMF2 represent the components corresponding to the second and first natural frequencies, respectively. This can also be concluded from the amplitude of IMF1 and IMF2 in Figure 5a.
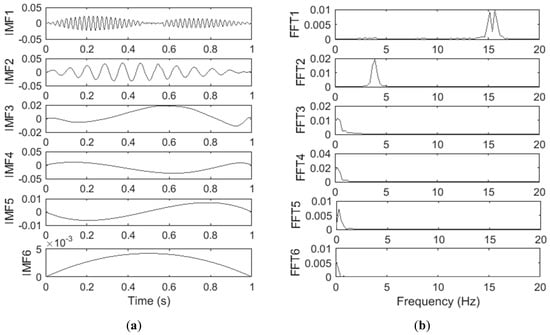
Figure 5.
(a) Intrinsic mode functions (IMFs) of the vehicle acceleration response and (b) FFT spectra of the IMFs of the vehicle acceleration response.
4.1. Effect of Road Surface Roughness
To investigate the effect of the bridge road surface roughness to the results, the high-level road surface roughness profile explained in Section 3 is adopted here. The simulation is repeated in the presence of a road profile. The acceleration response is decomposed using the EMD method. The IMFs obtained from the EMD and their FFT spectra are shown in Figure 6a,b. It shows that the presence of a road profile excites the vehicle frequencies. In this case, IMF5 corresponds to the first bridge natural frequency. In addition, the bridge’s second frequency is hardly detectable from any IMFs. The first frequency is estimated as 3.90 Hz in the presence of road roughness.
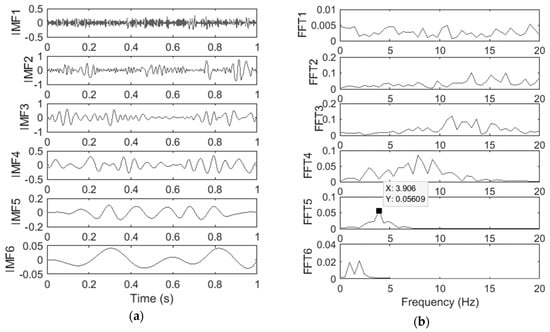
Figure 6.
(a) IMF components and (b) their FFT spectra in the presence of a road profile.
4.2. Effect of Noise
In practical cases, noise is a feature which cannot be avoided in measurements. Therefore, it is necessary to assess the effectiveness of the EMD in presence of measurement noise. White noise is added to the calculated vehicle responses to simulate the noise-polluted measurements:
where is the polluted acceleration, is the noise level, is a standard normal distribution vector with zero mean value and unit standard deviation, is the calculated acceleration and is its standard deviation. In this study, 5% noise is added to the calculated acceleration.
The EMD is applied to the noise-polluted measurements. The IMFs and their FFT obtained by EMD are shown in Figure 7a,b, respectively. The last IMF is the one associated with the first bridge natural frequency. This frequency is estimated as 3.42 Hz which is less accurate to the FE frequency of 3.83 Hz compared to the noise-free scenario.
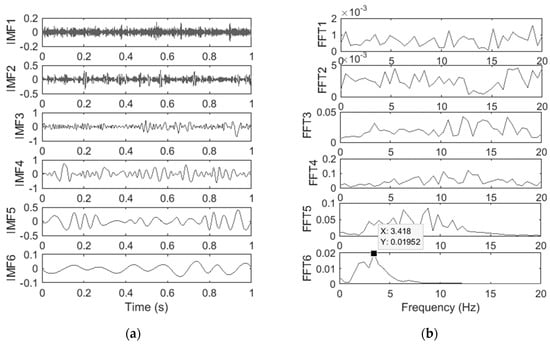
Figure 7.
(a) IMFs of the vehicle acceleration response and (b) FFT of the IMFs of the vehicle acceleration response in the presence of 5% noise.
4.3. Effect of Vehicle Velocity
Several researchers have shown the importance of the vehicle velocity for the successful identification of bridge natural frequencies from indirect measurements [4,10]. In this section, the same simulation is repeated with lower vehicle velocities to find if the EMD method can perform well in lower speeds. Figure 8a,b shows the FFT of the IMFs obtained while a vehicle moves at speeds of 10 m/s and 5 m/s, respectively. They show that it is hardly possible to detect the bridge natural frequencies for the lower vehicle speeds. This could be explained by the fact that the bridge is less excited when the vehicle passes with a lower speed. Therefore, the bridge response has a smaller contribution in the response measured on the vehicle which makes it harder to be detected by the EMD method. The results show that the EMD method fails to efficiently separate the bridge’s natural frequencies from others for different vehicle speeds.
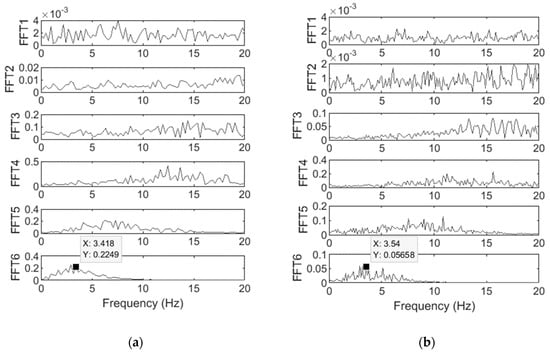
Figure 8.
FFT of the IMFs of the vehicle acceleration response when the vehicle speed is (a) 10 m/s and (b) 5 m/s.
5. Estimation of Vehicle Frequency Using the EEMD Method
The EEMD method is applied to the responses measured from the same model which adopt the same road roughness profile when the vehicle velocity is 15 m/s. The amplitude of the added white noise is set as 0.2 times the standard deviation of the original signal. This value is chosen using the index suggested by Wu and Huang [19]. However, they suggest that the sensitivity of the performance of the EEMD to the amplitude of noise is small within a certain range of noise amplitudes. They also recommend using a smaller noise amplitude when the signal contains high-frequency components and a larger noise amplitude when the signal is dominated by low-frequency components.
It is generally accepted that the greater number of times that white noise is added to the signal Ne (the higher the ensemble number Ne is), the better the mode mixing would be. It is found that Ne = 100 is sufficiently accurate for the acceleration signal investigation based on the recommendation in [19]. The IMFs and FFT spectra of the IMFs obtained from the EEMD are illustrated in Figure 9a,b, respectively. The frequency extracted from FFT of IMF5 is the one related to the bridge first natural frequency, which is very close to the FE frequency.
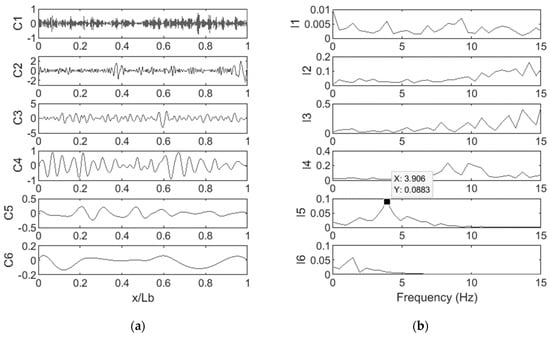
Figure 9.
(a) IMFs obtained from the EEMD of the vehicle acceleration response and (b) FFT spectra of the IMFs.
5.1. Effect of Measurement Noise
It is shown in the previous section that the performance of the EMD method in the presence of measurement noise is not reliable enough. In this section, 5% noise is added to the measurements to evaluate the performance of the EEMD method in presence of noise. The IMFs obtained from the EEMD and their FFT spectra are shown in Figure 10a,b, respectively. The frequency extracted from FFT of IMF6 is 3.906 Hz, which is the one related to the first natural bridge frequency. The results suggest that the EEMD method can provide better performance compared to the EMD method in the presence of measurement noise. The comparison of the results of these two methods is shown in Table 1.
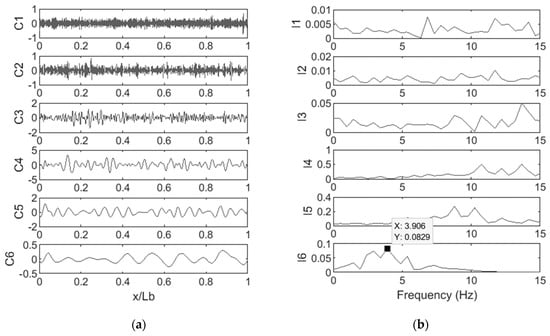
Figure 10.
(a) IMFs of the vehicle acceleration response and (b) FFT spectra of the vehicle acceleration response in presence.

Table 1.
Comparison of the first frequency estimated by EMD and EEMD in the presence of measurement noise (FE: finite element).
The results obtained in the presence of measurement noise simulate a more practical scenario. Therefore, these results are used to compare the performance of two methods for estimating the bridge frequency. Table 1 compares the frequencies estimated from the EMD and EEMD. It shows that the estimation error is improved from 10.73% to 2.01% when the EEMD is used compared to the EMD. This is a considerable improvement to the current FFT-based methods. It is also observed that in some cases (for both EMD and EEMD) IM5 contains the bridge frequency while in some other case IMF6 shows this frequency. This is due to randomness of the added measurement noise. This would change the frequency content of the whole signal in different random ways. Therefore, the bridge frequency would appear at different IMFs when the signal is decomposed by the EMD and EEMD.
5.2. Effect of Vehicle Velocity
It is shown in the previous section that the EMD can identify the first bridge natural frequency accurately when the vehicle moves at 15 m/s, but it does not perform well when the vehicle travels at a speed of 5 m/s or 10 m/s. The EEMD method is applied to the responses measured at these speeds. The IMFs and FFT spectra of the IMFs by the EEMD are illustrated in Figure 11 and Figure 12. It can be seen that the first bridge’s natural frequency can be approximately detected from the FFT of IMF6, which is shown to be 3.906 Hz. This confirms the performance of the EEMD for this case.
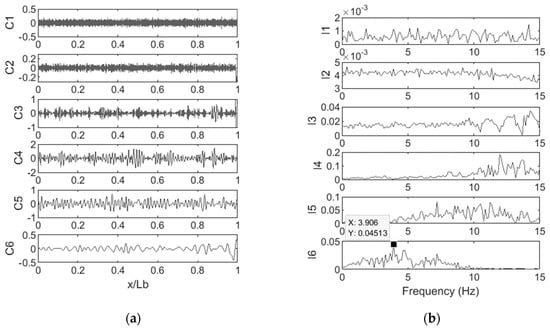
Figure 11.
(a) IMFs of the vehicle acceleration response and (b) FFT of IMFs when the vehicle speed is 5 m/s.
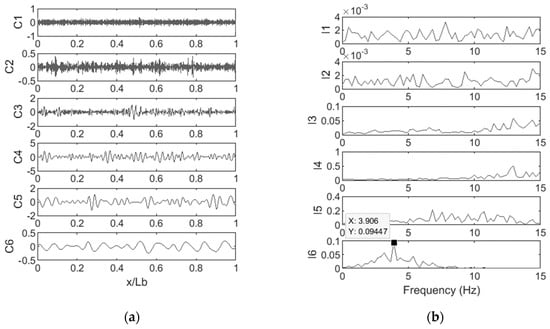
Figure 12.
(a) IMFs of the vehicle acceleration response and (b) FFT of IMFs when the vehicle speed is 10 m/s.
For 10 m/s, the IMFs and FFT spectra of IMFs by EEMD are presented in Figure 12a,b. It can also be seen in this case that the bridge’s first natural frequency can be detected with great accuracy, shown to be 3.906 Hz. Thus, the results for both 5 m/s and 10 m/s vehicle velocities suggest that the EEMD method performs much better compared to the EMD on a wider range of vehicle velocity, which is demonstrated in Table 2.

Table 2.
Comparison of the frequency estimated by EMD and EEMD for different vehicle velocities.
Table 2 provides a comparison between the estimation error obtained from two methods. It shows for the vehicle speeds of 5 and 10 m/s, the estimation errors are improved from 7.55% and 10.73% to 2.01%, respectively. This clearly shows the advantage of using the EEMD over EMD for the indirect estimation of bridge natural frequency.
6. Conclusions
In this paper, the EMD and EEMD methods are adopted for the identification of bridge natural frequencies from the vehicle response. A vehicle bridge interaction (VBI) model is created using the finite element (FE) method in Matlab. It is shown that in an ideal situation, the EMD method can be an effective method for the identification of bridge natural frequencies. However, the application of EMD is limited to certain vehicle speeds since the results from lower speeds cannot show bridge natural frequencies clearly. It is also observed that the results obtained from EMD are sensitive to measurement noise. The use of EEMD is proposed in this paper to improve the performance of the identification of bridge natural frequencies from drive-by measurements. It is shown that EEMD can perform better compared to the EMD method. It is demonstrated that the EEMD is relatively less sensitive to measurement noise. The bridge’s first natural frequency is detected with higher accuracy in the presence of noise compared to the EMD. It is also numerically confirmed that the EEMD performs well in a wider range of vehicle speeds. However, there are still some challenges in the application of the EEMD. For example, the amplitude of the added random white noise needs to be carefully chosen. Therefore, a more accurate method is required for precise defining of this number in this application. The number of trials also has an important influence on the quality of the results. It is recommended to introduce a proper method for defining this number that can work for different bridge cases. In addition, more datasets need to be used to achieve a statically meaningful application of the proposed method. Therefore, the authors will use multiple measurements from multiple vehicles to use the proposed method for the purpose of damage detection.
Author Contributions
This research was carried out by L.Z. under supervision of A.M. Both authors discussed the results and contributed to the final manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Carden, E.P.; Fanning, P. Vibration based condition monitoring: A review. Struct. Health Monit. 2004, 3, 355–377. [Google Scholar] [CrossRef]
- Yang, Y.B.; Lin, C.W.; Yau, J.D. Extracting bridge frequencies from the dynamic response of a passing vehicle. J. Sound Vib. 2004, 272, 471–493. [Google Scholar] [CrossRef]
- Malekjafarian, A.; McGetrick, P.J.; OBrien, E.J. A Review of Indirect Bridge Monitoring Using Passing Vehicles. Shock Vib. 2015, 2015. [Google Scholar] [CrossRef]
- Yang, Y.B.; Yang, J.P. State-of-the-Art Review on Modal Identification and Damage Detection of Bridges by Moving Test Vehicles. Int. J. Struct. Stab. Dyn. 2018, 18, 1850025. [Google Scholar] [CrossRef]
- Bu, J.Q.; Law, S.S.; Zhu, X.Q. Innovative bridge condition assessment from dynamic response of a passing vehicle. J. Eng. Mech. 2006, 132, 1372–1379. [Google Scholar] [CrossRef]
- Oshima, Y.; Yamaguchi, T.; Kobayashi, Y.; Sugiura, K. Eigenfrequency estimation for bridges using the response of a passing vehicle with excitation system. In Proceedings of the Fourth International Conference on Bridge Maintenance, Safety and Management, Seoul, Korea, 13–17 July 2008; pp. 3030–3037. [Google Scholar]
- Yang, Y.B.; Chang, K.C. Extracting the bridge frequencies indirectly from a passing vehicle: Parametric study. Eng. Struct. 2009, 31, 2448–2459. [Google Scholar] [CrossRef]
- Gonzalez, A.; OBrien, E.J.; McGetrick, P.J. Identification of damping in a bridge using a moving instrumented vehicle. J. Sound Vib. 2012, 331, 4115–4131. [Google Scholar] [CrossRef]
- Malekjafarian, A.; Brien, E.J. Identification of bridge mode shapes using Short Time Frequency Domain Decomposition of the responses measured in a passing vehicle. Eng. Struct. 2014, 81, 386–397. [Google Scholar] [CrossRef]
- Malekjafarian, A.; OBrien, E.J. On the use of a passing vehicle for the estimation of bridge mode shapes. J. Sound Vib. 2017, 397, 77–91. [Google Scholar] [CrossRef]
- Yang, J.P.; Lee, W.C. Damping Effect of a Passing Vehicle for Indirectly Measuring Bridge Frequencies by EMD Technique. Int. J. Struct. Stab. Dyn. 2018, 18, 1850008. [Google Scholar] [CrossRef]
- OBrien, E.J.; Malekjafarian, A.; Gonzalez, A. Application of empirical mode decomposition to drive-by bridge damage detection. Eur. J. Mech. A-Solids 2017, 61, 151–163. [Google Scholar] [CrossRef]
- Dhakal, S.; Malla, R.B. Determination of Natural Frequencies of a Steel Railroad Bridge Using Onboard Sensors. In Proceedings of the 16th Biennial ASCE Aerospace Division International Conference on Engineering, Science, Construction, and Operations in Challenging Environments, Cleveland, OH, USA, 9–12 April 2018; pp. 1034–1046. [Google Scholar]
- Kong, X.; Cai, C.S.; Deng, L.; Zhang, W. Using Dynamic Responses of Moving Vehicles to Extract Bridge Modal Properties of a Field Bridge. J. Bridge Eng. 2017, 22, 04017018. [Google Scholar] [CrossRef]
- Mei, Q.; Gül, M.; Boay, M. Indirect health monitoring of bridges using Mel-frequency cepstral coefficients and principal component analysis. Mech. Syst. Signal Process. 2019, 119, 523–546. [Google Scholar] [CrossRef]
- Mei, Q.; Gül, M. A crowdsourcing-based methodology using smartphones for bridge health monitoring. Struct. Health Monit. 2018. [Google Scholar] [CrossRef]
- Aied, H.; Gonzalez, A.; Cantero, D. Identification of sudden stiffness changes in the acceleration response of a bridge to moving loads using ensemble empirical mode decomposition. Mech. Syst. Signal Process. 2016, 66, 314–338. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.L.C.; Shih, H.H.; Zheng, Q.N.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- International Standard Organization. Mechanical Vibration-Road Surface Profiles-Reporting of Measured Data; ISO8608:1995; International Organization for Standardization: Geneva, Switzerland, 1995. [Google Scholar]
- Tedesco, J.W.; McDougal, W.G.; Ross, C.A. Structural dynamics: Theory and Applications; Longman; Addison Wesley: Boston, MA, USA, 1999. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).