A New MPPT-Based Extended Grey Wolf Optimizer for Stand-Alone PV System: A Performance Evaluation versus Four Smart MPPT Techniques in Diverse Scenarios
Abstract
:1. Introduction
1.1. Motivations
1.2. State of the Art
1.3. Contributions
1.4. Structure Overview
2. PV System Plant Modeling
2.1. PV Mathematical Model
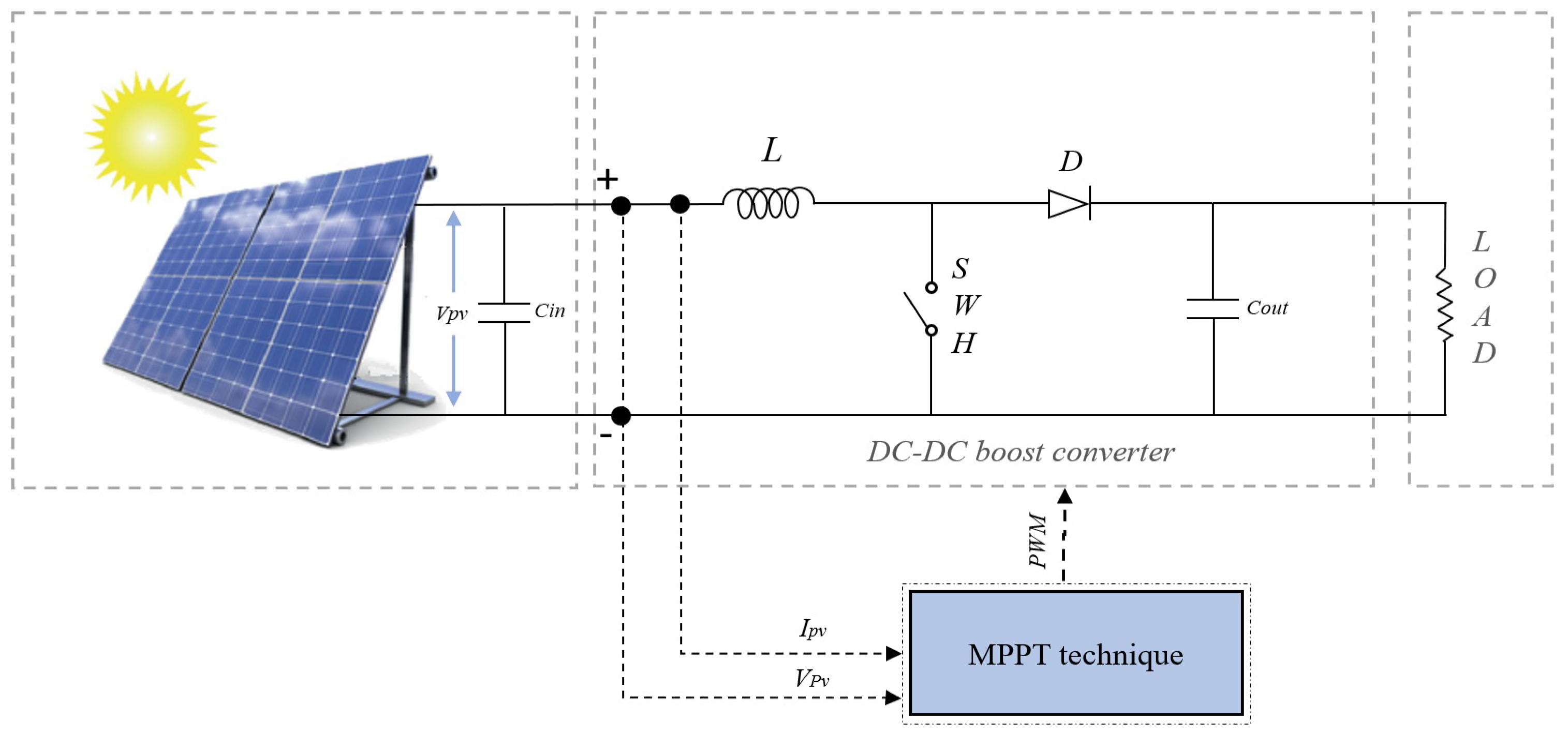
2.2. DC/DC Boost Converter
3. MPPT Control Method
3.1. Extended and Grey Wolf Optimizers
3.1.1. GWO Mathematical Model
- Social Hierarchy: The social hierarchy of the wolves is represented by four positions: , , and . These positions represent the best, second-best, third-best and the rest of the wolves in the population, respectively.
- Encircling behavior: Entails the coordinated movement of group members toward a specific target position while tightening the search area around it. The wolves concentrate their exploration around influential leaders (, , ), optimizing the balance between exploration and exploitation. This approach enables the algorithm to effectively discover optimal or near-optimal solutions for complex optimization problems. The encircling behavior equations are given as follows [49]:where is the updated position of the wolf at time step , is the current position of the wolf, is the position of the targeted wolf, and are random coefficients vectors that determine the encircling behavior which lies in the range [−1, 1]. The equation to generate the and vectors are given as follows [49]:where is a random coefficient vector with elements uniformly decreased from 2 to 0, and , are random coefficient vectors with elements uniformly distributed in [−1, 1].
- Follow, hunt and approach the prey: The , , wolves guide the wolves toward promising regions. The updated position for each omega wolf is determined by the influence of the , and wolves as follows:Therefore, the updated position of all search agents is given by [49]:
3.1.2. EGWO Mathematical Model
3.1.3. EGWO and GWO Application for MPPT
- Initialization: The optimization process starts with the initialization of a population (represented by wolves) in the search space. The duty ratio is initialized (Equation (18)) randomly within the defined limits, ranging from to .
- Evaluation: The fitness values, corresponding to the PV power output, are calculated for each member of the population. The wolves with the highest PV power values are assigned as (the best solution), (the second-best solution) and (the third-best solution).
- Updating Positions: The positions (duty ratios) of the wolves in the population are updated based on the positions of , and , the best, second and the third-best solutions, respectively. This update aims to explore the search space more effectively and improve the duty ratios. The updated position of all search agents using GWO and EGWO is given as follows [52]:where , , are the duty cycle direction vectors for the , and wolves, respectively. In the EGWO and GWO algorithms with direct duty-cycle control for MPPT in PV systems, the updated duty cycle vector is determined based on the power output of the wolves. Hence, using Equations (15), (16), (19), (20) and (21), the duty cycle update equation for GWO and EGWO are given as follows, respectively:
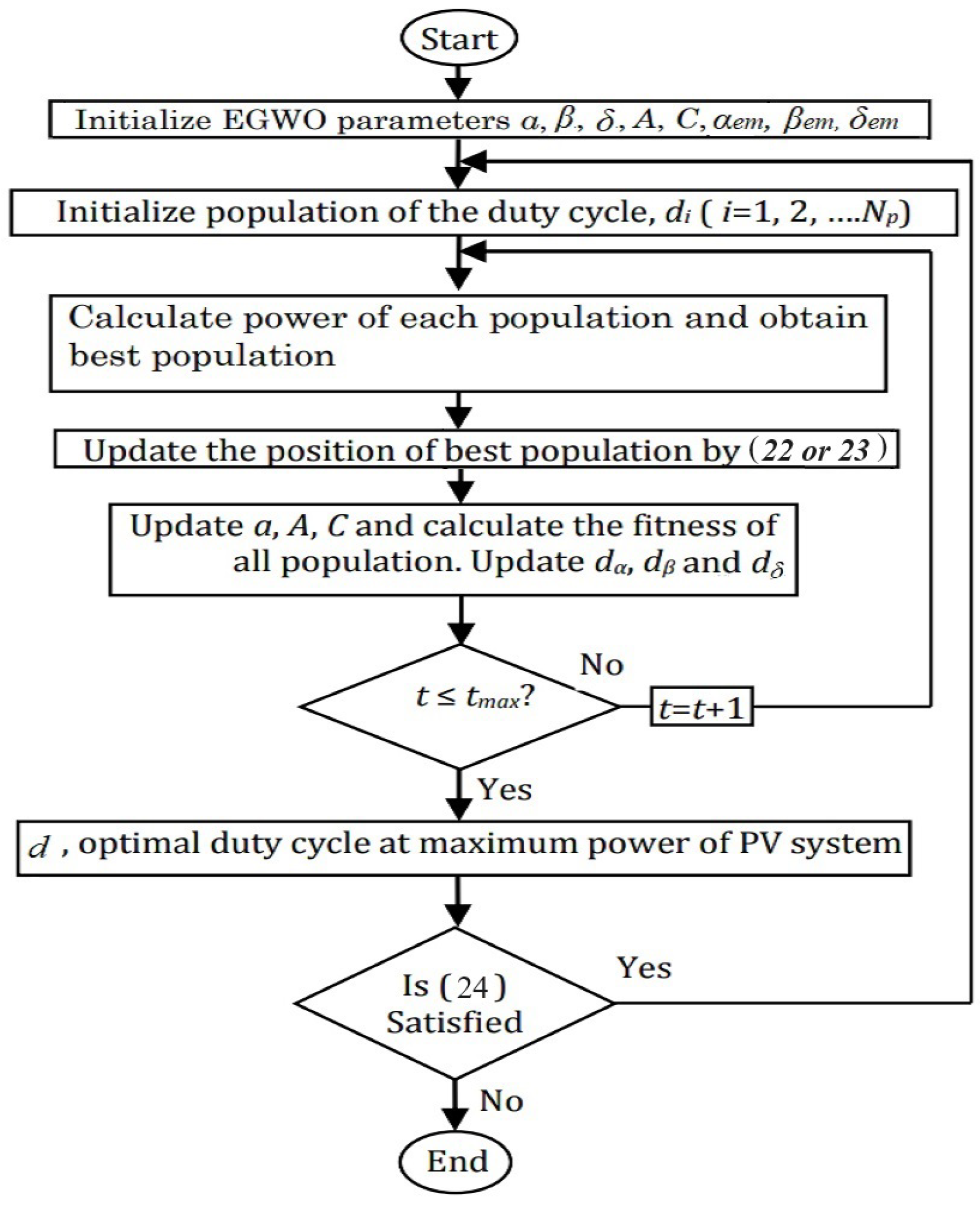
- Termination: The termination condition is determined by the maximum number of iterations reached or when the relative change in PV power compared to the previous iteration’s power becomes negligible. The termination criterion is defined as follows:where represents the PV power calculated for the current duty cycle, represents the PV power calculated for the previous duty cycle and is set to , representing the predefined threshold for the relative change in the PV power. The EGWO MPPT flowchart is given in Figure 2.
4. Simulation Results
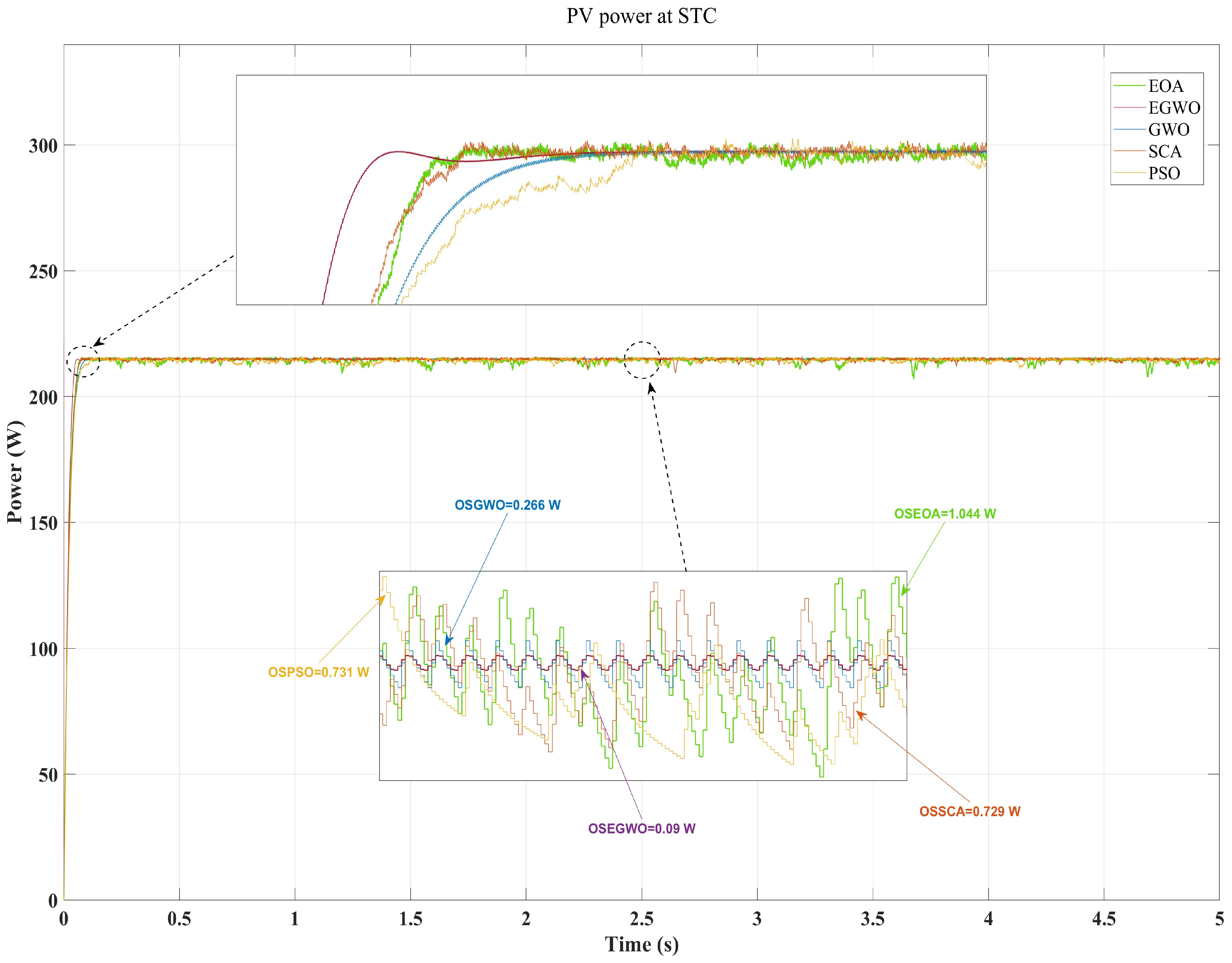
4.1. First Scenario: Under Standard Test Conditions (STC)
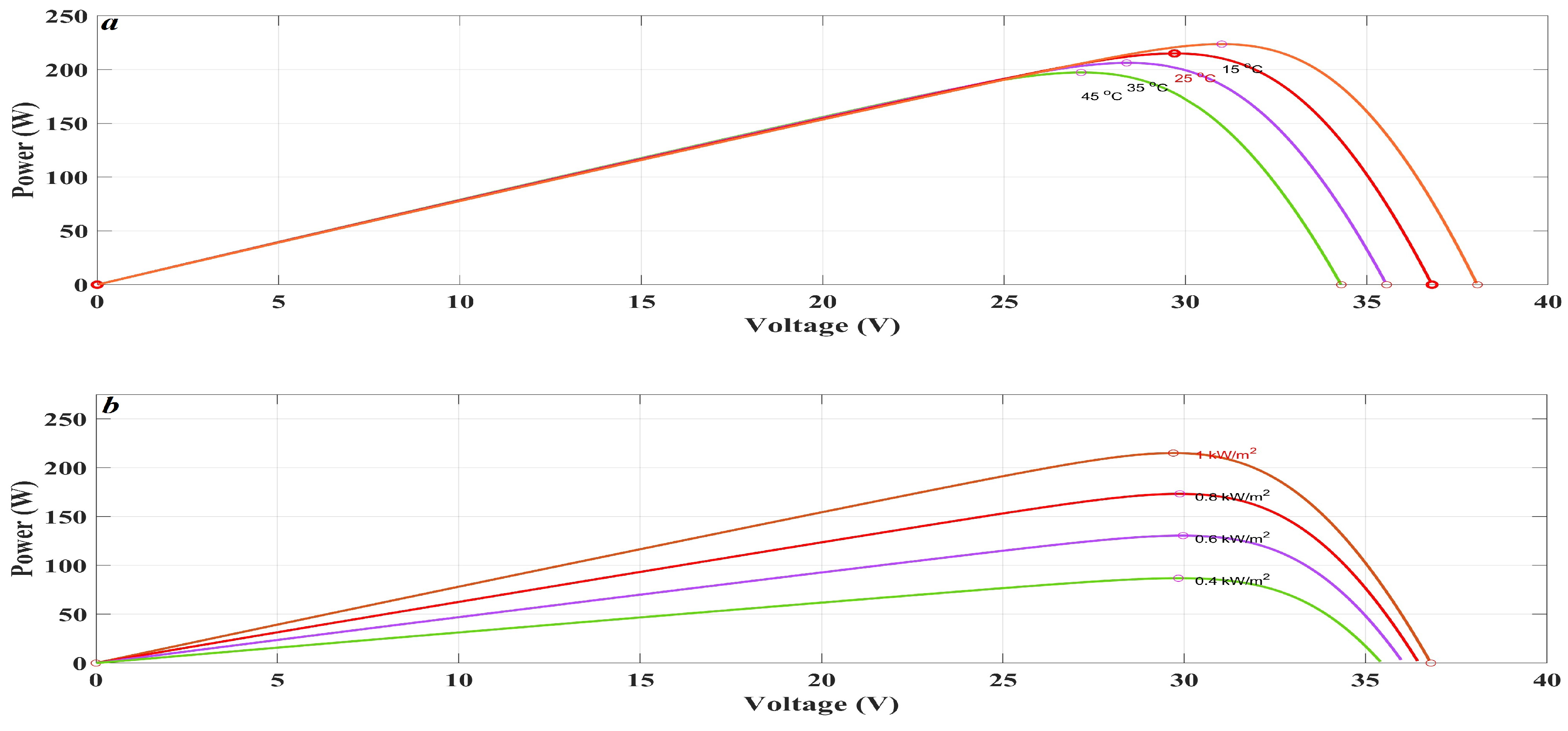
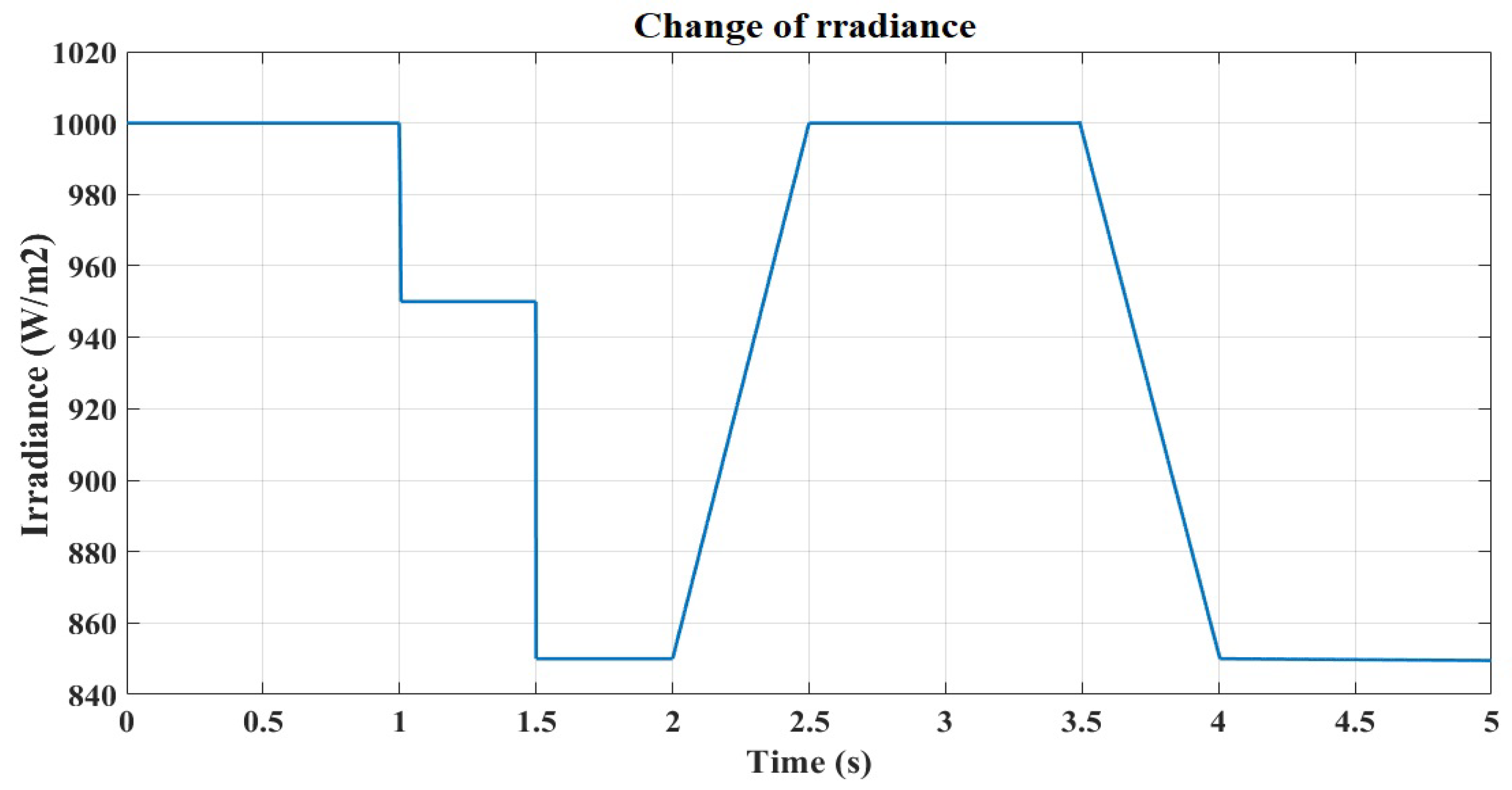
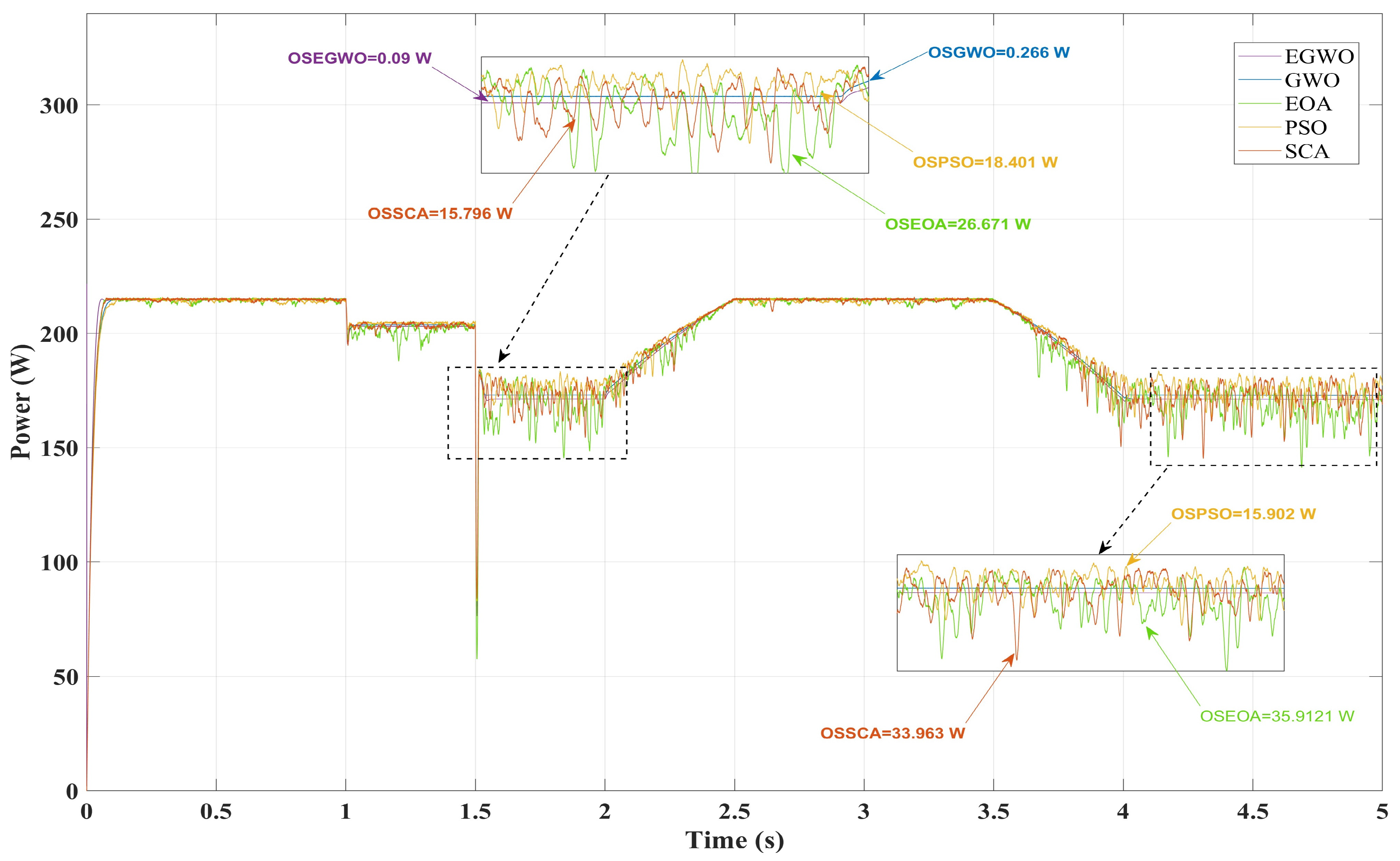
4.2. Second Scenario: Variable Irradiance and Constant Temperature
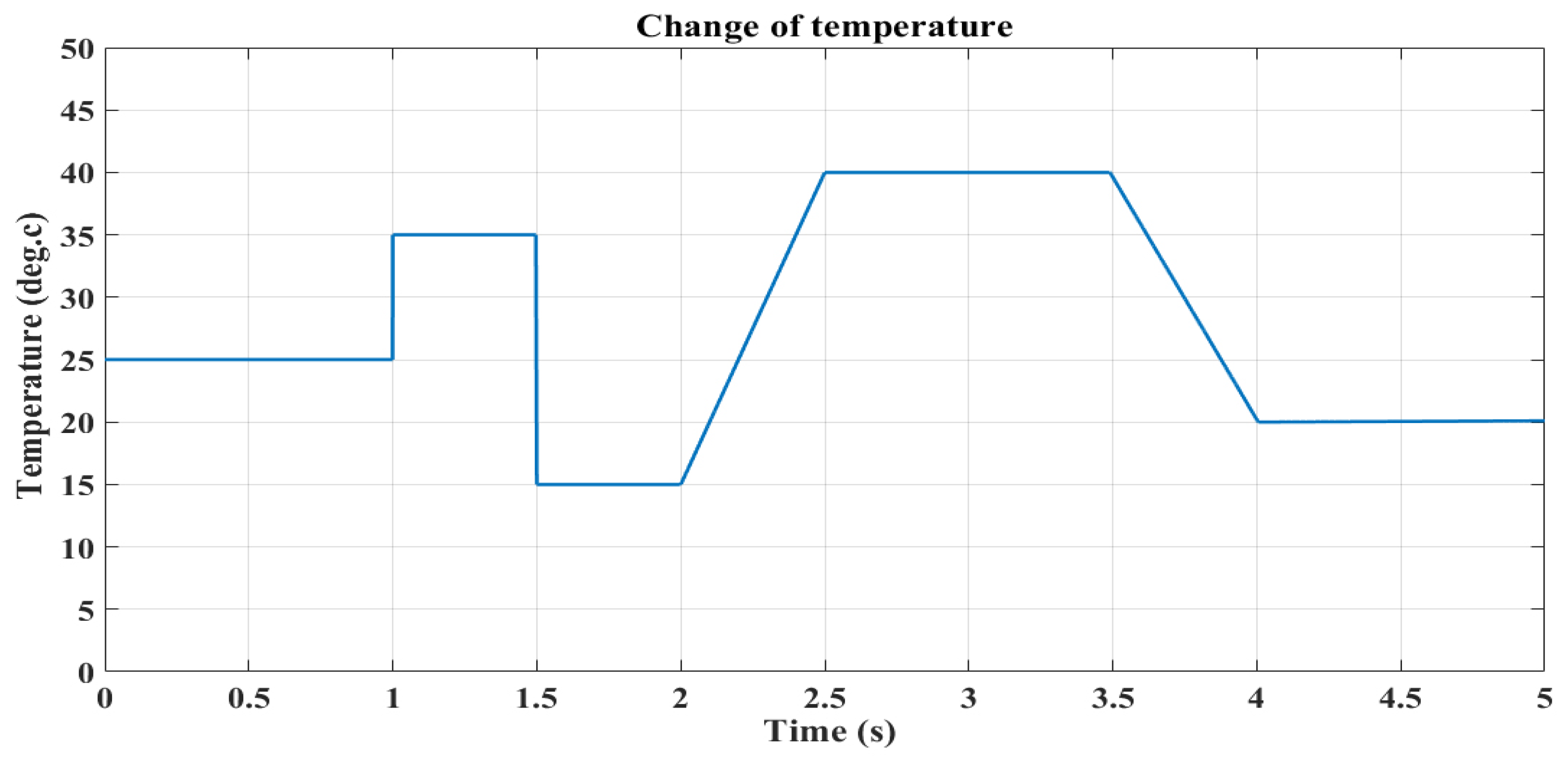
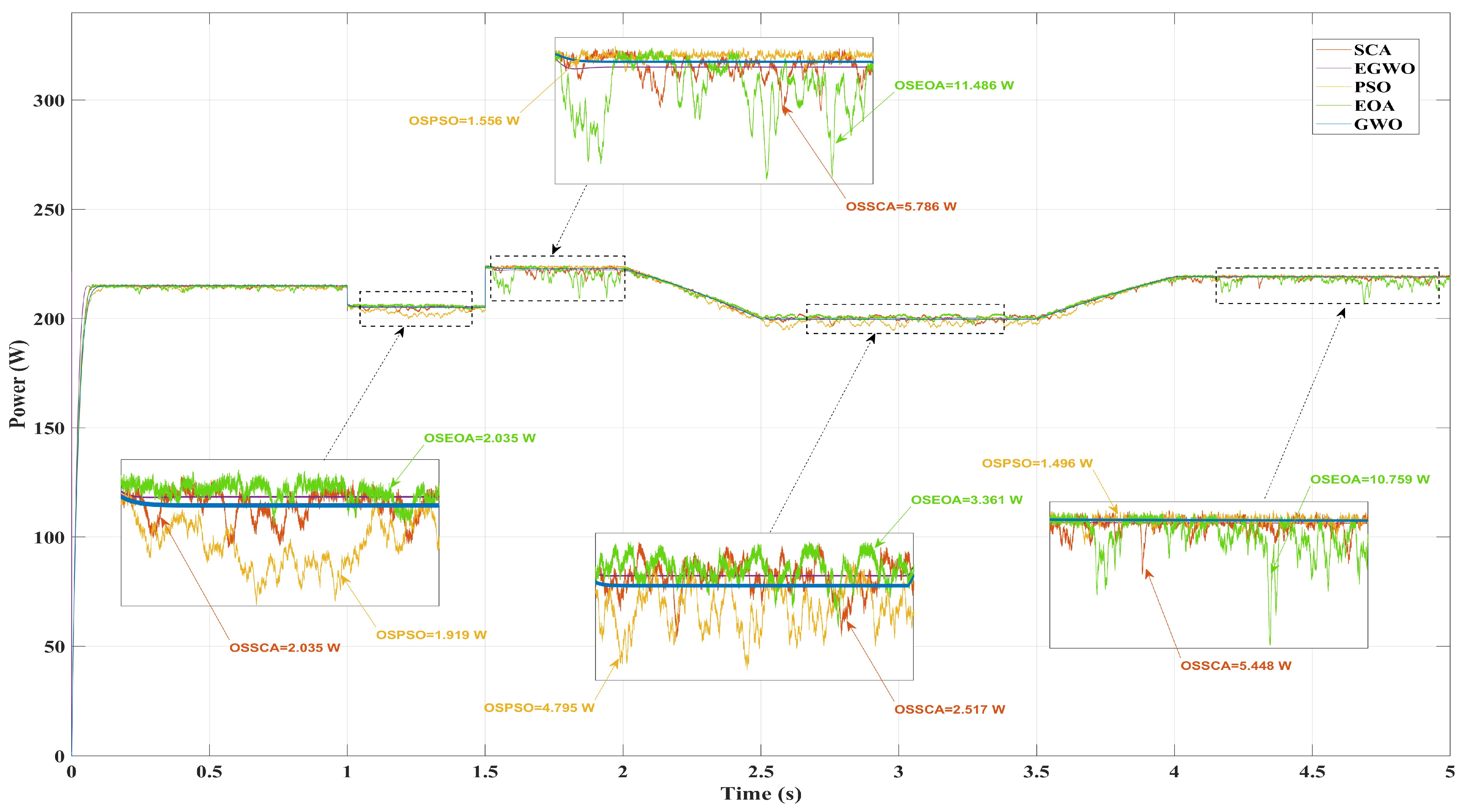
4.3. Third Scenario: Variable Temperature and Constant Irradiance
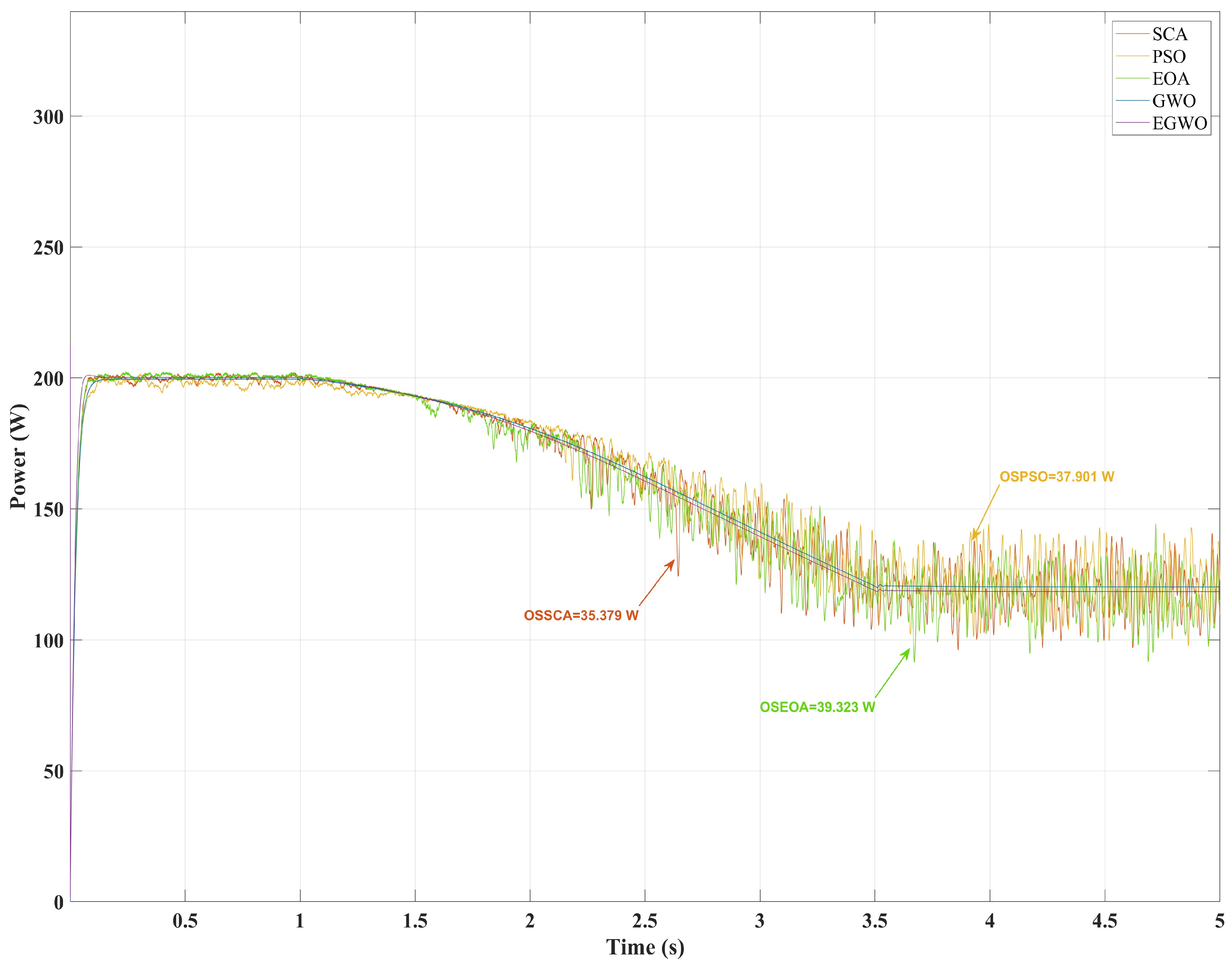
4.4. Fourth Scenario: Variable Temperature and Irradiance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MPPT | Maximum power point tracking |
| MPP | Maximum power point |
| EGWO | Extended grey wolf optimizer |
| GWO | Grey wolf optimizer |
| EOA | Equilibrium optimization algorithm |
| PSO | Particle swarm optimization |
| SCA | Sin cos algorithm |
| P&O | Perturb and observe |
| INC | Incremental conductance |
| FOCV | Fractional open circuit voltage |
| FSCC | Fractional short circuit current |
| HL | Hill climbing |
| ABC | Artificial bee colony algorithm |
| GA | Genetic algorithm |
| ACO | Colony optimization |
| FA | Firefly algorithm |
| WOA | Whale optimization algorithm |
| CS | Cuckoo search |
| AFSA | Artificial fish swarm algorithm |
| PWM | Pulse width modulation |
| d | Duty cycle |
| P | PV system power (W) |
| Cell current | |
| Current generated by light | |
| Diode’s current | |
| Current of the parallel resistance | |
| Reverse saturation current | |
| V | Voltage across the PV cell |
| Voltage of the equivalent diode | |
| Series resistance | |
| Parallel resistance | |
| G | Actual irradiance |
| Irradiance at standard rating conditions | |
| K | Boltzmann constant |
| q | Electron charge |
| Cell temperature | |
| Reference temperature | |
| n | Diode ideality factor |
| Number of series cells |
References
- Zhou, C.; Wang, Y.; Li, J.; Ma, X.; Li, Q.; Yang, M.; Zhao, X.; Zhu, Y. Simulation and economic analysis of an innovative indoor solar cooking system with energy storage. Sol. Energy 2023, 111816. [Google Scholar] [CrossRef]
- Falter, C.; Pitz-Paal, R. Energy analysis of solar thermochemical fuel production pathway with a focus on waste heat recuperation and vacuum generation. Sol. Energy 2018, 176, 230–240. [Google Scholar] [CrossRef]
- De Groote, O.; Pepermans, G.; Verboven, F. Heterogeneity in the adoption of photovoltaic systems in Flanders. Energy Econ. 2016, 59, 45–57. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Carli, R.; Dotoli, M. Robust day-ahead energy scheduling of a smart residential user under uncertainty. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 935–940. [Google Scholar]
- Halden, U.; Cali, U.; Dynge, M.F.; Stekli, J.; Bai, L. DLT-based equity crowdfunding on the techno-economic feasibility of solar energy investments. Sol. Energy 2021, 227, 137–150. [Google Scholar] [CrossRef]
- Ji, J.; Pei, G.; Chow, T.T.; Liu, K.; He, H.; Lu, J.; Han, C. Experimental study of photovoltaic solar assisted heat pump systems. Sol. Energy 2008, 82, 43–52. [Google Scholar] [CrossRef]
- Arsalan, M.; Iftikhar, R.; Ahmad, I.; Hasan, A.; Sabahat, K.; Javeria, A. MPPT for photovoltaic system using nonlinear backstepping controller with integral action. Sol. Energy 2018, 170, 192–200. [Google Scholar] [CrossRef]
- Vukadinović, A.; Radosavljević, J.; Đorđević, A.; Protić, M.; Petrović, N. Multi-objective optimization of energy performance for a detached residential building with a sunspace using the NSGA-II genetic algorithm. Sol. Energy 2021, 224, 1426–1444. [Google Scholar] [CrossRef]
- Jafari, M.; Malekjamshidi, Z. A topology of DC-DC converter based on multi-winding transformer for grid integration of multiple renewable energy resources. Inventions 2020, 5, 31. [Google Scholar] [CrossRef]
- Sachan, A.; Gupta, A.K.; Samuel, P. A review of MPPT algorithms employed in wind energy conversion systems. J. Green Eng. 2016, 6, 385–402. [Google Scholar] [CrossRef]
- Nedumgatt, J.J.; Jayakrishnan, K.B.; Umashankar, S.; Vijayakumar, D.; Kothari, D.P. Perturb and observe MPPT algorithm for solar PV systems-modeling and simulation. In Proceedings of the 2011 Annual IEEE India Conference, Hyderabad, India, 16–18 December 2011; pp. 1–6. [Google Scholar]
- Shahid, H.; Kamran, M.; Mehmood, Z.; Saleem, M.Y.; Mudassar, M.; Haider, K. Implementation of the novel temperature controller and incremental conductance MPPT algorithm for indoor photovoltaic system. Sol. Energy 2018, 163, 235–242. [Google Scholar] [CrossRef]
- Nadeem, A.; Sher, H.A.; Murtaza, A.F. Online fractional open-circuit voltage maximum output power algorithm for photovoltaic modules. IET Renew. Power Gener. 2020, 14, 188–198. [Google Scholar] [CrossRef]
- Alsulami, A.F.; Al Arefi, S.M. Fraction open circuit and fractional short circuit based incremental conductance maximum power point tracking controller. In Proceedings of the 2021 10th International Conference on Renewable Energy Research and Application (ICRERA), Ankara, Turkey, 26–29 September 2021; pp. 184–189. [Google Scholar]
- Jately, V.; Azzopardi, B.; Joshi, J.; Sharma, A.; Arora, S. Experimental Analysis of hill-climbing MPPT algorithms under low irradiance levels. Renew. Sustain. Energy Rev. 2021, 150, 111467. [Google Scholar] [CrossRef]
- Dolara, A.; Grimaccia, F.; Mussetta, M.; Ogliari, E.; Leva, S. An evolutionary-based MPPT algorithm for photovoltaic systems under dynamic partial shading. Appl. Sci. 2018, 8, 558. [Google Scholar] [CrossRef]
- Baatiah, A.O.; Eltamaly, A.M.; Alotaibi, M.A. Improving Photovoltaic MPPT Performance through PSO Dynamic Swarm Size Reduction. Energies 2023, 16, 6433. [Google Scholar] [CrossRef]
- Karaboga, D. Artificial bee colony algorithms. Scholarpedia 2010, 5, 6915. [Google Scholar] [CrossRef]
- Badis, A.; Mansouri, M.N.; Boujmil, M.H. A genetic algorithm optimized MPPT controller for a PV system with DC-DC boost converter. In Proceedings of the 2017 International Conference on Engineering & MIS (ICEMIS), Monastir, Tunisia, 8–10 May 2017; pp. 1–6. [Google Scholar]
- Huang, K.H.; Chao, K.H.; Lee, T.W. An Improved Photovoltaic Module Array Global Maximum Power Tracker Combining a Genetic Algorithm and Ant Colony Optimization. Technologies 2023, 11, 61. [Google Scholar] [CrossRef]
- Chao, K.H.; Zhang, S.W. An Maximum Power Point Tracker of Photovoltaic Module Arrays Based on Improved Firefly Algorithm. Sustainability 2023, 15, 8550. [Google Scholar] [CrossRef]
- Jing, L.; Song, B.; Zhu, Y.; Yang, B.; Shu, H. Grey wolf optimizer based MPPT control of centralized thermoelectric generator applied in thermal power stations. In Proceedings of the 2020 Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 29–31 May 2020; pp. 127–132. [Google Scholar]
- Silaa, M.Y.; Barambones, O.; Bencherif, A. A Novel Adaptive PID Controller Design for a PEM Fuel Cell Using Stochastic Gradient Descent with Momentum Enhanced by Whale Optimizer. Electronics 2022, 11, 2610. [Google Scholar] [CrossRef]
- Salah, Z.B.H.; Krim, S.; Hajjaji, M.A.; Alshammari, B.M.; Alqunun, K.; Alzamil, A.; Guesmi, T. A New Efficient Cuckoo Search MPPT Algorithm Based on a Super-Twisting Sliding Mode Controller for Partially Shaded Standalone Photovoltaic System. Sustainability 2023, 15, 9753. [Google Scholar] [CrossRef]
- Mao, M.; Duan, Q.; Duan, P.; Hu, B. Comprehensive improvement of artificial fish swarm algorithm for global MPPT in PV system under partial shading conditions. Trans. Inst. Meas. Control 2018, 40, 2178–2199. [Google Scholar] [CrossRef]
- Melhem, F.Y.; Grunder, O.; Hammoudan, Z.; Moubayed, N. Energy management in electrical smart grid environment using robust optimization algorithm. IEEE Trans. Ind. Appl. 2018, 54, 2714–2726. [Google Scholar] [CrossRef]
- Mohanty, P.; Bhuvaneswari, G.; Balasubramanian, R.; Dhaliwal, N.K. MATLAB based modeling to study the performance of different MPPT techniques used for solar PV system under various operating conditions. Renew. Sustain. Energy Rev. 2014, 38, 581–593. [Google Scholar] [CrossRef]
- Calvinho, G.; Pombo, J.; Mariano, S.; do Rosario Calado, M. Design and implementation of MPPT system based on PSO algorithm. In Proceedings of the 2018 International Conference on Intelligent Systems (IS), Funchal, Portugal, 25–27 September 2018; pp. 733–738. [Google Scholar]
- Rajkumar, M.V.; Mahakumar, M.; Manojkumar, M.; Hemaraj, M.; Kumaravel, E. A new DC-DC converter topology with grey wolf MPPT algorithm for photovoltaic system. Int. J. Emerg. Technol. Eng. Res. (IJETER) 2017, 5, 54–59. [Google Scholar]
- Soufyane Benyoucef, A.; Chouder, A.; Kara, K.; Silvestre, S. Artificial bee colony based algorithm for maximum power point tracking (MPPT) for PV systems operating under partial shaded conditions. Appl. Soft Comput. 2015, 32, 38–48. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Ramachandaramurthy, V.K.; Padmanaban, S.; Azam, F. An ant colony optimized MPPT for standalone hybrid PV-wind power system with single Cuk converters. Energies 2019, 12, 167. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A Maximum Power Point Tracking (MPPT) for PV system using Cuckoo Search with partial shading capability. Appl. Energy 2014, 119, 118–130. [Google Scholar] [CrossRef]
- Pilakkat, D.; Kanthalakshmi, S. An improved P&O algorithm integrated with artificial bee colony for photovoltaic systems under partial shading conditions. Sol. Energy 2019, 178, 37–47. [Google Scholar]
- Figueiredo, S.; e Silva, R.N.A.L. Hybrid mppt technique pso-p&o applied to photovoltaic systems under uniform and partial shading conditions. IEEE Lat. Am. Trans. 2021, 19, 1610–1617. [Google Scholar]
- Chao, K.H.; Rizal, M.N. A hybrid MPPT controller based on the genetic algorithm and ant colony optimization for photovoltaic systems under partially shaded conditions. Energies 2021, 14, 2902. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Mitani, Y.; Watanabe, M.; Küfeoǧlu, S.K. Robust virtual inertia control of an islanded microgrid considering high penetration of renewable energy. IEEE Access 2017, 6, 625–636. [Google Scholar] [CrossRef]
- Carli, R.; Dotoli, M. A decentralized resource allocation approach for sharing renewable energy among interconnected smart homes. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 5903–5908. [Google Scholar]
- Saleem, O.; Ali, S.; Iqbal, J. Robust MPPT Control of Stand-Alone Photovoltaic Systems via Adaptive Self-Adjusting Fractional Order PID Controller. Energies 2023, 16, 5039. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Almutairi, Z.A.; Abdelhamid, M.A. Modern Optimization Algorithm for Improved Performance of Maximum Power Point Tracker of Partially Shaded PV Systems. Energies 2023, 16, 5228. [Google Scholar] [CrossRef]
- Provensi, L.L.; de Souza, R.M.; Grala, G.H.; Bergamasco, R.; Krummenauer, R.; Andrade, C.M.G. Modeling and Simulation of Photovoltaic Modules Using Bio-Inspired Algorithms. Inventions 2023, 8, 107. [Google Scholar] [CrossRef]
- Ngo, S.; Chiu, C.S.; Ngo, T.D. A Novel Horse Racing Algorithm Based MPPT Control for Standalone PV Power Systems. Energies 2022, 15, 7498. [Google Scholar] [CrossRef]
- Hameed, W.I.; Saleh, A.L.; Sawadi, B.A.; Al-Yasir, Y.I.; Abd-Alhameed, R.A. Maximum power point tracking for photovoltaic system by using fuzzy neural network. Inventions 2019, 4, 33. [Google Scholar] [CrossRef]
- Silaa, M.Y.; Barambones, O.; Cortajarena, J.A.; Alkorta, P.; Bencherif, A. PEMFC Current Control Using a Novel Compound Controller Enhanced by the Black Widow Algorithm: A Comprehensive Simulation Study. Sustainability 2023, 18, 13823. [Google Scholar] [CrossRef]
- Sahu, B.; Rincón-Mora, G.A. A low voltage, dynamic, noninverting, synchronous buck-boost converter for portable applications. IEEE Trans. Power Electron. 2004, 19, 443–452. [Google Scholar] [CrossRef]
- Nahavandi, A.; Hagh, M.T.; Sharifian, M.B.B.; Danyali, S. A nonisolated multiinput multioutput DC–DC boost converter for electric vehicle applications. IEEE Trans. Power Electron. 2014, 30, 1818–1835. [Google Scholar] [CrossRef]
- Abdel-Rahim, O.; Orabi, M.; Abdelkarim, E.; Ahmed, M.; Youssef, M.Z. Switched inductor boost converter for PV applications. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC)s, Orlando, FL, USA, 5–9 February 2012; pp. 2100–2106. [Google Scholar]
- Khadmun, W.; Subsingha, W. High voltage gain interleaved dc boost converter application for photovoltaic generation system. Energy Procedia 2013, 34, 390–398. [Google Scholar] [CrossRef]
- Silaa, M.Y.; Bencherif, A.; Barambones, O. A novel robust adaptive sliding mode control using stochastic gradient descent for PEMFC power system. Int. J. Hydrog. Energy 2023, 48, 17277–17292. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Muro, C.; Escobedo, R.; Spector, L.; Coppinger, R.P. Wolf-pack (Canis lupus) hunting strategies emerge from simple rules in computational simulations. Behav. Process. 2011, 11, 192–197. [Google Scholar] [CrossRef] [PubMed]
- Silaa, M.Y.; Barambones, O.; Derbeli, M.; Napole, C.; Bencherif, A. Fractional order PID design for a proton exchange membrane fuel cell system using an extended grey wolf optimizer. Processes 2022, 10, 450. [Google Scholar] [CrossRef]
- Cherukuri, S.K.; Rayapudi, S.R. Enhanced grey wolf optimizer based MPPT algorithm of PV system under partial shaded condition. Int. J. Renew. Energy Dev. 2017, 6, 203. [Google Scholar] [CrossRef]

| Specifications | Value |
|---|---|
| Maximum power (W) | |
| Cells per module () | 60 |
| Open circuit voltage (V) | |
| Short-circuit current (A) | |
| Voltage at maximum power point (V) | |
| Current at maximum power point (A) | |
| Temperature coefficient of (%/deg.C) | |
| Temperature coefficient of (%/deg.C) |
| Specifications | Value |
|---|---|
| Inductance (L) | H |
| In capacitor (C) | 100 × 10 F |
| Out capacitor (C) | 470 × 10 F |
| Max | 10 kHz |
| Load | 32 Ohm |
| Parameter | EGWO | GWO | PSO | EOA | SCA |
|---|---|---|---|---|---|
| Population size () | 20 | 20 | 20 | 20 | 20 |
| Maximum number of iterations () | 100 | 100 | 100 | 100 | 100 |
| A and C | Random | Random | − | − | − |
| − | − | − | − | ||
| − | − | − | − | ||
| − | − | − | − | ||
| − | − | − | − | ||
| − | − | − | − | ||
| − | − | − | − | ||
| − | − | − | 2 | − | |
| − | − | − | 1 | − | |
| − | − | − | − | ||
| − | − | − | − | Random in |
| Algorithm | Scenario 1 (Oscillation) | Scenario 2 (Oscillation) | Scenario 3 (Oscillation) | Scenario 4 (Oscillation) |
|---|---|---|---|---|
| EGWO | Excellent (0.09 W) | Excellent (0.09 W) | Excellent (0.09 W) | Excellent (0.09 W) |
| GWO | Good (0.266 W) | Good (0.266 W) | Good (0.266 W) | Good (0.266 W) |
| PSO | Poor (0.731 W) | Poor (18.401 W) | Poor (1.919 W) | Poor (37.901 W) |
| EOA | Poor (1.044 W) | Poor (26.671 W) | Poor (2.035 W) | Poor (39.323 W) |
| SCA | Poor (0.729 W) | Poor (15.796 W) | Poor (2.035 W) | Poor (35.379 W) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silaa, M.Y.; Barambones, O.; Bencherif, A.; Rahmani, A. A New MPPT-Based Extended Grey Wolf Optimizer for Stand-Alone PV System: A Performance Evaluation versus Four Smart MPPT Techniques in Diverse Scenarios. Inventions 2023, 8, 142. https://doi.org/10.3390/inventions8060142
Silaa MY, Barambones O, Bencherif A, Rahmani A. A New MPPT-Based Extended Grey Wolf Optimizer for Stand-Alone PV System: A Performance Evaluation versus Four Smart MPPT Techniques in Diverse Scenarios. Inventions. 2023; 8(6):142. https://doi.org/10.3390/inventions8060142
Chicago/Turabian StyleSilaa, Mohammed Yousri, Oscar Barambones, Aissa Bencherif, and Abdellah Rahmani. 2023. "A New MPPT-Based Extended Grey Wolf Optimizer for Stand-Alone PV System: A Performance Evaluation versus Four Smart MPPT Techniques in Diverse Scenarios" Inventions 8, no. 6: 142. https://doi.org/10.3390/inventions8060142
APA StyleSilaa, M. Y., Barambones, O., Bencherif, A., & Rahmani, A. (2023). A New MPPT-Based Extended Grey Wolf Optimizer for Stand-Alone PV System: A Performance Evaluation versus Four Smart MPPT Techniques in Diverse Scenarios. Inventions, 8(6), 142. https://doi.org/10.3390/inventions8060142







