Measuring the Electron–Phonon Interaction in Two-Dimensional Superconductors with He-Atom Scattering
Abstract
1. Introduction
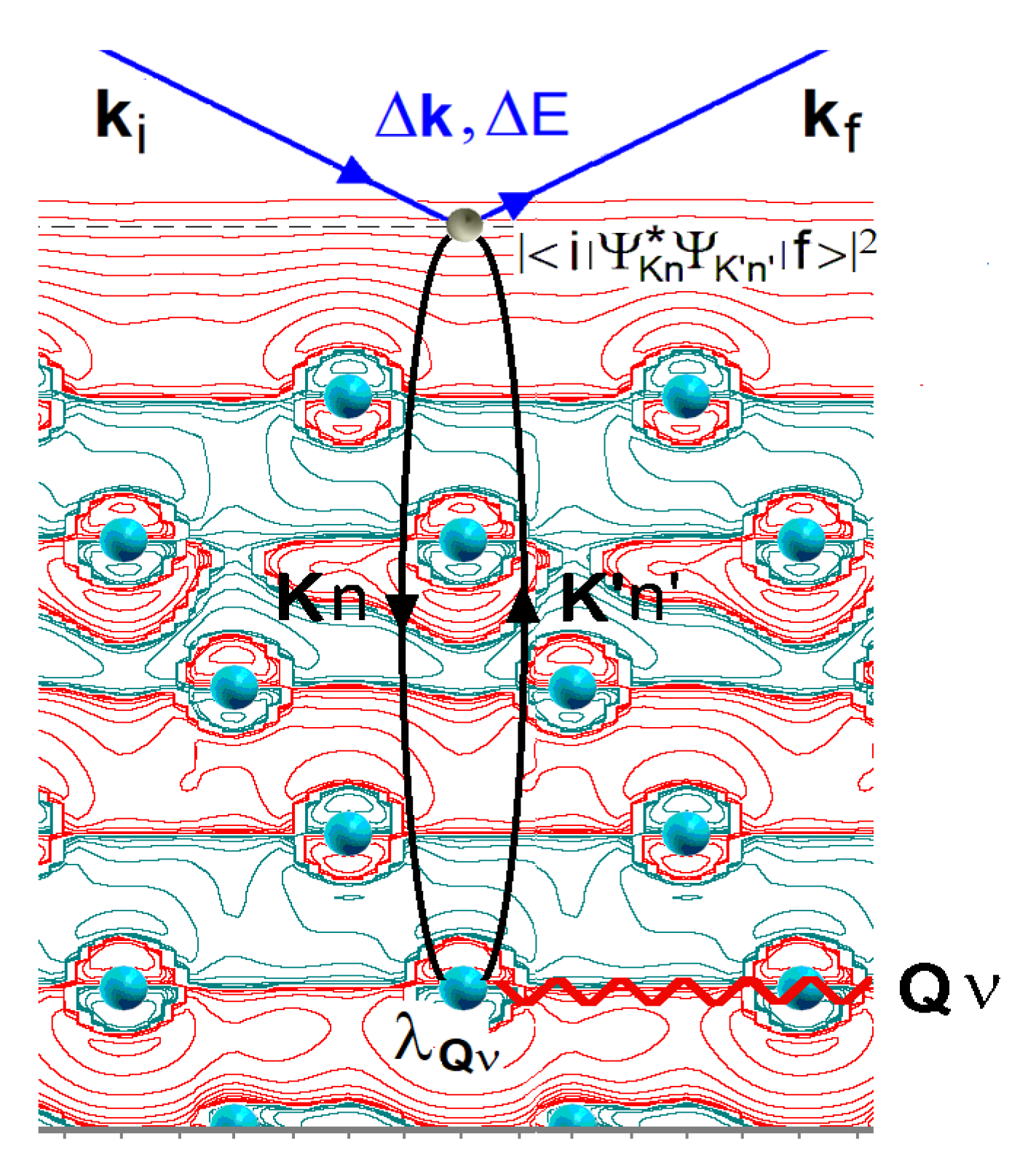
2. The Electron–Phonon Theory of He-Atom Scattering from Conducting Surfaces
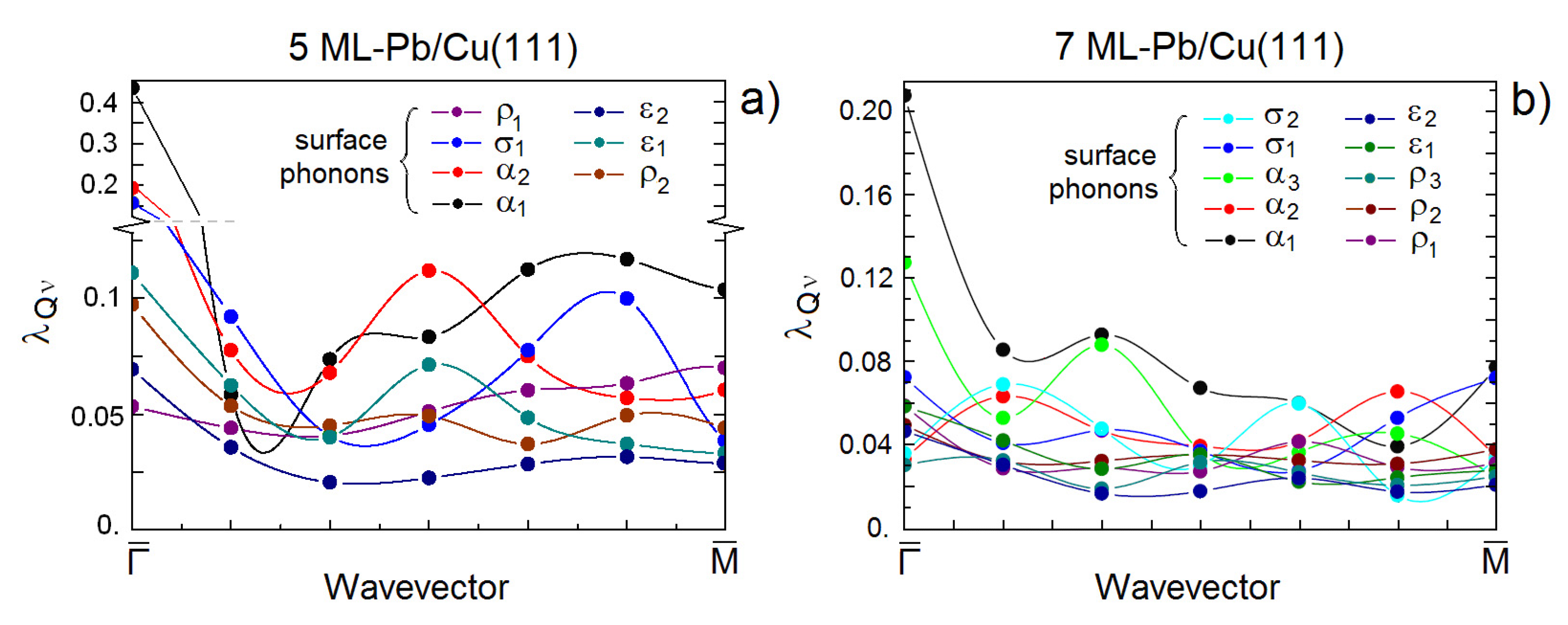
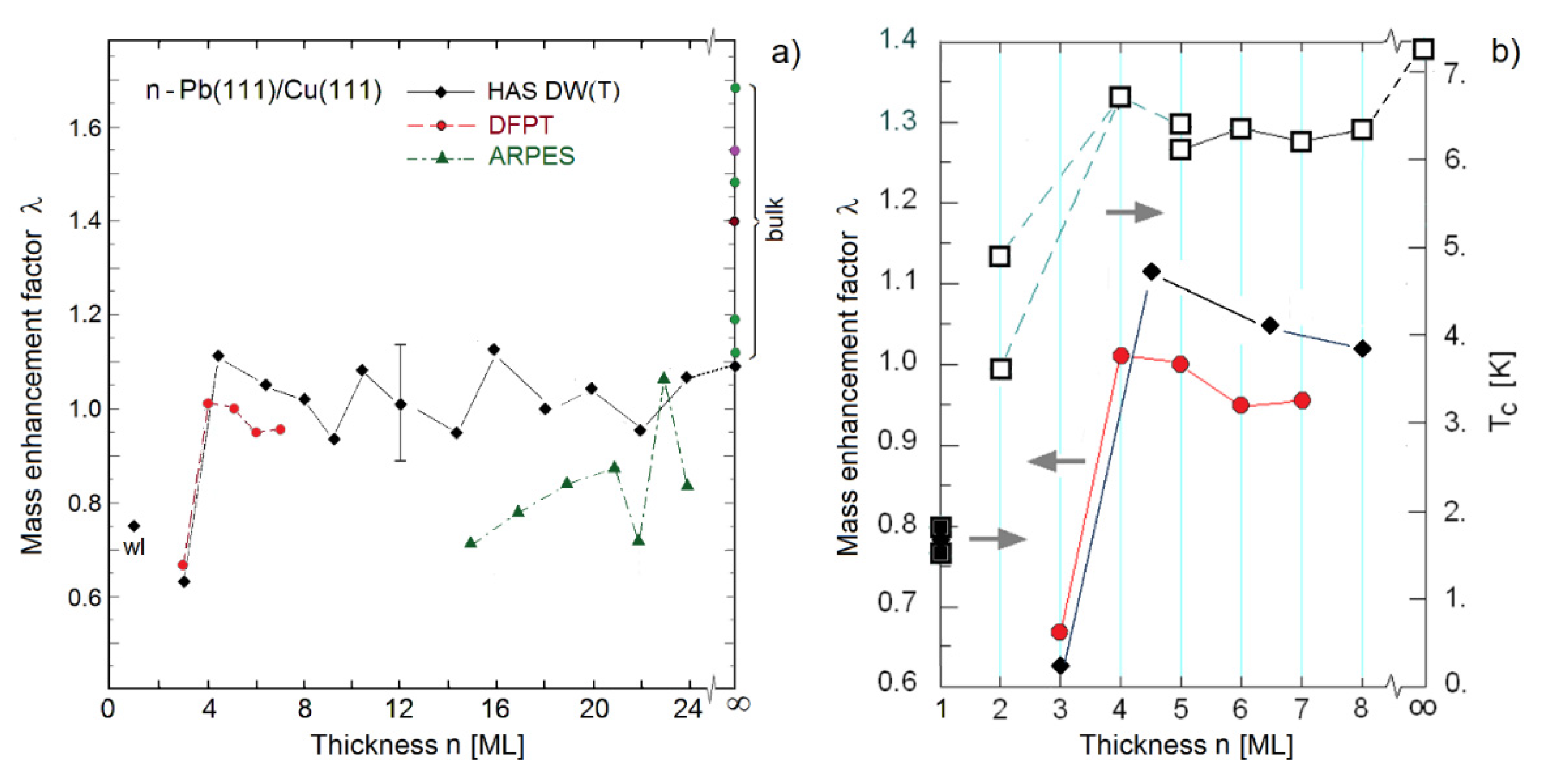
3. Mode-Selected Electron–Phonon Coupling from HAS: Lead Ultra-thin Films
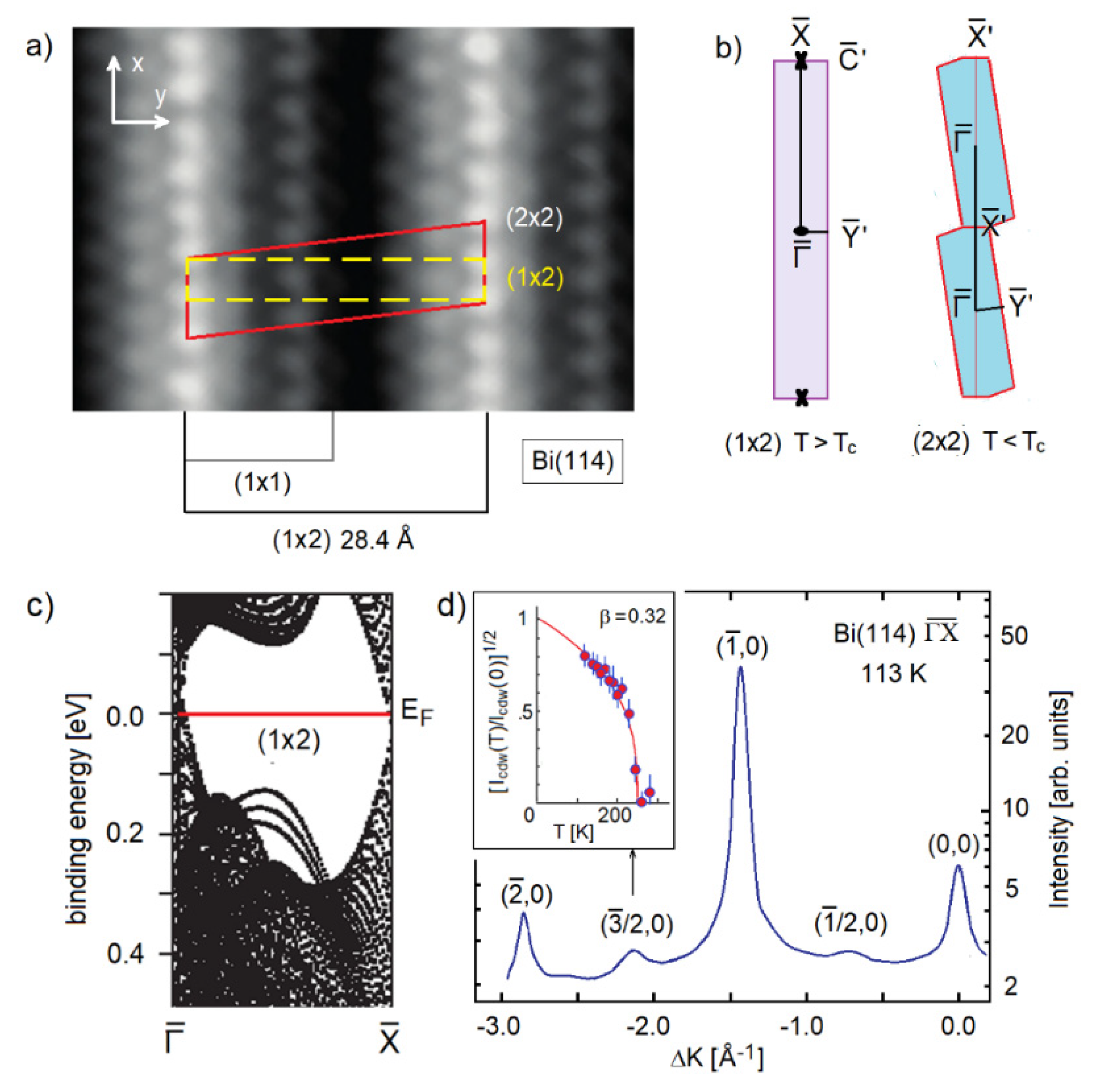
4. A Quasi-1D Metal: Bi(114)
5. Superconducting Layered Chalcogenides
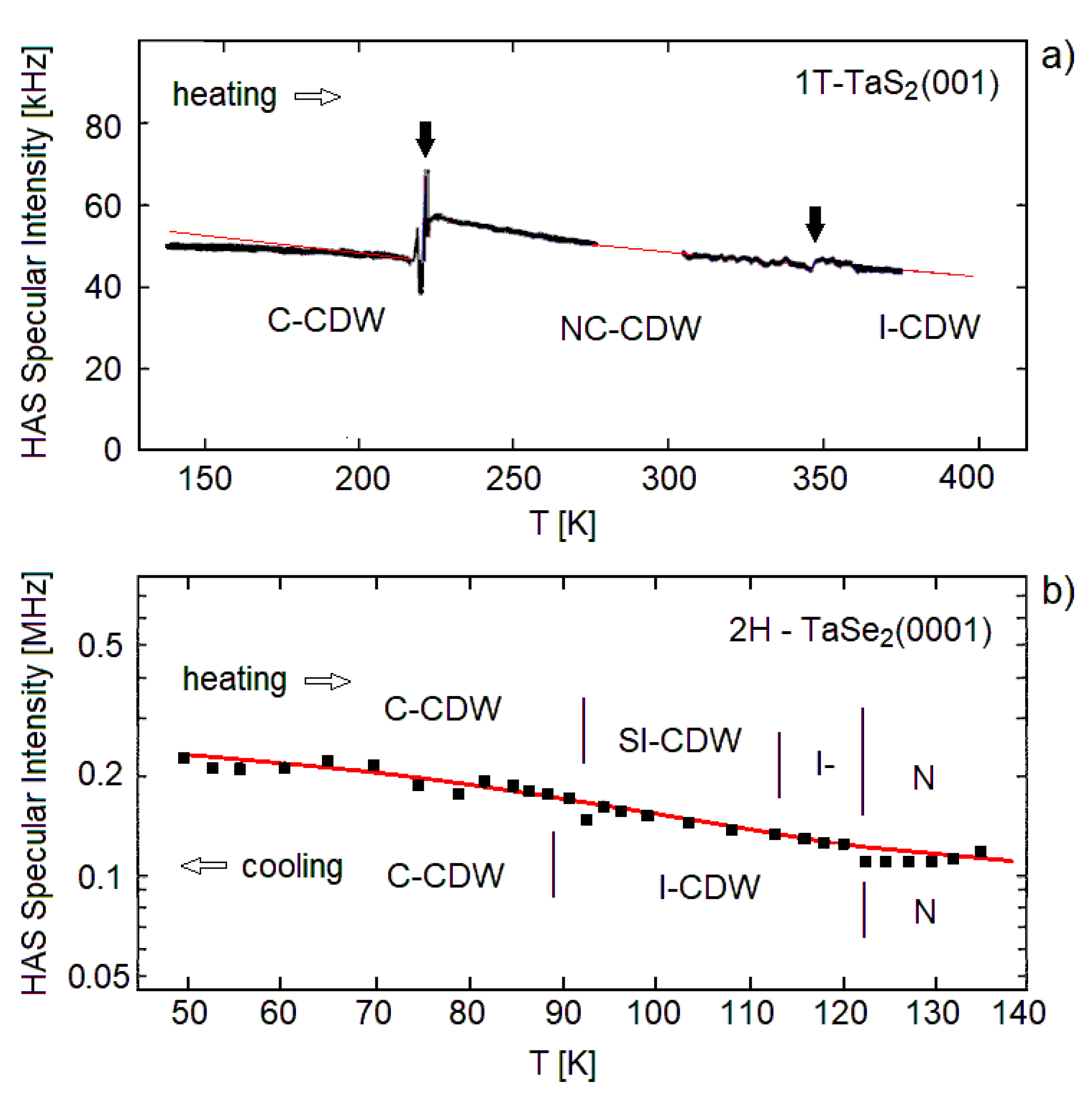
5.1. 1T-TaS2(001)
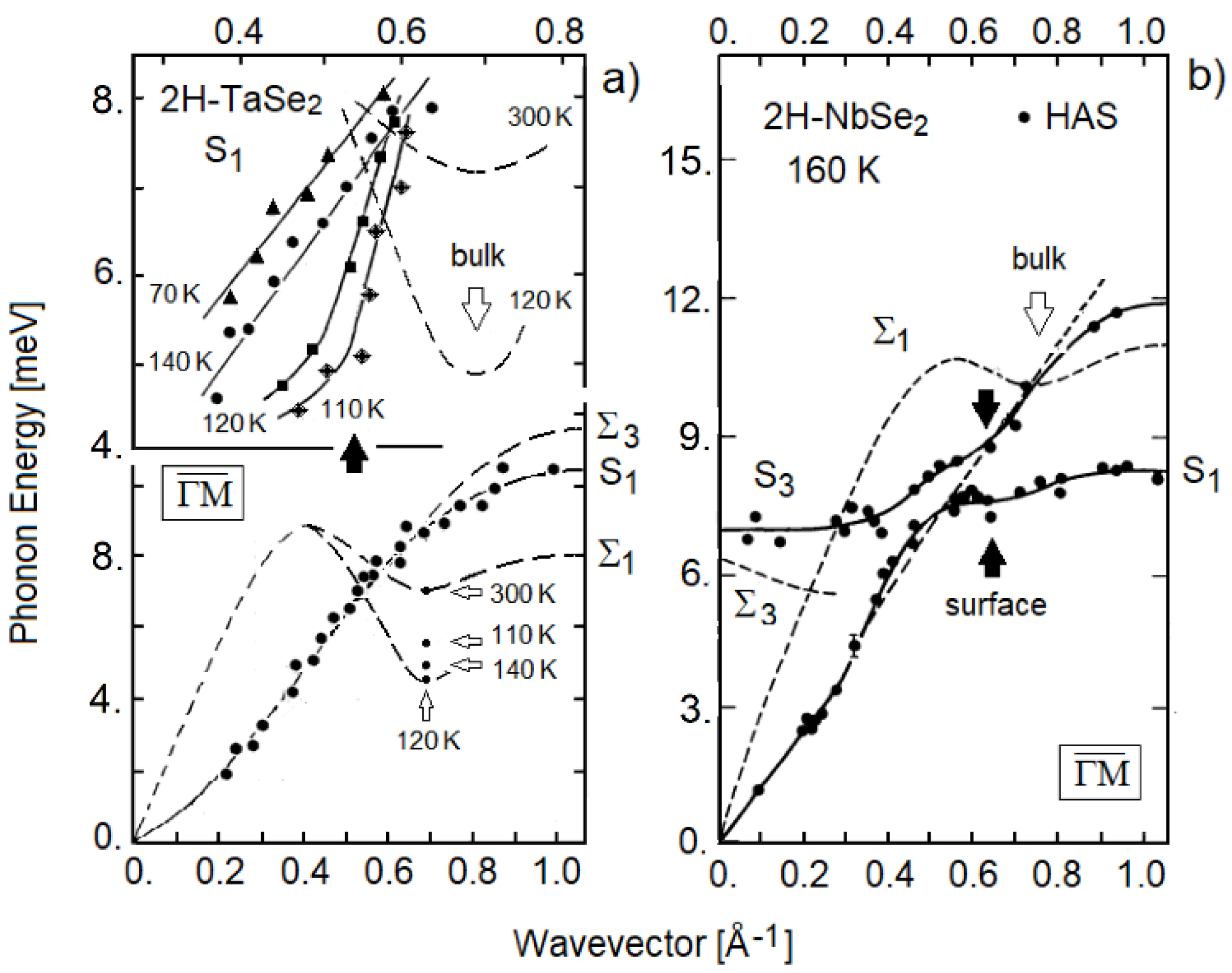
5.2. 2H-TaSe2(0001)
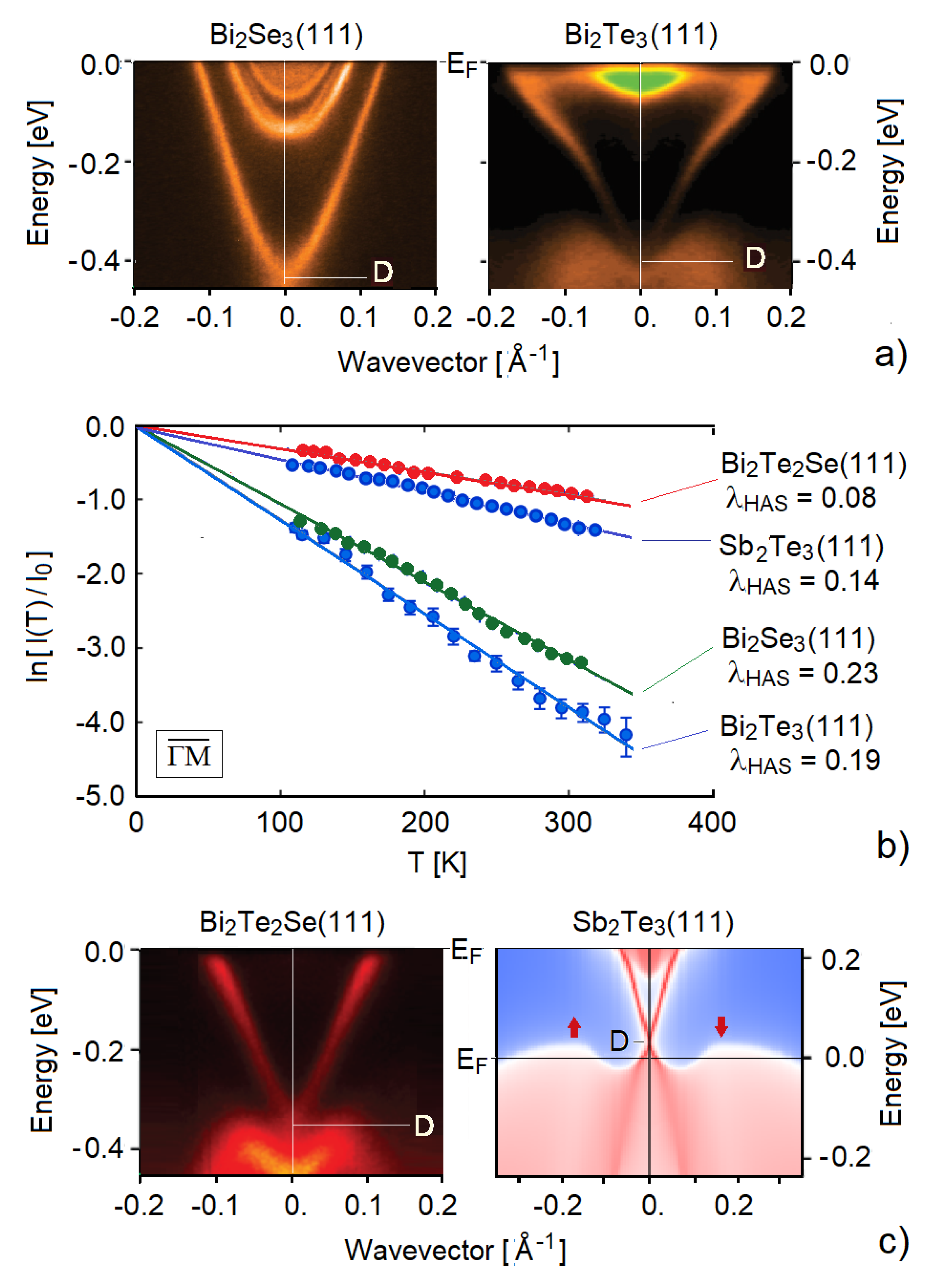
5.3. Pnictogen Chalcogenides
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Benedek, G.; Toennies, J.P. 2018 Atomic-Scale Dynamics at Surfaces—Theory and Experimental Studies with Helium Atom. Scattering; Springer: Berlin, Germany, 2018. [Google Scholar]
- Doak, R.B.; Harten, U.; Toennies, J.P. Anomalous Surface Phonon Dispersion Relations for Ag(111) Measured by Inelastic Scattering of He. Atoms Phys. Rev. Lett. 1983, 51, 578–581. [Google Scholar] [CrossRef]
- Harten, U.; Toennies, J.P.; Wöll, C. Helium time-of-flight spectroscopy of surface-phonon dispersion curves of the noble metals. Faraday Discuss. Chem. Soc. 1985, 80, 137–149. [Google Scholar] [CrossRef]
- Jayanthi, C.S.; Bilz, H.; Kress, W.; Benedek, G. Nature of surface-phonon anomalies in noble metals. Phys. Rev. Lett. 1987, 59, 795–798. [Google Scholar] [CrossRef] [PubMed]
- Kaden, C.; Ruggerone, P.; Toennies, J.P.; Zhang, G.; Benedek, G. Electronic pseudocharge model for the Cu(111) longitudinal-surface-phonon anomaly observed by helium-atom scattering. Phys. Rev. B 1992, 46, 13509–13525. [Google Scholar] [CrossRef] [PubMed]
- Benedek, G.; Bernasconi, M.; Chis, V.; Chulkov, E.; Echenique, P.M.; Hellsing, B.; Toennies, J.P. Theory of surface phonons at metal surfaces: Recent advances. J. Phys. Condens. Matter 2010, 22, 084020. [Google Scholar] [CrossRef] [PubMed]
- Sklyadneva, I.Y.; Benedek, G.; Chulkov, E.V.; Echenique, P.M.; Heid, R.; Bohnen, K.-P.; Toennies, J.P. Mode-Selected Electron-Phonon Coupling in Superconducting Pb Nanofilms Determined from He Atom Scattering. Phys. Rev. Lett. 2011, 107, 095502. [Google Scholar] [CrossRef]
- Tamtögl, A.; Ruckhofer, A.; Campi, D.; Allison, W.; Ernst, W.E. Atom-surface van der Waals Potentials of Topological Insulators and Semimetals from Scattering Measurements. Phys. Chem. Chem. Phys. 2020, in press. [Google Scholar]
- Benedek, G.; Bernasconi, M.; Bohnen, K.-P.; Campi, D.; Chulkov, E.V.; Echenique, P.M.; Heid, R.; Sklyadneva, I.Y.; Toennies, J.P. Unveiling mode-selected electron–phonon interactions in metal films by helium atom scattering. Phys. Chem. Chem. Phys. 2014, 16, 7159–7172. [Google Scholar] [CrossRef][Green Version]
- Manson, J.R.; Benedek, G.; Miret-Artés, S. Electron–Phonon Coupling Strength at Metal Surfaces Directly Determined from the Helium Atom Scattering Debye–Waller Factor. J. Phys. Chem. Lett. 2016, 7, 1016–1021. [Google Scholar] [CrossRef]
- Benedek, G.; Miret-Artés, S.; Toennies, J.P.; Manson, J.R. Electron–Phonon Coupling Constant of Metallic Overlayers from Specular He Atom Scattering. J. Phys. Chem. Lett. 2018, 9, 76–83. [Google Scholar] [CrossRef]
- Anemone, G.; Taleb, A.A.; Benedek, G.; Castellanos-Gomez, A.; Farías, D. Electron–Phonon Coupling Constant of 2H-MoS2(0001) from Helium-Atom Scattering. J. Phys. Chem. C 2019, 123, 3682–3686. [Google Scholar] [CrossRef]
- Anemone, G.; Garnica, M.; Zappia, M.; Aguilar, P.C.; Taleb, A.A.; Kuo, C.-N.; Lue, C.S.; Politano, A.; Benedek, G.; Parga, A.L.V.; et al. Experimental determination of surface thermal expansion and electron–phonon coupling constant of 1T-PtTe2. 2D Mater. 2020, 7, 025007. [Google Scholar]
- Tamtögl, A.; Kraus, P.; Mayrhofer-Reinhartshuber, M.; Benedek, G.; Bernasconi, M.; Dragoni, D.; Campi, D.; Ernst, W.E. Statics and dynamics of multivalley charge density waves in Sb(111). npj Quantum Mater. 2019, 4, 28. [Google Scholar] [CrossRef]
- Benedek, G.; Miret-Artés, S.; Manson, J.R.; Ruckhofer, A.; Ernst, W.E.; Tamtögl, A. Origin of the Electron–Phonon Interaction of Topological Semimetal Surfaces Measured with Helium Atom Scattering. J. Phys. Chem. Lett. 2020, 11, 1927–1933. [Google Scholar] [CrossRef]
- Hofmann, P.; Ugeda, M.M.; Tamtögl, A.; Ruckhofer, A.; Ernst, W.E.; Benedek, G.; Martínez-Galera, A.J.; Stróżecka, A.; Gómez-Rodríguez, J.M.; Rienks, E.; et al. Strong-coupling charge density wave in a one-dimensional topological metal. Phys. Rev. B 2019, 99, 035438. [Google Scholar] [CrossRef]
- Benedek, G.; Manson, J.R.; Miret-Artés, S. The Electron–Phonon Interaction of Low-Dimensional and Multi-Dimensional Materials from He Atom Scattering. Adv. Mater. 2020, 32, 2002072. [Google Scholar] [CrossRef]
- Benedek, G.; Manson, J.R.; Miret-Artés, S. The electron–phonon coupling constant for single-layer graphene on metal substrates determined from He atom scattering. Phys. Chem. Chem. Phys. 2020, in press. [Google Scholar] [CrossRef]
- Ruckhofer, A.; Campi, D.; Bremholm, M.; Hofmann, P.; Benedek, G.; Bernasconi, M.; Ernst, W.E.; Tamtögl, A. Terahertz surface modes and electron-phonon coupling on Bi2Se3(111). Phys. Rev. Res. 2020, 2, 023186. [Google Scholar] [CrossRef]
- Ruckhofer, A.; Halbritter, S.E.; Lund, H.; Holt, A.J.U.; Bianchi, M.; Bremholm, M.; Benedek, G.; Hofmann, P.; Ernst, W.E.; Tamtögl, A. Inelastic helium atom scattering from Sb2Te3(111): Phonon dispersion, focusing effects and surfing. Phys. Chem. Chem. Phys. 2020, in press. [Google Scholar] [CrossRef]
- Esbjerg, N.; Nørskov, J.K. Dependence of the He-Scattering Potential at Surfaces on the Surface-Electron-Density Profile. Phys. Rev. Lett. 1980, 45, 807–810. [Google Scholar] [CrossRef]
- Cole, M.W.; Toigo, F. Energy of immersing a He, Ne, or Ar atom or H2 molecule into a low-density electron gas. Phys. Rev. B 1985, 31, 727–729. [Google Scholar] [CrossRef] [PubMed]
- Manson, R.; Celli, V. Inelastic surface scattering of non-penetrating particles. Surf. Sci. 1971, 24, 495–514. [Google Scholar] [CrossRef]
- Grimvall, G. The Electron-Phonon Interaction in Normal. Metals Phys. Scr. 1976, 14, 63. [Google Scholar] [CrossRef]
- Allen, P.B. The Electron-Phonon Coupling Constant λ. In Handbook of Superconductivity; Poole, C.P., Jr., Ed.; Academic Press: New York, NY, USA, 1999; pp. 478–483. [Google Scholar]
- Hinch, B.J.; Koziol, C.; Toennies, J.P.; Zhang, G. Evidence for Quantum Size Effects Observed by Helium Atom Scattering during the Growth of Pb on Cu(111). Europhys. Lett. EPL 1989, 10, 341–346. [Google Scholar] [CrossRef]
- Zhang, G. Max-Planck-Institut für Strömungsforschung. Ph.D. Thesis, University of Göttingen, Göttingen, Germany, 1991. [Google Scholar]
- Braun, J.; Ruggerone, P.; Zhang, G.; Toennies, J.P.; Benedek, G. Surface phonon dispersion curves of thin Pb films on Cu(111). Phys. Rev. B 2009, 79, 205423. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, Y.-F.; Bao, X.-Y.; Han, T.-Z.; Tang, Z.; Zhang, L.-X.; Zhu, W.-G.; Wang, E.G.; Niu, Q.; Qiu, Z.Q.; et al. Superconductivity Modulated by Quantum Size Effects. Science 2004, 306, 1915–1917. [Google Scholar] [CrossRef]
- Eom, D.; Qin, S.; Chou, M.-Y.; Shih, C.K. Persistent Superconductivity in Ultrathin Pb Films: A Scanning Tunneling Spectroscopy Study. Phys. Rev. Lett. 2006, 96, 027005. [Google Scholar] [CrossRef]
- Özer, M.M.; Jia, Y.; Zhang, Z.; Thompson, J.R.; Weitering, H.H. Tuning the Quantum Stability and Superconductivity of Ultrathin Metal Alloys. Science 2007, 316, 1594–1597. [Google Scholar] [CrossRef]
- Qin, S.; Kim, J.; Niu, Q.; Shih, C.-K. Superconductivity at the Two-Dimensional Limit. Science 2009, 324, 1314–1317. [Google Scholar] [CrossRef]
- Brun, C.; Hong, I.-P.; Patthey, F.; Sklyadneva, I.Y.; Heid, R.; Echenique, P.M.; Bohnen, K.P.; Chulkov, E.V.; Schneider, W.-D. Reduction of the Superconducting Gap of Ultrathin Pb Islands Grown on Si(111). Phys. Rev. Lett. 2009, 102. [Google Scholar] [CrossRef]
- Zhang, T.; Cheng, P.; Li, W.-J.; Sun, Y.-J.; Wang, G.; Zhu, X.-G.; He, K.; Wang, L.; Ma, X.; Chen, X.; et al. Superconductivity in one-atomic-layer metal films grown on Si(111). Nat. Phys. 2010, 6, 104–108. [Google Scholar] [CrossRef]
- Zhang, Y.-F.; Jia, J.-F.; Han, T.-Z.; Tang, Z.; Shen, Q.-T.; Guo, Y.; Qiu, Z.Q.; Xue, Q.-K. Band Structure and Oscillatory Electron-Phonon Coupling of Pb Thin Films Determined by Atomic-Layer-Resolved Quantum-Well States. Phys. Rev. Lett. 2005, 95, 096802. [Google Scholar] [CrossRef] [PubMed]
- Prakash, O.; Kumar, A.; Thamizhavel, A.; Ramakrishnan, S. Evidence for bulk superconductivity in pure bismuth single crystals at ambient pressure. Science 2017, 355, 52–55. [Google Scholar] [CrossRef] [PubMed]
- Mata-Pinzón, Z.; Valladares, A.A.; Valladares, R.M.; Valladares, A. Superconductivity in Bismuth. A New Look at an Old Problem. PLoS ONE 2016, 11, e0147645. [Google Scholar]
- Tian, M.; Wang, J.; Ning, W.; Mallouk, T.E.; Chan, M.H.W. Surface Superconductivity in Thin Cylindrical Bi Nanowire. Nano Lett. 2015, 15, 1487–1492. [Google Scholar] [CrossRef]
- Wells, J.W.; Dil, J.H.; Meier, F.; Lobo-Checa, J.; Petrov, V.N.; Osterwalder, J.; Ugeda, M.M.; Fernandez-Torrente, I.; Pascual, J.I.; Rienks, E.D.L.; et al. Nondegenerate Metallic States on Bi(114): A One-Dimensional Topological Metal. Phys. Rev. Lett. 2009, 102, 096802. [Google Scholar] [CrossRef]
- Ma, T.; Wang, S. Phase Transition Dynamics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Liu, R.; Ma, T.; Wang, S.; Yang, J. Dynamic Theory of Fluctuations and Critical Exponents of Thermodynamic Phase Transitions. 2019. Available online: https://hal.archives-ouvertes.fr/hal-01674269 (accessed on 2 December 2020).
- Brusdeylins, G.; Heimlich, C.; Skofronick, J.G.; Toennies, J.P.; Vollmer, R.; Benedek, G. Determination of the Critical Exponent for a Charge Density Wave Transition in 2H-TaSe2 by Helium Atom Scattering. Europhys. Lett. 1989, 9, 563–568. [Google Scholar] [CrossRef]
- Brusdeylins, G.; Heimlich, C.; Skofronick, J.G.; Toennies, J.P.; Vollmer, R.; Benedek, G.; Miglio, L. He-atom scattering study of the temperature-dependent charge-density-wave surface structure and lattice dynamics of 2H-TaSe2(001). Phys. Rev. B 1990, 41, 5707–5716. [Google Scholar] [CrossRef]
- Requardt, H.; Kalning, M.; Burandt, B.; Press, W.; Currat, R. Critical x-ray scattering at the Peierls transition in the quasi-one-dimensional system. J. Phys. Condens. Matter 1996, 8, 2327–2336. [Google Scholar] [CrossRef]
- Lorenzo, J.E.; Currat, R.; Monceau, P.; Hennion, B.; Berger, H.; Levy, F. A neutron scattering study of the quasi-one-dimensional conductor. J. Phys. Condens. Matter 1998, 10, 5039–5068. [Google Scholar] [CrossRef]
- Wilson, J.A.; Salvo, F.J.D.; Mahajan, S. Charge-density waves and superlattices in the metallic layered transition metal dichalcogenides. Adv. Phys. 1975, 24, 117–201. [Google Scholar] [CrossRef]
- Nagata, S.; Aochi, T.; Abe, T.; Ebisu, S.; Hagino, T.; Seki, Y.; Tsutsumi, K. Superconductivity in the layered compound 2H-TaS2. J. Phys. Chem. Solids 1992, 53, 1259–1263. [Google Scholar] [CrossRef]
- Sipos, B.; Kusmartseva, A.F.; Akrap, A.; Berger, H.; Forró, L.; Tutiš, E. From Mott state to superconductivity in 1T-TaS2. Nat. Mater. 2008, 7, 960–965. [Google Scholar] [CrossRef] [PubMed]
- Navarro-Moratalla, E.; Island, J.O.; Mañas-Valero, S.; Pinilla-Cienfuegos, E.; Castellanos-Gomez, A.; Quereda, J.; Rubio-Bollinger, G.; Chirolli, L.; Silva-Guillén, J.A.; Agraït, N.; et al. Enhanced superconductivity in atomically thin TaS2. Nat. Commun. 2016, 7, 11043. [Google Scholar] [CrossRef]
- Yang, Y.; Fang, S.; Fatemi, V.; Ruhman, J.; Navarro-Moratalla, E.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Enhanced superconductivity upon weakening of charge density wave transport in 2H-TaS2 in the two-dimensional limit. Phys. Rev. B 2018, 98, 035203. [Google Scholar] [CrossRef]
- Peng, J.; Yu, Z.; Wu, J.; Zhou, Y.; Guo, Y.; Li, Z.; Zhao, J.; Wu, C.; Xie, Y. Disorder Enhanced Superconductivity toward TaS2 Monolayer. ACS Nano 2018, 12, 9461–9466. [Google Scholar] [CrossRef]
- Ribak, A.; Skiff, R.M.; Mograbi, M.; Rout, P.K.; Fischer, M.H.; Ruhman, J.; Chashka, K.; Dagan, Y.; Kanigel, A. Chiral superconductivity in the alternate stacking compound 4Hb-TaS2. Sci. Adv. 2020, 6, eaax9480. [Google Scholar] [CrossRef]
- Ritschel, T.; Trinckauf, J.; Garbarino, G.; Hanfland, M.; Zimmermann, M.V.; Berger, H.; Büchner, B.; Geck, J. Pressure dependence of the charge density wave in 1T-TaS2 and its relation to superconductivity. Phys. Rev. B 2013, 87, 125135. [Google Scholar] [CrossRef]
- Wagner, K.E.; Morosan, E.; Hor, Y.S.; Tao, J.; Zhu, Y.; Sanders, T.; McQueen, T.M.; Zandbergen, H.W.; Williams, A.J.; West, D.V.; et al. Tuning the charge density wave and superconductivity in CuxTaS2. Phys. Rev. B 2008, 78, 104520. [Google Scholar] [CrossRef]
- Wilson, J.A.; Salvo, F.J.D.; Mahajan, S. Charge-density waves and superlattices in the metallic layered transition metal dichalcogenides. Adv. Phys. 2001, 50, 1171–1248. [Google Scholar] [CrossRef]
- Coleman, R.V.; McNairy, W.W.; Slough, C.G. Amplitude modulation of charge-density-wave domains in 1T-TaS2 at 300 K. Phys. Rev. B 1992, 45, 1428–1431. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Yang, F.; Lu, X.F.; Yan, Y.J.; Cho, Y.-H.; Ma, L.; Niu, X.; Kim, S.; Son, Y.-W.; Feng, D.; et al. Gate-tunable phase transitions in thin flakes of 1T-TaS2. Nanotechnology 2015, 10, 270–276. [Google Scholar] [CrossRef] [PubMed]
- Cantini, P.; Boato, G.; Colella, R. Surface charge density waves observed by atomic beam diffraction. Physica B+C 1980, 99, 59–63. [Google Scholar] [CrossRef]
- Heimlich, C. Max-Planck Inst. für Strömungsforschung. Ph.D. Thesis, University of Göttingen, Göttingen, Germany, October 1987. [Google Scholar]
- Brusdeylins, G.; Heimlich, C.; Toennies, J.P. Helium scattering from the layered compound single crystal surface of 1T-TaS2 in the temperature region of charge density wave reconstruction. Surf. Sci. 1989, 211–212, 98–105. [Google Scholar] [CrossRef]
- Shimada, T.; Ohuchi, F.S.; Parkinson, B.A. Work Function and Photothreshold of Layered Metal Dichalcogenides. Jpn. J. Appl. Phys. 1994, 33. [Google Scholar] [CrossRef]
- Zhao, R.; Grisafe, B.; Ghosh, R.K.; Holoviak, S.; Wang, B.; Wang, K.; Briggs, N.; Haque, A.; Datta, S.; Robinson, J. Two-dimensional tantalum disulfide: Controlling structure and properties via synthesis. 2D Materials 2018, 5, 025001. [Google Scholar] [CrossRef]
- Rossnagel, K. On the origin of charge-density waves in select layered transition-metal dichalcogenides. J. Phys. Condens. Matter. 2011, 23, 213001. [Google Scholar] [CrossRef]
- Shiino, O.; Watanabe, T.; Endo, T.; Hanaguri, T.; Kitazawa, K.; Nohara, M.; Takagi, H.; Murayama, C.; Takeshita, N.; Môri, N.; et al. Metal–insulator transition in 1T-TaS2−xSex. Phys. B Condens. Matter 2000, 284–288, 1673–1674. [Google Scholar] [CrossRef]
- Balaguru-Rayappan, J.B.; Raj, S.A.C.; Lawrence, N. Thermal properties of 1T-TaS2 at the onset of charge density wave states. Phys. B Condens. Matter. 2010, 405, 3172–3175. [Google Scholar] [CrossRef]
- Liu, A.Y. Electron-phonon coupling in compressed 1T-TaS2: Stability and superconductivity from first principles. Phys. Rev. B 2009, 79, 220515. [Google Scholar] [CrossRef]
- Benedek, G.; Hofmann, F.; Ruggerone, P.; Onida, G.; Miglio, L. Surface phonons in layered crystals: Theoretical aspects. Surf. Sci. Rep. 1994, 20, 1–43. [Google Scholar] [CrossRef]
- Benedek, G.; Brusdeylins, G.; Hofmann, F.; Ruggerone, P.; Toennies, J.P.; Vollmer, R.; Skofronick, J.G. Strong coupling of Rayleigh phonons to charge density waves in 1T-TaS2. Surf. Sci. 1994, 304, 185–190. [Google Scholar] [CrossRef]
- McWhan, D.B.; Axe, J.D.; Youngblood, R. Pressure dependence of the striped-to-hexagonal charge-density-wave transition in 2H-TaSe2. Phys. Rev. B 1981, 24, 5391–5393. [Google Scholar] [CrossRef]
- Tsoutsou, D.; Aretouli, K.E.; Tsipas, P.; Marquez-Velasco, J.; Xenogiannopoulou, E.; Kelaidis, N.; Aminalragia-Giamini, S.; Dimoulas, A. Epitaxial 2D MoSe2 (HfSe2) Semiconductor/2D TaSe2 Metal van der Waals Heterostructures. ACS Appl. Mater. Interfaces 2016, 8, 1836–1841. [Google Scholar] [CrossRef]
- Moncton, D.E.; Axe, J.D.; DiSalvo, F.J. Neutron scattering study of the charge-density wave transitions in 2H−TaSe2 and 2H−NbSe2. Phys. Rev. B 1977, 16, 801–819. [Google Scholar] [CrossRef]
- Craven, R.A.; Meyer, S.F. Specific heat and resistivity near the charge-density-wave phase transitions in 2H−TaSe2 and 2H−TaS2. Phys. Rev. B 1977, 16, 4583–4593. [Google Scholar] [CrossRef]
- Bhoi, D.; Khim, S.; Nam, W.; Lee, B.S.; Kim, C.; Jeon, B.-G.; Min, B.H.; Park, S.; Kim, K.H. Interplay of charge density wave and multiband superconductivity in 2H-PdxTaSe2. Sci. Rep. 2016, 6, 24068. [Google Scholar] [CrossRef]
- Luo, H.; Xie, W.; Tao, J.; Inoue, H.; Gyenis, A.; Krizan, J.W.; Yazdani, A.; Zhu, Y.; Cava, R.J. Polytypism, polymorphism, and superconductivity in TaSe2−xTex. Proc. Natl. Acad. Sci. USA 2015, 112, E1174–E1180. [Google Scholar] [CrossRef]
- Kumakura, T.; Tan, H.; Handa, T.; Morishita, M.; Fukuyama, H. Charge density waves and superconductivity in 2H-TaSe2. Czechoslov. J. Phys. 1996, 46, 2611–2612. [Google Scholar] [CrossRef]
- Yokota, K.; Kurata, G.; Matsui, T.; Fukuyama, H. Superconductivity in the quasi-two-dimensional conductor 2H-TaSe2. Phys. B Condens. Matter. 2000, 284–288, 551–552. [Google Scholar] [CrossRef]
- Lian, C.-S.; Heil, C.; Liu, X.; Si, C.; Giustino, F.; Duan, W. Coexistence of Superconductivity with Enhanced Charge Density Wave Order in the Two-Dimensional Limit of TaSe2. J. Phys. Chem. Lett. 2019, 10, 4076–4081. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; He, J.; Liu, J.; Xing, H.; Mao, Z.; Liu, Y. Dimensional reduction and ionic gating induced enhancement of superconductivity in atomically thin crystals of 2H-TaSe2. Nanotechnology 2018, 30, 035702. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Shao, D.F.; Li, L.J.; Lu, W.J.; Zhu, X.D.; Tong, P.; Xiao, R.C.; Ling, L.S.; Xi, C.Y.; Pi, L.; et al. Nature of charge density waves and superconductivity in 1T−TaSe2−xTex. Phys. Rev. B 2016, 94, 045131. [Google Scholar] [CrossRef]
- Li, X.C.; Zhou, M.H.; Yang, L.H.; Dong, C. Significant enhancement of superconductivity in copper-doped 2H-TaSe2. Supercond. Sci. Technol. 2017, 30, 125001. [Google Scholar] [CrossRef]
- Benedek, G. Summary Abstract: Surface phonon dynamics of 2H–TaSe2(001). J. Vac. Sci. Technol. A 1987, 5, 1093–1094. [Google Scholar] [CrossRef]
- Benedek, G.; Brusdeylins, G.; Heimlich, C.; Miglio, L.; Skofronick, J.G.; Toennies, J.P.; Vollmer, R. Shifted surface-phonon anomaly in 2H-TaSe2. Phys. Rev. Lett. 1988, 60, 1037–1040. [Google Scholar] [CrossRef] [PubMed]
- Hulpke, E. Helium Atom Scattering from Surfaces; Springer: Berlin, Germany, 1992. [Google Scholar]
- Murphy, B.M.; Requardt, H.; Stettner, J.; Serrano, J.; Krisch, M.; Müller, M.; Press, W. Phonon Modes at the 2H−NbSe2 Surface Observed by Grazing Incidence Inelastic X-Ray Scattering. Phys. Rev. Lett. 2005, 95, 256104. [Google Scholar] [CrossRef]
- Weber, F.; Rosenkranz, S.; Castellan, J.-P.; Osborn, R.; Hott, R.; Heid, R.; Bohnen, K.-P.; Egami, T.; Said, A.H.; Reznik, D. Extended Phonon Collapse and the Origin of the Charge-Density Wave in 2H−NbSe2. Phys. Rev. Lett. 2011, 107, 107403. [Google Scholar] [CrossRef]
- Anemone, G.; Casado Aguilar, M.P.; Garnica, A.; Al Taleb, C.-N.; Kuo, C.; Shan-Lue, A.; Politano, A.L.; Vàzquez de Parga, G.; Benedek, D.; Farìas, R.M. Electron-Phonon Coupling in Superconducting 1T-PdTe2. To be publish.
- Hor, Y.S.; Williams, A.J.; Checkelsky, J.G.; Roushan, P.; Seo, J.; Xu, Q.; Zandbergen, H.W.; Yazdani, A.; Ong, N.P.; Cava, R.J. Superconductivity in CuxBi2Se3 and its Implications for Pairing in the Undoped Topological Insulator. Phys. Rev. Lett. 2010, 104, 057001. [Google Scholar] [CrossRef]
- Hor, Y.S.; Checkelsky, J.G.; Qu, D.; Ong, N.P.; Cava, R.J. Superconductivity and non-metallicity induced by doping the topological insulators Bi2Se3 and Bi2Te3. J. Phys. Chem. Solids 2011, 72, 572–576. [Google Scholar] [CrossRef]
- Bray-Ali, N. Anon How to turn a topological insulator into a superconductor. Physics 2010, 3, 11. [Google Scholar] [CrossRef]
- Yonezawa, S. Nematic Superconductivity in Doped Bi2Se3 Topological Superconductors. Condens. Matter. 2019, 4, 2. [Google Scholar] [CrossRef]
- Zhang, H.; Li, H.; He, H.; Wang, J. Enhanced superconductivity in Bi2Se3/Nb heterostructures. Appl. Phys. Lett. 2019, 115, 113101. [Google Scholar] [CrossRef]
- Matsubayashi, K.; Terai, T.; Zhou, J.S.; Uwatoko, Y. Superconductivity in the topological insulator Bi2Te3 under hydrostatic pressure. Phys. Rev. B 2014, 90, 125126. [Google Scholar] [CrossRef]
- Yano, R.; Hirose, H.T.; Tsumura, K.; Yamamoto, S.; Koyanagi, M.; Kanou, M.; Kashiwaya, H.; Sasagawa, T.; Kashiwaya, S. Proximity-Induced Superconducting States of Magnetically Doped 3D Topological Insulators with High Bulk Insulation. Condens. Matter. 2019, 4, 9. [Google Scholar] [CrossRef]
- Koren, G.; Kirzhner, T.; Lahoud, E.; Chashka, K.B.; Kanigel, A. Proximity-induced superconductivity in topological Bi2Te2Se and Bi2Se3 films: Robust zero-energy bound state possibly due to Majorana fermions. Phys. Rev. B 2011, 84, 224521. [Google Scholar] [CrossRef]
- Qin, H.; Guo, B.; Wang, L.; Zhang, M.; Xu, B.; Shi, K.; Pan, T.; Zhou, L.; Chen, J.; Qiu, Y.; et al. Superconductivity in Single-Quintuple-Layer Bi2Te3 Grown on Epitaxial FeTe. Nano Lett. 2020, 20, 3160–3168. [Google Scholar] [CrossRef]
- Charpentier, S.; Galletti, L.; Kunakova, G.; Arpaia, R.; Song, Y.; Baghdadi, R.; Wang, S.M.; Kalaboukhov, A.; Olsson, E.; Tafuri, F.; et al. Induced unconventional superconductivity on the surface states of Bi2Te3 topological insulator. Nat. Commun. 2017, 8, 2019. [Google Scholar] [CrossRef]
- Kong, P.P.; Zhang, J.L.; Zhang, S.J.; Zhu, J.; Liu, Q.Q.; Yu, R.C.; Fang, Z.; Jin, C.Q.; Yang, W.G.; Yu, X.H.; et al. Superconductivity of the topological insulator Bi2Se3 at high pressure. J. Phys. Condens. Matter 2013, 25, 362204. [Google Scholar] [CrossRef]
- Cai, S.; Kushwaha, S.K.; Guo, J.; Sidorov, V.A.; Le, C.; Zhou, Y.; Wang, H.; Lin, G.; Li, X.; Li, Y.; et al. Universal superconductivity phase diagram for pressurized tetradymite topological insulators. Phys. Rev. Mater. 2018, 2, 114203. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, S.; Kong, P.; Yang, L.; Jin, C.; Liu, Q.; Wang, X.; Yu, J. Pressure induced electronic phase transitions and superconductivity in n-type Bi2Te3. J. Appl. Phys. 2018, 123, 125901. [Google Scholar] [CrossRef]
- Zhang, S. Discovery of the Chiral Majorana Fermion and Its Application to Topological Quantum Computing; APS March Meeting: Nashville, TN, USA, 2018. [Google Scholar]
- Kauffman, L.H.; Lomonaco, S.J. Braiding, Majorana fermions, Fibonacci particles and topological quantum computing. Quantum Inf. Process. 2018, 17, 201. [Google Scholar] [CrossRef]
- Benedek, G. Majorana Fermions in Condensed Matter Scientific Papers of Ettore Majorana: A New Expanded Edition; Cifarelli, L., Ed.; Springer International Publishing: Cham, Switzerland, 2020; pp. 159–168. [Google Scholar]
- Volovik, G.E. Fermion zero modes on vortices in chiral superconductors. J. Exp. Theor. Phys. Lett. 1999, 70, 609–614. [Google Scholar] [CrossRef]
- Read, N.; Green, D. Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum Hall effect. Phys. Rev. B 2000, 61, 10267–10297. [Google Scholar] [CrossRef]
- Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 2006, 321, 2–111. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef]
- Akhmerov, A.R.; Nilsson, J.; Beenakker, C.W.J. Electrically Detected Interferometry of Majorana Fermions in a Topological Insulator. Phys. Rev. Lett. 2009, 102, 216404. [Google Scholar] [CrossRef]
- Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 2012, 75, 076501. [Google Scholar] [CrossRef]
- He, Q.L.; Pan, L.; Stern, A.L.; Burks, E.C.; Che, X.; Yin, G.; Wang, J.; Lian, B.; Zhou, Q.; Choi, E.S.; et al. Chiral Majorana fermion modes in a quantum anomalous Hall insulator–superconductor structure. Science 2017, 357, 294–299. [Google Scholar] [CrossRef]
- Xu, J.-P.; Wang, M.-X.; Liu, Z.L.; Ge, J.-F.; Yang, X.; Liu, C.; Xu, Z.A.; Guan, D.; Gao, C.L.; Qian, D.; et al. Experimental Detection of a Majorana Mode in the core of a Magnetic Vortex inside a Topological Insulator-Superconductor Bi2Te3/NbSe2 Heterostructure. Phys. Rev. Lett. 2015, 114, 017001. [Google Scholar] [CrossRef]
- Lee, E.J.H.; Jiang, X.; Houzet, M.; Aguado, R.; Lieber, C.M.; De Franceschi, S. Spin-resolved Andreev levels and parity crossings in hybrid superconductor–semiconductor nanostructures. Nat. Nanotechnol. 2014, 9, 79–84. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.-H.; Zhang, K.-W.; Hu, L.-H.; Li, C.; Wang, G.-Y.; Ma, H.-Y.; Xu, Z.-A.; Gao, C.-L.; Guan, D.-D.; Li, Y.-Y.; et al. Majorana Zero Mode Detected with Spin Selective Andreev Reflection in the Vortex of a Topological Superconductor. Phys. Rev. Lett. 2016, 116, 257003. [Google Scholar] [CrossRef] [PubMed]
- Kitaev, A. Periodic table for topological insulators and superconductors. AIP Conf. Proc. 2009, 1134, 22–30. [Google Scholar]
- Qi, X.-L.; Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef]
- Wang, M.-X.; Liu, C.; Xu, J.-P.; Yang, F.; Miao, L.; Yao, M.-Y.; Gao, C.L.; Shen, C.; Ma, X.; Chen, X.; et al. The Coexistence of Superconductivity and Topological Order in the Bi2Se3. Thin Films Sci. 2012, 336, 52–55. [Google Scholar]
- Tamtögl, A.; Campi, D.; Bremholm, M.; Hedegaard, E.M.J.; Iversen, B.B.; Bianchi, M.; Hofmann, P.; Marzari, N.; Benedek, G.; Ellis, J.; et al. Nanoscale surface dynamics of Bi2Te3(111): Observation of a prominent surface acoustic wave and the role of van der Waals interactions. Nanoscale 2018, 10, 14627–14636. [Google Scholar] [CrossRef]
- Tamtögl, A.; Kraus, P.; Avidor, N.; Bremholm, M.; Hedegaard, E.M.J.; Iversen, B.B.; Bianchi, M.; Hofmann, P.; Ellis, J.; Allison, W.; et al. Electron-phonon coupling and surface Debye temperature of B2Te3(111) from helium atom scattering. Phys. Rev. B 2017, 95, 195401. [Google Scholar] [CrossRef]
- Lund, H.E.; Campi, D.; Ruckhofer, A.; Halbritter, S.; Holt, A.J.U.; Bianchi, M.; Bremholm, M.; Benedek, G.; Hofmann, P.; Ernst, W.E.; et al. Electron-Phonon Coupling and (Bulk) Electronic Structure of Sb2Te3 with intrinsic doping. 2021; To be publish. [Google Scholar]
- Heid, R.; Sklyadneva, I.Y.; Chulkov, E.V. Electron-phonon coupling in topological surface states: The role of polar optical modes. Sci. Rep. 2017, 7, 1095. [Google Scholar] [CrossRef]
- Chen, C.; Xie, Z.; Feng, Y.; Yi, H.; Liang, A.; He, S.; Mou, D.; He, J.; Peng, Y.; Liu, X.; et al. Tunable Dirac Fermion Dynamics in Topological Insulators. Sci. Rep. 2013, 3, 2411. [Google Scholar] [CrossRef]
- Hatch, R.C.; Bianchi, M.; Guan, D.; Bao, S.; Mi, J.; Iversen, B.B.; Nilsson, L.; Hornekær, L.; Hofmann, P. Stability of the Bi2Se3(111) topological state: Electron-phonon and electron-defect scattering. Phys. Rev. B 2011, 83, 241303. [Google Scholar] [CrossRef]
- Zeljkovic, I.; Scipioni, K.L.; Walkup, D.; Okada, Y.; Zhou, W.; Sankar, R.; Chang, G.; Wang, Y.J.; Lin, H.; Bansil, A.; et al. Nanoscale determination of the mass enhancement factor in the lightly doped bulk insulator lead selenide. Nat. Commun. 2015, 6, 6559. [Google Scholar] [CrossRef] [PubMed]
- Campi, D.; Bernasconi, M.; Benedek, G. Ab-initio calculation of surface phonons at the Sb2Te3(111) surface. Surf. Sci. 2018, 678, 46–51. [Google Scholar] [CrossRef]
- Bussmann, A.; Bilz, H.; Roenspiess, R.; Schwarz, K. Oxygen polarizability in ferroelectric phase transitions. Ferroelectrics 1980, 25, 343–346. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Benedek, G.; Bilz, H.; Mokross, B. Microscopic polarizability model of ferroelectric soft modes. J. Phys. Colloq. 1981, 42, C6-409–C6-411. [Google Scholar] [CrossRef]
- Bilz, H.; Bussmann-Holder, A.; Benedek, G. Ferroelectricity in ternary compounds. Nuovo Cimento D 1983, 2, 1957–1963. [Google Scholar] [CrossRef]
- Bilz, H.; Benedek, G.; Bussmann-Holder, A. Theory of ferroelectricity: The polarizability model. Phys. Rev. B 1987, 35, 4840–4849. [Google Scholar] [CrossRef]
- Benedek, G.; Bussmann-Holder, A.; Bilz, H. Nonlinear travelling waves in ferroelectrics. Phys. Rev. B 1987, 36, 630–638. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Bilz, H.; Benedek, G. Applications of the polarizability model to various displacive-type ferroelectric systems. Phys. Rev. B 1989, 39, 9214–9223. [Google Scholar] [CrossRef]
- Bilz, H.; Büttner, H.; Bussmann-Holder, A.; Kress, W.; Schröder, U. Nonlinear Lattice Dynamics of Crystals with Structural Phase Transitions. Phys. Rev. Lett. 1982, 48, 264–267. [Google Scholar] [CrossRef]
- Bilz, H.; Büttner, H.; Bussmann-Holder, A.; Vogl, P. Phonon anomalies in ferroelectrics and superconductors. Ferroelectrics 1987, 73, 493–500. [Google Scholar] [CrossRef]
- Sigmund, E.; Müller, K.A. (Eds.) Phase Separation in Cuprate Superconductors. In Proceedings of the Second International Workshop on Phase Separation in Cuprate Superconductors, Cottbus, Germany, 4–10 September 1993; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Symmetry and Heterogeneity in High Temperature Superconductors; Bianconi, A., Ed.; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Shengelaya, A.; Müller, K.A. The intrinsic heterogeneity of superconductivity in the cuprates. Europhys. Lett. 2014, 109, 27001. [Google Scholar] [CrossRef]
- Bianconi, A. Resonances and Complexity: From Stripes to Superstripes. J. Supercond. Nov. Magn. 2011, 24, 1117–1121. [Google Scholar] [CrossRef]
- Bianconi, A.; Innocenti, D.; Campi, G. Superstripes and Superconductivity in Complex Granular Matter. J. Supercond. Nov. Magn. 2013, 26, 2585–2588. [Google Scholar] [CrossRef][Green Version]
- Bianconi, A. Superstripes in the Low Energy Physics of Complex Quantum Matter at the Mesoscale. J. Supercond. Nov. Magn. 2015, 28, 1227–1229. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A.; Poccia, N.; Bianconi, G.; Barba, L.; Arrighetti, G.; Innocenti, D.; Karpinski, J.; Zhigadlo, N.D.; Kazakov, S.M.; et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-Tc superconductor. Nature 2015, 525, 359–362. [Google Scholar] [CrossRef]
- Agrestini, S.; Saini, N.L.; Bianconi, G.; Bianconi, A. The strain of CuO2 lattice: The second variable for the phase diagram of cuprate perovskites. J. Phys. Math. Gen. 2003, 36, 9133–9142. [Google Scholar] [CrossRef]
- Jaouen, T.; Hildebrand, B.; Mottas, M.-L.; Di Giovannantonio, M.; Ruffieux, P.; Rumo, M.; Nicholson, C.W.; Razzoli, E.; Barreteau, C.; Ubaldini, A.; et al. Phase separation in the vicinity of Fermi surface hot spots. Phys. Rev. B 2019, 100, 075152. [Google Scholar] [CrossRef]
- Bianconi, A.; Poccia, N.; Sboychakov, A.O.; Rakhmanov, A.L.; Kugel, K.I. Intrinsic arrested nanoscale phase separation near a topological Lifshitz transition in strongly correlated two-band metals. Supercond. Sci. Technol. 2015, 28, 024005. [Google Scholar] [CrossRef]
- Kostylev, I.; Yonezawa, S.; Wang, Z.; Ando, Y.; Maeno, Y. Uniaxial-strain control of nematic superconductivity in SrxBi2Se3. Nat. Commun. 2020, 11, 4152. [Google Scholar] [CrossRef]
- Benedek, G.M.; Bernasconi, D.; Campi, I.V.; Silkin, I.P.; Chernov, V.M.; Silkin, E.V.; Chulkov, P.M.; Echenique, J.P.; Toennies, G.; Anemone, A.; et al. Evidence for Acoustic Surface Plasmons from Inelastic Atom Scattering. 2020; Unpublished work. [Google Scholar]
- Silkin, V.M.; García-Lekue, A.; Pitarke, J.M.; Chulkov, E.V.; Zaremba, E.; Echenique, P.M. Novel low-energy collective excitation at metal surfaces. Europhys. Lett. 2004, 66, 260. [Google Scholar] [CrossRef]
- Shvonski, A.; Kong, J.; Kempa, K. Plasmon-polaron of the topological metallic surface states. Phys. Rev. B 2019, 99, 125148. [Google Scholar] [CrossRef]
- Lemmens, L.F.; Devreese, J.T. Collective excitations of the polaron-gas. Solid State Commun. 1974, 14, 1339–1341. [Google Scholar] [CrossRef]
- Mott, N.F. The bipolaron theory of high-temperature superconductors. Phys. Stat. Mech. Appl. 1993, 200, 127–135. [Google Scholar] [CrossRef]
- Müller, K.A. Large, Small, and Especially Jahn–Teller Polarons. J. Supercond. 1999, 12, 3–7. [Google Scholar] [CrossRef]
- Müller, K.A. The unique properties of superconductivity in cuprates. J. Supercond Nov. Magn. 2014, 27, 2163–2179. [Google Scholar] [CrossRef]
- Müller, K.A. Essential Heterogeneities in Hole-Doped Cuprate Superconductors Superconductivity in Complex. Systems: Structure and Bonding; Müller, K.A., Bussmann-Holder, A., Eds.; Springer: Berlin, Germany, 2015; pp. 1–11. [Google Scholar]
- Zhao, G.; Conder, K.; Keller, H.; Müller, K.A. Oxygen isotope effects in: Evidence for polaronic charge carriers and their condensation. J. Phys. Condens. Matter 1998, 10, 9055–9066. [Google Scholar] [CrossRef]
- Perali, A.; Innocenti, D.; Valletta, A.; Bianconi, A. Anomalous isotope effect near a 2.5 Lifshitz transition in a multi-band multi-condensate superconductor made of a superlattice of stripes. Supercond. Sci. Technol. 2012, 25, 124002. [Google Scholar] [CrossRef]
- Lanzara, A.; Zhao, G.; Saini, N.L.; Bianconi, A.; Conder, K.; Keller, H.; Müller, K.A. Oxygen-isotope shift of the charge-stripe ordering temperature in La2-xSrxCuO4 from x-ray absorption spectroscopy. J. Phys. Condens. Matter. 1998, 11, L541. [Google Scholar] [CrossRef]
- Lanzara, A.; Bogdanov, P.V.; Zhou, X.J.; Kellar, S.A.; Feng, D.L.; Lu, E.D.; Yoshida, T.; Eisaki, H.; Fujimori, A.; Kishio, K.; et al. Evidence for ubiquitous strong electron–phonon coupling in high-temperature superconductors. Nature 2011, 412, 510–514. [Google Scholar] [CrossRef]
- Benedek, G. The Erice Legacy. Il Nuovo Saggiatore 2019, 35, 47. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benedek, G.; Manson, J.R.; Miret-Artés, S.; Ruckhofer, A.; Ernst, W.E.; Tamtögl, A.; Toennies, J.P. Measuring the Electron–Phonon Interaction in Two-Dimensional Superconductors with He-Atom Scattering. Condens. Matter 2020, 5, 79. https://doi.org/10.3390/condmat5040079
Benedek G, Manson JR, Miret-Artés S, Ruckhofer A, Ernst WE, Tamtögl A, Toennies JP. Measuring the Electron–Phonon Interaction in Two-Dimensional Superconductors with He-Atom Scattering. Condensed Matter. 2020; 5(4):79. https://doi.org/10.3390/condmat5040079
Chicago/Turabian StyleBenedek, Giorgio, Joseph R. Manson, Salvador Miret-Artés, Adrian Ruckhofer, Wolfgang E. Ernst, Anton Tamtögl, and Jan Peter Toennies. 2020. "Measuring the Electron–Phonon Interaction in Two-Dimensional Superconductors with He-Atom Scattering" Condensed Matter 5, no. 4: 79. https://doi.org/10.3390/condmat5040079
APA StyleBenedek, G., Manson, J. R., Miret-Artés, S., Ruckhofer, A., Ernst, W. E., Tamtögl, A., & Toennies, J. P. (2020). Measuring the Electron–Phonon Interaction in Two-Dimensional Superconductors with He-Atom Scattering. Condensed Matter, 5(4), 79. https://doi.org/10.3390/condmat5040079






