Abstract
K.A. Müller took a long route in science leaving many traces and imprints, which have been and are still today initiations for further research activities. We “walk” along this outstanding path but are certainly not able to provide a complete picture of it, since the way was not always straight, often marked by unintended detours, which had novel impact on the international research society.
1. Introduction
After World War II, science started a new blooming period, especially in solid state physics, which used to be the poor cousin in physics. In this early period, a number of novel systems were discovered, mostly in the need of applications to support the reconstruction of Europe. A lot of attention was devoted then to perovskite oxides, which, because of their ferroelectric properties, were excellent ultrasound transducers, piezoelectric converters, and pyroelectric devices. The most prominent members of this material class are PbTiO3 and its mixed ceramics with PbZrO3, still today installed in many applications, and being necessary ingredient for many techniques. BaTiO3 is similarly important, together with SrTiO3. Many other related compounds originated from this time, which all turned out to be of high scientific interest and relevant for new technologies (for a comprehensive review, see, Reference [1]). It was this exciting period when K.A. Müller started his research in experimental solid state physics.
2. Polar and Rotational Instabilities in Perovskite Oxides
In the early 1950s, the investigations of perovskites were enormously intense, since their ferroelectric properties were relevant for novel industrial applications. Understanding the background for the appearance of these phenomena intensified the experimental and theoretical activities and lead to new tools, like neutron scattering, nuclear and electron (para)magnetic resonance (NMR, EPR), and low-temperature techniques. These techniques evidenced that the ferroelectric perovskites have unique properties related to their dynamics, namely a distinct soft mode behavior of a long wave length transverse optic mode, where the related frozen-in ionic displacement pattern determines the low temperature structure and the magnitude of the polarization [2,3,4]. Thus, a unique characterization of ferroelectrics was possible through the identification of a soft optic mode. Besides the polar properties, further structural phase transitions were discovered, where, especially, SrTiO3 [5], LaAlO3 [6], and BaTiO3 were of uttermost interest. In the former two compounds, phase transitions from cubic to tetragonal, cubic to , were observed and believed to be characteristic for oxide perovskites [5]. The origin of these transitions remained unknown, however, for a decade, as well as their precise transition temperatures. This issue was clarified by K.A. Müller et al. in 1968 [7], who showed that the rotation angle φ of the oxygen ion octahedra is the order parameter of these phase transitions (see Figure 1, where the perovskite structure and the rotation of the octahedra are schematically illustrated).
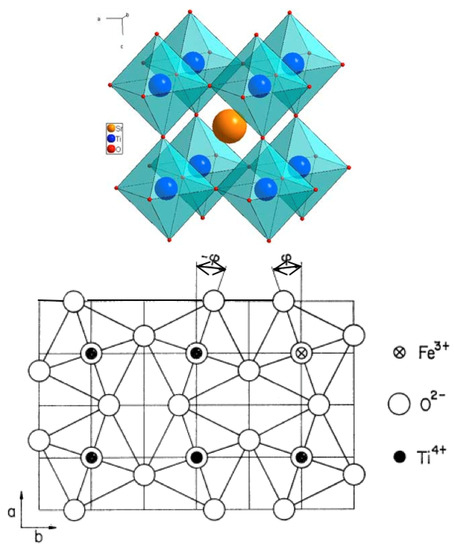
Figure 1.
(Top) Perovskite structure of SrTiO. (Bottom) Oxygen octahedra rotated around the tetragonal c-axis in SrTiO below the transition temperature . The rotation angle represents the order parameter of the structural phase transition below . (from References [5,8]).
He identified this assignment via electron paramagnetic resonance (EPR) experiments where tiny amounts of a magnetic ion (e.g., Fe as indicated in the lower part of Figure 1) were implanted in the respective samples. By comparing the normalized rotation angles of different perovskite oxides, he concluded that, indeed, a unique similarity between them was present, since the temperature dependence of the rotation angle follows one single law independent of the corresponding compound. Since the rotation angle continuously goes to zero upon approaching the phase transition temperature, the transition has been classified as second order type.
Prior to this well-known work, K.A. Müller was interested in the Jahn-Teller effect, which continued to remain in his focus throughout his career, also and importantly, in the search for superconductivity. Already, in 1937, Jahn and Teller showed that, for a polyatomic molecule, “All nonlinear nuclear configurations are unstable for an orbitally degenerate ground state”. Using EPR to detect impurity ions in Al2O3 and SrTiO3, he showed that line broadening due to resonance relaxation occurs already above room temperature. By determining the level splitting between the ground and excited levels, he concluded that phonons are sufficient to overcome this splitting, thereby arriving at the concept of the dynamic Jahn-Teller effect [9], which later turned out to be at the heart for the discovery of high-temperature superconductivity.
The previous observations of a soft transverse optic mode at gave rise to speculations that a coupling to an acoustic mode initiates the phase transition. This could rapidly be excluded, since the transition in LaAlO3 has been related to the softening of a transverse acoustic mode at with no further evidence of any other soft mode being present [10]. On the opposite side, in SrTiO3, there is indeed a soft transverse optic mode at . This observation led K.A. Müller et al. to propose that a second zone boundary soft acoustic mode must exist in SrTiO3. This idea was directly proven to be true by Raman scattering experiments and, shortly afterwards, additionally verified by inelastic neutron scattering [11].
An interesting discovery was made by K.A. Müller, as early as 1969, where he experimentally demonstrated the existence of a negative U-center in Ni-doped SrTiO3 [12]. At that time, this discovery did not draw much attention. However, six years later, P.W. Anderson [13], and, simultaneously and independently, R.A. Street and N.F. Mott [14], introduced theoretically the negative U centers to account for the fact that most glasses and amorphous semiconductors are diamagnetic. Obviously, they were unaware that this had already been discovered before experimentally [12]. There are important consequences from these centers for superconductivity, namely that there is an analogy between the existence of an effective attraction between electrons in a superconductor and the negative U centers in an insulating glass. Since the origin of this electron-electron attractive interaction stems from the lattice, it also bears a close resemblance to bipolaron formation, later on proposed by Chakraverty [15], to give rise to superconductivity.
The increasing interest in SrTiO3 and other perovskite titanates successfully encouraged crystal growers to optimize their growth conditions, and it became possible to obtain almost domain-free samples of SrTiO3 and LaAlO3 in their low-temperature tetragonal, phase. These were the starting point to investigate in deep detail, and with much improved resolution, the temperature dependence of the order parameter, the rotation angle , in the vicinity of the phase transition temperature (see Figure 1) [16]. While it was long taken for given that Landau theory universally describes the behavior of φ by the law: , being the phase transition temperature and , the better sample quality enabled to measure β with higher accuracy, especially in the vicinity of . The new data evidenced deviations from this law close to , thus questioning the global validity of Landau theory (). From this work, it was concluded that the temperature dependence of φ in SrTiO3 and LaAlO3, below the second-order phase transition temperatures , is described by an exponent (critical exponent of the order parameter) in the temperature region (critical region). For , there occurs a change to Landau behavior (mean-field behavior), as indicated by the solid line in Figure 2. This observation of static critical exponents near displacive phase transitions confirmed the notion of universality classes in this field [16].
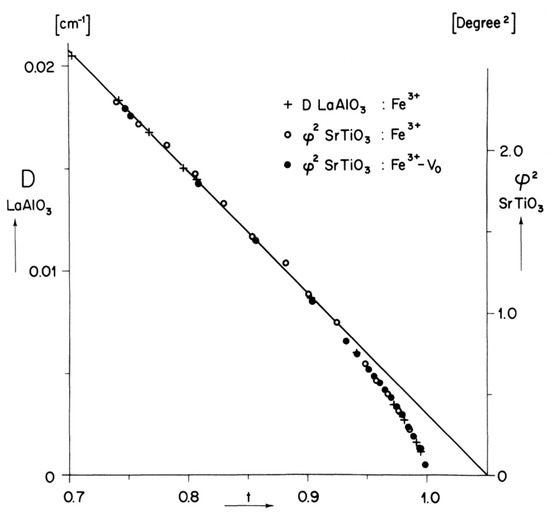
Figure 2.
of SrTiO and crystal field parameter D of LaAlO vs reduced temperature between 0.7 and 1, showing the changeover from Landau to critical behavior at (from Reference [16]).
The above comprehensive results on SrTiO3 set off more detailed investigations on the long wave length soft zone center transverse optic mode, which was speculated to be related to a ferroelectric phase transition in analogy to other titanites. However, a real transition had never been reported, but the extrapolation of this mode to zero led to a transition temperature around 20–30 K. Since the transverse optic soft mode driven phase transitions are related to a temperature dependent dielectric constant via the Lyddane-Sachs-Teller relation, measurements of can uniquely clarify the occurrence of a true phase transition. These were performed by Müller and Burkard [17] in 1979 and had the unexpected outcome that saturates below 4 K exhibiting extremely high values there (Figure 3). The results have been interpreted in terms of quantum fluctuations which suppress a true phase transition and coined the name “quantum paraelectricity” [17]. After the Nobel Prize awarded paper, it is the most frequently cited paper of K.A. Müller, as noted in a bibliographic study by Kremer et al. in Reference [18].
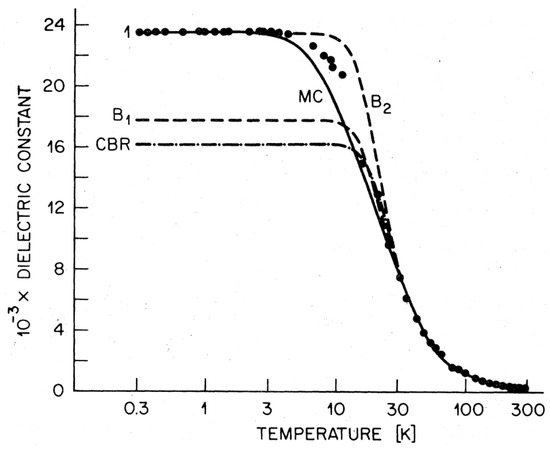
Figure 3.
Comparison of the temperature dependent dielectric constant of SrTiO in the quantum dominated temperature region with the mean-field theory; B1 adjusted to fit the crossover below 150 K; B2 adjusted to fit at ; CBR: effective acoustic mode coupling; MC dipolar mode coupling with biquadratic electron-phonon interaction (from Reference [17]).
In the search for superconductivity in perovskites, Binnig and coauthors went back to SrTiO3, which was already known to become superconducting at low temperature () upon changing the oxygen stoichiometry [19,20,21]. Instead of manipulating the oxygen content, they doped the compound with small amounts of Nb [22] in order to enhance the superconducting transition temperature . Even though this methodology did not lead to a significant enhancement of , they discovered that their compound has two superconducting gaps and verified, thereby, the long known prediction that superconductors can exhibit more than one gap [23,24]. The most amazing thing about Nb-doped SrTiO3 is, however, that it has an extremely low carrier concentration, such that its Fermi energy is smaller or comparable to the Debye energy. This “strange” behavior has very recently been taken up again and gave rise to new theoretical [25,26,27] and experimental interest, results, concepts, and speculations [28] (also see Scheerer et al. in Reference [29]). These will be discussed in more detail at the end of this paper.
For many years, the proximity of SrTiO3 to a polar instability has challenged researchers to induce this order by different means. A first success was achieved by electric field effects, where polar domains could be induced [30]. Pressure on the contrary proved to be counter-productive, since the soft mode was observed to harden [31,32,33]. Similar effects were observed with doping, where an increase in the carrier density reduces the gap but also enhances the soft mode frequency [34]. It was up to J. G. Bednorz and K.A. Müller to achieve a breakthrough by replacing tiny amounts of Sr with Ca in SrTiO3 [34]. Since Ca is smaller than Sr, a spontaneous polarization appears in the basal planes and not along the c-direction and is switchable between the two equivalent a-axes. This behavior was named “XY quantum ferroelectric” and shown to vanish rapidly with increasing Ca content [34]. An alternative approach has been undertaken by Itoh et al. by replacing O16 by its isotope O18 [35]. Indeed, ferroelectricity was observed there, but soon shown to be incomplete through theoretical modeling [36] and Raman spectroscopy [37]. By “incomplete”, it is meant that ferroelectricity is not of long-range order, but appears locally only. Kleemann et al., in Reference [38], focus exactly on the possibility to achieve a true polar ground state in SrTiO3 but also strive through doping-dependent novel phenomena achievable in this compound.
Even though the discovery of high-temperature superconductivity in the La-Ba-Cu-O perovskite slowed down the work of K.A. Müller with respect to oxide perovskites, he continued beforehand existing collaborations and produced interesting new results. Here, it is important to mention his work on BaTiO3, which exhibits three phase transitions with decreasing temperature: the first from cubic to tetragonal at 408 K induces ferroelectricity, the following at 278 K lowers the symmetry to orthorhombic and is accompanied by a change in the polarization direction; at 183 K, the symmetry becomes rhombohedral and again the polarization reorients. The mechanisms of all transitions remained controversial for a long time, since experimental data testing different time and length scales suggested different mechanisms to be at play. Local probe experiments were in accordance with order-disorder type transitions [39,40], whereas long range testing experiments were in accordance with purely displacive ones [41]. The puzzles could be resolved again by EPR, where Mn4+ ions were doped in BaTiO3 to randomly substitute for the isovalent Ti4+ ion. These experiments clearly showed that dynamic precursor clusters are formed above the respective transition temperature, which signify a coexistence of order/disorder and displacive features [42]. Depending on the testing tool, either of both appears dominant and yields a corresponding interpretation. Note that, in the paper by Bishop in Reference [43], similar aspects and beyond are addressed, and more detailed consequences are given.
A representative and comprehensive collection of the broad work of K.A. Müller on the properties of perovskites and other oxides (except cuprates) is presented in Reference [8] and supplemented in the work by Kool in Reference [44].
The above described results have an important consequence, since they suggest that perovskites are locally inhomogeneous with different coexisting time and length scales. As will be shown below, this is also true for cuprate superconductors, where distinctive properties stem from inherent inhomogeneity [45].
3. High-Temperature Superconductivity in Cuprates
3.1. Discovery of Superconductivity in the Cuprates
While K.A. Müller was already famous for his work on oxide perovskites in the eighties, he became inspired by the work on granular Al to move to superconductivity [46], a field he had never been interested in before. Granular Al has an extremely short coherence length, untypical for BCS superconductors, which later was shown to be also realized in cuprate superconductors [47]. For more details on the physical meaning of a short coherence length in unconventional superconductors, see the contribution of Deutscher in Reference [48].
K.A. Müller almost immediately turned to his favorite materials, the oxide perovskites, since the observation of a low carrier density and a large Debye energy yielded astonishingly high superconducting transition temperatures in oxides, incompatible with BCS theory. The above described discovery of two-band superconductivity in Nb-doped SrTiO3 was the first result in that direction and actually was considered as very disappointing from the perspective of J.G. Bednorz. However, he, together with K.A. Müller, did not give up, and, finally, they succeeded in their world famous discovery of the La-Ba-Cu-O compound, which was honored with the Nobel prize only a year later, the fastest Nobel prize [49,50,51,52].
This discovery was inspired, as mentioned above, by the observation of the combination of low carrier density and a rather large superconducting transition temperature and the knowledge of Jahn-Teller polarons [53]. From this observation, and theoretical results of Höck et al. [53], K.A. Müller concluded that the coupling between the ions and the electrons/holes must be extraordinarily strong and unconventional, as suggested by Chakravarty based on a (bi-) polaronic concept [15]. Indeed, the cuprates also have a smaller carrier density than conventional superconductors, which is why they were named “bad” metals. Already, in his Nobel prize award speech, K.A. Müller depicted this scenario with alternating CuO pyramids, being charge rich and charge poor (Figure 4) [52], which was shortly afterwards verified experimentally by the group of A. Bianconi [54], suggesting a stripe-like patterning consisting of alternating distorted (D) and undistorted (U) CuO6 octahedra with widths W and L (Figure 5). Having such a scenario in mind, it is obvious from the very beginning that cuprates, being non-stoichiometric, cannot be homogeneous. This is discussed in the next section.
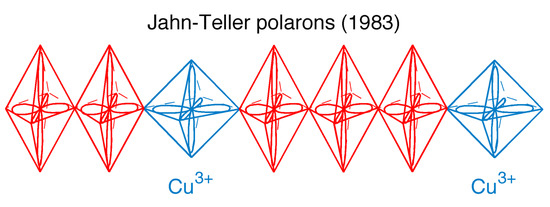
Figure 4.
Schematic representation of the Jahn-Teller polaron in a linear chain substitution of trivalent La by a divalent alkaline-earth element would lead to a symmetric change in the oxygen polyhedral in the presence of Cu (after Reference [52]).
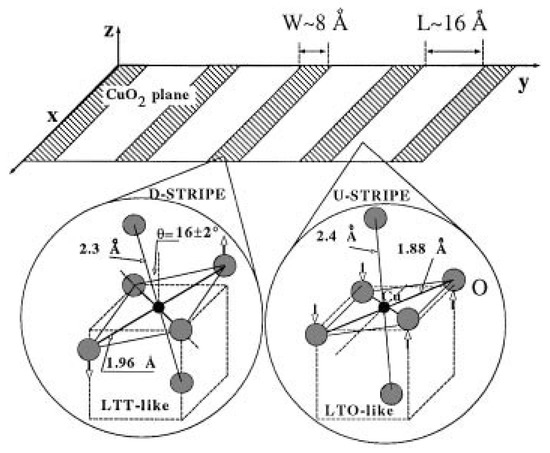
Figure 5.
Pictorial view of the distorted CuO octahedra, left side, of the “LTT (low-temperature tetragonal) type” assigned to the distorted stripe (D stripes) of width Å and of the undistorted octahedra, right side, of the “LTO (low-temperature orthorhombic) type” assigned to the undistorted stripes (U stripes) of width Å. The superlattice of quantum stripes of wavelength is shown in the upper part (from Reference [54]).
As mentioned above, the discovery of high-temperature superconductivity in the cuprates was not accidental but based on the idea that an unconventionally strong electron-lattice interaction may lead to superconductivity at high . A possible way to achieve such a strong coupling is the formation of Jahn-Teller (JT) polarons (bipolarons) in doped perovskite oxides, as proposed by Bednorz and Müller [49,50]. In order to test and support the polaron concept, K.A. Müller made, from the beginning, several suggestions for key experiments (see, e.g., References [55,56,57]). Some of his main proposals for experiments—dealing with inhomogeneity, mixed oder parameters, and unconventional isotope effects in cuprate superconductors—are discussed in the following sections.
3.2. Essential Heterogeneities and Mixed Order Parameters in Cuprate Superconductors
In spite of many efforts in understanding the electron (hole) pairing mechanism in these materials, K.A. Müller pursued his ideas which culminated - driven by not understood experimental results—in his suggestion that two coexisting order parameters are characteristic for these compounds [58,59]. In view of the majority line that cuprates have a single d-wave order parameter (see, e.g., References [60,61,62]), he intensely pointed out to a combination of wave order parameters [58], thereby supporting his viewpoint of intrinsic inhomogeneity [45] characterized by local and global features which are beyond lattice periodicity. These ideas have subsequently been supported by detailed muon-spin rotation (μSR) experiments on various families of cuprate superconductors by the University of Zurich group [63,64,65,66,67]. The temperature dependence of the magnetic penetration depth λ, which can be extracted from the μSR relaxation rate according to the relation [68], is sensitive to the gap symmetry.
As an example, Figure 6a shows the temperature dependence of the μSR relaxation rate for single-crystal La1.83Sr0.17CuO4 measured in various external magnetic fields perpendicular to the CuO2 plane [63]. In this case, , where is the in-plane magnetic penetration depth. Note that shows an inflection point at low temperature which is most pronounced in the lowest magnetic field of μ. By analyzing the μSR data within a two-component model with coupled -wave order parameters, a good agreement between experiment and theory was achieved [63,67], as demonstrated in Figure 6b. In particular, it is evident from the analysis that the s-wave gap contributes less to the superfluid density (32%) as compared to the d-wave gap (68%), but that its contribution is essential in order to describe the μSR data consistently. The fact that various cuprate families exhibit essentially the same behavior of the μSR relaxation rate [63,64,65] suggests that this behavior is generic to all cuprate superconductors and reflects also the intrinsic inhomogeneity of these materials [45,69].
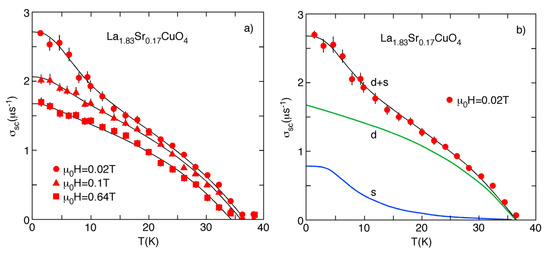
Figure 6.
(a) Temperature dependence of the muon-spin rotation (μSR) relaxation rate of single-crystal LaSrCuO measured at various magnetic fields, as indicated in the figure. The solid lines correspond to results from a two-gap model. (b) The green and blue lines represent the contributions of d- and s-wave gap (after Reference [63]).
Testing the gap symmetry experimentally crucially depends on the experimental technique involved. For example, ARPES (angle-resolved photoemission spectroscopy) or phase-sensitive tunneling experiments on single-crystal samples probe the gap symmetry near the surface, whereas μSR experiments probe the gap symmetry in the bulk. Inconsistent results concerning the gap symmetry determined by different experimental techniques [59], as well as group theoretical considerations inspired K.A. Müller, to conclude that the gap symmetry may change from purely d-wave near the surface to more s-wave, like in the bulk of the superconductor [69,70]. We investigated the temperature dependencies of the in-plane () and out-of-plane () magnetic field penetration depths near the surface and in the bulk of the electron-doped superconductor Sr0.9La0.1CuO2 by means of AC magnetization and μSR measurements [71]. These studies provide evidence that the scenario of coexisting mixed order parameters is indeed also realized in this electron-doped cuprate superconductor, as proposed by K.A. Müller [58,69]. The temperature dependence of was found to be consistent with a dominant d-wave component (≃96%) and only a tiny s-wave component near the surface of the sample, whereas is well described by a mixed order parameter with an s-wave component of more than 50% in the bulk. A comparison of the magnetization (surface probe) and the μSR (bulk probe) data for reveals that the s-wave component of the superfluid density is strongly suppressed by more than a factor of two near the surface of the sample, in accordance with the proposal of K.A. Müller [69]. For more details of this study, we refer to the contribution of Khasanov et al. in Reference [71].
Since the involvement of the lattice is essential in this model of mixed order parameters, K.A. Müller proposed to investigate isotope effects in the cuprate superconductors in order to highlight the important role played by the lattice. The most prominent isotope effects observed in cuprate superconductors are summarized in the following.
3.3. Unconventional Isotope Effects in Cuprate Superconductors
The observation of an isotope effect (IE) on the superconducting transition temperature in mercury in 1950 played a key role in the development of the weak-coupling microscopic BCS theory of superconductivity, where the electron-phonon interaction leads to the formation of Cooper pairs (two electrons with opposite spin and momentum) at . The isotope shift on is expressed by the relation
where M is the isotope mass, and is the IE exponent. Weak-coupling BCS theory predicts with . Indeed, for many low-temperature conventional superconductors, values of were found. The observation of an IE in conventional superconductors is thus consistent with the BCS theory of superconductivity, where the electron-phonon interaction is the pairing mechanism.
The discovery of high-temperature superconductivity in the cuprates by Bednorz and Müller [49] with transitions temperatures well above those found in conventional superconductors raised the question of the electron/hole pairing nature of superconductivity in these novel systems. The observation of only a tiny oxygen (16O/18O)-isotope effect (OIE) in optimally doped YBa2Cu3O [72] led many theoreticians to conclude that the electron-phonon interaction, or, more generally, lattice effects, cannot be the pairing glue in high-temperature superconductivity. Alternatively, several other models of purely electronic origin were proposed, and a majority of scientists working in the field ignored the role of the lattice in the cuprates. However, it is important to note that all cuprates show a finite OIE on at all doping levels, increasing substantially with reduced doping [73,74].
From the very beginning, K.A Müller was convinced that the IE plays a crucial role to understand the microscopic pairing mechanism in the cuprates. The concept of the Jahn-Teller (JT) polaron, which originally was his basic motivation to search for superconductivity in perovskite oxides, involves local lattice deformations. Consequently, strong lattice interactions and unconventional isotope effects are expected to be present in the cuprates. In an early paper, K.A. Müller reviews the importance of IEs in the cuprates [75]. In 1990, K.A. Müller, therefore, initiated a new project, Isotope Effects in Cupate Superconductors, at the University of Zurich (see, e.g., References [76,77,78]), in close collaboration with material scientists from the ETH Zurich and the Paul Scherrer Institute (PSI) (see the contribution of Conder et al. in Reference [79]). The main goal of this project was to investigate which oxygen atoms (plane (p), apical (a), or chain (c) oxygens) in the crystal lattice of YBa2Cu3O contribute mainly to the OIE on . It was expected that, within the JT concept, the apical oxygen ions should play a crucial role and give rise to a pronounced OIE. Experimentally, this can be tested by the so-called site-selective oxygen-isotope effect (SOIE) study on in optimally doped YBa2Cu3O [80]. For this purpose, fully 16O and 18O exchanged, as well as site-selective exchanged samples, were prepared. In the site-selective samples, the planar sites were substituted by 18O (16O) and the apical and chain sites by 16O (18O). Surprisingly, it was found that the planar oxygen atoms contribute dominantly (≥80%) to the total OIE shift on . This finding was later confirmed for YPrxBa2Cu3O for various dopings () [81,82]. All these SOIE results on for YPrxBa2Cu3O are summarized in Figure 7. It is evident that the main contribution to the OIE on for all dopings originates from the oxygen atoms in the CuO2 planes, opposite to what was expected by K.A. Müller in his original proposal, where he assumed that the apical oxygen ion displacement is subject to strong anharmonicity analogous to perovskite ferroelectrics [75,83]. Apparently, these assumptions did not meet the experimental results, which he immediately accepted.
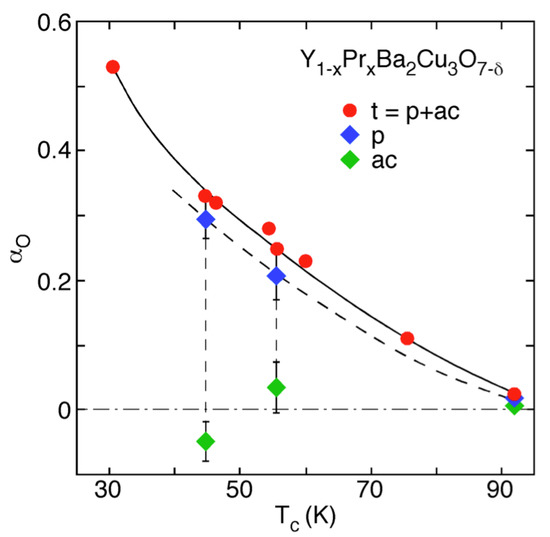
Figure 7.
Total (t) and partial (p, ac) oxygen-isotope exponent as a function of for YPrBaCuO (t = total: all oxygen sites, p: planar oxygen sites, ac: apex and chain oxygen sites). Solid and dashed lines are guides to the eye (after Reference [78]).
In subsequent years, doping dependent unconventional OIEs on several physical quantities (besides ) were observed, including, for instance, the antiferromagnetic transition temperature , the spin-glass transition temperature , the spin-stripe ordering tempertaure , the magnetic penetration depth , and the pseudogap temperature [67,76,77,78,84,85]. In the following, we will only focus on the OIEs on λ and .
The BCS theory is based on the Migdal adiabatic approximation, in which the effective mass of the supercarriers is not sensitive to the mass M of the lattice atoms. However, if the supercarriers interact strongly with the lattice as in a polaronic concept (JT representation), the adiabatic approximation is no longer valid, and depends on M (see, e.g., Reference [86]). A direct way to test this notion is to search for a possible IE on the magnetic penetration depth λ. In the simplest case of a spherical or ellipsoidal Fermi surface, the zero-temperture in-plane magnetic penetration depth may be expressed by the London formula [78]:
where is the superconducting carrier density, and is the in-plane effective mass of the carriers. The in-plane superfluid density is then given by the relation:
This means that a possible OIE shift of the superfluid density arises from an OIE shift of and/or according to the expression:
The first OIE experiments on the magnetic penetration depth in polycrystalline YBa2Cu3O6.94 were performed by means of magnetization measurements [87], and, later on, in fine-grained samples of LaSrxCuO4 () [76,88]. For LaSrxCuO4, the observed oxygen-isotope shift of was found to decrease substantially with increasing doping x [76,88]. For , an oxygen-isotope shift of was found [88].
In addition, we performed OIE studies on microcrystals of underdoped LaSrxCuO4 with and (volume by means of high-sensitive torque magnetometry [89]. A substantial OIE on was observed, namely for and −8(1)% for , respectively, in agreement with the results obtained for fine-grained powder samples [76,88].
The University of Zurich group carried out a μSR OIE study of in fine-grained powder samples of underdoped YPrxBa2Cu3O ( and 0.4) [90], which were in line with those of magnetic torque data for underdoped LaSrxCuO4 [89]. In order to investigate which oxygen atoms in the lattice mainly contribute to the OIE on , we initiated a site-selective OIE μSR study of in underdoped YPrBaCuO [82]. A substantial total OIE of , as well as of , is observed. Moreover, the SOIE experiments clearly indicates that the planar oxygens account within experimental error for 100% to both OIE shifts, yielding and , consistent with the SOIE results on presented above.
In a further OIE study, the low-energy μSR (LEμSR) technique was applied, which allows a direct measurement of the magnetic penetration depth by measuring the magnetic field profile inside a superconductor in the Meissner state just below a distance z from the surface [91,92]. From the measured , the magnetic penetration depth is then extracted directly. This method was used to detect the OIE on the in-plane penetration depth in a nearly optimally doped YBaCuO thin film (600 nm thick) [92]. The analysis of the LEμSR data for the O and O substituted thin films yielded nm and nm. Correcting for the incomplete O exchange of 95%, one obtains for the relative OIE shift % at 4 K. This value is in good correspondence with the values reported for optimally doped YBaCuO, LaSrCuO, and BiPbSrCaCuO evaluated indirectly from magnetization measurements [78].
The OIE results on and presented in this chapter are summarized in Figure 8, where the OIE shifts versus the OIE shifts are shown. In order to discuss these findings, we use the OIE shift , instead of . Figure 8 clearly demonstrates that there is a correlation between the OIE on and . At optimal doping, both isotope shifts are small, but finite with . With decreasing doping (decreasing ), remains almost constant as underlined by the blue dashed line, then starts to increase, and, in the underdoped regime, the two relative oxygen isotope shifts are almost equal (), as indicated by the red solid line. This behavior is apparently generic for different families of cuprates, and, at first glance, one may speculate that this is a direct consequence of the empirical Uemura relation [93,94]. In the underdoped regime, the simple relation with holds, and C is a “universal constant”. With this relation, one readily gets for the isotope shift on :
For (the Uemura relation), one obtains , as marked by the dashed red line in Figure 8, which deviates from the experimental data. In the underdoped regime, these are much better described by the red solid line with (). However, the physical meaning of this factor 2 remains unclear.
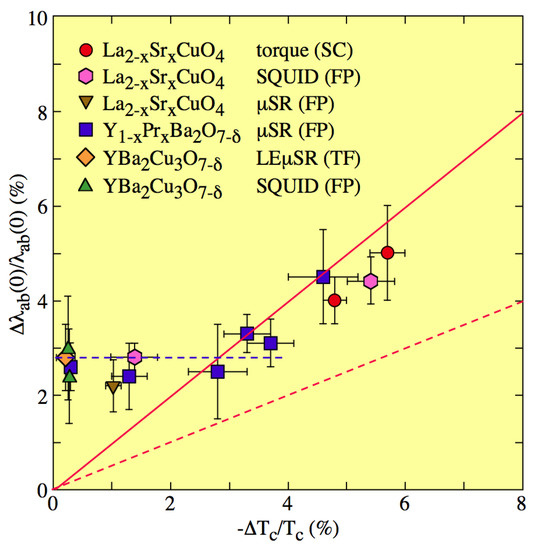
Figure 8.
Plot of the oxygen (O/O)-isotope effect (OIE) shift versus the OIE shift ) for LaSrCuO and YPrBaCuO using different experimental techniques as described in the text and various types of samples (SC: single crystal, FP: fine powder, TF: thin film). The meaning of the dashed lines is explained in the text (after Reference [78]).
S. Weyeneth and K.A. Müller [95] analyzed the doping dependence of the OIE on for various cuprate systems in terms of a “polaronic model” proposed by Kresin and Wolf [96,97], which was derived for polarons forming perpendicular to the superconducting CuO planes. It is important to note that, in References [96,97], polarons are not mentioned. However, S. Weyeneth and K. A. Müller [95] reinterpreted the model by them in terms of a polaronic one. The doping dependence of the measured OIE exponent follows well the predicted behavior, in agreement with previous results based on a purely empirical model [98]. In addition, the OIE exponent of the pseudogap temperature with reversed sign compared to that of is also described by this polaronic model. These findings suggest that superconductivity in the cuprates is driven by polaron, or rather bipolaron, formation in the CuO planes [95]. In this model, it is assumed that the isotope effect on is only determined by the isotope effect on the supercarrier density . The same argument holds for . Since , but , the two isotope effects are sign reversed (see Figure 9). However, this concept underestimates the observed OIE on in the underdoped regime by almost a factor 2, as shown by the dashed red line () in Figure 8, and even closer to optimal doping where . This suggests the conclusion that the OIE on must arise from an OIE on and , according to Equation (4).
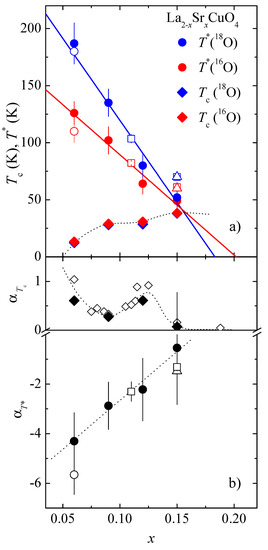
Figure 9.
(a) The superconducting transition temperature and the pseudogap temperature of LaSrCuO as a function of doping x for O (red symbols) and O (blue symbols). The solid lines are obtained from a linear fitting. The dashed line is a guide to the eye. The data are results from X-ray absorption near edge structure (XANES) and neutron crystal field spectroscopy (NCFS) experiments (see Reference [99]). (b) Doping dependence of the isotope effect exponent and for LaSrCuO. The data of are obtained by various XANES and NCFS experiments and data of are from magnetization measurements (see Reference [99]). The dashed lines are a guide to the eye (from Reference [99]).
In another project proposed by K.A. Müller, we explored a possible OIE on the pseudogap (charge-stripe ordering temperature) in cuprate superconductors. It is generally accepted that plays a fundamental role in understanding the complex phase diagram und the underlying physics of cuprates. However, from an experimental point of view, the quantity is ill defined, depending on the experimental technique and the corresponding time and length scales involved (see, e.g., Reference [99]). In addition, the meaning of and its origin are controversely discussed. Here, we define as the temperature where local deviations from the average structure occur (also named charge ordering temperature) and where no direct magnetic effects are present. Thereby, it is evident that OIE studies of are crucial to test lattice/polaron effects in the cuprates. Up to now, only a few such studies have been carried out [99,100,101,102,103,104,105]. The first OIE on was performed in underdoped LaSrCuO by means of Cu K-edge X-ray absorption near edge structure (XANES) studies [100], yielding a huge and sign reversed OIE exponent of . Later on, similar XANES experiments on LaSrCuO as a function of doping x () completed this result [99]. All XANES data, together with additional outcome from neutron crystal field spectroscopy (NCFS) studies of LaHoSrCuO [104,105], are summarized Figure 9. The observed OIE exponent changes almost linearly from for to for . This is in contrast to the doping dependence of the OIE exponent which exhibits a characteristic anomaly at (Figure 9), which is absent in , implying that there is no simple correlation between and , at least for LaSrCuO. Furthermore, NCFS experiments on slightly underdoped HoBaCuO [101] revealed , in agreement with values for LaSrCuO. Additional NCFS studies of the Cu/Cu isotope effect show a large negative isotope shift of for HoBaCuO [103], which was not observed for optimally doped LaHoSrCuO [104]. A consistent explanation of this observation was given by K.A. Müller [104]. In both compounds, single-layer LaHoSrCuO and double-layer HoBaCuO, local oxygen and copper lattice JT-type modes have to be considered. Whereas oxygen and copper modes are relevant for the bilayer compound, the umbrella-type copper modes are absent in the single-layer compound, thus explaining the observed oxygen and copper isotope effects on [104]. As shown in Figure 9a, the pseudogap temperature decreases linearly with increasing doping x with pronounced different slopes for O and O. The limit has frequently been interpreted as quantum critical point (see, e.g., References [106,107]). However, since, in this limit, an appreciable isotope effect is also observed, [] [99], a purely electronic model can be excluded as origin of this point.
A theoretical explanation of the above described isotope effects has been given in References [67,108], where it was shown that the original idea as introduced by K.A. Müller, namely Jahn-Teller (bi-) polarons [50,52], indeed provide a consistent explanation of them. Polaron formation occurs in the case of strong local electron-lattice coupling where the individual particles lose their meaning to form a new quasi-particle. In such a case, the electrons are renormalized by the lattice, and the lattice, in turn, is renormalized by the electrons. This introduces an exponential slowing down of the electron (hole) hopping, i.e., their kinetic energy, whereas the phonons are rigidly displaced. Upon adopting a three band picture to capture the essential physics of cuprates, namely nearest and next-nearest neighbor hopping , together with an inter-planar hopping term , their polaronic coupling consequences have been investigated. Interestingly, only the second and inter-planar couplings are relevant for the isotope effects and describe the correct trends as observed experimentally for all those compounds mentioned above. This observation admits to draw conclusions on the local displacement involved in the dynamics, namely a -type phonon mode, as shown in Figure 10.
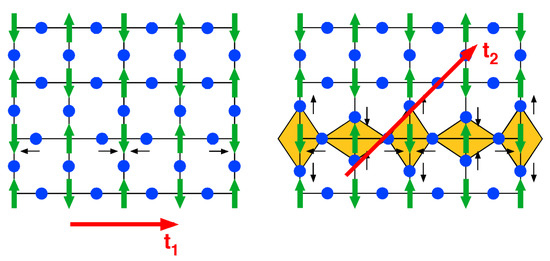
Figure 10.
The relevant ionic displacements in the CuO plane dominated by the nearest () and or second nearest () hopping integrals, giving rise to a -type phonon mode visualized by the yellow areas (from Reference [67]).
On the other hand, the lattice renormalization caused by the polaron formation plays a decisive role to understand experimental XAFS (X-ray absorption fine structure) data of LaSrCuO [109]. These show two anomalies as a function of temperature, namely an upturn at and a second anomaly at . Both are consistently explained by the polaronic approach [110], emerging in a picture where (bi)polarons become coherent at , being gaseous above , to adopt a stripe-type dynamical pattern below , as illustrated in Figure 11. At , the superconducting pairing condensate symmetry becomes relevant, since a divergence, as observed by XAFS, takes place only if the symmetry is s-wave-like or has at least a substantial s-wave contribution. For a purely d-wave order parameter, no divergence takes place. This substantiates the original suggestion of K.A. Müller that cuprates must have coexisting order parameters [58].
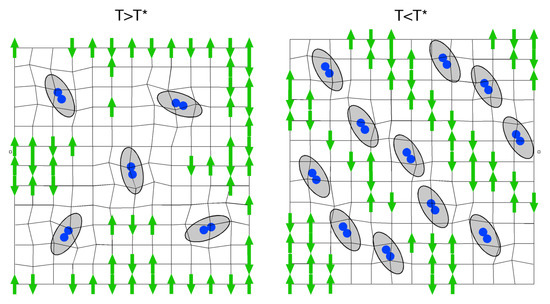
Figure 11.
Disordered bipolaron gas above (left) and ordered bipolaron liquid below (right) (from Reference [67]).
With these clear conclusions, we move back to SrTiO3 and one of the first famous papers of K.A. Müller, namely the introduction of quantum paraelectricity in this compound [17].
4. SrTiO3—An Exotic Low Carrier Density Superconductor
One of the most frequently cited papers of K.A. Müller is his work on the low-temperature behavior of the dielectric constant in SrTiO3 [17]. The saturation of the dielectric constant ε in this temperature regime has been termed “quantum paraelectricity” (see Figure 3) and gave rise to numerous speculations of its role played for superconductivity in doped or oxygen reduced SrTiO3. When, in the 1960s, superconductivity in this compound was first reported [19,20], the pairing mechanism was interpreted in terms of intervalley scattering or soft mode induced. A typical BCS pairing scheme was excluded, since the low carrier density does not support this. For a rather long period, the work on superconductivity in SrTiO3 slowed down, essentially until Binnig et al. [22] discovered multiband superconductivity in Nb-doped SrTiO3, inspired by K.A. Müller. With the discovery of high-temperature superconductivity in the cuprates, the majority interest was devoted to these compounds, and, only after many years of hype, novel or formerly discussed systems reemerged.
During the high-temperature superconductivity peak activities, SrTiO3 also gained renewed interest, since its lattice parameters match extraordinarily well with those of many cuprates, and, correspondingly, it was used as substrate material for the film growth of these superconductors. Scientifically, focused interest appeared in 2004 with the discovery of the two-dimensional electron (2DEG) or hole gas (2DHG) interface conductivity. In particular, the discovery of 2DEG at the interface between two oxide insulators LaAlO3 and SrTiO3 provided new opportunities for research and applications [111]. Especially, superconductivity [112] and magnetism [113] have been observed at these interface 2DEGs, which are not found in typical semiconductor interfaces. By using strain as an additional tuning parameter, a variety of new research areas have been reemerged [114,115,116].
The low carrier density of doped SrTiO3 has been in the focus during the last 5 years, since it was found that, even smaller than first thought, carrier densities support superconductivity [26,117]. These new findings gave rise to novel theories concentrating often on the proximity of SrTiO3 to quantum criticality and its incipient polar properties [25,118]. Experimentally, the carrier density has been determined from macroscopic measurements, namely conductivity, resistivity, and Hall measurements [117], thereby overlooking that all perovskite oxides have an inherent tendency to inhomogeneity, meaning that the doped carriers are not homogeneously distributed in the respective sample. This is already reflected in undoped perovskite oxides where finite size precursors occur, signaling locally distorted regions in an intact matrix [42,119]. In addition, extended X-ray absorption fine structure (EXAFS) [120,121], electron paramagnetic resonance (EPR) [8], atomic pair distribution function (PDF) (for a recent review, see, e.g., Reference [122]), and similar data are strong indications that the real space properties differ substantially from the momentum space derived ones. For this reason, novel experiments have been carried out in order to arrive at a clue for the understanding of the insulator/metal (I/M) and/or insulator/superconducting (I/S) transition. Both of these are achieved by either introducing oxygen vacancies or by doping the A or B site in ABO3 SrTiO3 by aliovalent ions. The data are interpreted by theoretical modeling based on the polarizability model [123,124,125].
From the latter approach, the dynamics of SrTiO3 can be studied in detail when concentrating on local anomalies in the momentum dependence of the two lowest transverse optic and acoustic modes, which represent the ferroelectric soft mode and the soft acoustic mode responsible for the antiferroelectric rotational instability. Anomalies in these two branches have already been analyzed previously and shown to be signatures for local polar and piezoelectric nano-regions [126]. By calculating the phonon group velocities for the two considered branches, the above described anomalies become very apparent and define the momentum at which local, spatially confined soft modes occur. The decisive momentum value is the one where the scattering between optic and acoustic mode is strongest. The corresponding squared local frequency is shown in Figure 12 as a function of carrier concentration, temperature, and momentum q.
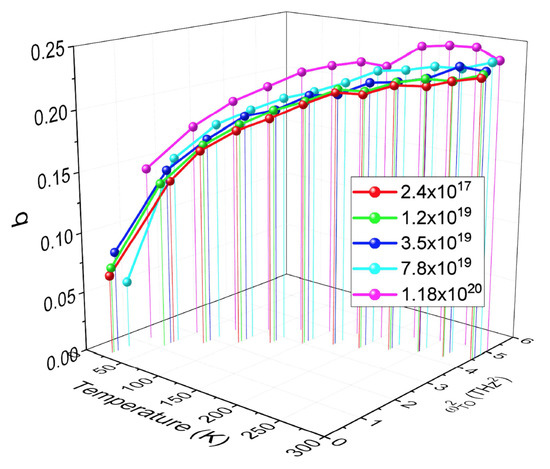
Figure 12.
The squared transverse local optic mode frequency as a function of temperature, momentum, and carrier concentration.
As is obvious from the figure, this local mode softens with decreasing temperature and simultaneously moves to lower momentum values but never reaches the long wave length limit. In addition, the softening slows down with increasing carrier concentration, and its momentum space spread increases, highlighting the growing spatial confinement of these polar nano-domains. In contrast to a long wave length “true” soft mode, it is not linearly dependent on temperature but substantially nonlinear below . Since , this mode is directly linked to the dielectric permittivity , which is reduced by approximately 40% as compared to the long wave length limit, but still exhibits an appreciable temperature dependence which is typical for an almost ferroelectric compound [127]. From the calculated thermal average of the displacement-displacement correlation function, a local dipole moment has been derived, which decreases with decreasing temperature and increasing carrier concentration (Figure 13), where the inset shows the zero temperature limit of it in dependence of the carrier concentration.
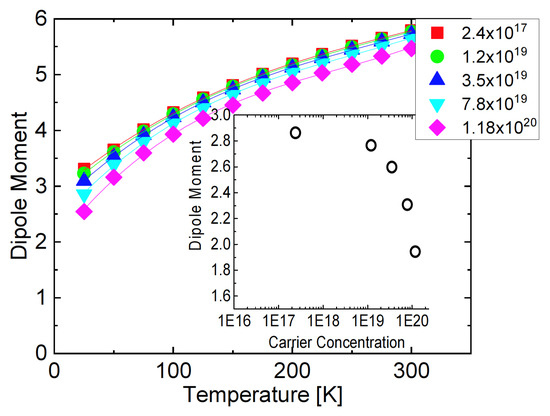
Figure 13.
Temperature dependence of the local dipole moment for various carrier concentrations. The inset shows the local dipole moment in the zero temperature limit as a function of the carrier concentration.
Experimentally, the electrical properties of doped SrTiO3 depend on the volume concentration of carriers which are, however, inhomogeneously distributed in the samples. Self-doped samples exhibit different electronic, chemical, and structural properties in highly doped regions as compared to the matrix, which is almost unaffected by doping [128]. According to References [129,130], the removal of oxygen preferentially takes place along extended defects, thus giving rise to a local reduction, which cannot be detected by average macroscopic property detecting methods, like, e.g., mobility and Hall measurements. This argument is supported by local conductivity atomic force microscopy (LC-AFM) data [131,132], which demonstrate that very low concentrations of oxygen deficiency assemble along these dislocations. In order to prove that a random distribution of “defects” is absent, a decisive experiment has been carried out, which underlines the important role of dislocations and filament formation on the electrical transport properties of reduced SrTiO3. As outlined above, even with increasing carrier density, mode softening persists on a dynamic time scale of ps and length scale of nm. This can be confirmed experimentally on the nano-scale by using, e.g., time-resolved infrared spectroscopy or scanning near-field optical microscopy (SNOM). Alternatively, piezoelectric force microscopy (PFM) offers the possibility of locally detecting a piezoelectric response which is an indirect probe of mode softening through the creation of induced dipole moments. This has been shown in Reference [133], where, in the vicinity of the core of edge dislocations in a SrTiO3 bicrystal, a polarization of the order of 20 μC/cm has been detected. This is shown in Figure 14, where, along a sharp step of a plastically deformed SrTiO3 crystal, corresponding to a broad band of dislocations, piezoelectric responses are observed.
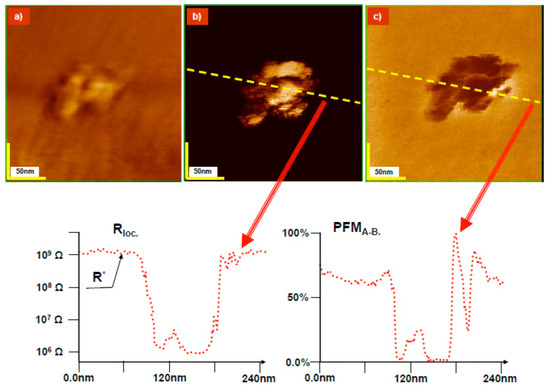
Figure 14.
Topographic image of the exit of a dislocation bundle in thermally reduced SrTiO: (a) the topography variation is about 0–4.8 nm. In the area of the bundle (local conductivity atomic force microscopy (LC-AFM)) (b) with metallic properties, the piezo response (c) is absent. This can be observed at the cross sections of LC-AFM (b) and piezoelectric force microscopy (PFM) (c) responses. The distribution of the resistance along the cross section (lower part of the figure) shows an anti-correlation with the distribution of the piezo activity on the cross section of the PFM. The resistance outside the bundle is much higher than on the cross section, which is related to the finite resolution of the analog-to-digital converters (here, 4 decades), so that, using additional measurements (only in this area), the resistance is higher than 10 (from Reference [127]).
As expected, this rapidly decreases with increasing carrier concentration and approaches a constant value for small densities, thus clearly supporting the polar character of the matrix and the inherent inhomogeneity of doped SrTiO3. Correspondingly, in the metallic and superconducting low carrier density limit of SrTiO3, metallicity is not globally present but appears only in filaments which coexist with elastically and polar distorted domains where the latter shrink in size with increasing carrier density and have completely vanished beyond a critical carrier density to give space for a homogeneous metal where superconductivity is absent. In terms of the electronic band structure, highly localized polaronic bands can be attributed to the matrix, whereas Luttinger liquid-type behavior must be present in the filaments. With increasing carrier density, the localized band adopts dispersion from the itinerant one, which corresponds to a steep band/flat band scenario, where superconductivity is a consequence of interband interactions [134].
In conclusion, the dynamical properties of SrTiO3 have been calculated as a function of carrier concentration. Up to a critical concentration , the lattice potential is of double-well character, and strong transverse optic mode softening takes place [127]. This is linked to the formation of polar nano-regions, which grow in size with decreasing temperature, implying substantial sample inhomogeneity. The “insulating” nano-domains coexist with the filamentary conductivity; hence, possible links to superconductivity are apparent. As long as this coexistence persists, metallicity/superconductivity survives. Thus, its essential origin must be associated with the polar character of the matrix and the two-component properties. Beyond , almost “normal” dynamics are observed with negligible mode softening and nano-domain formation. Typical metallicity is expected there, as well as homogeneous sample properties. The theoretical results are in agreement with experiments which demonstrate the local metallic character and the insulating behavior of the matrix, which are schematically summarized in Figure 15, where the change in the character of the potential along a core of dislocations and the entry into the matrix is depicted.
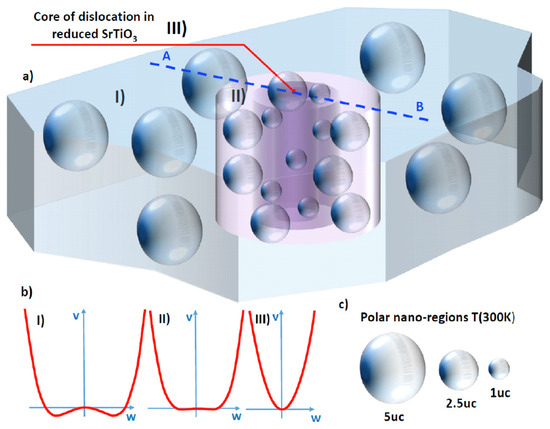
Figure 15.
(a) Schematic representation of the structural and chemical development along a pathway from A to B crossing a core of dislocations in SrTiO. (b) The change of the local potential along the same pathway where in the region I) an intact matrix is present, while, in II), a crossover region exists with flat potential, which changes over to single well in III), where the metallic properties of the dislocation core dominate. (c) Sizes of the polar nano-regions (uc: unit cell) (from Reference [127]).
5. Another Rather Mysterious Perovskite: WO3
WO3 is a perovskite where the A-site ion is missing or only in part occupied by M=Na, K, Rb, or Cs [135]. The dominating physics in these materials stem from the valence fluctuations of W, which dominantly adopts a 3 or 5 valency. Structurally, depending on the dopant atom M, carrier-doped tungsten oxides (MWO3) are classified into two different categories: perovskite or hexagonal. Both structures consist of WO octahedra that form a corner-sharing network, though, in many cases, each octahedron exhibits a significant distortion [136,137,138]. Early on, it was discovered that these tungsten bronzes become superconductors when small amounts x of M are added. Typical superconducting transition temperatures for the three compounds are shown in Figure 16.
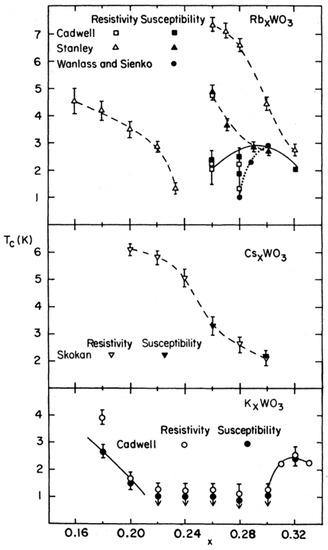
Figure 16.
Superconducting transition temperature as a function of x for RbWO, CsWO, and KWO (from Reference [135]).
As is obvious from the figure, there are two superconducting regions in the K- and Rb-doped compounds which adopt a dome or half-dome, like x-dependence. The highest s are observed for the Rb-doped system reaching more than 7 K. What is of particular interest in WO3 is the fact that charge accumulations occur around the W ion with the tendency to localization, i.e., polaron formation [139]. Early on, detailed experiments by Salje and Schirmer convincingly showed that these polarons pair to form bipolarons [140,141], which yielded one of the first realizations for obtaining bipolaronic superconductivity, the original concept behind the discovery of cuprates [49]. This connection was taken up by Reich and Tsabba [142] to get back to WO3 and search for superconductivity in a WO3 sample with surface composition of NaWO3. These crystals showed a sharp diamagnetic step in their magnetization at 91 K, and a magnetic hysteresis below this temperature. Transport measurements below 100 K show a sharp metal to insulator transition, which is followed by a rapid decrease in the resistivity when the temperature is lowered to about 90 K. These results point to a possible nucleation of a superconducting phase on the surface of these crystals. The results of Ref. [142] initialized an EPR and magnetic susceptibility study of Na-doped WO3 samples, suggesting traces of possible superconductivity [143]. In a later investigation of a related compound, namely lithium intercalated WO, a small superconducting fraction was observed [144]. The absence of a clear transition in resistivity measurements indicated, however, that the superconductivity is localized in small regions which do not percolate. EPR experiments showed the presence of W - W electron bipolarons in reduced tungsten oxide samples, thus rendering the compound as a promising candidate for high-temperature superconductivity. More details with respect to recent progress on superconductivity in WO3-type compounds can be found in the contributions of Shengelaya et al. [145] and Salje [146] in this issue.
6. Concluding Remarks
In our contribution to the special issue honoring K.A. Müller’s life work, we tried to walk along his scientific path, which is a long one and covers almost 7 decades. Since his productivity and scientific activity was enormous, we certainly cannot follow all the detours he made during his career, but we concentrated on the two uttermost important systems: SrTiO3, his scientific favorite child, and the cuprates. In addition, we added an outlook for the future research in the former where, again, superconductivity is in the focus with emphasis on its inherent heterogeneous filamentary character, parallelizing his viewpoints for cuprates. We both are deeply indebted to our friend, K. Alex Müller, who not only scientifically supported and inspired both of us, and never stopped encouraging us in following even controversial scientific topics but also for his open minded attitudes and his honest interest in our private life. His black humor has promoted us throughout our collaborations and beyond and today also adds spice to our life.
- Thank you very much, Alex! -
In order to come back to the starting ideas leading to high-temperature superconductivity, we finish our conclusions with the final Figure 17, the Jahn-Teller bipolaron [55,147], which is the essential ingredient and motivation for the discovery of high-temperature superconductivity [49,50,51,52].
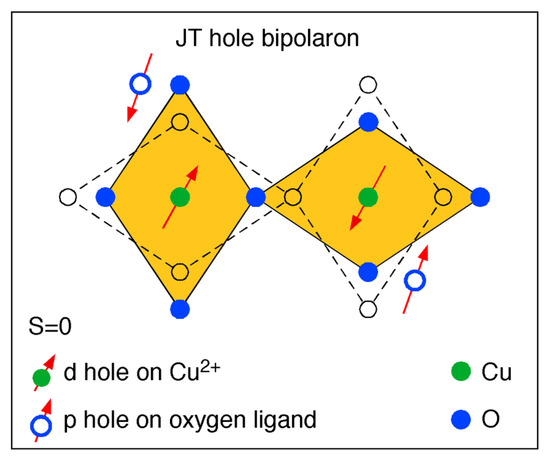
Figure 17.
Schematic sketch of the inter-site Jahn-Teller (JT) bipolaron (from Reference [67]).
Author Contributions
Both authors (A.B.-H. and H.K.) have contributed equally to this work. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We would like to thank K.A. Müller for the fruitful and encouraging collaboration, his great support, and his warm friendship over many years.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lines, M.E.; Glass, A.M. Principles and Applications of Ferroelectrics and Related Materials; Clarendon Press: Oxford, UK, 1977. [Google Scholar]
- Cochran, W. Crystal stability and the theory of ferroelectricity. Adv. Phys. 1960, 9, 387–423. [Google Scholar] [CrossRef]
- Anderson, P.W. Concepts in Solids; Benjamin: New York, NY, USA, 1963. [Google Scholar]
- Cowley, R.A. Lattice dynamics and phase transitions of strontium titanate. Phys. Rev. 1964, 134, A981–A997. [Google Scholar] [CrossRef]
- Müller, K.A. Paramagnetic Resonance of Fe3+ in SrTiO3 single crystals. Helv. Phys. Acta 1958, 31, 173–204. [Google Scholar]
- Geller, S.; Bala, V.B. Crystallographic studies of perovskite-like compounds. II. Rare earth alluminates. Acta Cryst. 1957, 9, 1019–1025. [Google Scholar] [CrossRef]
- Müller, K.A.; Berlinger, W.; Waldner, F. Characteristic Structural Phase Transitions in Perovskite-Type Compounds. Phys. Rev. Lett. 1968, 21, 814–817. [Google Scholar] [CrossRef]
- Müller, K.A.; Kool, T.W. Properties of Perovskites and Other Oxides; World Scientific Publishing: Singapore, 2010. [Google Scholar]
- Höchli, U.; Müller, K.A. Observation of the Jahn-Teller splitting of three-valent d7 ions via Orbach relaxation. Phys. Rev. Lett. 1964, 12, 730–733. [Google Scholar] [CrossRef]
- Cochran, W.; Zia, A. Structure and dynamics of perovskite-type crystals. Phys. Stat. Sol. 1968, 25, 273–283. [Google Scholar] [CrossRef]
- Fleury, P.A.; Scott, J.F.; Worlock, J.M. Soft Phonon Modes and the 110 K Phase Transition in SrTiO3. Phys. Rev. Lett. 1968, 21, 16–19. [Google Scholar] [CrossRef]
- Müller, K.A.; Berlinger, W.; Rubins, R.S. Observation of Two Charged States of a Nickel-Oxygen Vacancy Pair in SrTiO3 by Paramagnetic Resonance. Phys. Rev. 1969, 186, 361–371. [Google Scholar] [CrossRef]
- Anderson, P.W. Model for the electronic structure of amorphous semiconductors. Phys. Rev. Lett. 1975, 34, 953–956. [Google Scholar] [CrossRef]
- Street, R.A.; Mott, N.F. States in the Gap in Glassy Semiconductors. Phys. Rev. Lett. 1975, 35, 1293–1296. [Google Scholar] [CrossRef]
- Chakraverty, B.K. Possibility of insulator to superconductor phase transition. J. Phys. Lett. 1979, 40, 99–100. [Google Scholar] [CrossRef]
- Müller, K.A.; Berlinger, W. Static critical exponents at structural phase transitions. Phys. Rev. Lett. 1971, 26, 13–16. [Google Scholar] [CrossRef]
- Müller, K.A.; Burkard, H. SrTiO3: An intrinsic quantum paraelectric below 4 K. Phys. Rev. B 1979, 19, 3593–3602. [Google Scholar] [CrossRef]
- Kremer, R.K.; Bussmann-Holder, A.; Keller, H.; Haunschild, R. The Crucial Things in Science often Happen Quite Unexpectedly - Das Entscheidende in der Wissenschaft Geschieht of Ganz Unerwartet (K. Alex Müller). Condens. Matter 2020, 5, 43. [Google Scholar] [CrossRef]
- Schooley, F.; Hosler, W.R.; Cohen, M.L. Superconductivity in semiconducting SrTiO3. Phys. Rev. Lett. 1964, 12, 474–475. [Google Scholar] [CrossRef]
- Appel, J. Soft-mode superconductivity in SrTiO3-x. Phys. Rev. 1969, 180, 508–516. [Google Scholar] [CrossRef]
- Cohen, M.L. Superconductivity in many-valley semiconductors and in semimetals. Phys. Rev. 1964, 134, A511–A521. [Google Scholar] [CrossRef]
- Binnig, G.; Baratoff, A.; Hoenig, H.E.; Bednorz, J.G. Two-band superconductivity in Nb-doped SrTiO3. Phys. Rev. Lett. 1980, 45, 1352–1355. [Google Scholar] [CrossRef]
- Suhl, H.; Matthias, B.T.; Walker, L.R. Bardeen-Cooper-Schrieffer Theory of Superconductivity in the Case of Overlapping Bands. Phys. Rev. Lett. 1959, 3, 552–555. [Google Scholar] [CrossRef]
- Moskalenko, V. Superconductivity in metals with overlapped energy bands. Fiz. Metal. Metalloved. 1959, 8, 503–513. [Google Scholar]
- Gor’kov, L.P. Phonon mechanism in the most dilute superconductor n-type SrTiO3. Proc. Natl. Acad. Sci. USA 2016, 113, 4646–4651. [Google Scholar] [CrossRef]
- Thiemann, M.; Beutel, M.H.; Dressel, M.; Lee-Hone, N.R.; Broun, D.M.; Fillis-Tserakis, E.; Boschker, H.; Mannhart, J.; Scheffler, M. Single-Gap Superconductivity and Dome of Superfluid Density in Nb-Doped SrTiO3. Phys. Rev. Lett. 2018, 120, 37002. [Google Scholar] [CrossRef] [PubMed]
- Collignon, C.; Lin, X.; Rischau, C.W.; Fauqué, B.; Behnia, K. Metallicity and Superconductivity in Doped Strontium Titanate. Annual Rev. Cond. Mat. Phys. 2019, 10, 25–44. [Google Scholar] [CrossRef]
- For a recent review see: Gastiasoro, M.N.; Ruhman, J.; Fernandes, R.M. Superconductivity in dilute SrTiO3: A review. Ann. Phys. 2020, 417, 168107. [Google Scholar] [CrossRef]
- Scheerer, G.; Boselli, M.; Pulmannova, D.; Rischau, C.W.; Waelchli, A.; Gariglio, S.; Giannini, E.; van der Marel, D.; Triscone, J.M. Ferroelectricity, Superconductivity, and SrTiO3—Passions of K.A. Müller. Condens. Matter 2020, 5, 60. [Google Scholar] [CrossRef]
- Hemberger, J.; Lunkenheimer, P.; Viana, R.; Böhmer, R.; Loidl, A. Electric-field-dependent dielectric constant and nonlinear susceptibility in SrTiO3. Phys. Rev. B 1995, 52, 13159–13162. [Google Scholar] [CrossRef]
- Samara, G.A. Pressure and Temperature Dependences of the Dielectric Properties of the Perovskites BaTiO3 and SrTiO3. Phys. Rev. 1966, 151, 378–386. [Google Scholar] [CrossRef]
- Berre, B.; Fossheim, K.; Müller, K.A. Critical attenuation of the soft mode in SrTiO3. Phys. Rev. Lett. 1969, 23, 589–591. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Bilz, H.; Bäuerle, D.; Wagner, D. A polarizability model for the ferroelectric mode in semiconducting SrTiO3. Z. Physik B 1981, 41, 353–355. [Google Scholar] [CrossRef]
- Bednorz, J.G.; Müller, K.A. Sr1-xCaxTiO3: An XY Quantum Ferroelectric with Transition to Randomness. Phys. Rev. Lett. 1984, 52, 2289–2292. [Google Scholar] [CrossRef]
- Itoh, M.; Wang, R.; Inaguma, Y.; Yamaguchi, T.; Shan, Y.-J.; Nakamura, T. Ferroelectricity Induced by Oxygen Isotope Exchange in Strontium Titanate Perovskite. Phys. Rev. Lett. 1999, 82, 3540–3543. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Bishop, A.R. Incomplete ferroelectricity in SrTi18O3. Eur. Phys. J. B 2006, 53, 279–282. [Google Scholar] [CrossRef]
- Shigenari, T.; Abe, K. Raman Spectra of Soft Modes of SrTiO3. Ferroelectrics 2010, 369, 117–126. [Google Scholar] [CrossRef]
- Kleemann, W.; Dec, J.; Tkach, A.; Vilarinho, P.M. SrTiO3—Glimpses of an Inexhaustible Source of Novel Solid State Phenomena. Condens. Matter 2020, 5, 58. [Google Scholar] [CrossRef]
- Ravel, B.; Stern, E.A.; Verdinskii, R.I.; Kraizman, V. Local structure and the phase transitions of BaTiO3. Ferroelectrics 1998, 206–207, 407–430. [Google Scholar] [CrossRef]
- Zalar, B.; Laguta, V.V.; Blinc, R. NMR Evidence for the Coexistence of Order-Disorder and Displacive Components in Barium Titanate. Phys. Rev. Lett. 2003, 90, 037601. [Google Scholar] [CrossRef]
- Harada, J.; Axe, J.D.; Shirane, G. Neutron-Scattering Study of Soft Modes in Cubic BaTiO3. Phys. Rev. B 1971, 4, 155–162. [Google Scholar] [CrossRef]
- Völkel, G.; Müller, K.A. Order-disorder in the low-temperature phase of BaTiO3. Phys. Rev. B 2007, 76, 094105. [Google Scholar] [CrossRef]
- Bishop, A.R. A Lattice Litany for Transition Metal Oxides. Condens. Matter 2020, 5, 46. [Google Scholar] [CrossRef]
- Kool, T.W. Meetings with a Remarkable Man, Alex Müller—The Professor of SrTiO3. Condens. Matter 2020, 5, 44. [Google Scholar] [CrossRef]
- Müller, K.A. Essential Heterogeneities in Hole-Doped Cuprate Superconductors. In Superconductivity in Complex Systems; Müller, K.A., Bussman-Holder, A., Eds.; Structure and Bonding 114; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1–11. [Google Scholar]
- Deutscher, G.; Fenichel, H.; Gershenson, M.; Grünbaum, E.; Ovadyahu, Z. Transition to zero dimensionality in granular aluminum superconducting films. J. Low Temp. Phys. 1973, 10, 231–243. [Google Scholar] [CrossRef]
- Deutscher, G.; Müller, K.A. Origin of superconductive glassy state and extrinsic critical currents in high-Tc oxide. Phys. Rev. Lett. 1987, 59, 1745–1748. [Google Scholar] [CrossRef] [PubMed]
- Deutscher, G. The role of the Short Coherence Length in Unconventional Superconductors. Condens. Matter 2020, 5, 77. [Google Scholar] [CrossRef]
- Bednorz, J.G.; Müller, K.A. Possible High Tc Superconductivity in the Ba-La-Cu-O Sysyem. Z. Phys. B 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Bednorz, J.G.K. Alexander Müller Nobel Lecture. Available online: https://www.nobelprize.org/prizes/physics/1987/muller/lecture/ (accessed on 29 May 2020).
- Müller, K.A.; Bednorz, J.G. The Discovery of a Class of High-Temperature Superconductors. Science 1987, 237, 1133–1139. [Google Scholar] [CrossRef] [PubMed]
- Bednorz, J.G.; Müller, K.A. Perovskite-type oxides—The new approach to high-Tc superconductivity. Rev. Mod. Phys. 1988, 60, 585–600. [Google Scholar] [CrossRef]
- Höck, K.-H.; Nickisch, H.; Thomas, H. Jahn-Teller effect in itinerant electron systems: The Jahn-Teller polaron. Helv. Phys. Acta 1983, 56, 237–243. [Google Scholar]
- Bianconi, A.; Saini, N.L.; Lanzara, A.; Missori, M.; Rossetti, T.; Oyanagi, H.; Yamaguchi, H.; Oka, K.; Ito, T. Determination of the Local Lattice Distortions in the CuO2 Plane of La1.85Sr0.15CuO4. Phys. Rev. Lett. 1996, 76, 3412–3415. [Google Scholar] [CrossRef]
- Müller, K.A. On the superconductivity in hole doped cuprates. J. Phys. Condens. Matter 2007, 19, 251002. [Google Scholar] [CrossRef]
- Müller, K.A. The Unique Properties of Superconductivity in Cuprates. J. Supercond. Nov. Magn. 2014, 27, 2163–2179. [Google Scholar] [CrossRef]
- Müller, K.A. The Polaronic Basis for High-Temperature Superconductivity. J. Supercond. Nov. Magn. 2017, 30, 3007–3018. [Google Scholar] [CrossRef]
- Müller, K.A. Possible coexistence of s- and d-wave condensates in copper oxide superconductors. Nature 1995, 377, 133–135. [Google Scholar] [CrossRef]
- Müller, K.A.; Keller, H. s and d Wave Symmetry Components in High-Temperature Cuprate Superconductors. In High-Tc Superconductivity 1996: Ten Years after the Discovery; Kaldis, E., Liarokapis, E., Müller, K.A., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997; pp. 7–29. [Google Scholar]
- Wollman, D.A.; Van Harlingen, D.J.; Lee, W.C.; Ginsberg, D.M.; Leggett, A.J. Experimental determination of the superconducting pairing state in YBCO from the phase coherence of YBCO-Pb dc SQUIDs. Phys. Rev. Lett. 1993, 71, 2134–2137. [Google Scholar] [CrossRef]
- Tsuei, C.C.; Kirtley, J.R.; Chi, C.C.; Yu-Jahnes, L.S.; Gupta, A.; Shaw, T.; Sun, J.Z.; Ketchen, M.B. Pairing Symmetry and Flux Quantization in a Tricrystal Superconducting Ring of YBa2Cu3O7-δ. Phys. Rev. Lett. 1994, 73, 593–596. [Google Scholar] [CrossRef]
- Brawner, D.A.; Ott, H.R. Evidence for an unconventional superconducting order parameter in YBa2Cu3O6.9. Phys. Rev. B 1994, 50, 6530(R)–6533(R). [Google Scholar] [CrossRef]
- Khasanov, R.; Shengelaya, A.; Maisuradze, A.; La Mattina, F.; Bussmann-Holder, A.; Keller, H.; Müller, K.A. Experimental evidence for two gaps in the high-temperature La1.83Sr0.17CuO4 superconductor. Phys. Rev. Lett. 2007, 98, 057007. [Google Scholar] [CrossRef]
- Khasanov, R.; Strässle, S.; Di Castro, D.; Masui, T.; Miyasaka, S.; Tajima, S.; Bussmann-Holder, A.; Keller, H. Multiple gap symmetries for the order parameter of cuprate superconductors from penetration depth measurements. Phys. Rev. Lett. 2007, 99, 237601. [Google Scholar] [CrossRef]
- Khasanov, R.; Shengelaya, A.; Karpinski, J.; Bussmann-Holder, A.; Keller, H.; Müller, K.A. s-wave symmetry along the c-axis and s+d in-plane superconductivity in bulk YBa2Cu4O8. J. Supercond. Nov. Magn. 2008, 21, 81–85. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Khasanov, R.; Shengelaya, A.; Maisuradze, A.; La Mattina, F.; Keller, H.; Müller, K.A. Mixed order parameter symmetries in cuprate superconductors. Europhys. Lett. 2007, 77, 27002. [Google Scholar] [CrossRef][Green Version]
- Keller, H.; Bussmann-Holder, A.; Müller, K.A. Jahn-Teller physics and high-Tc superconductivity. Mater. Today 2008, 11, 38–46. [Google Scholar] [CrossRef]
- Zimmermann, P.; Keller, H.; Lee, S.L.; Savić, I.M.; Warden, M.; Zech, D.; Cubitt, R.; Forgan, E.M.; Kaldis, E.; Karpinski, J.; et al. Muon-spin rotation studies of the temperature dependence of the magnetic penetration depth in the YBa2Cu3Ox family and related compounds. Phys. Rev. B 1995, 52, 541–552. [Google Scholar] [CrossRef] [PubMed]
- Müller, K.A. On the macroscopic s- and d-wave symmetry in cuprate superconductors. Philos. Mag. Lett. 2002, 82, 279–288. [Google Scholar] [CrossRef]
- Iachello, F. A model of cuprate superconductors based on the analogy with atomic nuclei. Philos. Mag. Lett. 2002, 82, 289–295. [Google Scholar] [CrossRef]
- Khasanov, R.; Shengelaya, A.; Brütsch, R.; Keller, H. Suppression of the s-wave Order Parameter Near the Surface of the Infinite-Layer Electron-Doped Cuprate Superconductor Sr0.9La0.1Cu2. Condens. Matter 2020, 5, 50. [Google Scholar] [CrossRef]
- Batlogg, B.; Cava, R.J.; Jayaraman, A.; van Dover, R.B.; Kourouklis, G.A.; Sunshine, S.; Murphy, D.W.; Rupp, L.W.; Chen, H.S.; White, A.; et al. Isotope Effect in the High-Tc Superconductors Ba2YCu3O7 and Ba2EuCu3O7. Phys. Rev. Lett. 1987, 58, 2333–2336. [Google Scholar] [CrossRef]
- Franck, J.P.; Jung, J.; Mohamed, A.K.; Gygax, S.; Sproule, G.I. Observation of an oxygen isotope effect in superconducting (Y1-xPrx)Ba2Cu3O7-δ. Phys. Rev. B 1991, 44, 5318–5321. [Google Scholar] [CrossRef] [PubMed]
- Franck, J.P. Experimental studies of the isotope effect in high temperature superconductors. In Physical Properties of High Temperature Superconductors IV; Ginsberg, D.M., Ed.; World Scientific: Singapore, 1994; pp. 189–293. [Google Scholar]
- Müller, K.A. On the oxygen isotope effect and apex anharmonicity in high-Tc cuprates. Z. Phys. B Condens. Matter 1990, 80, 193–201. [Google Scholar] [CrossRef]
- Zhao, G.M.; Conder, K.; Keller, H.; Müller, K.A. Oxygen isotope effects in La2-xSrxCuO4: Evidence for polaronic charge carriers and their condensation. J. Phys. Condens. Matter 1998, 10, 9055–9066. [Google Scholar] [CrossRef]
- Zhao, G.M.; Keller, H.; Conder, K. Unconventional isotope effects in the high-temperature cuprate superconductors. J. Phys. Condens. Matter 2001, 13, R569–R587. [Google Scholar] [CrossRef]
- Keller, H. Unconventional Isotope Effects in Cuprate Superconductors. In Superconductivity in Complex Systems; Müller, K.A., Bussmann-Holder, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 143–169. [Google Scholar]
- Conder, K.; Furrer, A.; Pomjakushina, E. A Retrospective of Materials Synthesis at the Paul Scherrer Institut (PSI). Condens. Matter 2020, 5, 55. [Google Scholar] [CrossRef]
- Zech, D.; Keller, H.; Conder, K.; Kaldis, E.; Liarokapis, E.; Poulakis, N.; Müller, K.A. Site-selective oxygen isotope effect in optimally doped YBa2Cu3O6+x. Nature 1994, 371, 681–683. [Google Scholar] [CrossRef]
- Zhao, G.; Ager, J.W., III; Morris, D.E. Site dependence of large oxygen isotope effect in Y0.7Pr0.3Ba2Cu3O6.97. Phys. Rev. B 1996, 54, 14982–14985. [Google Scholar] [CrossRef] [PubMed]
- Khasanov, R.; Shengelaya, A.; Morenzoni, E.; Angst, M.; Conder, K.; Savić, I.M.; Lampakis, D.; Liarokapis, E.; Tatsi, A.; Keller, H. Site-selective oxygen isotope effect on the magnetic field penetration depth in underdoped Y0.6Pr0.4Ba2Cu3O7-δ. Phys. Rev. B 2003, 68, 220506(R). [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Genzel, L.; Bishop, A.R.; Simon, A. The role of apical oxygen in superconducting cuprates. Philos. Mag. B 1997, 75, 463–469. [Google Scholar] [CrossRef]
- Khasanov, R.; Shengelaya, A.; Di Castro, D.; Morenzoni, E.; Maisuradze, A.; Savić, I.M.; Conder, K.; Pomjakushina, E.; Bussmann-Holder, A.; Keller, H. Oxygen isotope effect on the superconducting transition and magnetic states within the phase diagram of Y1-xPrxBa2Cu3O7-δ. Phys. Rev. Lett. 2008, 101, 077001. [Google Scholar] [CrossRef] [PubMed]
- Guguchia, Z.; Khasanov, R.; Bendele, M.; Pomjakushina, E.; Conder, K.; Shengelaya, A.; Keller, H. Negative Oxygen Isotope Effect on the Static Spin Stripe Order in Superconducting La2-xBaxCuO4 (x=1/8) Observed by Muon-Spin Rotation. Phys. Rev. Lett. 2014, 113, 057002. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Mott, N.F. Spin and charge bipolaron kinetics of high Tc superconductors. Int. J. Mod. Phys. B 1994, 8, 2075–2109. [Google Scholar] [CrossRef]
- Zhao, G.; Morris, D.E. Observation of a possible oxygen isotope effect on the effective mass of carriers in YBa2Cu3O6.94. Phys. Rev. B 1995, 51, 16487–16490. [Google Scholar] [CrossRef]
- Zhao, G.M.; Hunt, M.B.; Keller, H.; Müller, K.A. Evidence for polaronic supercarriers in the copper oxide superconductors La2-xSrxCuO4. Nature 1997, 385, 236–239. [Google Scholar] [CrossRef]
- Hofer, J.; Conder, K.; Sasagawa, T.; Zhao, G.M.; Willemin, M.; Keller, H.; Kishio, K. Oxygen-isotope effect on the in-plane penetration depth in underdoped La2-xSrxCuO4 single crystals. Phys. Rev. Lett. 2000, 84, 4192–4195. [Google Scholar] [CrossRef] [PubMed]
- Khasonov, R.; Shengelaya, A.; Conder, K.; Morenzoni, E.; Savić, I.M.; Keller, H. The oxygen-isotope effect on the in-plane penetration depth in underdoped Y1-xPrxBa2Cu3O7-δ as revealed by muon-spin rotation. J. Phys. Condens. Matter 2003, 15, L17–L23. [Google Scholar] [CrossRef]
- Jackson, T.J.; Riseman, T.M.; Forgan, E.M.; Glückler, H.; Prokscha, T.; Morenzoni, E.; Pleines, M.; Niedermayer, C.; Schatz, G.; Luetkens, H.; et al. Depth-Resolved Profile of the Magnetic Field beneath the Surface of a Superconductor with a Few nm Resolution. Phys. Rev. Lett. 2000, 84, 4958–4961. [Google Scholar] [CrossRef] [PubMed]
- Khasanov, R.; Eshchenko, D.G.; Luetkens, H.; Morenzoni, E.; Prokscha, T.; Suter, A.; Garifinov, N.; Mali, M.; Roos, J.; Conder, K.; et al. Direct observation of the oxygen isotope effect on the in-plane magnetic field penetration depth in optimally doped YBa2Cu3O7-δ. Phys. Rev. Lett. 2004, 92, 057602. [Google Scholar] [CrossRef] [PubMed]
- Uemura, Y.J.; Luke, G.M.; Sternlieb, B.J.; Brewer, J.H.; Carolan, J.F.; Hardy, W.N.; Kadono, R.; Kempton, J.R.; Kiefl, R.F.; Kreitzman, S.R.; et al. Universal Correlations between Tc and ns/m* (Carrier Density over Effective Mass) in High-Tc Cuprate Superconductors. Phys. Rev. Lett. 1989, 62, 2317–2320. [Google Scholar] [CrossRef]
- Uemura, Y.J.; Le, L.P.; Luke, G.M.; Sternlieb, B.J.; Wu, W.D.; Brewer, J.H.; Riseman, T.M.; Seaman, C.L.; Maple, M.B.; Ishikawa, M.; et al. Basic similarities among cuprate, bismuthate, organic, Chevrel-phase, and heavy-fermion superconductors shown by penetration-depth measurements. Phy. Rev. Lett. 1991, 66, 2665–2668. [Google Scholar] [CrossRef]
- Weyeneth, S.; Müller, K.A. Oxygen Isotope Effect in Cuprates Results from Polaron-induced Superconductivity. J. Supercond. Nov. Magn. 2011, 24, 1235–1239. [Google Scholar] [CrossRef][Green Version]
- Kresin, V.Z.; Wolf, S.A. Microscopic model for the isotope effect in high-Tc oxides. Phys. Rev. B 1994, 49, 3652–3654. [Google Scholar] [CrossRef]
- Bill, A.; Kresin, V.Z.; Wolf, S.A. Isotope effect for the penetration depth in superconductors. Phys. Rev. B 1998, 57, 10814–10824. [Google Scholar] [CrossRef]
- Schneider, T.; Keller, H. Universal trends in extreme type-II superconductors. Phys. Rev. Lett. 1992, 69, 3374–3377. [Google Scholar] [CrossRef]
- Bendele, M.; von Rohr, F.; Gugchia, Z.; Pomjakushina, E.; Conder, K.; Bianconi, A.; Simon, A.; Bussmann-Holder, A.; Keller, H. Evidence for strong lattice effects as revealed from huge unconventional oxygen isotope effects on the pseudogap temperature in La2-xSrxCuO4. Phys. Rev. B 2017, 95, 014514. [Google Scholar] [CrossRef]
- Lanzara, A.; Zhao, G.; Saini, N.L.; Bianconi, A.; Conder, K.; Keller, H.; Müller, K.A. Oxygen-isotope effect of the charge-stripe ordering temperature in La2-xSrxCuO4 from X-ray absorption spectroscopy. J. Phys. Condens. Matter 1999, 11, L541–L546. [Google Scholar] [CrossRef]
- Rubio Temprano, D.; Mesot, J.; Janssen, S.; Conder, K.; Furrer, A.; Mutka, H.; Müller, K.A. Large Isotope Effect on the Pseudogap in the High-Temperature Superconductor HoBa2Cu4O8. Phys. Rev. Lett. 2000, 84, 1990–1993. [Google Scholar] [CrossRef] [PubMed]
- Rubio Temprano, D.; Furrer, A.; Conder, K.; Mutka, H. A neutron crystal-field study of the pseudogap in the underdoped high Tc superconductor HoBa2Cu418O8. Physica B 2000, 276–278, 762–763. [Google Scholar] [CrossRef]
- Rubio Temprano, D.; Mesot, J.; Janssen, S.; Conder, K.; Furrer, A.; Sokolov, A.; Trounov, V.; Kazakov, S.M.; Karpinski, J.; Müller, K.A. Large copper isotope effect on the pseudogap in the high-temperature superconductor HoBa2Cu4O8. Eur. Phys. J. B 2001, 19, 5–8. [Google Scholar] [CrossRef]
- Rubio Temprano, D.; Conder, K.; Furrer, A.; Mutka, H.; Trounov, V.; Müller, K.A. Oxygen and copper isotope effects on the pseudogap in the high-temperature superconductor La1.81Ho0.04Sr0.15CuO4 studied by neutron crystal-field spectroscopy. Phys. Rev. B 2002, 66, 184506. [Google Scholar] [CrossRef]
- Häfliger, P.S.; Podlesnyak, A.; Conder, K.; Pomjakushina, E.; Furrer, A. Pseudogap of the high-temperature superconductor La1.96-xSrxHo0.04CuO4 as observed by neutron crystal-field spectroscopy. Phys. Rev. B 2006, 74, 184520. [Google Scholar] [CrossRef]
- Varma, C.M. Non-Fermi-liquid states and pairing instability of a general model of copper oxide metals. Phys. Rev. B 1997, 55, 14554–14580. [Google Scholar] [CrossRef]
- Li, Y.; Balédent, V.; Barisić, N.; Cho, Y.; Fauqué, B.; Sidis, Y.; Yu, G.; Zhao, X.; Bourges, P.; Greven, M. Unusual magnetic order in the pseudogap region of the superconductor HgBa2CuO4+δ. Nature 2008, 455, 372–375. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Keller, H. Polaron Effects in High-Temperature Cuprate Superconductors. In Polarons in Advanced Materials; Alexandrov, S.A., Ed.; Springer: Dordrecht, The Netherlands, 2007; pp. 599–621. [Google Scholar]
- Zhang, C.J.; Oyanagi, H. Local lattice instability and superconductivity in La1.85Sr0.15Cu1-xMxO4 (M=Mn, Ni, and Co). Phys. Rev. B 2009, 79, 064521. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Simon, A.; Keller, H.; Bishop, A.R. Polaron signatures in the phonon dispersion of high-temperature superconducting copper oxides. Eur. Phys. Lett. 2013, 101, 47004. [Google Scholar] [CrossRef]
- Ohtomo, A.; Hwang, H.Y. A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 2004, 427, 423–426. [Google Scholar] [CrossRef] [PubMed]
- Reyren, N.; Thiel, S.; Caviglia, A.D.; Hammerl, G.; Richter, C.; Schneider, C.W.; Kopp, T.; Rüetschi, A.-S.; Jaccard, D.; Gabay, M.; et al. Superconducting interfaces between insulating oxides. Science 2007, 317, 1196–1199. [Google Scholar] [CrossRef] [PubMed]
- Brinkman, A.; Huijben, M.; van Zalk, M.; Huijben, J.; Zeitler, U.; Maan, J.C.; van der Wiel, W.; Rijnders, D.; Blank, D.H.A.; Hilgenkamp, H. Magnetic effects at the interface between non-magnetic oxides. Nat. Mater. 2007, 6, 493–496. [Google Scholar] [CrossRef] [PubMed]
- Mannhart, J.; Schlom, D.G. Oxide interfaces—An opportunity for electronics. Science 2010, 327, 1607–1611. [Google Scholar] [CrossRef]
- Zubko, P.; Gariglio, S.; Gabay, M.; Ghosez, P.; Triscone, J.-M. Interface physics in complex oxide heterostructures. Ann. Rev. Cond. Mat. Phys. 2011, 2, 141–156. [Google Scholar] [CrossRef]
- Hwang, H.Y.; Iwasa, Y.; Kawasaki, M.; Keimer, B.; Nagaosa, N.; Tokura, Y. Emergent phenomena at oxide interfaces. Nat. Mater. 2012, 11, 103–113. [Google Scholar] [CrossRef]
- Lin, X.; Zhu, Z.; Fauqué, B.; Behnia, K. Fermi surface of the most dilute superconductor. Phys. Rev. X 2013, 3, 021002. [Google Scholar] [CrossRef]
- Edge, J.M.; Kedem, Y.; Aschauer, U.; Spaldin, N.A.; Balatsky, A.V. Quantum critical origin of the superconducting dome in SrTiO3. Phys. Rev. Lett. 2015, 115, 247002. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Beige, H.; Völkel, G. Precursor effects, broken local symmetry, and coexistence of order-disorder and displacive dynamics in perovskite ferroelectrics. Phys. Rev. B 2009, 79, 18411. [Google Scholar] [CrossRef]
- Egami, T.; Billinge, S.J.L. Underneath the Bragg Peaks. In Structural Analysis of Complex Materials; Pergamon Press: New York, NY, USA, 2012. [Google Scholar]
- Sato, K.; Miyanaga, T.; Ikeda, S.; Diop, D. XAFS Study of Local Structure Change in Perovskite Titanates. Physica Scripta 2005, T115, 359–361. [Google Scholar] [CrossRef]
- Hou, D.; Zhao, C.; Paterson, A.R.; Li, S.; Jones, J.L. Local structures of perovskite dielectrics and ferroelectrics via pair distribution function analyses. J. Eur. Ceramic Soc. 2017, 38, 971–987. [Google Scholar] [CrossRef]
- Bilz, H.; Benedek, G.; Bussmann-Holder, A. Theory of ferroelectricity: The polarizability model. Phys. Rev. B 1987, 35, 4840–4848. [Google Scholar] [CrossRef] [PubMed]
- Bussmann-Holder, A.; Büttner, H. Ferroelectricity in oxides. Nature 1992, 360, 541. [Google Scholar] [CrossRef]
- Bussmann-Holder, A. The polarizability model for ferroelectricity in perovskite oxides. J. Phys. Condens. Matter 2012, 24, 273202. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Roleder, K.; Ko, J.-H. What makes the difference in perovskite titanates? J. Phys. Chem. Solids 2018, 117, 148–157. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Keller, H.; Simon, A.; Bihlmayer, G.; Roleder, K.; Szot, K. Unconventional Co-Existence of Insulating Nano-Regions and Conducting Filaments in Reduced SrTiO3: Mode Softening, Local Piezoelectricity, and Metallicity. Crystals 2020, 10, 437. [Google Scholar] [CrossRef]
- Calvani, P.; Capizzi, M.; Donato, F.; Lupi, S.; Maselli, P.; Peschiaroli, D. Observation of a midinfrared band in SrTiO3-y. Phys. Rev. B 1993, 47, 8917–8922. [Google Scholar] [CrossRef]
- Waser, R.; Dittmann, R.; Staikov, G.; Szot, K. Redox-Based Resistive Switching Memories—Nanoionic Mechanisms, Prospects, and Challenges. Adv. Mater. 2009, 21, 2632–2663. [Google Scholar] [CrossRef]
- Wrana, D.; Rodenbücher, C.; Bełza, W.; Szot, K.; Krok, F. In situ study of redox processes on the surface of SrTiO3 single crystals. Appl. Surf. Sci. 2018, 432, 46–52. [Google Scholar] [CrossRef]
- Rodenbücher, C.; Menzel, S.; Wrana, D.; Gensch, T.; Korte, C.; Krok, F.; Szot, K. Current channeling along extended defects during electroreduction of SrTiO3. arXiv 2019, arXiv:1910.02748. [Google Scholar] [CrossRef] [PubMed]
- Szot, K.; Speier, W.; Bihlmayer, G.; Waser, R. Switching the electrical resistance of individual dislocations in single-crystalline SrTiO3. Nat. Mater. 2006, 5, 312–320. [Google Scholar] [CrossRef] [PubMed]
- Gao, P.; Yang, S.; Ishikawa, R.; Li, N.; Feng, B.; Kumamoto, A.; Shibata, N.; Yu, P.; Ikuhara, Y. Atomic-Scale Measurement of Flexoelectric Polarization at SrTiO3 Dislocations. Phys. Rev. Lett. 2018, 120, 267601. [Google Scholar] [CrossRef] [PubMed]
- Bussmann-Holder, A.; Keller, H.; Simon, A.; Bianconi, A. Multi-Band Superconductivity and the Steep Band/Flat Band Scenario. Condens. Matter 2019, 4, 91. [Google Scholar] [CrossRef]
- Cadwell, L.H.; Morris, R.C.; Moulton, W.G. Normal and superconducting properties of KxWO3. Phys. Rev. B 1981, 23, 2219–2223. [Google Scholar] [CrossRef]
- Wiseman, P.J.; Dickens, P.G. Neutron diffraction studies of cubic tungsten bronzes. J. Solid State Chem. 1976, 17, 91–100. [Google Scholar] [CrossRef]
- Brusetti, R.; Bordet, P.; Bossy, J.; Schober, H.; Eibl, S. Superconductivity in the tungsten bronze RbxWO3 (0.20 ≤ x ≤ 0.33) in connection with its structure, electronic density of states, and phonon density of states. Phys. Rev. B 2007, 76, 174511. [Google Scholar] [CrossRef]
- Lee, K.S.; Seo, D.K.; Whangbo, M.H. Electronic Band Structure Study of the Anomalous Electrical and Superconducting Properties of Hexagonal Alkali Tungsten Bronzes AxWO3 (A = K, Rb, Cs). J. Am. Chem. Soc. 1997, 119, 4043–4049. [Google Scholar] [CrossRef]
- Bousquet, E.; Hamdi, H.; Aguado-Puente, P.; Salje, E.K.H.; Artacho, E.; Ghosez, P. First-principles characterization of single-electron polaron in WO3. Phys. Rev. Res. 2020, 2, 012052. [Google Scholar] [CrossRef]
- Schirmer, O.F.; Salje, E. Conducting bi-polarons in low-temperature crystalline WO3-x. J. Phys. C 1980, 13, 1067–1072. [Google Scholar] [CrossRef]
- Schirmer, O.F.; Salje, E. The W5+ polaron in crystalline low temperature WO3 ESR and optical absorption. Solid State Commun. 1980, 33, 333–336. [Google Scholar] [CrossRef]
- Reich, S.; Tsabba, Y. Possible nucleation of a 2D superconducting phase on WO3 single crystals surface doped with Na+. Eur. Phys. J. B 1999, 1, 1–4. [Google Scholar] [CrossRef]
- Shengelaya, A.; Reich, S.; Tsabba, Y.; Müller, K.A. Electron spin resonance and magnetic susceptibility suggest superconductivity in Na doped WO3 samples. Eur. Phys. J. B 1999, 12, 13–15. [Google Scholar] [CrossRef]
- Shengelaya, A.; Conder, K.; Müller, K.A. Signatures of filamentary superconductivity up to 94 K in tungsten oxide WO2.9. J. Supercond. Nov. Magn. 2020, 33, 301–306. [Google Scholar] [CrossRef]
- Shengelaya, A.; Mattina, F.L.; Conder, K. Unconventional Transport Properties of Reduced Tungsten Oxide WO2.9. Condens. Matter 2020, 5, 63. [Google Scholar] [CrossRef]
- Salje, E.K.H. Polaronic States and Superconductivity in WO3-x. Condens. Matter 2020, 5, 32. [Google Scholar] [CrossRef]
- Kochelaev, B.I.; Safina, A.M.; Shengelaya, A.; Keller, H.; Müller, K.A.; Conder, K. Three-Spin-Polarons and Their Elastic Interaction in Cuprates. Mod. Phys. Lett. B 2003, 17, 415–421. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).