Isotope Effect in the Translation-Invariant Bipolaron Theory of High-Temperature Superconductivity
Abstract
1. Introduction
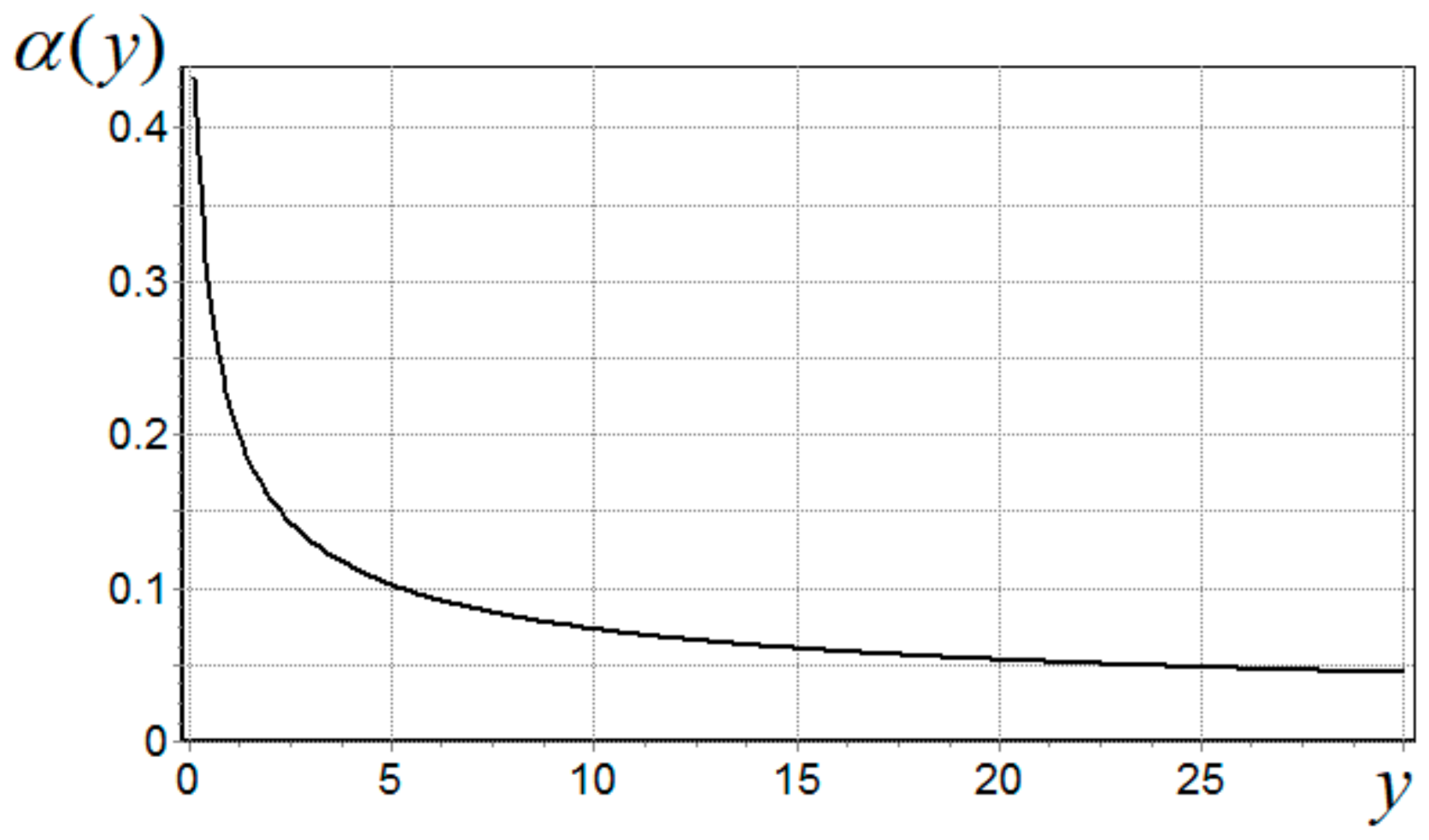
2. Isotope Influence on
3. Isotope Influence on London Penetration Depth
4. Discussion
Funding
Conflicts of Interest
Appendix A. Derivation of Formula (4)
Appendix B. The Criteria for D-Wave Phonon Input into Thermodynamic Properties of HTSC
References
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Bill, A.; Kresin, V.Z.; Wolf, S.A. The isotope Effect in Superconductors. In Pair Correlations in Many-Fermion Systems; Kresin, V.Z., Ed.; Plenum Press: New York, NY, USA, 1998. [Google Scholar]
- Lakhno, V.D. Superconducting Properties of 3D Low-Density Translation-Invariant Bipolaron Gas. Adv. Cond. Matt. Phys. 2018, 2018, 1380986. [Google Scholar] [CrossRef]
- Lakhno, V.D. Superconducting properties of a nonideal bipolaron gas. Phys. C Supercond. 2019, 561, 1–8. [Google Scholar] [CrossRef]
- Lakhno, V.D. Superconducting Properties of 3D Low-Density TI-Bipolaron Gas in Magnetic Field. Condens. Matter 2019, 4, 43. [Google Scholar] [CrossRef]
- Lakhno, V.D. Translational-Invariant Bipolarons and Superconductivity. Condens. Matter 2020, 5, 30. [Google Scholar] [CrossRef]
- Eliashberg, G.M. Interactions between Electrons and Lattice Vibrations in a Superconductor. Sov. Phys. JETP 1960, 11, 696–702. [Google Scholar]
- Chen, X.-J.; Liang, B.; Ulrich, C.; Lin, C.-T.; Struzhkin, V.V.; Wu, Z.; Hemley, R.J.; Mao, H.; Lin, H.-Q. Oxygen isotope effect in Bi2Sr2Can−1CunO2n+4+δ (n = 1,2,3) single crystals. Phys. Rev. B 2007, 76, 140502. [Google Scholar] [CrossRef]
- Franck, J.P. Experimental studies of the isotope effect in high temperature superconductors. In Physical Properties of High Temperature Superconductors IV; Ginsberg, D.M., Ed.; World Scientific: Singapore, 1994; p. 189. [Google Scholar] [CrossRef]
- Franck, J.; Jung, J.; Mohamed, M.A.-K.; Gygax, S.; Sproule, G.I. Observation of an oxygen isotope effect in superconducting (Y1−xPrx)Ba2Cu3O7−δ. Phys. Rev. B 1991, 44, 5318–5321. [Google Scholar] [CrossRef]
- Batlogg, B.; Kourouklis, G.A.; Weber, W.H.; Cava, R.J.; Jayaraman, A.; White, A.E.; Short, K.T.; Rupp, L.W.; Rietman, E.A. Nonzero isotope effect in La1.85Sr0.15CuO4. Phys. Rev. Lett. 1987, 59, 912–914. [Google Scholar] [CrossRef]
- Zech, D.; Keller, H.; Conder, K.; Kaldis, E.; Liarokapis, E.; Poulakis, N.; Müller, K.A. Site-selective oxygen isotope effect in optimally doped YBa2Cu3O6+x. Nature 1994, 371, 681–683. [Google Scholar] [CrossRef]
- Khasanov, R.; Eshchenko, D.G.; Luetkens, H.; Morenzoni, E.; Prokscha, T.; Suter, A.; Garifianov, N.; Mali, M.; Roos, J.; Conder, K.; et al. Direct Observation of the Oxygen Isotope Effect on the In-Plane Magnetic Field Penetration Depth in Optimally Doped YBa2Cu3O7−δ. Phys. Rev. Lett. 2004, 92, 057602. [Google Scholar] [CrossRef] [PubMed]
- Tallon, J.L.; Islam, R.S.; Storey, J.; Williams, G.V.M.; Cooper, J.R. Isotope Effect in the Superfluid Density of High-Temperature Superconducting Cuprates: Stripes, Pseudogap, and Impurities. Phys. Rev. Lett. 2005, 94, 237002. [Google Scholar] [CrossRef] [PubMed]
- Bill, A.; Kresin, V.Z.; Wolf, S.A. Isotope effect for the penetration depth in superconductors. Phys. Rev. B 1998, 57, 10814–10824. [Google Scholar] [CrossRef]
- Lakhno, V.D. Translation Invariant Bipolarons and Charge Density Waves in High-Temperature Superconductors. Keldysh Inst. Prepr. 2020, 57, 1–13. (In Russian) [Google Scholar] [CrossRef]
- Smilde, H.J.; Golubov, A.A.; Ariando Rijnders, G.; Dekkers, J.M.; Harkema, S.; Blank, D.H.; Rogalla, H.; Hilgenkamp, H. Admixtures to d-Wave Gap Symmetry in Untwinned YBa2Cu3O7 Superconducting Films Measured by Angle-Resolved Electron Tunneling. Phys. Rev. Lett. 2005, 95, 257001. [Google Scholar] [CrossRef]
- Kirtley, J.R.; Tsuei, C.C.; Ariando; Verwijs, C.J.M.; Harkema, S.; Hilgenkamp, H. Angle-resolved phase-sensitive determination of the in-plane gap symmetry in YBa2Cu3O7−δ. Nat. Phys. 2006, 2, 190–194. [Google Scholar] [CrossRef]
- Zhao, G.-M.; Hunt, M.; Conder, K.; Keller, H.; Müller, K. Oxygen isotope effects in the manganites and cuprates: Evidence for polaronic charge carriers. Phys. C Supercond. 1997, 282–287 (Pt 1), 202–205. [Google Scholar] [CrossRef]
- Božović, I.; He, X.; Wu, J.; Bollinger, A.T. Dependence of the critical temperature in overdoped copper oxides on superfluid density. Nature 2016, 536, 309–311. [Google Scholar] [CrossRef]
- Shengelaya, A.; Müller, K.A. Superconductivity in Oxides Generated by Percolating Electron or Hole Bipolarons. J. Supercond. Nov. Magn. 2019, 32, 3–6. [Google Scholar] [CrossRef]
- Müller, K.A. The Polaronic Basis for High-Temperature Superconductivity. J. Supercond. Nov. Magn. 2017, 30, 3007–3018. [Google Scholar] [CrossRef]
- Kochelaev, B.I.; Müller, K.A.; Shengelaya, A. Oxygen Isotope Effects on Tc Related to Polaronic Superconductivity in Underdoped Cuprates. J. Mod. Phys. 2014, 5, 473–476. [Google Scholar] [CrossRef]
- Müller, K.A. The Unique Properties of Superconductivity in Cuprates. J. Supercond. Nov. Magn. 2014, 27, 2163–2179. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Keller, H. Evidence for Polaron Formation in High-Temperature Superconducting Cuprates: Experiment and Theory. J. Supercond. Nov. Magn. 2009, 22, 123–129. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lakhno, V.D. Isotope Effect in the Translation-Invariant Bipolaron Theory of High-Temperature Superconductivity. Condens. Matter 2020, 5, 80. https://doi.org/10.3390/condmat5040080
Lakhno VD. Isotope Effect in the Translation-Invariant Bipolaron Theory of High-Temperature Superconductivity. Condensed Matter. 2020; 5(4):80. https://doi.org/10.3390/condmat5040080
Chicago/Turabian StyleLakhno, Victor D. 2020. "Isotope Effect in the Translation-Invariant Bipolaron Theory of High-Temperature Superconductivity" Condensed Matter 5, no. 4: 80. https://doi.org/10.3390/condmat5040080
APA StyleLakhno, V. D. (2020). Isotope Effect in the Translation-Invariant Bipolaron Theory of High-Temperature Superconductivity. Condensed Matter, 5(4), 80. https://doi.org/10.3390/condmat5040080




