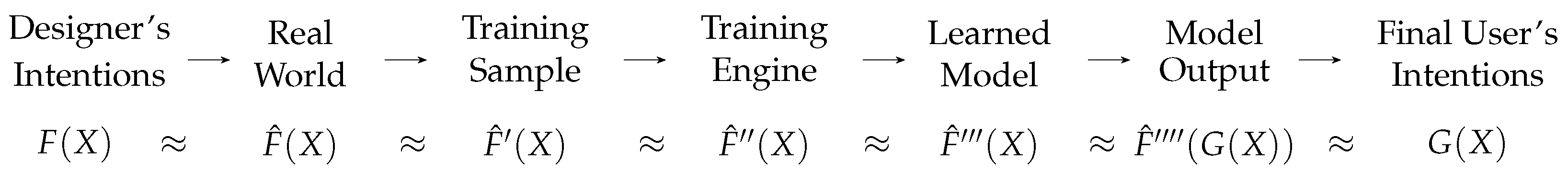A Philosophical Framework for Data-Driven Miscomputations

Abstract

This paper introduces a first approach to miscomputations for data-driven systems. First, we establish an ontology for data-driven learning systems and categorize various computational errors based on the Levels of Abstraction ontology. Next, we consider computational errors which are associated with users’ evaluation and requirements and consider the user level ontology, identifying two additional types of miscomputation.

1. Introduction

We have all wasted endless minutes waiting in vain for a web page to load; by now, we are so accustomed to this and other typical computational malfunctions that most of the time, almost automatically, we try to reload the blocked page or restart an application that does not respond to our commands. More rarely, we have to give in to their annoying presence and shut down the device, in the hope that a reboot will solve the problem and not end with a monochrome (black, blue, white, or gray) screen of death. As trivial as computational errors may seem in our everyday life, their existence is daunting for safety-critical systems (such as aircrafts, medical devices, etc.) and for the disciplines trying to address them, from philosophy and logic to theoretical computer science and software engineering.

From a philosophical point of view, the notion of miscomputation has been a central aspect of the Levels of Abstraction (LoAs) approach by [1], a fine-grained onto-epistemic account of computational artifacts, explicitly introducing a rigid normative structure with a top-down direction of governance from the specification to the rest of the system. However, this fixed direction seems limited in accounting for systems whose criteria of correctness are markedly dynamic, e.g., shift between multiple agents, feedback from the output, or possibly involve non-deterministic outputs. While the LoA ontology can still help us formulate a taxonomy of errors for data-driven systems, a User Level (UL) ontology [2] may offer a tool for analyzing and representing contexts in which the normative and semantic instances of different users (human or otherwise) can compete and possibly conflict. The latter also oversteps the standard qualification of the correct uses of computational artifacts, providing a taxonomy of the phenomena occurring in the unexplored limbo that extends between correctness and incorrectness.

In this paper, we intend to provide a first framework for understanding miscomputations in data-driven systems. We first offer a layered ontology of such computational artifacts which allows us to explore the issue of miscomputations from the LoA perspective. Next, we explore our understanding of implementation and specification from a pragmatic point of view, to extend the analysis from a UL perspective. This interpretation leads to the definition of two additional types of miscomputation.

This paper is structured as follows: Section 2 starts with an overview of contemporary philosophical accounts of miscomputation, ranging from the standard LoA approach to its recent pragmatic UL extension; Section 3 presents a series of non-standard cases from data-driven computational systems, and in particular generative artificial intelligence (genAI), that existing accounts struggle to categorize; Section 4 provides an ontological framework for machine learning (ML) systems and a detailed taxonomy for data-driven miscomputation on the basis of the LoA theory; in Section 5, this framework is complemented with a pragmatic perspective, offering a less rigid notion of correctness which forms a continuum with fairness and suggesting two types of ML miscomputation. We conclude with some indications for future research.

2. Miscomputation: The State of the Art

In the last two decades, the philosophical debate around computational errors has newly emerged after a short burst in the 1980s and 1990s centered around the methodological validity of formal verification [3,4,5]. The basis of this fresh interest in miscomputations in the philosophical arena has been the definition of an ontology of computational artifacts based on Floridi’s method of Levels of Abstraction (LoAs) [6]. Refs. [1,7] systematized the normative intuitions of earlier papers on this structure: each LoA identifies a pair consisting of an ontological domain and an epistemological construct that acts as a linguistic control device over the former. Every LoA is said to implement the LoA above, by acting as an ontological domain for the latter, and simultaneously is said to abstract the LoA below by expressing its epistemological control device ([7], pp. 174–175). The normative supremacy of the specification expressed by the layered notion of correctness ([7], pp. 194–195) is stressed by a layered definition of information [1], in which truthfulness, meaningfulness, and well-formedness are rigidly associated with specific LoAs. At the highest LoA, the architect’s intention acts as an epistemological control device on the problem at which it is aimed. Such intentional informational content is abstract and semantically loaded and determines the truth for the level below, in which it is realized in the form of an algorithm. The latter, besides satisfying the original intention, also fulfills a task in which the corresponding problem is reflected. At this level, abstract information is characterized by correct syntax and meaningfulness; it is correct in view of the intention; and it is truth-determining for the instructions associated with the programming language at the LoA below. This instructional information must have correct syntax and must be meaningful and becomes correct in view of the algorithm; however, being alethically neutral, it can only denote the operations performed by machine code at the lower level. Here, the operational information has correct syntax but not semantics, nor alethic value. It controls the structured physical data of the lowest LoA, in which the electrical charges realize actions.

Correctness requires matching across all of these levels. On this basis, ref. [8] proposed a taxonomy of computational errors that refines Turing’s distinction between errors of functioning and errors of conclusion [9], which refer, respectively, to failures in the physical execution of a program and failures in its design. Their miscomputation taxonomy includes mistakes, failures, slips, and operational malfunctions. Mistakes are conceptual errors occurring at the Functional Specification Level (FSL), at the Design Specification Level (DSL), at the Algorithm Design Level (ADL), and/or at the Algorithm Implementation Level (AIL) due to miscomprehension and misinterpretation between the agents responsible for different levels, e.g., the system designer’s interpretation of the architect’s intention or the engineer’s interpretation and translation of the system’s design. Failures are material errors that occur at the DSL, ADL, and AIL, e.g., when the requirements are wrongly formulated in the specification or when the latter is poorly implemented in an algorithm. Slips are syntactic and/or semantic errors occurring at the AIL: they are the least interesting errors for our purposes since in contemporary Software Development Kits (SDKs), they are checked (and hopefully corrected) during the coding or compilation phase and hence prevented from manifesting as proper errors. Lastly, operational malfunctions are runtime errors due to hardware failures.

If we exclude slips as philosophically less interesting, in the above taxonomy, miscomputation can be caused only by design errors or hardware failures, recalling again Turing’s distinction and then identifying an emergent normative structure which improves the classic theories of correctness and in which the specification dictates the behavior of the entire artifact. On this same basis, the work by [10] distinguishes between two kinds of malfunctions: the dysfunction (or negative malfunction) that occurs when an artifact does less than what it is supposed to do and misfunction (or positive malfunction), when it does more. The authors’ conclusion (to some extent, counterintuitive) is that software tokens can neither dysfunction nor misfunction since any malfunctioning is due to design errors or hardware failures. Hence, software results in a very peculiar kind of type of artifact whose tokens cannot malfunction. This underlines and reinforces the normative role of the specification with respect to other LoAs.

Recently, Ref. [11] questioned this conclusion, claiming that in light of the complexity of the contemporary landscape of software engineering, the presuppositions of complete control and self-containedness for software engineering practices, on which the above account is based, are no longer valid. In particular, they rely on a series of practical examples to show that many agential activities are involved in the development and execution of software; hence, under the aforementioned presuppositions, the LoA-based theory wrongly attributes too many responsibilities to software engineers. These initial assumptions are agreeable, and the theory of malfunction in [10] represents a strong position that requires appropriate framing in view of the role of agents. This is, however, not as straightforward as in [11].

While the attempt of [11] is to reduce the burden of responsibility on the software engineer, their approach ends up placing some of that responsibility on the shoulders of yet other software engineers (see, for example, their interpretation of the EVE Online bug, which ends up blaming Windows software engineers for not denying problematic file deletion requests ([11], p. 11)), possibly suggesting that giving up the self-containedness and complete control assumptions is not enough.

Starting from roughly the same philosophical worries as those of [11] in [2], another and more fundamental assumption of the LoA theory has been challenged, namely its rigid normative structure. The LoA-based account has been hence complemented with a pragmatic framework called the User Level (UL) theory. According to the UL account, computing is not to be considered an individual activity but rather a sequence of computational acts, akin to collective speech acts [12,13], with locutory, illocutory, and perlocutory parts embedded into the informational content of the different users involved. The specification loses its normative supremacy, to become the collector of all of the semantic and normative instances of all ULs, from the designer’s intentions to the idiosyncratic uses of end users, including programmers, designers, operating systems, compilers, applications, policy makers, and owners. From this plurality follows the failure of self-containedness and complete control, as discussed by [11].

According to the standard LoA account, a computational system is correct (or is functioning well) if and only if it is functionally, procedurally, and executionally correct, i.e., if it displays all and only the functionalities included in the specification with the intended efficiency; it correctly displays all and only the functionalities as intended by the algorithm; and it runs with no errors on the hardware on which it is installed [7]. Complementing this view, Ref. [2] points out that this account is highly theoretical and is ill equipped for the complexity of contemporary information technologies. The corresponding notion of pragmatic correctness is qualified as the convergence of all of the modes and requests of use of the artifact expressed at the different ULs ([2], p. 26). The two following examples will show how the standard LoA account of miscomputation fails in some interesting cases.

2.1. Excel Pixel Art

In 2000, Tatsuo Horiuchi retired and decided to devote himself to painting. He did not want to spend money on brushes, paints, and canvases, and he did not want to spend a lot of time cleaning up. So, he opted for digital painting, but he did not want to spend money on expensive graphics programs either. Then, he decided to use the programs pre-installed on his Windows computer, but he found Paint to be unintuitive and not user-friendly. Instead, he found the perfect instruments to create amazing digital art by means of Excel’s line tool (to draw shapes) and bucket tool (to fill such shapes with color and gradients), raising Excel art, which until then had just been pixel art created using cells, to a new level.

2.2. Malicious Software

During the same year, Onel de Guzman was a talented but poor 23-year-old student from the Pandacan district of Manila, besides being an activist devoted to the fight for the right to Internet access. Since he could not afford the cost of an Internet connection, he decided to create a password-stealing Macro virus written and compiled in Visual Basic, disguised as a common text file named LOVE-LETTER-FOR-YOU.TXT, and to attach it to an email with the subject “ILOVEYOU” containing the following text: “Kindly check the attached LOVELETTER coming from me.”. The virus was able to replicate itself, replacing Windows library files and other random files in the infected system; to resend itself to all of the addresses in Outlook’s address book; and (obviously) to steal passwords.

According to the LoA theory, both cases are cashed out as misfunctional uses of computational systems (incorrect uses with side effects) since their outputs are neither included in nor foreseen by the specification. In particular, both cases are included in the category of conceptual failures: the ILOVEYOU Trojan is a case of the selection of bad rules, while Excel art is a case of misformulation of good rules [14].

Nonetheless, there seems to be a straightforward difference between these two examples in terms of what these computational acts produced in the world that the LoA theory does not capture: while Onel de Guzman was charged by Philippines state prosecutors for the (in)famous Love Bug which affected 10% of Internet-connected computers, Tatsuo Horiuchi is now a well-known 80-year-old digital artist whose technique was promoted by Excel developers with the release of an improved set of drawing tools. At a more philosophical level, the Excel example is a virtuous use of a highly limited tool (spreadsheet line and bucket tools), while the virus example above can be seen as the malicious use of a very powerful tool (macros).

Developed on the basis of the ICE theory of function by [15], the UL theory vindicates the conceptual difference between these two examples by putting the focus on the sequence of computational acts triggered by the initial idiosyncratic uses of Excel and macros, respectively. Initially, these uses were neither included nor explicitly excluded by the original designer’s specification or any other UL. As idiosyncratic uses similar to the initial ones became more widespread, both cases evolved to the stage of innovative use: on the one hand, Excel art has never been so popular; on the other hand, more than 25 variants of ILOVEYOU were created and sent across the Internet. Then, they both evolved to the expert redesigning stage, when expert digital artists started to develop new techniques for creating art using spreadsheets and when new improved variations of Love Bug were developed by black hat developers and social engineers. The last stage of the array of uses, i.e., product design, is reached when the idiosyncratic use is accepted as part of the specification or is rejected as not correct and hence the specification is modified in order to prevent it. In both cases, a new version of the computational artifact is released by the original designer: in the first one, including new improved drawing tools and promoting their use and, in the second one, preventing by default the execution of any macro downloaded from the Internet and suggesting not to use them. The specification thus temporarily regains its normative role over the system, until the next idiosyncratic use, in an endless iteration of the same process sequence (see Figure 1).

This analysis offers the basis for identifying miscomputations from a pragmatic point of view:

Definition 1.

A physical artifact displays a pragmatic miscomputation when it allows the execution of a functionality which results from an idiosyncratic use that is explicitly disallowed by the specification.

In other words, a use that is not foreseen by the specification does not immediately count as a miscomputation. In fact, it might be seen as an idiosyncratic or innovative use, eventually resulting in an expert redesign of the artifact’s specification itself. In contrast, only uses that are explicitly forbidden by the specification qualify as miscomputations.

3. The Problem of Correctness for Data-Driven Systems

While our discussion has so far been limited to traditional computational artifacts, we now turn to the more complex case of data-driven computational systems—that include machine learning (ML) algorithms, as well as generative artificial intelligence (genAI)—to identify a novel categorization of their miscomputations. Note that we group ML and genAI technologies under the common label of data-driven computation here. While the underlying ontology of these technologies associates important structural properties with the models, e.g., the number of parameters and hyperparameters, we identify their non-deterministic behavior and associated miscomputations as essentially dependent on training.

To understand why the traditional LoA taxonomy recalled in Section 1 is not adequate anymore when it comes to data-driven artifacts, we might consider the case of an ML face recognition system that wrongly identifies somebody who is male with feminine traits as female and compare it to the opposite scenario in which the same recognition system correctly identifies him as male. Assuming that the intended function of the algorithm (its Functional Specification Level in LoA terms) is to classify faces based on their gender traits, in the former case, the system gets it right. Nonetheless, this causes incorrect predictions for certain data points—especially outliers like the one under consideration—with potentially negative societal impacts for certain minorities (e.g., for transgender men for the case considered) (for an analysis of this kind, see [16]). The latter scenario instead seems to be precisely the opposite: the data point is predicted correctly, although this seems to be hardly justified in terms of the training data the model was exposed to.

This example just intuitively shows that in ML systems, functional correctness does not imply the absence of incorrect outputs, and vice versa. On a broader scale, this consideration finds resonance with the Rashomon Effect [17], according to which given a dataset, many models might achieve an equivalent test performance yet produce contradictory predictions for single data points (a phenomenon also known as predictive multiplicity [18]).

Or consider the case of text-to-image generators, which typically output at least two different results for the same user prompt, as in Figure 2. Hence, what about non-deterministic data-driven miscomputation? How is it possible to establish correctness for a system that generates multiple alternative outputs starting from the same input? And more fundamentally, what does miscomputation mean for a non-deterministic system? An LoA-based account of correctness, while efficient in its standard understanding of computational errors for deterministic and well-specified software, seems to remain limited in accounting for these new and less straightforward cases. In this case, a pragmatic approach which includes the requirements of the users seems more apt.

In the next two sections, we explore the notion of computational error from the point of view of LoA and UL theory, respectively. The former approach can be seen as system-oriented, and it allows us to identify miscomputations as they arise at specific levels of the ontological structure underlying data-driven systems. The latter focuses on the (artificial and human) agents interacting with(in) the system, and it allows us to identify two additional forms of miscomputation.

4. An LoA Taxonomy of Errors for Data-Driven Systems

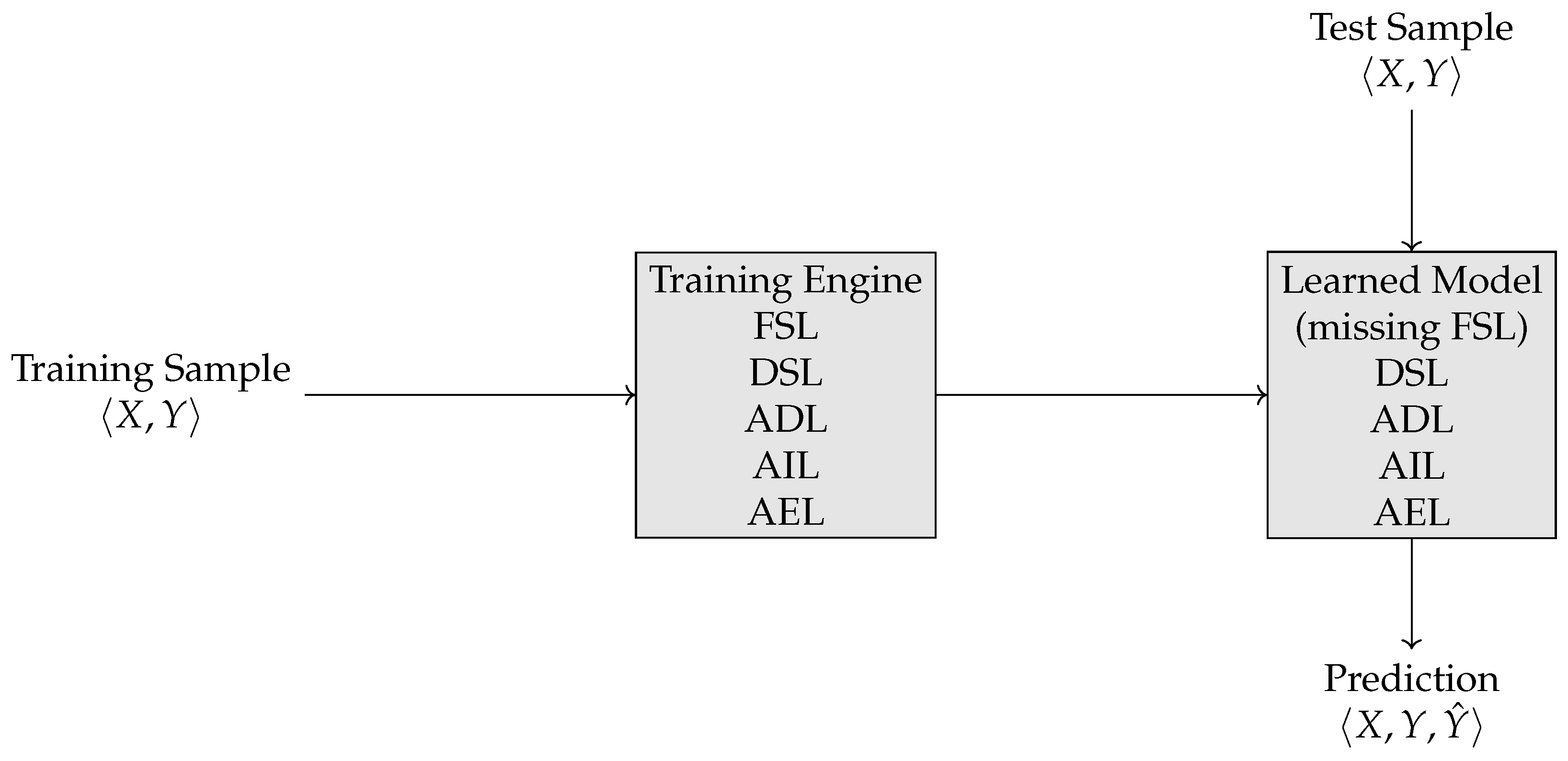
The ongoing paradigm shift from the methodology of manual coding to that of curing, which refers to the set of increasingly sophisticated techniques for pre-processing data in the context of data-driven technologies [19], is indicative of the pivotal role played by training data in determining the behavior of an ML model. In fact, it is during the training phase that the functionality of the model emerges from the training data, as if training itself could be seen as an automatic version of the traditional techniques of requirement elicitation. From the LoA perspective, data curing seems to suggest that ML models inherently lack a proper Functional Specification Level, as their specification is the output of an algorithmic process, i.e., the execution of the training engine on the training sample. Therefore, we argue, the ML model should not be considered in isolation but always associated with the training process through which its functionality was found. In other words, what we ought to consider is not an ML model but an ML system, as composed of three distinct, though functionally integrated, components [20] (see Figure 3):

• The training sample: The set of inputs used to train the ML model;
• The training engine: The computational process that allows the ML model to learn from data during the training process;
• The learned model: The resulting ML model obtained by running the training engine on a specific training sample.

Figure 3. The training sample, the test sample, and the prediction are data artifacts. The training engine and the learned model are, instead, computational artifacts. The training sample, training engine, and learned model together constitute an ML system.

Figure 3. The training sample, the test sample, and the prediction are data artifacts. The training engine and the learned model are, instead, computational artifacts. The training sample, training engine, and learned model together constitute an ML system.

Note that the three components are artifacts themselves: the training sample is a data artifact; the training engine is a traditional (non-data-driven) computational artifact; and the third is a computational artifact with no FSL. Accordingly, the traditional error taxonomy is revised in two distinct ways. In fact, any type of error occurring in the training sample and the training engine can be re-categorized as an error of design for the ML system (as discussed in Section 4.1). On the other hand, once training is over, the ML system shows two additional types of error that were not accounted for in the traditional taxonomy of miscomputations: errors of prediction (see Section 4.2) and errors of justification (see Section 4.3).

Table 1. The three basic components of a data-driven system, alongside their associated malfunctions: design, prediction, and justification errors.

Component	Description	ML Miscomputation
Training Sample	data artifact	design error
Training Engine	traditional computational artifact	design error
Learned Model	computational artifact with no FSL	justification error prediction error

summarizes the basic error mapping illustrated in the remainder of this section.

4.1. Errors of Design

In the context of traditional computational artifacts, errors of design refer to incorrect coupling between the function intended by the designer and the specification actually implemented by the system. The notion of design error was refined in [8]; when considering the Design Specification Level, a mistake in the form of a conceptual error corresponds to an inconsistent design, while a failure in the form of a material error corresponds to an incomplete design. However, when it comes to ML systems, any malfunctioning occurring at the level of the training engine or at the level of the training sample impacts the functionality of the resulting learned model and can therefore be seen as an error of design for the ML system. For both the training engine and the training sample, we hence distinguish between mistakes and failures.

Starting from the training engine, one important consideration is that this artifact specifies all of the hyperparameters, i.e., the technical details of the training process: the learning rate, the batch size, the loss function, the number of epochs, etc. Hence, hyperparameter choices may be considered erroneous to the extent that they are either inconsistent (mistakes) or incomplete (failures). Here, a mistake may occur when, for instance, the optimization method is not consistent with the loss function chosen: pairing a binary cross-entropy loss function with ReLU activation in the output layer violates the assumptions of the loss function and leads to undefined or misleading gradients. In contrast, a failure may occur when a critical hyperparameter is omitted. As an example, failing to specify a batch size in a deep learning pipeline can result in the use of an undesired default or incompatible value, ultimately causing runtime errors straight away or suboptimal training.

Coming to the training sample, data errors can be classified along a number of different data quality dimensions. Similarly to the distinction just made for hyperparameters, we can conceptually distinguish between inconsistent and incomplete data, respectively, corresponding to data mistakes and data failures. Recalling the discussion on data curing by [19], we notice that the process of data preparation (data cleaning, integration, resampling, etc.) constitutes a potential source of errors of both kinds. Furthermore, the training sample itself is frequently the result of an automated process known as feature learning. For instance, within the context of Natural Language Processing, feature learning involves the training of an additional ML model to embed lexical items as vectors such that lexically similar items are situated in close proximity within the vectorial space, while those that are dissimilar are positioned significantly further apart. In this scenario, an error within a training sample derived through feature embedding would simultaneously count as a design error, in relation to the training of the ML system, as well as a prediction error, in relation to the embedding methodology.

4.2. Errors of Prediction

Given an input, a prediction error occurs whenever a mismatch between the predicted label and its true value (ground truth) exists. The first obvious observation is that prediction errors are inevitable for ML systems. As the No Free Lunch Theorem [21] demonstrates, all supervised classification algorithms have the same test performance (i.e., accuracy, precision, and recall calculated on new inputs) when averaged over all possible datasets. This implies that while a model might exhibit a satisfactory performance on specific data points, it will inevitably demonstrate a suboptimal performance on others.

A first reason for this mismatch is given by the fact that unlike in traditional settings, in ML contexts, the model is learned from examples rather than manually coded. Hence, what is learned is an approximation of the target function, inferred on the available examples within the constraints imposed by the hyperparameters (see the previous subsection). Put differently, the ML system does not learn the target function $F\left(X\right)$ but a suitable approximation $\widehat{F}\left(X\right)$ thereof.

A second and more fundamental source of prediction error in ML systems arises from the inherent difference between the predicted and true labels, known as the irreducible minimum error, or the Bayes error [22]. In fact, $Y=F\left(X\right)+ϵ$, where the Bayes error $ϵ$, an independent random noise term, represents the influence of all sorts of unobservable factors on Y. Therefore, it is the lowest possible classification error achievable by any classifier, under the assumption that we know the true probability distribution of the data.

Just to exemplify the significance of predictive errors in today’s ML-based scientific practice, we can briefly touch upon the notion of adversarial examples. This refers to unusual input data that cause deep neural networks to output verdicts that look to humans like very bizarre prediction errors. For instance, in the widely cited study by [23], small, imperceptible perturbations were added to images that caused a well-performing image classification model to misclassify a panda as a gibbon with high confidence. Adversarial examples represent a paradigmatic type of “strange” ML prediction errors—to use the terminology of [24]—whose occurrence and content are substantially impossible to foresee. Adversarial examples are not only carefully crafted inputs that are intentionally designed to deceive machine learning models into making incorrect predictions. Rather, they naturally occur in datasets, like image datasets where textures, patterns, colors, and light conditions thereof can fool the ML system in the most bizarre ways. According to Alvarado [25], such unpredictability should count as a serious obstacle to securing a sufficient level of reliability for ML systems in science.

4.3. Errors of Justification

The training process might induce correlations in the model that, while not necessarily detrimental to the performance, are undesirable for some other reasons, like epistemological ones. The ML system might, for instance, return the right prediction for a data point but for the wrong reasons. We hence take these widespread kinds of ML malfunctions to be errors at the level of justification.

An illustrative instance of a justification error was presented in [26], where a classification algorithm was trained to classify images of wolves and dogs. Contingently, in the training dataset, wolves were often portrayed against a snowy background. Using an explainability technique called LIME, the authors showed that the resulting ML system had learned to classify new input pictures based on the color on the background, deeply questioning the trustworthiness of the system. Even if the classifier contingently performed well, in fact, one would still want to claim that an error had occurred in virtue of what justified such predictions.

The problem of misjustified ML predictions has particular import in the context of science, where we want well-defined epistemic guarantees to hold. Here, we limit ourselves to a brief discussion on the role of AI in the process of scientific discovery, starting with an example taken from computational chemistry.

In the case of molecular design, AI systems can achieve previously unthinkable results in terms of the speed of discovery and the efficiency of the result. On the basis of in-depth prior knowledge of the process and the vast amount of available previous data, ML systems can “generate a new chemical entity from data observations of past reactions to produce an ideal catalyst to solve a chemistry reaction problem” ([27], p. 8). In contrast with the wolf/dog classifier mentioned above, the prediction is justified this time by the “substantial amount of [previous] raw data from previous reaction routes” ([27], p. 8). According to the same author, this could even allow “the creative part of this process [of formulating a chemical hypothesis] to be progressively aided by a procedural logic” ([27], p. 13). However, to concede this, we should first examine what we mean by scientific creativity, whether there are different types thereof, and how these relate to scientific discoveries on the one hand and computational systems on the other.

Ref. [28] offers a simple and exhaustive taxonomy that distinguishes between three types of creativity in a broad sense (encompassing the artistic sphere) which are defined as “combinational”, “exploratory”, and “transformational”.

“The first type involves novel (improbable) combinations of familiar ideas. [The second] involves the generation of novel ideas by the exploration of structured conceptual spaces. This often results in structures (“ideas”) that are not only novel, but unexpected. [The third] involves the transformation of some (one or more) dimension of the space, so that new structures can be generated which could not have arisen before. The more fundamental the dimension concerned, and the more powerful the transformation, the more surprising the new ideas will be”.

([28], p. 348)

How these categories relate to the process of artistic creation is easily deducible. Consider the case of painting: combinational creativity is involved when we move within the same artistic style, such as the Flemish style or the Michelangelo school; exploratory creativity occurs when a new and unexpected figurative painting style is created, as in the case of the Impressionist school or Surrealism. The abandonment of the figurative form typical of abstract painting can instead be considered a form of transformational creativity.

With respect to the creation of new scientific knowledge, this taxonomy can be exemplified as follows: the abovementioned molecular design example can be placed at the first level of the taxonomy; research on mRNA vaccines, which began in the late 1980s, provides an excellent example of exploratory creativity; regarding the last level of creativity, we need to go back in time to the epochal discoveries that led to substantial paradigm shifts, such as the concept of quantum introduced by Max Planck, Albert Einstein’s theories of relativity, and Niels Bohr’s atomic model.

This taxonomy has already been used to evaluate the artistic capabilities of computational systems, both classical and data-driven: generative AI systems are primarily combinatorial systems, so the first level of creativity is assured. Exploratory and transformational creativity “shades into one another” ([28], p. 348), and ML systems have been shown to be able to express not only the former but also the latter, thanks to the introduction and manipulation of random values (e.g., temperature) capable of creating new and unexpected results.

Even though chance can create new and pleasant artistic forms, it would be dangerous to rely on randomness when dealing with scientific discovery. Using randomness to create new scientific knowledge obliterates the possibility of providing a justification based on the most probable statistical distribution: the more randomness we introduce to scale the hierarchical levels of creativity, the less likely we are to find a rationale for the results obtained. In other words, ML systems could provide scientifically reliable results only in the combinational setting, thanks to their brute force.

Even in these cases, the risk of falling into the temptations of pseudoscience is very high. Statistical systems, by their very nature, lend themselves to favoring homogeneous results and consequently to being vulnerable, on the one hand, to the risk of discrimination against outliers or minorities and, on the other, to the risk of dystopian Lombrosian research tendencies that excite eugenicists (see [29] for a widely criticized example). In these and other cases (such as credit scoring, recruitment, access to public services, etc.), the laws of statistics can serve as scientific justification for unfair results and unjust policies.

To conclude, the risk arising from the statistical nature of AI systems must be seriously taken into account, and particular attention must be paid to the even greater risks of using this type of technology to generate scientific theories that draw on forms of exploratory and transformational creativity.

5. A Pragmatic Approach to Data-Driven Miscomputation

The previous section has served the purpose of illustrating how a taxonomy of classical miscomputations can be extended to errors in data-driven systems. From a pragmatic point of view, the above schema is still limited: it offers a static snapshot, but it does not represent the inherently dynamic and evolutionary nature of data-driven computation since continuous training and optimization are key factors for any ML system. Furthermore, an LoA-based account still risks placing too much responsibility on those in charge of model development and training, as noted by [11] for software engineers. In contrast, the UL theory seems more able to capture the way normativity and responsibility flow back and forth among the different agents training, testing, validating, and using the AI system. This analysis is offered in the present section.

5.1. Miscomputation Chains

Consider again the three components of ML systems as identified in the previous section: the training sample, the training engine, and the learned model. As mentioned in Section 4, according to the LoA account, they are considered three distinct and different artifacts: the first is a data artifact; the second is a standard computational artifact; the third is a traditional computational artifact but without the FSL. In the UL framework, they are considered three different ULs (the training sample UL, the training engine UL, and the learning/learned model UL), constituting one computational system, together with the designer UL above them and the final user level (i.e., the level at which the model outcome comes to fruition for some agent) as the lower level. Recall from Section 2 that the UL ontology is characterized by different types of use, from idiosyncratic to innovative and expert redesign. We now want to explore the application of this framework to the ontology of ML systems.

For the sake of simplicity, let us start by applying this structure to the simple case of a multilayer perceptron (MLP) to exemplify the general behavior of an ML system, although it can easily be extended to more complex systems. At the very beginning of its life, when weights and biases (by bias, here, we mean the mathematical correction of the activation function in neural networks, not algorithmic prejudice intended to systemically discriminate against particular groups or individuals) are randomly distributed across the network, any input of the training sample UL will result in an idiosyncratic output in the model output UL since it is very unlikely that the system will perform with the intended accuracy, precision, specificity, and sensitivity. During the training, e.g., by means of backpropagation in supervised learning, idiosyncratic outcomes start to converge towards similar results, and innovative outcomes will start to emerge in the model output UL, whereas the performance of the system improves with the adjustment of weights and biases dictated by the minimization of the cost function. In hyperparameter tuning, the learning model UL and the training engine UL are involved in determining the optimal combination of, e.g., the number of hidden layers, the number of neurons for each layer, and the number of training epochs, by means of gridsearch and/or randomsearch algorithms, in a proper expert redesigning intervention from higher ULs (as the prefix hyper suggests).

This process has many similarities with the agile development methodology, as described in ([2], p. 7), as “the result of a dialogue between parties […] in a context of continuous communication and collaboration between the [ULs] involved in the process”. When the system satisfactorily approximates the performance intended by the designer UL, the phase of product design is reached, and the entire process can be reiterated, e.g., by means of final user UL feedback in reinforcement learning, again and again. Idiosyncratic and innovative outcomes, even if rejected as unsatisfactory, should be considered necessary constituents of the system for improving and evolving. These remarks illustrate an essential new aspect of a theory of computational artifacts which no longer assigns normative control over the behavior of the entire system to the specification alone. Once each user level is charged with at least some epistemic authority on the direction of governance of the system, the possibilities of conflicting and erroneous behavior multiply accordingly. The notion of idiosyncratic use illustrated in the examples from Section 2 explains this situation to some extent: a use deviating from the norm may emerge at each UL. The task of quantifying this deviation and accordingly measuring the possibility that the deviation may become normal again must be expressed properly in formal terms; see [30]. The associated conceptual issue of determining and quantifying responsibility is also in line with the present research topic, while it clearly deserves its own space. In the present context, we are interested in a preliminary definitional question: what does it mean for an ML system to satisfactorily approximate the intended performance? Or in other words, in which cases can we talk about data-driven miscomputation?

One answer is given by checking whether the distance between the outcome distribution and a reference correct distribution stands below a certain threshold (this is the strategy followed by the probabilistic typed natural deduction calculus TPTND [31,32,33] and its derivatives [34], grounding the algorithmic bias detection tool BRIO [35], which has already been used to account for risk in credit scoring [36]). But what is the reference that we should aim at? In classifiers like the ML face recognition system in Section 3, the reference distribution is variously identified. Recall the two erroneous behaviors mentioned: the case in which the system correctly labels someone who is male with female traits, despite these traits being more correlated with the female label, can be interpreted as a miscomputation due to the difference between the model’s outcome and the training sample, intended as a reference; the case in which the system wrongly identifies the same individual as female can instead be considered a miscomputation due to the distance between the training sample, e.g., containing only pictures of men with masculine traits and women with feminine traits, and the ground truth embedded in the real world, i.e., the presence of males with feminine traits, and, respectively, of females with masculine traits.

But in more complex systems, such as the case of the images generated in Figure 2, and leaving aside the more technical aspects (the embedding of the prompt into a semantic space and its conversion into an image by means of reverse diffusion), one should additionally consider as a reference how much the model’s output, i.e., the two images generated by the system, approximates the text prompt, i.e., the final user’s intentions. This shows that such systems have multiple ULs to consider.

Starting from a real-world distribution, data-driven miscomputations can spread across all of the ULs, involving the training sample UL, the training engine UL, the learning/learned model UL, and the final user UL, and at each link of this chain, the miscomputation can be amplified, i.e., the distance between the considered distribution and the reference distribution can increase. The intended function $F\left(X\right)$ is approximated by the function $\widehat{F}\left(X\right)$ representing the ground truth distribution in the real world, which in turn is approximated by the function $\widehat{F}\prime \left(X\right)$ corresponding to the training sample distribution, and so on (see Figure 4). At each step, the random error $ϵ$, representing all of the unmeasured and even unmeasurable variables, can increase, possibly also increasing the distance between the predicted feature Y and the reference distribution further.

In cases in which the ground truth embedded into the real-world distribution does not agree with the designer’s intentions, this chain can also be extended back to include the ideal reference distribution, as intended by the designer UL. Under this assumption, correctness is replaced by trustworthiness—when can we trust the results of a given computational system?—and fairness—which output do we consider fair with respect to some distribution of properties of the population of interest? The phenomenon whereby ML systems yield results that are skewed, partial, or inequitable in relation to certain groups or individuals is termed algorithmic bias. This issue has been extensively examined through statistical methodologies aiming to detect prejudices within machine learning systems and mitigate their impact.

5.2. Between Correctness and Fairness

First, it is worth noting that such a pragmatic approach stresses the human-in-the-loop perspective, in which the designer’s and the final user’s intentions, reflected in their modes and requests of use of the ML artifact, have to cohere and converge, as with all other UL modes and requests of use (e.g., the training sample UL, the training engine UL, and the learned model UL) (real-world scenarios may involve a larger number of ULs, e.g., the data-labeler UL, the data-sampler UL, etc., especially in the case of genAI, in which several systems can be combined to produce a complex result, e.g., in the generation of images, a Large Language Model (LLM) is usually paired with a reverse diffusion algorithm; however, the following analysis is limited to a smaller number of levels in order to avoid useless complications, but it is designed to be extended ad libitum), in order to result in a correct computation (see the definition of a pragmatically correct computational artifact in Section 2).

Secondly, we usually find ourselves having to choose a trade-off between correctness and fairness: for example, consider the case of a credit scoring system which always rejects requests for loans from everyone. Although it would intuitively be considered fair, since it treats everybody in the same exact way, everyone will agree on considering its predictions to be largely incorrect (and on deeming the system completely useless, of course). Or consider the case of a home insurance system correctly suggesting higher prices for people living in highly risky environments; it cannot be considered fair since it will systematically disadvantage those living close to a volcano, but to some degree, it will be considered correct. This phenomenon is well known [37,38,39] and has been analyzed from several points of view [40,41].

As noted above for miscomputation, bias can also be propagated and amplified at each UL, creating Bias Amplification Chains (BACs) [42], involving the entire ML life cycle [43]. Bias and prejudices present in real-world societies can be replicated and amplified in training datasets because of inaccurate collection, sampling, and captioning of the data [44]; the parameters, hyperparameters, and other technical factors (the model’s accuracy, capacity, or overconfidence, the amount of training data) can modify and amplify algorithmic bias further in the process of training a model [45]; when considering interactions with active human users, such as in the case of text prompts for generative AI, all of the biases collected across the chain can be amplified because of syntactical and semantical differences between training image captions and user prompts [46]; and lastly, the usual infra-marginal and context-unaware automatic mitigation processes can increase prejudicial results further [44]. This last link can transform the bias amplification chain into a loop, resulting in feedback that leads to results that are as dangerous as they are funny.

Consider the simple test results in Figure 5: when using as a text prompt “A person holding a spoon” or “A person holding a fork”, Microsoft Bing Image Creator gives us pretty accurate, photorealistic, and unbiased images, in which gender and race are fairly distributed, and even left-handed people are accurately represented with respect to their distribution in the real world. On the contrary, if we use as the prompt “A person holding a knife”, in order to prevent violent or racially biased images, automatic bias mitigation operations lead to results in which the photorealism disappears, together with gender equality and accuracy: not only are there only cartoon-like male characters in the last row of Figure 5 but also none of them are holding a knife, and in one case, the character is not even a person, but a happy and hungry cannibal tomato (this is only a selection of the tests conducted using Microsoft Bing Creator based on OpenAI’s DALL-E 3 models PR13 and PR16 from August 2024 to May 2025 (15 tests from August 2024 to September 2024, 15 tests from November 2024 to January 2025, and 34 tests from March 2025 to May 2025; these tests were conducted both in isolation and sequentially and always showed comparable results)).

This means that the taken-for-granted trade-off between fairness and correctness may have unexplored causes and therefore may be a false myth. In fact, by means of Chernoff information, Ref. [47] shows that it is always possible to find an ideal reference distribution that maximizes both the fairness and accuracy, without a trade-off, whereas such a trade-off is present when dealing with (possibly) biased datasets, concluding that accuracy for ML systems should be measured with respect to ideal, unbiased distributions. Under this framework, correctness and fairness form a continuum, and the bias amplification chain should be extended to also include the unbiased, ideal distribution, which, in turn, can serve to mitigate bias in the real world.

Human-driven mitigation operations can be performed at the beginning of the chain, in the designer’s UL, but also at the end of the chain, in the final user’s UL. Consider again the simple test in Figure 5: photorealistic, more accurate, and fair results can be achieved by injecting contextual information into the user prompt.

Figure 6 shows the effects of adding the contextual information “in the kitchen” to the sentence “A person holding a knife”: we regain photorealism, together with accuracy and an acceptable amount of racial and gender fairness. This may be due to the fact that such contextual information makes automatic mitigation operations useless, and hence, it frees the model from mitigation operations. The group of tokens included in “in the kitchen” is semantically associated with other tokens, e.g., cooking, which allow us to avoid associations with undesirable semantic subspaces, e.g., involving violence and racial bias. Accuracy and fairness, and hence the direction of normativity, are dictated by both the intentions of the designer and those of the end user writing the text prompt and, from the latter’s point of view, merge into trustworthiness. And this is true not only for generative systems but also for predictive ones; trust does not mean blind acceptance of the results of a predictive system; on the contrary, we should consider ML predictions as judgments to be verified. However, since correctness is asymptotically unattainable for an ML system, such a proof may not be available: from a pragmatic structuralist point of view, data-driven predictions should be consistent and coherent with the data, information, and knowledge bases of all ULs. Under this reasoning, two such forms of miscomputation are:

Definition 2 

(Implementation Miscomputation). An implementation miscomputation occurs when any of the lower ULs in the system (the training sample UL, the training engine UL, the learned model UL, and the model output UL) badly implements the designer’s intentions, as represented by an ideal unbiased distribution (when evaluating fairness) and/or by real-world ground truths (when evaluating accuracy).

Definition 3 

(Instruction Miscomputation). An instruction miscomputation arises when the output of the system is in contrast with the instruction provided by end users and/or their informational states.

Figure 6. Images (a–d) generated with Microsoft Bing Image Creator using “A person holding a knife in the kitchen” as the prompt.

Figure 6. Images (a–d) generated with Microsoft Bing Image Creator using “A person holding a knife in the kitchen” as the prompt.

Under this taxonomy, the first two rows of Figure 5 are to be considered pragmatically correct computations, whether accuracy is our goal or we are aiming for the fairness of the system, since they accurately implement the designer’s intentions and follow the final user’s instructions, while preserving a fair balance between genders and races (assuming for simplicity gender as a binary feature). Figure 6 can be seen as a case of implementation miscomputation with respect to gender fairness given the non-uniform distribution of male and female outcomes. The last row of Figure 5 represents a more severe case of pragmatic miscomputation, involving both implementation and instruction: it is an unfair implementation miscomputation, given the non-uniform gender distribution; it is an inaccurate implementation miscomputation, due to the cartoon-like style; and it is an instruction miscomputation because all of the characters are holding a wooden spoon instead of a knife, as requested by the end user’s text prompt.

6. Conclusions

In this paper, we have provided a first take on the taxonomy of miscomputations for data-driven systems. Our approach has consisted of presenting, first, an LoA-based ontology of ML systems, on whose grounds we distinguish three types of miscomputations. Next, we have suggested a pragmatic notion of correctness forming a continuum with the notion of fairness for cases which link to the user’s requirements. In such cases, two main forms of miscomputation may occur.

Future research lines emerge from this first attempt to categorize errors for data-driven computational systems. First, less simple ML artifacts should be considered, including LLMs in their agentic versions and used in orchestration. Second, the issue of epistemic authority mentioned earlier raises various important related conceptual questions: the problem of the chain of responsibility across agents (human and artificial) for an ML system’s decisions; the formalization of the accessibility relations to information between groups of users with different computational and expressive capabilities and possibly in contrast or conflict, as treated in the Logic for Pragmatic Information (LPI) [30]; and the extension to a Logic for Trustworthy Information (LTI), providing a formal framework for UL structures characterized by trust. Third, several methodological aspects that emerge from the classification of errors in ML/genAI contexts, like theory generation by AI, the distinction between explanation and prediction, understandability, and transparency, are all crucial. However, this goes far beyond the scope of the present article.