Interfacing Programming Language Semantics and Pragmatics: What Does “Hello, World” Mean?

Abstract

In 1978, Brian Kernighan and Dennis Ritchie insisted that the first program to write in a new language is one to print the words “hello, world.” From then until now, “hello, world” has frequently been the first exercise in introductory programming courses. On one hand, this does seem like a good first program because it makes something familiar—a greeting—appear on the screen. On the other hand, it is extremely strange. How can it be understood as a greeting? Who is greeting whom? Unfortunately, the bulk of formal means for defining programming languages provides very little help for assigning a meaning to the “hello, world” program. It is argued that the weakness of older theories and methods of programming language semantics is due to the historical, disciplinary segregation (in logic, semiotics, and linguistics) of semantics as a study apart from syntax and pragmatics. Drawing from both more recent work in programming language semantics that addresses side effects and on speech-act-based programming language design, this paper proposes a possible reintegration of semantics and pragmatics in order to better define the meaning of “hello, world” and the programming languages used to produce speech acts more generally.

1. Introduction: Hello World!

In their 1978 book, The C Programming Language, Brian Kernighan and Dennis Ritchie declare

The only way to learn a new programming language is by writing programs in it.

The first program to write is the same for all languages:

Print the words hello, world. In C, the program to print “hello, world” is

#include <stdio.h> include information about standard library

main()             define a function called main

                   that receives no argument values

{                  statements of main are enclosed in braces

   printf(“hello, world\n”); main calls library function printf

                            to print this sequence of characters

} [1] (pp. 9–10)

Searching a programming chrestomathy, one can find “hello, world” implemented in hundreds of languages (e.g., https://rosettacode.org/wiki/Hello_world (accessed on 24 July 2025)). In some languages, “hello, world” can be written much more succinctly. For example, in JavaScript it can be this: console.log(“hello, world!”);.

On one hand, this does seem like a good first program because it makes something familiar—a greeting—appear on the screen. On the other hand, it is extremely strange. How can it be understood as a greeting? Who is greeting whom? In this paper I will argue for an expanded approach to programming language analysis and design that stretches semantics to better represent programs like this.

The approach taken is an attempt to move from a conventional understanding of computing as calculation to a more expansive understanding of computing as coordination [2], specifically an understanding of computing as a force for coordinating people and things. How might the fields of programming language semantics and computer-supported cooperative work (CSCW) be brought into closer proximity?

In his recent book [3], computer scientist and philosopher Tomas Petricek provides another way of framing the issue at hand. Petricek identifies what he calls five “cultures of programming”: the mathematical culture, hacker culture, managerial culture, engineering culture, and humanistic culture. Each culture differs according to how it conceptualizes programs. According to Petricek, the mathematical culture of programming sees programs as mathematical entities. In contrast, the humanistic culture of programming is concerned with programs as sites of human interaction and influences on the shape of society [3] (p. 27). Petricek argues that great achievements of computing have resulted from the agonistic and collaborative exchange between these cultures with the development of programming languages as a case in point:

Despite the different interpretations, each of the cultures was able to contribute something to the shared notion of a programming language, be it a commercial motivation, compiler implementation or a language definition. I [Petricek] will even argue that such collaborations often advanced the state of the art of programming in ways that would unlikely happen within a single consistent culture [3] (p. 18).

In Petricek’s terms, this paper links the mathematical and the humanistic cultures of programming for the purpose of better understanding the languages that allow us to write programs like “hello, world,” programs that interpellate [4] us, as subjects, into the social, political, cultural, and economic institutions of everyday life.

2. The Paradox of printf and Its Arguments

Kernighan and Ritchie’s pedagogical claim is that we learn a programming language “by writing programs in it.” While this is a well-supported path to coding literacy [5], it is a very different path than that which would have the student start with a reading of a formal definition of the language. The latter would be analogous to asking the student of a natural language to begin with a reading of the grammar and a dictionary of the language. Following the latter path, one is immediately confronted by two problems with Kernighan and Ritchie’s suggestion that the student start by writing the “hello, world” program:

(1)

Like most other programming languages, in C input/output (I/O) functions (such as printf) are considered to be outside the formal definition of the language per se. Kernighan and Ritchie tell us this, almost at the very beginning of their book: “By the way, printf is not part of the C language; there is no input or output defined in C itself. printf is just a useful function from the standard library of functions that are normally accessible to C programs [1] (p. 14).” Thus, Kernighan and Ritchie are advocating that the first program one should write in the language highlights a function (printf) that is, formally speaking, not a part of the language.

(2)

From a formal perspective – from the perspective of “the mathematical culture”—“hello, world” is not a greeting, it is simply a sequence of characters, a string that has no motivated connection to the design and operation of the C language.

In other words, printf is not part of the C language and neither is “hello, world.” Consequently, while from a humanistic culture of programming, Kernighan and Ritchie’s suggestion seems like good pedagogy, from a mathematical cultural perspective it seems like a paradox: To learn a language, one should start by writing code that is not part of the language [6].

This paper will proceed by first examining in more depth the mathematical culture of the formal semantics of programming languages that makes the “hello, world” program seem to be conceptually complicated. The focus will be on how the output of programs has been conceptualized as “side effects” beyond the semantics of the programming language—and then move to narrate how semantics has been enlarged to take into account the meaning of side effects. Essentially, the first part will address how one can use the insights of recent developments in formal semantics to understand the meaning of the printf function. In the second part, the meaning of the actual output—i.e., “hello, world”—will be examined. To do so, a set of pioneering works will be highlighted, works from the history of programming language design wherein speech acts—like greetings, promises, etc.—are foundational constructs of the languages. This latter portion of the paper has a direct connection to the earliest work in CSCW, like the use of speech acts in the design of Terry Winograd and Fernando Flores’s Coordinator system [7].

3. On the Definition of printf

I/O operations and all other workings of a programming language that have some effect beyond the immediate environment of the computing machine produce “side effects,” i.e., changes to the context of the computing machine. Internal to the machine is an environment that can be defined by a set of bindings (variables to values). The state of the machine also comprises a set of operations that work on those bindings, a program also known as a sequence of operations, and a program counter that refers to the point in the program that is being executed at any given moment. Of course the environment, and so the machine, can be defined, circumscribed, or expanded in a number of ways, but, typically, the environment does not encompass, for instance, what appears on the screen or other concerns that can be called the “context” of a computation.

When one searches the literature of programming language semantics for mention of I/O operations, one usually finds two scenarios as follows:

• I/O operations are explicitly excluded from consideration: For example, in their work on the semantics of C, Yuri Gurevich and James K. Huggins state at the beginning, “We intended to cover all constructs of the C programming language, but not the C standard library functions (e.g., fprintf(), fscanf()) [8] (p. 274).”
• In works of formal semantics where I/O operations are covered, like Chucky Ellison and Grigore Rosu’s “An executable formal semantics of C with applications [9],” the semantics of I/O operations are defined as a computer program that can perform the operations in a way that is functionally equivalent to the way they are performed in the implementation of the language.

Ellison and Rosu’s approach to formal semantics, called operational semantics, defines the meaning of the implementation a programming language to be the implementation of the programming language in code structured differently and written in a different notation than the implementation. Not all operational semantics are executable programs, i.e., they are not all written in a notation that can be executed as a program on the computer—although Ellison and Rosu’s is so written [10,11].1 To count as an operational semantics of a programming language, it must be written in a very specific manner. If it is not, then it is considered a reference implementation and not a formal semantics of the language [12,13,14]. Many languages—like Ruby, PHP, and Perl 5—do not have a formal semantics but only a reference implementation.

EMCAScript, the standard for JavaScript (https://bit.ly/EMCAScript262_15thEdition_June2024 (accessed on 24 July 2025)), was defined with an operational semantics (inscribed as a term rewriting system) that can be automatically rendered as an executable interpreter for the language [15]. The authors call the result “KJS.” “Hello World” is the first example presented in the README instructing one how to install and use the interpreter derived from the semantics (https://github.com/kframework/javascript-semantics (accessed on 24 July 2025)). As Park, Stefanescu, and Rosu explain in the scientific paper, specifically in Section 3.4, “Standard Libraries,” “Although KJS aims at defining the semantics of the core JavaScript language, we have also given semantics to some essential standard built-in objects. For example, we completely defined the Object, Function, Boolean, and Error objects, because they expose internals of the language semantics [15] (p. 350).”

Note that Rosu is a co-author of KJS and also a co-author of the second formal semantics of C cited above. One might imagine Rosu et al.’s approach to be unusual because it is seemingly tautological or, perhaps, circular: defining the meaning of one computer program, that implements the interpretation of a language (its interpreter, its evaluator, or its compiler), as another computer program.

But one would be mistaken. In their approach, Rosu et al. are not unusual at all. The vast majority of modern programming language semantics are given as operational semantics. What distinguishes a reference implementation from an operational semantics is the latter is written as a set of functions without side effects, while the former need not be written without side effects.

Side effects are changes to the context of a computation. One way to compose an operational semantics for printf is to parameterize the context and thereby make it explicit in the semantics.

An example of such a definition for printf written in JavaScript follows. Note however that this is a simplification for a number of reasons, one of which is that printf has a much more complicated operation than what is assumed here. In C, printf can output values of several types; here, it is assumed that the value of the output has to be of type string. In C, printf can also be used to format the output string. In what follows, no formatting facility is defined.

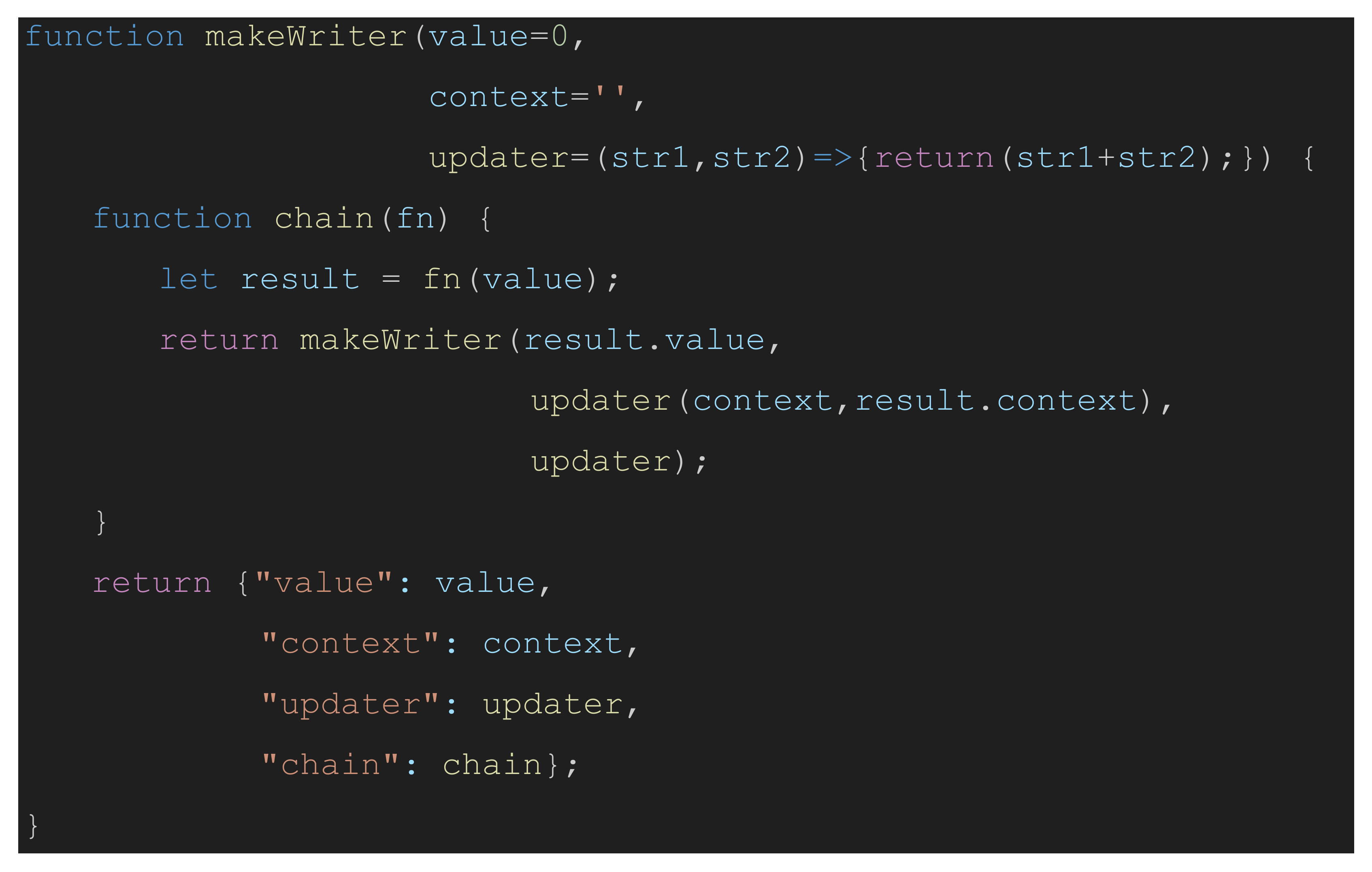
Figure 1 defines (in JavaScript) the central object necessary to parameterize the context of a computation. The object will be referred to as a “writer,” until later in the article when it will be compared to what is called a “writer monad” in the literature of formal semantics. makeWriter is a function that has three parameters: (1) a value that will be the input to some, as yet unspecified function, fn; (2) a context for the evaluation of the function fn; (3) an updater, a function that updates the current state of the context with any modifications produced via the execution of the function fn. The body of makeWriter composes a function called chain which, in the literature about monads, is also called “bind” or “flatMap,” and, in the programming language Haskell, is denoted by the symbol >>=. The function chain of the writer is designed to bundle together a value and a context; accept a function, fn; apply the function, fn, to the value; update the value and the context; and then return a new writer object containing the resultant value and the updated context.

If invoked without arguments, the value defaults to zero, the context defaults to the empty string, and updater is an anonymous function that concatenates its arguments together. The anonymous function is expressed as a lambda expression in JavaScript where => is the lambda operator. The object constructor makeWriter corresponds to what has been called “unit” or “return” in the literature on monads.

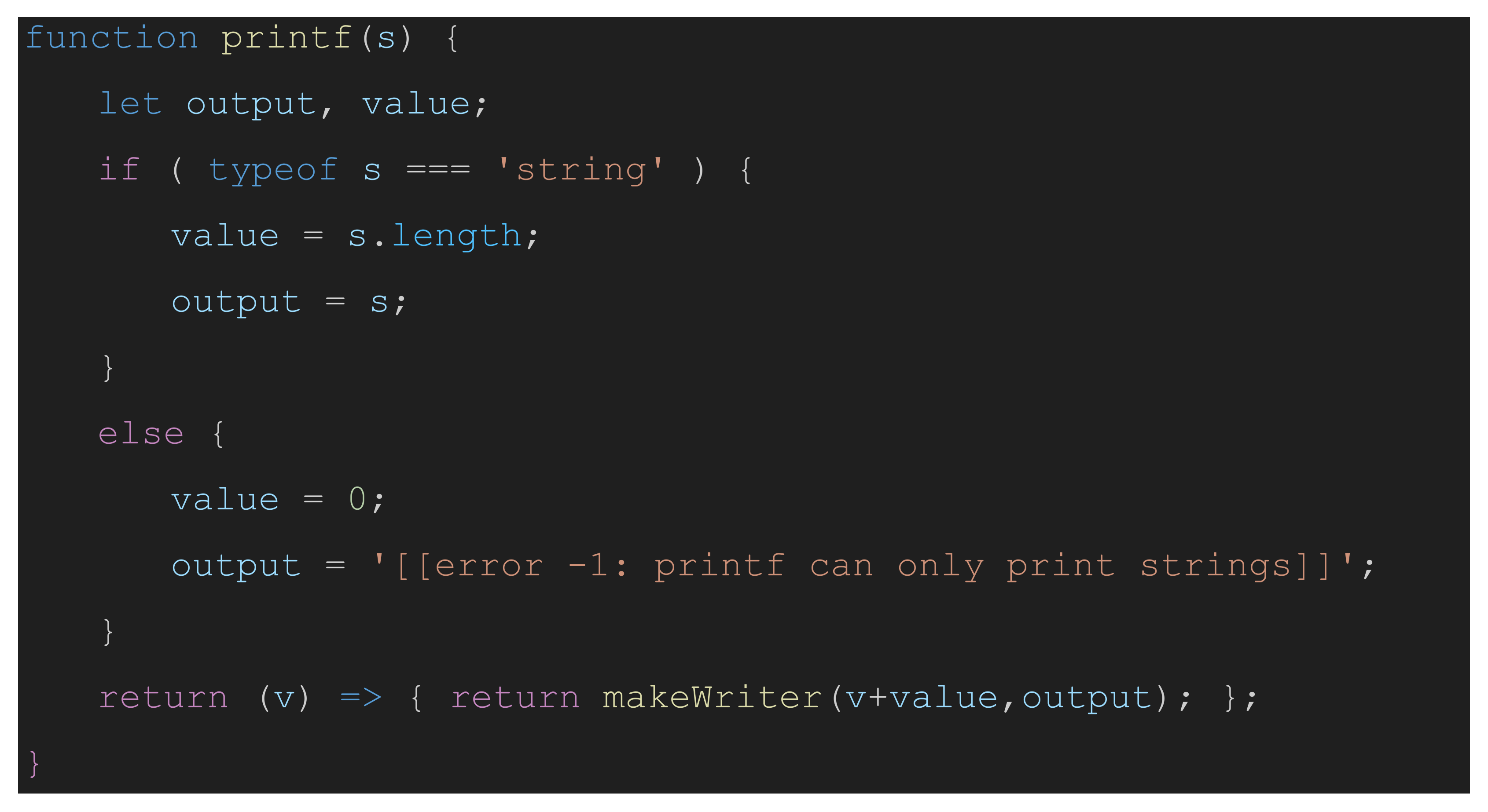
Given the definition of makeWriter, printf can be defined as a function without side effects. Given s as input, according to the semantics of C, it should return a value equal to the number of characters printed and should also output s to the screen. Thus, printf (“hello, world”); will output “hello, world” to the screen and return 12, the number of characters in the string “hello, world.” [16] 2 The definition of printf in Figure 2 accepts a string to be output and returns a function that, in turn, returns a writer containing a value equal to the number of characters printed, and the context—also known as the output.

To execute this definition of printf, one first creates a writer object to encapsulate the context and then calls the printf function with the chain method of the writer:

The result is a new writer object containing a value, 12, and a context of all that would have been printed to the screen: w1.value is 12 and w1.context is “hello, world.”

Outputting the string with two calls to printf provides an illustration of how sequential calls can be chained together:

The result, w2, is equal to w1 because sequential calls to printf, using chain, add the length of the next string onto the current value and concatenate the next string onto the current string that represents the context.

Attempting to print a value unsupported by printf could, in C, throw an error and stop the computation in medias res. The definition in Figure 2 will raise an error if one attempts to print a non-string, like the empty object (written {} in JavaScript). However, in this definition of printf, since the side effect, the error message, will simply be recorded into one of the parameters of the writer object, the computation will not suddenly halt. Executing the following results in the creation of w3, a writer object.

The resultant writer object, w3, has a value of 12 and a context of “hello,[[error −1: printf can only print strings]] world.” Note that the latter includes both the expected output and the error message.

4. Criteria of Formal Semantics

Criteria that motivate the rewriting of printf in this manner are criteria of formal semantics—including truth-conditional semantics, model-theoretic semantics, and the principle of compositionality—that were first developed in the nineteenth and twentieth centuries by the logicians Gottlob Frege [17], Alfred Tarski [18], and Rudolf Carnap [19].

With respect to Petricek’s cultures of programming, these criteria are central to mathematical culture. Members of the others—hacker culture, managerial culture, engineering culture, or humanistic culture—would all likely approach the definition of printf in JavaScript much more directly, taking advantage of, for instance, console.log, an analogous function in JavaScript. Thus, one might succinctly write Kernighan and Ritchie’s first program in JavaScript as console.log(“hello, world”);. To understand why the mathematical culture of formal semantics would motivate one to instead define printf via the rather complicated mechanics of writer objects and chain functions, it is worthwhile to consider the history of these criteria.3

Truth-conditional semantics: Frege argued that sentences have truth values as their referents.

Model-theoretic semantics: Tarski argued that truth is defined with respect to a model and any such model includes an interpretation function that maps constants to entities or sets.

Principle of compositionality: Frege, in his analysis of functions and arguments, implicitly defines this principle, a principle that Richard Montague [20] later formulates explicitly. Namely, the meaning of a complex expression is determined by the meanings of its parts and how they are combined. For example, we can think of the “parts” as the words in a lexicon and “how they are combined” as a grammar.

All of these criteria are dependent upon the definition of a function, a definition that has changed over the centuries. One can see in the Oxford English Dictionary (OED) that prior to Gottfried Wilhelm Leibniz, the term “function” was a very general term meaning, for example, “official duties” or “the kind of action proper to a person as belonging to a particular class.” These meanings are applicable to all kinds of work. After Leibniz, however, according to the OED, a new, more specialized, and specifically mathematical definition is introduced: “A variable quantity regarded in its relation to one or more other variables in terms of which it may be expressed, … This use of the Latin functio is due to Leibniz and his associates.”

In his nineteenth century work on functions and arguments, Frege wrote about functions that would be familiar in any algebra class: a function is a mapping from inputs to outputs, arguments to values, and can be expressed like this: f(x) = y. Frege defined predicates as functions from individuals to a set of truth values; e.g., Man(x) = {true, false}, so Man(Socrates) would map to the value true.

In the twentieth century, means were devised to write functions as syntactic constructs. Notably for formal semantics, Alonzo Church’s Lambda Calculus [21] provides the means for (1) function definition: the expression λx.E defines a function that has the parameter x and returns E, an expression; (2) function application: (F A) denotes the application of the function F to the argument A; (3) functions as first-class objects: functions can be arguments to other functions and functions can return functions. In the Lambda Calculus, roughly, Man = λx.E and applying the function Man to the argument Socrates would return true: (Man Socrates) → true.

Conceptually, monad operations (e.g., the makeWriter and chain functions defined above) extend this lineage by providing a way to combine local computations and their contexts. Monads are functors that include two operations: (1) referred to above as a constructor (e.g., makeWriter) and referred to in the literature on monads as a “unit” or “return” and (2) what is referred to above as a chain and in the literature as a “bind” or “flatMap.” The unit operation accepts a value and a context and “wraps” that value in a monad object. The signature for unit can be written like this:

unit (or constructor): x → M x

where x can contain both value and context.

The bind operation accepts a monad, unwraps the value it contains, applies the given function to the value, modifies the context according to the result, and wraps up the resulting value and the modified context into a new monad:

bind (or chain): M x → (x → M y) → M y

Writer monads are only one of a large variety of monads, each differing from the other with respect to the data structures they incorporate. For example, a state monad can incorporate a means to pair keys with values and so model a set of variable bindings. An introduction to monads, including the composition of a state monad, can be found in Philip Wadler’s 1995 paper “Monads for functional programming” [22]. All monads define the unit and bind/chain operations that conform to three “laws” of identity and associativity that insure compositionality.4 With monad operators, functions now can be composed to map values-in-context to values-in-context.

With monads, Frege’s truth-conditional semantics can be extended. For example, if we want to distinguish Socrates the actual man who lived in ancient Athens from “Socrates,” the dramatis persona invented by Plato in his dialogues, a predicate could be composed with a monad that includes reference to a specific historical or literary context. Analogously, an interpretation function of a Tarski-style model-theoretic semantics can also be extended to include context. And, finally, with respect to the principle of compositionality, the determination of the meaning of an expression according to the meanings of its parts can be extended to include context as one of those parts. This is especially important for examining pragmatic relations of anaphora and coherence between expressions or sentences. For example, one needs the context of the preceding sentences of a story to resolve what or who a specific pronoun refers to later in the story.

From a perspective of mathematical culture, monads provide the necessary means for defining the meaning of programming language constructs, like printf, that allow one to write programs like “hello, world.” However, from the perspective of what Petricek calls a humanistic culture, where foundational criteria of formal semantics—such as the Fregean idea that meanings can be modeled as functions and the composition of functions [23]5—are alien, the construct of the monad seems only obliquely related to an understanding of what programming languages mean. The only point of consensus on this issue between a mathematical culture and a humanistic culture may be a common belief that context is important. Finding something more substantial than an ambiguous understanding of context will require some historical insight.

5. What Was Programming Language Semantics?

Well into the 1950s, computers were bespoke—designed and assembled for a single site or purpose. They had unique names—ENIAC, EDVAC, Manchester Mark 1, etc.—and unique machine languages, so coding a given algorithm for one machine did not provide one with any help coding the same algorithm for a different machine. And so, as the historian Mark Priestley relates, in a chapter titled “The invention of programming languages,” this problem was recast as a question of translation: “In 1951, for example, Jack Good asked whether anybody had ‘studied the possibility of programme-translating programmes, i.e., given machines A and B, to produce a programme for machine A which will translate programmes for machine B into programmes for machine A’ [24] as cited by [25] (p. 225).” By the end of the 1950s, the notion of a programming language that could be used to program many different machines was invented. FORTRAN and COBOL were some of the first languages that could be used on multiple machines. ALGOL was the first such language that was defined not in terms of its translation to specific machine codes but in formalisms borrowed and extended from logic and mathematics [26,27].

In the 1960s and 1970s the development of approaches to programming language semantics served two purposes. The first was to untether the meaning of a program from its performance on a specific machine. The second was to ground the meaning of a program in logic and mathematics (i.e., formal semantics) so that, for example, algorithms could be seen as mathematical entities and not just step-by-step recipes for accomplishing a specific task or calculation, thus making programs subject to analysis and proof using methods from mathematical logic. For thoughts of the era on these criteria see, for instance, E.W. Dijkstra [28].

In other words, one can understand the discipline of programming language semantics as, at least originally, an effort to rise above the details of any given machine, both so that programming languages can be implemented on many different kinds of computer and so that one has tools for designing and refining the design of new programming languages.

6. The Divergence and Subsequent Convergence of Forms of Formal Semantics

Roughly speaking, two dominant approaches to programming language semantics6 can be identified:

(1)

Operational semantics proceeds by first articulating an abstract machine that could, in principle, be embodied in a variety of different hardware architectures and then developing a set of rules that rewrite constructs of a given programming language into a step-by-step program of the abstract machine. As seen above in the discussion of operational semantics for C and JavaScript, the abstract machine can be a computer program and so the operational semantics can be an executable program. Critically, however, any such abstract-machine-as-computer-program must be written in a programming language with an authoritative formal semantics (e.g., [9]). In general, an operational semantics is an abstract description of how a computation is accomplished in a programming language.

(2)

In contrast, a denotational semantics maps constructs of a programming language to mathematical functions. Thus, for example, imagine a programming language has a routine called ADD for adding together two numbers. An operational semantics of ADD could spell out step-by-step the details of how one must, for example, carry a 1 from one column to the next if the column sums to 10 or above. Excluded would be the “levels below” in which the decimal arithmetic is transcoded into binary arithmetic performed on logic circuits. A denotational semantics can simply state that ADD maps to the addition function of mathematics.

In “Understanding Programming Languages,” Raymond Turner distinguishes what is taken to be foundational to each approach [29]. He points to the history of operational semantics, to work performed by Peter Landin in 1964 [30], in which the meaning of a programming language is modeled with Alonzo Church’s Lambda Calculus [21] in conjunction with an abstract machine for evaluating expressions written in the Lambda Calculus. Landin provides a specification for this machine, the SECD machine.

The original work on denotational semantics, by Dana Scott [31] and Christopher Strachey [32], and later summarized in textbooks, such as Joseph Stoy’s [33], argues for a mathematical foundation to semantics, a foundation that ultimately has a set-theoretic interpretation.

As Turner explains [29] (p. 206), at the time, when each of the approaches was being developed, there was no set-theoretic interpretation of the Lambda Calculus but then, shortly thereafter, Dana Scott invented/discovered such an interpretation [34]. One can see Scott’s work as a means to understand operational semantics from a set theoretic perspective. Turner offers the converse, an operational understanding of set theory:

…in which we locate our understanding of sets, not in the sets themselves, but in the axioms and rules of set theory. This would be an operational view of set-theory. Our understanding of the programming language would then be unpacked in terms of these rules i.e., via the semantic clauses through the axioms and theorems of set theory, including the proof of any required theorems. Such understanding is constituted by the rules and axioms of the underlying semantic theory: when we teach a language, we teach the semantic rules etc. [29] (p. 212).

While practical, this operational approach to set theory is unpalatable to philosophers and mathematicians who are invested in the metaphysical and ontological status of set theory. For them, sets are ontologically true while rules and operations are only epistemological, a form of know-how. This philosophical division Turner names as Platonism versus formalism. Later in the article, Turner invokes Ludwig Wittgenstein to elaborate on the weakness of this distinction for those who do not have ontological investments in set theory as a foundation for truth. Ultimately, Turner argues the following:

[I]t seems clear that the formalist/Platonist perspectives do not line up with the operational/denotational divide in programming language semantics. One could hold either philosophical position with respect to any of the so-called operational or denotational accounts. Much the same is true of the more conventionalist stance of Wittgenstein: any form of semantics, be it based on the Lambda Calculus or set-theory, constitutes a form of life that is constituted by the appropriate training. Indeed, the difference between the various approaches to semantics is technical not conceptual or philosophical [my emphasis] [29] (pp. 214–215).

Without delving into the subtleties of the philosophical literature that distinguishes Wittgenstein’s “forms of life” from his discussions of “language-game,” “certainty,” “patterns of life,” “ways of living,” and “facts of living” [35], one can see that Turner’s use of Wittgenstein opens an entirely different approach to meaning that situates operational semantics and denotational semantics as convergent. In Ludwig Wittgenstein’s philosophy of language, the meaning of a word is considered to be its use [36] (I, sec. 43). The uses of the terms of denotational and operational semantics are technically different but philosophically homogenous or at least analogous. In Petricek’s terms, denotational and operational semantics both partake in a mathematical culture of programming.

7. A Short History of Syntax, Semantics, and Pragmatics

In his 1959 book, The Two Cultures and the Scientific Revolution, C.P. Snow condemns the British educational system for the production of two mutually unintelligible cultures, one of the sciences and the other of the humanities, with the members of each unable to understand the essential ideas of the other; scientists, for example, ignorant of Shakespeare and humanists ignorant of thermodynamics [37]. Snow’s two cultures parallel what Petricek calls mathematical and humanistic cultures. However, with respect to programming languages, what separates these two cultures is not an educational system per se, but (1) the belief natural languages can be interpreted with the theories and methods of formal (artificial) languages, or not; (2) whether or not the study of language can be divided into three parts: whether or not syntax, semantics, and pragmatics are distinct and independent enough to be decoupled and studied separately.

While one might equate semantics with the study of meaning, formal semantics is more precisely the study of a very specific tranche of meaning. For instance, in one language one might sum two numbers with this expression: ADD A B. In another one, might write A + B to mean the same thing. Semantics, as it has been formulated in logic, linguistics, and programming language design is neither concerned with syntax (e.g., that the operator precedes the parameters or is between them, or the lexical issue that the operator is written “ADD” instead of “+”); nor is it concerned with pragmatics (e.g., that A may refer to the number of apples or attorneys and B may refer to the number of bananas or bandits and their sum may be the resolution to a practical problem of a grocery store or a criminal court). For over a century, the distinction between semantics, syntax, and pragmatics has been established within formal semantics.

In one of the first (1979) textbooks to introduce denotational semantics to undergraduates, Michael JC Gordon wrote,

The study of a natural or artificial language is traditionally split into three areas: (i) Syntax: This deals with the form, shape, structure, etc., of the various expressions in the language. (ii) Semantics: This deals with the meaning of the language. (iii) Pragmatics: This deals with the uses of the language [38] (p. 6).

Gordon continues in the opening paragraph of his book: “We shall discuss our uses of ‘syntax’ and ‘semantics’ later in the book; the word ‘pragmatics’ will be avoided [38] (p. 6).” This tradition referred to by Gordon is inherited from semiotics and can be traced to Charles W. Morris’s 1938 work Foundations of the Theory of Signs [39]. The trichotomy is still important to contemporary linguistics, logic, and programming languages.

Paradoxically, Gordon rules out a study of the uses of words (pragmatics) and then states that the book will examine “our uses” [my emphasis] of two particular words (“syntax” and “semantics”). Thus, succinctly, he illustrates the difficulty of separating the study of semantics from the study of pragmatics, the uses of language by people.

One might point to the logician Rudolf Carnap for an earlier reference on the separation of semantics from pragmatics as important to mathematical logic and thus the foundations of programming languages:

If in an investigation explicit reference is made to the speaker, or to put it in more general terms, to the user of the language, then we assign it [the investigation] to the field of pragmatics … If we abstract from the user the language and analyze only the expressions and their designata, we are in the field of semantics. And, finally, if we abstract from the designata also and analyze only the relations between the expressions, we are in (logical) syntax [40] cited by [41] (p. 2).

Carnap was one of Morris’s contemporaries (e.g., they were both editors of the 1938 International Encyclopedia of Universal Science) but Carnap’s reformulation of this trichotomy is especially important due to his involvement in what he referred to as “constructed language systems.” For Carnap, this distinction between semantics and pragmatics was homologous with the investigation of constructed language systems versus natural languages (i.e., spoken and written). He found these two kinds of study, one study of the meaning of constructed language systems (semantics) and the other in the semiosis of natural language (pragmatics), to be “fundamentally different forms of analysis” [19] (p. 116).

8. Pragmatics Without People

Historian Mark Priestley traces the introduction of Carnap’s distinctions into the discourse of programming language design and analysis to a 1961 article by Saul Gorn [25] (pp. 230–231) in which Gorn writes,

The study of mechanical languages and their processors is fully “semiotic” in the sense of Charles Morris (see Carnap, Introduction to Symbolic Logic), i.e., it is concerned with “pragmatics,” as well as with “syntax” and “semantics.” Pragmatics is concerned with the relationship between symbols and their “users” or “interpreters.” We will “interpret” the words user and interpreter to have a mechanical sense, i.e., to mean “processor”; … The word “processor” in our context refers ambiguously to mechanisms, algorithms, programs for a machine, or systems and organizations composed of machines, programs, and algorithmized people [42] (p. 337).

To equate “users” to mechanical processors is an abrupt departure from Carnap for whom “users” were “speakers” and “pragmatics” was concerned with the semiosis of natural language. Nevertheless, Gorn’s highly restricted definition of pragmatics was met with enthusiasm in computer science. Heinz Zemanek (head of the lab that developed the Vienna Definition Language, an influential approach to operational semantics) in an address a few years later entitled “Semiotics and Programming Languages,” presented at the ACM Programming Languages and Pragmatics Conference endorsed Gorn’s idea:

So we have two kinds of pragmatics, the human pragmatics and the mechanical pragmatics, applying a term of S. Gorn. To illustrate the two kinds: to the first kind would belong an investigation to find out why a certain audience may break out into laughter when the name of a certain programming language is pronounced, and to the second, to find out how much of a certain programming language reflects a certain family of computers [43,44] (p. 142) 7

This conceptualization of a mechanical pragmatics that is separate from a human pragmatics persists in programming language research, even today. For example, the popular textbook (now in its fifth edition), Michael Scott’s Programming Language Pragmatics, [45] emphasizes the interplay between programming language design and programming language implementation but barely touches on what Zemanek called “human pragmatics.” [45] 8

9. Interfacing Semantics and Pragmatics in Linguistics, Philosophy, and Computer Science

Before proceeding to a discussion of the human pragmatics of “hello, world,” it is enlightening to quickly review how this bifurcation (of semantics from pragmatics) has been “sutured” elsewhere, especially in the formal semantics of natural languages.

So much has taken place at the boundary of the fields of linguistic semantics and pragmatics that it will only be possible to review a small fraction of the work. There are journals (e.g., the open access journal Semantics and Pragmatics published by the Linguistic Society of America: https://semprag.org/ (accessed on 24 July 2025)) and entire book series (e.g., the Oxford Studies in Semantics and Pragmatics: https://global.oup.com/academic/content/series/o/oxford-studies-in-semantics-and-pragmatics-ossmp (accessed on 24 July 2025)) devoted to studying this border. One might characterize this work as collaborative but also contentious. One well-known linguist has famously characterized it as a set of “border wars” with contending factions.

In reports filed from several fronts in the semantics/pragmatics border wars, I seek to bolster the loyalist (neo-)Gricean forces against various recent revisionist sorties [46].

Another, in less inflammatory terms, has called it an “interface.”

[T]he investigation of the semantics–pragmatics interface has proven to be one of the most vibrant areas of research in contemporary studies of meaning [47].

The relevance of this linguistics work to present purposes is easiest to see in formal semantics, an approach that is increasingly imbricated in the concerns of programming language semantics. One of the founders of that approach, Barbara Partee, describes the work of Richard Montague (1930–1971) as a key antecedent to contemporary formal semantics. Montague was a student of Alfred Tarski (1901–1983) who, along with Gottlob Frege (1848–1925) and Rudolf Carnap (1891–1970), developed the criteria of formal semantics, as described above. Partee writes,

Montague’s idea that a natural language like English could be formally described using logicians’ techniques was a radical one at the time. Most logicians believed that natural languages were not amenable to precise formalization, while most linguists doubted the appropriateness of logicians’ approaches to the domain of natural language semantics [48].

By introducing several features of logic to linguistics, Montague’s proposal to formalize the semantics of natural language was rendered feasible.

Montague’s use of a richly typed logic with lambda-abstraction [i.e., the abstraction of Church’s Lambda Calculus] made it possible for the first time to interpret noun phrases (NPs) like every man, the man, a man uniformly as semantic constituents, something impossible with the tools of first-order logic. More generally, Montague’s type theory represents an instantiation of Frege’s strategy of taking function argument application as the basic “semantic glue” by which meanings are combined. This view, unknown in linguistics at the beginning of the 1970’s, is now widely viewed as standard [48].

Partee and her colleagues considerably revised and extended Montague’s original work, and by the 1980s, formal semantics had become a mainstream approach in linguistics. See, for example, the two volumes of articles edited by Gennaro Chierchia, Partee, and Raymond Turner [49]. The work revising and extending Montague’s retains several key aspects of his proposals including, as stated above, function-argument application as the basic approach to combining meanings; and, the centrality of the so-called principle of compositionality: “The meaning of a whole is a function of the meanings of its parts and their mode of syntactic combination [48].”

While Montague’s very first formal semantics treats sentence meaning as a truth condition (i.e., mapping a sentence to its meaning irrespective of context), pragmatic phenomena require the interpretation of a sentence in context. Later, by 1973, Montague was working with his intentional logic that dealt with possible worlds, and thus context-dependency. Mapping a sentence to a formula that depends on the possible world in which it is evaluated does model context-dependence, but the earlier work lacked treatments of updating contexts.

Consider these two sentences from a Russian folktale: (1) A sorcerer gives Ivan a boat. (2) The boat takes him to another kingdom [50]. The context of the second sentence is given by the first sentence and thus allows the pronoun “him” in the second sentence to be resolved to the “Ivan” of the first sentence. To address the anaphoric interdependence between sequential sentences (and other relations between meaning and context), dynamic semantics was proposed in the 1980s and 1990s to extend Montague grammar with treatments to update context. The general idea is that the meaning of a sentence depends upon and changes its context.

Formal semanticists Theo M.V. Janssen and Thomas Ede Zimmermann, in the entry for “Montague Semantics,” [51] cite Montague’s 1970 Universal Grammar in which he already anticipates this concern: “meanings are functions of two arguments—a possible world and a context of use [20].” However, if function argument application is also used to combine meanings, it must be possible to chain together these functions of two arguments (informally a sentence and a context) that return two results (a meaning and a modified context), where the modified context is then the context for the subsequent sentence.

The function that calculates the meaning of a sentence returns an object containing both the meaning of the sentence and the modified context. We may roughly sketch out what its repeated application might look like:

• First Input:

Sentence: “A sorcerer gives Ivan a boat.”

Context: []

• First Output:

Meaning: Meaning for first sentence is recorded in a formal notation.

Context: Includes male characters in order of appearance: [sorcerer, Ivan].

• Second Input:

Sentence: “The boat takes him to another kingdom.”

Meaning and Context: Includes [sorcerer, Ivan].

• Second Output:

Meaning: Cumulative meaning for both sentences is recorded in a formal notation including the inference that “him” has been resolved to “Ivan,” the last male character to appear.

Context: Includes that the boat and Ivan are now in another kingdom.

That this structure could be expressed as a monad has been noted and developed by researchers of a particular line of formal semantics who see in computer science a means to structure insights about the semantics and pragmatics of natural languages. In his 2005 dissertation entitled “Linguistic side effects,” Chung-chieh Shan asserted that linguistic side effects were analogous to computational side effects.

Most computational side effects and many linguistic ones are thought of as the dynamic effect of executing a program or processing an utterance. This is the intuition underlying the term “side effects.” For example, it is intuitive to conceive of state (a computational side effect) and anaphora (a linguistic side effect) in similar, dynamic terms [my emphasis] [52] (p. 4).

In an earlier paper, Shan demonstrated how both computational and linguistic side effects could be expressed with monads [53]. In this guise, monads could be seen as a convenient tool, borrowed from computer science, to improve the articulation of the observations and findings of the formal semantics of linguists. But Shan finds a convergence between computer science and linguistics and not just a simple borrowing:

This dissertation is about computational linguistics, in two senses. First, we apply insights from computer science, especially programming-language semantics, to the science of natural languages. Second, we apply insights from linguistics, especially natural-language semantics, to the engineering of programming languages [52] (p. 1).

Shan’s work has inspired subsequent research, including a 2020 book by Ash Asudeh and Gianluca Giorgolo, Enriched Meanings: Natural Language Semantics with Category Theory:

Our [Asudeh and Giorgolo’s] original inspiration came from Shan (2001) [53], who sketched how monads could potentially be used to offer new solutions to certain problems in natural language semantics and pragmatics. The use of monads for the study of linguistic meaning is more of a research program than a specific result [my emphasis], so this book is mainly about further motivating the use of monads in semantics and pragmatics [54] (p. 1).

The monads of this new research program are the monads coded for functional programming languages, especially for the Haskell programming language.9 Perhaps the clearest representation of this approach is expressed in Simon Charlow’s 2014 dissertation where monads are taken to be a theory:

Following Shan’s 2002 pioneering work, I [Charlow] use monads (e.g., Moggi 1989, Wadler 1992, 1994, 1995) [22,55,56,57] as a way to think a bit more abstractly and systematically about what we do when we posit grammars that allow expressions to incur side effects. In other words, monads give a theory of side effects [my emphasis] [58] (p. 3).

In a recent book Charlow co-authored with Dylan Bumford, Effect-driven interpretation: Functors for natural language composition, phenomena on the border of semantics and pragmatics are analyzed (including “anaphora and binding, indeterminacy and questions, presupposition, quantification, supplementation, and association with focus” [59] (p. 1)). These analyses are implemented in the functional programming language Haskell. About their use of Haskell, they write,

[T]o make this all a little more concrete and a little more fun, we [Charlow and Bumford] include snippets of code throughout the text implementing key ideas. The code is written in the programming language Haskell, whose construction and development have been heavily influenced by the algebraic concepts we discuss. This makes the language almost eerily well-suited to linguistic analysis [59] (pp. 1–2).

This is a remarkable convergence between linguistics and computer science, foreseen by Shan, in which the Haskell programming language is “eerily well-suited to linguistic analysis.” In Turner’s terms (discussed above), the debate between the formalists and the Platonists in programming language semantics is, for these formal semanticists, definitively settled on the side of the formalists. If, from the perspective of this “research program” and “theory of monads,” the linguistic side effects of pragmatics can be understood as computational side effects and side effects of all kinds can be analyzed with monads, then one might imagine Carnap’s distinction between the semantics (of formal languages) and pragmatics (of natural languages) has been overcome; and Gorn’s differentiation of human pragmatics from mechanical pragmatics is unnecessary. In Petricek’s terms, if the criteria of formal semantics and pragmatics (of Frege, Tarski, Carnap, Montague, Partee, etc.) are best articulated in the idioms of side-effect-free functional programming, the mathematical culture of programming would seem to render redundant and so unnecessary any humanistic culture of programming. But the truth is more subtle.

Presently, it will be argued that the humanists’ criteria are not unnecessary but, instead, a crucial supplement to the criteria of formal semantics. Nevertheless, this thread of formal semantics would seem to provide support for understanding practically any form of natural language semantics and pragmatics with the concepts/constructs of functional programming. Consequently, the same formal means of analyzing programming language constructs, like C’s printf function, should be appropriate to the analysis of natural language utterances, like “hello, world.” In the following section, this idea will be sketched out for the semantics and pragmatics of speech acts.

10. Speech Acts, Institutions and Programming Languages

Employing the form of pragmatics originally articulated by J. L. Austin in How to do things with words [60] and further developed by philosopher John Searle, in a number of works [61], the locution “hello, world” could be described as a speech act, an oral (or written) performance that is not just a representation or description but also an action. The bulk of linguistics and philosophy work on speech acts has been directed to establishing the felicity conditions of their success according to the beliefs and intentions of the speaker and the hearer. The work has been, traditionally, divided into the analysis of (1) locutionary aspects (what is said or written), (2) illocutionary aspects (what the speaker intended to accomplish via the speech act), and (3) perlocutionary aspects (what of the hearer’s beliefs or intentions were changed by the speech act). These three aspects have been formalized by Searle, his collaborators (e.g., [62,63,64]), and many others in linguistics, philosophy, and computer science (e.g., [65]).

If we consider “hello, world” to be a greeting, it presupposes some kind of social contact between the speaker and the hearer and its locution commits the hearer to respond in kind. If the hearer reciprocates (e.g., “Hello!”), the commitment is fulfilled. If the hearer declines to reciprocate, the commitment is left unfulfilled perhaps for a variety of reasons including (a) the hearer did not receive (e.g., hear or see) the speaker’s greeting; (b) the hearer was not hailed by the speech act because they did not recognize themselves as the addressee; (c) the hearer is deliberately snubbing the speaker, refusing to acknowledge the greeting; etc. Just as commitments entail obligations on the part of the speaker and the hearer, unfulfilled commitments entail ongoing processes of accountability that are entangled with the prior relationship between the speaker and the hearer and the specific context of the speech act. For example, if the speaker and the hearer are good friends and in a noisy environment, a non-response from the hearer will likely be accounted for by the speaker as (a)—not (b) or (c)—and therefore taken to be an obligation to repeat the greeting more loudly. Ultimately, most speech acts are a means of coordinating people within a given institution though mutual commitments and processes of accountability. And, their felicitous performance is governed largely by their context, i.e., by formal institutions (retail stores, schools, etc.) and informal institutions (e.g., friendship, acquaintance, etc.).

Searle’s writing on artificial intelligence makes it clear that he thinks only humans and animals can have intentions: “Intentionality in human beings (and animals) is a product of causal features of the brain…. [And] Any attempt literally to create intentionality artificially (strong AI) could not succeed just by designing programs but would have to duplicate the causal powers of the human brain [66].” Following this line of reasoning, no computer program could produce a speech act because the computer program, by fiat of not having an organic brain, has no intentions and so cannot be said, according to Searle, to have any illocutionary force, no intended communicative effect. According to this reasoning, printf(“hello, world”) is not the locution of a speech act.

Of course, Searle’s essay on AI—known informally as “The Chinese Room Argument”—has now been subject to decades of critiques [67]. There are three objections of especial importance here: (1) Some person, with intentions, wrote the “hello, world” code or wrote the AI that wrote the code, and so one can hardly argue that there are no intentions behind the code even if one might argue that the code itself has no intentions. (2) Most of what counts as intentions and beliefs in the exchange of speech acts is not personal, is not due to a specific individual’s brain, but is, rather, imposed by the institutional context of the exchange. Searle’s later work seemed to acknowledge this second point since he increasingly placed more emphasis on an analysis of the institutions created by and contextualizing speech acts, even though he continued to focus on the role of individuals [68]. (3) Many social, political, cultural, and financial institutions have been replaced by digital platforms that encode sets of intentions. Consider the greeting a banking app produces upon a successful login: the intention to identify a specific customer has been fulfilled. Consider depositing a check via online banking. The platform, the app or web services of the bank, is obligated to increment the balance of the account once the check clears. Thus, the bank via the digital platform performs speech acts. This is known as the “Systems Reply” to the Chinese Room Argument and was not accepted by Searle.

Despite the fact that Searle’s stance would seem to rule out any possibility that a computer program could produce speech acts, many efforts have been made to design programming languages based on speech acts. Perhaps understandably, however, those who have employed speech act theory for programming language design have largely moved away from the mentalist concerns of intentions and beliefs. For example, Carl Hewitt wrote, “Illocutionary semantics is limited in scope to the psychological state of a speaker. However, it is unclear how to determine psychological state! [69]”

Munindar Singh, in a description of agent-based languages based on speech acts, expresses skepticism about the practicality of designs based on beliefs and intentions, despite some of his earlier work (see, for example, [70]). Instead, Singh advocates for the expression of publicly verifiable social agency:

A more promising approach is to consider communicative acts as part of an ongoing social interaction. Even if you can’t determine whether agents have a specific mental state, you can be sure that communicating agents are able to interact socially. … Practically and even philosophically, the compliance of an agent’s communication depends on whether it is obeying the conventions in its society, for example, by keeping promises and being sincere [71].

In an unpublished paper proposing the design of a programming language based on speech acts (Elephant 2000), John McCarthy also moves away from the mentalist focus of speech act theory: “Elephant 2000 started with the idea of making programs use performatives. However, as the ideas developed, it seemed useful to deviate from the notions of speech act discussed by J. L. Austin (1962) and John Searle (1969) [my emphasis] [72] (p. 4).” McCarthy, without argumentation, finds analogies between “input–output specifications” and illocutionary speech acts and between “accomplishment specifications” and perlocutionary acts [72] (p. 5), and then offers the following that seems to entirely dispense with mental states as an important aspect of speech acts:

Proving that a program meets accomplishment specifications must be based on assumptions about the world, the information it makes available to the program and the effects of the program’s actions as well on facts about the program itself. These specifications are external [my emphasis] in contrast to the intrinsic specifications of the happy performance of speech acts [72] (p. 6).

Indeed, by halfway through the article, when McCarthy provides a first example of a program written in his Elephant 2000 language, he has completely redefined “perlocutionary act” when he describes the physical act of allowing a passenger to board a flight as a perlocutionary act [72] (p. 10).

There is, of course, other work on the use of speech acts in programming language design that does not abandon what philosopher Daniel Dennett has termed the “intentional stance” (roughly the position that anything could be attributed intentions) [73,74] including, for instance, Yoav Shoham’s call for a programming paradigm he calls “agent-oriented programming,” an amalgam of object-oriented programming and Hewitt’s actors [75].

But both the programming language design work that abandons the mentalist foundation of speech act theory and the work that does not take commitment as a central construct. Responding to contemporary commentary [76] on work he did in the 1980s to reify networks of speech acts as software-based institutions [7], Terry Winograd articulates a position that seems to be shared by all of the subsequent work on speech-act-based software:

[T]he underlying philosophy reflected a deeper view of human relationships. It was centered on the role of commitment as the basis for language. The Coordinator’s structure [the system designed by Winograd and his coauthor Fernando Flores] was designed to encourage those who used it to be explicit in their own recognition and expressions of commitment, within their everyday practical communications. The theme of this and Flores’s subsequent work is of “instilling a culture of commitment” in our working relationships, allowing us to focus on what we are creating of value together [77].

For Hewitt too, the point of improving upon speech act theory is to better represent commitments:

Speech Act Theory has attempted to formalize the semantics of some kinds of expressions for commitments. Participatory Semantics for commitment can overcome some of the lack of expressiveness and generality in Speech Act Theory [69] (p. 293).

Singh’s approach also takes commitments as central.

In our approach, agents play different roles within a society. The roles define the associated social commitments or obligations to other roles. When agents join a group, they join in one or more roles, thereby acquiring the commitments that go with those roles…. Consequently, we specify protocols as sets of commitments [71] (p. 45).

For McCarthy’s Elephant 2000 proposal

Programs that carry out external communication need several features that substantially correspond to the ability to use speech acts. They need to ask questions, answer them, make commitments and make agreements. … Commitments are like specifications, but they are to be considered as dynamic, i.e., specific commitments are created as the program runs [72] (p. 18 and p. 26).

Thus, for McCarthy, proving the correctness of an Elephant 2000 program is tantamount to verifying that it has fulfilled all of its commitments. These commitments are made through the performance of a series of speech acts by the program. Consequently, they are visible in a recorded trace of the program execution:

Elephant 2000 programs can refer to the past directly. In one respect, this is not such a great difference, because the program can be regarded as having a single virtual history list or “journal.” It is then a virtual side effect of actions to record the action in the history list [my emphasis] [72] (p. 8).

But the trace record is not formatted as simply a series of strings, but rather in a more structured form:

Elephant speech acts are a step above strings, because the higher levels of the speech acts have a meaning independent of the application program [72] (p. 19).

Clearly, there is a rich set of work to draw from in speech-act-based programming language design if one wants to formalize a greeting as a programming language construct that could be used to write the “hello, world” program. If one were to structure the definition of such a programming language using monads, one would need a context modeled as an institution, a construct from the humanities and social sciences. The representation of institutions and the speech acts that animate them is an area of study that would draw from what Petricek has termed the “humanistic culture of programming.” It is a topic of possible collaboration between mathematical and humanistic cultures.

There is a large literature detailing possible ways to structure the representation of institutions, a literature that stretches back at least to the late nineteenth century when Émile Durkheim argued that sociology was the science of institutions. The revival of this approach in social sciences, known as “new institutionalism” [78] in the late twentieth century, provides many contemporary models. For example, the 2009 Nobel laureate, political scientist Elinor Ostrom and her colleague Sue Crawford provide what they call a “grammar of institutions” whereby they articulate a suitably exact formalism of institutions and also, by so doing, provide an overview of how similar constructs developed throughout the social sciences (rules, norms, schema, etc.) overlap and differ from their definition of institutions [79]. While not a new institutionalist himself—and quite dismissive of efforts to compare his work to Durkheim’s [80]—John Searle contextualized speech acts in institutions, as expressed in his penultimate book [68]. Finally, it would be useful to carefully compare the social science and philosophy with work on multi-agent systems aimed at formalizing institutions as computational systems, such as that of Nicoletta Fornara and her colleagues [81].

11. Conclusions

It is paradoxical that the “hello, world” program is simultaneously considered simple enough to be the first program for a novice to write and yet poses a challenge to programming language semantics. It is a challenge because the println function produces a side effect and its argument, the string “hello, world,” as a speech act, has no motivated relationship to the C programming language.

Recent developments of formal semantics provide us with both (1) a solution for formalizing computational side effects with the monad construct; and (2) a new optimism about Richard Montague’s idea that a natural language like English could be formally described using logicians’ techniques. Thus, for example, pragmatic phenomena of natural languages are considered to be “linguistic side effects” (Shan) and amenable to an analogous formal analysis with monads. Arguably, this new lease on life for Montague’s vision is due to a convergence of the logicians’ techniques and those of functional programming, especially the Haskell programming language.

This convergence may be counted as a net loss for Platonist mathematicians who prefer the idealized functions of mathematics and the purity of set theory to the computational machinery of Haskell. However, for formalist mathematicians, mathematical logicians, and linguists, it seems like a net gain. The design of Haskell and other functional languages has been so strongly influenced by mathematics that specific programming constructs (such as the monad) are considered to be analogous, if not exactly synonymous, with specific mathematical concepts; e.g., the monad was, first, prior to its arrival in functional programming, a concept of category theory. Employing these programming constructs qua mathematical concepts at the boundary of natural language semantics and pragmatics has produced new insights into linguistic phenomena, such as anaphora.

While speech act theory has yet to be given a thorough analysis employing the constructs/concepts of this newest form of computational formal semantics, this paper proposes that such an analysis could be feasible and fruitful. One might begin such an analysis with a reconsideration of several now-decades-old attempts to design speech-act-based programming languages for specific domains. From the perspective of linguistic theory, this approach can be seen as concordant with Richard Montague’s “method of fragments,” the writing of a complete syntax and semantics for a specified subset (“fragment”) of a language [82]. From the perspective of programming language research, this approach is concordant with what Paul Hudak, one of the designers of Haskell, and others have conceptualized as “domain specific embedded languages,” where the specific domain may be, say, music [83], the embedding performed in a semantically unproblematic language like Haskell, and the interpreter structured as what Hudak called a “modular monadic interpreter [84].”

The context of any speech act is a social, political, cultural, or economic institution, a context for coordinating people and things; thus, the effects of a speech act—like the greeting “hello, world”—are both enabled and circumscribed by its contextualizing institution. Attempting to define the semantics of a programming language based on speech acts and institutions would have to be situated in a deep understanding of how computing is not just a form of calculation but also the coordination of people and things—as is commonly accepted in the contemporary research of computer-supported cooperative work (CSCW) and human–computer interaction (HCI) [7,85].10

In Searle’s terminology, actions within an institutional context are defined by constitutive rules of the form “X counts as Y in context C [68] (p. 10)”; thus, “hello, world” counts as a greeting (although an odd one) in a bakery (among other places). The oddity of “hello, world” as a greeting raises a problem for any future formalization. Note that, in French it does not seem so odd: “bonjour tout le monde” literally translates to “good day all the world,” but, if translated back into English, would likely be rendered as “hello everyone” or “hello everybody,” since “tout le monde” is the idiomatic phrase for “everyone” or “everybody.” Thus, in French, the identities of the addressees of the analogous greeting are everyone and everybody in the bakery. In English, it is difficult to know which of the world’s many billion inhabitants are being addressed by the greeting “hello, world”.

The addressee, “world,” could be considered a deictic referent, one that changes with context, and analyzed in a manner akin to Roman Jakobson’s study of “shifters [86].” However, even in a given context, the addressee of the phrase “hello, world” is still ambiguous and only resolved when one or more possible interlocutors acknowledge(s) it as addressed to them. According to the philosopher Louis Althusser, those who accept the role of addressee are “interpellated” into an institution through such a speech act. Althusser’s example is the policeman on the street yelling “Hey, you there!” into a crowd. Those who are “hailed” by such an address are interpellated into the legal system represented by the policeman [4]. This complex, interactive process of assignment of an individual to a role in an institution would seem to be problematic if one were to attempt to do so with the semantics of value-to-variable assignment in an imperative programming language.

In conclusion, while it is likely to be technically and conceptually difficult to analyze the meaning of the “hello, world” program as a construct that participates in the coordination of actions and commitments between people and things, recent developments from the mathematical and humanistic cultures of programming could make it both feasible and fruitful.