Path Planning with Time Windows for Multiple UAVs Based on Gray Wolf Algorithm
Abstract
1. Introduction
2. Problem Statement
2.1. Graph Theory Basis
2.2. UAV Restraint Information and Environment Information
2.3. Fitness of Unmanned Aerial Vehicle
3. Gray Wolf Algorithm
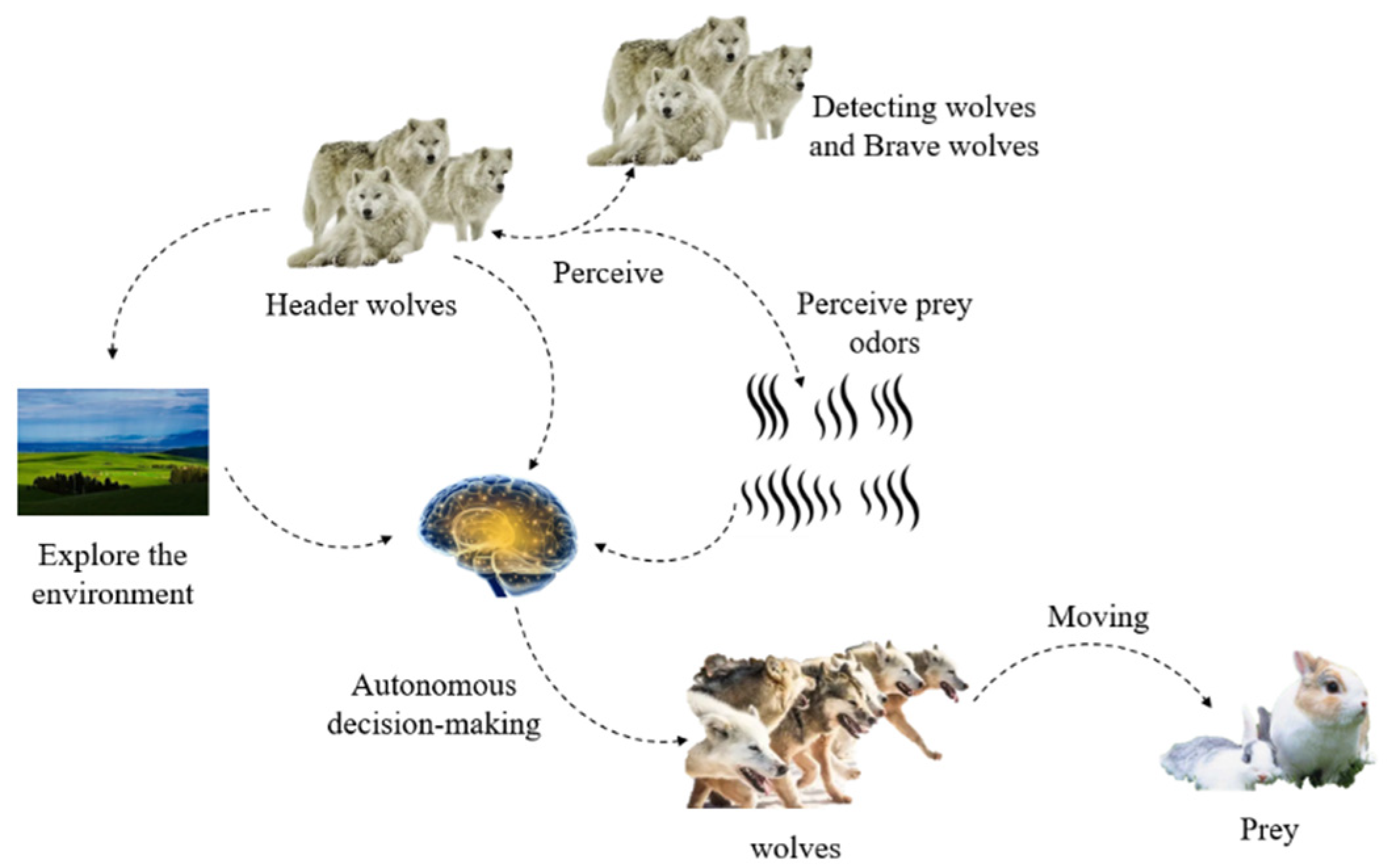
3.1. Intelligent Behavior of Wolves
3.2. Adjust the Flight Time of Each UAV
3.3. Steps of GWO to Solve the Multi-UAV Path Planning Problem
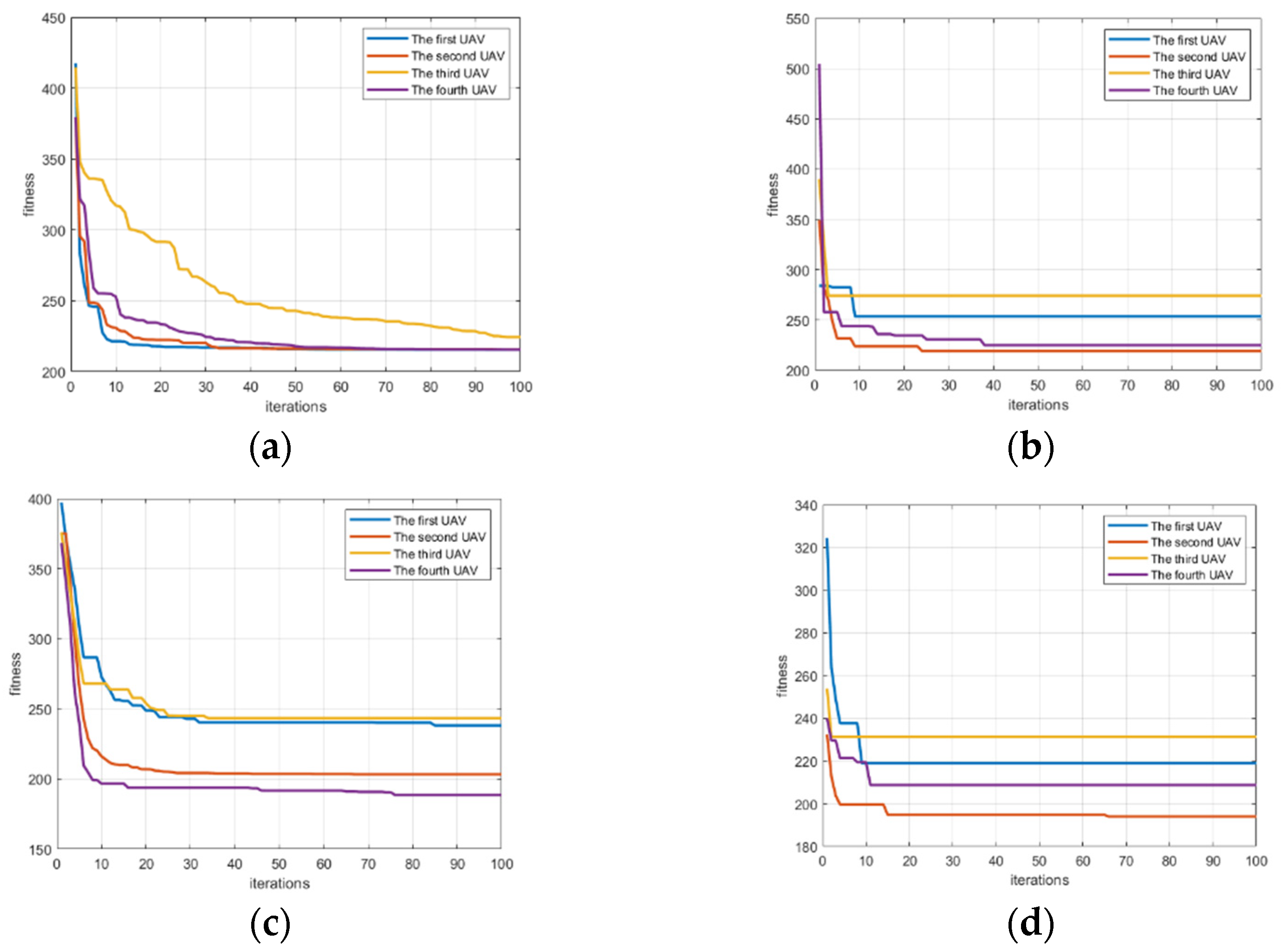
4. Simulation and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alevizos, E.; Oikonomou, D.; Argyriou, A.V.; Alexakis, D.D. Fusion of Drone-based RGB and Multispectral Imagery for Shallow Water Bathymetry Inversion. Remote Sens. 2022, 14, 1127. [Google Scholar] [CrossRef]
- Bandini, F.; Lopez-Tamayo, A.; Merediz-Alonso, G.; Olesen, D.; Jakobsen, J.; Wang, S.; Garcia, M.; Bauer-Gottwein, P. Unmanned Aerial Vehicle Observations of Water Surface Elevation and Bathymetry in the Cenotes and Lagoons of the Yucatan Peninsula, Mexico. Hydrogeol. J. 2018, 26, 2213–2228. [Google Scholar] [CrossRef]
- Specht, C.; Lewicka, O.; Specht, M.; Dąbrowski, P.; Burdziakowski, P. Methodology for Carrying out Measurements of the Tombolo Geomorphic Landform Using Unmanned Aerial and Surface Vehicles near Sopot Pier, Poland. J. Mar. Sci. Eng. 2020, 8, 384. [Google Scholar] [CrossRef]
- Specht, M.; Stateczny, A.; Specht, C.; Widźgowski, S.; Lewicka, O.; Wiśniewska, M. Concept of an Innovative Autonomous Unmanned System for Bathymetric Monitoring of Shallow Waterbodies (INNOBAT System). Energies 2021, 14, 5370. [Google Scholar] [CrossRef]
- Wang, D.; Xing, S.; He, Y.; Yu, J.; Xu, Q.; Li, P. Evaluation of a New Lightweight UAV-borne Topobathymetric LiDAR for Shallow Water Bathymetry and Object Detection. Sensors 2022, 22, 1379. [Google Scholar] [CrossRef] [PubMed]
- Cao, W.; Xu, S. Multiple Unmanned Aerial Vehicles Cooperation Architectures and Its Performances Analysis. Tactical Missile Technol. 2017, 3, 53–57. (In Chinese) [Google Scholar]
- Feng, Q.; Gao, J.; Deng, X. Path Planner for UAVs Navigation Based on A Algorithm Incorporating Intersection. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (IEEE CGNCC2016), Nanjing, China, 12–14 August 2016. [Google Scholar]
- Dong, Z.; Chen, Z.; Zhou, R.; Zhang, R. A hybrid approach of virtual force and A* search algorithm for UAV path re-planning. In Proceedings of the IEEE Conference on Industrial Electronics & Applications, Beijing, China, 21–23 June 2011. [Google Scholar]
- Li, X.; Fang, Y.; Fu, W. Obstacle Avoidance Algorithm for Multi-UAV Flocking Based on Artificial Potential Field and Dubins Path Planning. In Proceedings of the 2019 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 17–19 October 2019. [Google Scholar]
- Clerc, M. Particle Swarm Optimization; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Yong, L.; Yu, L.; Yipei, G.; Kejie, C. Cooperative path planning of robot swarm based on ACO. In Proceedings of the IEEE Information Technology, Networking, Electronic and Automation Control Conference, Chengdu, China, 15–17 December 2017. [Google Scholar]
- Zhou, J.; Dai, G.Z.; He, D.Q.; Ma, J.; Cai, X.Y. Swarm Intelligence: Ant-Based Robot Path Planning. In Proceedings of the Fifth International Conference on Information Assurance and Security, Xi’an, China, 18–20 August 2009. [Google Scholar]
- Agrawal, A.; Sudheer, A.P.; Ashok, S. Ant colony-based path planning for swarm robots. In Proceedings of the Conference on Advances in Robotics, Goa, India, 2–4 July 2015; pp. 1–5. [Google Scholar]
- Peng, J.; Li, X.; Qin, Z.Q.; Luo, G. Robot Global Path Planning Based on Improved Artificial Fish-Swarm Algorithm. Res. J. Appl. Sci. Eng. Technol. 2013, 5, 2042–2047. [Google Scholar] [CrossRef]
- Yi, Z.; Hua, Y. Path planning of mobile robot based on hybrid improved artificial fish swarm algorithm. Vibroeng. Procedia 2018, 17, 130–136. [Google Scholar]
- Yao, Z.H.; Ren, Z.H.; Zhu, X.H.; Li, S.C. Path Planning for Coalmine Rescue Robot based on Hybrid Adaptive Artificial Fish Swarm Algorithm. TELKOMNIKA Indones. J. Electr. Eng. 2014, 12, 7223–7232. [Google Scholar] [CrossRef]
- Duan, H.; Qiao, P. Pigeon-inspired optimization: A new swarm intelligence optimizer for air robot path planning. Int. J. Intell. Comput. Cybern. 2014, 7, 24–37. [Google Scholar] [CrossRef]
- Hidalgo-Paniagua, A.; Vega-Rodríguez, M.A.; Ferruz, J.; Pavón, N. Solving the multi-objective path planning problem in mobile robotics with a firefly-based approach. Soft Comput. 2017, 21, 949–964. [Google Scholar] [CrossRef]
- Chen, G.; Cruz, J.B. Genetic Algorithm for Task Allocation in UAV Cooperative Control. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Austin, TX, USA, 11–14 August 2003; p. 5582. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Gharesifard, B.; Cortés, J. Continuous-time distributed convex optimization on weight-balanced digraphs. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012. [Google Scholar]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Jepsen, T.C. Distributed Coordination of Multi-agent Networks; Springer: New York, NY, USA, 2013. [Google Scholar]
- Qu, Z. Cooperative Control of Dynamical Systems: Applications to Autonomous Vehicles; Springer: New York, NY, USA, 2009. [Google Scholar]
- Wei, R.; Beard, R.W.; Atkins, E.M. Information consensus in multivehicle cooperative control. IEEE Control Syst. Mag. 2007, 27, 71–82. [Google Scholar]
- Liu, Y.; Li, W.; Wu, H.; Song, W. Track Planning for Unmanned Aerial Vehicles Based on Wolf Pack Algorithm. J. Syst. Simul. 2015, 27, 1838. [Google Scholar]
- Mech, L.D. Leadership in Wolf, Canis lupus, Packs. Can. Field Nat. 2000, 114, 259–263. [Google Scholar]
- Muro, C.; Escobedo, R.; Spector, L.; Coppinger, R.P. Wolf-pack (Canis lupus) hunting strategies emerge from simple rules in computational simulations. Behav. Process. 2011, 88, 192–197. [Google Scholar] [CrossRef]
- Madden, J.D.; Arkin, R.C.; Macnulty, D.R. Multi-robot system based on model of wolf hunting behavior to emulate wolf and elk interactions. In Proceedings of the IEEE International Conference on Robotics & Biomimetics, Tianjin, China, 14–18 December 2010. [Google Scholar]
- Baan, C.; Bergmüller, R.; Smith, D.W.; Molnar, B. Conflict management in free-ranging wolves, Canis lupus. Anim. Behav. 2014, 90, 327–334. [Google Scholar] [CrossRef]
- Duan, H.; Yang, Q.; Deng, Y.; Li, P.; Qiu, H.; Zhang, T.; Zhang, D.; Huo, M.; Shen, Y. Unmanned aerial systems coordinate target allocation based on wolf behaviors. Sci. China Inf. Sci. 2019, 62, 205–207. [Google Scholar] [CrossRef]
- Bo, Z.; Duan, H.B. Three-Dimensional Path Planning for Uninhabited Combat Aerial Vehicle Based on Predator-Prey Pigeon-Inspired Optimization in Dynamic Environment. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017, 14, 97–107. [Google Scholar]
- Duan, H.; Li, P.; Shi, Y.; Zhang, X.; Sun, C. Interactive Learning Environment for Bio-Inspired Optimization Algorithms for UAV Path Planning. IEEE Trans. Educ. 2015, 58, 276–281. [Google Scholar] [CrossRef]
- Qiu, H.; Duan, H. Multiple UAV distributed close formation control based on in-flight leadership hierarchies of pigeon flocks. Aerosp. Sci. Technol. 2017, 70, 471–486. [Google Scholar] [CrossRef]




| Parameters of GWO | Numerical Value |
|---|---|
| Iterations | 100 |
| Dimensions | 3 |
| Total number of wolves | 100 |
| Scale factor of detecting wolves | 0.5 |
| Step factor | 20 |
| Number of directions to summoning | 20 |
| Critical distance | 10 |
| The maximum number of rounding up | 10 |
| Parameters of UAV Performance | Numerical Value |
|---|---|
| Minimum velocity | 100 |
| Maximum velocity | 3 |
| Maximum angle of turning | 100 |
| Maximum angle of downthrust | 0.5 |
| Minimum distance from the obstacle | 20 |
| Safe distance | 20 |
| Method | Optimal Value | Mean Value | Worst Value | Variance |
|---|---|---|---|---|
| PSO | 0.08 | 0.382 | 4.41 | 0.146 |
| GWO | 0.017 | 0.213 | 2.57 | 0.0453 |
| AFO | 0.05 | 0.315 | 5.19 | 0.0992 |
| GA | 0.029 | 0.825 | 2.69 | 0.703 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Liu, Y.; Hu, C. Path Planning with Time Windows for Multiple UAVs Based on Gray Wolf Algorithm. Biomimetics 2022, 7, 225. https://doi.org/10.3390/biomimetics7040225
Zhang C, Liu Y, Hu C. Path Planning with Time Windows for Multiple UAVs Based on Gray Wolf Algorithm. Biomimetics. 2022; 7(4):225. https://doi.org/10.3390/biomimetics7040225
Chicago/Turabian StyleZhang, Changchun, Yifan Liu, and Chunhe Hu. 2022. "Path Planning with Time Windows for Multiple UAVs Based on Gray Wolf Algorithm" Biomimetics 7, no. 4: 225. https://doi.org/10.3390/biomimetics7040225
APA StyleZhang, C., Liu, Y., & Hu, C. (2022). Path Planning with Time Windows for Multiple UAVs Based on Gray Wolf Algorithm. Biomimetics, 7(4), 225. https://doi.org/10.3390/biomimetics7040225







