Starling-Behavior-Inspired Flocking Control of Fixed-Wing Unmanned Aerial Vehicle Swarm in Complex Environments with Dynamic Obstacles
Abstract
1. Introduction
2. Model of Starling Behavior
2.1. The Behavioral Mechanism of Starlings
2.2. Bevioral Patterns Based on Bevioral Mechanisms of Starlings
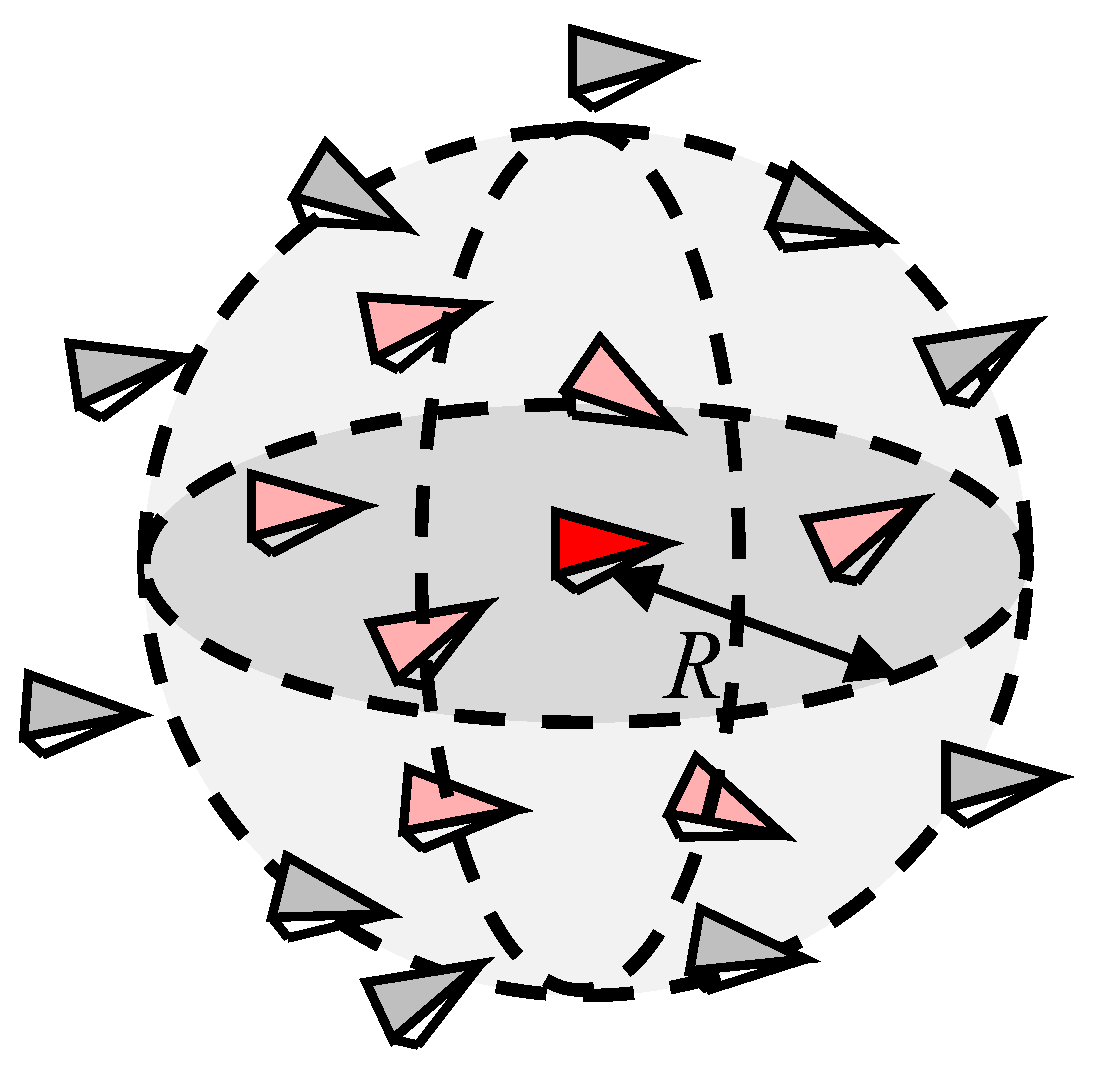
2.2.1. Collective Pattern
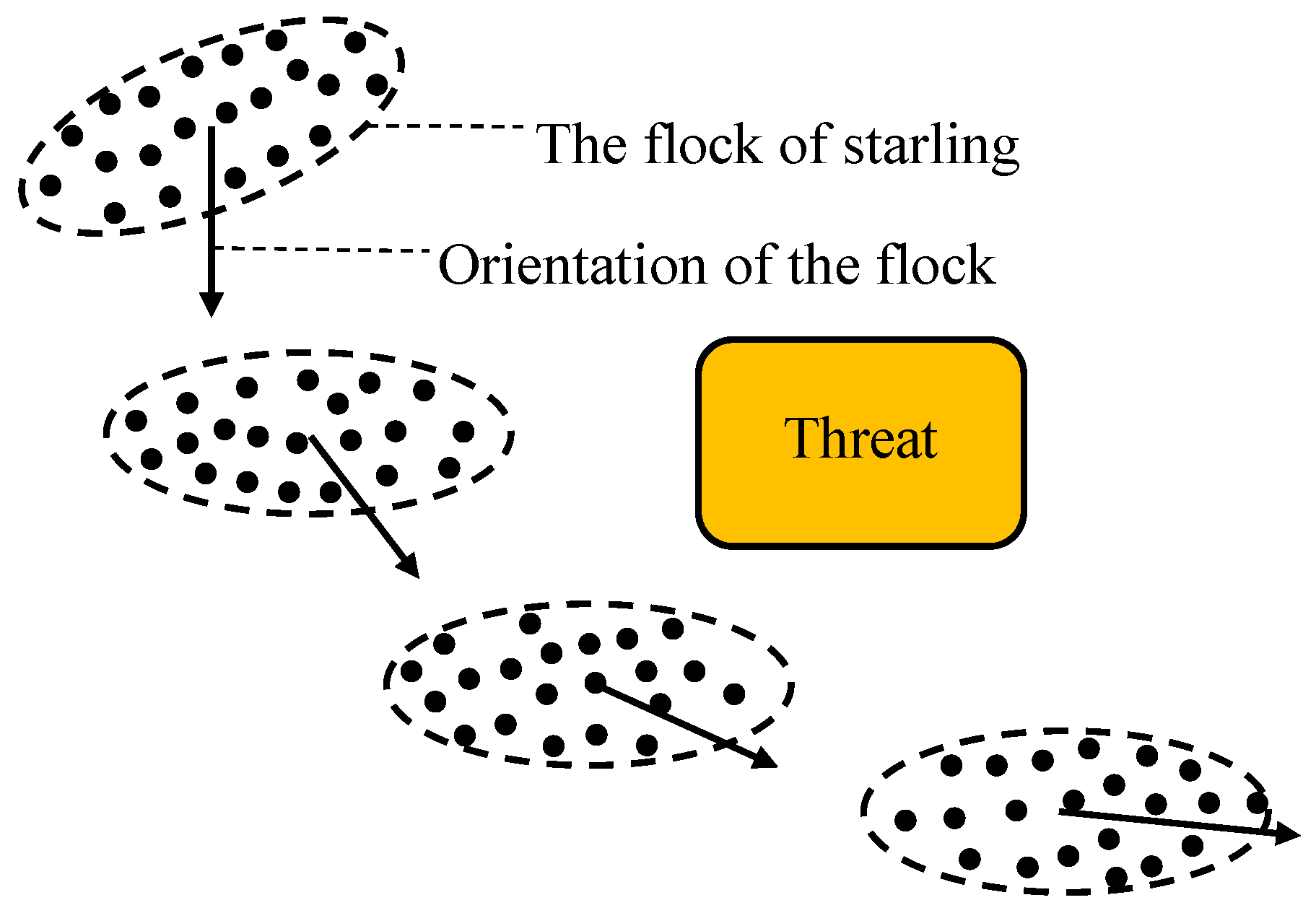
2.2.2. Evasion Pattern
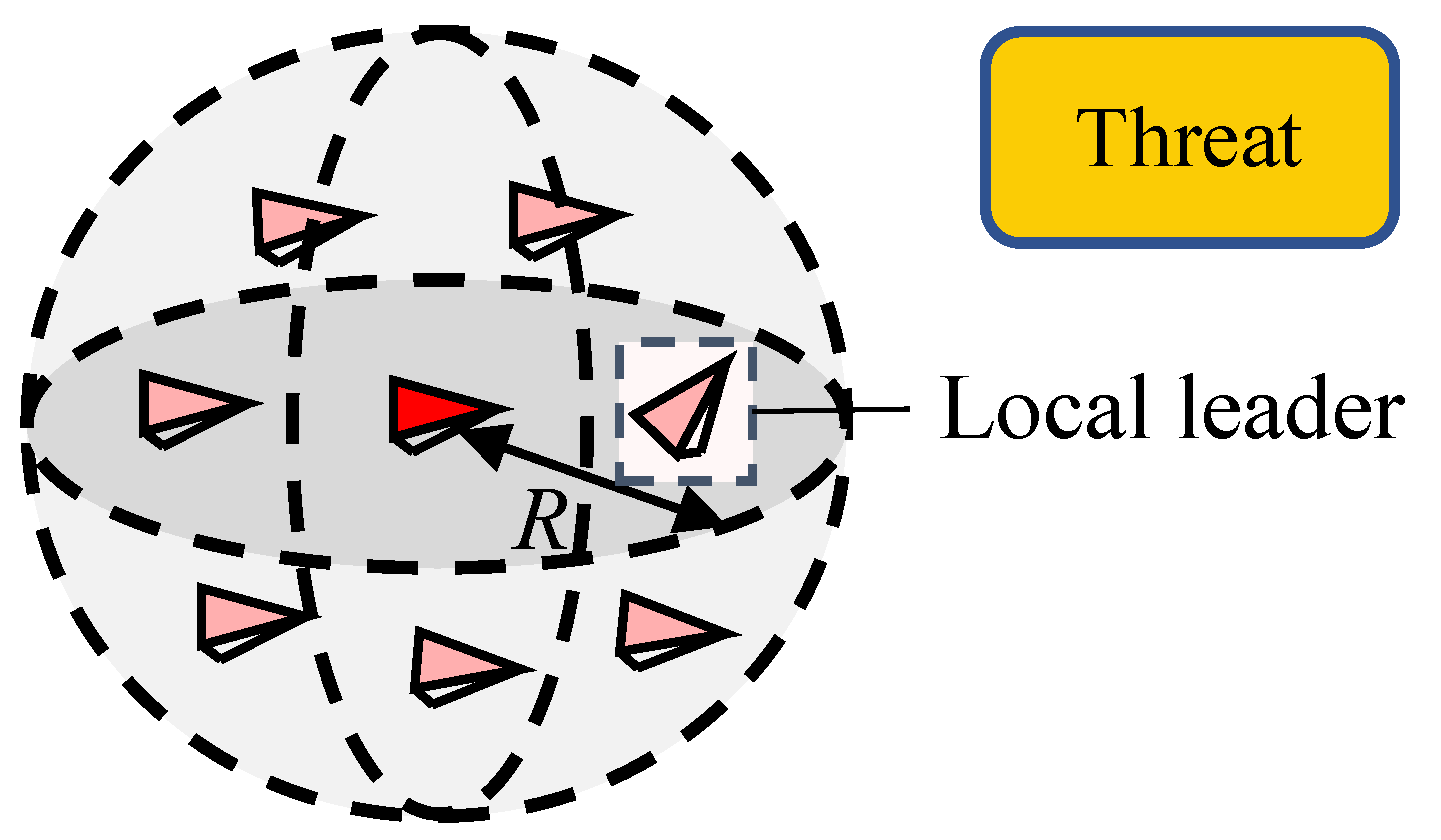
2.2.3. Local-Following Pattern
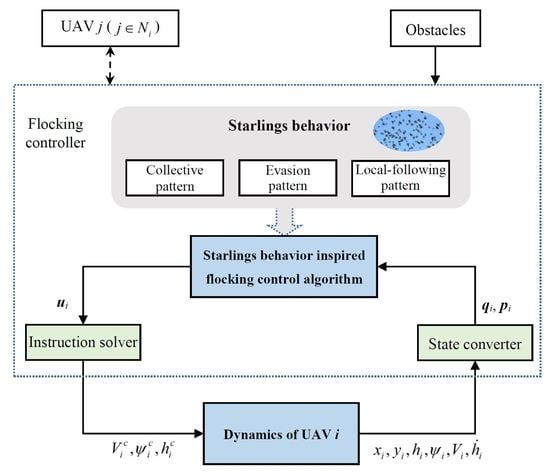
3. Starling-Behavior-Inspired Flocking Control for UAV Swarm
3.1. Model of UAV
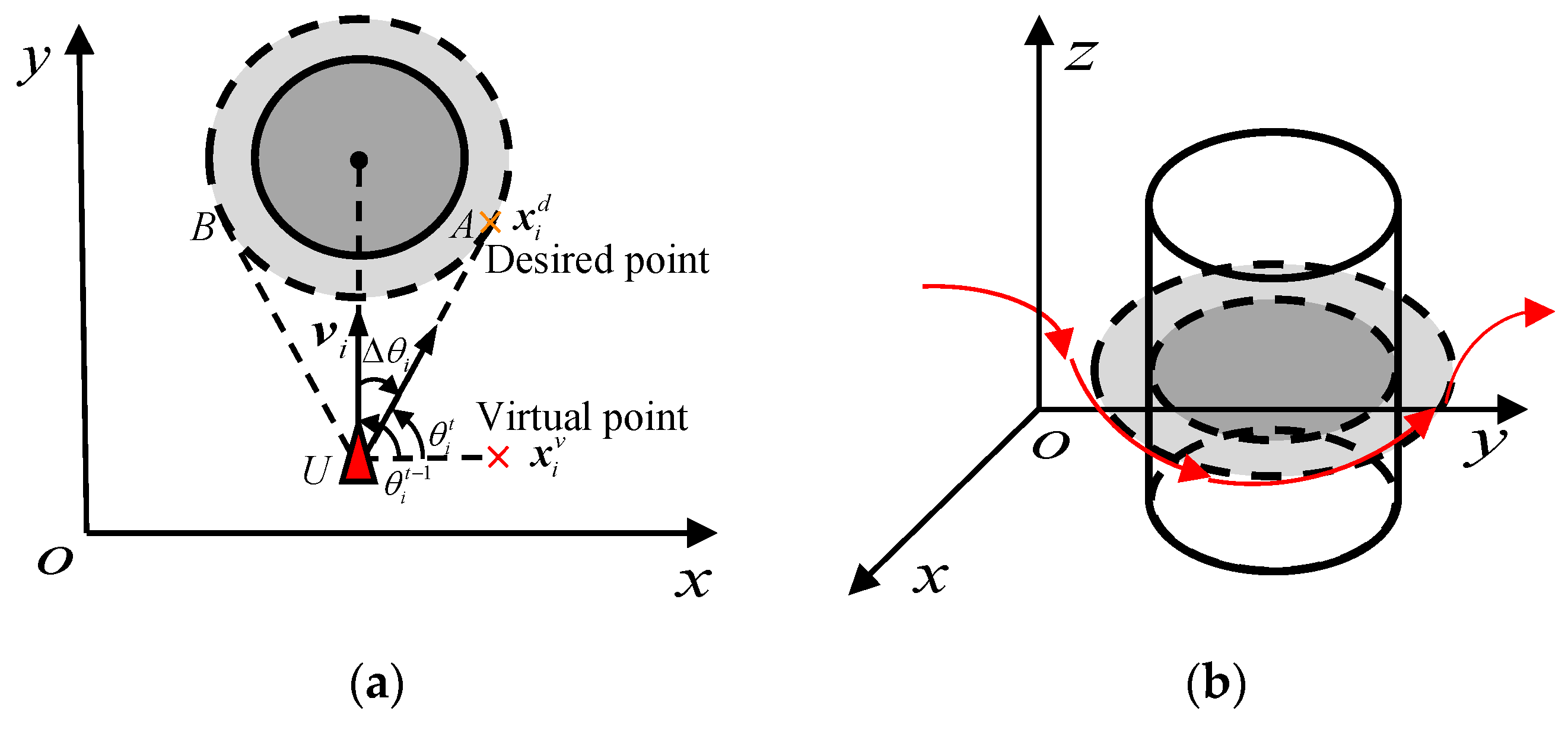
3.2. Collision Prediction Mechanism
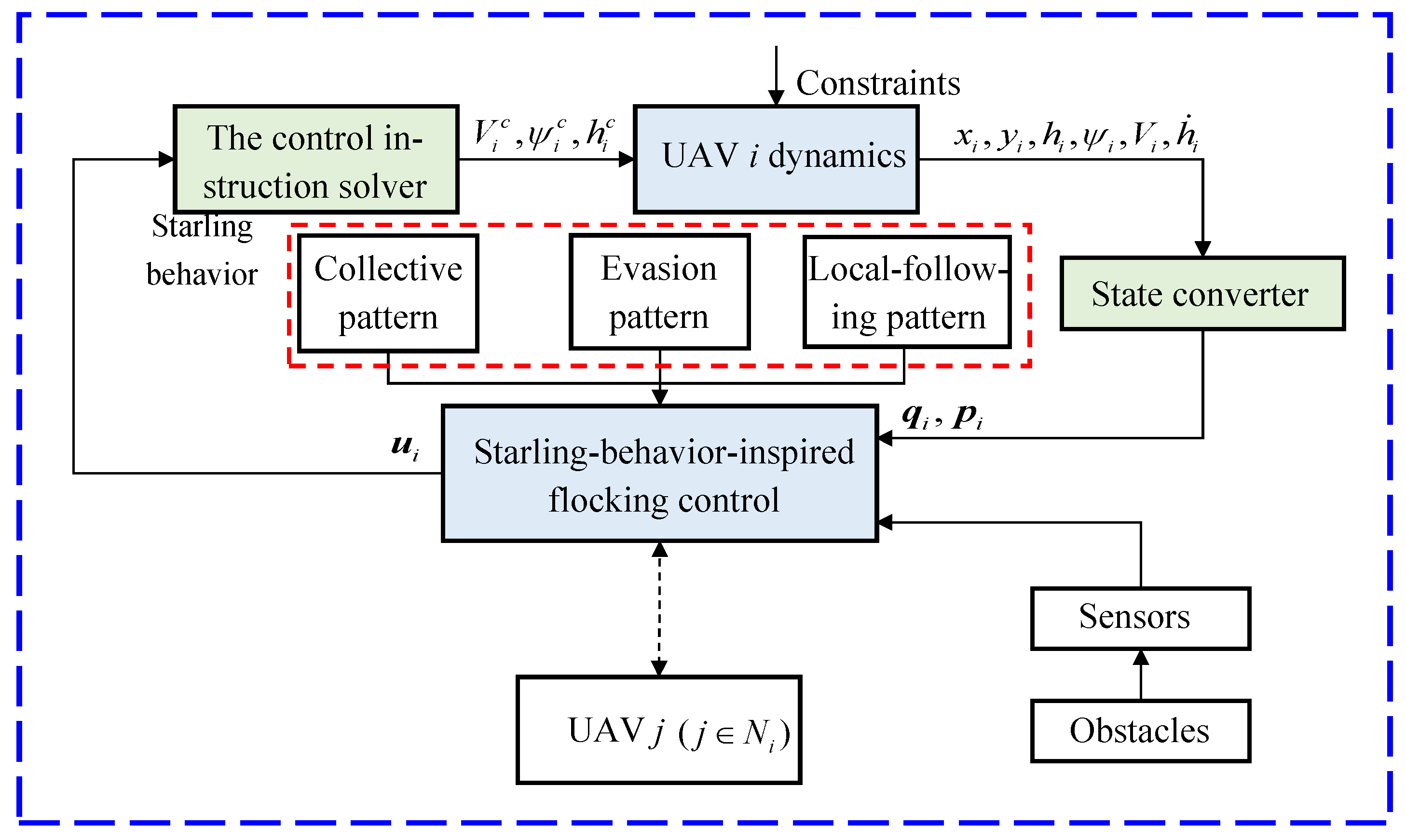
3.3. Mapping of the Intelligent Behavioral Patterns of Starlings
| Algorithm 1. Starling-behavior-inspired flocking control algorithm for UAVs |
| /*Initialization*/ Set initial parameters of the proposed algorithm and the model of fixed-wing UAV Generate the position of UAV i randomly /*Begin*/ for i = 1 to n for j = 1 to n Select neighbors according to Equation (1) if UAV j is the neighbor of UAV i UAV i interact with UAV j according to Equation (21) according to Equation (9) end if according to Equation (12) according to Equations (10) and (11) end for to Equation (16) Execute collision prediction according to Equation (17) Calculate the control signal of evasion pattern of UAV i according to Equation (22) end if if there exist a local leader li Set parameter β = 0 UAV i follows the local leader according to Equation (21) end if end if Follow the virtual leader according to Equation (23) /*Limitation*/ Set limitations according to Equation (15) Update the position and velocity according to Equations (24) and (25) end for |
3.4. Conversion of Patterns
4. Simulation Results and Analysis
4.1. Performance Metrics
- (1)
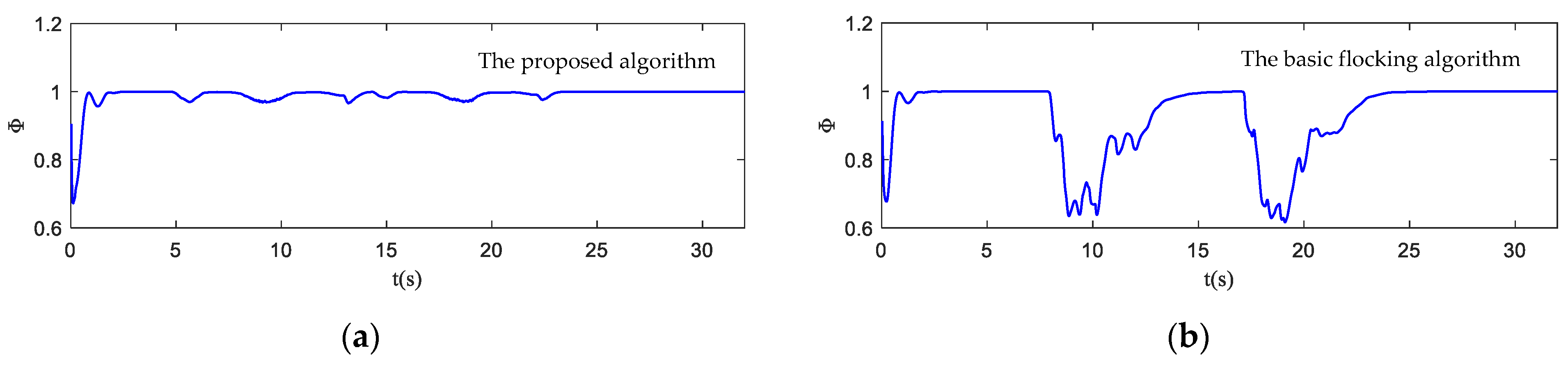
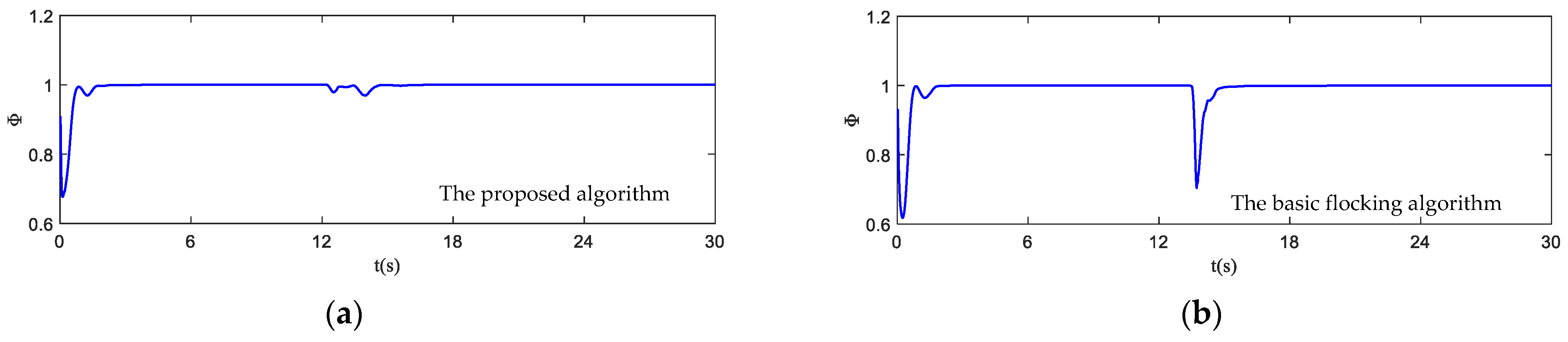
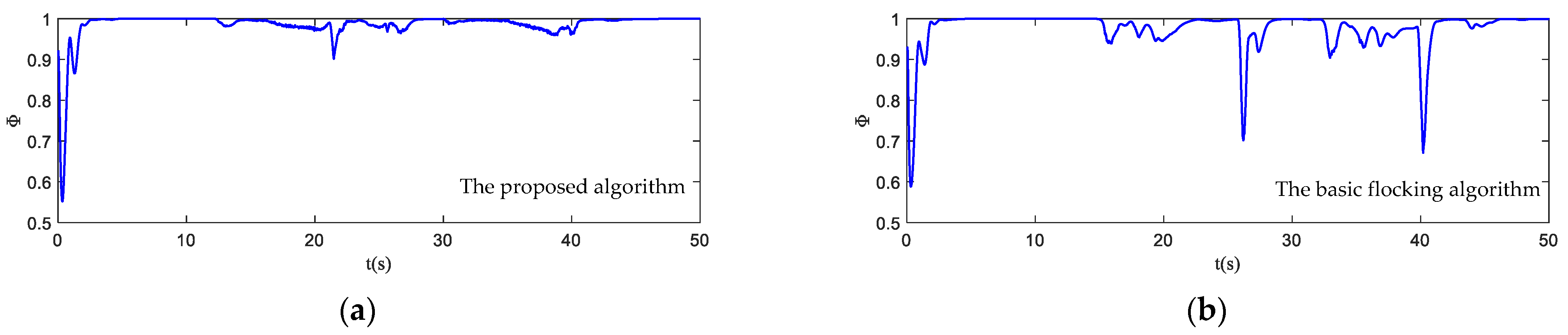
- Order parameter: it captures the coordination of the motion of the UAV swarm and represents the velocity alignment degree of all UAVs in the swarm.where varies from [0, 1]. indicates that the UAV swarm is in an ordered state while indicates that the UAV swarm is in a chaotic state.
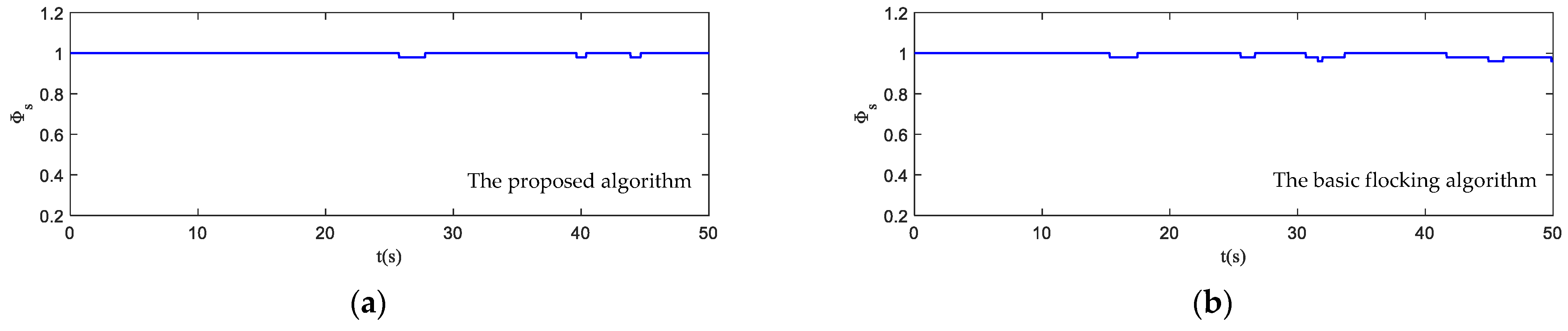
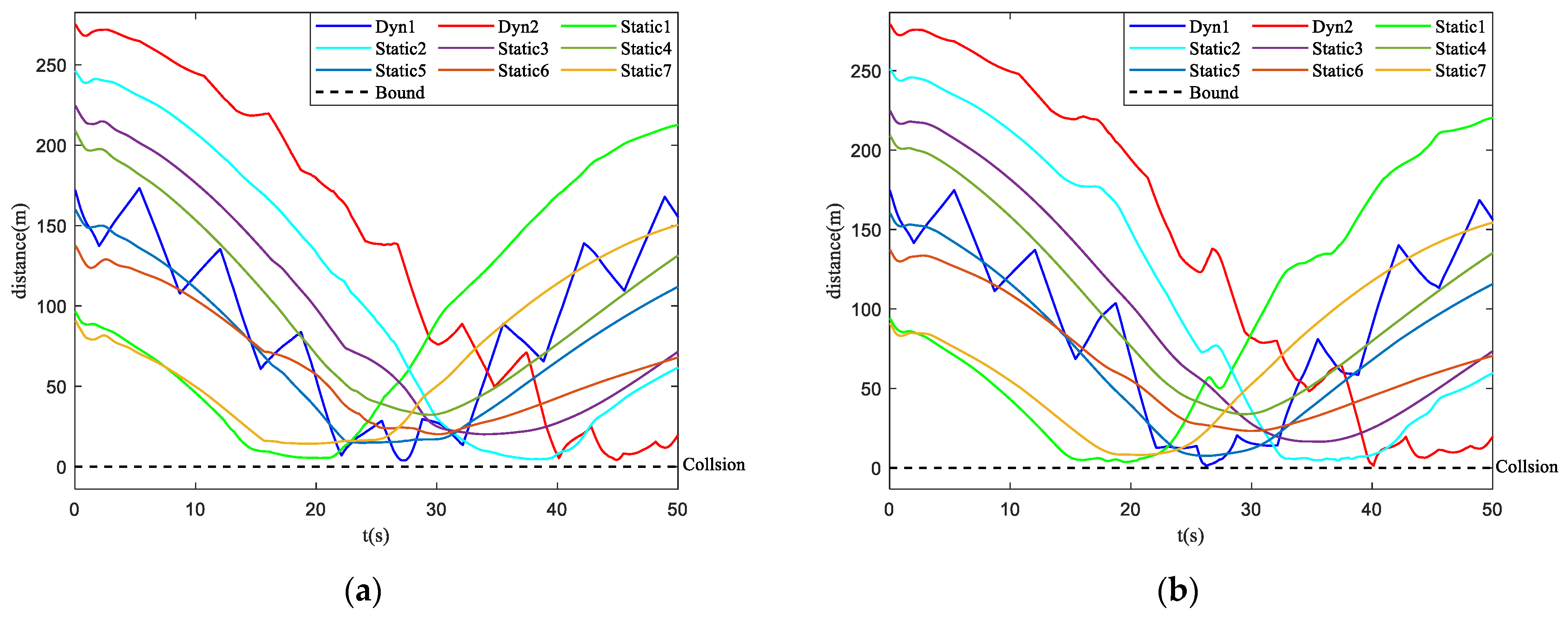
- (2)
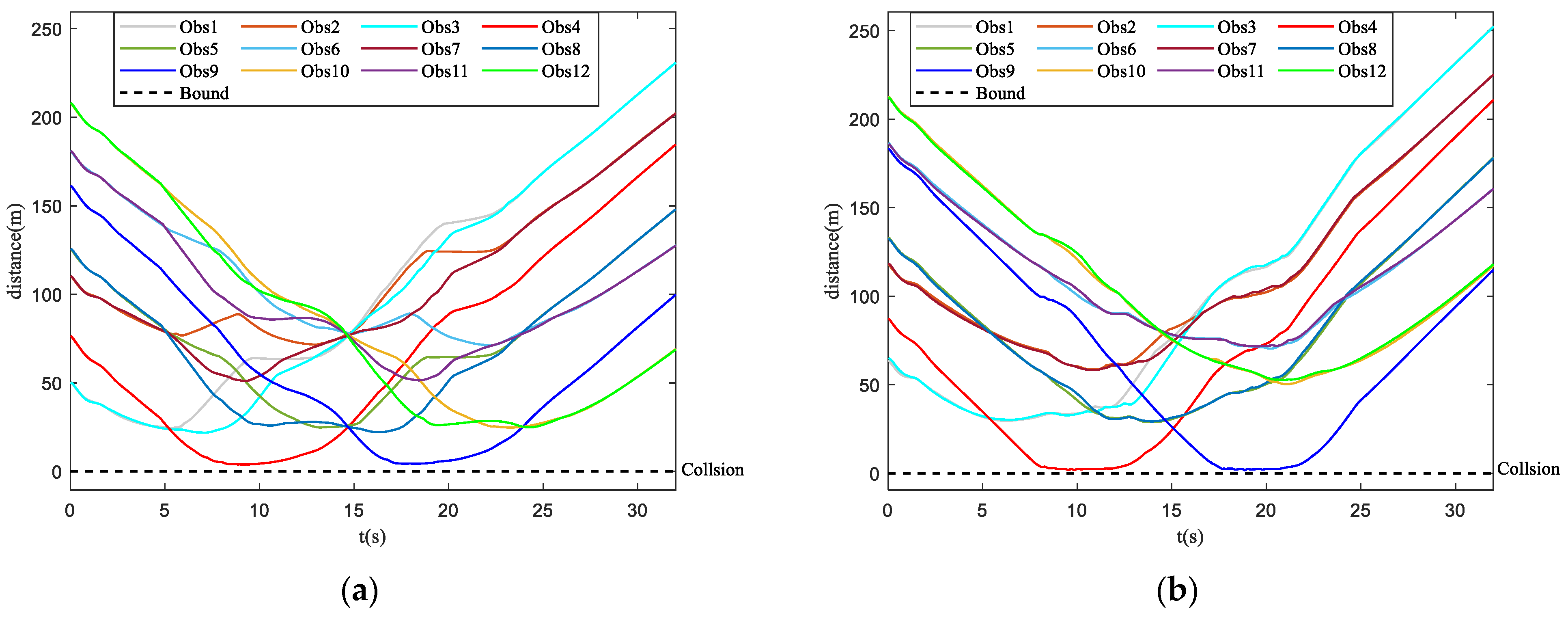
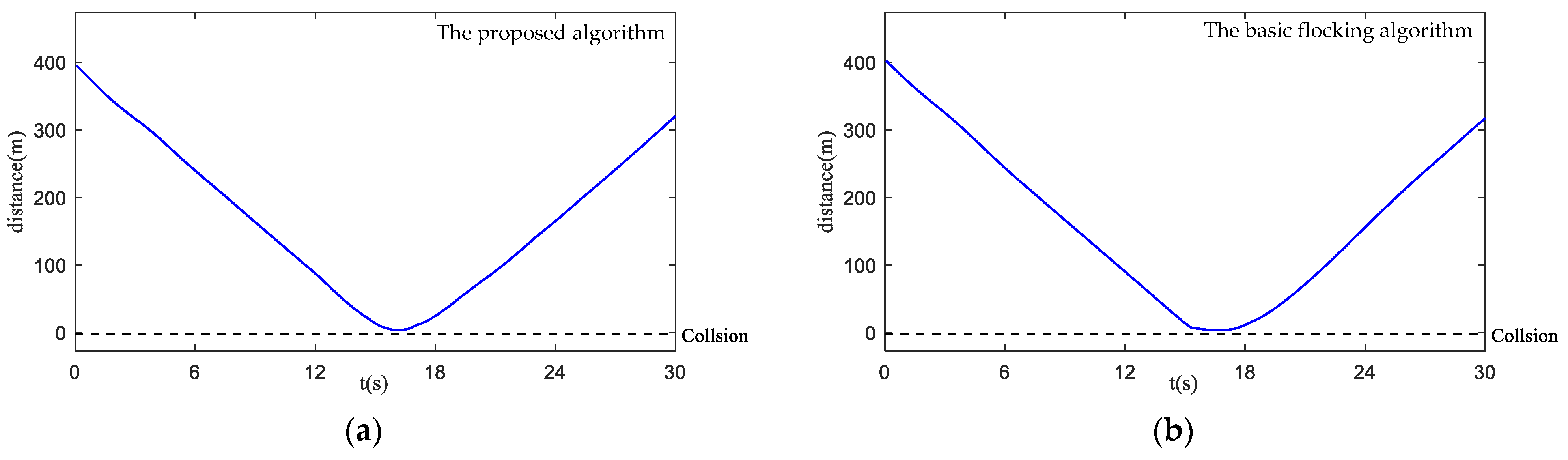
- Safety metrics: it measures the risk of collision between the UAV swarm and obstacles and assesses the ability of the UAV swarm to avoid collisions with the obstacles.where the number of UAV that enters the obstacle zone is . reveals that no UAVs enter the obstacle zone while reveals that the whole UAV swarm enters the obstacle zone.
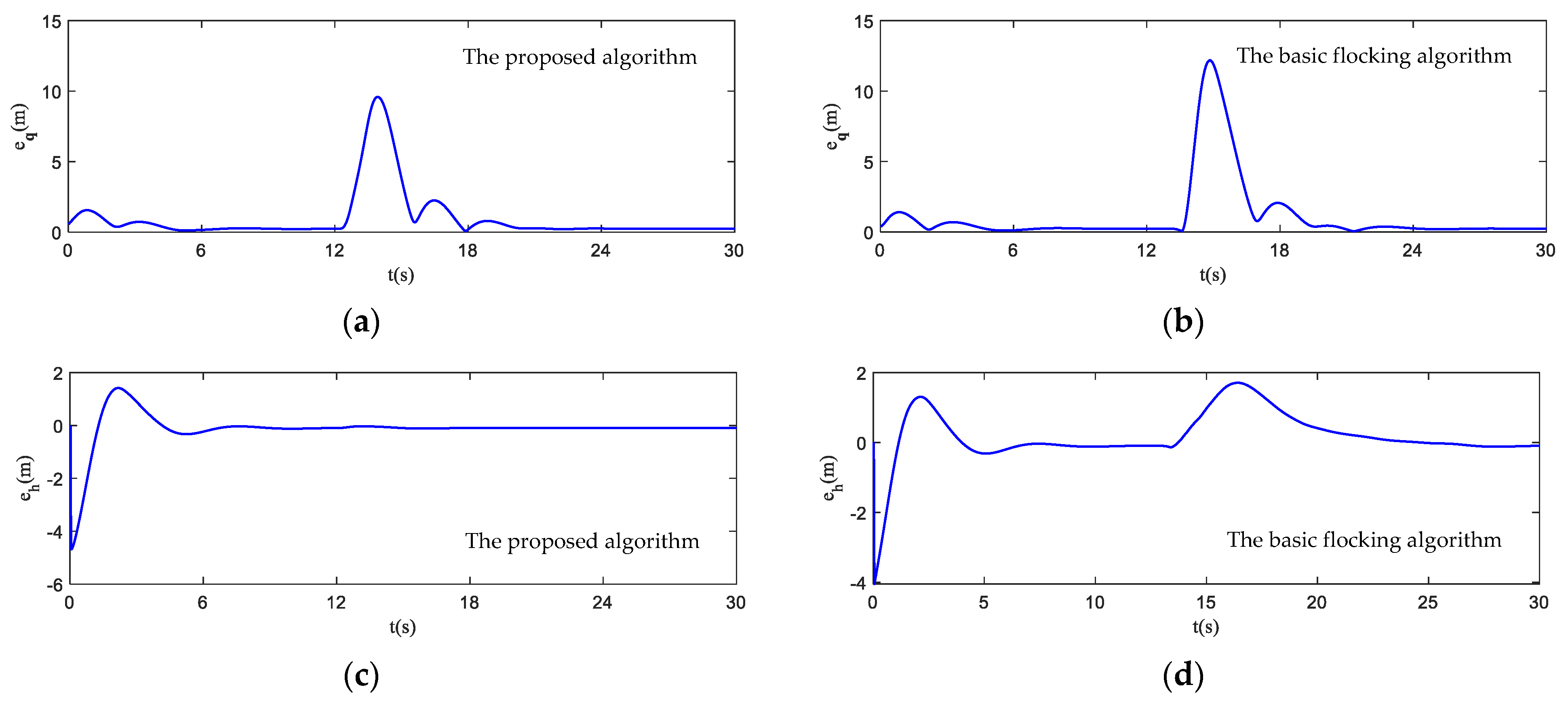
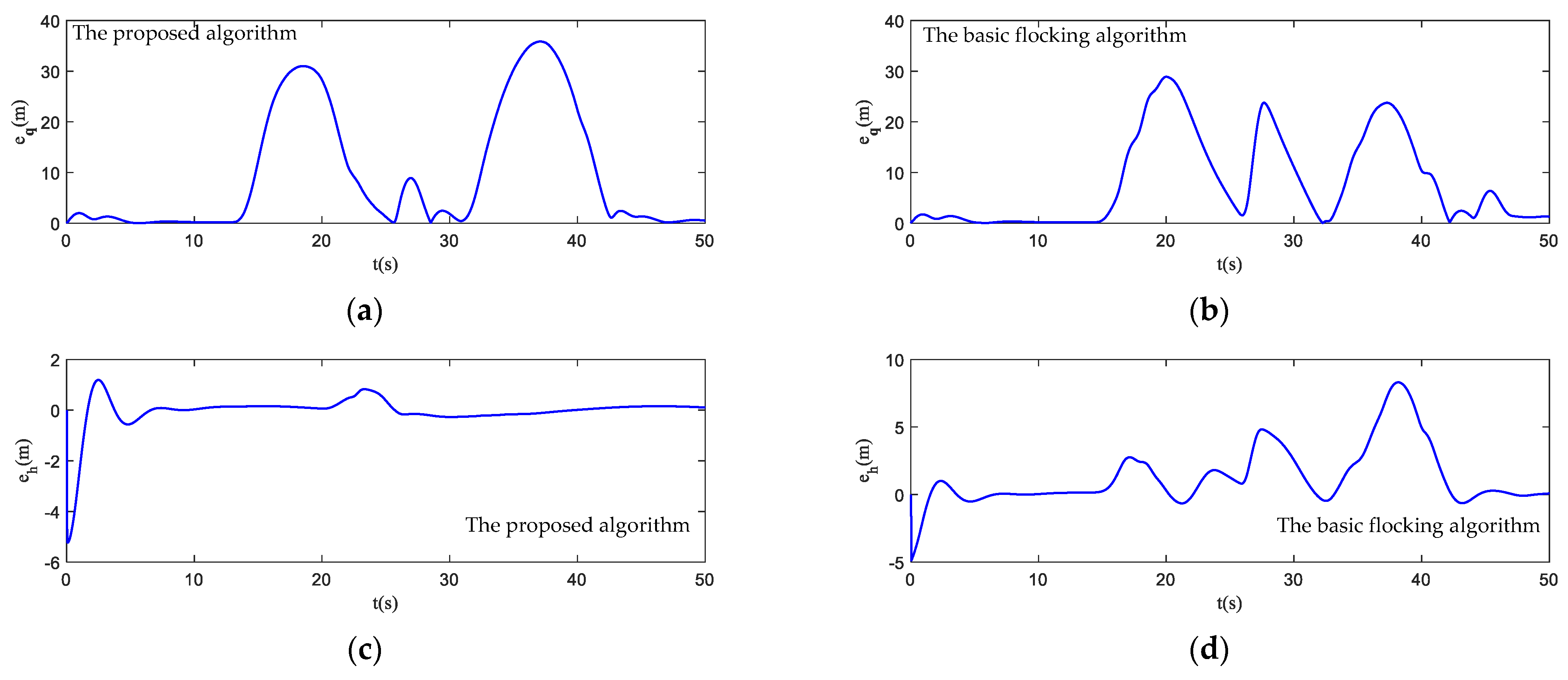
- (3)
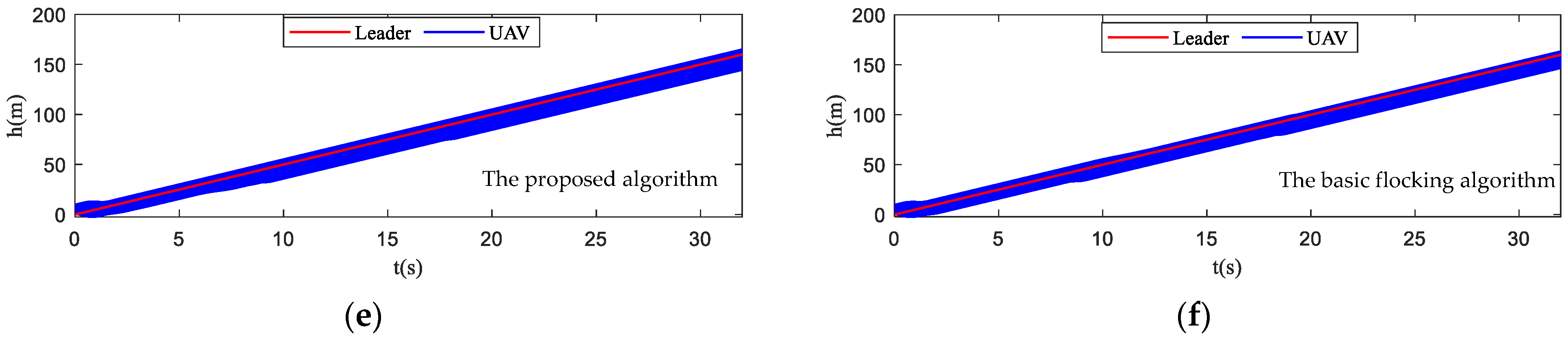
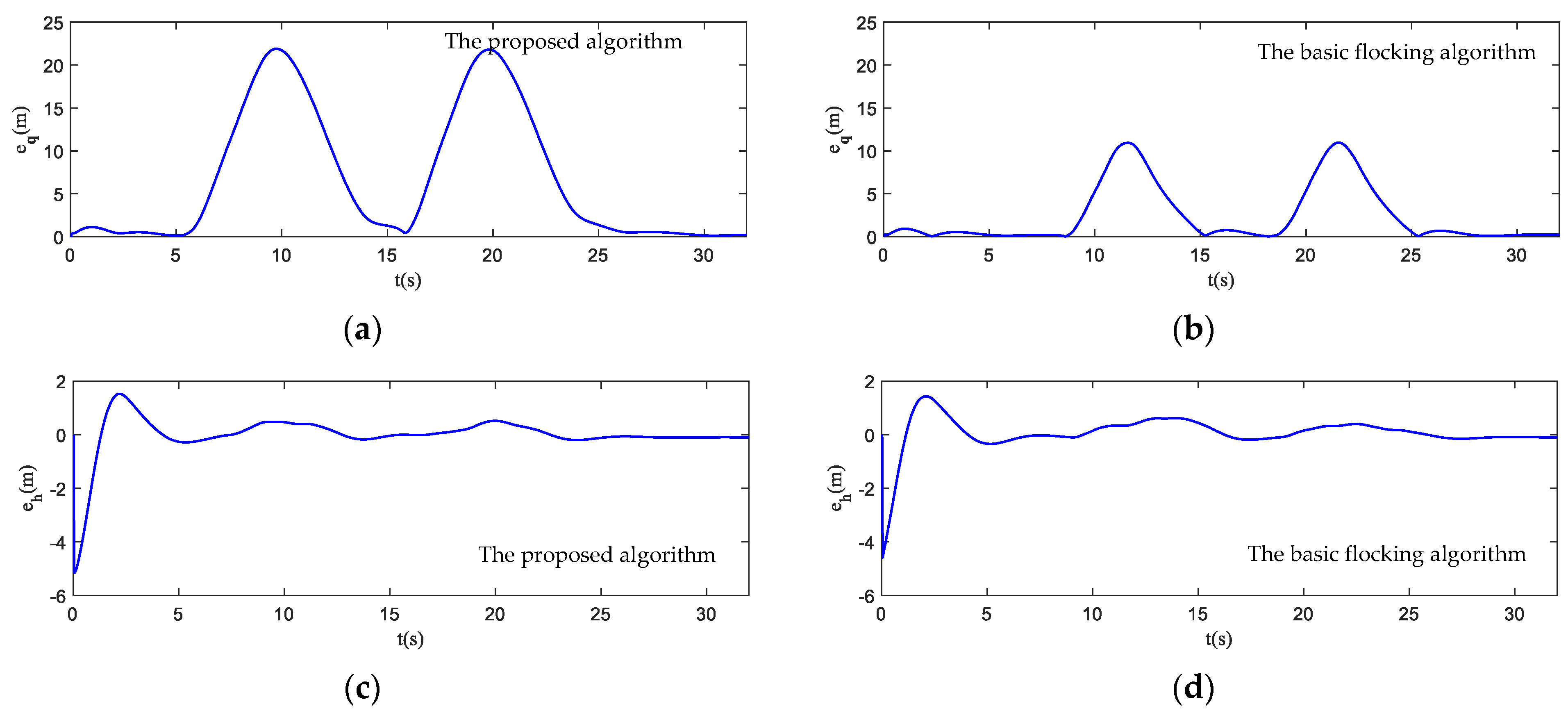
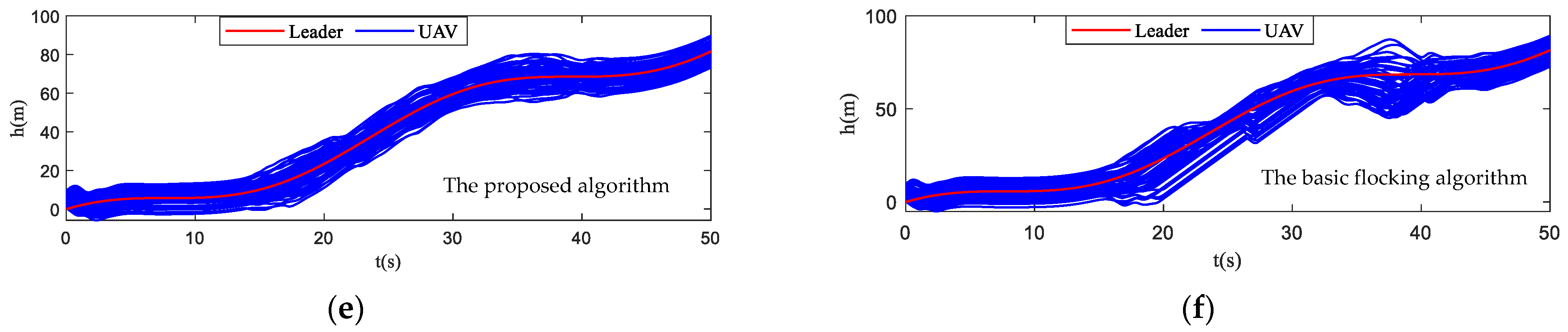
- Tracking error: it evaluates the tracking performance of the UAV swarm. The tracking error of position is error between the position of UAV swarm and virtual leader, which can be described as follows:The tracking error of altitude is error between the altitude of UAV swarm and virtual leader, which can be described as follows:
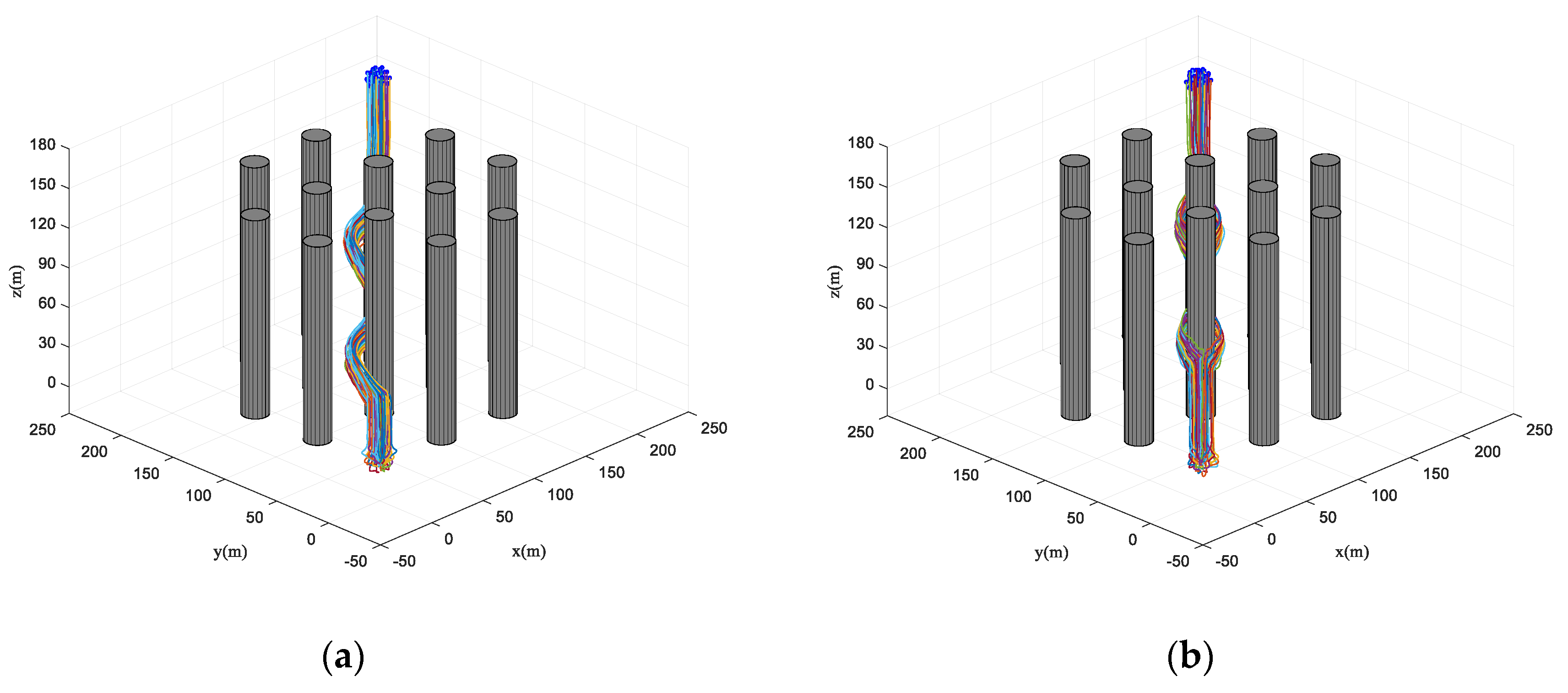
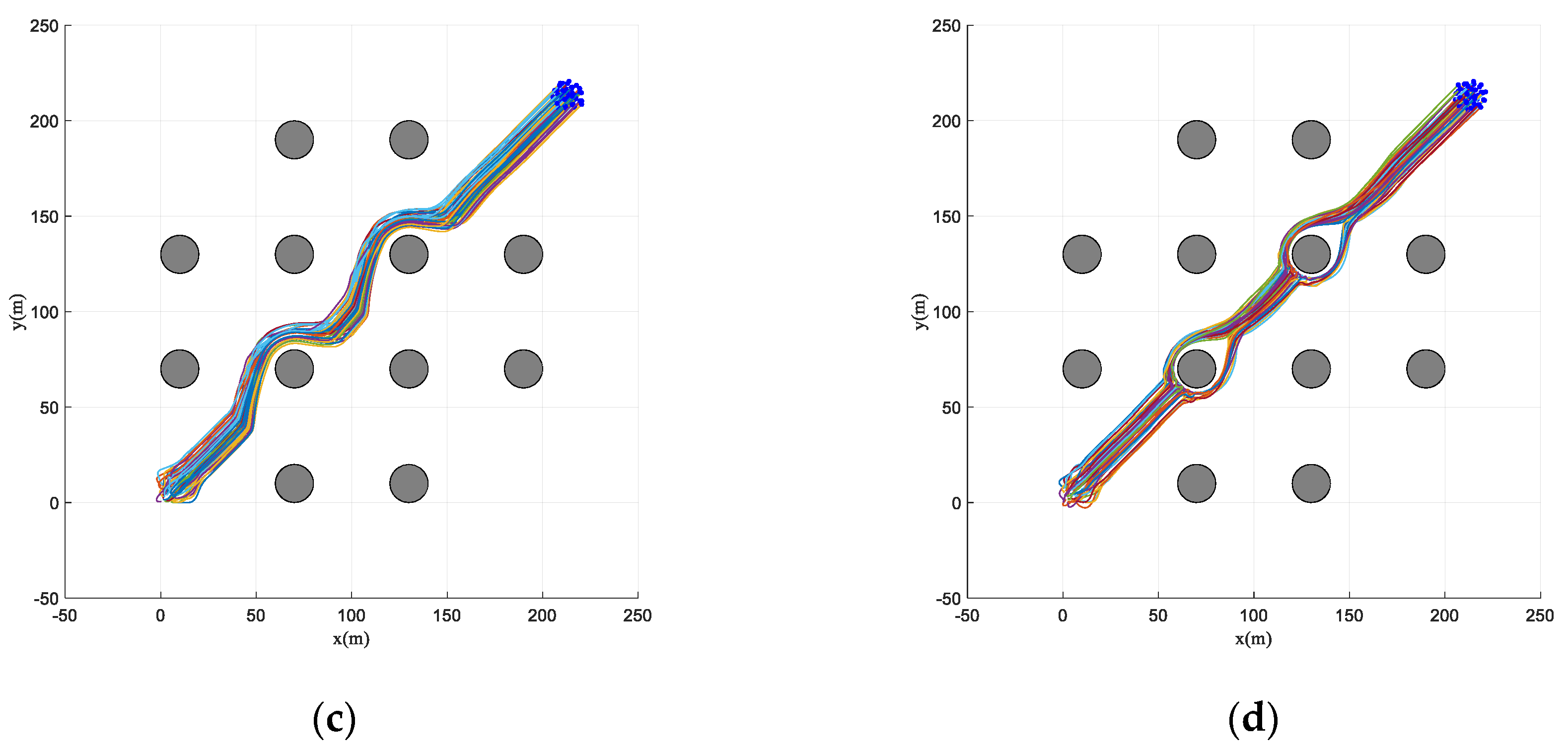
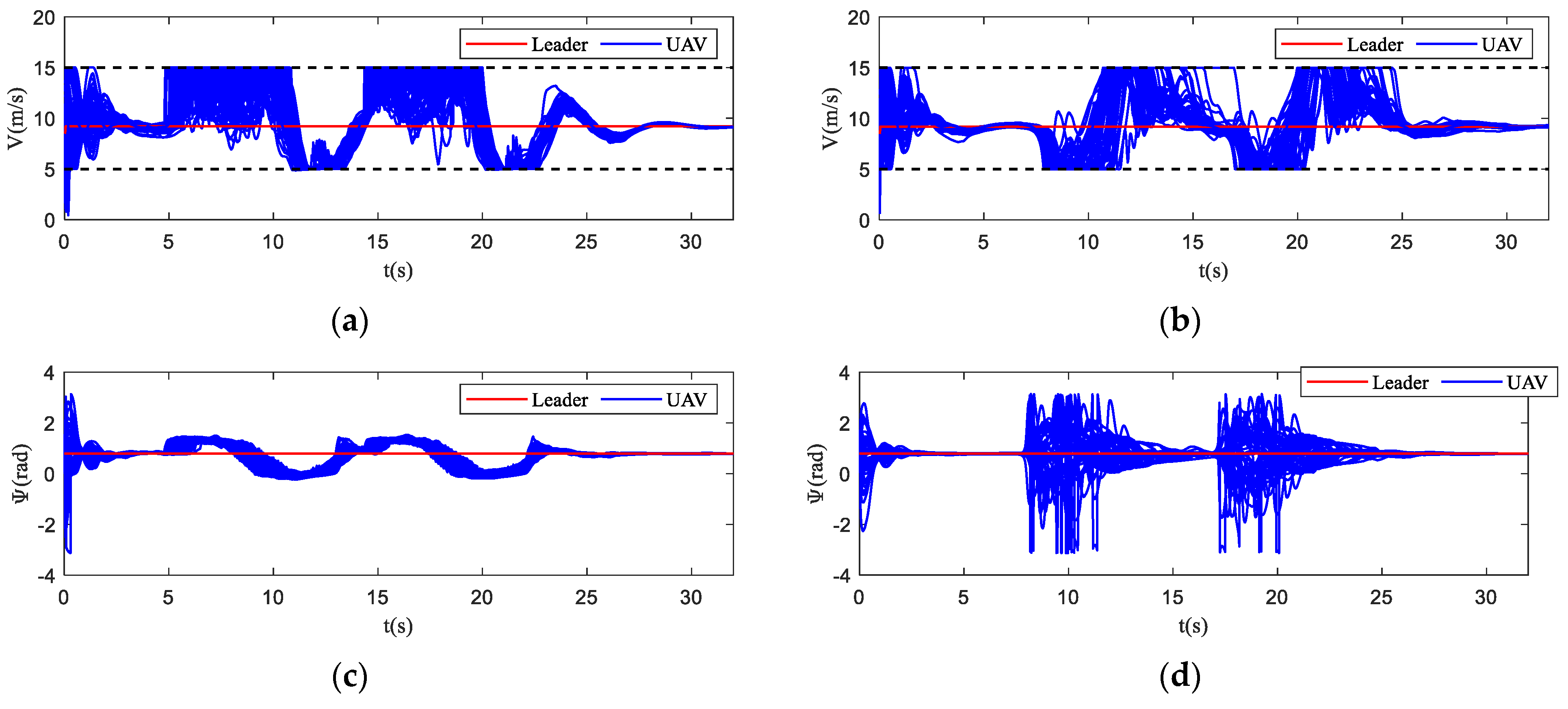
4.2. Simulation in Obstacle-Dense Environment
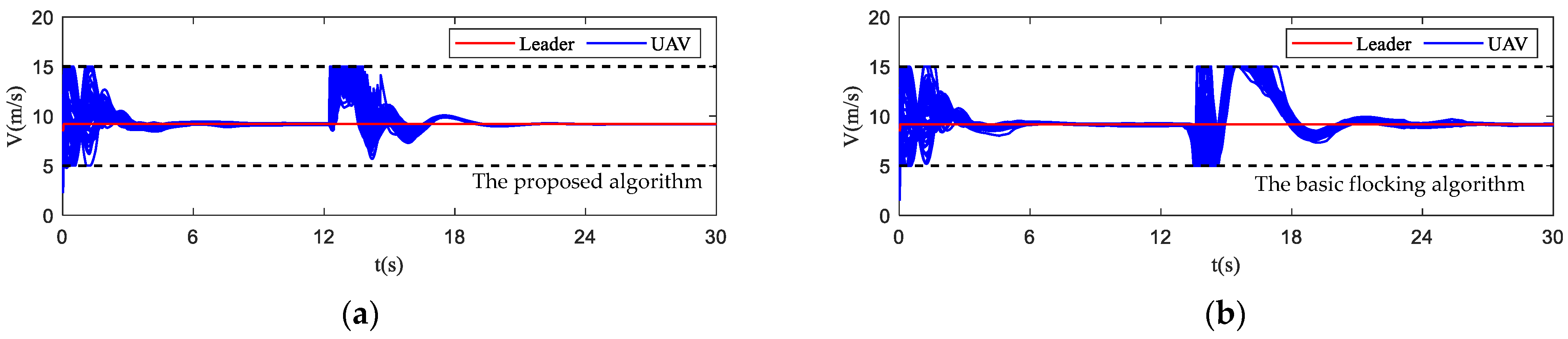
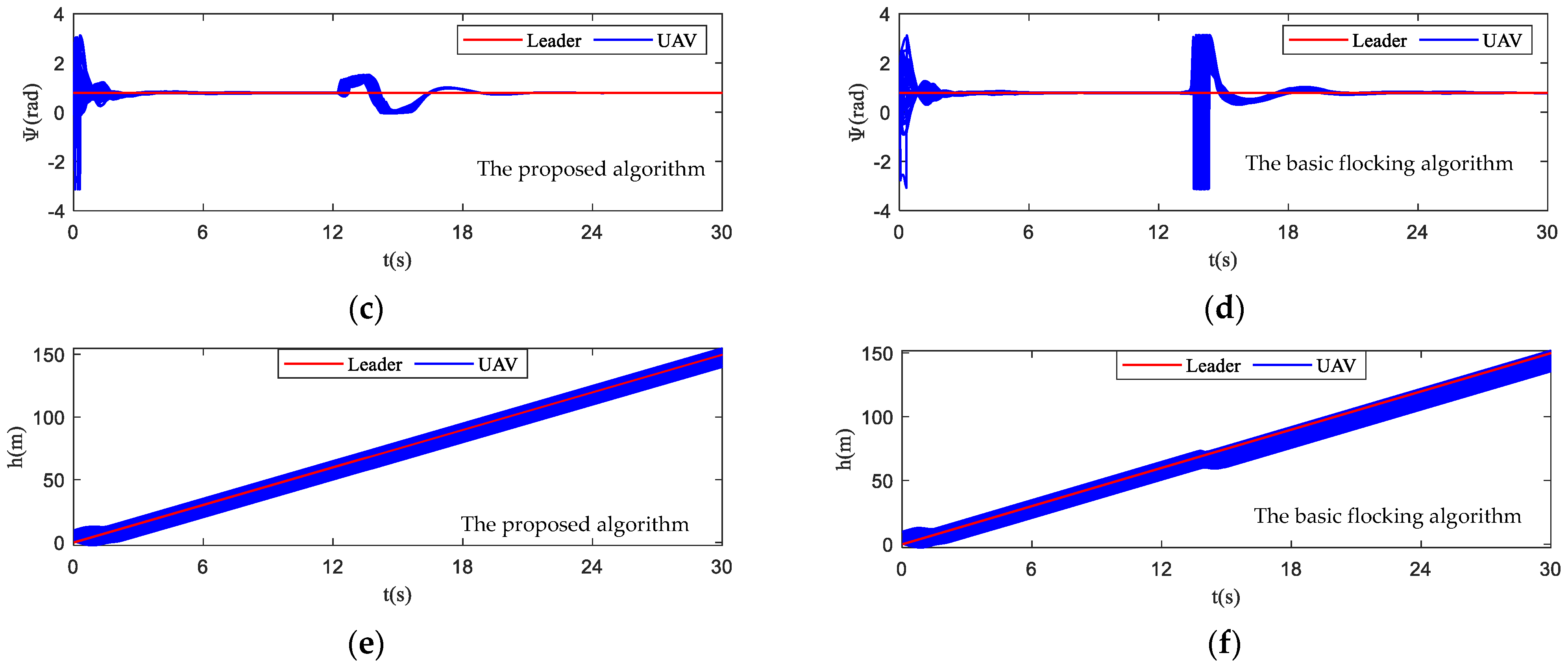
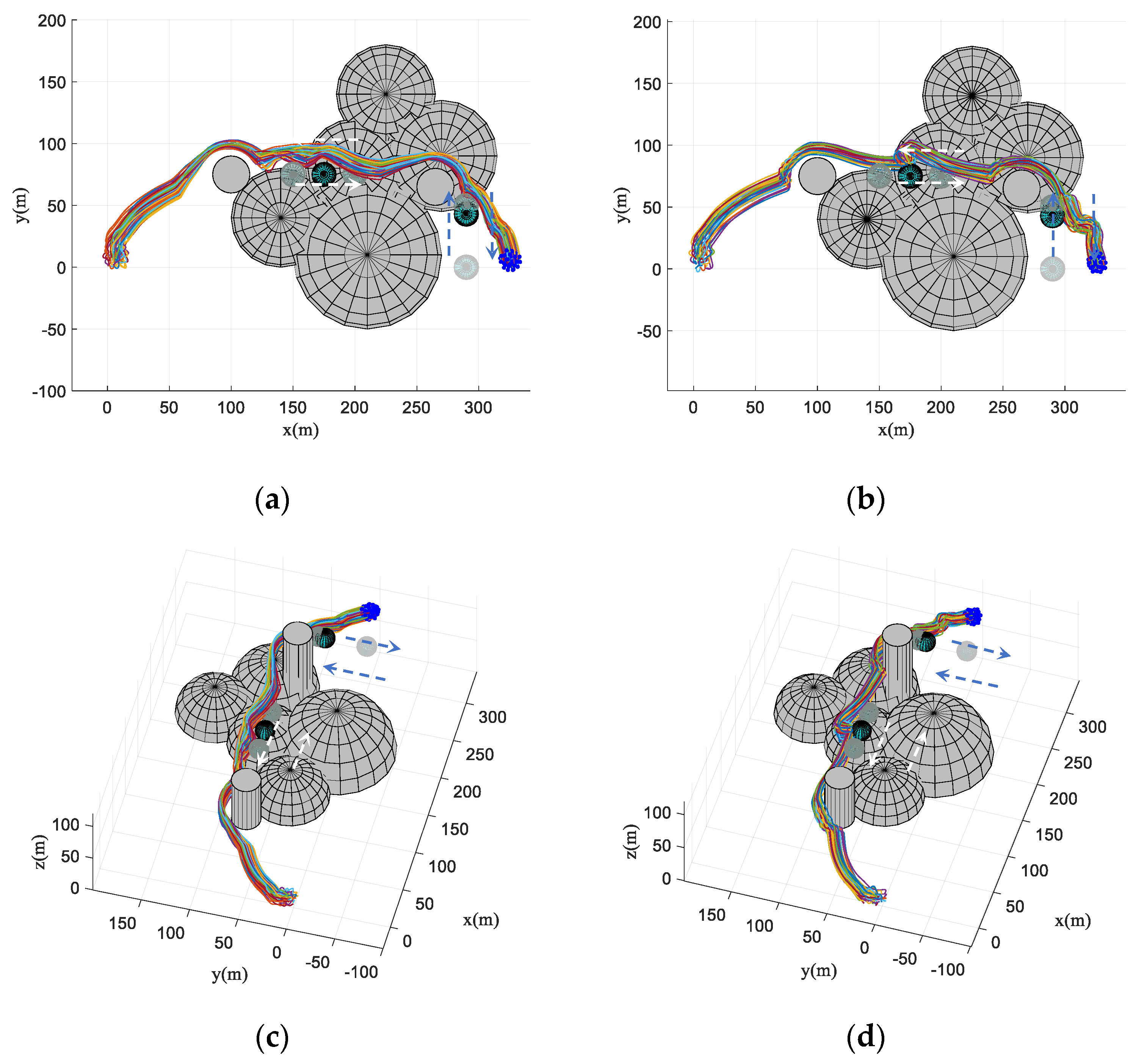
4.3. Simulation in Dynamic Threat Environment
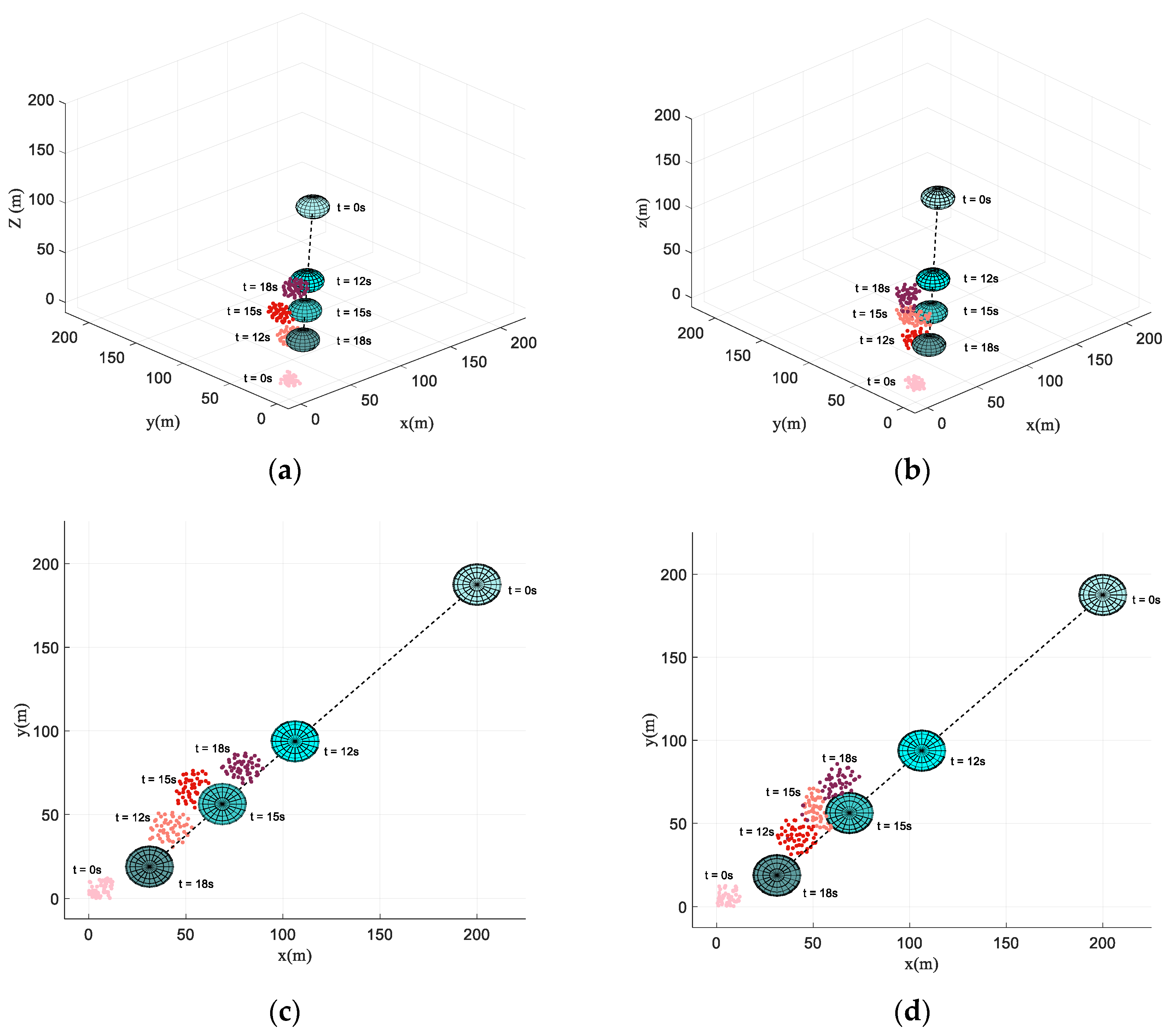
4.4. Simulation in Obstacle Environment with Static and Dynamic Obstacles
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Reynolds, A.; Mclvor, G. Stochastic modeling of bird flocks: Accounting for the cohesiveness of collective motion. J. R. Soc. Interface 2022, 19, 20210745. [Google Scholar] [CrossRef]
- Papadopoulou, M.; Hildenbrandt, H. Emergence of splits and collective turns in pigeon flocs under predation. R. Soc. Open Sci. 2022, 9, 211898. [Google Scholar] [CrossRef] [PubMed]
- Susumu, I.; Nariya, U. Emergence of a giant rotating cluster of fish in three dimensions by local interactions. J. Phys. Soc. Jpn. 2022, 91, 064806. [Google Scholar]
- Costanzo, A.; Hildenbrandt, H. Causes of variation of darkness in flocks of starlings, a computational model. Swarm Intell. 2022, 16, 91–105. [Google Scholar] [CrossRef]
- Hemelrijk, C.; Zuidam, L. What underlies waves of agitation in starling flocks. Behav. Ecol. Sociobiol. 2015, 69, 755–764. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, C. Flocks, herds and schools: A distributed behavioral model. Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- Vicsek, T.; Czirok, A. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 1995, 75, 1226–1229. [Google Scholar] [CrossRef] [PubMed]
- Couzin, I.; Krause, J. Collective memory and spatial sorting in animal groups. J. Theor. Biol. 2002, 218, 1–11. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control. 2006, 51, 401–420. [Google Scholar] [CrossRef]
- Tanner, H.G.; Jadbabaie, F. Flocking in fixed and switch networks. IEEE Trans. Autom. Control. 2007, 52, 863–868. [Google Scholar] [CrossRef]
- Duan, H.; Qiao, P. Pigeon-inspired optimization a new swarm intelligence optimizer for air robot path planning. Int. J. Intell. Comput. Cybern. 2014, 7, 24–37. [Google Scholar] [CrossRef]
- Zhang, X.; Xia, S. Quantum behavior-based enhanced fruit fly optimization algorithm with application to UAV path planning. Int. J. Comput. Intell. Syst. 2020, 13, 1315–1331. [Google Scholar] [CrossRef]
- Zhou, Z.; Duan, H. Unmanned aerial vehicle close formation control based on the behavior mechanism in wild geese. Sci. Sin. Technol. 2017, 47, 230–238. [Google Scholar] [CrossRef]
- Xie, R.; Gu, C. A starling swarm coordination algorithm. Wuhan Univ. (Nat. Sci. Ed.) 2019, 65, 229–237. [Google Scholar]
- Grammatikis, P.; Sarigianndis, P. A compilation of UAV applications for precision agriculture. Comput. Netw. 2020, 172, 107148. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, T. A hybrid optimization framework for UAV reconnaissance mission planning. Comput. Ind. Eng. 2022, 173, 108653. [Google Scholar] [CrossRef]
- Pei, J.; Chen, H. UAV-assisted connectivity enhancement algorithms for multiple isolated sensor networks in agricultural Internet of things. Comput. Netw. 2022, 207, 108854. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, Y. Multi-UAV cooperative reconnaissance mission planning novel method under multi-radar detection. Sci. Prog. 2022, 105, 1–20. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Liu, C. Dynamic anti-collision A-star algorithm for multi-ship encounter situations. Appl. Ocean. Res. 2022, 118, 102995. [Google Scholar] [CrossRef]
- Wu, Y.; Gou, J. A new consensus theory-based method for formation and obstacle avoidance of UAVs. Aerosp. Sci. Technol. 2020, 107, 106332. [Google Scholar] [CrossRef]
- Tian, S.; Li, Y. Multi-robot path planning in wireless sensor networks based on jump mechanism PSO and safety gap obstacle avoidance. Future Gener. Comput. Syst. 2021, 118, 37–47. [Google Scholar] [CrossRef]
- Vargas, S.; Becerra, H. MPC-based distributed formation control of multiple quadcopters with obstacle avoidance and connectivity maintenance. Control. Eng. Pract. 2022, 121, 105054. [Google Scholar] [CrossRef]
- Zhang, X.; Duan, H. Altitude consensus-based 3D flocking control for fixed-wing unmanned aerial vehicle swarm trajectory tracking. Proc. Inst. Mech.Eng. Part G J. Aerosp. Eng. 2016, 230, 2628–2638. [Google Scholar] [CrossRef]
- Qi, J.; Guo, J. Formation tracking and obstacle avoidance for multi quadrotors with static and dynamic obstacles. IEEE Robot. Autom. Lett. 2022, 7, 1713–1722. [Google Scholar] [CrossRef]
- Wu, J.; Wang, H. Learning-based fixed-wing UAV reactive maneuver control for obstacle avoidance. Aerosp. Sci. Technol. 2022, 316, 107623. [Google Scholar] [CrossRef]
- Liu, X.; Yan, C. Towards flocking navigation and obstacle avoidance for multi-UAV systems through hierarchical weighting Vicsek model. Aerospace 2021, 8, 286. [Google Scholar] [CrossRef]
- Fu, X.; Pan, J. A formation maintenance and reconstruction method of UAV swarm based on distributed control. Aerosp. Sci. Technol. 2020, 104, 105981. [Google Scholar] [CrossRef]
- Lim, J.; Pyo, S.; Kim, N.; Lee, J.; Lee, J. Obstacle magnification for 2-D collision and occlusion avoidance autonomous multirotor aerial vehicles. IEEE/ASME Trans. Mechatron. 2020, 25, 2428–2436. [Google Scholar] [CrossRef]
- Hemelrijk, C.; Hildenbrant, H. Diffusion and topological neighbors in flocks of starlings: Relating a model to empirical data. PLoS ONE 2015, 10, e0126913. [Google Scholar] [CrossRef] [PubMed]
- Ballerini, M.; Cabibbo, N. Empirical investigation of starling flocks: A benchmark study in collective animal behavior. Anim. Behav. 2008, 76, 201–215. [Google Scholar] [CrossRef]
- Carere, C.; Montanino, S. Aerial flocking patterns of wintering starlings, Sturnus vulgaris, under different predation risk. Anim. Behav. 2009, 77, 101–107. [Google Scholar] [CrossRef]
- Procaccini, A.; Orlandi, A. Propagating waves in starling, Sturnus vulgaris, flocks under predation. Anim. Behav. 2011, 82, 759–765. [Google Scholar] [CrossRef]
- Hogan, B.; Hidenbrandt, H. The confusion effect when attacking simulated three-dimensional starling flocks. R. Soc. Open Sci. 2017, 4, 160564. [Google Scholar] [CrossRef] [PubMed]
- Brown, J.; Bossomaier, T. Information transfer in finite flocks with topological interactions. J. Comput. Sci. 2021, 53, 101370. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Sharaki, M. Starling murmuration optimizer: A novel bio-inspired algorithm for global and engineering. Computer Methods in Applied Mechanics and Engineering. 2022, 392, 114616. [Google Scholar] [CrossRef]
- Storms, R.; Carere, C. Complex patterns of collective escape in starling flocks under predation. Behav. Ecol. Sociobiol. 2019, 73, 10. [Google Scholar] [CrossRef]
- Olcay, E.; Schuhmann, F. Collective navigation of a multi-robot system in an unknown environment. Robot. Auton. Syst. 2020, 132, 103604. [Google Scholar] [CrossRef]
- Yu, Y.; Duan, H. Turning control multiple UAVs imitating the super-maneuver behavior in massive starling. Robot 2020, 42, 385–393. [Google Scholar]
- Lei, X.; Liu, M. Fission control algorithm for swarm based on local following interaction. Control. Decis. 2013, 28, 741–746. [Google Scholar]
- Nagy, M.; Ákos, Z.; Biro, D.; Vicsek, T. Hierarchical group dynamic in pigeon flocks. Nature 2010, 464, 890–893. [Google Scholar] [CrossRef]
- Vásárhelyi, G.; Virágh, C. Optimized flocking of autonomous drone in confined environments. Sci. Robot. 2018, 3, 3536–3550. [Google Scholar] [CrossRef] [PubMed]



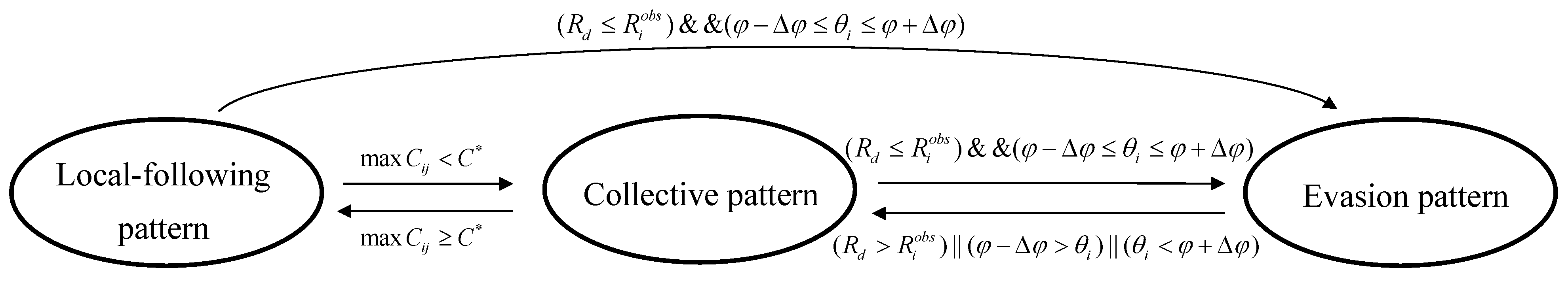
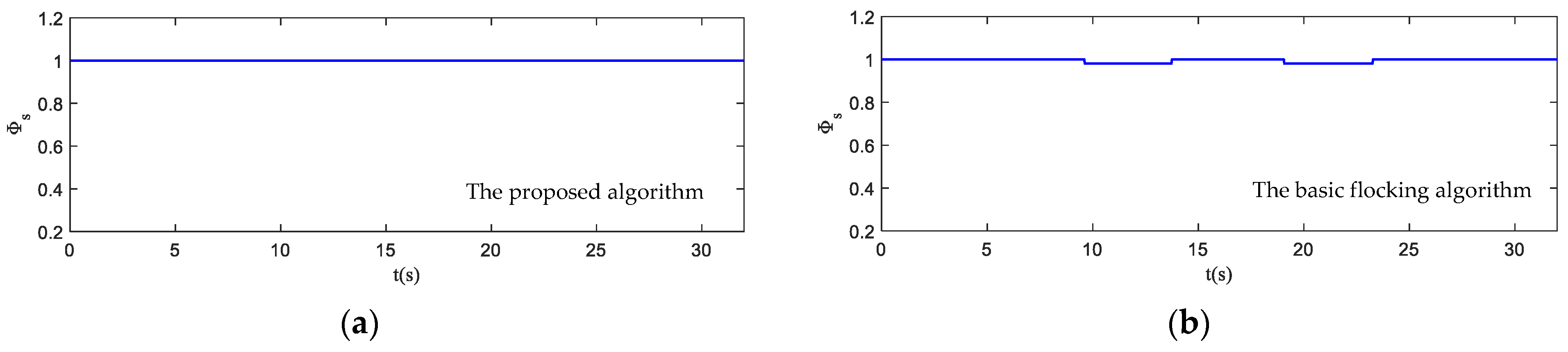


| Parameter | Value |
|---|---|
| Sensing range, R | 15 m |
| Desired distance between neighboring UAVs, d | 5 m |
| Desired distance between UAV and obstacle, | 15 m |
| Coefficient for the selection of local leader, | 2.5 |
| Control gains of local-following pattern, | 0.5, 2 |
| Step-size, | 0.025 s |
| Control gains of collective pattern, | 1, 4 |
| Control gains of evasion pattern, | 1 |
| Control gains of virtual leader-follower, | 1, 2 |
| Parameter | Value |
|---|---|
| Velocity time constant, | 5 |
| Heading angle time constant, | 0.75 |
| Altitude time constant, | 0.3, 1 |
| Minimum and maximum velocity, | 5 m/s, 15 m/s |
| Maximum lateral overload, | 5 g |
| Maximum climbing and gliding velocity, | −5 m/s, 5 m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, W.; Zhang, X.; Miao, Y. Starling-Behavior-Inspired Flocking Control of Fixed-Wing Unmanned Aerial Vehicle Swarm in Complex Environments with Dynamic Obstacles. Biomimetics 2022, 7, 214. https://doi.org/10.3390/biomimetics7040214
Wu W, Zhang X, Miao Y. Starling-Behavior-Inspired Flocking Control of Fixed-Wing Unmanned Aerial Vehicle Swarm in Complex Environments with Dynamic Obstacles. Biomimetics. 2022; 7(4):214. https://doi.org/10.3390/biomimetics7040214
Chicago/Turabian StyleWu, Weihuan, Xiangyin Zhang, and Yang Miao. 2022. "Starling-Behavior-Inspired Flocking Control of Fixed-Wing Unmanned Aerial Vehicle Swarm in Complex Environments with Dynamic Obstacles" Biomimetics 7, no. 4: 214. https://doi.org/10.3390/biomimetics7040214
APA StyleWu, W., Zhang, X., & Miao, Y. (2022). Starling-Behavior-Inspired Flocking Control of Fixed-Wing Unmanned Aerial Vehicle Swarm in Complex Environments with Dynamic Obstacles. Biomimetics, 7(4), 214. https://doi.org/10.3390/biomimetics7040214