The Plant-Like Structure of Lance Sea Urchin Spines as Biomimetic Concept Generator for Freeze-Casted Structural Graded Ceramics
Abstract
1. Introduction
2. Experimental Procedure
2.1. Lance Sea Urchin Spines
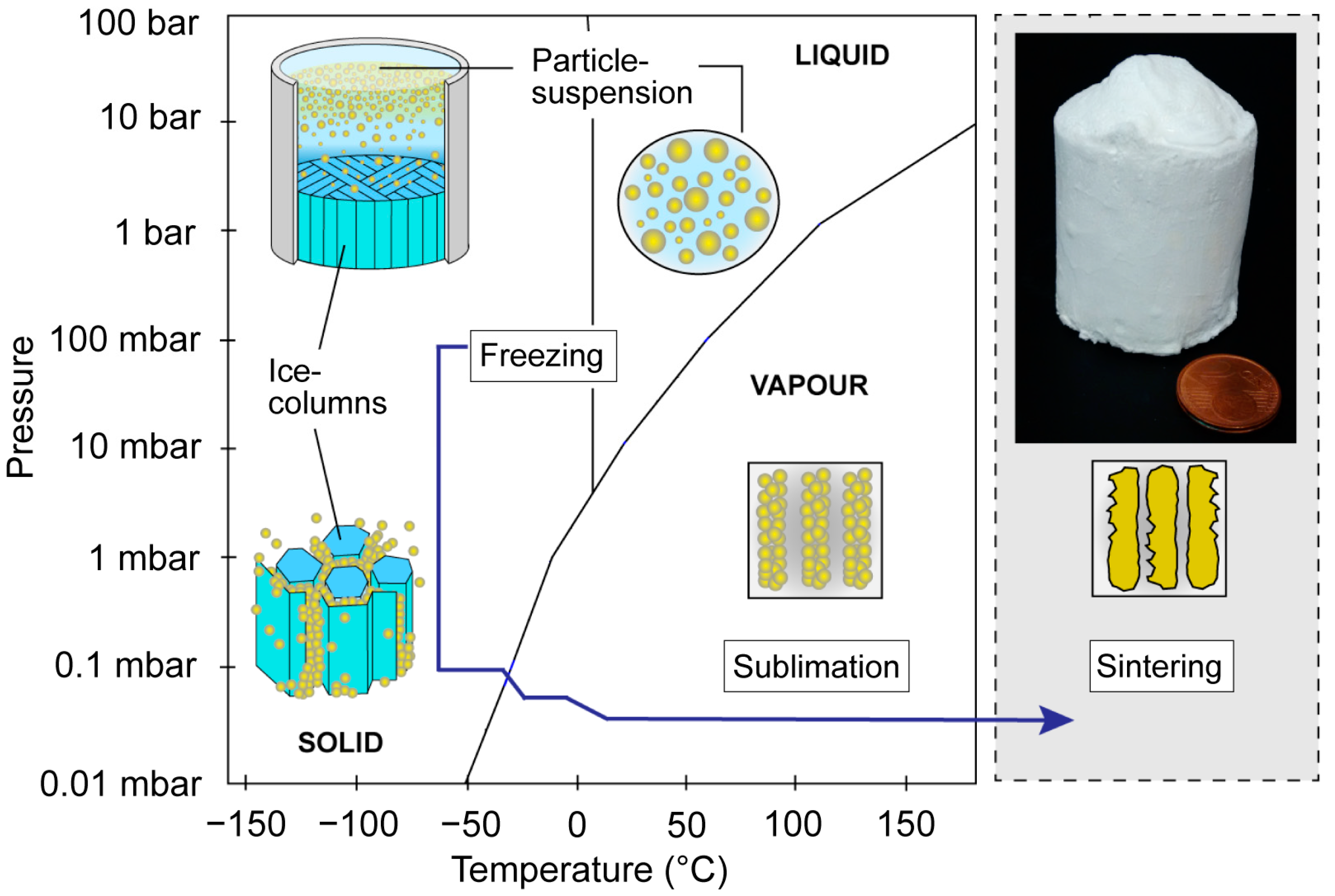
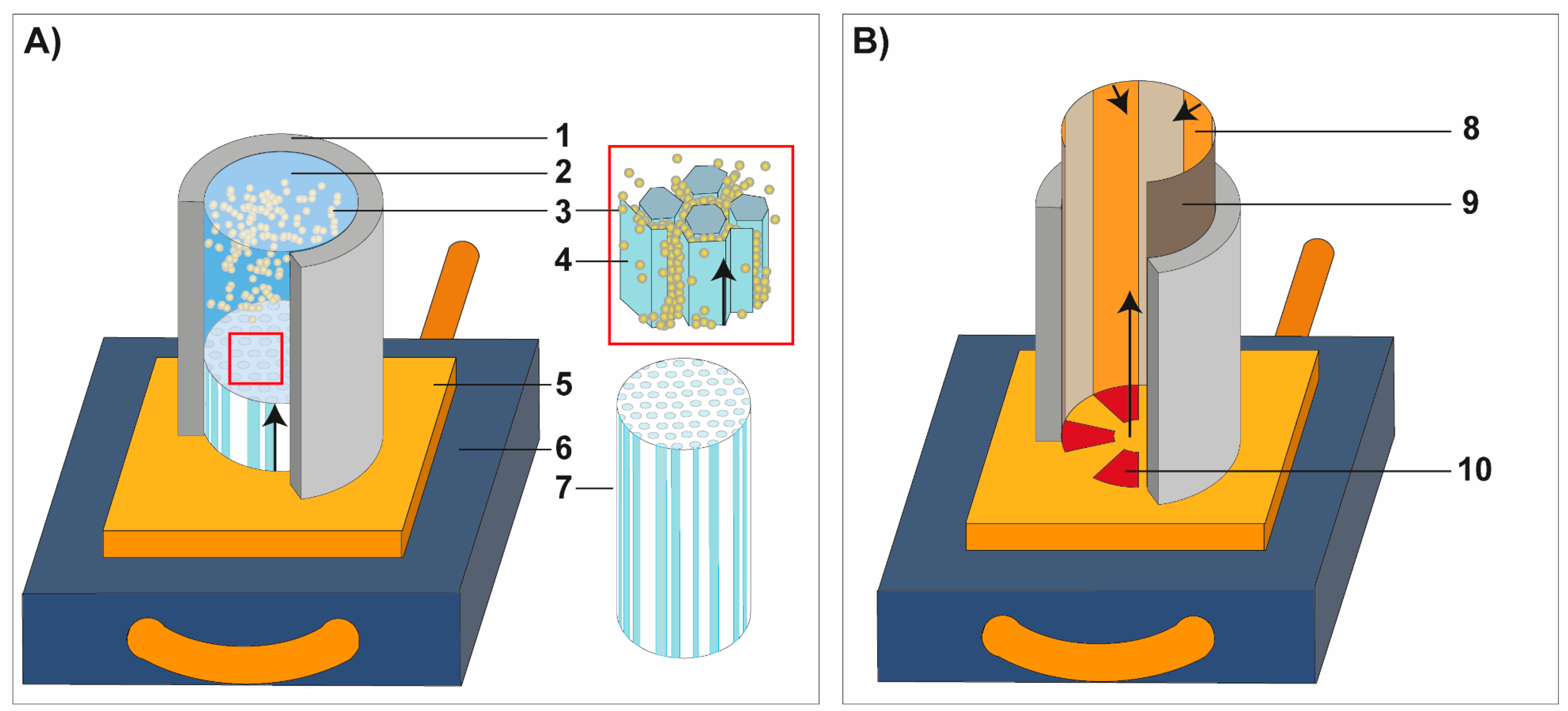
2.2. Freeze-Casting
2.3. Sample Preparation and Characterization
2.4. Scanning Electron Microscopy (SEM)
2.5. Micro Computed Tomography (µCT) and Data Processing
2.6. Mechanical Testing
3. Results
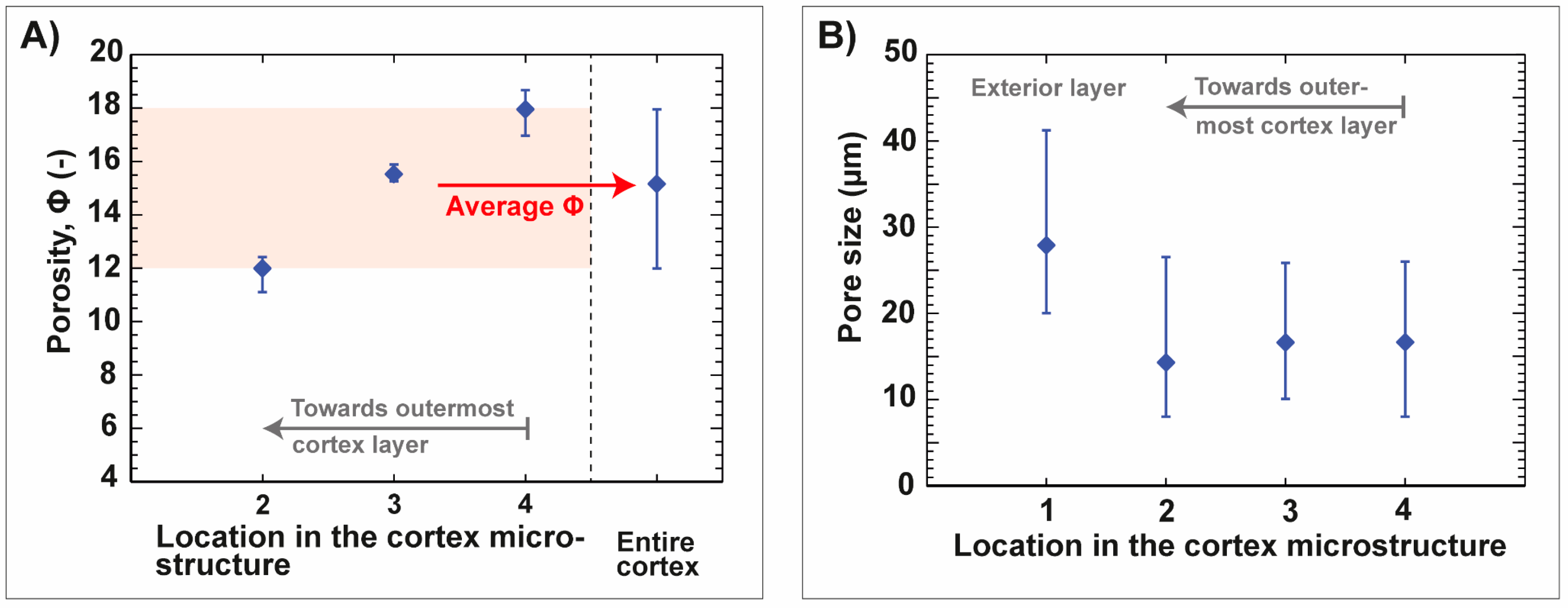
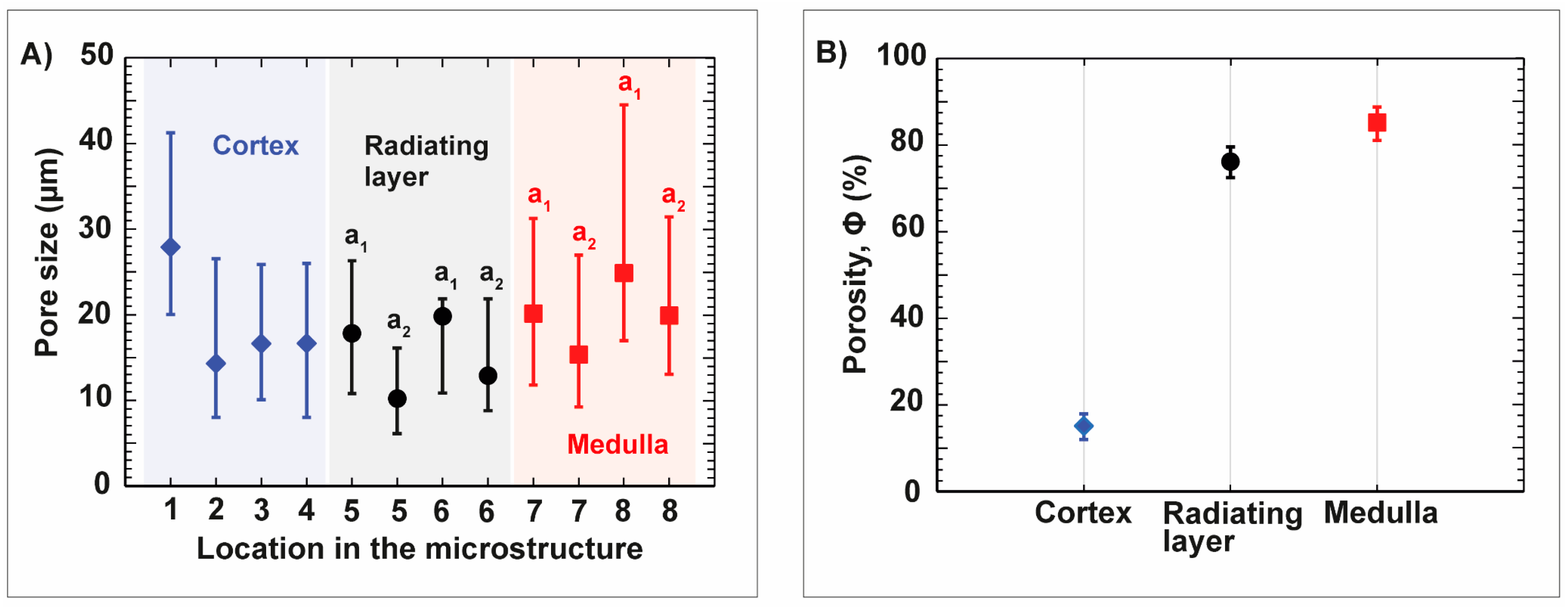
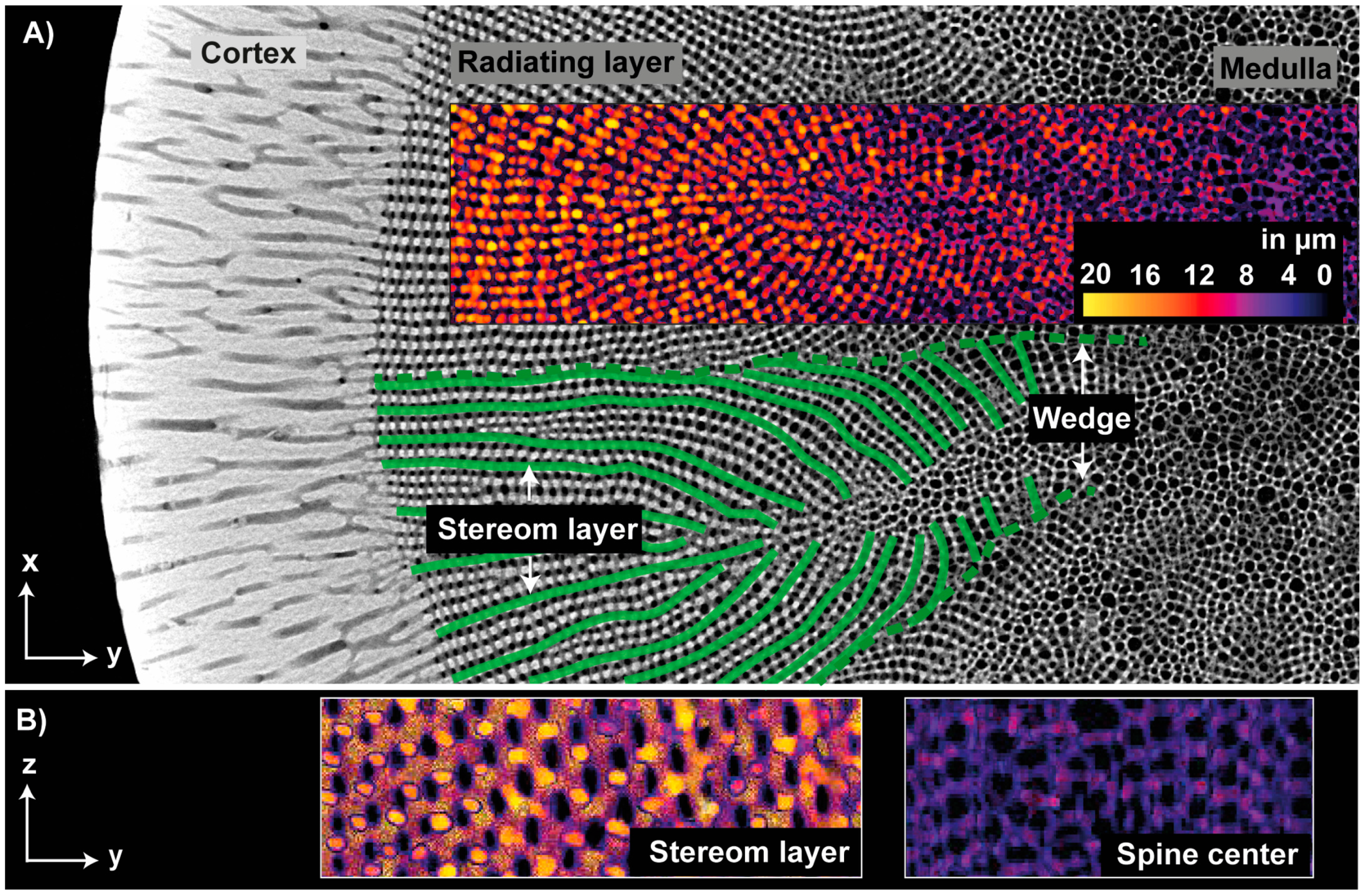
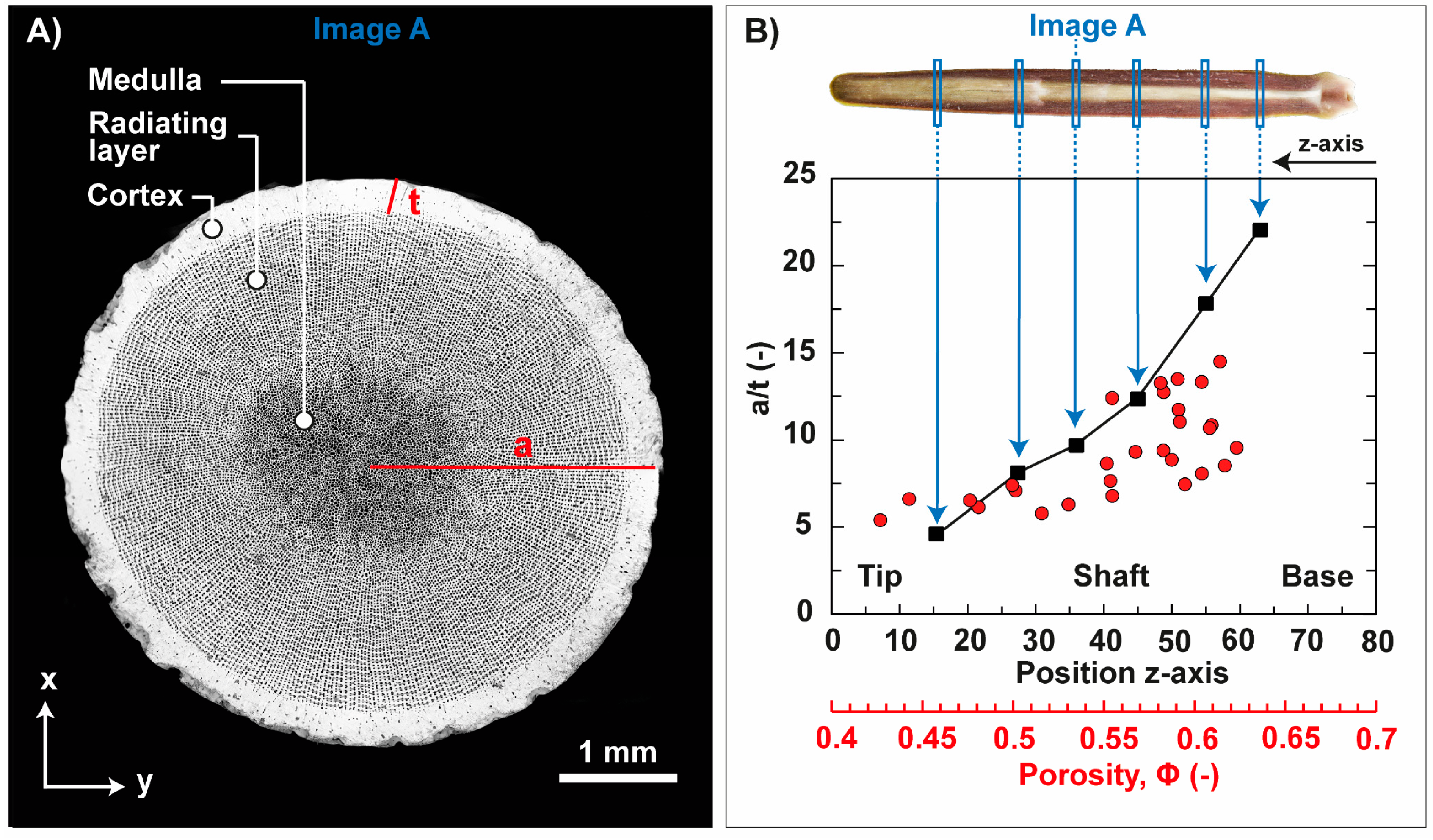
3.1. Sea Urchin Spine as Concept Generator
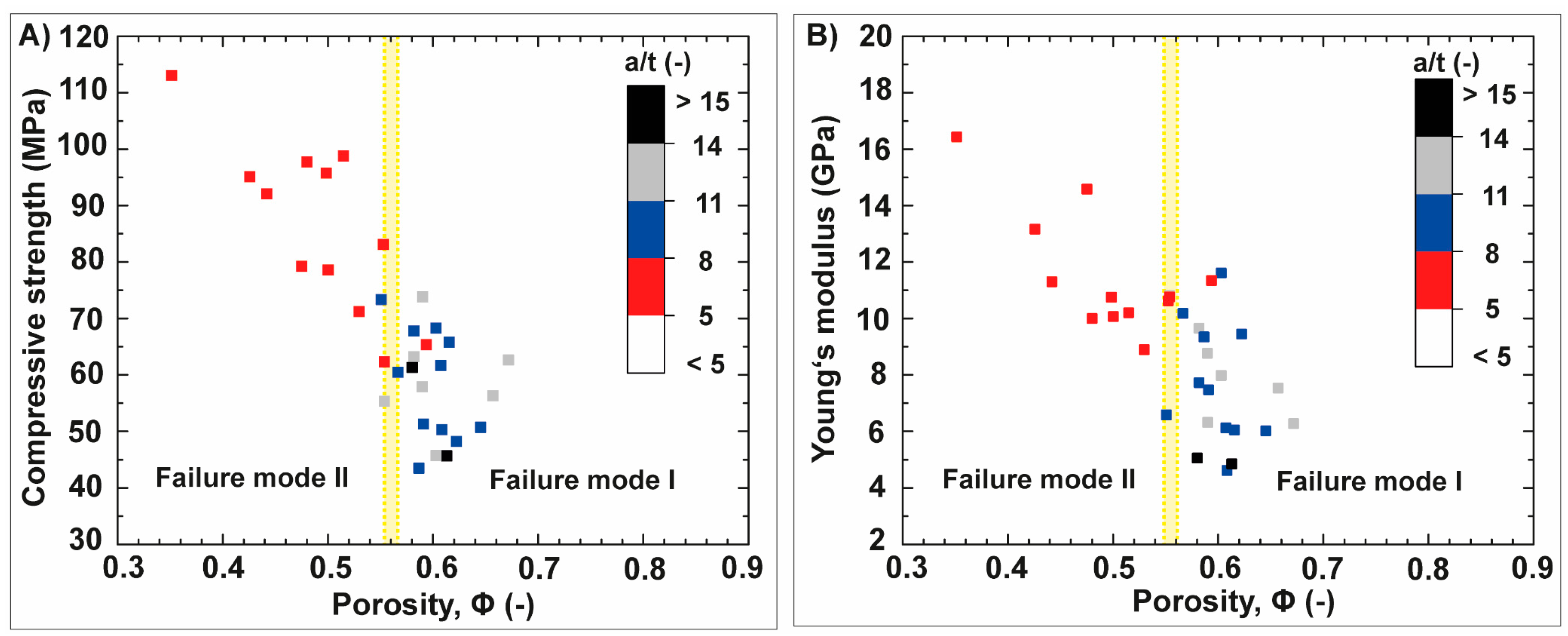
3.2. Anisotropic Ceramics
3.2.1. Bioinspired Structural Graded Ceramic
3.2.2. Ceramics with No Gradation
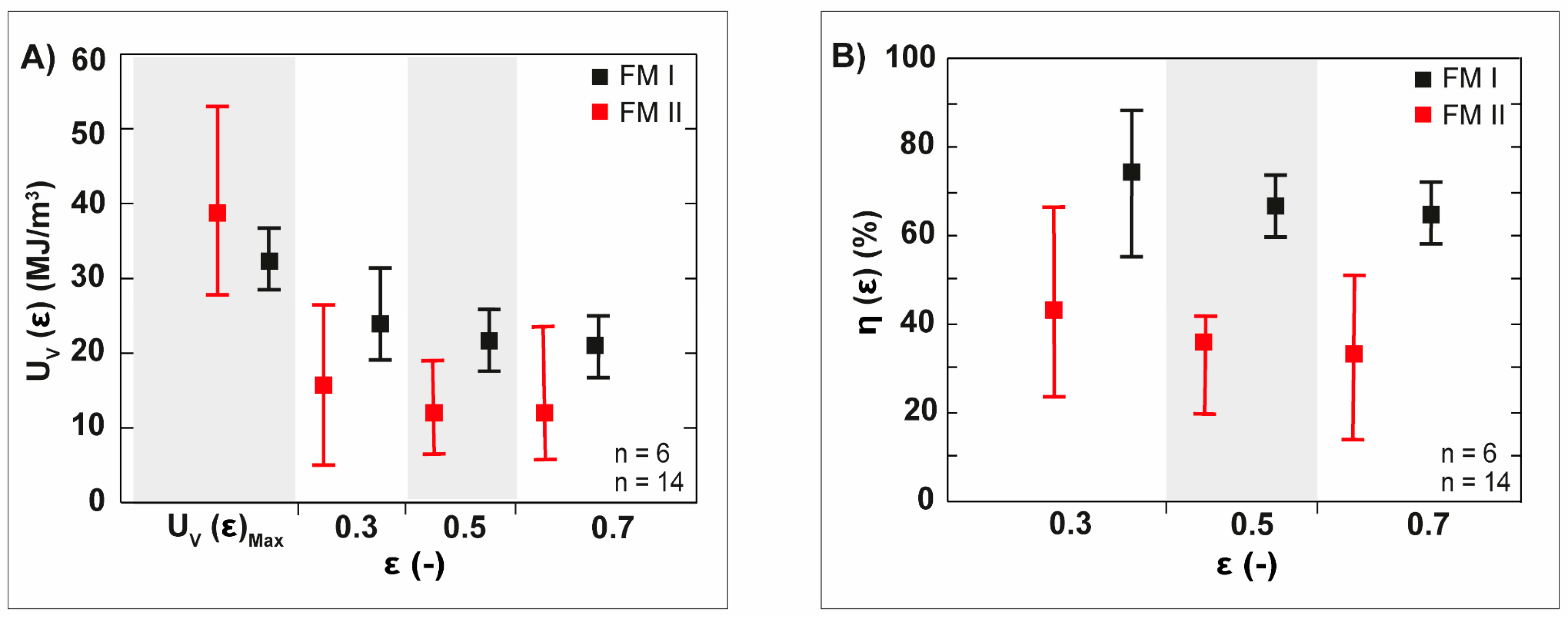
4. Discussion
4.1. Freeze-Casted Ceramic with Gradation Features Inspired by Natural Core–Shell Systems
4.2. Freeze-Casted Ceramics with Anisotropic Cellular Structures
4.3. The Plant Stem-Alike Core–Shell Construction in the Lance Sea Urchin Spines
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schmier, S.; Hosoda, N.; Speck, T. Hierarchical structure of the Cocos nucifera (coconut) endocarp: Functional morphology and its influence on fracture toughness. Molecules 2020, 25, 223. [Google Scholar] [CrossRef] [PubMed]
- Schmier, S.; Jentzsch, M.; Speck, T.; Thielen, M. Fracture mechanics of the endocarp of Cocos nucifera. Mater. Des. 2020, 195, 108944. [Google Scholar] [CrossRef]
- Bauer, G.; Speck, T.; Blömer, J.; Bertling, J.; Speck, O. Insulation capability of the bark of trees with different fire adaptation. J Mater. Sci. 2010, 45, 5950–5959. [Google Scholar] [CrossRef]
- Born, L.; Körner, A.; Schieber, G.; Westermeier, A.S.; Poppinga, S.; Sachse, R.; Bergmann, P.; Betz, O.; Bischoff, M.; Speck, T.; et al. Fiber-Reinforced Plastics with Locally Adapted Stiffness for Bio-Inspired Hingeless, Deployable Architectural Systems, 1st ed.; Trans Tech Publications Ltd.: Zurich, Switzerland, 2017; pp. 689–696. [Google Scholar] [CrossRef]
- Grun, T.B.; von Scheven, M.; Bischoff, M.; Nebelsick, J.H. Structural stress response of segmented natural shells: A numerical case study on the clypeasteroid echinoid Echinocyamus pusillus. J. R. Soc. Interface 2018, 15, 20180164. [Google Scholar] [CrossRef] [PubMed]
- Kovaleva, D.; Gericke, O.; Kappes, J.; Haase, W. Rosenstein-Pavilion: Towards resource efficiency by design. Beton Stahlbetonbau 2018, 113, 433–442. [Google Scholar] [CrossRef]
- Karam, G.N.; Gibson, L.J. Biomimicking of animal quills and plant stems: Natural cylindrical shells with foam cores. Mater. Sci. Eng. C 1994, 2, 113–132. [Google Scholar] [CrossRef]
- Schott, R.T.; Roth-Nebelsick, A. Ice nucleation in stems of trees and shrubs with different frost resistance. IAWA J. 2018, 39, 177–190. [Google Scholar] [CrossRef]
- Smith, A.B. Stereom Microstructure of the Echinoid Test. Spec. Pap. Palaeontol. 1980, 25, 1–324. [Google Scholar]
- Smith, A.B. Biomineralization in Echinoderms. In Skeletal Biomineralization: Patterns, Processes and Evolutionary Trends, 1st ed.; Carter, J.G., Ed.; VanNostrand Reinhold: New York, NY, USA, 1990; pp. 413–443. [Google Scholar]
- Märkel, K.; Kubanek, F.; Willgallis, A. Polycristalline calcite in sea urchins. Z. Zellforsch 1971, 119, 355–377. [Google Scholar] [CrossRef]
- Cölfen, H.; Antonietti, M. Mesocrystals and Nonclassical Crystallization; John Wiley and Sons: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Seto, J.; Zhang, Y.; Hamilton, P.; Wilt, F. The localization of occluded matrix proteins in calcareous spicules of sea urchin larvae. J. Struct. Biol. 2004, 148, 123–130. [Google Scholar] [CrossRef]
- Presser, V.; Schultheiß, S.; Berthold, C.; Nickel, K.G. Sea Urchin Spines as a Model-System for Permeable, Light-Weight Ceramics with Graceful Failure Behavior. Part, I. Mechanical Behavior of Sea Urchin Spines under Compression. J. Bionic Eng. 2009, 6, 203–213. [Google Scholar] [CrossRef]
- Presser, V.; Schultheiß, S.; Kohler, C.; Berthold, C.; Nickel, K.G.; Vohrer, A.; Finckh, H.; Stegmaier, T. Lessons from nature for the construction of ceramic cellular materials for superior energy absorption. Adv. Eng. Mater. 2011, 13, 1042–1049. [Google Scholar] [CrossRef]
- Klang, K.; Bauer, G.; Toader, N.; Lauer, C.; Termin, K.; Schmier, S.; Kovaleva, D.; Haase, W.; Berthold, C.; Nickel, K.G.; et al. Plants and Animals as Source of Inspiration for Energy Dissipation in Load Bearing Systems and Facades. In Biomimetic Research for Architecture and Building Construction: Biological Design and Integrative Structures, 1st ed.; Knippers, J., Nickel, K.G., Speck, T., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 109–133. [Google Scholar]
- Presser, V.; Kohler, C.; Živcová, Z.; Berthold, C.; Nickel, K.G.; Schultheiß, S.; Gregorová, E.; Pabst, W. Sea Urchin Spines as a Model-System for Permeable, Light-Weight Ceramics with Graceful Failure Behavior. Part II. Mechanical Behavior of Sea Urchin Spine Inspired Porous Aluminum Oxide Ceramics under Compression. J. Bionic Eng. 2009, 6, 357–364. [Google Scholar] [CrossRef]
- Tang, Z.; Kotov, N.A.; Magonov, S.; Ozturk, B. Nanostructured artificial nacre. Nat. Mater. 2003, 2, 413–418. [Google Scholar] [CrossRef]
- Podsiadlo, P.; Kaushik, A.K.; Arruda, E.M.; Waas, A.M.; Shim, B.S.; Xu, J.; Nandivada, H.; Pumplin, B.G.; Lahann, J.; Ramamoorthy, A.; et al. Ultrastrong and stiff layered polymer nanocomposites. Science 2007, 318, 80–83. [Google Scholar] [CrossRef]
- Yao, H.-B.; Fang, H.-Y.; Tan, Z.-H.; Wu, L.-H.; Yu, S.-H. Biologically inspired, strong, transparent, and functional layered organic-inorganic hybrid films. Angew. Chem. Int. Ed. 2010, 49, 2140–2145. [Google Scholar] [CrossRef]
- Cheng, Q.; Wu, M.; Li, M.; Jiang, L.; Tang, Z. Ultratough artificial nacre based on conjugated cross-linked graphene oxide. Angew. Chem. Int. Ed. 2013, 52, 3750–3755. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, Y.; Huang, L.; Xu, Z.; Li, C.; Shi, G. Multifunctional Pristine Chemically Modified Graphene Films as Strong as Stainless Steel. Adv. Mater. 2015, 27, 6708–6713. [Google Scholar] [CrossRef]
- Chavez-Valdez, A.; Shaffer, M.; Boccaccini, A.R. Applications of graphene electrophoretic deposition. A review. J. Phys. Chem. B 2013, 117, 1502–1515. [Google Scholar] [CrossRef] [PubMed]
- Fukasawa, T.; Ando, M.; Ohji, T.; Kanzaki, S. Synthesis of Porous Ceramics with Complex Pore Structure by Freeze-Dry Processing. J. Am. Ceram. Soc. 2001, 84, 230–232. [Google Scholar] [CrossRef]
- Deville, S. Freeze-casting of porous ceramics: A review of current achievements and issues. Adv. Eng. Mater. 2008, 10, 155–169. [Google Scholar] [CrossRef]
- Deville, S. Freeze-casting of porous biomaterials: Structure, properties and opportunities. Materials 2010, 3, 1913–1927. [Google Scholar] [CrossRef]
- Peppin, S.; Elliott, J.; Worster, M.G. Solidification of colloidal suspensions. J. Fluid Mech. 2006, 554, 147–166. [Google Scholar] [CrossRef]
- Peppin, S.; Worster, M.G.; Wettlaufer, J.S. Morphological instability in freezing colloidal suspensions. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 723–733. [Google Scholar] [CrossRef]
- Peppin, S.; Wettlaufer, J.S.; Worster, M.G. Experimental verification of morphological instability in freezing aqueous colloidal suspensions. Phys. Rev. Lett. 2008, 100, 238301. [Google Scholar] [CrossRef]
- Hunger, P.M.; Donius, A.E.; Wegst, U. Structure-property-processing correlations in freeze-cast composite scaffolds. Acta Biomater. 2013, 9, 6338–6348. [Google Scholar] [CrossRef] [PubMed]
- Lichtner, A.; Roussel, D.; Jauffrès, D.; Martin, C.L.; Bordia, R.K. Effect of Macropore Anisotropy on the Mechanical Response of Hierarchically Porous Ceramics. J. Am. Ceram. Soc. 2016, 99, 979–987. [Google Scholar] [CrossRef]
- Liu, X.; Rahaman, M.N.; Fu, Q.; Tomsia, A.P. Porous and strong bioactive glass (13-93) scaffolds prepared by unidirectional freezing of camphene-based suspensions. Acta Biomater. 2012, 8, 415–423. [Google Scholar] [CrossRef]
- Munch, E.; Saiz, E.; Tomsia, A.P.; Deville, S. Architectural control of freeze-cast ceramics through additives and templating. J. Am. Ceram. Soc. 2009, 92, 1534–1539. [Google Scholar] [CrossRef]
- Naviroj, M.; Voorhees, P.W.; Faber, K.T. Suspension- and solution-based freeze casting for porous ceramics. J. Mater. Res. 2017, 32, 3372–3382. [Google Scholar] [CrossRef]
- Fukushima, M.; Yoshizawa, Y.-I.; Ohji, T. Macroporous ceramics by gelation-freezing route using gelatin. Adv. Eng. Mater. 2014, 16, 607–620. [Google Scholar] [CrossRef]
- Speck, O.; Speck, D.; Horn, R.; Gantner, J.; Sedlbauer, K.P. Biomimetic bio-inspired biomorph sustainable? An attempt to classify and clarify biology-derived technical developments. Bioinspir. Biomimetics 2017, 12, 11004. [Google Scholar] [CrossRef] [PubMed]
- de Lamarck, J.B.M. Histoire Naturelle des Animaux sans Vertébres, Tome Deuxiéme; Bailliére Libraire: Paris, France, 1836; p. 568. [Google Scholar]
- DeFoe, O.K.; Compton, A.H. The density of rock salt and calcite. Phys. Rev. 1925, 25, 618–620. [Google Scholar] [CrossRef]
- Sun, Z.; Li, B.; Hu, P.; Ding, F.; Yuan, F. Alumina ceramics with uniform grains prepared from Al2O3 nanospheres. J. Alloy. Compd. 2016, 688, 933–938. [Google Scholar] [CrossRef]
- Hautcoeur, D.; Gonon, M.; Baudin, C.; Lardot, V.; Leriche, A.; Cambier, F. Alumina Porous Ceramics Obtained by Freeze Casting: Structure and Mechanical Behaviour under Compression. Ceramics 2018, 1, 8. [Google Scholar] [CrossRef]
- Ridler, T.W.; Calvard, S. Picture thresholding using an iterative selectction methode. IEEE Trans. Syst. Man. Cybern. 1978, 8, 630–632. [Google Scholar] [CrossRef]
- Doube, M.; Klosowski, M.M.; Arganda-Carreras, I.; Cordelières, F.P.; Dougherty, R.P.; Jackson, J.S.; Schmid, B.; Hutchinson, J.R.; Shefelbine, S.J. BoneJ: Free and extensible bone image analysis in ImageJ. Bone 2010, 47, 1076–1079. [Google Scholar] [CrossRef]
- Dawson, M.A.; Gibson, L.J. Optimization of cylindrical shells with compliant cores. Int. J. Solids Struct. 2007, 44, 1145–1160. [Google Scholar] [CrossRef]
- Karam, G.N.; Gibson, L.J. Elastic buckling of cylindrical shells with elastic cores-I. Analysis. Int. J. Solids Struct. 1995, 32, 1259–1283. [Google Scholar] [CrossRef]
- Karam, G.N.; Gibson, L.J. Elastic buckling of cylindrical shells with elastic cores-II. Experiments. Int. J. Solids Struct. 1995, 32, 1285–1306. [Google Scholar] [CrossRef]
- Yu, S.; Liu, J.; Wei, M.; Luo, Y.; Zhu, X.; Liu, Y. Compressive property and energy absorption characteristic of open-cell ZA22 foams. Mater. Des. 2009, 30, 87–90. [Google Scholar] [CrossRef]
- Speck, T.; Burgert, I. Plant Stems: Functional Design and Mechanics. Annu. Rev. Mater. Res. 2011, 41, 169–193. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Nebelsick, J.H. Echinoid distribution by fragment identification in the northern Bay of Safaga, Red Sea, Egypt. Palaios 1992, 7, 316–328. [Google Scholar] [CrossRef]
- Nebelsick, J.H. Biodiversity of shallow-water red sea echinoids: Implications for the fossil record. J. Mar. Biol. Assoc. UK 1996, 76, 185–194. [Google Scholar] [CrossRef]
- Magdans, U.; Gies, H. Single crystal structure analysis of sea urchin spine calcites: Systematic investigations of the Ca/Mg distribution as a function habitat of the sea urchin and the sample location in the spine. Eur. J. Mineral. 2004, 16, 261–268. [Google Scholar] [CrossRef]
- Dery, A.; Guibourt, V.; Catarino, A.I.; Compère, P.; Dubois, P. Properties, morphogenesis, and effect of acidification on spines of the cidaroid sea urchin Phyllacanthus imperialis. Invertebr. Biol. 2014, 133, 188–199. [Google Scholar] [CrossRef]




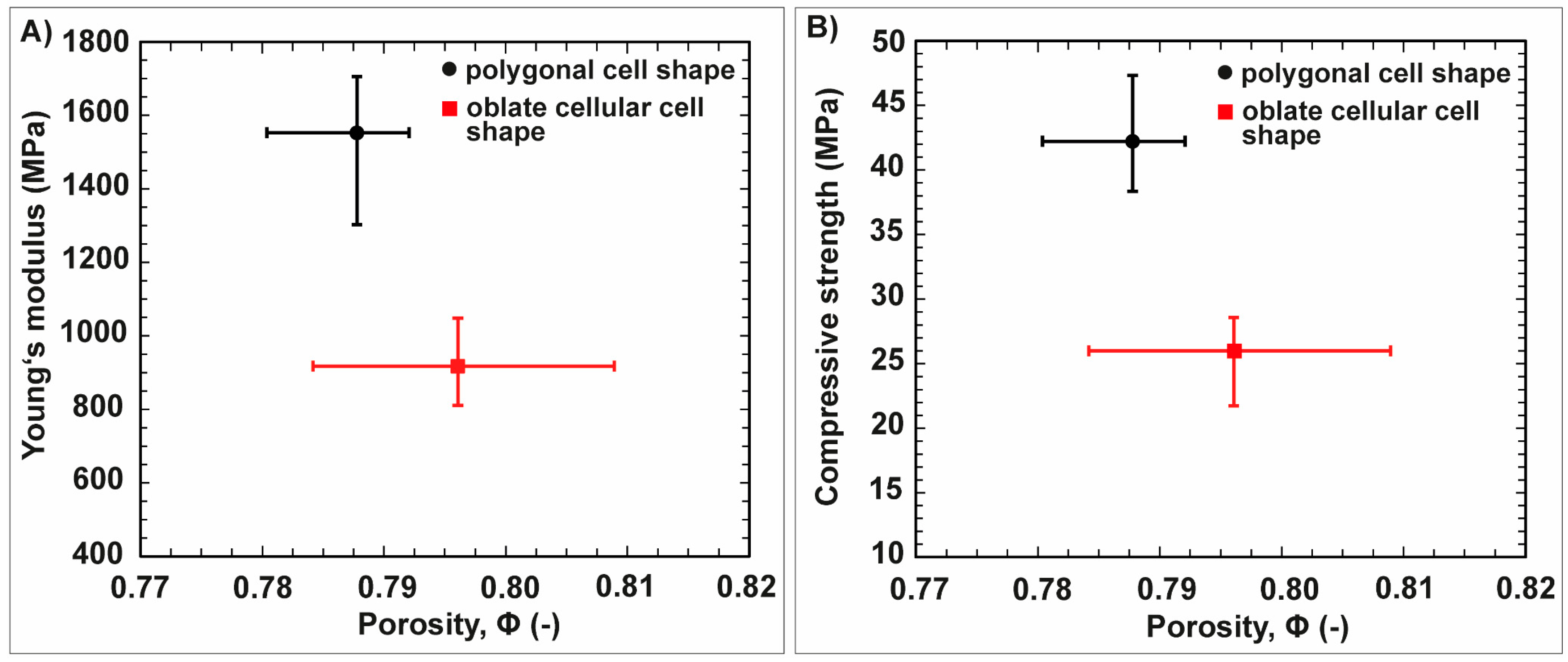
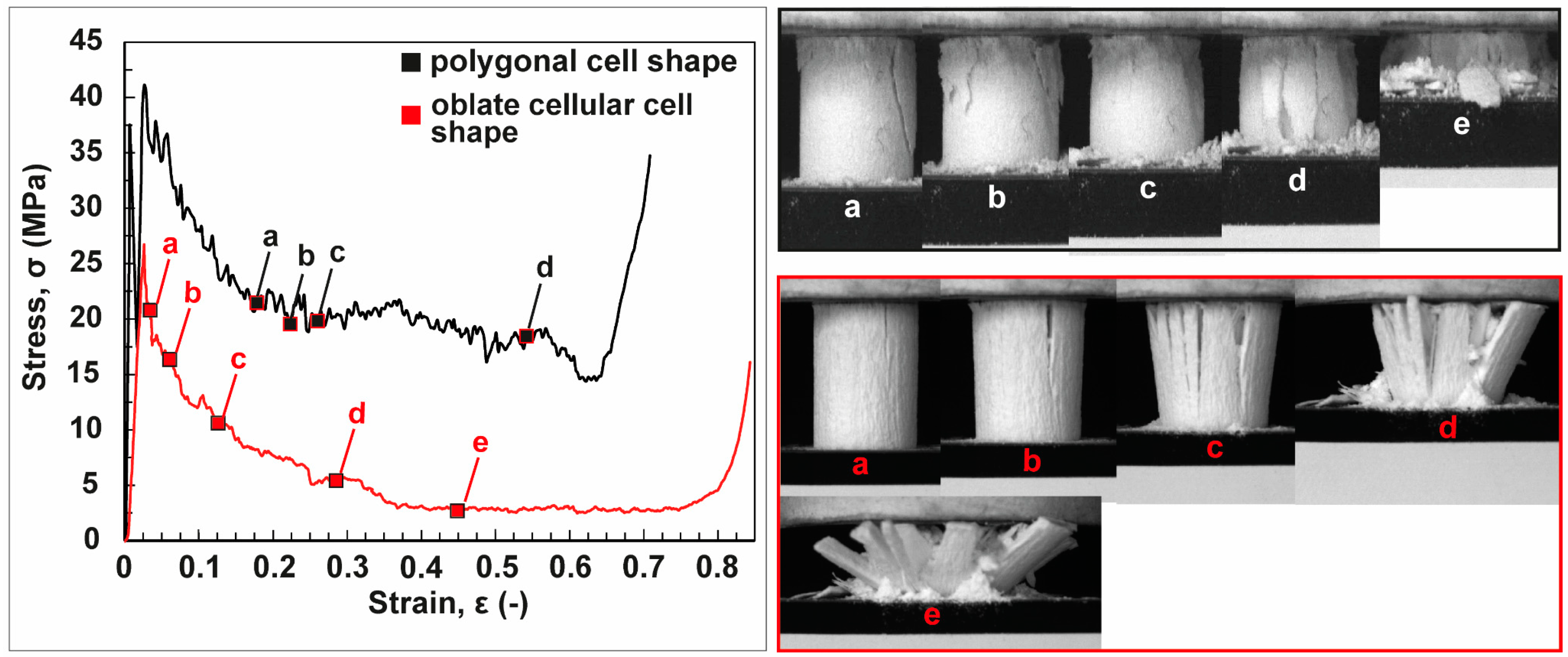
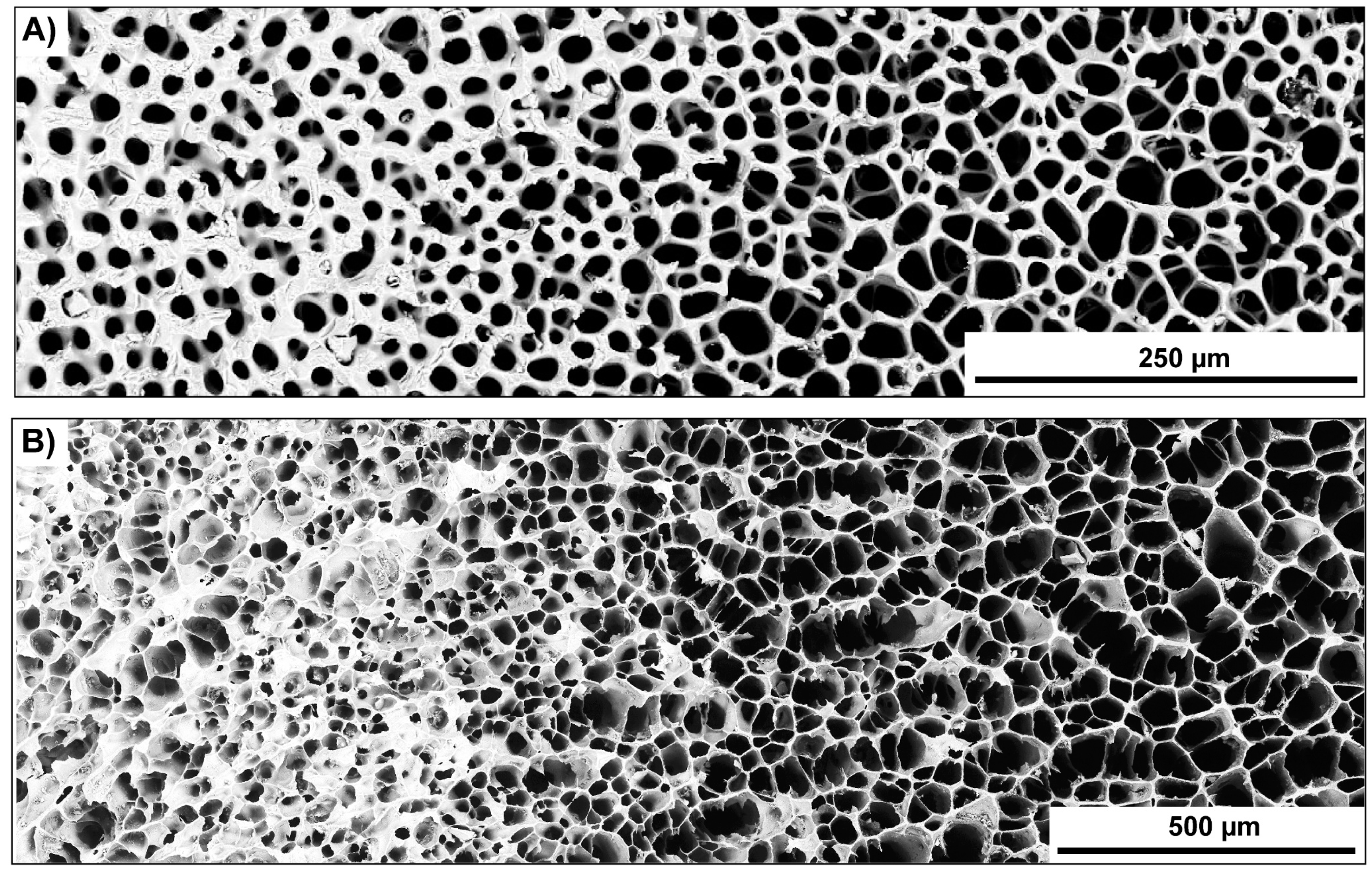

| Name | ϕ Sintered Foam | Total Concentration of Al2O3 | Total Concentration of Gelatin with Regard to Water | Dolapix CE 64 | ||
|---|---|---|---|---|---|---|
| (vol.%) | (wt.%) | (vol.%) | (wt.%) | (vol.%) | (cm3) | |
| Polygonal cells | 77–79 | 44.0 | 16.5 | 5 | 6.8 | 0.47 |
| Oblate cells | 77–79 | 44.0 | 16.5 | 2.5 | 3.5 | 0.47 |
| Graded ceramic | 77–79 | 44.0 | 16.5 | 5 | 6.8 | 0.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klang, K.; Nickel, K.G. The Plant-Like Structure of Lance Sea Urchin Spines as Biomimetic Concept Generator for Freeze-Casted Structural Graded Ceramics. Biomimetics 2021, 6, 36. https://doi.org/10.3390/biomimetics6020036
Klang K, Nickel KG. The Plant-Like Structure of Lance Sea Urchin Spines as Biomimetic Concept Generator for Freeze-Casted Structural Graded Ceramics. Biomimetics. 2021; 6(2):36. https://doi.org/10.3390/biomimetics6020036
Chicago/Turabian StyleKlang, Katharina, and Klaus G. Nickel. 2021. "The Plant-Like Structure of Lance Sea Urchin Spines as Biomimetic Concept Generator for Freeze-Casted Structural Graded Ceramics" Biomimetics 6, no. 2: 36. https://doi.org/10.3390/biomimetics6020036
APA StyleKlang, K., & Nickel, K. G. (2021). The Plant-Like Structure of Lance Sea Urchin Spines as Biomimetic Concept Generator for Freeze-Casted Structural Graded Ceramics. Biomimetics, 6(2), 36. https://doi.org/10.3390/biomimetics6020036






