3D Reticulated Actuator Inspired by Plant Up-Righting Movement Through a Cortical Fiber Network
Abstract
1. Introduction
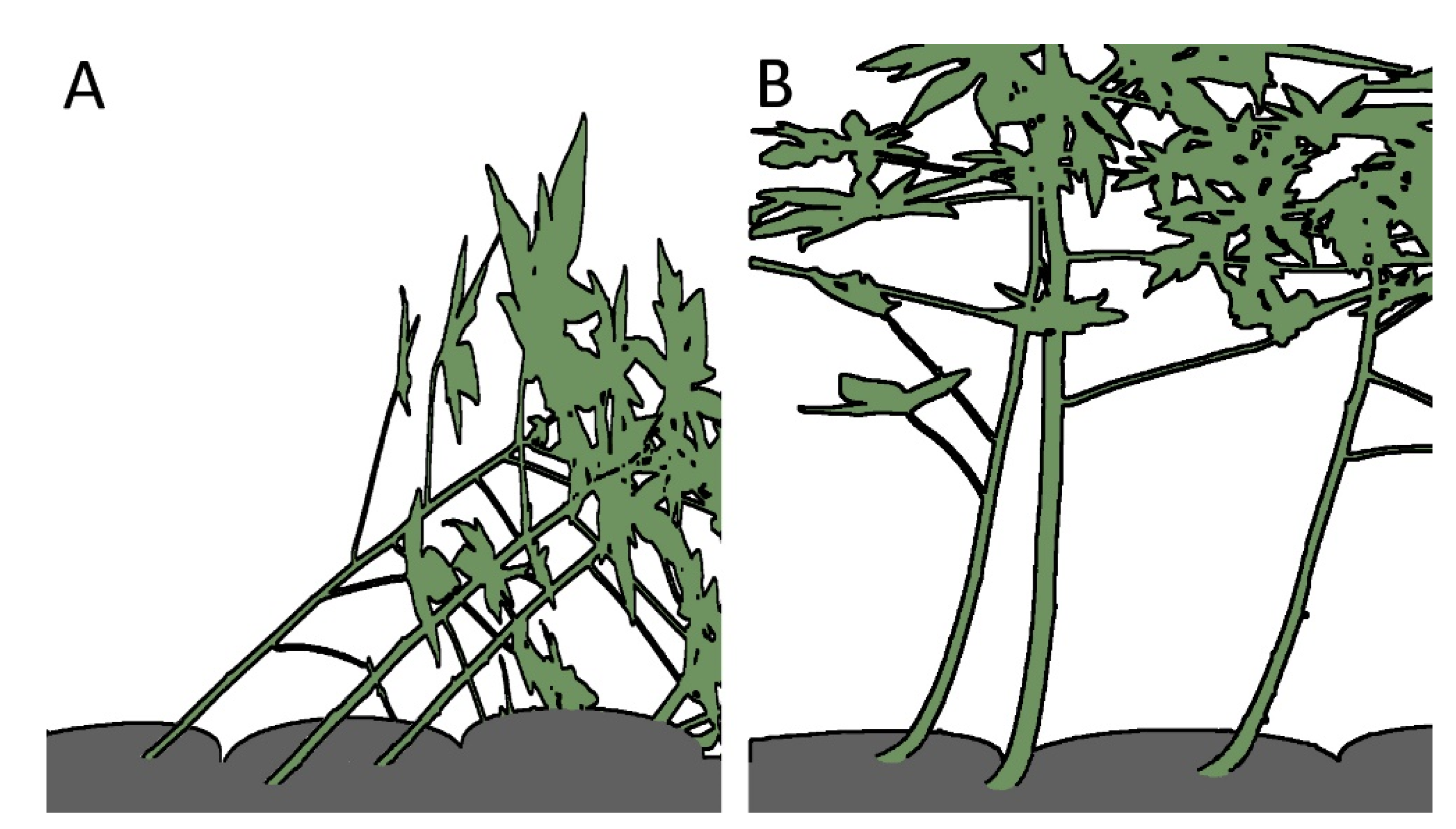
1.1. Movements of Plants
1.2. Plant-Inspired Actuators
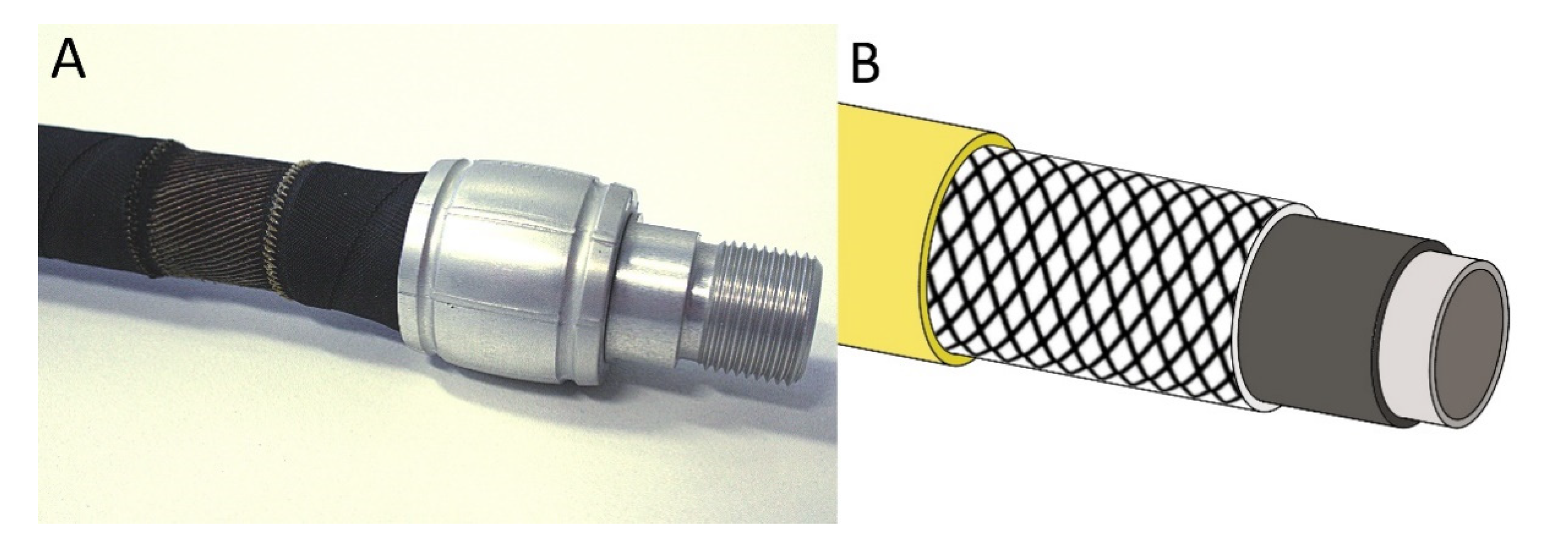
1.3. Conventional Technical Solutions
1.4. Aim of the Study
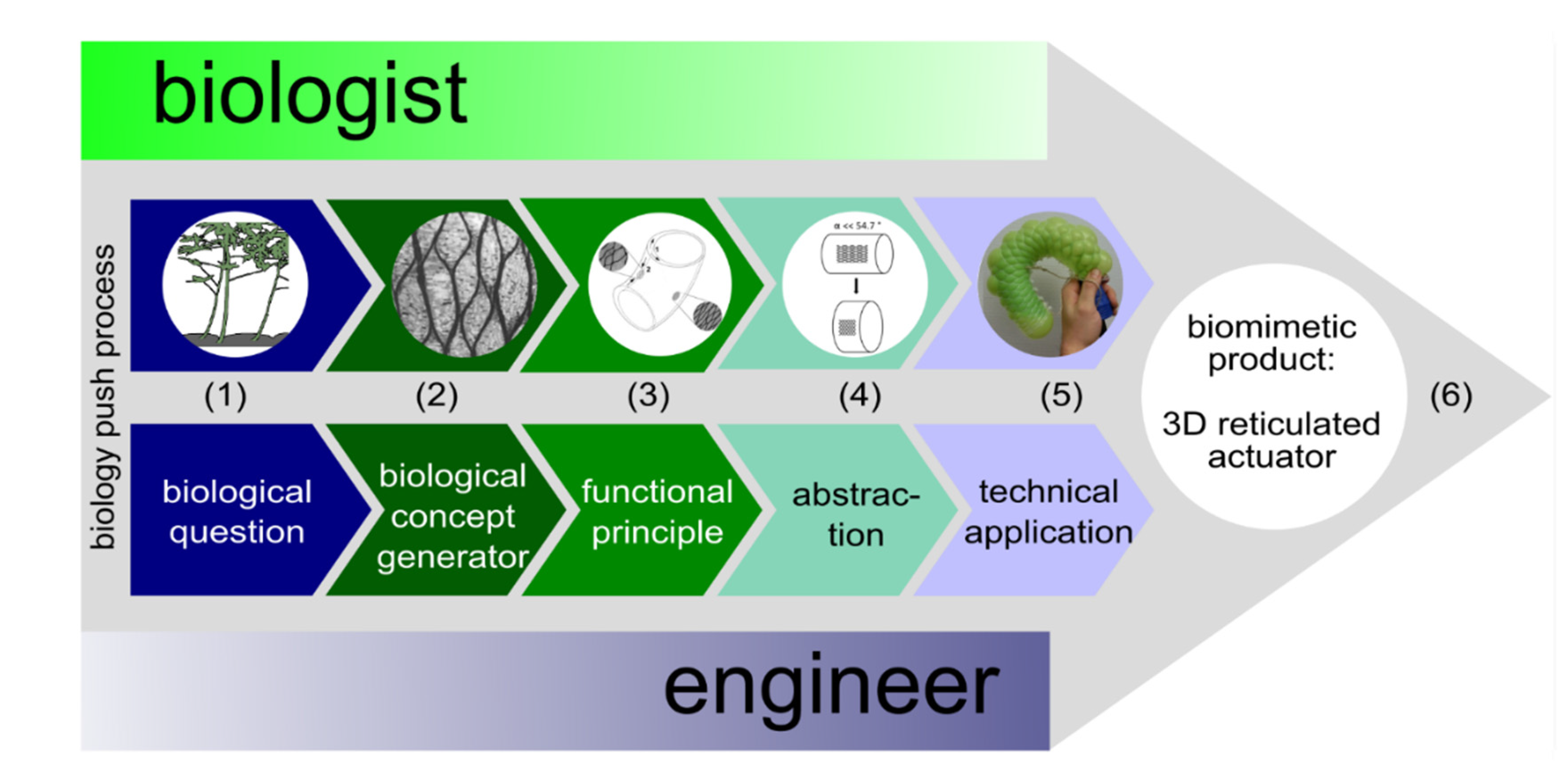
2. Biology Push Process (Biomimetic Bottom-Up Approach)
2.1. Biological Question
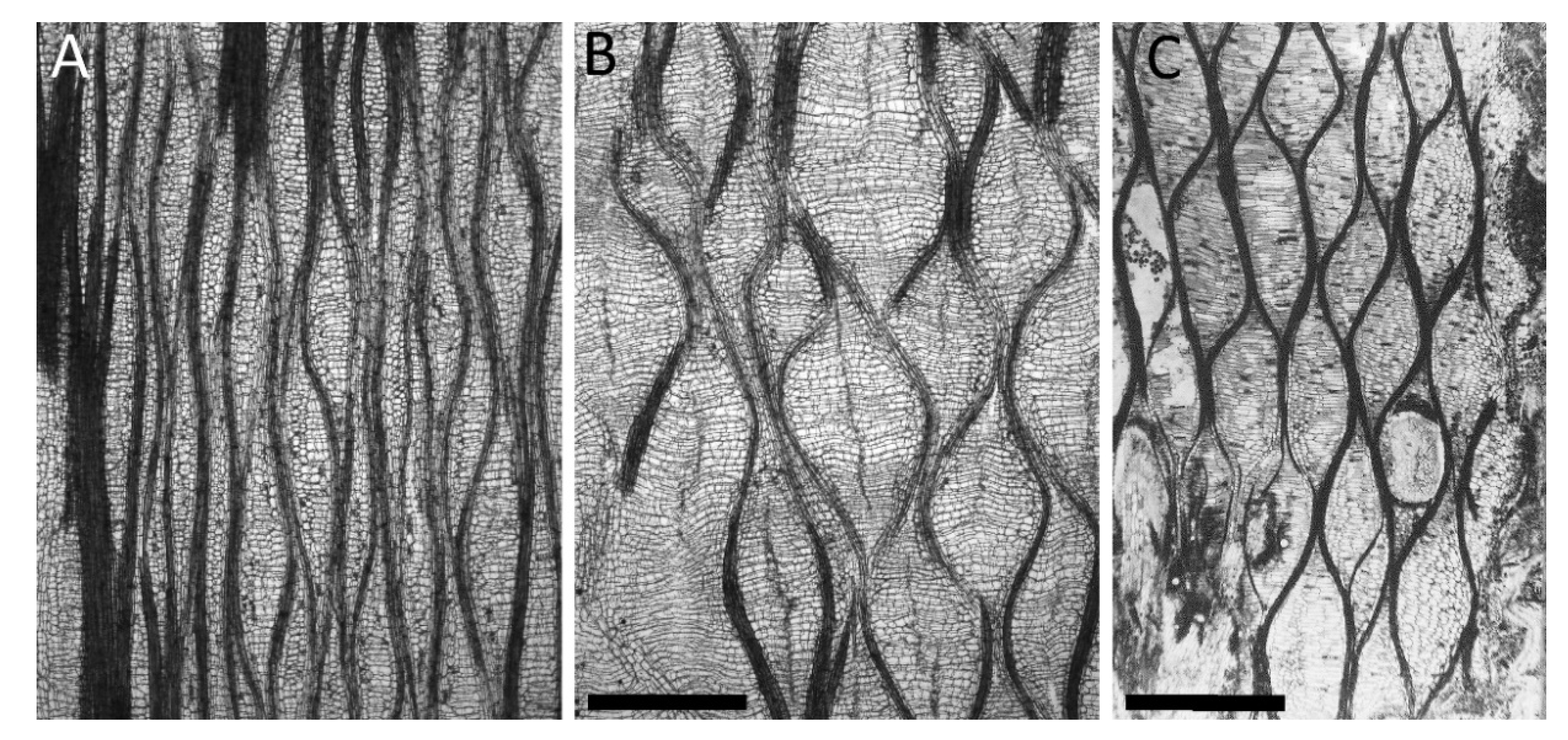
2.2. Biological Concept Generators
2.3. Functional Principle
2.4. Abstraction
2.5. Feasibility Studies
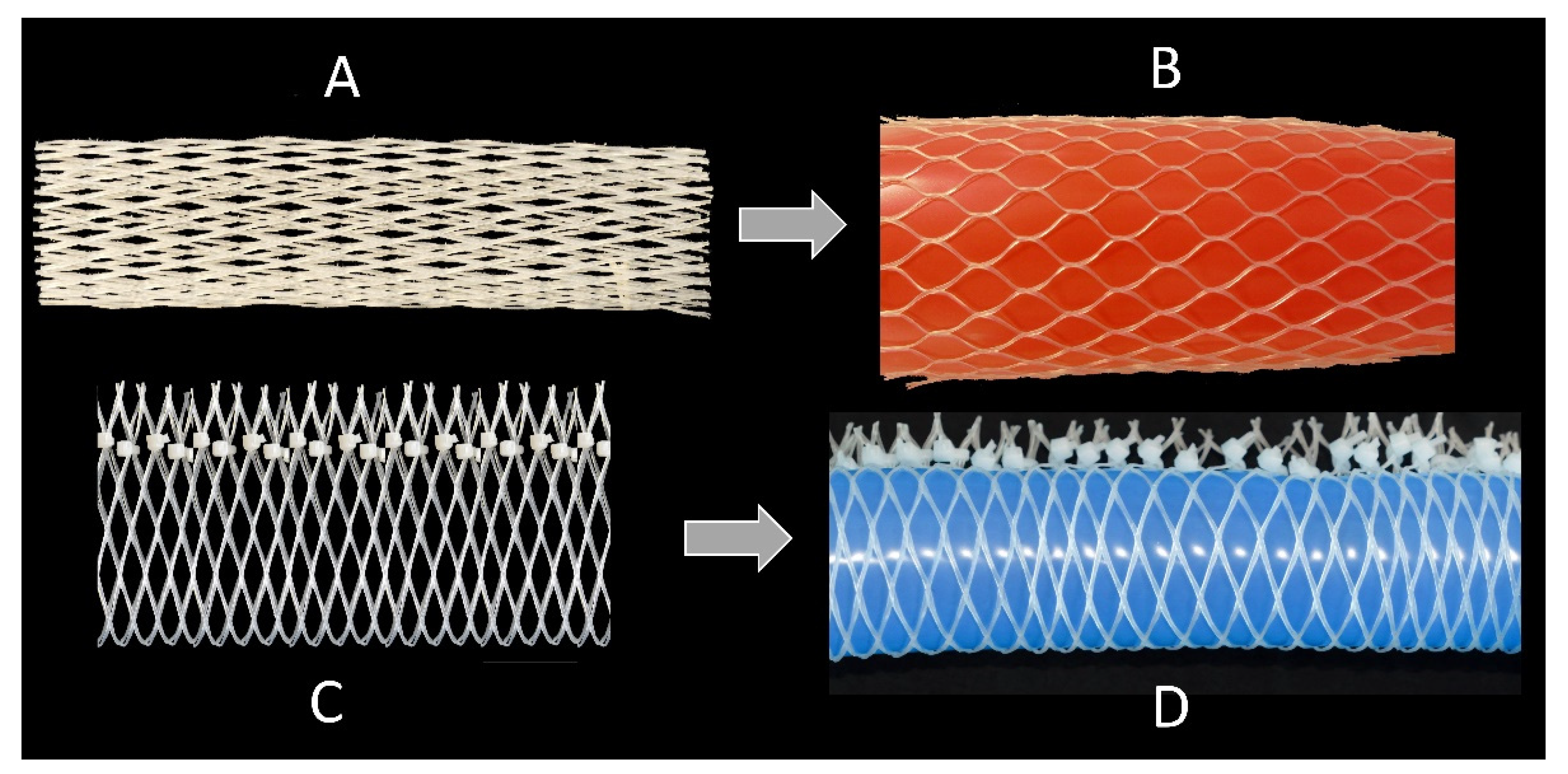
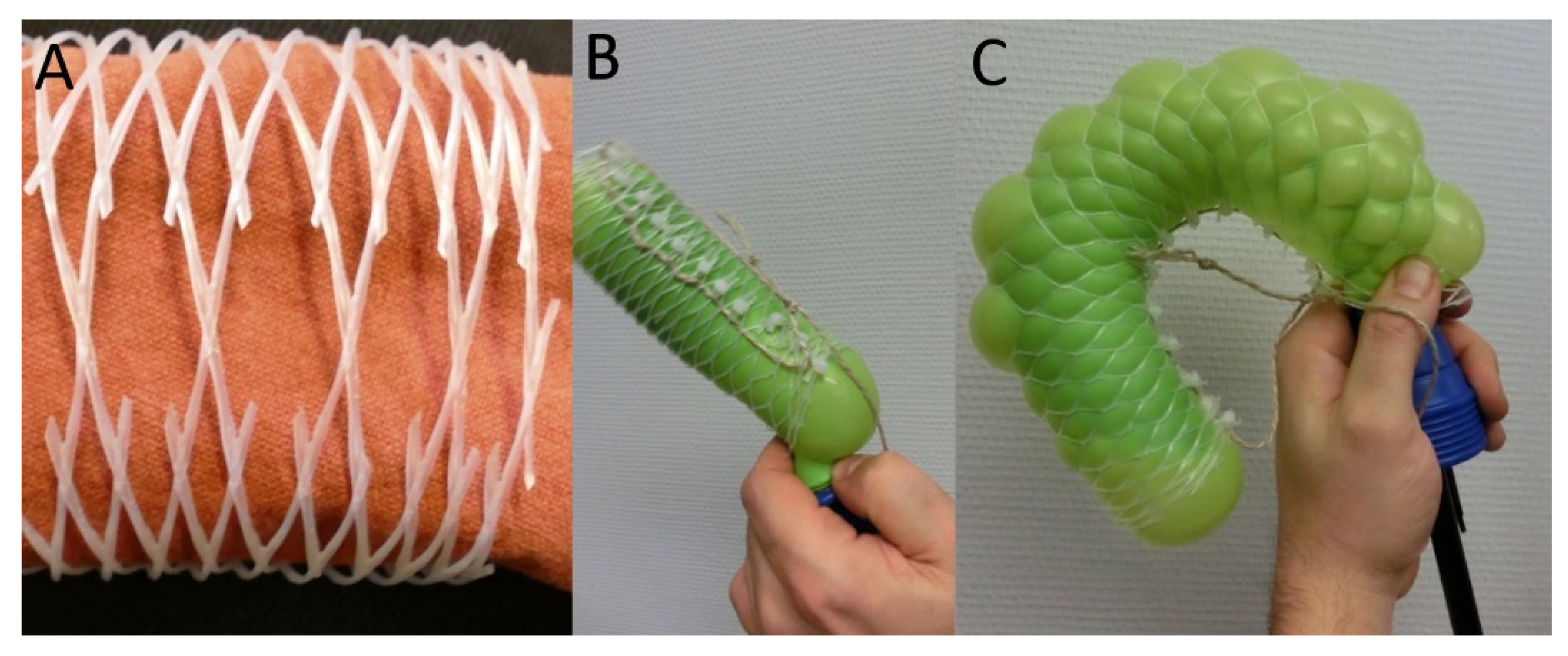
2.5.1. Technical Translation as Biomimetic Demonstrator with Linear Deformation
2.5.2. Technical Translation as Biomimetic Demonstrator with Asymmetric Deformation
3. Discussion
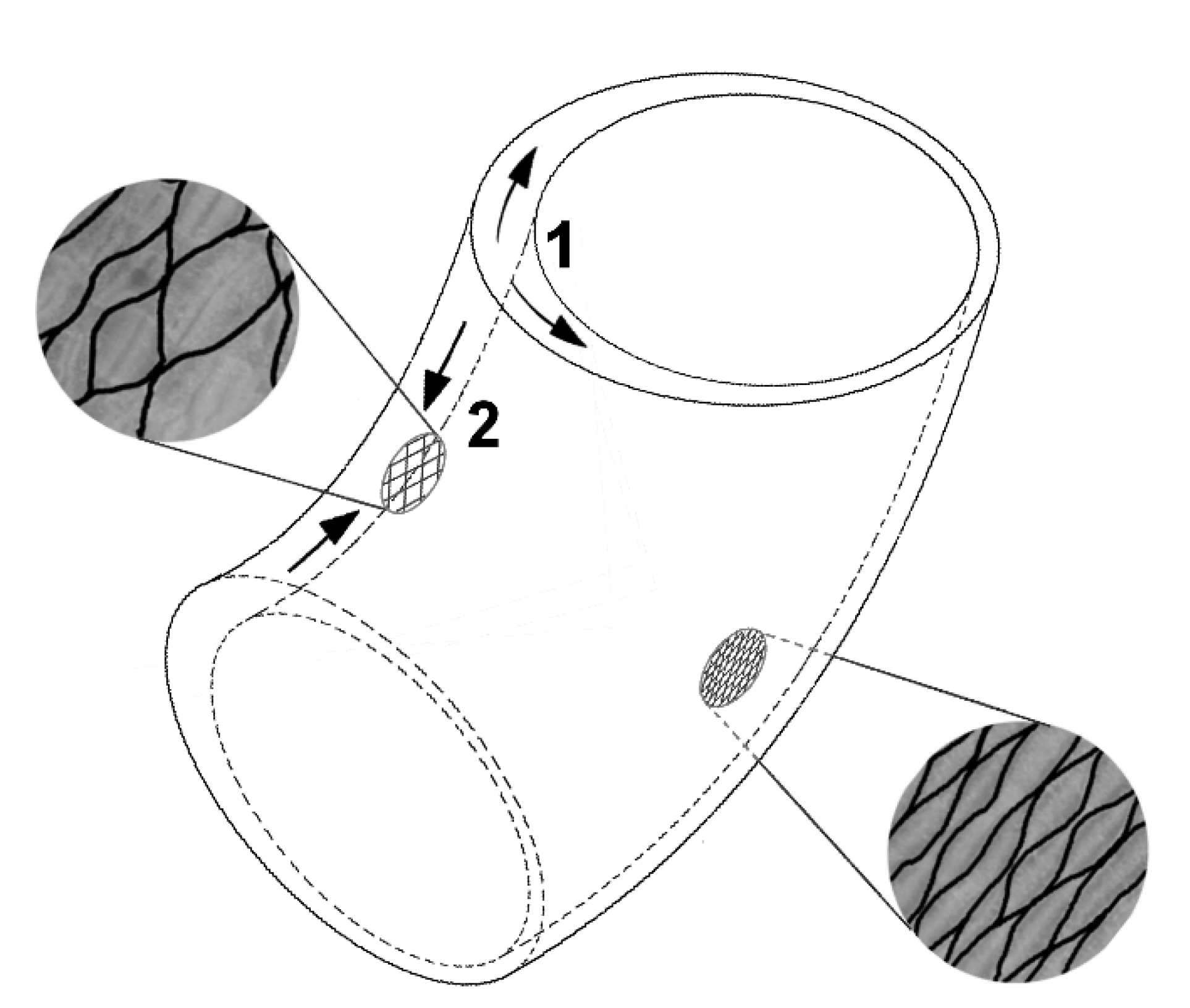
- Structure: The structural setup, i.e., a tubular geometry surrounded by a peripheral network of fibers, is similar in C. papaya, O. pyramidale, L. oldhamia, and the demonstrators of the bio-inspired 3D reticulated actuator.
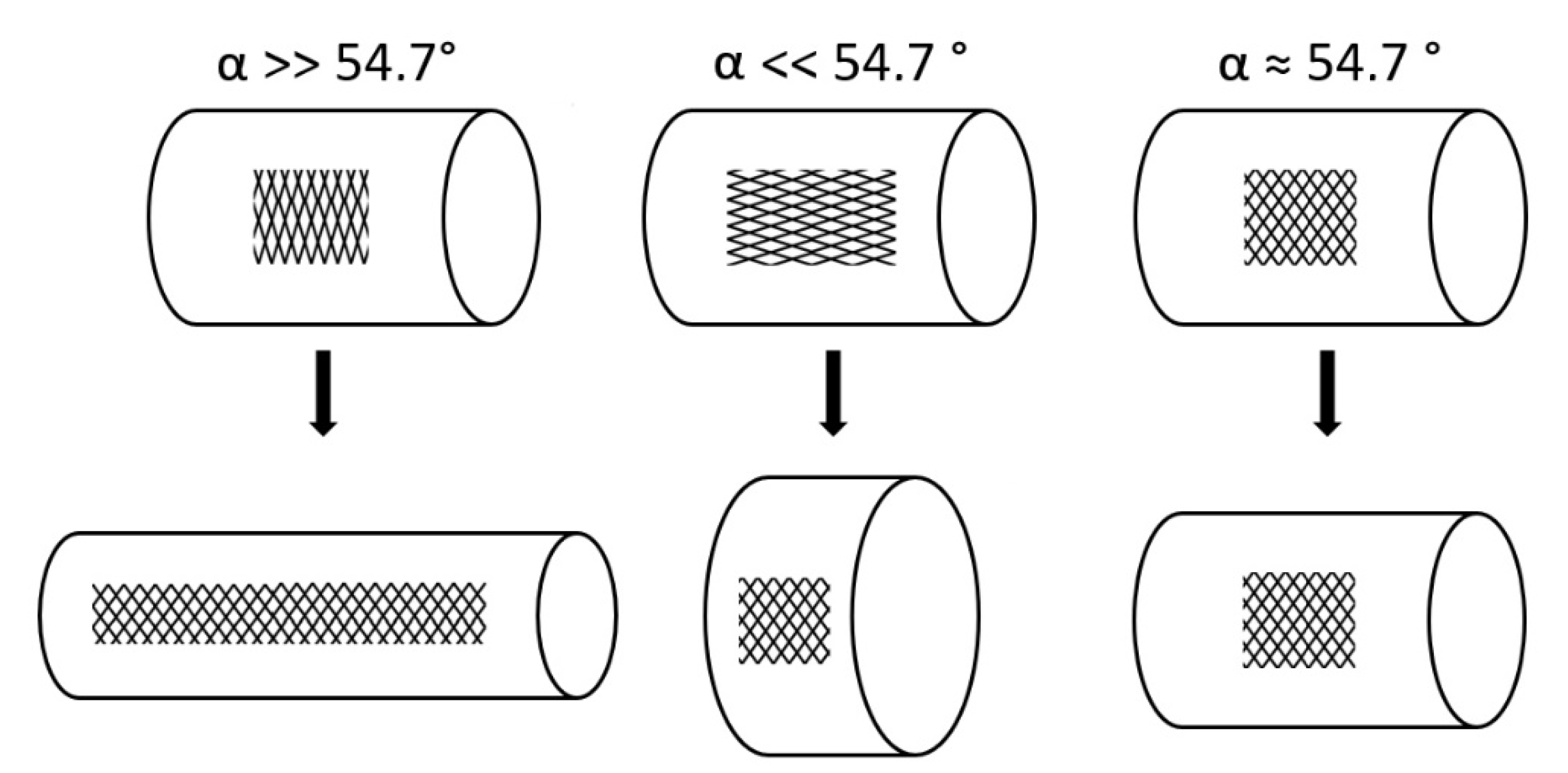
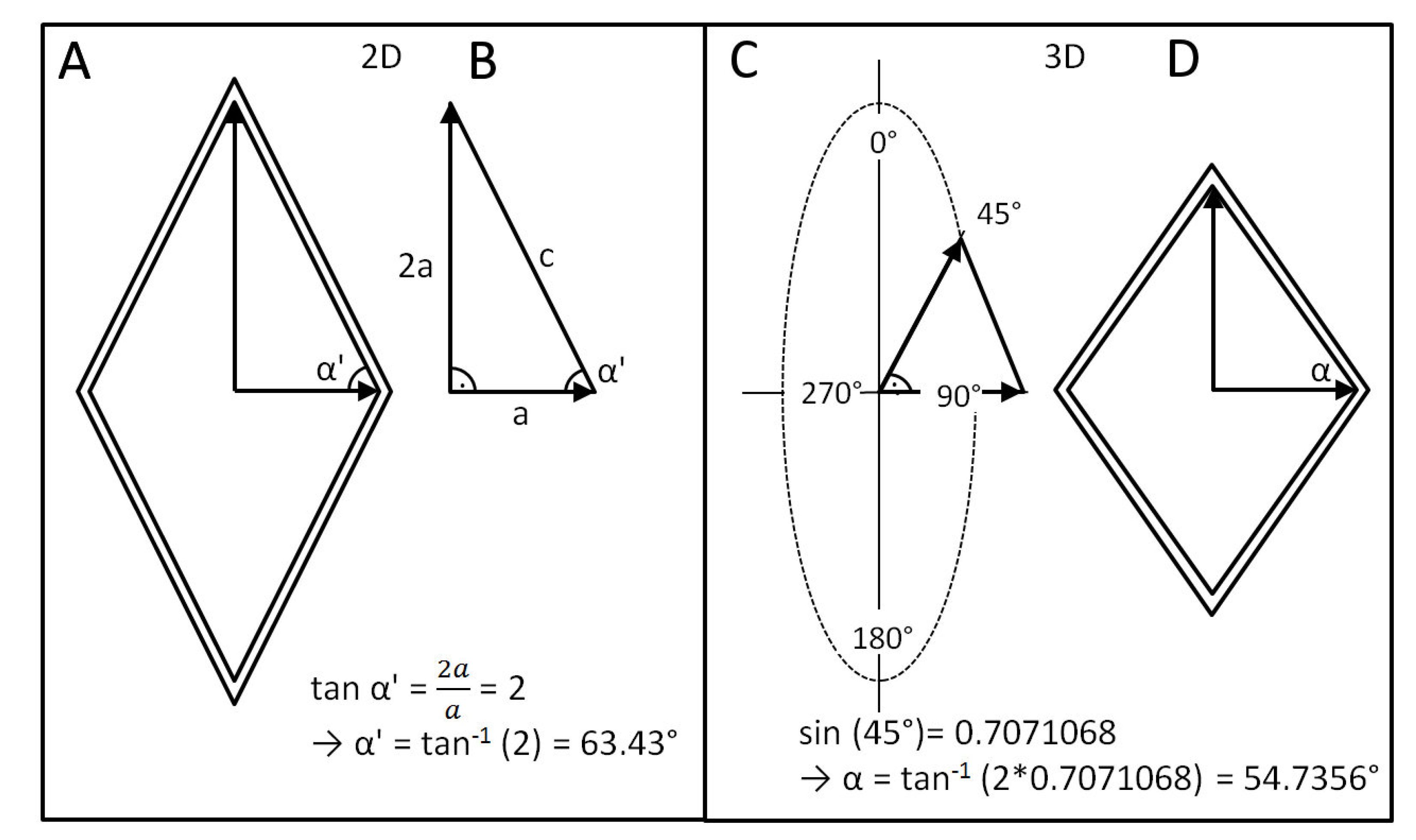
- Change of shape: Length–volume relationship depends on the fiber angle α between the spiral netted fibers and the longitudinal axis of the cylinder: leads to a maximal volume, but, under internal pressure, the cylinder elongates and thins when and shortens and thickens when °.
- Actuation: Shortening/elongation of the cylindrical net structures is often hydraulically driven in nature, e.g., the swelling of the so-called G-layer [34] in cell walls of reaction (tension) wood on the upper side of branches in deciduous trees. The increase in volume of the cylindrical cellular structure that occurs here is converted into a shortening of the wood cells in the axial longitudinal direction by a special enveloping layer [5,6]. Thus, tension is generated in the tension wood of deciduous trees. An additional example of this actuation principle by liquids is the movement of the feet of sea urchins and starfish, in which extension or contraction is actuated by pressure changes in the ambulacral system [13]. On a different scale, the similar deformations of the netted fibers in C. papaya, O. pyramidale, and L. oldhamia are actuated by growth-induced stresses. All of these examples have in common that the actuation is markedly different from the pneumatic pressurization used in the demonstrators (main difference: incompressible versus compressible actuation agents, see below).
- Speed of movement: Re-orientation of plant stems takes place by slow growth-induced processes, both in tension wood and in cortex-based (re-)erection, compared with the rapid inflation-based size and shape change in the demonstrator. Nevertheless, the time frame of the movements achieved with the bio-inspired demonstrators above shows more similarities with that of the shape changes in the feet of sea urchins and starfish.
- Reversibility: Re-orientation in the plants is irrevocable, whereas the pressurization of the demonstrators can easily be undone; this again shows similarities with the reversible motion of the feet of sea urchins and starfish.
- Power: Forces exerted by liquids (turgor pressure, swelling of G-layers, liquid-filled feet of sea urchins) or solids (secondary tissues) are higher than the forces attainable by inflation because of the incompressibility of liquids and solids as compared with compressible air.
- Curvature actuation: As detailed above, curvature is the result of asymmetric growth in C. papaya, O. pyramidale, and L. oldhamia, whereas it is a consequence of the asymmetric net structure in the technical translation.
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Poppinga, S.; Joyeux, M. Different mechanics of snap-trapping in the two closely related carnivorous plants Dionaea muscipula and Aldrovanda vesiculosa. Phys. Rev. 2011, 84, 041928. [Google Scholar] [CrossRef]
- Poppinga, S.; Bauer, U.; Speck, T.; Volkov, A.G. Motile traps. In Carnivorous Plants: Physiology, Ecology, and Evolution; Ellison, A.M., Adamec, L., Eds.; Oxford University Press: Oxford, UK, 2017; pp. 180–193. [Google Scholar] [CrossRef]
- Poppinga, S.; Daber, L.E.; Westermeier, A.S.; Kruppert, S.; Horstmann, M.; Tollrian, R.; Speck, T. Biomechanical analysis of prey capture in the carnivorous Southern bladderwort (Utricularia australis). Sci. Rep. 2017, 7, 1776. [Google Scholar] [CrossRef] [PubMed]
- Westermeier, A.S.; Fleischmann, A.; Müller, K.; Schäferhoff, B.; Rubach, C.; Speck, T.; Poppinga, S. Trap diversity and character evolution in carnivorous bladderworts (Utricularia, Lentibulariaceae). Sci. Rep. 2017, 7, 12052. [Google Scholar] [CrossRef] [PubMed]
- Goswami, L.; Dunlop, J.W.; Jungnikl, K.; Eder, M.; Gierlinger, N.; Coutand, C.; Jeronimidis, G.; Fratzl, P.; Burgert, I. Stress generation in the tension wood of poplar is based on the lateral swelling power of the G-layer. Plant J. 2008, 56, 531–538. [Google Scholar] [CrossRef]
- Burgert, I.; Fratzl, P. Actuation systems in plants as prototypes for bioinspired devices. Philos. Trans. R. Soc. 2009, 367, 1541–1557. [Google Scholar] [CrossRef]
- Speck, T.; Poppinga, S.; Speck, O.; Tauber, F. Bio-inspired life-like motile materials systems: Changing the boundaries between living and technical systems in the Anthropocene? Anthr. Rev. 2021. under review. [Google Scholar]
- Skotheim, J.M.; Mahadevan, L. Physical limits and design principles for plant and fungal movements. Science 2005, 308, 1308–1310. [Google Scholar] [CrossRef] [PubMed]
- Dumais, J.; Forterre, Y. “Vegetable dynamicks”: The role of water in plant movements. Annu. Rev. Fluid Mech. 2012, 44, 453–478. [Google Scholar] [CrossRef]
- Correa, D.; Poppinga, S.; Mylo, M.; Westermeier, A.S.; Bruchmann, B.; Menges, A.; Speck, T. 4D pine scale: Biomimetic 4D printed autonomous scale and flap structures capable of multi-phase movement. Philos. Trans. R. Soc. 2020, 378, 20190445. [Google Scholar] [CrossRef]
- Kempe, A.; Lautenschläger, T.; Neinhuis, C. Reorientation in tilted stems of papaya by differential growth. Int. J. Plant Sci. 2014, 175, 537–543. [Google Scholar] [CrossRef]
- Masselter, T.; Kempe, A.; Caliaro, S.; Neinhuis, C.; Speck, T. Comparing structure and biomechanics of extant Carica papaya and Ochroma pyramidale stems allows re-evaluating the functional morphology of the fossil ‘seed fern’ Lyginopteris oldhamia. Rev. Palaeobot. Palynol. 2017, 246, 258–263. [Google Scholar] [CrossRef]
- McCurley, R.S.; Kier, W.M. The functional morphology of starfish tube feet: The role of a crossed-fiber helical array in movement. Biol. Bull. 1995, 188, 197–209. [Google Scholar] [CrossRef] [PubMed]
- Heydari, S.; Johnson, A.; Ellers, O.; McHenry, M.J.; Kanso, E. Sea star inspired crawling and bouncing. J. R. Soc. Interface 2020, 17, 20190700. [Google Scholar] [CrossRef] [PubMed]
- Jonas, F.A.; Born, L.; Möhl, C.; Hesse, L.; Bunk, K.; Masselter, T.; Speck, T.; Gresser, G.; Knippers, J. Biomimetics for Architecture: Learning from Nature; Knippers, J., Schmid, U., Speck, T., Eds.; Birkhäuser Verlag: Basel, Switzerland, 2019. [Google Scholar]
- Poppinga, S.; Zollfrank, C.; Prucker, O.; Rühe, J.; Menges, A.; Cheng, T.; Speck, T. Towards a new generation of smart biomimetic actuators for architecture. Adv. Mater. 2018, 30, 1703653. [Google Scholar] [CrossRef] [PubMed]
- Correa, D.; Krieg, O.D.; Menges, A.; Reichert, S.; Rinderspacher, K. HygroSkin: A climate-responsive prototype project based on the elastic and hygroscopic properties of wood. Adapt. Archit. 2013, 33–41. [Google Scholar]
- Menges, A.; Knippers, J. Architecture Research Building ICD/ITKE, 2010–2020; Birkhäuser Verlag: Basel, Switzerland, 2020. [Google Scholar]
- Mader, A.; Langer, M.; Knippers, J.; Speck, O. Learning from plant movements triggered by bulliform cells: The biomimetic cellular actuator. J. R. Soc. Interface 2020, 17, 20200358. [Google Scholar] [CrossRef]
- Körner, A.; Born, L.; Mader, A.; Sachse, R.; Saffarian, S.; Westermeier, A.S.; Poppinga, S.; Bischoff, M.; Gresser, G.T.; Milwich, M.; et al. Flectofold—a biomimetic compliant shading device for complex free form facades. Smart Mater. Struct. 2017, 27, 017001. [Google Scholar] [CrossRef]
- Festo SE & Co. KG. Fluidic Muscle DMSP/MAS. Operating Instructions. 2018. p. 18. Available online: https://www.festo.com/net/SupportPortal/Files/492257/DMSP_MAS_2018-01f_8081496g1.pdf (accessed on 1 April 2021).
- Speck, O.; Boblan, I. Vom Luftballon zum künstlichen Muskel. Grundsch. Sachunterr. 2014, 62, 20–26. [Google Scholar]
- Behrens, R.; Poggendorf, M.; Schulenburg, E.; Elkmann, N. An elephant’s trunk-inspired robotic arm—Trajectory determination and control. In Proceedings of the ROBOTIK 2012, 7th German Conference on Robotics, Munich, Germany, 21–22 May 2012; pp. 1–5, ISBN 978-1-5231-0924-1. [Google Scholar]
- Boblan, I.; Schulz, A.; Tuchscherer, A.; Perfilov, I.; Bertrand, B. A compliant lightweight universal joint cascadable to a multi-joint kinematics—Tripedale Alternanzkaskade TAK. In Proceedings of the AMAM 2013, 6th International Symposium zur Bewegungsforschung, Darmstadt, Germany, 11–14 March 2013; p. 4. Available online: http://www.biorobotiklabor.de/pdfs/boblan-2013-AMAM2013.pdf (accessed on 22 March 2021).
- Speck, T.; Speck, O. Process sequences in biomimetic research. In Design and Nature IV; Brebbia, C.A., Ed.; WIT Press: Southampton, UK, 2008; pp. 3–11. ISBN 978-1-84564-120-7. [Google Scholar]
- ISO 18458:2015-05. Biomimetics—Terminology, Concepts and Methodology; Beuth: Berlin, Germany, 2015. [Google Scholar]
- Fisher, J.B.; Müller, R.J. Reaction anatomy and reorientation in leaning stems of balsa (Ochroma) and papaya (Carica). Can. J. Bot. 1983, 61, 880–887. [Google Scholar] [CrossRef]
- Masselter, T.; Speck, T.; Rowe, N.P. Ontogenetic reconstruction of the Carboniferous seed plant Lyginopteris oldhamia. Int. J. Plant Sci. 2006, 167, 147–166. [Google Scholar] [CrossRef]
- Masselter, T.; Speck, T. Secondary growth stresses in recent and fossil plants: Physical and mathematical modeling. Rev. Paleobot. Palynol. 2014, 201, 47–55. [Google Scholar] [CrossRef]
- Poppinga, S.; Speck, T. Bark, the neglected tree postural motor system. New Phytol. 2019, 221, 7–9. [Google Scholar] [CrossRef] [PubMed]
- Horgan, C.O.; Murphy, J.G. Magic angles in the mechanics of fibrous soft materials. Mech. Soft Mater. 2019, 1, 2. [Google Scholar] [CrossRef]
- Gordon, J.E. The New Science of Strong Materials, or Why You Don’t Fall through the Floor; Princeton University Press: Princeton, NJ, USA, 1976; p. 287. [Google Scholar]
- Takosoglu, J.E.; Laski, P.A.; Blasiak, S.; Bracha, G.; Pietrala, D. Determining the static characteristics of pneumatic muscles. Meas. Control 2016, 49, 62–71. [Google Scholar] [CrossRef]
- Gorshkova, T.; Chernova, T.; Mokshina, N.; Ageeva, M.; Mikshina, P. Plant ‘muscles’: Fibers with a tertiary cell wall. New Phytol. 2018, 218, 66–72. [Google Scholar] [CrossRef] [PubMed]
- Born, L.; Jonas, F.A.; Bunk, K.; Masselter, T.; Speck, T.; Knippers, J.; Gresser, G.T. Branched structures in plants and architecture. In Biomimetic Research for Architecture and Building Construction—Biological Design and Integrative Structures; Knippers, J., Speck, T., Nickel, K., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 195–215. ISBN 978-3-319-46374-2. [Google Scholar]
- Bunk, K.; Jonas, F.A.; Born, L.; Hesse, L.; Möhl, C.; Gresser, G.; Knippers, J.; Speck, T.; Masselter, T. From plant branchings to technical support structures. In Biomimetics for Architecture: Learning from Nature; Knippers, J., Schmid, U., Speck, T., Eds.; Birkhäuser: Basel, Switzerland, 2019; pp. 144–152. ISBN 987-3-0356-1786-3. [Google Scholar]
- Hesse, L.; Leupold, J.; Poppinga, S.; Wick, M.; Strobel, K.; Speck, T.; Masselter, T. Resolving form-structure-function relationships in plants with MRI for biomimetic transfer. Integr. Comp. Biol. 2019, 59, 1713–1726. [Google Scholar] [CrossRef] [PubMed]
- Jonas, F.A.; Born, L.; Möhl, C.; Hesse, L.; Bunk, K.; Masselter, T.; Speck, T.; Gresser, G.; Knippers, J. New branched loadbearing structures in architecture. In Biomimetics for Architecture: Learning from Nature; Knippers, J., Schmid, U., Speck, T., Eds.; Birkhäuser: Basel, Switzerland, 2019; pp. 153–162. ISBN 987-3-0356-1786-3. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masselter, T.; Speck, O.; Speck, T. 3D Reticulated Actuator Inspired by Plant Up-Righting Movement Through a Cortical Fiber Network. Biomimetics 2021, 6, 33. https://doi.org/10.3390/biomimetics6020033
Masselter T, Speck O, Speck T. 3D Reticulated Actuator Inspired by Plant Up-Righting Movement Through a Cortical Fiber Network. Biomimetics. 2021; 6(2):33. https://doi.org/10.3390/biomimetics6020033
Chicago/Turabian StyleMasselter, Tom, Olga Speck, and Thomas Speck. 2021. "3D Reticulated Actuator Inspired by Plant Up-Righting Movement Through a Cortical Fiber Network" Biomimetics 6, no. 2: 33. https://doi.org/10.3390/biomimetics6020033
APA StyleMasselter, T., Speck, O., & Speck, T. (2021). 3D Reticulated Actuator Inspired by Plant Up-Righting Movement Through a Cortical Fiber Network. Biomimetics, 6(2), 33. https://doi.org/10.3390/biomimetics6020033







