Abstract
Various methods published in recent years for reliable detection of battery faults (mainly internal short circuit (ISC)) raise the question of comparability and cross-method evaluation, which cannot yet be answered due to significant differences in training data and boundary conditions. This paper provides a Monte Carlo-like simulation approach to generate a reproducible, comprehensible and large dataset based on an extensive literature search on common assumptions and simulation parameters. In some cases, these assumptions are quite different from field data, as shown by comparison with experimentally determined values. Two relatively simple ISC detection methods are tested on the generated dataset and their performance is evaluated to illustrate the proposed approach. The evaluation of the detection performance by quantitative measures such as the Youden-index shows a high divergence with respect to internal and external parameters such as threshold level and cell-to-cell variations (CtCV), respectively. These results underline the importance of quantitative evaluations based on identical test data. The proposed approach is able to support this task by providing cost-effective test data generation with incorporation of known factors affecting detection quality.
1. Introduction
The transformation process towards electrical power systems such as from vehicles with combustion engines towards electrical vehicles (EV) has led to a significant increase in the demand for energy storage systems, which is mainly met by lithium-ion batteries (LIB) [1]. With increasing energy and power densities of such LIB, the thermal stability has captured great attention as potential failures might result in the explosive release of the stored chemical energy [2]. This destructive process called Thermal Runaway (TR) [3] has also come to public interest after the supra-regional media coverage of certain incidents and the consecutive recalls such as the grounding of Boeing 787 [4], the fire incidents of the Samsung Note 7 [5], burning electric buses [6] or problems with the Chevrolet Bolt [7].
The TR is characterized by a sequence of characteristic reactions which significantly influence the fault behaviour in certain temperature ranges. For more detailed information on the individual chemical reactions and mechanisms, please refer to the extensive work of Feng et al. in [2,8,9] as well as Li et al. [10] and Zheng et al. [11] in which the results of accelerating rate calorimetry tests is given. In [9], the authors also provide a detailed discussion of the various failure paths for initiating a TR.
Reported field failures as mentioned above often show a chain-reaction-like behaviour, since nearly every battery system in application consists of multiple cells forming battery modules and packs to fulfil the power and energy requirements. In case of a single-cell TR in such a dense-packed assembly, the released thermal energy can trigger a thermal failure of adjacent cells, propagating the TR through the whole battery system. Therefore, this failure is called Thermal Propagation (TP) and proposes significantly higher risks than a single TR due to the larger amounts of energy-release potential [12].
To address this problem—one of the greatest challenges in battery technology [13]—various solutions have been published and already integrated in battery systems. Despite the broad range of methods, in our previous work [14] three main approaches were identified:
- Reduction or delay of energy release by additives and alternative cell materials [15,16].
- Reduction in heat influx from adjacent TRs to slow down or rather prevent TP in accordance with the US Vehicle Battery Safety Roadmap Guidance, which states that TP must not be initiated [17] if a never fully excluded cell-level TR occurs [18]. Prevention by smart module design [19,20], active or passive cooling strategies [21,22] and/or thermal isolation [23].
- Detection of battery faults and abnormal conditions for countermeasures, warning and evacuation before a hazardous situation develops. Here, the Global Technical Regulation on Electrical Vehicle Safety (GTR-EVS) specifies at least 5 or enough time for egress [24].
The first two methods require the implementation of additional material into the battery system or supplementation, reducing the power and energy density or the performance per cost in exchange for increased safety and thermal stability [15,25]. It was also found that reduction in the heat transfer capabilities causes further disadvantages such as limited cooling performance [26] and increased thermal differences within the battery system [27]. In addition, Grabow et al. [28] have proven in a recent study that battery failures such as particle-induced internal short circuits (ISC) cannot be safely ruled out. A passive safety concept might advert, and the affected cell will remain in an unknown—most likely more unstable—state.
Through implementation of a fault detection method, however, both disadvantages can be addressed. The knowledge of the fault appearance even provides the possibility of active counter-measures such as increasing the cooling power or just the warning of operators and the surrounding. Therefore, various methods for fault detection have been proposed in recent years, as extensively summarized by Hu et al. [29]. In accordance with Klink et al. [14], who prove the advantage of evaluating the cell voltage compared to external sensors, these methods are mostly focused on the electrical quantities voltage and current—sometimes extended by temperature. The algorithms and methods utilized to evaluate the battery data originate from various scientific disciplines such as outlier detection [30] from statistics, neural networks from machine learning/data science [31] or modelling [32]. These adoptions of common techniques to improve the detection capabilities underline the importance of the topic.
Despite these very promising studies, no systematic side-by-side comparison of different methods has been published yet—not even in the context of recent extensive review studies [29,33,34,35]. There are, however, studies evaluating advantages and disadvantages of certain methods, e.g., by Hu et al. [29], but the classification based on measures such as sensitivity for noise or high precision [29] is rather subjective and vague [36]. In addition, some researches have published a brief comparison with alternative methods, e.g., [37,38,39], but both implementation and evaluation criteria are limited.
This lack of the ability for comparison is, inter alia, caused by the large variance in validation data and the known or unknown boundary conditions and due to the sensitivity of gathered results to the experimental design [40]. In addition, the results are often based on assumptions [41], which further hampers comparability. Especially, simulation studies are repeatedly criticized for the missing consideration of measurement noise [42] as well as possible cell-to-cell-variations (CtCV) [43,44,45,46,47] when investigating modules.
In summary, the combination of non-standardized evaluation criteria and lack of similar boundary conditions and assumptions hinders the comparison of published results. Therefore, the selection of the optimal method for a certain application from all published approaches is currently not possible. To address these issues, three requirements were identified. First, all methods should be validated on the same dataset. For statistical evaluations, this dataset must contain several test cases with variable default conditions. For the analysis of the detection performance, comprehensible data are advantageous. Second, the dataset should contain sources of uncertainty to represent real application. Consequently, the implemented uncertainty should be based on real world data. Third, the evaluation of the detection methods should be focused on quantitative and statistical measures to guarantee a fair and rational comparison.
This study proposes a methodology for the first two requirements by a data generation method leaned on Monte Carlo simulation. The Monte Carlo approach allows full controllability of boundary conditions and parameters, guarantees the comprehensibility of the data and simplifies the creation of large datasets. Although this work focusses on ISC faults, most statements are also valid for external short-circuit faults (ESC) due to the similar electrical behaviour. Furthermore, the main approach is applicable for other faults by changing the fault simulation part. Besides the variable fault simulation, further variance is integrated into the data by simulation of measurement noise and CtCV. Based on this comprehensible and large dataset the third requirement—qualitative evaluation—can be achieved using established statistical indicators.
The main contributions of this paper are:
- Extensive literature review of disturbances on the measurement signal and their magnitudes;
- Summary of common qualitative and quantitative evaluation criteria;
- Generation of test data with stochastic disturbances and variations with consideration of both fault-free and fault-containing samples with the scope of ISC and ESC;
- Example comparison based on binary classifiers and identification of optimum parameter combinations.
The remainder of this paper is organized as follows. First, the literature review on common assumptions and previous evaluation aspects is given in Section 2 side-by-side with experimentally determined values. In Section 3, the proposed Monte Carlo simulation framework and the underlying assumptions are described in detail. Furthermore, the simulation boundaries are defined as well as two exemplary fault detection methods briefly introduced. The performance of both methods is presented and discussed in Section 4 before the main findings are summarized in Section 5.
2. State of the Art
As mentioned above, recent methods for battery fault detection have been evaluated or criticized—mostly qualitatively—with respect to various measures. Although a complete overview of aspects is not possible due to the broad range, recurring aspects are listed below:
- Complexity or difficulty of the application, e.g.,
- -
- Large battery model parameter sets [31,32,39,41,48,49,50];
- -
- Large fault model parameter sets [30];
- -
- Model limitations [51,52,53,54];
- -
- Processing time [34,37,39,41,42,43,46,47,48,52,55,56,57,58,59,60,61,62,63,64,65,66,67,68];
- -
- Dependency of training data [30,34,37,38,39,41,42,52,56,69,70,71,72];
- -
- General complexity [44,64,66,70,73,74,75,76].
- Simplifications and assumptions concerning:
- -
- Imperfect monitoring data [41,42,50,62,63,64,66,70,76,77,78];
- -
- Deviation from homogeneous cell parameter [43,44,45,46,47,62,72].
- Limitation to single cells [43,45,79,80].
Therefore, origin, experimentally estimated values and implementations in testing of fault detection methods are briefly described in the following.
2.1. Measurement Uncertainty
It is commonly known that every practical measurement is distorted, and the quantity estimated as such is always just an—often sufficient—approximation of the true value due to the existence of random and systematic errors. To standardize definitions, procedures and for extensive reference, the guide to the expression of uncertainty in measurement (GUM) was published. Here, the definitions for the above-mentioned errors can be found at ([81], [B.2.20–B.2.22]). Following this vocabulary, this expected deviation is given as uncertainty of the measurement. The uncertainty itself generally results from various sources, e.g., the measurement device, the conducting person, environmental conditions, the measurement strategy and the measured object itself ([82], [transl.]).
It should be noted that strict adherence to the GUM requires each source to be identified and its individual contribution to the measurement uncertainty to be assessed. The GUM differentiates the origin of the information of the uncertainty, which either is by statistical analysis or by knowledge and classified as Type A and Type B, respectively.
In the context of the commonly used voltage measurements, the resolution and accuracy, sample rate, temperature correction and signal-to-noise ratio can be identified as possible sources of uncertainty. With respect to the finite resolution d of both the sensor and the corresponding analogue-to-digital converter, the estimate of the true value X can be expressed as . Here, the probability function is uniform and not (Gaussian) normally distributed. Strictly following GUM, a normal distribution must be used if the nature of the uncertainty and the probability function are unknown ([81], [4.3.7]).
It is obvious that this task becomes impractical with more complex systems outside well-controlled laboratory conditions. Here, the central limit theorem becomes handy when assuming the presence of multiple independent any-distributed uncertainties. It states that the sum of independently distributed variables will converge towards a normal distribution ([81], [G.2.1]). Thus, expressing measurement uncertainty with normally distributed behaviour, e.g., by Xia et al. and Zhao et al. [76,83], is feasible but still an approximation.
To model this normal distributed uncertainty, an additive component [73,79,84,85] with zero mean (Equation (1)) and given standard variation (Equation (2)) is commonly used [66,76,77,86] as the given exemplary for a voltage measurement by Equation (3).
Please note that in this simple approach, the uncertainty is independent of the measured quantity U.
For application of Equation (3) in simulation, a realistic value for the standard deviation has to be defined for each measurement quantity independently. Referencing recent approaches, this task is not trivial, as illustrated by the findings for voltage, current and temperature measurements presented in Table 1. On the one hand, investigation of measurement uncertainty in the context of fault detection is not often performed, despite the many mentions of advantages or disadvantages of certain detection methods. On the other hand, each study defines the uncertainty differently, e.g., in dB [39], as RMS [87], by variance [56], by standard deviation [50] or by accuracy [88]. Furthermore, in some studies the uncertainty seems to be meant Gaussian distributed, but only an amplitude is given [53,57], which is not a useful definition. For the representation in Table 1 a reference voltage of 3.7 V was assumed. The amplitudes and accuracy were treated as standard deviation.

Table 1.
Assumptions for the level of measurement uncertainty for the common battery system quantities cell voltage (U), current (I) and temperature () if modelled by zero-mean Gaussian noise with standard deviation . Displayed values were derived from publication if standard deviation was not given. Please refer to the table footnotes for limitations due to the provided data.
For further illustration, an incomplete overview of exemplary values for measurement uncertainty from application is given in Table 2. Here, given specifications for real monitoring systems from published studies are summarized as well as application notes, e.g., the guaranteed accuracy of battery management systems (BMS) integrated circuits (IC).

Table 2.
Reference values describing the measurement uncertainty from real application for common battery system quantities. For better comparability in case of percentages given, the absolute values were calculated based on 3.7 V and 44.4 V as nominal voltages for cell and module levels, respectively. The values derived as such are indicated by parenthesis.
With focus on the voltage measurement uncertainty, a significant deviation between some model representations given in Table 1 with values > 50 mV and the values from application < 10 mV is visible.
Assuming that the exemplary chosen commercial BMS-ICs represent close-to-application values of the measurement uncertainty a selection of 1 mV to 10 mV for seems feasible.
2.2. Cell-to-Cell Variations
For nearly every battery application, multiple cells have to be combined to achieve the electrical requirements. Since every cell in such a pack is subjected to small variations from production and material quality, for realistic simulation cell-to-cell variations (CtCV) have to be considered too. Since the CtCV are suspected for self-amplifying behaviour [18] the magnitude of variation is generally expected to increase over the module lifetime by individual ageing progresses [18]. Among other things, different operational conditions [97] such as temperature gradients cause uneven current distribution of parallel connected cells [98]. Similar to the measurement uncertainty, most approaches for describing the CtCV assume an underlying normal distribution. Thus, both mean and standard deviation (see Equations (1) and (2)) are used for quantifying the variations. Since both measures will change significantly with cell types and sizes, scaling the standard deviation with the mean as described by Equation (4) simplifies the comparability. This ratio from standard deviation relative to the mean is called coefficient of variation () [99] and is often given in %.
While CtCV should be incorporated into models for realistic results [100], there is no publicly available information on production quality of commercial cells. Thus, researchers have to assume proper variations based on educated guesses [101,102] or on the findings from extensive cell characterization studies. Within Table 3, a broad overview over recent studies and the corresponding results is given.

Table 3.
Overview of the literature on experimental determined CtCV of cell capacity and resistance, given as coefficient of variation (); see Equation (4). Please refer to Table 2 for comparison with common approximations for CtCV simulation. Cell specifications were taken from source; please refer to Wildfeuer et al. [103] for an in depth analysis of recent studies.
Please refer to Wildfeuer et al. [103] for an in-depth analysis of previous studies and measurement procedures.
As indicated by the presented findings, these studies focus on quantities such as capacity, internal resistance and sometimes weight, since these characteristics can be determined by standard measurement procedures with acceptable complexity and time effort. The internal origin of these externally expressed variations is theoretically understood and suspected, e.g., in variations of electrolyte, electrode balancing, etc., as extensively summarized by Beck et al. [127] but no internal root-cause analysis is performed in general by the listed studies. Paul et al. [107] have investigated this aspect by simulating the influence of internal variations on the external parameters R and C; backtracking measured variations onto variations on material level, however, is not possible. Therefore, the only valid data basis for simulating CtCV is external parameters on the basis of a simplified equivalent circuit.
With respect to the given capacities of the investigated cells, with a few exceptions, a clear focus on small size—often cylindrical 18650—formats is recognizable. Thus, cells with capacities < 5 Ah predominate the presented findings. In addition, only very few studies have achieved sample sizes ≈1000 as the majority are ≤200, which is relatively close to a statistical significant sample size. Nevertheless, a very good accordance over all estimated CVs for both capacity and resistance is observable, where seems to be smaller than in general. It was assumed that this behaviour is caused by the aim of the manufactures for lower variations of the capacity due to its property as the main performance indicator [114,123]. Recent findings by Wildfeuer et al. after revising previous datasets, however, indicate that the observed differences between and may originate significantly by uncompensated measurement errors [103]. Thus, approximation of the CtCV by values in the magnitude of and to 5% seems feasible.
It has to be mentioned that the authors of the listed studies identified both a high dependency on the cell batch and transformation of the normal distribution towards a Weibull distribution with the lifetime [102].
When consulting non-academic sources for close-to-application CtCV-values, a broad range from capacity variations of <2.5% [128] up to expected resistance variations of 15% [129] can be found. Since this range differs significantly from the experimentally determined values as given above, a proper definition of CtCV for implementation in simulation remains unclear.
This discrepancy is continued when revisiting the implemented levels of CtCV to validate fault detection methods, as summarized in Table 4. Similar to the non-academic range, the variation is assumed to be »1%, which is not supported by the experimentally determined values. Therefore, these values have to be understood as the worst case approximation. Based on the gathered findings, two configurations of CtCV simulation seem feasible:
- Orientation at statistical founded experimentally determined variations;
- Assessment of the worst case boundaries.

Table 4.
Assumptions of CtCV for both capacity (C) and resistance (R) utilized in recent studies in the context of battery fault detection evaluation. For three studies, no cell type was specified. Please refer to Table 3 for comparison with experimental determined CtCV values.
Table 4.
Assumptions of CtCV for both capacity (C) and resistance (R) utilized in recent studies in the context of battery fault detection evaluation. For three studies, no cell type was specified. Please refer to Table 3 for comparison with experimental determined CtCV values.
| Author et al. | Year | Cell | /Ah | Source | ||
|---|---|---|---|---|---|---|
| Dey | 2016 | 5, 10 and 15 | [77] | |||
| Chang | 2019 | 18650 cell | 2 | 10, 20 and 40 | 20 | [130] |
| Chen | 2019 | A123 ANR26650-M1A | 2300 | ±3 | [30] | |
| Dubarry | 2019 | 0.0, 3.75, 7.5, 12.5 and 15 | 0.0, 1.25, 2.5, 3.75 and 5 | [131] | ||
| Zhang | 2019 | −5, −3, 2 and 5 | −5, −3, 2 and 5 | [68] | ||
| Schmid | 2021 | Samsung INR18650-25R | 2500 | +10 | [42] | |
| Song | 2021 | 60 | 0, 1.5 and 2.8 | [132] |
Independent of the chosen configuration, the underlying design decisions and database should be disclosed.
Voltage Offset
Despite assumptions to the contrary [54], during the operation of battery packs, no perfect temperature homogeneity can be achieved [68], due to finite heat conductivity. Thus, the cells within a battery system are exposed to slightly different temperatures [21,133,134], which cause variations of the open circuit voltage (OCV) due to entropy effects. Since the entropy coefficient alters with respect to the state of charge (SOC), e.g., within −0.07 mV K−1 to 0.2 mV K−1 [135], no general statement of the effect can be made. With respect to published maximum temperature differences inside battery modules of <10 K [136,137,138,139,140] the voltage variation is expected to be <1 mV. In addition, the already mentioned CtCV causes further voltage variations since the differences in internal resistance will cause slight variations of the voltage-drop and overvoltage during charge and discharge, respectively.
Starting from an approximately identical state, the cells will drift as self-discharge [120], capacity and internal properties vary from cell-to-cell. To compensate for these influences and re-calibrate the cells towards a similar SOC, battery packs and systems are equipped with a monitoring unit (BMS) that will re-balance such deviations—usually by discharging cells with high voltage. Since this balancing causes losses and will never reach perfection due to the above-mentioned measurement uncertainty, a hysteresis is usually implemented. Due to this hysteresis, the open-circuit-voltage (OCV) of cells in battery packs will always slightly deviate. As the balancing is often performed at the end of the charge process, it can be assumed that the is approximately constant in-between. Please refer to Table 5 for an overview of exemplary values for this OCV offset. Similar to the previous aspects, the published range is rather wide and identification of a proper realistic value not trivial. When these magnitudes are compared with the values given for measurement uncertainty (Table 2), CtCV of the measured voltage is significantly more influenced by the balancing hysteresis—thus a constant voltage offset—than by the imperfection of measurement accuracy and resolution. Nevertheless, to best of our knowledge, the performance of fault detection methods have not yet been evaluated under the influence of constant OCV-offset.

Table 5.
Published values for the balancing hysteresis taken from sources close to field-application, such as application guidelines from BMS-manufacturers or accuracy values given for BMS in the academic literature.
2.3. Evaluation Aspects
Irrespective of the chosen approximations of the influencing factors discussed before for the test data, after applying a fault detection method to this dataset, the result needs to be evaluated. First, the calculated defect feature or detection signal can be analysed qualitatively, e.g., by visual inspection as seen in [37,39,146]. However, this simple approach quickly reaches its limits when the properties of interest go beyond, e.g., consistency among few variations. In particular, when different detection parameters, methods or datasets are to be compared, it is necessary to transform the complex fault characteristics and corresponding fault features into a low-dimensional measure. Therefore, the detection time has been used in many studies [41,43,50,51,52,72,73,75,77,79,92,147]. Here, the detection time is defined as the time between the trigger of the fault and the time of detection , as given by Equation (5). Using also evaluates the requirement for fault detection in an early stage due to the unpredictable development of ISC faults from mild towards sudden TR [148]. This measure is also in line with the GTR requirements mentioned above, where a time between the trigger of the thermal failure and a dangerous situation for the passenger is defined. In addition to the simple evaluation of , Liu et al. [79] have calculated the average (see Equation (1)), minimum and maximum value of for multiple repetitions of the same test.
By varying the fault size, both Dey et al. and Marcicki et al. have further investigated the smallest fault that was still detectable by their methods [77,86]. This becomes interesting when the disturbances discussed above are included in the test, as these are likely to mask the fault signal of a low magnitude fault.
The process of applying a detection method to a dataset with and without faults is not a battery specific task, but known as binary classifier from many other disciplines, such as pharmacy [149]. As indicated by its name, with each investigated sample two possible states are considered—e.g., a present fault and normal operation. In addition, the applied test has two outputs, indicating either a fault situation (positive) or no fault (negative). Based on these prerequisites, four outcomes of the applied test are possible, as summarized below:
| True positive | True negative | |||
| False positive | False negative |
If evaluated and summed over all conducted tests, the total number of, for example, true positive states is calculated. With these total counts, further measures are defined as listed in Table 6 as well as studies utilizing them.

Table 6.
Summary of quality indicators for evaluation of a binary test, their definition and usage in recent battery fault detection studies. See also [149,150]. Please note that the reference figure is different in-between indicators and therefore the sum is not equal to 1.
One observation of the given table is that—to the best of our knowledge—there is no published TNR in the context of battery fault detection yet. This illustrates that usually the presented detection methods are not tested against fault-free data and therefore . If TPR (sensitivity) and FNR (specificity) have been calculated for different detection method parameters and test boundaries, they can be plotted as conducted by Meng et al. [40]. The resulting curves are called the receiver operating characteristic (ROC) curve and provide the opportunity to identify the parameters for an optimized classification result. A similar assessment is possible with the Youden-index, in which both sensitivity and specificity are considered. Please note that TPR and FNR have to be evaluated together, since a method which always outputs the presence of a fault will obviously catch all faults () but is not useful at all (). Due to the severity of the TR, the response to a detection will be dramatic, such as immediate evacuation of an EV. Thus, must not occur regularly, which is measured by the FNR. Nevertheless, due to the severity, TR must not occur without warning (), which is incorporated in the TPR.
In addition, some studies have analysed the functionality of the investigated methods, such as the correct identification of the type of fault [52]. Similarly, the convergence of the employed algorithms has been evaluated [90,91]. Methods that estimate the fault magnitude, e.g., the resistance of the ISC, have been accessed on the basis of the accordance between the estimated and correct magnitude [38,51,55].
With respect to the intended application of the various methods within a BMS and in real-time, computational effort becomes a critical factor [67]—especially when tools from data-science are applied that are usually used on computational clusters. Thus, the computational time has been included into the analysis of recent studies [39,59,67,71,151]. This measure, however, has a significant drawback as it is very sensitive to the implementation of the algorithm in detail. To illustrate this problem, a comparison of different moving average implementations written in Python™ is given in the appendix (see Appendix A.1), while the result of all functions is the same, the computational time differs significantly. Thus, deriving an advantage or disadvantage just from the computational time is problematic and most likely biased from the algorithm design. In addition, the importance of this aspect is expected to decrease as the cost of computing power continues to decrease.
3. Material and Methods
To demonstrate a method that incorporates the before-mentioned requirements for a sensible data-generation, an exemplary workflow of fault simulation under the influence of disturbances and the subsequent detection and evaluation of detection methods is presented in the following. After the introduction of the cell chosen as sample for simulation in Section 3.1 the descriptions of model (Section 3.2) and fault detection (Section 3.4) follow.
Within Figure 1 the overall workflow is given—detailed descriptions on certain aspects can be found in the following. First, a simulation case is initialized by the definition of the simulation boundaries for the underlying random influences on the model. Under consideration of both Monte Carlo parameters and fault representation parameters, the model defined as such is repeatedly simulated for no-fault and fault conditions. These two datasets are evaluated using a chosen detection method configuration (see Section 3.4) which gives the fault feature signal for each simulation run. Based on the defined threshold, the fault feature under no-fault condition is evaluated, and a proper threshold is calculated. This value is then checked against the test dataset with mixed fault and no-fault conditions, and each simulation is classified with . Besides evaluation of individual simulation runs, the summary performance of the individual investigated configurations is analysed in the end.
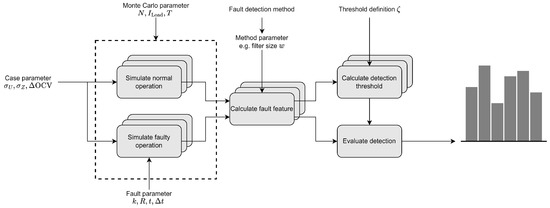
Figure 1.
Workflow for generating a dataset with variable characteristics (disturbances and faults) for setting up and validating different fault detection methods. External inputs represent parameter presets that are used either in the Monte Carlo-like data generation process or for different fault detection configurations.
3.1. Reference Cell
For this study, a commercial off-the-shelf pouch cell by Kokam has been chosen to represent common cell properties. The model name is SLPB98106100 and the nominal capacity is 10 Ah, which is in the range of typical industrially used large-format-sized cells. Following the classification of the manufacturer, the cell is a high energy version. Please refer to Table 7 for an overview of cell properties.

Table 7.
Selected datasheet properties of the SLPB98106100 pouch cell from Kokam that was used as reference cell for the simulation.
3.2. Model
This simulation study is based on an equivalent circuit model (ECM) as the representation of the dynamic cell behaviour. The model of cell and fault was implemented within Matlab/Simulink® [152] with pre- and post-processing was performed in native Matlab. As displayed in Figure 2, a second order ECM was chosen, which is in accordance with many other studies, where either a first or second order model was chosen as compromise between accuracy and complexity as investigated by Zhang et al. [153].
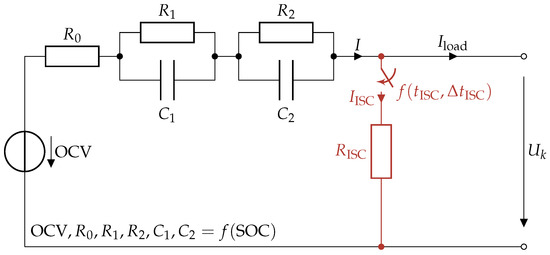
Figure 2.
Second order ECM as implemented in this simulation study to emulate the dynamic behaviour of one cell. All parameters describing the normal operation of the cell are implemented dependent on the SOC. Parallel simulation of multiple models results in the dynamic characteristics of one module in ks1p configuration. Emulation of ISC-fault by parallel resistance is indicated in red.
Using an ECM instead of elaborated models such as mathematical [154] or electrochemical models [88] comes with some advantages:
- Parameterization is doable by standard electrochemical tests;
- Implementation of parameter distribution is simplified;
- Fault representation (see below) is well-defined;
- Simulation time is fast.
To emulate a battery model in Ns1p configuration N cell models are simulated individually with the same load current. Within this study was chosen as common module configuration. In accordance with the ECM (see Figure 2) the individual cell voltage is calculated by Equation (6). The module voltage is then estimated by summation of all N cell voltages .
In accordance with previous studies such as [60,64,155] the dependency of the model parameters and the OCV by the SOC is incorporated as look-up-table (LUT). Values between provided points are approximated by linear interpolation. The required SOC is calculated using integration of the load current (coulomb-counting) as described by Equation (7).
For this study, the simulated sample-rate was set to 10 Hz and the simulation output was stored in as double data type.
As indicated in Figure 2 the thermal dependency of parameters was neglected. With respect to the mild ISC-resistances and short fault duration, this simplification seems reasonable. However, the proposed method is also applicable to more advanced battery models without changes.
3.2.1. ISC/ESC-Fault Representation
Besides some electrochemical fault simulation [88], simplified P2D-models [156] or reduced network models [157] in most cases both ISC and ESC faults are represented by a parallel fault resistance as highlighted by red colour in Figure 2 as well as in Equation (6). Thus, the cell voltage is further reduced by the internal voltage drop caused by the short circuit current. When the fault resistance is decreased, the deviation towards the normal cell behaviour increases.
The sudden fault appearance and clearance is realized by a time controlled switching behaviour.
3.2.2. Randomness and Variation
The influence of the previously discussed disturbance variables on a realistic voltage measurement signal should also be included in the generated test data. Thus, the ECM is extended to take into account both the imperfection of the measurement and the variation in the individual battery cells. The details of the implementation are described below.
Measurement Uncertainty
In accordance with most before-mentioned studies (see above, Section 2.1) additive zero-mean Gaussian noise () is used in this work to emulate a voltage signal with imperfect measurement. As indicated by the dependency of t and k, the noise value is generated randomly for each sample and cell.
Cell-to-Cell Variation
Both voltage offsets and impedance parameter variations are implemented into the simulation framework. Variances of cell capacity, however, are not considered separately. First, according to the literature review (see Section 2.2) the expected coefficient of variation is rather small (<1%), causing only small variations in the OCV-SOC behaviour. Second, this small variation is already implemented by the voltage offsets.
Unlike the measurement uncertainty, both variations are assumed to be approximately constant over the simulated time period. Therefore, the value is set for each cell during model initialization. In contrast to the , which is also implemented as an additive variation, the parameter variation causes a deviation relative to the reference cell parameter as exemplary shown in Equation (8) for (see Figure 2), where represents the relative deviation.
The LUT of all parameters given in Figure 2 (, ) are scaled analogously by the same value. Since the impedance has experimentally proven (see Section 2.2) to behave normally distributed, the scaling factor for each cell k is generated from a normal distribution with given standard deviation (). In contrast, the voltage offset has been found to be significantly influenced by the balancing hysteresis and resolution, which behave uniform distributed according to GUM. Thus, the was generated for each cell from a uniform distribution following where d is the selected hysteresis width.
3.2.3. Parameterization
The parameters of the ECM shown above were measured beforehand at 20° using the SL1002 6 V/1000 A/0.6 kW battery test bench from Keysight/Scienlab. For all tests, the cell was clamped between two aluminium plates to emulate the clamping force within a battery module [158]. Using screws to tighten the setup, a pre-tension of approximate 0.1 MPa was established, which is close to realistic applications [158,159]. Using screwed connections, the pouch cell tabs were connected to the battery test bench.
The correlation between OCV and SOC was measured by charging and discharging the cell at very low (0.05 C) current, which is called pseudo-OCV (P-OCV) measurement. Averaging the both voltage curves and normalization of the charge with the nominal capacity (see Table 7) gives the relationship. The passive parameters of the ECM pictured in Figure 2 were calculated based on current steps with 1 C and 2 C in charge and discharge direction. Both pulses were applied for 10 s and were followed by a 50 s relaxation. To incorporate the SOC-dependency of the parameters, this pulse procedure was conducted for every 10%-SOC increment. Due to the operational limits for 100% and 0% no charge, respectively, no discharge pulse was applied.
Using the SciPy implementation of the Powell-algorithm [160] the model parameters were fitted to the data. Here, both the pulse and the relaxation were considered as well as both currents directions and amplitudes and an overall fit was performed.
The parameterized model was evaluated by means of both standard and normalized root mean squared error (RMSE and NRMSE) compared with a reference dynamic drive cycle test. Please refer to Equations (9) and (10) for the calculation of both metrics. The dynamic load was emulated using the WLTP drive cycle [161] six time, which results in a validation time period of 10,800 s. The achieved simulation quality was 0.0253 V and 0.0286 for RMSE and NRMSE, respectively. These values are in range to similar published results [41,54].
3.3. Simulation Cases
For proof of concept of the above-described simulation framework, the following test cases were defined: First, only the measurement uncertainty is incorporated to the model (Default), which is the source of uncertainty most often used in recent studies. Second, the two other disturbances and are implemented both separately and combined to create test datasets with more kinds of variation. The values for all variations were chosen in accordance to the literature review given in Section 2.1 and Section 2.2 as given in Table 8. For investigation of the sensitivity of the detection results towards the magnitude of the disturbances, multiple modified (mod.) parameter sets were created as well. The considered ranges are given in Table 8.

Table 8.
Parameters of the Monte Carlo data generation, including simulated uncertainty and ISC-fault replication. The individual parameter-set was generated randomly based on either a uniform () or a Gaussian () distribution. Left: Values for the implemented model disturbances dependent on the simulation case, where measurement uncertainty only is considered as Default. Please refer to Section 2.1 and Section 2.2 for further details on the implementation. Right: Intervals for generation of a fault-simulation parameter-set based on a uniform distribution.
The fault appearance, however, was kept constant for all simulation cases and was based on the following assumptions:
- The fault chance is 80%;
- Only one cell fault per time;
- Only one fault event per simulation run.
All four fault-defining parameters were selected randomly from a uniform distribution. For incorporation of fault-free cases, the fault was applied with a chance of 80%, while the cell index k was chosen within the cell count, 1 to 12 the time of fault was chosen from the simulation duration T. Thus, for simulation of the WLTP 1 s to 1800 s were considered. In addition, 1 to 100 and were chosen as boundaries for the fault resistance and fault duration, respectively. The selected range is in accordance with various recent studies [40,49,61,88] and the range incorporates both resistances commonly considered as safety-critical (<4 [162], <10 [88] and mild criticality (1 to 100 [75,163], >10 [164].
3.4. Fault Detection Methods
To illustrate the proposed approach, two rather simple fault detection algorithms were implemented. Both the implementation of the detection methods and the pre- and post-processing were performed in Python™ (V3.9.12) and are heavily based on the NumPy (V1.21.5) [165], SciPy (V1.7.3) [166] and pandas (V1.4.2) [167] packages.
First, the deviation between individual cell voltages and the mean of the module is considered. Normalization of this deviation with the standard deviation leads to the z-score that is investigated as well. Please find the algorithms defined below. In accordance with other methods, a rolling window filter can be applied to the calculated fault signal for further signal refinement.
To eliminate small deviations stemming from the machine precision the calculated fault signal is rounded to the nearest 8 digits.
Based on the fault signals estimated as such, the required thresholds have to be defined. Within this study, a deterministic approach was chosen to ensure comparability. Since the threshold is often defined by trial-and-error with given reference and fault data, a deterministic approach as performed by Ouyang et al. [75] is seldom documented. The process is described as follows:
- Generate many samples without presence of a fault.
- Calculate the fault signals for the detection method for each sample.
- Determine the maximal fault signal value for each sample.
- Define the threshold as .
- If the fault signal is greater than a fault will be assumed.
Thus, by changing the threshold level the quality of the results (see Table 6), e.g., false positive values (FPR) can be altered. By approximation of an underlying normal distribution, the relationship between and the samples inside the so-defined boundaries is as given in Table 9. Due to the definition of the fault occurrence as excess of the threshold, the one side-probability is given in addition to the more common two-sided one. Within this work 1, 2 and 3 was investigated.

Table 9.
Probability of samples within multiple standard deviations around the mean of a normal distribution. The two-sided values describe and for the one-sided case . Here, the left side of the distribution is already fully incorporated.
3.4.1. Deviation from Mean
The input of the detection method is the voltage measurement matrix of the module with elements . Here, N represents the number of cells and T is the number of samples. For each sample step t, the vector is evaluated and the mean as well the difference to each cell is calculated as defined by Equations (12) and (11). In addition, following Equation (13) this fault signal vector can be smoothed by subsequent application of a rolling average filter with window length w using previous sample steps.
where
Assuming that of the cell under fault condition will be smaller than without an ISC due to the additional voltage drop (see Figure 2) a positive correlation between amplitude of the fault signal and fault magnitude is expected.
3.4.2. z-Score
The z-score as utilized inter alia in [59,168] is quite similar to the above-mentioned deviation from the mean. However, the deviation as calculated in Equation (11) is standardized by the standard deviation (see Equation (2) as shown by Equation (14). Thus, the resulting fault signal indicates its deviation from the mean relative to . Similar to before, by application of a moving average filter (see Equation (13)) the z-score can be smoothed, too.
As the definition is similar to Equation (11) and the difference just normalized, a positive correlation between fault magnitude and fault signal is expected as well.
4. Results and Discussion
Using the described simulation workflow, first the simulation setup and the validity of the gathered results are investigated in Section 4.1 and Section 4.2. Based on these prerequisites, the generated data and implemented fault detection methods are used to evaluate the fault detection functionality and transform the individual result per simulation into an overall describing metric within Section 4.3. The analysis is complemented by further investigations in Section 4.4 where individual simulation and evaluation parameters are investigated in detail.
4.1. Number of Simulations
Since the threshold definition is based on the estimated mean and standard deviation of the simulations without fault, the minimum number of simulations required for a good estimation of these statistics has to be determined. Due to the asymptotic convergence of the sample mean to the population mean with , increasing the estimation accuracy will significantly increase the number of simulations. Thus, a trade-off between the two aspects is necessary.
Assuming a normal distribution, the confidence interval of the estimated mean of a sample with size n is defined by the limits [81]. Here, is the sample mean, the corresponding standard deviation and z the quantile of the t-distribution associated with the sample size n and the desired confidence level, e.g., 95%. With , the t-distribution can be approximated by the normal distribution, thus (see Table 9). Rearranging the equation above gives
where is the acceptable deviation in %.
Evaluating both detection methods with different window sizes w for a sample of 300 simulations gives the statistics summarized in Table 10. The derived minimum number of simulations for a 2% deviation with 95% confidence is given as well. Thus, due to the small sample variation observed, even few simulations < 100 achieve high reliability.

Table 10.
Summary statistic coefficient of variation () for the default simulation case with 300 simulation runs. Evaluated maximum fault signal for deviation from mean and z-score z dependent on the filter window size w. Required minimal simulation runs N to achieve 2% accuracy results with 95% confidence.
In order to represent the additional variations due to the error simulation, at least 100 simulations for the loads Zero and CC and 1000 simulations for the WLTP are used arbitrarily in the following for no-fault simulations. With respect to the additional variations under fault simulation, here, the number of simulations were doubled. Please also refer to Table A3 for a comparison of the evaluation (see below) of two simulation studies with identical boundary conditions. The high agreement between the two datasets proves that the number of simulations is sufficient and that the gathered results are valid.
4.2. Distribution of Fault Feature
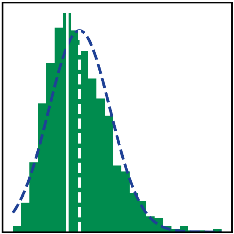
For both the definition of the threshold and the approximation of the required number of simulation runs, a normal distribution of the maximum values of the calculated fault signals was assumed. On the left side of Table 11 this maximum value distribution is exemplary visualized for the z-score -method of 1200 simulations (Zero load: 100, CC-load: 100, WLTP: 1000) and window as highlighted in Table 11. It is visible, that the average is shifted (skewed) towards the right relative to the peak of the distribution, which is quantified by positive values for the skewness (see Equation (17) from [169]). The calculated skewness for and further distinct windows sizes is given in Table 11. This behaviour is in accordance with the known properties of sample maximum distributions. These sample maximum distributions are either Weibull, Fréchet or Gumbel distributions dependent on the underlying population distribution. For an underlying normal distribution that can be assumed for this case due to the implementation of the disturbances, a Gumbel distribution is expected as sample maximum distribution [170].
where

Table 11.
Statistical properties average , standard deviation and skewness for the maximum fault signal distribution of the fault-free simulation setup with . Evaluated of the fault signals for the detection methods z and for different window sizes w. The corresponding FPR in % is calculated based on a threshold associated with which should result in a FPR of 0,18% according to Table 9. Left margin: Exemplary barplot of the maximum fault signal distribution for the z-score of (green, highlighted values) and approximation by a normal distribution based on the statistical properties , (blue). Skewness is visualized by marked peak position (white).
Due to the positive skewness, more values are located on the right side of the mean compared to the normal distribution. Thus, the assumed FPR associated with a certain -based threshold is underestimated, as shown in Table 11 for a -range. Based on this threshold, the FPR should result in the range of ≈0.18%, as given in Table 9. It is shown that with one exception the FPR is larger but ≤1.5%. Despite the rather small error due to the simplification of assuming a normal distribution, the comparison made should raise awareness that any assumptions regarding the basic distribution functions should be carefully examined in order to be able to estimate and explain the resulting behaviour.
4.3. Fault Detection
The voltage profile of a simulated ISC-fault (here cell 11) is presented exemplary within the top axis in Figure 3 in comparison to a fault-free cell (01) during dynamic WLTP load. For illustrational purposes, a severe ISC-fault of 1 was chosen, causing a significant voltage drop along the internal resistances as visible in the magnification on the right side. The fault was initiated at s and lasts for s, as marked within the right axis and indicated by the red background colour. Due to the additional discharge during the ISC-fault, a remaining voltage offset between the faulty cell and the unaffected cell is visible.
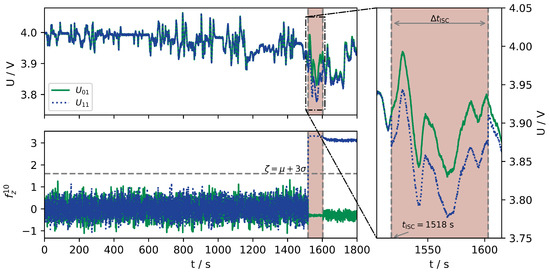
Figure 3.
Simulated voltages for faulty cell () and fault-free cell (here ) for simulation of 1 ISC-fault at 1518 s for 85 s. The period of fault is magnified at the right and marked in all axis in red colour. The corresponding z-score fault signal with ( ) is given in the lower figure, as well as the threshold level.
In addition, the corresponding fault signal of both cells is given in the bottom part of the Figure. Here, the z-score filtered by 10 sample periods, thereby 1 s, was chosen. Please note the detection threshold based on a interval as indicated by the horizontal line.
At the start of simulation—just under the influence of measurement noise—the fault signal is noisy but with the presence of the fault the z-score of the faulty cell increases virtually immediately and surpasses the threshold. Thus, the fault is already detected after 0.3 s. After the fault is gone, however, the fault signal remains above the threshold due to the above-mentioned voltage offset, while this sensitivity of the z-score to offsets simplifies the detection of smaller faults with less initial voltage-drop, it causes problems when voltage offsets exist already in fault-free samples, as discussed within Section 3.2.2.
Following the observations, this simulation in combination with the method and is classified as true positive (). Evaluating all 2400 simulations for this method and threshold gives the results presented on the left side of Figure 4. Here, each simulation is coloured based on the achieved classification, where is green and is red. Please also note the simulation discussed above marked by a star in the upper left part.
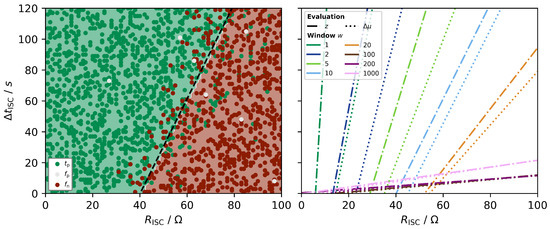
Figure 4.
Left: Classification of simulation runs to , and with respect to the fault resistance and fault duration for z-score and window size . Please note that (see Section 2.3) will not appear in this representation. The boundary between and is visualized by fitted model using linear support vector classification (SVC). Right: Decision boundaries for both detection methods and variable window sizes.
An approximate linear dependency between both fault resistance and fault duration and the achieved classification is observable. In contrast, no such dependency was observed for the classification that occurred randomly with low frequency. To illustrate the dependency between detection and no detection under the presence of a fault, the decision boundary for and was calculated by using a support vector machine (SVM) algorithm. This boundary is marked by a dashed line in the figure. Although the change from to is not so much sharp and other contrary classifications can be found beyond the boundary line, the chosen representation represents a good summary of the individual simulations:
First, the right and left hand side area approximates the FNR and TPR, respectively, since the figure displays all fault-cases (, see Table 6). Secondly, the intercept with the horizontal axis (bottom and top) indicates the smallest detectable fault (see Section 2.3). In combination with the slope of the boundary, the smallest detectable fault with respect to the fault duration can be approximated as well. Thus, the slope can be used to understand which parameter has more impact on the classification quality.
With these prerequisites, the results of both detection methods and with variable window sizes w can be compared as given on the right in Figure 4. Here, each line is the calculated decision boundary between and .
It is visible that with the same filter size the z-score is always left to the . Thus, the FNR is expected higher and the smallest detectable fault or rather the highest detectable fault resistance is smaller. In addition, both methods show similar behaviour when the filter size is increased as the slope decreases and the intercept with the horizontal axis increases, resulting in a significant better detection performance based on FNR and detectable resistances. For filter sizes , however, this trend is reversed, and a decreasing performance is observed.
This behaviour is due to two effects that occur with increasing filter size: First, the influence of the measurement noise on the fault signal is reduced, which also results in significant smaller threshold levels. Therefore, smaller faults can be detected since the signal-to-noise ratio increases. Secondly, the sudden fault signal deviation at fault appearance (see Figure 3) is filtered as well, which increases the time to surpass the threshold. Thus, the fault duration becomes more important on the detection results with increasing filter size. In addition, the charge difference between the faulty cell and the remaining cells also increases with the fault duration. Since both methods are biased by offsets, this developing deviation provides a second possibility for fault detection besides the initial voltage drop.
Therefore, an optimum between filtering noise and removing fault information has to be found, which was observed in this study at approximate .
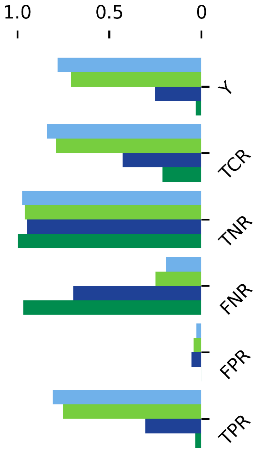
Within Table 12 the calculated quality indicators of the discussed study are given. The table is accompanied by a graphical illustration of the values for the z-score with for each given w.

Table 12.
Classification quality indicators for the fault detection with both z-score and for a fault simulation setup with and ≈80% fault cases under default measurement uncertainty. The classification is evaluated under different filter sizes w and underlying threshold level . Please refer to Table 6 for the definition of the indicators. The graphical illustration visualizes the values for , where the corresponding window is marked by colour.
Please note the decreasing FNR values with increasing w, as was visually analysed before. In addition, the approximately opposing characteristic of TPR is found in the data as well.
Taking TPR of the z-score at (Table 12, grey backfill) it seems that is the best option, since it has the highest value and nearly every fault was detected. The FPR, however, also gives a high rating, meaning that of fault-free cases were also classified as fault. Thus, the TPR alone is not a suitable measure, since identifying just every test case as fault would give . This problem can be solved by the Youden-index, since it combines both sensitivity and specificity into one indicator. Using this index, the visually determined best configuration of window and threshold level at and , respectively, is confirmed. While the former analysis is focused on the classification into fault and no-fault, other potential measures are feasible as well, e.g., the before-mentioned detection time . Due to its definition given in Equation (5), only cases with correct fault-detection () are considered by this indicator. Accordingly, the evaluation based on only can only provide a limited picture of the detection performance—similar to using just TPR. Especially with low TPR rates (see Table 12) using might remove significant chunks from the data.
However, since has been used in recent studies (see Section 2.3) the achieved times are given in Figure 5 with respect to the corresponding fault parameter value. In accordance with the fault parameter space described in Table 8 the variables are (a) the fault resistance , (b) the fault duration and (c) the time of fault . For the sake of clarity, only the z-score method is presented for the configuration , but similar behaviour can be observed for other configurations as well.
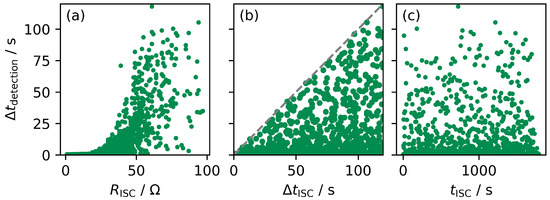
Figure 5.
Achieved detection times of the z-score method () with respect to (a) the fault resistance , (b) the fault duration and (c) the time of fault . Please note that only classified cases are considered in this analysis.
Despite the time-dependent load amplitude of the WLTP used, there is no correlation between and in (c). Thus, the commonly found validation with fixed may be less prone to a biased result.
Neither with regard to nor is a classical correlation to be observed. Instead, however, the range of possible detection times seems to change as a function of the variables, as can be seen from the relatively sharp edges in (a) and (b). The dashed border in (b) represents the duration of the fault itself, so that no fault could be detected after its clearing. This behaviour is disadvantageous for the application, as short faults may remain undetected. With regard to the resistance, a minimum size can be recognised, which is necessary for a detection within a certain period of time. This consideration is of particular interest for designs according to the 5 min criterion of the GTR-EVS mentioned at the beginning.
Removing all fault-cases without detection from the analysis for evaluating a fault detection method seems counter-intuitive; therefore, an opposing approach is described in the following:
For comparison of two not-detected ISC faults, the assessment of the corresponding criticality seems feasible. However, due to limited understanding of the ISC processes and the highly stochastic behaviour [171] the fault characteristic often remains unclear and the dynamic state not feasible for proper assessment [9,33,172].
Therefore, in the context of this study, the released energy during the fault duration starting at the ISC trigger is utilized for comparison. Since the energy increases with the and decreases with the fault resistance the fraction of both is taken as an approximation of the associated criticality of an unidentified fault as given in Equation (18).
Thus, in addition to the smallest detectable fault (see above), this indicator provides information on the severity of potential misses.
In Figure 6, the highest criticality value that was not detected is presented for the before-mentioned variations of detection methods and parameter are given. Here, a higher value represents an undetected fault with either longer fault duration or smaller resistance. Thus, for most applications, a small value is desired.
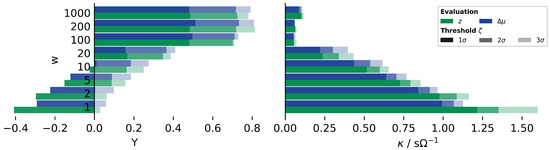
Figure 6.
Achieved detection quality for both methods and z-score with respect to the underlying threshold level and filter size w; Left: Youden-index (Y). Right: Approximation of criticality of faults that were not detected ().
It is clearly visible that with increasing filter size the most severe missed fault becomes less and less significant. Increasing the threshold limit, however, has a contrary effect. The former observation is most likely linked to the already identified improvement of the detection results with increasing filter size (see Figure 3). On the contrary, enlarging the threshold will cause longer detection times and misses of smaller faults, which leads to a higher not-detected criticality.
4.4. Further Investigations
For the previous analysis, the unlimited range of parameters had to be restricted to certain values in order to allow clear evaluation and comparison. The sensitivity of these restrictions is examined below.
4.4.1. Threshold Level
In the previous discussion, the dependence of the classification result on the chosen threshold was repeatedly observed. However, the observed characteristic of increasing performance with increasing threshold could not be predicted, as two effects are to be expected: On the one hand, increasing the threshold reduces the probability of . On the other hand, the significance of the error signal required to detect an error increases. Accordingly, an a priori consideration is difficult to make. Therefore, and since the values of 1, 2 and 3 were chosen rather arbitrary, the deviation of the Youden-index due to was evaluated.
The corresponding characteristics are given in Figure 7 for both methods and the known selection of w. First, the dependency between achieved detection performance—assessed by the Youden-index —and threshold level is clearly visible. This dependency is in high accordance to literature statements that the threshold definition has significant impact on the detection result [35,71]. The observation, however, calls into question the general validity of results obtained by means of the often described trial-and-error procedure based on experimental data, which was also used by the authors in previous work. Due to the limited amount of test data in the context of timely and expensive experimental abuse test and the large sample size needed [44], the trial-and-error procedure is advantageous.
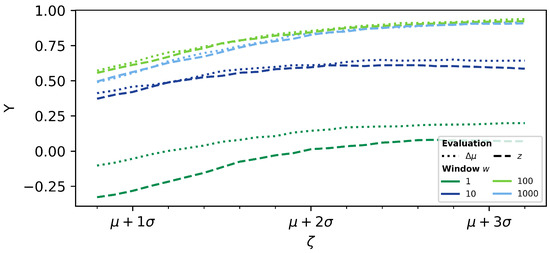
Figure 7.
Achieved detection quality for both methods and z-score with respect to the underlying filter size w dependent on the threshold level and corresponding threshold expressed by the Youden-index (Y).
The evaluation in Figure 7 additionally shows that the achievable improvement decreases asymptotically for both methods and for all filter sizes. Thus, the reduction in , which is associated with higher thresholds, is advantageous in terms of classification quality. However, due to the asymptotic behaviour, further increases such as the -level as described by Ouyang et al. [75] do not lead to large improvements.
4.4.2. Noise Level
For the preceding analysis, the default simulation case with normal distributed noise with mV was considered. Although this value was chosen based on the broad literature review in Section 2.1, this value is not physically derived. Thus, the influence of the underlying noise level on the achieved detection results has to be evaluated.
In Figure 8, the detection results for simulation studies with 0.5 mV, 1 mV, 2 mV and 5 mV as separated by colour are given. According to the previous discussion, the Youden-index is chosen to represent both sensitivity and specificity. For each filter size w, the Youden value of both z-score and is given side-by-side with different fill-patterns. Please note the different alpha levels corresponding to the threshold levels.
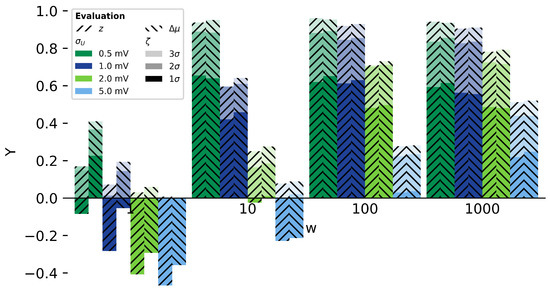
Figure 8.
Achieved classification accuracy of both methods and z-score (hatch) at discrete window sizes w under the influence of various levels of measurement noise . The result corresponding to each threshold level is indicated by the alpha level.
The decrease in classification quality with increasing noise level is clearly observable for each w, which even results in negative Youden values when only a small filter is utilized. In addition, the differences between certain noise levels diminish for higher filter sizes. Besides the unfiltered case (), no significant difference between z-score and can be observed— seem to be slightly higher more often.
The figure also shows the significant improvement of classification with higher threshold levels for all cases in accordance with the discussion before. Especially the improvement from to is advantageous for the overall performance.
Based on the results, no linear dependency between noise level and detection quality is identified. The level of decrease seems to be dependent on both w and in a non-linear fashion.
4.4.3. CtCV
In contrast to the investigated simplified simulation case with only consideration of the measurement uncertainty, the initial review has discussed further influences of disturbances. Thus, the preceding analysis was performed under the influence of additional CtCV in the form of parameter variation and voltage offset . The corresponding fault detection accuracy is given in Figure 9 based on the already utilized Youden-index. For reference, the simplified simulation case is also presented.
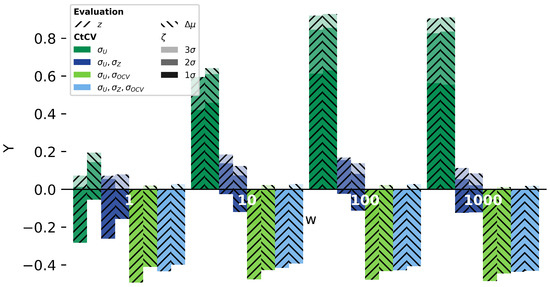
Figure 9.
Achieved classification accuracy of both methods and z-score (hatch) at discrete window sizes w under the influence of various kinds of disturbances. In addition to the default case with , parameter variation and as well as the combination of them was added. The result corresponding to each threshold level is indicated by the alpha level.
It is visually obvious that the performance of the investigated methods decreases significantly under the influence of additional disturbance that are either constant () or load dependent (). Especially, adding into the data generation prevents any reliable fault detection. Under consideration of the discussion of the fault feature characteristic in Figure 3 this behaviour has become apparent due to the sensitivity of the fault feature towards the remaining charge deviation or rather voltage offset.
Thus, both methods—as implemented in this study—are not suitable for proper fault detection under the influence of CtCV in addition to measurement uncertainty and optimization is required. Here, one solution could be to evaluate instead of to compensate for . As long as the load current is constant—which it is usually not—this will also work for the deviation between cells due to the slightly deviated cell impedance.
While the performance of the investigated methods is limited by these results, the importance of implementing CtCV into the test datasets of fault detection methods has been underlined. As presented in Section 2.2 this has not been conducted in general yet. Thus, the performance of the published detection methods has to be evaluated with respect to CtCV.
5. Conclusions
Within this publication, the well-known and much discussed factors influencing the measurement signal of battery systems, which can affect the possibilities of reliable detection of ISC faults, were presented first. In accordance with the literature, this overview was focused on the voltage signal. By comparing common assumptions in the literature of these influencing variables for the validation of fault detection methods and corresponding values from experimental investigations or from the application, significant differences could be identified, while the measurement inaccuracy and scatter of cell parameters tend to be overestimated, no considerations of voltage offsets due to BMS hysteresis could be found. With respect to the orders of magnitude to be expected here compared to, for example, measurement inaccuracy, this influence should be taken more into account in future work.
Based on this preliminary work, a simulation workflow was presented to generate test data for the validation of fault detection methods in a controllable manner, with different boundary conditions and in a statistically sufficient quantity.
The resulting possibilities were tested exemplarily on two simple detection methods and the obtained results were evaluated using various measures. Here, among other things, the greatest criticality of false-negative classifications was introduced as a modification of the smallest detectable fault. In addition, established indicators such as sensitivity, specificity and the Youden-index were used to test the methods under different boundary conditions. Based on the generated dataset, the limits of common evaluation indicators such as TPR-only or detection time were discussed, since they give no information on false-positive and false-negative detections. To obtain a complete picture of the detection performance, this study emphasizes both usage of non-fault validation data and consideration of FPR or similar indicators.
For both methods, the best performance was found for a filter width of using a sample rate of 10 Hz and a deterministic threshold definition of with . Here, and represent the mean and standard deviation of the fault signal under fault-free conditions, respectively. It could additionally be shown that the gain in performance decreases asymptotically by an additional increase in the limit value. Increasing the threshold limit further results in a higher energy release, as expressed by the criticality . By simulating variants with higher measurement noise and with additional parameter and OCV deviations, it could be shown that the performance decreases significantly with additional disturbances.
These observed dependencies have already been partially investigated in the literature, but not regularly or under non-uniform boundary conditions. The results of this work emphasize the necessity of investigating these confounding variables, since the detection performance is significantly affected. The partly significant deviations of the results depending on the definition of threshold and filter width show that published results are only comparable to a very limited extent if the boundary conditions and test data are not guaranteed to be identical. This results in the necessity mentioned above to compare the numerous published methods under identical conditions and on identical data. The adaptation of a Monte Carlo simulation for data generation presented here can be used very well for this purpose. The main underlying concept as displayed in Figure 1 can be also adopted to more advanced battery models and fault representation if required. Furthermore, by using a simulation approach, the extension of the investigation on the basis of another reference cell, as well as the investigation of a generic cell, is possible.
The identified influences of the signal disturbances on the detection quality can be further used to optimize the requirements of the BMS, e.g., an acceptable noise level with respect to the required detection accuracy.
Based on the preliminary work and methodology presented, the next step will be to expand the evaluation to include other established detection methods. Furthermore, it is planned to supplement the simulated data with experimentally determined faults in order to take into account the dynamic unsteady behaviour of a more realistic ISC.
Author Contributions
Conceptualization, J.K. and J.G.; methodology, J.K.; software, J.K.; validation, J.K. and N.O.; investigation, J.K.; data curation, J.K.; writing—original draft preparation, J.K.; writing—review and editing, J.K., J.G., N.O., R.B. and I.H.; visualization, J.K.; supervision, I.H. and H.-P.B.; project administration, R.B.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The simulation data are available from the corresponding author upon reasonable request.
Acknowledgments
We acknowledge financial support by the Open Access Publishing Fund of Clausthal University of Technology.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BMS | Battery management system |
| CC | Constant current |
| CtCV | Cell-to-cell variation |
| CV | Coefficient of variation |
| ECM | Equivalent circuit model |
| ESC | External short circuit |
| EV | Electric vehicle |
| FNR | False negative rate (specificity) |
| FPR | False positive rate |
| GTR | Global Technical Regulation |
| GTR-EVS | Global Technical Regulation on Electrical Vehicle Safety |
| GUM | Guide to the expression of uncertainty in measurement |
| IC | Integrated circuit |
| ISC | Internal short circuit |
| LIB | Lithium-ion battery |
| LUT | Look-up-table |
| MA | Moving average |
| NPV | Negative predictive value |
| NRMSE | Normalized root mean squared error |
| OCV | Open circuit voltage |
| P2D | Pseudo two-dimensional |
| P-OCV | Pseudo open circuit voltage |
| PPV | Positive predictive value |
| RMS | Root mean square |
| RMSE | Root mean squared error |
| ROC | Receiver operating characteristic |
| SOC | State of Charge |
| SVM | Support vector machine |
| TNR | True negative rate |
| TPR | True positive rate (sensitivity) |
| TR | Thermal runaway |
| WLTP | Worldwide Harmonized Light-Duty Vehicles Test Procedure |
| Y | Youden-Index |
Appendix A
Appendix A.1. Evaluation of Computational Effort
As discussed in Section 2.3, the complexity of individual methods with respect to application on a BMS in real-time has been repeatedly measured by the observed computational time. This comparison, however, can end significantly biased due to difference in the implementation of the certain algorithms and independent of the actual algorithm. To illustrate this problem, three different Python™ implementations of a rolling average algorithm are presented in the following. The algorithms are then both compared for calculation time and result.
To recreate the presented example the implementations as given in Listing 1 have to be saved in a file SampleFunctions.py and the remaining code of Listings 2, 3, 4 within a Jupyter notebook-file, e.g., Evaluation.ipynb.
The mathematical background of the implemented rolling average calculations is as follows. Given an array where n denotes the columns and m represents the number of rows, the moving average (MA) with window length w is calculated for each element—defined by row i and columns j—as shown in Equation (A1).
Values for are set to np.nan, which represents not a number.
The first implementation (rollingMeanPandas) is based on using the pandas package, which is known for broad functionally when handling tabular data. Thus, the application of the algorithm has low complexity and the already implemented optimizations are used. In contrast, the algorithm was also implemented using the more basic functionality of the NumPy package by iterating over each row. Since most NumPy-only algorithms can be easily converted into code that can be processed by Numba such an implementation was added as well.
| Listing 1. Implementation of the moving average algorithms using functions from pandas, NumPy and Numba. |
| import NumPy as np |
| from Numba import njit, prange, float64, int16 |
| def rollingMeanPandas(data, w=10): |
| return data.rolling(w).mean() |
| def rollingMeanNumPy(data, w=10): |
| result=np.empty_like(data) |
| for row in range(data.shape[0]): |
| window=np.zeros((w, data.shape[1])) |
| window[:]=np.nan # Initialise with np.nan |
| # Relevant for the first w rows |
| tmp=data[max(0,row−w+1):row+1, :] # Selection of data with window w |
| window[−len(tmp):, :]=tmp |
| result[row]= np.mean(window,axis=0) # Calculate mean over each column selection |
| return result |
| @njit(float64[:,:](float64[:,:],int16), parallel = True) # See above rollingMeanNumPy |
| def rollingMeanNumba(data, w=10): |
| result=np.empty_like(data) |
| for row in prange(data.shape[0]): |
| window=np.zeros((w, data.shape[1])) |
| window[:]=np.nan |
| tmp=data[max(0,row−w+1):row+1, :] |
| window[−len(tmp):, :]=tmp |
| avg=np.empty(window.shape[1], dtype=float64) |
| # np.mean(axis=0) is not implemented by Numba−>custom calculation |
| for col in range(window.shape[1]): |
| avg[col]=window[:,col].mean() |
| result[row]=avg |
| return result |
| Listing 2. Import of both functions and required packages. Random generation of test data with two different dimensions. |
| from SampleFunctions import ∗ |
| import pandas as pd |
| import NumPy as np |
| sampleData=np.random.rand(100000,12) |
| # SampleData=np.random.rand(100000,100) |
| sampleDF=pd.DataFrame(sampleData) |
| Listing 3. Evaluation of the computational time for each implemented function with respect to the required data structure. |
| timeit rollingMeanPandas(sampleDF, 10) |
| timeit rollingMeanNumba(sampleData, 10) |
| timeit rollingMeanNumPy(sampleData, 10) |
| Listing 4. Validation of correct implementation by pair-to-pair comparison of the calculated results based on the same random test data. |
| # Comparison of the evaluated arrays |
| print(np.allclose(rollingMeanNumba(sampleData, 10), |
| rollingMeanPandas(sampleDF, 10), equal_nan=True)) |
| print(np.allclose(rollingMeanNumPy(sampleData, 10), |
| rollingMeanPandas(sampleDF, 10), equal_nan=True)) |
| print(np.allclose(rollingMeanNumba(sampleData, 10), |
| rollingMeanNumPy(sampleData, 10), equal_nan=True)) |
To evaluate the three functions, sample data with both dimensions and were generated randomly. The same data were stored both as pandas DataFrame and NumPy array as shown in Listing 2.
The following results were obtained both on a standard notebook (A) and a dedicated simulation workstation (B). The specifications are given in Table A1.
The timeit function (see Listing 3) was used to evaluate the calculation time of each function. This function calls every implementation multiple times to reduce the influence of parallel processes. In addition, the similarity of all three results is verified in Listing 4.

Table A1.
Technical specifications utilized to calculate the moving average on both a standard notebook (A) and a simulation workstation (B).
Table A1.
Technical specifications utilized to calculate the moving average on both a standard notebook (A) and a simulation workstation (B).
| Specification | A | B |
|---|---|---|
| Processor | Intel Core i5-8265U | Intel Xeon W-2275 |
| Total cores | 4 | 14 |
| RAM | 8 GB | 256 GB |
| Year | 2020 | 2022 |
The summarized computational times for all three implementations are given in Table A2. For the same calculation, a significant variation in-between the different implementations is found. Furthermore, the step from to shows that both NumPy and Numba implementation scaling much better even by the reduction in the estimated computational time. Following these results, the initial hypothesis that computational time is significantly dependent on the implementation itself and therefore not feasible for comparison of different methods is confirmed.

Table A2.
Computational times of the investigated moving average implementations on both standard notebook (A) and simulation workstation (B) and sample sizes.
Table A2.
Computational times of the investigated moving average implementations on both standard notebook (A) and simulation workstation (B) and sample sizes.
| A | B | |||
|---|---|---|---|---|
| Implementation | ||||
| Pandas | 114 ms | 63.7 ms | 41.3 ms | 573 ms |
| NumPy | 2.34 s | 1.93 s | 1.34 s | 1.56 s |
| Numba | 23.1 ms | 18.3 ms | 15.2 ms | 24.1 ms |
Appendix A.2. Consistency of Separate Simulation Studies
Within Section 4.1 a proper number of simulations for generating a reproducible dataset was defined. The main goal is to ensure that the results gathered from evaluation of this dataset are significant and not biased by the influences implemented randomly into the data generation. To validate this desired property, the default case (see Table 8) was simulated twice with identical parameters but different random seeds. For comparison, the z-score method with was chosen, and the results are given for a selection of window sizes in Table A3. Both a completely fault-free simulation study and a simulation with ≈80% error rate are shown. The former configuration was used to define the trip limits, which were then used to evaluate the latter (see also diagram in Figure 1). It can be seen that for both variants, the differences between the two analyses (I and II) are neither non-existent nor negligible due to their magnitude. In particular, the overall behaviour such as the optimum at is seen in both variants with error replication. The slightly larger variation in the results obtained in comparison to the fault-free cases can be explained by the larger number of variation possibilities with the active error simulation, while the error-free simulations differ only by the measurement noise, the latter add the variance of the error resistance, the duration and the timing.
Thus, the chosen number of simulations was proven sufficient for generating valid results despite the random influences.

Table A3.
Achieved detection quality of z-score method with threshold level of for repetitive simulation of the default simulation case with no-fault condition (left) and with 80% failure rate (right). Results were obtained on the basis of 1200 and 2400 repetitions for fault-free and fault datasets, respectively. The mean of the maximum fault signal per simulation run is also given. For detailed information on the given indicators FPR and TNR please refer to Table 6.
Table A3.
Achieved detection quality of z-score method with threshold level of for repetitive simulation of the default simulation case with no-fault condition (left) and with 80% failure rate (right). Results were obtained on the basis of 1200 and 2400 repetitions for fault-free and fault datasets, respectively. The mean of the maximum fault signal per simulation run is also given. For detailed information on the given indicators FPR and TNR please refer to Table 6.
| FPR/% | TNR/% | FPR/% | TNR/% | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No | I | II | I | II | I | II | No | I | II | I | II |
| 1 | 3.108 | 3.110 | 0.167 | 0.167 | 99.833 | 99.833 | 1 | 0.600 | 0.832 | 99.400 | 99.168 |
| 10 | 1.369 | 1.364 | 1.000 | 0.833 | 99.000 | 99.167 | 10 | 2.183 | 3.854 | 97.817 | 96.146 |
| 100 | 0.408 | 0.408 | 1.083 | 1.500 | 98.917 | 98.500 | 100 | 3.523 | 2.474 | 96.477 | 97.526 |
| 1000 | 0.111 | 0.111 | 1.083 | 0.917 | 98.917 | 99.083 | 1000 | 1.394 | 2.053 | 98.606 | 97.947 |
References
- Yu, A.; Sumangil, M. Top Electric Vehicle Markets Dominate Lithium-ion Battery Capacity Growth; Technical Report; S&P Global Market Intelligence: New York, NY, USA, 2021. [Google Scholar]
- Feng, X.; Zheng, S.; Ren, D.; He, X.; Wang, L.; Cui, H.; Liu, X.; Jin, C.; Zhang, F.; Xu, C.; et al. Investigating the thermal runaway mechanisms of lithium-ion batteries based on thermal analysis database. Appl. Energy 2019, 246, 53–64. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Thermal runaway caused fire and explosion of lithium ion battery. J. Power Sources 2012, 208, 210–224. [Google Scholar] [CrossRef]
- National Transportation Safety Board. Auxiliary Power Unit Battery Fire Japan Airlines Boeing 787-8, JA829J, Boston, MA 7 January 2013: Incident Report; Technical Report NTSB/AIR-14/01; National Transportation Safety Board: Washington, DC, USA, 2014.
- Koh, D.J. Samsung Announces Cause of Galaxy Note7 Incidents in Press Conference, Seoul, Republic of Korea, 23 January 2017. Available online: https://news.samsung.com/us/Samsung-Electronics-Announces-Cause-of-Galaxy-Note7-Incidents-in-Press-Conference (accessed on 11 October 2021).
- Meza, E. Several German Cities Halt Use of E-Buses Following Series of Unresolved Cases of Fire. Clean Energy Wire. Available online: https://www.cleanenergywire.org/news/german-cities-demand-subsidised-e-buses-outstrips-expectations (accessed on 11 October 2021).
- Naughton, K.; Yang, Y. GM Recalls All Bolt EVs on Fire Risk; Sees $1 Billion Cost. Available online: https://www.bloomberg.com/news/articles/2021-08-20/gm-to-spend-1-billion-to-recall-all-bolt-evs-due-to-fire-risk (accessed on 21 August 2021).
- Feng, X.; Fang, M.; He, X.; Ouyang, M.; Lu, L.; Wang, H.; Zhang, M. Thermal runaway features of large format prismatic lithium ion battery using extended volume accelerating rate calorimetry. J. Power Sources 2014, 255, 294–301. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal runaway mechanism of lithium ion battery for electric vehicles: A review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Li, H.; Duan, Q.; Zhao, C.; Huang, Z.; Wang, Q. Experimental investigation on the thermal runaway and its propagation in the large format battery module with Li(Ni1/3Co1/3Mn1/3)O2 as cathode. J. Hazard. Mater. 2019, 375, 241–254. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Wang, L.; Feng, X.; He, X. Probing the heat sources during thermal runaway process by thermal analysis of different battery chemistries. J. Power Sources 2018, 378, 527–536. [Google Scholar] [CrossRef]
- Ouyang, D.; Liu, J.; Chen, M.; Weng, J.; Wang, J. Thermal Failure Propagation in Lithium-Ion Battery Modules with Various Shapes. Appl. Sci. 2018, 8, 1263. [Google Scholar] [CrossRef]
- Ruiz, V.; Pfrang, A. JRC Exploratory Research: Safer Li-ion Batteries by Preventing Thermal Propagation; Technical Report; European Commission: Petten, The Netherlands, 2018. [Google Scholar]
- Klink, J.; Hebenbrock, A.; Grabow, J.; Orazov, N.; Nylén, U.; Benger, R.; Beck, H.P. Comparison of Model-Based and Sensor-Based Detection of Thermal Runaway in Li-Ion Battery Modules for Automotive Application. Batteries 2022, 8, 34. [Google Scholar] [CrossRef]
- Tidblad, A.A.; Edström, K.; Hernández, G.; de Meatza, I.; Landa-Medrano, I.; Jacas Biendicho, J.; Trilla, L.; Buysse, M.; Ierides, M.; Horno, B.P.; et al. Future Material Developments for Electric Vehicle Battery Cells Answering Growing Demands from an End-User Perspective. Energies 2021, 14, 4223. [Google Scholar] [CrossRef]
- Liu, B.; Jia, Y.; Li, J.; Yin, S.; Yuan, C.; Hu, Z.; Wang, L.; Li, Y.; Xu, J. Safety issues caused by internal short circuits in lithium-ion batteries. J. Mater. Chem. A 2018, 6, 21475–21484. [Google Scholar] [CrossRef]
- Doughty, D.H.; Pesaran, A.A. Vehicle Battery Safety Roadmap Guidance; Technical Report; National Renewable Energy Laboratory: Golden, CO, USA, 2012. [CrossRef]
- Liaw, B.Y.; Wang, F.; Wei, Y.; Brandt, K.; Schultheiß, J.; Schweizer-Berberich, M.; Dandl, S.; Wöhrle, T.; Lamp, P.; Jeevarajan, A.J.; et al. Managing Safety Risk by Manufacturers. In Li-Battery Safety; Garche, J., Brandt, K., Eds.; Electrochemical Power Sources; Elsevier: San Diego, CA, USA, 2019; pp. 267–378. [Google Scholar] [CrossRef]
- Lopez, C.F.; Jeevarajan, J.A.; Mukherjee, P.P. Experimental Analysis of Thermal Runaway and Propagation in Lithium-Ion Battery Modules. J. Electrochem. Soc. 2015, 162, A1905–A1915. [Google Scholar] [CrossRef]
- Zhong, G.; Li, H.; Wang, C.; Xu, K.; Wang, Q. Experimental Analysis of Thermal Runaway Propagation Risk within 18650 Lithium-Ion Battery Modules. J. Electrochem. Soc. 2018, 165, A1925–A1934. [Google Scholar] [CrossRef]
- Chen, F.; Huang, R.; Wang, C.; Yu, X.; Liu, H.; Wu, Q.; Qian, K.; Bhagat, R. Air and PCM cooling for battery thermal management considering battery cycle life. Appl. Therm. Eng. 2020, 173, 115154. [Google Scholar] [CrossRef]
- Kim, G.H.; Pesaran, A. Analysis of Heat Dissipation in Li-Ion Cells & Modules for Modeling of Thermal Runaway (Presentation). Available online: https://www.nrel.gov/docs/fy07osti/41531.pdf (accessed on 15 May 2007).
- Darcy, E. Driving Factors for Mitigating Cell Thermal Runaway Propagation and Arresting Flames in High Performing Li-Ion Battery Designs. Available online: https://ntrs.nasa.gov/api/citations/20150003488/downloads/20150003488.pdf (accessed on 1 May 2015).
- UN Global Technical Regulation. Global Technical Regulation No. 20: Global Technical Regulation on the Electrical Vehicle Safety (EVS); Technical Report; United Nations: Geneva, Switzerland, 2018. [Google Scholar]
- Schipper, F.; Erickson, E.M.; Erk, C.; Shin, J.Y.; Chesneau, F.F.; Aurbach, D. Review—Recent Advances and Remaining Challenges for Lithium Ion Battery Cathodes. J. Electrochem. Soc. 2017, 164, A6220–A6228. [Google Scholar] [CrossRef]
- Feng, X.; Ren, D.; He, X.; Ouyang, M. Mitigating Thermal Runaway of Lithium-Ion Batteries. Joule 2020, 4, 743–770. [Google Scholar] [CrossRef]
- Chombo, P.V.; Laoonual, Y. A review of safety strategies of a Li-ion battery. J. Power Sources 2020, 478, 228649. [Google Scholar] [CrossRef]
- Grabow, J.; Klink, J.; Benger, R.; Hauer, I.; Beck, H.P. Particle Contamination in Commercial Lithium-Ion Cells—Risk Assessment with Focus on Internal Short Circuits and Replication by Currently Discussed Trigger Methods. Batteries 2023, 9, 9. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, K.; Liu, K.; Lin, X.; Dey, S.; Onori, S. Advanced Fault Diagnosis for Lithium-Ion Battery Systems: A Review of Fault Mechanisms, Fault Features, and Diagnosis Procedures. IEEE Ind. Electron. Mag. 2020, 14, 65–91. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, K.; Wei, J.; Dong, G. Voltage fault detection for lithium-ion battery pack using local outlier factor. Measurement 2019, 146, 544–556. [Google Scholar] [CrossRef]
- Yao, L.; Xiao, Y.; Gong, X.; Hou, J.; Chen, X. A novel intelligent method for fault diagnosis of electric vehicle battery system based on wavelet neural network. J. Power Sources 2020, 453, 227870. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Tian, J.; Shang, X.; Lu, J. Model-based fault diagnosis approach on external short circuit of lithium-ion battery used in electric vehicles. Appl. Energy 2016, 184, 365–374. [Google Scholar] [CrossRef]
- Zhang, G.; Wei, X.; Tang, X.; Zhu, J.; Chen, S.; Dai, H. Internal short circuit mechanisms, experimental approaches and detection methods of lithium-ion batteries for electric vehicles: A review. Renew. Sustain. Energy Rev. 2021, 141, 110790. [Google Scholar] [CrossRef]
- Wu, C.; Zhu, C.; Ge, Y.; Zhao, Y. A Review on Fault Mechanism and Diagnosis Approach for Li-Ion Batteries. J. Nanomater. 2015, 2015, 631263. [Google Scholar] [CrossRef]
- Tran, M.K.; Fowler, M. A Review of Lithium-Ion Battery Fault Diagnostic Algorithms: Current Progress and Future Challenges. Algorithms 2020, 13, 62. [Google Scholar] [CrossRef]
- Bhaskar, K.; Kumar, A.; Bunce, J.; Pressman, J.; Burkell, N.; Rahn, C.D. Data-Driven Thermal Anomaly Detection in Large Battery Packs. Batteries 2023, 9, 70. [Google Scholar] [CrossRef]
- Liu, P.; Sun, Z.; Wang, Z.; Zhang, J. Entropy-Based Voltage Fault Diagnosis of Battery Systems for Electric Vehicles. Energies 2018, 11, 136. [Google Scholar] [CrossRef]
- Seo, M.; Goh, T.; Park, M.; Koo, G.; Kim, S. Detection of Internal Short Circuit in Lithium Ion Battery Using Model-Based Switching Model Method. Energies 2017, 10, 76. [Google Scholar] [CrossRef]
- Shang, Y.; Lu, G.; Kang, Y.; Zhou, Z.; Duan, B.; Zhang, C. A multi-fault diagnosis method based on modified Sample Entropy for lithium-ion battery strings. J. Power Sources 2020, 446, 227275. [Google Scholar] [CrossRef]
- Meng, J.; Boukhnifer, M.; Delpha, C.; Diallo, D. Incipient short-circuit fault diagnosis of lithium-ion batteries. J. Energy Storage 2020, 31, 101658. [Google Scholar] [CrossRef]
- Liu, Z.; He, H. Model-based Sensor Fault Diagnosis of a Lithium-ion Battery in Electric Vehicles. Energies 2015, 8, 6509–6527. [Google Scholar] [CrossRef]
- Schmid, M.; Kneidinger, H.G.; Endisch, C. Data-Driven Fault Diagnosis in Battery Systems Through Cross-Cell Monitoring. IEEE Sens. J. 2021, 21, 1829–1837. [Google Scholar] [CrossRef]
- Yao, L.; Wang, Z.; Ma, J. Fault detection of the connection of lithium-ion power batteries based on entropy for electric vehicles. J. Power Sources 2015, 293, 548–561. [Google Scholar] [CrossRef]
- Xue, Q.; Li, G.; Zhang, Y.; Shen, S.; Chen, Z.; Liu, Y. Fault diagnosis and abnormality detection of lithium-ion battery packs based on statistical distribution. J. Power Sources 2021, 482, 228964. [Google Scholar] [CrossRef]
- Zheng, Y.; Han, X.; Lu, L.; Li, J.; Ouyang, M. Lithium ion battery pack power fade fault identification based on Shannon entropy in electric vehicles. J. Power Sources 2013, 223, 136–146. [Google Scholar] [CrossRef]
- Yang, R.; Xiong, R.; He, H.; Chen, Z. A fractional-order model-based battery external short circuit fault diagnosis approach for all-climate electric vehicles application. J. Clean. Prod. 2018, 187, 950–959. [Google Scholar] [CrossRef]
- Chen, W.; Chen, W.T.; Saif, M.; Li, M.F.; Wu, H. Simultaneous Fault Isolation and Estimation of Lithium-Ion Batteries via Synthesized Design of Luenberger and Learning Observers. IEEE Trans. Control Syst. Technol. 2014, 22, 290–298. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Liu, P. Big-Data-Based Thermal Runaway Prognosis of Battery Systems for Electric Vehicles. Energies 2017, 10, 919. [Google Scholar] [CrossRef]
- Seo, M.; Park, M.; Song, Y.; Kim, S.W. Online Detection of Soft Internal Short Circuit in Lithium-Ion Batteries at Various Standard Charging Ranges. IEEE Access 2020, 8, 70947–70959. [Google Scholar] [CrossRef]
- Xia, B.; Shang, Y.; Nguyen, T.; Mi, C. A correlation based fault detection method for short circuits in battery packs. J. Power Sources 2017, 337, 1–10. [Google Scholar] [CrossRef]
- Fill, A.; Koch, S.; Birke, K.P. Algorithm for the detection of a single cell contact loss within parallel-connected cells based on continuous resistance ratio estimation. J. Energy Storage 2020, 27, 101049. [Google Scholar] [CrossRef]
- Jiang, J.; Cong, X.; Li, S.; Zhang, C.; Zhang, W.; Jiang, Y. A Hybrid Signal-Based Fault Diagnosis Method for Lithium-Ion Batteries in Electric Vehicles. IEEE Access 2021, 9, 19175–19186. [Google Scholar] [CrossRef]
- Kang, Y.; Duan, B.; Zhou, Z.; Shang, Y.; Zhang, C. A multi-fault diagnostic method based on an interleaved voltage measurement topology for series connected battery packs. J. Power Sources 2019, 417, 132–144. [Google Scholar] [CrossRef]
- Zhang, H.; Pei, L.; Sun, J.; Song, K.; Lu, R.; Zhao, Y.; Zhu, C.; Wang, T. Online Diagnosis for the Capacity Fade Fault of a Parallel-Connected Lithium Ion Battery Group. Energies 2016, 9, 387. [Google Scholar] [CrossRef]
- Dey, S.; Mohon, S.; Pisu, P.; Ayalew, B. Sensor Fault Detection, Isolation, and Estimation in Lithium-Ion Batteries. IEEE Trans. Control Syst. Technol. 2016, 24, 2141–2149. [Google Scholar] [CrossRef]
- Dey, S.; Ayalew, B. A Diagnostic Scheme for Detection, Isolation and Estimation of Electrochemical Faults in Lithium-Ion Cells. In Proceedings of the ASME 8th Annual Dynamic Systems and Control Conference, Columbus, OH, USA, 29 October–3 November 2015; The American Society of Mechanical Engineers: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Kang, Y.; Duan, B.; Zhou, Z.; Shang, Y.; Zhang, C. Online multi-fault detection and diagnosis for battery packs in electric vehicles. Appl. Energy 2020, 259, 114170. [Google Scholar] [CrossRef]
- Kim, G.H.; Smith, K.; Ireland, J.; Pesaran, A. Fail-safe design for large capacity lithium-ion battery systems. J. Power Sources 2012, 210, 243–253. [Google Scholar] [CrossRef]
- Kim, T.; Makwana, D.; Adhikaree, A.; Vagdoda, J.S.; Lee, Y. Cloud-Based Battery Condition Monitoring and Fault Diagnosis Platform for Large-Scale Lithium-Ion Battery Energy Storage Systems. Energies 2018, 11, 125. [Google Scholar] [CrossRef]
- Klink, J.; Grabow, J.; Orazov, N.; Benger, R.; Börger, A.; Ahlberg Tidblad, A.; Wenzl, H.; Beck, H.P. Thermal fault detection by changes in electrical behaviour in lithium-ion cells. J. Power Sources 2021, 490, 229572. [Google Scholar] [CrossRef]
- Kong, X.; Zheng, Y.; Ouyang, M.; Lu, L.; Li, J.; Zhang, Z. Fault diagnosis and quantitative analysis of micro-short circuits for lithium-ion batteries in battery packs. J. Power Sources 2018, 395, 358–368. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z. A novel fault diagnosis method for lithium-Ion battery packs of electric vehicles. Measurement 2018, 116, 402–411. [Google Scholar] [CrossRef]
- Li, X.; Dai, K.; Wang, Z.; Han, W. Lithium-ion batteries fault diagnostic for electric vehicles using sample entropy analysis method. J. Energy Storage 2020, 27, 101121. [Google Scholar] [CrossRef]
- Sidhu, A.; Izadian, A.; Anwar, S. Adaptive Nonlinear Model-Based Fault Diagnosis of Li-Ion Batteries. IEEE Trans. Ind. Electron. 2015, 62, 1002–1011. [Google Scholar] [CrossRef]
- Singh, A.; Izadian, A.; Anwar, S. Fault diagnosis of Li-Ion batteries using multiple-model adaptive estimation. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2014; pp. 3524–3529. [Google Scholar] [CrossRef]
- Xia, B.; Nguyen, T.; Yang, J.; Mi, C. The improved interleaved voltage measurement method for series connected battery packs. J. Power Sources 2016, 334, 12–22. [Google Scholar] [CrossRef]
- Yan, W.; Zhang, B.; Wang, X.; Dou, W.; Wang, J. Lebesgue-Sampling-Based Diagnosis and Prognosis for Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2016, 63, 1804–1812. [Google Scholar] [CrossRef]
- Zhang, Z.; Kong, X.; Zheng, Y.; Zhou, L.; Lai, X. Real-time diagnosis of micro-short circuit for Li-ion batteries utilizing low-pass filters. Energy 2019, 166, 1013–1024. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Yao, Y. Fault prognosis of battery system based on accurate voltage abnormity prognosis using long short-term memory neural networks. Appl. Energy 2019, 251, 113381. [Google Scholar] [CrossRef]
- Singh, A.; Izadian, A.; Anwar, S. Model based condition monitoring in lithium-ion batteries. J. Power Sources 2014, 268, 459–468. [Google Scholar] [CrossRef]
- Son, J.; Du, Y. Model-Based Stochastic Fault Detection and Diagnosis of Lithium-Ion Batteries. Processes 2019, 7, 38. [Google Scholar] [CrossRef]
- Tran, M.K.; Fowler, M. Sensor Fault Detection and Isolation for Degrading Lithium-Ion Batteries in Electric Vehicles Using Parameter Estimation with Recursive Least Squares. Batteries 2020, 6, 1. [Google Scholar] [CrossRef]
- Liu, Z.; Ahmed, Q.; Zhang, J.; Rizzoni, G.; He, H. Structural analysis based sensors fault detection and isolation of cylindrical lithium-ion batteries in automotive applications. Control Eng. Pract. 2016, 52, 46–58. [Google Scholar] [CrossRef]
- Moeini, A.; Wang, S. Fast and Precise Detection of Internal Short Circuit on Li-Ion Battery. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2018; pp. 2759–2766. [Google Scholar] [CrossRef]
- Ouyang, M.; Zhang, M.; Feng, X.; Lu, L.; Li, J.; He, X.; Zheng, Y. Internal short circuit detection for battery pack using equivalent parameter and consistency method. J. Power Sources 2015, 294, 272–283. [Google Scholar] [CrossRef]
- Xia, B.; Mi, C. A fault-tolerant voltage measurement method for series connected battery packs. J. Power Sources 2016, 308, 83–96. [Google Scholar] [CrossRef]
- Dey, S.; Biron, Z.A.; Tatipamula, S.; Das, N.; Mohon, S.; Ayalew, B.; Pisu, P. Model-based real-time thermal fault diagnosis of Lithium-ion batteries. Control Eng. Pract. 2016, 56, 37–48. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Chen, Z.; Liu, X. Model based insulation fault diagnosis for lithium-ion battery pack in electric vehicles. Measurement 2019, 131, 443–451. [Google Scholar] [CrossRef]
- Liu, Z.; He, H. Sensor fault detection and isolation for a lithium-ion battery pack in electric vehicles using adaptive extended Kalman filter. Appl. Energy 2017, 185, 2033–2044. [Google Scholar] [CrossRef]
- Zhang, M.; Ouyang, M.; Lu, L.; He, X.; Feng, X.; Liu, L.; Xie, X. Battery Internal Short Circuit Detection. ECS Trans. 2017, 77, 217–223. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Uncertainty of Measurement: Part 3: Guide to the Expression of Uncertainty in Measurement (GUM:1995); ISO: Geneva, Switzerland, 2008. [Google Scholar]
- Mieke, S. Berechnung der Messunsicherheit nach GUM: Kurzfassung in 20 min. 2011. Available online: https://www.ptb.de/cms/fileadmin/internet/fachabteilungen/abteilung_8/8.4_mathematische_modellierung/277_PTB_SEMINAR/VORTRAEGE/11_Mieke_-_Berechnung_der_Messunsicherheit_nach_GUM__Kurzfassung_in_20.pdf (accessed on 7 May 2023).
- Zhao, S.; Duncan, S.R.; Howey, D.A. Observability Analysis and State Estimation of Lithium-Ion Batteries in the Presence of Sensor Biases. IEEE Trans. Control Syst. Technol. 2017, 25, 326–333. [Google Scholar] [CrossRef]
- Dirndorfer, T.; Botsch, M.; Knoll, A. Model-Based Analysis of Sensor-Noise in Predictive Passive Safety Algorithms. In Proceedings of the 22nd Enhanced Safety of Vehicles Conference, Washington, DC, USA, 13–16 June 2011; National Highway Traffic Safety Administration: Washington, DC, USA; p. 11-0251. [Google Scholar]
- Jerath, K.; Brennan, S.; Lagoa, C. Bridging the gap between sensor noise modeling and sensor characterization. Measurement 2018, 116, 350–366. [Google Scholar] [CrossRef]
- Marcicki, J.; Onori, S.; Rizzoni, G. Nonlinear Fault Detection and Isolation for a Lithium-Ion Battery Management System. In Proceedings of the ASME Dynamic Systems and Control Conference 2010, Cambridge, MA, USA, 12–15 September 2010; ASME: New York, NY, USA, 2010; pp. 607–614. [Google Scholar] [CrossRef]
- Zhang, C.; Allafi, W.; Dinh, Q.; Ascencio, P.; Marco, J. Online estimation of battery equivalent circuit model parameters and state of charge using decoupled least squares technique. Energy 2018, 142, 678–688. [Google Scholar] [CrossRef]
- Feng, X.; Weng, C.; Ouyang, M.; Sun, J. Online internal short circuit detection for a large format lithium ion battery. Appl. Energy 2016, 161, 168–180. [Google Scholar] [CrossRef]
- Alavi, S.M.M.; Fekriasl, S.; Niyakan, S.N.; Saif, M. Fault detection and isolation in batteries power electronics and chargers. J. Energy Storage 2019, 25, 100807. [Google Scholar] [CrossRef]
- Dey, S.; Perez, H.E.; Moura, S.J. Thermal fault diagnostics in Lithium-ion batteries based on a distributed parameter thermal model. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2018; pp. 68–73. [Google Scholar]
- Dey, S.; Perez, H.E.; Moura, S.J. Model-Based Battery Thermal Fault Diagnostics: Algorithms, Analysis, and Experiments. IEEE Trans. Control Syst. Technol. 2019, 27, 576–587. [Google Scholar] [CrossRef]
- Pan, Y.; Feng, X.; Zhang, M.; Han, X.; Lu, L.; Ouyang, M. Internal short circuit detection for lithium-ion battery pack with parallel-series hybrid connections. J. Clean. Prod. 2020, 255, 120277. [Google Scholar] [CrossRef]
- Zhang, K.; Hu, X.; Liu, Y.; Lin, X.; Liu, W. Multi-fault Detection and Isolation for Lithium-Ion Battery Systems. IEEE Trans. Power Electron. 2022, 37, 971–989. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, J.; Liu, P.; Zhang, L. Voltage fault diagnosis and prognosis of battery systems based on entropy and Z-score for electric vehicles. Appl. Energy 2017, 196, 289–302. [Google Scholar] [CrossRef]
- Analog Devices Inc. LTC6811-1/LTC6811-2: 12-Cell Battery Stack Monitor; Technical Report; Analog Devices Inc.: Wilmington, MA, USA, 2019. [Google Scholar]
- STMicroelectronics. Multicell Battery Monitoring and Balancing ICs. 2022. Available online: https://www.st.com/en/power-management/multicell-battery-monitoring-and-balancing-ics.html (accessed on 8 December 2022).
- Feng, F.; Hu, X.; Hu, L.; Hu, F.; Li, Y.; Zhang, L. Propagation mechanisms and diagnosis of parameter inconsistency within Li-Ion battery packs. Renew. Sustain. Energy Rev. 2019, 112, 102–113. [Google Scholar] [CrossRef]
- Könekamp, A.; Dudek, A.; Schilder, B. Cell Delta-Temperature Optimized Battery Module Configuration. U.S. Patent No 9,160,040, 13 October 2015. [Google Scholar]
- Joint Research Centre of the European Commission. Data Collection Framework: Definitions. 2023. Available online: https://www.wur.nl/en/research-results/statutory-research-tasks/centre-for-fisheries-research-1/data-collection-framework.htm (accessed on 5 June 2023).
- Dubarry, M.; Truchot, C.; Cugnet, M.; Liaw, B.Y.; Gering, K.; Sazhin, S.; Jamison, D.; Michelbacher, C. Evaluation of commercial lithium-ion cells based on composite positive electrode for plug-in hybrid electric vehicle applications. Part I: Initial characterizations. J. Power Sources 2011, 196, 10328–10335. [Google Scholar] [CrossRef]
- Kenney, B.; Darcovich, K.; MacNeil, D.D.; Davidson, I.J. Modelling the impact of variations in electrode manufacturing on lithium-ion battery modules. J. Power Sources 2012, 213, 391–401. [Google Scholar] [CrossRef]
- Rumpf, K.; Naumann, M.; Jossen, A. Experimental investigation of parametric cell-to-cell variation and correlation based on 1100 commercial lithium-ion cells. J. Energy Storage 2017, 14, 224–243. [Google Scholar] [CrossRef]
- Wildfeuer, L.; Lienkamp, M. Quantifiability of inherent cell-to-cell variations of commercial lithium-ion batteries. eTransportation 2021, 9, 100129. [Google Scholar] [CrossRef]
- Dubarry, M.; Vuillaume, N.; Liaw, B.Y. From single cell model to battery pack simulation for Li-ion batteries. J. Power Sources 2009, 186, 500–507. [Google Scholar] [CrossRef]
- Dubarry, M.; Vuillaume, N.; Liaw, B.Y. Origins and accommodation of cell variations in Li-ion battery pack modeling. Int. J. Energy Res. 2010, 34, 216–231. [Google Scholar] [CrossRef]
- Shin, D.; Poncino, M.; Macii, E.; Chang, N. A statistical model of cell-to-cell variation in Li-ion batteries for system-level design. In Proceedings of the International Symposium on Low Power Electronics and Design (ISLPED), Beijing, China, 4–6 September 2013; pp. 94–99. [Google Scholar] [CrossRef]
- Paul, S.; Diegelmann, C.; Kabza, H.; Tillmetz, W. Analysis of ageing inhomogeneities in lithium-ion battery systems. J. Power Sources 2013, 239, 642–650. [Google Scholar] [CrossRef]
- Baumhöfer, T.; Brühl, M.; Rothgang, S.; Sauer, D.U. Production caused variation in capacity aging trend and correlation to initial cell performance. J. Power Sources 2014, 247, 332–338. [Google Scholar] [CrossRef]
- Rothgang, S.; Baumhofer, T.; Sauer, D.U. Diversion of Aging of Battery Cells in Automotive Systems. In Proceedings of the 2014 IEEE Vehicle Power and Propulsion Conference (VPPC), Coimbra, Portugal, 27–30 October 2014; pp. 1–6. [Google Scholar]
- Schuster, S.F.; Brand, M.J.; Berg, P.; Gleissenberger, M.; Jossen, A. Lithium-ion cell-to-cell variation during battery electric vehicle operation. J. Power Sources 2015, 297, 242–251. [Google Scholar] [CrossRef]
- Devie, A.; Dubarry, M. Durability and Reliability of Electric Vehicle Batteries under Electric Utility Grid Operations. Part 1: Cell-to-Cell Variations and Preliminary Testing. Batteries 2016, 2, 28. [Google Scholar] [CrossRef]
- Campestrini, C.; Keil, P.; Schuster, S.F.; Jossen, A. Ageing of lithium-ion battery modules with dissipative balancing compared with single-cell ageing. J. Energy Storage 2016, 6, 142–152. [Google Scholar] [CrossRef]
- An, F.; Chen, L.; Huang, J.; Zhang, J.; Li, P. Rate dependence of cell-to-cell variations of lithium-ion cells. Sci. Rep. 2016, 6, 35051. [Google Scholar] [CrossRef]
- An, F.; Huang, J.; Wang, C.; Li, Z.; Zhang, J.; Wang, S.; Li, P. Cell sorting for parallel lithium-ion battery systems: Evaluation based on an electric circuit model. J. Energy Storage 2016, 6, 195–203. [Google Scholar] [CrossRef]
- Barreras, J.V.; Raj, T.; Howey, D.A.; Schaltz, E. Results of Screening over 200 Pristine Lithium-Ion Cells. In Proceedings of the 2017 IEEE Vehicle Power and Propulsion Conference (VPPC), Belfort, France, 14–17 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Devie, A.; Baure, G.; Dubarry, M. Intrinsic Variability in the Degradation of a Batch of Commercial 18650 Lithium-Ion Cells. Energies 2018, 11, 1031. [Google Scholar] [CrossRef]
- Oeser, D.; Ziegler, A.; Ackva, A. Single cell analysis of lithium-ion e-bike batteries aged under various conditions. J. Power Sources 2018, 397, 25–31. [Google Scholar] [CrossRef]
- Baumann, M.; Wildfeuer, L.; Rohr, S.; Lienkamp, M. Parameter variations within Li-Ion battery packs—Theoretical investigations and experimental quantification. J. Energy Storage 2018, 18, 295–307. [Google Scholar] [CrossRef]
- Zou, H.; Zhan, H.; Zheng, Z. A Multi-Factor Weight Analysis Method of Lithiumion Batteries Based on Module Topology. In Proceedings of the 2018 International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC), Xi’an, China, 15–17 August 2018; pp. 61–66. [Google Scholar] [CrossRef]
- Zilberman, I.; Sturm, J.; Jossen, A. Reversible self-discharge and calendar aging of 18650 nickel-rich, silicon-graphite lithium-ion cells. J. Power Sources 2019, 425, 217–226. [Google Scholar] [CrossRef]
- Zilberman, I.; Ludwig, S.; Jossen, A. Cell-to-cell variation of calendar aging and reversible self-discharge in 18650 nickel-rich, silicon-graphite lithium-ion cells. J. Energy Storage 2019, 26, 100900. [Google Scholar] [CrossRef]
- Zilberman, I.; Schmitt, J.; Ludwig, S.; Naumann, M.; Jossen, A. Simulation of voltage imbalance in large lithium-ion battery packs influenced by cell-to-cell variations and balancing systems. J. Energy Storage 2020, 32, 101828. [Google Scholar] [CrossRef]
- Schindler, M.; Sturm, J.; Ludwig, S.; Schmitt, J.; Jossen, A. Evolution of initial cell-to-cell variations during a three-year production cycle. eTransportation 2021, 8, 100102. [Google Scholar] [CrossRef]
- Oeser, D. From the Production of the Single Cell to the End of Life of The Battery Module: The Development of Parameter Variation of Lithium-Ion Cells. Ph.D. Thesis, Departament d’Enginyeria Elèctrica, UPC, Barcelona, Spain, 2022. [Google Scholar]
- Reiter, A.; Lehner, S.; Bohlen, O.; Sauer, D.U. Electrical cell-to-cell variations within large-scale battery systems—A novel characterization and modeling approach. J. Energy Storage 2023, 57, 106152. [Google Scholar] [CrossRef]
- Hein, T.; Oeser, D.; Ziegler, A.; Montesinos-Miracle, D.; Ackva, A. Aging Determination of Series-Connected Lithium-Ion Cells Independent of Module Design. Batteries 2023, 9, 172. [Google Scholar] [CrossRef]
- Beck, D.; Dechent, P.; Junker, M.; Sauer, D.U.; Dubarry, M. Inhomogeneities and Cell-to-Cell Variations in Lithium-Ion Batteries, a Review. Energies 2021, 14, 3276. [Google Scholar] [CrossRef]
- Buchmann, I. BU-803a: Cell Matching and Balancing; Technical Report; Battery University: Richmond, BC, Canada, 2021. [Google Scholar]
- Barsukov, Y. Battery Cell Balancing: What to Balance and How; Technical Report; Texas Instruments: Dallas, TX, USA, 2022. [Google Scholar]
- Chang, L.; Zhang, C.; Wang, T.; Yu, Z.; Cui, N.; Duan, B.; Wang, C. Correlations of cell-to-cell parameter variations on current and state-of-charge distributions within parallel-connected lithium-ion cells. J. Power Sources 2019, 437, 226869. [Google Scholar] [CrossRef]
- Dubarry, M.; Pastor-Fernández, C.; Baure, G.; Yu, T.F.; Widanage, W.D.; Marco, J. Battery energy storage system modeling: Investigation of intrinsic cell-to-cell variations. J. Energy Storage 2019, 23, 19–28. [Google Scholar] [CrossRef]
- Song, Z.; Yang, X.G.; Yang, N.; Delgado, F.P.; Hofmann, H.; Sun, J. A study of cell-to-cell variation of capacity in parallel-connected lithium-ion battery cells. eTransportation 2021, 7, 100091. [Google Scholar] [CrossRef]
- Dubey, P.; Pulugundla, G.; Srouji, A.K. Direct Comparison of Immersion and Cold-Plate Based Cooling for Automotive Li-Ion Battery Modules. Energies 2021, 14, 1259. [Google Scholar] [CrossRef]
- Thakur, A.K.; Prabakaran, R.; Elkadeem, M.R.; Sharshir, S.W.; Arıcı, M.; Wang, C.; Zhao, W.; Hwang, J.Y.; Saidur, R. A state of art review and future viewpoint on advance cooling techniques for Lithium–ion battery system of electric vehicles. J. Energy Storage 2020, 32, 101771. [Google Scholar] [CrossRef]
- Eddahech, A.; Briat, O.; Vinassa, J.M. Thermal characterization of a high-power lithium-ion battery: Potentiometric and calorimetric measurement of entropy changes. Energy 2013, 61, 432–439. [Google Scholar] [CrossRef]
- Iraola, U.; Aizpuru, I.; Gorrotxategi, L.; Segade, J.M.C.; Larrazabal, A.E.; Gil, I. Influence of Voltage Balancing on the Temperature Distribution of a Li-Ion Battery Module. IEEE Trans. Energy Convers. 2015, 30, 507–514. [Google Scholar] [CrossRef]
- Jilte, R.D.; Kumar, R. Numerical investigation on cooling performance of Li-ion battery thermal management system at high galvanostatic discharge. Eng. Sci. Technol. Int. J. 2018, 21, 957–969. [Google Scholar] [CrossRef]
- Ni, P.; Wang, X. Temperature field and temperature difference of a battery package for a hybrid car. Case Stud. Therm. Eng. 2020, 20, 100646. [Google Scholar] [CrossRef]
- Shahid, S.; Agelin-Chaab, M. Analysis of Cooling Effectiveness and Temperature Uniformity in a Battery Pack for Cylindrical Batteries. Energies 2017, 10, 1157. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, S.; Liu, Z.; Cheng, J. Numerical analysis of temperature uniformity of a liquid cooling battery module composed of heat-conducting blocks with gradient contact surface angles. Appl. Therm. Eng. 2020, 178, 115509. [Google Scholar] [CrossRef]
- DelRossi, R. Cell Balancing Design Guidelines. In Technical Report AN231; Microchip Technology Inc.: Chandler, AZ, USA, 2002. [Google Scholar]
- Ewert Energy Systems, I. How Cell Balancing Works. 2022. Available online: https://www.orionbms.com/manuals/utility_o2/param_balancing_description.html (accessed on 8 December 2022).
- Danae. Battery Pack Cell Voltage Difference and Solution: Part 1. 2021. Available online: https://www.grepow.com/blog/battery-pack-cell-voltage-difference-and-solution-part-1-battery-monday.html (accessed on 5 May 2023).
- Wang, Y.; Liu, D.; Shen, Y.; Tang, Y.; Chen, Y.; Zhang, J. Adaptive Balancing Control of Cell Voltage in the Charging/Discharging Mode for Battery Energy Storage Systems. Front. Energy Res. 2022, 10, 794191. [Google Scholar] [CrossRef]
- Brühl, M. Aktive Balancing-Systeme für Lithium-Ionen Batterien und deren Auswirkung auf die Zellalterung. Ph.D. Thesis, Université du Luxembourg, Luxemburg, 30 June 2017. [Google Scholar]
- Zhao, Y.; Liu, P.; Wang, Z.; Zhang, L.; Hong, J. Fault and defect diagnosis of battery for electric vehicles based on big data analysis methods. Appl. Energy 2017, 207, 354–362. [Google Scholar] [CrossRef]
- Gao, W.; Li, X.; Ma, M.; Fu, Y.; Jiang, J.; Mi, C. Case Study of an Electric Vehicle Battery Thermal Runaway and Online Internal Short-Circuit Detection. IEEE Trans. Power Electron. 2021, 36, 2452–2455. [Google Scholar] [CrossRef]
- Mallick, S.; Gayen, D. Thermal behaviour and thermal runaway propagation in lithium-ion battery systems—A critical review. J. Energy Storage 2023, 62, 106894. [Google Scholar] [CrossRef]
- Wikipedia contributors. Evaluation of Binary Classifiers. 2022. Available online: https://en.wikipedia.org/wiki/Evaluation_of_binary_classifiers (accessed on 7 May 2023).
- Hedderich, J.; Sachs, L. Angewandte Statistik; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Gao, W.; Zheng, Y.; Ouyang, M.; Li, J.; Lai, X.; Hu, X. Micro-Short-Circuit Diagnosis for Series-Connected Lithium-Ion Battery Packs Using Mean-Difference Model. IEEE Trans. Ind. Electron. 2019, 66, 2132–2142. [Google Scholar] [CrossRef]
- MathWorks. Matlab/Simulink. 2019. Available online: https://se.mathworks.com/products/simulink.html (accessed on 6 July 2020).
- Zhang, H.; Chow, M.Y. Comprehensive dynamic battery modeling for PHEV applications. In Proceedings of the IEEE PES General Meeting, Lake Buena Vista, FL, USA, 25–29 July 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Lei, Y.; Jia, F.; Lin, J.; Xing, S.; Ding, S.X. An Intelligent Fault Diagnosis Method Using Unsupervised Feature Learning Towards Mechanical Big Data. IEEE Trans. Ind. Electron. 2016, 63, 3137–3147. [Google Scholar] [CrossRef]
- Sangwan, V.; Sharma, A.; Kumar, R.; Rathore, A.K. Equivalent circuit model parameters estimation of Li-ion battery: C-rate, SOC and temperature effects. In Proceedings of the 2016 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Trivandrum, India, 14–17 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Kong, X.; Plett, G.L.; Scott Trimboli, M.; Zhang, Z.; Qiao, D.; Zhao, T.; Zheng, Y. Pseudo-two-dimensional model and impedance diagnosis of micro internal short circuit in lithium-ion cells. J. Energy Storage 2020, 27, 101085. [Google Scholar] [CrossRef]
- Chen, M.; Bai, F.; Lin, S.; Song, W.; Li, Y.; Feng, Z. Performance and safety protection of internal short circuit in lithium-ion battery based on a multilayer electro-thermal coupling model. Appl. Therm. Eng. 2019, 146, 775–784. [Google Scholar] [CrossRef]
- Barai, A.; Tangirala, R.; Uddin, K.; Chevalier, J.; Guo, Y.; McGordon, A.; Jennings, P. The effect of external compressive loads on the cycle lifetime of lithium-ion pouch cells. J. Energy Storage 2017, 13, 211–219. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. Stress evolution and capacity fade in constrained lithium-ion pouch cells. J. Power Sources 2014, 245, 745–751. [Google Scholar] [CrossRef]
- The SciPy community. SciPy. 2023. Available online: https://scipy.org/ (accessed on 7 May 2023).
- VDA Verband der Automobilindustrie. Abgasemissionen: WLTP—Weltweit Harmonisierter Zyklus für Leichte Fahrzeuge; VDA Verband der Automobilindustrie: Eisenach, Germany, 2020. [Google Scholar]
- Barnett, B. Lithium-Ion Cell Internal Shorting: 1. Early Detection 2. Simulation; National Transportation Safety Board (NTSB): Washington, DC, USA, 2017.
- Meng, J.; Boukhnifer, M.; Diallo, D. On-line Model-based Short Circuit Diagnosis of Lithium-Ion Batteries for Electric Vehicle Application. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Chengdu, China, 15–17 December 2019; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2019; pp. 6022–6027. [Google Scholar] [CrossRef]
- Seo, M.; Goh, T.; Koo, G.; Park, M.; Kim, S.W. Detection of Internal Short Circuit in Li-ion Battery by Estimating its Resistance. In Proceedings of the 4th IIAE International Conference on Intelligent Systems and Image Processing 2016, Kyoto, Japan, 8–12 September 2016; The Institute of Industrial Applications Engineers: Fukuoka, Japan, 2016; pp. 212–217. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- The Pandas Development Team. Pandas-Dev/Pandas: Pandas. 2023. Available online: https://zenodo.org/record/7344967 (accessed on 7 May 2023).
- Ma, M.; Wang, Y.; Duan, Q.; Wu, T.; Sun, J.; Wang, Q. Fault detection of the connection of lithium-ion power batteries in series for electric vehicles based on statistical analysis. Energy 2018, 164, 745–756. [Google Scholar] [CrossRef]
- Guthrie, W.F. NIST/SEMATECH e-Handbook of Statistical Methods (NIST Handbook 151); Technical Report; National Institute of Standards and Technology: Gaithersburg, MA, USA, 2020. [CrossRef]
- Hansen, A. The Three Extreme Value Distributions: An Introductory Review. Front. Phys. 2020, 8, 604053. [Google Scholar] [CrossRef]
- Brodd, R.J. Batteries for Sustainability; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Lai, X.; Jin, C.; Yi, W.; Han, X.; Feng, X.; Zheng, Y.; Ouyang, M. Mechanism, modeling, detection, and prevention of the internal short circuit in lithium-ion batteries: Recent advances and perspectives. Energy Storage Mater. 2021, 35, 470–499. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).