Comparative Analysis via CFD Simulation on the Impact of Graphite Anode Morphologies on the Discharge of a Lithium-Ion Battery
Abstract
1. Introduction
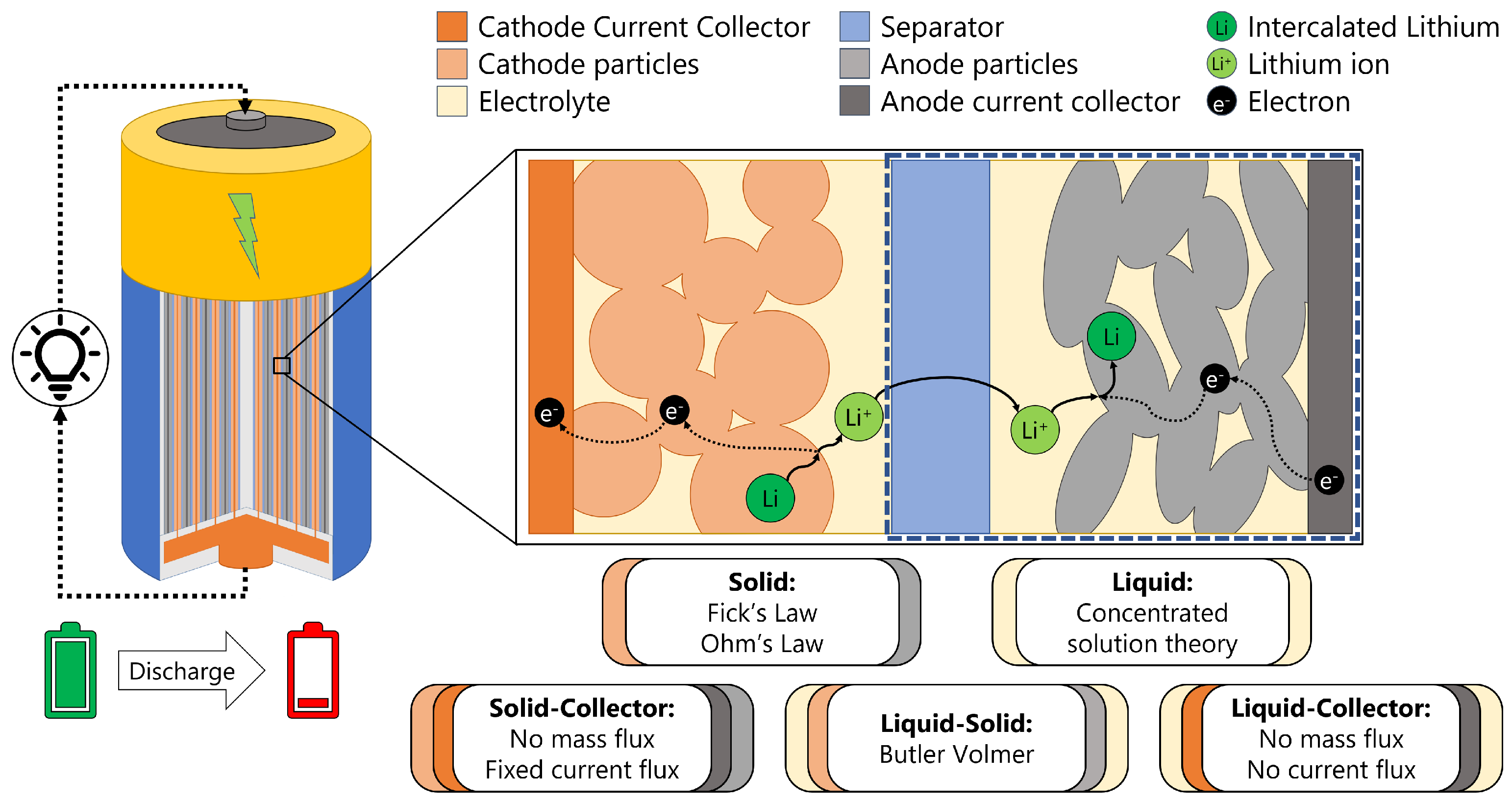
2. Governing Equations
3. Materials and Methods
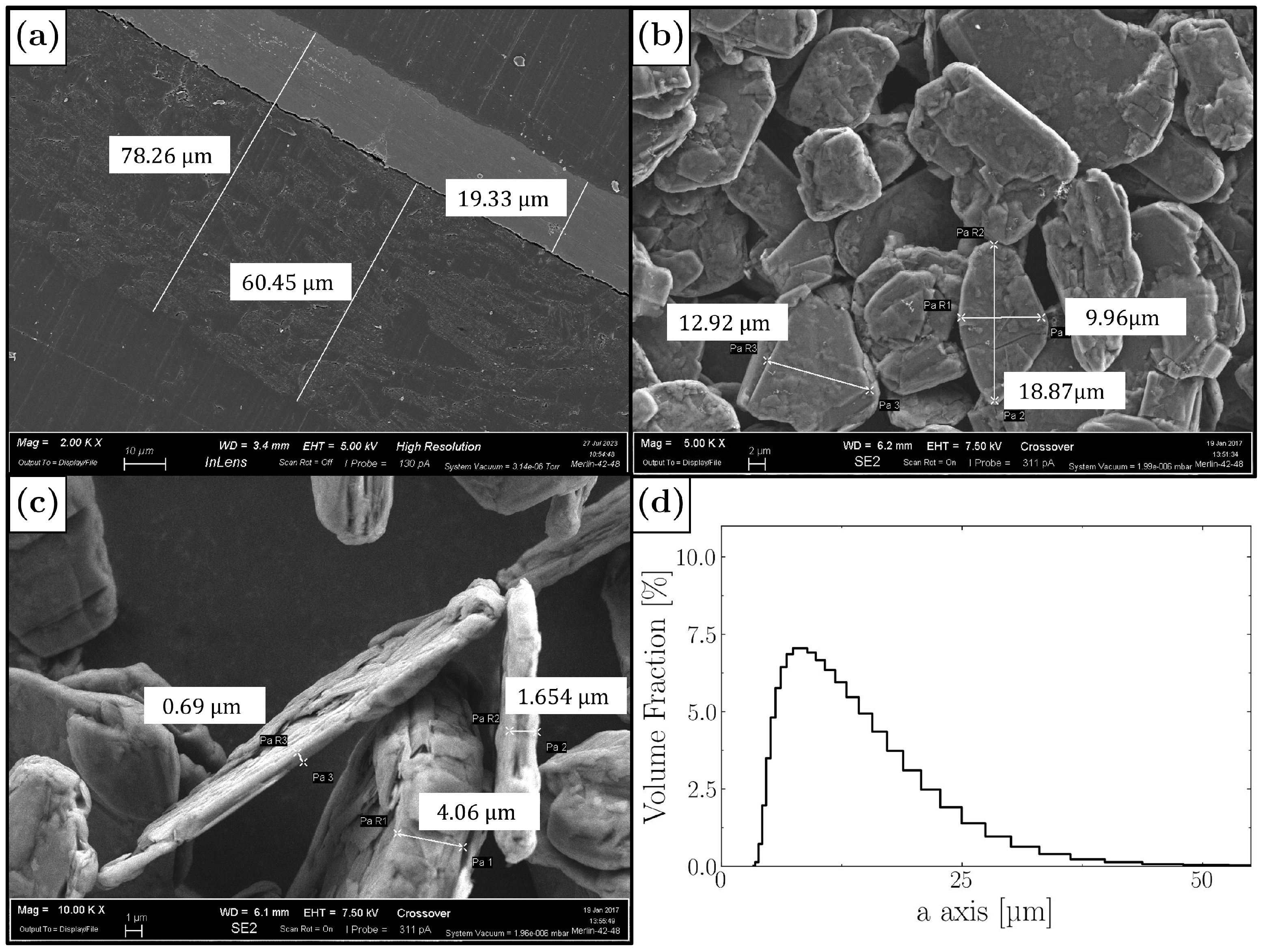
3.1. Experimental Analysis
3.2. The Creation of the Geometry of the Electrodes
3.3. DEM Simulation
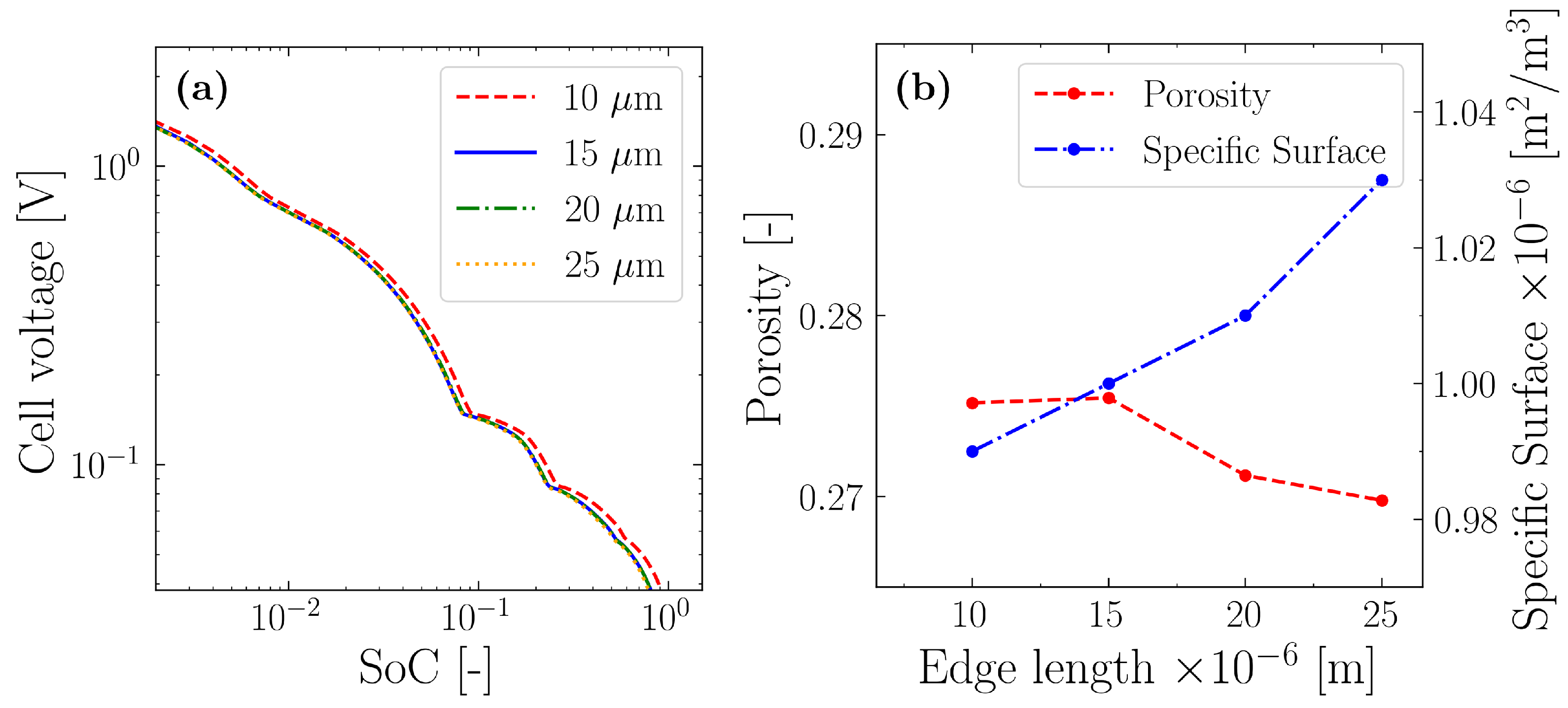
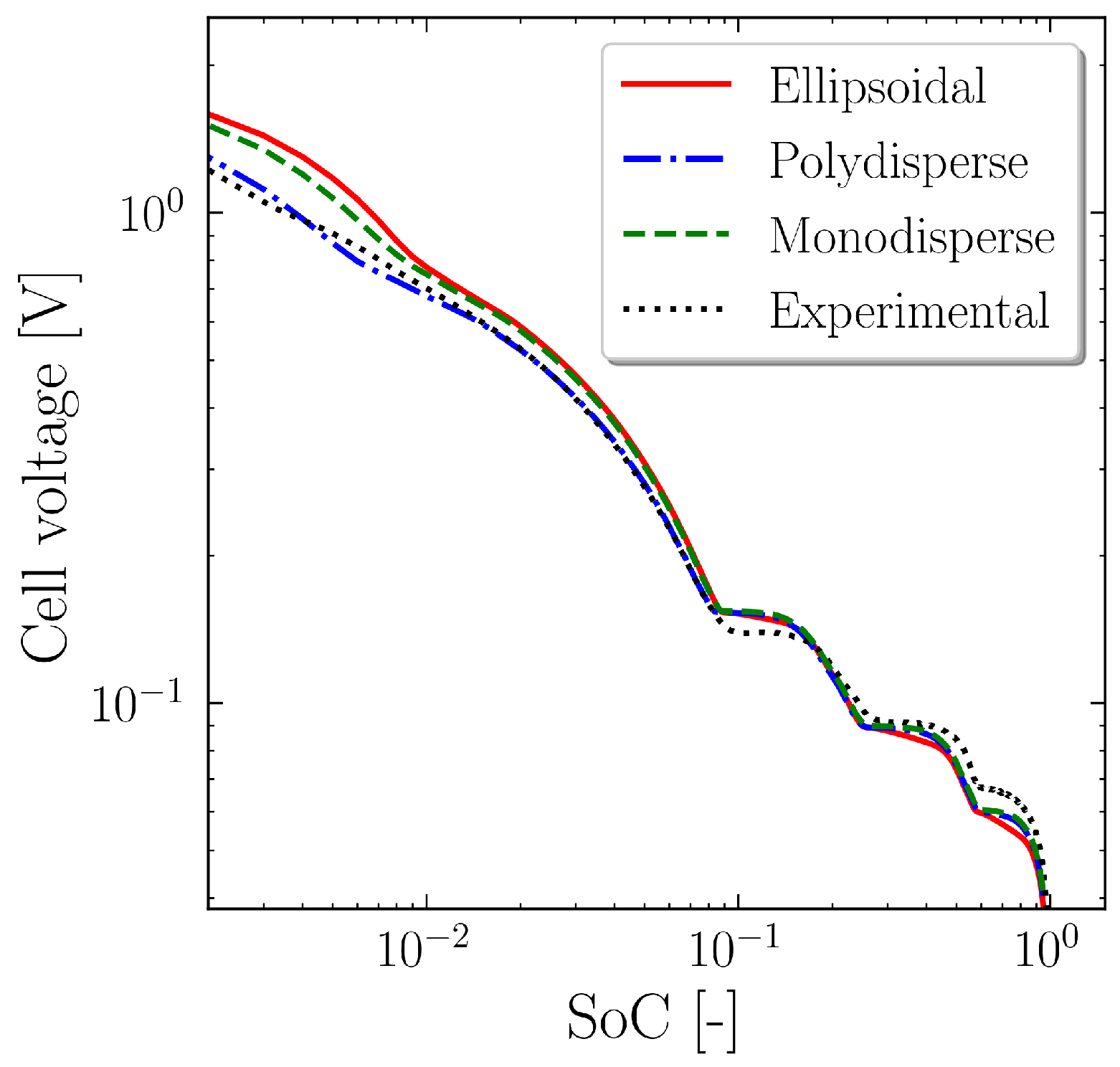
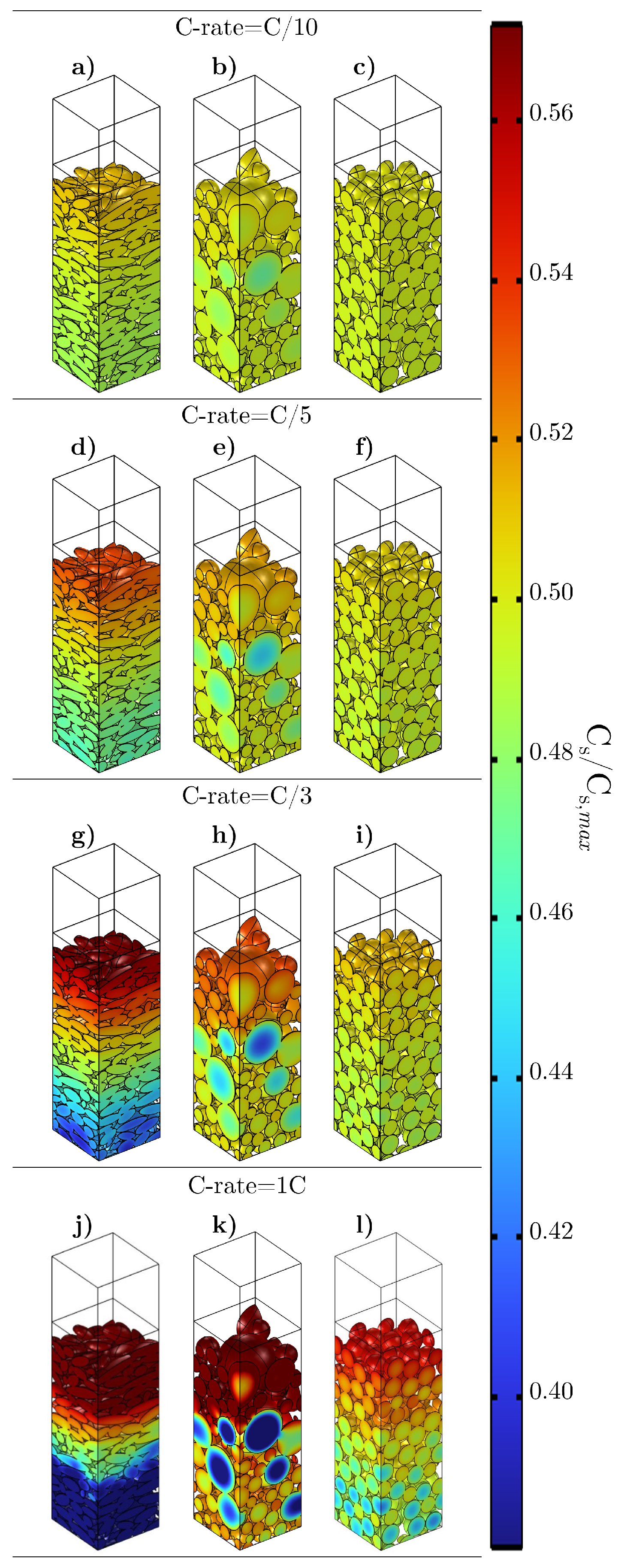
4. Results and Discussion
5. Conclusions
Reproducibility and Data FAIRness
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| T | Temperature |
| F | Faraday constant |
| R | Ideal gas constant |
| Electric potential | |
| c | Concentration |
| V | Volume |
| Referred to solid phase | |
| Referred to liquid phase | |
| Referred to anode side | |
| Referred to cathode side | |
| Referred to current collector | |
| Referred to a solid particle | |
| Referred to of the state of charge | |
| Initial condition | |
| Reference value | |
| Maximum value considered | |
| Minimum value considered | |
| i | Electric current |
| Electrical conductivity | |
| Diffusion coefficient | |
| t | Time |
| Mean molar activity | |
| Lithium-ion transference number | |
| A | Surface area |
| Over-potential | |
| m | Mass |
| M | Molar mass |
| Force | |
| Spatial position | |
| Inertia | |
| Gravitational acceleration | |
| Angular velocity | |
| Distance | |
| Young module | |
| Radius |
References
- Ziemann, S.; Müller, D.B.; Schebek, L.; Weil, M. Modeling the potential impact of lithium recycling from EV batteries on lithium demand: A dynamic MFA approach. Resour. Conserv. Recycl. 2018, 133, 76–85. [Google Scholar] [CrossRef]
- Zhao, Y.; Pohl, O.; Bhatt, A.; Collis, G.; Mahon, P.; Rüther, T.; Hollenkamp, A. A Review on Battery Market Trends, Second-Life Reuse, and Recycling. Sustain. Chem. 2021, 2, 167–205. [Google Scholar] [CrossRef]
- Xu, C.; Dai, Q.; Gaines, L.; Hu, M.; Tukker, A.; Steubing, B. Future material demand for automotive lithium-based batteries. Commun. Mater. 2020, 1, 99. [Google Scholar] [CrossRef]
- Li, H. Practical Evaluation of Li-Ion Batteries. Joule 2019, 3, 911–914. [Google Scholar] [CrossRef]
- Lu, X.; Bertei, A.; Finegan, D.P.; Tan, C.; Daemi, S.R.; Weaving, J.S.; O’Regan, K.B.; Heenan, T.M.M.; Hinds, G.; Kendrick, E.; et al. 3D microstructure design of lithium-ion battery electrodes assisted by X-ray nano-computed tomography and modelling. Nat. Commun. 2020, 11, 2079. [Google Scholar] [CrossRef]
- Gupta, A.; Manthiram, A. Designing Advanced Lithium-Based Batteries for Low-Temperature Conditions. Adv. Energy Mater. 2020, 10, 2001972. [Google Scholar] [CrossRef]
- Thompson, D.; Hartley, J.; Lambert, S.; Shiref, M.; Harper, G.; Kendrick, E.; Anderson, P.; Ryder, K.; Gaines, L.; Abbott, A. The importance of design in lithium ion battery recycling—A critical review. RSC Green Chem. 2020, 22, 7585–7603. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. The importance of the lithium ion transference number in lithium/polymer cells. Electrochim. Acta 1994, 39, 2073–2081. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526. [Google Scholar] [CrossRef]
- Jokar, A.; Rajabloo, B.; Désilets, M.; Lacroix, M. Review of simplified Pseudo-two-Dimensional models of lithium-ion batteries. J. Power Sources 2016, 327, 44–55. [Google Scholar] [CrossRef]
- Qiu, G.; Dennison, C.; Knehr, K.; Kumbur, E.; Sun, Y. Pore-scale analysis of effects of electrode morphology and electrolyte flow conditions on performance of vanadium redox flow batteries. J. Power Sources 2012, 219, 223–234. [Google Scholar] [CrossRef]
- Chung, D.D.L. Review Graphite. J. Mater. Sci. 2002, 37, 1475–1489. [Google Scholar] [CrossRef]
- Deprez, N.; McLachlan, D.S. The analysis of the electrical conductivity of graphite conductivity of graphite powders during compaction. J. Phys. D Appl. Phys. 1988, 21, 101. [Google Scholar] [CrossRef]
- Gottschalk, L.; Müller, J.; Schoo, A.; Baasch, E.; Kwade, A. Spherical Graphite Anodes: Influence of Particle Size Distribution and Multilayer Structuring in Lithium-Ion Battery Cells. Batteries 2024, 10, 40. [Google Scholar] [CrossRef]
- Bläubaum, L.; Röder, F.; Nowak, C.; Chan, H.S.; Kwade, A.; Krewer, U. Impact of Particle Size Distribution on Performance of Lithium-Ion Batteries. ChemElectroChem 2020, 7, 4755–4766. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, L.; Wang, W.; Yang, K.; Zhang, Z.; Liang, X.; Chen, S.; Yang, S.; Li, J.; Liu, X. Lithium-ion battery multi-scale modeling coupled with simplified electrochemical model and kinetic Monte Carlo model. iScience 2023, 26, 107661. [Google Scholar] [CrossRef]
- Lu, X.; Lagnoni, M.; Bertei, A.; Das, S.; Owen, R.E.; Li, Q.; O’Regan, K.; Wade, A.; Finegan, D.P.; Kendrick, E.; et al. Multiscale dynamics of charging and plating in graphite electrodes coupling operando microscopy and phase-field modelling. Nat. Commun. 2023, 14, 5127. [Google Scholar] [CrossRef] [PubMed]
- Danner, T.; Singh, M.; Hein, S.; Kaiser, J.; Hahn, H.; Latz, A. Thick electrodes for Li-ion batteries: A model based analysis. J. Power Sources 2016, 334, 191–201. [Google Scholar] [CrossRef]
- Westhoff, D.; Manke, I.; Schmidt, V. Generation of virtual lithium-ion battery electrode microstructures based on spatial stochastic modeling. Comput. Mater. Sci. 2018, 151, 53–64. [Google Scholar] [CrossRef]
- Kremer, L.S.; Hoffmann, A.; Danner, T.; Hein, S.; Prifling, B.; Westhoff, D.; Dreer, C.; Latz, A.; Schmidt, V.; Wohlfahrt-Mehrens, M. Manufacturing Process for Improved Ultra-Thick Cathodes in High-Energy Lithium-Ion Batteries. Energy Technol. 2020, 8, 1900167. [Google Scholar] [CrossRef]
- Hein, S.; Danner, T.; Westhoff, D.; Prifling, B.; Scurtu, R.; Kremer, L.; Hoffmann, A.; Hilger, A.; Osenberg, M.; Manke, I.; et al. Influence of Conductive Additives and Binder on the Impedance of Lithium-Ion Battery Electrodes: Effect of Morphology. J. Electrochem. Soc. 2020, 167, 013546. [Google Scholar] [CrossRef]
- Deng, Z.; Lin, X.; Huang, Z.; Meng, J.; Zhong, Y.; Ma, G.; Zhou, Y.; Shen, Y.; Ding, H.; Huang, Y. Recent progress on advanced imaging techniques for lithium-ion batteries. Adv. Energy Mater. 2021, 11, 2000806. [Google Scholar] [CrossRef]
- An, S.J.; Li, J.; Daniel, C.; Mohanty, D.; Nagpure, S.; Wood, D.L. The state of understanding of the lithium-ion-battery graphite solid electrolyte interphase (SEI) and its relationship to formation cycling. Carbon 2016, 105, 52–76. [Google Scholar] [CrossRef]
- Chouchane, M.; Arcelus, O.; Franco, A.A. Heterogeneous Solid-Electrolyte Interphase in Graphite Electrodes Assessed by 4D-Resolved Computational Simulations. Batter. Supercaps 2021, 4, 1457–1463. [Google Scholar] [CrossRef]
- Pron, V.; Versaci, D.; Amici, J.; Francia, C.; Santarelli, M.; Bodoardo, S. Electrochemical Characterization and Solid Electrolyte Interface Modeling of LiNi 0.5 Mn 1.5 O 4 -Graphite Cells. J. Electrochem. Soc. 2019, 166, A2255–A2263. [Google Scholar] [CrossRef]
- Heiskanen, S.K.; Kim, J.; Lucht, B.L. Generation and Evolution of the Solid Electrolyte Interphase of Lithium-Ion Batteries. Joule 2019, 3, 2322–2333. [Google Scholar] [CrossRef]
- Peled, E.; Menkin, S. Review—SEI: Past, Present and Future. J. Electrochem. Soc. 2017, 164, A1703. [Google Scholar] [CrossRef]
- Nie, M.; Lucht, B.L. Role of Lithium Salt on Solid Electrolyte Interface (SEI) Formation and Structure in Lithium Ion Batteries. J. Electrochem. Soc. 2014, 161, A1001. [Google Scholar] [CrossRef]
- Keil, P.; Schuster, S.F.; Wilhelm, J.; Travi, J.; Hauser, A.; Karl, R.C.; Jossen, A. Calendar Aging of Lithium-Ion Batteries. J. Electrochem. Soc. 2016, 163, A1872. [Google Scholar] [CrossRef]
- Goldin, G.M.; Colclasure, A.M.; Wiedemann, A.H.; Kee, R.J. Three-dimensional particle-resolved models of Li-ion batteries to assist the evaluation of empirical parameters in one-dimensional models. Electrochim. Acta 2012, 64, 118–129. [Google Scholar] [CrossRef]
- Newman, J.; Balsara, N.P. Electrochemical Systems; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Latz, A.; Zausch, J. Thermodynamic consistent transport theory of Li-ion batteries. J. Power Sources 2011, 196, 3296–3302. [Google Scholar] [CrossRef]
- Richardson, G.W.; Foster, J.M.; Ranom, R.; Please, C.P.; Ramos, A.M. Charge transport modelling of Lithium-ion batteries. Eur. J. Appl. Math. 2022, 33, 983–1031. [Google Scholar] [CrossRef]
- Kespe, M.; Nirschl, H. Numerical simulation of lithium-ion battery performance considering electrode microstructure. Int. J. Energy Res. 2015, 39, 2062–2074. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R.; White, H.S. Electrochemical Methods: Fundamentals and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Colclasure, A.M.; Kee, R.J. Thermodynamically consistent modeling of elementary electrochemistry in lithium-ion batteries. Electrochim. Acta 2010, 55, 8960–8973. [Google Scholar] [CrossRef]
- Karthikeyan, D.K.; Sikha, G.; White, R.E. Thermodynamic model development for lithium intercalation electrodes. J. Power Sources 2008, 185, 1398–1407. [Google Scholar] [CrossRef]
- Smilauer, V. Yade Documentation; The Yade Project: Lowestoft, UK, 2021; Available online: https://zenodo.org/records/5705394 (accessed on 9 June 2025).
- Filippov, S. Blender software platform as an environment for modeling objects and processes of science disciplines. Keldysh Inst. Prepr. 2018, 24, 1–42. [Google Scholar] [CrossRef]
- Park, J.H.; Yoon, H.; Cho, Y.; Yoo, C.Y. Investigation of Lithium Ion Diffusion of Graphite Anode by the Galvanostatic Intermittent Titration Technique. Materials 2021, 14, 4683. [Google Scholar] [CrossRef]
- Markevich, E.; Levi, M.; Aurbach, D. Comparison between potentiostatic and galvanostatic intermittent titration techniques for determination of chemical diffusion coefficients in ion-insertion electrodes. J. Electroanal. Chem. 2005, 580, 231–237. [Google Scholar] [CrossRef]
- Yang, H.; Bang, H.J.; Prakash, J. Evaluation of Electrochemical Interface Area and Lithium Diffusion Coefficient for a Composite Graphite Anode. J. Electrochem. Soc. 2004, 151, A1247. [Google Scholar] [CrossRef]
- Horner, J.S.; Whang, G.; Ashby, D.S.; Kolesnichenko, I.V.; Lambert, T.N.; Dunn, B.S.; Talin, A.A.; Roberts, S.A. Electrochemical Modeling of GITT Measurements for Improved Solid-State Diffusion Coefficient Evaluation. ACS Appl. Energy Mater. 2021, 4, 11460–11469. [Google Scholar] [CrossRef]
- Rabbani, A.; Salehi, S. Dynamic modeling of the formation damage and mud cake deposition using filtration theories coupled with SEM image processing. J. Nat. Gas Sci. Eng. 2017, 42, 157–168. [Google Scholar] [CrossRef]
- Ezeakacha, C.P.; Rabbani, A.; Salehi, S.; Ghalambor, A. Integrated Image Processing and Computational Techniques to Characterize Formation Damage. In Proceedings of the SPE International Conference and Exhibition on Formation Damage Control, Lafayette, LA, USA, 7–9 February 2018; p. D012S007R004. [Google Scholar] [CrossRef]
- Castillo, J.; Soria-Fernández, A.; Rodriguez-Peña, S.; Rikarte, J.; Robles-Fernández, A.; Aldalur, I.; Cid, R.; González-Marcos, J.A.; Carrasco, J.; Armand, M.; et al. Graphene-Based Sulfur Cathodes and Dual Salt-Based Sparingly Solvating Electrolytes: A Perfect Marriage for High Performing, Safe, and Long Cycle Life Lithium-Sulfur Prototype Batteries. Adv. Energy Mater. 2024, 14, 2302378. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Coumans, E. Bullet physics simulation. In Proceedings of the ACM SIGGRAPH 2015 Courses, Association for Computing Machinery, Los Angeles, CA, USA, 9–13 August 2015. [Google Scholar] [CrossRef]
- Boccardo, G.; Augier, F.; Haroun, Y.; Ferré, D.; Marchisio, D.L. Validation of a novel open-source work-flow for the simulation of packed-bed reactors. Chem. Eng. J. 2015, 279, 809–820. [Google Scholar] [CrossRef]
- Cooper, S.; Bertei, A.; Shearing, P.; Kilner, J.; Brandon, N. TauFactor: An open-source application for calculating tortuosity factors from tomographic data. SoftwareX 2016, 5, 203–210. [Google Scholar] [CrossRef]
- Yao, K.P.C.; Okasinski, J.S.; Kalaga, K.; Shkrob, I.A.; Abraham, D.P. Quantifying lithium concentration gradients in the graphite electrode of Li-ion cells using operando energy dispersive X-ray diffraction. Energy Environ. Sci. 2019, 12, 656–665. [Google Scholar] [CrossRef]


| Parameter | Value | Description |
|---|---|---|
| 0 [mol/m3] | Initial Li concentration in solid | |
| 1000 [mol/m3] | Initial Li+ concentration in liquid | |
| 31,507 [mol/m3] | Maximum Li concentration in solid | |
| 0.95 | Final particle lithiation level | |
| 0 | Initial particle lithiation level | |
| 100 [S/m] | Electrode electrical conductivity | |
| 0.743 [S/m] | Electrolyte electrical conductivity | |
| 1.317 [m2/s] | Electrode diffusion coefficient | |
| 3.613 [m2/s] | Electrolyte diffusion coefficient | |
| 0.5 | Anodic symmetry factor | |
| 0.5 | Cathodic symmetry factor | |
| 0.363 | Lithium-ion transference number | |
| 0.85 [µm] | Minimum mesh size | |
| 6.6 [µm] | Maximum mesh size | |
| 20 [µm] | Electrode thickness along X direction | |
| 20 [µm] | Electrode thickness along Y direction | |
| 60 [µm] | Electrode thickness along Z direction | |
| 20 [µm] | Separator thickness |
| Geometry | Exp. Porosity | Comp. Porosity | Comp. Specific Area [m2/m3] | Tortuosity |
|---|---|---|---|---|
| Monodispersed spheres | 0.376 | 9.29 | 2.05 | |
| Polydispersed ellipsoids | 0.300 | 0.271 | 9.90 | 7.8 |
| Polydispersed spheres | 0.301 | 5.93 | 2.33 |
| System | RMSE |
|---|---|
| Ellipsoidal | 0.3861 |
| Monodispersed | 0.3638 |
| Polydispersed | 0.3046 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lombardo Pontillo, A.; Marcato, A.; Versaci, D.; Marchisio, D.; Boccardo, G. Comparative Analysis via CFD Simulation on the Impact of Graphite Anode Morphologies on the Discharge of a Lithium-Ion Battery. Batteries 2025, 11, 252. https://doi.org/10.3390/batteries11070252
Lombardo Pontillo A, Marcato A, Versaci D, Marchisio D, Boccardo G. Comparative Analysis via CFD Simulation on the Impact of Graphite Anode Morphologies on the Discharge of a Lithium-Ion Battery. Batteries. 2025; 11(7):252. https://doi.org/10.3390/batteries11070252
Chicago/Turabian StyleLombardo Pontillo, Alessio, Agnese Marcato, Daniele Versaci, Daniele Marchisio, and Gianluca Boccardo. 2025. "Comparative Analysis via CFD Simulation on the Impact of Graphite Anode Morphologies on the Discharge of a Lithium-Ion Battery" Batteries 11, no. 7: 252. https://doi.org/10.3390/batteries11070252
APA StyleLombardo Pontillo, A., Marcato, A., Versaci, D., Marchisio, D., & Boccardo, G. (2025). Comparative Analysis via CFD Simulation on the Impact of Graphite Anode Morphologies on the Discharge of a Lithium-Ion Battery. Batteries, 11(7), 252. https://doi.org/10.3390/batteries11070252








