Research on SOC Estimation of Lithium-Ion Battery Based on CA-SVDUKF Algorithm
Abstract
1. Introduction
2. Development of the Lithium-Ion Battery Equivalent Model
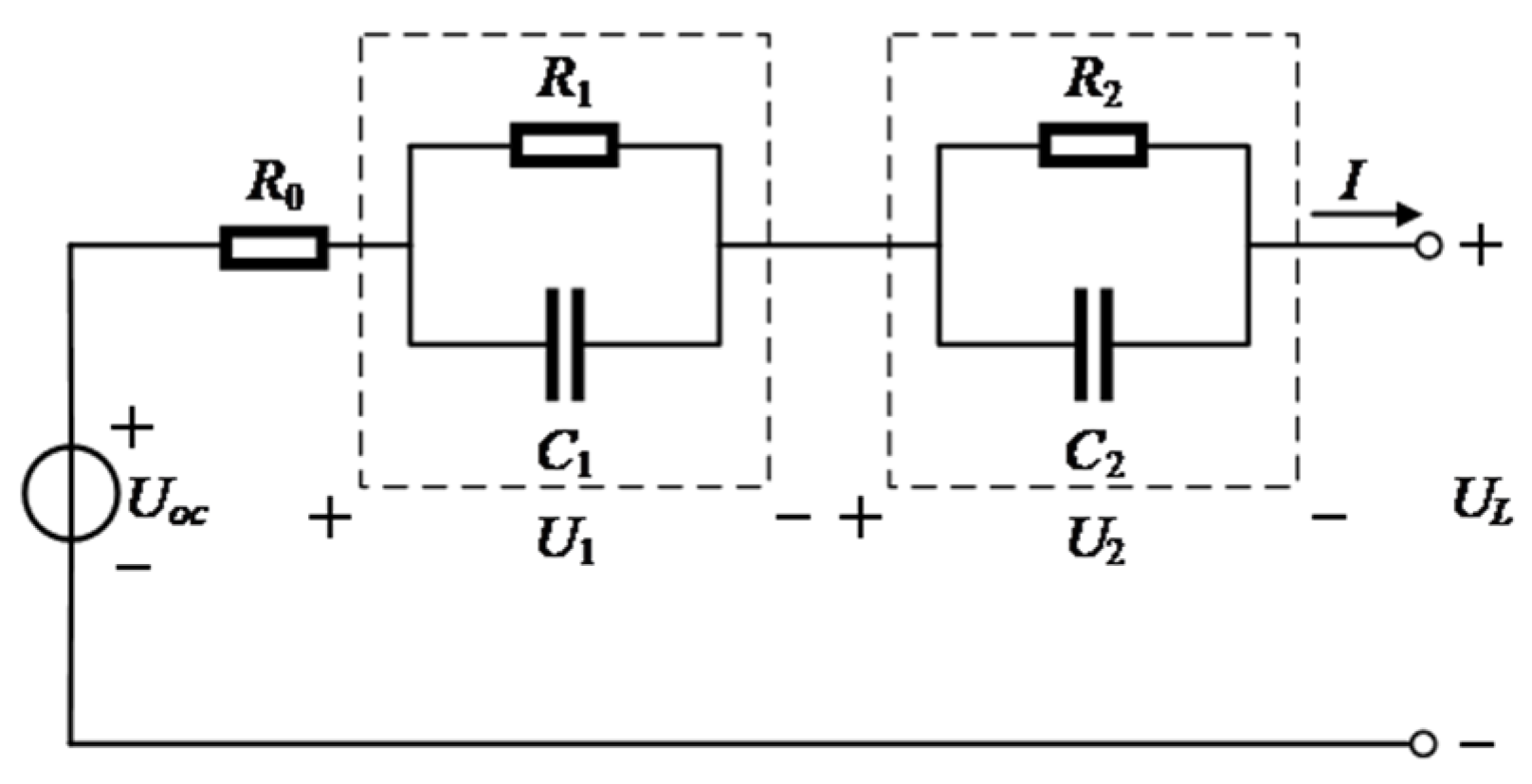
2.1. Second-Order RC Equivalent Circuit Model
2.2. State-Space Equations of the Battery
3. Online Parameter Identification of Battery Model
3.1. Identification Method Based on FFRLS Algorithm
3.2. Analysis of Online Identification Results
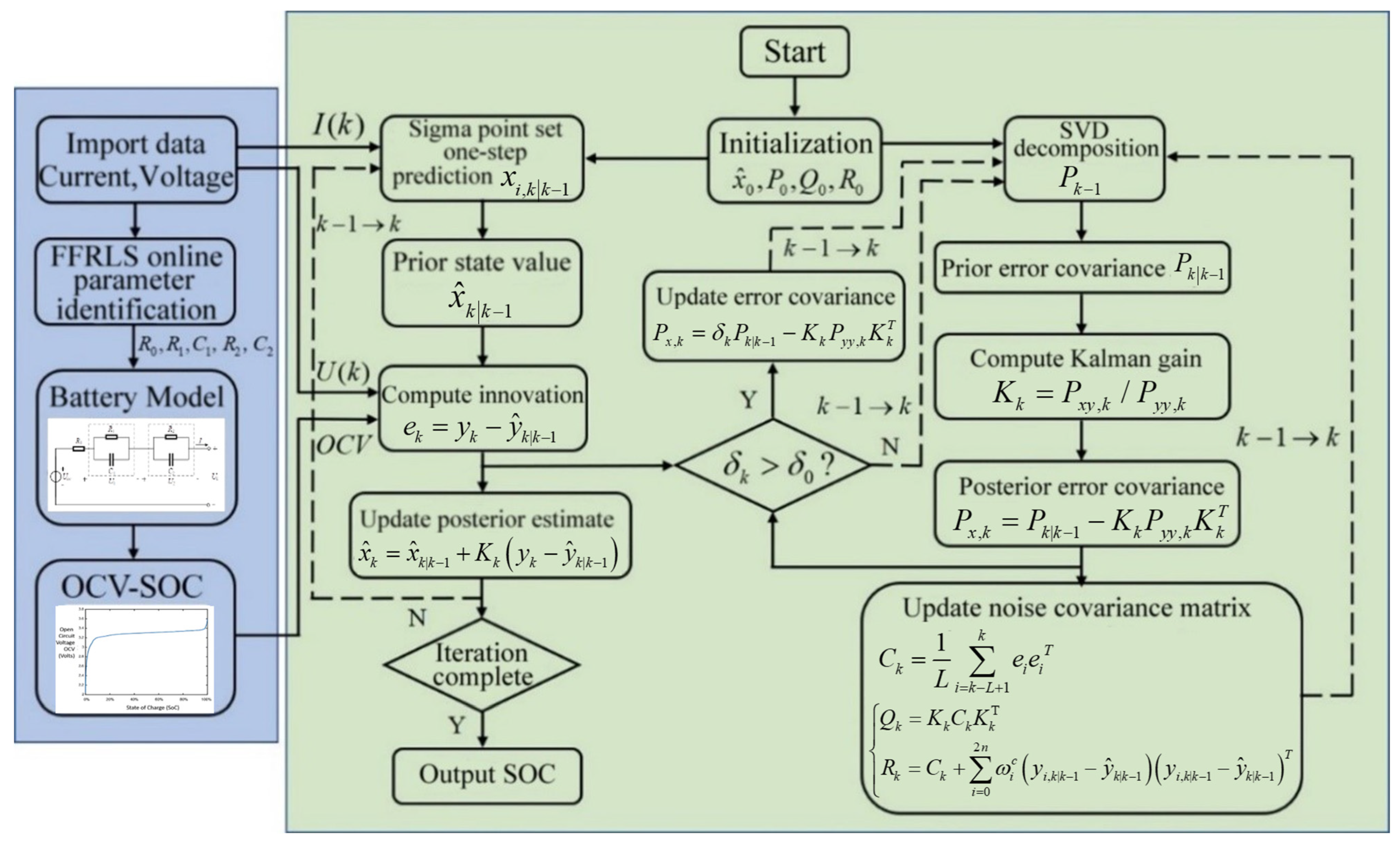
4. CA-SVDUKF Algorithm
4.1. Standard UKF Algorithm Procedure
4.2. Improvements to the UKF Algorithm
4.2.1. SVD-UKF Algorithm
4.2.2. Noise Covariance Matching Method
4.2.3. Adaptive Error Covariance Matrix Method
4.3. Design of the CA-SVDUKF Algorithm
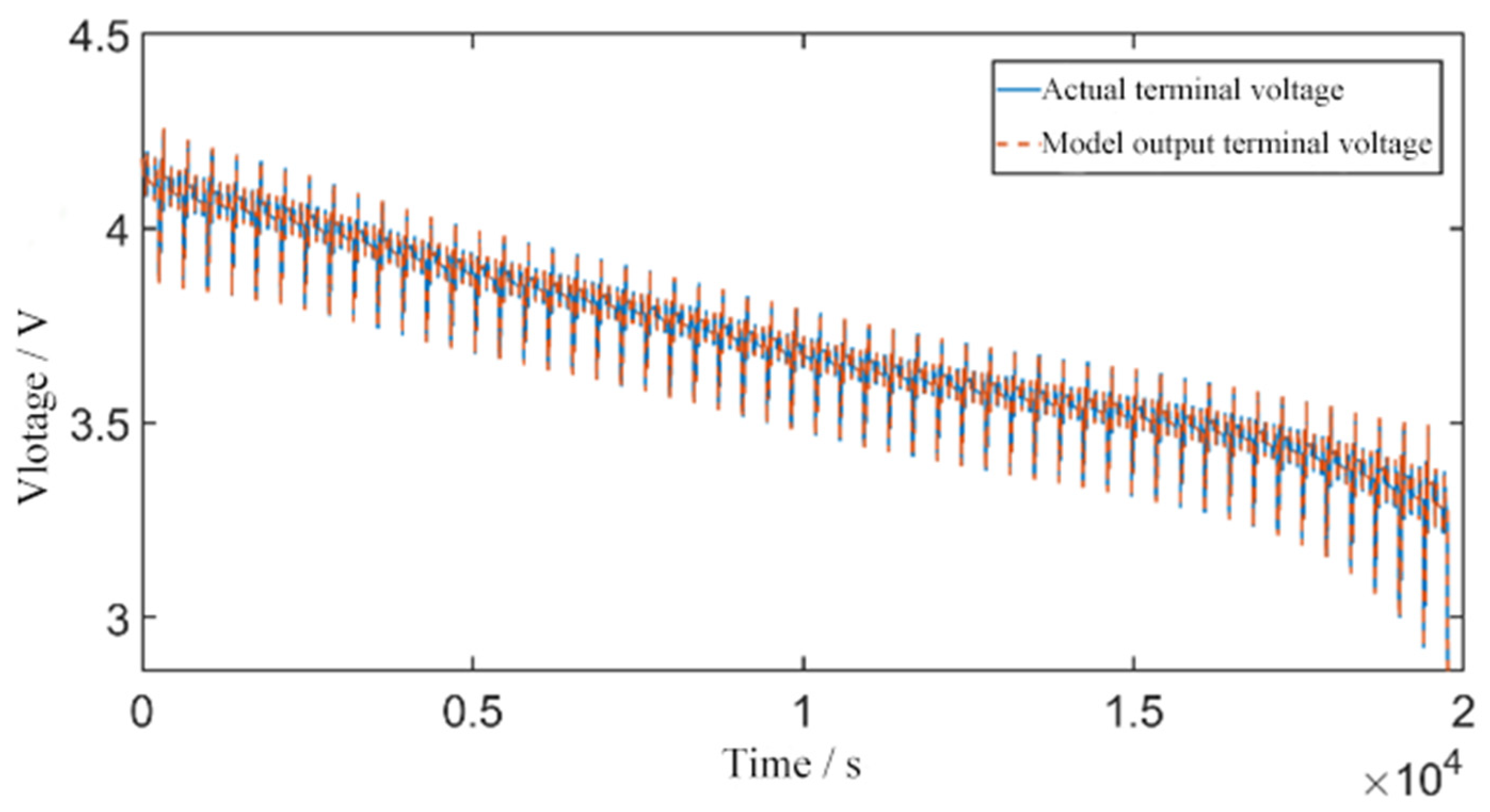
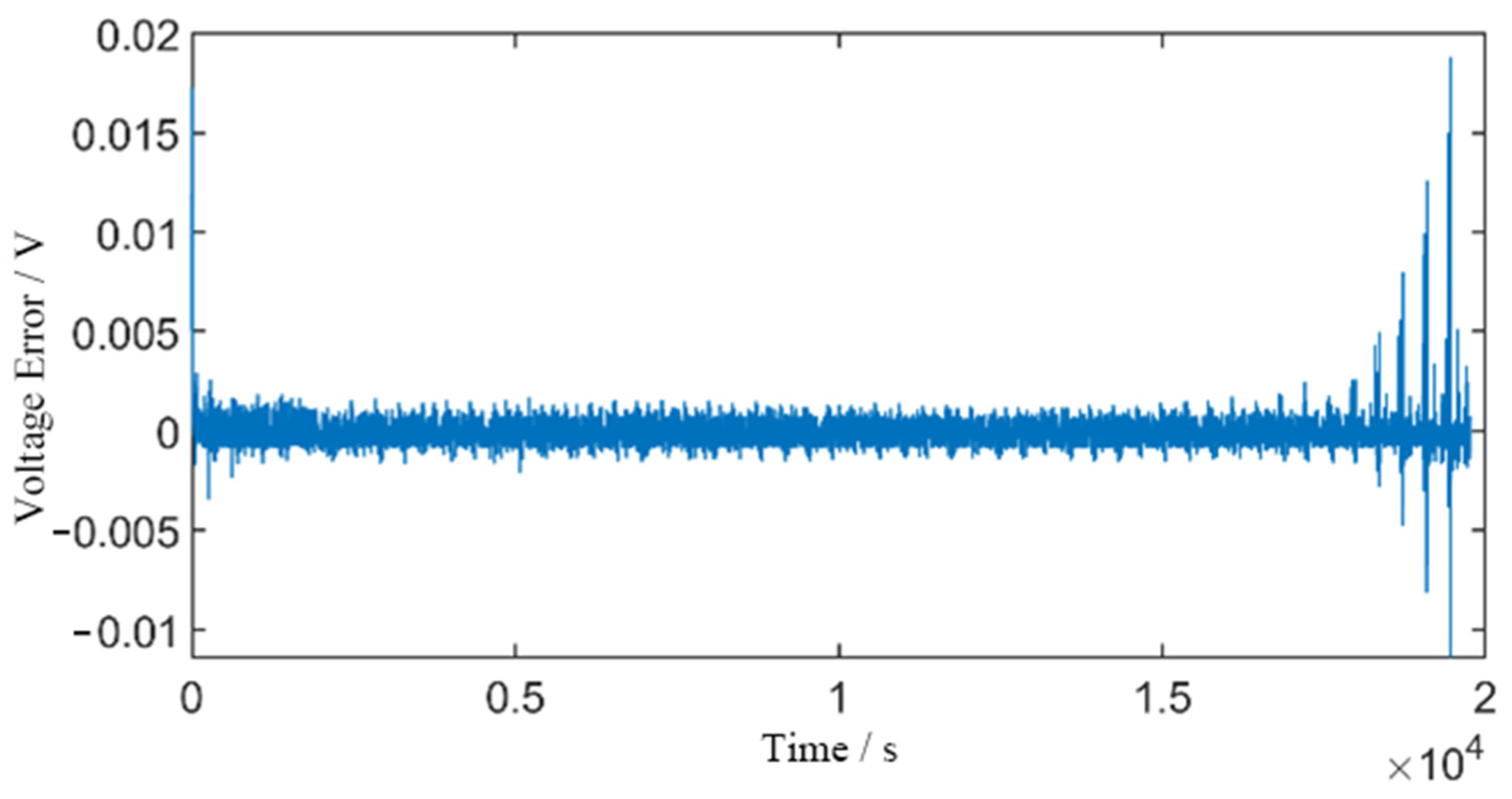
5. Verification of SOC Simulation Results
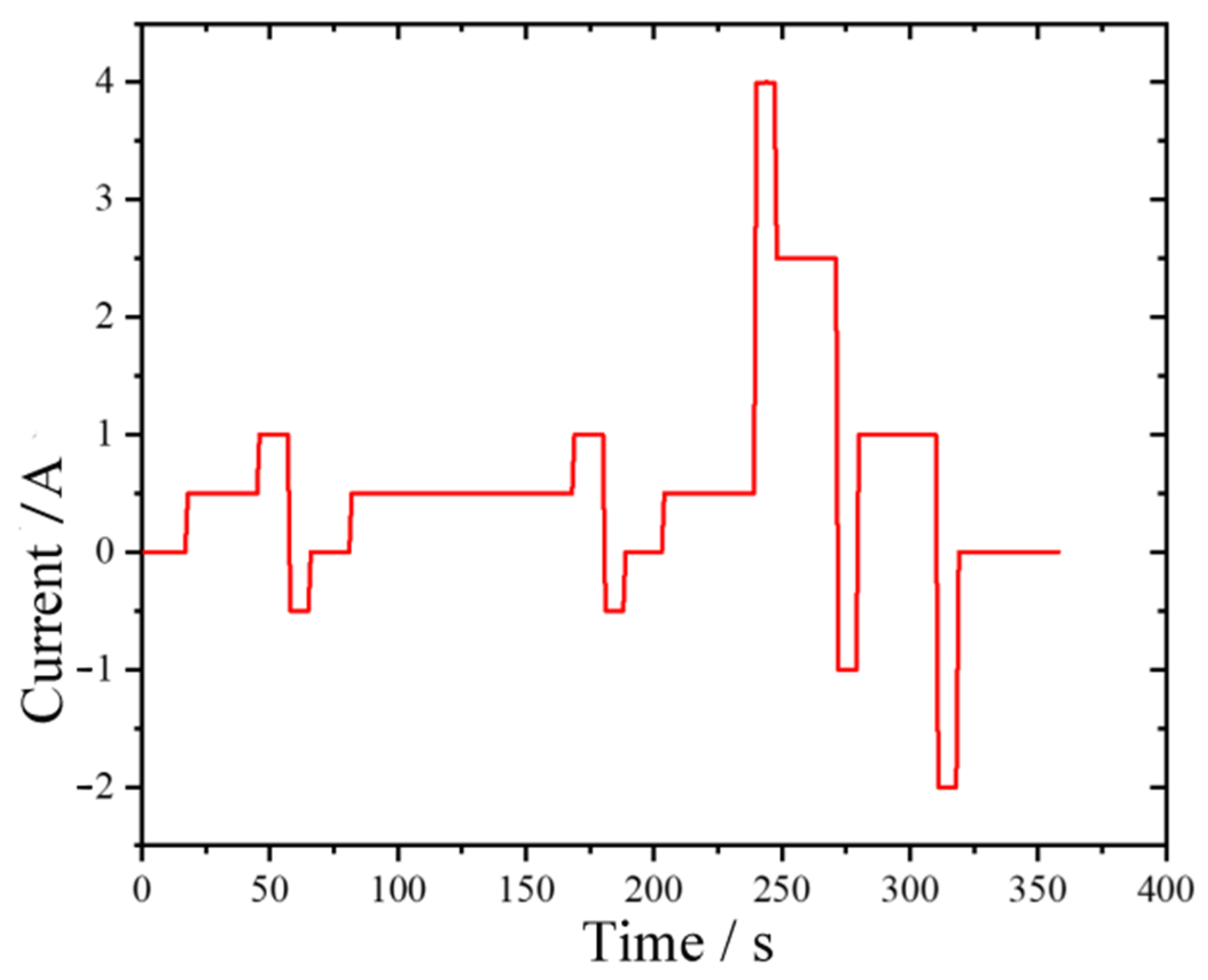
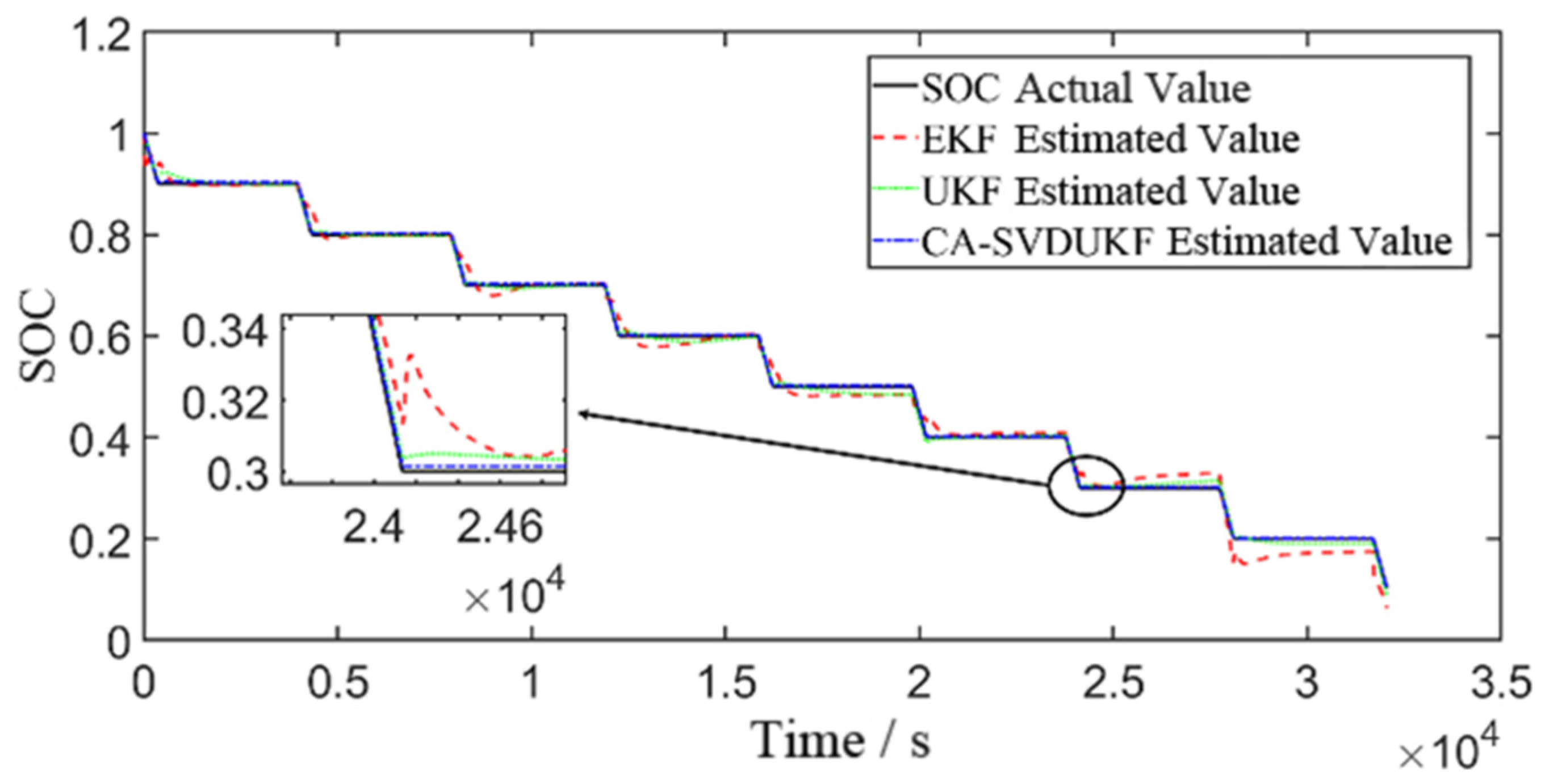
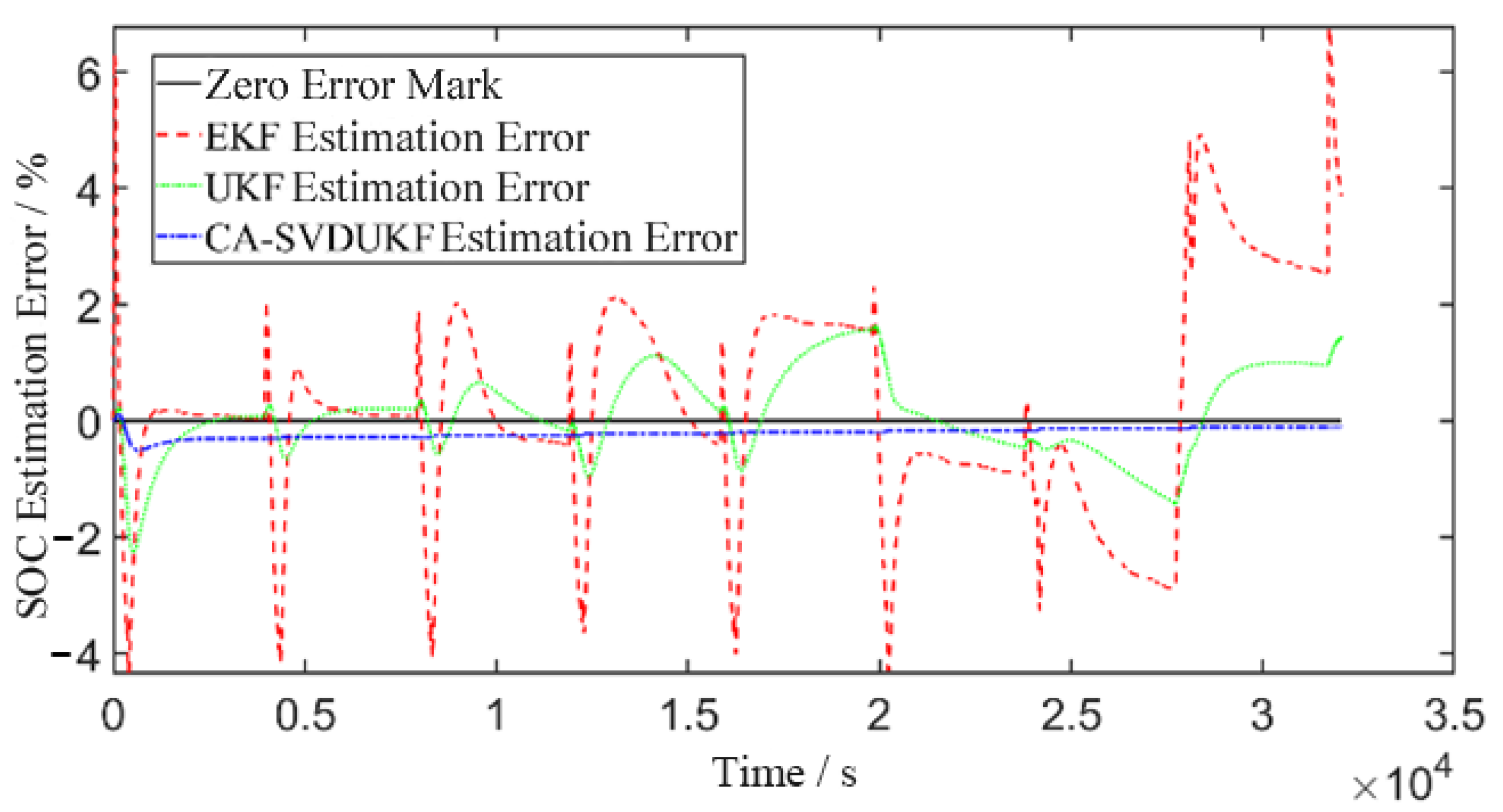
5.1. Standard Pulse Discharge Condition
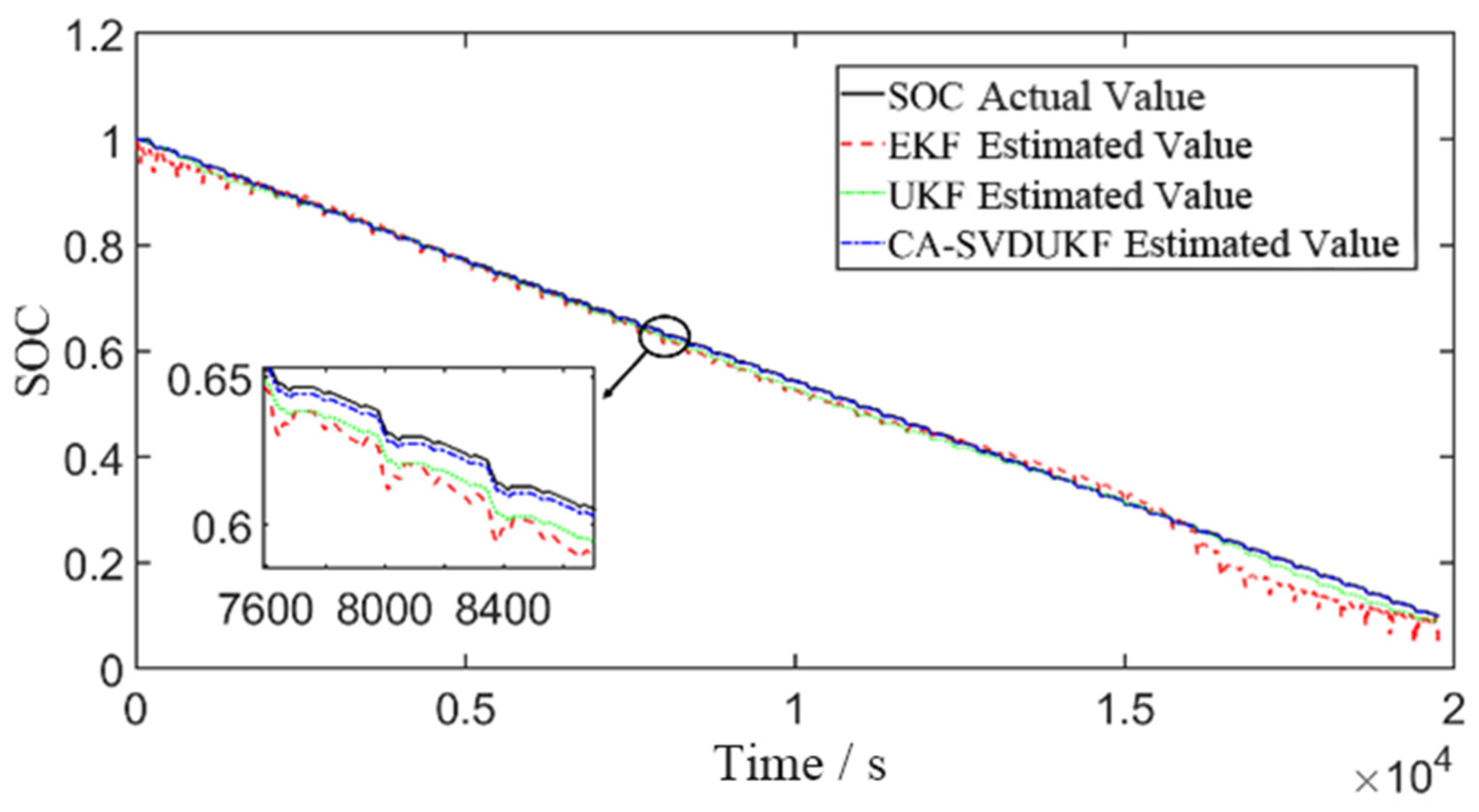
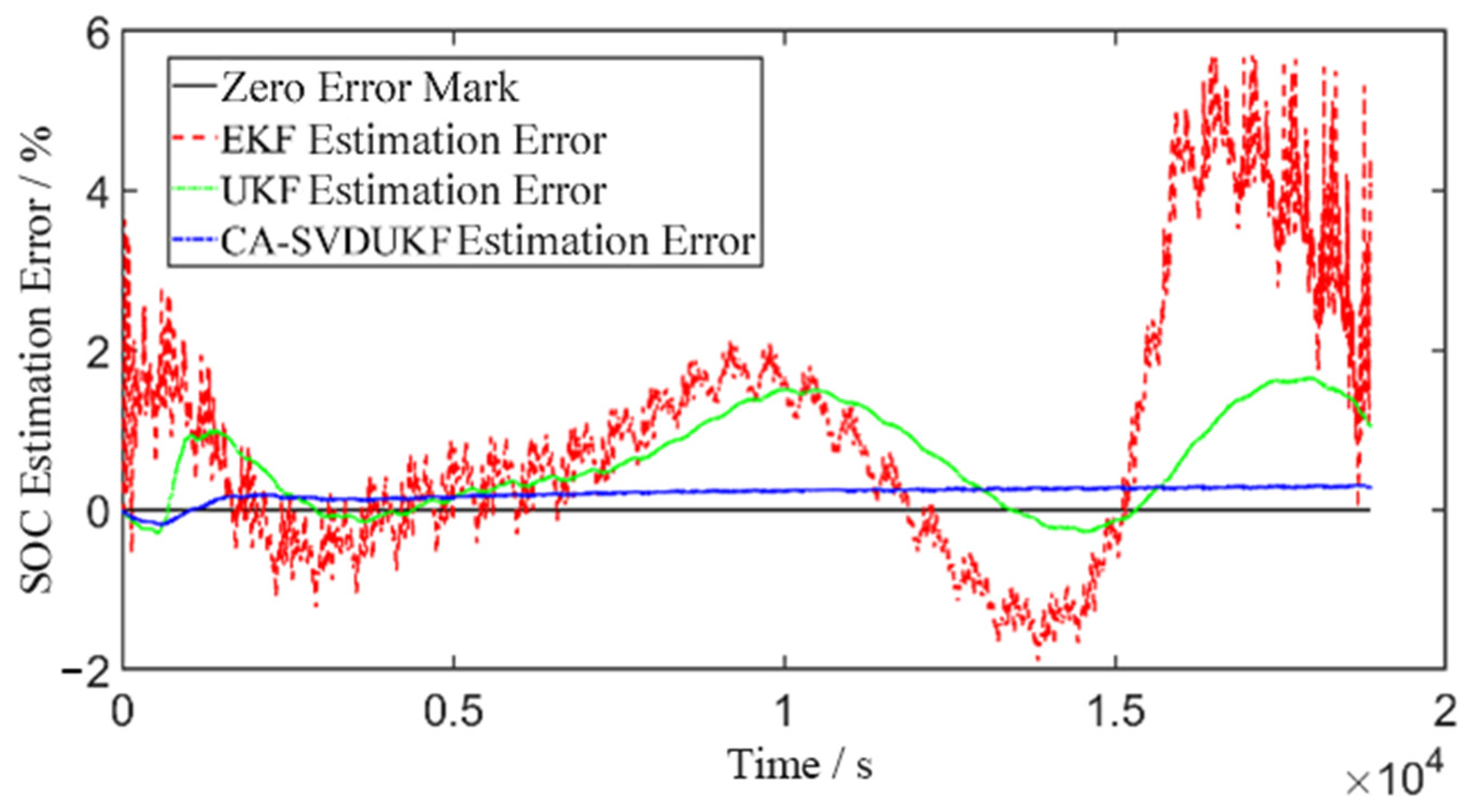
5.2. DST Condition
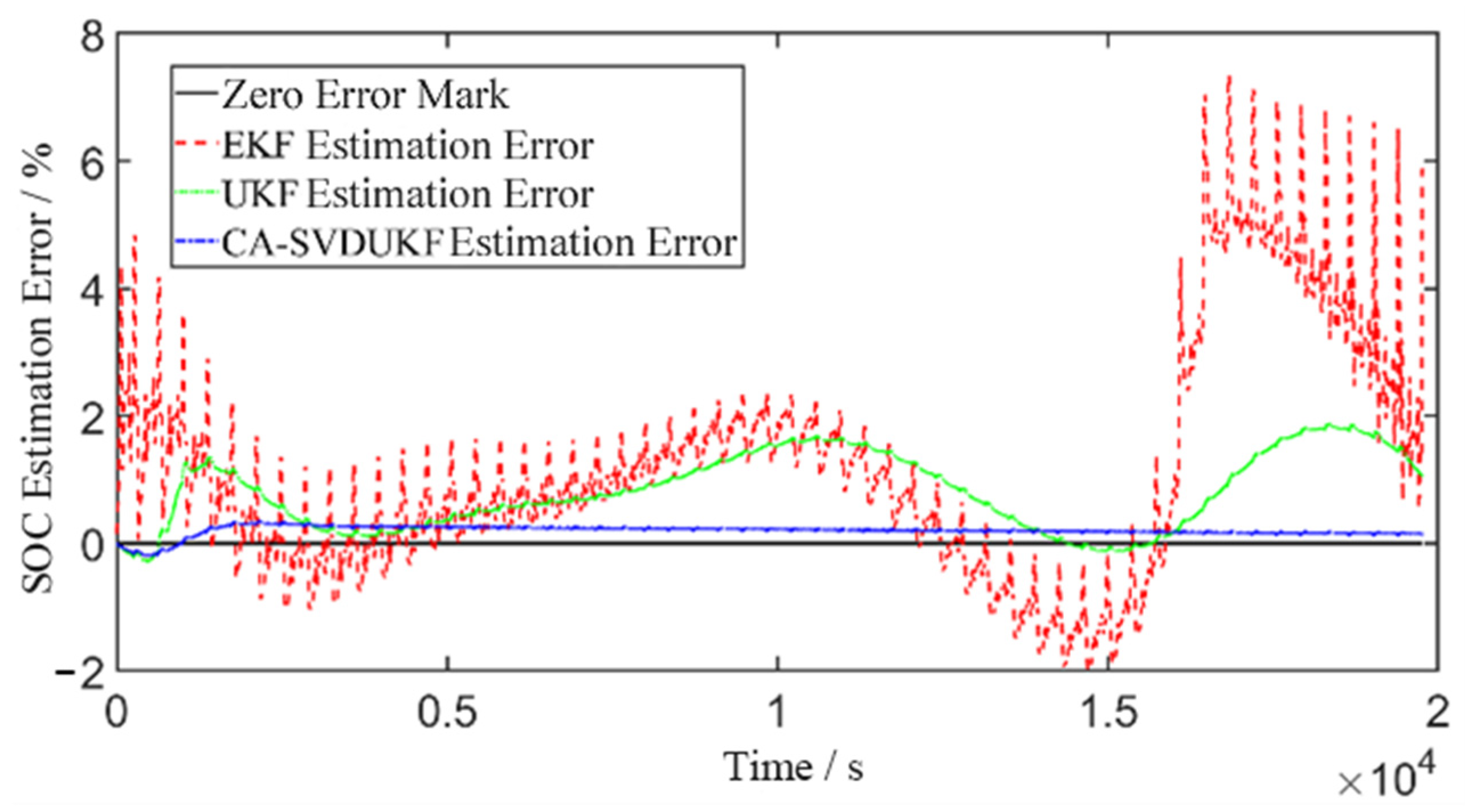
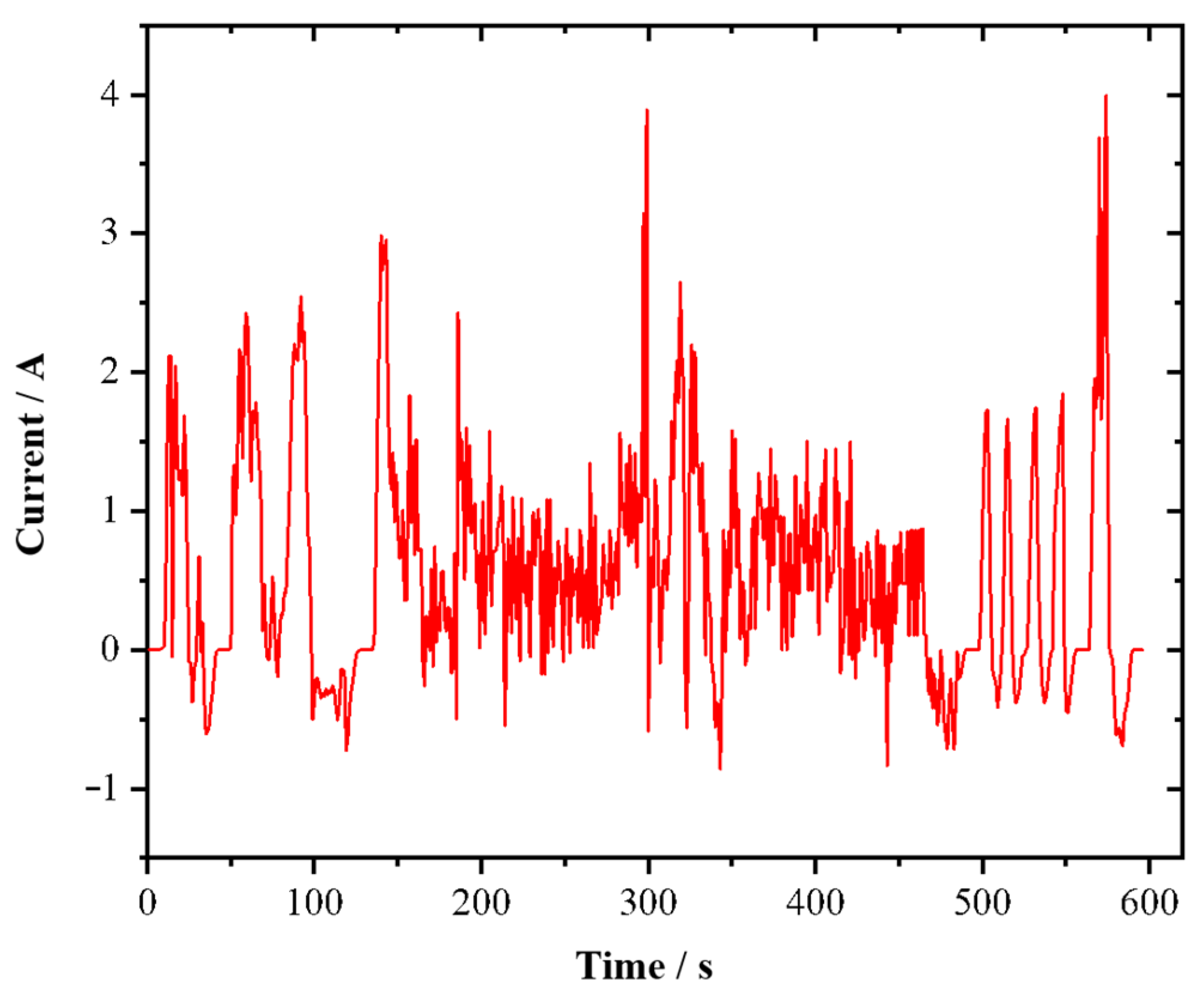
5.3. US06 Condition
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shen, M.; Gao, Q. A review on battery management system from the modeling efforts to its multiapplication and integration. Int. J. Energy Res. 2019, 43, 5042–5075. [Google Scholar] [CrossRef]
- Yu, Y.; Qian, X.; Yang, G. Accurate estimation of charge state of lithium battery based on fuzzy control. Electron. Meas. Technol. 2018, 41, 7–11. [Google Scholar] [CrossRef]
- Wu, X.; Li, X.; Du, J. State of Charge Estimation of Lithium-Ion Batteries Over Wide Temperature Range Using Unscented Kalman Filter. IEEE Access 2018, 6, 41993–42003. [Google Scholar] [CrossRef]
- Ali, M.U.; Zafar, A.; Nengroo, S.H.; Hussain, S.; Alvi, M.J.; Kim, H.-J. Towards a Smarter Battery Management System for Electric Vehicle Applications: A Critical Review of Lithium-Ion Battery State of Charge Estimation. Energies 2019, 12, 446. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- How, D.N.; Hannan, M.A.; Lipu, M.H.; Ker, P.J. State of Charge Estimation for Lithium-Ion Batteries Using Model-Based and Data-Driven Methods: A Review. IEEE Access 2019, 7, 136116–136136. [Google Scholar] [CrossRef]
- Wang, W.; He, F.; Jiang, X.; Zheng, Y.L. Research on state of charge estimation of lithium battery based on double extended Kalman filter. Electron. Meas. Technol. 2020, 43, 49–52. [Google Scholar] [CrossRef]
- He, Z.; Li, Y.; Sun, Y.; Zhao, S.; Lin, C.; Pan, C.; Wang, L. State-of-charge estimation of lithium ion batteries based on adaptive iterative extended Kalman filter. J. Energy Storage 2021, 39, 102593. [Google Scholar] [CrossRef]
- Gao, J.; Ai, T.; Xu, X.; Wang, F.F. Accurate SOC Estimation of the Lithium Iron Phosphate Battery Based on UKF. Electron. Meas. Technol. 2018, 41, 12–16. [Google Scholar] [CrossRef]
- An, Z.; Tian, M.; Zhao, L.; Chen, X.; Li, Y.; Si, X. SOC estimation of lithium battery based on adaptive untracked Kalman filter. Energy Storage Sci. Technol. 2019, 8, 856–861. [Google Scholar] [CrossRef]
- Zou, L.; Liu, J.; Ma, G.; Lang, J. Estimation of state of charge of lithium battery based on dual unscented Kalman filter. Chin. J. Power Sources 2021, 45, 450–454. [Google Scholar] [CrossRef]
- Deng, M.; Min, Q.; Yang, G.; Yu, M. Kalman Filter Estimation of Lithium Battery SOC Based on Model Capacity Updating. Energy Eng. 2022, 119, 739–754. [Google Scholar] [CrossRef]
- Dhanagare, T.; Singh, S.; Pandey, V. An Lstm-Driven Simulation Approach for Soc & Soh Estimation of a Lithium-Ion Cell. In Proceedings of the 2023 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Boston, MA, USA, 20–23 August 2023; Volume 5. [Google Scholar]
- Xing, L.; Ren, H.; Luo, W.; Zhang, Z.; Song, Y. Online estimation of lithium battery SOC based on fractional order FOUKF-FOMIUKF algorithm with multiple time scales. Energy Sci. Eng. 2024, 12, 508–523. [Google Scholar] [CrossRef]
- Wang, X.; Gao, Y.; Lu, D.; Li, Y.; Du, K.; Liu, W. Lithium Battery SoC Estimation Based on Improved Iterated Extended Kalman Filter. Appl. Sci. 2024, 14, 5868. [Google Scholar] [CrossRef]
- Li, H.; Chen, F.; Xu, T.; Luo, S.; Mao, Y. Estimation of the state of charge of lithium batteries based on EKF-AEKF. Appl. Technol. 2024, 51, 102–108. [Google Scholar]
- Son, D.; Park, S.; Oh, J.; Lee, T.; Kim, S.W. Physics-informed dual-stage network for lithium-ion battery state-of-charge estimation under various aging and temperature condition. Appl. Energy 2025, 401, 126770. [Google Scholar] [CrossRef]
- Wu, L.; Wei, X.; Lin, C.; Huang, Z.; Fan, Y.; Liu, C.; Fang, S. Battery SOC estimation with physics-constrained BiLSTM under different external pressures and temperatures. J. Energy Storage 2025, 117, 116205. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison study on the battery models used for the energy management of batteries in electric vehicles. Energy Convers. Manag. 2012, 64, 113–121. [Google Scholar] [CrossRef]
- You, D.; Liu, P.; Shang, W.; Zhang, Y.; Kang, Y.; Xiong, J. An Improved Unscented Kalman Filter Algorithm for Radar Azimuth Mutation. Int. J. Aerosp. Eng. 2020, 2020, 8863286. [Google Scholar] [CrossRef]
- Xie, Y.; He, Z.; Chen, D.; Zhou, H. SOC Estimation of Power Battery Based on AUKF. J. Beijing Jiaotong Univ. 2018, 42, 129–137. [Google Scholar] [CrossRef]

| Parameter of Apparatus | Specification |
|---|---|
| Model | MACCOR M4300 |
| Number of Independent Test Channels | 8 |
| Voltage Range | 0–5 V |
| Current Range | 60 uA–5 A |
| Minimum Step Time | 5 ms |
| Minimum Pulse Time | 100 us |
| Current Resolution/Accuracy | 16 Bit/±0.01% FS |
| Voltage Resolution/Accuracy | 0.076 mV/±0.02% FS |
| Battery Parameters | Specification |
|---|---|
| Rated Capacity | 3.4 Ah |
| Maximum/Minimum Voltage | 4.2 V/2.5 V |
| Nominal Voltage | 3.6 V |
| Cathode/Acceptor | Nickel–cobalt–aluminum oxide lithium/graphite |
| Weight | 48.5 g |
| Temperature Range | −20–60 °C |
| SOC Interval (%) | R0 (Ω) | R1 (Ω) | C1 (F) | R2 (Ω) | C2 (F) |
|---|---|---|---|---|---|
| 90–100 | 0.0132 | 0.0085 | 2150 | 0.0179 | 1480 |
| 80–90 | 0.0137 | 0.0089 | 2105 | 0.0185 | 1492 |
| 70–80 | 0.0143 | 0.0093 | 2070 | 0.0192 | 1505 |
| 60–70 | 0.0149 | 0.0098 | 2030 | 0.0201 | 1523 |
| 50–60 | 0.0156 | 0.0103 | 1992 | 0.0210 | 1538 |
| 40–50 | 0.0164 | 0.0109 | 1950 | 0.0220 | 1550 |
| 30–40 | 0.0173 | 0.0115 | 1908 | 0.0230 | 1567 |
| 20–30 | 0.0181 | 0.0122 | 1867 | 0.0243 | 1580 |
| 10–20 | 0.0190 | 0.0129 | 1820 | 0.0255 | 1602 |
| Parameter | EKF/UKF Value | Notes |
|---|---|---|
| Initial SOC estimate | 100% | Same for all algorithms |
| Initial polarization voltages | 0 V | For both RC branches |
| Initial state error covariance (P_0) | diag ([1 × 10−4, 1 × 10−4, 1 × 10−2]) | Corresponds to [V1, V2, SOC] |
| Process noise covariance (Q) | diag ([1 × 10−6, 1 × 10−6, 1 × 10−6]) | Tuned for stability and responsiveness |
| Measurement noise covariance (R) | 1 × 10−3 | Based on experimental noise characterization |
| Sampling interval | 1 s | Fixed across all experiments |
| OCV–SOC lookup | Pulse-derived and curve-fitted | Same lookup used across all filters |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, J.; Yang, K.; Hu, X. Research on SOC Estimation of Lithium-Ion Battery Based on CA-SVDUKF Algorithm. Batteries 2025, 11, 435. https://doi.org/10.3390/batteries11120435
Cheng J, Yang K, Hu X. Research on SOC Estimation of Lithium-Ion Battery Based on CA-SVDUKF Algorithm. Batteries. 2025; 11(12):435. https://doi.org/10.3390/batteries11120435
Chicago/Turabian StyleCheng, Jinrun, Kuo Yang, and Xing Hu. 2025. "Research on SOC Estimation of Lithium-Ion Battery Based on CA-SVDUKF Algorithm" Batteries 11, no. 12: 435. https://doi.org/10.3390/batteries11120435
APA StyleCheng, J., Yang, K., & Hu, X. (2025). Research on SOC Estimation of Lithium-Ion Battery Based on CA-SVDUKF Algorithm. Batteries, 11(12), 435. https://doi.org/10.3390/batteries11120435






