Abstract
We present detailed first-principles density functional theory-based studies on RbRE2Fe4As4O2 (RE = Sm, Tb, Dy, Ho) hybrid 12442-type iron-based superconducting compounds with particular emphasis on competing magnetic interactions and their effect on possible magneto-structural coupling and electronic structure. The stripe antiferromagnetic (sAFM) pattern across the xy plane emerges as the most favorable spin configuration for all the four compounds, with close competition among the different magnetic orders along the z-axis. The structural parameters, including arsenic heights, Fe-As-Fe angle, and other relevant factors that influence superconducting T and properties, closely match the experimental values in stripe antiferromagnetic arrangement of Fe spins. Geometry optimization with inclusion of explicit magnetic ordering predicts a spin–lattice coupling for all the four compounds, where a weak magneto–structural transition, a tetragonal-to-orthorhombic structural transition, takes place in the relaxed stripe antiferromagnetic spin configuration. Absence of any experimental evidence of such structural transition is possibly an indication of nematic transition in RE-12442 compounds. As a result of structural distortion, the lattice contracts (expands) along the direction with parallel (anti-parallel) alignment of Fe spins. Introduction of stripe antiferromagnetic order in Fe sub-lattice reconstructs the low-energy band structure, which results in significantly reduced number of bands crossing the Fermi level. Moreover, the dispersion of bands and their orbital characteristics also are severely modified in the stripe antiferromagnetic phase similar to BaFeAs. Calculations of exchange parameters were performed for all the four compounds. Exchange coupling along the anti-parallel alignment of Fe spins J is larger than that for the parallel aligned spins J. A crossover between the super-exchange-driven in-plane next-nearest-neighbor exchange coupling J and in-plane exchange coupling J due to lanthanide substitution was found. A large super-exchange-driven next-nearest-neighbor exchange interaction is justified using the construction of 32 maximally localized Wannier functions, where the nearest-neighbor Fe-As hopping amplitudes were found to be larger than the nearest- and the next-nearest-neighbor Fe-Fe hopping amplitudes. We compare the hopping parameters in the stripe antiferromagnetic pattern with non-magnetic configuration, and increased hopping amplitude was found along the anti-parallel spin alignment with more majority-spin electrons in Fe d and d but not in Fe d. On the other hand, the hopping amplitudes are increased in stripe antiferromagnetic phase along the parallel spin alignment with more majority-spin electrons in only Fe d. This difference in hopping amplitudes in the stripe antiferromagnetic order enables more isotropic hopping.
1. Introduction
The high-temperature iron-based superconductors (FeSCs) exhibit peculiar phase diagrams where tunable structural, magnetic and superconducting states play an intricate interconnecting role [1]. Superconductivity (SC) emerges in most of the FeSCs with disappearance of static magnetic order in their parent compounds; however, many FeSCs show coexistence of SC with long-range magnetic order [2,3,4,5,6]. FeSCs are generally categorized into distinct families based on the chemical proportions of constituent atoms found within a single formula unit of these compounds, such as 122 (BaFe2As2, KFe2As2, etc.), 1111 (SmFeAsO, ThFeAsN, etc.), 11 (FeSe, FeTe, etc.), 111 (LiFeAs, NaFeAs, etc.) and 245 (Rb2Fe4Se5, K0.8Fe1.60Se2, etc.). This classification aids in identifying common characteristics, studying superconducting properties, electronic structures and potential applications within each family. Neutron diffraction studies on 122, 111 and 1111 compounds have revealed the collinear AF order in their parent compounds except in LiFeAs, which is a superconducting compound but does not show any magnetic order [1]. The close coupling of magnetism and structural transition has been experimentally demonstrated frequently in FeSCs. The magnetic phase transition occurs simultaneously with a structural distortion in the 122 family of FeSCs [7,8]. For example, SrFeAs exhibits a close coupling between the appearance of magnetic order and tetragonal-to-orthorhombic structural transition [9]. On the other hand, structural transition is succeeded by the magnetic transition in 1111, 111 and 245 family [10] compounds. In 1111-type FeSCs [10], the structural distortion takes place at a temperature about 20–30 K higher than that at which magnetic transition takes place. Electronic nematicity is the lowering of the discrete rotational symmetry of a crystalline solid caused by electronic correlations. The point-group symmetry of the tetragonal FeSCs is lowered by such coincidental or succeeding structural transition to orthorhombic and is known to be driven by an electronic mechanism [11,12,13,14,15,16].
The newly discovered hybrid 1144 and 12442 FeSCs unlock a new avenue to investigate the existing orders and the consequent intriguing aspects related to the fundamentals of high-Tc SC. Stoichiometric AeAFeAs (Ae = Ca, Sr; A = K, Rb, Cs) does not show any structural or magnetic phase transition below 300 K [17]. Interestingly, electron and hole doping by substitution at the Fe site of 1144 compounds induce the magnetic order which coexists with SC. The suppression of magnetic moment below T in Ni-doped 1144 suggests competition and coexistence of a magnetic order with SC, and such suppression of ordered magnetic moment is not seen in Mn-doped counterparts, where Mn dopants may act as local magnetic impurities rather than hole dopants [18]. The newly discovered family of hybrid 12442 compounds are the result of intergrowth of 1111 and 122 FeSCs; these are the only materials which contain double Fe-As layers in between the two neighboring insulating layers. The 12442 FeSCs do not have an established phase diagram yet; nevertheless, transport measurements suggest no sign of magneto-structural phase transition in parent and Co-doped KCaFeAsF [19]. Mössbauer’s study observed a singlet pattern in RbREFeAsO (RE = Sm, Tb, Dy, Ho) compounds down to 5.9 K, indicating absence of any long-range static magnetic order [20]. Earlier in a Mössbauer study, no sign of magnetic ordering was observed above 4.2 K in iron chalcogenide FeSe [21]; however, the structural transition occurs at 90 K without any observed long-range magnetic order. Recent neutron and Raman scattering experimental studies on FeSe suggest a nearly frustrated stripe antiferromagnetic (sAFM) order [22,23]. The question of whether magnetic instability similar to FeSe is also present in hybrid 12442 compounds is yet to be addressed, and efforts are being made to understand the different phases that can exist at different conditions in these new and complex materials.
In the present paper, we investigated various magnetic interactions, their effects on the corresponding electronic structure and possibility of occurrence of structural phase transition in recently discovered self-hole-doped RbREFeAsO (RE = Sm, Tb, Dy, Ho) compounds. These compounds are hybrid structures formed through the intergrowth of already known RbFeAs and REFeAsO superconductors. The unit cell of all the compounds is composed of double FeAs layers, which are separated by an insulating REO layer. All the compounds are self-hole-doped hybrid superconductors with ∼0.25 holes/Fe atom. The superconducting critical temperature () of these compounds in increasing (decreasing) order of atomic number (ionic radius) of RE atoms (RE = Sm, Tb, Dy, Ho) is 35.8, 34.7, 34.3 and 33.8 K, respectively [24]. Several inelastic neutron scattering investigations indicate magnetism as a common origin of the SC pairing in iron-based superconductors, and a large number of intensive studies have been performed on magnetic properties of these systems [25,26,27]. These investigations bring out the importance of interplay between SC and magnetism in these compounds. It is worth investigating the role of magnetic interactions in rare-earth-containing hole-doped 12442 iron-based compounds. It was observed that lanthanide magnetism has negligible influence on the superconducting critical temperature of RbREFeAsO [24]. Explicit inclusion of magnetic ordering in the Fe sub-lattice and its effect on structural parameters was studied in the present work using collinear spin polarized DFT calculations, which resulted in sAFM as the magnetic ground state for all the four compounds. We further relaxed the structure and found that sAFM emerges as the lowest energy state among all the considered relaxed magnetic configurations.
A significant reduction in pnictogen height in the GGA calculated relaxed structure is seen in many iron-based superconductors, which is associated with the influence of strong magnetic fluctuations in FeSC [28,29,30,31]. It was found in electron-doped 12442 FeSC that incorporating magnetic ordering in Fe lattice results in accurate anion heights. Spin polarized DFT calculations on an electron-doped 12442 iron-based superconductor BaThFeAs(NO) showed close agreement of structural parameters with the experimental data in the ground state: sAFM [32]. Anion heights h, h as well as lattice parameters and atomic positions of fully relaxed structure were very close to the experimental data. Earlier, first-principles calculations on RbGdFeAsO [33] and KCaFeAsF [34] predicted sAFM as the lowest energy configuration. Hence, it was speculated that these 12442 compounds may undergo a tetragonal-to-orthorhombic structural transition at low temperatures. The classical stability condition for the sAFM state is J> J/2. Spins in stripe spin configuration are aligned antiferromagnetically along the diagonal direction due to a large next-nearest-neighbor exchange coupling J, resulting in parallel and anti-parallel alignment of spins along a/b axes, respectively. Thus, the J interaction cannot be defined, and the system is called frustrated. sAFM order with ordering wave vector (, ) results from interlocking of two AFM Néel sub-lattices with AFM wave vector (, 0). Frustration in the system is known to be usually destroyed by either a structural distortion or by an effective spin–spin interaction mediated by quantum and thermal fluctuations of the spins [7]. Work by P. Chandra and co-workers showed earlier that in the process of gluing two Néel sub-lattices together one can also have the Ising-nematic term, which has the same symmetry as that of the tetragonal-to-orthorhombic phase transition [35]. Taking into consideration the possibility of coupling between structural and magnetic phase leading to transition from tetragonal (I4/mmm) to orthorhombic (Cmme) structural symmetry, we performed full structural optimization for all the lattice parameters, angles and atomic positions. All our geometry optimization calculations are based on the experimentally obtained room temperature crystallographic data of RbREFeAsO compounds [24] as input. Results of first-principles calculations in the sAFM phase indicates that the symmetry indeed changes from tetragonal to orthorhombic in the sAFM phase for all the four compounds. Furthermore, the calculated structural parameters in relaxed sAFM configuration are closer to the experimental value than in any other spin configuration.
A general description of the effect of sAFM order on the electronic structure of RE12442 compounds is presented along the high-symmetry axes. In high-resolution measurements it was observed earlier that, due to the stripe magnetic order, the electronic structure changes severely in BaFeAs [36]. By comparing the results with first-principles calculations, they argued that in general it is magnetism, rather than orbital/nematic ordering, that primarily reconstructs the low-energy electronic structure in BaFeAs. In a similar manner, band structure is affected severely in present study on hybrid 12442 compounds due to the effect of sAFM order. In accordance with earlier theoretical prediction [37], we see reconstruction of the low-energy electronic structure with formation of Dirac-like dispersion along the high-symmetry axis. The essential microscopic Hamiltonian for both non-magnetic (NM) and magnetic phases is also further presented. The comparison of tetragonal NM hopping parameters with those of sAFM ordering indicates the presence of anisotropic spin ordering and may open an additional route for d-d and d-d hopping for majority-spin electrons along the anti-parallel and parallel alignment of Fe spins, respectively. Furthermore, our study elaborates the role of substitution on the strength of exchange interaction and elucidates its effects on physical properties.We calculated the in-plane and out-of-plane spin interactions. A large next-nearest-neighbor in-plane exchange coupling parameter J was found for all the four compounds. In order to illustrate the microscopic origin of larger next-nearest neighbor exchange interactions between the Fe spins, we describe a 32-band model with five Fe-d and three As-p orbitals for each Fe and As atom. The Hamiltonian was constructed on the maximally localized Wannier function basis, which includes essential low-energy physics corresponding to the interaction between Fe spins.
The rest of this manuscript is organized as follows. The computational methods used are provided in Section 2. The ground-state energy among all the considered spin configurations and their effect on structural parameters are presented in Section 3. We found sAFM as the magnetic ground state for all the four 12442 compounds. Geometry optimization, considering explicit magnetic ordering, reveals a spin–lattice coupling in all the four compounds. Structural transition occurs from a tetragonal to an orthorhombic structure in the relaxed sAFM spin configuration. Furthermore, the general description of the electronic structure due to sAFM ordering is provided using the electronic band structure and low-energy tight-binding Hamiltonian in Section 4 and Section 5, respectively. The introduction of sAFM order in the iron (Fe) sub-lattice leads to a reconstruction of the low-energy band structure, resulting in a significantly reduced number of bands crossing the Fermi level (Fl). Additionally, the dispersion and orbital characteristics of the bands undergo significant modifications in the sAFM phase. The influence of magnetic order on the Fe-Fe hopping processes is studied using Wannier function representation, which is based on the twenty Fe 3d orbitals. By studying the strength and spin dependence of Fe-Fe hopping processes, we deepen our understanding of the electronic and magnetic properties in materials with magnetic order. We found an isotropic hopping in both the x- and y-direction due to introduction of stripe magnetic order in the Fe sub-lattice. The effect of introducing stripe magnetic order is that significant hopping amplitudes were found along both the anti-parallel or parallel alignment of spins, thus opening an additional hopping route for electrons. Such modification of hopping parameters is due to explicitly introducing anisotropic magnetic ordering (sAFM) in the Fe sub-lattice. Results of mapping the DFT energies with those of Heisenberg Hamiltonian are presented in Section 6. The classical stability conditions for the sAFM state in the low-temperature orthorhombic structure are J > J and J > J/2, which were found to be satisfied for all the four RE12442 compounds. In Section 7, we provide conclusions of our first-principles studies.
2. Computational Methods
Density-functional-theory-based first-principles calculations were performed for RbRE FeAsO (RE = Sm, Tb, Dy, Ho) iron-based superconductors. All the DFT-based ab initio calculations were performed using Quantum Espresso suite [38], which is based on a plane wave pseudopotential method. The generalized gradient approximation (GGA) was implemented in the electronic exchange correlation with the Perdew–Burke–Enzerhof (PBE) functional [39]. The chosen pseudopotential within GGA in the DFT approach exhibits satisfactory accuracy, as evidenced in Appendix A.4; a close agreement between the optimized structures of the compounds and the measured ones was found. Geometry optimization was performed under the Broyden–Fletcher–Goldfrab–Shanno (BFGS) scheme with the experimental structure as the initial input [24]. The convergence threshold on total energy (a.u) and forces (a.u) is and , respectively, for optimizing the structures. Spin ordering is explicitly defined for FM, c-AFM, s-AFM1, s-AFM2 and s-AFM3 magnetic configurations, where s-AFM magnetic unit cells are that of the conventional chemical unit cell. The plane wave cut-off energy (E) for Kohn–Sham valence states was taken as 60 Ry for all the four compounds after performing a rigorous convergence test. We employed the WANNIER90 package [40] implemented in Quantum Espresso suite to simulate the low-energy tight-binding model.
3. Magnetic Ground State and Structural Phase Transition
Magnetic order and its implications on physical properties such as structural parameters and electronic structure are so far not studied for recently discovered RbREFeAsO compounds. There exists no established phase diagram of the youngest 12442 family of FeSCs. Therefore, it is worth investigating the existing ground-state magnetic order and the modification of structural parameters due to magnetic order in the Fe square sub-lattice. For this purpose, we first examined the relative total energies of different possible magnetically ordered arrangements of four self-hole-doped 12442 compounds. In the magnetic unit cell, the c axis remains the same as in the conventional unit cell, whereas the a and b axes are rotated by 45 in the x-y plane, and their magnitude is times that of a and b axes of the conventional unit cell, respectively (Figure 1). Thus, the number of atoms in the magnetic unit cell are four times that in the primitive chemical unit cell. Spin is flipped either up or down at each magnetic center to obtain ferromagnetic and distinctly arranged antiferromagnetic unit cells. All the nearest-neighbor spins are antiferromagnetically aligned along the x-, y- and z-directions in the c-AFM configuration. Spins in three arrangements, s-AFM1, s-AFM2 and s-AFM3, are identical in the xy plane and are aligned antiferromagnetically along the x-axis and ferromagnetically along the y-axis. The difference between these three configurations is that they have different spin arrangements along the z-axis. Although the magnetic unit cells of only the s-AFM configuration are two times those of their conventional chemical unit cell, for the purpose of relative comparison of energies, we constructed non-magnetic (NM) and five other magnetic unit cells of the same size.
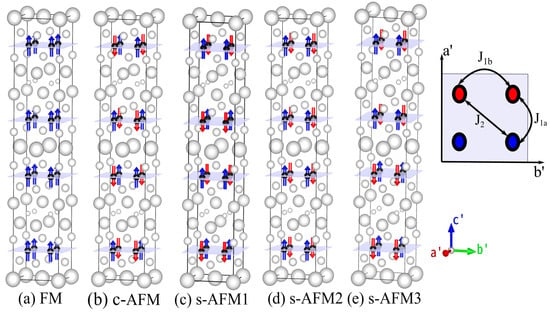
Figure 1.
Arrangement of Fe spins (black atoms) in Fe square lattice is shown for various spin configurations, where other non-magnetic ions are shown with white color. Four exchange parameters corresponding to different distance between magnetic centers are shown. Five different Fe spin configurations are considered to calculate exchange coupling parameters.
We calculated the relative energies incorporating experimental and fully relaxed crystal structure in each spin configuration. In Table 1, calculated relative energies and magnetic moment per Fe site are shown for each compound in NM, FM, cAFM, s-AFM1, s-AFM2 and s-AFM3 spin configurations. All the energies shown in the table are relative to the energy of non-magnetic configuration after optimization. s-AFM configuration is the lowest energy configuration in all the four RbREFeAsO compounds in the experimental as well as in the optimized structure. In the Sm12442 compound, s-AFM3 emerges as the ground-state magnetic order. In contrast, s-AFM1 is the ground-state spin order in other three compounds. The small differences among the energies of three s-AFM configurations indicate that there exists strong competition among different AFM orderings along the z-axis. In Figure 1, all the ground-state energies in the relaxed structure are shown with bold text, and the energies calculated with the tetragonal symmetry constraint are denoted by E. In the relaxed unit cell, the sAFM spin arrangements have energies −1.190 eV, −1.143 eV, −1.118 eV and −1.105 eV relative to the energy of the relaxed NM unit cell for RE = Sm, Tb, Dy and Ho RbREFeAsO compounds, respectively. It is interesting to note that all the spin configurations can be stabilized, with the sAFM configuration having the lowest energy. One can also see that the relative energies of Dy12442 and Ho12442 compounds are close to each other in all configurations. In the last column of Table 1, the magnetic moment (in ) per Fe atom in each relaxed unit cell is shown for all the four RE12442 compounds. The calculated Fe magnetic moment in c-AFM arrangement is larger than that of s-AFM configuration for all the four compounds. The calculated magnetic moments per Fe atom of RbREFeAsO compounds in s-AFM configuration are 1.71, 1.58, 1.54 and 1.52 for RE = Sm, Tb, Dy and Ho, respectively. GGA calculations often overestimate the value of moment as compared to the experimental value in FeSC [31], and the complex nature of spin-fluctuation in these compounds is yet to be comprehended completely [41]. As mentioned earlier, relaxing the lattice parameters and atomic positions in non-magnetic structure results in shortened anion heights in all the four compounds. Consequently, electronic structure calculated with theoretically determined structural parameters differs significantly from that obtained using experimental structure. Hence, in the next step, we illustrate the variation in structural parameters due to the effect of magnetic order. In Table 2, experimental and theoretically calculated structural parameters in various Fe spin configurations for all the four RbREFeAsO compounds are shown. It is conspicuous that the lattice parameters (a, b and c) decrease monotonically in both experimental and calculated non-magnetic structures with decreasing RE radius. Similar to previously studied FeSC, arsenic heights h and h are reduced significantly (by 6 to 10%) in non-magnetic relaxed structure for all the four RbREFeAsO compounds. This deviation of calculated arsenic heights from experimental values has been reported several times in other iron-based superconductors and has been considered to be associated with magnetic fluctuations present in these multi-orbital complex materials [29,42,43,44]. Consequently, the values of and increase in the relaxed NM structure due to reduction in arsenic heights. Furthermore, all the lattice parameters a, b and c are decreased in the NM relaxed structure, and hence the volume of the relaxed cell is also reduced. For example, in RbSmFeAsO, the experimental cell volume is 964.8 Å, which reduces to 938.8 Å in the relaxed NM unit cell. Relaxed structural parameters for the ferromagnetic configuration are shown in Table 2 below the FM column for each RbREFeAsO compound. Arsenic heights decrease even more after geometry optimization in FM configuration. However, changes in lattice parameters, arsenic heights, As-Fe-As angles and two Fe plane distances are smaller in case of the FM configuration as compared to the changes in structural parameters of the NM relaxed unit cell. In the column on the right of FM in Table 2, relaxed structural parameters for cAFM spin configurations are shown. In contrast to NM and FM configurations, lattice parameters a and b are increased in relaxed cAFM spin arrangement for all the four RbREFeAsO compounds, and the lattice parameter c is slightly reduced in all the four 12442 compounds. Arsenic heights in relaxed cAFM unit cell are smaller than experimental value though deviation from experimental height is smaller than those in NM and FM cases in all the four 12442 compounds. Next, we will discuss the calculated structural parameters in the relaxed ground-state sAFM unit cell. For brevity, we only show structural parameters for the lowest energy s-AFM unit cell. In the relaxed s-AFM unit cell, the calculated arsenic heights as well as other structural parameters that are known to control superconducting T are closer to the experimental values than in other relaxed spin configurations. It is evident from Table 2 that d, the two As-Fe-As angles, approach the experimental values in the relaxed s-AFM magnetic unit cell. d is slightly overestimated in the relaxed s-AFM structure and is closer to the experimental value in the optimized unit cell of the c-AFM spin arrangement.

Table 1.
Theoretically calculated relative energies and magnetic moments in various spin configurations for RbREFeAsO compounds.

Table 2.
Comparison of theoretically calculated structural parameters with experimental results of RbREFeAsO.
It is evident from Table 2 that for all the four compounds, the lattice parameter a (b) increases (decreases) in the relaxed s-AFM unit cell. In the relaxed structure, the lattice expands (contracts) along the anti-parallel (parallel) alignment of the Fe spins. Our results indicate the possibility of a structural distortion in all the four compounds, where the crystal symmetry changes from tetragonal to orthorhombic. In order to quantify the variation in crystal symmetry from tetragonal to orthorhombic, we defined a structural distortion parameter = . This parameter is shown in the bottom row of Table 2. Obtained values of in s-AFM spin arrangement are 9.30, 10.2, 9.71 and 10.1 (×) for RE = Sm, Tb, Dy and Ho RbREFeAsO compounds, respectively. Obtained values signify the possibility of spin–lattice interaction leading to tetragonal-to-orthorhombic structural distortion. The structural distortion factor is nearly equal to in all the four compounds, suggesting lanthanide substitution hardly alters the extent of the structural distortion. In a frustrated magnetic state such as sAFM, frustration is usually known to be removed by structural distortion. T. Yildirim [7] demonstrated that an orthorhombic distortion occurs in a sAFM spin configuration employing a spin-Peierles-like model. It is evident from Table 1 that sAFM configuration is the most stable state, where all the axes and angles are free to move during the geometry optimization. Such optimization results in a structural distortion, leading to orthorhombic symmetry of the system. For all the four compounds, the relaxed energy values in Table 1 corresponding to the orthorhombic phase (highlighted in bold text) and tetragonal phase E show that the orthorhombic structural phase is the most stable one. Experimentally, however, SDW order or orthorhombic structural phase was absent in parent and electron-doped KCaFeAsF compounds [19]. The calculated energy differences are nearly equal to 0.5 meV per atom in between the two cases: one when the lattice undergoes tetragonal-to-orthorhombic structural transition and the other when the tetragonal symmetry of the crystal structure remains unchanged. Thus, a structural phase transition from tetragonal to orthorhombic symmetry may be unlikely to occur in these hybrid compounds at finite temperatures. However, experimental studies at low temperatures are desirable to investigate whether any long-range spin ordering or structural distortion takes place in hole-doped RbREFeAsO compounds.
4. Electronic Band Structure
In the previous section, we see in all the four compounds that the sAFM emerges as the most stable configuration in both unit cells obtained before and after the optimization. After the full optimization, the obtained sAFM orthorhombic structural phase is the most stable one, with energy per atom 0.5 meV less than that of tetragonal unit cell. In this section, we highlight the significant influence of stripe antiferromagnetic (AFM) order on the observed variations in the low energy electronic structure. In Figure 2, Figure 3, Figure 4 and Figure 5, the electronic structure enforcing the non-magnetic solution is compared with that of introducing the sAFM order in RE = Sm, Tb, Dy and Ho 12442 compounds, respectively. Non-magnetic orthorhombic calculations result in a band structure typical of hybrid 12442 compounds in Figure 2a, where multiple bands with multi-orbital characteristics cross the Fermi level (Fl) at around the and M-point. However, the orbital characteristics of bands with mixed d/d are now separated due to the orthorhombic structure. In Figure 2a, there are six hole pockets near the -point in the orthorhombic NM phase. Back-folding the four electron bands at the M-point, one might expect a total of ten bands at around the Gamma point in the AFM phase; however, only four bands are crossing the Fermi level (Fl) along the -M. The effect of the AFM ordering is severe, such that none of the bands of the orthorhombic NM phase in Figure 2a, Figure 3a, Figure 4a and Figure 5a are recognizable to bands of the sAFM phase in Figure 2b, Figure 3b, Figure 4b and Figure 5b. In the ground-state s-AFM unit cell, the electron bands at the zone corner M-points are expected to be mapped back to the -point, thus hybridizing strongly with the hole bands at around the -point. Bands crossing the Fl in Figure 2b have dominant d, d and d characteristics. Around the center of the high-symmetry axis -M, four bands cross the Fl. These four bands cross each other at around the center of symmetry axis. In Appendix A.3 Figure A1, there are two bands crossing the Fl along the high-symmetry line -M. The number of bands crossing the Fl in Figure 2b is doubled due to unfolding with slight asymmetric dispersion around the symmetry axis. Surely, backfolding the NM band structure in Figure 2a, one can not obtain the sAFM band structure in Figure 2b; hence, sAFM of RE12442 is not weak coupling SDW. It was shown earlier in the spin density wave state of FeSCs that hybridization of certain bands at exactly the high-symmetry points is forbidden with the nodal nature of SDW state; this leads to the formation of a Dirac-like dispersion localized at the high-symmetry axis [36,37]. The magnetic order completely reconstructs the band structure, and dispersion along all the paths changes considerably. The low-energy electronic structure is altered with a complete change in number of bands crossing the Fl as well as their orbital characteristics and dispersion.
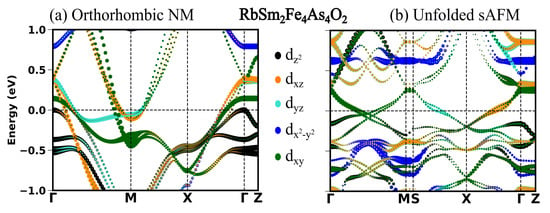
Figure 2.
(a) Orbital projected band structure in orthorhombic NM configuration along high-symmetry points with space group Fmmm and (b) band structure in s-AFM spin configuration in the tetragonal Brillouin zone with space group I4/mmm. The reciprocal lattice points in the Brillouin zone for space group Fmmm are (0, 0, 0), M (0, 0.5, 0.5), X (0.25, 0.25, 0.5), Z (0.5, 0.5, 0.0). The reciprocal lattice points in the Brillouin zone for space group I4/mmm are (0, 0, 0), M (0, 0, 0.5), S (0.25, 0.25, 0.25), X (0.0, 0.5, 0.0), Z (0.5, 0.5, −0.5). The reciprocal points are given in the linear combination of reciprocal lattice vectors of the corresponding primitive cell.
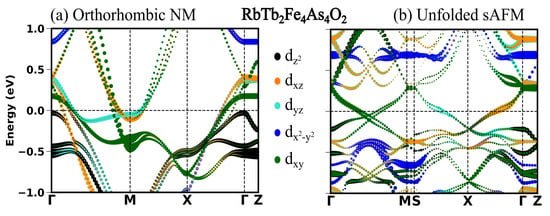
Figure 3.
(a) Orbital projected band structure in s-AFM spin configuration and (b) band structure in NM orthorhombic phase.
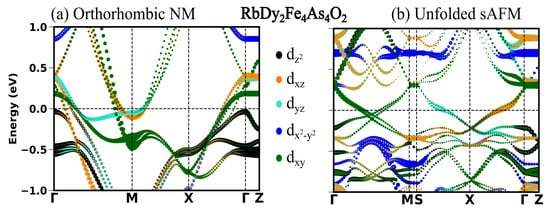
Figure 4.
(a) Orbital projected band structure in s-AFM spin configuration and (b) band structure in NM orthorhombic phase.
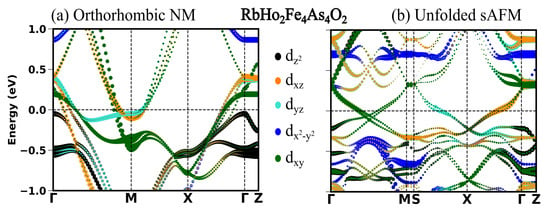
Figure 5.
(a) Orbital projected band structure in s-AFM spin configuration and (b) band structure in NM orthorhombic phase.
5. Tight-Binding Hopping Parameters
In order to study the local effect of anisotropic spin ordering on hopping amplitudes along the x- and y-axis in the stripe phase, the tight-binding Hamiltonian in five Fe-d orbitals was compared for NM and s-AFM phases. In our previous calculations, we calculated nearest-neighbor (NN) and next-nearest-neighbor (NNN) hopping parameters in the non-magnetic unit cell [45], where NN hopping amplitudes were found to be significantly larger than NNN hopping amplitudes. Table 3 and Table 4 present the hopping parameters (in eV) of d, d and d orbitals of the Fe1 atom to all the five Fe d-orbitals of the two nearest-neighbor Fe2, Fe4 atoms and next-nearest neighbor Fe3 atom in Sm12442 and Ho12442 compounds, respectively (see Figure 6 for the definition of Fe atoms). We take the x- and y-axis along the nearest-neighbor Fe-Fe bond as shown in Figure 6. It is evident from Table 3 in the NM phase that t = t = −0.346 eV is greater than t = t = −0.06 eV, where t denotes hopping amplitude of d-d along the y-axis. This indicates that the hopping d-d (d-d) of Fe-d (Fe-d) electrons along the y (x) direction are more favorable along the x (y) direction. Thus, the hopping (through As atoms) of Fe d and d electrons is not isotropic in the NM phase. The equivalence of x- and y-directions is maintained since the hopping of the electrons in the two orbitals occurs in different directions, and global tetragonal symmetry still remains. Further, it is well known fact that phonons can influence the hopping integrals tij [46]. Hence, the modulations found in the hopping integrals due to presence of explicit spin arrangements in sAFM magnetic cell indicate an indirect e–p coupling through the spin-channel (see below), and while the direct impact of the lattice effect on the properties of Fe pnictides is small, e–p coupling through the spin-channel and hence superconductivity might be considerably more significant than usually believed.

Table 3.
The hopping amplitudes (in eV) of d, d and d orbitals of the Fe1 atom to five d-orbitals of its nearest atoms (Fe2, Fe4) and next-neighbor atom Fe3 in the NM and stripe-AFM Fe spin configurations of RbSmFeAsO compound using 20-band model; x-axis is along the nearest neighbor Fe-Fe bond.

Table 4.
The hopping amplitudes (in eV) of d, d and d orbitals of the Fe1 atom to five d-orbitals of its nearest atoms (Fe2, Fe4) and next-neighbor atom Fe3 in the NM and stripe-AFM Fe spin configurations of RbHoFeAsO compound using 5 d-band model; x-axis is along the nearest neighbor Fe-Fe bond.
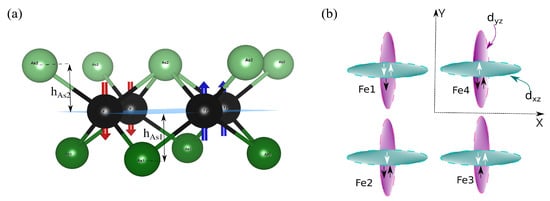
Figure 6.
(a) A side view of Fe-As layer, where Fe and As atoms are shown with black and green colors, respectively. Red and blue arrows indicate down- and upspin, respectively. A typical stripe spin antiferromagnetic (s-AFM) configuration is shown, where the Fe spins are aligned ferromagnetically along the x-direction and antiferromagnetically along the y-direction. (b) Schematic presentation of ferro-orbital ordering of iron atoms in s-AFM configuration, which is a favorable ordering in iron pnictides due to kinetic energy gain from the nearest-neighbor hopping [47].
The change in hopping amplitudes in the s-AFM phase is related to the modification of the corresponding WFs. In Table 3, hopping amplitude t of majority-spin electrons is increased along the anti-parallel alignment of spins (Fe1–Fe2 bond direction) from −0.060 to −0.257 eV; this opens an extra route to electron hopping along the x-direction in addition to the y-direction. The increased hopping amplitudes in s-AFM configuration are shown with bold text. Along the same anti-parallel spin direction, the d-d hopping amplitude of the majority-spin electron increases significantly in the s-AFM case. In the NM configuration, d-d hopping amplitude is the same in both the x- and y-directions due to symmetry, the absolute value of which is 0.178 eV. It is evident in Table 3 that the absolute value increases from 0.178 to 0.344 eV along the anti-parallel spin direction in the s-AFM configuration for majority-spin electrons. This variation indicates a major effect of broken symmetry in the surroundings of the d orbital. It is interesting to note that any such significant change for majority-spin electrons in case of d-d hopping is absent along the anti-parallel Fe spins. Furthermore, the d-d hopping amplitude is increased from 0.06 to 0.23 eV along the parallel spin alignment. In the NM configuration, hoppings between d-d or d-d occur mainly in the y- or x-direction, which can now occur in both directions in the s-AFM phase.
6. Calculation of Exchange Parameters
We determined in-plane nearest-neighbor (NN) interaction (J, J), in-plane next-nearest-neighbor (NNN) interaction (J) and nearest-neighbor interaction along the c-axis (J and J) using the difference of total energies obtained in various spin configurations of Fe sub-lattices. Different spin interactions existing in magnetic structure J, J, J, J and J are distinct according to the physical distances between magnetic centers and their neighboring magnetic centers. In order to calculate the four exchange parameters J, J, J, J and J, we performed spin polarized DFT calculations on six different magnetic unit cells, each having distinctly ordered collinear Fe spin configurations. Exchange interactions J, J and J are defined in Figure 1. J and J are the exchange parameters along the z-direction interaction in alternate layers corresponding to a distance d and d, respectively. In order to calculate the exchange parameters, we employed the following Heisenberg Hamiltonian
where summations in Equation (1) are over distinct pairs of spins. and denote the summation over in-plane nearest and in-plane next-nearest-neighbor, respectively, while denotes the sum over nearest-neighbor pair of spins along the c-axis. S is the magnitude of the spin, and is the unit vector of the ith spin. Throughout the present work, a positive J denotes an antiferromagnetic interaction, whereas a negative J corresponds to a ferromagnetic interaction.
The estimated values of Heisenberg exchange coupling parameters are shown in Table 5 for all the four 12442 compounds, indicating a possible interconnection of T with both the planer as well as out-of-planer magnetic couplings. A large next-nearest-neighbor coupling J is predicted, which is an attribute of iron-based high-T superconductors [48,49]. Cr/Mn-based counterparts of Fe-based compounds do not show high-temperature SC. In contrast to Cr/Mn-based compounds, iron-based superconductors have large next-nearest-neighbor coupling [50]. Prediction of large next-nearest-neighbor (NNN) exchange coupling indicates its essential role in SC. Antiferromagnetic coupling between the nearest-neighbor (NN) spins indicates that the superexchange mechanism is responsible for the interaction. NNN coupling (J) is the result of mainly superexchange interaction due to d–p coupling. The exchange parameter along the anti-parallel spins is larger than the one along the parallel spin alignment. Moreover, J is larger than the NNN exchange parameter J in the Sm12442 compound. However, with lanthanide substitution, the calculated value of NNN coupling parameter J exceeds the NN exchange parameter J in the Tb12442 compound and remains larger than J for other substituted compounds in order of decreasing lanthanide radii. To understand the origin of these exchange interactions, we calculated the charge density and electron localization function in the Fe square plane and along the (001) plane crossing the Fe-As and Sm-O atomic chains in the Sm12442 compound. The areas with high electron localization function (ELF) values indicate the localization of the electron. It is clear from the charge density plot in Figure 7a that only superexchange pairing via As non-magnetic ions is possible along the diagonal Fe-Fe bond, since charge density is negligible between the two diagonals of the Fe square. Therefore, large Fe-As hopping amplitudes and nearly empty charge density around the center of Fe square indicate J is associated with the superexchange coupling mediated via non-magnetic As ions. On the other hand, significant charge is distributed along the nearest Fe-Fe bond; hence, superexchange and direct exchange both together engender nearest-neighbor interaction. However, direct exchange interaction plays a sub-dominant role in pairing between nearest-neighbor spins due to antiferromagnetic ordering of Fe spins along the a-axis and ferromagnetic alignment along the b-axis. Presence of strong Hund’s coupling between Fe spins drives a ferromagnetic alignment of spins, whereas superexchange interaction causes antiferromagnetic alignment of spins. Thus, in the s-AFM ground-state configuration, spins are antiferromagnetically aligned along each diagonal direction and are parallel/anti-parallel along the x/y direction.

Table 5.
Theoretically calculated Exchange parameters for RbREFeAsO compounds.
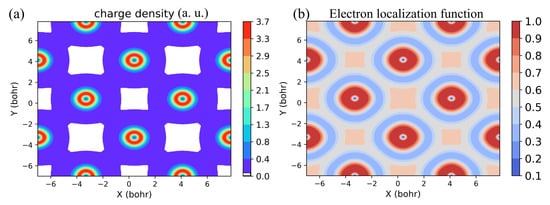
Figure 7.
Total charge-density distribution of RbSmFeAsO (a) in the (001) Fe square lattice plane and (b) electron localization function (ELF) in the (001) plane.
7. Conclusions
In this study, we compared the influence of different magnetic configurations using first-principles methods focused on their relative energies, electronic structure and magneto-structural coupling, leading to the possibility of structural phase transition in four newly discovered hybrid RbREFeAsO (RE = Sm, Tb, Dy and Ho) iron-based superconductors. Explicitly incorporating magnetic order in Fe square lattice results in stripe antiferromagnetic (sAFM) spin configuration as the lowest energy state for all the four 12442 compounds. Arsenic heights as well as the other structural parameters considered crucial in determining superconducting properties of FeSCs are in good agreement with the experimental values in optimized s-AFM unit cell. A spin–lattice interaction was found in all the four compounds, due to which a tetragonal-to-orthorhombic structural transition may occur. The crystals undergo structural distortion from tetragonal to orthorhombic symmetry only in the s-AFM configuration, which suggests that the structural distortion is the manifestation of the frustration due to the nearest-neighbor anisotropic spin configuration in the s-AFM spin arrangement. In the relaxed s-AFM unit cell, the lattice expands along the anti-parallel spins and contracts along the parallel spin alignment. The calculated energy difference in between the relaxed tetragonal and orthorhombic structural phases for the s-AFM spin configuration indicates low possibility of structural transition at sufficiently large temperatures. Such unlikelihood of structural distortion supports the experimental report of the absence of any orthorhombic phase in intrinsically hole-doped 12442 compounds [19].
Similar to previous results in the BaFeAs compound [36], the low-energy electronic structure is severely affected due to explicit introduction of the sAFM order in the Fe sub-lattice. As compared to the NM orthorhombic band structure, the number of bands crossing the Fl, their dispersion along the high-symmetry axes and orbital characteristics are critically modified due to the sAFM order for all the four compounds. Further, tight-binding representation based on DFT Wannier functions of Fe 3d orbitals in both NM and s-AFM configurations provides the effect of anisotropic spin-ordering. In the non-magnetic case, both d and d orbital electrons have different hopping amplitudes corresponding to the x- and y-direction due to the nature of the surroundings of As atoms. In the NM phase of Sm12442, d-d hopping amplitude along the anti-parallel spin direction is 0.06 eV, which is small as compared to the d-d hopping amplitude along the parallel spin direction, which is 0.346 eV. Along the anti-parallel spin direction in the sAFM phase, d-d hopping amplitude of majority-spin electrons increases to 0.257 eV from its NM phase value 0.06 eV. Similarly, d-d hopping amplitude increases from 0.178 eV in the NM phase to 0.344 eV in the sAFM phase along the anti-parallel spin alignment. No change occurs for the d-d hopping along the anti-parallel spin alignment. However, d-d hopping amplitude increases to open an additional route for the electron to hop along the parallel spin direction. The major effect of such a counter-intuitive increase in hopping amplitudes in sAFM ordering is that d and d electrons may hop to both the x- and y-direction, resulting in isotropic hopping.
Furthermore, employing the Heisenberg Hamiltonian, we obtained large next-nearest-neighbor exchange coupling for all the four compounds. Our study predicts that there are strong antiferromagnetic next-nearest-neighbor superexchange interactions between the Fe local moments mediated by As-4p orbitals. The exchange parameter along the anti-parallel alignment of spins J was found to be larger than that along the parallel aligned spins J. The calculated value of J is slightly larger than the NNN exchange parameter J in Sm12442 compound. A crossover in between the J and J was found due to lanthanide substitution. J remains larger than J in all three Tb-, Dy- and Ho-containing 12442 compounds. To understand the origin of these exchange interactions, we calculated charge density in Fe square plane and along the (001) plane crossing the Fe-As and Dy-O atomic chains. It is clear from the charge density plot in Figure 7a that only superexchange pairing via As non-magnetic ions is possible along the diagonal Fe-Fe bond, since charge density is negligible between the two diagonals of the Fe square. Therefore, J is associated with the superexchange coupling mediated via non-magnetic As ions. Prediction of large next-nearest-neighbor (NNN) exchange coupling indicates its essential role in SC. The tight-binding 32-band model fitted using construction of maximally localized Wannier functions provides more insight into the essential physics within the conducting Fe-As layer. Calculated NN Fe-As transfer integrals in the MLWF basis were found to be very large as compared to the NN Fe-Fe hopping amplitudes. Therefore, a large superexchange-driven NNN exchange coupling J was found, where the NN exchange interaction, on the other hand, may be driven by both the direct and superexchange mechanisms.
Author Contributions
Conceptualization, H.G. and A.P.; methodology, H.G.; software, A.P. and S.S.; validation, A.P., A.G. and S.S.; formal analysis, A.P.; investigation, A.P. and A.G.; resources, H.G. and S.S.; data curation, A.P. and S.S.; writing—original draft preparation, A.P. and A.G.; writing—review and editing, H.G.; visualization, H.G.; supervision, H.G.; project administration, H.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was not funded by any specific grant from the public, commercial, or non-profit sectors.
Data Availability Statement
Data will be available upon request.
Acknowledgments
A.P. acknowledges the HBNI and RRCAT for financial support and encouragement. A.P. acknowledges fruitful discussion with Soumyadeep Ghosh. All the authors acknowledge Computer Center RRCAT for providing computational facilities.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. 32-Band Tight-Binding Hamiltonian
In Table A1, tight-binding hopping parameters are presented for NM phase on a total 32 Wannier basis which consists of 20 Fe-d (five d-orbitals for each Fe atom) and 12 As-p (three for each As atom) orbitals. The hopping amplitudes of Table A1 differ from those of earlier shown Table 3 and Table 4 for two reasons. First, projection of arsenic p-orbitals is included in this case, and second, the x- and y-direction are along the diagonal of the Fe square. Hence in this case, both d-d and d-d hopping amplitudes are equal due to symmetry. Fe-As1 and Fe-As2 hopping amplitudes are nearly equal, and hence we present the hopping amplitudes only for Fe-As1. It is conspicuous from Table A1 that the Fe-As2 hoppings are larger than the Fe-Fe hopping amplitudes, since the Fe-As bond length is smaller by 0.4 Å. This large Fe-As hopping indicates electrons hop mainly through As atoms. Moreover, this results in a large next-nearest-neighbor exchange interaction, which is mainly derived from the Fe-As-Fe superexchange, as discussed in Section 6 of the main text.

Table A1.
Nearest-neighbor (NN) hopping parameters (in eV) calculated using 32-band model; x-axis is along the diagonal of Fe square.
Table A1.
Nearest-neighbor (NN) hopping parameters (in eV) calculated using 32-band model; x-axis is along the diagonal of Fe square.
| (a) RbSmFeAsO | |||||
| Nearest-Neighbor (NN) | |||||
| −0.170 | 0.024 | 0.035 | −0.022 | −0.203 | |
| 0.024 | 0.110 | −0.184 | 0.120 | 0.071 | |
| 0.035 | −0.184 | 0.110 | −0.120 | 0.017 | |
| −0.022 | 0.120 | −0.120 | 0.302 | −0.022 | |
| −0.203 | 0.071 | 0.017 | −0.022 | −0.347 | |
| −0.604 | 0.000 | 0.034 | −0.631 | 0.000 | |
| 0.000 | −0.575 | 0.000 | 0.000 | 0.823 | |
| −0.261 | 0.000 | 0.839 | 0.211 | 0.000 | |
| (b) RbTbFeAsO | |||||
| Nearest-Neighbor (NN) | |||||
| −0.182 | 0.021 | 0.028 | −0.021 | −0.208 | |
| 0.021 | 0.120 | −0.185 | 0.111 | 0.062 | |
| 0.028 | −0.185 | 0.120 | −0.107 | 0.010 | |
| −0.021 | 0.111 | −0.107 | 0.329 | −0.020 | |
| −0.208 | 0.063 | 0.010 | −0.020 | −0.355 | |
| −0.847 | 0.000 | −0.088 | −0.908 | 0.000 | |
| 0.000 | −0.550 | 0.000 | 0.000 | 0.765 | |
| −0.270 | 0.000 | 0.830 | 0.212 | 0.000 | |
| (c) RbDyFeAsO | |||||
| Nearest-Neighbor (NN) | |||||
| −0.179 | 0.028 | 0.029 | −0.016 | −0.210 | |
| 0.028 | 0.116 | −0.190 | 0.112 | 0.063 | |
| 0.029 | −0.190 | 0.116 | −0.115 | 0.014 | |
| −0.016 | 0.112 | −0.115 | 0.325 | −0.015 | |
| −0.210 | 0.063 | 0.014 | −0.015 | −0.355 | |
| −0.850 | 0.000 | −0.064 | −0.624 | 0.000 | |
| 0.000 | −0.574 | 0.000 | 0.000 | 0.752 | |
| −0.307 | 0.000 | 0.802 | 0.172 | 0.000 | |
| (d) RbHoFeAsO | |||||
| Nearest-Neighbor (NN) | |||||
| −0.179 | 0.032 | 0.031 | −0.014 | −0.214 | |
| 0.032 | 0.117 | −0.189 | 0.117 | 0.065 | |
| 0.031 | −0.189 | 0.117 | −0.121 | 0.015 | |
| −0.014 | 0.117 | −0.121 | 0.317 | −0.015 | |
| −0.214 | 0.065 | 0.015 | −0.015 | −0.357 | |
| −0.863 | 0.000 | −0.291 | −1.063 | 0.000 | |
| 0.000 | −0.541 | 0.000 | 0.000 | 0.746 | |
| −0.310 | 0.000 | 0.824 | 0.226 | 0.000 | |
Appendix A.2. Calculation of Heisenberg Exchange Parameters
We applied the energy expressions obtained with high spin state S = 2 for Fe per spin site. We see that average magnetic moment per Fe site varies from 0.55 to 1.71 in different spin configurations. The total classical energies of the considered five different magnetic configurations in Figure 1 are
Equating the energy differences between the various magnetic unit cells obtained from the DFT calculations to the corresponding energy differences obtained from the Heisenberg Hamiltonian, we obtain the values of exchange parameters.
Appendix A.3. Electronic Structure in Folded Brillouin Zone
The DOS spectra and band structures in the lowest energy s-AFM configuration are shown in Figure A1, Figure A2, Figure A3 and Figure A4 for all the four RbREFeAsO compounds where RE is Sm, Tb, Dy and Ho, respectively. Total DOS spectra are roughly similar for s-AFM and non-magnetic RbREFeAsO compounds (see Figure A1a, Figure A2a, Figure A3a and Figure A4a). The Fermi level (Fl) is denoted by black dotted vertical line in DOS spectra. Specifically, in all DOS spectra, a valley can be seen near the Fl, where the Fermi level (Fl) is located at the lower slope side of the valley. In Figure A1b, the band structure for s-AFM RbSmFeAsO is presented. Bands cross the Fl along -M, -X and Z-X symmetry paths. Most of the bands are flat along -Z, displaying the quasi-two-dimensional characteristic of electronic structure. As we substituted different lanthanides in the RE site, the total number of the bands crossing the Fl remains the same. At the X-point in Figure A1b, four nearly degenerate bands are just below the Fl for Sm12442 compounds. These four degenerate bands shift close to the Fl with lanthanide substitution. For compound Ho12442, four degenerate bands cross the Fl exactly at the X-point. These bands are now flat around the X-point, which is the band edge Van Hove singularity, thus resulting in increased local DOS at X-point for compound RbHoFeAsO. In Figure A5a–d, orbital projected partial density of states per Fe atom is presented in the s-AFM configuration. It is evident for each compound that the DOS at Fl for downspin is higher than that for the upspin. The Fe majority downspin-channel DOS at Fl is 1.26, 1.25, 1.24, 1.21 states/Fe for RE = Sm, Tb, Dy, Ho 12442 compounds, respectively.
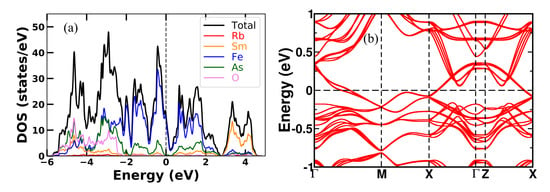
Figure A1.
Calculated (a) density of states and (b) band structure of stripe antiferromagnetic RbSmFeAsO.
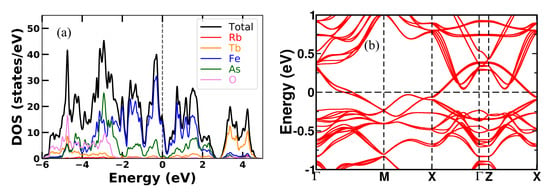
Figure A2.
Calculated (a) density of states and (b) band structure of stripe antiferromagnetic RbTbFeAsO.
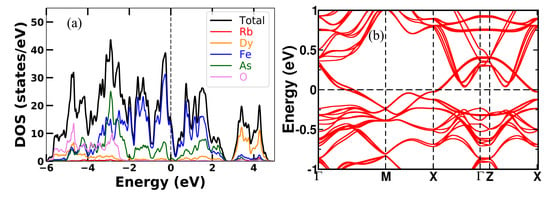
Figure A3.
Calculated (a) density of states and (b) band structure of stripe antiferromagnetic RbDyFeAsO.
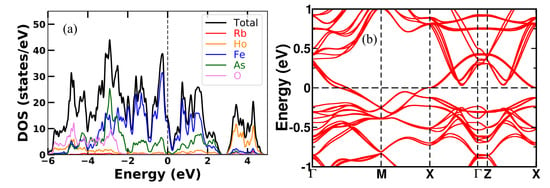
Figure A4.
Calculated (a) density of states and (b) band structure of stripe antiferromagnetic RbHoFeAsO.
Appendix A.4. Effect of On-Site Electron Correlation
We shown in Figure A6 the change in volume due to relaxation of the crystal structure for NM, FM, cAFM and sAFM structures in Sm12442 and Tb12442 compounds. The change in volume is large in NM and FM configurations, while the volumes as well as other structural parameters are closer to the experiment in AFM structures. We further show the reliability of our results with respect to the variation in on-site electron correlation U. In Figure A7, we show GGA+U results with the inclusion of distinct magnetic ordering in Tb12442 compound. A zoomed image at Hubbard U = 0.0 eV is shown in the left side of Figure A7, where sAFM can be clearly seen as the lowest energy spin configuration. In the right side of Figure A7, sAFM remains the lowest energy configuration for the moderate on-site electron correlation U. In Figure A8, the volume difference is shown for non-magnetic primitive unit cells of RE12442 compounds. At U = 0.0 eV, the volume of the relaxed unit cell decreases in all the four compounds by nearly 6 Å. The magnitude of differences in between volumes of relaxed and experimental structures further increases with moderate increase in on-site electron correlation U. Furthermore, we optimized the stripe AFM magnetic cell of Sm12442 with inclusion of on-site Hubbard U. In Figure A9, the volume of the relaxed magnetic unit cell with respect to the volume of experimental unit cell is shown for the Sm12442 compound. It is conspicuous from Figure A9 that the volume of the relaxed unit cell is closer to the measured one at Hubbard U = 0.0 eV. This slight reduction in volume is not an indication of correlation effect but the “Magneto-Volume Effect” in Fe pnictides [46].
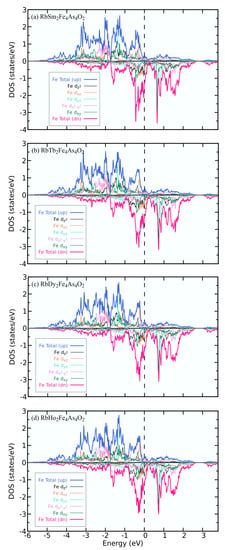
Figure A5.
Spin polarized density of states per Fe atom of RbREFeAsO (RE = Sm, Tb, Dy and Ho) compounds.
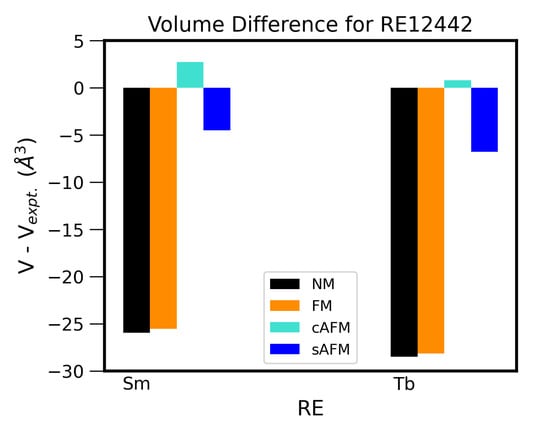
Figure A6.
Volume differences are shown for relaxed crystal structures of RbREFeAsO (RE = Sm, Tb) in different spin configurations with respect to the experimental value.
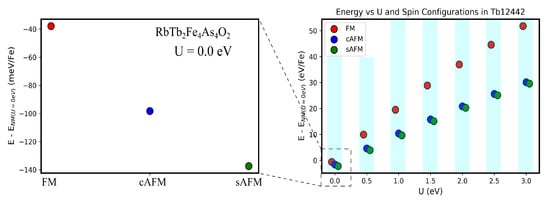
Figure A7.
Energies of three spin configurations, FM (red), cAFM (blue) and sAFM (green) with respect to the NM (non-magnetic) unit cell are plotted against gradually increasing on-site Hubbard correlation U. For better visualization, circles representing each spin configuration are slightly shifted in the x-axis to reduce their overlap, where the value of on-site electron correlation is the same within each vertical stripe.
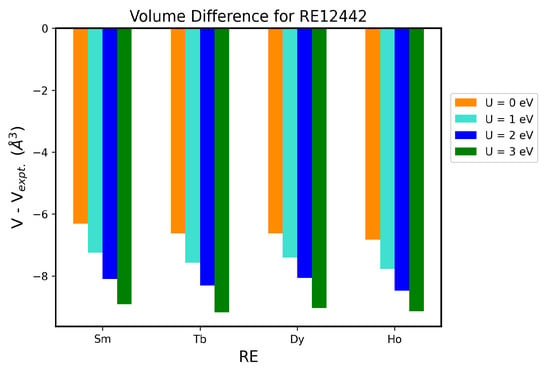
Figure A8.
Volume difference is shown with respect to the experimental volume for relaxed NM primitive unit cell in RbREFeAsO (RE = Sm, Tb, Dy and Ho) for different on-site Hubbard correlation U.
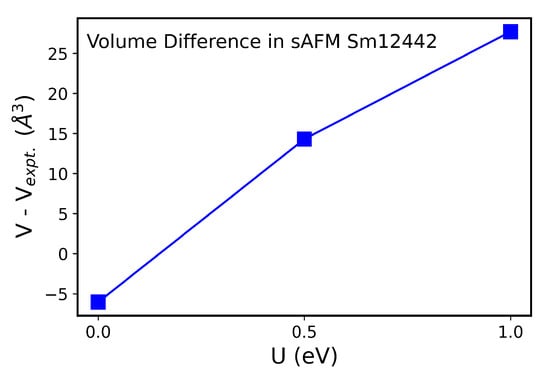
Figure A9.
Change in volume (after optimization) with gradual increase in on-site correlation U (eV) in the sAFM spin configuration of the Sm12442 compound, where volume is subtracted from the experimental value.
References
- Dai, P. Antiferromagnetic order and spin dynamics in iron-based superconductors. Rev. Mod. Phys. 2015, 87, 855. [Google Scholar] [CrossRef]
- Liu, R.H.; Wu, G.; Wu, T.; Fang, D.F.; Chen, H.; Li, S.Y.; Liu, K.; Xie, Y.L.; Wang, X.F.; Yang, R.L.; et al. Anomalous Transport Properties and Phase Diagram of the FeAs-Based SmFeAsO1−xFx Superconductors. Phys. Rev. Lett. 2008, 101, 087001. [Google Scholar] [CrossRef]
- Sasmal, K.; Lv, B.; Lorenz, B.; Guloy, A.M.; Chen, F.; Xue, Y.-Y.; Chu, C.-W. Superconducting Fe-Based Compounds (A1−xSrx)Fe2As2 with A=K and Cs with Transition Temperatures up to 37 K. Phys. Rev. Lett. 2008, 101, 107007. [Google Scholar] [CrossRef]
- Rotundu, C.R.; Keane, D.T.; Freelon, B.; Wilson, S.D.; Kim, A.; Valdivia, P.N.; Bourret-Courchesne, E.; Birgeneau, R.J. Phase diagram of the PrFeAsO1−xFx superconductor. Phys. Rev. B 2009, 80, 144517. [Google Scholar] [CrossRef]
- Huang, Q.; Zhao, J.; Lynn, J.W.; Chen, G.F.; Luo, J.L.; Wang, N.L.; Dai, P. Doping evolution of antiferromagnetic order and structural distortion in LaFeAsO1−xFx. Phys. Rev. B 2008, 78, 054529. [Google Scholar] [CrossRef]
- Kordyuk, A.A. Iron-based superconductors: Magnetism, superconductivity, and electronic structure (Review Article). Low Temp. Phys. 2012, 38, 888. [Google Scholar] [CrossRef]
- Yildirim, T. Frustrated magnetic interactions, giant magneto–elastic coupling, and magnetic phonons in iron–pnictides. Phys. C SC 2009, 469, 425. Available online: https://www.sciencedirect.com/science/article/pii/S092145340900077X (accessed on 15 June 2009). [CrossRef]
- Zhao, J.; Adroja, D.T.; Yao, D.X.; Bewley, R.; Li, S.; Wang, X.F.; Wu, G.; Chen, X.H.; Hu, J.; Dai, P. Spin waves and magnetic exchange interactions in CaFe2As2. Nat. Phys. 2009, 5, 555–560. [Google Scholar] [CrossRef]
- Kaneko, K.; Hoser, A.; Caroca-Canales, N.; Jesche, A.; Krellner, C.; Stockert, O.; Geibel, C. Columnar magnetic structure coupled with orthorhombic distortion in the antiferromagnetic iron arsenide SrFe2As2. Phys. Rev. B 2008, 78, 212502. [Google Scholar] [CrossRef]
- Cruz, C.d.; Huang, Q.; Lynn, J.W.; Li, J.; Zarestky, W.R.I.I.L.; Mook, H.A.; Chen, G.F.; Luo, J.L.; Wang, N.L.; Dai, P. Magnetic order close to superconductivity in the iron-based layered LaO1−xFx FeAs systems. Nature 2008, 453, 899. [Google Scholar] [CrossRef]
- Ghosh, H.; Sen, S.; Ghosh, A. Electronic origin of structural transition in 122 Fe based superconductors. J. Phys. Chem. Solids 2017, 102, 157. [Google Scholar] [CrossRef]
- Sen, S.; Ghosh, H. Nematicity, magnetic fluctuation and ferro-spin-orbital ordering in BaFe2As2 family. J. Alloys Compd. 2016, 675, 416. Available online: https://www.sciencedirect.com/science/article/pii/S0925838816305916 (accessed on 5 August 2016). [CrossRef]
- Fernandes, R.M.; Van Bebber, L.H.; Bhattacharya, S.; Chandra, P.; Keppens, V.; Mandrus, D.; McGuire, M.A.; Sales, B.C.; Sefat, A.S.; Schmalian, J. Effects of Nematic Fluctuations on the Elastic Properties of Iron Arsenide Superconductors. Phys. Rev. Lett. 2010, 105, 157003. [Google Scholar] [CrossRef]
- Nandi, S.; Kim, M.G.; Kreyssig, A.; Fernandes, R.M.; Pratt, D.K.; Thaler, A.; Ni, N.; Bud’ko, S.L.; Canfield, P.C.; Schmalian, J.; et al. Anomalous Suppression of the Orthorhombic Lattice Distortion in Superconducting Ba(Fe1−xCox)2As2 Single Crystals. Phys. Rev. Lett. 2010, 104, 057006. [Google Scholar] [CrossRef]
- Böhmer, A.E.; Chu, J.-H.; Lederer, S.; Yi, M. Nematicity and nematic fluctuations in iron-based superconductors. Nat. Phys. 2022, 18, 1412. [Google Scholar] [CrossRef]
- Chu, J.-H.; Kuo, H.-H.; Analytis, J.G.; Fisher, I.R. Divergent Nematic Susceptibility in an Iron Arsenide Superconductor. Science 2012, 337, 710. [Google Scholar] [CrossRef]
- Meier, W.R.; Kong, T.; Kaluarachchi, U.S.; Taufour, V.; Jo, N.H.; Drachuck, G.; Böhmer, A.E.; Saunders, S.M.; Sapkota, A.; Kreyssig, A.; et al. Anisotropic thermodynamic and transport properties of single-crystalline CaKFe4As4. Phys. Rev. B 2016, 94, 064501. [Google Scholar] [CrossRef]
- Wilde, J.M.; Sapkota, A.; Ding, Q.P.; Xu, M.; Tian, W.; Bud’ko, S.L.; Furukawa, Y.; Kreyssig, A.; Canfield, P.C. Antiferromagnetic order and its interplay with superconductivity in CaK(Fe1−xMnx)4As4. arXiv 2023, arXiv:2301.06336. [Google Scholar] [CrossRef]
- Ishida, J.; Iimura, S.; Hosono, H. Effects of disorder on the intrinsically hole-doped iron-based superconductor KCa2Fe4As4F2 by cobalt substitution. Phys. Rev. B 2017, 96, 174522. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y.; Wang, Z.; Cao, G.; Zhang, B.; Pang, H.; Li, F. Study of the Rare Earth Effects on the Magnetic Fluctuations in RbLn2Fe4As4O2 (Ln = Tb, Dy, and Ho) by Mössbauer Spectroscopy. J. Supercond. Nov. Magn. 2019, 32, 361. [Google Scholar] [CrossRef]
- Mizuguchi, Y.; Furubayashi, T.; Deguchi, K.; Tsuda, S.; Yamaguchi, T.; Takano, Y. Mössbauer studies on FeSe and FeTe. Phys. C Supercond. Its Appl. 2010, 470, S338. Available online: https://www.sciencedirect.com/science/article/pii/S0921453409008594 (accessed on 1 December 2010). [CrossRef]
- Wang, Q.; Shen, Y.; Pan, B.; Zhang, X.; Ikeuchi, K.; Iida, K.; Christianson, A.D.; Walker, H.C.; Adroja, D.T.; Abdel-Hafiez, M.; et al. Magnetic ground state of FeSe. Nat. Commun. 2016, 7, 12182. [Google Scholar] [CrossRef]
- Baum, A.; Ruiz, H.N.; Lazarević, N.; Wang, Y.; Böhm, T.; Ahangharnejhad, R.H.; Adelmann, P.; Wolf, T.; Popović, Z.V.; Moritz, B.; et al. Frustrated spin order and stripe fluctuations in FeSe. Commun. Phys. 2019, 2, 14. [Google Scholar] [CrossRef]
- Wang, Z.-C.; He, C.-Y.; Wu, S.-Q.; Tang, Z.-T.; Liu, Y.; Cao, G.-H. Synthesis, Crystal Structure and Superconductivity in RbLn2Fe4As4O2 (Ln = Sm, Tb, Dy, and Ho). Chem. Mater. 2017, 29, 1805. [Google Scholar] [CrossRef]
- Christianson, A.D.; Goremychkin, E.A.; Osborn, R.; Rosenkranz, S.; Lumsden, M.D.; Malliakas, C.D.; Todorov, I.S.; Claus, H.; Chung, D.Y.; Kanatzidis, M.G.; et al. Unconventional superconductivity in Ba0.6K0.4Fe2As2 from inelastic neutron scattering. Nature 2008, 456, 930. [Google Scholar] [CrossRef]
- Hong, W.; Song, L.; Liu, B.; Li, Z.; Zeng, Z.; Li, Y.; Wu, D.; Sui, Q.; Xie, T.; Danilkin, S.; et al. Neutron Spin Resonance in a Quasi-Two-Dimensional Iron-Based Superconductor. Phys. Rev. Lett. 2020, 125, 117002. [Google Scholar] [CrossRef]
- Adroja, D.T.; Kirschner, F.K.K.; Lang, F.; Smidman, M.; Hillier, A.D.; Wang, Z.-C.; Cao, G.-H.; Stenning, G.B.G.; Blundell, S.J. Multigap Superconductivity in RbCa2Fe4As4F2 Investigated Using μSR Measurements. J. Phys. Soc. Jpn. 2018, 87, 124705. [Google Scholar] [CrossRef]
- Mazin, I.I.; Johannes, M.D.; Boeri, L.; Koepernik, K.; Singh, D.J. Problems with reconciling density functional theory calculations with experiment in ferropnictides. Phys. Rev. B 2008, 78, 085104. [Google Scholar] [CrossRef]
- Sen, S.; Ghosh, H. Interdependence of spin structure, anion height and electronic structure of BaFe2As2. AIP Conf. Proc. 2016, 1728, 020180. [Google Scholar] [CrossRef]
- Bondino, F.; Magnano, E.; Malvestuto, M.; Parmigiani, F.; McGuire, M.A.; Sefat, A.; Sales, B.C.; Jin, R.; Mandrus, D.; Plummer, E.; et al. Evidence for strong itinerant spin fluctuations in the normal state of CeFeAsO0.89 F0.11 iron-oxypnictide superconductors. Phys. Rev. Lett. 2008, 101, 267001. Available online: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.101.267001 (accessed on 23 December 2008). [CrossRef]
- Singh, D.J. ThFeAsN in relation to other iron-based superconductors. J. Alloys Compd. 2016, 687, 786. Available online: https://www.sciencedirect.com/science/article/pii/S0925838816318710 (accessed on 5 December 2016). [CrossRef]
- Pokhriyal, A.; Ghosh, A.; Ghosh, H. Electronic structure, magnetic order and Lifshitz transition in electron doped new structure 12442 type Fe-based superconductors. J. Phys. Chem. Solids 2022, 172, 111085. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, G.; Tian, X. Electronic structure and magnetism of RbGd2Fe4As4O2. J. Alloys Compd. 2017, 708, 392. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0925838817307867 (accessed on 25 June 2017). [CrossRef]
- Wang, G.; Wang, Z.; Shi, X. Self-hole-doping–induced superconductivity in KCa2Fe4As4F2. Europhys. Lett. 2016, 116, 37003. [Google Scholar] [CrossRef]
- Chandra, P.; Coleman, P.; Larkin, A.I. Ising transition in frustrated Heisenberg models. Phys. Rev. Lett. 1990, 64, 88. [Google Scholar] [CrossRef]
- Watson, M.D.; Dudin, P.; Rhodes, L.C.; Evtushinsky, D.V.; Iwasawa, H.; Aswartham, S.; Wurmehl, S.; Büchner, B.; Hoesch, M.; Kim, T.K. Probing the reconstructed Fermi surface of antiferromagnetic BaFe2As2 in one domain. npj Quantum Mater. 2019, 4, 36. [Google Scholar] [CrossRef]
- Ran, Y.; Wang, F.; Zhai, H.; Vishwanath, A.; Lee, D.-H. Nodal spin density wave and band topology of the FeAs-based materials. Phys. Rev. B 2009, 79, 014505. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Pizzi, G.; Vitale, V.; Arita, R.; Blügel, S.; Freimuth, F.; Géranton, G.; Gibertini, M.; Gresch, D.; Johnson, C.; Koretsune, T.; et al. Wannier90 as a community code: New features and applications. J. Phys. Condens. Matter 2020, 32, 165902. [Google Scholar] [CrossRef]
- Johnston, D.C. The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Adv. Phys. 2010, 59, 803. [Google Scholar] [CrossRef]
- Mazin, I.I.; Singh, D.J.; Johannes, M.D.; Du, M.H. Unconventional Superconductivity with a Sign Reversal in the Order Parameter of LaFeAsO1−xFx. Phys. Rev. Lett. 2008, 101, 057003. [Google Scholar] [CrossRef]
- Singh, D.J. Electronic structure and doping in BaFe2As2 and LiFeAs: Density functional calculations. Phys. Rev. B 2008, 78, 094511. [Google Scholar] [CrossRef]
- Sen, S.; Ghosh, H.; Sinha, A.K.; Bharathi, A. Origin of structural and magnetic transitions in BaFe2−xRuxAs2 materials. Supercond. Sci. Technol. 2014, 27, 122003. [Google Scholar] [CrossRef]
- Pokhriyal, A.; Ghosh, A.; Ghosh, H. Electronic structure studies of RbLn2Fe4As4O2 (Ln = Sm, Tb, Dy and Ho) compounds. Mater. Today Commun. 2023, 35, 106210. [Google Scholar] [CrossRef]
- Egami, T.; Fine, B.V.; Parshall, D.; Subedi, A.; Singh, D.J. Spin-Lattice Coupling and Superconductivity in Fe Pnictides. Adv. Condens. Matter Phys. 2010, 2010, 164916. [Google Scholar] [CrossRef]
- Lee, C.-C.; Yin, W.-G.; Ku, W. Ferro-Orbital Order and Strong Magnetic Anisotropy in the Parent Compounds of Iron-Pnictide Superconductors. Phys. Rev. Lett. 2009, 103, 267001. [Google Scholar] [CrossRef]
- Ma, F.; Lu, Z.-Y.; Xiang, T. Arsenic-bridged antiferromagnetic superexchange interactions in LaFeAsO. Phys. Rev. B 2008, 78, 224517. [Google Scholar] [CrossRef]
- Wang, W.; Li, B.; Liu, S.; Liu, M.; Xing, Z.W. Magnetic fluctuation and frustration in new iron-based layered SrFe1−xCoxAsF superconductors. J. Appl. Phys. 2010, 107, 123906. [Google Scholar] [CrossRef]
- Hu, J. Identifying the genes of unconventional high temperature superconductors. Sci. Bull. 2016, 61, 561. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).