Dynamic Footprints of the Specific Artificial Spin Ice Microstate on Its Spin Waves
Abstract
1. Introduction
2. Materials and Methods
Micromagnetic Framework and Simulations
3. Results
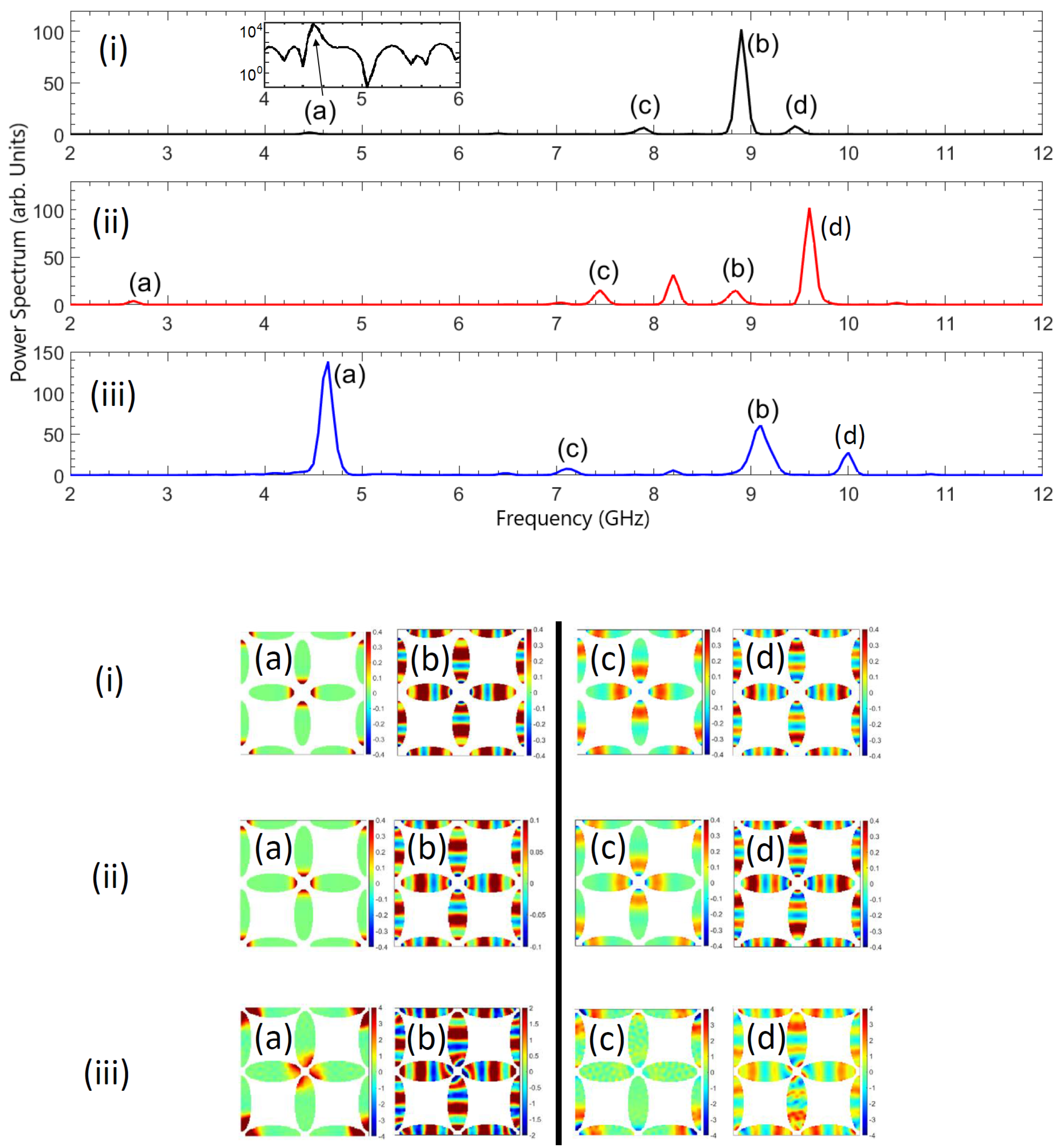
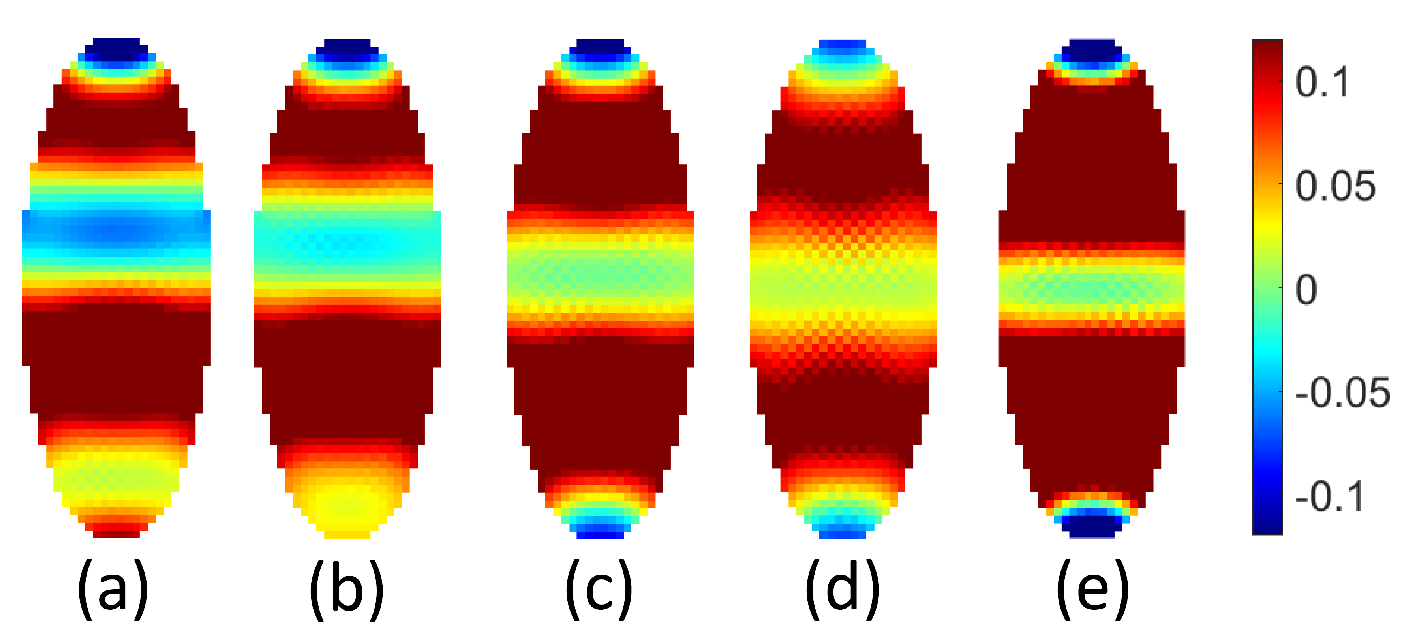
3.1. Footprints of the Microstate on the Fundamental Mode
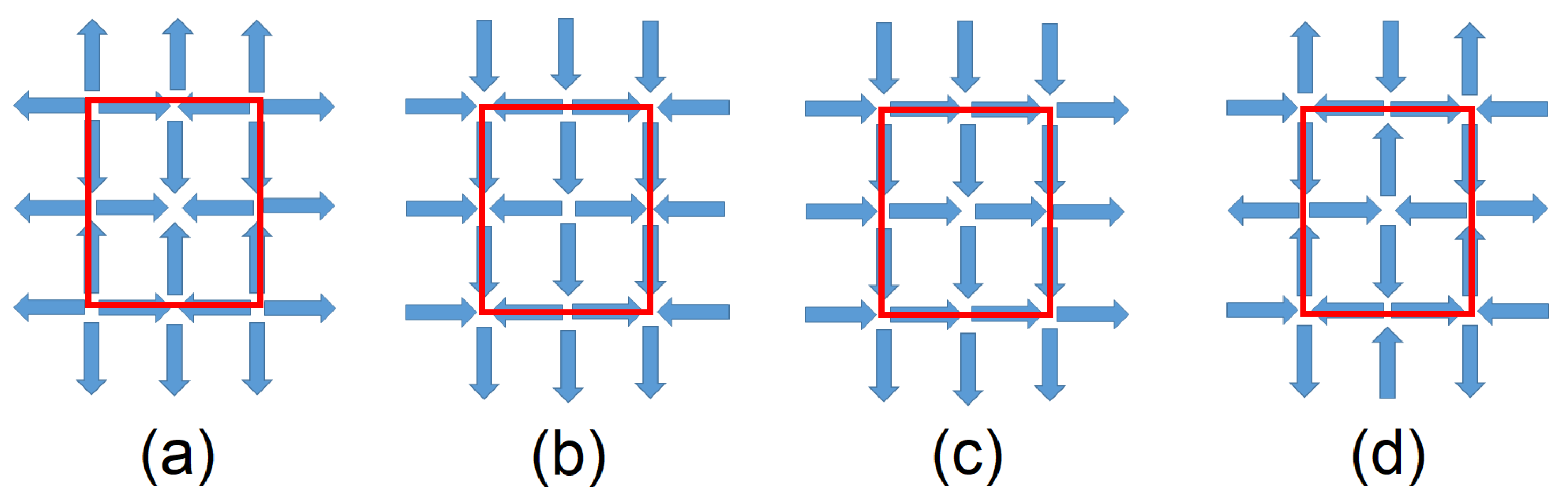
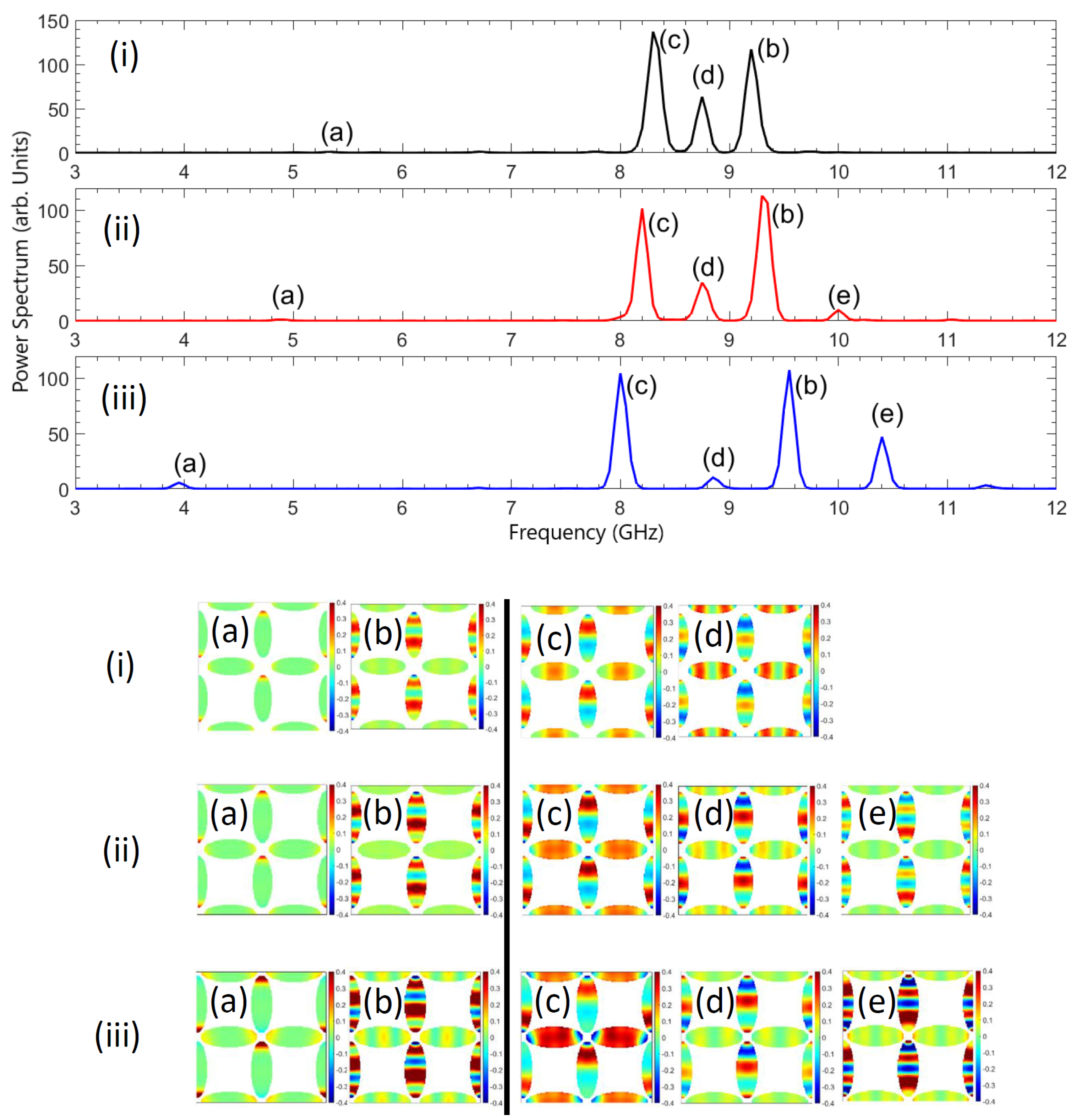
3.2. Main Effects in the Spectra Due to the Different Vertex Configurations
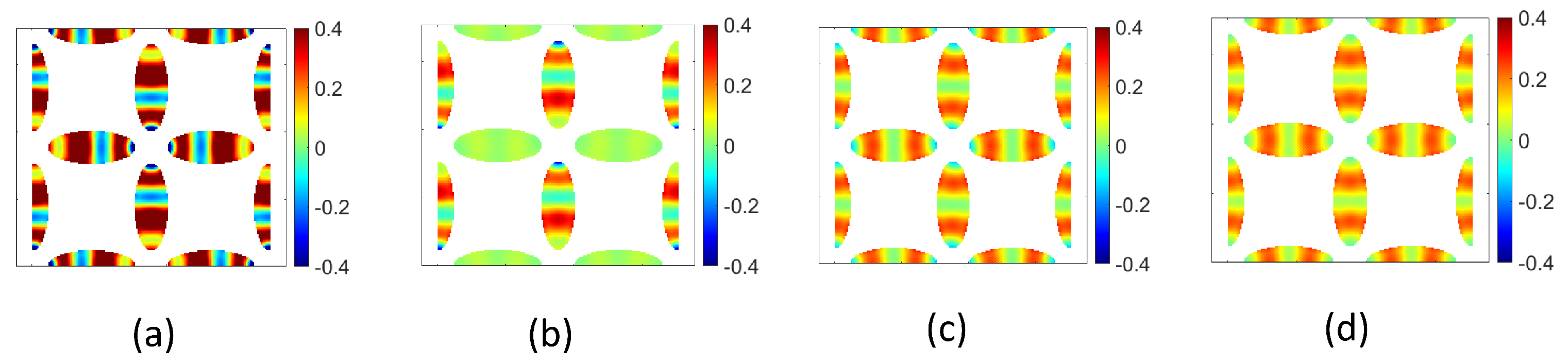
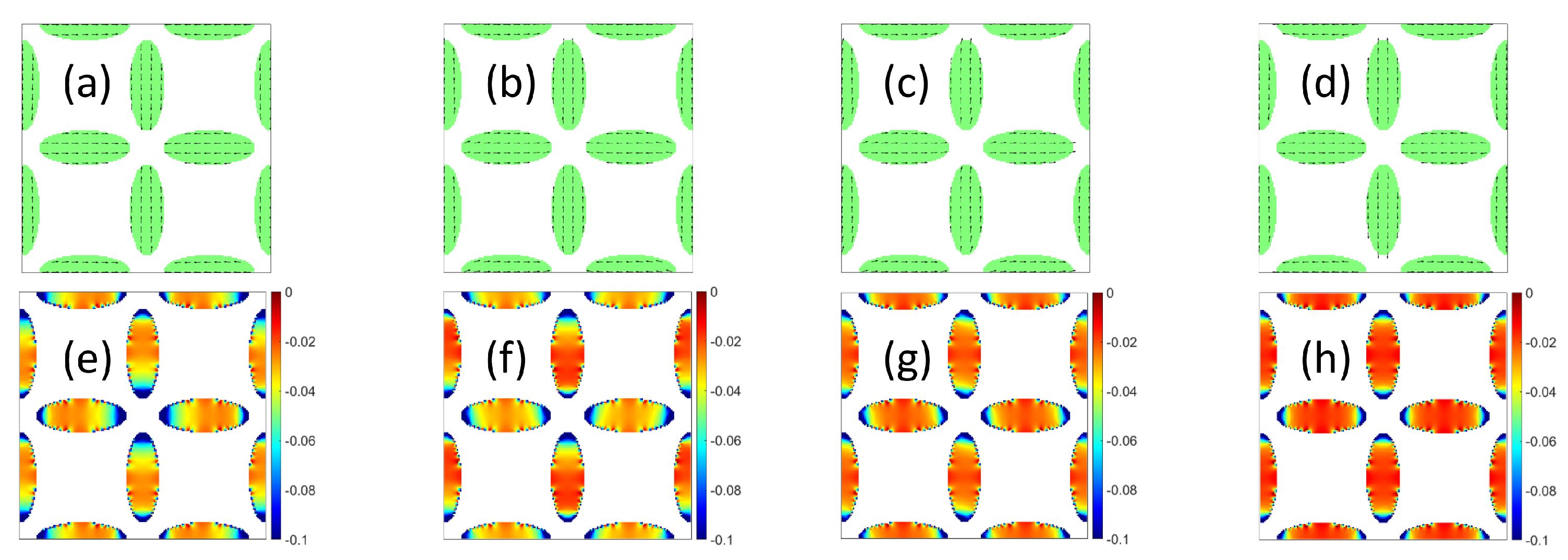
3.2.1. Lattice Interaction and SW Profile
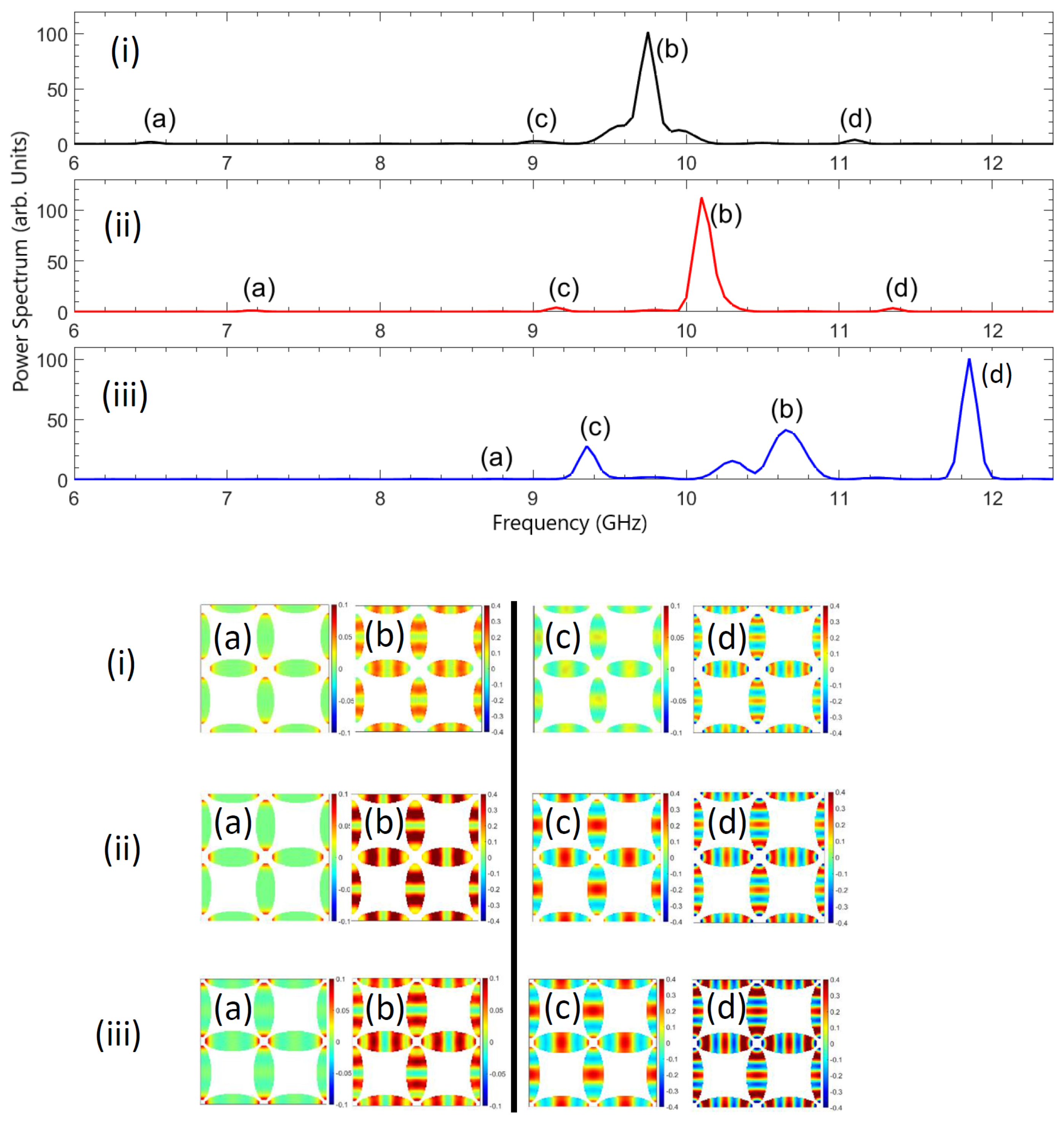
3.2.2. Macrospin Size
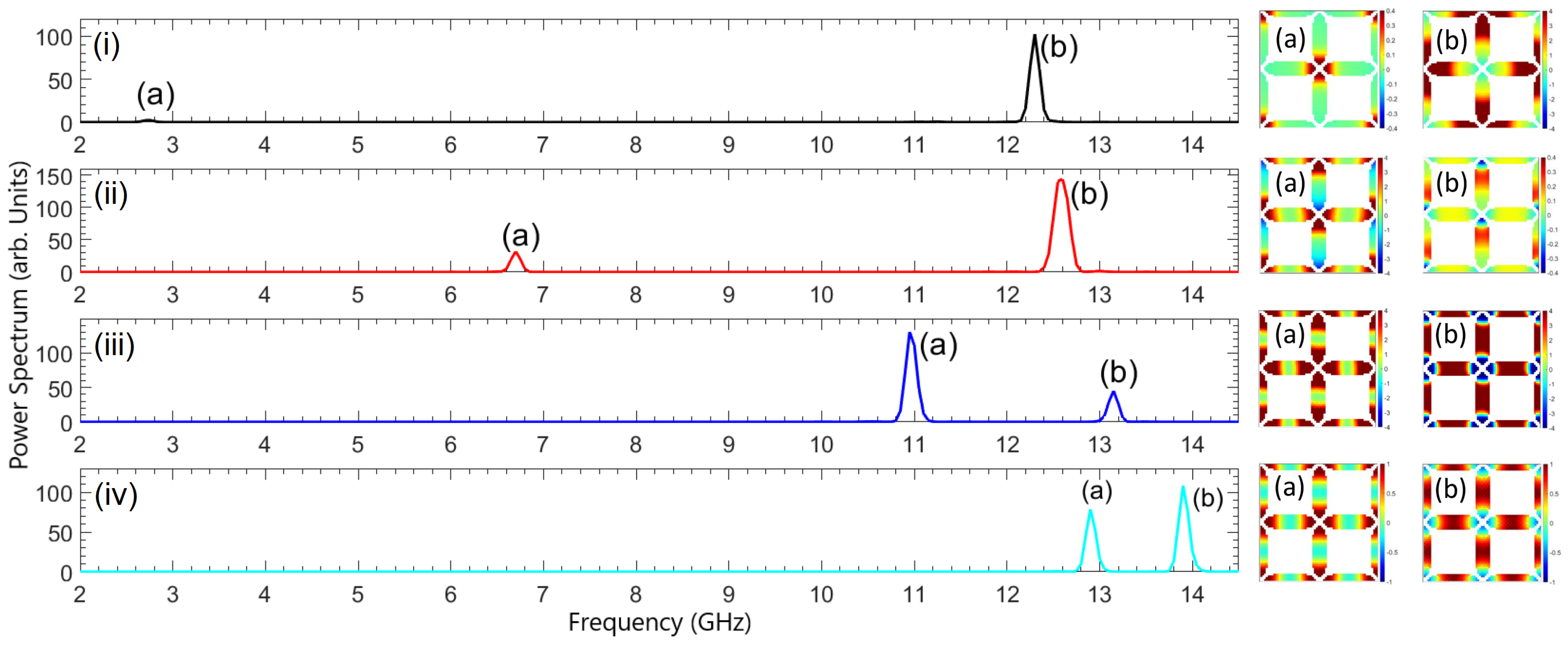
3.2.3. Aspect Ratio
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Morris, D.J.P.; Tennant, D.A.; Grigera, S.A.; Klemke, B.; Castelnovo, C.; Moessner, R.; Czternasty, C.; Meissner, M.; Rule, K.C.; Hoffmann, J.U.; et al. Dirac Strings and Magnetic Monopoles in the Spin Ice Dy2Ti2O7. Science 2009, 326, 411. [Google Scholar] [CrossRef] [PubMed]
- Bramwell, S.T.; Harris, M.J. The history of spin ice. J. Phys. Condens. Matter 2020, 32, 374010. [Google Scholar] [CrossRef]
- Wang, R.F.; Nisoli, C.; Freitas, R.S.; Li, J.; McConville, W.; Cooley, B.J.; Lund, M.S.; Samarth, N.; Leighton, C.; Crespi, V.H.; et al. Artificial ‘spin ice’ in a geometrically frustrated lattice of nanoscale ferromagnetic islands. Nature 2006, 439, 303–306. [Google Scholar] [CrossRef] [PubMed]
- Skjærvø, S.H.; Marrows, C.H.; Stamps, R.L.; Heyderman, L.J. Advances in artificial spin ice. Nat. Rev. Phys. 2020, 2, 13. [Google Scholar] [CrossRef]
- Farhan, A.; Derlet, P.M.; Anghinolfi, L.; Kleibert, A.; Heyderman, L.J. Magnetic charge and moment dynamics in artificial kagome spin ice. Phys. Rev. B 2017, 96, 064409. [Google Scholar] [CrossRef]
- Morrison, M.J.; Nelson, T.R.; Nisoli, C. Unhappy vertices in artificial spin ice: New degeneracies from vertex frustration. New J. Phys. 2013, 15, 045009. [Google Scholar] [CrossRef]
- Pollard, S.D.; Volkov, V.; Zhu, Y. Propagation of magnetic charge monopoles and Dirac flux strings in an artificial spin-ice lattice. Phys. Rev. B 2012, 85, 180402(R). [Google Scholar] [CrossRef]
- Mengotti, E.; Heyderman, L.J.; Rodríguez, A.F.; Nolting, F.; Hügli, R.V.; Braun, H.B. Real-space observation of emergent magnetic monopoles and associated Dirac strings in artificial kagome spin ice. Nat. Phys. 2011, 7, 68–74. [Google Scholar] [CrossRef]
- Le, B.L.; Park, J.; Sklenar, J.; Chern, G.W.; Nisoli, C.; Watts, J.D.; Manno, M.; Rench, D.W.; Samarth, N.; Leighton, C.; et al. Understanding magnetotransport signatures in networks of connected permalloy nanowires. Phys. Rev. B 2017, 95, 060405(R). [Google Scholar] [CrossRef]
- Sander, D.; Valenzuela, S.O.; Makarov, D.; Marrows, C.H.; Fullerton, E.E.; Fischer, P.; McCord, J.; Vavassori, P.; Mangin, S.; Pirro, P.; et al. The 2017 Magnetism Roadmap. J. Phys. D Appl. Phys. 2017, 50, 363001. [Google Scholar] [CrossRef]
- Lendinez, S.; Jungfleisch, M.B. Magnetization dynamics in artificial spin ice. J. Physics Condens. Matter 2019, 32, 013001. [Google Scholar] [CrossRef] [PubMed]
- Gliga, S.; Kákay, A.; Hertel, R.; Heinonen, O.G. Spectral Analysis of Topological Defects in an Artificial Spin-Ice Lattice. Phys. Rev. Lett. 2013, 110, 117205. [Google Scholar] [CrossRef] [PubMed]
- Montoncello, F.; Gubbiotti, G. Controlling the three dimensional propagation of spin waves in continuous ferromagnetic films with an increasing out of plane undulation. Sci. Rep. 2021, 11, 21344. [Google Scholar] [CrossRef]
- Graczyk, P.; Krawczyk, M.; Dhuey, S.; Yang, W.G.; Schmidt, H.; Gubbiotti, G. Magnonic band gap and mode hybridization in continuous permalloy films induced by vertical dynamic coupling with an array of permalloy ellipses. Phys. Rev. B 2018, 98, 174420. [Google Scholar] [CrossRef]
- Saha, S.; Zhou, J.; Hofhuis, K.; Kákay, A.; Scagnoli, V.; Heyderman, L.J.; Gliga, S. Spin-Wave Dynamics and Symmetry Breaking in an Artificial Spin Ice. Nano Lett. 2021, 21, 2382. [Google Scholar] [CrossRef]
- Bhat, V.S.; Watanabe, S.; Baumgaertl, K.; Kleibert, A.; Schoen, M.A.W.; Vaz, C.A.F.; Grundler, D. Magnon Modes of Microstates and Microwave-Induced Avalanche in Kagome Artificial Spin Ice with Topological Defects. Phys. Rev. Lett. 2020, 125, 117208. [Google Scholar] [CrossRef]
- Ghosh, A.; Ma, F.; Lourembam, J.; Jin, X.; Maddu, R.; Yap, Q.J.; Lim, S.T. Emergent Dynamics of Artificial Spin-Ice Lattice Based on an Ultrathin Ferromagnet. Nano Lett. 2020, 20, 109. [Google Scholar] [CrossRef]
- Gartside, J.C.; Vanstone, A.; Dion, T.; Stenning, K.D.; Arroo, D.M.; Kurebayashi, H.; Branford, W.R. Reconfigurable magnonic mode-hybridisation and spectral control in a bicomponent artificial spin ice. Nat. Commun. 2021, 12, 2488. [Google Scholar] [CrossRef]
- Dion, T.; Arroo, D.M.; Yamanoi, K.; Kimura, T.; Gartside, J.C.; Cohen, L.F.; Kurebayashi, H.; Branford, W.R. Tunable magnetization dynamics in artificial spin ice via shape anisotropy modification. Phys. Rev. B 2019, 100, 054433. [Google Scholar] [CrossRef]
- Iacocca, E.; Gliga, S.; Stamps, R.L.; Heinonen, O. Reconfigurable wave band structure of an artificial square ice. Phys. Rev. 2016, 93, 134420. [Google Scholar] [CrossRef]
- Ladak, S.; Fernández-Pacheco, A.; Fischer, P. Science and technology of 3D magnetic nanostructures. APL Mater. 2022, 10, 5. [Google Scholar] [CrossRef]
- Negrello, R.; Montoncello, F.; Kaffash, M.T.; Jungfleisch, M.B.; Gubbiotti, G. Dynamic coupling and spin-wave dispersions in a magnetic hybrid system made of an artificial spin-ice structure and an extended NiFe underlayer. APL Mater. 2022, 10, 091115. [Google Scholar] [CrossRef]
- Montoncello, F.; Kaffash, M.T.; Carfagno, H.; Doty, M.F.; Gubbiotti, G.; Jungfleisch, M.B. A Brillouin light scattering study of the spin-wave magnetic field dependence in a magnetic hybrid system made of an artificial spin-ice structure and a film underlayer. J. Appl. Phys. 2023, 133, 083901. [Google Scholar] [CrossRef]
- Barman, A.; Gubbiotti, G.; Ladak, S.; Adeyeye, A.O.; Krawczyk, M.; Gräfe, J.; Adelmann, C.; Cotofana, S.; Naeemi, A.; Vasyuchka, V.I.; et al. The 2021 Magnonics Roadmap. J. Physics Condens. Matter 2021, 33, 413001. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, S.; May, A.; van Den Berg, A.; Mondal, A.K.; Ladak, S.; Barman, A. Observation of Coherent Spin Waves in a Three-Dimensional Artificial Spin Ice Structure. Nano Lett. 2021, 21, 4629. [Google Scholar] [CrossRef] [PubMed]
- Gubbiotti, G. Three-Dimensional Magnonics: Layered, Micro- and Nanostructures; Jenny Stanford Publishing: Singapore, 2019. [Google Scholar]
- Iacocca, E.; Gliga, S.; Heinonen, O.G. Tailoring Spin-Wave Channels in a Reconfigurable Artificial Spin Ice. Phys. Rev. Appl. 2020, 13, 044047. [Google Scholar] [CrossRef]
- Iacocca, E.; Heinonen, O. Topologically Nontrivial Magnon Bands in Artificial Square Spin Ices with Dzyaloshinskii-Moriya Interaction. Phys. Rev. Applied 2017, 8, 034015. [Google Scholar] [CrossRef]
- Jungfleisch, M.B.; Zhang, W.; Iacocca, E.; Sklenar, J.; Ding, J.; Jiang, W.; Zhang, S.; Pearson, J.E.; Novosad, V.; Ketterson, J.B.; et al. Dynamic response of an artificial square spin ice. Phys. Rev. B 2016, 93, 100401(R). [Google Scholar] [CrossRef]
- Bang, W.; Sturm, J.; Silvani, R.; Kaffash, M.T.; Hoffmann, A.; Ketterson, J.B.; Montoncello, F.; Jungfleisch, M.B. Influence of the Vertex Region on Spin Dynamics in Artificial Kagome Spin Ice. Phys. Rev. Appl. 2020, 14, 014079. [Google Scholar] [CrossRef]
- Sebastian, T.; Schultheiss, K.; Obry, B.; Hillebrands, B.; Schultheiss, H. Micro-focused Brillouin light scattering: Imaging spin waves at the nanoscale. Front. Phys. 2015, 3, 35. [Google Scholar] [CrossRef]
- Madami, M.; Montoncello, F.; Capuzzo, G.; Giovannini, L.; Nizzoli, F.; Gubbiotti, G.; Tacchi, S.; Carlotti, G.; Tanigawa, H.; Ono, T. Experimental Evidence of Field-Induced Localization of Spin Excitations in NiFe Elliptical Rings by Micro-Focused Brillouin Light Scattering. IEEE Trans. Magn. 2010, 46, 1531. [Google Scholar] [CrossRef]
- Berweger, S.; Tyrell-Ead, R.; Chang, H.; Wu, M.; Zhu, N.; Tang, H.X.; Nembach, H.; Karl Stupic, T.; Russek, S.; Wallis, T.M.; et al. Imaging of magnetic excitations in nanostructures with near-field microwave microscopy. J. Magn. Magn. Mater. 2022, 546, 168870. [Google Scholar] [CrossRef]
- Keatley, P.S.; Loughran, T.H.J.; Hendry, E.; Barnes, W.L.; Hicken, R.J.; Childress, J.R.; Katine, J.A. A platform for time-resolved scanning Kerr microscopy in the near-field. Rev. Sci. Instruments 2017, 88, 123708. [Google Scholar] [CrossRef]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Van Waeyenberge, B. The design and verification of MuMax3. AIP Adv. 2014, 4, 107133. [Google Scholar] [CrossRef]
- Fangohr, H.; Bordignon, G.; Franchin, M.; Knittel, A.; de Groot, P.A.J.; Fischbacher, T. A new approach to (quasi) periodic boundary conditions in micromagnetics: The macrogeometry. J. Appl. Phys. 2009, 105, 07D529. [Google Scholar] [CrossRef]
- De Wiele, B.V.; Montoncello, F. A continuous excitation approach to determine time-dependent dispersion diagrams in 2D magnonic crystals. J. Phys. D Appl. Phys. 2014, 47, 315002. [Google Scholar] [CrossRef]
- Gubbiotti, G.; Carlotti, G.; Okuno, T.; Grimsditch, M.; Giovannini, L.; Montoncello, F.; Nizzoli, F. Spin dynamics in thin nanometric elliptical Permalloy dots: A Brillouin light scattering investigation as a function of dot eccentricity. Phys. Rev. B 2005, 72, 184419. [Google Scholar] [CrossRef]
- Gubbiotti, G.; Xiong, L.L.; Montoncello, F.; Giovannini, L.; Adeyeye, A.O. pin wave dispersion and intensity correlation in width-modulated nanowire arrays: A Brillouin light scattering study. J. Appl. Phys. 2018, 124, 083903. [Google Scholar] [CrossRef]
- Bang, W.; Montoncello, F.; Hoffmann, A.; Giovannini, L.; Ketterson, J.B. Thickness dependence of spin wave dynamics in three-fold nano-ellipse clusters. AIP Adv. 2018, 8, 101502. [Google Scholar] [CrossRef]
- Madami, M.; Tacchi, S.; Gubbiotti, G.; Carlotti, G.; Montoncello, F.; Capuzzo, G.; Giovannini, L.; Nizzoli, F.; Tanigawa, H.; Ono, T. Spin Modes in Elliptical Nanorings in the Vortex State: Two-Dimensional Mapping by Micro-Focused Brillouin Light Scattering. IEEE Trans. Magn. 2010, 46, 199. [Google Scholar] [CrossRef]
- Perzlmaier, K.; Buess, M.; Back, C.H.; Demidov, V.E.; Hillebrands, B.; Demokritov, S.O. Spin-Wave Eigenmodes of Permalloy Squares with a Closure Domain Structure. Phys. Rev. Lett. 2005, 94, 057202. [Google Scholar] [CrossRef] [PubMed]
- Schneider, T.; Serga, A.A.; Leven, B.; Hillebrands, B.; Stamps, R.L.; Kostylev, M.P. Realization of spin-wave logic gates. Appl. Phys. Lett. 2008, 92, 022505. [Google Scholar] [CrossRef]
- Lee, K.S.; Kim, S.K. Conceptual design of spin wave logic gates based on a Mach–Zehnder-type spin wave interferometer for universal logic functions. J. Appl. Phys. 2008, 104, 053909. [Google Scholar] [CrossRef]
- Csaba, G.; Papp, Á.; Porod, W. IPerspectives of using spin waves for computing and signal processing. Phys. Lett. A 2017, 381, 1471. [Google Scholar] [CrossRef]
- Damon, R.; Eshbach, J. Magnetostatic modes of a ferromagnet slab. J. Phys. Chem. Solids 1961, 19, 308–320. [Google Scholar] [CrossRef]
- Jorzick, J.; Demokritov, S.O.; Hillebrands, B.; Bailleul, M.; Fermon, C.; Guslienko, K.; Slavin, A.N.; Berkov, D.; Gorn, N.L. Spin Wave Wells in Nonellipsoidal Micrometer Size Magnetic Elements. Phys. Rev. Lett. 2002, 88, 047204. [Google Scholar] [CrossRef]
- Bailleul, M.; Höllinger, R.; Fermon, C. Microwave spectrum of square Permalloy dots: Quasisaturated state. Phys. Rev. B 2006, 73, 104424. [Google Scholar] [CrossRef]
- Montoncello, F.; Giovannini, L.; Nizzoli, F.; Vavassori, P.; Grimsditch, M. Dynamic origin of first and second order phase transitions in magnetization reversal of elliptical nanodots. Phys. Rev. B 2008, 77, 214402. [Google Scholar] [CrossRef]
- Yuan, H.Y.; Duine, R.A. Universal field dependence of magnetic resonance near zero frequency. Phys. Rev. B 2021, 103, 134440. [Google Scholar] [CrossRef]
- Montoncello, F.; Giovannini, L.; Bang, W.; Ketterson, J.B.; Jungfleisch, M.B.; Hoffmann, A.; Farmer, B.W.; De Long, L.E. Mutual influence between macrospin reversal order and spin-wave dynamics in isolated artificial spin-ice vertices. Phys. Rev. B 2018, 97, 014421. [Google Scholar] [CrossRef]
- Montoncello, F.; Giovannini, L.; Farmer, B.; De Long, L.E. Dynamic origin of segment magnetization reversal in thin-film Penrose tilings. J. Magn. Magn. Mater. 2017, 423, 158–163. [Google Scholar] [CrossRef]
- Montoncello, F.; Giovannini, L. Bandwidth broadening and asymmetric softening of collective spin waves in magnonic crystals. Appl. Phys. Lett. 2014, 104, 242407. [Google Scholar] [CrossRef]
- Montoncello, F.; Giovannini, L.; Nizzoli, F.; Vavassori, P.; Grimsditch, M.; Ono, T.; Gubbiotti, G.; Tacchi, S.; Carlotti, G. Soft spin waves and magnetization reversal in elliptical Permalloy nanodots: Experiments and dynamical matrix results. Phys. Rev. B 2007, 76, 024426. [Google Scholar] [CrossRef]
- Mamica, S. Influence of the demagnetizing field on the spin-wave softening in bicomponent magnonic crystals. J. Magn. Magn. Mater. 2022, 546, 168690. [Google Scholar] [CrossRef]

| s (nm) | 96 | 64 | 56 | 48 | 40 |
|---|---|---|---|---|---|
| Frequency (GHz) | 4.5 | 2.6 | 1.0 | 3.2 | 4.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Micaletti, P.; Montoncello, F. Dynamic Footprints of the Specific Artificial Spin Ice Microstate on Its Spin Waves. Magnetochemistry 2023, 9, 158. https://doi.org/10.3390/magnetochemistry9060158
Micaletti P, Montoncello F. Dynamic Footprints of the Specific Artificial Spin Ice Microstate on Its Spin Waves. Magnetochemistry. 2023; 9(6):158. https://doi.org/10.3390/magnetochemistry9060158
Chicago/Turabian StyleMicaletti, Pietro, and Federico Montoncello. 2023. "Dynamic Footprints of the Specific Artificial Spin Ice Microstate on Its Spin Waves" Magnetochemistry 9, no. 6: 158. https://doi.org/10.3390/magnetochemistry9060158
APA StyleMicaletti, P., & Montoncello, F. (2023). Dynamic Footprints of the Specific Artificial Spin Ice Microstate on Its Spin Waves. Magnetochemistry, 9(6), 158. https://doi.org/10.3390/magnetochemistry9060158







