Nano-Magnonic Crystals by Periodic Modulation of Magnetic Parameters
Abstract
1. Introduction
2. Materials and Methods
2.1. Analytical Derivation
2.1.1. Exchange Constant Modulation
2.1.2. DMI Modulation
2.2. Micromagnetic Simulations
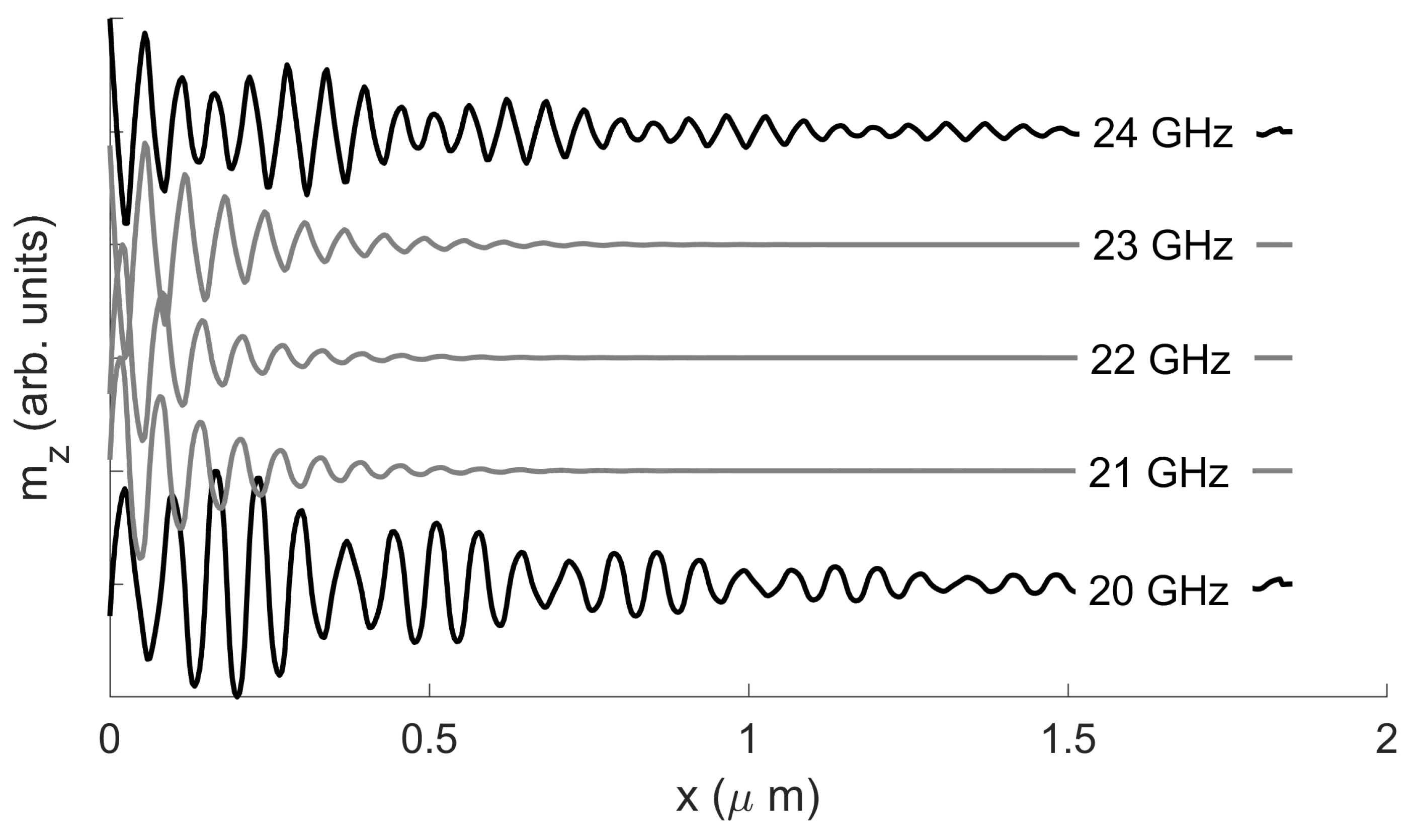
2.2.1. Sinc Excitation
2.2.2. Local Microwave Field
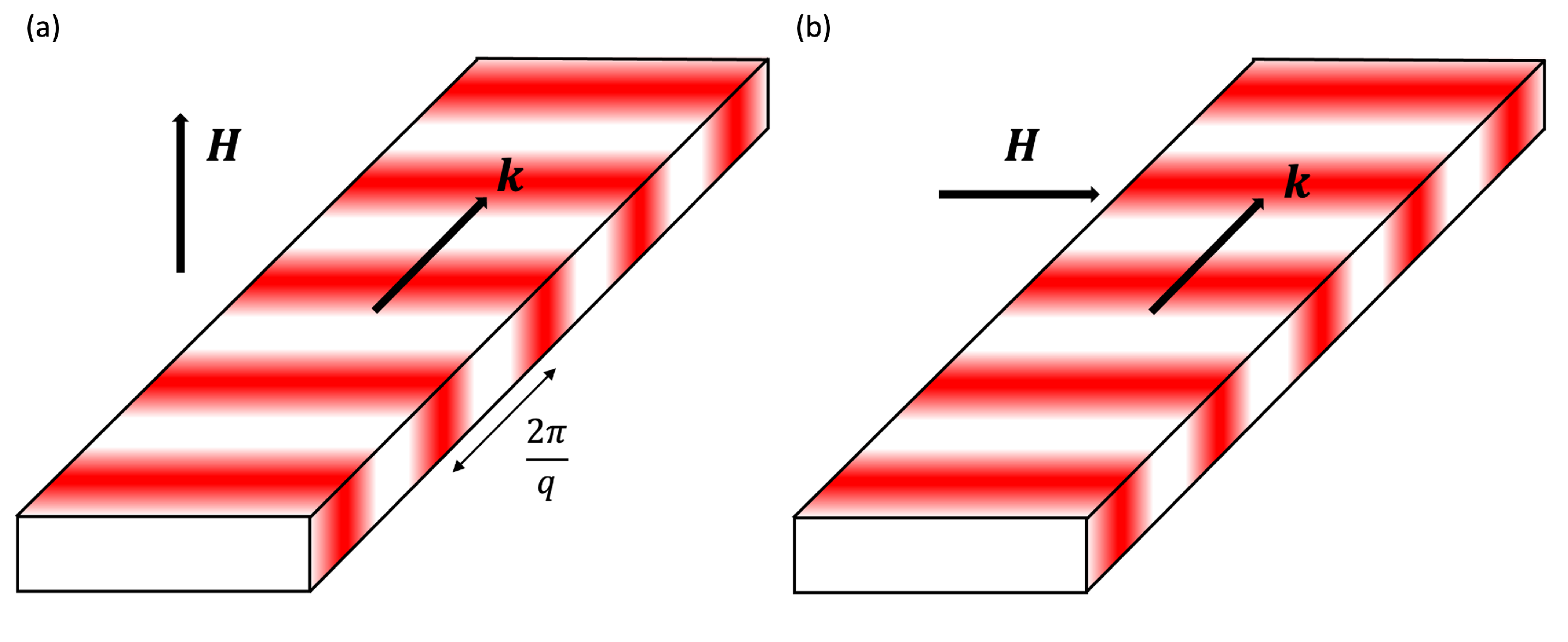
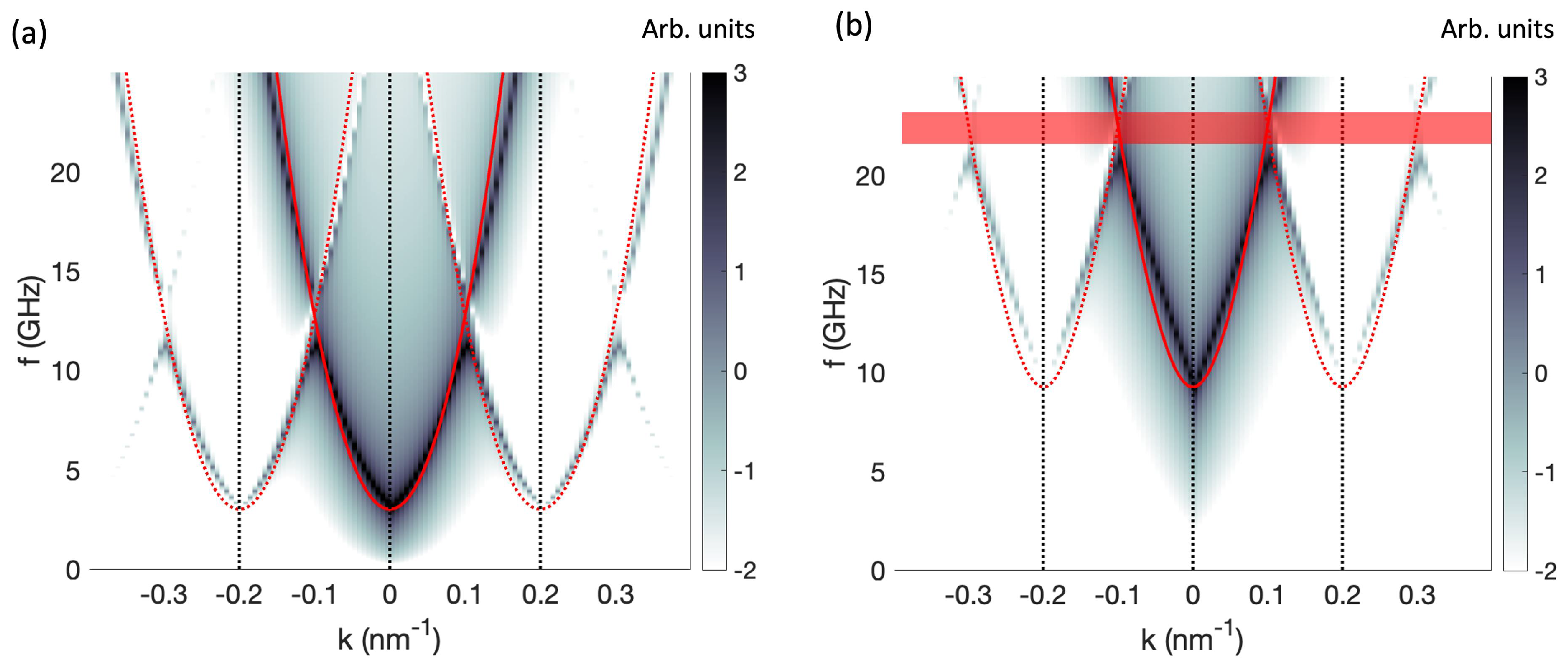
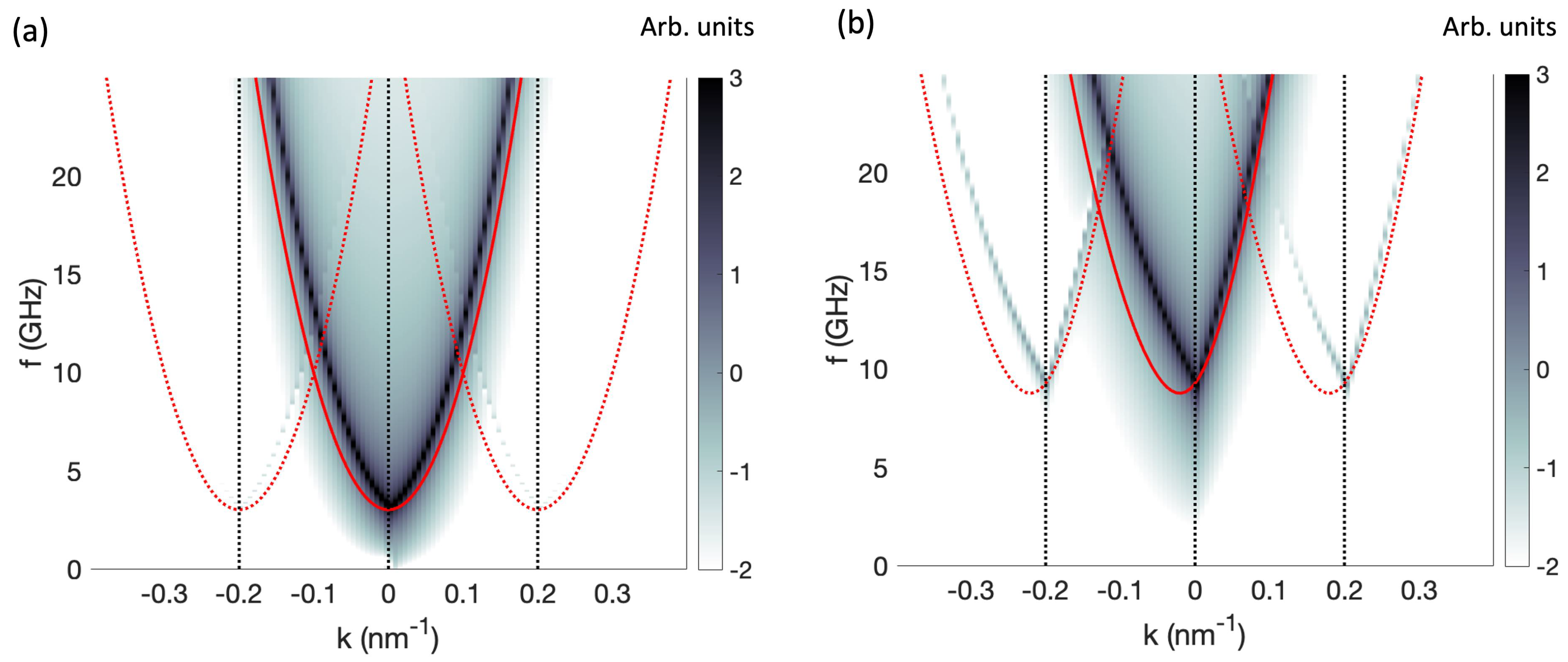
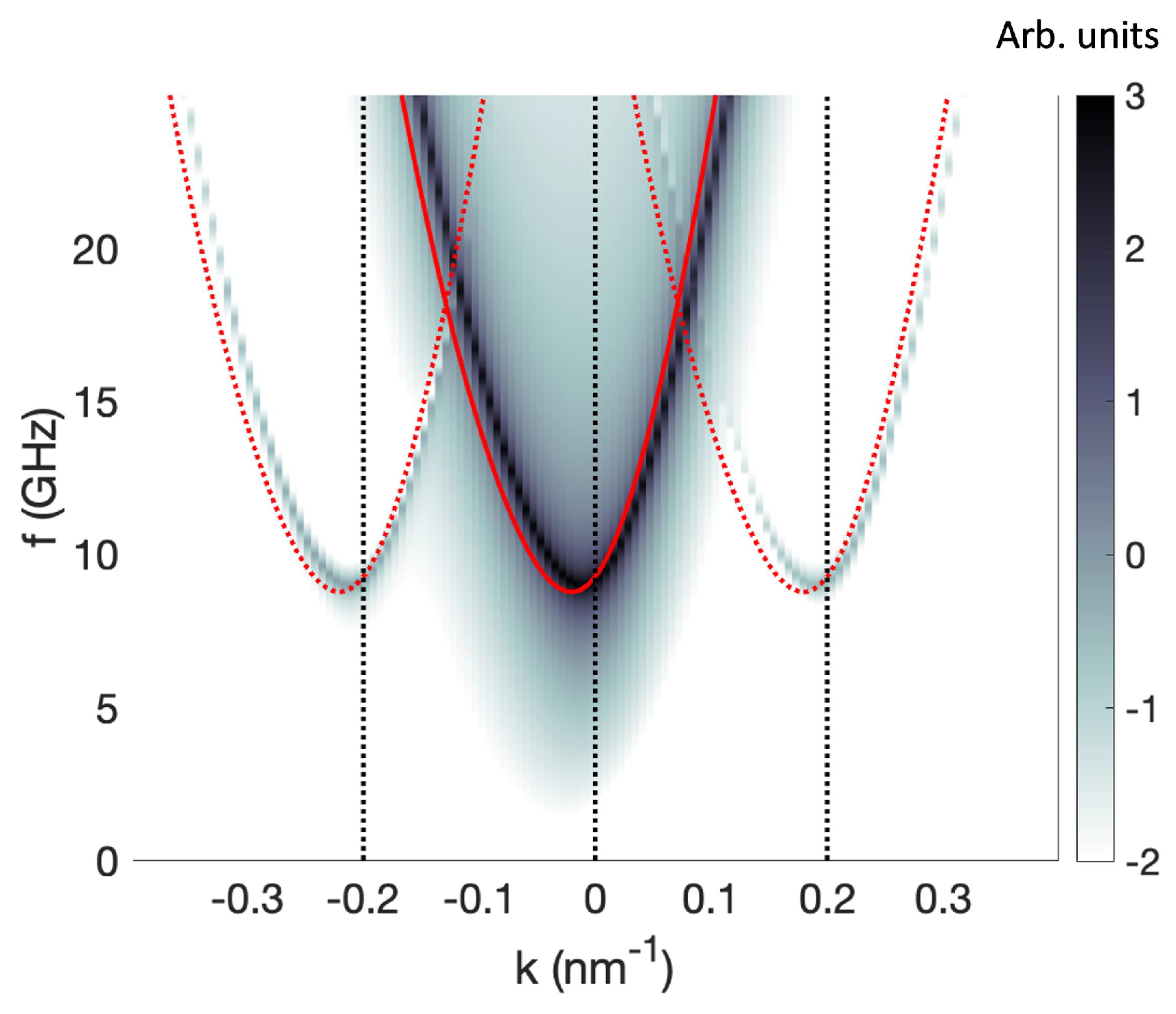
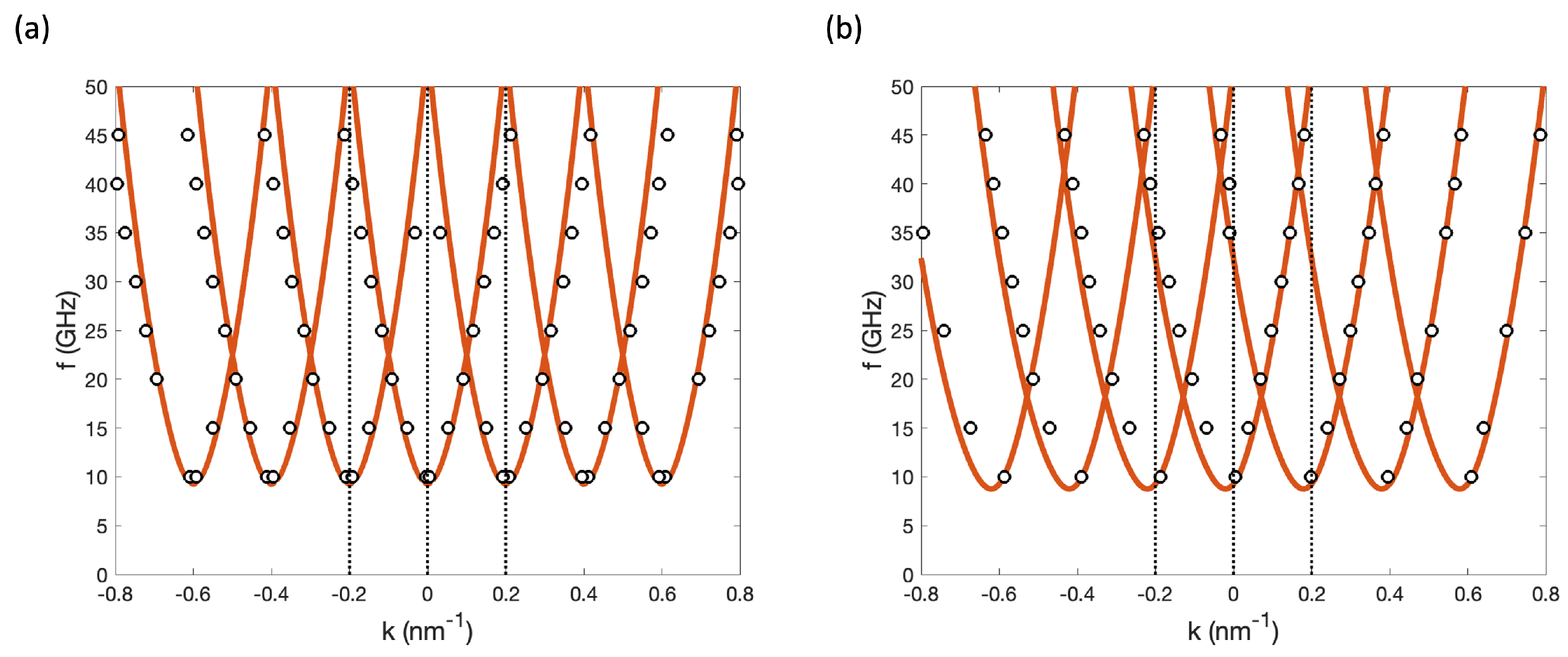
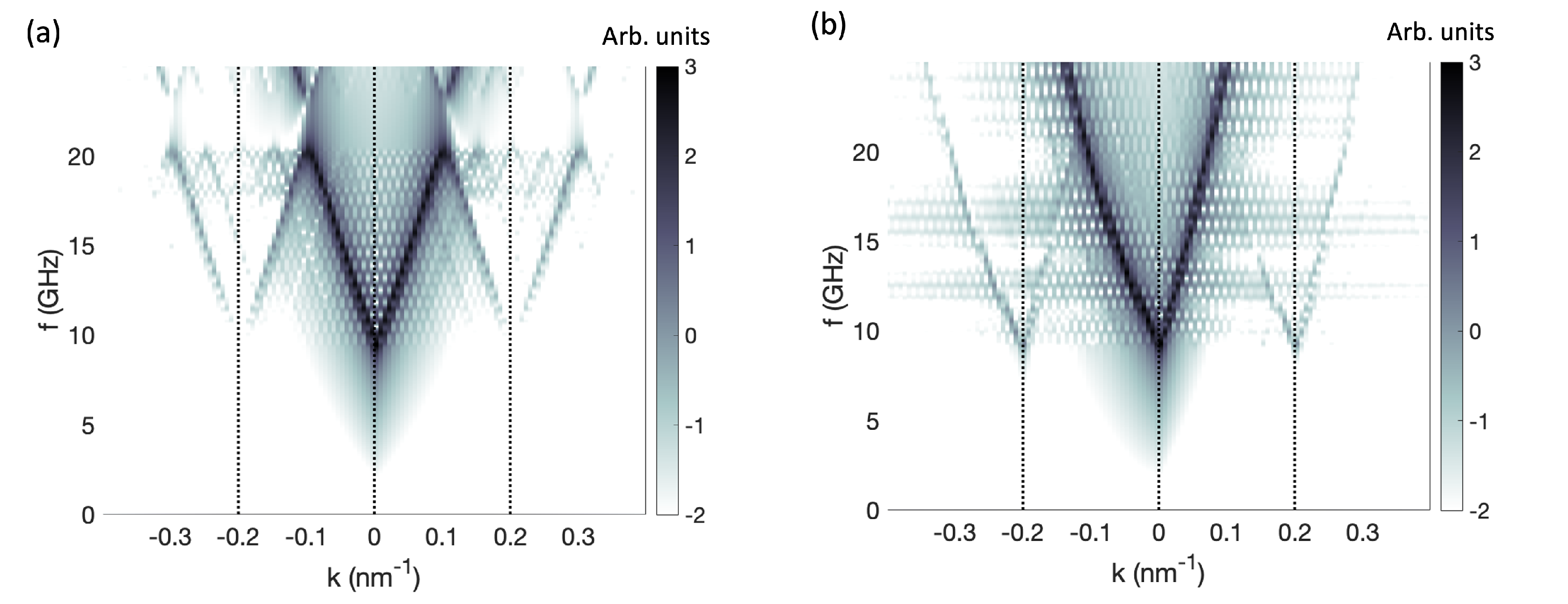
3. Results
3.1. Dispersion Relations
3.1.1. Local Microwave Field
3.2. Square Modulations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Balkanski, M.; Wallis, R. Semiconductor Physics and Applications; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Kruglyak, V.V.; Demokritov, S.O.; Grundler, D. Magnonics. J. Phys. D Appl. Phys. 2010, 43, 264001. [Google Scholar] [CrossRef]
- Grundler, D. Reconfigurable Magnonics Heats Up. Nat. Phys. 2015, 11, 438–441. [Google Scholar] [CrossRef]
- Serga, A.A.; Chumak, A.V.; Hillebrands, B. YIG magnonics. J. Phys. D Appl. Phys. 2010, 43, 264002. [Google Scholar] [CrossRef]
- Chumak, A.V.; Vasyuchka, V.I.; Serga, A.A.; Hillebrands, B. Magnon Spintronics. Nat. Phys. 2015, 11, 453–461. [Google Scholar] [CrossRef]
- Barman, A.; Gubbiotti, G.; Ladak, S.; Adeyeye, A.O.; Krawczyk, M.; GrÄfe, J.; Adelmann, C.; Cotofana, S.; Naeemi, A.; Vasyuchka, V.I.; et al. The 2021 Magnonics Roadmap. J. Phys. Condens. Matter. 2021, 33, 413001. [Google Scholar] [CrossRef]
- Chumak, A.V.; Kabos, P.; Wu, M.; Abert, C.; Adelmann, C.; Adeyeye, A.O.; Åkerman, J.; Aliev, F.G.; Anane, A.; Awad, A.; et al. Advances in Magnetics Roadmap on Spin-Wave Computing. IEEE Trans. Magn. 2022, 58, 1–72. [Google Scholar] [CrossRef]
- Nikitov, S.; Tailhades, P.; Tsai, C. Spin Waves in Periodic Magnetic Structures-Magnonic Crystals. J. Magn. Magn. Mater. 2001, 236, 320–330. [Google Scholar] [CrossRef]
- Wang, Z.K.; Zhang, V.L.; Lim, H.S.; Ng, S.C.; Kuok, M.H.; Jain, S.; Adeyeye, A.O. Observation of frequency band gaps in a one-dimensional nanostructured magnonic crystal. Appl. Phys. Lett. 2009, 94, 083112. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, V.; Lim, H.; Ng, S.; Kuok, M.; Jain, S.; Adeyeye, A. Nanostructured magnonic crystals with size-tunable bandgaps. ACS Nano 2010, 4, 643–648. [Google Scholar] [CrossRef] [PubMed]
- Frey, P.; Nikitin, A.A.; Bozhko, D.A.; Bunyaev, S.A.; Kakazeri, G.N.; Ustinov, A.B.; Kalinikos, B.A.; Ciubotaru, F.; Chumak, A.V.; Wang, Q.; et al. Reflection-less width-modulated magnonic crystal. Npj Commun. Phys. 2020, 3, 17. [Google Scholar] [CrossRef]
- Krawczyk, M.; Puszkarski, H. Plane-wave theory of three-dimensional magnonic crystals. Phys. Rev. B 2008, 77, 054437. [Google Scholar] [CrossRef]
- Tacchi, S.; Montoncello, F.; Madami, M.; Gubbiotti, G.; Carlotti, G.; Giovannini, L.; Zivieri, R.; Nizzoli, F.; Jain, S.; Adeyeye, A.O.; et al. Band Diagram of Spin Waves in a Two-Dimensional Magnonic Crystal. Phys. Rev. Lett. 2011, 107, 127204. [Google Scholar] [CrossRef]
- Zivieri, R.; Montoncello, F.; Giovannini, L.; Nizzoli, F.; Tacchi, S.; Madami, M.; Gubbiotti, G.; Carlotti, G.; Adeyeye, A.O. Collective spin modes in chains of dipolarly interacting rectangular magnetic dots. Phys. Rev. B 2011, 83, 054431. [Google Scholar] [CrossRef]
- Kumar, D.; Kłos, J.W.; Krawczyk, M.; Barman, A. Magnonic band structure, complete bandgap, and collective spin wave excitation in nanoscale two-dimensional magnonic crystals. J. Appl. Phys. 2014, 115, 043917. [Google Scholar] [CrossRef]
- Tacchi, S.; Gubbiotti, G.; Madami, M.; Carlotti, G. Brillouin light scattering studies of 2D magnonic crystals. J. Phys. Condens. Matter. 2017, 29, 073001. [Google Scholar] [CrossRef] [PubMed]
- Skjærvø, S.H.; Marrows, C.H.; Stamps, R.L.; Heyderman, L.J. Advances in artificial spin ice. Nat. Rev. Phys. 2020, 2, 13–28. [Google Scholar] [CrossRef]
- Gliga, S.; Kákay, A.; Hertel, R.; Heinonen, O.G. Spectral Analysis of Topological Defects in an Artificial Spin-Ice Lattice. Phys. Rev. Lett. 2013, 110, 117205. [Google Scholar] [CrossRef]
- Iacocca, E.; Gliga, S.; Stamps, R.L.; Heinonen, O. Reconfigurable Wave Band Structure of an Artificial Square Ice. Phys. Rev. B 2016, 93, 134420. [Google Scholar] [CrossRef]
- Jungfleisch, M.B.; Zhang, W.; Iacocca, E.; Sklenar, J.; Ding, J.; Jiang, W.; Zhang, S.; Pearson, J.E.; Novosad, V.; Ketterson, J.B.; et al. Dynamic Response of an Artificial Square Spin Ice. Phys. Rev. B 2016, 93, 100401. [Google Scholar] [CrossRef]
- Iacocca, E.; Heinonen, O. Topologically Nontrivial Magnon Bands in Artificial Square Spin Ices with Dzyaloshinskii-Moriya Interaction. Phys. Rev. Appl. 2017, 8, 034015. [Google Scholar] [CrossRef]
- Iacocca, E.; Gliga, S.; Heinonen, O.G. Tailoring Spin-Wave Channels in a Reconfigurable Artificial Spin Ice. Phys. Rev. Appl. 2020, 13, 044047. [Google Scholar] [CrossRef]
- Gliga, S.; Iacocca, E.; Heinonen, O.G. Dynamics of reconfigurable artificial spin ice: Toward magnonic functional materials. APL Mater. 2020, 8, 040911. [Google Scholar] [CrossRef]
- Negrello, R.; Montoncello, F.; Kaffash, M.T.; Jungfleisch, M.B.; Gubbiotti, G. Dynamic coupling and spin-wave dispersions in a magnetic hybrid system made of an artificial spin-ice structure and an extended NiFe underlayer. APL Mater. 2022, 10, 091115. [Google Scholar] [CrossRef]
- Lendinez, S.; Kaffash, M.T.; Heinonen, O.G.; Gliga, S.; Iacocca, E.; Jungfleisch, M.B. Nonlinear multi-magnon scattering in artificial spin ice. Nat. Commun. 2023, 14, 3419. [Google Scholar] [CrossRef] [PubMed]
- Heyderman, L.J.; Stamps, R.L. Artificial Ferroic Systems: Novel Functionality from Structure, Interactions and Dynamics. J. Phys. Condens. Matter. 2013, 25, 363201. [Google Scholar] [CrossRef] [PubMed]
- Lendinez, S.; Jungfleisch, M.B. Magnetization dynamics in artificial spin ice. J. Phys. Condens. Matter. 2019, 32, 013001. [Google Scholar] [CrossRef] [PubMed]
- Arroo, D.M.; Gartside, J.C.; Branford, W.R. Sculpting the spin-wave response of artificial spin ice via microstate selection. Phys. Rev. B 2019, 100, 214425. [Google Scholar] [CrossRef]
- Bhat, V.S.; Watanabe, S.; Baumgaertl, K.; Kleibert, A.; Schoen, M.A.W.; Vaz, C.A.F.; Grundler, D. Magnon Modes of Microstates and Microwave-Induced Avalanche in Kagome Artificial Spin Ice with Topological Defects. Phys. Rev. Lett. 2020, 125, 117208. [Google Scholar] [CrossRef] [PubMed]
- Caravelli, F.; Nisoli, C. Logical gates embedding in artificial spin ice. New J. Phys. 2020, 22, 103052. [Google Scholar] [CrossRef]
- Kaffash, M.T.; Lendinez, S.; Jungfleisch, M.B. Nanomagnonics with artificial spin ice. Phys. Lett. A 2021, 402, 127364. [Google Scholar] [CrossRef]
- Gartside, J.C.; Stenning, K.D.; Vanstone, A.; Holder, H.H.; Arroo, D.M.; Dion, T.; Caravelli, F.; Kurebayashi, H.; Branford, W.R. Reconfigurable training and reservoir computing in an artificial spin-vortex ice via spin-wave fingerprinting. Nat. Nanotechnol. 2022, 17, 460–469. [Google Scholar] [CrossRef]
- Gallardo, R.A.; Cortés-Ortuño, D.; Schneider, T.; Roldán-Molina, A.; Ma, F.; Troncoso, R.E.; Lenz, K.; Fangohr, H.; Lindner, J.; Landeros, P. Flat Bands, Indirect Gaps, and Unconventional Spin-Wave Behavior Induced by a Periodic Dzyaloshinskii-Moriya Interaction. Phys. Rev. Lett. 2019, 122, 067204. [Google Scholar] [CrossRef]
- Albisetti, E.; Petti, D.; Pancaldi, M.; Madami, M.; Tacchi, S.; Curtis, J.; King, W.P.; Papp, A.; Csaba, G.; Porod, W.; et al. Nanopatterning reconfigurable magnetic landscapes via thermally assisted scanning probe lithography. Nat. Nanotechnol. 2016, 11, 545–551. [Google Scholar] [CrossRef]
- Levati, V.; Girardi, D.; Pellizzi, N.; Panzeri, M.; Vitali, M.; Petti, D.; Albisetti, E. Phase Nanoengineering via Thermal Scanning Probe Lithography and Direct Laser Writing. Adv. Mater. Technol. 2023, 8, 2300166. [Google Scholar] [CrossRef]
- Auric, P.; Bouat, S.; Rodmacq, B. Structural and magnetic properties of annealed multilayers studied by Mössbauer spectroscopy, X-ray diffraction and magnetization measurements. J. Phys. Condens. Matter. 1998, 10, 3755. [Google Scholar] [CrossRef]
- Yin, Y.; Pan, F.; Ahlberg, M.; Ranjbar, M.; Dürrenfeld, P.; Houshang, A.; Haidar, M.; Bergqvist, L.; Zhai, Y.; Dumas, R.K.; et al. Tunable permalloy-based films for magnonic devices. Phys. Rev. B 2015, 92, 024427. [Google Scholar] [CrossRef]
- Khan, R.A.; Shepley, P.M.; Hrabec, A.; Wells, A.W.J.; Ocker, B.; Marrows, C.H.; Moore, T.A. Effect of annealing on the interfacial Dzyaloshinskii-Moriya interaction in Ta/CoFeB/MgO trilayers. Appl. Phys. Lett. 2016, 109, 132404. [Google Scholar] [CrossRef]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Van Waeyenberge, B. The Design and Verification of MuMax3. AIP Adv. 2014, 4, 107133. [Google Scholar] [CrossRef]
- Sprenger, P.; Hoefer, M.A.; Iacocca, E. Magnonic Band Structure Established by Chiral Spin-Density Waves in Thin-Film Ferromagnets. IEEE Magn. Lett. 2019, 10, 4501605. [Google Scholar] [CrossRef]
- Szulc, K.; Tacchi, S.; Hierro-Rogríguez, A.; Díaz, J.; Gruszecki, P.; Graczyk, P.; Quirós, C.; Markó, D.; Martín, J.I.; Vélez, M.; et al. Reconfigurable Magnonic Crystals Based on Imprinted Magnetization Textures in Hard and Soft Dipolar-Coupled Bilayers. ACS Nano 2022, 16, 14168–14177. [Google Scholar] [CrossRef] [PubMed]
- Nembach, H.T.; Shaw, J.M.; Weiler, M.; Jué, E.; Silva, T.J. Linear relation between Heisenberg exchange and interfacial Dzyaloshinskii-Moriya Interaction in metal films. Nat. Phys. 2015, 11, 825. [Google Scholar] [CrossRef]
- Venkat, G.; Kumar, D.; Franchin, M.; Dmytriiev, O.; Mruczkiewicz, M.; Fangohr, H.; Barman, A.; Krawczyk, M.; Prabhakar, A. Proposal for a standard micromagnetic problem: Spin wave dispersion in a magnonic waveguide. IEEE Trans. Magn. 2013, 49, 524. [Google Scholar] [CrossRef]
- Tacchi, S.; Troncoso, R.E.; Ahlberg, M.; Gubbiotti, G.; Madami, M.; Åkerman, J.; Landeros, P. Interfacial Dzyaloshinskii-Moriya Interaction in Pt/CoFeB Films: Effect of the Heavy-Metal Thickness. Phys. Rev. Lett. 2017, 118, 147201. [Google Scholar] [CrossRef] [PubMed]
- Madami, M.; Bonetti, S.; Consolo, G.; Tacchi, S.; Carlotti, G.; Gubbiotti, G.; Mancoff, F.B.; Yar, M.A.; Åkerman, J. Direct observation of a propagating spin wave induced by spin-transfer torque. Nat. Nanotechnol. 2011, 6, 635–638. [Google Scholar] [CrossRef]
- Madami, M.; Iacocca, E.; Sani, S.; Gubbiotti, G.; Tacchi, S.; Dumas, R.K.; Åkerman, J.; Carlotti, G. Propagating spin waves excited by spin-transfer torque: A combined electrical and optical study. Phys. Rev. B 2015, 92, 024403. [Google Scholar] [CrossRef]
- Yu, H.; Duerr, G.; Huber, R.; Bahr, M.; Schwarze, T.; Brandl, F.; Grundler, D. Omnidirectional Spin-Wave Nanograting Coupler. Nat. Commun. 2013, 4, 2702. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roxburgh, A.; Iacocca, E. Nano-Magnonic Crystals by Periodic Modulation of Magnetic Parameters. Magnetochemistry 2024, 10, 14. https://doi.org/10.3390/magnetochemistry10030014
Roxburgh A, Iacocca E. Nano-Magnonic Crystals by Periodic Modulation of Magnetic Parameters. Magnetochemistry. 2024; 10(3):14. https://doi.org/10.3390/magnetochemistry10030014
Chicago/Turabian StyleRoxburgh, Alison, and Ezio Iacocca. 2024. "Nano-Magnonic Crystals by Periodic Modulation of Magnetic Parameters" Magnetochemistry 10, no. 3: 14. https://doi.org/10.3390/magnetochemistry10030014
APA StyleRoxburgh, A., & Iacocca, E. (2024). Nano-Magnonic Crystals by Periodic Modulation of Magnetic Parameters. Magnetochemistry, 10(3), 14. https://doi.org/10.3390/magnetochemistry10030014





