Quantum Chemical Approaches to the Calculation of NMR Parameters: From Fundamentals to Recent Advances
Abstract
1. Introduction
2. Theoretical Background
2.1. Nonrelativistic Representation of NMR Parameters
2.2. Relativistic Representation of NMR Parameters
3. Quantum Chemical Methods for Calculating NMR Parameters
3.1. Configuration Interaction Methods
3.2. Coupled Clusters Methods
3.3. Density Functional Theory
- GGAs:
- Hybrid GGA functionals:
- Meta-GGA functionals:
- Hybrid meta-GGA functionals:
- and
- Long-range corrected hybrid functionals:
3.4. Polarization Propagator Methods
3.5. Methods Based on the Many-Body Perturbation Theory
4. Computational Factors Influencing the Accuracy of NMR Spectrum Modeling
4.1. Specialized Basis Sets
4.1.1. Specialized Basis Sets for Calculating Spin–Spin Coupling Constants
4.1.2. Specialized Basic Sets for Calculating NMR Chemical Shifts
4.2. Vibrational Corrections
4.2.1. Vibrational Corrections to Spin–Spin Coupling Constants
4.2.2. Vibrational Corrections to NMR Shielding Constants
4.3. Solvation Models
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gauss, J.; Stanton, J.F. Electron-correlated methods for the calculation of NMRchemical shifts. In Calculation of NMR and EPR Parameters, Theory and Applications, 1st ed.; Kaupp, M., Bühl, M., Malkin, V.G., Eds.; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2004; Chapter 8; pp. 123–139. [Google Scholar]
- Fukui, H. Theory and calculation of nuclear shielding constants. Prog. Nucl. Magn. Reson. Spectrosc. 1997, 31, 317–342. [Google Scholar] [CrossRef]
- Fukui, H. Theoretical aspects of spin–spin couplings. Nucl. Magn. Reson. 2007, 36, 113–130. [Google Scholar] [CrossRef]
- Webb, G.A.; Fukui, H.; Baba, T. Theoretical Aspects of Spin-spin coupling constants. In Nuclear Magnetic Resonance, 1st ed.; Webb, G.A., Ed.; Royal Society of Chemistry: London, UK, 2003; Volume 32, pp. 126–145. [Google Scholar] [CrossRef]
- Helgaker, T.; Coriani, S.; Jørgensen, P.; Kristensen, K.; Olsen, J.; Ruud, K. Recent advances in wave function-based methods of molecular-property calculations. Chem. Rev. 2012, 112, 543–631. [Google Scholar] [CrossRef]
- Helgaker, T.; Jaszuński, M.; Pecul, M. The quantum-chemical calculation of NMR indirect spin-spin coupling constants. Prog. Nucl. Magn. Reson. Spectrosc. 2008, 53, 249–268. [Google Scholar] [CrossRef]
- Helgaker, T.; Jaszuński, M.; Ruud, K. Ab initio methods for the calculation of NMR shielding and indirect spin-spin coupling constants. Chem. Rev. 1999, 99, 293–352. [Google Scholar] [CrossRef]
- Helgaker, T.; Pecul, M. Spin-Spin Coupling Constants with HF and DFT Methods. In Calculation of NMR and EPR Parameters: Theory and Applications, 1st ed.; Kaupp, M., Bühl, M., Malkin, V.G., Eds.; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2004; Chapter 7; pp. 101–121. [Google Scholar]
- Contreras, R.H.; Ferraro, M.B.; de Azúa, M.C.R.; Aucar, G.A. Brief account of nonrelativistic theory of NMR parameters. In High Resolution NMR Spectroscopy, Understanding Molecules and Their Electronic Structures, 1st ed.; Contreras, R.H., Ed.; Elsevier B.V.: London, UK, 2013; Volume 3, Chapter 2; pp. 9–39. [Google Scholar]
- Contreras, R.H.; Tormena, C.F.; Ducati, L.C. Transmission mechanisms of the Fermi-contact term of spin-spin couplings. In High Resolution NMR Spectroscopy, Understanding Molecules and Their Electronic Structures, 1st ed.; Contreras, R.H., Ed.; Elsevier B.V.: London, UK, 2013; Volume 3, Chapter 8; pp. 245–284. [Google Scholar]
- Aucar, G.A.; Romero, R.H.; Maldonado, A.F. Polarization propagators: A powerful theoretical tool for a deeper understanding of NMR spectroscopic parameters. Int. Rev. Phys. Chem. 2010, 29, 1–64. [Google Scholar] [CrossRef]
- Aucar, G.A.; de Azúa, M.C.R.; Giribet, C.G. The polarization propagator approach as a tool to study electronic molecular structures from high-resolution NMR parameters. In High Resolution NMR Spectroscopy, Understanding Molecules and Their Electronic Structures, 1st ed.; Contreras, R.H., Ed.; Elsevier B.V.: London, UK, 2013; Volume 3, Chapter 5; pp. 119–159. [Google Scholar]
- Autschbach, J.; Le Guennic, B. Analyzing and Interpreting NMR Spin–Spin Coupling Constants Using Molecular Orbital Calculations. J. Chem. Educ. 2007, 84, 156–171. [Google Scholar] [CrossRef]
- Autschbach, J. The Calculation of NMR Parameters in Transition Metal Complexes. In Principles and Applications of Density Functional Theory in Inorganic Chemistry I, Structure and Bonding, 1st ed.; Kaltsoyannis, N., McGrady, J.E., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 112, pp. 1–48. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, W.; Autschbach, J. Relativistic Theories of NMR Shielding. In Handbook of Relativistic Quantum Chemistry, 1st ed.; Liu, W., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–33. [Google Scholar] [CrossRef]
- Autschbach, J. Calculating NMR Chemical Shifts and J-Couplings for Heavy Element Compounds. In Encyclopedia of Analytical Chemistry: Applications, Theory and Instrumentation, Nuclear Magnetic Resonance and Electron Spin Resonance Spectroscopy, 1st ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014; pp. 1–14. [Google Scholar] [CrossRef]
- Faber, R.; Kaminsky, J.; Sauer, S.P.A. Rovibrational and Temperature Effects in Theoretical Studies of NMR Parameters. In Gas Phase NMR, 1st ed.; Jackowski, K., Jaszuński, M., Eds.; Royal Society of Chemistry: London, UK, 2016; Volume 6, Chapter 7; pp. 218–266. [Google Scholar] [CrossRef]
- Lazzeretti, P. Electronic current densities induced by magnetic fields and nuclear magnetic dipoles: Theory and computation of NMR spectral parameters. In High Resolution NMR Spectroscopy, Understanding Molecules and Their Electronic Structures, 1st ed.; Contreras, R.H., Ed.; Elsevier B.V.: London, UK, 2013; Volume 3, Chapter 7; pp. 209–243. [Google Scholar]
- Cremer, D.; Gräfenstein, J. Calculation and analysis of NMR spin-spin coupling constants. Phys. Chem. Chem. Phys. 2007, 9, 2791–2816. [Google Scholar] [CrossRef]
- De la Vega, J.M.G.; Fabián, J.S. Analysis of Contributions to Spin-Spin Coupling Constants by the Natural J-Coupling Method. In High Resolution NMR Spectroscopy, Understanding Molecules and Their Electronic Structures, 1st ed.; Contreras, R.H., Ed.; Elsevier B.V.: London, UK, 2013; Volume 3, Chapter 6; pp. 161–207. [Google Scholar]
- Rusakov, Y.Y.; Krivdin, L.B. Modern quantum chemical methods for calculating spin-spin coupling constants: Theoretical basis and structural applications in chemistry. Russ. Chem. Rev. 2013, 82, 99–130. [Google Scholar] [CrossRef]
- Rusakova, I.L.; Rusakov, Y.Y.; Krivdin, L.B. Theoretical grounds of relativistic methods for calculation of spin-spin coupling constants in nuclear magnetic resonance spectra. Russ. Chem. Rev. 2016, 85, 365–426. [Google Scholar] [CrossRef]
- Rusakova, I.L.; Rusakov, Y.Y. Quantum chemical calculations of 77Se and 125Te nuclear magnetic resonance spectral parameters and their structural applications. Magn. Reson. Chem. 2020, 59, 359–407. [Google Scholar] [CrossRef]
- Krivdin, L.B.; Rusakov, Y.Y. Structural and Stereochemical Applications of Computational NMR Using 29Si–1H and 77Se–1H Indirect Spin–Spin Coupling Constants. eMagRes 2014, 3, 87–110. [Google Scholar] [CrossRef]
- Krivdin, L.B.; Contreras, R.H. Recent advances in theoretical calculations of indirect spin-spin coupling constants. Annu. Rep. NMR Spectrosc. 2007, 61, 133–245. [Google Scholar] [CrossRef]
- Krivdin, L.B. Theoretical calculations of carbon-hydrogen spin-spin coupling constants. Prog. Nucl. Magn. Reson. Spectrosc. 2018, 108, 17–73. [Google Scholar] [CrossRef]
- Krivdin, L.B. Computational protocols for calculating 13C NMR chemical shifts. Prog. Nucl. Magn. Reson. 2019, 112, 103–156. [Google Scholar] [CrossRef]
- Krivdin, L.B. Calculation of 15N NMR chemical shifts: Recent advances and perspectives. Prog. Nucl. Magn. Reson. 2017, 102, 98–119. [Google Scholar] [CrossRef]
- Krivdin, L.B. Carbon-carbon spin-spin coupling constants: Practical applications of theoretical calculations. Prog. Nucl. Magn. Reson. 2018, 105, 54–99. [Google Scholar] [CrossRef]
- Krivdin, L.B. Computational NMR of Carbohydrates: Theoretical Background, Applications, and Perspectives. Molecules 2021, 26, 2450. [Google Scholar] [CrossRef]
- Krivdin, L.B. Computational 1H NMR: Part 1. Theoretical background. Magn. Reson. Chem. 2019, 57, 897–914. [Google Scholar] [CrossRef]
- Krivdin, L.B. Recent advances in computational 31P NMR: Part 1. Chemical shifts. Magn. Reson. Chem. 2020, 58, 478–499. [Google Scholar] [CrossRef]
- Krivdin, L.B. Recent advances in computational 31P NMR: Part 2. Spin–spin coupling constants. Magn. Reson. Chem. 2020, 58, 500–511. [Google Scholar] [CrossRef]
- Krivdin, L.B. Computational 1H NMR: Part 2. Chemical applications. Magn. Reson. Chem. 2020, 58, 5–14. [Google Scholar] [CrossRef]
- Krivdin, L.B. Computational 1H NMR: Part 3. Biochemical studies. Magn. Reson. Chem. 2020, 58, 15–30. [Google Scholar] [CrossRef]
- Krivdin, L.B. Computational NMR of charged systems. Magn. Reson. Chem. 2022, 60, 8–79. [Google Scholar] [CrossRef]
- Krivdin, L.B. Computational liquid-phase and solid-state 29Si NMR. Russ. Chem. Rev. 2020, 89, 449–468. [Google Scholar] [CrossRef]
- Krivdin, L.B. Computational aspects of 19F NMR. Russ. Chem. Rev. 2020, 89, 1040–1073. [Google Scholar] [CrossRef]
- Krivdin, L.B. Recent advances in computational liquid-phase 77Se NMR. Russ. Chem. Rev. 2021, 90, 265–279. [Google Scholar] [CrossRef]
- Krivdin, L.B. Computational NMR of heavy nuclei involving 109Ag, 113Cd, 119Sn, 125Te, 195Pt, 199Hg, 205Tl, and 207Pb. Russ. Chem. Rev. 2021, 90, 1166–1212. [Google Scholar] [CrossRef]
- Mulder, F.A.A.; Filatov, M. NMR chemical shift data and ab initio shielding calculations: Emerging tools for protein structure determination. Chem. Soc. Rev. 2010, 39, 578–590. [Google Scholar] [CrossRef]
- Pyykkö, P. Theory of NMR parameters. From Ramsey to Relativity, 1953 to 1983. In Calculation of NMR and EPR Parameters, Theory and Applications, 1st ed.; Kaupp, M., Bühl, M., Malkin, V.G., Eds.; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2004; Chapter 2; pp. 7–19. [Google Scholar]
- Facelli, J.C. Chemical shift tensors: Theory and application to molecular structural problems. Prog. Nucl. Magn. Reson. 2011, 58, 176–201. [Google Scholar] [CrossRef]
- Webb, G.A.; Jameson, C.J.; De Dios, A.C. Theoretical and physical aspects of nuclear shielding. In Nuclear Magnetic Resonance, 1st ed.; Webb, G.A., Ed.; Royal Society of Chemistry: London, UK, 2003; Volume 32, pp. 43–74. [Google Scholar] [CrossRef]
- Ebraheem, K.A.K.; Webb, G.A. Semi-empirical calculations of the chemical shifts of nuclei other than protons. Prog. Nucl. Magn. Reson. 1977, 11, 149–181. [Google Scholar] [CrossRef]
- O’Reilly, D.E. Chapter 1 Chemical shift calculations. Prog. Nucl. Magn. Reson. 1967, 2, 1–61. [Google Scholar] [CrossRef]
- Vaaraa, J.; Jokisaari, J.; Wasylishen, R.E.; Bryce, D.L. Spin–spin coupling tensors as determined by experiment and computational chemistry. Prog. Nucl. Magn. Reson. 2002, 41, 233–304. [Google Scholar] [CrossRef]
- Murrell, J.N. Chapter 1 The theory of nuclear spin-spin coupling in high resolution NMR spectroscopy. Prog. Nucl. Magn. Reson. 1970, 6, 1–60. [Google Scholar] [CrossRef]
- Jameson, C.J. Parameters, Calculation of Nuclear Magnetic Resonance. In Encyclopedia of Analytical Chemistry: Applications, Theory and Instrumentation, Nuclear Magnetic Resonance and Electron Spin Resonance Spectroscopy, 1st ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014; pp. 1–38. [Google Scholar] [CrossRef]
- Ramsey, N.F. Magnetic shielding of nuclei in molecules. Phys. Rev. 1950, 78, 699–703. [Google Scholar] [CrossRef]
- Ramsey, N.F. Electron coupled interactions between nuclear spins in molecules. Phys. Rev. 1953, 91, 303–307. [Google Scholar] [CrossRef]
- Lamb, W.E., Jr. Internal diamagnetic fields. Phys. Rev. 1941, 60, 817–819. [Google Scholar] [CrossRef]
- Harris, R.K.; Becker, E.D.; de Menezes, S.M.C.; Goodfellow, R.; Granger, P. NMR nomenclature. Nuclear spin properties and conventions for chemical shifts (IUPAC Recommendations 2001). Pure Appl. Chem. 2001, 73, 795–1818. [Google Scholar] [CrossRef]
- Harris, R.K.; Becker, E.D.; de Menezes, S.M.C.; Granger, P.; Hoffman, R.E.; Zilm, K.W. Further conventions for NMR shielding and chemical shifts (IUPAC Recommendations 2008). Pure Appl. Chem. 2008, 80, 59–84. [Google Scholar] [CrossRef]
- Becker, E.D. High Resolution NMR, Theory and Chemical Applications, 3rd ed.; Academic Press: London, UK, 2000; pp. 1–424. [Google Scholar]
- Kutzelnigg, W. Ab initio calculations of molecular properties. J. Mol. Struct. THEOCHEM 1989, 202, 11–61. [Google Scholar] [CrossRef]
- Robinson, P.D. Hypervirial Theorems and Perturbation Theory in Quantum Mechanics. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1965, 283, 229–237. [Google Scholar] [CrossRef]
- Pedersen, T.B.; Koch, H.; Hättig, C. Gauge invariant coupled cluster response theory. J. Chem. Phys. 1999, 110, 8318–8327. [Google Scholar] [CrossRef]
- Epstein, S.T. Gauge Invariance of the Hartree-Fock Approximation. J. Chem. Phys. 1965, 42, 2897–2898. [Google Scholar] [CrossRef]
- Ditchfield, R. Self-consistent perturbation theory of diamagnetism. Mol. Phys. 1974, 27, 789–807. [Google Scholar] [CrossRef]
- Kutzelnigg, W. Theory of magnetic susceptibilities and NMR chemical shifts in terms of localized quantities. Isr. J. Chem. 1980, 19, 193–200. [Google Scholar] [CrossRef]
- Schindler, M.; Kutzelnigg, W. Theory of magnetic susceptibilities and NMR chemical shifts in terms of localized quantities. II. Application to some simple molecules. J. Chem. Phys. 1982, 76, 1919–1933. [Google Scholar] [CrossRef]
- Hansen, A.E.; Bouman, T.D. Localized orbital/local origin method for calculation and analysis of NMR shieldings. Applications to 13C shielding tensors. J. Chem. Phys. 1985, 82, 5035–5047. [Google Scholar] [CrossRef]
- Arduengo, A.J., III; Dixon, D.A.; Kumashiro, K.K.; Lee, C.; Power, W.P.; Zilan, K. Chemical shielding tensor of a carbene. J. Am. Chem. Soc. 1994, 116, 6361–6367. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Hameka, H. On the nuclear magnetic shielding in the hydrogen molecule. Mol. Phys. 1958, 1, 203–215. [Google Scholar] [CrossRef]
- Hameka, H. Berechnung der magnetischen Eigenschaften des Wasserstoffmoleküls. Z. Naturforsch. A Phys. Sci. 1959, 14, 599–602. [Google Scholar] [CrossRef]
- Ditchfield, R. Molecular orbital theory of magnetic shielding and magnetic susceptibility. J. Chem. Phys. 1972, 56, 5688–5691. [Google Scholar] [CrossRef]
- Schreckenbach, G.; Ziegler, T. Calculation of NMR shielding tensors using gauge-including atomic orbitals and modern density functional theory. J. Phys. Chem. 1995, 99, 606–611. [Google Scholar] [CrossRef]
- Rauhut, G.; Puyear, S.; Wolinski, K.; Pulay, P. Comparison of NMR shieldings calculated from Hartree-Fock and density functional wave functions using gauge-including atomic orbitals. J. Phys. Chem. 1996, 100, 6310–6316. [Google Scholar] [CrossRef]
- Cheesemann, J.R.; Trucks, G.W.; Keith, T.A.; Frisch, M.J. A comparison of models for calculating nuclear magnetic resonance shielding tensors. J. Chem. Phys. 1996, 104, 5497–5509. [Google Scholar] [CrossRef]
- Jørgensen, P.; Simons, J. Introduction to Second-Quantization Methods. In Second Quantization-Based Methods in Quantum Chemistry, 1st ed.; Jørgensen, P., Simons, J., Eds.; Elsevier, Academic Press: New York, NY, USA, 1981; Chapter 1; pp. 1–17. [Google Scholar] [CrossRef]
- Sauer, S.P.A. Molecular Electromagnetism, A Computational Chemistry Approach, 1st ed.; Oxford University Press: Oxford, UK, 2011; pp. 1–306. [Google Scholar] [CrossRef]
- Reiher, M.; Wolf, A. Relativistic Quantum Chemistry, The Fundamental Theory of Molecular Science, 1st ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2009; pp. 1–669. [Google Scholar]
- Rose, M.E. Relativistic Electron Theory, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1961; pp. 1–302. [Google Scholar] [CrossRef]
- Moss, R.E. Advanced Molecular Quantum Mechanics: An Introduction to Relativistic Quantum Mechanics and the Quantum Theory of Radiation, 1st ed.; Chapman and Hall: London, UK, 1973; pp. 1–300. [Google Scholar]
- Strange, P. Relativistic Quantum Mechanics: With Applications in Condensed Matter and Atomic Physics, 1st ed.; Cambridge University Press: New York, NY, USA, 1998; pp. 1–612. [Google Scholar] [CrossRef]
- Dyall, K.G.; Faegri, K., Jr. Introduction to Relativistic Quantum Chemistry, 1st ed.; Oxford University Press: New York, NY, USA, 2007; pp. 1–544. [Google Scholar] [CrossRef]
- Schwerdtfeger, P. Relativistic Electronic Structure Theory, Part 1. Fundamentals, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 2002; pp. 1–946. [Google Scholar]
- Schwerdtfeger, P. Relativistic Electronic Structure Theory, Part 2. Applications, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 2004; pp. 1–1124. [Google Scholar]
- Eliav, E.; Kaldor, U. Four-component electronic structure methods. In Relativistic Methods for Chemists, 1st ed.; Barysz, M., Ishikawa, Y., Eds.; Springer: Heidelberg/Berlin, Germany, 2010; Chapter 7; pp. 279–349. [Google Scholar]
- Liu, W. Handbook of Relativistic Quantum Chemistry, 1st ed.; Springer-Verlag: Heidelberg/Berlin, Germany, 2017; pp. 1–907. [Google Scholar] [CrossRef]
- Kaldor, U.; Wilson, S. Theoretical Chemistry and Physics of Heavy and Superheavy Elements, 1st ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003; Volume 11, pp. 1–584. [Google Scholar]
- Grant, I.P. Relativistic Quantum Theory of Atoms and Molecules: Theory and Computation, 1st ed.; Springer: New York, NY, USA, 2007; Volume 40, pp. 1–800. [Google Scholar] [CrossRef]
- Wilson, S.; Grant, I.P.; Gyorffy, B.L. The effects of Relativity in Atoms, Molecules and the Solid State, 1st ed.; Springer: New York, NY, USA, 1991; pp. 1–360. [Google Scholar]
- Hess, B.A. Relativistic Effects in Heavy-Element Chemistry and Physics, 1st ed.; Wiley: New York, NY, USA, 2003; pp. 1–350. [Google Scholar]
- Hirao, K.; Ishikawa, Y. Recent Advances in Relativistic Molecular Theory, 1st ed.; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2004; Volume 5, pp. 1–327. [Google Scholar]
- Pyper, N.C. The relativistic theory of the chemical shift. Chem. Phys. Lett. 1983, 96, 204–210. [Google Scholar] [CrossRef]
- Pyper, N.C. Relativistic theory of nuclear shielding in one-electron atoms 1. Theoretical foundations and first-order terms. Mol. Phys. 1999, 97, 381–390. [Google Scholar] [CrossRef]
- Pyper, N.C.; Zhang, Z.C. Relativistic theory of nuclear shielding in one-electron atoms 2. Analytical and numerical results. Mol. Phys. 1999, 97, 391–413. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Webb, G.A. On the relativistic molecular orbital theory of diamagnetism and NMR chemical shifts. J. Mol. Struct. THEOCHEM 1983, 104, 439–444. [Google Scholar] [CrossRef]
- Pyykkö, P. On the relativistic theory of NMR chemical shifts. Chem. Phys. 1983, 74, 1–7. [Google Scholar] [CrossRef]
- Pyykkö, P.; Görling, A.; Rösch, N. A transparent interpretation of the relativistic contribution to the N.M.R. ‘heavy atom chemical shift’. Mol. Phys. 1987, 61, 195–205. [Google Scholar] [CrossRef]
- Nakatsuji, H.; Takashima, H.; Hada, M. Spin-orbit effect on the magnetic shielding constant using the ab initio UHF method. Chem. Phys. Lett. 1995, 233, 95–101. [Google Scholar] [CrossRef]
- Nakatsuji, H.; Hada, M.; Tejima, T.; Nakajima, T.; Sugimoto, M. Spin-orbit effect on the magnetic shielding constant using the ab initio UHF method. Electronic mechanism in the aluminum compounds, AlX4- (X = H, F, Cl, Br and I). Chem. Phys. Lett. 1996, 249, 284–289. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Nakajima, T.; Hada, M.; Nakatsuji, H. Relativistic theory of the magnetic shielding constant: A Dirac–Fock finite perturbation study. Chem. Phys. Lett. 1998, 283, 119–124. [Google Scholar] [CrossRef]
- Fukuda, R.; Hada, M.; Nakatsuji, H. Quasirelativistic theory for the magnetic shielding constant. I. Formulation of Douglas-Kroll-Hess transformation for the magnetic field and its application to atomic systems. J. Chem. Phys. 2003, 118, 1015–1026. [Google Scholar] [CrossRef]
- Fukuda, R.; Hada, M.; Nakatsuji, H. Quasirelativistic theory for magnetic shielding constants. II. Gauge-including atomic orbitals and applications to molecules. J. Chem. Phys. 2003, 118, 1027–1035. [Google Scholar] [CrossRef]
- Fukuda, R.; Nakatsuji, H. Quasirelativistic theory for the magnetic shielding constant. III. Quasirelativistic second-order Møller–Plesset perturbation theory and its application to tellurium compounds. J. Chem. Phys. 2005, 123, 044101. [Google Scholar] [CrossRef]
- Fukui, H.; Baba, T.; Inomata, H. Calculation of nuclear magnetic shieldings. X. Relativistic effects. J. Chem. Phys. 1996, 105, 3175–3186, Erratum in J. Chem. Phys. 1997, 106, 2987. [Google Scholar] [CrossRef]
- Fukui, H.; Baba, T. Calculation of nuclear magnetic shieldings. XV. Ab initio zeroth-order regular approximation method. J. Chem. Phys. 2002, 117, 7836–7844. [Google Scholar] [CrossRef]
- Xiao, Y.; Peng, D.; Liu, W. Four-component relativistic theory for nuclear magnetic shielding constants: The orbital decomposition approach. J. Chem. Phys. 2007, 126, 081101. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, W.; Cheng, L.; Peng, D. Four-component relativistic theory for nuclear magnetic shielding constants: Critical assessments of different approaches. J. Chem. Phys. 2007, 126, 214101. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Xiao, Y.; Liu, W. Four-component relativistic theory for nuclear magnetic shielding: Magnetically balanced gauge-including atomic orbitals. J. Chem. Phys. 2009, 131, 244113. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Sun, Q.; Liu, W. Fully relativistic theories and methods for NMR parameters. Theor. Chem. Acc. 2012, 131, 1080. [Google Scholar] [CrossRef]
- Kutzelnigg, W.; Liu, W. Relativistic theory of nuclear magnetic resonance parameters in a Gaussian basis representation. J. Chem. Phys. 2009, 131, 044129. [Google Scholar] [CrossRef]
- Sun, Q.; Xiao, Y.; Liu, W. Exact two-component relativistic theory for NMR parameters: General formulation and pilot application. J. Chem. Phys. 2012, 137, 174105. [Google Scholar] [CrossRef]
- Aucar, G.A.; Aucar, I.A. Recent developments in absolute shielding scales for NMR spectroscopy. In Annual Reports on NMR Spectroscopy, 1st ed.; Webb, G., Ed.; Academic Press: London, UK, 2019; Volume 96, Chapter 3; pp. 77–141. [Google Scholar]
- Aucar, G.A.; Maldonado, A.F.; Montero, M.D.A.; Cruz, T.S. Theoretical developments and applications of polarization propagators. Int. J. Quantum Chem. 2019, 119, e25722. [Google Scholar] [CrossRef]
- Melo, J.I.; de Azua, M.C.R.; Giribet, C.G.; Aucar, G.A.; Romero, R.H. Relativistic effects on the nuclear magnetic shielding tensor. J. Chem. Phys. 2003, 118, 471–486. [Google Scholar] [CrossRef]
- Melo, J.I.; de Azua, M.C.R.; Giribet, C.G.; Aucar, G.A.; Provasi, P.F. Relativistic effects on nuclear magnetic shielding constants in HX and CH3X (X = Br, I) based on the linear response within the elimination of small component approach. J. Chem. Phys. 2004, 121, 6798–6808. [Google Scholar] [CrossRef]
- Gomez, S.S.; Romero, R.H.; Aucar, G.A. Fully relativistic calculation of nuclear magnetic shieldings and indirect nuclear spin-spin couplings in group-15 and -16 hydrides. J. Chem. Phys. 2002, 117, 7942–7946. [Google Scholar] [CrossRef]
- Aucar, G.A.; Oddershede, J. Relativistic theory for indirect nuclear spin–spin couplings within the polarization propagator approach. Int. J. Quantum Chem. 1993, 47, 425–435. [Google Scholar] [CrossRef]
- Maldonado, A.F.; Aucar, G.A.; Melo, J.I. Core-dependent and ligand-dependent relativistic corrections to the nuclear magnetic shieldings in MH4−nYn (n = 0–4; M = Si, Ge, Sn, and Y = H, F, Cl, Br, I) model compounds. J. Mol. Model. 2014, 20, 2417. [Google Scholar] [CrossRef] [PubMed]
- Aucar, G.A.; Saue, T.; Visscher, L.; Jensen, H.J.A. On the origin and contribution of the diamagnetic term in four-component relativistic calculations of magnetic properties. J. Chem. Phys. 1999, 110, 6208–6218. [Google Scholar] [CrossRef]
- Vaara, J.; Malkina, O.L.; Stoll, H.; Malkin, V.G.; Kaupp, M. Study of relativistic effects on nuclear shieldings using density-functional theory and spin–orbit pseudopotentials. J. Chem. Phys. 2001, 114, 61–71. [Google Scholar] [CrossRef]
- Vaara, J.; Ruud, K.; Vahtras, O. Second- and third-order spin-orbit contributions to nuclear shielding tensors. J. Chem. Phys. 1999, 111, 2900–2909. [Google Scholar] [CrossRef][Green Version]
- Vaara, J.; Ruud, K.; Vahtras, O.; Ågren, H.; Jokissari, J. Quadratic response calculations of the electronic spin-orbit contribution to nuclear shielding tensors. J. Chem. Phys. 1998, 109, 1212–1222. [Google Scholar] [CrossRef]
- Manninen, P.; Lantto, P.; Vaara, J.; Ruud, K. Perturbational ab initio calculations of relativistic contributions to nuclear magnetic resonance shielding tensors. J. Chem. Phys. 2003, 119, 2623–2637. [Google Scholar] [CrossRef]
- Autschbach, J. Calculation of heavy-nucleus chemical shifts. relativisticall-electron methods. In Calculation of NMR and EPR Parameters, Theory and Applications, 1st ed.; Kaupp, M., Bühl, M., Malkin, V.G., Eds.; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2004; Chapter 14; pp. 69–117. [Google Scholar]
- Autschbach, J. Perspective: Relativistic effects. J. Chem. Phys. 2012, 136, 150902. [Google Scholar] [CrossRef]
- Autschbach, J. Relativistic Effects on NMR Parameters. In High Resolution NMR Spectroscopy, Understanding Molecules and Their Electronic Structures, 1st ed.; Contreras, R.H., Ed.; Elsevier B.V.: London, UK, 2013; Volume 3. [Google Scholar]
- Autschbach, J.; Ziegler, T. Relativistic computation of NMR shieldings and spin-spin coupling constants. In Encyclopedia of Nuclear Magnetic Resonance: Advances in NMR, 1st ed.; Grant, D.M., Harris., R.K., Eds.; John Wiley and Sons: Chichester, UK, 2002; Volume 9, pp. 306–323. [Google Scholar]
- Manninen, P. Breit-Pauli Hamiltonian and Molecular Magnetic Resonance Properties. Ph.D. Thesis, University of Oulu, Department of Physical Sciences, Oulu, Finland, 2004. [Google Scholar]
- Vaara, J.; Manninen, P.; Lantto, P. Perturbational and ECP calculation of relativistic effectsin NMR shielding and spin-spin coupling. In Calculation of NMR and EPR Parameters, Theory and Applications, 1st ed.; Kaupp, M., Bühl, M., Malkin, V.G., Eds.; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2004; Chapter 13; pp. 209–226. [Google Scholar]
- Manninen, P.; Ruud, K.; Lantto, P.; Vaara, J. Leading-order relativistic effects on nuclear magnetic resonance shielding tensors. J. Chem. Phys. 2005, 122, 114107, Erratum in: J. Chem. Phys. 2006, 124, 149901. [Google Scholar] [CrossRef]
- Schnack-Petersen, A.K.; Simmermacher, M.; Fasshauer, E.; Jensen, H.J.A.; Sauer, S.P.A. The second-order-polarization-propagator-approximation (SOPPA) in a four-component spinor basis. J. Chem. Phys. 2020, 152, 134113. [Google Scholar] [CrossRef]
- Morishima, I.; Endo, K.; Yonezawa, T. Effect of the heavy atom on the nuclear shielding constant. I. The proton chemical shifts in hydrogen halides. J. Chem. Phys. 1973, 59, 3356–3364. [Google Scholar] [CrossRef]
- Oprea, C.I. Theoretical Calculations of Heavy Atom Effects in Magnetic Resonance Spectroscopy. Ph.D. Thesis, Theoretical Chemistry School of Biotechnology Royal Institute of Technology, Stockholm, Sweden, 2006. [Google Scholar]
- Iliaš, M.; Saue, T.; Enevoldsen, T.; Jensen, H.J.A. Gauge origin independent calculations of nuclear magnetic shieldings in relativistic four-component theory. J. Chem. Phys. 2009, 131, 124119. [Google Scholar] [CrossRef]
- Jaszuński, M.; Ruud, K. Nuclear magnetic resonance shielding constants in XH4 group XIV hydrides. Mol. Phys. 2006, 104, 2139–2148. [Google Scholar] [CrossRef]
- Wolff, S.K.; Ziegler, T. Calculation of DFT-GIAO NMR shifts with the inclusion of spin-orbit coupling. J. Chem. Phys. 1998, 109, 895–905. [Google Scholar] [CrossRef]
- Kaupp, M. Relativistic effects on NMR chemical shifts. In Relativistic Electronic Structure Theory, Part 2: Applications, Theoretical and Computational Chemistry, 1st ed.; Schwerdtfeger, P., Ed.; Elsevier B.V.: Amsterdam, The Netherlands, 2004; Volume 14, Chapter 9; pp. 552–597. [Google Scholar]
- Pestka, G.; Karwowski, J. Structure of Dirac-Coulomb-Breit Hamiltonian. In Symmetry and Structural Properties of Condensed Matter, 1st ed.; World Scientific: Singapore, 2001; pp. 111–115. [Google Scholar] [CrossRef]
- Foldy, L.L.; Wouthuysen, S.A. On the Dirac theory of spin 1/2 particles and its non-relativistic limit. Phys. Rev. 1950, 78, 29–36. [Google Scholar] [CrossRef]
- Heully, J.-L.; Lindgren, I.; Lindroth, E.; Lundqvist, S.; Martensson-Pendrill, A.-M. Diagonalisation of the Dirac Hamiltonian as a basis for a relativistic many-body procedure. J. Phys. B At. Mol. Phys. 1986, 19, 2799–2815. [Google Scholar] [CrossRef]
- Vícha, J.; Patzschke, M.; Marek, R. A relativistic DFT methodology for calculating the structures and NMR chemical shifts of octahedral platinum and iridium complexes. Phys. Chem. Chem. Phys. 2013, 15, 7740–7754. [Google Scholar] [CrossRef]
- Kaupp, M.; Malkina, O.L.; Malkin, V.G.; Pyykkö, P. How do spin-orbit-induced heavy-atom effects on NMR chemical shifts function? Validation of a simple analogy to spin-spin coupling by Density Functional Theory (DFT) calculations on some iodo compounds. Chem. Eur. J. 1998, 4, 118–126. [Google Scholar] [CrossRef]
- Kaupp, M.; Malkina, O.L.; Malkin, V.G. The role of π-type nonbonding orbitals for spin-orbit induced NMR chemical shifts: DFT study of 13C and 19F shifts in the series CF3IFn (n = 0, 2, 4, 6). J. Comput. Chem. 1999, 20, 1304–1313. [Google Scholar] [CrossRef]
- Vícha, J.; Straka, M.; Munzarová, M.L.; Marek, R. Mechanism of spin-orbit effects on the ligand NMR chemical shift in transition-metal complexes: Linking NMR to EPR. J. Chem. Theor. Comput. 2014, 10, 1489–1499. [Google Scholar] [CrossRef]
- Asenjo, F.A.; Zamanian, J.; Marklund, M.; Brodin, G.; Johansson, P. Semi-relativistic effects in spin-1/2 quantum plasmas. New J. Phys. 2012, 14, 073042. [Google Scholar] [CrossRef]
- Sherrill, C.D.; Schaefer III, H.F. The configuration interaction method: Advances in highly correlated approaches. Adv. Quantum Chem. 1999, 34, 143–269. [Google Scholar] [CrossRef]
- Siegbahn, P.E.M. The configuration interaction method. In Quantum Chemistry: European Summer School in Quantum Chemistry, 1st ed.; Roos, B.O., Ed.; Springer-Verlag: New York, NY, USA, 1992; Volume 58, pp. 255–293. [Google Scholar]
- Karwowski, J. The configuration interaction approach to electron correlation. In Methods in Computational Molecular Physics, 1st ed.; Wilson, S., Diercksen, G.H.F., Eds.; Plenum Press: New York, NY, USA, 1992; pp. 65–98. [Google Scholar]
- Kowalewski, J.; Roos, B.; Siegbahn, P.; Vestin, R. Large configuration interaction calculations of nuclear spin-spin coupling constants. I. HD molecule. Chem. Phys. 1974, 3, 70–77. [Google Scholar] [CrossRef]
- Brueckner, K.A. Many-body problem for strongly interacting particles. II. Linked cluster expansion. Phys. Rev. 1955, 100, 36–45. [Google Scholar] [CrossRef]
- Hugenholtz, A. Perturbation theory of large quantum systems. Physica 1957, 23, 481–532. [Google Scholar] [CrossRef]
- Goldstone, J. Derivation of the Brueckner many-body theory. Proc. R. Soc. Lond. 1957, 239, 267–279. [Google Scholar] [CrossRef]
- Bartlett, R.J. Many-body perturbation theory and coupled cluster theory for electron correlation in molecules. Annu. Rev. Phys. Chem. 1981, 32, 359–401. [Google Scholar] [CrossRef]
- Hanrath, M. On the concepts of connectivity, separability, and consistency: An illustration by partitioned diagrams and numerical probing. Chem. Phys. 2009, 356, 31–38. [Google Scholar] [CrossRef]
- Pecul, M. The nuclear spin–spin coupling constant in He2. J. Chem. Phys. 2000, 113, 10835–10836. [Google Scholar] [CrossRef]
- Auer, A.A.; Gauss, J.; Pecul, M. Full configuration-interaction and coupled-cluster calculations of the indirect spin-spin coupling constant of BH. Chem. Phys. Lett. 2003, 368, 172–176. [Google Scholar] [CrossRef]
- Vizioli, C.V.; de Azua, M.C.R. NMR 1J(HD) coupling in HD as a function of interatomic distance in the presence of an external magnetic field. Mol. Phys. 2000, 98, 891–897. [Google Scholar] [CrossRef]
- Helgaker, T.; Jaszuński, M.; Ruud, K. Full CI calculations of magnetic properties of the H2 molecule in the B1Σ+u state. Pol. J. Chem. 1998, 72, 1405–1410. [Google Scholar]
- Del Bene, J.; Ditchfield, R.; Pople, J.A. Self-Consistent Molecular Orbital Methods. X. Molecular Orbital Studies of Excited States with Minimal and Extended Basis Sets. J. Chem. Phys. 1971, 55, 2236–2241. [Google Scholar] [CrossRef]
- Foresman, J.B.; Head-Gordon, M.; Pople, J.A.; Frisch, M. Toward a systematic molecular orbital theory for excited states. J. Phys. Chem. 1992, 96, 135–149. [Google Scholar] [CrossRef]
- Maurice, D.; Head-Gordon, M. Configuration interaction with single substitutions for excited states of open-shell molecules. Int. J. Quantum Chem. 1995, 56, 361–370. [Google Scholar] [CrossRef]
- Head-Gordon, M.; Rico, R.J.; Oumi, M.; Lee, T.J. A doubles correction to electronic excited states from configuration interaction in the space of single substitutions. Chem. Phys. Lett. 1994, 219, 21–29. [Google Scholar] [CrossRef]
- Cremer, D. From configuration interaction to coupled cluster theory: The quadratic configuration interaction approach. WIREs Comput. Mol. Sci. 2013, 3, 482–503. [Google Scholar] [CrossRef]
- Harrison, R.J.; Handy, N.C. Full CI calculations on BH, H2O, NH3, and HF. Chem. Phys. Lett. 1983, 95, 386–391. [Google Scholar] [CrossRef]
- Pople, J.A. Theoretical models for chemistry. In Energy, Structure and Reactivity, 1st ed.; Smith, D.W., McRae, W.B., Eds.; John Wiley & Sons: New York, NY, USA, 1973; pp. 51–61. [Google Scholar]
- Szalay, P.G. Configuration Interaction: Corrections for Size-Consistency. In Encyclopedia of Computational Chemistry; von Ragué Schleyer, P., Jorgensen, W.L., Schaefer, H.F., III, Schreiner, P., Thiel, W., Glen, R., Eds.; John Wiley & Sons, Ltd.: New York, NY, USA, 2004; pp. 1–47. [Google Scholar] [CrossRef]
- Kutzelnigg, W. Pair Correlation Theories. In Methods of Electronic Structure Theory, 1st ed.; Schaefer, H.F., III, Eds.; Plenum Press: New York, NY, USA, 1977; Chapter 5; pp. 129–188. [Google Scholar] [CrossRef]
- Čížek, J. On the Use of the Cluster Expansion and the Technique of Diagrams in Calculations of Correlation Effects in Atoms and Molecules. Adv. Chem. Phys. 1969, 14, 35–89. [Google Scholar] [CrossRef]
- Kelly, H.P.; Sessler, A.M. Correlation Effects in Many-Fermion Systems: Multiple-Particle Excitation Expansion. Phys. Rev. 1963, 132, 2091–2095. [Google Scholar] [CrossRef]
- Kelly, H.P. Correlation Effects in Many Fermion Systems. II. Linked Clusters. Phys. Rev. 1964, 134, A1450–A1453. [Google Scholar] [CrossRef]
- Meyer, W. PNO–CI Studies of electron correlation effects. I. Configuration expansion by means of nonorthogonal orbitals, and application to the ground state and ionized states of methane. J. Chem. Phys. 1973, 58, 1017–1035. [Google Scholar] [CrossRef]
- Meyer, W. PNO-CI and CEPA studies of electron correlation effects II. Potential curves and dipole moment functions of the OH radical. Theor. Chim. Acta 1974, 35, 277–292. [Google Scholar] [CrossRef]
- Koch, S.; Kutzelnigg, W. Comparison of CEPA and CP-MET methods. Theor. Chim. Acta 1981, 59, 387–411. [Google Scholar] [CrossRef]
- Ahlrichs, R.; Scharf, P.; Ehrhardt, C. The coupled pair functional (CPF). A size consistent modification of the CI(SD) based on an energy functional. J. Chem. Phys. 1985, 82, 890–898. [Google Scholar] [CrossRef]
- Sherrill, C.D.; Schaefer III, H.F. Compact Variational Wave Functions Incorporating Limited Triple and Quadruple Substitutions. J. Phys. Chem. 1996, 100, 6069–6075. [Google Scholar] [CrossRef]
- Cremer, D.; He, Z. Size-extensive QCISDT—Implementation and application. Chem. Phys. Lett. 1994, 222, 40–45. [Google Scholar] [CrossRef]
- He, Z.; Kraka, E.; Cremer, D. Application of quadratic CI with singles, doubles, and triples (QCISDT): An attractive alternative to CCSDT. Int. J. Quantum Chem. 1996, 57, 157–172. [Google Scholar] [CrossRef]
- He, Y.; He, Z.; Cremer, D. Size-extensive quadratic CI methods including quadruple excitations: QCISDTQ and QCISDTQ(6)—On the importance of four-electron correlation effects. Chem. Phys. Lett. 2000, 317, 535–544. [Google Scholar] [CrossRef]
- Cramer, C.J. Essentials of Computational Chemistry, Theories and Models, 2nd ed.; John Wiley & Sons Ltd.: Chichester, UK, 2004; pp. 1–596. [Google Scholar]
- Jensen, F. Introduction to Computational Chemistry, 2nd ed.; John Wiley & Sons Ltd.: Chichester, UK, 2007; pp. 1–599. [Google Scholar]
- Piela, L. Chapter 2—Correlation and Anticorrelation of Electronic Motions. In Ideas of Quantum Chemistry, Volume Two: Interactions, 3rd ed.; Elsevier B.V.: Amsterdam, The Netherlands, 2020; Chapter 2; pp. 81–190. [Google Scholar] [CrossRef]
- Andersson, K.; Malmqvist, P.-Å.; Roos, B.O. Second-order perturbation theory with a complete active space self-consistent field reference function. J. Chem. Phys. 1992, 96, 1218–1226. [Google Scholar] [CrossRef]
- Andersson, K.; Malmqvist, P.-Å.; Roos, B.O.; Sadlej, A.J.; Wolinski, K. Second-order perturbation theory with a CASSCF reference function. J. Phys. Chem. 1990, 94, 5483–5488. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.P. Introduction of n-electron valence states for multireference perturbation theory. J. Chem. Phys. 2001, 114, 10252–10264. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.P. N-electron valence state perturbation theory: A fast implementation of the strongly contracted variant. Chem. Phys. Lett. 2001, 350, 297–305. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.P. n-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants. J. Chem. Phys. 2002, 117, 9138–9153. [Google Scholar] [CrossRef]
- Havenith, R.W.A.; Taylor, P.R.; Angeli, C.; Cimiraglia, R.; Ruud, K. Calibration of the n-electron valence state perturbation theory approach. J. Chem. Phys. 2004, 120, 4619–4625. [Google Scholar] [CrossRef] [PubMed]
- Angeli, C.; Pastore, M.; Cimiraglia, R. New perspectives in multireference perturbation theory: The n-electron valence state approach. Theor. Chim. Acta 2007, 117, 743–754. [Google Scholar] [CrossRef]
- Angeli, C.; Borini, S.; Cestari, M.; Cimiraglia, R. A quasidegenerate formulation of the second order 𝑛-electron valence state perturbation theory approach. J. Chem. Phys. 2004, 121, 4043–4049. [Google Scholar] [CrossRef]
- Angeli, C.; Bories, B.; Cavallini, A.; Cimiraglia, R. Third-order multireference perturbation theory: The 𝑛-electron valence state perturbation-theory approach. J. Chem. Phys. 2006, 124, 054108. [Google Scholar] [CrossRef]
- Witek, H.A.; Nakano, H.; Hirao, K. Multireference Perturbation Theory with Optimized Partitioning. I. Theoretical and Computational Aspects. J. Chem. Phys. 2003, 118, 8197–8206. [Google Scholar] [CrossRef]
- Dyall, K.G. The Choice of a Zeroth-Order Hamiltonian for Second-Order Perturbation Theory with a Complete Active Space Self-Consistent-Field Reference Function. J. Chem. Phys. 1995, 102, 4909–4918. [Google Scholar] [CrossRef]
- Yost, S.R.; Head-Gordon, M. Size consistent formulations of the perturb-then-diagonalize Møller-Plesset perturbation theory correction to non-orthogonal configuration interaction. J. Chem. Phys. 2016, 145, 054105. [Google Scholar] [CrossRef]
- Olsen, J.; Roos, B.O.; Jǿrgensen, P.; Jensen, H.J.A. Determinant based configuration interaction algorithms for complete and restricted configuration interaction spaces. J. Chem. Phys. 1988, 89. [Google Scholar] [CrossRef]
- Moszynski, R. Theory of intermolecular forces: An introductory account. In Challenges and Advances in Computational Chemistry and Physics, Vol. 4, Molecular Materials with Specific Interactions, Modeling and Design, 1st ed.; Sokalski, W.A., Leszczynski, J., Eds.; Springer: Dordercht, The Netherlands, 2007; Volume 4, Chapter 1; pp. 1–152. [Google Scholar]
- Gendron, F.; Sharkas, K.; Autschbach, J. Calculating NMR chemical shifts for paramagnetic metal complexes from first-principles. J. Phys. Chem. Lett. 2015, 6, 2183–2188. [Google Scholar] [CrossRef] [PubMed]
- Jaszuński, M.; Helgaker, T.; Ruud, K.; Bak, K.L.; Jǿrgensen, P. MCSCF calculations of nitrogen NMR shielding constants using London atomic orbitals. Chem. Phys. Lett. 1994, 220, 154–160. [Google Scholar] [CrossRef]
- Ruud, K.; Helgaker, T.; Kobayashi, R.; Jørgensen, P.; Bak, K.L.; Jensen, H.-J.A. Multiconfigurational self-consistent field calculations of nuclear shieldings using London atomic orbitals. J. Chem. Phys. 1994, 100, 8178–8185. [Google Scholar] [CrossRef]
- Jaszuński, M.; Rizzo, A.; Yeager, D.L. A multiconfigurational linear response study of N2. Chem. Phys. 1989, 136, 385–397. [Google Scholar] [CrossRef]
- San Fabián, J.; Gasanueva, J.; San Fabián, E.; Guilleme, J. MCSCF calculations of NMR spin–spin coupling constant of the HF molecule. J. Chem. Phys. 2000, 112, 4143–4152. [Google Scholar] [CrossRef]
- Guilleme, J.; San Fabián, J. Basis sets and active space in multiconfigurational self-consistent field calculations of nuclear magnetic resonance spin–spin coupling constants. J. Chem. Phys. 1998, 109, 8181–8186. [Google Scholar] [CrossRef]
- Guilleme, J.; San Fabián, J.; Gasanueva, J.; Díez, E. Vicinal proton–proton coupling constants: MCSCF ab initio calculations of ethane. Chem. Phys. Lett. 1999, 314, 168–175. [Google Scholar] [CrossRef]
- Jaszuński, M.; Ruud, K. Spin-spin coupling constants in C2H2. Chem. Phys. Lett. 2001, 336, 473–478. [Google Scholar] [CrossRef]
- Helgaker, T.; Jaszuński, M.; Ruud, K.; Gorska, A. Basis-set dependence of nuclear spin-spin coupling constants. Theor. Chem. Acc. 1998, 99, 175–182. [Google Scholar] [CrossRef]
- Bryce, D.L.; Wasylishen, R.E. Indirect nuclear spin-spin coupling tensors in diatomic molecules: a comparison of results obtained by experiment and first principles calculations. J. Am. Chem. Soc. 2000, 122, 3197–3205. [Google Scholar] [CrossRef]
- Barszczewicz, A.; Helgaker, T.; Jaszuński, M.; Jǿrgensen, P.; Ruud, K. Multiconfigurational self-consistent field calculations of nuclear magnetic resonance indirect spin–spin coupling constants. J. Chem. Phys. 1994, 101, 6822–6828. [Google Scholar] [CrossRef]
- Barszczewicz, A.; Helgaker, T.; Jaszuński, M.; Jǿrgensen, P.; Ruud, K. NMR shielding tensors and indirect spin-spin coupling tensors in HCN, HNC, CH3CN, and CH3NC molecules. J. Magn. Reson. Ser. 1995, 114, 212–218. [Google Scholar] [CrossRef]
- Pecul, M.; Sadlej, J. The spin-spin coupling constants in the ammonia dimer. Chem. Phys. Lett. 2002, 360, 272–282. [Google Scholar] [CrossRef]
- Pecul, M.; Helgaker, T. The Spin-spin coupling constants in ethane, methanol and methylamine: A comparison of DFT, MCSCF and CCSD Results. Int. J. Mol. Sci. 2003, 4, 143–157. [Google Scholar] [CrossRef]
- Jaszuński, M.; Helgaker, T.; Ruud, K. Ab initio studies of the [AX]2 spin systems of cis- and trans-N2F2. Magn. Reson. Chem. 1996, 34, 646–649. [Google Scholar] [CrossRef]
- Vahtras, O.; Ågren, H.; Jørgensen, P.; Jensen, H.J.A.; Padkjær, S.B.; Helgaker, T. Indirect nuclear spin–spin coupling constants from multiconfiguration linear response theory. J. Chem. Phys. 1992, 96, 6120–6125. [Google Scholar] [CrossRef]
- Visscher, L.; Saue, T.; Nieuwpoort, W.C.; Fægri, K.; Gropen, O. The electronic structure of the PtH molecule: Fully relativistic configuration interaction calculations of the ground and excited states. J. Chem. Phys. 1993, 99, 6704–6715. [Google Scholar] [CrossRef]
- Jensen, H.J.A.; Dyall, K.G.; Saue, T.; Fægri, K. Relativistic 4-component multiconfigurational self-consistent field theory for molecules: Formalism. J. Chem. Phys. 1996, 104, 4083–4097. [Google Scholar] [CrossRef]
- Monkhorst, H.J. Calculation of properties with the coupled-cluster method. Int. J. Quantum Chem. Symp. 1977, 12, 421–432. [Google Scholar] [CrossRef]
- Dalgaard, E.; Monkhorst, H.J. Some aspects of the time-dependent coupled-cluster approach to dynamic response functions. Phys. Rev. 1983, 28, 1217–1222. [Google Scholar] [CrossRef]
- Takahashi, M.; Paldus, J. Time-dependent coupled cluster approach: Excitation energy calculation using an orthogonally spin-adapted formalism. J. Chem. Phys. 1986, 85, 1486–1501. [Google Scholar] [CrossRef]
- Koch, H.; Jørgensen, P. Coupled cluster response functions. J. Chem. Phys. 1990, 93, 3333–3344. [Google Scholar] [CrossRef]
- Koch, H.; Jensen, H.J.A.; Jørgensen, P.; Helgaker, T. Excitation energies from the coupled cluster singles and doubles linear response function (CCSDLR). Applications to Be, CH+, CO, and H2O. J. Chem. Phys. 1990, 93, 3345–3350. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Purvis, G.D., III. Molecular applications of coupled cluster and many-body perturbation methods. Phys. Scr. 1980, 21, 255–265. [Google Scholar] [CrossRef]
- Lee, Y.S.; Kucharski, S.A.; Bartlett, R.J. A coupled cluster approach with triple excitations. J. Chem. Phys. 1984, 81, 5906–5912. [Google Scholar] [CrossRef]
- Christiansen, O. Coupled cluster theory with emphasis on selected new developments. Theor. Chem. Acc. 2006, 116, 106–123. [Google Scholar] [CrossRef]
- Paldus, J.; Wormer, P.E.S.; Visser, F.; van der Avoird, A. Relationship between configuration interaction and coupled cluster approaches. J. Chem. Phys. 1982, 76, 2458–2470. [Google Scholar] [CrossRef]
- Gauss, J.; Stanton, J.F. Perturbative treatment of triple excitations in coupled-cluster calculations of nuclear magnetic shielding constants. J. Chem. Phys. 1996, 104, 2574–2583. [Google Scholar] [CrossRef]
- Koch, H.; Sánchez de Merás, A.; Helgaker, T.; Christiansen, O. The integral-direct coupled cluster singles and doubles model. J. Chem. Phys. 1996, 104, 4157–4165. [Google Scholar] [CrossRef]
- Gauss, J.; Stanton, J.F. Analytic CCSD(T) second derivatives. Chem. Phys. Lett. 1997, 276, 70–77. [Google Scholar] [CrossRef]
- Kállay, M.; Gauss, J. Analytic second derivatives for general coupled-cluster and configuration-interaction models. J. Chem. Phys. 2004, 120, 6841–6848. [Google Scholar] [CrossRef]
- Christiansen, O.; Koch, H.; Jørgensen, P. The second-order approximate coupled cluster singles and doubles model CC2. Chem. Phys. Lett. 1995, 243, 409–418. [Google Scholar] [CrossRef]
- Auer, A.A.; Gauss, J. Triple excitation effects in coupled-cluster calculations of indirect spin–spin coupling constants. J. Chem. Phys. 2001, 115, 1619–1622. [Google Scholar] [CrossRef]
- Knizia, G.; Adler, T.B.; Werner, H.-J. Simplified CCSD(T)-F12 methods: Theory and benchmarks. J. Chem. Phys. 2009, 130, 054104. [Google Scholar] [CrossRef] [PubMed]
- Urban, M.; Noga, J.; Cole, S.J.; Bartlett, R.J. Towards a full CCSDT model for electron correlation. J. Chem. Phys. 1985, 83, 4041–4046. [Google Scholar] [CrossRef]
- Scuseria, G.E.; Janssen, C.L.; Schaefer, H.F. An efficient reformulation of the closed-shell coupled cluster single and double excitation (CCSD) equations. J. Chem. Phys. 1988, 89, 7382–7387. [Google Scholar] [CrossRef]
- Raghavachari, K.; Trucks, G.W. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Noga, J.; Bartlett, R.J.; Urban, M. Towards a full CCSDT model for electron correlation. CCSDT-n models. Chem. Phys. Lett. 1987, 134, 126–132. [Google Scholar] [CrossRef]
- Noga, J.; Bartlett, R.J. The full CCSDT model for molecular electronic structure. J. Chem. Phys. 1987, 86, 7041–7050. [Google Scholar] [CrossRef]
- Purvis, G.D., III; Bartlett, R.J. A full coupled-cluster singles and doubles model: The inclusion of disconnected triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Musiał, M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 2007, 79, 291–352. [Google Scholar] [CrossRef]
- Scuseria, G.E.; Schaefer, H.F., III. A new implementation of the full CCSDT model for molecular electronic structure. Chem. Phys. Lett. 1988, 152, 382–386. [Google Scholar] [CrossRef]
- Kucharskia, S.A.; Bartlett, R.J. The coupled-cluster single, double, triple, and quadruple excitation method. J. Chem. Phys. 1992, 97, 4282–4288. [Google Scholar] [CrossRef]
- Oliphant, N.; Adamowicz, L. Coupled-cluster method truncated at quadruples. J. Chem. Phys. 1991, 95, 6645–6651. [Google Scholar] [CrossRef]
- Kucharski, S.A.; Bartlett, R.J. Recursive intermediate factorization and complete computational linearization of the coupled-cluster single, double, triple, and quadruple excitation equations. Theor. Chem. Acc. 1991, 80, 387–405. [Google Scholar] [CrossRef]
- Matthews, D.A. Accelerating the convergence of higher-order coupled-cluster methods II: Coupled-cluster Λ equations and dynamic damping. Mol. Phys. 2020, 118, e1757774. [Google Scholar] [CrossRef]
- Christiansen, O.; Koch, H.; Jørgensen, P. Response functions in the CC3 iterative triple excitation model. J. Chem. Phys. 1995, 103, 7429–7441. [Google Scholar] [CrossRef]
- Čížek, J.; Paldus, J. Stability Conditions for the Solutions of the Hartree-Fock Equations for Atomic and Molecular Systems. Application to the Pi-Electron Model of Cyclic Polyenes. J. Chem. Phys. 1967, 47, 3976–3985. [Google Scholar] [CrossRef]
- Crawford, T.D.; Stanton, J.F.; Allen, W.D.; Schaefer, H.F., III. Hartree–Fock orbital instability envelopes in highly correlated single-reference wave functions. J. Chem. Phys. 1997, 107, 10626–10632. [Google Scholar] [CrossRef]
- Vahtras, O.; Almlöf, J.E.; Feyereisen, M.W. Integral approximations for LCAO-SCF calculations. Chem. Phys. Lett. 1993, 213, 514–518. [Google Scholar] [CrossRef]
- Feyereisen, M.W.; Fitzgerald, G.; Komornicki, A. Use of approximate integrals in ab initio theory. An application in MP2 energy calculations. Chem. Phys. Lett. 1993, 208, 359–363. [Google Scholar] [CrossRef]
- Hättig, C.; Weigend, F. CC2 excitation energy calculations on large molecules using the resolution of the identity approximation. J. Chem. Phys. 2000, 113, 5154–5161. [Google Scholar] [CrossRef]
- Rendell, A.P.; Lee, T.J. Coupled-cluster theory employing approximate integrals: An approach to avoid the input/output and storage bottlenecks. J. Chem. Phys. 1994, 101, 400–408. [Google Scholar] [CrossRef]
- Koch, H.; Kobayashi, R.; Jørgensen, P. Calculation of size-intensive transition moments from the coupled cluster singles and doubles linear response function. J. Chem. Phys. 1994, 100, 4393–4400. [Google Scholar] [CrossRef]
- Kobayashi, R.; Koch, H.; Jørgensen, P. Calculation of frequency-dependent polarizabilities using coupled-cluster response theory. Chem. Phys. Lett. 1994, 219, 30–35. [Google Scholar] [CrossRef]
- Geertsen, J.; Rittby, M.; Bartlett, R.J. The equation-of-motion coupled-cluster method: Excitation energies of Be and CO. Chem. Phys. Lett. 1989, 164, 57–62. [Google Scholar] [CrossRef]
- Stanton, J.F.; Bartlett, R.J. The equation of motion coupled-cluster method. A systematic biorthogonal approach to molecular excitation energies, transition probabilities, and excited state properties. J. Chem. Phys. 1993, 98, 7029–7039. [Google Scholar] [CrossRef]
- Perera, S.A.; Nooijen, M.; Bartlett, R.J. Electron correlation effects on the theoretical calculation of nuclear magnetic resonance spin-spin coupling constants. J. Chem. Phys. 1996, 104, 3290–3305. [Google Scholar] [CrossRef]
- Cheng, L.; Gauss, J. Analytic second derivatives for the spin-free exact two-component theory. J. Chem. Phys. 2011, 135, 244104. [Google Scholar] [CrossRef]
- Cheng, L.; Gauss, J.; Stanton, J.F. Treatment of scalar-relativistic effects on nuclear magnetic shieldings using a spin-free exact-two-component approach. J. Chem. Phys. 2013, 139, 054105. [Google Scholar] [CrossRef] [PubMed]
- Perera, S.A.; Sekino, H.; Bartlett, R.J. Coupled-cluster calculations of indirect nuclear coupling constants: The importance of non-Fermi contact contributions. J. Chem. Phys. 1994, 101, 2186–2191. [Google Scholar] [CrossRef]
- Del Bene, J.E.; Alkorta, I.; Elguero, J. Systematic comparison of second-order polarization propagator approximation (SOPPA) and equation-of-motion coupled cluster singles and doubles (EOM-CCSD) spin-spin coupling constants for molecules with C, N, and O double and triple bonds and selected f-substituted derivatives. J. Chem. Theory Comput. 2009, 5, 208–216. [Google Scholar] [CrossRef] [PubMed]
- Del Bene, J.E.; Alkorta, I.; Elguero, J. A systematic comparison of second-order polarization propagator approximation and equation-of-motion coupled cluster singles and doubles C-C, C-N, N-N, C-H, and N-H spin-spin coupling constants. J. Phys. Chem. 2009, 113, 12411–12420. [Google Scholar] [CrossRef] [PubMed]
- Gauss, J.; Stanton, J.F. Gauge-invariant calculation of nuclear magnetic shielding constants at the coupled-cluster singles and doubles level. J. Chem. Phys. 1995, 102, 251–253. [Google Scholar] [CrossRef]
- Gauss, J.; Stanton, J.F. Coupled-cluster calculations of nuclear magnetic resonance chemical shifts. J. Chem. Phys. 1995, 103, 3561–3577. [Google Scholar] [CrossRef]
- Auer, A.A.; Gauss, J.; Stanton, J.F. Quantitative prediction of gas-phase 13C nuclear magnetic shielding constants. J. Chem. Phys. 2003, 118, 10407–10417. [Google Scholar] [CrossRef]
- Gauss, J. Analytic second derivatives for the full coupled-cluster singles, doubles, and triples model: Nuclear magnetic shielding constants for BH, HF, CO, N2, N2O, and O3. J. Chem. Phys. 2002, 116, 4773–4776. [Google Scholar] [CrossRef]
- Sundholm, D.; Gauss, J.; Schäfer, A. Rovibrationally averaged nuclear magnetic shielding tensors calculated at the coupled-cluster level. J. Chem. Phys. 1996, 105, 11051–11059. [Google Scholar] [CrossRef]
- Stanton, J.F.; Gauss, J.; Siehl, H.-U. CCSD(T) calculation of NMR chemical shifts: Consistency of calculated and measured 13C chemical shifts in the 1-cyclopropylcyclopropylidenemethyl cation. Chem. Phys. Lett. 1996, 262, 183–186. [Google Scholar] [CrossRef]
- Christe, K.; Wilson, W.W.; Sheehy, J.A.; Boatz, J.A. N5+: A novel homoleptic polynitrogen ion as a high energy density material. Angew. Chem. Int. Ed. Engl. 1999, 38, 2004–2009. [Google Scholar] [CrossRef]
- Rasul, G.; Surya Prakash, G.K.; Olah, G.A. Comparative study of the hypercoordinate ions C7H9+ and C8H9+ by the ab initio/GIAO-CCSD(T) method. J. Phys. Chem. 2006, 110, 11320–11323. [Google Scholar] [CrossRef] [PubMed]
- Faber, R.; Sauer, S.P.A. On the convergence of the ccJ-pVXZ and pcJ-n basis sets in CCSD calculations of nuclear spin–spin coupling constants: Some difficult cases. Theor. Chem. Acc. 2018, 137, 35. [Google Scholar] [CrossRef]
- Benedikt, U.; Auer, A.A.; Jensen, F. Optimization of augmentation functions for correlated calculations of spin–spin coupling constants and related properties. J. Chem. Phys. 2008, 129, 064111. [Google Scholar] [CrossRef]
- Jensen, F. The basis set convergence of spin–spin coupling constants calculated by density functional methods. J. Chem. Theory. Comput. 2006, 2, 1360–1369. [Google Scholar] [CrossRef] [PubMed]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Del Bene, J.E.; Alkorta, I.; Elguero, J. A systematic comparison of second-order polarization propagator approximation (SOPPA) and equation-of-motion coupled cluster singles and doubles (EOM-CCSD) spin–spin coupling constants for selected singly bonded molecules, and the hydrides NH3, H2O, and HF and their protonated and deprotonated ions and hydrogen-bonded complexes. J. Chem. Theory Comput. 2008, 4, 967–973. [Google Scholar] [CrossRef]
- Schäfer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
- Faber, R.; Sauer, S.P.A.; Gauss, J. Importance of Triples Contributions to NMR Spin–Spin Coupling Constants Computed at the CC3 and CCSDT Levels. J. Chem. Theory Comput. 2017, 13, 696–709. [Google Scholar] [CrossRef]
- Jaszuński, M.; Sauer, S.P.A.; Faber, R.; Wilson, D.J.D. NMR parameters of FNNF as a test for coupled-cluster methods: CCSDT shielding and CC3 spin–spin coupling. Phys. Chem. Chem. Phys. 2020, 37, 21350–21359. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Dreizler, R.M.; Gross, E.K.U. Density Functional Theory, An Approach to the Quantum Many-Body Problem, 1st ed.; Springer-Verlag: Heidelberg/Berlin, Germany, 1990; pp. 1–302. [Google Scholar]
- Fiolhais, C.; Nogueira, F.; Marques, M.A.L. A Primer in Density Functional Theory, 1st ed.; Springer: Berlin, Germany, 2003; pp. 1–258. [Google Scholar] [CrossRef]
- Koch, W.; Holthausen, M.C. A Chemist’s Guide to Density Functional Theory, 2nd ed.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2001; pp. 1–300. [Google Scholar]
- Baer, R. Electron Density Functional Theory: Lecture Notes, 1st ed.; The Hebrew University of Jerusalem, Fritz Haber Center for Molecular Dynamics at the Hebrew University: Jerusalem, Israel, 2016; pp. 1–109. [Google Scholar]
- Lutnæs, O.B. Density-Functional-Theory Calculations of Second-Order Magnetic Properties. Ph.D. Thesis, University of Oslo, CTCC—Centre for Theoretical and Computational Chemistry, Department of Chemistry Faculty of Mathematics and Natural Sciences, Oslo, Norway, 2009. [Google Scholar]
- Dirac, P.A.M. Note on exchange phenomena in the Thomas atom. Math. Proc. Camb. Philos. Soc. 1930, 26, 376–385. [Google Scholar] [CrossRef]
- Slater, J.C.; Phillips, J.C. Quantum Theory of Molecules and Solids: The Self-Consistent Field for Molecules and Solids, 1st ed.; McGraw-Hill: New York, NY, USA, 1974; Volume 4, pp. 1–583. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 59, 1200–1211. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys Rev. 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Perdew, J. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Perdew, J.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Becke, A.D. Exchange–correlation approximations in density-functional theory. In Modern Electronic Structure Theory, part II; Yarkony, D.R., Ed.; World Scientific: Singapore, 1995; pp. 1022–1046. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Malkin, V.G.; Malkina, O.L.; Salahub, D.R. Calculations of NMR shielding constants by uncoupled density functional theory. Chem. Phys. Lett. 1993, 204, 80–86. [Google Scholar] [CrossRef]
- Malkin, V.G.; Malkina, O.L.; Casida, M.E.; Salahub, D.R. Nuclear Magnetic Resonance Shielding Tensors Calculated with a Sum-over-States Density Functional Perturbation Theory. J. Am. Chem. Soc. 1994, 116, 5898–5908. [Google Scholar] [CrossRef]
- Malkin, V.G.; Malkina, O.L.; Erikson, L.A.; Salahub, D.R. Modern Density Functional Theory: A Tool for Chemistry, 1st ed.; Politzer, P., Seminario, J.M., Eds.; Elsevier: Amsterdam, The Netherlands, 1995; Volume 2, pp. 273–347. [Google Scholar]
- Lee, A.M.; Handy, N.C.; Colwell, S.M. The density functional calculation of nuclear shielding constants using London atomic orbitals. J. Chem. Phys. 1995, 103, 10095–10109. [Google Scholar] [CrossRef]
- Olsson, L.; Cremer, D. Sum-overs-tates density functional perturbation theory: Prediction of reliable 13C, 15N, and 17O nuclear magnetic resonance chemical shifts. J. Chem. Phys. 1996, 105, 8995–9006. [Google Scholar] [CrossRef]
- Rajagopal, A.K.; Callaway, J. Inhomogeneous electron gas. Phys. Rev. 1973, 7, 1912–1919. [Google Scholar] [CrossRef]
- Rajagopal, A.K. Inhomogeneous relativistic electron gas. J. Phys. Solid State Phys. 1978, 11, L943–L948. [Google Scholar] [CrossRef]
- Vignale, G.; Rasolt, M. Current- and spin-density-functional theory for inhomogeneous electronic systems in strong magnetic fields. Phys. Rev. 1988, 37, 10685–10696. [Google Scholar] [CrossRef]
- Becke, A.D. Current-density dependent exchange-correlation functionals. Can. J. Chem. 1996, 74, 995–997. [Google Scholar] [CrossRef]
- Malkin, V.G.; Malkina, O.L.; Salahub, D.R. Calculation of spin—spin coupling constants using density functional theory. Chem. Phys. Lett. 1994, 221, 91–99. [Google Scholar] [CrossRef]
- Malkina, O.L.; Salahub, D.R.; Malkin, V.G. Nuclear magnetic resonance spin–spin coupling constants from density functional theory: Problems and results. J. Chem. Phys. 1996, 105, 8793–8800. [Google Scholar] [CrossRef]
- Hricovíni, M.; Malkina, O.L.; Bízik, F.; Turi Nagy, L.; Malkin, V.G. Calculation of NMR Chemical Shifts and Spin−Spin Coupling Constants in the Monosaccharide Methyl-β-d-xylopyranoside Using a Density Functional Theory Approach. J. Phys. Chem. 1997, 101, 9756–9762. [Google Scholar] [CrossRef]
- Dickson, R.M.; Ziegler, T. NMR Spin-Spin Coupling Constants from Density Functional Theory with Slater-Type Basis Functions. J. Phys. Chem. 1996, 100, 5286–5290. [Google Scholar] [CrossRef]
- Sychrovsky, V.; Gräfenstein, J.; Cremer, D. Nuclear magnetic resonance spin–spin coupling constants from coupled perturbed density functional theory. J. Chem. Phys. 2000, 113, 3530–3547. [Google Scholar] [CrossRef]
- Helgaker, T.; Watson, M.; Handy, N.C. Analytical calculation of nuclear magnetic resonance indirect spin–spin coupling constants at the generalized gradient approximation and hybrid levels of density-functional theory. J. Chem. Phys. 2000, 113, 9402–9409. [Google Scholar] [CrossRef]
- Watson, M.A.; Handy, N.C.; Cohen, A.J.; Helgaker, T. Density-functional generalized-gradient and hybrid calculations of electromagnetic properties using Slater basis sets. J. Chem. Phys. 2004, 120, 7252–7261. [Google Scholar] [CrossRef]
- Joyce, S.A.; Yates, J.R.; Pickard, C.J.; Mauri, F. A first principles theory of nuclear magnetic resonance 𝐽-coupling in solid-state systems. J. Chem. Phys. 2007, 127, 204107. [Google Scholar] [CrossRef]
- Alkorta, I.; Elguero, J. Review on DFT and ab initio Calculations of Scalar Coupling Constants. Int. J. Mol. Sci. 2003, 4, 64–92. [Google Scholar] [CrossRef]
- Malkin, V.G.; Malkina, O.L.; Salahub, D.R. Calculations of NMR shielding constants beyond uncoupled density functional theory. IGLO approach. Chem. Phys. Lett. 1993, 204, 87–95. [Google Scholar] [CrossRef]
- Schreckenbach, G.; Ziegler, T. The calculation of NMR shielding tensors based on density functional theory and the frozen-core approximation. Int. J. Quantum Chem. 1996, 60, 753–766. [Google Scholar] [CrossRef]
- Schreckenbach, G.; Dickson, R.M.; Ruiz-Morales, Y.; Ziegler, T. The calculation of NMR parameters by density-functional theory—An approach based on gauge including atomic orbitals. In Chemical Applications of Density Functional Theory; Laird, B.B., Ross, R.B., Ziegler, T., Eds.; ACS Symposium Series, 629; American Chemical Society: Washington, DC, USA, 1996; pp. 328–341. [Google Scholar]
- Schreckenbach, G.; Ziegler, T. Calculation of NMR shielding tensors based on density functional theory and a scalar relativistic Pauli-type Hamiltonian. The application to transition metal complexes. Int. J. Quantum Chem. 1997, 61, 899–918. [Google Scholar] [CrossRef]
- Schreckenbach, G.; Ziegler, T. Density functional calculations of NMR chemical shifts and ESR g-tensors. Theor. Chem. Acc. 1998, 99, 71–82. [Google Scholar] [CrossRef]
- Laskowski, R.; Blaha, P.; Tran, R. Assessment of DFT functionals with NMR chemical shifts. Phys. Rev. 2013, 87, 195130. [Google Scholar] [CrossRef]
- Zahn, S.L.V.; Hammerich, O.; Hansen, P.E.; Sauer, S.P.A. The best density functional theory functional for the prediction of 1H and 13C chemical shifts of protonated alkylpyrroles. J. Comput. Chem. 2021, 42, 1248–1262. [Google Scholar] [CrossRef]
- Vila, J.A.; Baldoni, H.A.; Scheraga, H.A. Performance of Density Functional Models to Reproduce Observed 13Cα Chemical Shifts of Proteins in Solution. J. Comput. Chem. 2009, 30, 884–892. [Google Scholar] [CrossRef] [PubMed]
- Maximoff, S.N.; Peralta, J.E.; Barone, V.; Scuseria, G.E. Assessment of density functionals for predicting one-bond carbon-hydrogen NMR spin−spin coupling constants. J. Chem. Theory Comput. 2005, 1, 541–545. [Google Scholar] [CrossRef] [PubMed]
- San Fabián, J.; García de la Vega, J.M.; San Fabián, E. Improvements in DFT calculations of spin-spin coupling constants. J. Chem. Theory Comput. 2014, 10, 4938–4949. [Google Scholar] [CrossRef] [PubMed]
- Lutnæs, O.B.; Helgaker, T.; Jaszunski, M. Spin–spin coupling constants and triplet instabilities in Kohn–Sham theory. Mol. Phys. 2010, 108, 2579–2590. [Google Scholar] [CrossRef]
- De Giovanetti, M.; Bitencourt, L.F.F.; Cormanich, R.; Sauer, S.P.A. On the Unexpected Accuracy of the M06L Functional in the Calculation of 1JFC Spin–Spin Coupling Constants. J. Chem. Theory Comput. 2021, 17, 7712–7723. [Google Scholar] [CrossRef]
- Jaszuński, M.; Świder, P.; Sauer, S.P.A. Through-space spin–spin coupling constants involving fluorine: Benchmarking DFT functionals. Mol. Phys. 2019, 117, 1469–1480. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. ERRATA for: Generalized gradient approximation made simple. Phys. Rev. Lett. 1997, 78, 1396, Erratum [Phys. Rev. Lett. 1996, 77, 3865–3868]. [Google Scholar] [CrossRef]
- Burke, K.; Perdew, J.P.; Wang, Y. Derivation of a Generalized Gradient Approximation: The PW91 Density Functional. In Electronic Density Functional Theory, 1st ed.; Dobson, J.F., Vignale, G., Das, M.P., Eds.; Springer: Boston, MA, USA, 1998; pp. 81–111. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Keal, T.W.; Tozer, D.J. The exchange-correlation potential in Kohn-Sham nuclear magnetic resonance shielding calculations. J. Chem. Phys. 2003, 119, 3015–3024. [Google Scholar] [CrossRef]
- Keal, T.W.; Tozer, D.J. A semiempirical generalized gradient approximation exchange-correlation functional. J. Chem. Phys. 2004, 121, 5654–5660. [Google Scholar] [CrossRef]
- Hamprecht, F.A.; Cohen, A.J.; Tozer, D.J.; Handy, N.C. Development and assessment of new exchange-correlation functionals. J. Chem. Phys. 1998, 109, 6264–6271. [Google Scholar] [CrossRef]
- Boese, A.D.; Doltsinis, N.L.; Handy, N.C.; Sprik, M. New generalized gradient approximation functionals. J. Chem. Phys. 2000, 112, 1670–1678. [Google Scholar] [CrossRef]
- Boese, A.D.; Handy, N.C. A new parametrization of exchange–correlation generalized gradient approximation functionals. J. Chem. Phys. 2001, 114, 5497–5503. [Google Scholar] [CrossRef]
- Handy, N.C.; Cohen, A.J. Left-right correlation energy. Mol. Phys. 2001, 99, 403–412. [Google Scholar] [CrossRef]
- Hoe, W.-M.; Cohen, A.J.; Handy, N.C. Assessment of a new local exchange functional OPTX. Chem. Phys. Lett. 2001, 341, 319–328. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, A.; Xu, X.; Yan, Y. OPBE: A promising density functional for the calculation of nuclear shielding constants. Chem. Phys. Lett. 2006, 421, 383–388. [Google Scholar] [CrossRef]
- Perdew, J.P. Unified Theory of Exchange and Correlation Beyond the Local Density Approximation. In Electronic Structure of Solids, 91st ed.; Ziesche, P., Eschig, H., Eds.; Akademie Verlag: Berlin, Germany, 1991; pp. 11–20. [Google Scholar]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. 1992, 46, 6671–6687. [Google Scholar] [CrossRef] [PubMed]
- Adamo, C.; Barone, V. Exchange functionals with improved long-range behavior and adiabatic connection methods without adjustable parameters: The 𝑚PW and 𝑚PW1PW models. J. Chem. Phys. 1998, 108, 664–675. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. V. Systematic optimization of exchange-correlation functionals. J. Chem. Phys. 1997, 107, 8554–8560. [Google Scholar] [CrossRef]
- Wilson, P.J.; Bradley, T.J.; Tozer, D.J. Hybrid exchange-correlation functional determined from thermochemical data and ab initio potentials. J. Chem. Phys. 2001, 115, 9233–9242. [Google Scholar] [CrossRef]
- Keal, T.W.; Tozer, D.J. Semiempirical hybrid functional with improved performance in an extensive chemical assessment. J. Chem. Phys. 2005, 123, 121103. [Google Scholar] [CrossRef]
- Xu, X.; Goddard, W.A. The X3LYP extended density functional for accurate descriptions of nonbond interactions, spin states, and thermochemical properties. Proc. Natl. Acad. Sci. USA 2004, 101, 2673–2677. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ernzerhof, M.; Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Schmider, H.L.; Becke, A.D. Optimized density functionals from the extended G2 test set. J. Chem. Phys. 1998, 108, 9624–9631. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable adiabatic connection models free from adjustable parameters. Chem. Phys. Lett. 1997, 274, 242–250. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Perdew, J.P. Generalized gradient approximation to the angle- and system-averaged exchange hole. J. Chem. Phys. 1998, 109, 3313–3320. [Google Scholar] [CrossRef]
- Boese, A.D.; Handy, N.C. New exchange-correlation density functionals: The role of the kinetic-energy density. J. Chem. Phys. 2002, 116, 9559–9569. [Google Scholar] [CrossRef]
- Van Voorhis, T.; Scuseria, G.E. A novel form for the exchange-correlation energy functional. J. Chem. Phys. 1998, 109, 400–410. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef] [PubMed]
- Peverati, R.; Truhlar, D.G. M11-L: A Local Density Functional That Provides Improved Accuracy for Electronic Structure Calculations in Chemistry and Physics. J. Phys. Chem. Lett. 2012, 3, 117–124. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. IV. A new dynamical correlation functional and implications for exact-exchange mixing. J. Chem. Phys. 1996, 104, 1040–1046. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Scuseria, G.E. Assessment of a long-range corrected hybrid functional. J. Chem. Phys. 2006, 125, 234109. [Google Scholar] [CrossRef] [PubMed]
- Keal, T.W.; Tozer, D.J.; Helgaker, T. GIAO shielding constants and indirect spin–spin coupling constants: Performance of density functional methods. Chem. Phys. Lett. 2004, 391, 374–379. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward chemical accuracy in the computation of NMR shieldings: The PBE0 model. Chem. Phys. Lett. 1998, 298, 113–119. [Google Scholar] [CrossRef]
- Perdew, J.P.; Schmidt, K. Jacob’s ladder of density functional approximations for the exchange-correlation energy. AIP Conf. Proc. 2001, 577, 1–20. [Google Scholar] [CrossRef]
- Helgaker, T.; Lutnæs, O.B.; Jaszuński, M. Density-Functional and Coupled-Cluster Singles-and-Doubles Calculations of the Nuclear Shielding and Indirect Nuclear Spin−Spin Coupling Constants of o-Benzyne. J. Chem. Theory Comput. 2007, 3, 86–94. [Google Scholar] [CrossRef]
- Komorovsky, S.; Repisky, M.; Malkina, O.L.; Malkin, V.G.; Ondik Malkin, I.; Kaupp, M.J. A fully relativistic method for calculation of nuclear magnetic shielding tensors with a restricted magnetically balanced basis in the framework of the matrix Dirac–Kohn–Sham equation. Chem. Phys. 2008, 128, 104101. [Google Scholar] [CrossRef]
- Repiský, M.; Komorovský, S.; Malkina, O.L.; Malkin, V.G. Restricted magnetically balanced basis applied for relativistic calculations of indirect nuclear spin–spin coupling tensors in the matrix Dirac–Kohn–Sham framework. Chem. Phys. 2009, 356, 236–242. [Google Scholar] [CrossRef]
- Malkin, V.G.; Malkina, O.L.; Reviakine, R.; Arbuznikov, A.V.; Kaupp, M.; Schimmelpfennig, B.; Malkin, I.; Repiský, M.; Komorovský, S.; Hrobárik, P.; et al. ReSpect Program, version 3.1. 2007. Available online: http://www.respectprogram.org (accessed on 25 March 2022).
- Liu, W.; Hong, G.; Dai, D.; Li, L.; Dolg, M. The Beijing four-component density functional program package (BDF) and its application to EuO, EuS, YbO and YbS. Theor. Chem. Acc. 1997, 96, 75–83. [Google Scholar] [CrossRef]
- Liu, W.; Wang, F.; Li, L. The Beijing Density Functional (BDF) Program Package: Methodologies and Applications. J. Theor. Comput. Chem. 2003, 2, 257–272. [Google Scholar] [CrossRef]
- Sun, Q.; Liu, W.; Xiao, Y.; Cheng, L. Exact two-component relativistic theory for nuclear magnetic resonance parameters. J. Chem. Phys. 2009, 131, 081101. [Google Scholar] [CrossRef] [PubMed]
- Olejniczak, M.; Bast, R.; Saue, T.; Pecul, M. A simple scheme for magnetic balance in four-component relativistic Kohn-Sham calculations of nuclear magnetic resonance shielding constants in a Gaussian basis. J. Chem. Phys. 2012, 136, 014108. [Google Scholar] [CrossRef] [PubMed]
- DIRAC. A Relativistic ab Initio Electronic Structure Program, Release DIRAC22. Jensen, H.J.A., Bast, R., Gomes, A.S.P., Saue, T., Visscher, L., Bakken, V., Chibueze, C., Creutzberg, J., Dyall, K.G., Dubillard, S., et al., Eds.; 2022. Available online: http://www.diracprogram.org. [CrossRef]
- Autschbach, J. Relativistic calculations of magnetic resonance parameters: Background and some recent developments. Philos. Trans. R. Soc. 2014, 372, 20120489. [Google Scholar] [CrossRef] [PubMed]
- Peng, D.; Reiher, M. Exact decoupling of the relativistic Fock operator. Theor. Chem. Acc. 2012, 131, 1081. [Google Scholar] [CrossRef]
- Dyall, K.G. Interfacing relativistic and nonrelativistic methods. I. Normalized elimination of the small component in the modified Dirac equation. J. Chem. Phys. 1997, 106, 9618–9626. [Google Scholar] [CrossRef]
- Dyall, K.G. Interfacing relativistic and nonrelativistic methods. II. Investigation of a low-order approximation. J. Chem. Phys. 1998, 109, 4201–4208. [Google Scholar] [CrossRef]
- Dyall, K.G.; Enevoldsen, T. Interfacing relativistic and nonrelativistic methods. III. Atomic 4-spinor expansions and integral approximations. J. Chem. Phys. 1999, 111, 10000–10007. [Google Scholar] [CrossRef]
- Dyall, K.G. Interfacing relativistic and nonrelativistic methods. IV. One- and two-electron scalar approximations. J. Chem. Phys. 2001, 115, 9136–9143. [Google Scholar] [CrossRef]
- Dyall, K.G. A systematic sequence of relativistic approximations. J. Comput. Chem. 2002, 23, 786–793. [Google Scholar] [CrossRef]
- Filatov, M.; Cremer, D. Representation of the exact relativistic electronic Hamiltonian within the regular approximation. J. Chem. Phys. 2003, 119, 11526–11540. [Google Scholar] [CrossRef]
- Filatov, M.; Cremer, D. Connection between the regular approximation and the normalized elimination of the small component in relativistic quantum theory. J. Chem. Phys. 2005, 122, 064104. [Google Scholar] [CrossRef] [PubMed]
- Zou, W.; Filatov, M.; Cremer, D. An improved algorithm for the normalized elimination of the small-component method. Theor. Chem. Acc. 2011, 130, 633–644. [Google Scholar] [CrossRef]
- Seino, J.; Hada, M. Magnetic shielding constants calculated by the infinite-order Douglas-Kroll-Hess method with electron-electron relativistic corrections. J. Chem. Phys. 2010, 132, 174105. [Google Scholar] [CrossRef] [PubMed]
- Barysz, M.; Sadlej, A.J. Two-component methods of relativistic quantum chemistry: From the Douglas-Kroll approximation to the exact two-component formalism. J. Mol. Struct. THEOCHEM 2001, 573, 181–200. [Google Scholar] [CrossRef]
- Barysz, M.; Sadlej, A.J. Infinite-order two-component theory for relativistic quantum chemistry. J. Chem. Phys. 2002, 116, 2696–2704. [Google Scholar] [CrossRef]
- Kedziera, D.; Barysz, M. Two-component relativistic methods for the heaviest elements. J. Chem. Phys. 2004, 121, 6719–6727. [Google Scholar] [CrossRef]
- Kedziera, D.; Barysz, M. Non-iterative approach to the infinite-order two-component (IOTC) relativistic theory and the non-symmetric algebraic Riccati equation. Chem. Phys. Lett. 2007, 446, 176–181. [Google Scholar] [CrossRef]
- Wolff, S.K.; Ziegler, T.; van Lenthe, E.; Baerends, E.J. Density functional calculations of nuclear magnetic shieldings using the zeroth-order regular approximation (ZORA) for relativistic effects: ZORA nuclear magnetic resonance. J. Chem. Phys. 1999, 110, 7689–7698. [Google Scholar] [CrossRef]
- Chang, C.; Pelissier, M.; Durand, M. Regular Two-Component Pauli-like effective Hamiltonians in Dirac theory. Phys. Scr. 1986, 34, 394–404. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic regular two-component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
- Hamaya, S.; Maeda, H.; Funaki, M.; Fukui, H. Relativistic calculation of nuclear magnetic shielding tensor using the regular approximation to the normalized elimination of the small component. III. Introduction of gauge-including atomic orbitals and a finite-size nuclear model. J. Chem. Phys. 2008, 129, 224103. [Google Scholar] [CrossRef] [PubMed]
- Douglas, M.; Kroll, N.M. Quantum electrodynamical corrections to the fine structure of helium. Ann. Phys. 1974, 82, 89–155. [Google Scholar] [CrossRef]
- Reiher, M. Douglas-Kroll-Hess Theory: A relativistic electrons-only theory for chemistry. Theor. Chem. Acc. 2006, 116, 241–252. [Google Scholar] [CrossRef]
- Hess, B.A. Relativistic electronic-structure calculations employing a two-component no-pair formalism with external-field projection operators. Phys. Rev. 1986, 33, 3742–3748. [Google Scholar] [CrossRef]
- Jensen, G.; Hess, B.A. Revision of the Douglas-Kroll transformation. Phys. Rev. 1989, 39, 6016–6017. [Google Scholar] [CrossRef]
- Nakajima, T.; Hirao, K. The higher-order Douglas-Kroll transformation. J. Chem. Phys. 2000, 113, 7786–7789. [Google Scholar] [CrossRef]
- Nakajima, T.; Hirao, K. Numerical illustration of third-order Douglas-Kroll method: Atomic and molecular properties of superheavy element 112. Chem. Phys. Lett. 2000, 329, 511–516. [Google Scholar] [CrossRef]
- Wolf, A.; Reiher, M.; Hess, B.A. The generalized Douglas-Kroll transformation. J. Chem. Phys. 2002, 117, 9215–9226. [Google Scholar] [CrossRef]
- Van Wüllen, C. Relation between different variants of the generalized Douglas-Kroll transformation through sixth order. J. Chem. Phys. 2004, 120, 7307–7313. [Google Scholar] [CrossRef]
- Filatov, M.; Cremer, D. Calculation of indirect nuclear spin-spin coupling constants within the regular approximation for relativistic effects. J. Chem. Phys. 2004, 120, 11407–11422. [Google Scholar] [CrossRef] [PubMed]
- Dyall, K.G.; van Lenthe, E. Relativistic regular approximations revisited: An infinite-order relativistic approximation. J. Chem. Phys. 1999, 111, 1366–1372. [Google Scholar] [CrossRef]
- Wu, W.; Rehe, D.; Hrobárik, P.; Kornienko, A.Y.; Emge, T.J.; Brennan, J.G. Molecular Thorium Compounds with Dichalcogenide Ligands: Synthesis, Structure, 77Se NMR Study, and Thermolysis. Inorg. Chem. 2018, 57, 14821–14833. [Google Scholar] [CrossRef] [PubMed]
- Brownridge, S.; Calhoun, L.; Jenkins, H.D.B.; Laitinen, R.S.; Murchie, M.P.; Passmore, J.; Pietikäinen, J.; Rautiainen, J.M.; Sanders, J.C.P.; Schrobilgen, G.J.; et al. 77Se NMR Spectroscopic, DFT MO, and VBT Investigations of the Reversible Dissociation of Solid (Se6I2)[AsF6]2·2SO2 in Liquid SO2 to Solutions Containing 1,4-Se6I22+ in Equilibrium with Sen2+ (n = 4, 8, 10) and Seven Binary Selenium Iodine Cations: Preliminary Evidence for 1,1,4,4-Se4Br42+ and cyclo-Se7Br+. Inorg. Chem. 2009, 48, 1938–1959. [Google Scholar] [CrossRef] [PubMed]
- Ringgold, M.; Rehe, D.; Hrobárik, P.; Kornienko, A.Y.; Emge, T.J.; Brennan, J.G. Thorium Cubanes−Synthesis, Solid-State and Solution Structures, Thermolysis, and Chalcogen Exchange Reactions. Inorg. Chem. 2018, 57, 7129–7141. [Google Scholar] [CrossRef]
- Rautiainen, J.M.; Way, T.; Schatte, G.; Passmore, J.; Laitinen, R.S.; Suontamo, R.J.; Valkonen, J. A Computational and Experimental Study of the Structures and Raman and 77Se NMR Spectra of SeX3+ and SeX2 (X = Cl, Br, I): FT-Raman Spectrum of (SeI3)[AsF6]. Inorg. Chem. 2005, 44, 1904–1913. [Google Scholar] [CrossRef]
- Oddershede, J.; Jørgensen, P.; Yeager, D.L. Polarization propagator methods in atomic and molecular calculations. Comput. Phys. Rep. 1984, 2, 33–92. [Google Scholar] [CrossRef]
- Goscinski, O.; Lukman, B. Moment-conserving decoupling of green functions via pade approximants. Chem. Phys. Lett. 1970, 7, 573–576. [Google Scholar] [CrossRef]
- Löwdin, P.-O. Studies in perturbation theory. X. Lower bounds to energy eigenvalues in perturbation-theory ground state. Phys. Rev. 1965, 139, A357–A372. [Google Scholar] [CrossRef]
- Oddershede, J. Response and propagator methods. In Methods in Computational Molecular Physics, 1st ed.; Wilson, S., Diercksen, G.H.F., Eds.; Plenum Press: New York, NY, USA, 1992; Chapter 11; pp. 303–324. [Google Scholar]
- Wigglesworth, R.D.; Raynes, W.T.; Sauer, S.P.A.; Oddershede, J. The calculation and analysis of isotope effects on the nuclear spinspin coupling constants of methane at various temperatures. Mol. Phys. 1997, 92, 77–88. [Google Scholar] [CrossRef]
- Wigglesworth, R.D.; Raynes, W.T.; Sauer, S.P.A.; Oddershede, J. Calculated spin-spin coupling surfaces in the water molecule; prediction and analysis of J(O,H), J(O,D) and J(H,D) in water isotopomers. Mol. Phys. 1998, 94, 851–862. [Google Scholar] [CrossRef]
- Enevoldsen, T.; Oddershede, J.; Sauer, S.P.A. Correlated calculations of indirect nuclear spin-spin coupling constants using second-order polarization propagator approximations: SOPPA and SOPPA(CCSD). Theor. Chem. Acc. 1998, 100, 275–284. [Google Scholar] [CrossRef]
- Wigglesworth, R.D.; Raynes, W.T.; Kirpekar, S.; Oddershede, J.; Sauer, S.P.A. Nuclear spin-spin coupling in the acetylene isotopomers calculated from ab initio correlated surfaces for 1𝐽(C, H), 1𝐽(C, C), 2𝐽(C, H), and 3𝐽(H, H). J. Chem. Phys. 2000, 112, 3735–3746. [Google Scholar] [CrossRef]
- Nielsen, E.S.; Jørgensen, P.; Oddershede, J. Transition moments and dynamic polarizabilities in a second order polarization propagator approach. J. Chem. Phys. 1980, 73, 6238–6246. [Google Scholar] [CrossRef]
- Bak, K.L.; Koch, H.; Oddershede, J.; Christiansen, O.; Sauer, S.P.A. Atomic integral driven second order polarization propagator calculations of the excitation spectra of naphthalene and anthracene. J. Chem. Phys. 2000, 112, 4173–4185. [Google Scholar] [CrossRef]
- Kjær, H.; Sauer, S.P.A.; Kongsted, J. Benchmarking NMR indirect nuclear spin-spin coupling constants: SOPPA, SOPPA(CC2), and SOPPA(CCSD) versus CCSD. J. Chem. Phys. 2010, 133, 144106. [Google Scholar] [CrossRef]
- Sauer, S.P.A. Second-order polarization propagator approximation with coupled-cluster singles and doubles amplitudes—SOPPA(CCSD): The polarizability and hyperpolarizability of Li−. J. Phys. 1997, 30, 3773–3780. [Google Scholar] [CrossRef]
- Sauer, S.P.A.; Raynes, W.T.; Nicholls, R.A. Nuclear spin-spin coupling in silane and its isotopomers: Ab initio calculation and experimental investigation. J. Chem. Phys. 2001, 115, 5994–6006. [Google Scholar] [CrossRef]
- Sauer, S.P.A.; Raynes, W.T. Unexpected differential sensitivity of nuclear spin-spin-coupling constants to bond stretching in BH4−, NH4+, and SiH4. J. Chem. Phys. 2000, 113, 3121–3129. [Google Scholar] [CrossRef]
- Provasi, P.F.; Aucar, G.A.; Sauer, S.P.A. The use of locally dense basis sets in the calculation of indirect nuclear spin-spin coupling constants: The vicinal coupling constants in H3C–CH2X (X = H, F, Cl, Br, I). J. Chem. Phys. 2000, 112, 6201–6208. [Google Scholar] [CrossRef]
- Sauer, S.P.A.; Paidarová, I.; Oddershede, J. Correlated and gauge origin independent calculations of magnetic properties. Mol. Phys. 1993, 81, 87–118. [Google Scholar] [CrossRef]
- Provasi, P.F.; Aucar, G.A.; Sauer, S.P.A. The effect of lone pairs and electronegativity on the indirect nuclear spin–spin coupling constants in CH2X (X = CH2, NH, O, S): Ab initio calculations using optimized contracted basis sets. J. Chem. Phys. 2001, 115, 1324–1334. [Google Scholar] [CrossRef]
- Tew, D.P.; Klopper, W.; Helgaker, T. Electron correlation: The many-body problem at the heart of chemistry. J. Comput. Chem. 2007, 28, 1307–1320. [Google Scholar] [CrossRef] [PubMed]
- Rose, J.; Shibuya, T.; McKoy, V. Application of the equations-of-motion method to the excited states of N2, CO, and C2H4. J. Chem. Phys. 1973, 58, 74–83. [Google Scholar] [CrossRef]
- Shibuya, T.; Rose, J.; McKoy, V. Equations-of-motion method including renormalization and double-excitation mixing. J. Chem. Phys. 1973, 58, 500–507. [Google Scholar] [CrossRef]
- Haase, P.A.B.; Faber, R.; Provasi, P.F.; Sauer, S.P.A. Noniterative Doubles Corrections to the Random Phase and Higher Random Phase Approximations: Singlet and Triplet Excitation Energies. J. Comput. Chem. 2019, 41, 43–55. [Google Scholar] [CrossRef]
- Head-Gordon, M.; Maurice, D.; Oumi, M. A perturbative correction to restricted open shell configuration interaction with single substitutions for excited states of radicals. Chem. Phys. Lett. 1995, 246, 114–121. [Google Scholar] [CrossRef]
- Head-Gordon, M.; Oumi, M.; Maurice, D. Quasidegenerate second-order perturbation corrections to single-excitation configuration interaction. Mol. Phys. 1999, 96, 593–602. [Google Scholar] [CrossRef]
- Christiansen, O.; Bak, K.L.; Koch, H.; Sauer, S.P.A. A second-order doubles correction to excitation energies in the random-phase approximation. Chem. Phys. Lett. 1998, 284, 47–55. [Google Scholar] [CrossRef]
- Åstrand, P.-O.; Ramanujam, P.S.; Hvilsted, S.; Bak, K.L.; Sauer, S.P.A. Ab Initio Calculation of the Electronic Spectrum of Azobenzene Dyes and Its Impact on the Design of Optical Data Storage Materials. J. Am. Chem. Soc. 2000, 122, 3482–3487. [Google Scholar] [CrossRef]
- Åstrand, P.-O.; Sommer-Larsen, P.; Hvilsted, S.; Ramanujam, P.S.; Bak, K.L.; Sauer, S.P.A. Five-membered rings as diazo components in optical data storage devices: An ab initio investigation of the lowest singlet excitation energies. Chem. Phys. Lett. 2000, 325, 115–119. [Google Scholar] [CrossRef]
- Falden, H.H.; Falster-Hansen, K.R.; Bak, K.L.; Rettrup, S.; Sauer, S.P.A. Benchmarking Second Order Methods for the Calculation of Vertical Electronic Excitation Energies: Valence and Rydberg States in Polycyclic Aromatic Hydrocarbons. J. Phys. Chem. 2009, 113, 11995–12012. [Google Scholar] [CrossRef] [PubMed]
- Sauer, S.P.A.; Pitzner-Frydendahl, H.F.; Buse, M.; Jensen, H.J.A.; Thiel, W. Performance of SOPPA-based methods in the calculation of vertical excitation energies and oscillator strengths. Mol. Phys. 2015, 113, 2026–2045. [Google Scholar] [CrossRef]
- Schnack-Petersen, A.K.; Haase Pi, A.B.; Faber, R.; Provasi, P.F.; Sauer, S.P.A. RPA(D) and HRPA(D): Two new models for calculations of NMR indirect nuclear spin–spin coupling constants. J. Comput. Chem. 2018, 39, 2647–2666. [Google Scholar] [CrossRef]
- Møller, C.H.S.; Schnack-Petersen, A.K.; Sauer, S.P.A. RPA(D) and HRPA(D): Calculation of carbon–carbon spin–spin coupling constants for saturated cycloalkanes. Mol. Phys. 2020, 118, e1757773. [Google Scholar] [CrossRef]
- Engelmann, A.R.; Contreras, R.H. Transmission mechanisms of spin-spin coupling constants within the CHF approximation: Their study using inner projections of the polarization propagator. Int. J. Quantum Chem. 1983, 23, 1033–1045. [Google Scholar] [CrossRef]
- Diz, A.C.; Giribet, C.G.; Ruiz de Azua, M.C.; Contreras, R.H. The use of localized molecular orbitals and the polarization propagator to identify transmission mechanisms in nuclear spin-spin couplings. Int. J. Quantum Chem. 1990, 37, 663–677. [Google Scholar] [CrossRef]
- Pople, J.A.; Beveridge, D.L. Approximate Molecular Orbital Theory, 1st ed.; McGraw-Hill: New York, NY, USA, 1970; pp. 1–214. [Google Scholar]
- Dewar, M.J.S.; Thiel, W. Ground states of molecules. 38. The MNDO method. Approximations and parameters. J. Am. Chem. Soc. 1977, 99, 4899–4907. [Google Scholar] [CrossRef]
- Dewar, M.J.S.; Zoebisch, E.J.; Healy, E.F.; Stewart, J.P. Development and use of quantum mechanical molecular models. 76. AM1: A new general purpose quantum mechanical molecular model. J. Am. Chem. Soc. 1985, 107, 3902–3909. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods II. Applications. J. Comput. Chem. 1989, 10, 221–264. [Google Scholar] [CrossRef]
- Zerner, M.C.; Loew, G.H.; Kirchner, R.F.; Mueller-Westerhoff, U.T. An intermediate neglect of differential overlap technique for spectroscopy of transition-metal complexes. Ferrocene. J. Am. Chem. Soc. 1980, 102, 589–599. [Google Scholar] [CrossRef]
- Ruiz de Azua, M.C.; Giribet, C.G.; Vizioli, C.V.; Contreras, R.H. Ab initio IPPP-CLOPPA approach to perform bond contribution analysis of NMR coupling constants: 1J(NH) in NH3 as a function of pyramidality. J. Mol. Struct. THEOCHEM 1998, 433, 141–150. [Google Scholar] [CrossRef]
- Zarycz, N.; Aucar, G.A. Analysis of electron correlation effects and contributions of NMR J-couplings from occupied localized molecular orbitals. J. Phys. Chem. 2012, 116, 1272–1282. [Google Scholar] [CrossRef] [PubMed]
- Ligabue, A.; Sauer, S.P.A.; Lazzeretti, P. Correlated and gauge invariant calculations of nuclear magnetic shielding constants using the continuous transformation of the origin of the current density approach. J. Chem. Phys. 2003, 118, 6830–6845. [Google Scholar] [CrossRef]
- Lazzeretti, P.; Malagoli, M.; Zanasi, R. Computational approach to molecular magnetic properties by continuous transformation of the origin of the current density. Chem. Phys. Lett. 1994, 220, 299–304. [Google Scholar] [CrossRef]
- Coriani, S.; Lazzeretti, P.; Malagoli, M.; Zanasi, R. On CHF calculations of second-order magnetic properties using the method of continuous transformation of origin of the current density. Theor. Chim. Acta 1994, 89, 181–192. [Google Scholar] [CrossRef]
- Lazzeretti, P. Ring currents. Prog. Nucl. Magn. Reson. Spectrosc. 2000, 36, 1–88. [Google Scholar] [CrossRef]
- Keith, T.A.; Bader, R.F.W. Calculation of magnetic response properties using a continuous set of gauge transformations. Chem. Phys. Lett. 1993, 210, 223–231. [Google Scholar] [CrossRef]
- Keith, T.A.; Bader, R.F.W. Topological analysis of magnetically induced molecular current distributions. J. Chem. Phys. 1993, 99, 3669–3682. [Google Scholar] [CrossRef]
- Keith, T.A.; Bader, R.F.W. Properties of atoms in molecules: Nuclear magnetic shielding. Can. J. Chem. 1996, 74, 185–200. [Google Scholar] [CrossRef]
- Schirmer, J. Beyond the random-phase approximation: A new approximation scheme for the polarization propagator. Phys. Rev. 1982, 26, 2395–2416. [Google Scholar] [CrossRef]
- Rusakova, I.L.; Krivdin, L.B.; Rusakov, Y.Y.; Trofimov, A.B. Algebraic-diagrammatic construction polarization propagator approach to indirect nuclear spin–spin coupling constants. J. Chem. Phys. 2012, 137, 044119. [Google Scholar] [CrossRef] [PubMed]
- Dempwolff, A.L.; Paul, A.C.; Belogolova, A.M.; Trofimov, A.B.; Dreuw, A. Intermediate state representation approach to physical properties of molecular electron-detached states. I. Theory and implementation. J. Chem. Phys. 2020, 152, 024113. [Google Scholar] [CrossRef] [PubMed]
- Pyykkö, P. Relativistic theory of nuclear spin-spin coupling in molecules. Chem. Phys. 1977, 22, 289–296. [Google Scholar] [CrossRef]
- Visscher, L.; Enevoldsen, T.; Saue, T.; Jensen, H.J.A.; Oddershede, J. Full four-component relativistic calculations of NMR shielding and indirect spin-spin coupling tensors in hydrogen halides. J. Comput. Chem. 1999, 20, 1262–1273. [Google Scholar] [CrossRef]
- Enevoldsen, T.; Visscher, L.; Saue, T.; Jensen, H.J.A.; Oddershede, J. Relativistic four-component calculations of indirect nuclear spin-spin couplings in MH4 (M = C, Si, Ge, Sn, Pb) and Pb(CH3)3H. J. Chem. Phys. 2000, 112, 3493–3498. [Google Scholar] [CrossRef]
- Antušek, A.; Pecul, M.; Sadlej, J. Relativistic calculation of NMR properties of XeF2, XeF4 and XeF6. Chem. Phys. Lett. 2006, 427, 281–288. [Google Scholar] [CrossRef]
- Quiney, H.M.; Skaane, H.; Grant, I.P. Relativistic, quantum electrodynamic and many-body effects in the water molecule. Chem. Phys. Lett. 1998, 290, 473–480. [Google Scholar] [CrossRef]
- Quiney, H.M.; Skaane, H.; Grant, I.P. Ab initio relativistic quantum chemistry: Four-components good, two-components bad! Adv. Quantum Chem. 1998, 32, 1–49. [Google Scholar] [CrossRef]
- Grant, I.P.; Quiney, H.M. Application of relativistic theories and quantum electrodynamics to chemical problems. Int. J. Quantum Chem. 2000, 80, 283–297. [Google Scholar] [CrossRef]
- Maldonado, A.F.; Aucar, G.A. The UKB prescription and the heavy atom effects on the nuclear magnetic shielding of vicinal heavy atoms. Phys. Chem. Chem. Phys. 2009, 11, 5615–5627. [Google Scholar] [CrossRef] [PubMed]
- Saue, T.; Helgaker, T. Four-component relativistic Kohn-Sham theory. J. Comput. Chem. 2002, 23, 814–823. [Google Scholar] [CrossRef]
- Salek, P.; Helgaker, T.; Saue, T. Linear response at the 4-component relativistic density-functional level: Application to the frequency-dependent dipole polarizability of Hg, AuH and PtH2. Chem. Phys. 2005, 311, 187–201. [Google Scholar] [CrossRef]
- Vaara, J.; Pyykkö, P. Relativistic, nearly basis-set-limit nuclear magnetic shielding constants of the rare gases He-Rn: A way to absolute nuclear magnetic resonance shielding scales. J. Chem. Phys. 2003, 118, 2973–2976. [Google Scholar] [CrossRef]
- Cremer, D. Møller–Plesset perturbation theory: From small molecule methods to methods for thousands of atoms. WIREs Comput. Mol. Sci. 2011, 1, 509–530. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Silver, D.M. Correlation energy in LiH, BH, and HF with many-body perturbation theory using Slater-type atomic orbitals. Int. J. Quantum Chem. 1974, S8, 271–276. [Google Scholar] [CrossRef]
- Binkley, J.S.; Pople, J.A. Møller–Plesset theory for atomic ground state energies. Int. J. Quantum Chem. 1975, 9, 229–236. [Google Scholar] [CrossRef]
- Gauss, J.; Stanton, J.F. Electron-correlated approaches for the calculation of NMR chemical shifts. In Advances in Chemical Physics, 1st ed.; Prigogine, I., Rice, S.A., Eds.; John Wiley & Sons, Inc.: New York, NY, USA, 2002; Volume 123, pp. 355–422. [Google Scholar]
- Pulay, P. Analytical derivative methods in quantum chemistry. In Advances in Chemical Physics: Ab Initio Methods in Quantum Chemistry Part 2, 1st ed.; Lawley, K.P., Ed.; John Wiley & Sons Ltd.: New York, NY, USA, 1987; Volume 65, pp. 241–286. [Google Scholar]
- Dupuis, M.; Rys, J.; King, H.F. Evaluation of molecular integrals over Gaussian basis functions. J. Chem. Phys. 1976, 65, 111–116. [Google Scholar] [CrossRef]
- McMurchie, L.E.; Davidson, E.R. One- and two-electron integrals over cartesian gaussian functions. J. Comp. Phys. 1978, 26, 218–231. [Google Scholar] [CrossRef]
- Obara, S.; Saika, A. Efficient recursive computation of molecular integrals over Cartesian Gaussian functions. J. Chem. Phys. 1986, 84, 3963–3974. [Google Scholar] [CrossRef]
- Gauss, J. Calculation of NMR chemical shifts at second-order many-body perturbation theory using gauge-including atomic orbitals. Chem. Phys. Lett. 1992, 191, 614–620. [Google Scholar] [CrossRef]
- Gauss, J. Effects of electron correlation in the calculation of nuclear magnetic resonance chemical shifts. J. Chem. Phys. 1993, 99, 3629–3643. [Google Scholar] [CrossRef]
- Bühl, M.; Gauss, J.; Hofmann, M.; Schleyer, P.v.R. Decisive electron correlation effects on computed boron-11 and carbon-13 NMR chemical shifts. Application of the GIAO-MP2 method to boranes and carbaboranes. J. Am. Chem. Soc. 1993, 115, 12385. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Gauss, J.; Bühl, M.; Greatrex, R.; Fox, M. Even more reliable NMR chemical shift computations by the GIAO-MP2 method. J. Chem. Soc. Chem. Commun. 1993, 23, 1766–1768. [Google Scholar] [CrossRef]
- Sieber, S.; Schleyer, P.v.R.; Gauss, J. The accurate C2v phenonium and benzenonium ion structures confirmed by correlated GIAO-MP2 NMR chemical shift calculations. J. Am. Chem. Soc. 1993, 115, 6987–6988. [Google Scholar] [CrossRef]
- Sieber, S.; Schleyer, P.v.R.; Otto, A.H.; Gauss, J.; Reichel, F.; Cremer, D. Structure, stabilization energies and chemical shifts of the cyclobutenyl cation. Does it have ‘aromatic’ homocyclopropenium ion character? An ab initio study. J. Phys. Org. Chem. 1993, 6, 445–464. [Google Scholar] [CrossRef]
- Buzek, P.; Schleyer, P.v.R.; Vancik, H.; Mihalic, Z.; Gauss, J. Erzeugung des Allyl-Kations in supersaurer Tieftemperatur-Matrix. Angew. Chem. 1994, 104, 470–473. [Google Scholar] [CrossRef]
- Siehl, H.-U.; Fuss, M.; Gauss, J. The 1-(Trimethylsilyl)bicyclobutonium Ion: NMR Spectroscopy, Isotope Effects, and Quantum Chemical Ab Initio Calculations of a New Hypercoordinated Carbocation. J. Am. Chem. Soc. 1995, 117, 5983–5991. [Google Scholar] [CrossRef]
- Gauss, J. GIAO-MBPT(3) and GIAO-SDQ-MBPT(4) calculations of nuclear magnetic shielding constants. Chem. Phys. Lett. 1994, 229, 198–203. [Google Scholar] [CrossRef]
- Pople, J.A.; Binkley, J.S.; Seeger, R. Theoretical models incorporating electron correlation. Int. J. Quantum. Chem. Symp. 1976, 10, 1–19. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Shavitt, I. Comparison of high-order many-body perturbation theory and configuration interaction for H2O. Chem. Phys. Lett. 1977, 50, 190–198. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Purvis, G.D. The potential energy curve for the X1Σg+ g state of Mg2 calculated with many-body perturbation theory. J. Chem. Phys. 1978, 68, 2114–2124. [Google Scholar] [CrossRef]
- Krishnan, R.; Pople, J.A. Approximate fourth-order perturbation theory of the electron correlation energy. Int. J. Quantum Chem. 1978, 14, 91–100. [Google Scholar] [CrossRef]
- Krishnan, R.; Frisch, M.; Pople, J.A. Contribution of triple substitutions to the electron correlation energy in fourth order perturbation theory. J. Chem. Phys. 1980, 72, 4244–4245. [Google Scholar] [CrossRef]
- Weigend, F.; Häser, M. RI-MP2: First derivatives and global consistency. Theor. Chem. Acc. 1997, 97, 331–340. [Google Scholar] [CrossRef]
- Dyall, K.G. Second-order Moller-Plesset perturbation theory for molecular Dirac-Hartree-Fock wavefunctions. Theory for up to two open-shell electrons. Chem. Phys. Lett. 1994, 224, 186–194. [Google Scholar] [CrossRef]
- Sapirstein, J. Theoretical methods for the relativistic atomic many-body problem. Rev. Mod. Phys. 1998, 70, 55–76. [Google Scholar] [CrossRef]
- Ishikawa, Y. Relativistic many-body perturbation theory using discrete basis expansion method: Accurate representation of second-order energy of Xe atom with contracted well-tempered Gaussian basis set. Can. J. Chem. 1992, 70, 399–403. [Google Scholar] [CrossRef]
- Johnson, W.R. Applications of relativistic MBPT to lithium-like atoms. AIP Conf. Proc. 1989, 189, 209–216. [Google Scholar] [CrossRef]
- Savukov, I.M.; Filin, D.; Chu, P.; Malone, M.W. Relativistic Configuration-Interaction and Perturbation Theory Calculations for Heavy Atoms. Atoms 2021, 9, 104. [Google Scholar] [CrossRef]
- Brown, G.E.; Ravenhall, D.G. On the interaction of two electrons. Proc. R. Soc. Lond. 1951, 208, 552–559. [Google Scholar] [CrossRef]
- Kutzelnigg, W. The relativistic many-body problem in molecular theory. Phys. Scr. 1987, 36, 416–431. [Google Scholar] [CrossRef]
- Sucher, J. S-Matrix Formalism for Level-Shift Calculations. Phys. Rev. 1957, 107, 1448–1449. [Google Scholar] [CrossRef]
- Sucher, J. Relativistic many-electron Hamiltonians. Phys. Scr. 1987, 36, 271–281. [Google Scholar] [CrossRef]
- Sucher, J. QED and Relativity in Atomic Physics. In Atoms in Unusual Situations, 1st ed.; Briand, J.P., Ed.; Springer: Boston, MA, USA, 1986; Volume 143, pp. 251–300. [Google Scholar] [CrossRef]
- Chesnut, D.B.; Byrd, E.F.C. The use of locally dense basis sets in correlated NMR chemical shielding calculations. Chem. Phys. 1996, 213, 153–158. [Google Scholar] [CrossRef]
- Sanchez, M.; Provasi, P.F.; Aucar, G.A.; Sauer, S.P.A. On the usage of locally dense basis sets in the calculation of NMR indirect nuclear spin-spin coupling constants: Vicinal fluorine-fluorine couplings. Adv. Quantum Chem. 2005, 48, 161–183. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. IV. Calculation of static electrical response properties. J. Chem. Phys. 1994, 100, 2975–2988. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. V. Core-valence basis sets for boron through neon. J. Chem. Phys. 1995, 103, 4572–4585. [Google Scholar] [CrossRef]
- Sadlej, J. Medium-size polarized basis sets for high-level correlated calculations of molecular electric properties. Collect. Czech. Chem. Commun. 1988, 53, 1995–2016. [Google Scholar] [CrossRef]
- Sadlej, J. Medium-size polarized basis sets for high-level-correlated calculations of molecular electric properties. II. Second-row atoms: Si through Cl. Theor. Chim. Acta 1991, 79, 123–140. [Google Scholar] [CrossRef]
- Sadlej, J. Medium-size polarized basis sets for high-level-correlated calculations of molecular electric properties. IV. Third-row atoms: Ge through Br. Theor. Chim. Acta 1991, 81, 45–63. [Google Scholar] [CrossRef]
- Sadlej, J. Medium-size polarized basis sets for high-level-correlated calculations of molecular electric properties. V. Fourth-row atoms: Sn through I. Theor. Chim. Acta 1992, 81, 339–354. [Google Scholar] [CrossRef]
- Huzinaga, S. Gaussian-type functions for polyatomic systems. I. J. Chem. Phys. 1965, 42, 1293–1302. [Google Scholar] [CrossRef]
- Provasi, P.F.; Sauer, S.P.A. Optimized basis sets for the calculation of indirect nuclear spin-spin coupling constants involving the atoms B, Al, Si, P, and Cl. J. Chem. Phys. 2010, 133, 054308. [Google Scholar] [CrossRef] [PubMed]
- Barone, V.; Provasi, P.F.; Peralta, J.E.; Snyder, J.P.; Sauer, S.P.A.; Contreras, R.H. Substituent effects on scalar 2J(19F,19F) and 3J(19F,19F) NMR couplings: a comparison of SOPPA and DFT methods. J. Phys. Chem. 2003, 107, 4748–4754. [Google Scholar] [CrossRef]
- Hedegård, E.D.; Kongsted, J.; Sauer, S.P.A. Optimized basis sets for calculation of electron paramagnetic resonance hyperfine coupling constants: Aug-cc-pVTZ-J for the 3d atoms Sc-Zn. J. Chem. Theory Comput. 2011, 7, 4077–4087. [Google Scholar] [CrossRef]
- Steinmann, C.; Sauer, S.P.A. The aug-cc-pVTZ-J basis set for the p-block fourth-row elements Ga, Ge, As, Se, and Br. Magn. Reson. Chem. 2021, 59, 1134–1145. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Rusakova, I.L. Hierarchical basis sets for the calculation of nuclear magnetic resonance spin–spin coupling constants involving either selenium or tellurium nuclei. J. Phys. Chem. 2019, 123, 6564–6571. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Rusakova, I.L. Efficient J-oriented tin basis sets for the correlated calculations of indirect nuclear spin-spin coupling constants. Magn. Reson. Chem. 2021, 59, 713–722. [Google Scholar] [CrossRef] [PubMed]
- Dyall, K.G. Relativistic and nonrelativistic finite nucleus optimized triple-zeta basis sets for the 4p, 5p and 6p elements. Theor. Chem. Acc. 2002, 108, 335–340. [Google Scholar] [CrossRef]
- Dyall, K.G. Relativistic quadruple-zeta and revised triple-zeta and double-zeta basis Sets for the 4p, 5p, and 6p elements. Theor. Chem. Acc. 2006, 115, 441–447. [Google Scholar] [CrossRef]
- Kjær, H.; Sauer, S.P.A. Pople style basis sets for the calculation of NMR spin-spin coupling constants: The 6-31G-J and 6-311G-J basis sets. J. Chem. Theory Comput. 2011, 7, 4070–4076. [Google Scholar] [CrossRef] [PubMed]
- Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self-consistent molecular orbital methods. xii. further extensions of gaussian-type basis sets for use in molecular orbital studies of organic molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Jensen, F. The optimum contraction of basis sets for calculating spin–spin coupling constants. Theor. Chem. Acc. 2010, 126, 371–382. [Google Scholar] [CrossRef]
- Aggelund, P.A.; Sauer, S.P.A.; Jensen, F. Development of polarization consistent basis sets for spin-spin coupling constant calculations for the atoms Li, Be, Na, and Mg. J. Chem. Phys. 2018, 149, 044117. [Google Scholar] [CrossRef]
- Jensen, F. Polarization consistent basis sets: Principles. J. Chem. Phys. 2001, 115, 9113–9125. [Google Scholar] [CrossRef]
- Jensen, F. Polarization consistent basis sets. II. Estimating the Kohn–Sham basis set limit. J. Chem. Phys. 2002, 116, 7372–7379. [Google Scholar] [CrossRef]
- Jensen, F.; Helgaker, T. Polarization consistent basis sets. V. The elements Si–Cl. J. Chem. Phys. 2004, 121, 3463–3470. [Google Scholar] [CrossRef] [PubMed]
- Jensen, F. Polarization Consistent Basis Sets. 4: The Elements He, Li, Be, B, Ne, Na, Mg, Al, and Ar. J. Phys. Chem. 2007, 111, 11198–11204. [Google Scholar] [CrossRef] [PubMed]
- Jensen, F. Polarization consistent basis sets. III. The importance of diffuse functions. J. Chem. Phys. 2002, 117, 9234–9240. [Google Scholar] [CrossRef]
- Chong, D.P. Completeness profiles of one-electron basis sets. Can. J. Chem. 1995, 73, 79–83. [Google Scholar] [CrossRef]
- Manninen, P.; Vaara, J. Systematic Gaussian basis-set limit using completeness-optimized primitive sets. A case for magnetic properties. J. Comput. Chem. 2006, 27, 434–445. [Google Scholar] [CrossRef]
- Lehtola, J.; Manninen, P.; Hakala, M.; Hämäläinen, K. Completeness-optimized basis sets: Application to ground-state electron momentum densities. J. Chem. Phys. 2012, 137, 104105. [Google Scholar] [CrossRef]
- Lehtola, J.; Manninen, P.; Hakala, M.; Hämäläinen, K. Contraction of completeness-optimized basis sets: Application to ground-state electron momentum densities. J. Chem. Phys. 2013, 138, 044109. [Google Scholar] [CrossRef]
- Lehtola, S. Automatic algorithms for completeness-optimization of Gaussian basis sets. J. Comput. Chem. 2015, 36, 335–347. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Rusakov, I.L. An efficient method for generating property-energy consistent basis sets. New pecJ-n (n = 1, 2) basis sets for high-quality calculations of indirect nuclear spin–spin coupling constants involving 1H, 13C, 15N, and 19F nuclei. Phys. Chem. Chem. Phys. 2021, 23, 14925–14939. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef]
- Harrison, R.L. Introduction to Monte Carlo Simulation. AIP Conf. Proc. 2010, 1204, 17–21. [Google Scholar] [CrossRef] [PubMed]
- Del Moral, P.; Doucet, A.; Jasra, A. Sequential Monte Carlo samplers. J. R. Stat. Soc. 2006, 68, 411–436. [Google Scholar] [CrossRef]
- d’Antuono, P.; Botek, E.; Champagne, B.; Spassova, M.; Denkova, P. Theoretical investigation on 1H and 13C NMR chemical shifts of small alkanes and chloroalkanes. J. Chem. Phys. 2006, 125, 144309. [Google Scholar] [CrossRef]
- Wu, A.; Cremer, D.; Gauss, J. 17O NMR chemical shifts of polyoxides in gas phase and in solution. J. Phys. Chem. 2003, 107, 8737–8745. [Google Scholar] [CrossRef]
- Gordon, M.S.; Binkley, J.S.; Pople, J.A.; Pietro, W.J.; Hehre, W.J. Self-consistent molecular-orbital methods. 22. Small split-valence basis sets for second-row elements. J. Am. Chem. Soc. 1982, 104, 2797–2803. [Google Scholar] [CrossRef]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-consistent molecular-orbital methods. IX. an extended gaussian-type basis for molecular-orbital studies of organic molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
- Spitznagel, G.W.; Clark, T.; von Ragué Schleyer, P.; Hehre, W.J. An evaluation of the performance of diffuse function-augmented basis sets for second row elements, Na-Cl. J. Comput. Chem. 1987, 8, 1109–1116. [Google Scholar] [CrossRef]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z = 11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Francl, M.M.; Pietro, W.J.; Hehre, W.J.; Binkley, J.S.; Gordon, M.S.; DeFrees, D.J.; Pople, J.A. Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row elements. J. Chem. Phys. 1982, 77, 3654–3665. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; von Ragué Schleyer, P. Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first-row elements, Li-F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Widmark, P.-O.; Malmqvist, P.-Å.; Roos, B.O. Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions. I. First row atoms. Theor. Chim. Acta 1990, 77, 291–306. [Google Scholar] [CrossRef]
- Widmark, P.-O.; Persson, B.J.; Roos, B.O. Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions. II. Second row atoms. Theor. Chim. Acta 1991, 79, 419–432. [Google Scholar] [CrossRef]
- Pou-Amérigo, R.; Merchán, M.; Nebot-Gil, I.; Widmark, P.-O.; Roos, B.O. Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions. III. First row transition metal atoms. Theor. Chim. Acta 1995, 92, 149–181. [Google Scholar] [CrossRef]
- Carmichael, I. Ab initio quadratic configuration interaction calculation of indirect NMR spin-spin coupling constants. J. Phys. Chem. 1993, 97, 1789–1792. [Google Scholar] [CrossRef]
- Jensen, F. Basis set convergence of nuclear magnetic shielding constants calculated by density functional methods. J. Chem. Theory Comput. 2008, 4, 719–727. [Google Scholar] [CrossRef]
- Jensen, F. Segmented contracted basis sets optimized for nuclear magnetic shielding. J. Chem. Theory Comput. 2015, 11, 132–138. [Google Scholar] [CrossRef]
- Raffenetti, R.C. General contraction of Gaussian atomic orbitals: Core, valence, polarization, and diffuse basis sets; molecular integral evaluation. J. Chem. Phys. 1973, 58, 4452–4458. [Google Scholar] [CrossRef]
- Franzke, Y.J.; Tress, R.; Pazdera, T.M.; Weigend, F. Error-consistent segmented contracted all-electron relativistic basis sets of double- and triple-zeta quality for NMR shielding constants. Phys. Chem. Chem. Phys. 2019, 21, 16658–16664. [Google Scholar] [CrossRef]
- Pollak, P.; Weigend, F. Segmented contracted error-consistent basis sets of double- and triple-ζ valence quality for one- and two-component relativistic all-electron calculations. J. Chem. Theory Comput. 2017, 13, 3696–3705. [Google Scholar] [CrossRef]
- Nielsen, H.H. The Vibration-Rotation Energies of Molecules. Rev. Mod. Phys. 1951, 23, 90–136. [Google Scholar] [CrossRef]
- Herman, R.C.; Shuler, K.E. Vibrational Intensities in Diatomic Infrared Transitions. The Vibrational Matrix Elements for CO. J. Chem. Phys. 1954, 22, 481–490. [Google Scholar] [CrossRef]
- Wilson, E.B., Jr.; Decius, J.C.; Cross, P.C. Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra, 1st ed.; McGraw-Hill: New York, NY, USA, 1955; pp. 1–388. [Google Scholar]
- Herschbach, D.R.; Laurie, V.W. Influence of Vibrations on Molecular Structure Determinations. I. General Formulation of Vibration—Rotation Interactions. J. Chem. Phys. 1962, 37, 1668–1686. [Google Scholar] [CrossRef]
- Morino, Y.; Kuchitsu, K.; Oka, T. Internuclear Distance Parameters. J. Chem. Phys. 1962, 36, 1108–1109. [Google Scholar] [CrossRef]
- Toyama, M.; Oka, T.; Morino, Y. Effect of vibration and rotation on the internuclear distance. J. Mol. Spectrosc. 1964, 13, 193–213. [Google Scholar] [CrossRef]
- Morino, Y.; Kuchitsu, K.; Yamamoto, S. The anharmonic constants and average structure of ammonia. Spectrochim. Acta Mol. Spectrosc. 1968, 24, 335–352. [Google Scholar] [CrossRef]
- Buckingham, A.D. Temperature-Dependent Chemical Shifts in the NMR Spectra of Gases. J. Chem. Phys. 1962, 36, 3096. [Google Scholar] [CrossRef]
- Buckingham, A.D.; Cordle, J.E. Nuclear motion corrections to some electric and magnetic properties of diatomic molecules. Mol. Phys. 1974, 28, 1037–1047. [Google Scholar] [CrossRef]
- Buckingham, A.D.; Urland, W. Isotope effects on molecular properties. Chem. Rev. 1975, 75, 113–117. [Google Scholar] [CrossRef]
- Hoy, A.R.; Mills, I.M.; Strey, G. Anharmonic force constant calculations. Mol. Phys. 1972, 24, 1265–1290. [Google Scholar] [CrossRef]
- Lucas, N.J.D. On the vibrationally averaged structure and vibrational expectation values. Mol. Phys. 1972, 23, 825–826. [Google Scholar] [CrossRef]
- Kern, C.W.; Matcha, R.L. Nuclear corrections to electronic expectation values: Zero-point vibrational effects in the water molecule. J. Chem. Phys. 1968, 49, 2081–2091. [Google Scholar] [CrossRef]
- Ermler, W.C.; Kern, C.W. Zero-Point vibrational corrections to one-electron properties of the water molecule in the Near-Hartree-Fock limit. J. Chem. Phys. 1971, 55, 4851–4860. [Google Scholar] [CrossRef]
- Krohn, B.J.; Ermler, W.C.; Kern, C.W. Nuclear corrections to molecular properties. IV. Theory for low-lying vibrational states of polyatomic molecules with application to the water molecule near the Hartree-Fock limit. J. Chem. Phys. 1974, 60, 22–33. [Google Scholar] [CrossRef]
- Ermler, W.C.; Krohn, B.J. Nuclear corrections to molecular properties. V. Refinements in ab initio normal-coordinate potential energy and property surfaces for water and their effect on the vibrational analysis. J. Chem. Phys. 1977, 67, 1360–1374. [Google Scholar] [CrossRef]
- Krohn, B.J.; Kern, C.W. Nuclear corrections to molecular properties. VI. Vibrational transition moments in asymmetric-top molecules. J. Chem. Phys. 1978, 69, 5310–5313. [Google Scholar] [CrossRef]
- Harding, L.B.; Ermler, W.C. Polyatomic, anharmonic, vibrational–rotational analysis. Application to accurate ab initio results for formaldehyde. J. Comput. Chem. 1985, 6, 13–27. [Google Scholar] [CrossRef]
- Hargiss, L.O.; Ermler, W.C. Vibrational-rotational analysis of ab initio potential energy surfaces for symmetric-top molecules: Application to ammonia isotopomers. J. Phys. Chem. 1988, 92, 300–306. [Google Scholar] [CrossRef]
- Hsieh, H.C.; Ermler, W.C. Ab initio vibrational transition dipole moments and intensities of formaldehyde. J. Comput. Chem. 1988, 9, 95. [Google Scholar] [CrossRef]
- Ermler, W.C.; Hsieh, H.C. Analytical Representation and Vibrational-Rotational Analysis of Ab Initio Potential Energy and Properties Surfaces. In Advances in Molecular Electronic Structure Theory: Calculation and Characterization of Potential Energy Surfaces, 1st ed.; Dunning, T.H., Jr., Ed.; JAI Press, Inc.: Greenwich, CN, USA, 1990; pp. 1–44. [Google Scholar]
- Herbert, J.M.; Ermler, W.C. Symbolic Implementation of Arbitrary-Order Perturbation Theory Using Computer Algebra: Application to Vibrational-Rotational Analysis of Diatomic Molecules. Comput. Chem. 1998, 22, 169–184. [Google Scholar] [CrossRef]
- Zhang, Q.; Day, P.N.; Truhlar, D.G. The accuracy of second order perturbation theory for multiply excited vibrational energy levels and partition functions for a symmetric top molecular ion. J. Chem. Phys. 1988, 98, 4948–4958. [Google Scholar] [CrossRef]
- Truhlar, D.G.; Isaacson, A.D. Simple perturbation theory estimates of equilibrium constants from force fields. J. Chem. Phys. 1991, 94, 357–359. [Google Scholar] [CrossRef]
- Lounila, J.; Wasser, R.; Diehl, P. Effects of anharmonic vibrations on molecular properties. Mol. Phys. 1987, 62, 19–31. [Google Scholar] [CrossRef]
- Fowler, P.W.; Raynes, W.T. The effects of rotation, vibration and isotopic substitution on the electric dipole moment, the magnetizability and the nuclear magnetic shielding of the water molecule. Mol. Phys. 1981, 43, 65–82. [Google Scholar] [CrossRef]
- Fowler, P.W.; Raynes, W.T. The effects of vibration-rotation on the quadrupole moment, rotational g-factor and spin-rotation parameters of the water molecule. Mol. Phys. 1982, 45, 667–680. [Google Scholar] [CrossRef]
- Raynes, W.T. The 17O nuclear magnetic shielding in H217O and D217O. Mol. Phys. 1983, 49, 443–447. [Google Scholar] [CrossRef]
- Fowler, P.W. Vibrational effects on properties of spherical tops. Mol. Phys. 1984, 51, 1423–1428. [Google Scholar] [CrossRef]
- Raynes, W.T.; Fowler, P.W.; Lazzeretti, P.; Zanasi, R.; Grayson, M. The effects of rotation and vibration on the carbon-13 shielding, magnetizabilities and geometrical parameters of some methane isotopomers. Mol. Phys. 1988, 64, 143–162. [Google Scholar] [CrossRef]
- Bishop, D.M.; Pipin, J. Vibrational effects for the dispersion-energy and dispersion-polarizability coefficients for interactions between H, He, and H2. J. Chem. Phys. 1993, 98, 522–524. [Google Scholar] [CrossRef]
- Bishop, D.M.; Cybulski, S.M. Vibrational corrections for some electric and magnetic properties of H2, N2, HF, and CO. J. Chem. Phys. 1994, 101, 2180–2185. [Google Scholar] [CrossRef]
- Carney, G.D.; Sprandel, L.L.; Kern, C.W. Variational Approaches to Vibration-Rotation Spectroscopy for Polyatomic Molecules. Adv. Chem. Phys. 1978, 37, 305–379. [Google Scholar] [CrossRef]
- Whitehead, R.J.; Handy, N.C. Variational calculation of vibration-rotation energy levels for triatomic molecules. J. Mol. Spectrosc. 1975, 55, 356–373. [Google Scholar] [CrossRef]
- Sexton, G.J.; Handy, N.C. Ab initio calculation for the fundamental frequencies of H2O. Mol. Phys. 1984, 51, 1321–1330. [Google Scholar] [CrossRef]
- Handy, N.C. The calculation of vibrational energy levels by semiclassical and quantum methodology: A review. Int. Rev. Phys. Chem. 1988, 8, 275–288. [Google Scholar] [CrossRef]
- Bačić, Z.; Light, J.C. Theoretical Methods for Rovibrational States of Floppy Molecules. Annu. Rev. Phys. Chem. 1989, 40, 469–498. [Google Scholar] [CrossRef]
- Choi, S.E.; Light, J.C. Highly excited vibrational eigenstates of nonlinear triatomic molecules. Application to H2O. J. Chem. Phys. 1992, 97, 7031–7054. [Google Scholar] [CrossRef]
- Åstrand, P.-O.; Ruud, K.; Taylor, P.R. Calculation of the vibrational wave function of polyatomic molecules. J. Chem. Phys. 2000, 112, 2655–2667. [Google Scholar] [CrossRef]
- Ruud, K.; Åstrand, P.-O.; Taylor, P.R. An efficient approach for calculating vibrational wave functions and zero-point vibrational corrections to molecular properties of polyatomic molecules. J. Chem. Phys. 2000, 112, 2668–2683. [Google Scholar] [CrossRef]
- Aidas, K.; Angeli, C.; Bak, K.L.; Bakken, V.; Bast, R.; Boman, L.; Christiansen, O.; Cimiraglia, R.; Coriani, S.; Dahle, P.; et al. The Dalton quantum chemistry program system. WIREs Comput. Mol. Sci. 2014, 4, 269–284. [Google Scholar] [CrossRef]
- Ruden, T.A.; Ruud, K. Ro-Vibrational Corrections to NMR Parameters. In Calculation of NMR and EPR Parameters: Theory and Applications, 1st ed.; Kaupp, M., Malkin, V.G., Bühl, M., Eds.; Wiley-VCH: Weinheim, Germany, 2004; Chapter 10; pp. 153–173. [Google Scholar]
- Ruden, T.A.; Lutnæs, O.B.; Helgaker, T.; Ruud, K. Vibrational corrections to indirect nuclear spin-spin coupling constants calculated by density-functional theory. J. Chem. Phys. 2003, 118, 9572–9581. [Google Scholar] [CrossRef]
- Bass, S.M.; DeLeon, R.L.; Muenter, J.S. Stark, Zeeman, and hyperfine properties of ν = 0, ν =1, and the equilibrium configuration of hydrogen fluoride. J. Chem. Phys. 1987, 86, 4305–4312. [Google Scholar] [CrossRef]
- Muenter, J.S.; Klemperer, W. Hyperfine structure constants of HF and DF. J. Chem. Phys. 1970, 52, 6033–6037. [Google Scholar] [CrossRef]
- Åstrand, P.-O.; Ruud, K.; Mikkelsen, K.V.; Helgaker, T. Rovibrationally averaged magnetizability, rotational g factor, and indirect spin-spin coupling of the hydrogen fluoride molecule. J. Chem. Phys. 1999, 110, 9463–9468. [Google Scholar] [CrossRef][Green Version]
- Sneskov, K.; Stanton, J.F. Effects of vibrational averaging on coupled cluster calculations of spin-spin coupling constants for hydrocarbons. Mol. Phys. 2012, 110, 2321–2327. [Google Scholar] [CrossRef]
- Kirpekar, S.; Enevoldsen, T.; Oddershede, J.; Raynes, W.T. Vibrational and thermal averaging of the indirect nuclear spin-spin coupling constants of CH4, SiH4, GeH4 and SnH4. Mol. Phys. 1997, 91, 897–908. [Google Scholar] [CrossRef]
- Yachmenev, A.; Yurchenko, S.N.; Paidarová, I.; Jensen, P.; Thiel, W.; Sauer, S.P.A. Thermal averaging of the indirect nuclear spin-spin coupling constants of ammonia: The importance of the large amplitude inversion mode. J. Chem. Phys. 2010, 132, 114305. [Google Scholar] [CrossRef]
- Jordan, M.J.T.; Toh, J.S.-S.; Del Bene, J.E. Vibrational averaging of NMR properties for an N-H-N hydrogen bond. Chem. Phys. Lett. 2001, 346, 288–292. [Google Scholar] [CrossRef]
- Del Bene, J.E.; Jordan, M.J.T.; Perera, S.A.; Bartlett, R.J. Vibrational Effects on the F−F Spin−Spin Coupling Constant (2hJF-F) in FHF- and FDF-. J. Phys. Chem. 2001, 105, 8399–8402. [Google Scholar] [CrossRef]
- Kutzelnigg, W.; Fleischer, U.; Schindler, M. NMR—Basic Principles and Progress, 1st ed.; Springer: Berlin, Germany, 1990; Volume 23, pp. 1–165. [Google Scholar]
- Geertsen, J.; Oddershede, J.; Scuseria, G.E. Spin–spin coupling constants of CO and N2. J. Chem. Phys. 1987, 87, 2138–2142. [Google Scholar] [CrossRef]
- Bennett, B.; Raynes, W.T.; Anderson, C.W. Temperature dependences of J(C,H) and J(C,D) in 13CH4 and some of its deuterated isotopomers. Spectrochim. Acta 1989, 45, 821–827. [Google Scholar] [CrossRef]
- Sauer, S.P.A.; Møller, C.K.; Koch, H.; Paidarová, I.; Špirko, V. The vibrational and temperature dependence of the indirect nuclear spin–spin coupling constants of the oxonium (H3O+) and hydroxyl (OH−) ions. Chem. Phys. 1998, 238, 385–399. [Google Scholar] [CrossRef]
- Ruden, T.A.; Helgaker, T.; Jaszuński, M. The NMR indirect nuclear spin-spin coupling constants for some small rigid hydrocarbons: Molecular equilibrium values and vibrational corrections. Chem. Phys. 2004, 296, 53–62. [Google Scholar] [CrossRef]
- Wigglesworth, R.D.; Raynes, W.T.; Kirpekar, S.; Oddershede, J.; Sauer, S.P.A. Nuclear magnetic shielding in the acetylene isotopomers calculated from correlated shielding surfaces. J. Chem. Phys. 2000, 112, 736–746. [Google Scholar] [CrossRef]
- Sundholm, D.; Gauss, J. Isotope and temperature effects on nuclear magnetic shieldings and spin-rotation constants calculated at the coupled-cluster level. Mol. Phys. 1997, 92, 1007–1014. [Google Scholar] [CrossRef]
- Chesnut, D.B. On the calculation of hydrogen NMR chemical shielding. Chem. Phys. 1997, 214, 73–79. [Google Scholar] [CrossRef]
- Jameson, C.J.; Jameson, A.K.; Cohen, S.M.; Parker, H.; Oppusunggu, D.; Burrell, P.M.; Wille, S. Temperature dependence of the 15N and 1H nuclear magnetic shielding in NH3. J. Chem. Phys. 1981, 74, 1608–1612. [Google Scholar] [CrossRef]
- Sanders, J.K.M.; Hunter, B.K.; Jameson, C.J.; Romeo, G. Isotope effects on proton chemical shifts and coupling constants in the ammonium ions 15, 14NH4-nDn+. Chem. Phys. Lett. 1988, 143, 471–476. [Google Scholar] [CrossRef]
- Jameson, C.J.; de Dios, A.C. Nuclear magnetic shielding of nitrogen in ammonia. J. Chem. Phys. 1991, 95, 1069–1079. [Google Scholar] [CrossRef]
- Jameson, C.J.; de Dios, A.C. The 31P shielding in phosphine. J. Chem. Phys. 1991, 95, 9042–9053. [Google Scholar] [CrossRef]
- Paidarova, I.; Spirko, V.; Oddershede, J. The Temperature Dependence and Isotope Shift of Nitrogen Shielding in Ammonia. J. Mol. Spectrosc. 1993, 160, 311–314. [Google Scholar] [CrossRef]
- Sauer, S.P.A.; Špirko, V.; Paidarová, I.; Oddershede, J. The vibrational and temperature dependence of the magnetic properties of the oxonium ion (H3O+). Chem. Phys. 1994, 184, 1–11. [Google Scholar] [CrossRef]
- Jameson, C.J.; Osten, H.J. The effect of anharmonic vibration and centrifugal distortion on nuclear shielding in linear triatomic molecules: NNO and CO2. J. Chem. Phys. 1984, 81, 2556–2561. [Google Scholar] [CrossRef]
- Fukui, H.; Baba, T.; Narumi, J.; Inomata, H.; Miura, K.; Matsuda, H. Calculation of nuclear magnetic shieldings. XI. Vibrational motion effects. J. Chem. Phys. 1996, 105, 4692–4699. [Google Scholar] [CrossRef][Green Version]
- Lounila, J.; Vaara, J.; Hiltunen, Y.; Pulkkinen, A.; Jokisaari, J.; Ala-Korpela, M.; Ruud, K. Isotope and temperature effects on the 13C and 77Se nuclear shielding in carbon diselenide. J. Chem. Phys. 1997, 107, 1350–1361. [Google Scholar] [CrossRef]
- Sauer, S.P.A.; Špirko, V.; Paidarova, I.; Kraemer, W.P. The vibrational dependence of the hydrogen and oxygen nuclear magnetic shielding constants in OH− and OH−·H2O. Chem. Phys. 1997, 214, 91–101. [Google Scholar] [CrossRef]
- Cooley, J.W. An improved eigenvalue corrector formula for solving the Schrödinger equation for central fields. Math. Comp. 1961, 15, 363–374. [Google Scholar] [CrossRef]
- Špirko, V.; Kraemer, W.P.; Čejchan, A. Vibrational dynamics of hydrogen bonds: The system OH−·H2O. J. Mol. Spectrosc. 1989, 136, 340–355. [Google Scholar] [CrossRef]
- Minaev, B.; Vaara, J.; Ruud, K.; Vahtras, O.; Ågren, H. Internuclear distance dependence of the spin–orbit coupling contributions to proton NMR chemical shifts. Chem. Phys. Lett. 1998, 295, 455–461. [Google Scholar] [CrossRef]
- Wigglesworth, R.D.; Raynes, W.T.; Sauer, S.P.A.; Oddershede, J. Calculated nuclear shielding surfaces in the water molecule; prediction and analysis of σ(O), σ(H) and σ(D) in water isotopomers. Mol. Phys. 1999, 96, 1595–1607. [Google Scholar] [CrossRef]
- Auer, A.A. Quantitative prediction of gas-phase 17O nuclear magnetic shielding constants. J. Chem. Phys. 2009, 131, 024116. [Google Scholar] [CrossRef]
- Kupka, T.; Stachów, M.; Kaminsky, J.; Sauer, S.P.A. Estimation of isotropic nuclear magnetic shieldings in the CCSD(T) and MP2 complete basis set limit using affordable correlation calculations. Magn. Reson. Chem. 2013, 51, 482–489. [Google Scholar] [CrossRef] [PubMed]
- Puzzarini, C.; Cazzoli, G.; Harding, M.E.; Vazquez, J.; Gauss, J. A new experimental absolute nuclear magnetic shielding scale for oxygen based on the rotational hyperfine structure of H217O. J. Chem. Phys. 2009, 131, 234304. [Google Scholar] [CrossRef] [PubMed]
- Vaara, J.; Lounila, J. Rovibrational effects, temperature dependence, and isotope effects on the nuclear shielding tensors of water: A new 17O absolute shielding scale. J. Chem. Phys. 1998, 109, 8388–8397. [Google Scholar] [CrossRef]
- Gauss, J.; Sundholm, D. Coupled-cluster calculations of spin-rotation constants. Mol. Phys. 1997, 91, 449–458. [Google Scholar] [CrossRef]
- Komorovsky, S.; Repisky, M.; Malkin, E.; Ruud, K.; Gauss, J. Communication: The absolute shielding scales of oxygen and sulfur revisited. J. Chem. Phys. 2015, 142, 091102. [Google Scholar] [CrossRef]
- Faber, R.; Buczek, A.; Kupka, T.; Sauer, S.P.A. On the convergence of zero-point vibrational corrections to nuclear shieldings and shielding anisotropies towards the complete basis set limit in water. Mol. Phys. 2016, 115, 144–160. [Google Scholar] [CrossRef]
- Rusakova, I.L.; Rusakov, Y.Y.; Krivdin, L.B. Calculation of 125Te NMR Chemical Shifts at the Full Four-Component Relativistic Level with Taking into Account Solvent and Vibrational Corrections: A Gateway to Better Agreement with Experiment. J. Phys. Chem. 2017, 121, 4793–4803. [Google Scholar] [CrossRef] [PubMed]
- Barfield, M.; Johnston, M.D., Jr. Solvent Dependence of Nuclear Spin-Spin Coupling Constants. Chem. Rev. 1973, 73, 53–73. [Google Scholar] [CrossRef]
- Raynes, W.T.; Sutherley, T.A.; Buttery, H.J.; Fenton, C.M. Solvent dependence of nuclear spin-spin couplings. Mol. Phys. 1968, 14, 599–600. [Google Scholar] [CrossRef]
- Raynes, W.T. An empirical correlation concerning the solvent dependence of nuclear spin-spin couplings. Mol. Phys. 1968, 15, 435–438. [Google Scholar] [CrossRef]
- Buckingham, A.D.; Schaefer, T.; Schneider, W.G. Solvent Effects in Nuclear Magnetic Resonance Spectra. J. Chem. Phys. 1960, 32, 1227–1233. [Google Scholar] [CrossRef]
- Giribet, C.G.; Vizioli, C.V.; de Azúa, M.C.R.; Contreras, R.H.; Dannenberg, J.J.; Masunov, A. Proximity effects on nuclear spin–spin coupling constants. Part 2.—The electric field effect on 1J(CH) couplings. J. Chem. Soc. Faraday Trans. 1996, 92, 3029–3033. [Google Scholar] [CrossRef]
- Mennucci, B.; Martínez, J.M.; Tomasi, J. Solvent Effects on Nuclear Shieldings: Continuum or Discrete Solvation Models To Treat Hydrogen Bond and Polarity Effects? J. Phys. Chem. 2001, 105, 7287–7296. [Google Scholar] [CrossRef]
- Miertus, S.; Scrocco, E.; Tomasi, J. Electrostatic interaction of a solute with a continuum. A direct utilizaion of AB initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
- Cammi, R.; Tomasi, J. Remarks on the use of the apparent surface charges (ASC) methods in solvation problems: Iterative versus matrix-inversion procedures and the renormalization of the apparent charges. J. Comput. Chem. 1995, 16, 1449–1458. [Google Scholar] [CrossRef]
- Johnston, M.D.; Barfield, M. Theoretical studies of solvent effects on nuclear spin-spin coupling constants. I. the reaction field model. J. Chem. Phys. 1971, 54, 3083–3096. [Google Scholar] [CrossRef]
- Cancés, E.; Mennucci, B. Linear response theory for the polarizable continuum model. J. Chem. Phys. 1999, 110, 9877–9886. [Google Scholar] [CrossRef]
- Cancés, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Mennucci, B.; Cancés, E.; Tomasi, J. Evaluation of Solvent Effects in Isotropic and Anisotropic Dielectrics and in Ionic Solutions with a Unified Integral Equation Method: Theoretical Bases, Computational Implementation, and Numerical Applications. J. Phys. Chem. 1997, 101, 10506–10517. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cancès, E. The IEF version of the PCM solvation method: An overview of a new method addressed to study molecular solutes at the QM ab initio level. THEOCHEM 1999, 464, 211–226. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
- Onsager, L.J. Electric Moments of Molecules in Liquids. J. Am. Chem. Soc. 1936, 58, 1486–1493. [Google Scholar] [CrossRef]
- Sadlej, J.; Pecul, M.; Barone, V.; Cimino, P.; Pavone, M.; Cappelli, C.; Stephens, P.J.; Devlin, F.J.; Ruud, K.; Hug, W.; et al. Computational modeling of the solvent–solute effect on NMR molecular parameters by Polarizable Continuum Model approach. In Continuum Solvation Models in Chemical Physics: From Theory to Applications, 1st ed.; Mennucci, B., Cammi, R., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2007. [Google Scholar] [CrossRef]
- Klamt, A.; Schüürman, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 1993, 799–805. [Google Scholar] [CrossRef]
- Klamt, A. Conductor-like screening model for real solvents: A new approach to the quantitative calculation of solvation phenomena. J. Phys. Chem. 1995, 99, 2224–2235. [Google Scholar] [CrossRef]
- Pye, C.C.; Ziegler, T. An Implementation of the Conductor-Like Screening Model of Solvation within the Amsterdam Density Functional Package. Theor. Chem. Acc. 1999, 101, 396–408. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
- Hoshi, H.H.; Sakurai, M.; Inoue, Y.; Chujo, R. Medium effects on the molecular electronic structure. I. The formulation of a theory for the estimation of a molecular electronic structure surrounded by an anisotropic medium. J. Chem. Phys. 1987, 87, 1107–1115. [Google Scholar] [CrossRef]
- Klamt, A.; Jonas, V.; Bürger, T.; Lohrenz, J.C.W. Refinement and Parametrization of COSMO-RS. J. Phys. Chem. 1998, 102, 5074–5085. [Google Scholar] [CrossRef]
- Mikkelsen, K.V.; Ågren, H.; Jensen, H.J.A.; Helgaker, T. A multiconfigurational self-consistent reaction-field method. J. Chem. Phys. 1988, 89, 3086–3095. [Google Scholar] [CrossRef]
- Mikkelsen, K.V.; Luo, Y.; Ågren, H.; Jørgensen, P. Solvent induced polarizabilities and hyperpolarizabilities of para-nitroaniline studied by reaction field linear response theory. J. Chem. Phys. 1994, 100, 8240–8250. [Google Scholar] [CrossRef]
- Mikkelsen, K.V.; Jørgensen, P.; Jensen, H.J.A. A multiconfiguration self-consistent reaction field response method. J. Chem. Phys. 1994, 100, 6597–6607. [Google Scholar] [CrossRef]
- Åstrand, P.-O.; Mikkelsen, K.V.; Jørgensen, P.; Ruud, K.; Helgaker, T. Solvent effects on nuclear shieldings and spin–spin couplings of hydrogen selenide. J. Chem. Phys. 1998, 108, 2528–2537. [Google Scholar] [CrossRef]
- Rivail, J.L.; Rinaldi, D. Polarisabilites moléculaires et effet diélectrique de milieu à l’état liquide. Étude théorique de la molécule d’eau et de ses diméres. Theor. Chim. Acta 1973, 32, 57–70. [Google Scholar] [CrossRef]
- Rivail, J.L.; Rinaldi, D. Liquid-state quantum chemistry: Computational applications of the polarizable continuum models. In Computational Chemistry, Review of Current Trends, 1st ed.; Leszczynski, J., Ed.; World Scientific: Singapore, 1996; Volume 1, pp. 139–174. [Google Scholar] [CrossRef]
- Rinaldi, D.; Ruiz-López, M.F.; Rivail, J.L. Ab initio SCF calculations on electrostatically solvated molecules using a deformable three axes ellipsoidal cavity. J. Chem. Phys. 1983, 78, 834–838. [Google Scholar] [CrossRef]
- Warshel, A.; Levitt, M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol. 1976, 103, 227–249. [Google Scholar] [CrossRef]
- Noell, J.O.; Morokuma, K. A simple model of solvation within the molecular orbital theory. Chem. Phys. Lett. 1975, 36, 465–469. [Google Scholar] [CrossRef]
- Singh, U.C.; Kollman, P.A. A combined ab initio quantum mechanical and molecular mechanical method for carrying out simulations on complex molecular systems: Applications to the CH3Cl + Cl− exchange reaction and gas phase protonation of polyethers. J. Comput. Chem. 1986, 7, 718–730. [Google Scholar] [CrossRef]
- Field, M.J.; Bash, P.A.; Karplus, M. A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations. J. Comput. Chem. 1990, 11, 700–733. [Google Scholar] [CrossRef]
- Thole, B.T.; van Duijnen, P.T. The direct reaction field hamiltonian: Analysis of the dispersion term and application to the water dimer. Chem. Phys. 1982, 71, 211–220. [Google Scholar] [CrossRef]
- Thompson, M.A. QM/MMpol: A Consistent Model for Solute/Solvent Polarization. Application to the Aqueous Solvation and Spectroscopy of Formaldehyde, Acetaldehyde, and Acetone. J. Phys. Chem. 1996, 100, 14492–14507. [Google Scholar] [CrossRef]
- Gao, J.L.; Xia, X.F. A Priori Evaluation of Aqueous Polarization Effects through Monte Carlo QM-MM Simulations. Science 1992, 258, 631–635. [Google Scholar] [CrossRef] [PubMed]
- Dupuis, M.; Kawashima, Y.; Hirao, K. A polarizable mixed Hamiltonian model of electronic structure for solvated excited states. II. Application to the blue shift of the H2CO 1(π*←n) excitation in water. J. Chem. Phys. 2002, 117, 1256–1268. [Google Scholar] [CrossRef]
- Jensen, L.; van Duijnen, P.T.; Snijders, J.G. A discrete solvent reaction field model within density functional theory. J. Chem. Phys. 2003, 118, 514–521. [Google Scholar] [CrossRef]
- Sauer, J.; Sierka, M. Combining quantum mechanics and interatomic potential functions in ab initio studies of extended systems. J. Comput. Chem. 2000, 21, 1470–1493. [Google Scholar] [CrossRef]
- Brandle, M.; Sauer, J.; Dovesi, R.; Harrison, N.M. Comparison of a combined quantum mechanics/interatomic potential function approach with its periodic quantum-mechanical limit: Proton siting and ammonia adsorption in zeolite chabazite. J. Chem. Phys. 1998, 109, 10379–10389. [Google Scholar] [CrossRef]
- Öhrn, A.; Karlström, G. Hybrid Monte Carlo simulations of vertical electronic transitions in acetone in aqueous solution. Theor. Chem. Acc. 2007, 117, 441–449. [Google Scholar] [CrossRef][Green Version]
- Coutinho, K.; Saavedra, N.; Canuto, S. Theoretical analysis of the hydrogen bond interaction between acetone and water. J. Mol. Struct. THEOCHEM 1999, 466, 69–75. [Google Scholar] [CrossRef]
- Moriarty, N.W.; Karlström, G. Geometry optimization of a water molecule in water. A combined quantum chemical and statistical mechanical treatment. J. Chem. Phys. 1997, 106, 6470–6474. [Google Scholar] [CrossRef]
- Poulsen, T.D.; Kongsted, J.; Osted, A.; Ogilby, P.R.; Mikkelsen, K.V. The combined multiconfigurational self-consistent-field/molecular mechanics wave function approach. J. Chem. Phys. 2001, 115, 2393–2400. [Google Scholar] [CrossRef]
- Nielsen, C.B.; Christiansen, O.; Mikkelsen, K.V.; Kongsted, J. Density functional self-consistent quantum mechanics/molecular mechanics theory for linear and nonlinear molecular properties: Applications to solvated water and formaldehyde. J. Chem. Phys. 2007, 126, 154112. [Google Scholar] [CrossRef]
- Kongsted, J.; Osted, A.; Mikkelsen, K.V.; Christiansen, O. The QM/MM approach for wavefunctions, energies and response functions within self-consistent field and coupled cluster theories. Mol. Phys. 2002, 100, 1813–1828. [Google Scholar] [CrossRef]
- Kongsted, J.; Osted, A.; Mikkelsen, K.V.; Christiansen, O. Linear response functions for coupled cluster/molecular mechanics including polarization interactions. J. Chem. Phys. 2003, 118, 1620–1633. [Google Scholar] [CrossRef]
- Kongsted, J.; Osted, A.; Mikkelsen, K.V.; Christiansen, O. Coupled Cluster/Molecular Mechanics Method: Implementation and Application to Liquid Water. J. Phys. Chem. 2003, 107, 2578–2588. [Google Scholar] [CrossRef]
- Kongsted, J.; Nielsen, C.B.; Mikkelsen, K.V.; Christiansen, O.; Ruud, K. Nuclear magnetic shielding constants of liquid water: Insights from hybrid quantum mechanics/molecular mechanics models. J. Chem. Phys. 2007, 126, 034510. [Google Scholar] [CrossRef]
- Møgelhøj, A.; Aidas, K.; Mikkelsen, K.V.; Sauer, S.P.A.; Kongsted, J. Prediction of spin-spin coupling constants in solution based on combined density functional theory/molecular mechanics. J. Chem. Phys. 2009, 130, 134508. [Google Scholar] [CrossRef]
- Bakowies, D.; Thiel, W. Hybrid Models for Combined Quantum Mechanical and Molecular Mechanical Approaches. J. Phys. Chem. 1996, 100, 10580–10594. [Google Scholar] [CrossRef]
- Ruud, K.; Frediani, L.; Cammi, R.; Mennucci, B. Solvent Effects on the Indirect Spin–Spin Coupling Constants of Benzene: The DFT-PCM Approach. Int. J. Mol. Sci. 2003, 4, 119–134. [Google Scholar] [CrossRef]
- Cammi, R. Nuclear magnetic shieldings in solution: Gauge invariant atomic orbital calculation using the polarizable continuum model. J. Chem. Phys. 1999, 110, 7627–7638. [Google Scholar] [CrossRef]
- Cui, Q.; Karplus, M. Molecular Properties from Combined QM/MM Methods. 2. Chemical Shifts in Large Molecules. J. Phys. Chem. 2000, 104, 3721–3743. [Google Scholar] [CrossRef]
- Di Remigio, R.; Bast, R.; Frediani, L.; Saue, T. Four-Component Relativistic Calculations in Solution with the Polarizable Continuum Model of Solvation: Theory, Implementation, and Application to the Group 16 Dihydrides H2X (X = O, S, Se, Te, Po). J. Phys. Chem. 2015, 119, 5061–5077. [Google Scholar] [CrossRef]
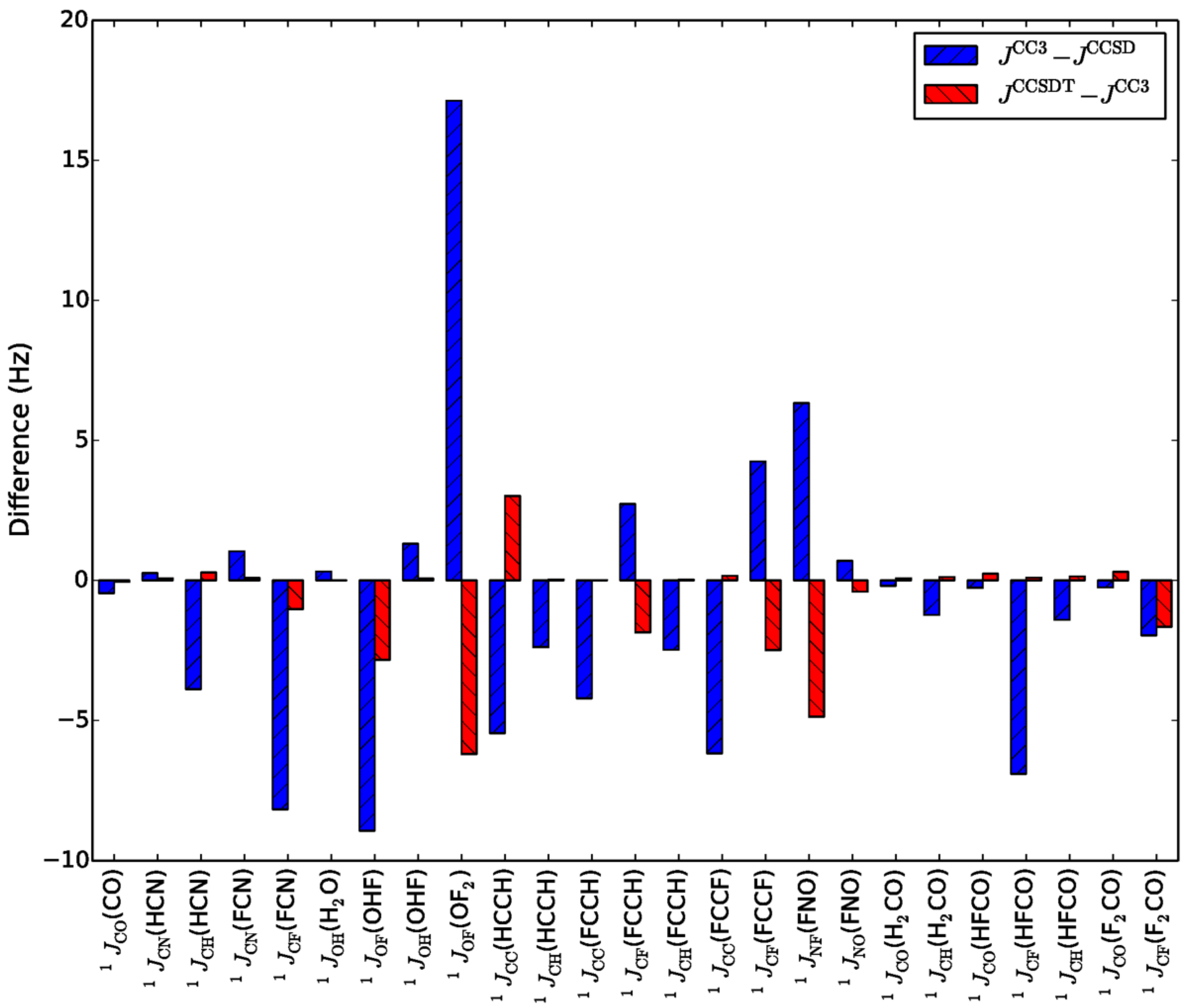
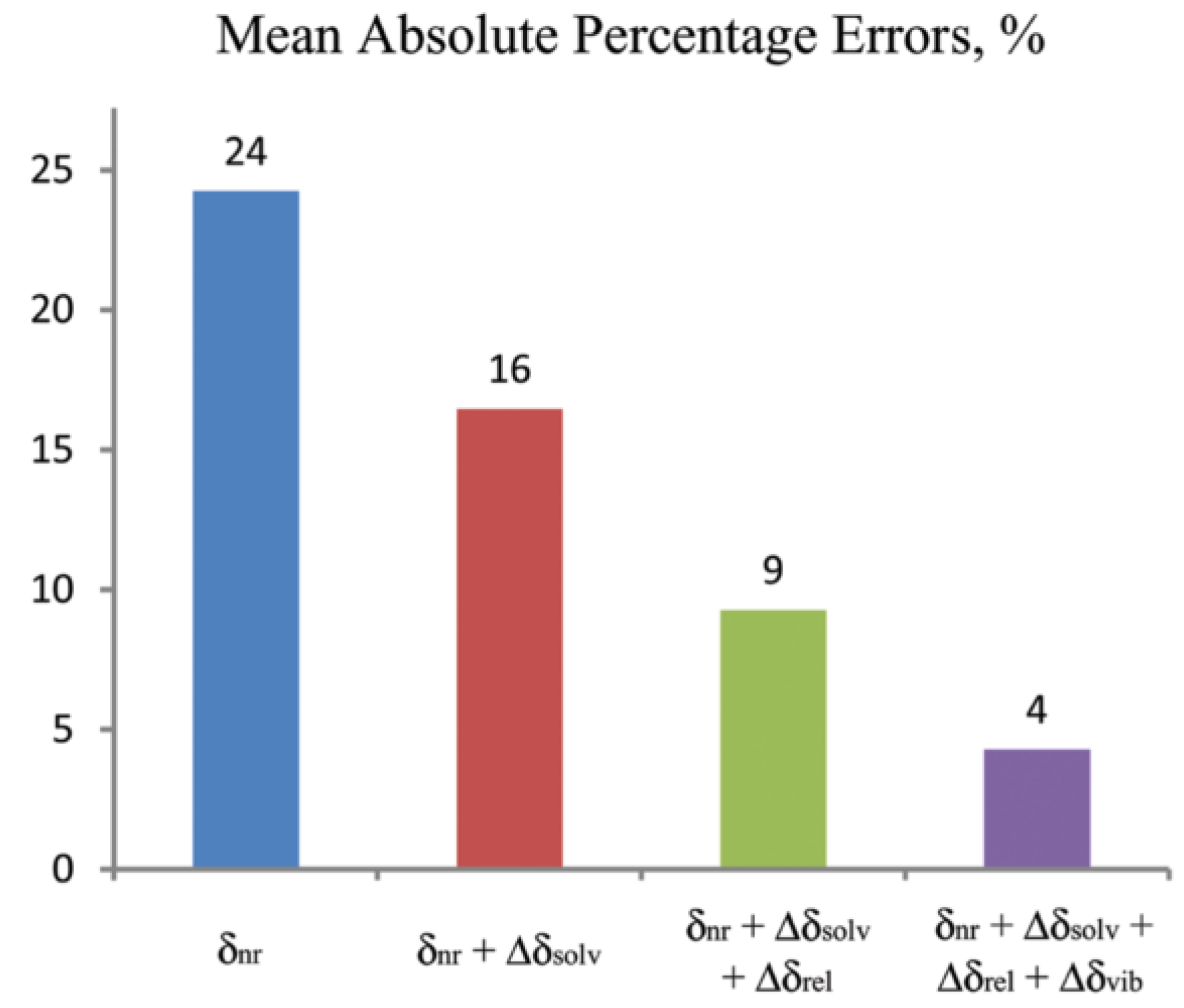
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rusakova, I.L. Quantum Chemical Approaches to the Calculation of NMR Parameters: From Fundamentals to Recent Advances. Magnetochemistry 2022, 8, 50. https://doi.org/10.3390/magnetochemistry8050050
Rusakova IL. Quantum Chemical Approaches to the Calculation of NMR Parameters: From Fundamentals to Recent Advances. Magnetochemistry. 2022; 8(5):50. https://doi.org/10.3390/magnetochemistry8050050
Chicago/Turabian StyleRusakova, Irina L. 2022. "Quantum Chemical Approaches to the Calculation of NMR Parameters: From Fundamentals to Recent Advances" Magnetochemistry 8, no. 5: 50. https://doi.org/10.3390/magnetochemistry8050050
APA StyleRusakova, I. L. (2022). Quantum Chemical Approaches to the Calculation of NMR Parameters: From Fundamentals to Recent Advances. Magnetochemistry, 8(5), 50. https://doi.org/10.3390/magnetochemistry8050050





