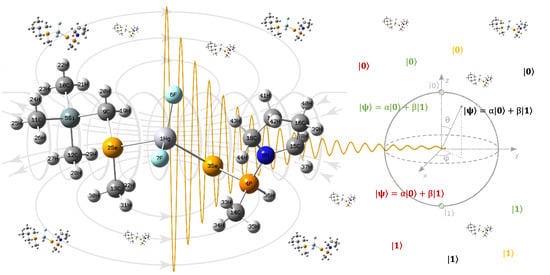
Extending NMR Quantum Computation Systems by Employing Compounds with Several Heavy Metals as Qubits
Abstract
:1. Introduction
2. Computational Details
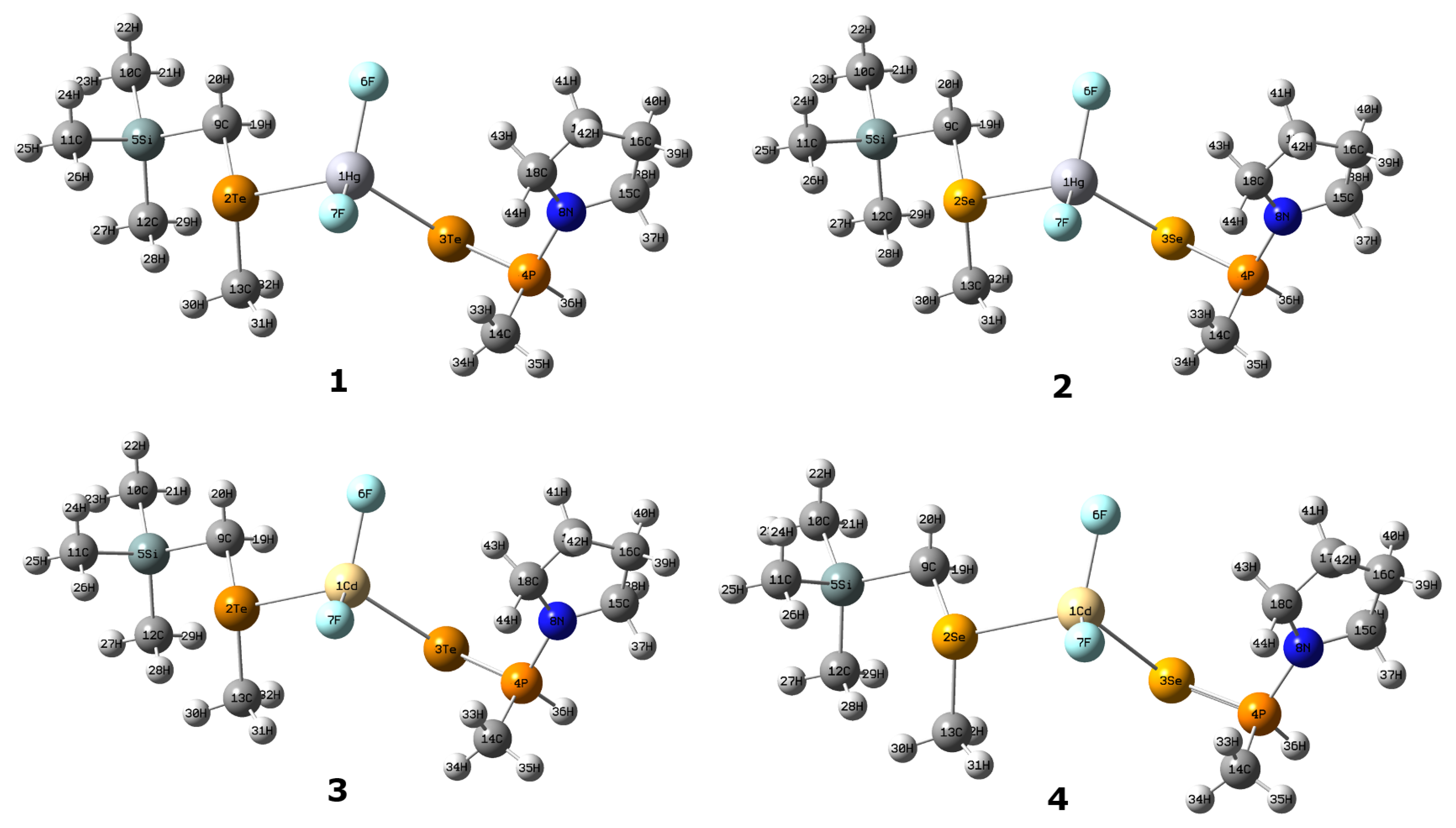
3. Results and Discussion
3.1. Conformational Flexibility
3.2. Spectroscopic Parameters: Chemical Shift Values
3.3. Spectroscopic Parameters: Spin–Spin Coupling Constant Values
3.4. Correlation Time and Spectral Density
Validation of the Theoretical Methodology
3.5. Spectroscopic Parameters: Relaxation Times
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Glaser, S.J.; Marx, R.; Reiss, T.; Schulte-Herbrüggen, T.; Khaneja, N.; Myers, J.M.; Fahmy, A.F. Increasing the Size of NMR Quantum Computers. In Quantum Information Processing; John Wiley & Sons, Ltd.: Weinheim, Germany, 2005; Chapter 5; pp. 58–69. [Google Scholar] [CrossRef]
- Jones, J.A. Quantum computing with NMR. Prog. NMR Spectrosc. 2011, 59, 91–120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vind, F.A.; Foerster, A.; Oliveira, I.S.; Sarthour, R.S.; Soares-Pinto, D.O.; Souza, A.M.; Roditi, I. Experimental realization of the Yang-Baxter Equation via NMR interferometry. Sci. Rep. 2016, 6, 20789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, D.; Li, K.; Li, J.; Katiyar, H.; Park, A.J.; Feng, G.; Xin, T.; Li, H.; Long, G.; Brodutch, A.; et al. Enhancing quantum control by bootstrapping a quantum processor of 12 qubits. npj Quantum Inf. 2017, 3, 45. [Google Scholar] [CrossRef] [Green Version]
- Peterson, J.P.; Sarthour, R.S.; Laflamme, R. Enhancing Quantum Control by Improving Shaped-Pulse Generation. Phys. Rev. Appl. 2020, 13, 054060. [Google Scholar] [CrossRef]
- Sauer, S.P.A. Molecular Electromagnetism: A Computational Chemistry Approach; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Vaara, J. Theory and computation of nuclear magnetic resonance parameters. Phys. Chem. Chem. Phys. 2007, 9, 5399–5418. [Google Scholar] [CrossRef]
- Helgaker, T.; Jaszuński, M.; Pecul, M. The quantum-chemical calculation of NMR indirect spin–spin coupling constants. Prog. NMR Spectrosc. 2008, 53, 249–268. [Google Scholar] [CrossRef]
- Helgaker, T.; Coriani, S.; Jørgensen, P.; Kristensen, K.; Olsen, J.; Ruud, K. Recent Advances in Wave Function-Based Methods of Molecular-Property Calculations. Chem. Rev. 2012, 112, 543–631. [Google Scholar] [CrossRef]
- Autschbach, J. Relativistic calculations of magnetic resonance parameters: Background and some recent developments. Philos. Trans. R. Soc. A 2014, 372, 20120489. [Google Scholar] [CrossRef] [Green Version]
- Krivdin, L.B. Computational 1H NMR: Part 1. Theoretical background. Magn. Reson. Chem. 2019, 57, 897–914. [Google Scholar] [CrossRef]
- Krivdin, L.B. Recent advances in computational liquid–phase 77Se NMR. Russ. Chem. Rev. 2021, 90, 265–279. [Google Scholar] [CrossRef]
- DiVincenzo, D.P. The Physical Implementation of Quantum Computation. Fortschr. Phys. 2000, 48, 771–783. [Google Scholar] [CrossRef] [Green Version]
- Ladd, T.D.; Jelezko, F.; Laflamme, R.; Nakamura, Y.; Monroe, C.; O’Brien, J.L. Quantum computers. Nature 2010, 464, 45–53. [Google Scholar] [CrossRef] [Green Version]
- Marx, R.; Pomplun, N.; Bermel, W.; Zeiger, H.; Engelke, F.; Fahmy, A.F.; Glaser, S.J. Engineering of an all-heteronuclear 5-qubit NMR quantum computer. Magn. Reson. Chem. 2015, 53, 442–447. [Google Scholar] [CrossRef]
- Lino, J.B.d.R.; Rocha, E.P.; Ramalho, T.C. Value of NMR parameters and DFT calculations for quantum information processing utilizing phosphorus heterocycles. J. Chem. Phys. A 2017, 121, 4486–4495. [Google Scholar] [CrossRef]
- Mawhinney, R.C.; Schreckenbach, G. NMR quantum computing: Applying theoretical methods to designing enhanced systems. Magn. Reson. Chem. 2004, 42, S88–S98. [Google Scholar] [CrossRef]
- Lino, J.B.d.R.; Ramalho, T.C. Exploring Through-Space Spin–Spin Couplings for Quantum Information Processing: Facing the Challenge of Coherence Time and Control Quantum States. J. Phys. Chem. A 2019, 123, 1372–1379. [Google Scholar] [CrossRef]
- Lino, J.B.d.R.; Gonçalves, M.A.; Ramalho, T.C. Value of NMR relaxation parameters of diamagnetic molecules for quantum information processing: Optimizing the coherent phase. Theor. Chem. Acc. 2021, 140, 1432–2234. [Google Scholar] [CrossRef]
- Lino, J.B.d.R.; Sauer, S.P.A.; Ramalho, T.C. Enhancing NMR Quantum Computation by Exploring Heavy Metal Complexes as Multiqubit Systems: A Theoretical Investigation. J. Phys. Chem. A 2020, 124, 4946–4955. [Google Scholar] [CrossRef]
- Cory, D.G.; Fahmy, A.F.; Havel, T.F. Ensemble quantum computing by NMR spectroscopy. Proc. Natl. Acad. Sci. USA 1997, 94, 1634–1639. [Google Scholar] [CrossRef] [Green Version]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef]
- Lenthe, E.V.; Baerends, E.J.; Snijders, J.G. Relativistic regular two–component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Chen, X.Y.; Landis, C.R.; Neese, F. All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms. J. Chem. Theory Comput. 2008, 4, 908–919. [Google Scholar] [CrossRef]
- Baerends, E.J.; Ziegler, T.; Atkins, A.J.; Autschbach, J.; Bashford, D.; Baseggio, O.; Bérces, A.; Bickelhaupt, F.M.; Bo, C.; Boerritger, P.M.; et al. ADF2017, SCM, Theoretical Chemistry; Vrije Universiteit: Amsterdam, The Netherlands, 2017; Available online: https://www.scm.com (accessed on 15 April 2022).
- Van Lenthe, E.; Baerends, E.J. Optimized Slater-type basis sets for the elements 1–118. J. Comp. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef]
- Bryce, D.L.; Autschbach, J. Relativistic hybrid density functional calculations of indirect nuclear spin–spin coupling tensors—Comparison with experiment for diatomic alkali metal halides. Can. J. Chem. 2009, 87, 927–941. [Google Scholar] [CrossRef] [Green Version]
- Radula-Janik, K.; Kupka, T.; Ejsmont, K.; Daszkiewicz, Z.; Sauer, S.P.A. Molecular modeling and experimental studies on structure and NMR parameters of 9-benzyl-3,6-diiodo-9H-carbazole. Struct. Chem. 2015, 26, 997–1006. [Google Scholar] [CrossRef] [Green Version]
- Morsing, T.J.; Reinholdt, A.; Sauer, S.P.A.; Bendix, J. Ligand Sphere Conversions in Terminal Carbide Complexes. Organometallics 2016, 35, 100–105. [Google Scholar] [CrossRef]
- Radula-Janik, K.; Kupka, T.; Ejsmont, K.; Daszkiewicz, Z.; Sauer, S.P.A. DFT and experimental studies on structure and spectroscopic parameters of 3,6-diiodo-9-ethyl-9H-carbazole. Struct. Chem. 2016, 27, 199–207. [Google Scholar] [CrossRef] [Green Version]
- Glent-Madsen, I.; Reinholdt, A.; Bendix, J.; Sauer, S.P.A. Importance of Relativistic Effects for Carbon as an NMR Reporter Nucleus in Carbide-Bridged [RuCPt] Complexes. Organometallics 2021, 40, 1443–1453. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Rusakova, I.L. Hierarchical basis sets for the calculation of nuclear magnetic resonance spin–spin coupling constants involving either selenium or tellurium nuclei. J. Phys. Chem. A 2019, 123, 6564–6571. [Google Scholar] [CrossRef]
- Wodyński, A.; Repiskỳ, M.; Pecul, M. A comparison of two-component and four-component approaches for calculations of spin–spin coupling constants and NMR shielding constants of transition metal cyanides. J. Chem. Phys. 2012, 137, 014311. [Google Scholar] [CrossRef]
- Repisky, M.; Komorovsky, S.; Kadek, M.; Konecny, L.; Ekström, U.; Malkin, E.; Kaupp, M.; Ruud, K.; Malkina, O.L.; Malkin, V.G. ReSpect: Relativistic spectroscopy DFT program package. J. Chem. Phys. 2020, 152, 184101. [Google Scholar] [CrossRef] [PubMed]
- De Azevedo Santos, L.; van Der Lubbe, S.C.; Hamlin, T.A.; Ramalho, T.C.; Matthias Bickelhaupt, F. A Quantitative Molecular Orbital Perspective of the Chalcogen Bond. ChemistryOpen 2021, 10, 391–401. [Google Scholar] [CrossRef] [PubMed]
- Cardin, A.D.; Ellis, P.D.; Odom, J.D.; Howard, J.W. Cadmium-113 Fourier transform nuclear magnetic resonance spectroscopy. J. Am. Chem. Soc. 1975, 97, 1672–1679. [Google Scholar] [CrossRef]
- Pecul, M.; Urbańczyk, M.; Wodyński, A.; Jaszuński, M. DFT calculations of 31P spin–spin coupling constants and chemical shift in dioxaphosphorinanes. Magn. Reson. Chem. 2011, 49, 399–404. [Google Scholar] [CrossRef] [PubMed]
- Jameson, A.; Jameson, C.J. Gas-phase 13C chemical shifts in the zero-pressure limit: Refinements to the absolute shielding scale for 13C. Chem. Phys. Lett. 1987, 134, 461–466. [Google Scholar] [CrossRef]
- Gonçalves, M.A.; Santos, L.S.; Peixoto, F.C.; Ramalho, T.C. NMR relaxation and relaxivity parameters of MRI probes revealed by optimal wavelet signal compression of molecular dynamics simulations. Int. J. Quantum Chem. 2019, 119, e25896. [Google Scholar] [CrossRef]
- Grivet, J.P. NMR relaxation parameters of a Lennard-Jones fluid from molecular-dynamics simulations. J. Chem. Phys. 2005, 123, 034503. [Google Scholar] [CrossRef]
- MATLAB Optimization Toolbox; The MathWorks: Natick, MA, USA, 2008; Available online: https://www.mathworks.com/products/optimization (accessed on 15 April 2022).
- Mallek, R.; Sanhoury, M.; Dhia, M.B.; Khaddar, M. Cadmium(II) complexes with phosphine tellurides: Synthesis and multinuclear (31P, 125Te, and 113Cd) NMR characterization in solution. J. Coord. Chem. 2014, 67, 1541–1549. [Google Scholar] [CrossRef]
- Riedel, S.; Straka, M.; Kaupp, M. Can Weakly Coordinating Anions Stabilize Mercury in Its Oxidation State +IV? Chem. Eur. J. 2005, 11, 2743–2755. [Google Scholar] [CrossRef]
- Vigo, L.; Salin, P.; Oilunkaniemi, R.; Laitinen, R.S. Formation and structural characterization of mercury complexes from Te(R)CH2SiMe3 (R=Ph, CH2SiMe3) and HgCl2. J. Organomet. Chem. 2009, 694, 3134–3141. [Google Scholar] [CrossRef]
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An open chemical toolbox. J. Cheminf. 2011, 3, 33. [Google Scholar] [CrossRef] [Green Version]
- Criger, B.; Park, D.; Baugh, J. Few–qubit magnetic resonance quantum information processors: Simulating chemistry and physics. In Quantum Information and Computation for Chemistry; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014; pp. 193–227. [Google Scholar] [CrossRef] [Green Version]
- Havel, T.F.; Cory, D.G.; Lloyd, S.; Boulant, N.; Fortunato, E.M.; Pravia, M.A.; Teklemariam, G.; Weinstein, Y.S.; Bhattacharyya, A.; Hou, J. Quantum information processing by nuclear magnetic resonance spectroscopy. Am. J. Phys. 2002, 70, 345–362. [Google Scholar] [CrossRef]
- Nelson, J.H. (Ed.) Nuclear Magnetic Resonance Spectroscopy; Pearson Education: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Vandersypen, L.M.K.; Chuang, I.L. NMR techniques for quantum control and computation. Rev. Mod. Phys. 2005, 76, 1037–1069. [Google Scholar] [CrossRef] [Green Version]
- Helgaker, T.; Jaszuński, M.; Ruud, K. Ab Initio Methods for the Calculation of NMR Shielding and Indirect Spin–Spin Coupling Constants. Chem. Rev. 1999, 99, 293–352. [Google Scholar] [CrossRef]
- Coutinho, K.; Canuto, S.; Zerner, M.C. A Monte Carlo-quantum mechanics study of the solvatochromic shifts of the lowest transition of benzene. J. Chem. Phys. 2000, 112, 9874–9880. [Google Scholar] [CrossRef] [Green Version]
- Coutinho, K.; Canuto, S. Solvent Effects from a Sequential Monte Carlo - Quantum Mechanical Approach. Adv. Quantum Chem. 1997, 28, 89–105. [Google Scholar] [CrossRef]
- Devra, A.; Prabhu, P.; Singh, H.; Arvind; Dorai, K. Efficient experimental design of high-fidelity three-qubit quantum gates via genetic programming. Quantum Inf. Process. 2018, 17, 67. [Google Scholar] [CrossRef] [Green Version]
- Gonçalves, M.A.; da Cunha, E.F.; Peixoto, F.C.; Ramalho, T.C. Probing thermal and solvent effects on hyperfine interactions and spin relaxation rate of δ-FeOOH(100) and [MnH3buea(OH)]2−: Toward new MRI probes. Comput. Theor. Chem. 2015, 1069, 96–104. [Google Scholar] [CrossRef]
- Patinec, V.; Rolla, G.A.; Botta, M.; Tripier, R.; Esteban-Gómez, D.; Platas-Iglesias, C. Hyperfine Coupling Constants on Inner-Sphere Water Molecules of a Triazacyclononane-based Mn(II) Complex and Related Systems Relevant as MRI Contrast Agents. Inorg. Chem. 2013, 52, 11173–11184. [Google Scholar] [CrossRef]
- Gonçalves, M.A.; Santos, L.S.; Prata, D.M.; Peixoto, F.C.; da Cunha, E.F.; Ramalho, T.C. Optimal wavelet signal compression as an efficient alternative to investigate molecular dynamics simulations: Application to thermal and solvent effects of MRI probes. Theor. Chem. Acc. 2017, 136, 1–13. [Google Scholar] [CrossRef]
- Xin, T.; Wang, B.X.; Li, K.R.; Kong, X.Y.; Wei, S.J.; Wang, T.; Ruan, D.; Long, G.L. Nuclear magnetic resonance for quantum computing: Techniques and recent achievements. Chin. Phys. B 2018, 27, 020308. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Negrevergne, C.; Mahesh, T.S.; Ryan, C.A.; Ditty, M.; Cyr-Racine, F.; Power, W.; Boulant, N.; Havel, T.; Cory, D.G.; Laflamme, R. Benchmarking Quantum Control Methods on a 12-Qubit System. Phys. Rev. Lett. 2006, 96, 170501. [Google Scholar] [CrossRef] [Green Version]
- Cory, D.; Laflamme, R.; Knill, E.; Viola, L.; Havel, T.; Boulant, N.; Boutis, G.; Fortunato, E.; Lloyd, S.; Martinez, R.; et al. NMR Based Quantum Information Processing: Achievements and Prospects. Fortschr. Phys. 2000, 48, 875–907. [Google Scholar] [CrossRef] [Green Version]
| Nucleus | Shielding | Nucleus | Shielding |
|---|---|---|---|
| Hg (HgMe2) | 9197.834 | Si (TMS) | 368.108 |
| Cd (CdMe2) | 3561.291 | F (CFCl3) | 184.172 |
| Te (TeMe2) | 3557.070 | C (TMS) | 191.333 |
| Se (SeMe2) | 1930.599 | H (TMS) | 31.553 |
| P (PH3) | 607.566 |
| Nucleus | Complex 1 | Complex 2 | Complex 3 | Complex 4 |
|---|---|---|---|---|
| −1513.02 | −1387.93 | 326.71 | 303.00 | |
| −46.23 | 58.59 | −188.55 | −10.28 | |
| −565.29 | −195.80 | −700.37 | −250.82 | |
| −18.67 | 25.03 | −22.51 | 24.25 | |
| 4.41 | 3.00 | 4.50 | 2.32 | |
| −202.22 | −220.33 | −231.50 | −244.14 | |
| −148.50 | −145.68 | −175.97 | −185.88 | |
| 1.59 | 20.69 | −2.00 | 19.18 | |
| −1.01 | −0.34 | −0.92 | 1.26 | |
| 0.06 | −1.01 | −0.23 | −1.77 | |
| −0.65 | −1.88 | −0.74 | −1.03 | |
| −6.62 | 15.57 | −8.88 | 14.59 | |
| 20.48 | 19.14 | 19.63 | 18.47 | |
| 53.53 | 50.95 | 53.88 | 50.77 | |
| 28.63 | 29.00 | 28.71 | 29.31 | |
| 30.96 | 30.70 | 30.23 | 30.09 | |
| 51.55 | 51.47 | 50.72 | 50.66 | |
| 1.38 | 1.47 | 1.39 | 1.73 | |
| 4.22 | 3.71 | 3.43 | 3.66 | |
| −0.03 | 0.27 | 0.35 | −0.03 | |
| 0.95 | −0.05 | −0.03 | 0.16 | |
| −0.13 | −0.02 | −0.03 | 0.04 | |
| 1.71 | −0.08 | 0.02 | 0.02 | |
| −0.14 | −0.14 | −0.03 | −0.22 | |
| −0.19 | 1.16 | 0.51 | 2.50 | |
| −0.03 | −0.15 | −0.14 | 0.07 | |
| 0.26 | 1.56 | 1.98 | 0.24 | |
| −0.02 | −0.01 | −0.22 | 0.02 | |
| 1.38 | 1.59 | 1.47 | 1.85 | |
| 1.44 | 1.72 | 1.42 | 1.84 | |
| 6.07 | 5.64 | 5.27 | 3.82 | |
| 7.62 | 7.09 | 6.34 | 5.75 | |
| 1.66 | 1.54 | 1.67 | 1.53 | |
| 2.63 | 2.01 | 2.66 | 2.04 | |
| 7.76 | 8.30 | 7.57 | 8.15 | |
| 2.45 | 2.62 | 2.43 | 2.57 | |
| 3.36 | 3.62 | 3.54 | 3.85 | |
| 1.45 | 1.46 | 1.40 | 1.47 | |
| 3.76 | 3.98 | 4.03 | 3.90 | |
| 2.11 | 2.09 | 2.14 | 2.07 | |
| 1.62 | 1.65 | 1.66 | 1.70 | |
| 4.50 | 4.60 | 4.55 | 4.82 | |
| 2.74 | 2.85 | 2.76 | 2.85 |
| Complex 1 | Complex 2 | Complex 3 | Complex 4 | |||||
|---|---|---|---|---|---|---|---|---|
| M1–E2 | 3302.70 | 96,802,165 | −835.01 | 8,435,780 | −481.12 | 66,742,136 | 105.44 | 21,582,334 |
| M1–E3 | 5102.88 | 96,686,569 | −1485.00 | 8,401,607 | −878.27 | 66,628,154 | 233.79 | 21,614,648 |
| M1–F6 | −2621.28 | 535,132,459 | −2483.84 | 535,104,716 | 783.72 | 505,084,765 | 677.95 | 505,080,108 |
| M1–F7 | −2405.23 | 535,167,977 | −2330.77 | 535,154,067 | 784.66 | 505,121,481 | 691.68 | 505,118,628 |
| E2–C9 | −15.82 | 46,039,162 | −83.82 | 42,314,827 | 195.52 | 46,008,099 | −81.18 | 42,323,811 |
| E2–C13 | −24.25 | 46,040,612 | −69.38 | 42,313,921 | 163.74 | 46,009,316 | −69.04 | 42,322,999 |
| E3–P4 | 1411.66 | 61,967,771 | −607.71 | 150,249,393 | 1504.62 | 61,996,763 | −660.24 | 150,256,563 |
| P4–C14 | 20.86 | 107,887,999 | 28.34 | 107,900,668 | 22.47 | 107,887,060 | 29.75 | 107,900,565 |
| P4–H36 | 422.22 | 417,965,157 | 448.08 | 417,953,108 | 428.45 | 417,966,118 | 451.89 | 417,953,223 |
| Si5–C9 | −34.38 | 37,025,106 | −34.41 | 37,028,676 | −33.74 | 37,024,459 | −32.89 | 37,028,505 |
| Si5–C10 | −41.49 | 37,024,645 | −37.33 | 37,024,961 | −38.53 | 37,024,649 | −39.00 | 37,025,340 |
| Si5–C11 | −41.75 | 37,024,835 | −42.01 | 37,024,843 | −40.35 | 37,024,771 | −42.09 | 37,024,804 |
| Si5–C12 | −37.53 | 37,024,710 | −41.88 | 37,024,688 | −41.38 | 37,024,681 | −39.32 | 37,024,935 |
| C15–C16 | 26.44 | 4398 | 26.40 | 3878 | 26.27 | 4447 | 26.22 | 3791 |
| C16–C17 | 23.53 | 410 | 23.53 | 300 | 23.64 | 268 | 23.76 | 138 |
| C17–C18 | 26.76 | 3637 | 26.82 | 3670 | 26.85 | 3620 | 26.73 | 3634 |
| C9–H19 | 123.68 | 525,852,016 | 122.91 | 525,848,702 | 123.92 | 525,852,654 | 124.00 | 525,849,153 |
| C9–H20 | 135.65 | 525,854,011 | 136.23 | 525,850,273 | 133.03 | 525,854,085 | 132.86 | 525,850,508 |
| C10–H21 | 112.77 | 525,851,482 | 111.88 | 525,851,574 | 112.46 | 525,851,732 | 112.68 | 525,851,083 |
| C10–H22 | 117.10 | 525,852,170 | 112.07 | 525,851,354 | 112.23 | 525,851,464 | 112.86 | 525,851,213 |
| C10–H23 | 112.22 | 525,851,414 | 111.99 | 525,851,373 | 111.84 | 525,851,467 | 112.27 | 525,851,130 |
| C11–H24 | 119.40 | 525,852,519 | 112.53 | 525,851,447 | 112.84 | 525,851,377 | 112.07 | 525,851,650 |
| C11–H25 | 111.88 | 525,851,220 | 112.21 | 525,851,409 | 112.37 | 525,851,343 | 110.23 | 525,851,481 |
| C11–H26 | 110.67 | 525,851,181 | 118.19 | 525,852,321 | 115.41 | 525,851,725 | 120.02 | 525,853,393 |
| C12–H27 | 112.02 | 525,851,417 | 111.54 | 525,851,552 | 111.82 | 525,851,358 | 112.22 | 525,851,556 |
| C12–H28 | 111.68 | 525,851,624 | 119.15 | 525,852,752 | 119.44 | 525,852,844 | 113.36 | 525,851,678 |
| C12–H29 | 112.20 | 525,851,429 | 111.67 | 525,851,649 | 110.88 | 525,851,304 | 113.30 | 525,851,523 |
| C13–H30 | 132.24 | 525,853,467 | 131.56 | 525,849,693 | 132.76 | 525,853,929 | 133.17 | 525,850,045 |
| C13–H31 | 129.49 | 525,853,505 | 127.68 | 525,849,787 | 128.90 | 525,853,895 | 128.17 | 525,850,038 |
| C13–H32 | 151.11 | 525,856,759 | 150.06 | 525,852,540 | 150.00 | 525,856,598 | 144.53 | 525,851,434 |
| C14–H33 | 134.29 | 525,853,058 | 133.34 | 525,852,924 | 133.78 | 525,852,312 | 133.42 | 525,852,103 |
| C14–H34 | 123.44 | 525,848,870 | 123.40 | 525,849,024 | 123.77 | 525,849,030 | 123.26 | 525,849,137 |
| C14–H35 | 121.84 | 52,5849,553 | 121.41 | 525,849,354 | 121.87 | 525,849,729 | 120.86 | 525,849,499 |
| C15–H37 | 129.93 | 525,843,591 | 129.48 | 525,844,164 | 130.37 | 525,843,517 | 129.55 | 525,844,160 |
| C15–H38 | 128.27 | 525,844,233 | 129.07 | 525,844,865 | 128.31 | 525,844,291 | 129.42 | 525,845,060 |
| C16–H39 | 121.40 | 525,847,283 | 121.31 | 525,847,231 | 121.09 | 525,847,240 | 121.22 | 525,847,184 |
| C16–H40 | 129.67 | 525,848,911 | 130.16 | 525,848,998 | 130.18 | 525,849,087 | 129.51 | 525,848,891 |
| C17–H41 | 126.03 | 525,847,341 | 125.78 | 525,847,371 | 125.49 | 525,847,492 | 124.91 | 525,847,466 |
| C17–H42 | 116.70 | 525,846,995 | 116.72 | 525,847,064 | 116.85 | 525,847,149 | 117.18 | 525,847,205 |
| C18–H43 | 141.85 | 525,845,384 | 141.07 | 525,845,467 | 138.72 | 525,845,563 | 137.77 | 525,845,763 |
| C18–H44 | 129.44 | 525,844,147 | 129.09 | 525,844,233 | 129.06 | 525,844,302 | 129.05 | 525,844,379 |
| Structures | Correlation Times (fs) | |
|---|---|---|
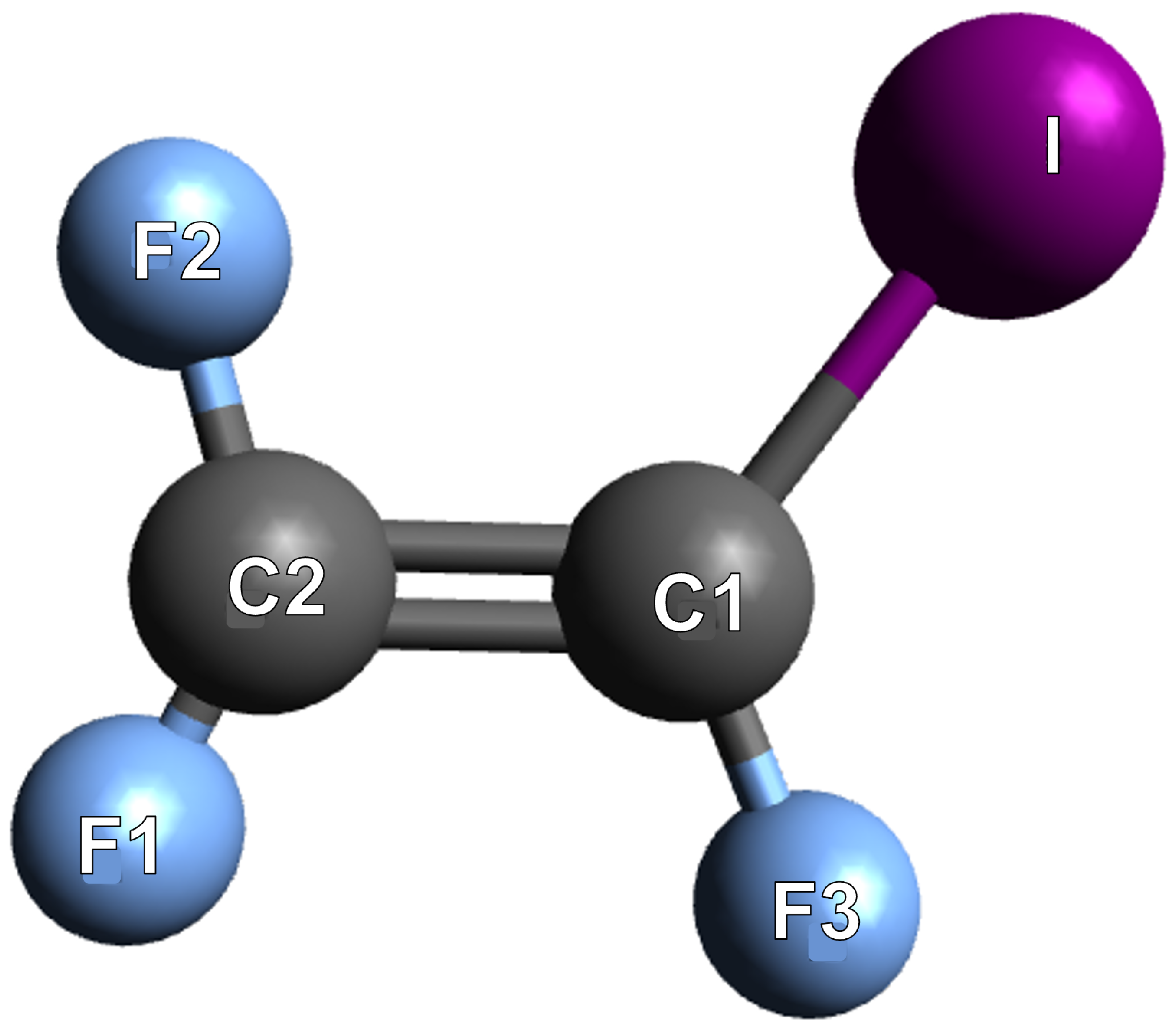
| TFE | 19 | 47.71 |
| Complex 1 | 28 | 36.13 |
| Complex 2 | 24 | 41.37 |
| Complex 3 | 8 | 137.52 |
| Complex 4 | 8 | 137.15 |
| (s) | (s) | (s) | (s) | ||
|---|---|---|---|---|---|
| TFE (F1–F3) | Theoretical | 5.29 | 0.19 | 0.18 | 5.26 |
| Experimental | 5.37 | 0.14 | 0.19 | 7.14 | |
| TFE (F1–F2) | Theoretical | 5.25 | 0.15 | 0.19 | 6.66 |
| Experimental | 5.56 | 0.12 | 0.18 | 8.33 |
| Hg | Cd | Te | Se | P | Si | F | C | H | |
|---|---|---|---|---|---|---|---|---|---|
| Complex 1 | |||||||||
| (s) | 21.27 | - | 7.17 | - | 1.20 | 44.80 | 1.22 | 1.95 | 1.05 |
| (s) | 2.04 | - | 1.02 | - | 0.63 | 3.52 | 1.12 | 1.49 | 0.46 |
| (s) | 0.04 | - | 0.14 | - | 0.83 | 0.02 | 0.82 | 0.51 | 0.95 |
| (s) | 0.49 | - | 0.98 | - | 1.58 | 0.28 | 0.89 | 0.67 | 2.17 |
| Complex 2 | |||||||||
| (s) | 32.77 | - | - | 30.44 | 2.77 | 11.87 | 2.12 | 2.58 | 1.30 |
| (s) | 1.51 | - | - | 2.59 | 1.28 | 9.34 | 1.60 | 1.27 | 0.45 |
| (s) | 0.03 | - | - | 0.03 | 0.36 | 0.08 | 0.47 | 0.38 | 0.76 |
| (s) | 0.66 | - | - | 0.39 | 0.78 | 0.11 | 0.63 | 0.78 | 2.22 |
| Complex 3 | |||||||||
| (s) | - | 7.82 | 9.22 | - | 2.01 | 13.99 | 2.72 | 2.56 | 0.95 |
| (s) | - | 1.05 | 2.05 | - | 0.37 | 1.10 | 1.97 | 1.25 | 0.35 |
| (s) | - | 0.13 | 0.11 | - | 0.50 | 0.07 | 0.37 | 0.39 | 1.05 |
| (s) | - | 0.95 | 0.49 | - | 2.70 | 0.91 | 0.81 | 0.80 | 2.85 |
| Complex 4 | |||||||||
| (s) | - | 6.06 | - | 21.56 | 2.70 | 15.89 | 1.67 | 2.53 | 1.20 |
| (s) | - | 2.09 | - | 1.83 | 0.58 | 9.97 | 1.08 | 1.24 | 0.38 |
| (s) | - | 0.17 | - | 0.05 | 0.37 | 0.06 | 0.59 | 0.36 | 0.83 |
| (s) | - | 0.48 | - | 0.55 | 1.72 | 0.10 | 0.93 | 0.81 | 2.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lino, J.B.d.R.; Gonçalves, M.A.; Sauer, S.P.A.; Ramalho, T.C. Extending NMR Quantum Computation Systems by Employing Compounds with Several Heavy Metals as Qubits. Magnetochemistry 2022, 8, 47. https://doi.org/10.3390/magnetochemistry8050047
Lino JBdR, Gonçalves MA, Sauer SPA, Ramalho TC. Extending NMR Quantum Computation Systems by Employing Compounds with Several Heavy Metals as Qubits. Magnetochemistry. 2022; 8(5):47. https://doi.org/10.3390/magnetochemistry8050047
Chicago/Turabian StyleLino, Jéssica Boreli dos Reis, Mateus Aquino Gonçalves, Stephan P. A. Sauer, and Teodorico Castro Ramalho. 2022. "Extending NMR Quantum Computation Systems by Employing Compounds with Several Heavy Metals as Qubits" Magnetochemistry 8, no. 5: 47. https://doi.org/10.3390/magnetochemistry8050047
APA StyleLino, J. B. d. R., Gonçalves, M. A., Sauer, S. P. A., & Ramalho, T. C. (2022). Extending NMR Quantum Computation Systems by Employing Compounds with Several Heavy Metals as Qubits. Magnetochemistry, 8(5), 47. https://doi.org/10.3390/magnetochemistry8050047