Next Article in Journal
Redox Activity as a Powerful Strategy to Tune Magnetic and/or Conducting Properties in Benzoquinone-Based Metal-Organic Frameworks
Next Article in Special Issue
Structure and Magnetic Properties of Fe-B-La-Al Alloy
Previous Article in Journal
Methods and Models of Theoretical Calculation for Single-Molecule Magnets
Previous Article in Special Issue
Artificial Intelligence—Engineering Magnetic Materials: Current Status and a Brief Perspective
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Magnetochemistry
Volume 7
Issue 8
10.3390/magnetochemistry7080108
magnetochemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

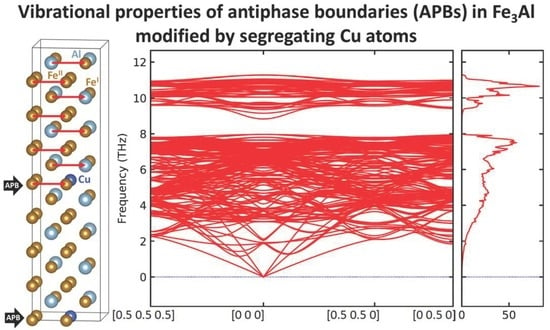
The Impact of Vibrational Entropy on the Segregation of Cu to Antiphase Boundaries in Fe3Al

by
Martin Friák
1,2,*,
Miroslav Černý
2,3 and
Mojmír Šob
4,1
1
Institute of Physics of Materials, v.v.i., Czech Academy of Sciences, Žižkova 22, CZ-616 00 Brno, Czech Republic
2
Central European Institute of Technology (CEITEC), Brno University of Technology, Technická 2, CZ-616 69 Brno, Czech Republic
3
Faculty of Mechanical Engineering, Brno University of Technology, Technická 2, CZ-616 69 Brno, Czech Republic
4
Department of Chemistry, Faculty of Science, Masaryk University, Kotlářská 2, CZ-611 37 Brno, Czech Republic
*
Author to whom correspondence should be addressed.
Magnetochemistry 2021, 7(8), 108; https://doi.org/10.3390/magnetochemistry7080108
Submission received: 18 June 2021 / Revised: 2 July 2021 / Accepted: 22 July 2021 / Published: 2 August 2021
(This article belongs to the Special Issue Advances in Amorphous and Nanocrystalline Magnetic Materials)
Browse Figures
Versions Notes

Abstract

We performed a quantum mechanical study of segregation of Cu atoms toward antiphase boundaries (APBs) in Fe 3 Al. The computed concentration of Cu atoms was 3.125 at %. The APBs have been characterized by a shift of the lattice along the ⟨001⟩ crystallographic direction. The APB energy turns out to be lower for Cu atoms located directly at the APB interfaces and we found that it is equal to 84 mJ/m 2 . Both Cu atoms (as point defects) and APBs (as extended defects) have their specific impact on local magnetic moments of Fe atoms (mostly reduction of the magnitude). Their combined impact was found to be not just a simple sum of the effects of each of the defect types. The Cu atoms are predicted to segregate toward the studied APBs, but the related energy gain is very small and amounts to only 4 meV per Cu atom. We have also performed phonon calculations and found all studied states with different atomic configurations mechanically stable without any soft phonon modes. The band gap in phonon frequencies of Fe 3 Al is barely affected by Cu substituents but reduced by APBs. The phonon contributions to segregation-related energy changes are significant, ranging from a decrease by 16% at T = 0 K to an increase by 17% at T = 400 K (changes with respect to the segregation-related energy difference between static lattices). Importantly, we have also examined the differences in the phonon entropy and phonon energy induced by the Cu segregation and showed their strongly nonlinear trends.

Graphical Abstract

1. Introduction

The Fe 3 Al intermetallic compound belongs to a promising class of Fe-Al-based materials possessing relatively low density, unusual resistance to oxidation, and low cost of raw materials [1,2,3]; some of them suffer from room-temperature brittleness [4,5,6,7,8]. Earlier experimental studies of these materials [9,10,11,12,13,14,15,16,17,18,19] were recently complemented by research focused on their use in high-temperature coatings [20,21,22,23,24,25,26] or composites [27,28,29,30,31], novel preparation techniques [32,33,34,35], and their materials properties [36,37]. Theoretical studies cover quantum mechanical calculations of single-phase materials [38,39,40,41,42,43,44,45,46,47] as well as nanocomposites [48,49], calculations of magnetic properties [50,51], combinations of methods [52,53,54,55], and analysis of point defects [56,57,58] and extended defects [59,60]. Our current research is focused on extended defects called antiphase boundaries (APBs). They separate two parts of the crystal mutually shifted such that the sublattices that would normally not interface do so. The APBs can form during crystallization (thermal APBs) or due to the motion of dislocations (deformation APBs). As the D0 3 structure of Fe 3 Al has three sublattices (one with the Al atoms and two with the Fe atoms), APBs are among defects previously simulated in Fe 3 Al [61,62,63,64].
Regarding experimental studies of APBs, there were two types found in the D0 3 superlattice of Fe 3 Al using transmission electron microscopy (TEM) techniques [65,66]. The first one is characterized by a shift of the interfacing grains in the 〈100〉 direction by a half of the lattice parameter defined for a 16-atom cube-shaped D0 3 cell (see red arrows in Figure 1b,c) and is associated solely with the D0 3 superlattice (D0 3 -type of APBs). We have recently computed properties of D0 3 -APBs in (i) Fe 3 Al with and without Cr additions [67] as well as (ii) in Fe-Al-Ti compounds [68]. The second type can appear both in the D0 3 superlattice and in the B2 lattice (a B2-type of APBs) when two parts of the crystal are shifted in the 〈111〉 direction by a half of the lattice parameter of the B2 cell containing two atoms (we recently examined them in Fe 70 Al 30 alloy [69]). Both types were found separating partials of superdislocations in Fe-Al alloys [70,71,72]. Other findings related to APBs may be found, for example, in papers [73,74,75,76,77].
The properties of iron aluminides can be fine-tuned by alloying, see, e.g., [78,79,80,81,82,83,84], but the complexity of interactions of the solute atoms with extended defects are quite rarely studied (see an example in [85]). Therefore, our study is aimed at filling in this gap in the common knowledge. We have chosen to focus on Fe 3 Al because (i) it belongs to industrially important iron aluminides [1,2,3], (ii) it is known to contain extended defects including APBs, and (iii) properties of Fe 3 Al are routinely modified by additions, but (iv) a thorough theoretical analysis of interactions of copper atoms with APBs (possibly segregation tendencies to them) in Fe 3 Al has not been performed yet. Therefore, we have applied quantum mechanical calculations to compute properties of Fe 3 Al compound with Cu atoms (see Figure 1a) with and without APBs. Regarding the coexistence of both Cu atoms and APBs, we have examined both the case with Cu atoms at the APB interfaces (see Figure 1b) and far away from them (see Figure 1c). Importantly, we have performed our calculations not only for static lattices, but we have also evaluated contributions related to thermal vibrations. Our analysis has allowed us to thoroughly assess segregation tendencies of Cu atoms toward APBs in Fe 3 Al even at elevated temperatures.

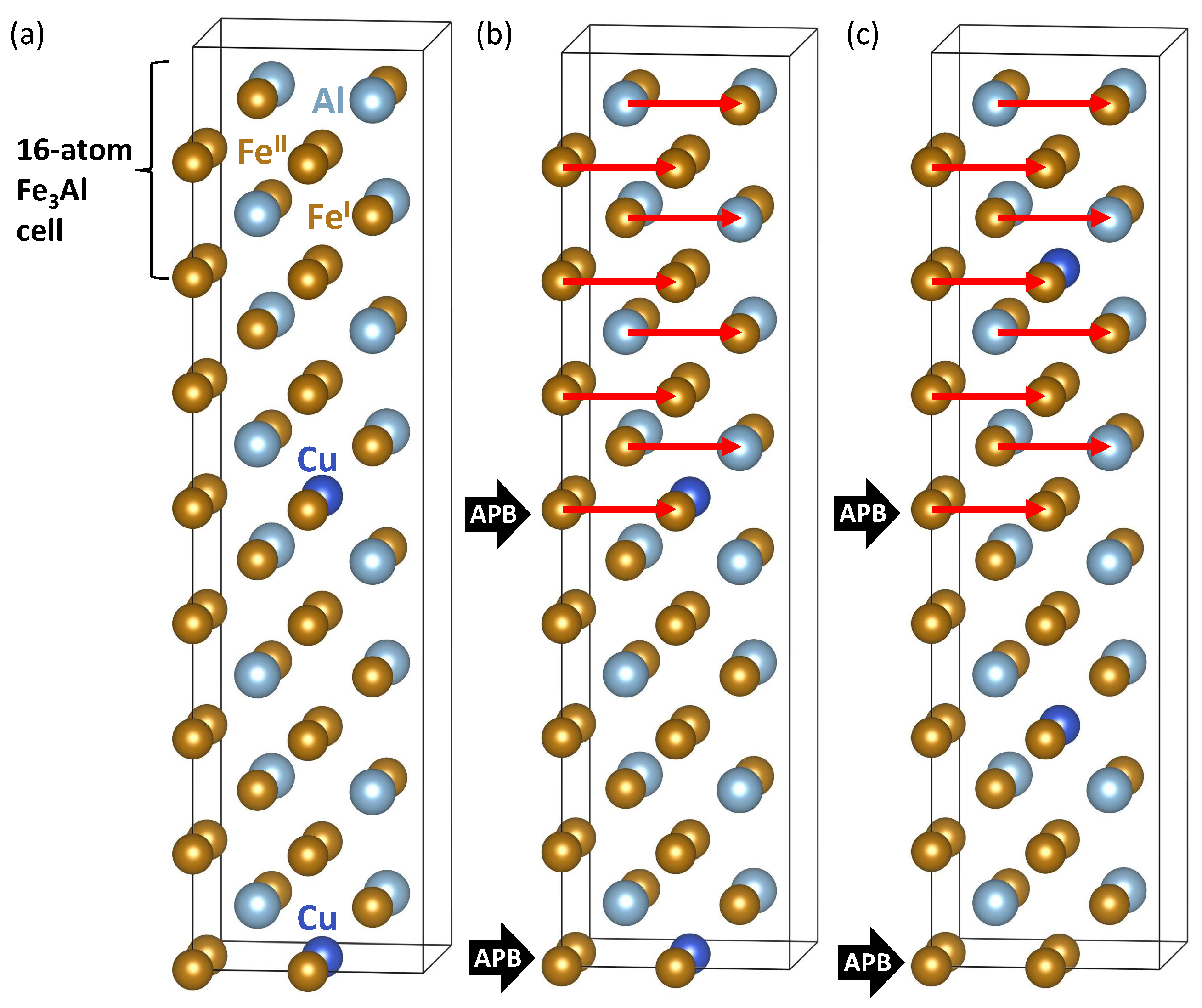
2. Methods

Our first-principles calculations were performed with the help of the Vienna Ab initio Simulation Package (VASP) [86,87] implementing the density functional theory [88,89]. Projector augmented wave (PAW) pseudopotentials [90,91] were used together with the generalized gradient approximation (GGA) in the parametrization according to Perdew and Wang [92] (PW91) in combination with the Vosko–Wilk–Nusair correction [93] for the exchange and correlation energy. This specific setup was chosen as it correctly predicts the ground state of Fe 3 Al to be the D0 3 structure (its energy is lower than that of Fe 3 Al with the L1 2 structure by about 5.5 meV/atom [94]). We have employed 64-atom supercells as a stacking of 16-atom cube-shaped cell of Fe 3 Al (see Figure 1). They are 1 × 1 × 4 multiples of the 16-atom cell (Figure 1). For phonon calculations, 256-atom supercells were generated by the PHONOPY software [95] as 2 × 2 × 1 multiples of the above-mentioned 64-atom supercells. Having computed the phonon frequencies ω ( q ν ) for a dense set of reciprocal-space vectors q and all modes ν , we evaluated also the Helmholtz free energy F, the entropy S, harmonic phonon energy E, and constant-volume heat capacity C v [95]:
F = 1 2 ∑ q ν ℏ ω ( q ν ) + k B T ∑ q ν ln [ 1 − exp ( − ℏ ω ( q ν ) / k B T ) ] , S = − ∂ F ∂ T , E = ∑ q ν ℏ ω ( q ν ) 1 2 + 1 exp ( ℏ ω ( q ν ) / k B T ) − 1 , C v = − ∂ E ∂ T v .
Our calculations were performed with the plane-wave energy cutoff of 400 eV and the product of the number of Monkhorst–Pack k-points and the number of atoms was equal to 27,648 (e.g., 12 × 12 × 3 k-point mesh in the case of 64-atom supercells shown in Figure 1). We have fully relaxed all studied supercells, i.e., the energy was minimized with respect to internal atomic positions, cell shape, and the volume (forces acting upon atoms were reduced under 0.001 eV/Å in the case of 64-atom supercells). All local magnetic moments were initially set up as parallel (a ferromagnetic state).

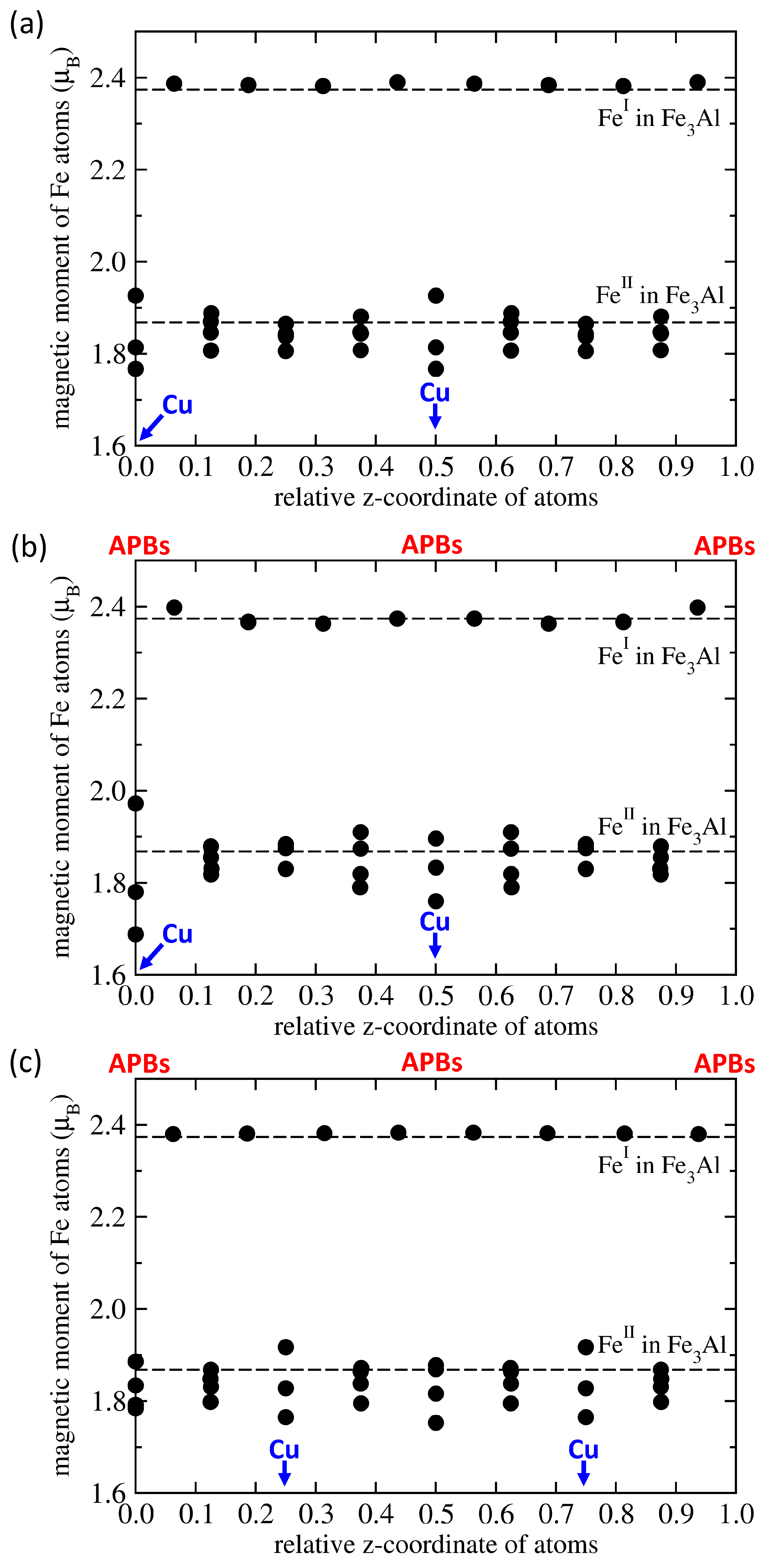
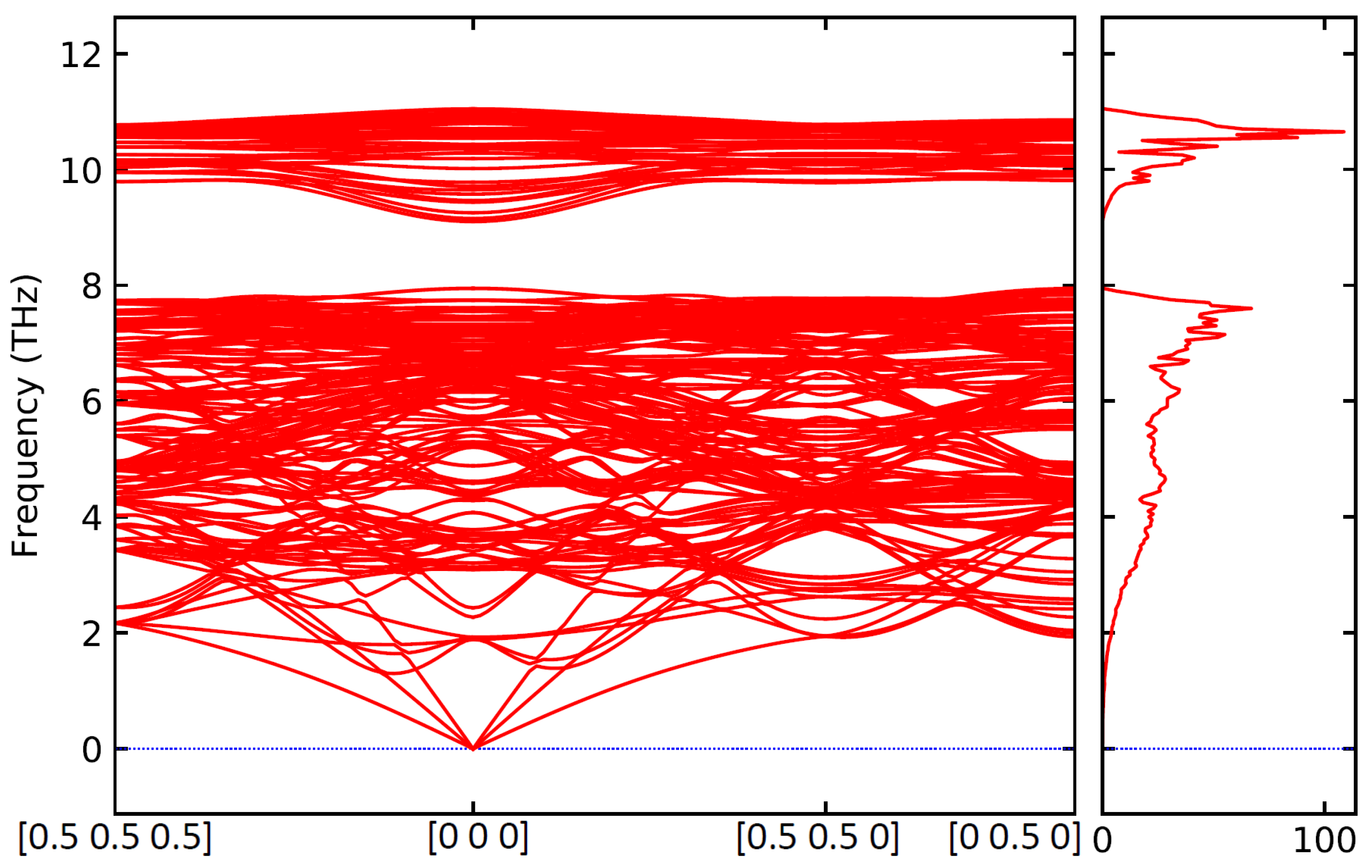
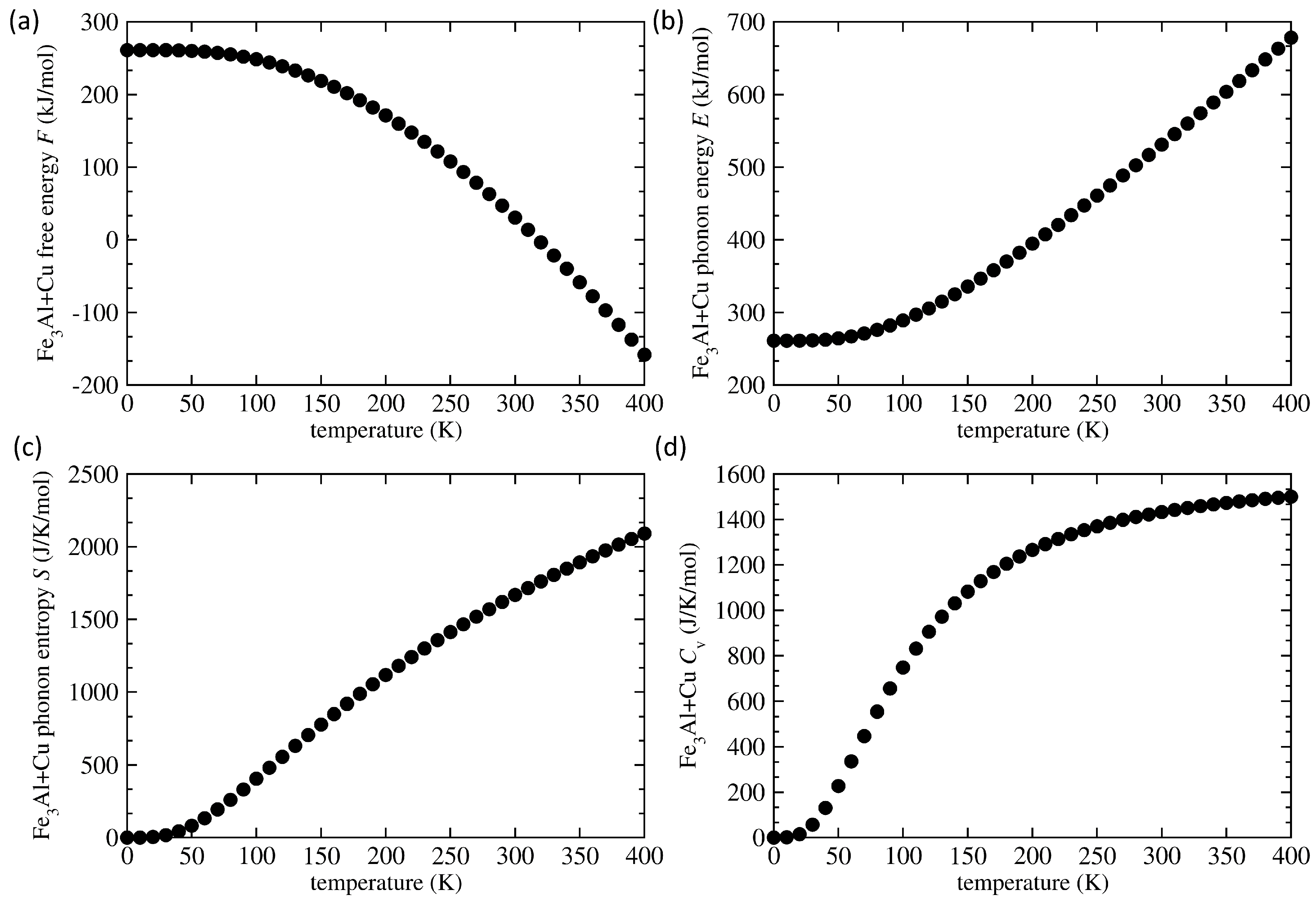
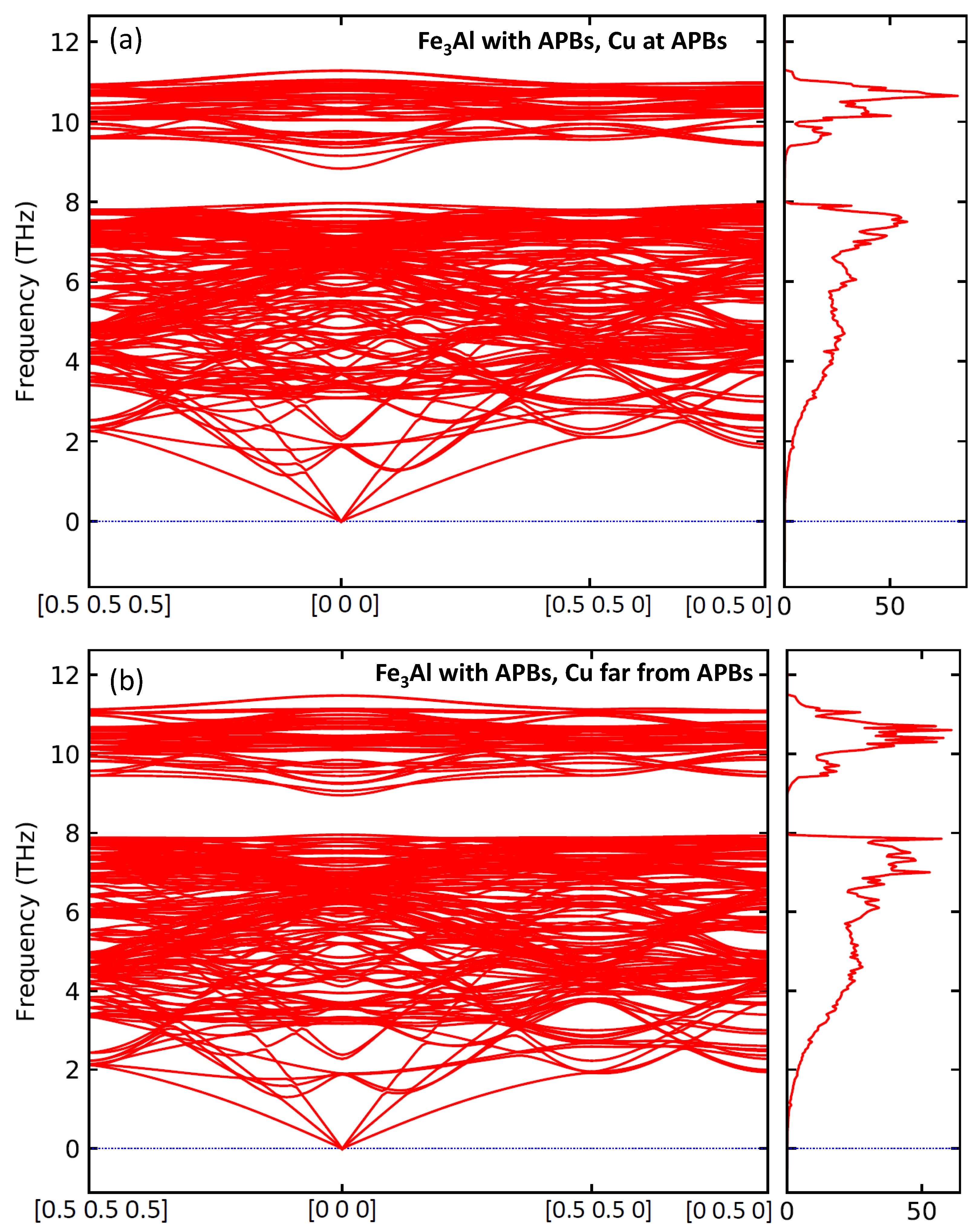
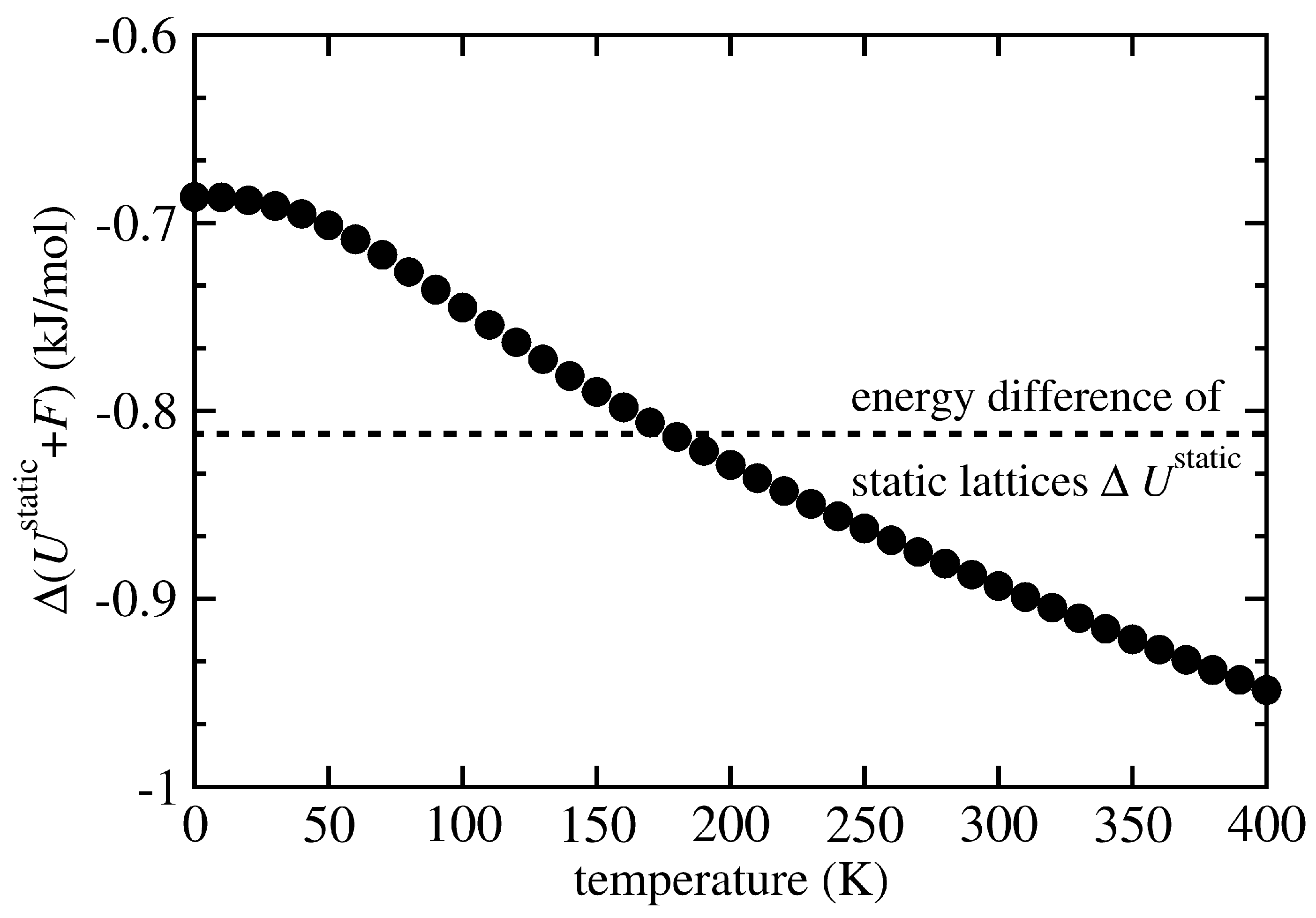
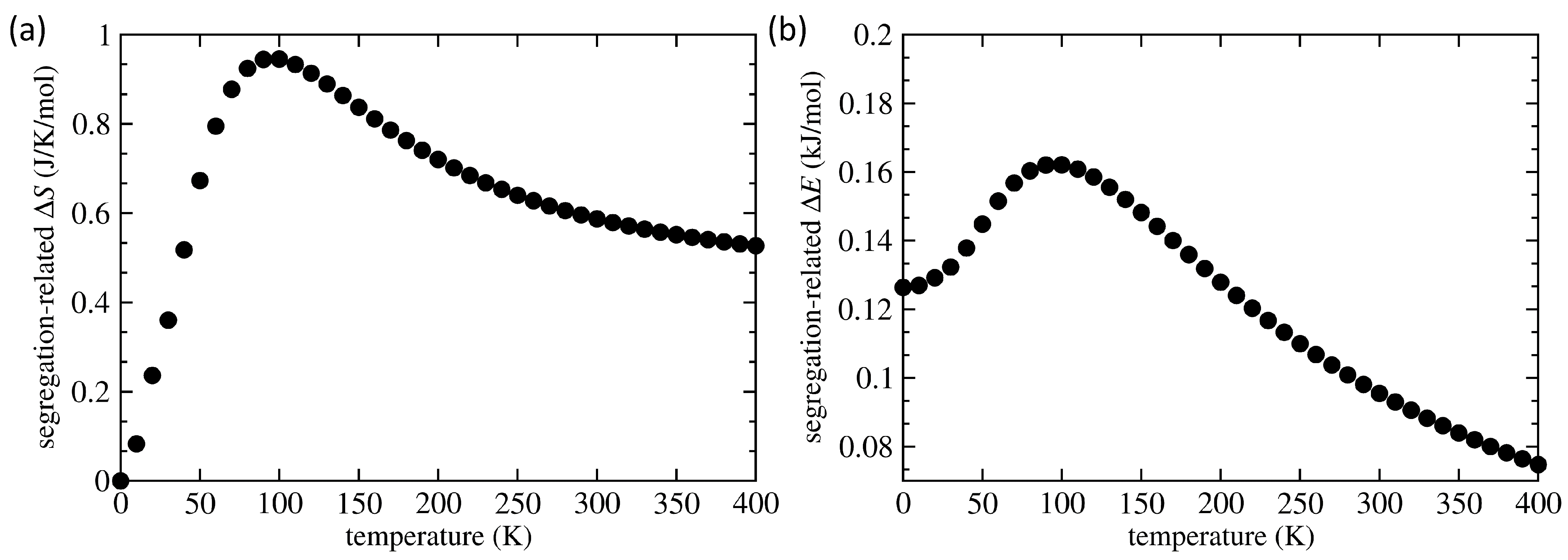
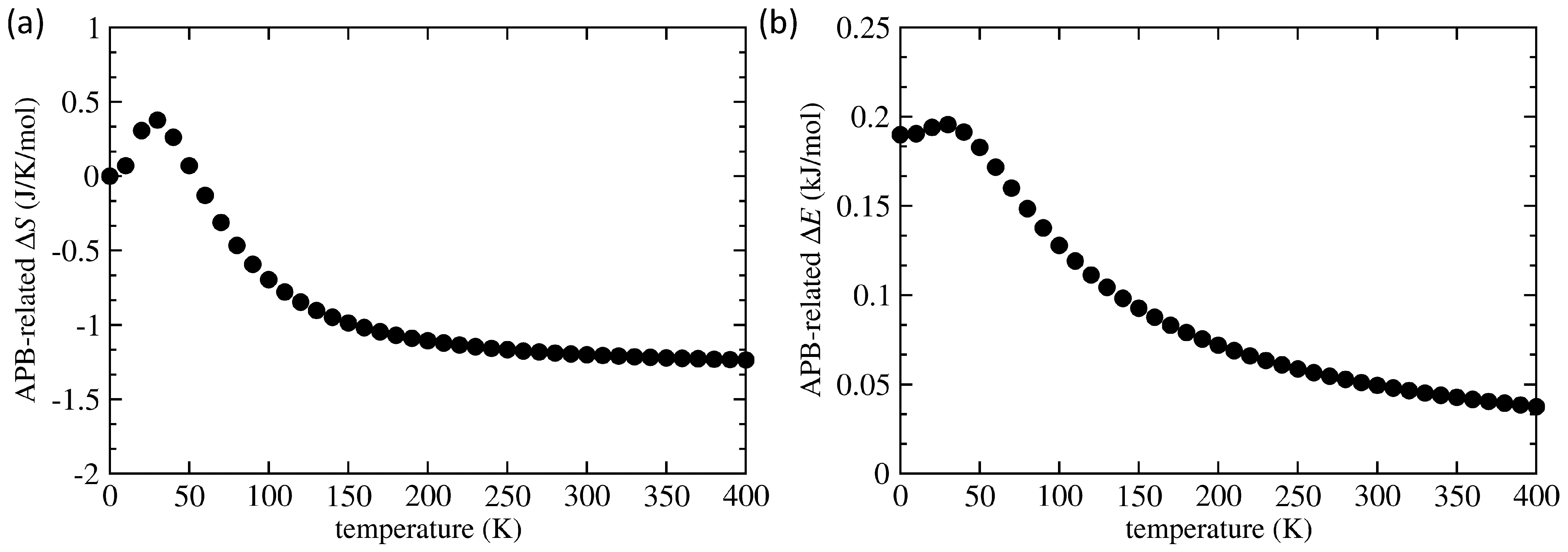
3. Results

Starting with calculations of static lattices, i.e., without phonons, we first examined the impact of Cu solutes on surrounding atoms. As mentioned in the introduction above, there are two sublattices of iron atoms in the defect-free Fe 3 Al. The Fe I atoms have eight iron atoms in the first nearest neighbors (1NN) shell and their magnetic moment is equal to 2.37 μ B . Twice more abundant Fe II atoms have four iron atoms and four aluminum atoms in their 1NN shell and their magnetic moment is lower, equal to 1.87 μ B . We have computed the local magnetic moments of all Fe atoms in all three supercells shown in Figure 1 and the resulting values are compared with the above-mentioned Fe 3 Al-bulk values in Figure 2. The Cu atoms substitute the Fe II atoms because it was shown that it is energetically preferred over the Fe I site (see, e.g., [83]). As seen in Figure 1a, there are three Fe II atoms per one Cu atom in the (001) atomic planes. The supercell Figure 1a has a simple tetragonal symmetry with only eight symmetry operations (point group D2 d ). Two of these three Fe II atoms have the Cu atoms as second nearest neighbors and their local magnetic moments are slightly reduced (see Figure 2a). The third of these three Fe II atoms has the Cu atoms as the third nearest neighbor and its magnetic moment is slightly increased (Figure 2a). Magnetic moments of other Fe atoms are influenced to a lesser extent.
The same trends, i.e., either increased or decreased local magnetic moments of Fe atoms, were found also in the case when the APBs are introduced (see Figure 2b,c). However, the APBs have their own rather complex type of impact on iron atoms close to the APB interfaces. The effect of APBs is better separated from that related to the Cu atoms when the Cu substituents are located away from the APBs (see Figure 2c). The local magnetic moments of Fe atoms in the same {001} plane as the Cu atoms are similar for both Cu substituents in the supercell shown in Figure 1c.
A qualitatively similar statement is true also in the case of the two APB interfaces; they lead to similar changes of the local magnetic moments as shown in Figure 2c. Interestingly, when the impact of Cu substituents combines with that of APBs, their overall influence is nontrivial and rather complicated trends emerge (see Figure 2b). For example, the local magnetic moments of Fe I atoms in the upper parts of Figure 2a,c are either equal to or slightly higher than the value in the defect-free Fe 3 Al bulk. In contrast to that, the combined impact of both Cu atoms and APB interfaces leads to local magnetic moments that are lower for some of the Fe I atoms, see the upper part of Figure 2b. Interactions of point defects and extended defects are, therefore, rather complex in Fe 3 Al and their influence on magnetic moments of Fe is not additive in any straightforward manner. This lack of a simple additivity in the case of the two types of studied defects is visible also in the case of other local magnetic moments of atoms, particularly those of the Fe II atoms in the lower part of Figure 2b.
When using the energies of static lattices U static , we have also evaluated the static lattice antiphase boundary energy. Comparing the two APB-containing supercells in Figure 1b,c, we found that the energy of the APB-containing supercell with the Cu atoms located directly at the APB interfaces (see Figure 1b) is lower than that when the Cu atoms are farther apart from the APB interfaces (see Figure 1c). Therefore, we have used the energy difference Δ U static between (i) the APB-containing supercell shown in Figure 1b and (ii) that one without any APB in Figure 1a for our evaluation of the APB energy. As there are two APBs per supercell, we have divided the above-mentioned energy difference by twice the area of the supercell within the {001} planes, i.e., the crystallographic orientation of the studied APB interfaces. The static lattice APB interface energy turns out to be equal to 84 mJ/m 2 . This rather low value obtained for Fe 3 Al with 3.125 at % of Cu atoms (i.e., 2 per 64 atoms) is slightly higher than the APB energy of 80 mJ/m 2 that we obtained for Fe 3 Al with the APBs characterized by the same shift in the 〈100〉 crystallographic direction and the same 64-atom supercell size in [67]. But the difference in the APB energy induced by the Cu atoms is very small and within an expected error bar of our calculations. This statement stems from the results of our comparative analysis of a series of supercells with different sizes and different separation of APBs in our previous study [67]. The APB energy in Fe 3 Al in our previous research exhibited values from the range of 80 ± 25 mJ/m 2 . Therefore, we conclude that the above discussed increase of the static lattice APB energy due to the presence of Cu atoms is rather insignificant.
Now, focusing on the main topic of our work, that is, the segregation of Cu atoms toward the antiphase boundaries in Fe 3 Al, we evaluated the segregation-related energy difference Δ U static determined from the static lattice calculations. We found this quantity to be small, only −4.2 meV per Cu atom (the negative value means an energy gain). This difference can be formulated as −0.81 kJ/mol as an energy difference between the supercells in Figure 1b,c with one mole defined as that of 64-atom supercell with two segregating Cu atoms. In what follows, we do not express the segregation energy in a traditional manner per one segregating Cu atom. We rather analyze energy differences between 64-atoms supercells Δ U static in order to be able to smoothly combine static lattice energy differences discussed here with thermodynamic phonon-related terms as obtained directly from the PHONOPY software (see the discussion below).
Next, we have determined phonon modes for the supercells visualized in Figure 1. Starting with the APB-free Fe 3 Al with Cu substituents, the computed phonon spectra and the overall density of phonon states are shown in Figure 3. The band gap in vibrational frequencies above 8 THz is matching that in perfect Fe 3 Al bulk that we reported in our previous study [59]. Interestingly, the point defects represented here by Cu atoms do not close this gap in phonon frequencies in contrast to some APBs that, as we have shown, can close it nearly completely (see [59]). Importantly, the obtained phonon spectrum does not contain any soft phonon modes with imaginary frequencies. Therefore, we assume that the studied system of APB-free Fe 3 Al with Cu atoms is mechanically stable.
Next, we evaluated Helmholtz free energy F, the entropy S, harmonic phonon energy E, and constant-volume heat capacity C v (see them visualized in Figure 4).
As our phonon calculations are performed only for the static lattice minimum-energy volume (the harmonic approximation), we present these quantities only up to T = 400 K (for which, we hope, thermal expansion does not alter the results too much). The dependences are qualitatively similar to those that we previously obtained for Fe 3 Al [59].
Next, we have determined phonon modes for both supercells containing APBs visualized in Figure 1b,c. The calculated spectra along selected higher-symmetry directions in the reciprocal space and the overall phonon densities of states are shown in Figure 5. Again, there are no soft phonon modes and, therefore, both studied systems with APBs (with the Cu atoms located directly at the APB interfaces or positioned away from them) are mechanically stable.
The APBs make the band gap of phonon frequencies narrower, in particular when the Cu substituents are located directly at the APB interfaces, see Figure 5a. These findings are in line with the results of our previous study in which APBs (of a different type) nearly closed the gap of phonon frequencies [59]. In the present study, the gap is narrower but not completely closed.
Having detailed information related to phonon modes of both APB-containing systems available, it is possible to focus on the main topic of our research, segregation trends of Cu atoms toward the studied APBs. These are expected to occur as the formation energy of point defects represented by Cu atoms in Fe 3 Al is positive and the point-defect formation energy is equal to 0.192 eV/atom as shown by Park and coworkers in [83]. The ab initio calculations in [83] are relevant despite of the fact that a higher concentration of Cu atoms (6.25 at %) was studied (there is a decent solubility of a few atomic percent of Cu in Fe 3 Al when 5 at % was reported in [82]). The segregation-related difference of the static lattice energy added to the phonon free energy Δ ( U static + F ) per 64 atoms (including 2 segregating Cu atoms) is shown in Figure 6. The comparison with the energy difference of static lattice Δ U static (see the horizontal dashed line in Figure 6) indicates that the phonon contributions are reducing the segregation-related energy gain (when compared with the static lattice value Δ U static ) to −0.69 kJ/mol at T = 0 K. As the temperature increases from T = 0 K, the vibronic contributions into the segregation-related energy difference enhance the segregation tendency (the energy gain due to segregation is increased). The static lattice energy difference Δ U static (the above-discussed value of −0.81 kJ/mol) is reached at approximately T = 180 K and the free-energy gain due to the segregation then steadily increases for yet higher temperatures. Due to the fact that the static lattice segregation-related energy difference Δ U static is so small, vibrational degrees of freedom that are rather small themselves, represent an important part of the combined Δ ( U static + F ) energy difference. In particular, they can represent a decrease by 16% for T = 0 K or an increase by 17% for T = 400 K (expressed relatively with respect to the segregation-related Δ U static value).
The above-discussed segregation-related energy differences Δ ( U static + F ) can be linked to the changes in the phonon entropy S and phonon energy E. Their differences between the two supercells containing APBs with differently located Cu atoms are shown in Figure 7. Their trends are nonlinear and nonmonotonous. They increase from their value at T = 0 K up to about T = 95 K and then decrease for higher temperatures. It is worth noting that the studied type of APBs alternates the distribution of atoms at the APB interfaces only slightly when compared to the APB-free lattice. Therefore, interatomic bonds are modified only weakly and the changes in thermal vibrations (and related terms in the free energy) are small. The phonon-related contributions into the segregation-related Δ ( U static + F ) are nevertheless significant (up to 16–17% discussed above). In contrast, their importance is much smaller (up to 1.5%) in the case the APB-related energy differences (again expressed as the energy difference between 64-atom supercells Δ ( U static + F ) ), as see Figure 8.
The APB-related static lattice energy difference Δ U static is about 40 times bigger than the segregation-related energy difference discussed above, whereas the phonon-related contributions into the APB-related Δ ( U static + F ) difference are similar in their magnitude. Consequently, the vibronic contributions into the APB-related Δ ( U static + F ) are relatively much smaller than the segregation-related ones as seen in the comparison of Figure 6 and Figure 8. The phonon contributions into the APB-related energy difference Δ ( U static + F ) , particularly the entropy difference Δ S and phonon energy difference Δ E , are shown in Figure 9. They exhibit qualitatively similar trends as the segregation-related ones in Figure 7, but their combined impact is positive for the whole studied temperature range, i.e., they only increase the APB-related energy difference (see Figure 8). Finally, while we are not aware of any quantitative experimental data related to segregation of Cu atoms toward APBs in Fe 3 Al, we hope that our theoretical predictions will initiate such a research in future.

4. Conclusions

We performed an ab initio study of segregation of Cu atoms toward antiphase boundaries in Fe 3 Al. The studied concentration of Cu atoms was 3.125 at % (two Cu atoms per 64-atom supercells). When simulating APBs, one Cu atoms was approaching each of the two identical APBs inside the supercells. The Cu atoms substitute Fe II atoms, i.e., sublattice with the Fe atoms where the first nearest neighbor shell contains an equal amount of both Fe and Al atoms. The APBs have been characterized by a shift of the lattice along the 〈001〉 crystallographic direction and have the {001} orientation of their sharp interfaces. The APB energy turns out to be lower for Cu atoms located directly at the APB interfaces and we found it equal to 84 mJ/m 2 . Both Cu atoms (as point defects) and APBs (as extended defects) have their specific impact on local magnetic moments of Fe atoms (mostly reduction of the magnitude) close to these defects. Their combined impact was found not to be a simple linear addition of the impact of each of the defect types. The Cu atoms are predicted to segregate toward the studied APBs, but the related energy gain is small and amounts to only 4.2 meV per Cu atom.
As an extension of our study of static lattices, we have also performed phonon calculations for lattices with and without APBs (and the former with and without segregated Cu atoms) at their equilibrium volume (the harmonic approximation). All studied systems are mechanically stable without any soft phonon modes. The band gap in phonon frequencies of Fe 3 Al is barely affected by Cu substituents but slightly reduced by APBs. The phonon-related contributions into segregation-related energy difference were found significant, ranging from a decrease by 16% at T = 0 K to an increase by 17% at T = 400 K when compared with the segregation-related energy difference determined for static lattices. We have examined the differences in the phonon entropy and phonon energy between the states with (i) Cu atoms segregated to APB interfaces and (ii) the Cu atoms being away from them and found strongly nonlinear trends in both quantities.

Author Contributions

Writing—original draft preparation, visualization, M.F.; conceptualization, M.Č., M.F., and M.Š.; methodology, M.Č., M.F., and M.Š.; writing—review and editing, M.F., M.Č., and M.Š.; resources, project administration, funding acquisition, M.Č.; supervision, M.Š. All authors have read and agreed to the published version of the manuscript.

Funding

The authors acknowledge the Czech Science Foundation for the financial support received under the Project No. 20-08130S (M.Č. and M.F.).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

Computational resources were provided by the Ministry of Education, Youth and Sports of the Czech Republic under the Projects e-INFRA CZ (ID:90140) at the IT4Innovations National Supercomputing Center and e-Infrastruktura CZ (e-INFRA LM2018140) at the MetaCentrum as well as the CERIT-Scientific Cloud (Project No. LM2015085), all granted within the program Projects of Large Research, Development and Innovations Infrastructures. The Figure 1 was visualized using the VESTA [96,97,98].

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Sauthoff, G. Intermetallics; VCH Verlagsgesellschaft: Weinheim, Germany, 1995. [Google Scholar]
  2. Liu, C.T.; Stringer, J.; Mundy, J.N.; Horton, L.L.; Angelini, P. Ordered intermetallic alloys: An assessment. Intermetallics 1997, 5, 579–596. [Google Scholar] [CrossRef]
  3. Stoloff, N.S. Iron aluminides: Present status and future prospects. Mater. Sci. Eng. A 1998, 258, 1–14. [Google Scholar] [CrossRef]
  4. Liu, C.T.; Lee, E.H.; McKamey, C.G. An environmental-effect as the major cause for room-temperature embrittlement in FeAl. Scr. Metall. Mater. 1989, 23, 875–880. [Google Scholar] [CrossRef]
  5. Lynch, R.J.; Heldt, L.A.; Milligan, W.W. Effects of alloy composition on environmental embrittlement of B2 ordered iron aluminides. Scr. Metall. Mater. 1991, 25, 2147–2151. [Google Scholar] [CrossRef]
  6. Liu, C.T.; McKamey, C.G.; Lee, E.H. Environmental-effects on room-temperature ductility and fracture in Fe3Al. Scr. Metall. Mater. 1990, 24, 385–389. [Google Scholar] [CrossRef]
  7. Lynch, R.J.; Gee, K.A.; Heldt, L.A. Environmental embrittlement of single-crystal and thermomechanically processed B2-ordered iron aluminides. Scr. Metall. Mater. 1994, 30, 945–950. [Google Scholar] [CrossRef]
  8. Zamanzade, M.; Barnoush, A.; Motz, C. A Review on the Properties of Iron Aluminide Intermetallics. Crystals 2016, 6, 10. [Google Scholar] [CrossRef]
  9. Kattner, U.; Burton, B. Al-Fe (Aluminium-Iron). In Phase Diagrams of Binary Iron Alloys; Okamoto, H., Ed.; ASM International: Materials Park, OH, USA, 1993; pp. 12–28. [Google Scholar]
  10. Palm, M.; Inden, G.; Thomas, N. The Fe-Al-Ti system. J. Phase Equilibria 1995, 16, 209–222. [Google Scholar] [CrossRef]
  11. Vernieres, J.; Benelmekki, M.; Kim, J.H.; Grammatikopoulos, P.; Bobo, J.F.; Diaz, R.E.; Sowwan, M. Single-step gas phase synthesis of stable iron aluminide nanoparticles with soft magnetic properties. APL Mater. 2014, 2, 116105. [Google Scholar] [CrossRef]
  12. Jirásková, Y.; Pizúrová, N.; Titov, A.; Janičkovič, D.; Friák, M. Phase separation in Fe-Ti-Al alloy–Structural, magnetic, and Mössbauer study. J. Magn. Magn. Mater. 2018, 468, 91–99. [Google Scholar] [CrossRef]
  13. Palm, M.; Lacaze, J. Assessment of the Al-Fe-Ti system. Intermetallics 2006, 14, 1291–1303. [Google Scholar] [CrossRef]
  14. Dobeš, F.; Dymáček, P.; Friák, M. Force-to-Stress Conversion Methods in Small Punch Testing Exemplified by Creep Results of Fe-Al Alloy with Chromium and Cerium Additions. IOP Conf. Ser. Mater. Sci. Eng. 2018, 461, 012017. [Google Scholar] [CrossRef]
  15. Dobeš, F.; Dymáček, P.; Friák, M. Small punch creep of Fe-Al-Cr alloy with Ce addition and its relation to uniaxial creep tests. Kovové Materiály Met. Mater. 2018, 56, 205. [Google Scholar] [CrossRef]
  16. Palm, M.; Sauthoff, G. Deformation behaviour and oxidation resistance of single-phase and two-phase L21-ordered Fe-Al-Ti alloys. Intermetallics 2004, 12, 1345–1359. [Google Scholar] [CrossRef]
  17. Sundman, B.; Ohnuma, I.; Dupin, N.; Kattner, U.R.; Fries, S.G. An assessment of the entire Al-Fe system including D0(3) ordering. Acta Mater. 2009, 57, 2896–2908. [Google Scholar] [CrossRef]
  18. Dymáček, P.; Dobeš, F.; Jirásková, Y.; Pizúrová, N.; Friák, M. Tensile, creep and fracture testing of prospective Fe-Al-based alloys using miniature specimens. Theor. Appl. Fract. Mech. 2019, 99, 18–26. [Google Scholar] [CrossRef]
  19. Dobeš, F.; Dymáček, P.; Friák, M. The Influence of Niobium Additions on Creep Resistance of Fe-27 at.% Al Alloys. Metals 2019, 9, 739. [Google Scholar] [CrossRef]
  20. Grigorchik, A.N.; Astrashab, V.E.; Kukareko, V.A.; Belotserkovsky, M.A.; Sosnovsky, V.A. High-temperature heat treatment of hypersonic metallization coatings from pseudoalloy “Fe-Al”. Lett. Mater. 2021, 11, 198–203. [Google Scholar] [CrossRef]
  21. Deevi, S.C. Advanced intermetallic iron aluminide coatings for high temperature applications. Prog. Mater. Sci. 2021, 118. [Google Scholar] [CrossRef]
  22. Tolochyn, O.I.; Baglyuk, G.A.; Tolochyna, O.V.; Evych, Y.I.; Podrezov, Y.M.; Molchanovska, H.M. Structure and Physicomechanical Properties of the Fe3Al Intermetallic Compound Obtained by Impact Hot Compaction. Mater. Sci. 2021, 56, 499–508. [Google Scholar] [CrossRef]
  23. Komarov, O.N.; Zhilin, S.G.; Predein, V.V.; Popov, A.V. Mechanisms for Forming Iron-Containing Intermetallics Prepared by Aluminothermy and the Effect of Special Treatment Methods on their Properties. Metallurgist 2020, 64, 810–821. [Google Scholar] [CrossRef]
  24. Vodickova, V.; Svec, M.; Hanus, P.; Novak, P.; Zadera, A.; Keller, V.; Prokopcakova, P.P. The Effect of Simultaneous Si and Ti/Mo Alloying on High-Temperature Strength of Fe3Al-Based Iron Aluminides. Molecules 2020, 25, 4268. [Google Scholar] [CrossRef]
  25. Luo, X.; Cao, J.; Meng, G.; Chuan, Y.; Yao, Z.; Xie, H. Systematical investigation on the microstructures and tribological properties of Fe-Al laser cladding coatings. Appl. Surf. Sci. 2020, 516. [Google Scholar] [CrossRef]
  26. Luo, X.; Cao, J.; Meng, G.; Yu, F.; Jiang, Q.; Zhang, P.; Xie, H. Double Glow Plasma Surface Metallurgy Technology Fabricated Fe-Al-Cr Coatings with Excellent Corrosion Resistance. Coatings 2020, 10, 575. [Google Scholar] [CrossRef]
  27. Teker, T.; Yilmaz, S.O. Synthesis and structural characterization of Fe based Ti+Ni3Al+Al2O3 reinforcement composite produced by mechanical alloying. Rev. Metal. 2020, 56. [Google Scholar] [CrossRef]
  28. Zhang, X.; Sun, Y.; Niu, M.; Shao, M.; Geng, X. Microstructure and mechanical behavior of in situ TiC reinforced Fe3Al (Fe-23Al-3Cr) matrix composites by mechanical alloying and vacuum hot-pressing sintering technology. Vacuum 2020, 180. [Google Scholar] [CrossRef]
  29. Ghazanfari, H.; Blais, C.; Gariepy, M.; Savoie, S.; Schulz, R.; Alamdari, H. Improving wear resistance of metal matrix composites using reinforcing particles in two length-scales: Fe3Al/TiC composites. Surf. Coat. Technol. 2020, 386. [Google Scholar] [CrossRef]
  30. Khodaei, M. Characterization of Al2O3 in Fe3Al-30 vol.% Al2O3 Nanocomposite Powder Synthesized by Mechanochemical Process. J. Nanostruct. 2020, 10, 456–462. [Google Scholar] [CrossRef]
  31. Altunin, R.R.; Moiseenko, E.T.; Zharkov, S.M. Structural Phase Transformations during a Solid-State Reaction in a Bilayer Al/Fe Thin-Film Nanosystem. Phys. Solid State 2020, 62, 200–205. [Google Scholar] [CrossRef]
  32. Tolochyn, O.I.; Tolochyna, O.V.; Bagliuk, H.A.; Yevych, Y.I.; Podrezov, Y.M.; Mamonova, A.A. Influence of Sintering Temperature on the Structure and Properties of Powder Iron Aluminide Fe3Al. Powder Metall. Met. Ceram. 2020, 59, 150–159. [Google Scholar] [CrossRef]
  33. Adler, L.; Fu, Z.; Koerner, C. Electron beam based additive manufacturing of Fe3Al based iron aluminides - Processing window, microstructure and properties. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2020, 785. [Google Scholar] [CrossRef]
  34. Michalcova, A.; Ozkan, M.; Mikula, P.; Marek, I.; Knaislova, A.; Kopecek, J.; Vojtech, D. The Influence of Powder Milling on Properties of SPS Compacted FeAl. Molecules 2020, 25, 2263. [Google Scholar] [CrossRef] [PubMed]
  35. Peska, M.; Karczewski, K.; Rzeszotarska, M.; Polanski, M. Direct Synthesis of Fe-Al Alloys from Elemental Powders Using Laser Engineered Net Shaping. Materials 2020, 13, 531. [Google Scholar] [CrossRef]
  36. Luo, X.; Cao, J.; Meng, G.; Zhou, Y.; Xie, H. Long-range-ordered Fe3Al with excellent electromagnetic wave absorption. J. Mater. Sci. Mater. Electron. 2020, 31, 15608–15615. [Google Scholar] [CrossRef]
  37. Ismail, A.; Bahanan, W.; Bin Hussain, P.; Saat, A.M.; Shaik, N.B. Diffusion Bonding of Al-Fe Enhanced by Gallium. Processes 2020, 8, 824. [Google Scholar] [CrossRef]
  38. Watson, R.E.; Weinert, M. Transition-metal aluminide formation: Ti, V, Fe, and Ni aluminides. Phys. Rev. B 1998, 58, 5981–5988. [Google Scholar] [CrossRef]
  39. Gonzales-Ormeno, P.; Petrilli, H.; Schon, C. Ab-initio calculations of the formation energies of BCC-based superlattices in the Fe-Al system. Calphad-Comput. Coupling Phase Diagrams Thermochem. 2002, 26, 573. [Google Scholar] [CrossRef]
  40. Connetable, D.; Maugis, P. First principle calculations of the kappa-Fe3AlC perovskite and iron-aluminium intermetallics. Intermetallics 2008, 16, 345–352. [Google Scholar] [CrossRef]
  41. Kellou, A.; Grosdidier, T.; Raulot, J.M.; Aourag, H. Atomistic study of magnetism effect on structural stability in Fe3Al and Fe3AlX (X = H, B, C, N, O) alloys. Phys. Status Solidi B-Basic Solid State Phys. 2008, 245, 750–755. [Google Scholar] [CrossRef]
  42. Šesták, P.; Friák, M.; Holec, D.; Všianská, M.; Šob, M. Strength and brittleness of interfaces in Fe-Al superalloy nanocomposites under multiaxial loading: An ab initio and atomistic study. Nanomaterials 2018, 8, 873. [Google Scholar] [CrossRef] [PubMed]
  43. Lechermann, F.; Fähnle, M.; Meyer, B.; Elsässer, C. Electronic correlations, magnetism, and structure of Fe-Al subsystems: An LDA+U study. Phys. Rev. B 2004, 69, 165116. [Google Scholar] [CrossRef]
  44. Airiskallio, E.; Nurmi, E.; Heinonen, M.H.; Vayrynen, I.J.; Kokko, K.; Ropo, M.; Punkkinen, M.P.J.; Pitkanen, H.; Alatalo, M.; Kollar, J.; et al. High temperature oxidation of Fe-Al and Fe-Cr-Al alloys: The role of Cr as a chemically active element. Corros. Sci. 2010, 52, 3394–3404. [Google Scholar] [CrossRef]
  45. Lechermann, F.; Welsch, F.; Elsässer, C.; Ederer, C.; Fähnle, M.; Sanchez, J.; Meyer, B. Density-functional study of Fe3Al: LSDA versus GGA. Phys. Rev. B 2002, 65, 132104. [Google Scholar] [CrossRef]
  46. Friák, M.; Slávik, A.; Miháliková, I.; Holec, D.; Všianská, M.; Šob, M.; Palm, M.; Neugebauer, J. Origin of the low magnetic moment in Fe2AlTi: An Ab initio study. Materials 2018, 11, 1732. [Google Scholar] [CrossRef]
  47. Ju, J.; Kang, M.; Zhou, Y.; Yang, C.; Wang, K.; Li, J.; Wang, R.; Fu, H.; Wang, J. First-principles investigations of the stability, electronic structures, mechanical properties and thermodynamic properties of FexAlyCz compounds in Fe-Cr-B-Al-C alloy. J. Phys. Chem. Solids 2020, 143. [Google Scholar] [CrossRef]
  48. Miháliková, I.; Friák, M.; Jirásková, Y.; Holec, D.; Koutná, N.; Šob, M. Impact of Nano-Scale Distribution of Atoms on Electronic and Magnetic Properties of Phases in Fe-Al Nanocomposites: An Ab Initio Study. Nanomaterials 2018, 8, 1059. [Google Scholar] [CrossRef]
  49. Friák, M.; Holec, D.; Šob, M. Quantum-Mechanical Study of Nanocomposites with Low and Ultra-Low Interface Energies. Nanomaterials 2018, 8, 1057. [Google Scholar] [CrossRef]
  50. Kulikov, N.I.; Postnikov, A.V.; Borstel, G.; Braun, J. Onset of magnetism in B2 transition-metal aluminides. Phys. Rev. B 1999, 59, 6824–6833. [Google Scholar] [CrossRef]
  51. Friák, M.; Neugebauer, J. Ab initio study of the anomalous volume-composition dependence in Fe-Al alloys. Intermetallics 2010, 18, 1316–1321. [Google Scholar] [CrossRef]
  52. Ipser, H.; Semenova, O.; Krachler, R. Intermetallic phases with D0(3)-structure: A statistical-thermodynamic model. J. Alloys Compd. 2002, 338, 20–25. [Google Scholar] [CrossRef]
  53. Fähnle, M.; Drautz, R.; Lechermann, F.; Singer, R.; Diaz-Ortiz, A.; Dosch, H. Thermodynamic properties from ab-initio calculations: New theoretical developments, and applications to various materials systems. Phys. Status Solidi B-Basic Solid State Phys. 2005, 242, 1159–1173. [Google Scholar] [CrossRef]
  54. Kirklin, S.; Saal, J.E.; Hegde, V.I.; Wolverton, C. High-throughput computational search for strengthening precipitates in alloys. Acta Mater. 2016, 102, 125–135. [Google Scholar] [CrossRef]
  55. Liu, S.; Duan, S.; Ma, B. First-principles calculation of vibrational entropy for Fe-Al compounds. Phys. Rev. B 1998, 58, 9705–9709. [Google Scholar]
  56. Čížek, J.; Lukáč, F.; Procházka, I.; Kužel, R.; Jirásková, Y.; Janičkovič, D.; Anwand, W.; Brauer, G. Characterization of quenched-in vacancies in Fe-Al alloys. Phys. B 2012, 407, 2659–2664. [Google Scholar] [CrossRef]
  57. Miháliková, I.; Friák, M.; Koutná, N.; Holec, D.; Šob, M. An Ab Initio Study of Vacancies in Disordered Magnetic Systems: A Case Study of Fe-Rich Fe-Al Phases. Materials 2019, 12, 1430. [Google Scholar] [CrossRef]
  58. Amara, H.; Fu, C.C.; Soisson, F.; Maugis, P. Aluminum and vacancies in α-iron: Dissolution, diffusion, and clustering. Phys. Rev. B 2010, 81, 174101. [Google Scholar] [CrossRef]
  59. Friák, M.; Černý, M.; Všianská, M.; Šob, M. Impact of Antiphase Boundaries on Structural, Magnetic and Vibrational Properties of Fe3Al. Materials 2020, 13, 4884. [Google Scholar] [CrossRef]
  60. Li, Y.; Liu, Y.; Yang, J. First principle calculations and mechanical properties of the intermetallic compounds in a laser welded steel/aluminum joint. Opt. Laser Technol. 2020, 122. [Google Scholar] [CrossRef]
  61. Wang, K.; Wang, Y. The partitioning behavior of dual solutes at the antiphase domain boundary in the B2 intermetallic: A microscopic phase-field study. J. Alloys Compd. 2020, 824, 153923. [Google Scholar] [CrossRef]
  62. Koizumi, Y.; Allen, S.M.; Ouchi, M.; Minamino, Y. Effects of solute and vacancy segregation on antiphase boundary migration in stoichiometric and Al-rich Fe3Al: A phase-field simulation study. Intermetallics 2010, 18, 1297–1302. [Google Scholar] [CrossRef][Green Version]
  63. Koizumi, Y.; Allen, S.M.; Minamino, Y. Effects of solute and vacancy segregation on migration of a/4〈111〉 and a/2〈100〉 antiphase boundaries in Fe3Al. Acta Mater. 2009, 57, 3039–3051. [Google Scholar] [CrossRef][Green Version]
  64. Koizumi, Y.; Allen, S.M.; Ouchi, M.; Minamino, Y.; Chiba, A. Phase-Field Simulation of D03-Type Antiphase Boundary Migration in Fe3Al with Vacancy and Solute Segregation. Solid State Phenom. 2011, 172–174, 1313–1319. [Google Scholar] [CrossRef]
  65. Marcinkowski, M.; Brown, N. Theory and direct observation of dislocations in the Fe3Al superlattices. Acta Metall. 1961, 9, 764–786. [Google Scholar] [CrossRef]
  66. Marcinkowski, M.J.; Brown, N. Direct Observation of Antiphase Boundaries in the Fe3Al Superlattice. J. Appl. Phys. 1962, 33, 537–552. [Google Scholar] [CrossRef]
  67. Friák, M.; Všianská, M.; Šob, M. A Quantum-Mechanical Study of Clean and Cr-Segregated Antiphase Boundaries in Fe3Al. Materials 2019, 12, 3954. [Google Scholar] [CrossRef] [PubMed]
  68. Friák, M.; Buršíková, V.; Pizúrová, N.; Pavlů, J.; Jirásková, Y.; Homola, V.; Miháliková, I.; Slávik, A.; Holec, D.; Všianská, M.; et al. Elasticity of Phases in Fe-Al-Ti Superalloys: Impact of Atomic Order and Anti-Phase Boundaries. Crystals 2019, 9, 299. [Google Scholar] [CrossRef]
  69. Friák, M.; Golian, M.; Holec, D.; Koutná, N.; Šob, M. An Ab Initio Study of Magnetism in Disordered Fe-Al Alloys with Thermal Antiphase Boundaries. Nanomaterials 2020, 10, 44. [Google Scholar] [CrossRef] [PubMed]
  70. McKamey, C.G.; Horton, J.A.; Liu, C.T. Effect of chromium on properties of Fe3Al. J. Mater. Res. 1989, 4, 1156–1163. [Google Scholar] [CrossRef]
  71. Morris, D.; Dadras, M.; Morris, M. The influence of Cr addition on the ordered microstructure and deformation and fracture-behavior of a Fe-28-%-Al intermetallic. Acta Metall. Mater. 1993, 41, 97–111. [Google Scholar] [CrossRef]
  72. Kral, F.; Schwander, P.; Kostorz, G. Superdislocations and antiphase boundary energies in deformed Fe3Al single crystals with chromium. Acta Mater. 1997, 45, 675–682. [Google Scholar] [CrossRef]
  73. Allen, S.; Cahn, J. Microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 1979, 27, 1085–1095. [Google Scholar] [CrossRef]
  74. Wang, K.; Wang, Y.; Cheng, Y. The Formation and Dynamic Evolution of Antiphase Domain Boundary in FeAl Alloy: Computational Simulation in Atomic Scale. Mater. Res. Ibero-Am. J. Mater. 2018, 21. [Google Scholar] [CrossRef]
  75. Balagurov, A.M.; Bobrikov, I.A.; Sumnikov, V.S.; Golovin, I.S. Antiphase domains or dispersed clusters? Neutron diffraction study of coherent atomic ordering in Fe3Al-type alloys. Acta Mater. 2018, 153, 45–52. [Google Scholar] [CrossRef]
  76. Murakami, Y.; Niitsu, K.; Tanigaki, T.; Kainuma, R.; Park, H.S.; Shindo, D. Magnetization amplified by structural disorder within nanometre-scale interface region. Nat. Commun. 2014, 5, 4133. [Google Scholar] [CrossRef]
  77. Oguma, R.; Matsumura, S.; Eguchi, T. Kinetics of B2-and D03 type ordering and formation of domain structures in Fe-Al alloys. J. Phys. Condens. Matter 2008, 20, 275225. [Google Scholar] [CrossRef]
  78. Nishino, Y.; Kumada, C.; Asano, S. Phase stability of Fe3Al with addition of 3d transition elements. Scr. Mater. 1997, 36, 461–466. [Google Scholar] [CrossRef]
  79. Friák, M.; Deges, J.; Stein, F.; Palm, M.; Frommeyer, G.; Neugebauer, J. Ab Initio Study of Elastic Properties in Fe3Al-based Alloys. MRS Proc. 2008, 1128, 1128-U02-04. [Google Scholar] [CrossRef]
  80. Nishino, Y.; Asano, S.; Ogawa, T. Phase stability and mechanical properties of Fe3Al with addition of transition elements. Mater. Sci. Eng. A 1997, 234–236, 271–274. [Google Scholar] [CrossRef]
  81. Friák, M.; Deges, J.; Krein, R.; Frommeyer, G.; Neugebauer, J. Combined ab initio and experimental study of structural and elastic properties of Fe3Al-based ternaries. Intermetallics 2010, 18, 1310. [Google Scholar] [CrossRef]
  82. Rosalbino, F.; Carlini, R.; Zanicchi, G.; Scavino, G. Effect of copper alloying addition on the electrochemical corrosion behaviour of Fe3Al intermetallic in sulphuric acid solution. Mater. Corros. 2016, 67, 1042–1048. [Google Scholar] [CrossRef]
  83. Park, N.; Lee, S.C.; Cha, P.R. Effects of alloying elements on the stability and mechanical properties of Fe3Al from first-principles calculations. Comput. Mater. Sci. 2018, 146, 303–309. [Google Scholar] [CrossRef]
  84. Liu, Y.; Zhang, L.; Cui, S.; Li, W. Effects of transition metal (Cr, Mn, Mo, Ni, Ti, and V) doping on the mechanical, electronic and thermal properties of Fe3Al. Vacuum 2021, 185. [Google Scholar] [CrossRef]
  85. Gomell, L.; Katnagallu, S.; Diack-Rasselio, A.; Maier, S.; Perrière, L.; Scheu, C.; Alleno, E.; Gault, B. Chemical segregation and precipitation at anti-phase boundaries in thermoelectric Heusler-Fe2VAl. Scr. Mater. 2020, 186, 370–374. [Google Scholar] [CrossRef]
  86. Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
  87. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
  88. Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, B864–B871. [Google Scholar] [CrossRef]
  89. Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. A 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
  90. Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
  91. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  92. Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
  93. Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200. [Google Scholar] [CrossRef]
  94. Všianská, M.; Friák, M.; Šob, M. An ab initio study of Fe3Al: A critical review of generalized gradient approximation. to be published.
  95. Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
  96. Momma, K.; Izumi, F. An integrated three-dimensional visualization system VESTA using wxWidgets. Comm. Crystallogr. Comput. IUCr Newslett. 2006, 7, 106. [Google Scholar] [CrossRef]
  97. Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
  98. Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
Magnetochemistry 07 00108 g001
Figure 1. Supercells used in our study. Part (a) shows a 64-atom supercell as an 1 × 1 × 4 multiple of the 16-atom elementary cell of Fe 3 Al. Parts (b,c) visualize the studied types of antiphase boundaries (APBs) with Cu atoms located either directly at the APB interfaces (b) or away from them (c), respectively. The subfigures (b,c) include red vectors defining a 〈100〉 shift that is characteristic for the studied APBs and applied to the upper halves of the 64-atom supercells.
Figure 1. Supercells used in our study. Part (a) shows a 64-atom supercell as an 1 × 1 × 4 multiple of the 16-atom elementary cell of Fe 3 Al. Parts (b,c) visualize the studied types of antiphase boundaries (APBs) with Cu atoms located either directly at the APB interfaces (b) or away from them (c), respectively. The subfigures (b,c) include red vectors defining a 〈100〉 shift that is characteristic for the studied APBs and applied to the upper halves of the 64-atom supercells.
Magnetochemistry 07 00108 g001
Magnetochemistry 07 00108 g002
Figure 2. Calculated local magnetic moments of iron atoms in Fe 3 Al with Cu substituents without antiphase boundaries (a), with Cu atoms located at the interface of the studied antiphase boundaries (b), and with the Cu substituents away from the APBs (c). The magnetic moments are compared with values for the Cu-free and defect-free bulk Fe 3 Al (horizontal dashed lines).
Figure 2. Calculated local magnetic moments of iron atoms in Fe 3 Al with Cu substituents without antiphase boundaries (a), with Cu atoms located at the interface of the studied antiphase boundaries (b), and with the Cu substituents away from the APBs (c). The magnetic moments are compared with values for the Cu-free and defect-free bulk Fe 3 Al (horizontal dashed lines).
Magnetochemistry 07 00108 g002
Magnetochemistry 07 00108 g003
Figure 3. Computed phonon frequencies along selected directions in the reciprocal space and the density of phonon states in the case of Cu-containing crystals of Fe 3 Al (without APBs).
Figure 3. Computed phonon frequencies along selected directions in the reciprocal space and the density of phonon states in the case of Cu-containing crystals of Fe 3 Al (without APBs).
Magnetochemistry 07 00108 g003
Magnetochemistry 07 00108 g004
Figure 4. Calculated Helmholtz free energy F (a) and the harmonic phonon energy E (b) of defect-free Fe 3 Al containing the Cu atoms together with derived vibrational entropy S (c) and constant-volume heat capacity C v (d), respectively. The elementary entity for defining one mol is the 64-atom supercell, i.e., we talk about one mole of 64-atom supercells.
Figure 4. Calculated Helmholtz free energy F (a) and the harmonic phonon energy E (b) of defect-free Fe 3 Al containing the Cu atoms together with derived vibrational entropy S (c) and constant-volume heat capacity C v (d), respectively. The elementary entity for defining one mol is the 64-atom supercell, i.e., we talk about one mole of 64-atom supercells.
Magnetochemistry 07 00108 g004
Magnetochemistry 07 00108 g005
Figure 5. Computed phonon frequencies along selected directions in the reciprocal space and the density of phonon states in Fe 3 Al containing antiphase boundaries (APBs) with the Cu atoms located either within the APB interface plane (a) or as far from the APB interface as possible within our computational supercell (b).
Figure 5. Computed phonon frequencies along selected directions in the reciprocal space and the density of phonon states in Fe 3 Al containing antiphase boundaries (APBs) with the Cu atoms located either within the APB interface plane (a) or as far from the APB interface as possible within our computational supercell (b).
Magnetochemistry 07 00108 g005
Magnetochemistry 07 00108 g006
Figure 6. Calculated segregation-related energy difference (per 64-atom supercell) that includes both the static lattice energy U static and the phonon free energy F. The difference is between the states with (i) two Cu atoms at the APB interfaces and (ii) far away from them as a function of temperature. It is compared with the segregation-related energy difference of static lattices Δ U static (see horizontal dashed line). As one mol, we mean one mol of 64-atom supercells.
Figure 6. Calculated segregation-related energy difference (per 64-atom supercell) that includes both the static lattice energy U static and the phonon free energy F. The difference is between the states with (i) two Cu atoms at the APB interfaces and (ii) far away from them as a function of temperature. It is compared with the segregation-related energy difference of static lattices Δ U static (see horizontal dashed line). As one mol, we mean one mol of 64-atom supercells.
Magnetochemistry 07 00108 g006
Magnetochemistry 07 00108 g007
Figure 7. Computed entropy difference Δ S (a) and phonon energy difference Δ E (b) (both per 64-atom supercell) between the states with Cu at the APB interfaces and far away from them.
Figure 7. Computed entropy difference Δ S (a) and phonon energy difference Δ E (b) (both per 64-atom supercell) between the states with Cu at the APB interfaces and far away from them.
Magnetochemistry 07 00108 g007
Magnetochemistry 07 00108 g008
Figure 8. Calculated APB-related energy difference Δ ( U static + F ) (per 64-atom supercell) between (i) the state with two Cu atoms at the APB interfaces and (ii) the state without APBs as a function of temperature in comparison with the static lattice difference (see horizontal dashed line). The elementary entity for defining one mole is the 64-atom supercell.
Figure 8. Calculated APB-related energy difference Δ ( U static + F ) (per 64-atom supercell) between (i) the state with two Cu atoms at the APB interfaces and (ii) the state without APBs as a function of temperature in comparison with the static lattice difference (see horizontal dashed line). The elementary entity for defining one mole is the 64-atom supercell.
Magnetochemistry 07 00108 g008
Magnetochemistry 07 00108 g009
Figure 9. Computed entropy difference Δ S (a) and phonon energy difference Δ E (b) (both per 64-atom supercell) between (i) the states of Fe 3 Al with Cu but without APBs and (ii) with the Cu atoms at the APB interfaces.
Figure 9. Computed entropy difference Δ S (a) and phonon energy difference Δ E (b) (both per 64-atom supercell) between (i) the states of Fe 3 Al with Cu but without APBs and (ii) with the Cu atoms at the APB interfaces.
Magnetochemistry 07 00108 g009
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Friák, M.; Černý, M.; Šob, M. The Impact of Vibrational Entropy on the Segregation of Cu to Antiphase Boundaries in Fe3Al. Magnetochemistry 2021, 7, 108. https://doi.org/10.3390/magnetochemistry7080108

AMA Style

Friák M, Černý M, Šob M. The Impact of Vibrational Entropy on the Segregation of Cu to Antiphase Boundaries in Fe3Al. Magnetochemistry. 2021; 7(8):108. https://doi.org/10.3390/magnetochemistry7080108

Chicago/Turabian Style

Friák, Martin, Miroslav Černý, and Mojmír Šob. 2021. "The Impact of Vibrational Entropy on the Segregation of Cu to Antiphase Boundaries in Fe3Al" Magnetochemistry 7, no. 8: 108. https://doi.org/10.3390/magnetochemistry7080108

APA Style

Friák, M., Černý, M., & Šob, M. (2021). The Impact of Vibrational Entropy on the Segregation of Cu to Antiphase Boundaries in Fe3Al. Magnetochemistry, 7(8), 108. https://doi.org/10.3390/magnetochemistry7080108

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop