Methods and Models of Theoretical Calculation for Single-Molecule Magnets

Abstract

Theoretical calculation plays an important role in the emerging field of single-molecule magnets (SMMs). It can not only explain experimental phenomena but also provide synthetic guidance. This review focuses on discussing the computational methods that have been used in this field in recent years. The most common and effective method is the complete active space self-consistent field (CASSCF) approach, which predicts mononuclear SMM property very well. For bi- and multi-nuclear SMMs, magnetic exchange needs to be considered, and the exchange coupling constants can be obtained by Monte Carlo (MC) simulation, ab initio calculation via the POLY_ANISO program and density functional theory combined with a broken-symmetry (DFT-BS) approach. Further application for these calculation methods to design high performance SMMs is also discussed.

1. Introduction

With the advent of the big data era, the capacity of information storage is in high demand. Distinctive to the traditional magnetic material, single-molecule magnets (SMMs) are synthesized from coordination chemistry and have uniformed tiny size, high transparency and chemical modifiable features. Thus, SMMs possess potential applications in interdisciplinary fields, such as spintronics [1,2], quantum computers [3,4] and high-density information storage [5,6]. The first case of SMM {Mn₁₂} was discovered in the early 1990s with typical slow relaxation of magnetization [7,8]. After almost one decade, the first lanthanide-based SMM [Pc₂Tb][N(C₄H₉)₄] was reported [9], which exhibits slower magnetization relaxation owing to the fact that some rare-earth ions can provide stronger magnetic anisotropy and be more sensitive to the crystal field [10]. After years of efforts to improve the effective energy barrier (U_eff) and magnetic blocking temperature (T_B), as two figure-of-merits, multitudinous SMMs have been synthesized, which can be classified as mono-, bi- and multi-nuclear molecules due to the diversity of synthesis methods [11,12,13,14,15,16,17]. Among them, two families of dysprosium(III) SMMs, namely the pentagonal–bipyramidal (PB) family with local D_5h symmetry and the cyclopentadienyl (Cp) family with a sandwich structure, are broadly paid attention to, especially for the representative complexes of [Dy(py)₅(O^tBu)₂][BPh₄] (U_eff = 1815 K, T_B = 14 K) and [(η⁵-Cp*)Dy(η⁵-Cp^iPr5)][B(C₆F₅)₄] (U_eff = 2220 K, T_B = 77 K) [18,19]. Evidently, the material is far from large-scale practical application, as its blocking temperature is still far below the room temperature. How to build higher performance SMMs is undoubtedly an urgent problem for synthetic chemists and theoretical researchers.

As one of the most active fields, the development of computational chemistry can not only analyze the experimental data but also predict ideal model complexes to inspire synthetic chemists [20]. At present, the main theoretical calculation methods used for molecular magnets are density functional theory (DFT) and ab initio calculation methods. For the latter, the complete active space self-consistent field (CASSCF) method is widely adopted in the prediction of static magnetic properties for SMMs. Moreover, the development of related software packages also promotes the prediction of SMM properties and the understanding of magnetic relaxation processes. Neese, Charbotaru and Ungur et al. developed two software packages, ORCA and Molcas, respectively, which have been successfully and widely used in the study of SMMs [21,22]. Their output g values, crystal field parameters, transition magnetic moment matrix and susceptibility and magnetization curves are significant information to understand the magnetic relaxation process of SMMs. Especially the POLY_ANISO [23] program, based on the Lines model, which can realize the fitting of the magnetic interactions between the metal centers of bi- or multi-nuclear systems. It is worth mentioning that Monte Carlo (MC) simulation is also a good choice for more complicated many-body systems with low symmetry, and their dc magnetic measurement data can be reproduced by random sampling [24,25,26,27,28]. Additionally, the Gaussian [29] software package, as one of the most popular electronic structure calculation programs, provides a large amount of information about structural chemistry. In the field of SMMs, it can accurately simulate the vibrational and electronic spectra of compounds; output the charge distribution information, electrostatic potentials and bond orders through population analysis; obtain the specific strength of weak interaction; and generate wave functions for analysis.

Herein, we summarize the common calculation methods and models of mono-, bi- and poly-nuclear systems of SMMs, respectively, and explain the guiding role of theoretical calculation in synthetic chemistry by combining it with the practical work of our research group.

2. Mononuclear Single-Molecule Magnets

For transition metal SMMs, according to the Heisenberg exchange theory, the spin Hamiltonian of SMM without an external magnetic field and other impacts can be described as Equation (1). However, for mononuclear SMMs, the third item about exchange couplings can be neglected. The items are equatorial and axial magnetic anisotropy energy, respectively, where D and E, namely zero-field splitting constant and equatorial anisotropy constant, are what we focus on. $\widehat{S}$, ${\widehat{S}}_x$, ${\widehat{S}}_y$ and ${\widehat{S}}_z$ express molecular total spin and the components of spin in x, y and z directions, respectively. The energy barrier is a function of D and the ground-state total spin S_T, specifically: $U_{eff}=\left|D{S}_{\mathrm{T}}^2\right|$ (S_T is an integer) or $U_{eff}=\left|D\left(S_{\mathrm{T}}^2-\frac{1}{4}\right)\right|$ (S_T is a half-integer). Some studies have pointed out that D and S_T cannot increase simultaneously [30], making the improvement of the energy barrier a challenge. For rare-earth SMMs, the situation is much more complicated, and their spin Hamiltonian cannot be directly expressed as an aforementioned equation. In total, four sections need to be considered: spin–orbit (SO) coupling, crystal field effect, exchange coupling and Zeeman splitting (Equation (2)). Similarly, here, the last item should be ignored. Although the magnitude of the SO effect is larger than the crystal field effect in the 4f system, based on chemical synthesis modification, the contribution of the crystal field to the anisotropic energy barrier is also undeniably significant. The operator on the crystal field can be written as Equation (3). In the formula, ${\widehat{O}}_k^q$ is the Wybourne operator (the real combinations of the spherical harmonics), and ${\widehat{B}}_k^q$ is the crystal field parameter of rank k and projection q, reflecting the symmetry of the crystal field: when q is 0, it represents the axial crystal field parameter; when q is not 0, it stands for the equatorial one. When the latter value is large, the overall axial anisotropy of the entire molecule is weakened, leading to quantum tunnelling behavior for Kramers ions with half-integer spin, which is not conducive to enhancing the high energy barrier of SMMs. Therefore, some studies have pointed out that [31,32,33] regulating ligands to synthesize complexes with high geometric symmetry, such as C_∞v, D_∞h, D_4d, D_5h and D_6d, can realize the equatorial crystal field parameters close to zero, helping to suppress quantum tunnelling and improve the blocking temperature and energy barrier. Nevertheless, compared with 3d systems, the existence of other thermal relaxation processes and quantum tunnelling effects makes the above energy barrier relationship unsuitable for rare-earth SMMs [34]. There are four types of relaxation processes existing: the direct relaxation process, Orbach process, Raman process and quantum tunnelling process (QTM). The direct relaxation process should be negligible without an external magnetic field. Hence, the relationship between relaxation time (τ) and temperature (T) can be described using Equation (4), where ${\tau }_0^{-1}$ is a pre-exponential factor of the Arrhenius term, C is the coefficient in the Raman process term and ${\tau }_{QTM}^{-1}$ expresses the QTM process. The Orbach process is a two-phonon process through a successive transition between microstates m_J split from ground state J. The Raman process is a two-phonon process leading to a relatively low temperature zone. 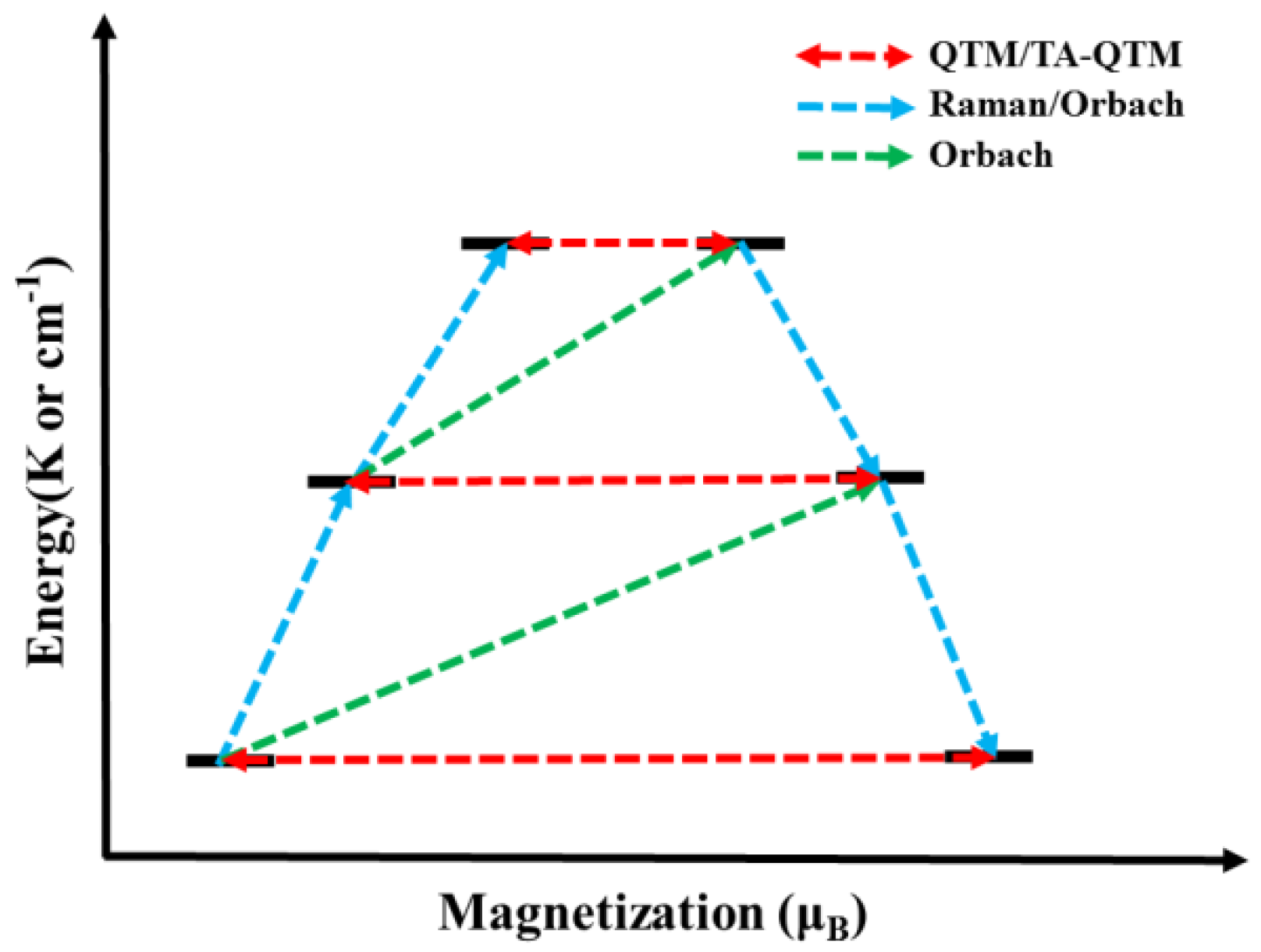QTM normally takes place in the lowest temperature zone, independent of temperature and existing between ground doublets m_J, as well as thermally assisted quantum tunnelling of magnetization (TA-QTM). All of the possible magnetic relaxation paths in rare-earth SMMs are shown in Figure 1 [35]. Among them, the existence of Raman and QTM processes, especially the latter, significantly descends the anisotropic energy barrier, so it needs to be suppressed. Furthermore, while constructing mononuclear SMMs with high performance, researchers have also been trying to explore and reveal the specific mechanism of the slow relaxation process for further guiding chemical design and synthesis.

$$\widehat{H}=D({\widehat{S}}_z^2-\frac{1}{3}{\widehat{S}}^2)+E({\widehat{S}}_x^2-{\widehat{S}}_y^2)+{{\displaystyle \sum }}_{i>j}-J_{ij}{\widehat{S}}_i{\widehat{S}}_j$$

(1)

$$\widehat{H}={\widehat{H}}_{SO}+{\widehat{H}}_{CF}+{\widehat{H}}_{ZEE}+{\widehat{H}}_{EX}$$

(2)

$${\widehat{H}}_{CF}={\displaystyle \sum }_{-k}^k{B}_k^q{\widehat{O}}_k^q$$

(3)

$${\tau }^{-1}={\tau }_0^{-1}\exp (-U_{eff}/T)C{T}^n+{\tau }_{QTM}^{-1}$$

(4)

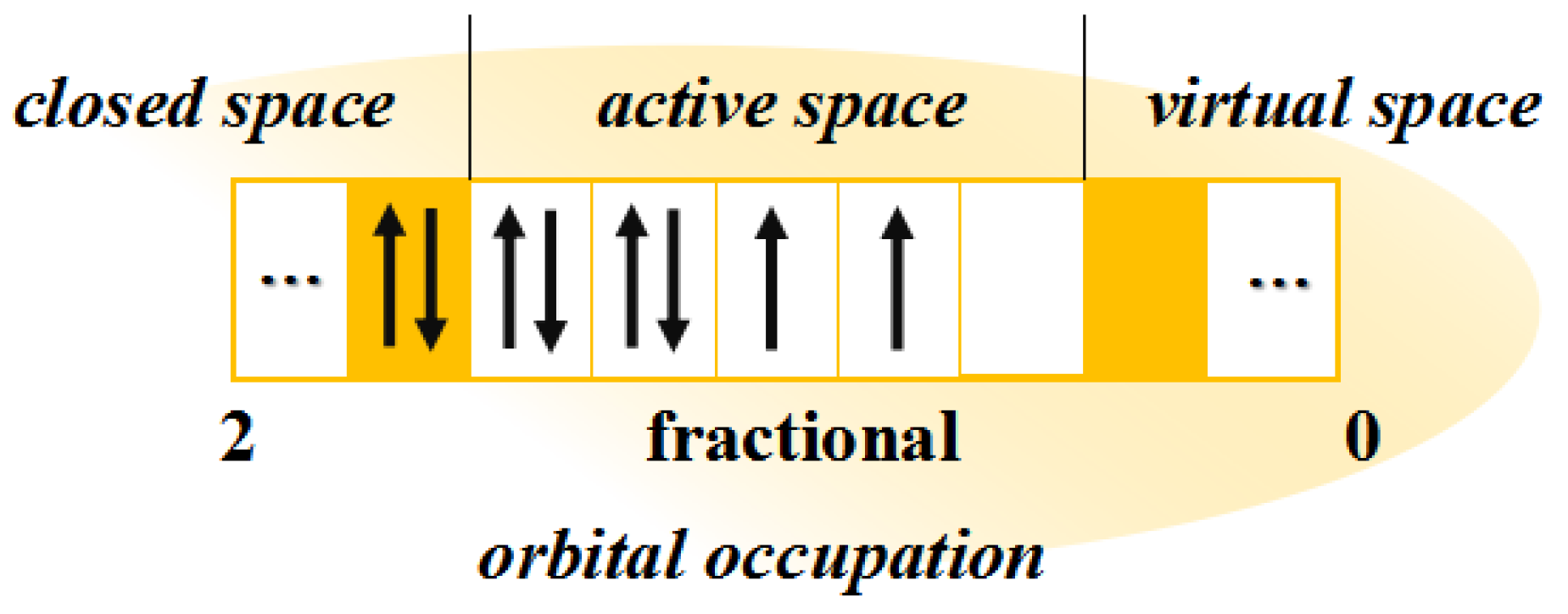
CASSCF is one of the central methods in dealing with metal complexes, successful at possessing the static correlation of multibody wave functions through fine zeroth-order wavefunction. Three varieties of orbitals are segregated from the whole orbitals in molecule systems, such as closed space, active space and virtual space (Figure 2). In this method, dynamic correlation is not originally fully taken into account, while the complete active space perturbation theory (CASPT2) [36,37,38], N-electron valence state perturbation theory (NEVPT2) [39,40] and multi-reference configuration interaction method (MRCI) [41,42] can realize the approximation of the full configuration interaction (CI) to recover dynamic correlation effect and acquire relatively pinpoint parameters. It is noted that the pivot of this approach in actual calculation processes is to determine appropriate and reasonable active space, which is relevant to the properties we study, namely active orbitals and electrons. For example, when performing calculations toward the Dy(III) system, we can regard its nine 4f-electrons and seven 4f-orbitals as active space, or CAS(9,7). That is to say, active space is case specific and needs particular analysis. When studying the magnetism of 3d transition metallic or lanthanide complexes, the smallest active space can be designated as the outermost five 3d or seven 4f orbitals and corresponding filled electrons, which is sufficient in most cases to guarantee metallic properties of the chosen orbitals elementarily. Under certain conditions, active space should be broadened when coordination bond orbitals with metallic properties emerge. Normally, we employ the ORCA software package for transition ion SMMs and Molcas for lanthanide systems.

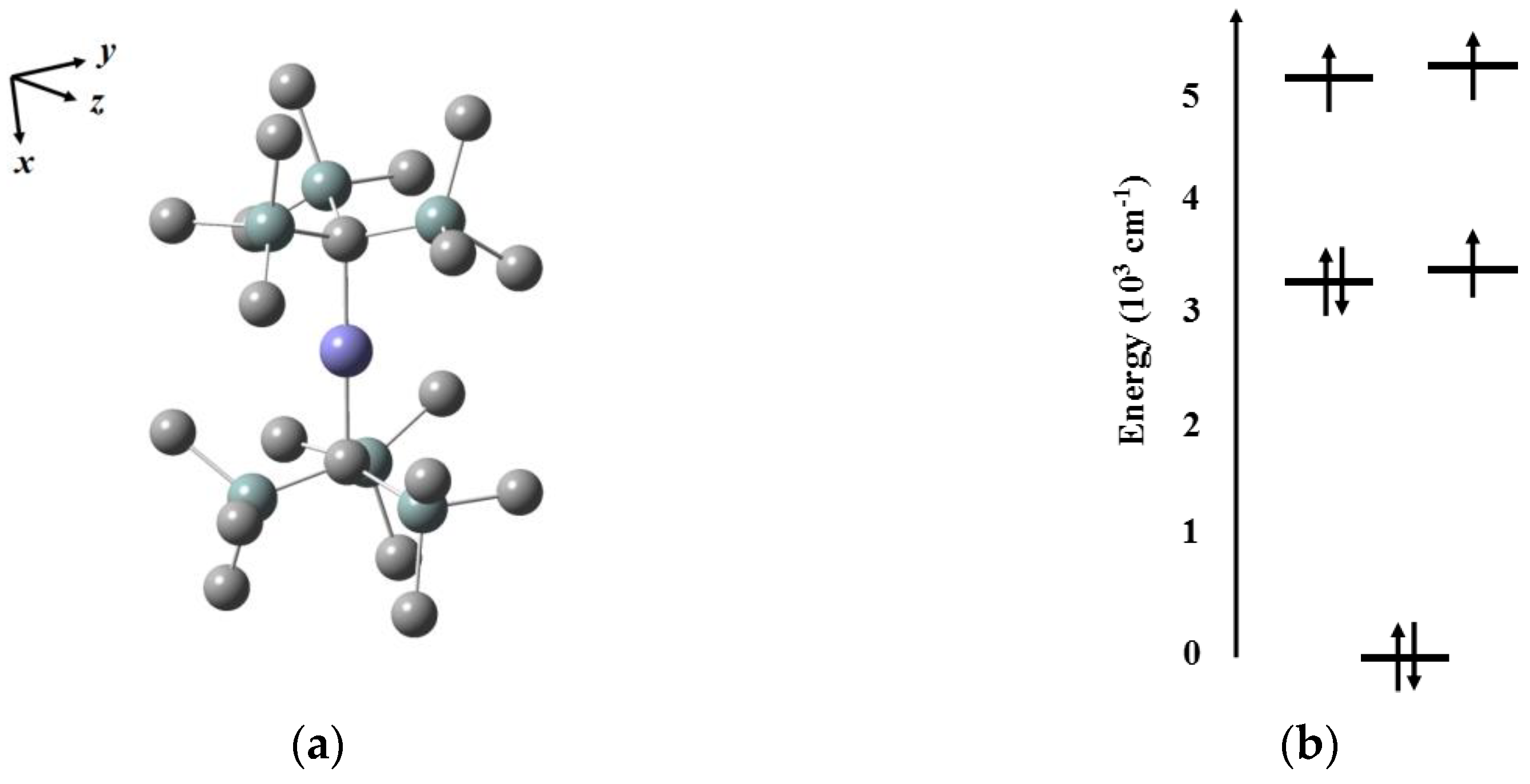
In 2013, Long’s group prepared one linear two-coordinate Fe(I) compound [Fe(C(SiMe₃)₃)₂]⁻ with a 3d⁷ electron configuration and 3/2 as the ground-state spin, exhibiting high performance that U_eff arrives at 226 cm⁻¹, and the hysteresis loop can be observed below 4.5 K [43]. In this compound, the existence of D_∞h local symmetry and a weak ligand field environment induces specific crystal field splitting: $d_{xz}, d_{yz}>d_{xy}, d_{x^2-y^2}>d_{z^2}$ from CASSCF and NEVPT2 calculations considering state averaging over the 10 quartets and 40 doublet states (Figure 3). The calculated energy gap between the ground doublet and the first excited doublet is 210 cm⁻¹, which is close to the experimental fitting value, suggesting Orbach relaxation passes through the latter doublet. In light of the results, they point out that a low coordination number and a low oxidation state matching with a weak ligand field create a large axial magnetic anisotropy and set out the vision for the future that the energy of $d_{z^2}$ orbital needs a lower and minimum quenching of orbital angular momentum, which can be realized by modifying ligands.

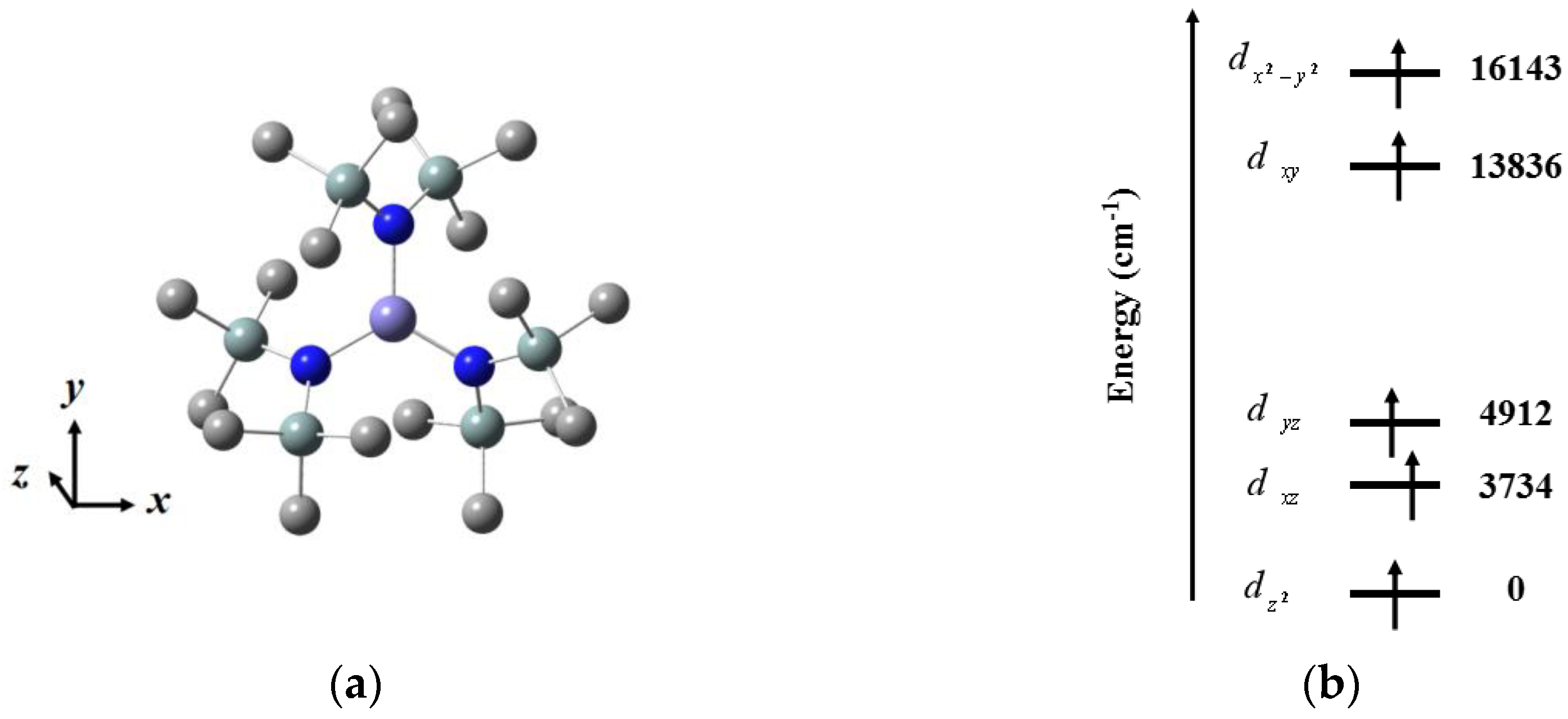
Normally, Fe(III) ion with half-filled 3d orbitals (S = 5/2) is not thought to be a suitable choice for composing SMMs with high U_eff as a result of the less orbital degeneracy of the ground state. Moreover, the Fe(III) complexes without intermediate spin S = 3/2 show positive D values, while the existence of intervening spin S = 3/2 makes it possible to generate a large negative D value. Our group carried out a detailed study on Fe[N(SiMe₃)₂]₃ with perfect local D_3h symmetry to explore its magnetic anisotropy (Figure 4) [44]. Three classes of methods were performed to acquire D: least-square fitting toward data from high-frequency EPR (HF-EPR) and ab initio calculation and data fitting based on spin Hamiltonian. In addition to the experimental value obtained by the first way, the theoretical values were generated from the other two means. As expected, the D values from distinctive aspects are basically in accordance with each other (−1.15, −1.48 and −1.62, respectively), and the Orbach energy barriers are 6.91 cm⁻¹ by magnetic dynamic analysis, as well as 6.90 cm⁻¹ by calculation. CASSCF with NEVPT2 calculation was performed to understand the origin of easy-axis magnetic anisotropy and acquire the information on the energy level of the 3d orbitals. In this case, the active space was determined as CAS(5,5), and 1 sextet state, 24 quartet states and 75 doublet states were chosen for the state average. From the d-orbital energy diagram, a weak z-axis crystal field reduces the energy of $d_{z^2}$ orbital, while a strong crystal field in the xy plane improves the energy of $d_{xy}$ and $d_{x^2-y^2}$ orbitals, making the ground state electron configuration ($d_{z^2}$)¹($d_{xz}$)¹($d_{yz}$)¹($d_{x^2-y^2}$)¹($d_{xy}$)¹. This result is suggestive of the fact that the energy difference between the ⁶A₁ ground state and the quartet excited states produced by ⁴G furnishes axial magnetic anisotropy.

Dysprosium(III) ion plays an increasingly important position in SMM research with its total orbital angular momentum J = 15/2, which can create large magnetic anisotropy. In the last decade, researchers have been exploring high performance Dy(III)-based SMMs via effectively suppressing the Raman and QTM, which are detrimental to magnetic relaxation, such as designing ligands with expected crystal fields, maintaining local high symmetry of metal centers and introducing transition metal ions or free radicals to utilize magnetic exchange [45,46].

Long et al. summarized a qualitative method that can produce high magnetic anisotropy for various 4f element ions (Figure 5) and proposed that since most rare-earth metal trivalent ions have oblate electron density, such as Dy(III) and Tb(III), to ensure axial anisotropy, axial enrichment of negative charge is essential, so axial ligand environment coordination is needed; for Yb(III) and Er(III), their electron density is elongated and the anisotropic barrier can be produced by the equatorial coordination environment [47]. Therefore, the reason why the Cp ligand can significantly improve SMM properties is that it has multi-dentate characteristics and can provide three pairs of lone pair electrons to the central Dy(III) ion. The imido ligand has similar electron donors, and more electrons concentrate on coordination atom N. Our group exploited 1,3-bis(2,6-diisopropylphenyl) imidazolin-2-imine (Im^DippNH) to synthesize one case of mononuclear SMM (1), whose experimental energy barrier is nearly 803 K (Figure 6) [48]. In sharp contrast, the energy barrier of similar analogous alkoxide ligand SMM (2) is merely 53 K. Ab initio calculations at the SA CASSCF/RASSI level were performed to understand the magnetic properties from the microscopic electronic structure using Molcas software. In the RASSCF module, 21 sextets, 224 quartets and 490 doublets optimized are considered, and, in the RASSI module, 21 sextets, 128 quartets and 130 doublets are constructed and diagonalized in spin–orbit (SO) coupling Hamiltonian. Then, these SO states are transmitted toward SINGLE_ANISO, which is a magnetism of complexes program and calculates zero-field splitting and the pseudospin Hamiltonians for Zeeman interaction, as well as temperature- and field-dependent magnetic properties. Ultimately, the parameters and information we are concerned with are printed, comprising crystal field parameters, g values, susceptibility curves, magnetization curves and transition magnetic moment matrix. The calculated U_eff of 1 and 2 are 759 K and 585 K; however, the probability of QTM between the first excited doublets in 2 is 0.5 ${\mu }_B^2$, which is non-ignorable, leading to the existence of a smaller experimental fitting value. DFT calculations reveal that the Mayer bond order of Dy-X (X = N or O) in 1 and 2 are 2.23 (σ + π) and 1.03 (σ), indicating that the formation of multiple bonds enhances the rigidity of axial ligands, weakens the intramolecular vibration, suppresses the Raman process and improves the magnetic anisotropy. Moreover, the theoretical prediction shows that the U_eff of a linear molecule with Cl ions and THF eliminated arrives at almost 4000 K, along with attenuation of the QTM process. Therefore, one of the strategies to improve the performance of SMM is to introduce multiple bonds in the axial coordination sites.

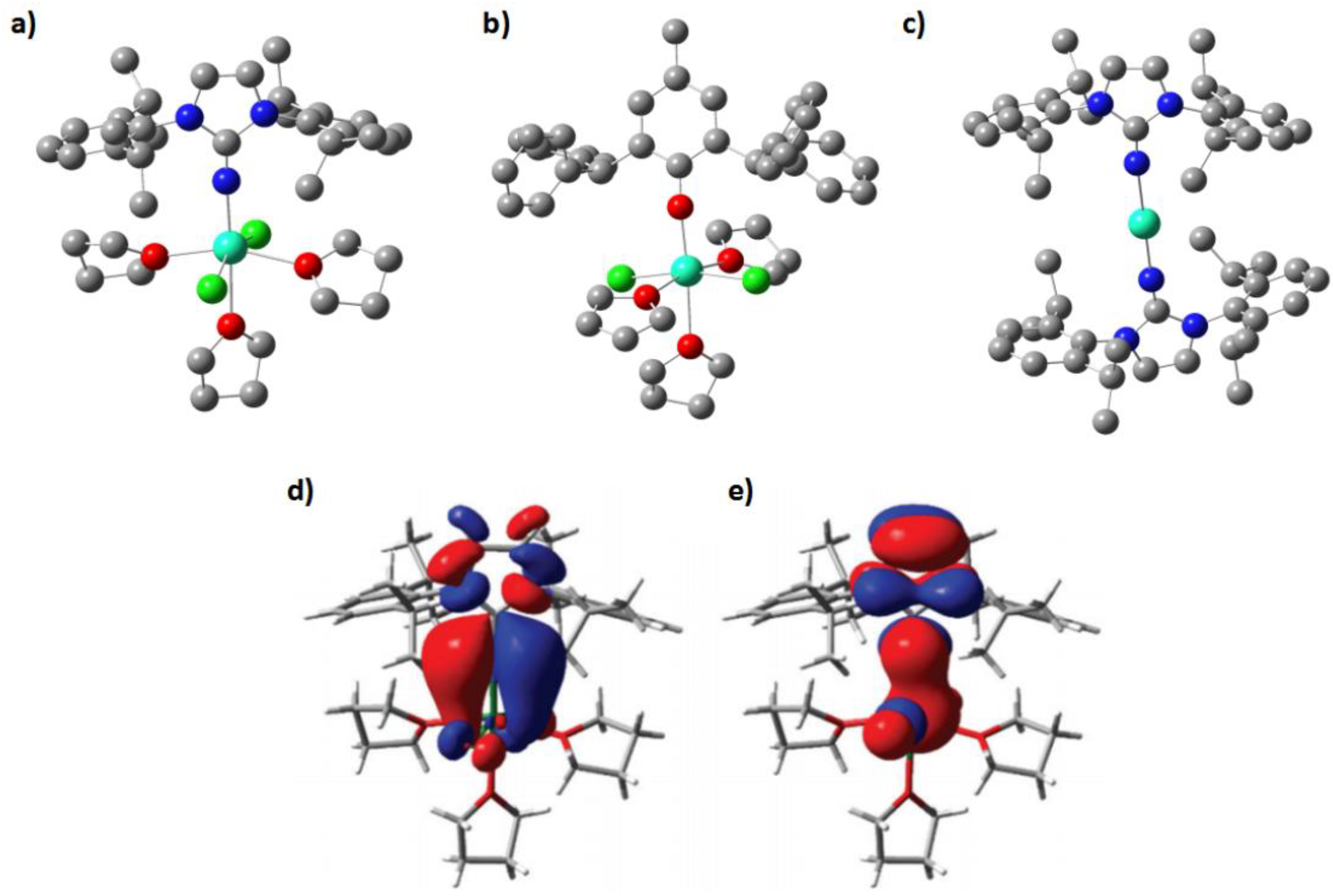
Later, our group reported one chiral isomeric SMM case [Dy(L)₂(py)₅][BPh₄] (HL=1-phenylethanol) (3 and 4, Figure 7), which has an energy barrier of 1130 (20) cm⁻¹ [49], and it also exhibits hysteresis at a blocking temperature of 22 K, which is much higher than [Dy(O^tBu)₂(py)₅]⁺. The crystal structure and intermolecular packing diagram were investigated, and the appearance of C-H…π and π…π interactions would increase the rigidity of the whole molecule. A DFT calculation confirms that there are strong intramolecular C-H…π interactions (~20.4 KJ/mol), intermolecular π…π (~5.7 KJ/mol) and C-H…π (~19.1 KJ/mol) interactions. An ab initio spin dynamic study demonstrates that the existence of such forces is beneficial to improve molecular rigidity, leading to the increase of blocking temperature.

Except for chemical regulatory means, Rajaraman et al. proposed a physical method to enhance magnetic anisotropy in Ln(III) SMMs using an external electric field (EEF) [50]. The introduction of EEF can largely change the geometry of molecules, thus affecting charge distribution, and ultimately transforms the electronic structure and its related properties, especially chemical reaction activity [51]. This research exerted oriented external electric field (OEEF) toward three types of classical complexes ([Dy(Py)₅(O^tBu)₂]⁺, [Er{N(SiMe₃)₂}₃Cl]⁻ and [Dy(CpMe₃)₂Cl] and acquired relevant principles through combining DFT structural optimization with the field keyword available using Gaussian 09, and, then, the electronic structure and magnetic properties were studied by means of the CASSCF method in Molcas software. For Ln(III) with oblate electron density, such as Dy(III), exerting EEF along the equatorial direction is beneficial to heighten the energy barrier, while for Ln(III) with elongated electron density, such as Er(III), the adaptable direction must be near the axial Ln-L bond. Despite the physical method being represented for the first time, the strength of the electric field, which effectively enhances the energy barrier of SMMs, is about ca. 10⁹ V/m, which is almost impossible to reproduce in an experimental method.

3. Bi- and Multi-Nuclear Single-Molecule Magnets

With regard to binuclear SMMs with both magnetic ion centers, even multinuclear compounds, when describing the spin Hamiltonian of these systems, the magnetic couplings between metal ions require consideration (Equation (5)), where ${\widehat{S}}_i$ and ${\widehat{S}}_j$ are spin operators of two central ions, and J_ij is the exchange coupling constant between i and j. For compounds with relatively weak SO coupling, particularly those containing transition metal ions, density functional theory combined with the broken symmetry (DFT-BS) approach proposed by Noodleman is a universal method to calculate the J value [52,53]. In the process of derivation, to produce a mixed spin state wave function, the single configuration model, which consists of nonorthogonal magnetic orbitals, was combined with unrestricted Hartree–Fock (HF) theory or density functional theory (DFT), putting forward that it is in the direct ratio between the J value and the energy difference within the high spin state, E(S_max), and the mixed spin state, E_B, indicating that this exchange constant can be calculated by Equation (6) when both energies are acquired, where S and A₁(S) mean spin quantum number and square of Clebsh–Gordan coefficient. Ultimately, due to ${\displaystyle \sum }_{S=0}^{S_{max}}{A}_1\left(S\right)·S\left(S+1\right)$ being equal to S_max, J can be obtained from Equation (7). One of the superiorities of this means is handling larger compounds comprising hundreds of atoms, while for circumstances with stronger SO coupling, for instance, when there are existing lanthanide ions, it cannot meet the requirements toward the accuracy of the parameters.

For rare-earth SMMs, even weak magnetic interactions can tremendously affect the slow relaxation process at a low temperature, which has two aspects: first, its presence will cause the coupling of adjacent spin ions, inducing the molecules’ direct relaxation or accelerating the quantum tunnelling process; furthermore, the generation of the internal magnetic field will inhibit quantum tunnelling to a certain extent. The 4f orbitals, as Ln(III) ions’ internal orbitals, are rarely involved in magnetic interaction; therefore, most binuclear SMMs emerge with similar effective energy barriers when compared with mononuclear complexes. Taking one binuclear SMM composed of two lanthanide metal ions as an example, the total exchange interaction (J_total) within both magnetic centers primarily consists of magnetic exchange (J_exch) and dipole–dipole exchange (J_dip), namely J_total = J_exch + J_dip. This relation is in a position to be expressed by the Hamiltonian as Equation (8) when the ground state of magnetic centers can be regarded as the Ising limit state [54]. Where J_dip, as a long-range interaction, frequently plays a dominant role in Ln(III) dimer complexes and can be calculated directly via Equation (9) under Ising approximation. Where g₁, g₂ and g_1z, g_2z are g tensors of two magnetic centers and their components in the z-direction; r is the distance within both lanthanide ions; θ is the angle between the anisotropic axes of two magnetic sites; and μ_B² is a constant, almost 0.43297 cm⁻¹/T. The formula illustrates that the dipole–dipole interaction depends on the distance between the two dipoles and the angle between the magnetic moments of the magnetic centers. The positive or negative sign of J_total intimates that the interaction between two magnetic sites is ferro- or antiferro-magnetic, respectively.

$${\widehat{H}}_{ex}={\displaystyle \sum }_{i>j}-J_{ij}{\widehat{S}}_i{\widehat{S}}_j$$

(5)

$$E\left(S_{\max }\right)-E_{\mathrm{B}}=(-S_{\max }(S_{\max }+1)+{{\displaystyle \sum }}_{\mathrm{S}=0}^{{\mathrm{S}}_{\max }}{A}_1\left(S\right)·S\left(S+1\right))J$$

(6)

$$J=\frac{E\left(S_{\max }\right)-E_{\mathrm{B}}}{-S_{\max }^2}$$

(7)

$$\widehat{H}={\widehat{H}}_{exch}+{\widehat{H}}_{dip}=-(J_{exch}{\tilde{\widehat{S}}}_{1z}{\tilde{\widehat{S}}}_{2z}+J_{dip}{\tilde{\widehat{S}}}_{1z}{\tilde{\widehat{S}}}_{2z})$$

(8)

$$J_{dip}=\frac{{\mu }_B^2}{{\left|r\right|}^3}[\overrightarrow{g_1}·\overrightarrow{g_2}-3(\overrightarrow{g_1}·\overrightarrow{r})(\overrightarrow{r}·\overrightarrow{g_2})]=\frac{{\mu }_B^2}{{\left|r\right|}^3}\overrightarrow{g_{1z}}·\overrightarrow{g_{2z}}(1-3co{s}^2\theta )$$

(9)

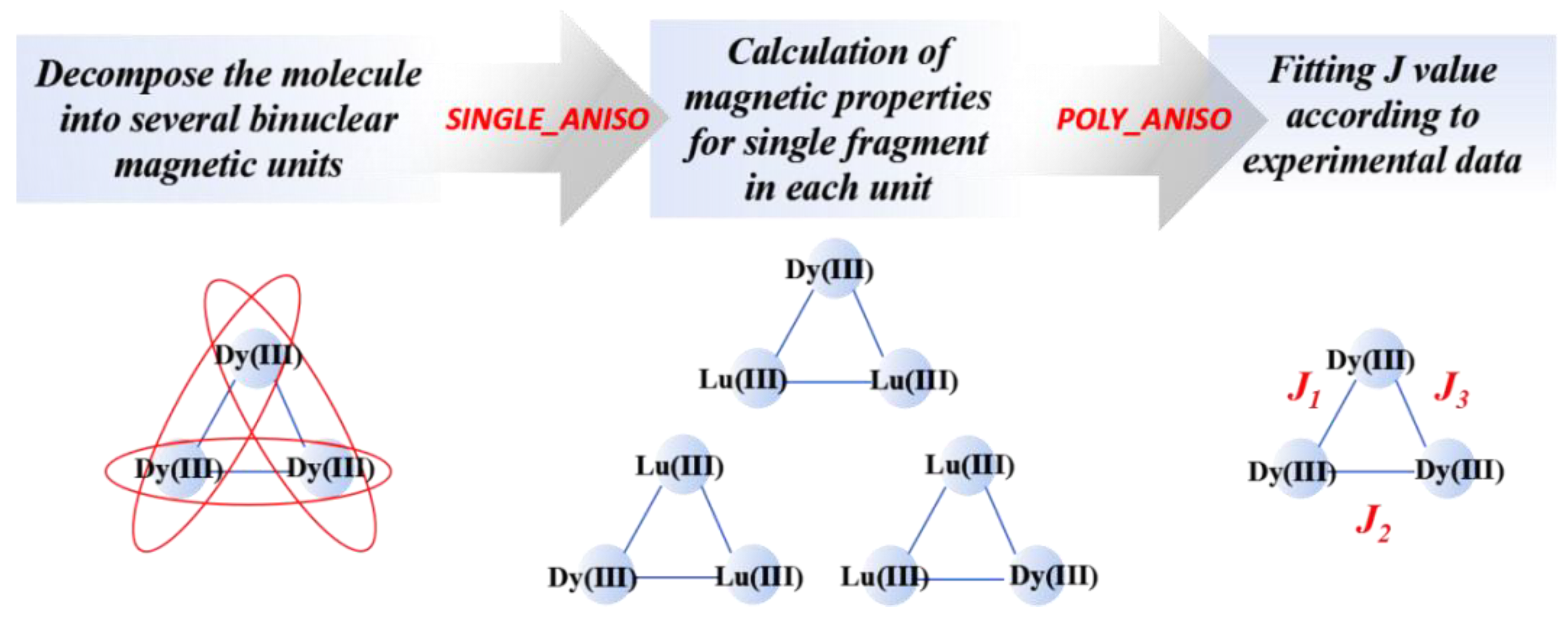
Charbotaru and Ungur developed one program, POLY_ANISO, to fit magnetic coupling interaction constants within rare-earth ions or transition metallic and rare-earth ions via M-H and χ_T-T data. This fitting method based on the Lines model has been successful in numerous molecules [55,56,57,58]. Meanwhile, this model is particularly suitable for the following circumstances: interactions within isotropic spins, between isotropic spin and Ising spin and both Ising spins. In the Molcas software package, the specific calculation processes are as follows: primarily, the magnetic property and electronic structure information of a single magnetic ion need computing through the SINGLE_ANISO module, and, then, a file named “ANISOINPUT” should be invoked to the POLY_ANISO module to output exchange the coupling constants cooperated with molecular susceptibility and magnetization data. To simplify the calculation, when dealing with multinuclear systems, the whole molecule is capable of being segregated into several independent binuclear sections, but it will bring about large errors. Consequently, one more reliable approach is to retain the magnetic centers that we calculate while replacing the other ones to diamagnetic ions of the same charge, for example, replacing Co(II) with Zn(II), or Dy(III) with La(III), Lu(III), Sc(III), etc. Figure 8 describes a simple flow chart of the whole calculation process.

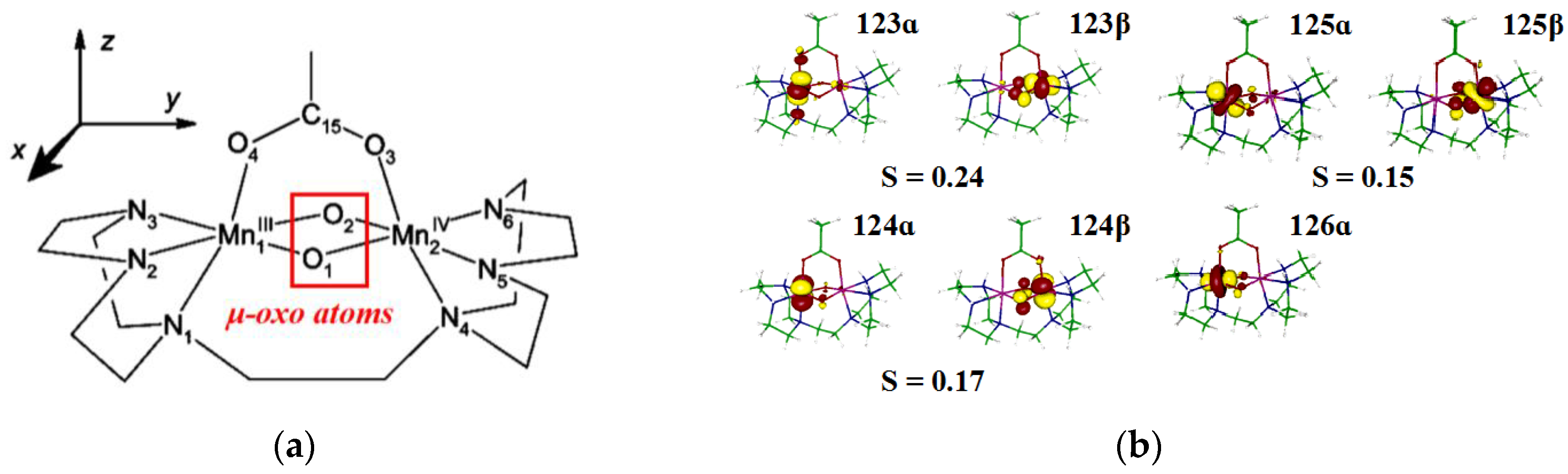
Neese et al. investigated the EPR parameters of one mixed-valence manganese compound [Mn^IIIMn^IV(μ-O)₂(μ-OAc)DTNE]²⁺ for the first time (Figure 9) [59]. After geometry optimization toward the structures of high spin (hs) and broken symmetry states (bs), utilizing different density functionals and basis sets, g tensors, hyperfine parameters, exchange coupling constant J and nuclear quadrupole coupling constants were determined from the DFT-BS method via ORCA and ADF software, which are consistent with the experimental results. Compared with single crystal data, the optimized coordinates from pure functional BP are more pinpoint than those from hybrid functional B3LYP. B3LYP overestimates the spin densities of Mn ions, which is traceable in the hybrid functional with reduced self-interaction error, and, for the calculation of J constant, B3LYP is superior to BP, which produces three or four times larger values. Moreover, molecular orbitals (MOs) for the bs state in this system are conducive to understanding the exchange interaction at the level of electronic structure, and MOs 123–126 indicate that exchange interaction passes through μ-oxo atoms.

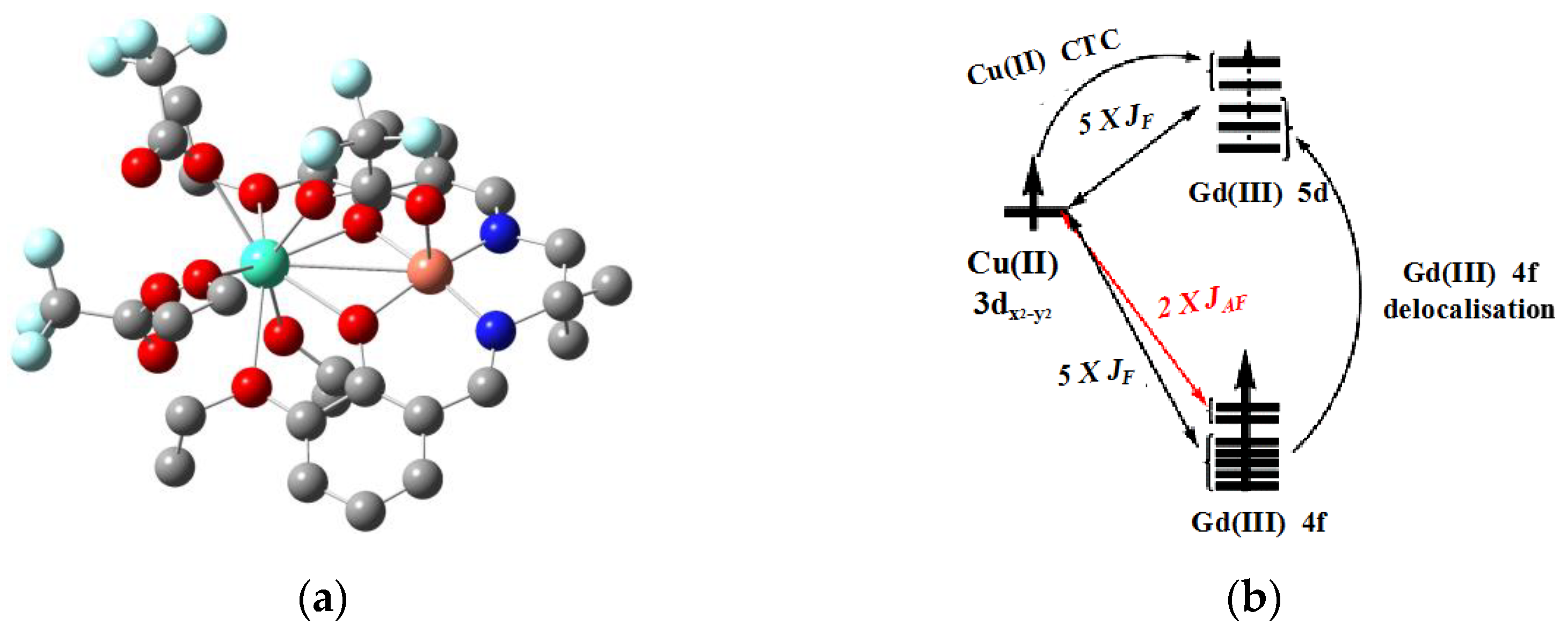
Rajaraman et al. specifically studied one complex of 3d-4f [LCuGd(O₂CCF₃)₃(C₂H₅OH)₂](L=N,N-bis(3-ethoxy-salicylidene)-1,2-diamino-2-methylpropanato) with DFT calculations to comprehend magnetic coupling and magneto-structural relations (Figure 10) [60]. After testing and comparing several functional methods, they recommend using a B3LYP hybrid functional and effective core potential (ECP) basis set to obtain the calculated value of magnetic exchange constant (−5.8 cm⁻¹), which is closely consistent with the experimental value (−4.42 cm⁻¹). When amply considering the relativistic effect of the rare-earth ion system, zeroth-order regular approximation (ZORA) or Douglas–Kroll–Hess (DKH) means should be performed. After analyzing MOs and spin density distribution, they found that 5d orbitals of Gd(III) acquire charge densities from 3d orbitals of Cu(II) and 4f ones of Gd(III) through charge transfer, showing a direct interaction between both sites. Furthermore, an authentic exponential relation within J and O-Cu-O-Gd dihedral angles was established.

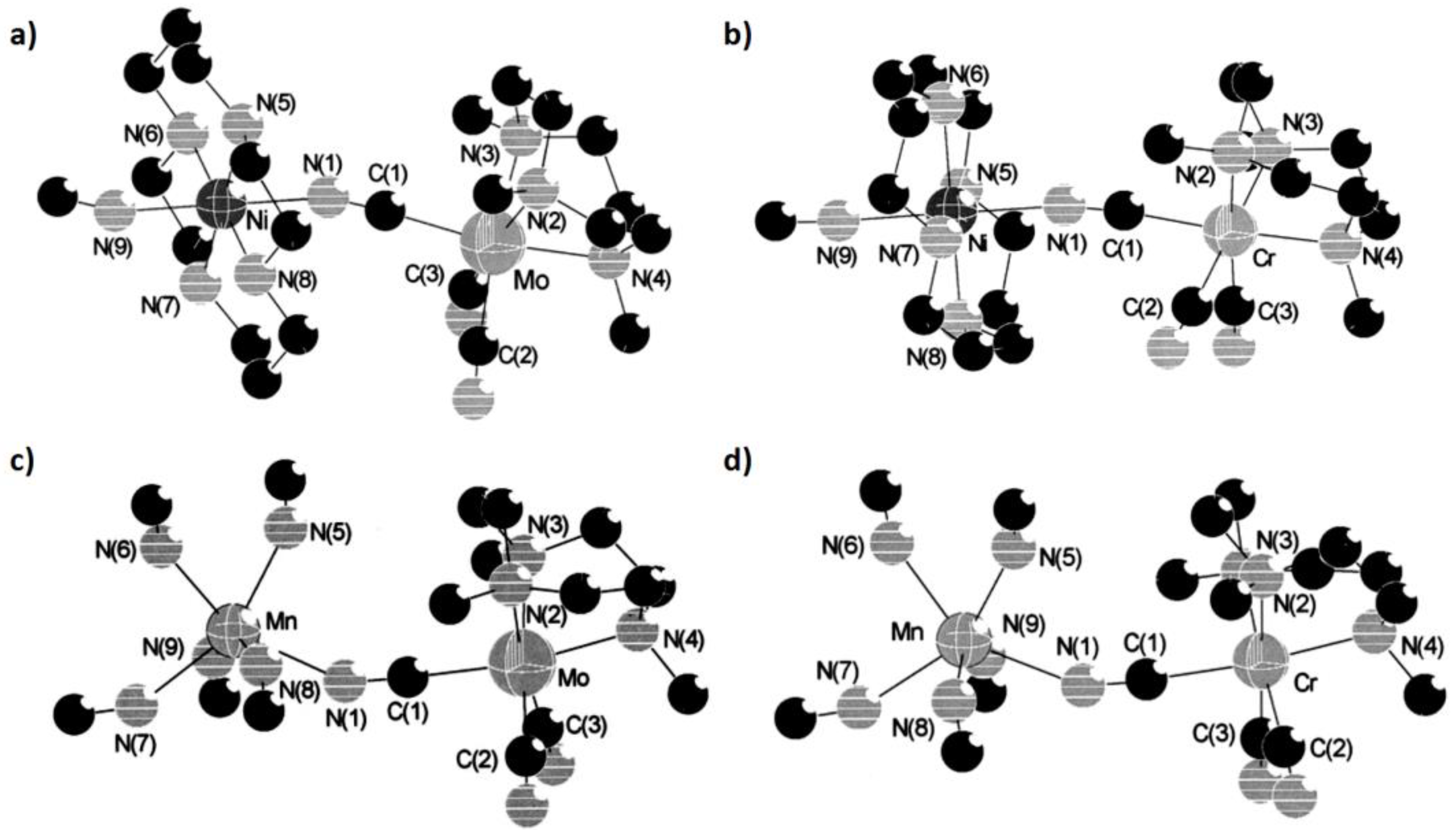
Zhang’s group carried out a detailed study on a group of cyano-bridged compounds with first and second transition metal magnetic centers using the DFT-BS method [61]. Four model complexes marked A, B, C and D, whose structures are from synthesized complexes [−(Me₃tacn)₂(cyclam)NiMo₂(CN)₆]²⁺, [−(Me₃tacn)₂(cyclam)Ni-Cr₂(CN)₆]²⁺, [(Me₃tacn)₆MnMo₆(CN)₁₈]²⁺ and [(Me₃tacn)₆MnCr₆(CN)₁₈]²⁺ (Me₃tacn = N,N’,N’’’-trimethyl-1,4,7-triazacyclononane), were investigated using diverse functionals in ADF and Gaussian software to evaluate the magnetic couplings within Ni(II) and Mo(III), Ni(II) and Cr(III), Mn(II) and Mo(III) and Mn(II) and Cr(III), respectively (Figure 11). For models A and B, the ferromagnetic exchange interaction was promoted after replacing Mo(III) with Cr(III) using Operdew, OPBE, O3LYP and B3LYP functionals, while the antiferromagnetic exchange interaction was enhanced after the same operation for C and D under the usage of XCs and B3LYP functionals. In brief, this type of substitution indeed strengthens the magnetic exchange interaction in this system.

Long et al. reported a series of free radical bridged SMMs [62,63]: {[(Me₃Si)₂N]₂(THF)Ln}₂(μ-η²:η²-N₂)⁻(Ln = Gd, Tb, Dy, Ho, Er) (Figure 12), whose Dy(III) and Tb(III) homologues possess evident slow magnetic relaxation properties attributed to the high magnetic anisotropy of central ions and the strong magnetic coupling between them: their U_eff are 178 K and 327 K, their blocking temperature approaches 8.3 K and 14 K (the temperature in which hysteresis loop opens, T_B) and the coercive field of hysteresis loop of the latter is up to 5 T at 11 K, making itself the hardest SMM at that time. Gao and his co-workers studied the magnetic anisotropy and coupling effect for this series using DFT and CASSCF calculations [64]. The exchange coupling constants (J) of them were computed via the spin-projected approach, the results indicating that coupling effects in Ln-N₂³⁻ are stronger than in Ln-Ln, and the types of coupling for them are antiferromagnetic except for Er(III) due to its orthogonal magnetic orbitals between Er(III) and the radical. The comparison between Tb₂N₂³⁻ and Er₂N₂³⁻ intimates large magnetic anisotropy for the mononuclear fragment combined with strong coupling within Ln-N₂³⁻, which leads to a high energy barrier in this dinuclear system. Thus, the introduction of free radical bridging becomes a novel synthesis idea for high-energy barrier lanthanide dinuclear SMMs.

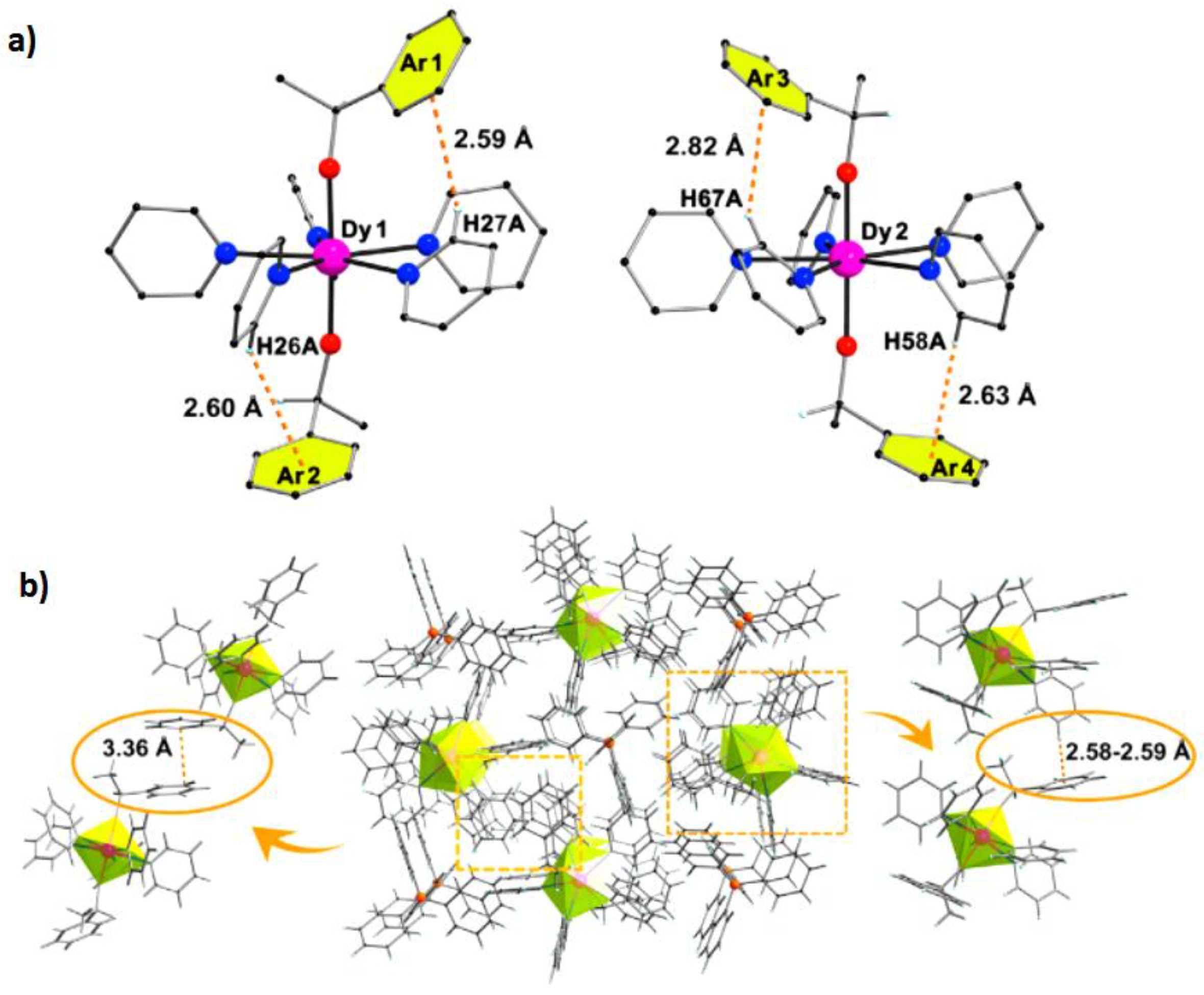
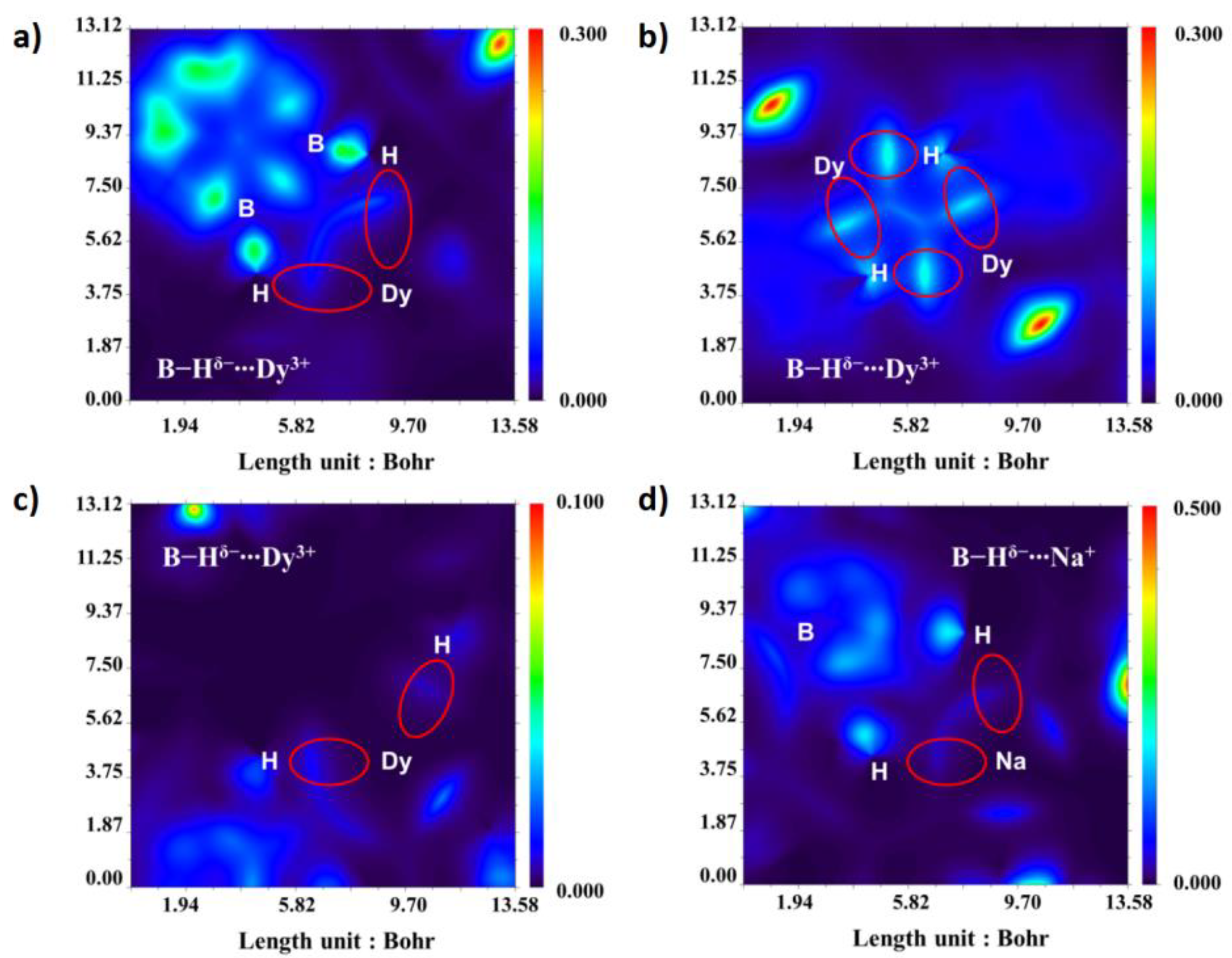
Recently, our group minutely studied a battery of lanthanacarborane complexes, which are provided with one kind of peculiar bridging form, namely B-H^δ−…Mⁿ⁺, considered as inverse hydrogen bonds (IHBs) [65]. DFT calculations confirm that IHBs in this system are relatively strong and larger than 24 kJ/mol (B-H^δ−…Dy³⁺) in order of magnitude by establishing model complexes extracted from original geometry and considering Grimme’s D3 dispersion correction. The electrostatic potential (ESP) plots of Dy³⁺ and B-H^δ− surface explain the formation of this type of interaction, showing that the surface of carboranyl with negative electrostatic potential has a strong interaction with Dy³⁺. The distribution of IHBs is reflected more intuitively via fingerprint plots, color-mapped isosurface graphs of Hirshfeld surface and variable sections based on the independent gradient model (IGM) (Figure 13), which are visual analyses means of intra- and inter-molecular interactions. Among these complexes, three dimer ones were studied which are named 2Dy, 4Dy and 6Dy. The combination of imidazolin-iminato ligands and Dy(III) can promote strong magnetic axiality, and the introduction of IHBs leads to the evident exchange biasing effect. In the aspect of magnetism, the Zeeman splitting diagrams explain this phenomenon with the help of CASSCF calculations and magnetic exchange constant fittings, and the magnetic exchange constant of a single crystal sample reaches −2.0 cm⁻¹, which is equivalent to that of a single atom-bridged binuclear complex system. Moreover, the bonding strengths of B-H^δ−…Mⁿ⁺ IHBs are cation dependent and decreased to 14 kJ/mol for B-H^δ−…Na⁺. The total exchange constant (J_total) decreases, and the exchange biasing effect disappears with the more distant path of magnetic exchange. This work is conducive to the understanding of the influence of IHBs on the magnetism of SMMs.

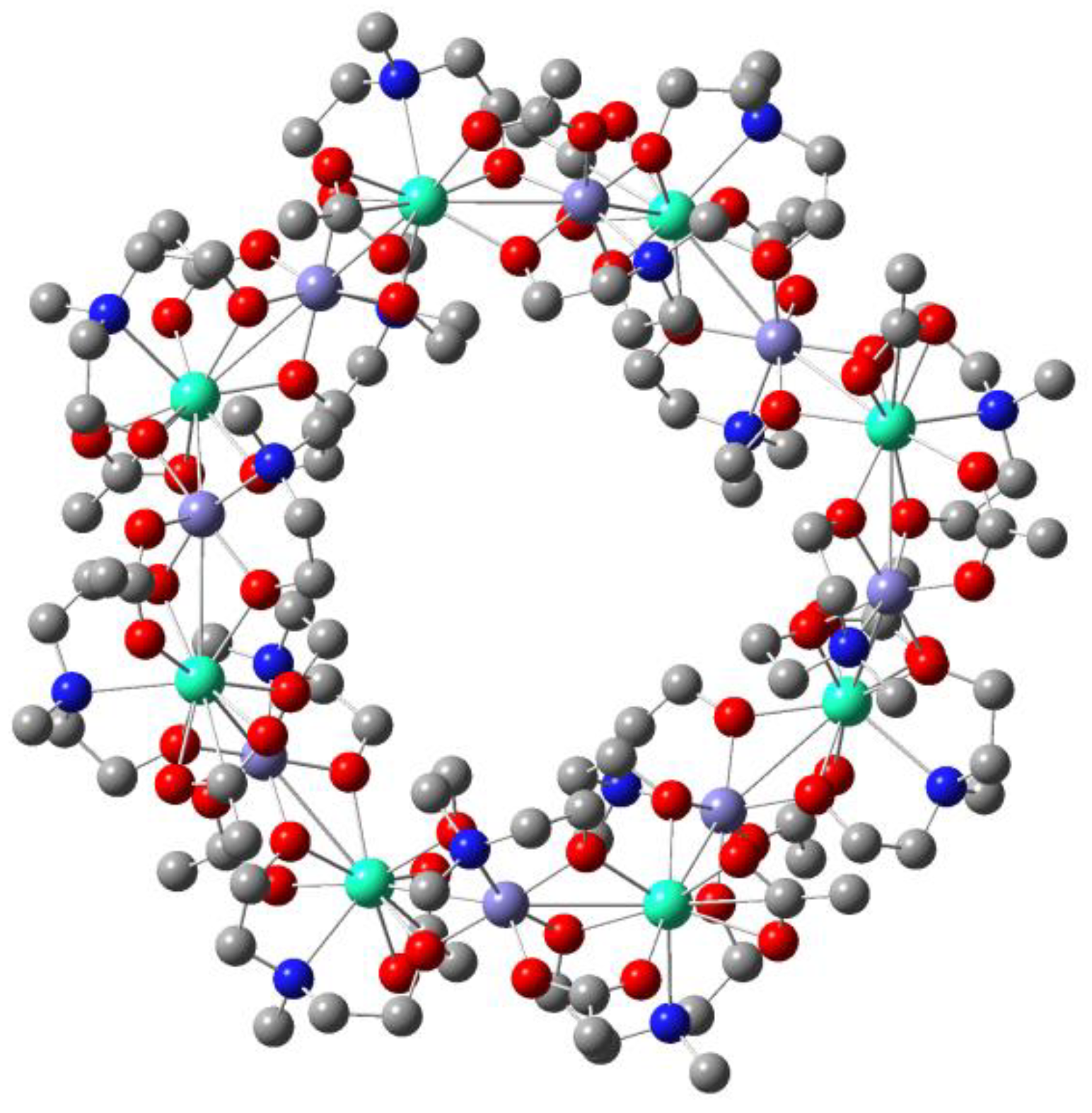
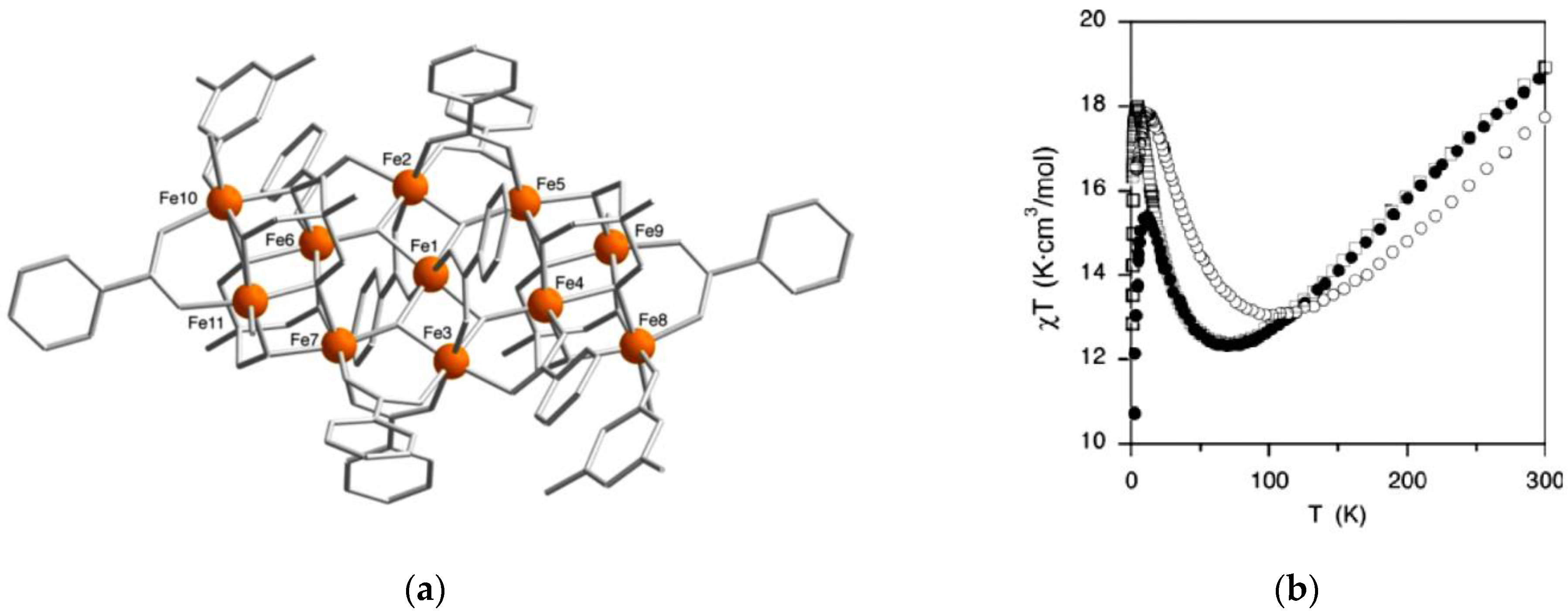
For more complicated multinuclear SMMs, our group successfully prepared one circular molecule of [Fe₈Dy₈(mdea)₁₆(CH₃COO)₁₆]∙CH₃CN∙18H₂O ({Fe₈Dy₈}), which contains 16 alternating magnetic centers (Figure 14) [17]. From the dc magnetic measurement, a local “S” shape curve was observed at 0.23 Tesla and 0.5 K. Combining with ab initio calculations and high-frequency/high-field electron paramagnetic resonance spectroscopy experiments (HF-EPR), the characteristic of a net toroidal moment was determined. Meanwhile, its isomorphic compounds of {Fe₈Y₈} and {Al₈Dy₈} were synthesized by replacing Fe(III) and Dy(III) with diamagnetic Al(III) and Y(III) to obtain magnetic interactions and understand the origin of the annular magnetic moment. The calculated Zeeman spectrum reveals that the strong ferromagnetic exchange interaction between Fe(III) and Dy(III) ensures a large energy gap between the first excited state and the ground state, which belongs to non-magnetic quadruple degenerate states. From the perspective of potential applications, the insertion of Fe, to some extent, can make compounds avoid interference of external magnetic field and realize information storage more steadily.

In addition to the above method of fitting the J value, Monte Carlo (MC) simulation is a good choice for the many-body systems with lower symmetry and has been successfully performed in copious molecular clusters with SMM properties to reproduce their magnetic behavior. In essence, MC simulation is a kind of method based on random sampling. Generally speaking, it can be divided into two categories according to the quantum nature of magnetic centers: one is the classical Monte Carlo (CMC) method for large local spin values, which is based on the Metropolis algorithm, and the other is for systems whose local spins (S) are $\frac{1}{2}$, called quantum Monte Carlo (QMC). Although this method possesses universal applicability, there are not many applications in the field of SMMs. Herein, we just give a few examples of MC simulation in solving spin Hamiltonian.

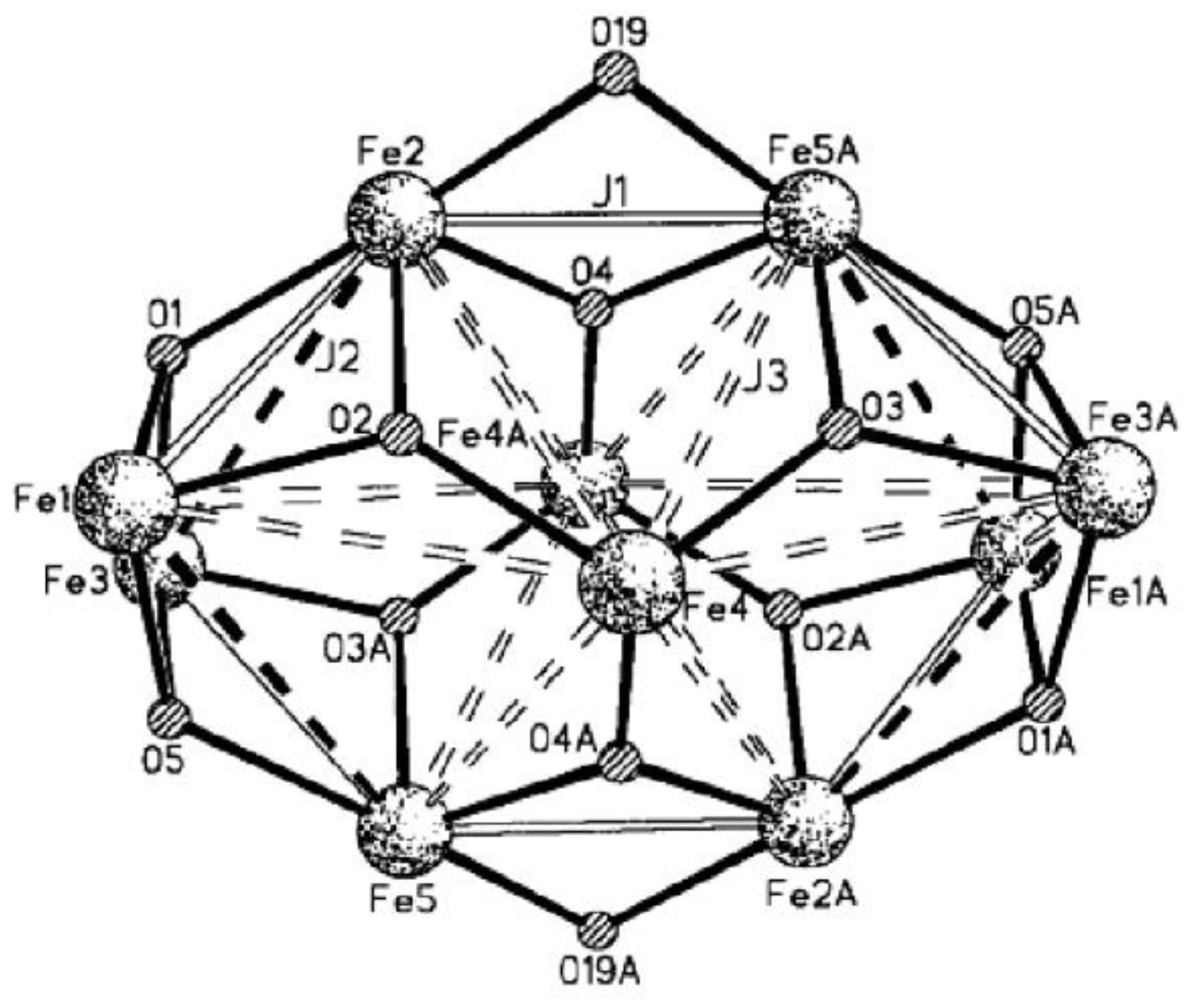
Winpenny et al. reported one {${\mathrm{Fe}}_{10}^{\mathrm{III}}$} cage, and its ground-state spin value (S) is 11 [66]. In virtue of low symmetry with C_2h and a large size of cage, matrix-diagonalization techniques cannot be utilized to fit its susceptibility curve. They first used CMC methods to study the discrete cluster, and the high-spin ground state was corroborated. Considering its actual crystal structure, three types of exchange parameters were determined as J₁, J₂ and J₃. The constant J₁ accounts for all superexchange interactions bridged by two atoms in this cage, while J₂ and J₃ describe couplings mediated through single hydroxide and oxide bridges, respectively (Figure 15). The best fitting gives J₁ = −44 cm⁻¹, J₂ = −13 cm⁻¹ and J₃ = −10 cm⁻¹, and these constants perfectly reproduced the susceptibility behavior of this cage in the temperature range of 300–40 K.

Ruiz’s group performed DFT calculations and MC simulations toward a Fe₁₁ complex with S = $\frac{11}{2}$ to calculate J values and understand its magnetic behavior [67]. Ten coupling constants were introduced due to its low symmetry. After DFT calculations using the PBE functional, CMC simulations were performed to output the susceptibility curve by using the set of calculated exchange parameters, and this curve is close to the experimental data. Then, they took the calculated values as the starting point and continued modifying the shape of the susceptibility curve through CMC simulations, until outputting the magnetic susceptibility curve in near agreement with the experimental data (Figure 16). These results indicate that the trend of all J values is the same as other polynuclear Fe(III) complexes, and μ₃-O bridging ligands are beneficial to construct stronger antiferromagnetic coupling. Accordingly, the combination of DFT calculations and CMC simulations can produce consistent results with the experimental susceptibility curve.

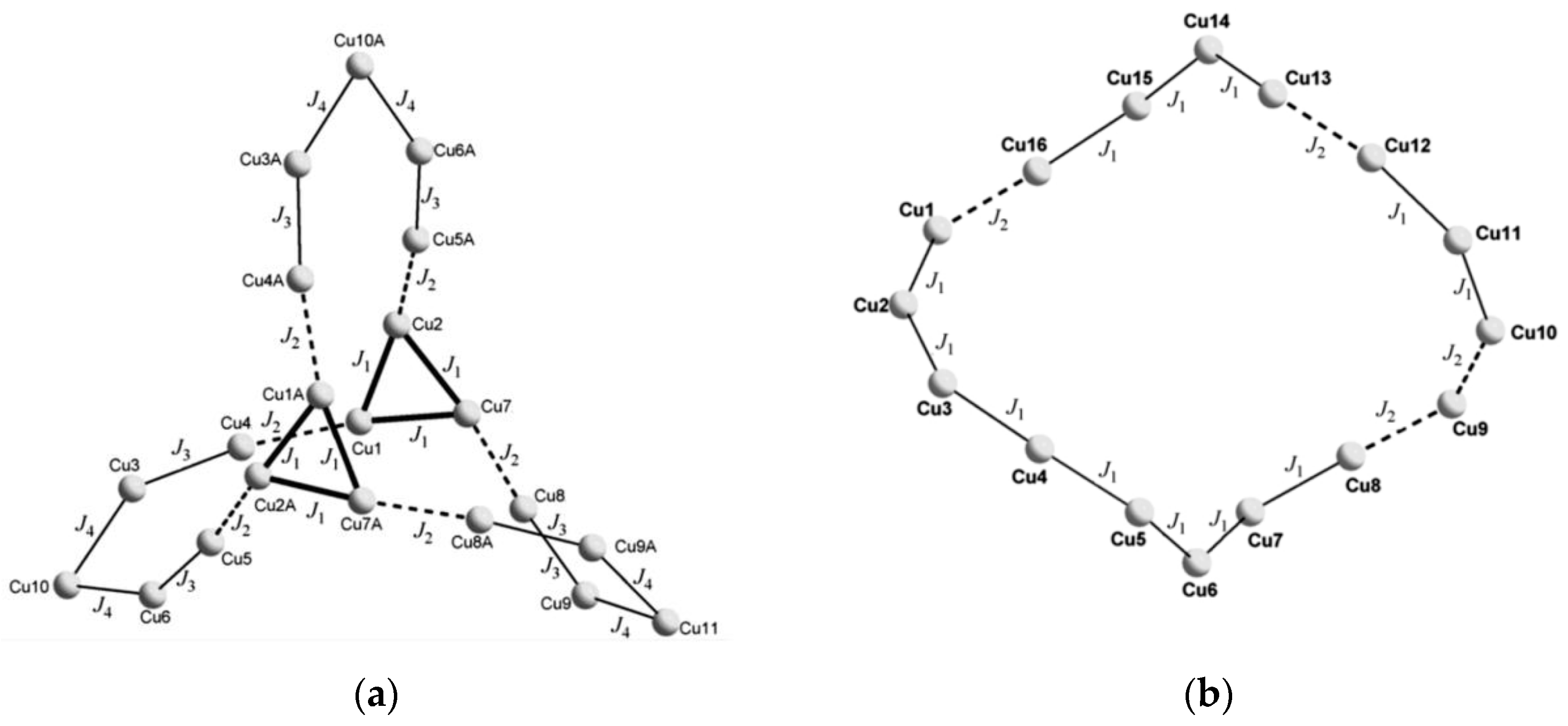
Tao and his collaborators reported two cases of molecular magnets, which are high-nuclearity copper cage compounds Cu₂₁ and Cu₁₆, and their molecular configurations are tricorne and saddlelike cyclic, respectively [68]. Their temperature-dependent susceptibility curves hint at overall antiferromagnetic interactions. Then, QMC simulations were performed to study exchange interactions between copper ions. Considering different bridging modes, four exchange constants were defined for Cu₂₁, while two coupling parameters were defined for Cu₁₆ in view of the nearest Cu…Cu distances (Figure 17). For the former complex, to avoid overparameterization, they supposed J₃ = J₄ in light of both interactions accounting for Cu(II) ions bridged by the pyrazolato and phenoxo groups. The magnetic susceptibility curve through fitting is consistent with that of the dc magnetic measurement. The data show ferro- and antiferro-magnetic interactions in Cu₂₁ and strong antiferromagnetic interactions in Cu₁₆.

4. Conclusions and Perspectives

After years of effort, many excellent single-molecule magnets have been reported, which has depended on the joint efforts of synthetic chemists and theoretical researchers. Theoretical calculations can not only help us analyze and understand the experimental phenomena but also explore the magneto-structural relations and guide the subsequent synthesis. Generally speaking, the commonly used static magnetic calculation methods are ab initio and density functional theory combined with the broken symmetry (DFT-BS) approach. ORCA and Molcas are commonly employed software packages. The former is used more in transition metallic systems, while the latter is used for rare-earth SMMs. For distinctive systems, corresponding calculation methods and models should be selected according to actual situations, for instance, considering whether or not to use DFT-BS to calculate the magnetic exchange constants in light of calculation resources and the atomic numbers of compounds. It should be noted that the reasonable consideration of active space is critical, and, in actual calculations, we can start from the minimum active space. For more complicated many-body systems with low symmetry, Monte Carlo (MC) simulation is a good method for reproducing the magnetic behavior of molecules. In this review, the calculation methods and models proverbially utilized in the field of SMMs in recent years are summarized, and considerable classic cases are enumerated to illustrate them. However, at the theoretical level, there are still many problems to be solved, such as the relationship between the blocking temperature and other physical quantities, the correlation between the Raman process and optical and acoustic phonons and the relaxation mechanisms of other rare-earth ion SMMs. Despite all this, we have reason to believe that with the development of computer processing abilities and the improvement of calculation methods, our understanding of SMMs will grow more and more in-depth to better promote this type of material to the application level.