The results are presented in two parts. First, we report the neutron diffraction results determining the low temperature cell parameters, the mode of magnetic ordering, and the orientation of the easy spin axis. The second part of the data reports the inelastic neutron results, which allow us to determine the internal magnetic field in the ordered state and the anisotropy parameters for the spin states. In addition to the S = 35/2 ground state multiplet, six excited state multiplets were identified from the data with spin values ranging from 31/2 to 39/2.
3.1. Diffraction
Cell parameters were obtained from the neutron data at 1.5 K and were found to be broadly consistent with those reported at 150 K with X-rays [
11], after allowing for a modest thermal contraction that reduces the cell volume by around 2% (
Table 1).
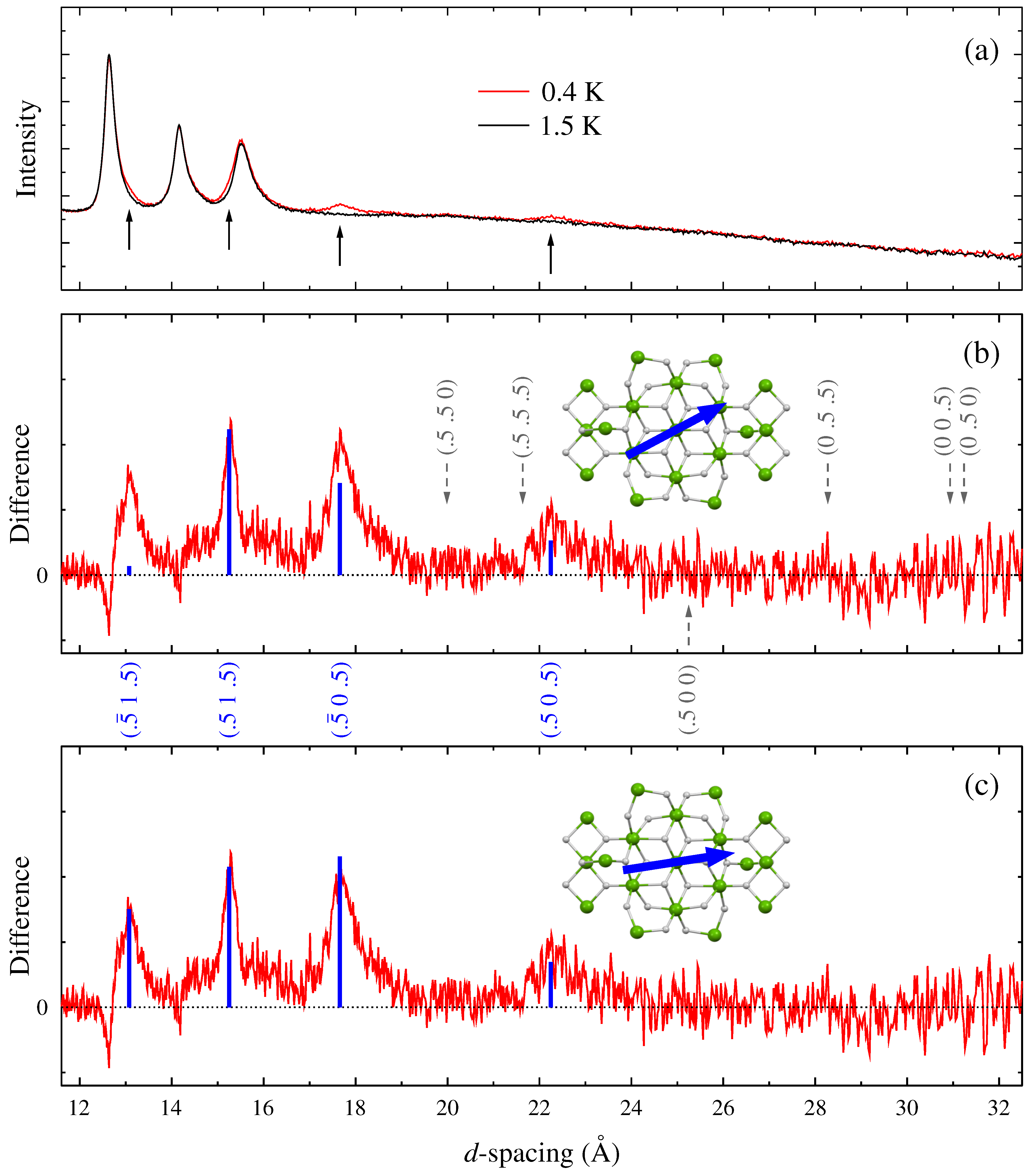
New magnetic diffraction peaks appeared below the AF ordering transition, as can be seen in
Figure 2a, where four extra peaks are seen, and these are made clearer in the difference plots of
Figure 2b,c. Information about the spin structure and the easy axis orientation may be obtained from the relative intensities of these magnetic peaks. The intensity of the magnetic peaks can be written here as a product of three terms
The first term in Equation (
1) is a factor from the component of the scattering vector
that is perpendicular to the magnetic moment axis
. The second term in Equation (
1) is the structure factor for magnetic ordering, which is summed over the lattice vectors
defining the magnetic cell, i.e.,
The third term in Equation (
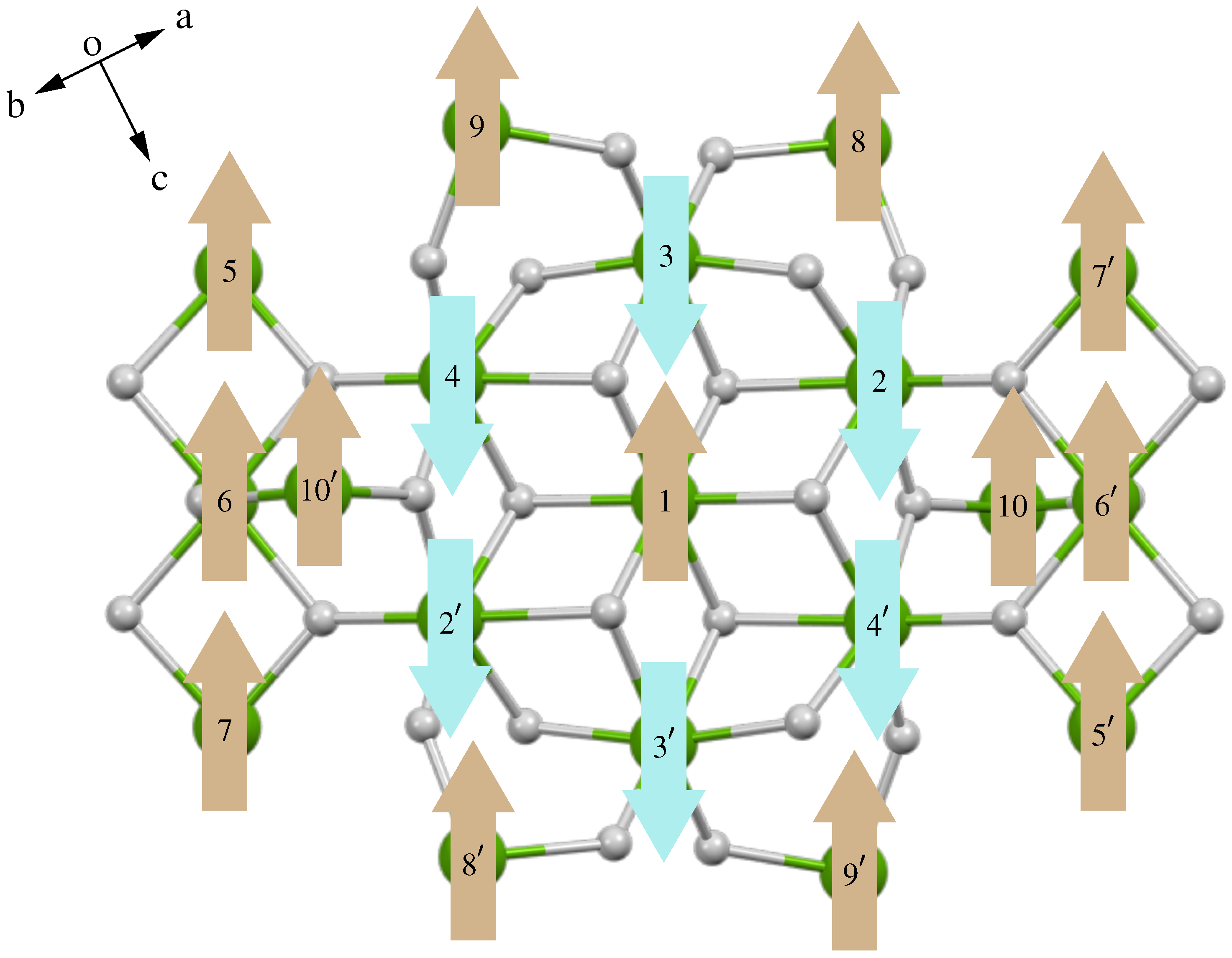
1) is the structure factor for the spatial arrangement of the up and down magnetic moments of the Fe sites within the molecule, as shown in
Figure 1, i.e.,
Note that no atomic form factors are needed in Equation (
3), as we only have one type of magnetic site, and the
Q values are too low to produce any difference in form factor between the magnetic peaks. The low symmetry triclinic cell also ensures that the magnetic peaks correspond to unique scattering planes, rather than to a superposition of magnetically inequivalent symmetry-related planes as is often found in higher symmetry structures.
The four magnetic peaks were found to be consistent only with an AF ordering whose propagation wave vector was (0.5 0 0.5). Thus, the (0 0 0.5) mode and all other modes that might be associated with purely dipolar-driven ordering are excluded (see
Table 2). This indicates that there is a significant contribution from superexchange to the magnetic coupling between the molecules. The relative scale of the interactions will be discussed in
Section 4.
The calculated intensities for the magnetic peaks are shown in
Figure 2b for the
S = 35/2 arrangement of spins in the molecule as defined in
Figure 1, with the ordering mode set to (0.5 0 0.5) and
aligned in the Fe1–Fe2 easy axis direction, which was reported in a previous EPR study [
13]. These intensities are seen to be a relatively poor overall match to the measured data with the intensity of the (−0.5 1 0.5) peak being strongly underestimated. A significant improvement was obtained by allowing the easy axis to rotate toward the long axis of the molecule, and this provided a very good match with the intensities, as shown in
Figure 2c.
Table 2.
Dipolar stabilisation energies for the S = 35/2 ground state of Fe calculated for different modes of magnetic ordering using, firstly, the previously proposed Fe1-Fe2 easy spin axis, for which (0 0 0.5) is the most stable mode, and secondly the axis determined from this study. A spherical sample is assumed for the case of the (0 0 0) ferromagnetic ordering mode. Negative values are unstable.
Table 2.
Dipolar stabilisation energies for the S = 35/2 ground state of Fe calculated for different modes of magnetic ordering using, firstly, the previously proposed Fe1-Fe2 easy spin axis, for which (0 0 0.5) is the most stable mode, and secondly the axis determined from this study. A spherical sample is assumed for the case of the (0 0 0) ferromagnetic ordering mode. Negative values are unstable.
| Ordering Mode | Dipolar Energy (K) | Dipolar Energy (K) |
|---|
| (−1.12, 1, 0.06) Easy Axis | (−0.45, 1, −0.34) Easy Axis |
|---|
| 0 | 0 | 0.5 | 0.809 | 0.436 |
| 0.5 | 0.5 | 0 | 0.575 | 0.219 |
| 0 | 0 | 0 | 0.561 | 0.662 |
| 0.5 | 0.5 | 0.5 | 0.515 | 0.533 |
| 0.5 | 0 | 0.5 | −0.271 | −0.337 |
| 0 | 0.5 | 0 | −0.425 | −1.028 |
| 0 | 0.5 | 0.5 | −0.556 | −0.024 |
| 0.5 | 0 | 0 | −0.792 | −0.144 |
The easy axis vector obtained from fitting the data is shown in
Table 3. We found this to be quite close to the Fe1–Fe10 axis and making an angle of 12° to that axis, whereas it is at 26° to the originally proposed Fe1–Fe2 axis. Although the molecule only has crystallographic inversion symmetry, the molecular symmetry conforms closely to 2/
m, with the twofold axis defined by Fe3–Fe1–Fe3
. It is, thus, very likely that the orientation of the easy axis also conforms to this symmetry (either parallel to the twofold axis or perpendicular to it). The axis orientation found here, lying close to the molecular mirror plane (defined by Fe10–Fe2–Fe1–Fe2
–Fe10
) is, thus, more consistent with this expectation than that suggested by the earlier EPR study.
Table 3.
For an easy axis vector specified in cell units (
), the direction is fully determined by two parameters. The orientation obtained here is compared with the Fe1–Fe10 direction and also the Fe1–Fe2 direction suggested by the previous EPR study [
13]. The fitted orientation is close to the plane formed by the Fe1, Fe2, and Fe10 sites and is close to the Fe1–Fe10 axis as shown by the angle given in the final column.
Table 3.
For an easy axis vector specified in cell units (
), the direction is fully determined by two parameters. The orientation obtained here is compared with the Fe1–Fe10 direction and also the Fe1–Fe2 direction suggested by the previous EPR study [
13]. The fitted orientation is close to the plane formed by the Fe1, Fe2, and Fe10 sites and is close to the Fe1–Fe10 axis as shown by the angle given in the final column.
| | S | S | S | Angle (°) |
|---|
| This study | −0.45(2) | 1 | −0.34(2) | |
| Fe1–Fe10 | −0.18 | 1 | −0.42 | 12 |
| Fe1–Fe2 (EPR) | −1.12 | 1 | 0.06 | 26 |
3.2. Inelastic Neutron Scattering
In addition to the appearance of new magnetic diffraction peaks, the magnetic phase transition can also be observed via changes in the low energy inelastic neutron scattering spectra with temperature. This provides a measurement of the effective internal field that appears below the transition. Using measurements at low energies, taken just above the transition at 1.2 K, the low lying excitations are determined. Further excitations are also found at higher energies, and the combined measurements allow the seven lowest energy spin states to be identified. The data obtained are analysed with a spin Hamiltonian for each spin state
S taking the form
where
D and
E are axial and rhombic anisotropy parameters defining the zero field splitting (
z is the direction of the anisotropy axis) and
B is a spontaneous static internal magnetic field that is only present in the magnetically ordered state. The energy levels
are determined by the eigenvalues of each spin state, offset by
, the energy gap of the lowest level of the spin state multiplet with respect to the
S = 35/2,
= 35/2 ground state. When
B is present, a shift in the energy levels occurs, which is mainly determined by the
z component of the field, which we will label
.
For the current simplified model, we have treated each
S-state independently within the Giant-Spin-Approximation using Equation (
4). We note that, besides the anisotropy contribution from crystal field and dipole–dipole interactions,
S-state mixing [
23] can also contribute to the effective
D and
E terms in the Spin Hamiltonian.
3.2.1. Internal Field
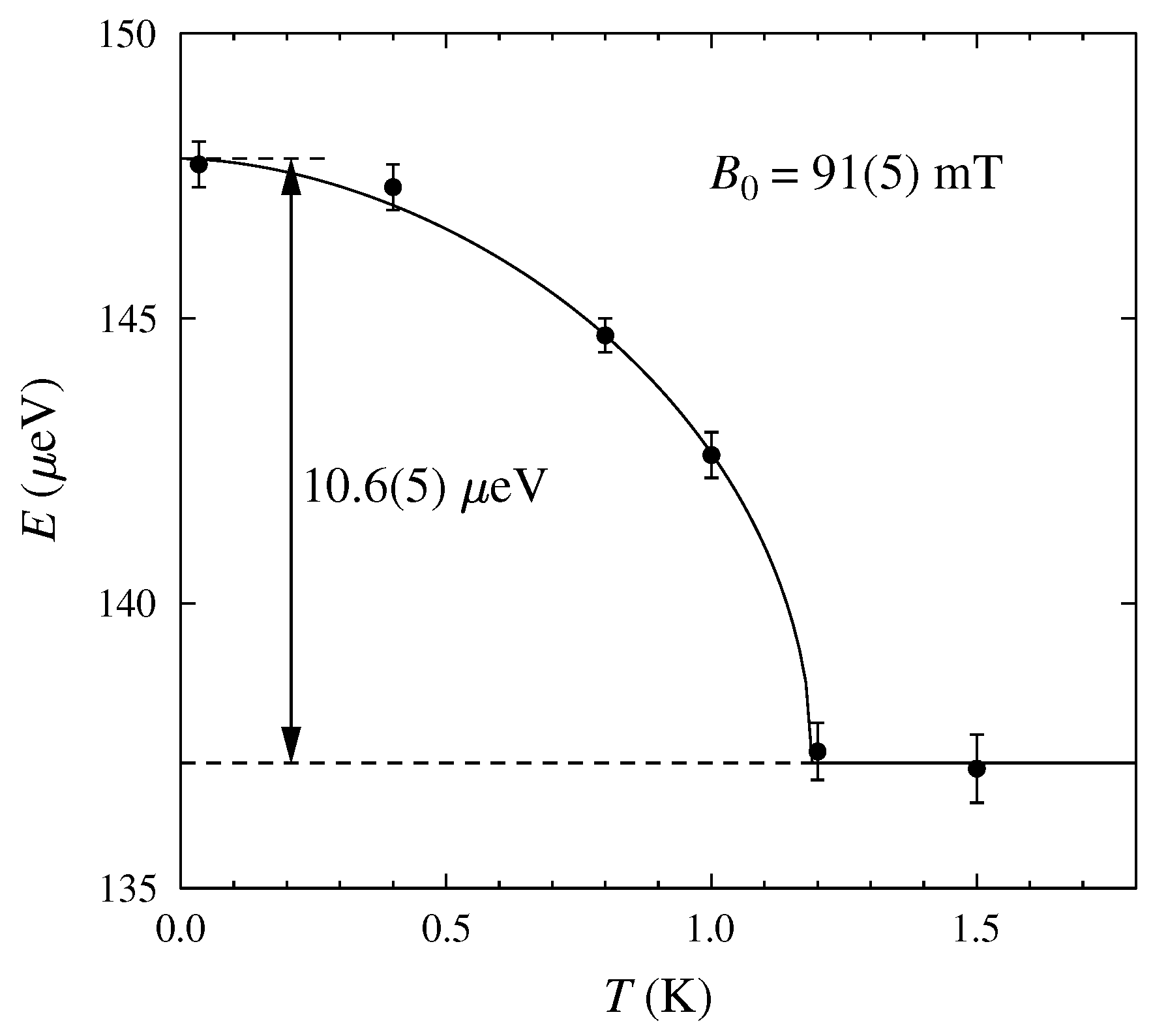
The temperature dependence of the position of the lowest energy transition is shown in
Figure 3. The magnetic transition just below 1.2 K is clearly seen in this data as an upward shift in the excitation energy. This shift is due to the different splittings of the
= 35/2 and
= 33/2 levels in the effective internal field of the ordered state
, which is obtained from the energy shift as
The energy shift reflects intermolecular interactions that can have contributions from both dipolar and exchange mechanisms. Since the dipolar contribution can be determined exactly from knowledge of the spin structure, the measured value of
allows the exchange contribution to be precisely quantified. This will be explored further in
Section 4.
3.2.2. Low Temperature Excitation Spectrum
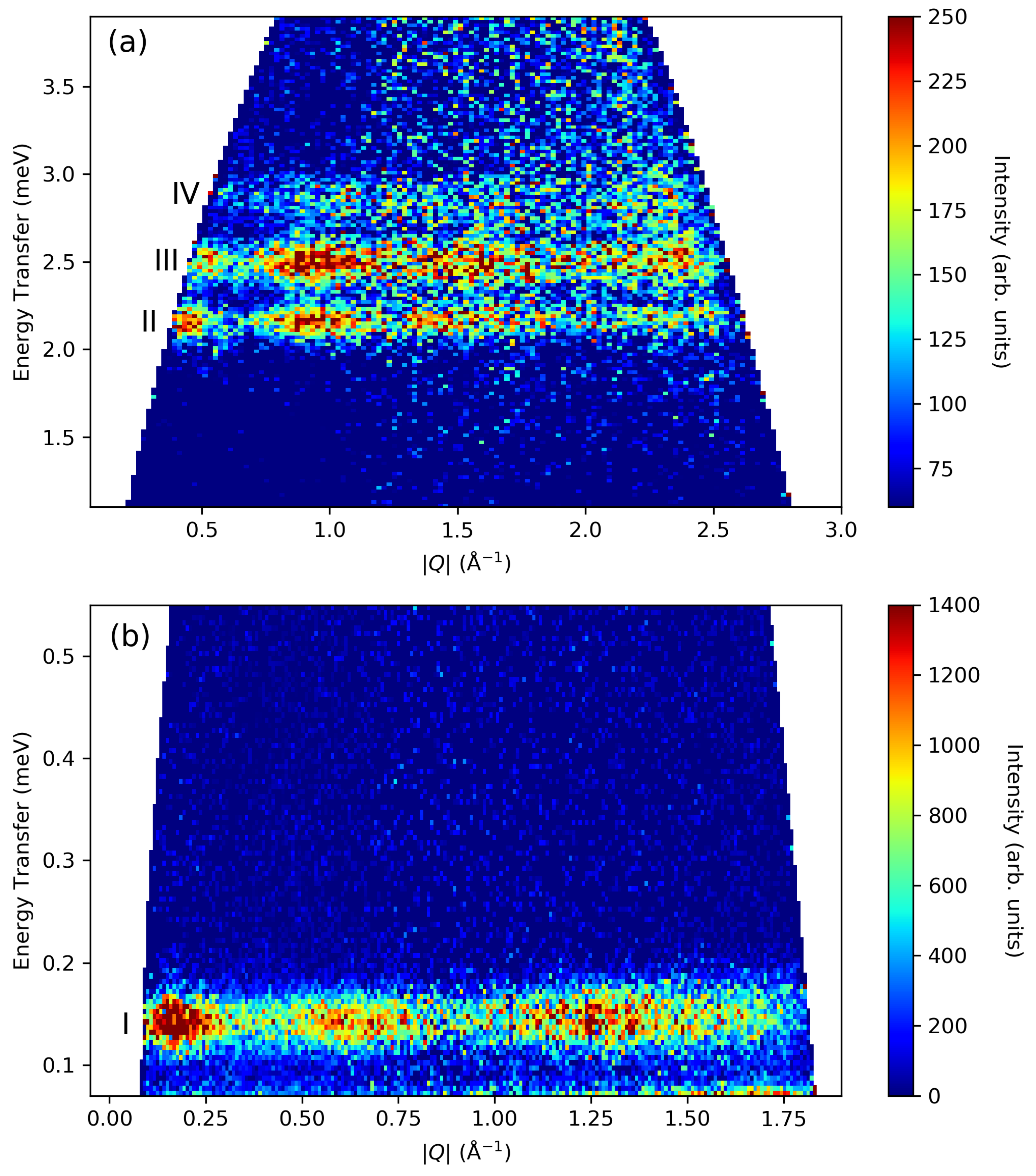
The excitation spectrum measured at a temperature of 35 mK is shown in
Figure 4a. This plot combines data for
= 2.00 meV and
= 5.15 meV. At this low temperature, all of the excitations originate from the ground state. There are four excitation bands labelled I to IV in
Figure 4a. Labelling the states as (
S,
), band I is assigned to the transition from the (35/2, 35/2) ground state to the next level in the 35/2 spin state, i.e., (35/2, 33/2) (
Figure 4b). Gaussian fits of bands II to IV are shown in
Figure 4a, with the parameters listed in
Table 4.
Consideration of the selection rules for allowed magnetic dipole transitions can assist in the assignment of these bands. These are
= 0 ± 1 and
= 0 ± 1. Hence, a single transition is expected for
= −1, whereas two closely spaced transitions would be expected for
= 0 and three closely spaced transitions for
= +1. The relative intensities within the sets of closely spaced transitions depend on matrix elements whose ratios within a given multiplet can be determined via the Wigner–Eckart theorem, leading to the following expression for the intensity
where the six element array is the Wigner 3-j symbol. The relative intensity values are shown in
Table 5, where it can be seen that the lowest energy transition within the set is always the strongest. The second transition, when allowed, is reduced from the first transition by a factor of
and the third transition, when allowed, is smaller than the first transition by a factor of
. The transitions with high intensity according to Equation (
6) and
Table 5 are signified by the thicker lines in
Figure 4b.
Since the fitted widths of the Gaussians are comparable for bands II and III and 50% larger for band IV, we take this as an indication of unresolved multiple transitions in band IV, leading to the assignments shown in
Table 4 and
Figure 4b with bands II and III corresponding to transitions to two
S = 35/2 excited states and band IV corresponding to a superposition of two transitions having
= ±1. In
Figure 4b, we illustrate one possibility for band IV with transitions to
S = 33/2 (IVa) and to
S = 37/2 (IVb). The four states associated with bands II to IV span a region of 25 to 33 K above the ground state.
The
Q dependence (
Figure 5) provides further support for this assignment [
24,
25,
26], with the intensities of bands II and III tracking each other and remaining large at low
Q, consistent with
= 0, whereas band IV is weaker at low
Q, consistent with
= ±1. We also considered whether bands II and III could be two transitions into a single
S = 35/2 excited state; however, their separation would require the magnitude of the
D parameter to be more than double that of the ground state, which we believe to be less likely than having two separate
S = 35/2 excited states.
3.2.3. Low Lying Thermally Accessible Spin Excitations
An EPR study [
13] suggested the presence of an excited spin state at 8 K rather than at 25 K; however, we observed here no direct transitions in the associated 0.7 meV spectral region (
Figure 4a). A thermal population of low lying excited states will produce additional low energy transitions, which allows such states to be identified, even when direct transitions from the ground state are not allowed.
Further information is contained in the relative intensities of the transitions, which are determined by the matrix elements for magnetic dipole transitions under Equation (
4). The temperature dependence of the spectra in the band I region are shown in
Figure 4c. These spectra were analysed using the energy levels and matrix elements derived from Equation (
4), taking into account the thermal occupancies of the levels given by
where
. The relatively low anisotropy of the Fe
system prevents us from being able to resolve the individual transitions within a spin state multiplet in the way that was possible for previous inelastic neutron studies on systems with larger anisotropy, such as Fe
[
27] and Mn
[
28]. Nevertheless, the characteristic asymmetric shape of the broadened scattering profile still enables us to extract important parameters from the data.
A global fit of the spectra obtained between 1.2 and 10 K below 0.2 meV (
Figure 4c) assigns the spectral features to the superposition of internal transitions within three spin states corresponding to the
S = 35/2 ground state and two low lying states for which direct transitions from the
S = 35/2 ground state are forbidden—namely
S = 31/2 and
S = 39/2. The spectral fits are shown as the blue curves in
Figure 4c, and the parameters obtained from this analysis are shown in
Table 6. The gaps obtained for these two states are 1.5 and 3 K, significantly lower than the 8 K gap to the
S = 33/2 state suggested from the EPR data. The
D parameter of the ground state at −51 mK is a little larger in magnitude than the value of −43 mK obtained from the EPR.
The
ratios here were found to be around 0.2, four times larger than the ratio of 0.05 that was suggested in the EPR study. The primary effect of a large
ratio is to increase the minimum level separation in the upper levels of the spin multiplet (
Figure 4b). This shows up most clearly in the data as a relatively pronounced low energy cutoff for the 5 and 10 K spectra (
Figure 4c). The value of
per degree of freedom for the global fit shown in
Figure 4c is 1.65. If the excited states are not included at all, then the
value becomes increased by a factor of 8 compared to the two excited state fit. If only one excited state is included, then the
value increases by a factor of 1.5 compared to the two excited state fit.
Figure 4.
(
a) Inelastic spectra measured on LET at 35 mK. Data below 1 meV are for incident energy
= 2.00 meV and data above 1 meV are for
= 5.15 meV (with a linear background subtracted). Gaussian fits to bands II to IV are indicated, with fit parameters given in
Table 4. (
b) The assignment of band I is the lowest
= 0 transition of the
S = 35/2 multiplet. Bands II to IV are due to magnetic-dipole-allowed transitions with
= 0, +1, or −1. On the basis of width, amplitude, and
Q dependence, bands II and III are assigned to two distinct
S = 35/2 excited states and band IV to unresolved transitions into excited states with
= ±1. One possibility is shown here for band IV with transitions to the
S = 33/2 and
S = 37/2 states. (
c) The temperature dependence of the low energy spectral region allows two low lying excited spin states to be identified. The blue lines show the fitted thermal dependence that is well described by three spin states, with the corresponding fit parameters given in
Table 6.
Figure 4.
(
a) Inelastic spectra measured on LET at 35 mK. Data below 1 meV are for incident energy
= 2.00 meV and data above 1 meV are for
= 5.15 meV (with a linear background subtracted). Gaussian fits to bands II to IV are indicated, with fit parameters given in
Table 4. (
b) The assignment of band I is the lowest
= 0 transition of the
S = 35/2 multiplet. Bands II to IV are due to magnetic-dipole-allowed transitions with
= 0, +1, or −1. On the basis of width, amplitude, and
Q dependence, bands II and III are assigned to two distinct
S = 35/2 excited states and band IV to unresolved transitions into excited states with
= ±1. One possibility is shown here for band IV with transitions to the
S = 33/2 and
S = 37/2 states. (
c) The temperature dependence of the low energy spectral region allows two low lying excited spin states to be identified. The blue lines show the fitted thermal dependence that is well described by three spin states, with the corresponding fit parameters given in
Table 6.
![Magnetochemistry 07 00074 g004 Magnetochemistry 07 00074 g004]()
Figure 5.
The Q dependence of the scattering intensity measured at 35 mK with an incident neutron energy of (a) 5.15 meV, showing bands II, III, and IV, and (b) 2.00 meV, showing band I.
Figure 5.
The Q dependence of the scattering intensity measured at 35 mK with an incident neutron energy of (a) 5.15 meV, showing bands II, III, and IV, and (b) 2.00 meV, showing band I.