Next Article in Journal
Nano-Structured Dilute Magnetic Semiconductors for Efficient Spintronics at Room Temperature
Previous Article in Journal
Magnetic Nanoparticles as In Vivo Tracers for Alzheimer’s Disease
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Magnetochemistry
Volume 6
Issue 1
10.3390/magnetochemistry6010014
magnetochemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effect of Terbium Ion Substitution in Inverse Spinel Nickel Ferrite: Structural and Magnetic Study

by
Deepa Guragain
1,*,
Binod Kumar Rai
2,
Sunghyun Yoon
3,
Tej Prasad Poudel
1,
Subash Chandra Bhandari
1 and
Sanjay R Mishra
1
1
Department of Physics, The University of Memphis, Memphis, TN 38152, USA
2
Materials Science and Technology Division, Oak Ridge National Laboratory, Oak Ridge, TN 37381, USA
3
Department of Physics, Kunsan National University, Gunsan 573-701, Korea
*
Author to whom correspondence should be addressed.
Magnetochemistry 2020, 6(1), 14; https://doi.org/10.3390/magnetochemistry6010014
Submission received: 30 January 2020 / Revised: 28 February 2020 / Accepted: 2 March 2020 / Published: 10 March 2020
Browse Figures
Versions Notes

Abstract

:
Doping rare-earth ions into spinel ferrites can alter their electrical and magnetic properties. The present study delineates the structure–property relationship of the effect of rare-earth terbium doping in NiFe2O4 ferrite. X-ray diffraction analysis (XRD) showed unit cell lattice expansion with increased Tb3+ content. The Fourier transform infrared spectroscopy (FTIR) results indicate preferential occupancy of Tb3+ at the octahedral B site. The magnetic parameters derived from room temperature hysteresis loops where both the saturation magnetization, Ms, and coercivity, Hc, value decreased with the Tb3+ substitution and reached a minimum value of Ms ~30.6 emu/g at x = 0.1 and Hc ~102 Oe at x = 0.075. The temperature-dependent magnetocrystalline anisotropy derived from the magnetic isotherm was observed to be the highest for x = 0.1 at 5 K with the value K1 ~1.09 × 106 J/m3. The Tb3+ doping also resulted in the Curie temperature reduction from 938 K at x = 0.0 to 899 K at x = 0.1.

1. Introduction

Nickel ferrite (NiFe2O4) with a spinel structure has the general formula AB2O4 [1], where all Ni ions are located at the B (Octahedral) site, and iron ions are at both the A (Tetrahedral) and B sites [2]. Nickel ferrite is highly used in electronic devices due to its large permeability at high frequency, low cost, chemically stability, higher electric resistivity, and higher mechanical hardness [3]. The magnetic and dielectric properties of NiFe2O4 are highly dependent on the cation distribution, which in turn are strongly dependent on the preparation method [4,5,6,7]. Different types of magnetic [8,9] and nonmagnetic atoms for cations [10,11,12,13,14,15] have been explored to create atomic-level changes in ferrites. This selection affects the Fe3+–O2−–Fe3+ interaction, which changes the crystal structure of ferrites and hence the magnetic properties of the compound [16].
The crystal structure of NiFe2O4 is face-centered, where the unit cell contains 32 O2−, 8 Ni2+, and 16 Fe3+ ions, where oxygen ions form 64 tetrahedral and 32 octahedral sites, and 24 cations are distributed [17]. Octahedral and tetrahedral sites are populated with eight Fe3+ ions each, and eight Ni2+ cations occupy half of the octahedral sites [18]. The bulk NiFe2O4 is a familiar inverse spinel with the Ni ion occupying the B site with structure (Fe3+1−δ)A[Ni2+δFe3+1+δ]B, while at the nanoscale, the mixed spinel structure of NiFe2O4 with Ni2+ ions occupying both A- and B-sites was observed.
Aside from replacing Fe3+ ions with magnetic and non-magnetic ions, researchers have studied the substitution of rare-earth elements [16,19,20]. Larger ionic radii of the rare-earth ions compared to Fe3+ were observed to bring lattice expansion in ferrites, which can alter the superexchange interaction of Fe3+–O2−–Fe3+ [21]. It has been observed that the substitution of rare-earth elements such as Nd3+, Gd3+, Ho3+, Er3+, Tm3+, Y3+, and Lu3+ decreases the Curie temperature [16,20,22] compared to pure ferrites, and become more useful for magneto-optical recording [20,23]. Additionally, the substitution of rare-earth ions at the octahedral site affects the hole transfer rate between Ni2+ and Ni3+, which increases the electrical resistivity of the compound and hence enables its high-frequency application.
To the best of our knowledge, scant reports are available in the literature on the structural and magnetic properties of Tb3+ doped NiFe2O4 ferrite nanoparticles. Tb3+ was chosen for the substitution, specifically to understand its effect on the magnetic properties of NiFe2O4 as Tb3+ ions present a large Bohr magneton number, μeff = 9.7–9.8, higher than Gd3+ (μeff = 7.8–7.9) [24]. Thus, the presence of Tb3+ can greatly alter the A–B site interaction via Fe3+–O2−–Fe3+(Tb3+) interaction. Considering the importance of the substituted NiFe2O4, we report the synthesis of the Tb3+ doped NiFe2−xTbxO4 (0.0 ≤ x ≤ 0.1) ferrite nanoparticles via the sol-gel method. The experimental results show an increase in the lattice parameter along with the reduction of crystalline size, Curie temperature, magnetization, and coercivity upon Tb3+ substitution.

2. Experimental

Terbium doped NiFe2-xTbxO4 (x = 0.00, 0.025, 0.05, 0.075, and 0.1) were prepared via the sol-gel method [25]. Nitrate precursors viz. nickel nitrate hexahydrate, ferric nitrate hexahydrate, and terbium nitrate hexahydrate were used for the synthesis of NiFe2−xTbxO4. A homogenous mixture was prepared by mixing a stoichiometric amount of precursor in 10 mL of ethylene glycol and stirred for 30 min at room temperature. A dry gel was obtained by heating the mixture at 70 °C for 4 h. Subsequently, the gel was dried in a furnace at 120 °C for 3 h. The as-obtained dry gel was later ground and calcined at 600 °C for 3 h in a box furnace. The structural and phase analysis of samples was performed using an X-ray diffractometer (XRD), where the patterns were collected using Cu Kα radiation in the 2Θ = 25–70° range at a step size of 0.0485 and acquisition time of 0.2 s. The room temperature magnetic properties of the samples were investigated using a vibrating sample magnetometer (VSM). Additionally, magnetic isotherms were obtained in the field of ±60 kOe and in the temperature range of 5–300 K via SQUID (Quantum Design). The infrared spectrum of samples was collected using the Fourier transfer infrared spectrometer (FTIR, Thermo Nicolet iS 10). The Curie (Neel) temperature (Tc) of the samples was measured using a modified thermogravimetric analyzer (TGA, Instrument Specialists Inc., Memphis, USA) equipped with a permanent magnet.

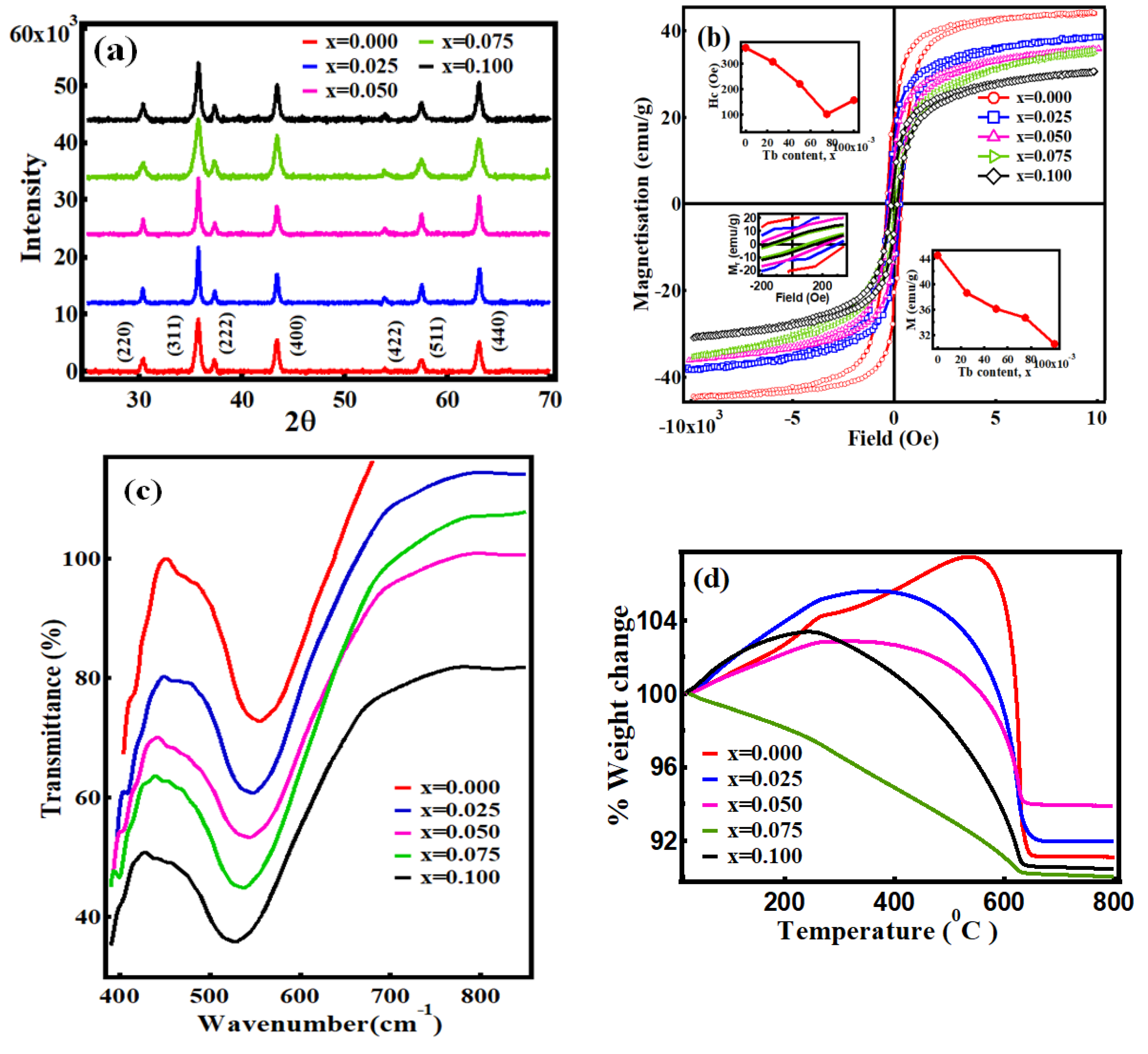
3. Results and Discussion

Figure 1a shows the XRD pattern of the calcined NiTbxFe2−xO4 (x = 0.00, 0.025, 0.05, 0.075, and 0.1) ferrites. All the Tb3+ substituted nickel ferrites showed a single-phase spinel structure. No impurity peaks were detected within the detection limit of the instrument. Table 1 shows that the lattice parameter “a” for NiTbxFe2−xO4 linearly increased with the Tb3+ content. The increase in the lattice parameter upon Tb3+ substitution was due to the larger Tb3+ ions (ionic radii ~0.923 Å) replacing Fe3+ ions (ionic radii ~0.645 Å). The X-ray density was calculated using the relation [26]: ρx = 8 M/NAa3, where M is the relative molecular mass, NA is the Avogadro’s number, and ‘a’ is the lattice parameter. The multiplication factor 8 was used as there is an 8-formula unit in a unit cell. Table 1 shows that the X-ray density increases with the Tb3+ content. This is because the molecular mass increased with the increase in the Tb3+ content due to the higher atomic weight of Tb than that of Fe.
The interionic distances (i.e., cation–anion distances at the A-site (dAL) and B-site (dBL), together with the distance of the closest anion–anion approach, tetrahedral edge, dAE, and shared and unshared octahedral edges, dBE, dBEU) are calculated according to the following equations [27,28],
dAL = a√3(u − 0.25),
dBL = a(3u2 − 11/4u + 43/64)1/2,
dAE = a√2(2u − 0.5),
dBE = a√2(1 − 2u),
dBEU = a(4u2 − 3u + 11/16)1/2
where u is the oxygen parameter (u = 0.3811 for NiFe2O4) [29]. Additionally, the distances LA and LB between the magnetic ions at the A-sites and B-sites (the jump length or hopping length), respectively, can be obtained where LA = a√3/4, and LB = a√2/4 [30]. Table 2 lists the calculated parameters. The values of dAL, dBL, dAE, dBE, dBEU, and the hopping length, LA and LB, increases with Tb3+ content due to the replacement of smaller Fe3+ via larger radii ions Tb3+ in octahedral sites. The ionic radius of a rare-earth ion is larger than the tetrahedral site radii, and therefore energetics force the rare-earth ions to occupy octahedral sites. The preferred rare-earth occupancy for the octahedral site has been also corroborated by Mossbauer spectroscopy [16,20].
Figure 1c shows the infrared absorption spectra of samples. The spectra show two distinct absorption bands with peaks at 554.3 (ν1) cm−1 (Mtetra↔O stretching) and 413.5  cm−1 (ν2) (Mocta↔O stretching). The band positions were found to agree with the characteristic infrared absorption bands of the AB2O4 type spinel [31]. The higher frequency band (ν1) was found to shift from 554.3 cm−1 to 543.3 cm−1 while the lower frequency band (ν2) shifted from 413.5 cm−1 to 406.2 cm−1. Similar band shifting with the doping in NiFe2O4 has been reported in the literature [16,27,32,33]. The difference in the band positions is expected because of the difference in the Fe–O distances for the A and B sites. The Fe–O distance (1.89 Å) for the A site was smaller than that of a B site (1.99 Å) [34]. Thus, a high degree of covalency between Fe–O at the A site was expected, compared to that at the B site, which resulted in vibration stretching at higher wavenumbers. The increase in the site radius reduced the fundamental frequency, thus shifting the central frequency toward the lower frequency side [35]. Upon replacement of smaller Fe3+ ions by bigger Tb3+ ions, an increase in site radius is expected.
Figure 1b shows the room temperature (RT) hysteresis loops of the NiFe2-xTbxO4 samples measured in the ±12 kOe field range. The inset in Figure 1b shows the saturation magnetization, Ms, and coercivity, Hc, as a function of Tb3+ content in NiFe2−xTbxO4. The hysteresis loop for NiFe2O4 exhibits saturation magnetization MS ~44.5 emu/g, Mr ~19.8 emu/g, and the coercivity was ~363 Oe. The Ms value of the doped NiFe2−xTbxO4 samples decreased with the increase in Tb3+ content from 44.5 emu/g for x = 0.0 to 30.6 emu/g for x = 0.1. This reduction in Ms value could mainly arise from the replacement of magnetic Fe3+ with non-magnetic Tb3+ ions. An increase in the magnetization value at low temperature, at 60 kOe, for samples x = 0.075 and x = 0.1 could be attributed to the freezing of surface spin [36]. With the decrease in the crystallite size due to broken surface bond symmetry, the number of uncompensated spins was expected to increase. Later, upon freezing at low temperatures, they could align and hence increase the net magnetization of the particles [37]. Additionally, the saturation magnetization in ferrites has been observed to decrease with decreasing crystallite size due to the existence of spin canting in nanoparticles [38]. As discussed above, the spin canting originates from the finite-size and the surface effects. Additionally, the size effects in nanoparticles can cause a reduction in the magnetization values compared with the bulk counterpart. Furthermore, the non-linear decrease in Ms value with Tb3+ may also result from the induced strain distorting bond angle (Fe3+–O2−–Fe3+ (Tb3+)), which could weaken the superexchange interaction. Additionally, with the doping, NiFe2-xTbxO4 may move from a mixed spinel to inverse spinel structure [16,39], resulting in the large cancelation of moments between two sites. The HC value of the NiFe2-xTbxO4 measured from the M(H) loops at 300 K is shown in the inset of Figure 1b. The HC value decreased with the Tb3+ content. The HC value of ferrite NPs is reported to be sensitive to a synthesis method including heat treatment, particle size, and anisotropy constant. It is known that the effective anisotropy constant increases with decreasing particle sizes, as dictated by the expression for spherical nanoparticles as Keff = KV + 6/d (Ks), where Keff, KV, and KS denote the effective, volume, and surface anisotropy constants, respectively [40]. With the grain refinement upon Tb3+ substitution, the thermal energy becomes enough to overcome the volume-dependent anisotropy energy (KeffV), enabling the easier reversal of the moments, thereby leading to the lower critical fields for these small-size nanoparticles [41,42]. This leads to a decrease in the coercivity of particles with increasing Tb3+ content. The squareness ratio value rapidly decreased from the 0.44 for x = 0.0 to 0.20 for x = 0.1 sample. According to the Stoner–Wohlfarth theory, the squareness ratio can take two values including one around 0.83 associated with the cubic anisotropy and another around 0.5 that corresponds to uniaxial anisotropy [43]. The squareness ratio value, Mr/Ms ≥ 0.5 indicates that the particles are in the single magnetic domain, and those <0.5 indicate particles with a multi-domain structure [35]. Furthermore, squareness ratio is a characteristic parameter of the prepared samples and depends on the anisotropy, indicating the ease with which the magnetization direction is reoriented to the nearest easy axis magnetization direction after the magnetic field is removed. The lower the Mr/Ms ratio value, the less anisotropic the material will be. The values of the Mr/Ms value ranges from 0.45 to 0.17 with increasing Tb3+ content from x = 0 to 0.1, Table 2. Additionally, the low value of Mr/Ms can be attributed to the increased fraction of superparamagnetic fraction and spin canting [44].
Isothermal magnetization, M, for the NiFe2-xTbxO4, is displayed in Figure 2a,b. Figure 2c shows the magnetization reduction with the temperature for all samples. The temperature-dependent reduction in magnetization could result from the breaking of ground state ferro/ferrimagnetic spin order by low energy excitations of the spins in the core and the disordered surface of ferromagnetic nanoparticles. The anisotropy constant, K1, for NiFe2-xTbxO4 samples were obtained from fitting the M vs. H data, Figure 2a,b to the expression [16], M = Ms [1 − (8/105)(K1/MsH)2] = Ms(1 − β/H2), where β = (8/105)(K1/Ms)2, consequently, the slope of the linear fitting provides the constant β, which is related to the magnetocrystalline anisotropy constant K1, via, K1 = Ms(105β/8)1/2. The numerical coefficient 8/105 holds for random polycrystalline samples with cubic anisotropy. The calculated value of K1 as a function of temperature for the NiFe2-xTbxO4 samples is plotted in Figure 2d and is listed in Table 2. The determined value of K1 for NiFe2O4 at 5 K was 3.90 × 105 J/m3, and at 300 K was 2.51 × 105 J/m3. These values agreed with the earlier reported K1 values measured at room temperature for nanocrystalline ferrites such as CoFe2O4 (2 × 106 J/m3), MnFe2O4 (3 × 104 J/m3), NiFe2O4 (0.7 × 105 J/m3), and Fe3O4 (0.9 × 105 J/m3) [45]. From Figure 2d, it is observed that the (1) K1 value decreases with the temperature, and (2) K1 increases with the Tb3+ content. The magnetocrystalline anisotropy depends on the crystalline field created by the ions in the environment of a given magnetic ion. While the magnetic anisotropy dictates the preferential alignment of spins along one direction and this magnetic anisotropy may originate for the sample shape, the stress, the surface structure of the grains, and by the crystalline structure of the grains. Higher K1 value was recorded for the Tb3+ doped samples at all temperatures in comparison to that of the undoped NiFe2O4 samples. Due to the so-called orbital quenching in the weak ligand field, transition metal oxides are marked by weak spin-orbit coupling [46,47]; however, the hybridization of Fe 3d-orbitals with O 2p-orbitals may occur if there are some distorted Fe-polyhedra in the non-ideal lattice [48,49]. Thus, the unquenched orbitals can increase magnetocrystalline anisotropy. This could possibly be the reason for the observed increase in K1 value in doped NiFe2−xTbxO4. Furthermore, surface anisotropy also adds to the effective anisotropy value with the grain refinement upon Tb3+ substitution [50]. The low-temperature K1 values are one order of magnitude larger than that at 300 K. This is indicative of the presence of inter-particle interaction, which is more marked for smaller particles that get unblocked at lower temperatures. However, the K1 value increases with Tb content. This increase in K1 could be related to the grain size reduction along with a reduction in Ms value due to magnetic dilution [51,52].
The Curie temperature (Neel temperature for the ferrimagnetic system), Tc, of all samples is listed in Table 2. A decreasing trend in Tc was observed with the increase in Tb3+ content in NiFe2−xTbxO4, reaching a value of 899 K for x = 0.1, Figure 1d. The measured Tc of pure NiFe2O4 was ~938 K. Thus, an ~6% reduction for Tc was noticed for the x = 0.1 sample. This Tc reduction could result from (1) the decrease in the number of pairs of some super-exchange interactions due to the magnetic dilution effect; (2) spin canting; and (3) the strength of interaction due to the Fe3+–O2−–Fe3+ bond angle deviation from the optimum angle for super-exchange interaction [53,54].

4. Summary

The substitution of a small amount of Tb3+ for Fe3+ affects the structural and magnetic properties of the ferrite. The substitution Fe3+ with larger ionic size Tb3+ leads to lattice expansion and possibly Fe3+–O2−–Fe3+ bond angle distortion, which eventually weakens super-exchange interaction. The decrease in the Ms, Mr/Ms, and Tc is the result of the weakening of super-exchange interaction. The substitution of Tb3+ at the B site was observed to improve magnetocrystalline anisotropy K1. On the other hand, K1 decreased with the temperature. The effect of Tb3+ ion substitution in NiFe2O4 was to create a moderate reduction in Ms and Tc, but a significant reduction in coercivity. This makes the rare-earth-doped ferrite, NiFe2−xTbxO4, a better candidate for soft-magnetic applications such as inductor cores and high-frequency applications.

Author Contributions

Conceptualization, S.R.M. and D.G.; methodology, D.G. and T.P.P.; software, S.Y., B.K.R. and D.G.; validation, S.R.M., B.K.R. and S.Y.; formal analysis, S.R.M. and D.G.; investigation, S.R.M.; resources, S.R.M.; data curation, D.G. and S.C.B.; writing—original draft preparation, D.G.; writing—review and editing, S.R.M.; visualization, D.G.; supervision, S.R.M.; project administration, S.R.M.; funding acquisition, S.R.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Pérez, E.; Marquez, G.; Sagredo, V. Effect of calcination on characteristics of nickel ferrite nanoparticles synthesized by sol-gel method. Iraqi J. Appl. Phys. 2019, 15, 13–17. [Google Scholar]
  2. Dixit, G.; Negi, P.; Singh, J.P.; Srivastava, R.C.; Agrawal, H.M. Effect of Ce Doping on the Magnetic Properties of NiFe2O4 Nanoparticles. J. Supercond. Nov. Magn. 2013, 26, 1015–1019. [Google Scholar] [CrossRef]
  3. Singhal, S.; Chandra, K. Cation distribution and magnetic properties in chromium-substituted nickel ferrites prepared using aerosol route. J. Sol. State Chem. 2007, 180, 296–300. [Google Scholar] [CrossRef]
  4. Krishna, K.R.; Ravinder, D.; Kumar, K.V.; Lincon, C.A. Synthesis, XRD & SEM studies of zinc substitution in nickel ferrites by citrate gel technique. World J. Cond. Matt. Phys. 2012, 2, 153. [Google Scholar]
  5. Dormann, J.L.; Nogues, M. Magnetic structures in substituted ferrites. J. Phys. Cond. Matt. 1990, 2, 1223. [Google Scholar] [CrossRef]
  6. Rezlescu, N.; Rezlescu, E.; Pasnicu, C.; Craus, M.L. Effects of the rare-earth ions on some properties of a nickel-zinc ferrite. J. Phys. Cond. Matt. 1994, 6, 5707. [Google Scholar] [CrossRef]
  7. Virden, A.E.; O’Grady, K. Structure and magnetic properties of NiZn ferrite nanoparticles. J. Magn. Magn. Mater. 2005, 290, 868–870. [Google Scholar] [CrossRef]
  8. Batoo, K.M. Microstructural and Mössbauer properties of low temperature synthesized Ni-Cd-Al ferrite nanoparticles. Nanoscale Res. Let. 2011, 6, 499. [Google Scholar] [CrossRef] [Green Version]
  9. Sharma, R.K.; Suwalka, O.P.; Lakshmi, N.; Venugopalan, K. Hyperfine fields in nano particles of Cr0.25Co0.25Zn0.5Fe2O4. Indian J. Pure Appl. Phys. 2007, 45, 830–833. [Google Scholar]
  10. Wang, L.; Rai, B.K.; Mishra, S.R. Structural and magnetic study of Al3+ doped Ni0.75Zn0.25Fe2−xAlxO4 nanoferrites. Mater. Res. Bull. 2015, 65, 183–194. [Google Scholar] [CrossRef]
  11. Borhan, A.I.; Iordan, A.R.; Palamaru, M.N. Correlation between structural, magnetic and electrical properties of nanocrystalline Al3+ substituted zinc ferrite. Mater. Res. Bull. 2013, 48, 2549–2556. [Google Scholar] [CrossRef]
  12. Hashim, M.; Kumar, S.; Ali, S.; Koo, B.H.; Chung, H.; Kumar, R. Structural, magnetic and electrical properties of Al3+ substituted Ni–Zn ferrite nanoparticles. J. Alloy. Compd. 2012, 511, 107–114. [Google Scholar] [CrossRef]
  13. Lakhani, V.K.; Zhao, B.; Wang, L.; Trivedi, U.N.; Modi, K.B. Negative magnetization, magnetic anisotropy and magnetic ordering studies on Al3+-substituted copper ferrite. J. Alloy. Compd. 2011, 509, 4861–4867. [Google Scholar] [CrossRef]
  14. Lakhani, V.K.; Pathak, T.K.; Vasoya, N.H.; Modi, K.B. Structural parameters and X-ray Debye temperature determination study on copper-ferrite-aluminates. Solid State Sci. 2011, 13, 539–547. [Google Scholar] [CrossRef]
  15. Sharifi, I.; Shokrollahi, H. Structural, magnetic and Mössbauer evaluation of Mn substituted Co–Zn ferrite nanoparticles synthesized by co-precipitation. J. Magn. Magn. Mater. 2013, 334, 36–40. [Google Scholar] [CrossRef]
  16. Poudel, T.P.; Rai, B.K.; Yoon, S.; Guragain, D.; Neupane, D.; Mishra, S.R. The effect of gadolinium substitution in inverse spinel nickel ferrite: Structural, Magnetic, and Mössbauer study. J. Alloy. Compd. 2019, 802, 609–619. [Google Scholar] [CrossRef]
  17. Jacob, B.P.; Kumar, A.; Pant, R.P.; Singh, S.; Mohammed, E.M. Influence of preparation method on structural and magnetic properties of nickel ferrite nanoparticles. B. Mater. Sci. 2011, 34, 1345–1350. [Google Scholar] [CrossRef]
  18. Sontu, U.B.; Yelasani, V.; Musugu, V.R.R. Structural, electrical and magnetic characteristics of nickel substituted cobalt ferrite nano particles, synthesized by self combustion method. J. Magn. Magn. Mater. 2015, 374, 376–380. [Google Scholar] [CrossRef]
  19. Almessiere, M.A.; Slimani, Y.; Güngüneş, H.; Ali, S.; Manikandan, A.; Ercan, I.; Baykal, A.; Trukhanov, A.V. Magnetic attributes of NiFe2O4 nanoparticles: Influence of dysprosium Ions (Dy3+) substitution. Nanomaterials 2019, 9, 820. [Google Scholar] [CrossRef] [Green Version]
  20. Cheng, F.X.; Jia, J.T.; Xu, Z.G.; Zhou, B.; Liao, C.S.; Yan, C.H.; Chen, L.Y.; Zhao, H.B. Microstructure, magnetic, and magneto-optical properties of chemical synthesized Co–RE (RE= Ho, Er, Tm, Yb, Lu) ferrite nanocrystalline films. J. Appl. Phys. 1999, 86, 2727–2732. [Google Scholar] [CrossRef]
  21. Morrish, A.H. The physical principles of magnetism. In The Physical Principles of Magnetism; Morrish, A.H., Ed.; Wiley-VCH: Hoboken, NJ, USA, 2001; p. 696. [Google Scholar]
  22. Bharathi, K.K.; Chelvane, J.A.; Markandeyulu, G. Magnetoelectric properties of Gd and Nd-doped nickel ferrite. J. Magn. Magn. Mater. 2009, 321, 3677–3680. [Google Scholar] [CrossRef]
  23. Şabikoğlu, İ.; Paralı, L.; Malina, O.; Novak, P.; Kaslik, J.; Tucek, J.; Pechousek, J.; Navarik, J.; Schneeweiss, O. The effect of neodymium substitution on the structural and magnetic properties of nickel ferrite. Prog. Nat. Sci. Mater. 2015, 25, 215–221. [Google Scholar] [CrossRef] [Green Version]
  24. Lueken, H. Course of Lectures on Magnetism of Lanthanide Ions under Varying Ligand and Magnetic Fields; Institute of Inorganic Chemistry, RWTH Aachen: Aachen, Germany, 2008. [Google Scholar]
  25. Jacob, B.P.; Thankachan, S.; Xavier, S.; Mohammed, E.M. Effect of Tb3+ substitution on structural, electrical and magnetic properties of sol–gel synthesized nanocrystalline nickel ferrite. J. Alloy. Compd. 2013, 578, 314–319. [Google Scholar] [CrossRef]
  26. Smith, J.; Wijn, H.P.J. Ferrites; John Wiley: New York, NY, USA, 1959. [Google Scholar]
  27. Pandit, A.A.; More, S.S.; Dorik, R.G.; Jadhav, K.M. Structural and magnetic properties of Co1+ySnyFe2-2y-xCrxO4 ferrite system. B Mater. Sci. 2003, 26, 517–521. [Google Scholar] [CrossRef]
  28. Abbas, T.J. X-ray Diffraction and Site Preference Analysis of Ni-Substituted MgFe2O4 Ferrites. J. Appl. Sci. 2002, 2, 1110–1114. [Google Scholar]
  29. Wohlfarth, E.P. Ferromagnetic Materials; North-Holland Publication Co.: Amsterdam, The Netherlands, 1982. [Google Scholar]
  30. Dhiman, R.L.; Taneja, S.P.; Reddy, V.R. Preparation and Characterization of Manganese Ferrite Aluminates. Adv. Condens. Matter Phys. 2008, 7. [Google Scholar] [CrossRef] [Green Version]
  31. Waldron, R.D. Infrared spectra of ferrites. Phys. Rev. 1955, 99, 1727. [Google Scholar] [CrossRef]
  32. Hemeda, O.M.; Barakat, M.M.; Hemeda, D.M. Structural, Electrical and Spectral Studies on Double Rare-Earth Orthoferrites La{1-x} NdxFeO3. J. Turk. Phys. 2003, 27, 537. [Google Scholar]
  33. Shinde, T.J.; Gadkari, A.B.; Vasambekar, P.N. Influence of Nd3+ substitution on structural, electrical and magnetic properties of nanocrystalline nickel ferrites. J. Alloy. Compd. 2012, 513, 80–85. [Google Scholar] [CrossRef]
  34. Evans, B.J.; Hafner, S.S. Mössbauer resonance of Fe57 in oxidic spinels containing Cu and Fe. J. Phys. Chem. Solids 1968, 29, 1573–1588. [Google Scholar] [CrossRef]
  35. Modi, K.B.; Rangolia, M.K.; Chhantbar, M.C.; Joshi, H.H. Study of infrared spectroscopy and elastic properties of fine and coarse grained nickel–cadmium ferrites. J. Mater. Sci. 2006, 41, 7308–7318. [Google Scholar] [CrossRef]
  36. Kodama, R.H.; Berkowitz, A.E.; McNiff, E.J., Jr.; Foner, S. Surface spin disorder in NiFe2O4 nanoparticles. Phys. Rev. Lett. 1996, 77, 394–397. [Google Scholar] [CrossRef] [PubMed]
  37. Berkowitz, A.E.; Kodama, R.H.; Makhlouf, S.A.; Parker, F.T.; Spada, F.E.; McNiff, E.J., Jr.; Foner, S. Anomalous properties of magnetic nanoparticles. J. Magn. Magn. Mater. 1999, 196, 591–594. [Google Scholar] [CrossRef]
  38. Hemeda, O.M.; Said, M.Z.; Barakat, M.M. Spectral and transport phenomena in Ni ferrite-substituted Gd2O3. J. Magn. Magn. Mater. 2001, 224, 132–142. [Google Scholar] [CrossRef]
  39. Šepelák, V.; Baabe, D.; Mienert, D.; Schultze, D.; Krumeich, F.; Litterst, F.J.; Becker, K.D. Evolution of structure and magnetic properties with annealing temperature in nanoscale high-energy-milled nickel ferrite. J. Magn. Magn. Mater. 2003, 257, 377–386. [Google Scholar] [CrossRef]
  40. Bødker, F.; Mørup, S.; Linderoth, S. Surface effects in metallic iron nanoparticles. Rev. Lett. 1994, 72, 282. [Google Scholar] [CrossRef] [Green Version]
  41. Pfeiffer, H. Determination of anisotropy field distribution in particle assemblies taking into account thermal fluctuations. Phys. Status solidi A 1990, 118, 295–306. [Google Scholar] [CrossRef]
  42. Vestal, C.R.; Zhang, Z.J. Synthesis and magnetic characterization of Mn and Co spinel ferrite-silica nanoparticles with tunable magnetic core. Nano. Lett. 2003, 3, 1739–1743. [Google Scholar] [CrossRef]
  43. Stoner, E.C.; Wohlfarth, E.P. Philos. Handbook of Nanomaterials for Industrial Applications. T. R. Soc. S-A 1948, 240, 599–642. [Google Scholar]
  44. Jiang, J.Z.; Goya, G.F.; Rechenberg, H.R. Magnetic properties of nanostructured CuFe2O4. J. Phys. Condens Mat. 1999, 11, 4063. [Google Scholar] [CrossRef] [Green Version]
  45. Robert, C.O.; Handley, O. Modern Magnetic Materials: Principles and Applications; John Wiley & Sons, Inc.: New York, NY, USA, 2000. [Google Scholar]
  46. Merer, A.J. Spectroscopy of the diatomic 3d transition metal oxides. Annu. Rev. Phys. Chem. 1989, 40, 407–438. [Google Scholar] [CrossRef]
  47. Ham, F.S. Dynamical Jahn-Teller effect in paramagnetic resonance spectra: Orbital reduction factors and partial quenching of spin-orbit interaction. Phys. Rev. 1965, 138, A1727–A1740. [Google Scholar] [CrossRef]
  48. Kim, J.Y.; Koo, T.Y.; Park, J.H. Orbital and bonding anisotropy in a half-filled GaFeO3 magnetoelectric ferrimagnet. Phys. Rev. Lett. 2006, 96, 047205–047209. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  49. Arima, T.; Higashiyama, D.; Kaneko, Y.; He, J.P.; Goto, T.; Miyasaka, S.; Kimura, T.; Oikawa, K.; Kamiyama, T.; Kumai, R.; et al. Structural and magnetoelectric properties of Ga2−xFexO3 single crystals grown by a floating-zone method. Phys. Rev. B 2004, 70, 064426. [Google Scholar] [CrossRef]
  50. Yoon, S.; Krishnan, K.M. Temperature dependence of magnetic anisotropy constant in manganese ferrite nanoparticles at low temperature. J. Appl. Phys. 2011, 109, 07B534. [Google Scholar] [CrossRef] [Green Version]
  51. Shenker, H. Magnetic anisotropy of cobalt ferrite (Co1.01Fe2.00O3.62) and nickel cobalt ferrite (Ni0.72 Fe0.20Co0.08Fe2O4). Phys. Rev. 1957, 107, 1246. [Google Scholar] [CrossRef]
  52. Gao, R.W.; Feng, W.C.; Liu, H.Q.; Wang, B.; Chen, W.; Han, G.B.; Zhang, P.; Li, H.; Li, W.; Guo, Y.Q.; et al. Exchange-coupling interaction, effective anisotropy and coercivity in nanocomposite permanent materials. J. Appl. Phys. 2003, 94, 664–668. [Google Scholar] [CrossRef]
  53. Gilleo, M.A. Superexchange interaction energy for Fe3+-O2−-Fe3+ linkages. Phys. Rev. 1958, 109, 777. [Google Scholar] [CrossRef]
  54. Goldman, A. Modern Ferrite Technology; Van Nostrand Reinhold: New York, NY, USA, 1990; p. 145. [Google Scholar]
Magnetochemistry 06 00014 g001 550
Figure 1. (a) X-ray diffraction (XRD) patterns of the NiTbxFe2−xO4 (0.0 ≤ x ≤ 0.1) nanoparticles. (b) Hysteresis loops at room temperature, M vs. H of NiTbxFe2−xO4. (c) Fourier transform infrared spectra of NiTbxFe2−xO4. (d) Thermogravimetric Analysis (TGA) curves of NiTbxFe2−xO4. TGA measurement was done in the presence of the magnetic field, thus the %Wt. change refers to the change in magnetic force.
Figure 1. (a) X-ray diffraction (XRD) patterns of the NiTbxFe2−xO4 (0.0 ≤ x ≤ 0.1) nanoparticles. (b) Hysteresis loops at room temperature, M vs. H of NiTbxFe2−xO4. (c) Fourier transform infrared spectra of NiTbxFe2−xO4. (d) Thermogravimetric Analysis (TGA) curves of NiTbxFe2−xO4. TGA measurement was done in the presence of the magnetic field, thus the %Wt. change refers to the change in magnetic force.
Magnetochemistry 06 00014 g001
Magnetochemistry 06 00014 g002 550
Figure 2. (a) Magnetic isotherms. (a) x = 0.000 and (b) x = 0.100 Tb3+ content in NiTbxFe2−xO4. (c) Magnetization vs. temperature curves as a function of Tb3+ content in NiTbxFe2−xO4 recorded at the 60 kOe field. (d) K1 obtained from fitting M vs. T using the law of approach to the saturation magnetization for NiTbxFe2−xO4 as a function of Tb3+ content.
Figure 2. (a) Magnetic isotherms. (a) x = 0.000 and (b) x = 0.100 Tb3+ content in NiTbxFe2−xO4. (c) Magnetization vs. temperature curves as a function of Tb3+ content in NiTbxFe2−xO4 recorded at the 60 kOe field. (d) K1 obtained from fitting M vs. T using the law of approach to the saturation magnetization for NiTbxFe2−xO4 as a function of Tb3+ content.
Magnetochemistry 06 00014 g002
Table
Table 1. Values from the magnetic isotherms and Curie temperature, Tc, of NiTbxFe2−xO4.
Table 1. Values from the magnetic isotherms and Curie temperature, Tc, of NiTbxFe2−xO4.
xMs
(emu/g)		Mr
(emu/g)		Mr/MsHc (Oe)K1 × 105
(5K) (J/m3)		K1 × 105
(300K) (J/m3)		Tc (K)
0.00044.519.80.443633.92.5938
0.02538.611.90.303088.35.7923
0.05036.110.80.292216.35.6913
0.07534.78.60.2510210.16.5903
0.10030.66.20.2015710.96.3899
Table
Table 2. Lattice parameters and Bond length of A-sites dAL and B-sites dBL, the tetrahedral edge dAE, the shared and unshared octahedral edges, dBE and dBEU and the hopping length at A-site LA and B- site LB for NiTbxFe2-xO4 samples.
Table 2. Lattice parameters and Bond length of A-sites dAL and B-sites dBL, the tetrahedral edge dAE, the shared and unshared octahedral edges, dBE and dBEU and the hopping length at A-site LA and B- site LB for NiTbxFe2-xO4 samples.
xLattice
Parameter
(Å)		Avg.
Crystallite
size (nm)		X-ray
Density
(g/cm3)		dAL (Å)dBL (Å)dAE (Å)dBE (Å)dBEU (Å)LA (Å)LB (Å)
0.0008.3039(06)36.415.441.88552.02653.07912.79262.93763.59562.9358
0.0258.3076(04)25.425.491.88642.02753.08052.79382.93893.59732.9371
0.0508.3089(04)22.495.551.88672.02783.08092.79422.93933.59792.9376
0.0758.3093(02)17.505.611.88682.02793.08112.79442.93953.59802.9378
0.1008.3105 (05)16.005.661.88702.02813.08152.79482.93993.59852.9382

Share and Cite

MDPI and ACS Style

Guragain, D.; Rai, B.K.; Yoon, S.; Poudel, T.P.; Bhandari, S.C.; Mishra, S.R. Effect of Terbium Ion Substitution in Inverse Spinel Nickel Ferrite: Structural and Magnetic Study. Magnetochemistry 2020, 6, 14. https://doi.org/10.3390/magnetochemistry6010014

AMA Style

Guragain D, Rai BK, Yoon S, Poudel TP, Bhandari SC, Mishra SR. Effect of Terbium Ion Substitution in Inverse Spinel Nickel Ferrite: Structural and Magnetic Study. Magnetochemistry. 2020; 6(1):14. https://doi.org/10.3390/magnetochemistry6010014

Chicago/Turabian Style

Guragain, Deepa, Binod Kumar Rai, Sunghyun Yoon, Tej Prasad Poudel, Subash Chandra Bhandari, and Sanjay R Mishra. 2020. "Effect of Terbium Ion Substitution in Inverse Spinel Nickel Ferrite: Structural and Magnetic Study" Magnetochemistry 6, no. 1: 14. https://doi.org/10.3390/magnetochemistry6010014

APA Style

Guragain, D., Rai, B. K., Yoon, S., Poudel, T. P., Bhandari, S. C., & Mishra, S. R. (2020). Effect of Terbium Ion Substitution in Inverse Spinel Nickel Ferrite: Structural and Magnetic Study. Magnetochemistry, 6(1), 14. https://doi.org/10.3390/magnetochemistry6010014

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop