A Dinuclear Dysprosium(III) Single Molecule Magnet of Benzo[h]quinolin-10-ol
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Synthesis of [Dy2(HOBQ)4Cl6] (1)
2.3. X-Ray Data Collection and Structure Refinement
3. Results
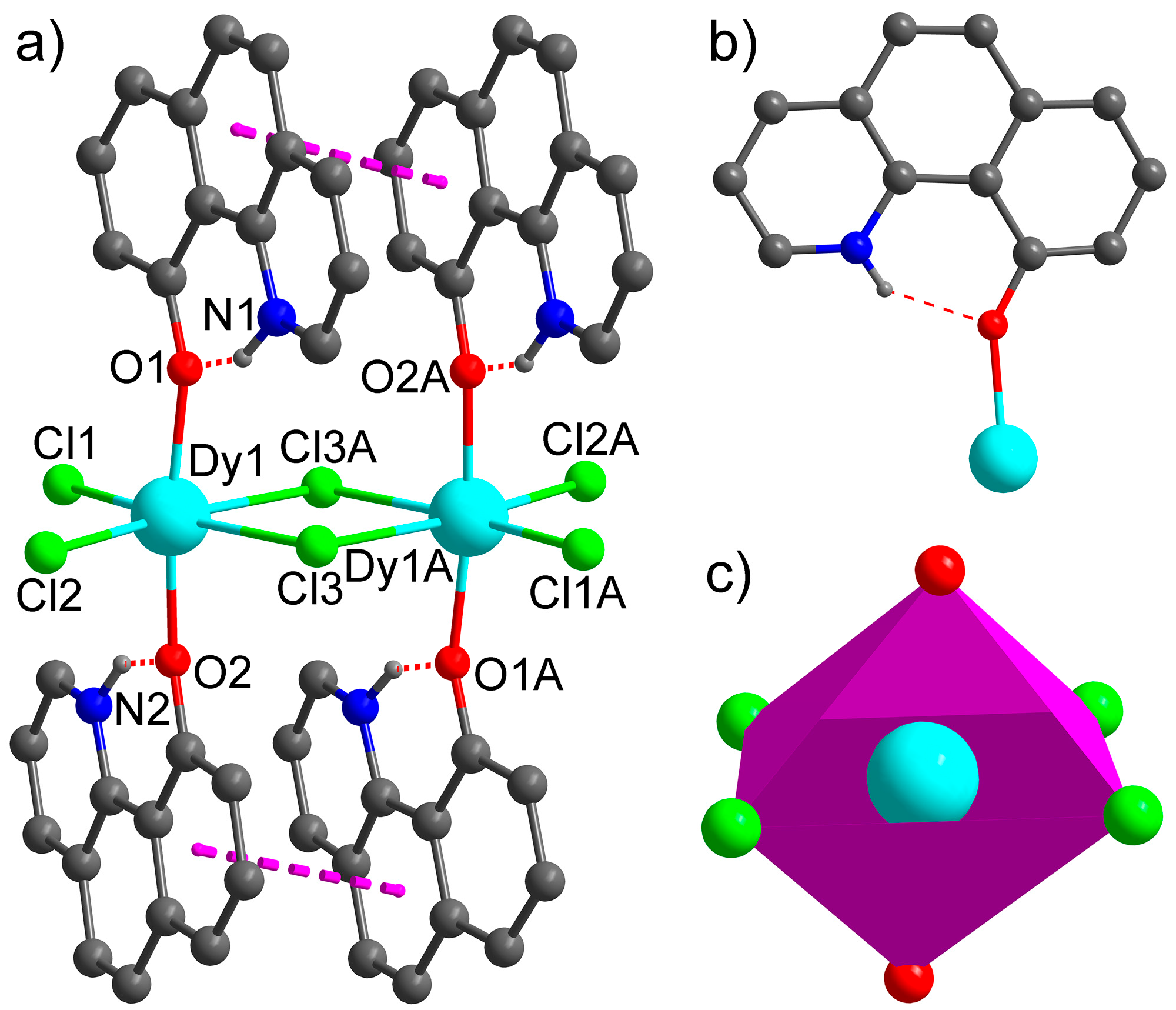
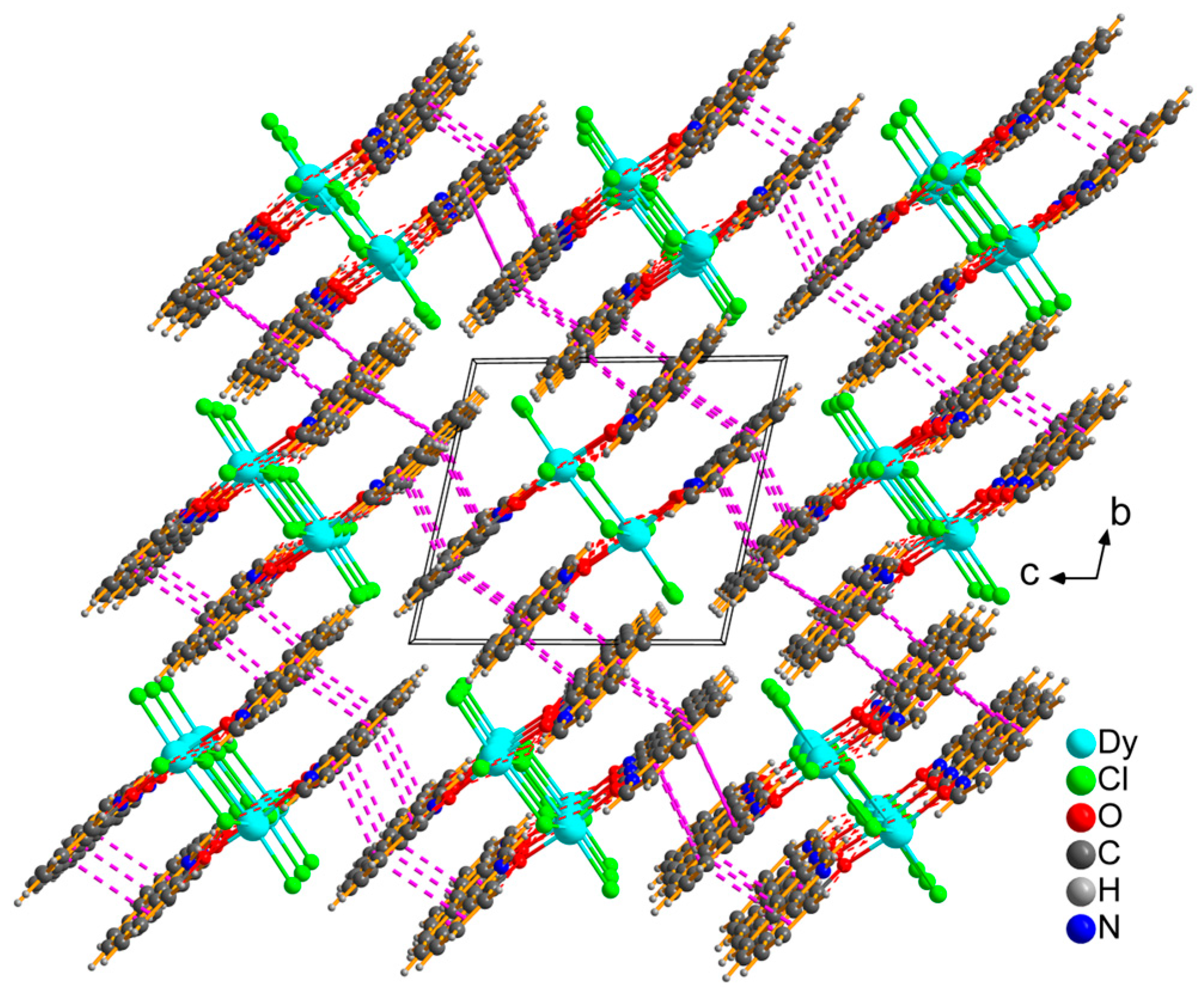
3.1. Synthesis and Structural Characterization of 1
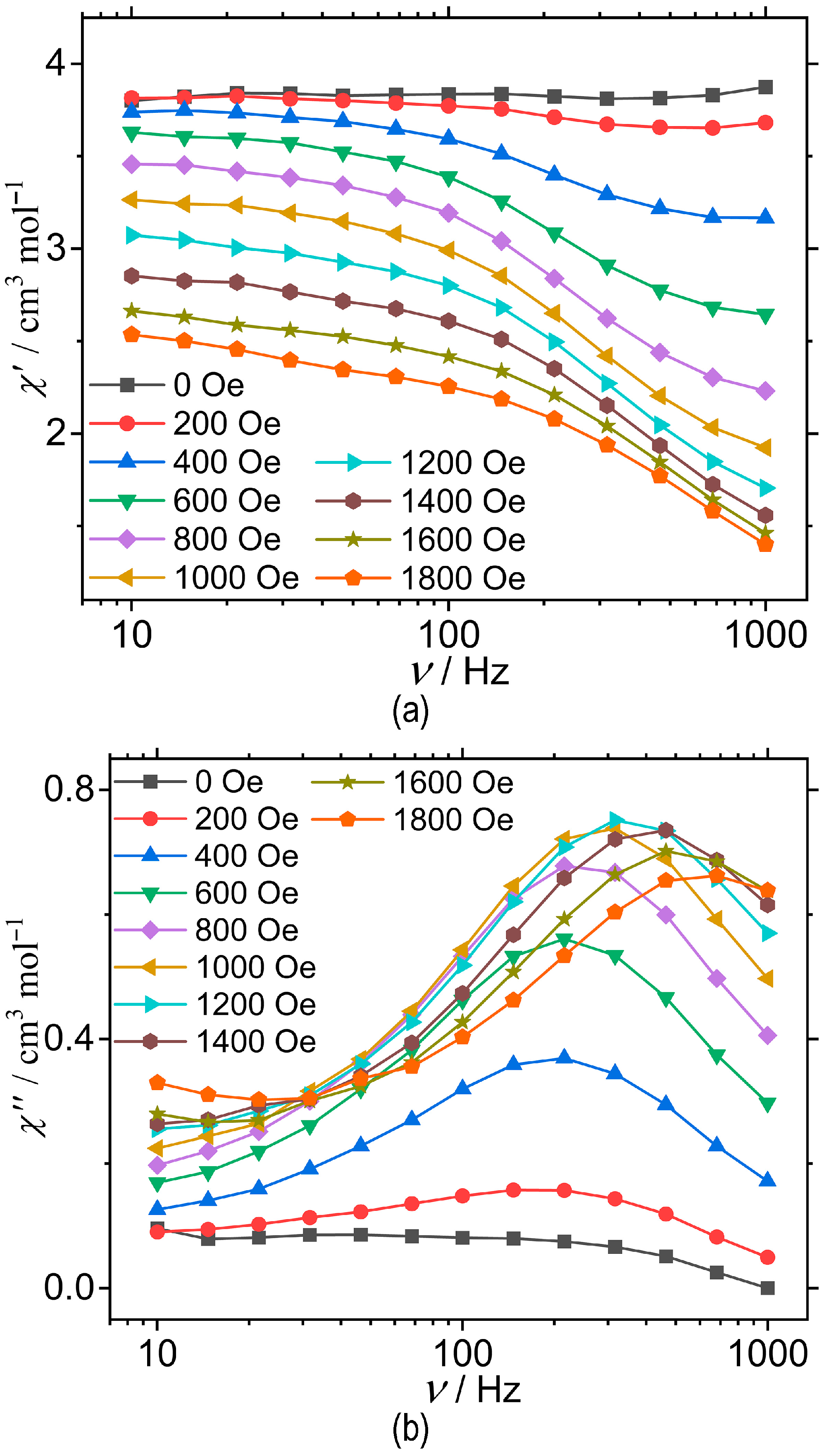
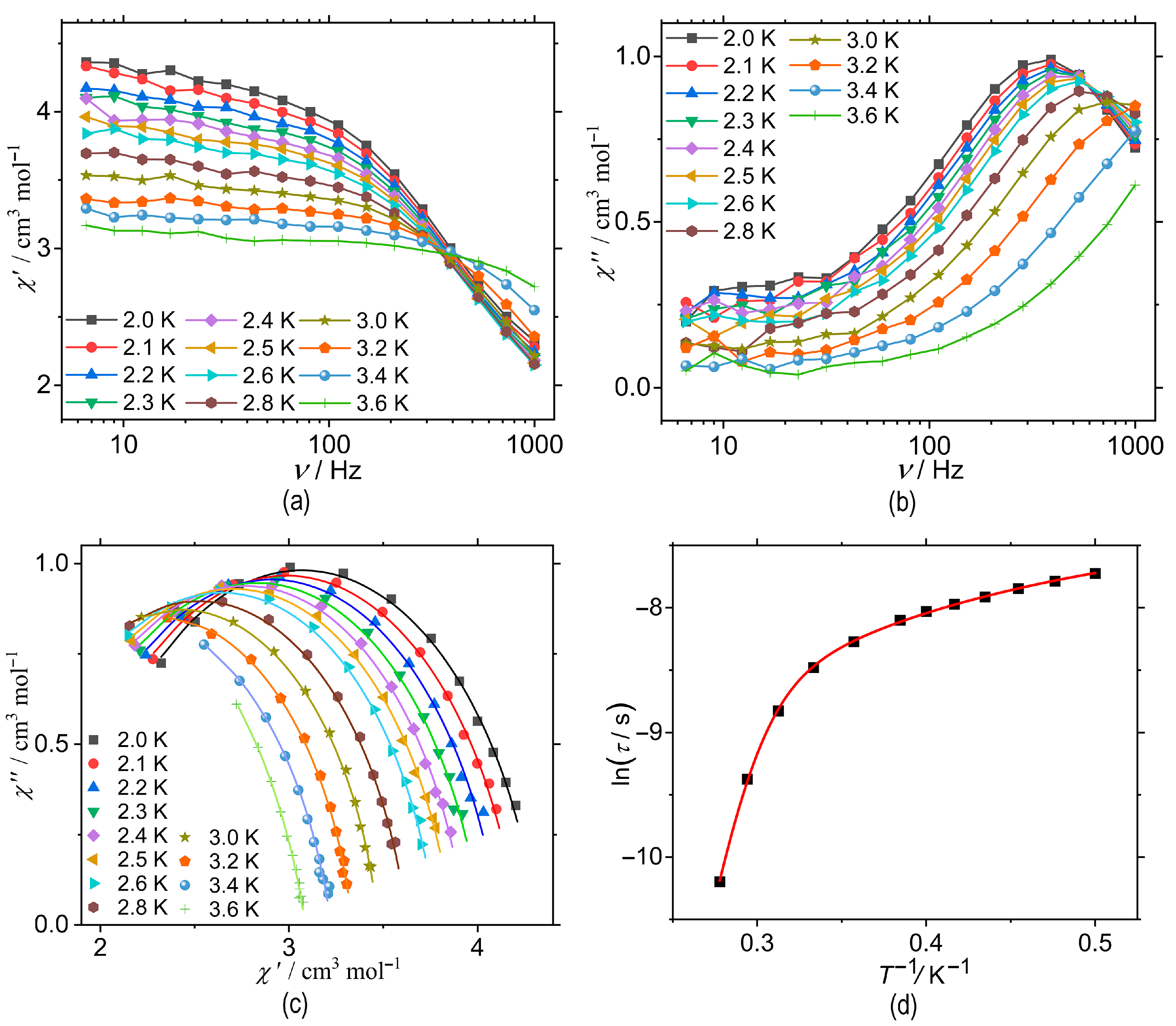
3.2. Magnetic Properties
3.3. Theoretical Calculation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Benner, F.; Jena, R.; Odom, A.L.; Demir, S. Magnetic Hysteresis in a Dysprosium Bis(amide) Complex. J. Am. Chem. Soc. 2025, 147, 8156–8167. [Google Scholar] [CrossRef]
- Kong, H.; Wang, J.-Y.; Liu, J.-C.; Zhang, L.; Liao, P.-Y.; Qi, Y.-Q.; Liu, Z.; Wu, S.-G.; Tong, M.-L. Photochromic Dysprosium Single-Molecule Magnet Featuring Reversible Redox Transformation of Polyoxomolybdate Moiety. Angew. Chem. Int. Ed. 2025, 64, e202422557. [Google Scholar] [CrossRef]
- Ling, B.-K.; Chang, M.; Zhai, Y.-Q.; Deng, J.; Kofu, M.; Guo, H.; Zhao, J.; Fu, Z.; Zheng, Y.-Z. Quantum Spin Wave Excited from a Cr–Dy Single-Molecule Magnet. J. Am. Chem. Soc. 2025, 147, 10935–10942. [Google Scholar] [CrossRef] [PubMed]
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Qu, Y.-X.; Liao, P.-Y.; Chen, Y.-C.; Tong, M.-L. Functional lanthanide complexes with N,N′-bis(2-hydroxybenzyl)-N,N′-bis(pyridin-2-ylmethyl)ethylenediamine (H2bbpen) derivatives: Coordination chemistry, single-molecule magnetism and optical properties. Coord. Chem. Rev. 2023, 475, 214880. [Google Scholar] [CrossRef]
- Vieru, V.; Gómez-Coca, S.; Ruiz, E.; Chibotaru, L.F. Increasing the Magnetic Blocking Temperature of Single-Molecule Magnets. Angew. Chem. Int. Ed. 2023, 63, e202303146. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.-B.; Gui, L.-A.; Li, L.-H.; Xiao, T.-T.; Hand, A.T.; Tin, P.; Ozerov, M.; Peng, Y.; Ouyang, Z.; Wang, Z.; et al. CoII single-ion magnet and its multi-dimensional aggregations: Influence of the structural rigidity on magnetic relaxation process. Chin. Chem. Lett. 2025, 36, 109600. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhao, C.; Feng, T.; Liu, X.; Ying, X.; Li, X.-L.; Zhang, Y.-Q.; Tang, J. Air-Stable Chiral Single-Molecule Magnets with Record Anisotropy Barrier Exceeding 1800 K. J. Am. Chem. Soc. 2021, 143, 10077–10082. [Google Scholar] [CrossRef]
- Xu, W.-J.; Luo, Q.-C.; Li, Z.-H.; Zhai, Y.-Q.; Zheng, Y.-Z. Bis-Alkoxide Dysprosium(III) Crown Ether Complexes Exhibit Tunable Air Stability and Record Energy Barrier. Adv. Sci. 2024, 11, 2308548. [Google Scholar] [CrossRef]
- Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef]
- Ding, Y.-S.; Chilton, N.F.; Winpenny, R.E.P.; Zheng, Y.-Z. On Approaching the Limit of Molecular Magnetic Anisotropy: A Near-Perfect Pentagonal Bipyramidal Dysprosium(III) Single-Molecule Magnet. Angew. Chem. Int. Ed. 2016, 55, 16071–16074. [Google Scholar] [CrossRef] [PubMed]
- Peng, S.; Ouyang, X.; Wang, Y.; Teng, Q.; Li, Y.; Zhang, X.; Hu, Z.; Wang, K.; Liang, F. In situ synthesized homochiral dysprosium-oxo clusters with threonine Schiff bases. Chin. Chem. Lett. 2023, 34, 108044. [Google Scholar] [CrossRef]
- Armenis, A.S.; Bakali, G.P.; Paul, S.; Pantelis, K.N.; Cunha-Silva, L.; Tang, J.; Alexandropoulos, D.I.; Wernsdorfer, W.; Moreno-Pineda, E.; Stamatatos, T.C. Deciphering the Magnetostructural Criteria in DyIII and HoIII Macrocycle-Based Single-Molecule Magnets with Pseudo-D5h Symmetry: A Combined Single-Crystal Hysteresis and Theoretical Study. Inorg. Chem. 2025, 64, 11476–11489. [Google Scholar] [CrossRef]
- Baka, K.H.; Liu, D.; Paul, S.; Wernsdorfer, W.; Tang, J.; Chibotaru, L.F.; Stamatatos, T.C. Unveiling the Werner-Type Cluster Chemistry of Heterometallic 4f/Post-Transition Metals: A {Dy3Bi8} Complex Exhibiting Quantum Tunneling Steps in the Hysteresis Loops and its 1-D Congener. Inorg. Chem. 2025, 64, 1962–1974. [Google Scholar] [CrossRef] [PubMed]
- Armenis, A.S.; Mondal, A.; Giblin, S.R.; Alexandropoulos, D.I.; Tang, J.; Layfield, R.A.; Stamatatos, T.C. ‘Kick-in the head’: High-performance and air-stable mononuclear DyIII single-molecule magnets with pseudo-D6h symmetry from a [1 + 1] Schiff-base macrocycle approach. Inorg. Chem. Front. 2025, 12, 1214–1224. [Google Scholar] [CrossRef]
- Zhu, Z.; Paul, S.; Zhao, C.; Wu, J.; Ying, X.; Ungur, L.; Wernsdorfer, W.; Meyer, F.; Tang, J. Record Quantum Tunneling Time in an Air-Stable Exchange-Bias Dysprosium Macrocycle. J. Am. Chem. Soc. 2024, 146, 18899–18904. [Google Scholar] [CrossRef]
- Du, J.; Wei, S.; Jiang, Z.; Ke, H.; Sun, L.; Zhang, Y.; Chen, S. Influence of lattice water molecules on the magnetization dynamics of binuclear dysprosium(III) compounds: Insights from magnetic and ab initio calculations. Phys. Chem. Chem. Phys. 2023, 25, 11717–11724. [Google Scholar] [CrossRef]
- Zhu, Z.; Ying, X.; Zhao, C.; Zhang, Y.-Q.; Tang, J. A new breakthrough in low-coordinate Dy(III) single-molecule magnets. Inorg. Chem. Front. 2022, 9, 6061–6066. [Google Scholar] [CrossRef]
- Bazhenova, T.A.; Kopotkov, V.A.; Korchagin, D.V.; Yureva, E.A.; Zhidkov, M.V.; Dmitriev, A.I.; Yakushev, I.A.; Efimov, N.N.; Babeshkin, K.A.; Mironov, V.S.; et al. Pentagonal-bipyramidal dysprosium(III) complexes with two apical phosphine oxide ligands and equatorial pentadentate N3O2 Schiff-base ligands: Breakdown of the apical magnetic axiality by a strong equatorial crystal field. Inorg. Chem. Front. 2025, 12, 231–252. [Google Scholar] [CrossRef]
- Wu, X.; Li, J.-F.; Yin, B. The interpretation and prediction of lanthanide single-ion magnets from ab initio electronic structure calculation: The capability and limit. Dalton Trans. 2022, 51, 14793–14816. [Google Scholar] [CrossRef]
- Long, B.-F.; Li, Y.-L.; Zhu, Z.-H.; Wang, H.-L.; Liang, F.-P.; Zou, H.-H. Assembly of pinwheel/twist-shaped chiral lanthanide clusters with rotor structures by an annular/linear growth mechanism and their magnetic properties. Dalton Trans. 2022, 51, 17040–17049. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Tong, M.-L. Single-molecule magnets beyond a single lanthanide ion: The art of coupling. Chem. Sci. 2022, 13, 8716–8726. [Google Scholar] [CrossRef]
- Liu, J.-L.; Chen, Y.-C.; Tong, M.-L. Symmetry strategies for high performance lanthanide-based single-molecule magnets. Chem. Soc. Rev. 2018, 47, 2431–2453. [Google Scholar] [CrossRef]
- Wang, J.; Li, Q.-W.; Wu, S.-G.; Chen, Y.-C.; Wan, R.-C.; Huang, G.-Z.; Liu, Y.; Liu, J.-L.; Reta, D.; Giansiracusa, M.J.; et al. Opening Magnetic Hysteresis by Axial Ferromagnetic Coupling: From Mono-Decker to Double-Decker Metallacrown. Angew. Chem. Int. Ed. 2021, 60, 5299–5306. [Google Scholar] [CrossRef]
- Le Roy, J.J.; Ungur, L.; Korobkov, I.; Chibotaru, L.F.; Murugesu, M. Coupling Strategies to Enhance Single-Molecule Magnet Properties of Erbium–Cyclooctatetraenyl Complexes. J. Am. Chem. Soc. 2014, 136, 8003–8010. [Google Scholar] [CrossRef] [PubMed]
- Hilgar, J.D.; Bernbeck, M.G.; Rinehart, J.D. Million-fold Relaxation Time Enhancement across a Series of Phosphino-Supported Erbium Single-Molecule Magnets. J. Am. Chem. Soc. 2019, 141, 1913–1917. [Google Scholar] [CrossRef]
- Gould, C.A.; McClain, K.R.; Reta, D.; Kragskow, J.G.C.; Marchiori, D.A.; Lachman, E.; Choi, E.-S.; Analytis, J.G.; Britt, R.D.; Chilton, N.F.; et al. Ultrahard magnetism from mixed-valence dilanthanide complexes with metal-metal bonding. Science 2022, 375, 198–202. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Qiu, Y.; Xu, W.; Cao, M.; Deng, X.; Lin, W. Slow magnetic relaxation behaviors and diamagnetic dilution studies of a carboxyl bridged dinuclear dysprosium(III) complex. J. Rare Earths 2024, 42, 2088–2096. [Google Scholar] [CrossRef]
- Long, J.; Habib, F.; Lin, P.-H.; Korobkov, I.; Enright, G.; Ungur, L.; Wernsdorfer, W.; Chibotaru, L.F.; Murugesu, M. Single-Molecule Magnet Behavior for an Antiferromagnetically Superexchange-Coupled Dinuclear Dysprosium(III) Complex. J. Am. Chem. Soc. 2011, 133, 5319–5328. [Google Scholar] [CrossRef]
- Long, J.; Tolpygin, A.O.; Cherkasov, A.V.; Lyssenko, K.A.; Guari, Y.; Larionova, J.; Trifonov, A.A. Single-molecule magnet behavior in heterolopetic Dy3+-chloro-diazabutadiene complexes: Influence of the nuclearity and ligand redox state. Dalton Trans. 2020, 49, 11890–11901. [Google Scholar] [CrossRef] [PubMed]
- Acharya, J.; Ahmed, N.; Flores Gonzalez, J.; Kumar, P.; Cador, O.; Singh, S.K.; Pointillart, F.; Chandrasekhar, V. Slow magnetic relaxation in a homo dinuclear Dy(III) complex in a pentagonal bipyramidal geometry. Dalton Trans. 2020, 49, 13110–13122. [Google Scholar] [CrossRef]
- Kalita, P.; Ahmed, N.; Bar, A.K.; Dey, S.; Jana, A.; Rajaraman, G.; Sutter, J.-P.; Chandrasekhar, V. Pentagonal Bipyramidal Ln(III) Complexes Containing an Axial Phosphine Oxide Ligand: Field-induced Single-ion Magnetism Behavior of the Dy(III) Analogues. Inorg. Chem. 2020, 59, 6603–6612. [Google Scholar] [CrossRef]
- Zhu, W.-H.; Xiong, X.; Gao, C.; Li, S.; Zhang, Y.; Wang, J.; Zhang, C.; Powell, A.K.; Gao, S. A family of one-dimensional lanthanide complexes bridged by two distinct carboxylate ligands with the Dy analogue displaying magnetic relaxation behaviour. Dalton Trans. 2017, 46, 14114–14121. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-H.; Gao, Z.-N.; Liang, S.; Wei, W.-J.; Han, S.-D.; Zhang, Y.-Q.; Hu, J.-X.; Wang, G.-M. Synergism of Light-Induced [4 + 4] Cycloaddition and Electron Transfer Toward Switchable Photoluminescence and Single-Molecule Magnet Behavior in a Dy4 Cubane. Research 2024, 7, 0411. [Google Scholar] [CrossRef]
- Zhang, Q.; Han, S.-D.; Li, Q.; Hu, J.-X.; Wang, G.-M. Electron transfer photochromism of Ln-based (Ln = Dy, Tb) coordinated polymers for reversibly switching off/on single-molecule magnetic behavior. Sci. China Mater. 2022, 65, 788–794. [Google Scholar] [CrossRef]
- Chen, L.; Niu, B.; Mansikkamäki, A.; Liu, K.; Sun, L.; Wang, W.; Xie, G.; Chen, S.; Ke, H. Alcohol-bridged dinuclear dysprosium single-molecule magnets. J. Mol. Struct. 2025, 1320, 139673. [Google Scholar] [CrossRef]
- Zhang, K.; Guo, F.-S.; Wang, Y.-Y. Synthesis, crystal structure and magnetic properties of a dinuclear dysprosium single-molecule magnet. Inorg. Chem. Commun. 2017, 76, 95–99. [Google Scholar] [CrossRef]
- Ke, H.; Yang, Y.; Wei, W.; Jiang, Y.; Zhang, Y.-Q.; Xie, G.; Chen, S. Synergistic effect of mixed ligands on the anisotropy axis of two dinuclear dysprosium complexes. Dalton Trans. 2020, 49, 10594–10602. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.-N.; Sun, R.; Ma, F.; Yang, J.; Huang, X.-X.; Sun, H.-L.; Gao, S. Coordination-driven assembly of dysprosium layers into a framework featuring enhanced energy barriers and quantum tunneling of magnetization. Inorg. Chem. Front. 2024, 11, 4686–4694. [Google Scholar] [CrossRef]
- Yao, X.; Yan, P.; An, G.; Li, Y.; Li, W.; Li, G. Investigation of magneto-structural correlation based on a series of seven-coordinated β-diketone Dy(III) single-ion magnets with C2v and C3v local symmetry. Dalton Trans. 2018, 47, 3976–3984. [Google Scholar] [CrossRef]
- Ge, Y.; Huang, Y.; Montenegro, J.L.B.; Cui, Y.; Liu, W.; Li, Y.; Wang, B.-L. Synthesis, Structures, and Single-Molecule Magnetic Properties of Three Dy2 Complexes. Chem. Asian J. 2019, 14, 986–994. [Google Scholar] [CrossRef]
- Wang, T.-T.; Che, Z.-W.; Chen, J.-T.; Yan, H.; Zhou, T.-D.; Zhang, Y.-Q.; Sun, W.-B. Tetranuclear lanthanide complexes display significant slow magnetic relaxation with an open hysteresis loop and the magnetocaloric effect. Inorg. Chem. Front. 2023, 10, 1501–1510. [Google Scholar] [CrossRef]
- Klementyeva, S.V.; Gamer, M.T.; Schulze, M.; Suryadevara, N.; Bogomyakov, A.S.; Abramov, P.A.; Konchenko, S.N.; Ruben, M.; Wernsdorfer, W.; Moreno-Pineda, E. Dinuclear Rare-Earth β-Diketiminates with Bridging 3,5-Ditert-butyl-catecholates: Synthesis, Structure, and Single-Molecule Magnet Properties. Inorg. Chem. 2025, 64, 701–715. [Google Scholar] [CrossRef] [PubMed]
- Bartolomé, E.; Arauzo, A.; Luzón, J.; Melnic, S.; Shova, S.; Prodius, D.; Nlebedim, I.C.; Bartolomé, F.; Bartolomé, J. High relaxation barrier in neodymium furoate-based field-induced SMMs. Dalton Trans. 2019, 48, 15386–15396. [Google Scholar] [CrossRef] [PubMed]
- Xémard, M.; Cordier, M.; Molton, F.; Duboc, C.; Le Guennic, B.; Maury, O.; Cador, O.; Nocton, G. Divalent Thulium Crown Ether Complexes with Field-Induced Slow Magnetic Relaxation. Inorg. Chem. 2019, 58, 2872–2880. [Google Scholar] [CrossRef] [PubMed]
- Zhong, X.; Rana, R.; Luo, T.-K.; Fang Wu, Y.; Peng, Y.; Liu, S.-J.; Rajaraman, G.; Wen, H.-R. Systematically study of ligands field effect on a pseudo-D6h Dy(III) single-ion magnet with axially asymmetric ligands. J. Mol. Struct. 2025, 1338, 142270. [Google Scholar] [CrossRef]
- Luo, T.-K.; Luo, Q.-C.; Cao, C.; Hu, Z.-B.; Zhong, X.; Peng, Y.; Niu, Z.-G.; Zheng, Y.-Z.; Liu, S.-J.; Wen, H.-R. Remote substituents effect on the valence and magnetic behavior in mononuclear cobalt complexes. J. Mol. Struct. 2025, 1344, 142997. [Google Scholar] [CrossRef]
- Athanasopoulou, A.A.; Baldoví, J.J.; Carrella, L.M.; Rentschler, E. Field-induced slow magnetic relaxation in the first Dy(III)-centered 12-metallacrown-4 double-decker. Dalton Trans. 2019, 48, 15381–15385. [Google Scholar] [CrossRef]
- Goodwin, C.A.P.; Reta, D.; Ortu, F.; Chilton, N.F.; Mills, D.P. Synthesis and Electronic Structures of Heavy Lanthanide Metallocenium Cations. J. Am. Chem. Soc. 2017, 139, 18714–18724. [Google Scholar] [CrossRef]
- Shrivastava, K.N. Theory of Spin-Lattice Relaxation. Phys. Status Solidi B 1983, 117, 437–458. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Software update: The ORCA program system—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Malmqvist, P.-Å.; Roos, B.O. The CASSCF state interaction method. Chem. Phys. Lett. 1989, 155, 189–194. [Google Scholar] [CrossRef]
- Chibotaru, L.F.; Ungur, L. Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin Hamiltonians and their derivation. J. Chem. Phys. 2012, 137, 064112. [Google Scholar] [CrossRef]
- Ungur, L.; Chibotaru, L.F. Ab Initio Crystal Field for Lanthanides. Chem. Eur. J. 2017, 23, 3708–3718. [Google Scholar] [CrossRef] [PubMed]
- Lines, M.E. Orbital Angular Momentum in the Theory of Paramagnetic Clusters. J. Chem. Phys. 1971, 55, 2977–2984. [Google Scholar] [CrossRef]
- Chibotaru, L.F.; Ungur, L.; Aronica, C.; Elmoll, H.; Pilet, G.; Luneau, D. Structure, Magnetism, and Theoretical Study of a Mixed-Valence CoII3CoIII4 Heptanuclear Wheel: Lack of SMM Behavior despite Negative Magnetic Anisotropy. J. Am. Chem. Soc. 2008, 130, 12445–12455. [Google Scholar] [CrossRef] [PubMed]
- Chibotaru, L.F.; Ungur, L.; Soncini, A. The Origin of Nonmagnetic Kramers Doublets in the Ground State of Dysprosium Triangles: Evidence for a Toroidal Magnetic Moment. Angew. Chem. Int. Ed. 2008, 47, 4126–4129. [Google Scholar] [CrossRef]
- Luo, Q.-C.; Yu, K.-X.; Jin, P.-B.; Liu, Y.-Y.; Zhai, Y.-Q.; Zheng, Y.-Z. Strong Antiferromagnetic Exchange-Coupling Observed in Hydride-Bridged Dimeric Dysprosium(III) Single-Molecule Magnet. Chin. J. Chem. 2024, 42, 391–396. [Google Scholar] [CrossRef]
- Aravena, D.; Neese, F.; Pantazis, D.A. Improved Segmented All-Electron Relativistically Contracted Basis Sets for the Lanthanides. J. Chem. Theory Comput. 2016, 12, 1148–1156. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Briganti, M.; Garcia, G.F.; Jung, J.; Sessoli, R.; Le Guennic, B.; Totti, F. Covalency and magnetic anisotropy in lanthanide single molecule magnets: The DyDOTA archetype. Chem. Sci. 2019, 10, 7233–7245. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Zhang, C.; Shi, M.; Zhou, Y.; Li, H.; Liu, R.; Zheng, S.; Yuan, A.; Chen, L.; Chen, S.-Y.; et al. A high-performance dysprosium single-ion magnet with local pseudo cubic geometry. Inorg. Chem. Front. 2025, 12, 1090–1101. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Wang, Y.-X.; Yang, Q.-Q.; Yin, B. Auxiliary Rather Than Dominant. The Role of Direct Dy–S Coordination in Single-Molecule Magnet Unveiled via ab initio Study. J. Phys. Chem. A 2024, 128, 5285–5297. [Google Scholar] [CrossRef]
- Nakajima, T.; Hirao, K. The Douglas–Kroll–Hess Approach. Chem. Rev. 2012, 112, 385–402. [Google Scholar] [CrossRef]
- Yin, B.; Li, C.-C. A method to predict both the relaxation time of quantum tunneling of magnetization and the effective barrier of magnetic reversal for a Kramers single-ion magnet. Phys. Chem. Chem. Phys. 2020, 22, 9923–9933. [Google Scholar] [CrossRef] [PubMed]
- Aravena, D.; Ruiz, E. Shedding Light on the Single-Molecule Magnet Behavior of Mononuclear DyIII Complexes. Inorg. Chem. 2013, 52, 13770–13778. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Lv, H.; Liang, Y.; Liu, D.; Yao, Z.; Luo, S.; Chen, Z. A Dinuclear Dysprosium(III) Single Molecule Magnet of Benzo[h]quinolin-10-ol. Magnetochemistry 2025, 11, 73. https://doi.org/10.3390/magnetochemistry11090073
Zhou L, Lv H, Liang Y, Liu D, Yao Z, Luo S, Chen Z. A Dinuclear Dysprosium(III) Single Molecule Magnet of Benzo[h]quinolin-10-ol. Magnetochemistry. 2025; 11(9):73. https://doi.org/10.3390/magnetochemistry11090073
Chicago/Turabian StyleZhou, Limin, Hongling Lv, Yuning Liang, Dongcheng Liu, Zaiheng Yao, Shuchang Luo, and Zilu Chen. 2025. "A Dinuclear Dysprosium(III) Single Molecule Magnet of Benzo[h]quinolin-10-ol" Magnetochemistry 11, no. 9: 73. https://doi.org/10.3390/magnetochemistry11090073
APA StyleZhou, L., Lv, H., Liang, Y., Liu, D., Yao, Z., Luo, S., & Chen, Z. (2025). A Dinuclear Dysprosium(III) Single Molecule Magnet of Benzo[h]quinolin-10-ol. Magnetochemistry, 11(9), 73. https://doi.org/10.3390/magnetochemistry11090073






