Effect of Microstructural Changes on the Magnetization Dynamics Mechanisms in Ferrofluids Subjected to Alternating Magnetic Fields

Abstract

We investigated the effects of chemical and physical changes on the interplay between the Néel and Brown superspin relaxation mechanisms in ferrofluids containing 18 nm-diameter Co_0.2Fe_2.8O₄ magnetic nanoparticles. We attempted to tune the ferrofluid’s magnetization dynamics via three methods: (i) changing the carrier fluid from Isopar M to kerosene (ii) doubling the Co-doping level from x = 0.2 to x = 0.4, and (iii) diluting the Co_0.2Fe_2.8O₄/Isopar M nanomagnetic fluid from δ = 1 mg/mL to δ = 0.1 mg/mL. We used temperature-resolved ac-susceptibility measurements at different frequencies, χ″ vs. T|_f, to gain insight into the thermally driven superspin dynamics of the nanoparticles within the ferrofluid. Our data demonstrates that both increasing x and using a different carrier fluid quantitatively alter the temperature dependence of the Néel and Brown relaxation frequency (f_N vs. T and f_B vs. T) by changing the nanoparticles’ magnetic moments and the fluid’s viscosity. Yet, the two mechanisms remain decoupled, as indicated by the presence of two magnetic events (peaks in the χ″ vs. T|_f datasets) one corresponding to the Néel and the other to Brown relaxation. On the other hand, diluting the ferrofluid leads to a qualitative change in the collective superspin dynamics behavior. Indeed, there is just one χ″-peak in the data from the δ = 0.1 mg/mL nanofluid, and its f vs. T dependence is well-described by a model that includes coupled contributions from both the Néel and Brown relaxation: $\mathrm{f}\left(\mathrm{T}\right)=\mathrm{p}·{\displaystyle \frac{T}{{\gamma }_0}}·\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{{\mathrm{E}}^{\prime }}{{\mathrm{k}}_{\mathrm{B}}\left(\mathrm{T}-{\mathrm{T}}_0^{\prime }\right)}}\right]+$ (1 − p) ${\mathrm{f}}_0\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{{\mathrm{E}}_{\mathrm{B}}}{{\mathrm{k}}_{\mathrm{B}}\left(\mathrm{T}-{\mathrm{T}}_0\right)}}\right]$. This is a remarkable behavior that demonstrates the ability to control a ferrofluids magnetization dynamics through simple chemical and physical changes.

1. Introduction

Nanomagnetic fluids (or ferrofluids) are colloidal suspensions of magnetic nanoparticles coated with a surfactant and immersed in a hydrocarbon-based carrier fluid. The surfactant prevents the nanoparticles from clumping under the action of magnetic dipole interactions and other forces. Ferrofluids are typically made of ferromagnetic or ferrimagnetic nanoparticles but become superparamagnetic upon heating. They have received a lot of attention in recent years, mainly due to their existing and potential applications in a broad range of areas including magnetic resonance imaging (MRI) [1,2,3], dynamic loudspeakers [4,5], magneto-optic sensors [6,7], and heat generation [8,9,10]. Ferrofluids are very sensitive to external magnetic fields, and their response to such fields depends on the physical and chemical properties of the nanoparticle and carrier liquid constituents.

Nanomagnetic fluids can be used to generate heat by subjecting them to alternating magnetic fields. This is based on the dynamics of the nanoparticles’ giant magnetic moments (the superspins), which undergo a thermally activated rotation both within the nanoparticle and within the carrier liquid. The former process is the Néel relaxation mechanism that occurs via the superspin flip across an energy barrier to magnetization reversal, E_B, that depends on the nanoparticles’ volume, V, and anisotropy constant, K, according to E_B = KV. For a single, isolated magnetic nanoparticle, the number on full flips per unit time—the frequency of the Néel relaxation—is given by a simple Arrhenius activation law, ${\mathrm{f}}_{\mathrm{N}}={\mathrm{f}}_0\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{{\mathrm{E}}_{\mathrm{B}}}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}}\right]$, where f₀ is the attempt frequency, T is the temperature and k_B the Boltzmann constant. For real nanoparticle ensembles, where interparticle interactions are always present, several models have also been developed [11,12]. Among them, a Vogel-Fulcher (VF) law that introduces an interaction strength parameter T₀ [13]:

$${\mathrm{f}}_{\mathrm{N}}={\mathrm{f}}_0\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{{\mathrm{E}}_{\mathrm{B}}}{{\mathrm{k}}_{\mathrm{B}}\left(\mathrm{T}-{\mathrm{T}}_0\right)}}\right]$$

(1)

has been extensively used to analyze this type of superspin dynamics in magnetic nanosystems [14,15]. The Néel mechanism does not require the presence of a liquid and is active in magnetic nanoparticle ensembles caught in a solid matrix, such as a powder [16], and in ferrofluids where the carrier liquid is frozen [17]. At temperatures above the freezing point of the carrier liquid, T_F, the superspins in a ferrofluid can also relax through a different mechanism, where the entire nanoparticle rotates within the fluid. The frequency of this so-called Brown relaxation mechanism, f_B, depends on the temperature through the temperature dependence of the carrier fluid’s viscosity according to [18]:

$${\mathrm{f}}_{\mathrm{B}}={\displaystyle \frac{\mathrm{T}}{{\mathsf{\gamma }}_0}}·\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{{\mathrm{E}}^{\prime }}{{\mathrm{k}}_{\mathrm{B}}\left(\mathrm{T}-{\mathrm{T}}_0^{\prime }\right)}}\right]$$

(2)

This is a phenomenological relationship, where T₀′ is the divergence temperature of the viscosity, E′ is an activation energy, and ${\mathsf{\gamma }}_0={\displaystyle \frac{3{\mathsf{\eta }}_0{\mathrm{V}}_{\mathrm{H}}}{{\mathrm{k}}_{\mathrm{B}}}}$ is a constant, where V_H is the hydrodynamic volume of the nanoparticles and η₀ depends on the carrier fluid type. On the other hand, Equation (1) is non-phenomenological in nature as there is no physical basis for the divergence of the relaxation frequency as T approaches T₀. Yet, T₀ does describe the interparticle interaction strength, and empirical relationships between the ferrofluid’s concentration and the exponential part of the VF law in Equation (1) have been established [17,18]. As a result, the nanoparticle concentration has a significantly stronger effect on the Néel superspin relaxation frequency than on its Brown counterpart. As the two mechanisms act concomitantly in a ferrofluid at temperatures above T_F, there is an effective relaxation frequency, f, or correspondingly an effective relaxation time τ = 1/2πf. Rosensweig developed a model where the effective relaxation time is given by the 1/τ = 1/τ_N + 1/τ_B, or f = f_N + f_B [19]. This “coupling” between the Néel and the Brown mechanisms has been extensively used to analyze the collective superspin dynamics in ferrofluids [20,21,22]. Such analyses are critical to understand and ultimately control the ability of these systems to generate heat when subjected to alternating magnetic fields because energy dissipation by magnetic nanoparticle ensembles in their superparamagnetic regime is not hysteretic but primarily depends on the above-described magnetization dynamics processes.

Magnetic ac-susceptibility measurements carried out at different temperatures and frequencies, χ″ vs. T|_f, are an ideal tool to get insight into the details of superspin dynamics in magnetic nanoparticle ensembles. Whether such measurements are performed on magnetic nanopowders or on ferrofluids, χ″ exhibits a peak at the temperature where the relaxation frequency (or time) is equal to the measurement frequency, regardless of the underlying mechanism of the superspin relaxation: Néel, Brown, or a combination of both. Consequently, by following the peak temperature shift with the measurement frequency—which is typically varied throughout a broad range spanning several orders of magnitude—one can experimentally determine the temperature dependence of the relevant superspin relaxation mechanism: f_N vs. T, f_B vs. T, or f = f_N + F_B vs. T. Eventually, analysis of these data in the framework of the Néel and Brown relaxation models described by Equations (1) and (2) is used to uncover qualitative and quantitative details of the microscopic dynamics responsible for the collective superspin relaxation of the studied nanoparticle ensemble.

One important biomedical application of nanomagnetic fluids is hyperthermia cancer therapy, a procedure based on the known fact that malignant cells die at temperatures just a few degrees lower than those at which normal cell apoptosis occurs [23,24,25]. Briefly, magnetic nanoparticles delivered by injection are driven to the tumor site and an external alternating magnetic field is applied to generate heat. Obviously, both the Néel and the Brown dissipation mechanisms can be active as the magnetic nanoparticles are immersed in a fluid. Currently, magnetic cancer hyperthermia is mostly used as an adjoint procedure to radiation and chemotherapy, despite its tremendous potential to kill cancer selectively and without side effects. This is primarily because the specific heat generation power by all currently used materials is significantly below what is needed for magnetic nanoparticle hyperthermia to become a mainstream stand-alone cancer therapy. Consequently, much research effort has been aimed at studying the relationship between the microstructure of these systems and their magnetization dynamics. Studies have initially focused on the effect of the average size and interparticle distances on the superspin relaxation in biocompatible Fe₃O₄ magnetic nanoparticles [26]. More recently, chemical manipulation has also been used [27], and attempts have been made at isolating [28] or even de-coupling [22] the Néel and the Brown mechanisms in ferrofluids to better understand their contributions to the overall relaxation. Much progress has been made, but the complex interplay between the two mechanisms is not fully understood, and the ability to control it via microstructural and chemical changes has not been thoroughly investigated.

Here, we present a study of the effects of chemical and physical changes on the interplay between the Néel and Brown superspin relaxation mechanisms in ferrofluids containing 18 nm diameter Co_0.2Fe_2.8O₄ magnetic nanoparticles. We used ac-susceptibility measurements at different temperatures and frequencies of the driving magnetic field to uncover the microscopic details of the magnetization dynamics in three nanofluid systems. First, we replaced the Isopar M carrier liquid with kerosene and found that the Néel and Brown components remain separated, each showing robust χ″-peaks at temperatures around 245 K and 275 K, respectively. In addition, the Co_0.2Fe_2.8O₄/kerosene ferrofluid exhibits a quantitatively different temperature behavior (γ₀ = 2.3 × 10⁻⁹ s·K, T₀′ = 220 K and E′/k_B= 930 K) compared with its Isopar M counterpart [29]. Second, we increased the level of Co doping from x = 0.2 to x = 0.4. This leads to a slight reduction of the gap between the Néel and Brown peak temperatures (as they shift in opposite directions upon the increase of x), and a 10% decrease in the energy barrier to magnetization reversal and the interaction strength parameter T₀. Finally, diluting the ferrofluid from δ = 1 mg/mL to δ = 0.1 mg/mL, induces the most significant change observed here. Indeed, the Néel and Brown relaxation become coupled as demonstrated by the presence of a single χ″-peak whose temperature varies with the frequency according to a linear combination of Equations (1) and (2):

$$\mathrm{f}(\mathrm{T})=\mathrm{p}·{\displaystyle \frac{\mathrm{T}}{{\mathsf{\gamma }}_0}}·\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{{\mathrm{E}}^{\prime }}{{\mathrm{k}}_{\mathrm{B}}\left(\mathrm{T}-{\mathrm{T}}_0^{\prime }\right)}}\right]+(1-\mathrm{p}) {\mathrm{f}}_0\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{{\mathrm{E}}_{\mathrm{B}}}{{\mathrm{k}}_{\mathrm{B}}\left(\mathrm{T}-{\mathrm{T}}_0\right)}}\right]$$

(3)

where p is a parameter associated with the percentage contribution of the two mechanisms to the overall superspin relaxation. Fits of Equation (3) to the χ″ vs. T|_f data collected on the diluted (δ = 0.1 mg/mL) Co_0.2Fe_2.8O₄/Isopar M sample allowed us to determine not only the parameters associated with the Brown and the Néel relaxation, but also their contributions to the observed relaxation: 58% and 42%, respectively. This is a remarkable result that demonstrates the ability to engineer the magnetization dynamics response of a magnetic nanofluid via physical and chemical manipulation of the nanoparticles and carrier liquid.

2. Materials and Methods

All ferrofluids used in this study were synthesized using Co_0.2Fe_2.8O₄ and Co_0.4Fe_2.6O₄ magnetic nanoparticles coated with oleic acid and immersed in Isopar M or kerosene. The as prepared ferrofluids have a concentration of 1 mg nanoparticles/1 mL carrier liquid. The 10× diluted (0.1 mg/ mL) Co_0.2Fe_2.8O₄/Isopar M sample was made by adding liquid carrier to the corresponding as prepared ferrofluid. The Co_0.2Fe_2.8O₄ and Co_0.4Fe_2.6O₄ magnetic nanoparticle ensembles were synthesized using the co-precipitation method. To make Co_0.2Fe_2.8O₄ nanoparticles, the following reactants were used FeCl₃·6H₂O, FeCl₂·4H₂O, and CoCl₂·4H₂O. The appropriate molar ratio (6.0:0.2:2.8) was dissolved in 50 mL deionized water, then NaOH was added dropwise under magnetic stirring at 750 rpm to induce precipitation (until the pH reached a value of 10). The resulting precipitate was then filtered and dried at a temperature of 175 °C for a few hours. The same process was employed to synthesize Co_0.4Fe_2.6O₄ magnetic nanoparticles, but this time a (6.0:0.4:2.6) molar ratio of FeCl₃, FeCl₂, and CoCl₂ was used.

The magnetic nanoparticle ensembles were initially characterized by transmission electron microscopy (TEM) using a Hitachi H-9500 high-resolution microscope (Hitachi, Schaumburg, IL USA). The instrument, which includes a CCD digital camera and goniometer-tilt stage, was operated at 300 kV. The main purpose of these measurements was to determine the nanoparticles’ shape, average size, and size distribution.

The magnetic ac-susceptibility measurements were performed on a Quantum Design^® Physical Property Measurement System (PPMS) (Quantum Design, San Diego, CA, USA) in applied alternating magnetic fields of 3 Oe amplitude at temperatures between 150 K and 350 K. The imaginary (out-of-phase) susceptibility χ″ was recorded upon heating in 5 K steps at six different frequencies of the driving field: 10 Hz, 100 Hz, 500 Hz, 1000 Hz, 5000 Hz, and 10,000 Hz. The resulting χ″ vs. T|_f datasets contain information about the microscopic aspects of the magnetization dynamics as they exhibit peaks at temperatures, T_p, where the measurement frequency is the same as the superspin relaxation (flip) frequency. Furthermore, the relationship between the measurement frequency and the χ″ peak temperature, f(T_p), can reveal the type the superspin relaxation mechanism and the strength of the magnetic dipole interactions among the nanoparticles in the ensemble.

3. Results and Discussion

Figure 1a presents a TEM image collected from nanopowders obtained by evaporating the carrier fluid from the Co_0.2Fe_2.8O₄/kerosene ferrofluid, whereas Figure 2b shows an image of two individual nanoparticles in the ensemble used throughout this study.

These images indicate that the nanoparticles are spherical, and they appear to be separated from one another within the ensemble, which is most likely due to their oleic acid coatings. The size distribution of the Co_0.2Fe_2.8O₄ nanoparticles (obtained from the TEM image in Figure 1a) is shown in Figure 1c. The nanoparticles show a sharp and symmetric distribution that yields an average diameter <D> = 18 nm and a standard deviation σ = 2.38 nm. The average size of the nanoparticles is critical for this type of experiment, where we need the Néel and the Brown relaxation to be simultaneously active at temperatures above the freezing point of the carrier fluid T_F.

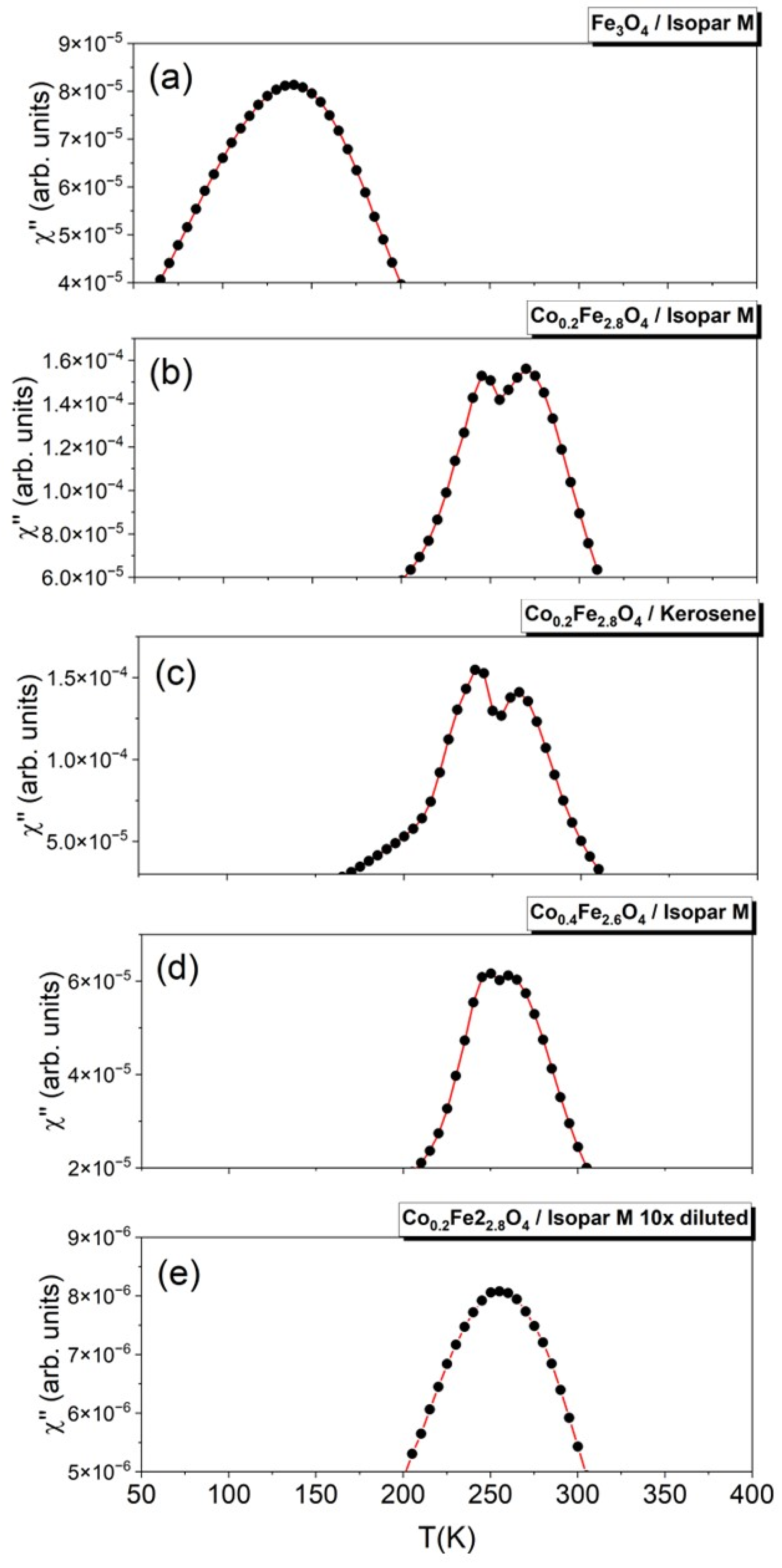
The out of phase component of the ac susceptibility measured upon heating at a frequency of the driving magnetic field f = 500 Hz is shown in Figure 2 for five different magnetic nanofluids: (a) Fe₃O₄/Isopar M, (b) Co_0.2Fe_2.8O₄/Isopar M, (c), Co_0.2Fe_2.8O₄/kerosene, (d) Co_0.4Fe_2.6O₄/Isopar M, and (e) 10× diluted Co_0.2Fe_2.8O₄/Isopar M.

The most salient feature of these χ″ vs. T|_500Hz datasets is that they exhibit major changes—both quantitative and qualitative—upon microstructural physical and chemical modifications to the nanoparticle ensemble and/or the carrier liquid component of the ferrofluid. First, doping cobalt into the Fe₃O₄, while keeping the same carrier liquid (Isopar M) has two major effects: the blocking temperature increases by more than 100 K, and a double-peak feature occurs in the temperature dependence of the susceptibility of Co_0.2Fe_2.8O₄/Isopar M. The blocking temperature shift was explained by the magnetic anisotropy increase and the interparticle magnetic interaction strengthening upon Co-doping, whereas the double χ″ vs. T peak was shown to be due to the strong dominance of the Néel and Brown superspin relaxation at two different temperatures [29]. Yet, several questions remain about how further microstructural and chemical changes can be used to alter the magnetization dynamics of these nanofluids.

The Néel and Brown dynamics depend on several parameters in a complex way. For example, the magnetic anisotropy of the nanoparticles only affects the Néel relaxation, and the viscosity of the carrier fluid only affects its Brown counterpart, whereas the interparticle interaction strength has an influence on both mechanisms. Our χ″ vs. T|_500Hz data in Figure 2c,d show that replacing the Isopar M carrier liquid by kerosene or increasing the Co doping in Co_xFe_3-xO₄ from x = 0.2 to x = 0.4 leaves the superspin relaxation mechnaisms decoupled, as indicated by the presence of two magnetic events (peaks in the χ″ vs. T datasets) one corresponding to the Néel and the other to Brown relaxation. Yet, as our frequency-resolved ac susceptibility data will demonstrate, the kerosene- based and strongly Co-doped ferrofluids (Co_0.2Fe_2.8O₄/kerosene and Co_0.4Fe_2.6O₄/Isopar M) do exhibit significant quantitative changes in the microscopic parameters that define their magnetization dynamics (e.g., E_B, T₀, E′, γ₀) compared to the original, Co_0.2Fe_2.8O₄/Isopar M ferrofluid. On the hand, the χ″ vs. T|_500Hz data in Figure 2e shows the presence of a single peak, which strongly suggests that diluting the Co_0.2Fe_2.8O₄/Isopar M ferrofluid from a from δ = 1 mg/mL to δ = 0.1 mg/mL leads to a qualitative change in the nanoparticles’ magnetization dynamics where the two mechanisms, Néel and Brown, are coupled and bring comparable contributions to the overall (effective) superspin relaxation.

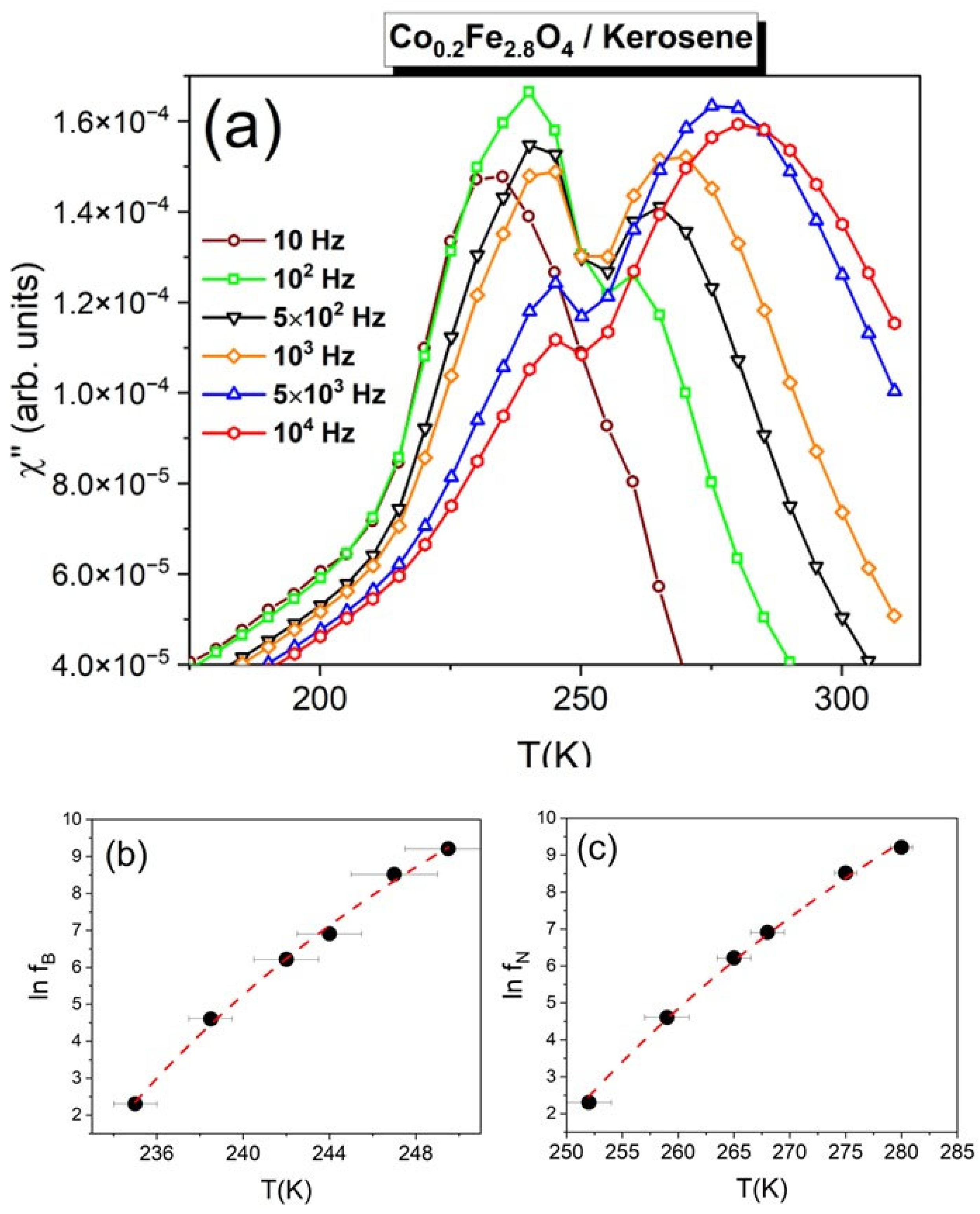
The six datasets in Figure 3a present the temperature dependence of the imaginary (out-of-phase) magnetic ac-susceptibility component, χ″, recorded on the Co_0.2Fe_2.8O₄/kerosene nanofluid at different frequencies of the applied magnetic field: 10 Hz (dark red), 100 Hz (green), 500 Hz (black), 1000 Hz (orange), 5000 Hz (blue), and 10,000 Hz (red). At all frequencies, χ″ exhibits two peaks, the temperature of which increase with the increase of the measurement frequency. The solid symbols in Figure 3b show this f(T) dependence for the low temperature χ″ peak, within the 235 K–250 K temperature range. Its higher temperature (255 K–290 K) counterpart is presented in Figure 3c. As this nanofluid was obtained by using Co_0.2Fe_2.8O₄ nanoparticles in a kerosene carrier (instead of Isopar M), we analyzed the lower temperature peak shift with the frequency using a hydrodynamic model described by Equation (2), ${\mathrm{f}}_{\mathrm{B}}={\displaystyle \frac{\mathrm{T}}{{\mathsf{\gamma }}_0}}·\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{{\mathrm{E}}^{\prime }}{{\mathrm{k}}_{\mathrm{B}}\left(\mathrm{T}-{\mathrm{T}}_0^{\prime }\right)}}\right]$, and the higher temperature peak shift using the Vogel-Fulcher law described by Equation (1), ${\mathrm{f}}_{\mathrm{N}}={\mathrm{f}}_0\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{{\mathrm{E}}_{\mathrm{B}}}{{\mathrm{k}}_{\mathrm{B}}\left(\mathrm{T}-{\mathrm{T}}_0\right)}}\right]$. This implies that the lower temperature peak is described by the Brown superspin relaxation and the higher temperature one by the Néel mechanism, which is similar to what was found for Co_0.2Fe_2.8O₄/Isopar M. The red dashed line in Figure 3b shows the best fit of Equation (2), which converges to low residuals (reduced χ_R² = 0.035) and yields the following parameters for the Brown relaxation: γ₀ = 2.3 × 10⁻⁹ s·K, T₀′ = 220 K and E′/k_B= 930 K. This is consistent with the new carrier liquid that has a different viscosity (from Isopar M) and a different freezing point (T_F = 225 K for pure kerosene). The red dashed line in Figure 3c represents the best fit of Equation (1) to the data.

This fit also converges (χ_R² = 0.019) upon the simultaneous variation of three parameters and yields a reduced energy barrier to magnetization reversal E_B/k_B= 2510 K and an interparticle interaction strength parameter T₀ = 165 K. Overall, these results show that changing the carrier liquid of a nanofluid based on 18 nm Co_0.2Fe_2.8O₄ nanoparticles alters the microscopic parameters that describe the Brown relaxation (γ₀, T₀′, E′/k_B) but preserves de-coupling of the two relaxation mechanisms—Néel and Brown—which show peaks within different temperature intervals.

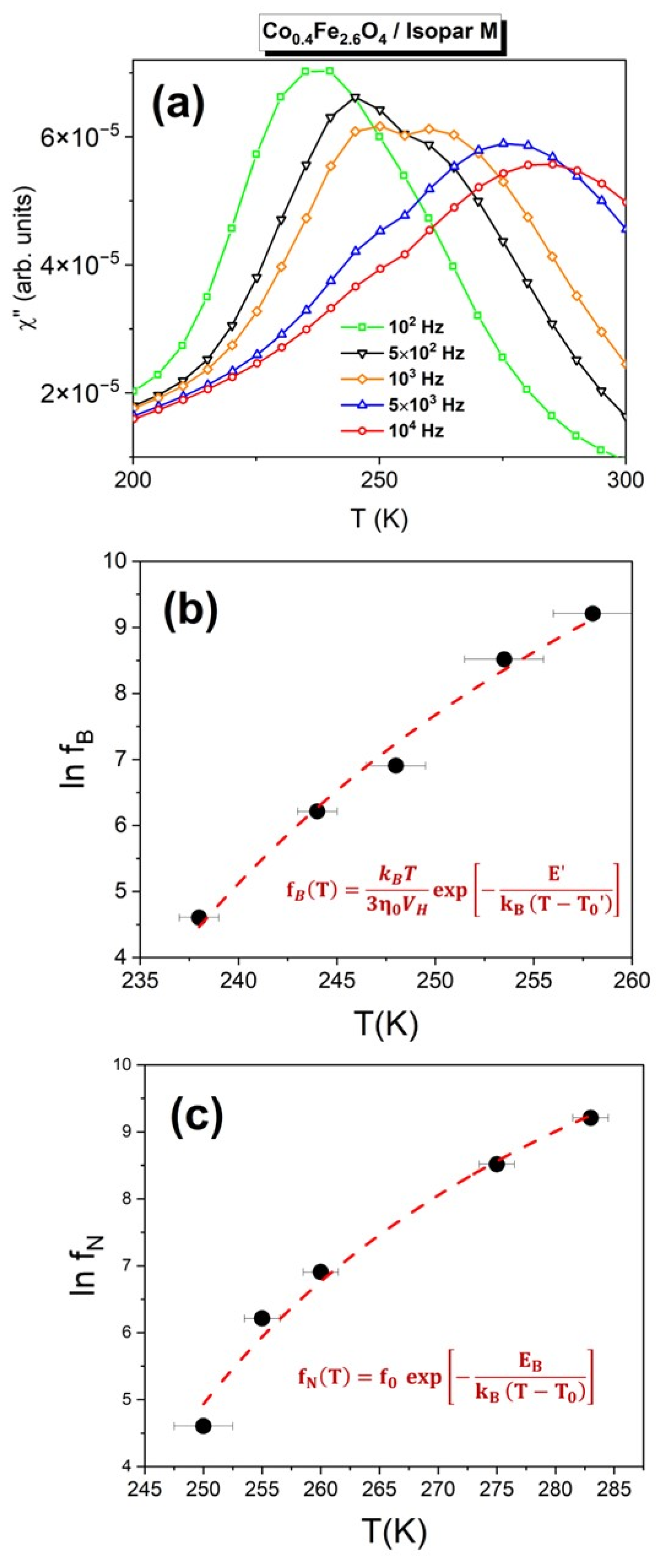
Next, we studied the effect of increasing Co-doping in Co_xFe_3−xO₄ from x = 0.2 to x = 0.4. As preliminarily shown by the χ″ vs. T|_{500 Hz} data collected on the Co_0.2Fe_2.8O₄/Isopar M (x = 0.4) ferrofluid (Figure 2d), the double χ″-peak feature is still present, but less pronounced that in the x = 0.2 sample. We therefore carried out the same type of measurements and analyses as the ones performed on the kerosene-based ferrofluid (discussed above).

Figure 4a shows the ac-susceptibility data collected at five different frequencies ranging from 100 Hz to 10,000 Hz. Figure 4b presents the frequency dependence of the lower temperature peak f_B(T). The filled circles are data obtained from ac-susceptibility measurements, whereas the dashed line represents the best fit of the hydrodynamic model based on the temperature dependence of the viscosity that describes the Brown relaxation dynamics. The best fit parameters resulting from this analysis of the x = 0.4 sample are: γ₀ = 8.3 × 10⁻⁸ s·K, T₀′ = 197 K and E′/k_B= 572 K. T₀′ is very close to the freezing point of Isopar M (205 K), as expected, and γ₀ has a four times higher value than the one reported on the x = 0.2 ferrofluid [29]. Doubling the Co-doping also has an effect on the higher temperature peak, whose frequency dependence on the temperature is related to the Néel superspin relaxation mechanism. Figure 4c shows this f_N(T) dependence, including the data (solid symbols) and the best fit of a Vogel-Fulcher law (dashed line) that yields a reduced energy barrier to magnetization reversal E_B/k_B= 2186 K and an interparticle interaction strength parameter T₀ = 135 K. Both these values are notably lower than the ones reported for the x = 0.2 ferrofluid, which, corroborated with the decrease of the viscosity’s activation energy E′/k_B described above, leads to the observed reduction of the gap between the Néel and Brown peak temperatures (as they shift in opposite directions upon the increase of x).

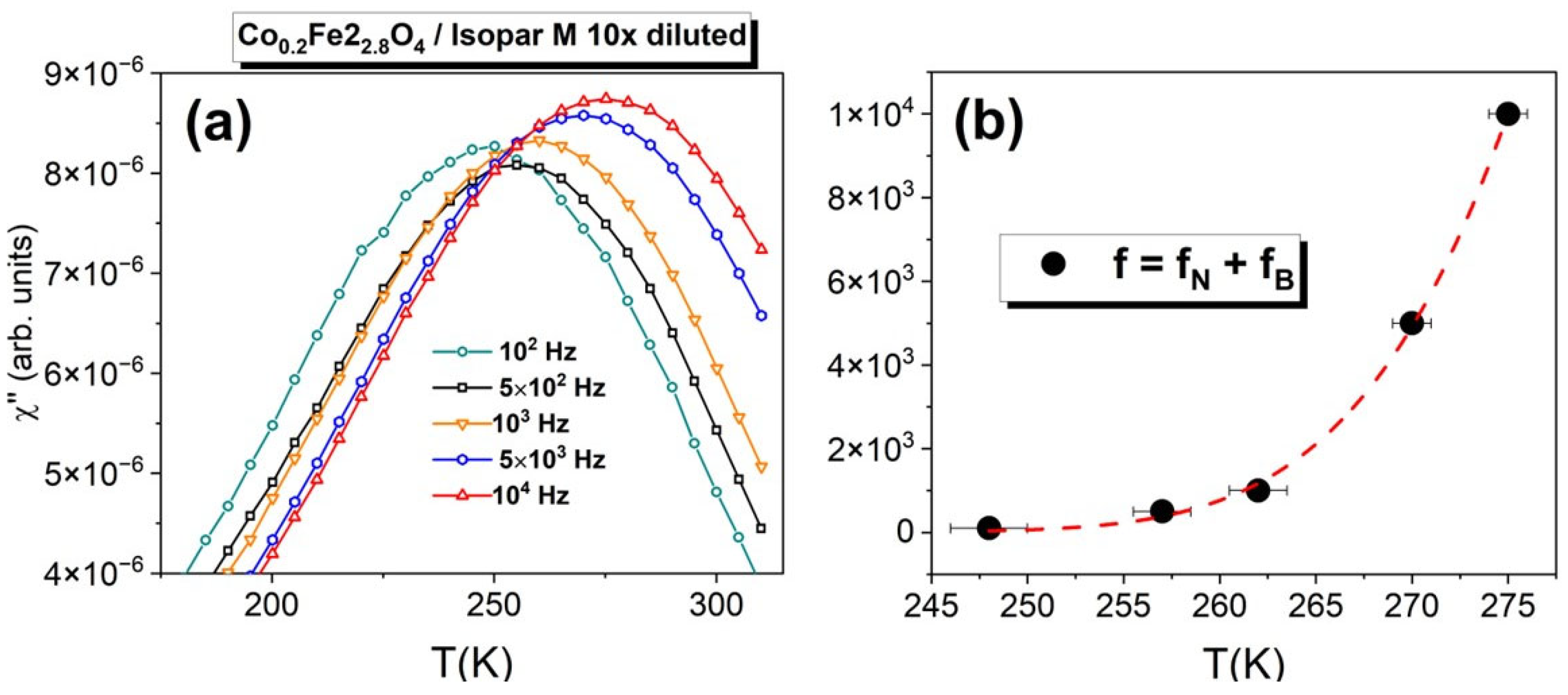
Our main finding comes from magnetic ac-susceptibility data recorded on the sample obtained by diluting the Co_0.2Fe_2.8O₄/Isopar M ferrofluid from δ = 1 mg/mL to δ = 0.1 mg/mL. Figure 5a shows these χ″ vs. T|_f, curves measured at five different frequencies: 100 Hz (green), 500 Hz (black), 1000 Hz (orange), 5000 Hz (blue), and 10,000 Hz (red).

The most striking feature of these data is that χ″ only exhibits one peak, as opposed to the other Co-doped nanofluids studies here. As we showed above, the reason for the double peak feature in the χ″ vs. T|_f curves is that the Néel and Brown mechanisms are separated, i.e., their corresponding superspin relaxation frequencies match the frequency of the applied filed at temperatures that are tens of degrees apart (e.g., ~40 K for the 1 mg/mL Co_0.2Fe_2.8O₄/kerosene ferrofluid). Consequently, we believe that dilution results in the recoupling of the two mechanisms. To test this hypothesis, we start with Rosensweig’s formula, which indicates that, when the Néel and Brown mechanisms are coupled, one measures an overall relaxation time, τ = 1/2πf, which includes contributions from both according to ${\displaystyle \frac{1}{\mathsf{\tau }\left(\mathrm{T}\right)}}={\displaystyle \frac{1}{{\mathsf{\tau }}_{\mathrm{N}}\left(\mathrm{T}\right)}}+{\displaystyle \frac{1}{{\mathsf{\tau }}_{\mathrm{B}}\left(\mathrm{T}\right)}}$ or, equivalently, $\mathrm{f}\left(\mathrm{T}\right)={\mathrm{f}}_{\mathrm{N}}\left(\mathrm{T}\right)+{\mathrm{f}}_{\mathrm{B}}\left(\mathrm{T}\right)$. It is important to mention that this formalism has been developed for isolated magnetic nanoparticles, and although it has been extensively used to successfully explain the magnetization dynamics of ferrofluids, several recent studies have pointed out possible deviations from the behavior predicted by Rosensweig’s formula [30,31]. Here, we obtained the temperature dependence of the overall superspin relaxation frequency, f(T), from the temperature shift of the χ″ peak upon the increase of the measurement frequency in Figure 5a. This yields the five data points shown by the filled symbols in Figure 5b. The dashed line in Figure 5b shows a fit of Equation (3) to the f(T) data. Equation (3) is based on the Rosensweig coupling between the Neel and the Brown relaxation, uses a Vogel-Fulcher for the former and a hydrodynamic model based on the temperature dependence of the viscosity for the latter, and introduces a parameter, p, that quantitatively describes the individual contribution of each mechanism to the overall relaxation. The fit yields the following parameters: E_B/k_B= 2658 K and T₀ = 140 K for the Néel relaxation, γ₀ = 1.5 × 10⁶ s·K, T₀′ = 210 K, and E′/k_B= 392 K for the Brown relaxation, and p = 0.58 for the Brown mechanism contribution to the overall relaxation. There are three important observations about these results. First, the energy barrier to magnetization reversal via Néel relaxation, E_B, and the interaction strength parameter, T₀, are reduced by less than 15% with respect to their counterparts in the non-diluted nanofluids. On the other hand, dilution affects the Brown relaxation parameters to a much greater extent. Indeed, the activation energy that describes the viscosity’s variation with temperature, E′, decreases by almost 50% and the viscosity pre-factor, γ₀, decreases by two orders of magnitude. This indicates that the rotation of the superspin together with the nanoparticle within the viscous fluid plays a predominant role in the re-coupling of the two superspin relaxation mechanisms. This is not unexpected, as the viscosity is known to play an important and multifaceted role in a ferrofluid’s dynamics [32]. Finally, the 0.58 value of the p coefficient reveals that the Brown and Néel mechanisms contribute to the effective magnetic moment relaxation by 58% and 42%, respectively. Overall, our results are significant because they demonstrate the ability to control the magnetization dynamics response of ferrofluid through physical and chemical changes to the nanoparticles and carrier liquid.

4. Conclusions

In this study we used physical and chemical modifications of both the nanoparticle and the carrier liquid components of nanomagnetic fluids based on 18-nm average diameter Co_0.2Fe_2.8O₄ nanoparticles to alter their magnetic behavior under alternating magnetic fields. Specifically, we replaced the Isopar M carrier fluid with kerosene, increased the Co-doping level from x = 0.2 to x = 0.4, and diluted the ferrofluid from δ = 1 mg/mL to δ = 0.1 mg/mL. We investigated the effect of the above-described changes on the magnetization dynamics of the ferrofluid using magnetic ac-susceptibility measurements, where the out-of-phase component is recorded within the 50 K to 350 K temperature range at six different frequencies of the driving magnetic field: 10 Hz, 100 Hz, 500 Hz, 1000 Hz, 5000 Hz, and 10,000 Hz. These χ″ vs. T|_f datasets show peaks at temperatures where the measurement frequency is the same as the superspin relaxation frequency. The observed shift of the χ″-peak temperature with the frequency of the driving magnetic field yields the temperature dependences of the Néel and Brown relaxation frequency: f_N(T) and f_B(T). We modeled these using a Vogel-Fulcher activation type law, ${\mathrm{f}}_{\mathrm{N}}={\mathrm{f}}_0\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{{\mathrm{E}}_{\mathrm{B}}}{{\mathrm{k}}_{\mathrm{B}}\left(\mathrm{T}-{\mathrm{T}}_0\right)}}\right]$, for the Néel mechanism and a hydrodynamic model based on the temperature dependence of the viscosity, ${\mathrm{f}}_{\mathrm{B}}={\displaystyle \frac{\mathrm{T}}{{\mathsf{\gamma }}_0}}·\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{{\mathrm{E}}^{\prime }}{{\mathrm{k}}_{\mathrm{B}}\left(\mathrm{T}-{\mathrm{T}}_0^{\prime }\right)}}\right]$, for its Brown counterpart. We found that replacing the Isopar M carrier liquid with kerosene leaves the Néel and Brown mechanisms separated: they show χ″-peaks at temperatures around 245 K and 275 K, respectively. In addition, the Co_0.2Fe_2.8O₄/kerosene ferrofluid exhibits a temperature behavior of the Brown relaxation frequency that only differs quantitatively from the one in Co_0.2Fe_2.8O₄/Isopar M. Increasing the level of Co doping from x = 0.2 to x = 0.4 leads to a slight reduction of the gap between the Néel and Brown peak temperatures (as they shift in opposite directions upon the increase of x) in the context of an unexpected 10% reduction of the energy barrier to magnetization reversal an the interparticle interaction strength parameter.

Our main finding is related to diluting the Co_0.2Fe_2.8O₄/Isopar M ferrofluid from δ = 1 mg/mL to δ = 0.1 mg/mL. This leads to a re-coupling of the Néel and Brown mechanisms demonstrated by the presence of a single χ″-peak whose temperature varies with the frequency according $\mathrm{f}(\mathrm{T})=\mathrm{p}·{\displaystyle \frac{\mathrm{T}}{{\mathsf{\gamma }}_0}}·\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{{\mathrm{E}}^{\prime }}{{\mathrm{k}}_{\mathrm{B}}\left(\mathrm{T}-{\mathrm{T}}_0^{\prime }\right)}}\right]+$(1 − p)·$\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{{\mathrm{E}}_{\mathrm{B}}}{{\mathrm{k}}_{\mathrm{B}}\left(\mathrm{T}-{\mathrm{T}}_0\right)}}\right].$ The best fit of this model to the χ″ vs. T|_f data collected on the diluted ferrofluid allowed us to determine the parameters associated to the Brown and the Néel relaxation and their contributions to the observed relaxation: 58% and 42%, respectively. It is important to mention that the validity of this model appears to be restricted to the weak magnetic dipole interaction regime. Our results are important because they prove the ability to control the superspin relaxation of ferrofluids by minute physical and chemical changes to the nanoparticles and carrier liquid constituents.