Magnetic Properties of an Ensemble of Core-Shell Fe/FeO_X Nanoparticles: Experimental Study and Micromagnetic Simulation

Abstract

Spherical magnetic nanoparticles consisting of an iron core and iron oxide shell (α-Fe/FeO_X) were fabricated by the electric explosion of the wire technique (EEW). The structure and magnetic properties of synthesized nanoparticles were experimentally investigated. Magnetic properties of an iron nanoparticle ensemble for individual defect-free, non-interacting iron-based nanoparticles having different diameters were calculated using micromagnetic modeling. Experimental and calculated magnetic hysteresis loops were comparatively analyzed.

1. Introduction

Magnetic nanoparticles (MNPs) based on iron (α-Fe) and iron oxides (magnetite Fe₃O₄) or maghemite (γ-Fe₂O₃) can be employed in various biomedical applications. Iron oxides are suitable for diagnostics using magnetic resonance imaging (MRI) or evaluation of the volumetric flow rate of ferrofluids (FF) along arteries with stenosis [1,2,3]. They are also necessary for magnetic hyperthermia, targeted drug delivery combined with magnetic biodetection [4,5]. Fe₃O₄ and γ-Fe₂O₃ have the necessary chemical stability and biocompatibility for their biomedical applications. In contrast, iron nano- and microparticles are characterized by quite high chemical activity and toxicity. However, their key advantage is a very high saturation magnetization, which is beneficial for certain drug delivery protocols and magnetic biosensing [6,7]. In order to reduce the cytotoxicity of iron particles, encapsulation or specialized surface treatments are employed to mitigate the adverse effects [8,9]. In addition, the ability of metallic iron to bind oxygen, taking it away from other components of biological systems, can be used in various treatments, for example, as a complementary part of cancer therapy. Specifically, introducing iron nanoparticles into the tumor area through its blood vessel system can inhibit tumor growth via oxygen starvation caused by the chemical oxidation of iron to different oxides. A similar effect can occur in the course of the treatment of infectious diseases using iron particles [9,10].

For certain biomedical applications, for example, such as enhancing hyperthermia efficiency, magnetic particles with high magnetization and non-zero coercivity are required. Another important application of magnetic materials is magnetic resonance imaging. It is a technique used in radiology for visualization of the organs or processes inside the body, employing strong magnetic fields. In order to improve the image quality, special contrast agents may be administered either orally or intravenously. Currently, gadolinium-based contrast agents dominate clinical practice due to their ability to shorten the relaxation times of nuclei within body tissues. However, the significant toxicity of gadolinium-containing drugs has prompted an ongoing search for MRI contrast agents with lower toxicity levels, even at the potential expense of reduced contrast quality. Iron oxide nanoparticles were among the first alternative candidates for MRI applications under specific conditions [10,11,12].

The use of pure iron nanoparticles is difficult due to the complexity of controlling their oxidation states: high chemical activity and a tendency to oxidation are causing these difficulties. As an alternative, it is proposed to use core/shell type nanoparticles [1,13,14] and doping of iron oxide particles with rare earth elements such as Gd or Tb [15,16,17]. Magnetic particles with an iron core and gadolinium shell are of special interest as contrast agents for resonance imaging and as materials for achieving the high therapeutic effects in radiotherapy. For instance, core-shell magnetic nanoparticles Fe₃O₄/Gd₂O₃ are used as T₁-T₂ dual modal MRI agents [17] that can decrease the risk of pseudo-positive signals in diagnosing lesions [18,19,20,21].

Due to the high requirements for nanomedical materials characterized by the state of polydispersity, comprehensive certification of the same parameter using several modern methods is necessary [22]. The fulfillment of the latter requirement is directly related to the batch size of the resulting nanomaterial. The problem can be solved by creating technologies for the synthesis of nanoparticles by combining the high-performance electrophysical and physical techniques, which include electric explosion of the wire (EEW), laser target evaporation, and ball milling [23,24,25]. These methods make it possible to vary the composition, size, and structure of nanoparticles, as well as to obtain core-shell nanocomposites with different compositions and structures of each component [26,27]. In this case the shell composition is conditioned by the very small additions to the gas atmosphere during MNPs fabrication. The most often used additives are either nitrogen or oxygen.

As iron MNPs might be toxic, it is important to ensure the high degree of their surface passivation, which can be completed by additional ball milling treatment (BM). Development of complex two-stage production technology (EEW + ball milling) of magnetic nanoparticles requires understanding of magnetic properties of obtained materials, including magnetic domain structures, magnetic hysteresis, ferromagnetic absorption in the high frequency range, etc. Experimentally it is impossible to obtain a monodisperse ensemble of MNPs consisting of indistinguishable MNPs. In addition, the larger the batch, the more difficult it is to obtain a narrow particle size distribution due to inevitable variations in local conditions of the synthesis.

Micromagnetic simulation can be very helpful in solving this problem and saving time and effort in the course of detailed understanding of magnetic processes that appeared in the particles of different types as well as in ensembles with different particle size distributions. Of course, the formulated predictions for different batches of MNPs-based materials require experimental verification. However, the successful combination of micromagnetic modeling and experimental verification can significantly simplify the search for optimum solutions.

In this study, ensembles of core-shell Fe/FeO_X magnetic nanoparticles were synthesized by the electric explosion of the wire technique. Magnetic properties, including magnetic structures and magnetic hysteresis loops, of individual magnetic iron nanoparticles were obtained by micromagnetic simulation techniques for batches of spherical MNPs with experimentally measured diameter distribution. A comparative analysis was conducted between the experimentally measured and computationally predicted magnetic hysteresis loops of a magnetostatically non-interacting Fe-based nanoparticle ensemble.

2. Materials and Methods

Iron MNPs were synthesized by an EEW setup originally designed and fabricated at the Institute of Electrophysics, RAS (Ekaterinburg, RF) [13,27]. The EEW system consisted of the following components: an explosion chamber, a gas trap for the large particles’ separation from the fine fraction, and a filter for collecting the fine MNPs. The chamber was filled with a gas mixture of argon (70%) and nitrogen (30%) at a working pressure of 0.12 MPa. A gas turbine maintained continuous gas circulation at a flow rate of 150 L min⁻¹.

A steel wire n, grade Ct3 of 0.47 mm diameter and a low carbon content (0.07 wt%) (MS Grupp, Moscow, RF) was continuously fed into the explosion chamber from a reel situated on top of the device. One explosion corresponded to an 89 mm wire portion and one 30 kV voltage pulse with 2 μs duration. The electrical energy corresponding to each wire exploded portion during each pulse ensured 130% excess energy in comparison with the sublimation energy of the metal iron (424 KJ mol⁻¹). The wire portion was first vaporized and then condensed into the shape of non-agglomerated spherical metallic iron MNPs. The synthesized material was collected in the filter where it was passivated by oxygen with a flow rate of about 0.5 cm³ s⁻¹ before opening the setup. A detailed description of the EEW method can be found elsewhere [28,29,30].

X-ray diffraction (XRD) analysis was completed using a standard diffractometer (Bruker D8 Discover, Bruker Corporation, Billerica, MA, USA) with a graphite monochromator operating with Cu-Kα radiation with the wavelength λ = 1.5418 Å. Quantitative analysis was carried out with TOPAS-3 software. The average size of coherent diffraction domains was estimated following the Scherrer approach [31].

Electron microscopy studies were performed by transmission electron microscopy (TEM) using a JEOL JEM2100 microscope (JEOL Corp., Tokyo, Japan) operated at 200 kV. In addition, the specific surface area of the ensemble of nanoparticles was measured by low-temperature nitrogen adsorption technique Brunauer-Emmett-Teller physical adsorption or BET using Micromeritics TriStar3000 automatic sorption analyzer (Micromeritics, Norcross, GA, USA).

The magnetic properties of Fe nanoparticles were investigated using a vibrating sample magnetometer, Lake Shore Cryotronics (VSM, Lake Shore 7404, Westerville, OH, USA), at room and liquid nitrogen temperatures. For the measurements, samples of Fe nanoparticles were prepared using a two-magnet system and GE-7031-CT Thermal Varnish (CRYO-Technics, Büttelborn, Germany) (polyvinyl butyral, PVB). PVB is a random terpolymer composed of vinyl alcohol and vinyl butyral with relatively small amounts of vinyl acetate [32].

Based on experimental data micromagnetic simulations were performed for iron nanoparticles at a temperature of 293 K. The simulation parameters are listed in Table 1. It should be noted that micromagnetic simulations of large particles require significant processing power. For example, in this study, micromagnetic simulations of nanoparticles with diameters from 10 nm to 230 nm with 20 nm steps took approximately one month. The calculations were performed using a workstation based on the SuperMicro 4U 7047A-T server platform (Super Micro Computer, San Jose, CA, USA) with 128 GB of RAM, 32 cores of an Intel XeonX5 CPU (Intel Corporation, Santa Clara, CA, USA) with a rate of 3.3 GHz, and a Gigabyte Geforce RTX 4060 Ti GPU (Gigabyte Technology, New Taipei City, Taiwan).

Micromagnetic models were designed using the Mumax3 (ver. 3.11) software by dynamically solving the Landau-Lifshitz-Gilbert Equation (1) on a mesh built by finite differences.

$$\dot{\mathit{m}}=-{\displaystyle \frac{\gamma }{1+{\alpha }^2}}\left[\mathit{m}\times {\mathit{H}}_{eff}+\alpha \mathit{m}\times (\mathit{m}\times {\mathit{H}}_{eff})\right]$$

(1)

where m = M/Ms represents reduced magnetization (a unit vector), Ms is the saturation magnetization, α is the damping parameter, γ is the gyromagnetic ratio, and H_eff is the effective magnetic field. The effective field H_eff is derived from the total free energy E that describes the micromagnetic model (see Equation (2)).

$${\mathit{H}}_{eff}=-{\displaystyle \frac{1}{{M_s\mu }_0}}{\displaystyle \frac{dE}{d\mathit{m}}}$$

(2)

The following contributions to the total free energy were considered in this work: Zeeman energy, exchange energy, magnetostatic energy, and magnetocrystalline anisotropy energy. While thermal fluctuation energy represents another important contribution for micromagnetic simulations, our model focuses on the α-Fe core and excludes surface layers with complex magnetic behavior. Accounting for thermal fluctuations would unnecessarily complicate the model while providing negligible benefits for our system. Thermal fluctuations would induce superparamagnetic effects in small nanoparticles. The critical diameter for superparamagnetic behavior can be estimated using Equation (3) [33,34], where T is temperature, k_b is the Boltzmann constant, and K_c1 is the cubic magnetocrystalline anisotropy constant. Using the parameters from Table 1, we estimate that α-Fe particles below 15 nm in diameter would exhibit superparamagnetic behavior. However, as these particles constitute a negligible fraction (<5%) (Figure 1d) of the investigated ensemble, their influence on the overall magnetic properties is insignificant.

A detailed description of the equations and capabilities of the Mumax3 (ver. 3.11) software can be found in references [35,36]. These energy contributions are enabled by setting the appropriate parameters in the program code. In Mumax3 (ver. 3.11), the geometry of simulated objects is defined by a mesh of rectangular cuboid cells with specified dimensions. Within each cell, magnetic moments must be uniformly distributed; otherwise, the model becomes incorrect. This means that the cell size should not exceed the magnetic exchange length l_ex (Equation (4)). The above-mentioned parameter characterizes competition between the exchange interaction A_ex (it leads to parallel direction of spins in cell) and the magnetostatic interaction K_d (it leads to opposite direction of spins in cell). For magnetic material with dominant crystalline anisotropy and Bloch-type domain wall profile, instead of K_d, using K_c1, but for α-Fe, the ratio K_d/K_c1 ≈ 10 [36,37,38].

$$d_{sp}={\left({\displaystyle \frac{150k_{b}T}{K_{c1}\pi }}\right)}^{1/3}$$

(3)

$$l_{ex}=\sqrt{{\displaystyle \frac{A_{ex}}{K_d}}}=\sqrt{{\displaystyle \frac{2A_{ex}}{{\mu }_0{M_s}^2}}}$$

(4)

with µ₀ = 4π × 10⁻⁷ Tm A⁻¹ the vacuum permeability.

Table 1. Magnetic parameters of Fe at different temperatures.

Material	Aex, pJ/m	Ms, MA/m	Kc1, J/m3	Kc2, J/m3	lex, nm
Fe (293 K)	21.0	1.75	52.0 × 103	0.1 × 103	3

Here, A_ex is the exchange stiffness constant; M_s is the magnetization saturation; K_c1 and K_c2 are the first and second order constants for cubic anisotropy of Fe; and l_ex is the magnetic exchange length [37,38,39,40,41].

Table 1. Magnetic parameters of Fe at different temperatures.

Material	Aex, pJ/m	Ms, MA/m	Kc1, J/m3	Kc2, J/m3	lex, nm
Fe (293 K)	21.0	1.75	52.0 × 103	0.1 × 103	3

Here, A_ex is the exchange stiffness constant; M_s is the magnetization saturation; K_c1 and K_c2 are the first and second order constants for cubic anisotropy of Fe; and l_ex is the magnetic exchange length [37,38,39,40,41].

3. Results and Discussion

3.1. Structure and Morphology of Fe Nanoparticles

XRD analysis (Figure 1a) shows that the iron powder consists of 96% α-Fe and 4% iron oxide FeO_X. The iron oxide layer was intentionally formed on the nanoparticle surfaces during production by adding oxygen. Otherwise, powder can explode at the moment of contact with air due to a high level of pyrophoricity. The specific surface area of the Fe MNPs, measured by low-temperature nitrogen adsorption was 7.3 m² g⁻¹. The calculated value of average diameter using the BET technique was about 100 nm, which is in good agreement with the median of the PSD and the average size of coherent diffraction domains.

The magnetic nanoparticles exhibited a nearly spherical morphology without visible agglomerations. Their size distribution (Figure 1b) was determined from TEM analysis. Particle size distributions by number and by weight were calculated through graphical analysis of approximately N₀ = 350 particles [27,42].

The particle size distribution by number was well approximated by a lognormal function (5) (A, σ, d_n—parameters of approximation), which allows us to estimate the number-averaged mean diameter (d_n = 50 nm). Particles of this size represent the most frequently occurring fraction in the batch (Figure 1c). However, since magnetic properties at the nanoscale are determined not only by the material itself but also by MNP size, the particles with the largest total volume will dominate the magnetic properties of the batch. The volume-averaged mean diameter (d_w = 130 nm) describes the particles that contribute the most to the magnetic properties. Since the size distribution by weight cannot be approximated by a lognormal function, d_w is calculated using Equation (6), where d_i represents the average size of particles in a specific size range, and N(d_i) is the number of particles with diameter d_i. The particle size distribution allows the magnetic hysteresis loop to be calculated for the entire Fe batch based on the magnetic hysteresis loops for individual particles with specific diameters (Figure 1d).

$$N/N_0(d)={\displaystyle \frac{A}{\sqrt{2\pi }\sigma d}}{e}^{{\displaystyle \frac{-{\left(ln\frac{d}{d_n}\right)}^2}{2{\sigma }^2}}}\times 100\%$$

(5)

Here, A is the parameter of non-normalized lognormal function; σ is the standard deviation of the natural logarithm (characterizes the particle size dispersion); and d_n is the number-averaged mean diameter.

$$d_w={\displaystyle \frac{\sum N\left(d_i\right)·{d_i}^4}{\sum N\left(d_i\right)·{d_i}^3}}$$

(6)

3.2. Magnetic Properties of Fe Nanoparticles: Simulation and Experiment

The specific magnetic moment of the nanoparticles was measured using vibration sample magnetometry at a room temperature of 293 K. The values of the coercivity (H_c), the residual specific magnetic moment (m_r), and the specific magnetic moment of technical saturation (m_s) defined for the external field intensity of 1.8 T are shown in

Table 2. Magnetic properties of Fe powders.

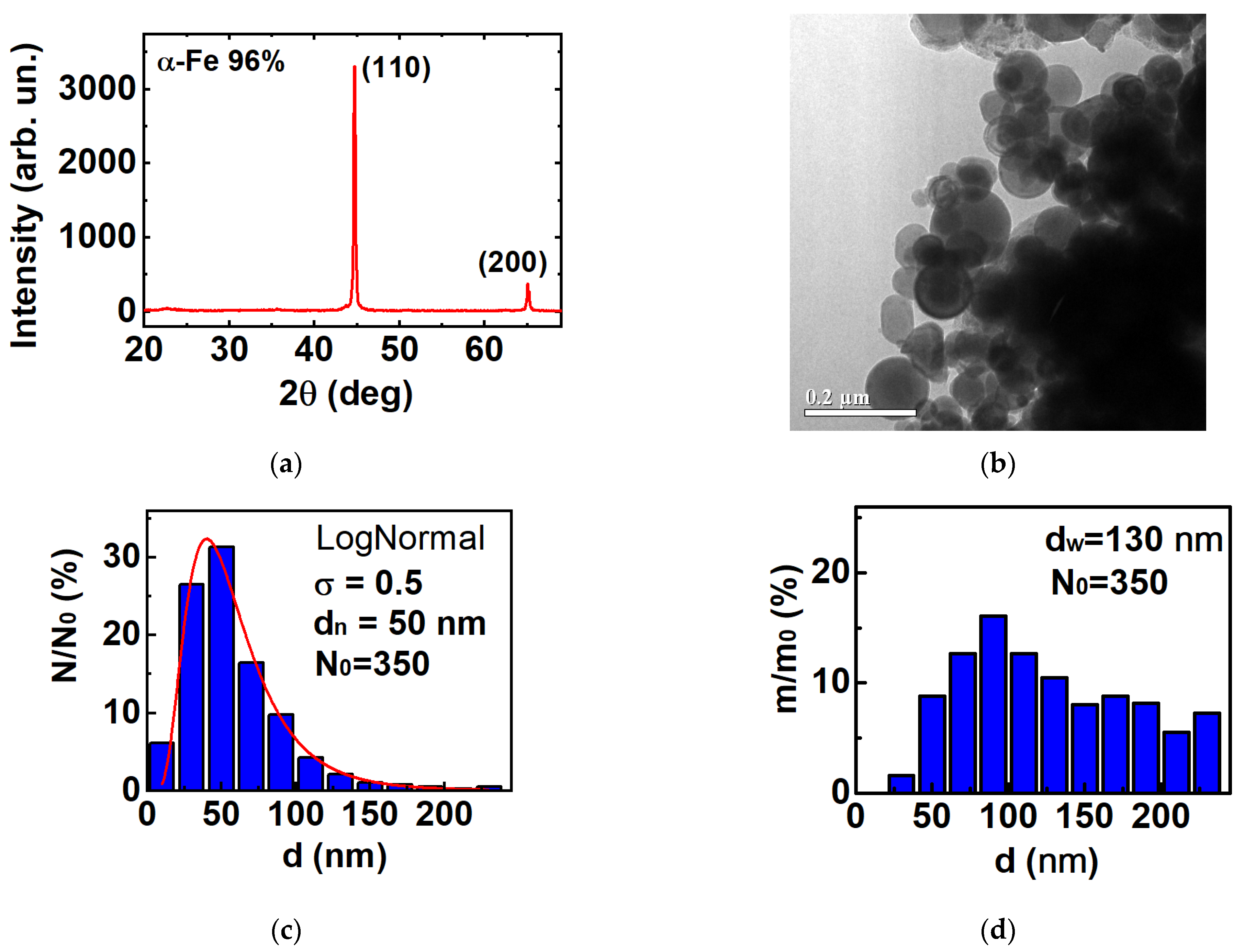
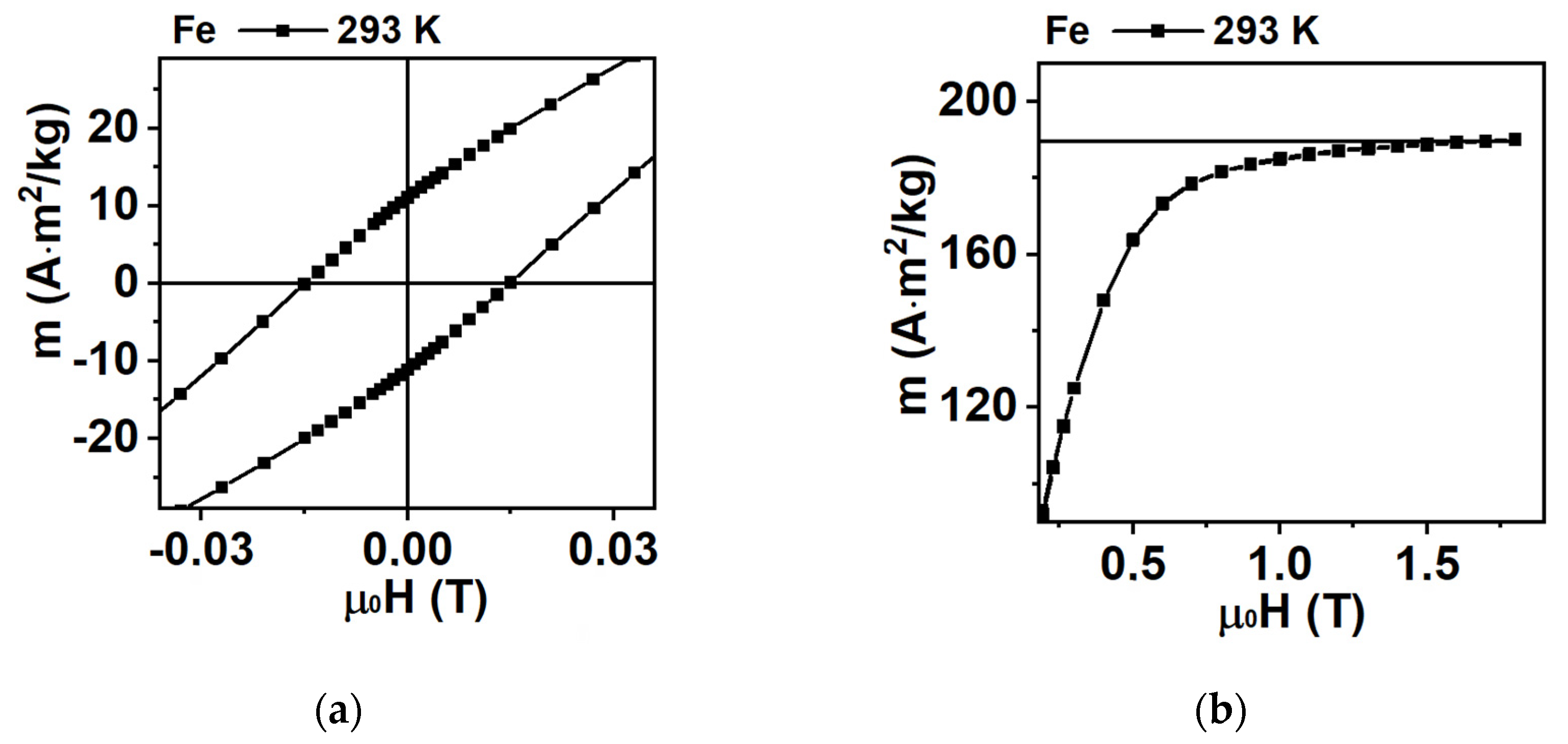
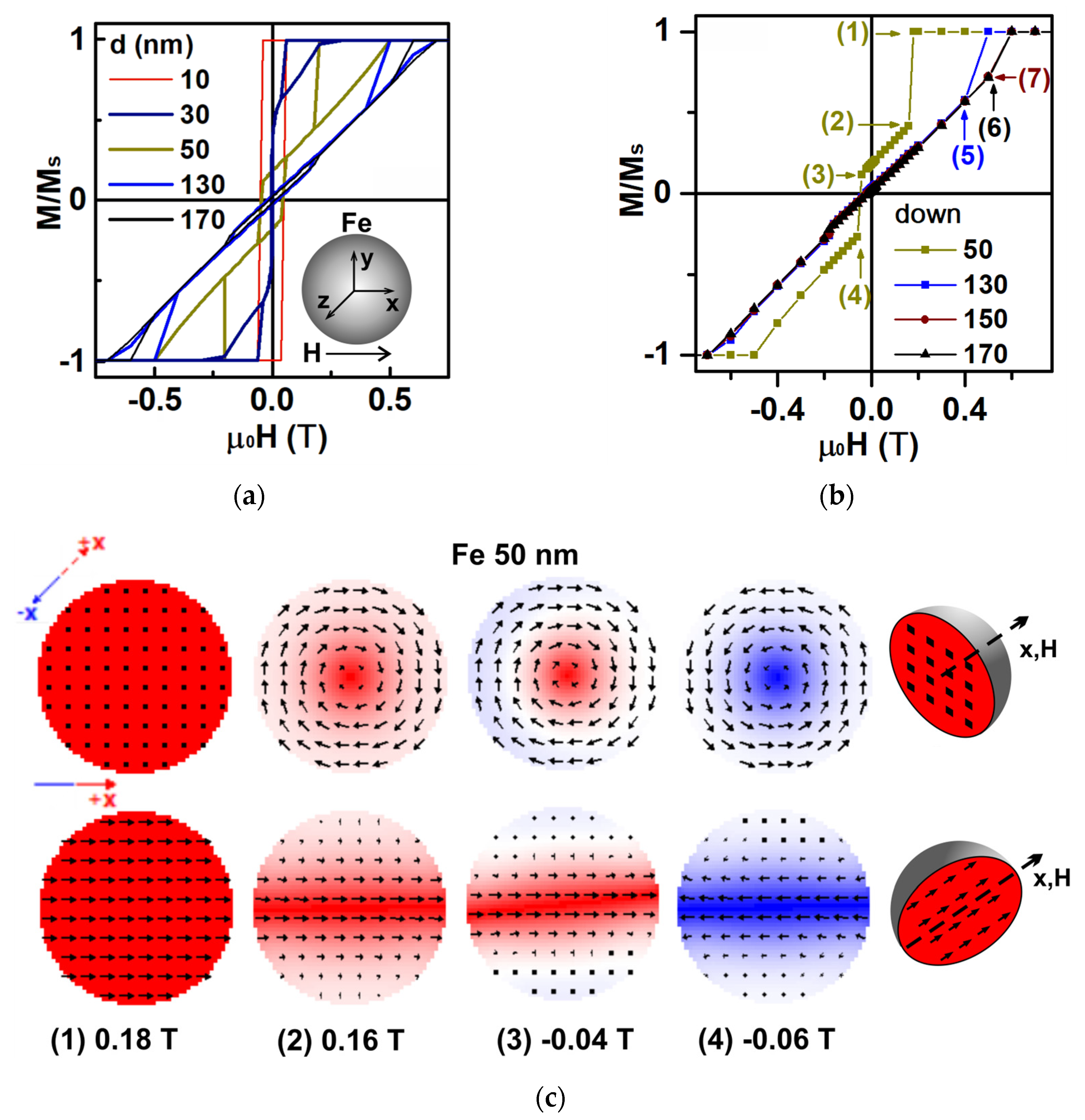
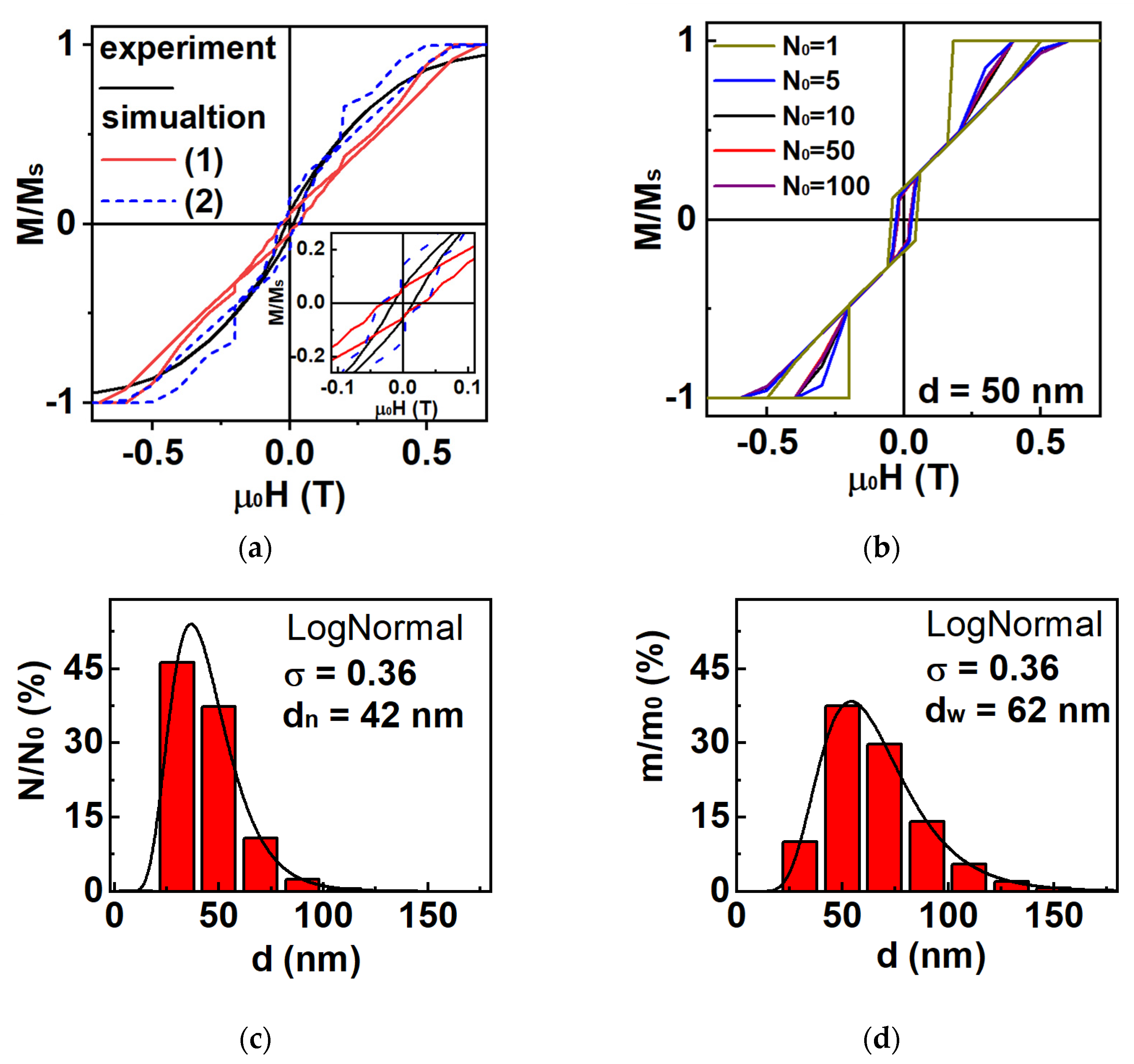
Batch	ms (H = 1.8 T), Am2/kg	mr, Am2/kg	Hc, mT
Fe (293 K)	190	11	15

. In the higher fields, the m_s changed by less than 2% (Figure 2). The specific magnetic moment of technical saturation of Fe nanoparticles, m_s = 190 Am²/kg, is lower than that for pure bulk iron (220 Am²/kg) [43,44,45]. This reduction arises from the nanoscale decrease of magnetization and due to the presence of iron oxide phases (e.g., Fe₃O₄ or γ-Fe₂O₃) forming the shell around the α-Fe core. Magnetite and maghemite exhibit specific magnetic moments at least two times smaller compared to pure iron. The oxide layer is assumed to be non-magnetic because the surface atoms lack sufficient neighboring exchange interactions. The diameter of magnetic core d_core is calculated using Equation (7) [30], where ρ_core = 7.87 g/cm³ (density of α-Fe), ρ_shell = 5.2 g/cm³ (density of FeO_X), d (diameter of nanoparticle), m_core = 220 Am²/kg (specific magnetic moment of saturation α-Fe core). For nanoparticles with d = 50 nm, the diameter of the magnetic core is about 46 nm.

$$d_{core}=d·{\left({\displaystyle \frac{{\rho }_{shell}/{\rho }_{core}}{{\rho }_{shell}/{\rho }_{core}+(m_{core}-m_s)/m_s}}\right)}^{1/3}$$

(7)

Micromagnetic simulations of magnetic hysteresis loops were carried out using the magnetic parameters listed in Table 1 at 293 K. The cubic magnetic anisotropy axes were directed along coordinate axes (along x, y, and z) according to the scheme of particles represented in Figure 3. Micromagnetic simulations were performed for individual defect-free particles with a diameter range from 10 nm to 230 nm in 20 nm increments.

Figure 3 shows magnetic structures of selected particles with diameters of 10 nm, 30 nm, and 50 nm in the remanent magnetization state. The magnetic properties of the Fe powder ensemble depend on the size of the individual particles of the ensemble. Iron particles with a diameter of 10 nm are homogeneously magnetized along one of the easy magnetization axes (x-axis) of cubic magnetic anisotropy in the remanent state. Particles with a diameter of 30 nm exhibit a rather complex multidomain structure. Particles with 50 nm have a vortex-type magnetic structure with a core aligned along the easy magnetization x-axis. The magnetic structure and magnetic hysteresis loops (Figure 4a) for 10 nm, 30 nm, and 50 nm were found to be in good agreement with other works [46,47,48,49].

Let us consider the simulated magnetization process for an individual particle with a diameter of 50 nm. Figure 4a,b shows the magnetic hysteresis loop, while Figure 4c,d displays the corresponding magnetic structures at selected field points. The external magnetic field H is applied along the x-axis and decreased from 1 T to −1 T (down), then increased from −1 T to 1 T (up). The number assigned to the magnetic structure (Figure 4c,d) corresponds to the number indicated on the hysteresis loop (Figure 4b). As the magnetic field is decreasing, the magnetic structure changes by jumping from a uniform saturated magnetization state (Figure 4b,c; the point (1)) to a magnetic structure with a “core” parallel to the magnetic field and a “vortex” partially directed along a magnetic field (Figure 4b,c; the point (2)). The “Core” is a central part of a particle with magnetic moments along the x-axis (m_y = m_z = 0). The “Vortex” is a region with magnetic moments that are perpendicular to the x-axes (m_x = 0) and formed around the “core” (Figure 3). Between states (Figure 4b,c; the point (2)) and (Figure 4b,c; the point (3)), the magnetization process occurs with the appearance of the mx magnetic moment component in “vortex” with the opposite direction of the external magnetic field. Then, the jump magnetization reversal of the “core” is observed at the transition from (Figure 4b,c; the point (3)) to (Figure 4b,c; the point (4)) states. At the same time, the direction of the “vortex” magnetic moments changes from clockwise to counterclockwise. Further magnetization process occurs by rotation of “vortex” magnetic moments along the external magnetic field direction until a state of uniform magnetization is reached.

Similar behavior was observed for all particles with diameters larger than 50 nm up to the 130 nm case (Figure 4b). For the MNPs with the diameters below 150 nm, as the field decreases, the magnetization evolves smoothly from uniform saturation to a vortex state via domain wall nucleation, without sudden transitions (Figure 4b,d; the points (6,7)). At zero external magnetic fields, the particles are also characterized by a “core” and “vortex” magnetic structure.

The simulated magnetic hysteresis loops of individual magnetic particles and particle size distributions can be used to calculate the magnetic hysteresis loop of an ensemble of Fe MNPs following the procedure described below. For this purpose, the normalized hysteresis loops (Figure 4a) for each particle size are multiplied by the corresponding weight fraction m/m₀ from the particle size distribution (Figure 1d). The weight concentration ratio m/m₀ is used because the magnetic properties of an ensemble are primarily determined by particles with the largest total volume. For instance, one particle with a diameter of 150 nm in the considered batch contributes to the magnetic properties equivalently to 30 particles with a diameter of 50 nm. Afterwards, all magnetic hysteresis loops for each one of the particle sizes were summarized, and the hysteresis loop for the ensemble was calculated.

The simulated magnetic hysteresis loop of the ensemble based on the experimental weight concentration ratio m/m₀ (Figure 1d) is marked by “1” (Figure 5a, red curve). It is characterized by a smaller angle of inclination relative to the H axis than the experimental magnetic hysteresis loop (Figure 5a, black curve) that is seen by deviations between loops (Figure 5a). According to the magnetic hysteresis loop for individual particles (Figure 4a), a smaller angle of loop inclination relative to the H-axis corresponds to larger nanoparticles. Consequently, the ensemble consists of smaller particles than shown by experimental particle size distribution (Figure 1a). It is related to the fact that the micromagnetic model describes magnetic properties of the α-Fe core without a surface layer of FeO_X. For instance, a nanoparticle (d = 50 nm) with a core of α-Fe (d_core = 46 nm) and a surface layer of FeO_X (thickness 2 nm, Equation (7)) corresponds to a micromagnetic model with d = 46 nm. Taking this fact into account, refined distribution (Figure 5d) was derived by optimizing the simulated hysteresis loop of the ensemble (Figure 5a, blue curve, marked by “2”) to closely match the experimental data. As the magnetic hysteresis loop of an individual nanoparticle is highly size-dependent, this method can be used as an alternative to electron microscopy for the determination of size distribution. Electron microscopy analysis of magnetic particles is limited by the small number of particles analyzed and operator-dependent subjectivity, while magnetic measurements probe a large ensemble of particles. As a result, the calculated size distribution by magnetic measurement accurately represents the entire ensemble. Additionally, magnetic measurements are less costly than electron microscopy.

Simulated magnetic hysteresis loop “2” (Figure 5a, blue curve) based on refined distribution (Figure 5d) is characterized by a “step-like” shape. The coercivity values are H_c = 14 mT for the experimental loop and H_c = 30 mT for the simulated one. Starting from 0.2 T, the experimental and simulated curves diverge due to the expansion of the simulated loop. These behaviors can be explained by the following reasons. The first reason is the discrete number of micromagnetic models with specific diameter steps (the diameter of micromagnetic models ranges from 10 nm to 230 nm with a step of 20 nm). The second reason, since the calculation was carried out for the case where the magnetic field H is aligned along one of the cubic magnetic anisotropy axes, the simulation corresponds to an ensemble of MNPs having a magnetic texture. However, in the experiment, different orientations of the anisotropy axes relative to the magnetic field are possible. Figure 5b shows simulated magnetic hysteresis loops for N₀ nanoparticles with d = 50 nm with random directions of anisotropy axes. Accounting for the dispersion of the axes narrows the hysteresis loop at fields above 0.2 T, while the coercivity decreases from 45 mT to 20 mT. It is shown that N₀ = 5 is sufficient to account for the contribution of anisotropy axis dispersion. Thus, calculating the magnetic hysteresis loop with the anisotropy axis dispersion significantly increases the calculation time. The third reason is that the simulation does not include the contribution of magnetic interactions between nanoparticles, which leads to a decrease in coercivity and an increase in the angle of inclination relative to the H-axis [50]. Other reasons may be related to the specific magnetization behavior of the nanoparticle shell, which consists of nanocrystalline FeO_X and 1–2 surface atomic layers [51]. Moreover, magnetic interactions between individual nanoparticles can be neglected in materials with a low nanoparticle concentration (e.g., magnetic polymers) due to the large interparticle distances. In contrast, both dipole-dipole interactions and exchange coupling in core-shell individual particles can play a crucial role in determining the magnetic properties of the ensemble.

It should be noticed that this method is not applicable to the description of magnetic properties of nanoparticles in a superparamagnetic state. The diameter of the superparamagnetic state is d_sp = 15 nm for α-Fe nanoparticles (Equation (3)). However, in this study, since these particles represent a negligible weight fraction, their impact on the magnetic properties is insignificant.

The refined nanoparticle size distribution by number (Figure 5c) is characterized by a lower dispersion σ = 0.36 and a number-averaged mean diameter d_n = 42 nm compared to the experimental distribution (Figure 1c). The distribution is shifted toward smaller diameters, representing only α-Fe core of the core-shell Fe/FeO_X ensemble. The number-averaged mean diameter (d_n = 42 nm) allows for estimating the FeO_X shell thickness at 4 nm. The size distribution by weight approximates a lognormal function well (see Equation (5)) compared to the experimental distribution (Figure 1d). This may indicate that larger particles are less abundant in the ensemble than the experimental distribution (obtained from a limited number of nanoparticles) suggests.

Modern fabrication techniques enable the production of MNP batches with widely varying dispersion parameters. For example, ensembles with similar specific surface area values may correspond to completely different particle size distributions and magnetic properties of batch materials. Simulation techniques serve as a powerful tool for understanding the relationship between structural and magnetic properties across different ensembles. One promising practical application of these findings is the design of new composite materials by mixing precisely controlled quantities of MNPs from different batches with well-characterized properties. This new ensemble of mixed batches can be difficult to obtain by direct synthesis.

Although the simplification of the micromagnetic model to defect-free, non-interacting magnetic particles was necessary at the first step of the research, the simulated magnetic hysteresis loops of individual particles can be used in order to describe the magnetic hysteresis loop of an ensemble. This approach can be applied to determine the particle size distribution by approximating the experimental magnetic hysteresis loop of the ensemble. However, it requires a database of magnetic hysteresis loops and magnetic structures for individual particles across a wide range of sizes. The micromagnetic simulation described in this work is an appropriate method for this purpose.

4. Conclusions

Magnetic nanoparticles consisting of an α-Fe core and an iron oxide shell of a few nanometers were fabricated by the electric explosion of the wire technique (EEW). As a result, ensembles of core-shell Fe/FeO_X magnetic nanoparticles were obtained. Their structure and magnetic properties were experimentally investigated. The magnetic properties of Fe nanoparticles—an ensemble of individual defect-free, non-interacting iron-based nanoparticles having non-magnetic shells with different diameters from 10 to 230 nm—were calculated using micromagnetic modeling. Experimental and calculated magnetic hysteresis loops were comparatively analyzed, showing reasonable agreement.