Evolution of Griffiths-like Anomaly in Isostructural Swedenborgite Compounds Ho1−xErxBaCo4O7+δ
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Structural Characterization
3.1.1. XRD and Structure
3.1.2. Valence State of Co-Ions from XANES (X-Ray Absorption near Edge Spectroscopy) Studies
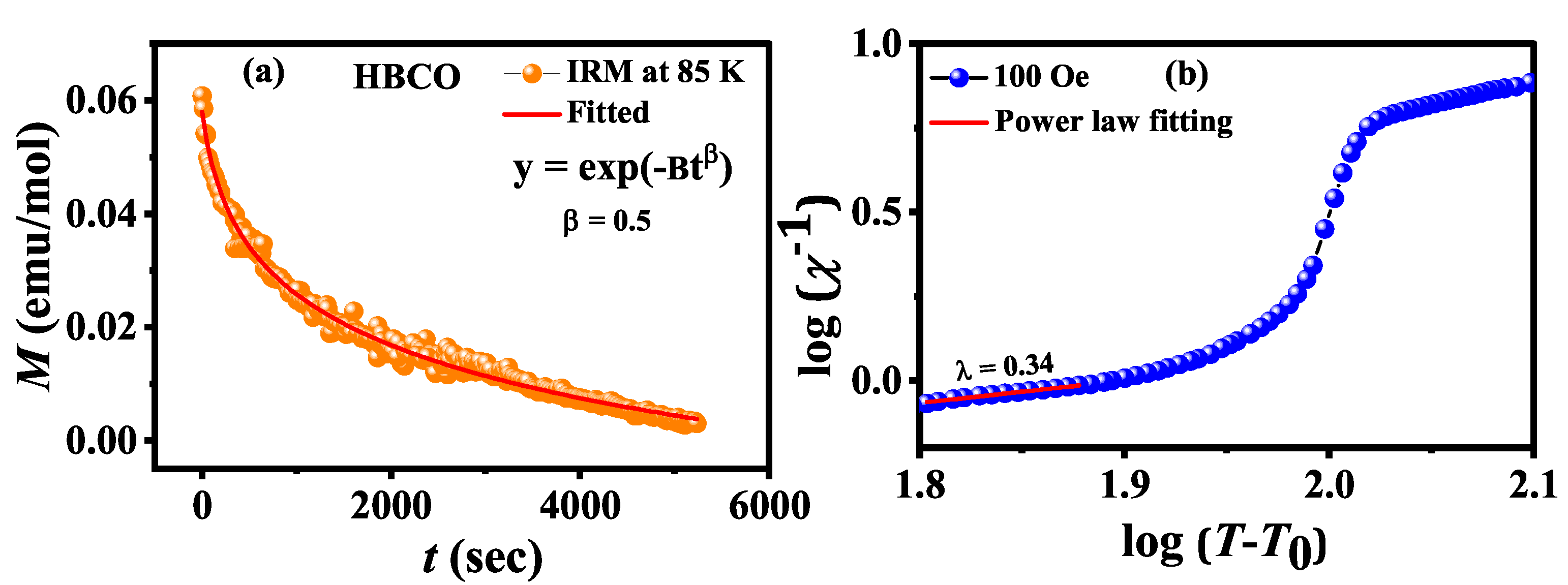
3.2. Magnetic Properties
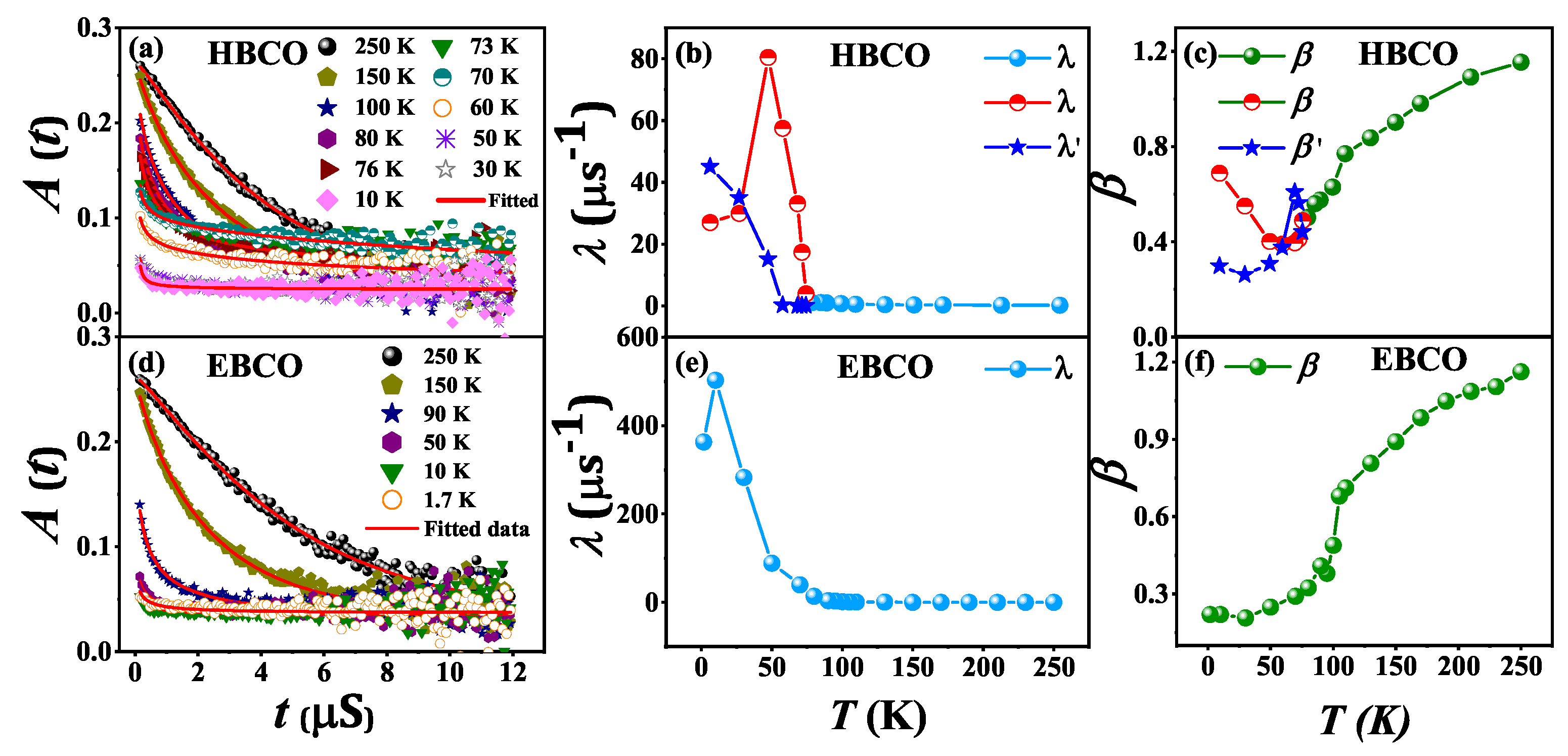
4. SR Measurement
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grinstein, G. Fundamental Problems in Statistical Mechanics VI, 4th ed.; Elsevier: New York, NY, USA, 1985. [Google Scholar]
- Vojta, T. Disorder-Induced Rounding of Certain Quantum Phase Transitions. Phys. Rev. Lett. 2003, 90, 107202. [Google Scholar] [CrossRef]
- Griffiths, R.B. Nonanalytic Behavior Above the Critical Point in a Random Ising Ferromagnet. Phys. Rev. Lett. 1969, 23, 17–19. [Google Scholar] [CrossRef]
- McCoy, B.M. Incompleteness of the Critical Exponent Description for Ferromagnetic Systems Containing Random Impurities. Phys. Rev. Lett. 1969, 23, 383–386. [Google Scholar] [CrossRef]
- Deisenhofer, J.; Braak, D.; Krug von Nidda, H.A.; Hemberger, J.; Eremina, R.M.; Ivanshin, V.A.; Balbashov, A.M.; Jug, G.; Loidl, A.; Kimura, T.; et al. Observation of a Griffiths Phase in Paramagnetic La1-xSrxMnO3. Phys. Rev. Lett. 2005, 95, 257202. [Google Scholar] [CrossRef]
- Jiang, W.; Zhou, X.; Williams, G.; Mukovskii, Y.; Glazyrin, K. Griffiths phase and critical behavior in single-crystal La0.7Ba0.3MnO3: Phase diagram for La1-xBaxMnO3 (x⩽0.33). Phys. Rev. B 2008, 77, 064424. [Google Scholar] [CrossRef]
- Zhou, S.; Guo, Y.; Zhao, J.; He, L.; Shi, L. Size-induced Griffiths phase and second-order ferromagnetic transition in Sm0.5Sr0.5MnO3 nanoparticles. J. Phys. Chem. C 2011, 115, 1535–1540. [Google Scholar] [CrossRef]
- Pramanik, A.K.; Banerjee, A. Griffiths phase and its evolution with Mn-site disorder in the half-doped manganite Pr0.5Sr0.5Mn1-yGayO3 (y=0.0, 0.025, and 0.05). Phys. Rev. B 2010, 81, 024431. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Castilla, G.; Jones, B.A. Non-Fermi Liquid Behavior and Griffiths Phase in f-Electron Compounds. Phys. Rev. Lett. 1998, 81, 3531–3534. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Wang, H.; Huo, D.; Tan, W. Room-temperature magnetoresistive and magnetocaloric effect in La1-xBaxMnO3 compounds: Role of Griffiths phase with ferromagnetic metal cluster above Curie temperature. J. Appl. Phys. 2022, 131, 043901. [Google Scholar] [CrossRef]
- Pereira, A.M.; Morellon, L.; Magen, C.; Ventura, J.; Algarabel, P.A.; Ibarra, M.R.; Sousa, J.B.; Araújo, J.P. Griffiths-like phase of magnetocaloric R5(SixGe1-x)4 (R=Gd, Tb, Dy, and Ho). Phys. Rev. B 2010, 82, 172406. [Google Scholar] [CrossRef]
- Krivoruchko, V.N. The Griffiths phase and the metal-insulator transition in substituted manganites (Review Article). Low Temp. Phys. 2014, 40, 586–599. [Google Scholar] [CrossRef]
- Magen, C.; Algarabel, P.A.; Morellon, L.; Araújo, J.P.; Ritter, C.; Ibarra, M.R.; Pereira, A.M.; Sousa, J.B. Observation of a Griffiths-like Phase in the Magnetocaloric Compound Tb5Si2Ge2. Phys. Rev. Lett. 2006, 96, 167201. [Google Scholar] [CrossRef]
- Ghosh, K.; Mazumdar, C.; Ranganathan, R.; Mukherjee, S. Griffiths phase behaviour in a frustrated antiferromagnetic intermetallic compound. Sci. Rep. 2015, 5, 15801. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Tong, P.; Cui, D.; Yanh, J.; Lin, S.; Wang, B.; Tong, W.; Zhang, L.; Zou, Y.; Sun, Y. Unusual ferromagnetic critical behavior owing to short-range antiferromagnetic correlations in antiperovskite Cu1-xNMn3+x (0.1 ≤ x ≤ 0.4). Sci. Rep. 2015, 5, 7933. [Google Scholar] [CrossRef]
- Ubaid-Kassis, S.; Vojta, T.; Schroeder, A. Quantum Griffiths Phase in the Weak Itinerant Ferromagnetic Alloy Ni1-xVx. Phys. Rev. Lett. 2010, 104, 066402. [Google Scholar] [CrossRef]
- Wang, R.; Gebretsadik, A.; Ubaid-Kassis, S.; Schroeder, A.; Vojta, T.; Baker, P.J.; Pratt, F.L.; Blundell, S.J.; Lancaster, T.; Franke, I.; et al. Quantum Griffiths Phase Inside the Ferromagnetic Phase of Ni1-xVx. Phys. Rev. Lett. 2017, 118, 267202. [Google Scholar] [CrossRef] [PubMed]
- Ahad, A.; Shukla, D.; Rahman, F.; Gautam, K.; Dey, K.; Majid, S.; Sharma, S.; Coaquira, J. Griffiths-like phase and charge-spin glass state in La1.5Sr0.5CoO4. Appl. Phys. Lett. 2018, 113, 102405. [Google Scholar] [CrossRef]
- Lu, C.L.; Wang, K.F.; Dong, S.; Wan, J.G.; Liu, J.M.; Ren, Z.F. Specific heat anomalies and possible Griffiths-like phase in La0.4Ca0.6MnO3 nanoparticles. J. Appl. Phys. 2008, 103, 07F714. [Google Scholar] [CrossRef]
- Ouyang, Z.W.; Xia, N.M.; Wu, Y.Y.; Sheng, S.S.; Chen, J.; Xia, Z.C.; Li, L.; Rao, G.H. Short-range ferromagnetic correlations in the spin-chain compound Ca3CoMnO6. Phys. Rev. B 2011, 84, 054435. [Google Scholar] [CrossRef]
- Kumar, J.; Panja, S.N.; Dengre, S.; Nair, S. Identification of a Griffiths singularity in a geometrically frustrated antiferromagnet. Phys. Rev. B 2017, 95, 054401. [Google Scholar] [CrossRef]
- Khalyavin, D.D.; Manuel, P.; Mitchell, J.F.; Chapon, L.C. Spin correlations in the geometrically frustrated RBaCo4O7 antiferromagnets: Mean-field approach and Monte Carlo simulations. Phys. Rev. B 2010, 82, 094401. [Google Scholar] [CrossRef]
- Raveau, B. The crucial role of mixed valence in the magnetoresistance properties of manganites and cobaltites. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 366, 83–92. [Google Scholar] [CrossRef]
- Chapon, L.C.; Radaelli, P.G.; Zheng, H.; Mitchell, J.F. Competing magnetic interactions in the extended Kagomé system YBaCo4O7. Phys. Rev. B 2006, 74, 172401. [Google Scholar] [CrossRef]
- Buhrandt, S.; Fritz, L. Antiferromagnetic Ising model on the swedenborgite lattice. Phys. Rev. B 2014, 90, 094415. [Google Scholar] [CrossRef]
- Gao, S.; Kocsis, V.; Soda, M.; Ye, F.; Liu, Y.; May, A.F.; Taguchi, Y.; Tokura, Y.; Arima, T.h.; Schweika, W.; et al. Suppressed incommensurate order in swedenborgite Ca0.5Y0.5BaCo4O7. Phys. Rev. B 2021, 104, L140408. [Google Scholar] [CrossRef]
- Schweika, W.; Valldor, M.; Reim, J.D.; Rößler, U.K. Chiral Spin Liquid Ground State in YBaCo3FeO7. Phys. Rev. X 2022, 12, 021029. [Google Scholar] [CrossRef]
- Kazei, Z.A.; Snegirev, V.V.; Stolyarenko, M.S. Phase Transitions in Frustrated Slightly Nonstoichiometric ErBaCo4O7 + x (x≈ 0 and 0.03) Cobaltites. JETP Lett. 2020, 112, 180–185. [Google Scholar] [CrossRef]
- Kazei, Z.A.; Snegirev, V.V.; Stolyarenko, M.S. Phase Transitions in Frustrated ErBaCo4O7 + x (x = 0–0.06) Cobaltites at a Small Deviation from Stoichiometry. J. Exp. Theor. Phys. 2021, 133, 591–598. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B Condens. Matter 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Huq, A.; Mitchell, J.; Zheng, H.; Chapon, L.; Radaelli, P.; Knight, K.; Stephens, P. Structural and magnetic properties of the Kagomé antiferromagnet YbBaCo4O7. J. Solid State Chem. 2006, 179, 1136–1145. [Google Scholar] [CrossRef]
- Avci, S.; Chmaissem, O.; Zheng, H.; Huq, A.; Manuel, P.; Mitchell, J.F. Oxygen Stoichiometry in the Geometrically Frustrated Kagomé System YBaCo4O7+δ: Impact on Phase Behavior and Magnetism. Chem. Mater. 2013, 25, 4188–4196. [Google Scholar] [CrossRef]
- Schiesaro, I.; Battocchio, C.; Venditti, I.; Prosposito, P.; Burratti, L.; Centomo, P.; Meneghini, C. Structural characterization of 3d metal adsorbed AgNPs. Phys. E Low-Dimens. Syst. Nanostruct. 2020, 123, 114162. [Google Scholar] [CrossRef]
- Randeria, M.; Sethna, J.P.; Palmer, R.G. Low-Frequency Relaxation in Ising Spin-Glasses. Phys. Rev. Lett. 1985, 54, 1321–1324. [Google Scholar] [CrossRef] [PubMed]
- Bray, A.J. Dynamics of dilute magnets above Tc. Phys. Rev. Lett. 1988, 60, 720–723. [Google Scholar] [CrossRef]
- Bray, A.J. Nature of the Griffiths phase. Phys. Rev. Lett. 1987, 59, 586–589. [Google Scholar] [CrossRef] [PubMed]
- Vazquez, F.; Bonachela, J.A.; López, C.; Muñoz, M.A. Temporal Griffiths Phases. Phys. Rev. Lett. 2011, 106, 235702. [Google Scholar] [CrossRef] [PubMed]
- Blundell, S.J. Spin-polarized muons in condensed matter physics. Contemp. Phys. 1999, 40, 175–192. [Google Scholar] [CrossRef]
- Ryan, D.H.; van Lierop, J.; Cadogan, J.M. Zero-field muon spin relaxation studies of frustrated magnets: Physics and analysis issues. J. Phys. Condens. Matter 2004, 16, S4619–S4638. [Google Scholar] [CrossRef]
- de Réotier, P.D.; Yaouanc, A. Muon spin rotation and relaxation in magnetic materials. J. Phys. Condens. Matter 1997, 9, 9113–9132. [Google Scholar] [CrossRef]
- Sannigrahi, J.; Pramanick, S.; Chatterjee, S.; Lord, J.S.; Khalyavin, D.; Hillier, A.D.; Adroja, D.T.; Majumdar, S. Magnetic states of Ni-Mn-Sn based shape memory alloy: A combined muon spin relaxation and neutron diffraction study. Phys. Rev. B 2019, 99, 224401. [Google Scholar] [CrossRef]
- Lee, S.; Lee, W.; Lee, K.J.; Kim, B.; Suh, B.J.; Zheng, H.; Mitchell, J.F.; Choi, K.Y. Muon spin relaxation study of spin dynamics in the extended kagome systems YBaCo4O7+δ(δ=0,0.1). Phys. Rev. B 2018, 97, 104409. [Google Scholar] [CrossRef]
- Teyssier, J.; Giannini, E.; Guritanu, V.; Viennois, R.; van der Marel, D.; Amato, A.; Gvasaliya, S.N. Spin-glass ground state in Mn1-xCoxSi. Phys. Rev. B 2010, 82, 064417. [Google Scholar] [CrossRef]
- Uemura, Y.J.; Harshman, D.R.; Senba, M.; Ansaldo, E.J.; Murani, A.P. Zero-field muon-spin relaxation in CuMn spin-glasses compared with neutron and susceptibility experiments. Phys. Rev. B 1984, 30, 1606–1608. [Google Scholar] [CrossRef]
- Tripathi, R.; Das, D.; Biswas, P.K.; Adroja, D.T.; Hillier, A.D.; Hossain, Z. Quantum Griffiths phase near an antiferromagnetic quantum critical point: Muon spin relaxation study of Ce(Cu 1-xCox)2Ge2. Phys. Rev. B 2019, 99, 224424. [Google Scholar] [CrossRef]
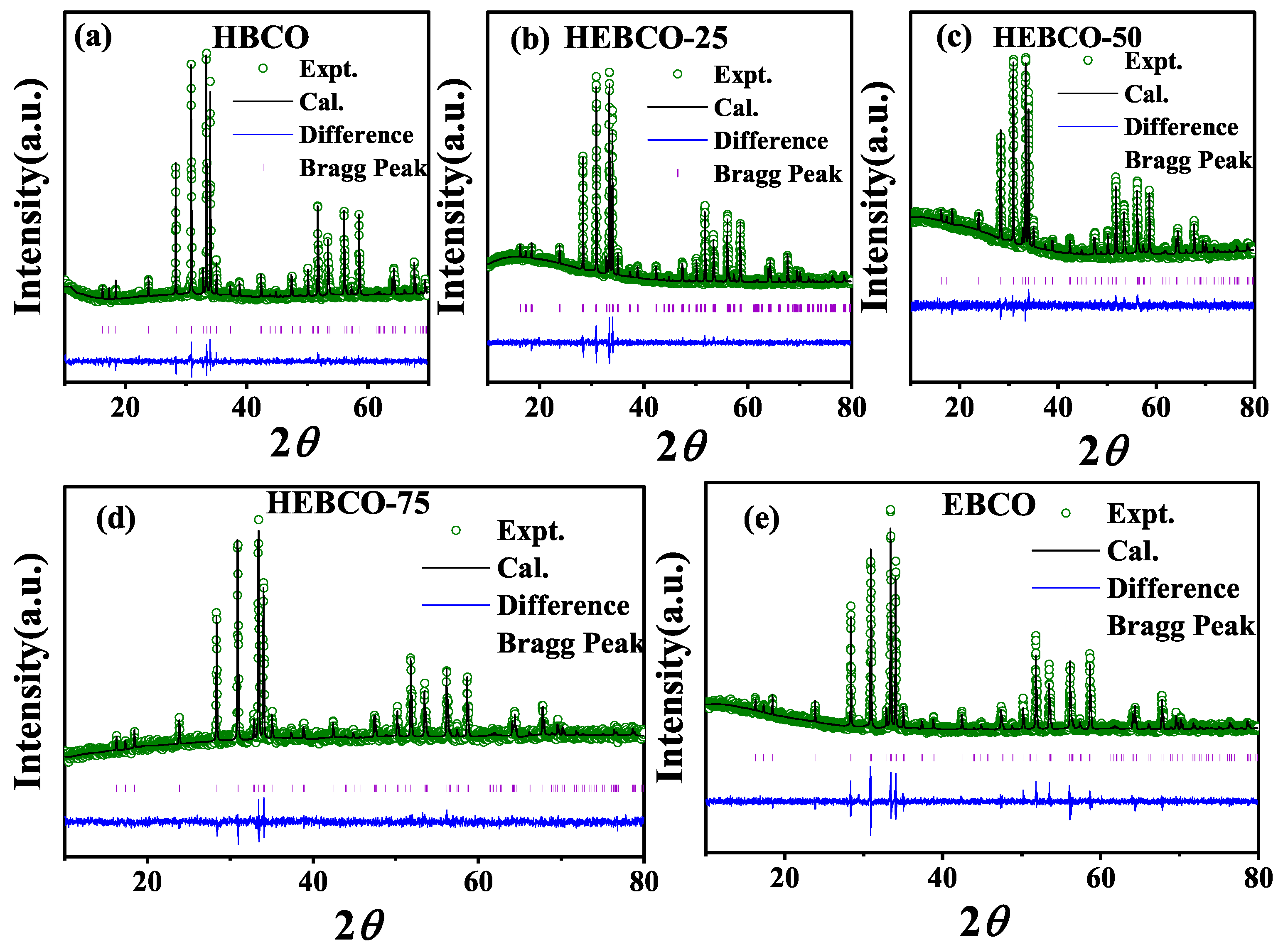
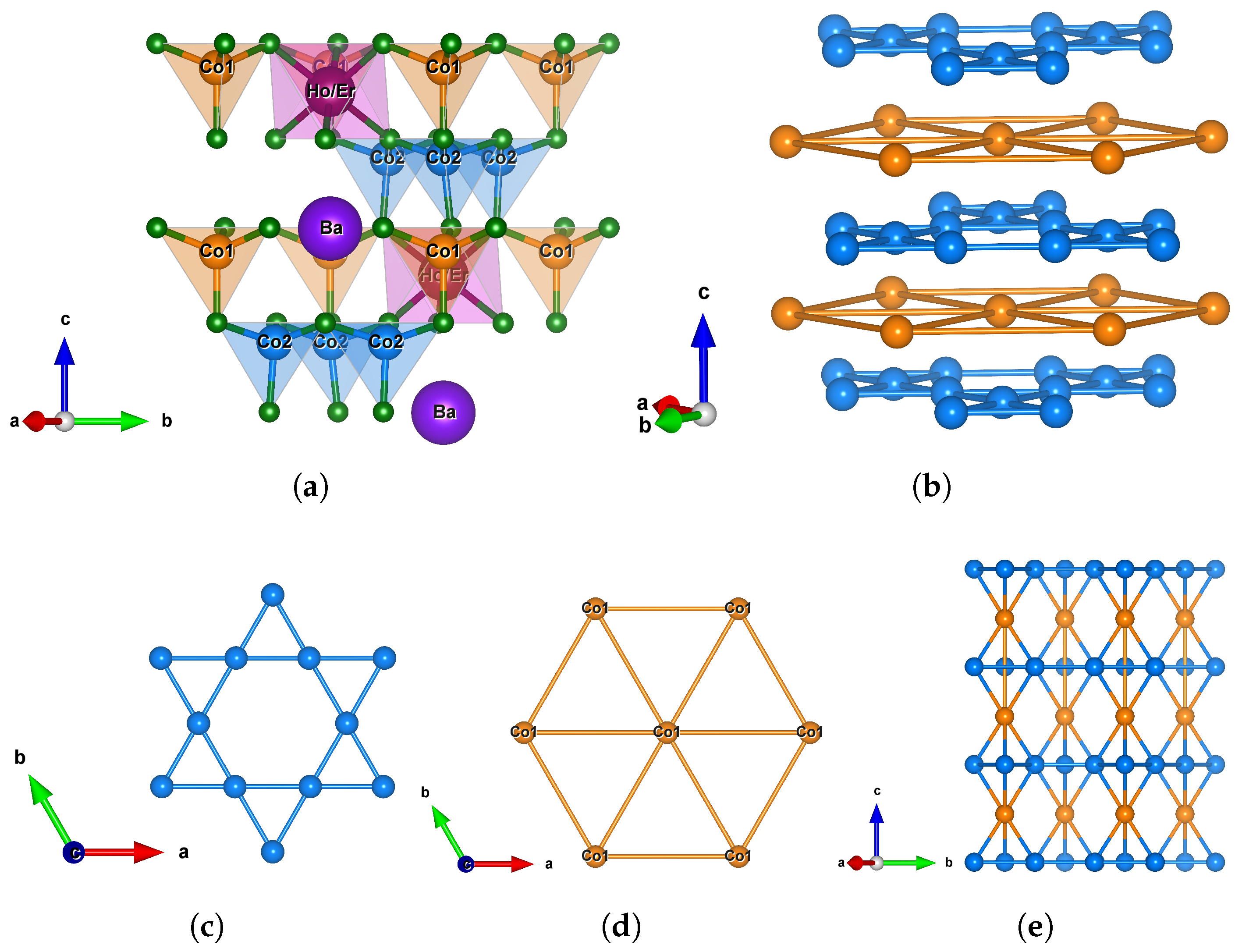
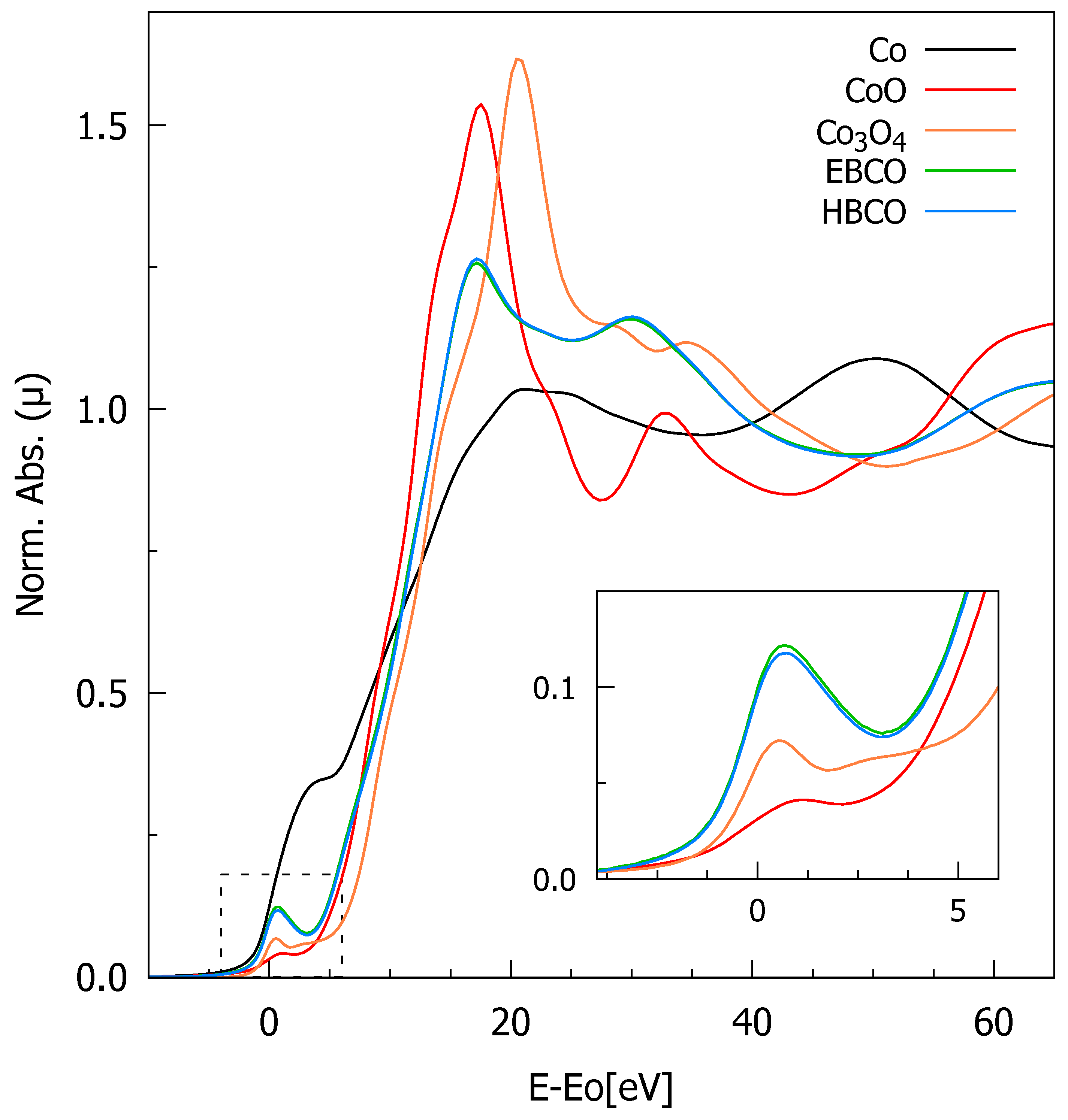
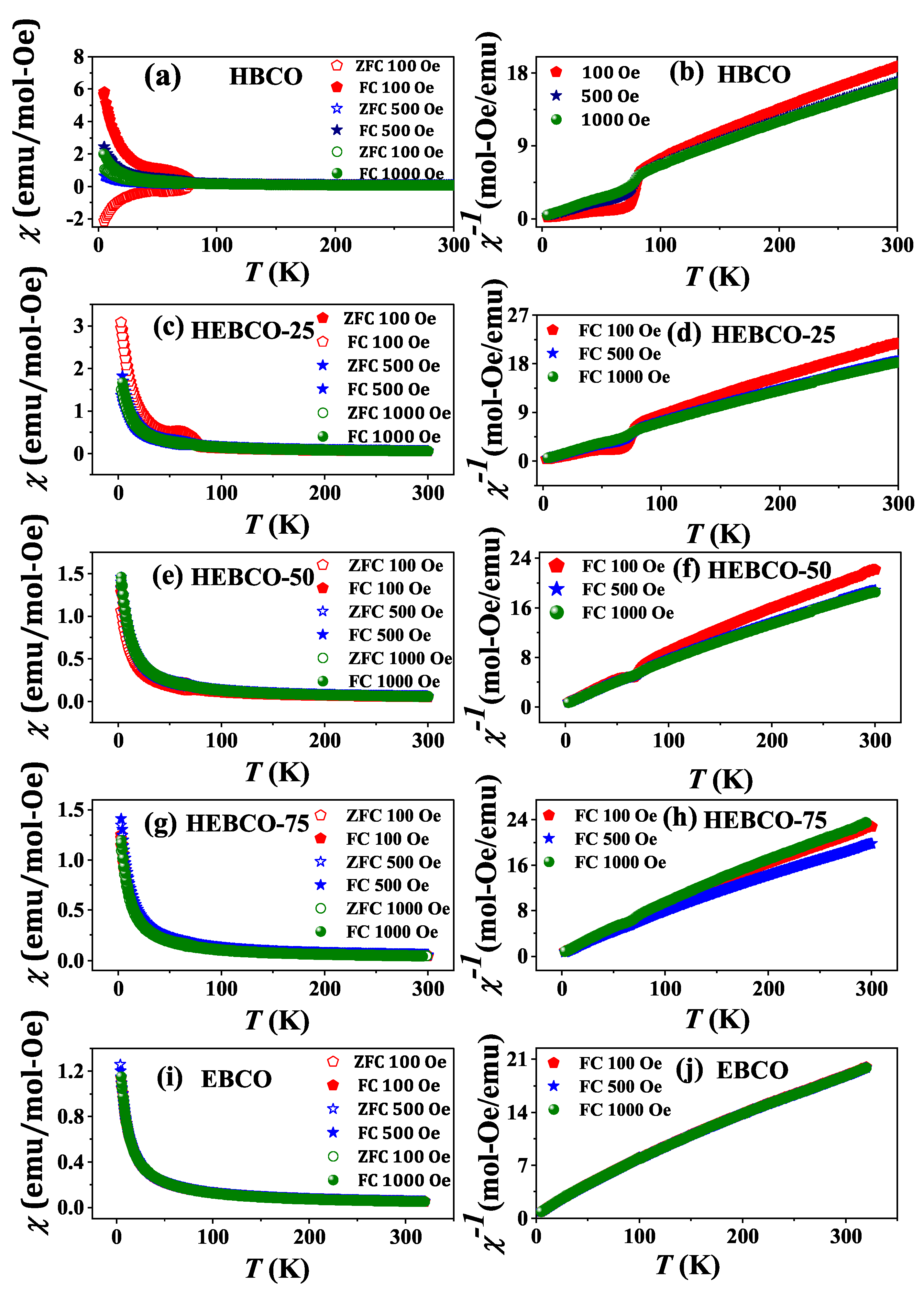
| Parameter | |||||
|---|---|---|---|---|---|
| = 0.0 | = 0.25 | = 0.50 | = 0.75 | = 1.0 | |
| 0.12 | 0.15 | 0.09 | 0.12 | 0.09 | |
| Space group | P31c | P31c | P31c | P31c | P31c |
| a (Å) | 6.303 (1) | 6.30 (1) | 6.29 (7) | 6.29 (4) | 6.29 (1) |
| b (Å) | 6.30 (7) | 6.30 (1) | 6.29 (7) | 6.29 (4) | 6.29 (1) |
| c (Å) | 10.24 (7) | 10.24 (4) | 10.24 (2) | 10.23 (5) | 10.24 (2) |
| Sample | & | (LS) | (HS) | Cal. Value (HS) | Cal. Value (LS) | Expt. Value | |
|---|---|---|---|---|---|---|---|
| x = 0 | 10.61 | 3.87 | 2.82 | 4.9 | 13.47 | 12.97 | 11.12 |
| x = 0.25 | 10.35 | 3.87 | 2.82 | 4.9 | 13.27 | 12.77 | 10.55 |
| x = 0.50 | 10.09 | 3.87 | 2.82 | 4.9 | 13.08 | 12.56 | 10.27 |
| x = 0.75 | 9.83 | 3.87 | 2.82 | 4.9 | 12.88 | 12.36 | 10.10 |
| x = 1.0 | 9.58 | 3.87 | 2.82 | 4.9 | 12.67 | 12.14 | 9.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pakhuria, B.; Saha, R.A.; Meneghini, C.; Bert, F.; Kundu, S.; Ray, S. Evolution of Griffiths-like Anomaly in Isostructural Swedenborgite Compounds Ho1−xErxBaCo4O7+δ. Magnetochemistry 2025, 11, 55. https://doi.org/10.3390/magnetochemistry11070055
Pakhuria B, Saha RA, Meneghini C, Bert F, Kundu S, Ray S. Evolution of Griffiths-like Anomaly in Isostructural Swedenborgite Compounds Ho1−xErxBaCo4O7+δ. Magnetochemistry. 2025; 11(7):55. https://doi.org/10.3390/magnetochemistry11070055
Chicago/Turabian StylePakhuria, Biplab, Rafikul Ali Saha, Carlo Meneghini, Fabrice Bert, Shruti Kundu, and Sugata Ray. 2025. "Evolution of Griffiths-like Anomaly in Isostructural Swedenborgite Compounds Ho1−xErxBaCo4O7+δ" Magnetochemistry 11, no. 7: 55. https://doi.org/10.3390/magnetochemistry11070055
APA StylePakhuria, B., Saha, R. A., Meneghini, C., Bert, F., Kundu, S., & Ray, S. (2025). Evolution of Griffiths-like Anomaly in Isostructural Swedenborgite Compounds Ho1−xErxBaCo4O7+δ. Magnetochemistry, 11(7), 55. https://doi.org/10.3390/magnetochemistry11070055







