Next Article in Journal
Rhenium-Induced Negative Magnetoresistance in Monolayer Graphene
Next Article in Special Issue
Multifunctional Synergistic Response Induced by Phase Transition in Molecular Compounds
Previous Article in Journal
Case Study on Homogeneous–Heterogeneous Chemical Reactions in a Magneto Hydrodynamics Darcy–Forchheimer Model with Bioconvection in Inclined Channels
Previous Article in Special Issue
Magnetic Relaxation in a Heterolanthanide Binuclear Complex Involving a Nitronyl Nitroxide Biradical
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Magnetochemistry
Volume 11
Issue 5
10.3390/magnetochemistry11050038
magnetochemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Synthesis, X-Ray Crystal Structures, and Magnetic Properties of a Series of Trinuclear Rare-Earth Hepta-Chloride Clusters †

by
Yingying Pan
1,2,
You-Song Ding
1,2,*,
Lei Li
1,2 and
Zhiping Zheng
1,2,*
1
Department of Chemistry, Southern University of Science and Technology, Shenzhen 518055, China
2
Key University Laboratory of Rare Earth Chemistry of Guangdong, Southern University of Science and Technology, Shenzhen 518055, China
*
Authors to whom correspondence should be addressed.
†
Dedicated to Prof. Dai-Zheng Liao on the occasion of his 85th birthday.
Magnetochemistry 2025, 11(5), 38; https://doi.org/10.3390/magnetochemistry11050038
Submission received: 15 April 2025 / Revised: 28 April 2025 / Accepted: 30 April 2025 / Published: 2 May 2025
(This article belongs to the Special Issue Molecular Magnetism: A Themed Issue in Honor of Professor Dai-Zheng Liao on the Occasion of His 85th Birthday)
Browse Figures
Versions Notes

Abstract

:
Organometallic rare-earth complexes have attracted considerable attention in recent years due to their unique structures and exceptional magnetic properties. In this study, we report the synthesis and magnetic characteristics of a family of monopentamethylcyclopentadienyl-coordinated trinuclear rare-earth hepta-chloride clusters [(Li(THF)(Et2O))(Cp*RE)3(μ-Cl)4(μ3-Cl)2(μ4-Cl)] (RE3: RE =Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu; Cp* = pentamethylcyclopentadienide). These clusters were synthesized by reacting LiCp* with RECl3 in a 1:1 molar ratio within a mixed solvent system (THF: Et2O = 1:9), resulting in high solubility in common organic solvents such as DCM, THF, and Et2O. Magnetic studies conducted on these paramagnetic clusters reveal the coexistence of ferromagnetic and antiferromagnetic superexchange interactions in Gd3. Additionally, Dy3 exhibits both ferromagnetic and antiferromagnetic intramolecular dipolar interactions. Notably, slow magnetic relaxation was observed in Dy3 below 23 K under a zero DC applied field with an energy barrier of 125(6) cm−1.

1. Introduction

Since the pioneering isolation of organometallic rare-earth complexes by Wilkinson and Birmingham in 1954 [1], the synthesis, reactivity, and physical properties of these complexes have attracted considerable attention across various fields due to the distinctive electronic structures of rare-earth ions [2,3,4,5,6]. Notably, significant advancements have been made in this area in recent years. For instance, cyclic multidecker sandwich rare-earth complexes have been successfully isolated and characterized [7]; metal–metal bonding, ligand–metal double bonds, and multicenter chemical bonding involving rare-earth ions have been realized [8,9,10,11,12,13]; molecular complexes featuring rare-earth ions in unconventional oxidation states (Pr(IV), Pr(V), and Tb(IV)) have been investigated [14,15,16,17,18,19]; and rare-earth telluride clusters were isolated through an efficient reduction method utilizing KC8 [20,21]. Certain organometallic rare-earth complexes can be employed for the regio- and stereoselective hydroalkynylation of internal alkynes [22,23]. The complexes [(C5Me4R)Eu(μ-BH4)(THF)2]2 (R = H, Me, Ph, SiMe3, GeMe3, and P(NMe2)2) serve as potential candidates for luminescence thermometers [24,25]. Some divalent rare-earth complexes also exhibit potential as qubits [26,27,28]. Furthermore, several organometallic rare-earth complexes demonstrate exceptionally high energy barriers (Ueff) and blocking temperatures (TB) as single-molecule magnet (SMMs) [29,30,31,32,33,34,35].
SMMs have emerged as one of the most promising molecular-based advanced functional materials in recent years, owing to their capability to store information within a single molecule. This unique property positions them as leading candidates for ultra-high-density data storage [3,5]. The characteristics of SMMs are typically assessed through Ueff, TB, or hysteresis temperatures (TH). These parameters are primarily influenced by the magnetic anisotropy of spin centers and the exchange coupling between spins within the molecules [36,37]. Consequently, organometallic rare-earth complexes have opened new avenues for research into SMMs [8,12,29,30,31,32,33,34,35,37]. The single-ion anisotropy of lanthanide ions can be significantly enhanced by intercalating Dy(III) ions between compact aromatic rings [29,30,31,32,33,34,35] or by utilizing low coordination numbers [38,39,40,41,42,43,44,45]. To facilitate robust exchange couplings, radical ligands are often used to bridge lanthanide ions [46,47]. More recently, metal–metal bonding between lanthanide ions has been successfully achieved, which can also result in significant magnetic exchange coupling in truncated SMMs exhibiting ultrahard magnetism [8,12]. Moreover, the manipulation of intramolecular dipolar interactions has been successfully accomplished in dinuclear rare-earth organometallic complexes by introducing an additional Cl− ion [48]. To further enhance the exchange couplings in lanthanide complexes, it is essential to develop a comprehensive understanding of the relationships between exchange couplings and structural characteristics [49].
The monopentamethylcyclopentadienyl-coordinated rare-earth fragments {Cp*RE} (where Cp* = pentamethylcyclopentadienide) are of particular interest, as they frequently serve as key components in various intriguing organometallic rare-earth complexes, including chalcogenides [20,21,50], bismuth compounds [51], and hydride clusters of rare-earth elements [52]. The starting materials employed typically consist of a mixture of KCp* and RECl3, or bis-Cp*-coordinated rare-earth complexes, or half-sandwich bis(aminobenzyl) rare-earth complexes [20,21,50,51,52]. We propose that mono-Cp*-coordinated rare-earth complexes can be atomically precise and cost-effective precursors for synthesizing these clusters. Such mono-Cp*-coordinated rare-earth complexes can be synthesized by reacting MCp* (M = Li, Na, K) and RECl3 in a 1:1 molar ratio (Scheme 1). Previous studies have demonstrated that the hexanuclear complex [(Cp*Dy)6K4Cl16(THF)6] can be synthesized using KCp* [53]. In contrast, when NaCp* is employed, a dimeric complex {Na(μ-THF)[Cp*Gd(THF)]2(μ-Cl)2}2 is isolated, with Cp*GdCl2(THF)3 coexisting in the mother liquor [54]. In this study, we report on the reaction between LiCp* and RECl3 at a 1:1 ratio in a mixed solvent system (THF: Et2O = 1:9), resulting in the formation of a family of mono-Cp*-coordinated trinuclear rare-earth hepta-chloride clusters [(Li(THF)(Et2O))(Cp*RE)3(μ-Cl)4(μ3-Cl)2(μ4-Cl)] (RE3: RE =Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu). These clusters’ structures and magnetic properties were investigated; Dy3 emerged as a new SMM, exhibiting an energy barrier of 125(6) cm−1.

2. Materials and Methods

2.1. Materials and Instruments

All manipulations were conducted using standard Schlenk techniques or within a glovebox under an argon atmosphere. The glassware was dried overnight at 120 °C before use. Diethyl ether (Et2O, 99+%) (Yonghua Chemical, Changshu, China) was dried over activated alumina and stored over a potassium mirror before utilization. Anhydrous rare-earth chlorides, RECl3, and Cp*Li, were synthesized following the established procedures from the literature [55,56]. All other reagents (AR) were procured from Energy-Chemical, (Shanghai, China) and utilized without further purification. Elemental analyses for carbon (C) and hydrogen (H) were performed usinga Thermo FLASH2000 elemental analyzer (Waltham, MA, USA).

2.2. Syntheses of Complex RE3

The clusters were synthesized through the reaction of an equimolar mixture of Cp*Li and anhydrous RECl3, which was dispersed in a mixed solvent (THF: Et2O = 1:9). The resulting mixture was stirred overnight at room temperature. After filtration, the precipitate LiCl (a byproduct) was removed, followed by the evaporation of the solvent under vacuum. The residue was then dissolved in 5 mL of Et2O. Finally, the slow volatilization of Et2O yielded crystals of RE3 suitable for X-ray diffraction after one day, with yields of approximately 25% for RE = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, and Lu, based on anhydrous RECl3. The elemental analyses calculated (found) the following for C42H71Cl7Ln3LiO3: Y3: C, 43.99 (43.60); H, 6.20 (6.16); Gd3: C, 37.31 (37.50); H, 5.26 (5.31); Tb3: C, 37.17 (37.21); H, 5.24 (5.24); Dy3: C, 36.88 (36.68); H, 5.20 (5.51); Ho3: C, 36.68 (36.84); H, 5.17 (5.46); Er3: C, 36.50 (36.45); H, 5.14 (5.44); Tm3: C, 36.37 (36.15); H, 5.12 (5.42); Yb3: C, 36.10 (36.23); H, 5.09 (5.39); and Lu3: C, 36.16 (36.27); H, 5.09 (5.10).

2.3. Crystal Structure Determination

Single-crystal X-ray diffraction (SXRD) studies were conducted using Bruker D8 Venture (Mo Kα radiation (λ = 0.71073 Å)) (Bruker, Berlin, Germany) at 100 K for RE3 (where RE = Gd, Ho-Lu, and Y), and at 200 K for Tb3 and Dy3. Using Olex2 (v1.5), the structure was solved with the SHELXT structure solution program using Intrinsic Phasing and refined with the SHELXL refinement package using least squares minimization [57,58,59]. All hydrogen atoms were placed in calculated, ideal positions and refined as riding on their respective carbon atoms, with displacement parameters also dependent on the parent carbon atom Ueq value. The Cambridge Crystallographic Data Centre contains the crystal structures under the following CCDC numbers: 2441413 (Gd3), 2441414 (Tb3), 2441415 (Dy3), 2441416 (Ho3), 2441417 (Er3), 2441418 (Tm3), 2441419 (Yb3), 2441420 (Lu3), and 2441421 (Y3). Crystal data and structure refinement are summarized in Table S1.

2.4. Magnetic Measurements

Crushed polycrystalline samples were sealed with melted eicosane in an NMR tube under vacuum for magnetic measurements. Magnetic susceptibilities were measured with a Quantum Design MPMS-3 SQUID magnetometer (Quantum Design, San Diego, CA, USA) between 2 and 300 K.

2.5. Ab Initio Calculations

OpenMolcas [60] (version: v21.06) was employed to conduct the CASSCF-SO calculations of the electronic structures of Dy3, utilizing molecular geometries derived from crystallographic analyses. No optimization was performed except for selecting the largest disorder component. Relativistic effects were incorporated using the second-order Douglas–Kroll–Hess Hamiltonian, and basis sets from the ANO-RCC library were utilized accordingly [61,62]. Specifically, VTZP quality basis sets were applied for Dy atoms, VDZP quality for coordinating C and Cl atoms, and VDZ quality for all other atoms. To conserve disk space and reduce computational demands, the Cholesky decomposition of two-electron integrals was executed with a threshold set at 10−8. The state-averaged CASSCF orbitals corresponding to sextets, quartets, and doublets were optimized with 21, 224, and 490 states, respectively, through the RASSCF module. For constructing and diagonalizing the spin–orbit (SO) coupling Hamiltonian using the RASSI module, 21 sextets, 128 quartets, and 130 doublets were selected. The resulting spin–orbit wavefunctions were decomposed into their corresponding crystal field (CF) wavefunctions. Subsequently, the ground atomic multiplet, associated tensors, energy barrier, and principal magnetic axes for each Dy(III) ion were calculated using SINGLE_ANISO [63]. Additionally, POLY_ANISO was utilized to compute dipolar interactions within Dy3 [64,65].

3. Results and Discussion

3.1. Syntheses and Structural Characterization

All title RE3 compounds were synthesized using a consistent procedure, wherein equimolar amounts of Cp*Li and RECl3 were dispersed in a mixed solvent (THF: Et2O = 1:9) and stirred overnight at room temperature. The byproduct LiCl precipitated out and was subsequently separated by filtration. Notably, the products obtained after solvent removal under vacuum exhibited high solubility in common organic solvents, including DCM, THF, and Et2O. Single crystals suitable for X-ray diffraction studies were acquired through the slow evaporation of saturated Et2O solutions of these complexes at room temperature within a glove box.
As revealed by X-ray diffraction, the nine RE3 isostructural compounds crystallized in the same orthorhombic noncentrosymmetric space group Pmn21 (Table S1). The cluster-type molecule (Figure 1a) for RE3 consists of three {Cp*RE} units, one Li+, seven Cl−, and three coordinated solvent molecules, which include two THF and one Et2O. The three {Cp*RE} fragments and the Li+ ion are interconnected by four μ2-Cl, two μ3-Cl, and one μ4-Cl (Figure 1b), resulting in a distorted heterometallic tetrahedron (Figure 1c). The μ4-Cl ion is situated within a seesaw-type polyhedron formed by four metal ions, which have been documented in a limited number of rare-earth clusters [66,67,68,69,70]. It is noteworthy that the structures of these clusters bear resemblance to [Cp*LuCl2]3[LiCl(THF)2], which was identified as a byproduct during the activation of white phosphorus with organometallic rare-earth complexes [66]. The primary distinction lies in the coordination environments of the Li+ ions. In this study’s RE3 complex, the Li+ ion at the vertex of [Cp*RE]3 is coordinated to one Et2O molecule and one disordered THF molecule. In contrast, it is coordinated with two THF molecules in [Cp*LuCl2]3[LiCl(THF)2].
All three RE(III) ions in RE3 are capped by a Cp*, with RE1 and RE1# coordinated to five Cl− ligands, while RE2 is associated with four Cl− ligands and one oxygen atom from THF. The distances between the RE and Cl bonds, ranging from 2.54 Å to 3.00 Å (Tables S2–S10), align well with those reported for other RE–Cl compounds [49,50,53,54]. Similarly, the distances of the RE–C bonds fall within the range of 2.54–2.68 Å (Tables S2–S10), and the distances from the RE(III) ions to the centroid of the coordinated Cp* rings vary from 2.31 Å to 2.36 Å (Tables S2–S10). These measurements also correspond closely with previously documented values for RE-Cp* complexes [47,48,49,50,51,52,53,54]. The three RE ions are interconnected through three bridging Cl atoms, resulting in an interionic distance ranging from 3.92 Å to 4.05 Å (Table S11). Notably, it should be mentioned that RE1 and RE1# are bridged by two μ3-Cl ligands and one μ4-Cl ligand; conversely, either pair consisting of (RE1 and RE2) or (RE1# and RE2) is connected via one μ2-Cl ligand along with one μ3-Cl ligand and one μ4-Cl ligand. This distinction results in slightly longer interionic distances for the former case than those observed in the latter. Furthermore, in terms of coordination geometry, the Cp* ligands attached to [RECl3RE] units (Figure 2a) adopt a ‘cis conformation’ in cases involving both RE1 and RE1#, whereas they exhibit a ‘trans conformation’ when considering pairs such as (RE1 and RE2) or (RE1# and RE2). This variation may influence different magnetic exchange couplings, as discussed further below.

3.2. Static-Field Magnetic Susceptibilities for RE3

To assess the static magnetic properties and intramolecular magnetic interactions in RE3, we measured the static-field magnetic susceptibilities under an applied DC field of 1000 Oe across a temperature range of 2–300 K. Additionally, field-dependent magnetic susceptibilities were recorded up to 7 T at low temperatures (Figure 2b and Figure 3). The static-field magnetic susceptibilities for RE3 exhibited remarkably similar trends (Figure 2b and Figure 3). The experimental χT values at 300 K closely align with the expected values for the corresponding RE(III) ions (Table 1) [71,72]. The decrease in χT values upon cooling for RE3 (RE = Tb–Yb) can be attributed to the thermal depopulation of Stark levels, anisotropy effects, and/or antiferromagnetic interactions [71,72]. Furthermore, the maximum magnetic moment observed at 2 K and 7 T for Gd3 corresponds well with the saturation value of 7 μB per Gd(III) ion. In contrast, the experimental values for the other RE3 compounds (RE = Tb–Yb) are significantly lower than their respective saturation values, indicating a pronounced anisotropy associated with these complexes.
Using the PHI program (version 3.1.6), the intramolecular magnetic interactions in Gd3 can be assessed by fitting the temperature- and field-dependent magnetic susceptibilities [73]. As previously mentioned, two types of ‘conformations’ correspond to the different magnetic exchange couplings in Gd3 (Figure 2a). Consequently, the Hamiltonian expressed as H ^ = −2J1( S ^ Gd1· S ^ Gd1#) − 2J2( S ^ Gd1· S ^ Gd2 + S ^ Gd1#· S ^ Gd2) is employed to describe these magnetic exchange couplings. Here, J1 represents the super-exchange constant for the interaction between Gd1 and Gd1#, while J2 pertains to the interactions involving either Gd1 with Gd2 or Gd1# with Gd2. The super-exchange constants (J1 and J2) derived from this Hamiltonian indicate a ferromagnetic exchange coupling when the value is positive (J > 0). Conversely, an antiferromagnetic exchange coupling can be identified if the value is negative. As illustrated in Figure 2b, the optimal fits (solid lines) combined with a variable g-factor in the Zeeman Hamiltonian and the isotropic exchange Hamiltonian mentioned above yielded values of J1 = 6.14 × 10−3 cm−1, and J2 = −1.29 × 10−2 cm−1 with g = 1.97 for Gd3. Such weak superexchange interactions among Gd(III) ions are not particularly surprising given that the 4f electrons are confined within contracted 4f orbitals and superexchange interactions mediated by non-radical ligands tend to exhibit inherently weak characteristics [50,51,74].

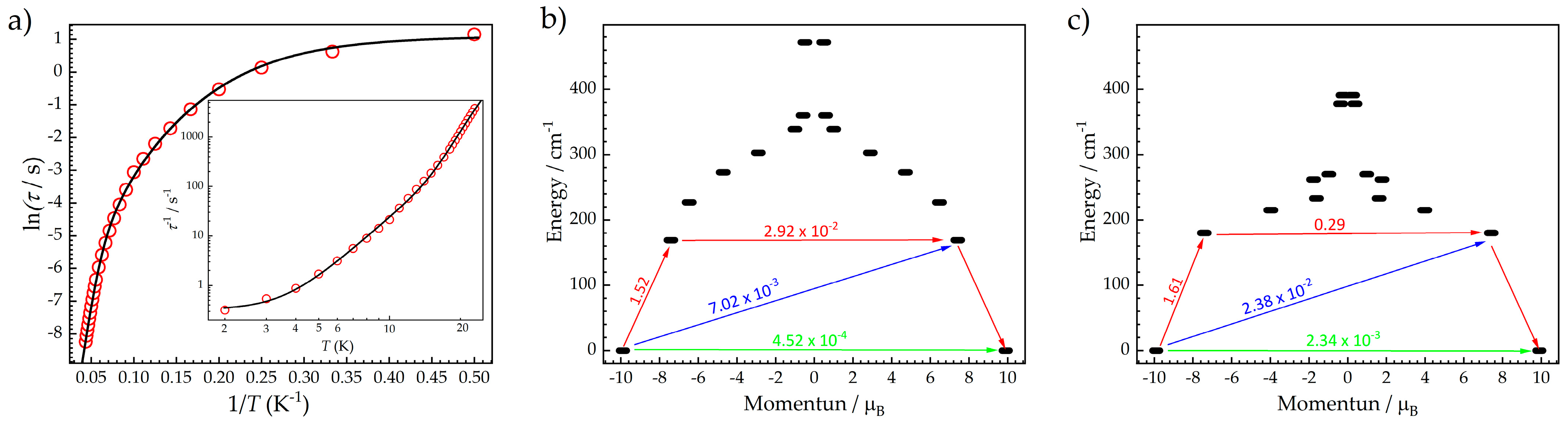
3.3. Dynamic Magnetic Susceptibilities for Dy3

The dynamic magnetic properties of RE3 were examined through AC magnetic susceptibilities measured under a zero applied field at low temperatures (Figures S1–S6). Notably, only Dy3 exhibited slow magnetic relaxations at these low temperatures, likely attributable to the capacity of Cp* ligands to effectively enhance the single-ion anisotropy of Dy(III) ions. The frequency-dependent AC susceptibilities under a zero applied field were subsequently collected from 2 K to 23 K (Figure 4) and fitted using the generalized Debye model (Figure S7), yielding relaxation times and corresponding α parameters (Table S12). [36,75,76]. The α parameters range from 0.3 to 0.5, indicating a relatively wide distribution of relaxation times. This variation may arise from the differing coordination environments of Dy1 and Dy2 (Figure 1d,e) within Dy3 and the trimer interactions [74].
As illustrated in Figure 5a, the relaxation profiles (ln(τ)) for Dy3 exhibit a rapid increase with rising values of 1/T when 1/T is less than 0.1 (corresponding to temperatures above 10 K). Subsequently, this increase slows down, ultimately reaching a nearly temperature-independent regime at 1/T = 0.5 (at a temperature of 2 K). The log–log version for the plot of the magnetic relaxation rate versus the temperature for Dy3 (inset in Figure 5a) indicates that the Raman process (the linear part) is dominated in the temperature range of 4–15 K [76]. Thus, the relaxation profiles for Dy3 can be fitted with Equation (1), which combines the Orbach process (Ueff is the effective energy barrier, and τ0 is the attempt frequency of the Orbach process), the Raman process (CTn), and the quantum tunneling of magnetization (QTM) process (τQTM). The parameters obtained are as follows: Ueff = 125(6) cm−1, τ0 = 1.4(5) × 10−7 s, C = 1.5(3) × 10−3 s, n = 4.2(1) and τQTM = 3.1(2) s. The Ueff is lower than the calculated energy gap between the first excited Kramers doublets, and the ground states for the Dy(III) ions in Dy3, probably because of the significant contribution of the Raman process to the magnetic relaxations up to 23 K (inset in Figure 5a) and a strong QTM.
τ − 1 = τ 0 − 1 e x p − U eff / T + C T n + τ Q T M − 1

3.4. Ab Initio Calculations for Dy3

The electronic states of the Dy(III) ions in Dy3 were studied with OpenMolcas by complete active space self-consistent field spin–orbit (CASSCF-SO) calculations (Table S13) [60]. For both Dy1 and Dy2 in Dy3, the ground states are predominantly characterized by the most magnetic component of mJ = ±15/2, accounting for over 98%. In contrast, the excited states exhibit various magnetic components (see Table 2 and Table 3). The energy gaps between the first excited Kramers doublets and the ground states are 169 cm−1 for Dy1 and 180 cm−1 for Dy2 (Figure 5b,c). The principal magnetic axes of the ground Kramers’ doublets obtained are oriented along the centroid of the coordinated Cp* ring relative to the Dy(III) ion (Figure 1d,e). This orientation indicates that the single-ion anisotropy of the Dy(III) ion is predominantly influenced by the Cp*− ligand, while THF and Cl− exhibit a similar effect on the single-ion anisotropy of the Dy(III) ion.
The intramolecular dipolar interactions, which play an essential role for the low temperature magnetic property of polynuclear complexes [48,49,77,78,79], can be calculated accurately using the program POLY_ANISO [63,64]. As shown in Figure 6a, the calculated principal magnetic axes for Dy1 and Dy1# in Dy3 are oriented along the Dy-μ4-Cl direction and the Dy-μ3-Cl direction for Dy2. For Dy1 and Dy1#, the principal magnetic axes are in-plane crossed (Figure 6b), while the principal magnetic axes are out-of-plane crossed for Dy1 and Dy2 or Dy1# and Dy2 (Figure 6c). Such arrangements of the principal magnetic axes cannot minimize the transversal component of the intramolecular dipolar field, so the QTM in Dy3 remains strong, as mentioned above [48,49,77,78,79]. The dipolar interaction between Dy1 and Dy1# is antiferromagnetic with an exchange constant of −0.92 cm−1, which is ferromagnetic with an exchange constant of 0.39 cm−1 for Dy1 and Dy or Dy1# and Dy2. These values are close to the dipolar interactions in other polynuclear Dy(III) complexes [65].

4. Conclusions

The synthesis, structure determinations, magnetic properties, and electronic structures of novel trinuclear rare-earth hepta-chloride clusters were reported. These mono-Cp*-coordinated rare-earth complexes obtained by the reaction of LiCp* and RECl3 in a 1:1 ratio can serve as starting materials for more interesting organometallic rare-earth clusters due to their high solubility in common organic solvents. Complex Dy3 is a novel single-molecule magnet that exhibits a significant contribution from the Orbach process, the Raman process, and QTM. The energy barrier of 125(6) cm−1 is primarily attributed to the single-ion anisotropy associated with its Dy(III) ions. Further magnetic studies indicate that the ‘cis conformation’ of the Cp* ligands coordinated to the [RECl3RE] units results in ferromagnetic superexchange interactions in Gd3, while it leads to antiferromagnetic intramolecular dipolar interactions in Dy3. Conversely, the ‘trans conformation’ exhibits opposing effects. It remains unclear how the ligands control the exchange interactions. The investigation into the control of exchange interactions in molecular magnetic materials is ongoing, which may pave the way for the development of more advanced molecular magnetic materials.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/magnetochemistry11050038/s1. Table S1: Crystal data and structure refinement for RE3 (RE=Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu, Y); Table S2–S10: Selected bond distances (Å) for Gd3, Tb3, Dy3, Ho3, Er3, Tm3, Yb3, Lu3 and Y3; Table S11: Selected RE–RE distances (Å) for RE3; Table S12: Relaxation fitting parameters obtained using a generalized Debye model for Dy3 from 23 K to 2 K under zero DC field; Table S13: Ab initio calculated crystal field parameters ( B q k ) for Dy1 and Dy2 in Dy3; Figures S1–S6: Temperature-dependence of the in-phase (χ′, top) and out-of-phase (χ″, bottom) AC susceptibility signals under zero DC field by standard AC susceptibility measurements for Tb3, Dy3, Ho3, Er3, Tm3 and Yb3 at indicated frequencies; Figure S7: Cole–Cole plots using the frequency-dependence AC susceptibility data under the zero DC field for Dy3 from 2 K (blue) to 23 K (red). The solid lines are the best fits.

Author Contributions

Synthesis and characterization of the materials: Y.P. and L.L.; measurement and analysis of magnetic data, ab initio calculations: Y.-S.D.; supervision and writing—review: Y.-S.D. and Z.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (22101116, 92261203, and 21971106), the Stable Support Plan Program of Shenzhen Natural Science Fund (20200925161141006), and the Shenzhen Fundamental Research Program (JCYJ20220530115001002 and JCYJ20220818100417037).

Data Availability Statement

The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding authors.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Wilkinson, G.; Birmingham, J.M. Cyclopentadienyl compounds of Sc, Y, La, Ce and some lanthanide elements. J. Am. Chem. Soc. 1954, 76, 6210. [Google Scholar] [CrossRef]
  2. Zimmermann, M.; Anwander, R. Homoleptic rare-earth metal complexes containing Ln–C σ-Bonds. Chem. Rev. 2010, 110, 6194–6259. [Google Scholar] [CrossRef]
  3. Harriman, K.L.M.; Murugesu, M. An organolanthanide building block approach to single-molecule magnets. Acc. Chem. Res. 2016, 49, 1158–1167. [Google Scholar] [CrossRef] [PubMed]
  4. Nishiura, M.; Guo, F.; Hou, Z. Half-sandwich rare-earth-catalyzed olefin polymerization, carbometalation, and hydroarylation. Acc. Chem. Res. 2015, 48, 2209–2220. [Google Scholar] [CrossRef]
  5. Day, B.M.; Guo, F.-S.; Layfield, R.A. Cyclopentadienyl ligands in lanthanide single-molecule magnets: One ring to rule them all? Acc. Chem. Res. 2018, 51, 1880–1889. [Google Scholar] [CrossRef]
  6. Ortu, F. Rare earth starting materials and methodologies for synthetic chemistry. Chem. Rev. 2022, 122, 6040–6116. [Google Scholar] [CrossRef]
  7. Münzfeld, L.; Gillhuber, S.; Hauser, A.; Lebedkin, S.; Hädinger, P.; Knöfel, N.D.; Zovko, C.; Gamer, M.T.; Weigend, F.; Kappes, M.M.; et al. Synthesis and properties of cyclic sandwich compounds. Nature 2023, 620, 92–96. [Google Scholar] [CrossRef]
  8. Gould, C.A.; McClain, K.R.; Reta, D.; Kragskow, J.G.C.; Marchiori, D.A.; Lachman, E.; Choi, E.-S.; Analytis, J.G.; Britt, R.D.; Chilton, N.F.; et al. Ultrahard magnetism from mixed-valence dilanthanide complexes with metal-metal bonding. Science 2022, 375, 198–202. [Google Scholar] [CrossRef] [PubMed]
  9. McClain, K.R.; Kwon, H.; Chakarawet, K.; Nabi, R.; Kragskow, J.G.C.; Chilton, N.F.; Britt, R.D.; Long, J.R.; Harvey, B.G. A trinuclear gadolinium cluster with a three-center one-electron bond and an S = 11 ground state. J. Am. Chem. Soc. 2023, 145, 8996–9002. [Google Scholar] [CrossRef]
  10. Wedal, J.C.; Anderson-Sanchez, L.M.; Dumas, M.T.; Gould, C.A.; Beltrán-Leiva, M.J.; Celis-Barros, C.; Páez-Hernández, D.; Ziller, J.W.; Long, J.R.; Evans, W.J. Synthesis and crystallographic characterization of a reduced bimetallic yttrium ansa-metallocene hydride complex, [K(crypt)][(μ-CpAn)Y(μ-H)]2 (CpAn = Me2Si[C5H3(SiMe3)-3]2), with a 3.4 Å yttrium-yttrium distance. J. Am. Chem. Soc. 2023, 145, 10730–10742. [Google Scholar] [CrossRef]
  11. Wang, Y.; Liang, J.; Deng, C.; Sun, R.; Fu, P.-X.; Wang, B.-W.; Gao, S.; Huang, W. Two-electron oxidations at a single cerium center. J. Am. Chem. Soc. 2023, 145, 22466–22474. [Google Scholar] [CrossRef] [PubMed]
  12. Kwon, H.; McClain, K.R.; Kragskow, J.G.C.; Staab, J.K.; Ozerov, M.; Meihaus, K.R.; Harvey, B.G.; Choi, E.S.; Chilton, N.F.; Long, J.R. Coercive fields exceeding 30 T in the mixed-valence single-molecule magnet (CpiPr5)2Ho2I3. J. Am. Chem. Soc. 2024, 146, 18714–18721. [Google Scholar] [CrossRef]
  13. Guo, Y.; Jiang, X.-L.; Wu, Q.-Y.; Liu, K.; Wang, W.; Hu, K.-q.; Mei, L.; Chai, Z.-f.; Gibson, J.K.; Yu, J.-p.; et al. 4f/5d hybridization induced single-electron delocalization in an azide-bridged dicerium complex. J. Am. Chem. Soc. 2024, 146, 7088–7096. [Google Scholar] [CrossRef] [PubMed]
  14. Palumbo, C.T.; Zivkovic, I.; Scopelliti, R.; Mazzanti, M. Molecular Complex of Tb in the +4 Oxidation State. J. Am. Chem. Soc. 2019, 141, 9827–9831. [Google Scholar] [CrossRef]
  15. Willauer, A.R.; Palumbo, C.T.; Scopelliti, R.; Zivkovic, I.; Douair, I.; Maron, L.; Mazzanti, M. Stabilization of the Oxidation State +IV in Siloxide-Supported Terbium Compounds. Angew. Chem. Int. Ed. 2020, 59, 3549–3553. [Google Scholar] [CrossRef]
  16. Willauer, A.R.; Palumbo, C.T.; Fadaei-Tirani, F.; Zivkovic, I.; Douair, I.; Maron, L.; Mazzanti, M. Accessing the +IV Oxidation State in Molecular Complexes of Praseodymium. J. Am. Chem. Soc. 2020, 142, 5538–5542. [Google Scholar] [CrossRef] [PubMed]
  17. Rice, N.T.; Popov, I.A.; Russo, D.R.; Bacsa, J.; Batista, E.R.; Yang, P.; Telser, J.; La Pierre, H.S. Design, Isolation, and Spectroscopic Analysis of a Tetravalent Terbium Complex. J. Am. Chem. Soc. 2019, 141, 13222–13233. [Google Scholar] [CrossRef]
  18. Xue, T.; Yang, Q.-S.; Li, L.; Chang, X.-Y.; Ding, Y.-S.; Zheng, Z. Supramolecular assemblies of tetravalent terbium complex units: Syntheses, structure, and materials properties. Chem. Sci. 2025, 16, 6805–6811. [Google Scholar] [CrossRef] [PubMed]
  19. Boggiano, A.C.; Studvick, C.M.; Roy Chowdhury, S.; Niklas, J.E.; Tateyama, H.; Wu, H.; Leisen, J.E.; Kleemiss, F.; Vlaisavljevich, B.; Popov, I.A.; et al. Praseodymium in the formal +5 oxidation state. Nat. Chem. 2025. [Google Scholar] [CrossRef]
  20. Ding, Y.-S.; Jiang, X.-L.; Li, L.; Xu, C.-Q.; Li, J.; Zheng, Z. Atomically precise semiconductor clusters of rare-earth tellurides. Nat. Synth. 2024, 3, 655–661. [Google Scholar] [CrossRef]
  21. Li, L.; Ding, Y.-S.; Zheng, Z. Lanthanide-based molecular magnetic semiconductors. Angew. Chem. Int. Ed. 2024, 63, e202410019. [Google Scholar] [CrossRef] [PubMed]
  22. Hao, N.; Jiao, T.; Sun, Z.; Mishra, A.; Zhuo, Q.; Nishiura, M.; Hou, Z.; Cong, X. Regio- and stereoselective hydroalkynylation of internal alkynes with terminal alkynes by half-sandwich rare-earth catalysts. J. Am. Chem. Soc. 2025, 147, 6149–6161. [Google Scholar] [CrossRef] [PubMed]
  23. Ma, Y.; Mishra, A.; Jiao, T.; Chang, W.; Lou, S.-J.; Nishiura, M.; Cong, X.; Hou, Z. Heteroatom-assisted regio- and stereoselective hydrosilylation of unsymmetric internal alkynes by scandium catalyst. Angew. Chem. Int. Ed. 2025, 64, e202502665. [Google Scholar] [CrossRef]
  24. Diaz-Rodriguez, R.M.; Gálico, D.A.; Chartrand, D.; Suturina, E.A.; Murugesu, M. Toward opto-structural correlation to investigate luminescence thermometry in an organometallic Eu(II) complex. J. Am. Chem. Soc. 2022, 144, 912–921. [Google Scholar] [CrossRef] [PubMed]
  25. Diaz-Rodriguez, R.M.; Gálico, D.A.; Chartrand, D.; Murugesu, M. Ligand effects on the emission characteristics of molecular Eu(II) luminescence thermometers. J. Am. Chem. Soc. 2024, 146, 34118–34129. [Google Scholar] [CrossRef]
  26. Kundu, K.; White, J.R.K.; Moehring, S.A.; Yu, J.M.; Ziller, J.W.; Furche, F.; Evans, W.J.; Hill, S. A 9.2-GHz clock transition in a Lu(II) molecular spin qubit arising from a 3,467-MHz hyperfine interaction. Nat. Chem. 2022, 14, 392–397. [Google Scholar] [CrossRef]
  27. Smith, P.W.; Hruby, J.; Evans, W.J.; Hill, S.; Minasian, S.G. Identification of an X-Band clock transition in Cp’3Pr− enabled by a 4f25d1 configuration. J. Am. Chem. Soc. 2024, 146, 5781–5785. [Google Scholar] [CrossRef]
  28. Nodaraki, L.E.; Ariciu, A.-M.; Huh, D.N.; Liu, J.; Martins, D.O.T.A.; Ortu, F.; Winpenny, R.E.P.; Chilton, N.F.; McInnes, E.J.L.; Mills, D.P.; et al. Ligand effects on the spin relaxation dynamics and coherent manipulation of organometallic La(II) potential qudits. J. Am. Chem. Soc. 2024, 146, 15000–15009. [Google Scholar] [CrossRef]
  29. Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef]
  30. Guo, F.-S.; Day, B.M.; Chen, Y.-C.; Tong, M.-L.; Mansikkamäki, A.; Layfield, R.A. A dysprosium metallocene single-molecule magnet functioning at the axial limit. Angew. Chem. Int. Ed. 2017, 56, 11445–11449. [Google Scholar] [CrossRef]
  31. Guo, F.-S.; Day, B.M.; Chen, Y.-C.; Tong, M.-L.; Mansikkamäki, A.; Layfield, R.A. Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet. Science 2018, 362, 1400–1403. [Google Scholar] [CrossRef] [PubMed]
  32. Guo, F.-S.; He, M.; Huang, G.-Z.; Giblin, S.R.; Billington, D.; Heinemann, F.W.; Tong, M.-L.; Mansikkamäki, A.; Layfield, R.A. Discovery of a dysprosium metallocene single-molecule magnet with two high-temperature orbach processes. Inorg. Chem. 2022, 61, 6017–6025. [Google Scholar] [CrossRef]
  33. Jin, P.-B.; Luo, Q.-C.; Gransbury, G.K.; Vitorica-Yrezabal, I.J.; Hajdu, T.; Strashnov, I.; McInnes, E.J.L.; Winpenny, R.E.P.; Chilton, N.F.; Mills, D.P.; et al. Thermally stable terbium(II) and dysprosium(II) bis-amidinate complexes. J. Am. Chem. Soc. 2023, 145, 27993–28009. [Google Scholar] [CrossRef] [PubMed]
  34. Wang, Y.; Luo, Q.-C.; Zheng, Y.-Z. Organolanthanide single-molecule magnets with heterocyclic ligands. Angew. Chem. Int. Ed. 2024, 63, e202407016. [Google Scholar] [CrossRef]
  35. Liu, M.; Chen, Y.-C.; Zheng, J.; Peng, X.-H.; Tong, M.-L.; Mansikkamäki, A.; Guo, F.-S. Isolation and single-molecule magnetism of neutral rare-earth(III) sandwich complexes supported by compact aromatic rings. Sci. China Chem. 2025. [Google Scholar] [CrossRef]
  36. Liu, J.-L.; Chen, Y.-C.; Tong, M.-L. Symmetry strategies for high performance lanthanide-based single-molecule magnets. Chem. Soc. Rev. 2018, 47, 2431–2453. [Google Scholar] [CrossRef]
  37. Chen, Y.-C.; Tong, M.-L. Single-molecule magnets beyond a single lanthanide ion: The art of coupling. Chem. Sci. 2022, 13, 8716–8726. [Google Scholar] [CrossRef] [PubMed]
  38. Meng, Y.-S.; Xu, L.; Xiong, J.; Yuan, Q.; Liu, T.; Wang, B.-W.; Gao, S. Low-coordinate single-ion magnets by intercalation of lanthanides into a phenol matrix. Angew. Chem. Int. Ed. 2018, 57, 4673–4676. [Google Scholar] [CrossRef]
  39. Wang, C.; Sun, R.; Chen, Y.; Wang, B.-W.; Wang, Z.-M.; Gao, S. Assembling high-temperature single-molecule magnets with low-coordinate bis(amido) dysprosium unit [DyN2]+ via Cl–K–Cl linkage. CCS Chem. 2020, 2, 362–368. [Google Scholar] [CrossRef]
  40. Sun, R.; Wang, C.; Wang, B.-W.; Wang, Z.-M.; Chen, Y.-F.; Tamm, M.; Gao, S. Low-coordinate bis(imidazolin-2-iminato) dysprosium(III) single-molecule magnets. Inorg. Chem. Front. 2023, 10, 485–492. [Google Scholar] [CrossRef]
  41. Sun, R.; Li, C.-Y.; Huang, Z.-N.; Wang, C.; Chen, Y.; Sun, H.-L.; Wang, Z.-M.; Wang, B.-W.; Gao, S. One is better than two: Improved performance in mono(imidazolin-2-iminato) dysprosium(III) single-molecule magnets featuring short Dy–N bond. CCS Chem. 2024. [CrossRef]
  42. Emerson-King, J.; Gransbury, G.K.; Whitehead, G.F.S.; Vitorica-Yrezabal, I.J.; Rouzières, M.; Clérac, R.; Chilton, N.F.; Mills, D.P. Isolation of a bent dysprosium bis(amide) single-molecule magnet. J. Am. Chem. Soc. 2024, 146, 3331–3342. [Google Scholar] [CrossRef]
  43. Benner, F.; Jena, R.; Odom, A.L.; Demir, S. Magnetic hysteresis in a dysprosium bis(amide) complex. J. Am. Chem. Soc. 2025, 147, 8156–8167. [Google Scholar] [CrossRef] [PubMed]
  44. Yang, Q.-Q.; Wang, Y.-F.; Wang, Y.-X.; Tang, M.-J.; Yin, B. Ab initio prediction of key parameters and magneto-structural correlation of tetracoordinated lanthanide single-ion magnets. Phys. Chem. Chem. Phys. 2023, 25, 18387–18399. [Google Scholar] [CrossRef]
  45. Wang, Y.-X.; Wang, Y.-F.; Yin, B. Theoretical study of pentacoordinated lanthanide single-ion magnets via ab initio electronic structure calculation. Magnetochemistry 2025, 11, 3. [Google Scholar] [CrossRef]
  46. Zhang, P.; Luo, Q.-C.; Zhu, Z.; He, W.; Song, N.; Lv, J.; Wang, X.; Zhai, Q.-G.; Zheng, Y.-Z.; Tang, J. Radical-bridged heterometallic single-molecule magnets incorporating four lanthanoceniums. Angew. Chem. Int. Ed. 2023, 62, e202218540. [Google Scholar] [CrossRef]
  47. Bajaj, N.; Mavragani, N.; Kitos, A.A.; Chartrand, D.; Maris, T.; Mansikkamäki, A.; Murugesu, M. Hard single-molecule magnet behavior and strong magnetic coupling in pyrazinyl radical-bridged lanthanide metallocenes. Chem 2024, 10, 2484–2499. [Google Scholar] [CrossRef]
  48. Huang, J.-Q.; Chen, Q.-W.; Ding, Y.-S.; Zhu, X.-F.; Wang, B.-W.; Pan, F.; Zheng, Z. Enhancement of single-molecule magnet properties by manipulating intramolecular dipolar interactions. Adv. Sci. 2025, 12, 2409730. [Google Scholar] [CrossRef]
  49. David, G.; Le Guennic, B.; Reta, D. Promoting exchange coupling in (CpiPr5)2Gd2X3 complexes. Chem. Commun. 2024, 60, 11988–11991. [Google Scholar] [CrossRef]
  50. Li, L.; Xue, T.-J.; Ding, Y.-S.; Zheng, Z. Rare-earth chalcogenidotetrachloride clusters (RE3ECl4, RE = Dy, Gd, Y.; E = S, Se, Te): Syntheses and materials properties. J. Mater. Chem. C 2024, 12, 16506–16514. [Google Scholar]
  51. Zhang, P.; Benner, F.; Chilton, N.F.; Demir, S. Organometallic lanthanide bismuth cluster single-molecule magnets. Chem. 2022, 8, 717–730. [Google Scholar] [CrossRef]
  52. Shima, T.; Nishiura, M.; Hou, Z. Tetra-, penta-, and hexanuclear yttrium hydride clusters from half-sandwich bis(aminobenzyl) complexes containing various cyclopentadienyl ligands. Organometallics. 2011, 30, 2513–2524. [Google Scholar] [CrossRef]
  53. Wu, J.; Demeshko, S.; Dechert, S.; Meyer, F. Hexanuclear [Cp*Dy]6 single-molecule magnet. Chem. Commun. 2020, 56, 3887–3890. [Google Scholar] [CrossRef]
  54. Shen, Q.; Qi, M.; Lin, Y. Synthesis and X-ray crystal structure of a monopentamethylcyclopentadienyl derivative of gadolinium {Na(μ-THF)[Cp*Gd(THF)]2(μ-Cl)2}2·6THF. J. Organomet. Chem. 1990, 399, 247–254. [Google Scholar] [CrossRef]
  55. Huang, W.; Upton, B.M.; Khan, S.I.; Diaconescu, P.L. Synthesis and characterization of paramagnetic lanthanide benzyl complexes. Organometallics. 2013, 32, 1379–1386. [Google Scholar] [CrossRef]
  56. Watson, P.L.; Whitney, J.F.; Harlow, R.L. (Pentamethylcyclopentadienyl)ytterbium and -lutetium complexes by metal oxidation and metathesis. Inorg. Chem. 1981, 20, 3271–3278. [Google Scholar] [CrossRef]
  57. Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Cryst. 2009, 42, 339–341. [Google Scholar] [CrossRef]
  58. Sheldrick, G. SHELXT-Integrated space-group and crystal-structure determination. Acta Crystallogr. A 2015, 71, 3–8. [Google Scholar] [CrossRef]
  59. Sheldrick, G. Crystal structure refinement with SHELXL. Acta Crystallogr. C 2015, 71, 3–8. [Google Scholar] [CrossRef]
  60. Li Manni, G.; Fdez. Galván, I.; Alavi, A.; Aleotti, F.; Aquilante, F.; Autschbach, J.; Avagliano, D.; Baiardi, A.; Bao, J.J.; Battaglia, S.; et al. The OpenMolcas web: A community-driven approach to advancing computational chemistry. J. Chem. Theory. Comput. 2023, 19, 6933–6991. [Google Scholar] [CrossRef]
  61. Roos, B.O.; Lindh, R.; Malmqvist, P.-Å.; Veryazov, V.; Widmark, P.-O. Main group atoms and dimers studied with a new relativistic ANO basis set. J. Phys. Chem. A 2004, 108, 2851–2858. [Google Scholar] [CrossRef]
  62. Roos, B.O.; Lindh, R.; Malmqvist, P.-Å.; Veryazov, V.; Widmark, P.-O. New relativistic ANO basis sets for transition metal atoms. J. Phys. Chem. A 2005, 109, 6575–6579. [Google Scholar] [CrossRef] [PubMed]
  63. Ungur, L.; Chibotaru, L.F. Ab Initio Crystal Field for Lanthanides. Chem. Eur. J. 2017, 23, 3708–3718. [Google Scholar] [CrossRef]
  64. Chibotaru, L.F.; Ungur, L.; Soncini, A. The origin of nonmagnetic kramers doublets in the ground state of dysprosium triangles: Evidence for a toroidal magnetic moment. Angew. Chem. Int. Ed. 2008, 47, 4126–4129. [Google Scholar] [CrossRef] [PubMed]
  65. Ungur, L.; Van den Heuvel, W.; Chibotaru, L.F. Ab initio investigation of the non-collinear magnetic structure and the lowest magnetic excitations in dysprosium triangles. New J. Chem. 2009, 33, 1224–1230. [Google Scholar] [CrossRef]
  66. Du, S.; Yin, J.; Chi, Y.; Xu, L.; Zhang, W.-X. Dual functionalization of white phosphorus: Formation, characterization, and reactivity of rare-earth-metal cyclo-P3 complexes. Angew. Chem. Int. Ed. 2017, 56, 15886–15890. [Google Scholar] [CrossRef]
  67. Dubé, T.; Gambarotta, S.; Yap, G.P.A.; Conoci, S. Preparation and characterization of two mixed-valence samarium octameric clusters. Organometallics 2000, 19, 115–117. [Google Scholar] [CrossRef]
  68. Gromada, J.; Mortreux, A.; Chenal, T.; Ziller, J.W.; Leising, F.; Carpentier, J.-F. Neodymium alkoxides: Synthesis, characterization and their combinations with dialkylmagnesiums as unique systems for polymerization and block copolymerization of ethylene and methyl methacrylate. Chem. Eur. J. 2002, 8, 3773–3788. [Google Scholar] [CrossRef]
  69. Dietrich, H.M.; Schuster, O.; Törnroos, K.W.; Anwander, R. Heterobimetallic half-lanthanidocene clusters: Novel mixed tetramethylaluminato/chloro coordination. Angew. Chem. Int. Ed. 2006, 45, 4858–4863. [Google Scholar] [CrossRef]
  70. Evans, W.J.; Champagne, T.M.; Davis, B.L.; Allen, N.T.; Nyce, G.W.; Johnston, M.A.; Lin, Y.-C.; Khvostov, A.; Ziller, J.W. Structural studies of mono(pentamethylcyclopentadienyl)lanthanide complexes. J. Coord. Chem. 2006, 59, 1069–1087. [Google Scholar] [CrossRef]
  71. Tang, J.; Zhang, P. A basis for lanthanide single-molecule magnets. In Lanthanide Single Molecule Magnets; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–39. [Google Scholar]
  72. Jiang, S.-D.; Wang, B.-W.; Gao, S. Advances in lanthanide single-ion magnets. In Molecular Nanomagnets and Related Phenomena; Gao, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 111–141. [Google Scholar]
  73. Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes. J. Comput. Chem. 2013, 34, 1164–1175. [Google Scholar] [CrossRef]
  74. Han, T.; Ding, Y.-S.; Li, Z.-H.; Yu, K.-X.; Zhai, Y.-Q.; Chilton, N.F.; Zheng, Y.-Z. A dichlorido-bridged dinuclear Dy(III) single-molecule magnet with an effective energy barrier larger than 600 K. Chem. Commun. 2019, 55, 7930–7933. [Google Scholar] [CrossRef] [PubMed]
  75. Guo, Y.-N.; Xu, G.-F.; Guo, Y.; Tang, J. Relaxation dynamics of dysprosium(III) single-molecule magnets. Dalton Trans. 2011, 40, 9953–9963. [Google Scholar] [CrossRef] [PubMed]
  76. Reta, D.; Chilton, N.F. Uncertainty estimates for magnetic relaxation times and magnetic relaxation parameters. Phys. Chem. Chem. Phys. 2019, 21, 23567–23575. [Google Scholar] [CrossRef] [PubMed]
  77. Deng, W.; Du, S.-N.; Ruan, Z.-Y.; Zhao, X.-J.; Chen, Y.-C.; Liu, J.-L.; Tong, M.-L. Aggregation-induced suppression of quantum tunneling by manipulating intermolecular arrangements of magnetic dipoles. Aggregate 2024, 5, e441. [Google Scholar] [CrossRef]
  78. Ding, Y.-S.; Chen, Q.-W.; Huang, J.-Q.; Zhu, X.-F.; Zheng, Z. Sandwich-type single-molecule magnets complexes of Er(III) with ansa-cyclooctatetraenyl ligands. Chin. J. Chem. 2024, 42, 3099–3106. [Google Scholar] [CrossRef]
  79. Chen, Q.; Ding, Y.; Zhu, X.; Wang, B.; Zheng, Z. Tuning intramolecular dipole interactions in dinuclear single-molecule magnetic complexes of Er(III) with monosubstituted cyclooctatetraenide ligands. J. Rare. Earth. 2024. [CrossRef]
Magnetochemistry 11 00038 sch001
Scheme 1. Synthesis of mono-Cp*-coordinated rare-earth complexes through the reaction of MCp* (where M = Li, Na, K) with RECl3 in a 1:1 molar ratio.
Scheme 1. Synthesis of mono-Cp*-coordinated rare-earth complexes through the reaction of MCp* (where M = Li, Na, K) with RECl3 in a 1:1 molar ratio.
Magnetochemistry 11 00038 sch001
Magnetochemistry 11 00038 g001
Figure 1. Ball-and-stick representations of RE3 (a) and side views of the RE3Cl7 core within RE3 (b,c). The local coordination environments for RE1 (d) and RE2 (e) in RE3 are illustrated. The yellow arrows indicate the principal magnetic axes of the ground doublets derived from CASSCF-SO calculations for Dy3. The color code is as follows: violet, RE; green, Cl; grey, C; and red, O. H atoms are omitted for clarity. Symmetry codes are as follows: #, 1 − x, +y, +z.
Figure 1. Ball-and-stick representations of RE3 (a) and side views of the RE3Cl7 core within RE3 (b,c). The local coordination environments for RE1 (d) and RE2 (e) in RE3 are illustrated. The yellow arrows indicate the principal magnetic axes of the ground doublets derived from CASSCF-SO calculations for Dy3. The color code is as follows: violet, RE; green, Cl; grey, C; and red, O. H atoms are omitted for clarity. Symmetry codes are as follows: #, 1 − x, +y, +z.
Magnetochemistry 11 00038 g001
Magnetochemistry 11 00038 g002
Figure 2. (a) The two types of intramolecular magnetic interactions of RE3 with the corresponding [RECl3RE] units coordinated to Cp* ligands. The symmetry codes are as follows: #, 1 − x, +y, +z. (b) The χT versus T plot for Gd3 under a 1000 Oe DC field. Inset: the field-dependent magnetization plots at indicated temperatures. The solid lines are the best fits.
Figure 2. (a) The two types of intramolecular magnetic interactions of RE3 with the corresponding [RECl3RE] units coordinated to Cp* ligands. The symmetry codes are as follows: #, 1 − x, +y, +z. (b) The χT versus T plot for Gd3 under a 1000 Oe DC field. Inset: the field-dependent magnetization plots at indicated temperatures. The solid lines are the best fits.
Magnetochemistry 11 00038 g002
Magnetochemistry 11 00038 g003
Figure 3. The χT versus T plot for (a) Tb3, (b) Dy3, (c) Ho3, (d) Er3, (e) Tm3, and (f) Yb3 under a 1000 Oe DC field. Inset: the field-dependent magnetization plots at indicated temperatures.
Figure 3. The χT versus T plot for (a) Tb3, (b) Dy3, (c) Ho3, (d) Er3, (e) Tm3, and (f) Yb3 under a 1000 Oe DC field. Inset: the field-dependent magnetization plots at indicated temperatures.
Magnetochemistry 11 00038 g003
Magnetochemistry 11 00038 g004
Figure 4. The in-phase (χ′, left) and out-of-phase (χ″, right) frequency-dependent AC susceptibility signals for Dy3 under a zero DC field, measured from 2 K (blue) to 23 K (red). The solid lines represent the best fit according to the generalized Debye model.
Figure 4. The in-phase (χ′, left) and out-of-phase (χ″, right) frequency-dependent AC susceptibility signals for Dy3 under a zero DC field, measured from 2 K (blue) to 23 K (red). The solid lines represent the best fit according to the generalized Debye model.
Magnetochemistry 11 00038 g004
Magnetochemistry 11 00038 g005
Figure 5. The ln(τ) vs. 1/T plots for Dy3 (inset: log–log version for plot of the magnetic relaxation rate versus the temperature for Dy3) (a). The solid lines best fit with Equation (1), including the Orbach, Raman, and QTM processes. The electronic states from the CASSCF-SO calculations for Dy1 (b) and Dy2 (c) in Dy3. The thick black lines represent the Kramers doublets as a function of their magnetic moment along the magnetic axis. The red arrows represent the most probable relaxation pathway for the Orbach process. The green lines correspond to the QTM through the ground states. The blue line represents the off-diagonal relaxation process. The numbers at each arrow represent the mean absolute value of the corresponding matrix element of the transition magnetic moment.
Figure 5. The ln(τ) vs. 1/T plots for Dy3 (inset: log–log version for plot of the magnetic relaxation rate versus the temperature for Dy3) (a). The solid lines best fit with Equation (1), including the Orbach, Raman, and QTM processes. The electronic states from the CASSCF-SO calculations for Dy1 (b) and Dy2 (c) in Dy3. The thick black lines represent the Kramers doublets as a function of their magnetic moment along the magnetic axis. The red arrows represent the most probable relaxation pathway for the Orbach process. The green lines correspond to the QTM through the ground states. The blue line represents the off-diagonal relaxation process. The numbers at each arrow represent the mean absolute value of the corresponding matrix element of the transition magnetic moment.
Magnetochemistry 11 00038 g005
Magnetochemistry 11 00038 g006
Figure 6. Arrangements of the principal magnetic axes for Dy3 (a), for Dy1 and Dy1# (b), for Dy1 and Dy2 or Dy1# and Dy2 (c). The yellow arrows represent the principal magnetic axes of the ground doublets obtained from the CASSCF-SO calculations.
Figure 6. Arrangements of the principal magnetic axes for Dy3 (a), for Dy1 and Dy1# (b), for Dy1 and Dy2 or Dy1# and Dy2 (c). The yellow arrows represent the principal magnetic axes of the ground doublets obtained from the CASSCF-SO calculations.
Magnetochemistry 11 00038 g006
Table 1. The total spin momentum (S), total orbit momentum (L), total angular quantum number (J), and g values for the ground states of free RE(III) ions [71,72], χT values, and magnetic moments per RE(III) ion in RE3.
Table 1. The total spin momentum (S), total orbit momentum (L), total angular quantum number (J), and g values for the ground states of free RE(III) ions [71,72], χT values, and magnetic moments per RE(III) ion in RE3.
RE(III)SLJgχTValue (cm3 mol−1 K)Magnetic Moments (μB)
ExpectedExperimentalSaturatedExperimental
300 K300 K2 K
Gd7/207/227.878.047.0376.92
Tb3363/211.8211.867.8694.74
Dy5/2515/24/314.1714.0310.59104.69
Ho2685/414.0714.759.17104.86
Er3/2615/26/511.4811.484.4995.09
Tm1567/67.157.111.8373.14
Yb1/237/28/72.572.521.2041.80
Table 2. The electronic structure of Dy1 in Dy3 was calculated with the crystal field parameters obtained from CASSCF-SO at the crystal structure. Each row corresponds to a Kramers doublet. Other components with low contributions are not displayed.
Table 2. The electronic structure of Dy1 in Dy3 was calculated with the crystal field parameters obtained from CASSCF-SO at the crystal structure. Each row corresponds to a Kramers doublet. Other components with low contributions are not displayed.
Energy
(cm−1)		g1g2g3Wavefunction
0.001.04 × 10−31.67 × 10−319.8198.9%|± 15/2⟩…
168.9116.26 × 10−29.52 × 10−217.6458.2%| ± 13/2⟩ + 14.5%| ± 11/2⟩ + 14.5%| ± 9/2⟩ + 7.9%| ± 7/2⟩…
227.0381.60 × 10−22.86 × 10−214.4937.3%| ± 13/2⟩ + 17.1%| ± 9/2⟩ + 16%| ± 11/2⟩ + 16%| ± 7/2⟩…
273.4313.534.7210.0748.1%| ± 11/2⟩ + 16.8%| ± 5/2⟩ + 13.3%| ± 7/2⟩ + 10.8%| ± 3/2⟩…
302.7172.565.6210.5642.8%| ± 9/2⟩ + 18.8%| ± 7/2⟩ + 11.9%| ± 11/2⟩ + 10.8%| ± 3/2⟩…
338.5000.142.6513.2030.6%| ± 5/2⟩ + 25.8%| ± 1/2⟩ + 25.6%| ± 7/2⟩+8.1%| ± 9/2⟩…
360.0750.561.9714.9839.1%| ± 3/2⟩ + 20.2%| ± 5/2⟩ + 16.1%| ± 1/2⟩ + 10.9%| ± 7/2⟩…
472.1222.36 × 10−23.85 × 10−219.7742.9%| ± 1/2⟩ + 28.9%| ± 3/2⟩ + 15.6%| ± 5/2⟩ + 7.5%| ± 7/2⟩…
Table 3. The electronic structure of Dy2 in Dy3 was calculated with the crystal field parameters obtained from CASSCF-SO at the crystal structure. Each row corresponds to a Kramers doublet. Other components with low contributions are not displayed.
Table 3. The electronic structure of Dy2 in Dy3 was calculated with the crystal field parameters obtained from CASSCF-SO at the crystal structure. Each row corresponds to a Kramers doublet. Other components with low contributions are not displayed.
Energy
(cm−1)		g1g2g3Wavefunction
0.006.24 × 10−39.61 × 10−319.8499.5%| ± 15/2⟩…
180.3030.800.8516.2373.3%| ± 13/2⟩ + 8.8%| ± 5/2⟩ + 5.8%| ± 11/2⟩ + 5.6%| ± 7/2⟩…
214.56310.207.122.7531.6%|± 9/2⟩ + 23.4%| ± 11/2⟩ + 11.2%| ± 3/2⟩ + 10.7%| ± 13/2⟩…
233.3520.684.138.9431.4%| ± 11/2⟩ + 21.6%| ± 7/2⟩ + 11.9%| ± 9/2⟩+10.6%| ± 13/2⟩…
261.85310.857.671.0446.8%| ± 7/2⟩+42.4%| ± 9/2⟩ + 4.3%| ± 5/2⟩ +3.3%| ± 11/2⟩…
270.3988.775.420.4844.4%| ± 5/2⟩ + 30.6%| ± 11/2⟩ + 16.9%| ± 3/2⟩ + 3.6%| ± 13/2⟩…
378.2500.582.7314.2353%| ± 3/2⟩ + 32.6%| ± 5/2⟩ + 5%| ± 1/2⟩ + 4.5%| ± 7/2⟩…
390.6060.393.2615.0268.9%| ± 1/2⟩ + 11.5%| ± 7/2⟩ + 8.8%| ± 9/2⟩ + 8.2%| ± 3/2⟩…
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Pan, Y.; Ding, Y.-S.; Li, L.; Zheng, Z. Synthesis, X-Ray Crystal Structures, and Magnetic Properties of a Series of Trinuclear Rare-Earth Hepta-Chloride Clusters. Magnetochemistry 2025, 11, 38. https://doi.org/10.3390/magnetochemistry11050038

AMA Style

Pan Y, Ding Y-S, Li L, Zheng Z. Synthesis, X-Ray Crystal Structures, and Magnetic Properties of a Series of Trinuclear Rare-Earth Hepta-Chloride Clusters. Magnetochemistry. 2025; 11(5):38. https://doi.org/10.3390/magnetochemistry11050038

Chicago/Turabian Style

Pan, Yingying, You-Song Ding, Lei Li, and Zhiping Zheng. 2025. "Synthesis, X-Ray Crystal Structures, and Magnetic Properties of a Series of Trinuclear Rare-Earth Hepta-Chloride Clusters" Magnetochemistry 11, no. 5: 38. https://doi.org/10.3390/magnetochemistry11050038

APA Style

Pan, Y., Ding, Y.-S., Li, L., & Zheng, Z. (2025). Synthesis, X-Ray Crystal Structures, and Magnetic Properties of a Series of Trinuclear Rare-Earth Hepta-Chloride Clusters. Magnetochemistry, 11(5), 38. https://doi.org/10.3390/magnetochemistry11050038

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop