Abstract
Attributed to the lack of an Earth-like global intrinsic dipole magnetic field on Mars, the induced electromagnetic field environment plays a crucial role in the evolution of its atmosphere. The dominant motional electric field () induced by the bulk motion of the magnetic field within the Martian magnetosheath serves to accelerate ions toward escape velocity, thereby forming a plume escape channel. However, the distribution morphology of itself has received limited attention in previous research. In this study, by taking advantage of the multi-fluid Hall-MHD model cooperating with the Martian crustal field model, we focus on elucidating the physical mechanisms underlying the asymmetrical distribution of and examining the influence of the crustal field on this asymmetry. The results obtained from the simulation conducted in the absence of the crustal field indicate that the is more intense within the magnetosheath, where is directed toward Mars, primarily due to its corresponding higher velocity and a stronger magnetic field at lower solar zenith angles. The Martian crustal field has the ability to enhance the local around the inner boundary of the magnetosheath by amplifying both the magnetic field and its associated velocity. Accordingly, these findings provide valuable insights into the asymmetric nature of within the Martian magnetosheath under typical quiet-time solar wind conditions.
1. Introduction
The solar wind, predominantly consisting of protons and electrons in a plasma state together with the solar magnetic field [1], is emitted continuously from the Sun’s corona and traverses the entire solar system at supersonic velocities ranging from 250 to 900 km/s [2]. When the solar wind encounters an obstacle, it undergoes deceleration at the bow shock, transitioning from supersonic to subsonic flow. As the solar wind decelerates, individual electrons undergo energization to higher energies mostly caused by the cross-shock ambipolar potential [3]. The bulk flow is subsequently decelerated and deflected downstream of the bow shock, known as the magnetosheath, leading to the phenomenon of the frozen interplanetary magnetic field (IMF) “draping” around the obstacle [4,5,6].
Despite the analogous functions performed by the bow shock and magnetosheath on Mars, Earth, and other planets within our solar system, significant distinctions emerge as a result of Mars’ small radius and absence of a global intrinsic dipole magnetic field. On Mars, the solar wind tends to directly interact with its upper atmosphere, and the magnetosheath has a thickness comparable to the ion gyroradius, implying that the solar wind is unlikely to be fully thermalized [7]. Moreover, the draped IMFs are capable of penetrating deep into the Martian ionosphere due to the potential for the solar wind dynamic pressure to surpass the thermal pressure of the Martian ionosphere [8]. At the lowest altitudes within the magnetosheath, there is a distinct transition region referred to as the ion composition boundary (ICB), which serves to separate the solar wind plasma from planetary ionospheric ions [9]. Charged particles, picked up and accelerated from the Martian ionosphere, exhibit a predominant orientation alignment with the solar wind motional/convection electric field within the magnetosheath [10,11,12]. However, in the instance of large planetary systems with a radius notably exceeding the ions’ gyroradius, there is evidence of ions displaying a ring distribution [13].
The solar wind motional electric field (), sometimes called the convection electric field, arises from the bulk motion of the magnetic field, accelerating ions to form a plume escape channel responsible for about 23% of the total Martian ion escape rate [10,14,15,16]. To assess the impact of such an electric field, the Mars Solar Electric (MSE) coordinate has been developed [17,18] and extensively employed in observation statistical analysis, where is parallel to the points from Mars toward the Sun, and completes the right-handed coordinate system. It is crucial to emphasize that the asymmetry features displayed within the MSE coordinate system represent the global average and are exclusively influenced by , rather than being attributed to the Martian crustal magnetic field predominantly situated in the southern hemisphere [19,20].
The local motional electric field () was quantified for the first time in the MSE coordinate system by integrating simultaneous measurements of solar wind plasma flow velocities () and magnetic field vectors () obtained during the initial months of the Mars Atmosphere and Volatile EvolutioN (MAVEN) observation [21]. These measurements revealed a predominant distribution in the magnetosheath, with a higher magnitude observed in the magnetosheath, as also confirmed by simulations [22,23]. It is evident that the characteristics of are dependent on the distribution of the solar wind velocity and magnetic field, given that the magnitude of is equivalent to , where is the angle between the and .
Actually, the distributions of and also exhibit asymmetry. Due to the comparable scale size of the Martian magnetosheath with the Larmor radius of solar wind protons, but significantly less than that of heavy ionospheric ions, pickup heavy ions initially acquire momentum along the direction. In order to maintain the momentum conservation postulate of a multi-ion fluid system, it is imperative that the solar wind protons undergo deflection in the opposite direction (). Phenomena associated with this asymmetrical deflection of the solar wind have been revealed in the Martian magnetosheath [24,25,26]. As for the magnetic field, both observations and simulations indicate that the dayside pileup of the draping magnetic fields is inclined to shift toward the direction [27,28]. Moreover, the significance of in relation to the magnitude of cannot be ignored. Recently, Qiao et al. [12] conducted a study on the impact of in enhancing the magnitude of only on the hemisphere. Therefore, the underlying physical mechanism driving the asymmetrical distribution of remains unclear.
Additionally, the north–south asymmetry in distributions of and can be attributed to the presence of the Martian crustal magnetic field. Observations and simulations both confirm that the crustal field possesses the inherent ability to locally deflect the solar wind streams and to elevate the position of the dayside magnetic pileup boundary [29,30,31,32,33], leading to distinctive modifications in the within the magnetosheath [12]. However, the complexity associated with the effectiveness of the crustal magnetic field in concurrently attenuating , augmenting , and perturbing between the vectors underlies inadequately understood physical reasons for the enhancement of within the Martian southern magnetosheath.
In this study, by employing a multi-fluid Hall magnetohydrodynamic (MHD) model [16,34], we devote ourselves to elucidating the underlying physical mechanisms responsible for the asymmetrical distributions of the solar wind motional electric field within the Martian magnetosheath. The following sections of this paper are organized as follows: Section 2 outlines the model description, Section 3 presents the simulation results, and Section 4 offers conclusions for our study.
2. Model Description
The three-dimensional four-species multi-fluid Hall-MHD model utilized in this study, which treats each ion species as a distinct fluid governed by Navier–Stokes (NS) equations coupled to the magnetic induction equation considering the Hall term, has been validated as a reliable method for simulating large-scale solar wind–Mars interactions [16,33,34,35,36,37].
When conducting the multi-fluid Hall-MHD simulations, the self-consistent production of four ion species () can be achieved by incorporating an atmospheric profile () [38] and considering the solar extreme ultraviolet flux [39], as well as accounting for the physical collisions and chemical reactions among them [40]. Subsequently, the characteristics of individual ion species within the Martian electromagnetic field environment can be accurately described by a set of discrete NS equations with respect to mass, momentum, and energy, followed by the temporal evolution of the electromagnetic environments derived by solving the magnetic induction equation. The system of equations governing the multi-fluid Hall-MHD model can be formulated as follows [15,16]:
where (1)–(3) are conservative NS equations and (4) is the magnetic induction equation. Here, and are the individual mass density, velocity, pressure, number density, and charge of the species s, respectively. is the identity matrix, , and is the polytropic index chosen to be 5/3. are the pressure and number density of electrons. is the charge-averaged ion velocity . The motional electric field () is equivalent to in our simulations. The electric current density can be obtained from .
The source terms , , and on the rightmost side of Equations (1)–(3) capture the variations in mass, momentum, and energy of the ion fluid resulting from physical collisions and chemical reactions among all species (Table 1), including photoionization, charge exchange, and recombination reactions [15,16,40].

Table 1.
Chemical reactions and associated rates considered in the Hall-MHD model.
A spherical simulation grid consisting of 960,000 cells under the Mars-centered Solar Orbital (MSO) coordinate frame was utilized in our simulation, where the X-axis (, is the radius of Mars) is oriented from Mars toward the Sun, with the Z-axis () being perpendicular to the X-axis and positively directed toward the north celestial pole. The Y-axis () completes the right-handed coordinate system. The inner boundary, located above the Martian surface, has a minimum grid size of . At this location, ion velocities are assumed to be zero, and the densities are determined through chemical reactions (Table 1) reaching a state of equilibrium, while the density of is considered to be 0.3 times that of the solar wind protons’ densities.
According to the typical quiet time solar wind parameters upstream of Mars [41], the upstream velocity and density of the solar wind plasma are set at and respectively, and the upstream interplanetary magnetic field is assumed to follow a Parker spiral angle of with a magnitude of 3 nT in the XY plane (), indicating that the MSO and MSE are the same coordinate in our simulations. The subsolar point corresponds to the 180° longitude at the equator, suggesting that the most intense crustal field areas are situated on the dayside. We conducted two simulation cases, as detailed in Table 2: the first case excluded the Martian crustal field to explore the inherent asymmetry distribution of within the Martian magnetosheath, while the second case incorporated the G110 crustal field model [42] to assess the influence of the crustal field on the asymmetrical distribution’s morphology. The simulation tends to approach equilibrium at approximately 750,000 simulation steps, as indicated by the minimal maximum residual error achieved.

Table 2.
Upstream solar wind conditions and crustal field setting of simulation cases.
3. Simulation Results
3.1. The Inherent Asymmetry Distribution of
During the solar wind–Mars interaction, the solar wind plasma undergoes deceleration upon encountering the Martian bow shock, initiating a process of mass loading through the ionization of neutral atomic oxygen species that are prevalent in the Martian exosphere, predominantly occurring within the Martian magnetosheath. To illustrate the outcomes of the solar wind mass loading process within the magnetosheath, Figure 1a,b present the distributions of in the XY (Z = 0) and XZ (Y = 0) planes overlaid with contour lines of 4.1 individually, as extracted from simulation Case 1, excluding the Martian crustal field. Both panels clearly indicate a constant density of 4 in the upstream, followed by a sudden increase of nearly three times in the Martian magnetosheath, which is in accordance with previous statistical observations [43]. Additionally, the symmetry of hydrogen density distributions originating from the solar wind is evident in the magnetosheath, with the highest concentration near the subsolar position. Furthermore, it is apparent that there also exists a significant density of hydrogen present in the Martian ionosphere due to the lack of differentiation between hydrogen derived from solar wind and that originating from the ionosphere. Accordingly, in this study, the Martian magnetosheath is delineated by the region where the density of solar wind protons exceeds that of the upstream initial conditions, as indicated by the space between the contour lines representing the bow shock and ICB, as depicted in Figure 1a,b.
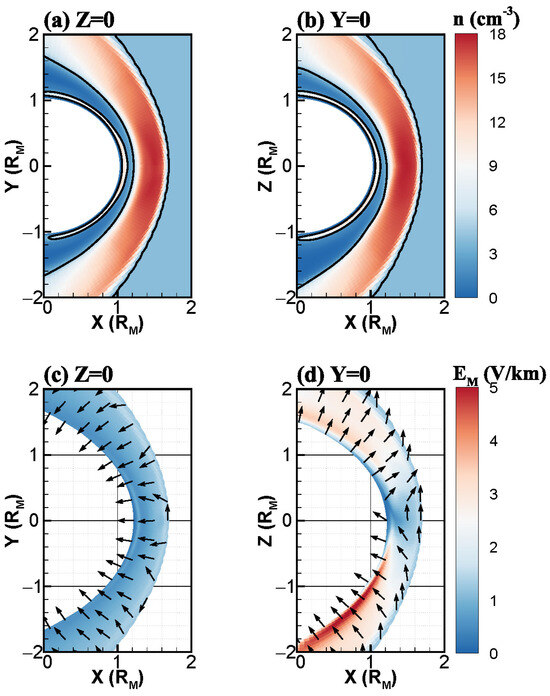
Figure 1.
The distributions of (a,b) density and (c,d) the motional electric field overlapped with its vectors (black arrows) in the XY and XZ plane derived from the simulation conducted without the influence of the Martian crustal field (Case 1).
In order to illustrate the distribution characteristics of in the Martian magnetosheath, Figure 1c,d depict the in the XY and XZ magnetosheath plane, along with the corresponding vectors, respectively. The symmetrical distribution of with a magnitude of approximately is clearly evident in the XY magnetosheath, oriented inward toward Mars. In contrast, displays an apparent asymmetrical distribution in the XZ magnetosheath, with a stronger of about near the inner boundary of the magnetosheath compared to the in the magnetosheath, consistent with previous observations [21]. Based on the orientation of the vectors in the XZ magnetosheath, it can be deduced that ions exhibit a tendency to precipitate toward Mars in the hemisphere, while being accelerated to escape from Mars in the hemisphere, thus forming a plume-like escape channel [14].
In order to elucidate the physical mechanisms underlying the asymmetrical distribution of , as described by , Figure 2 provides the distributions of the (a,b) velocity , (c,d) magnetic field , and (e,f) the angle between and in the XY and XZ magnetosheath separately, along with corresponding vectors in panels (a–d). The deceleration and deflection of plasma velocity in the magnetosheath are clearly demonstrated in Figure 2a,b. Furthermore, the velocity distribution exhibits symmetry in the XY magnetosheath but asymmetry in the XZ magnetosheath, indicating a higher near the inner boundary of the magnetosheath compared to its counterparts (). These findings are consistent with previous statistical observations presented in the MSE coordinate [24,25,26]. The interplanetary magnetic fields drape the planet as they traverse the bow shock and pile up around the inner boundary of the magnetosheath, as depicted in Figure 2c, while the draping magnetic fields are observed to be stronger near the inner boundary of the magnetosheath () compared to the corresponding (, Figure 2d), which is consistent with previous studies [27,28]. However, the asymmetry features of the velocity and magnetic field in the XZ magnetosheath cannot be reproduced by a single-fluid multi-species MHD model due to the assumption that all ion species, which are decoupled in our multi-fluid model, are coupled to share the same velocity and temperature during the single-fluid simulations [28,30]. Therefore, the asymmetrical feature of is not observed in the study by Qiao et al. [12], attributed to their employment of a single-fluid MHD model. The angle between and in the magnetosheath can be inferred from Figure 2e,f. Specifically, it is observed that they are predominantly parallel in the magnetosheath, anti-parallel in the magnetosheath, and quasi-vertical in the XZ magnetosheath. This behavior is primarily attributed to the initial solar wind velocity directed only along the , as well as to an upstream interplanetary magnetic field aligned with the XY plane following a Parker spiral angle. Due to the absence of significant asymmetry characteristics in the distribution of within the XZ magnetosheath, it can be deduced that the asymmetrical features of and , namely the stronger magnitude of in the magnetosheath and stronger in the magnetosheath, are likely responsible for driving the inherent asymmetric distribution of in the XZ magnetosheath.
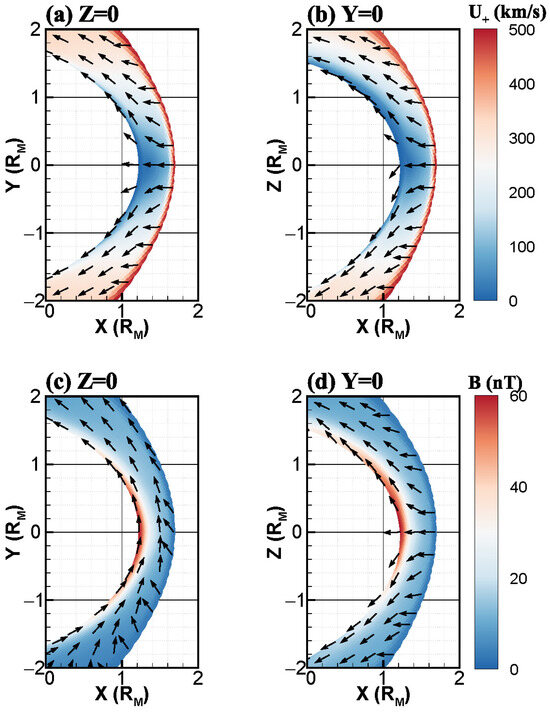
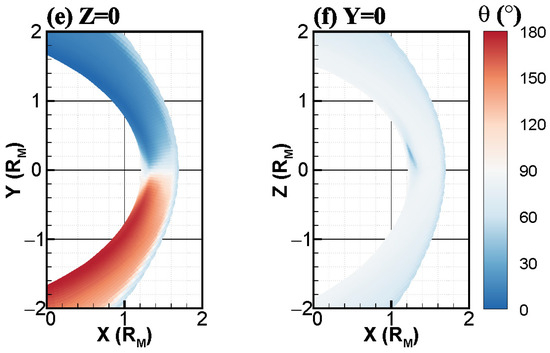
Figure 2.
The distributions of (a,b) the bulk velocity , (c,d) magnetic field , and (e,f) the angle between them in the XY and XZ magnetosheath obtained from the simulation conducted without the influence of the Martian crustal field (Case 1). The black arrows in (a–d) represent the corresponding vectors.
To quantitatively analyze the relative significance of velocity, magnetic field, and the angle between them in relation to the asymmetrical distributions of motional electric fields within the magnetosheath, Figure 3 illustrates the magnitudes of (c) , (d) , and (e) at the (a) altitude (R) where the peak strength of is observed within each solar zenith angle (SZA) interval of the (red lines) and (blue lines) magnetosheath, as depicted in Figure 1d. According to panel 3b, it is evident that the highest intensities are greater within the magnetosheath, increasing with SZA and peaking at at SZA = 60°, which exceeds the corresponding in the magnetosheath, followed by a decrease in the with SZA. These are in accordance with a previous observation [21] that revealed that the intensity in the magnetosheath is approximately double that of the magnetosheath. As depicted in panel 3c, the plasma bulk velocities, which increase with SZA, exhibit greater speed in the magnetosheath compared to their counterparts. However, it is obvious from Figure 3d that the magnitudes of at the most intense positions of the magnetosheath are greater than those of the magnetosheath when , but smaller than those when . As a result of interplanetary magnetic field pileup at the inner boundary of the magnetosheath, locations closer to this boundary tend to exhibit a stronger magnetic field. Accordingly, this phenomenon can be attributed to the fact that the locations where the peak strength of exists are closer to the inner boundary of the () magnetosheath when (), as illustrated in Figure 3a. As for , in the absence of Martian crustal fields, there are no significant differences in at altitudes R within the magnetosheath. Hence, it can be inferred from Figure 3 that the inherent asymmetry distribution of within the magnetosheath is primarily attributed to the higher in the magnetosheath. Additionally, at a lower SZA, the stronger resulting from the positioning of the most intense closer to the inner boundary of the magnetosheath also contributes to this asymmetry.
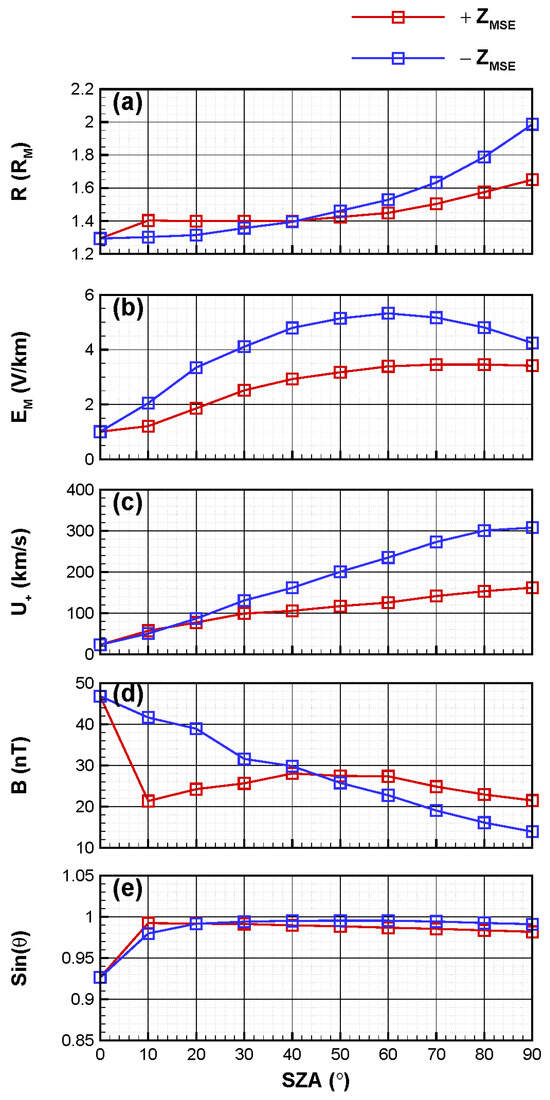
Figure 3.
The variations in the (c) velocity , (d) magnetic field and (e) with respect to the solar zenith angle (SZA) at the (a) altitudes R where the largest magnitudes of the (b) motional electric field exist within the SZA interval of the (red lines) and (blue lines) magnetosheath in the XZ plane extracted from the simulation without consideration of the crustal field (Case 1).
3.2. The Impact of the Crustal Field on the Asymmetry Distribution of
To investigate the influence of the Martian crustal field on the asymmetry distribution of within the magnetosheath, we conducted an additional simulation with the region of the strongest crustal field positioned at the subsolar longitude. The distributions of (a) , (b) , (c) and (d) obtained from this simulation case in the XZ magnetosheath are depicted in Figure 4, following the same format as the preceding figures in this study. It is important to emphasize that MSO and MSE represent identical coordinates in our simulations. In order to avoid confusion with previous expressions of the figures in this study, we will continue to present our results in the MSE coordinate instead of the MSO coordinate system. In this MSE coordinate, the hemisphere corresponds to the southern hemisphere in the MSO coordinate. The asymmetry distributions of , and in the magnetosheath are obvious in panels 4a–c. Additionally, the magnitudes of , and near the inner boundary of the magnetosheath exhibit slightly greater strength compared to corresponding simulation results that do not account for the crustal field. In comparison to Figure 2c, the magnetic field vectors exhibit a disordered pattern, particularly within the inner boundary of the magnetosheath, as a result of the interaction between the Martian crustal and interplanetary magnetic fields. When comparing Figure 2f and Figure 4d, another noticeable distinction arises. The Martian crustal field leads to a greater in the subsolar region and a smaller in the magnetosheath, particularly near the inner boundary. This indicates that the velocity and magnetic field become more anti-parallel in the subsolar region and parallel in the magnetosheath. Accordingly, it can be deduced that the influence of the crustal field on the within the magnetosheath is manifested by amplifying and , as well as perturbing the angle between them.

Figure 4.
The distributions of (a) motional electric field , (b) velocity , (c) magnetic field , and (d) the angle between the and in the XZ magnetosheath derived from the simulation incorporating the Martian crustal field (Case 2). The black arrows in (a–c) denote the respective vectors.
In order to visually illustrate the influence of the Martian crustal field on the , Figure 5 presents the maximum values obtained from simulations with uncoupled (Case 1, blue lines) and coupled (Case 2, green lines) crustal fields at each SZA interval within the magnetosheath in the XZ plane separately. It is obvious from panel 5a that there is no significant discrepancy in the derived from the two simulation cases within the magnetosheath. However, within the magnetosheath, the enhancements in by the Martian crustal fields are clearly observed in Figure 5b, particularly within the range of SZA = 20° to SZA = 60°, where the influences of crustal fields are predominant. More specifically, the most significant disparity in derived from the two simulation cases occurs at SZA = 30° within the magnetosheath, where the presence of a crustal field results in an increase in the peak value of from to .
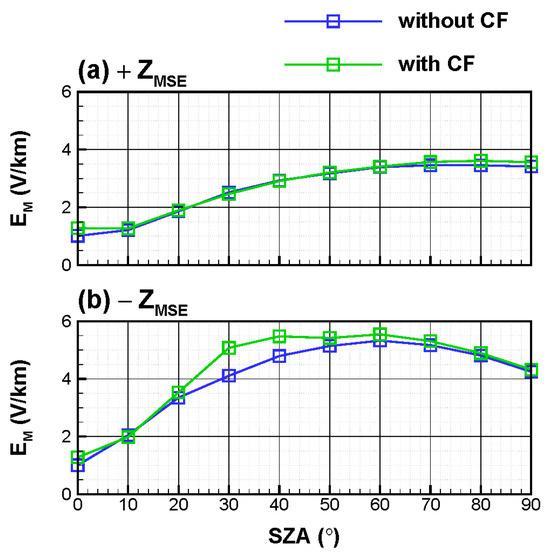
Figure 5.
The variations in the maximum magnitudes of the motional electric field , as derived from the simulation without (Case 1, blue lines) and with (Case 2, green lines) Martian crustal field, with respect to the solar zenith angle (SZA) within the (a) and (b) magnetosheath in the XZ plane.
To quantitatively analyze the physical mechanisms underlying the enhancement of by Martian crustal fields, Figure 6 illustrates the variations in the magnitudes of (a) , (b) , and (c) at the same location as shown in Figure 5b, with respect to SZA ranging from 20° to 60°. The deflection of the plasma by the Martian crustal field results in a faster around SZA = 20–40° and a slightly slower velocity compared to the case without consideration of the crustal field at SZA = 40–60° (panel 6a). Furthermore, the Martian magnetic anomalies contribute to an increase in the magnitude of (panel 6b). Due to the reconnection between interplanetary and crustal magnetic fields, as well as the deflection effect posed by the crustal fields, the angles between and within SZA = 20–60° are no longer quasi-vertical. This is evident from Figure 6c, which illustrates that becomes smaller under the impact of the crustal fields, suggesting that the angles are smaller than 90°. Specifically, at SZA = 30° within the magnetosheath, the peak value of and its associated , , and obtained from the simulation incorporating the crustal field are , , , and 0.82, respectively. These values correspond to , , , and 0.99 in the absence of the crustal field condition. Consequently, it can be deduced that the increase in due to Martian crustal fields is primarily attributed to the augmentation of and , despite causing a deviation in the angle between them from being quasi-vertical.
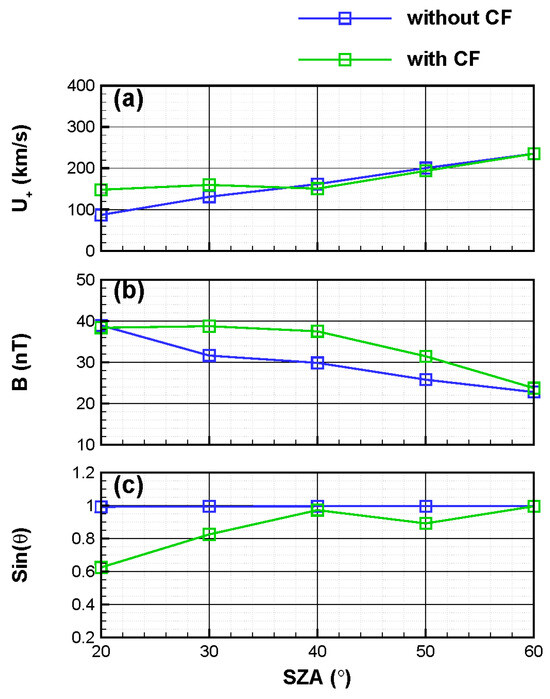
Figure 6.
The variations in the (a) velocity , (b) magnetic field and (c) , as derived from the simulation without (Case 1, blue lines) and with (Case 2, green lines) Martian crustal field, with respect to the solar zenith angle (SZA = 20–60°) at the position where the largest magnitudes of the motional electric field exist at the SZA interval within the magnetosheath in the XZ plane.
4. Discussion and Conclusions
In this study, by employing a well-developed multi-fluid Hall-MHD model, we reproduced the inherent asymmetrical distribution of within the magnetosheath revealed by previous MAVEN statistical observations [21]. Additionally, the physical reasons responsible for this asymmetry are elucidated, and the impact of the Martian crustal field on the asymmetry distribution is investigated.
The inherent asymmetry distribution of can be formed without any influence from the crustal field, which primarily results from the faster and low-SZA that is stronger at the location of the strongest within the magnetosheath than the correspondences in the magnetosheath. Furthermore, by analyzing the simulation results derived from the Hall-MHD model coupled with the Martian crustal field model, we find that the crustal fields tend to enhance the asymmetry of through an enlarged and .
The simulation results in this study represent the Martian environment during quiet-time solar wind conditions. However, the asymmetry distributions of and are impacted by the interplanetary magnetic field, solar wind velocity, and density [25,26,27,28]. Hence, the degree of the asymmetry distribution of within the magnetosheath can be influenced by upstream solar wind conditions, especially some extreme space weather events. Moreover, the fact that the MSO coordinate aligns with the MSE coordinate in our simulations, attributed to the specific initial inputs of the solar wind velocity and interplanetary magnetic field adopted in conducting the model, requires special attention. However, in reality, often deviates from , depending upon the upstream solar wind conditions. Therefore, it can be deduced that if the hemisphere corresponds to the Martian southern hemisphere, the extent of the asymmetry distribution of within the magnetosheath should be reduced due to the enhancement of by the crustal field in the magnetosheath. The impact of external solar wind conditions on the extent of the asymmetry distribution of deserves further investigation.
Author Contributions
Formal analysis, S.L.; Funding acquisition, H.L.; Investigation, S.L.; Methodology, S.L., H.L. and J.C.; Supervision, H.L.; Validation, J.C., X.W. and X.Z.; Visualization, S.L.; Writing—original draft, S.L.; Writing—review and editing, N.C., Y.S., J.W., Y.C. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grants 42241114, 42074214, and 12150008, the B-type Strategic Priority Program of the Chinese Academy of Sciences (Grant XDB41000000), the Postdoctoral Fellowship Program of CPSF under Grant GZC20233367 and the National Key R&D Program of China (Grant No. 2021YFA0718600).
Data Availability Statement
The MHD simulation data used in the analyses are publicly available online at https://zenodo.org/records/12792031 (accessed on 22 July 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Parker, E.N. Dynamics of the Interplanetary Gas and Magnetic Fields. Astrophys. J. 1958, 128, 664–676. [Google Scholar] [CrossRef]
- McComas, D.J.; Elliott, H.A.; Schwadron, N.A.; Gosling, J.T.; Skoug, R.M.; Goldstein, B.E. The three-dimensional solar wind around solar maximum. Geophys. Res. Lett. 2003, 30, 1517. [Google Scholar] [CrossRef]
- Scudder, J.D.; Mangeney, A.; Lacombe, C.; Harvey, C.C.; Aggson, T.L. The resolved layer of a collisionless, high β, supercritical, quasi-perpendicular shock wave, 2. Dissipative fluid electrodynamics. J. Geophys. Res. 1986, 91, 11053–11074. [Google Scholar] [CrossRef]
- Spreiter, J.R.; Summers, A.L.; Alksne, A.Y. Hydromagnetic flow around the magnetosphere. Planet. Space Sci. 1966, 14, 223–253. [Google Scholar] [CrossRef]
- Mazelle, C.; Winterhalter, D.; Sauer, K.; Trotignon, J.G.; Acuña, M.H.; Baumgärtel, K.; Bertucci, C.; Brain, D.; Brecht, S.; Delva, M.; et al. Bow shock and upstream phenomena at Mars. Space Sci. Rev. 2004, 111, 115–181. [Google Scholar] [CrossRef]
- Nagy, A.F.; Winterhalter, D.; Sauer, K.; Cravens, T.E.; Brecht, S.; Mazelle, C.; Crider, D.; Kallio, E.; Zakharov, A.; Dubinin, E.; et al. The plasma environment of Mars. Space Sci. Rev. 2004, 111, 33–114. [Google Scholar] [CrossRef]
- Moses, S.L.; Coroniti, F.V.; Scarf, F.L. Expectations for the microphysics of the Mars-solar wind interaction. Geophys. Res. Lett. 1988, 15, 429–432. [Google Scholar] [CrossRef]
- Sanchez-Cano, B.; Narvaez, C.; Lester, M.; Mendillo, M.; Mayyasi, M.; Holmstrom, M.; Halekas, J.; Andersson, L.; Fowler, C.M.; McFadden, J.P.; et al. Mars’ ionopause: A matter of pressures. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028145. [Google Scholar] [CrossRef]
- Halekas, J.S.; Ruhunusiri, S.; McFadden, J.P.; Espley, J.R.; DiBraccio, G.A. Ion composition boundary layer instabilities at mars. Geophys. Res. Lett. 2019, 46, 10303–10312. [Google Scholar] [CrossRef]
- Dong, Y.; Fang, X.; Brain, D.A.; McFadden, J.P.; Halekas, J.S.; Connerney, J.E.P.; Eparvier, F.; Andersson, L.; Mitchell, D.; Jakosky, B.M. Seasonal variability of Martian ion escape through the plume and tail from MAVEN observations. J. Geophys. Res. Space Phys. 2017, 122, 4009–4022. [Google Scholar] [CrossRef]
- Shuvalov, S.; Andersson, L.; Halekas, J.S.; Fowler, C.M.; Hanley, K.G.; DiBraccio, G. Ionospheric plasma transported into the Martian magnetosheath. Geophys. Res. Lett. 2024, 51, e2023GL107953. [Google Scholar] [CrossRef]
- Qiao, F.; Li, L.; Xie, L.; Li, W.; Kong, L.; Tang, B.; Zhang, Y.; Zhang, A.; Xu, Q.; Wang, L.; et al. Acceleration of pick-up ions in the Martian magnetosheath: A Tianwen-1 case study. J. Geophys. Res. Space Phys. 2024, 129, e2024JA032461. [Google Scholar] [CrossRef]
- Wilson, L.B. Low Frequency Waves at and Upstream of Collisionless Shocks; American Geophysical Union Geophysical Monograph Series: Washington, DC, USA, 2016; Volume 216, pp. 269–291. [Google Scholar]
- Dong, Y.; Fang, X.; Brain, D.A.; McFadden, J.P.; Halekas, J.S.; Connerney, J.E.; Curry, S.M.; Harada, Y.; Luhmann, J.G.; Jakosky, B.M. Strong plume fluxes at Mars observed by MAVEN: An important planetary ion escape channel. Geophys. Res. Lett. 2015, 42, 8942–8950. [Google Scholar] [CrossRef]
- Najib, D.; Nagy, A.F.; Tóth, G.; Ma, Y. Three-dimensional, multifluid, high spatial resolution MHD model studies of the solar wind interaction with Mars. J. Geophys. Res. 2011, 116, A05204. [Google Scholar] [CrossRef]
- Li, S.B.; Lu, H.Y.; Cui, J.; Yu, Y.Q.; Mazelle, C.; Li, Y.; Cao, J.B. Effects of a dipole-like crustal field on solar wind interaction with Mars. Earth Planet. Phys. 2020, 4, 23–31. [Google Scholar] [CrossRef]
- Russell, C.T.; Mulligan, T.; Delva, M.; Zhang, T.-L.; Schwingenschuh, K. A simple test of the induced nature of the martian tail. Planet. Space Sci. 1995, 43, 875–879. [Google Scholar] [CrossRef]
- Dubinin, E.; Sauer, K.; Lundin, R.; Norberg, O.; Trotignon, J.-G.; Schwingenschuh, K.; Delva, M.; Riedler, W. Plasma characteristics of the boundary layer in the martian magnetosphere. J. Geophys. Res. 1996, 101, 27061–27075. [Google Scholar] [CrossRef]
- Dubinin, E.; Fraenz, M.; Modolo, R.; Pätzold, M.; Tellmann, S.; Vaisberg, O.; Shuvalov, S.; Zelenyi, L.; Chai, L.; Wei, Y.; et al. Induced magnetic fields and plasma motions in the inner part of the martian magnetosphere. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029542. [Google Scholar] [CrossRef]
- Dubinin, E.; Fraenz, M.; Pätzold, M.; Tellmann, S.; Modolo, R.; DiBraccio, G.; McFadden, J.; Espley, J. Magnetic fields and plasma motions in a hybrid martian magnetosphere. J. Geophys. Res. Space Phys. 2023, 128, e2022JA030575. [Google Scholar] [CrossRef]
- Connerney, J.E.P.; Espley, J.R.; DiBraccio, G.A.; Gruesbeck, J.R.; Oliversen, R.J.; Mitchell, D.L.; Halekas, J.; Mazelle, C.; Brain, D.; Jakosky, B.M. First results of the MAVEN magnetic field investigation. Geophys. Res. Lett. 2015, 42, 8819–8827. [Google Scholar] [CrossRef]
- Bößwetter, A.; Bagdonat, T.; Motschmann, U.; Sauer, K. Plasma boundaries at Mars: A 3-D simulation study. Ann. Geophys. 2004, 22, 4363–4379. [Google Scholar] [CrossRef]
- Li, S.; Lu, H.; Cao, J.; Cui, J.; Ge, Y.; Zhang, X.; Rong, Z.; Li, G.; Li, Y.; Gao, J.; et al. Global electric fields at Mars inferred from Multifluid hall-MHD simulations. Astrophys. J. 2023, 949, 88. [Google Scholar] [CrossRef]
- Dubinin, E.; Fraenz, M.; Pätzold, M.; Halekas, J.S.; Mcfadden, J.; Connerney, J.E.P.; Jakosky, B.M.; Vaisberg, O.; Zelenyi, L. Solar wind deflection by mass loading in the Martian magnetosheath based on MAVEN observations. Geophys. Res. Lett. 2018, 45, 2574–2579. [Google Scholar] [CrossRef]
- Romanelli, N.; DiBraccio, G.; Halekas, J.; Dubinin, E.; Gruesbeck, J.; Espley, J.; Poh, G.; Ma, Y.; Luhmann, J.G. Variability of the solar wind flow asymmetry in the Martian magnetosheath observed by MAVEN. Geophys. Res. Lett. 2020, 47, e2020GL090793. [Google Scholar] [CrossRef]
- Dubinin, E.; Fraenz, M.; Pätzold, M.; Tellmann, S.; McFadden, J.; Halekas, J.; DiBraccio, G. Solar wind—Ionosphere interface at Mars. Ion dynamics, asymmetry, plasma jets. Geophys. Res. Lett. 2024, 51, e2023GL105073. [Google Scholar] [CrossRef]
- Zhang, C.; Rong, Z.; Klinger, L.; Nilsson, H.; Shi, Z.; He, F.; Gao, J.; Li, X.; Futaana, Y.; Ramstad, R.; et al. Three-dimensional configuration of induced magnetic fields around Mars. J. Geophys. Res. Planets 2022, 127, e2022JE007334. [Google Scholar] [CrossRef]
- Ma, Y.J.; Dong, C.F.; Toth, G.; van der Holst, B.; Nagy, A.F.; Russell, C.T.; Bougher, S.; Fang, X.; Halekas, J.S.; Espley, J.R.; et al. Importance of ambipolar electric field in driving ion loss from Mars: Results from a multifluid MHD model with the electron pressure equation included. J. Geophys. Res. Space Phys. 2019, 124, 9040–9057. [Google Scholar] [CrossRef]
- Crider, D.H.; Acuña, M.H.; Connerney, J.E.P.; Vignes, D.; Ness, N.F.; Krymskii, A.M.; Breus, T.K.; Rème, H.; Mazelle, C.; Mitchell, D.L.; et al. Observations of the latitude dependence of the location of the Martian magnetic pileup boundary. Geophys. Res. Lett. 2002, 29, 11-1–11-4. [Google Scholar] [CrossRef]
- Ma, Y.J.; Nagy, A.F.; Sokolov, I.V.; Hansen, K.C. Three-dimensional, multispecies, high spatial resolution MHD studies of the solar wind interaction with Mars. J. Geophys. Res. 2004, 109, A07211. [Google Scholar] [CrossRef]
- Harnett, E.M.; Winglee, R.M. The influence of a mini-magnetopause on the magnetic pileup boundary at Mars. Geophys. Res. Lett. 2003, 30, 2074. [Google Scholar] [CrossRef]
- Fan, K.; Fraenz, M.; Wei, Y.; Cui, J.; Rong, Z.; Chai, L.; Dubinin, E. Deflection of global ion flow by the Martian crustal magnetic fields. Astrophys. J. Lett. 2020, 898, L54. [Google Scholar] [CrossRef]
- Li, S.; Lu, H.; Cao, J.; Cui, J.; Zhou, C.; Wild, J.A.; Li, G.; Li, Y. Deflection of ion flow by magnetic fields in the Martian ionosphere. Astrophys. J. 2022, 941, 198. [Google Scholar] [CrossRef]
- Li, S.; Lu, H.; Cao, J.; Mazelle, C.; Cui, J.; Rong, Z.; Wild, J.A.; Yu, Y.; Li, X.; Li, Y.; et al. The impact and mechanism of the magnetic inclination angle on escape from Mars. Astrophys. J. 2022, 931, 30. [Google Scholar] [CrossRef]
- Song, Y.; Lu, H.; Cao, J.; Li, S.; Yu, Y.; Wang, S.; Ge, Y.; Zhang, X.; Zhou, C.; Wang, J. Effects of force in the martian plasma environment with solar wind dynamic pressure enhancement. J. Geophys. Res. Space Phys. 2023, 128, e2022JA031083. [Google Scholar] [CrossRef]
- Song, Y.; Lu, H.; Cao, J.; Wu, X.; Liu, Y.; Li, S.; Wang, S.; Wild, J.A.; Zhou, C.; Wang, J.; et al. Effects of solar wind density and velocity variations on the Martian ionosphere and plasma transport—A MHD model study. J. Geophys. Res. Space Phys. 2023, 128, e2023JA031788. [Google Scholar] [CrossRef]
- Li, S.; Lu, H.; Cao, J.; Cui, J.; Ip, W.-H.; Wild, J.A.; Zhang, X.; Chen, N.; Song, Y.; Wang, J. Asymmetrical looping magnetic fields and marsward flows on the nightside of Mars. Geophys. Res. Lett. 2024, 51, e2024GL109186. [Google Scholar] [CrossRef]
- Bougher, S.W.; Engel, S.; Hinson, D.P.; Forbes, J.M. Mars global surveyor radio science electron density profiles: Neutral atmosphere implications. Geophys. Res. Lett. 2001, 28, 3091–3094. [Google Scholar] [CrossRef]
- Huestis, D.L. Accurate evaluation of the chapman function for atmospheric attenuation. J. Quant. Spectrosc. Radiat. Transf. 2001, 69, 709–721. [Google Scholar] [CrossRef]
- Schunk, R.; Nagy, A. Ionospheres: Physics, Plasma Physics, and Chemistry; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Liu, D.; Rong, Z.; Gao, J.; He, J.; Klinger, L.; Dunlop, M.W.; Yan, L.; Fan, K.; Wei, Y. Statistical properties of solar wind upstream of Mars: MAVEN observations. Astrophys. J. 2021, 911, 113. [Google Scholar] [CrossRef]
- Gao, J.W.; Rong, Z.J.; Klinger, L.; Li, X.Z.; Liu, D.; Wei, Y. A spherical harmonic Martian crustal magnetic field model combining data sets of MAVEN and MGS. Earth Space Sci. 2021, 8, e2021EA001860. [Google Scholar] [CrossRef]
- Halekas, J.S.; Brain, D.A.; Luhmann, J.G.; DiBraccio, G.A.; Ruhunusiri, S.; Harada, Y.; Fowler, C.M.; Mitchell, D.L.; Connerney, J.E.; Espley, J.R.; et al. Flows, fields, and forces in the Mars-solar wind interaction. J. Geophys. Res. Space Phys. 2017, 122, 11320–11341. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).