Abstract
The generally accepted model of the magnetic structure of an iron oxide core–shell nanoparticle includes a single-domain magnetically ordered core surrounded by a layer with a frozen spin disorder. Due to the exchange coupling between the shell and core, the spin disorder should lead to nonuniform magnetization in the core. Suppression of this inhomogeneity by an external magnetic field causes the nonlinear behavior of the magnetization as a function of the field in the region of the approach to magnetic saturation. The equation proposed to describe this effect is tested using a micromagnetic simulation. Analysis of the approach to magnetic saturation of iron oxide nanoparticles at different temperatures using this equation can be used to estimate the temperature evolution of the core–shell coupling energy and the size of the uniformly magnetized nanoparticle core and the temperature behavior of this size.
1. Introduction
Magnetic nanoparticles of the magnetite–maghemite series have attracted close attention in various fields, from paleomagnetism to biomedicine [1,2,3,4,5,6,7,8,9,10]. Bulk magnetite Fe3O4 and maghemite Fe2O3 belong to the class of magnetically ordered substances with negative exchange interactions, which results in the ferrimagnetic structure [11,12]. In nanoparticles, ferrimagnetism is characteristic of the magnetic structure of the particle core and causes the formation of the particle magnetic moment <μ>. The magnetic moments of atoms in the surface layers of a particle are frustrated; therefore, the particle shell is in a state with a frozen magnetic disorder (spin-frustrated configuration) [13,14,15,16]. The ordered core/spin-frustrated shell structure manifests itself both in the magnetization dynamics of a particle and in its total magnetic moment <μ> [17,18,19,20]. The quantity <μ> has been well studied experimentally by describing the magnetization curves of the particles in the superparamagnetic regime using the Langevin equations [21,22,23]. In addition, the study of the temperature evolution of the magnetization using the ZFC–FC protocol (zero field cooled-field cooled curves) made it possible to estimate the mean blocking temperature at the specific measuring time used in a selected method [24,25,26,27]. In combination with the value of the particle size, this allowed the researcher to extract the effective magnetic anisotropy constant [25]. For blocked nanoparticles (at temperatures below the blocking temperature), one can expect the behavior described within the Stoner–Wohlfarth model [28,29,30]. For ensembles of the particles that obey this model, the magnetic anisotropy constant can be determined using the law of approach to magnetic saturation (LAMS) [31,32,33,34,35]. The advantage of this technique is the ability to estimate the temperature evolution of the magnetic anisotropy constant of a nanoparticle, while the estimation based on the blocking temperature suggests the anisotropy constant to be temperature-independent. In the LAMS, in its classical form, a uniform rotation of magnetization within an individual particle is assumed. Since particles have the composite core–shell structure, one can expect the experimental manifestation of both the separate core and shell contributions to the magnetization curve and the effects of the core–shell interactions. As a result of the exchange interaction between the core and the shell, the spin disorder in the shell would induce inhomogeneous magnetization in the core. Suppression of this inhomogeneity by an external magnetic field causes the specific behavior of the magnetization in the region of the approach to saturation. In this study, to describe this effect, a new form of the LAMS is proposed and tested. It is shown that the analysis of the approach to magnetic saturation of iron oxide nanoparticles at different temperatures with this equation can be used to separate the contributions of the surface anisotropy related to the core–shell interface and the random effective anisotropy that stabilizes the spin-disordered state in the shell.
2. The Forms of the LAMS
The magnetization of an ensemble of blocked single-domain particles with a randomly oriented easy magnetization axis approaches saturation according to the law [31,36]
where is the saturation magnetization and is the magnetic anisotropy field of a particle related to the magnetic anisotropy constant as . This formula implies the uniform rotation of the particle magnetization. The additive contribution of the spin-frustrated shell of a composite particle can be taken into account using the term [15]. Due to the core–shell exchange coupling in a nanoparticle, the spin disorder of the shell should induce the inhomogeneous magnetization in its core. The depth of propagation of the magnetization disturbance from the surface layer can be estimated using the so-called exchange size [37], where is exchange constant. Taking values of and for magnetite, we obtain . This means that if the core diameter in a spherical particle is less than 16 nm, the magnetization perturbation propagating from the particle surface will cover the entire core volume. Suppression of this inhomogeneity by an external magnetic field should lead to the nanoparticle core magnetization behavior being more complex than predicted by Equation (1) in the region of the approach to saturation. Here, we propose the equation for the approach to saturation that takes into account the competition between the exchange coupling, which promotes uniform magnetization, and the disordering impact of the shell:
where is the local random field induced by the core and spin-frustrated shell interaction. This equation is empirical and built by analogy with the expression for ferromagnetic media with the random magnetic anisotropy [38]. It has already been used to describe the approach to magnetic saturation in nanoparticles [35,39,40,41,42,43], but, unfortunately, this formula has not been well discussed and tested yet. In this work, we, to some extent, eliminate this gap by discussing the meaning and parameters of the proposed equation. Additionally, we report on its testing by the numerical experiment and experience using it for obtaining a description of the nanoparticle magnetization curves.
The effect of the LAMS from competition between disorders induced by random magnetic anisotropy and the ordering influence of positive exchange interaction has been well studied within the theory of a ferromagnetic medium with random magnetic anisotropy [44,45,46]. A nonuniform magnetization is induced by a local random field, but it becomes more homogeneous when exposed to external and exchange fields. In the case of a particle, there will also be competition between the random field induced by the core coated by spin-frustrated shell coupling and the external field, as well as the exchange field, which favors uniform magnetization within the core. An analogy can be drawn by giving the following meaning to the characteristic fields in Equation (2). The exchange field related to size of the uniformly magnetized particle core and exchange constant is the field that separates the regimes of the correlated (Figure 1a) and uncorrelated (Figure 1b) inhomogeneity of the magnetization in the core, while the field is the local random field induced by the core and spin-frustrated shell interaction. The type of the magnetization correlations in the core will be determined by the correlation length . The field dependence of this length leads to different asymptotic regimes in Equation (2), which are related to different inhomogeneity modes in the fields (, ) and (, ).
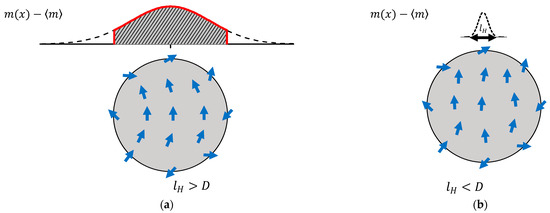
Figure 1.
Nonuniform magnetization in the core of a particle caused by the frozen spin disorder on its surface (the external field is directed from bottom to top): (a) the mode with () and (b) the mode with (). D is the particle diameter.
Let us clarify the first inequality: the condition can be converted into , which implies or , considering that the particle diameter D gives a good approximation of the magnetization correlation length . In addition, this inequality allows us to neglect the first term in the denominator in Equation (2). Hence, we have . In the opposite case, , based on the same logic, we have the inversion or . The physical meaning of the inequalities can be seen in Figure 1. In the case shown in Figure 1a, the correlation length of the transverse-to-field magnetization component of exceeds the diameter of the particle, which leads to a quasi-uniform transverse component of magnetization in its core (the external field in Figure 1 is directed from bottom to top). In the case shown in Figure 1b, the correlation length of magnetization is noticeably smaller than the particle diameter, which leads to inhomogeneity of the magnetization components transverse to the field. This, in turn, entails another power-law behavior of the LAMS.
3. Micromagnetic Testing
Some of the above statements can be verified using the micromagnetic simulation. The calculation of the micromagnetic states and magnetization curves was carried out by solving numerically the Landau–Lifshitz equation using the finite difference method using the OOMMF (Object-Oriented MicroMagnetic Framework 2.1) platform [47]. The total energy of the particle was presented as , where is the exchange energy, is the magnetic anisotropy energy, is the Zeeman energy, is the magneto-dipole energy. The total energy of the system is calculated as the sum of the magnetic moments of the cells. Each equilibrium state of the magnetic system corresponds to a local minimum of the total energy functional. The exchange energy contribution from cell i is given by , where is the set consisting of the 6 nearest cells to cell i, is the exchange coefficient between cells i and j, and is the discretization step size, between cell i and cell j, is the component of reduced (normalized) magnetization vector . The anisotropy energy for cell i is given by , where , , , for reduced (normalized) magnetization and orthonormal anisotropy axes , , and . The Zeeman energy for cell i is given by , where is saturation magnetization and is an applied field. The Standard demagnetization energy term in the OOMMF package, built upon the assumption that the magnetization is constant in each cell. It computes the average demagnetization field in each cell using formulae from [48,49] and convolution via the Fast Fourier Transform.
Spherical nanoparticles 4–10 nm in size were examined. The cell size was chosen within 0.5–1 nm, which is close to the magnetite unit cell size (0.84 nm). A nanoelement simulating a spherical particle, even being composed of such fine cells, is not an ideal sphere (Figure 1 and Figure 2), which, however, reproduces, to a certain extent, the discrete structure of real particles containing one crystalline grain. The shell thickness was chosen to be approximately equal to the size of 1–2 cells (a layer with broken chemical bonds and exchange couplings). The exchange constant was chosen to be J/m in the core and J/m in the shell. This model makes it possible to investigate the coupling between the magnetically ordered core and the shell with the antiferromagnetic interaction. The cubic magnetic anisotropy constant was chosen to be equal to the constant for bulk magnetite: J/m3 [50].
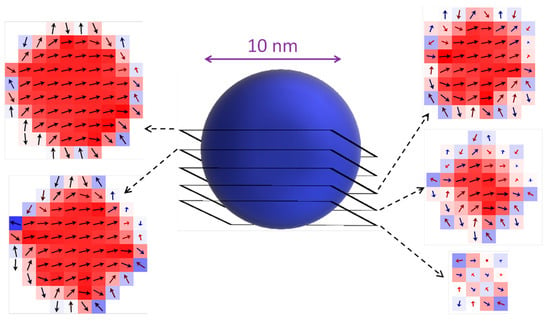
Figure 2.
Cross sections of a core–shell particle. The ordered magnetization states in the core and the disordered states on the surface can be seen.
In the surface layer of a particle, the frustrated (disordered) states of the magnetic moment are observed (Figure 2), which are caused by the symmetry violation and a number of nearest neighbors of the cell on the particle surface [15,16].
As can be seen from several particle cross sections presented in Figure 2, the magnetic order is preserved in the particle core and is not observed on the particle surface. In the particle core, the magnetization is somewhat non-uniform, which is noticeable when compared with a particle of the same size that has no shell (Figure 3). This confirms the ideas accompanying the discussion of Equation (2) and illustrated in Figure 1.
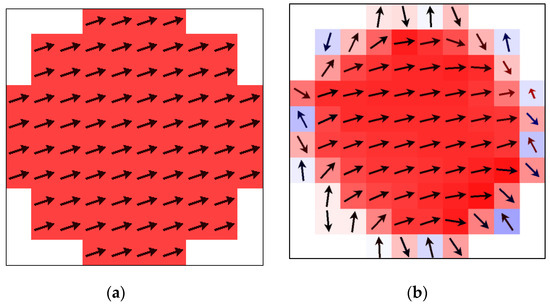
Figure 3.
The exchange coupling between the magnetically ordered core and magnetically disordered shell leads to the inhomogeneous magnetization in the core: (a) Particle without shell and (b) particle with the disordered magnetic shell.
The particle core, being single-domain, is magnetized by coherent rotation in fields comparable with the anisotropy field of bulk maghemite (250 Oe [51]). In these fields, the frozen magnetic disorder of the shell barely contributes to the particle magnetic moment (see upper left inset in Figure 4). This is reflected in the fact that the saturation moment determined from such loops is related to the parameter (there, is the shell thickness and R is the particle radius) as ; i.e., it is proportional to the volume fraction of the particle core (see lower right inset in Figure 4). In the fields much stronger than the magnetocrystalline anisotropy field, the average projection of the magnetization to the applied field slowly grows (see Figure 4). Against the background of the main linear contribution, a certain nonlinear contribution can also be seen in this portion, which may result from the above-described effect of the core–shell coupling leading to the behavior described by Equation (2). The description of this segment of the approach to magnetic saturation by a sum of the linear contribution and Equation (2) yields a satisfactory result (Figure 4).
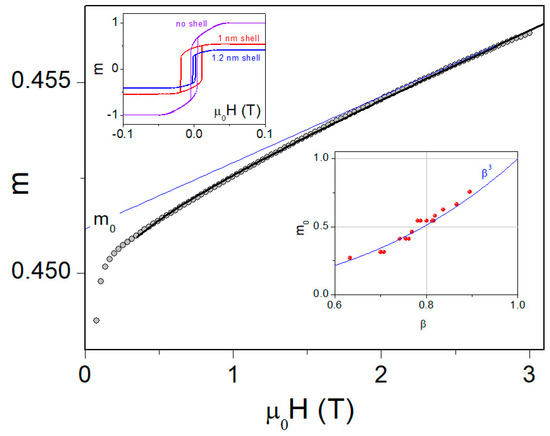
Figure 4.
Approach to magnetic saturation in the numerical simulation (m = M/Ms). The blue line shows the contribution of the spin-frustrated shell and the black solid line, the total nanoparticle response described by Equation (2). Upper left inset: hysteresis loops for a particle without and with a shell. Dependence of the technical saturation magnetization of a particle on the parameter .
4. Experimental Testing
The description of the experimental data on the approach to magnetic saturation in magnetite and maghemite nanoparticles using the expressions based on Equation (2) was first proposed in [17] and continued in [34,35,36,43,52,53,54,55]. Here, we summarize the experience of such a description, supplementing it with the new data obtained on magnetite nanoparticles coated with different biocompatible shells.
Since there are usually both superparamagnetic and blocked particles in a measured powder sample, we have to give some additional explanations concerning the approach to magnetic saturation behavior. For particles in the blocked state, at temperatures well below the blocking temperature, one can expect the behavior typical of the single-domain ferromagnetic particle described by the Stoner–Wohlfahrt model. In the superparamagnetic regime, the average magnetization of a system of particles is described by the Langevin function. Super-paramagnetic particles are meant to be the ones with the magnetic moment repeatedly passing between several stable states during the measurement. These states are determined by the balance between the magnetic anisotropy energy and the Zeeman energy. Thus, the boundary temperature between superparamagnetic and blocked particles (the blocking temperature), being a measure of the height of the potential barrier between stable states, turns out to be the function of an external field and measurement time. As the field increases, the barrier height decreases, leading to a decrease in the blocking temperature [56,57]. In a sufficiently strong field, where the magnetic energy of a particle is determined by the single minimum, the subdivision into the superparamagnetic and blocked states seems to lose meaning. The magnetization of superparamagnetic particles is described by the Langevin function. Note that the use of the Langevin function is justified by the fact that we deal with classical spins. In this approach, the average magnetization is only determined by the ratio between the Zeeman energy and the energy of thermal fluctuations of the magnetic moment of a particle: , where V is the particle volume. This model suggests the validity of the strong inequality , where is the nanoparticle anisotropy constant. The behavior of the magnetization in strong fields within this “superparamagnetic” limit is described as . The allowance for the anisotropy energy leads to the behavior [58]:
for the particles with a randomly oriented easy magnetization axis. The anisotropy-dependent term corresponds to the well-known behavior of polycrystalline ferromagnets in strong fields [31,37] or systems of single-domain particles at (see Equation (1) and the discussion about it). Taking into account the above arguments, we describe the experimental magnetization curves in strong fields using the expression with the last term described by Equation (2) with allowance for the response of the particle spin-frustrated shell :
where and (the both a and b in [A/m] units).
Fitting the approach to magnetic saturation using such an expression usually provides a perfect description of the magnetization evolution in strong fields. Figure 5 shows an example of fitting the magnetization curve for polyethylene glycol-coated iron oxide nanoparticles at 50 K.
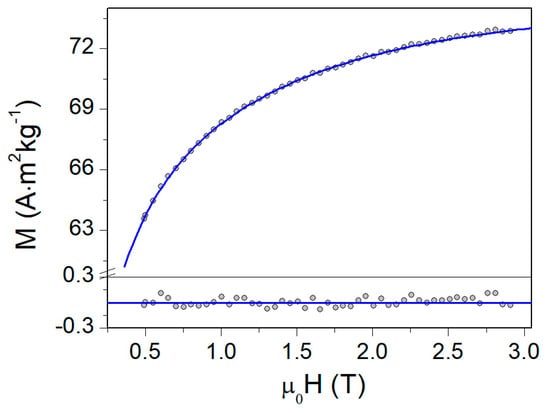
Figure 5.
Approach to magnetic saturation in polyethylene glycol-coated magnetite nanoparticles at 50 K [36] and data fitting using Equation (4). The lower panel shows the residual plot (the difference between the measured M value and the predicted by Equation (4)).
The synthesis and some properties of these particles were described in [54]. Taking into account the particle size (~10 nm) and the magnetization ( (92 Am2 kg−1) for magnetite) at T ≈ 50 K in a field of H ~ 1 T, the contribution in Equation (4) is about . The deviations of the magnetization from saturation, which we deal with in the strong-field mode (Figure 5), are 1÷2 orders of magnitude greater than the term . Thus, in this case, we can assume that the main contribution to the M(H) dependence is related to the next term in brackets in Equation (4). The parameters used for fitting in Figure 5 are , , , and and the correlation best-fit parameter R2 is 0.988. The values of parameters b and obtained by fitting the magnetization curves for different magnetite nanoparticle samples at different temperatures using Equation (4) are presented in Figure 6. These parameters show a significant spread in b and values and, at the same time, there is a noticeable correlation between b and .
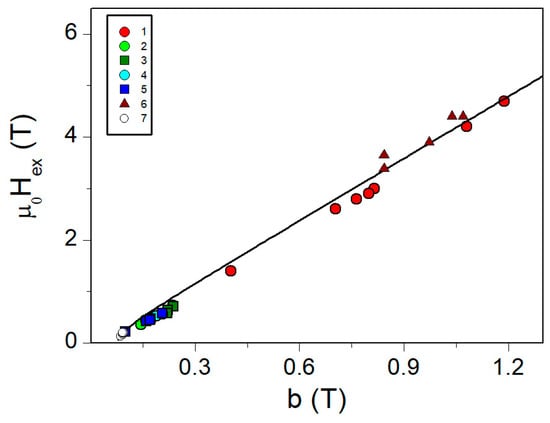
Figure 6.
Correlation of parameters b and Hex in different magnetite nanoparticle samples: (1) magnetite nanoparticles with the polyethylene glycol shell [59] (magnetization curves were measured at different temperatures, so one sample corresponds to several points); (2,3) magnetite nanoparticles with the SiO2 shell [59] (4,5) magnetite nanoparticles with minopropyltriethoxysilane and aminopropyltriethoxysilane/tetraethoxysilicate shells [60], (6) maghemite nanoparticles [17], and (7) lamellar magnetite nanoparticles [55].
The observed correlation suggests the apparent interplay between the field responsible for the core–shell exchange coupling and the exchange field inside the core (supposing the negligible value of as compared with ), as well as the universality of Equation (2) in describing the approach to magnetic saturation of magnetite-like particles. The data shown in Figure 6 concern particles with non-metallic shells. Considering that, in recent years, a lot of the research has been devoted to metallic shells such as Au and Ag, it will be interesting to test the applicability and universality of Equations (2) and (4) to such objects in the future. Describing the interplay between the fields and as and using the definition (see Equation (4) with the description), we express the correlation between and : . The dependence expressed by this formula (see solid line in Figure 6) is similar to the data obtained at and 3 T. The correlation in Figure 6 is almost linear. This means that the contribution of to the measured parameter b is the basic one. The core anisotropy constant recalculated as is . This is noticeably greater in the absolute value than the constant of the magnetocrystalline anisotropy of magnetite: [51]. However, the anisotropy constant of a nanoparticle also contains the contributions of the surface magnetic anisotropy and dipole–dipole interaction of a particle with the environment. The surface magnetic anisotropy contribution can be estimated as [61] ( is the particle diameter and surface magnetic anisotropy constant for magnetite). In ensembles, where particles are, as a rule, arranged in chains, the magnetostatic contribution can be estimated as ), where is the spin-frustrated shell thickness. For a magnetite nanoparticle with a core diameter of and [17], the sum of the bulk, surface, and magnetostatic contributions is about . In the experimental particle samples, for the data that are shown in Figure 6, the sizes lie within the range used in the estimation. Thus, it can be seen that this estimate is consistent with the estimate made from the data presented in Figure 6.
In Figure 6, not only are the data for different samples consistent, but so are the data obtained on the same sample, the magnetization curve of which was measured at different temperatures. This can be understood with the help of Figure 7, which shows the temperature dependences for the parameters of Fe3O4 coated by SiO2 nanoparticles synthesized and characterized as described in [60]. The size of the uniformly magnetized particle core was calculated as and the parameter was found as . The growth of the value with temperature should enhance core magnetization. This is precisely the behavior observed in Figure 7 since the enhanced inhomogeneity should lead to a decrease in . Note that the ability to obtain information about the magnetic inhomogeneity of an individual nanoparticle is an interesting problem; to solve it, the authors of [62] performed complex magnetic small-angle neutron scattering (SANS) and small-angle X-ray scattering (SAXS) measurements. The method used by us to obtain such information is much more accessible. In Figure 7, next to the size , the average particle size determined by transmission electron microscopy in [60] is presented.

Figure 7.
Energy Ksc of the core–shell coupling and size Lc of a uniformly magnetized core with the example of Fe3O4 coated by SiO2 nanoparticles.
The difference between this size and can be considered as an estimate of the double thickness of the spin-frustrated shell of a particle (the particle diameter is where the is assumed to be the core diameter and the is the shell thickness). The thickness of the magnetically disordered shell estimated from our data in such a way is 0.5÷1 nm, which agrees well with the thickness of 0.3÷0.6 nm estimated in [53,62].
5. Conclusions
An equation has been proposed for the approach to magnetic saturation in magnetite-like ferrimagnetic nanoparticles, which takes into account the exchange coupling between the magnetically disordered shell and the core of a particle. Experimental and micromagnetic testing was used to confirm the validity and universality of this equation. It was shown that analysis of the approach to magnetic saturation of iron oxide nanoparticles at different temperatures using the proposed equation makes it possible to estimate the temperature behavior of the core–shell coupling energy, as well as the size of the uniformly magnetized nanoparticle core and the temperature behavior of this size.
Author Contributions
Conceptualization, methodology, writing—original draft preparation S.V.K.; software, micromagnetic simulation, S.V.K., V.A.F. and A.A.M.; validation, R.S.I.; formal analysis, S.V.K.; investigation, D.A.V. and S.V.K.; data curation, S.V.S.; writing—review and editing, S.V.K. and R.S.I.; visualization, A.A.M.; supervision, S.V.S. All authors discussed the results and implications and commented on the manuscript at all stages. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Russian Science Foundation and the Krasnoyarsk Territorial Foundation for Support of Scientific and R&D Activities, project No. 22-14-20020.
Institutional Review Board Statement
This work did not involve humans or animals and therefore it did not require the Institutional Review Board Statement and approval.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pankhurst, Q.A.; Connolly, J.; Jones, S.K.; Dobson, J. Applications of Magnetic Nanoparticles in Biomedicine. J. Phys. D Appl. Phys. 2003, 36, R167–R181. [Google Scholar] [CrossRef]
- Mohammed, L.; Gomaa, H.G.; Ragab, D.; Zhu, J. Magnetic Nanoparticles for Environmental and Biomedical Applications: A Review. Particuology 2017, 30, 1–14. [Google Scholar] [CrossRef]
- Rancourt, D.G. Magnetism of Earth, Planetary, and Environmental Nanomaterials. Rev. Mineral. Geochem. 2001, 44, 217–292. [Google Scholar] [CrossRef]
- Ma, Y.; Zou, Y.; Meng, L.; Cai, L.; Xiong, S.; Chen, G.; Dong, C.; Guan, H. Ni@C/PPy Composites Derived from Ni-MOF Materials for Efficient Microwave Absorption. Magnetochemistry 2024, 10, 24. [Google Scholar] [CrossRef]
- Ziogas, P.G.; Bourlinos, A.B.; Chatzopoulou, P.; Dimitrakopulos, G.P.; Markou, A.; Douvalis, A.P. Novel Hybrid Ferromagnetic Fe–Co/Nanodiamond Nanostructures: Influence of Carbon on Their Structural and Magnetic Properties. Magnetochemistry 2024, 10, 35. [Google Scholar] [CrossRef]
- Moacă, E.-A.; Socoliuc, V.; Stoian, D.; Watz, C.; Flondor, D.; Păcurariu, C.; Ianoș, R.; Rus, C.I.; Barbu-Tudoran, L.; Semenescu, A.; et al. Synthesis and Characterization of Bioactive Magnetic Nanoparticles from the Perspective of Hyperthermia Applications. Magnetochemistry 2022, 8, 145. [Google Scholar] [CrossRef]
- Levin, C.S.; Hofmann, C.; Ali, T.A.; Kelly, A.T.; Morosan, E.; Nordlander, P.; Whitmire, K.H.; Halas, N.J. Magnetic−Plasmonic Core−Shell Nanoparticles. ACS Nano 2009, 3, 1379–1388. [Google Scholar] [CrossRef] [PubMed]
- Rajabi-Moghaddam, H.; Naimi-Jamal, M.R.; Tajbakhsh, M. Fabrication of Copper(II)-Coated Magnetic Core-Shell Nanoparticles Fe3O4@SiO2-2-Aminobenzohydrazide and Investigation of Its Catalytic Application in the Synthesis of 1,2,3-Triazole Compounds. Sci. Rep. 2021, 11, 2073. [Google Scholar] [CrossRef] [PubMed]
- Tsamos, D.; Krestou, A.; Papagiannaki, M.; Maropoulos, S. An Overview of the Production of Magnetic Core-Shell Nanoparticles and Their Biomedical Applications. Metals 2022, 12, 605. [Google Scholar] [CrossRef]
- Mittal, A.; Roy, I.; Gandhi, S. Magnetic Nanoparticles: An Overview for Biomedical Applications. Magnetochemistry 2022, 8, 107. [Google Scholar] [CrossRef]
- Coey, J.M.D. Noncollinear Spin Arrangement in Ultrafine Ferrimagnetic Crystallites. Phys. Rev. Lett. 1971, 27, 1140–1142. [Google Scholar] [CrossRef]
- Gareev, K.G. Diversity of Iron Oxides: Mechanisms of Formation, Physical Properties and Applications. Magnetochemistry 2023, 9, 119. [Google Scholar] [CrossRef]
- Silva, N.J.O.; Amaral, V.S.; Urtizberea, A.; Bustamante, R.; Millán, A.; Palacio, F.; Kampert, E.; Zeitler, U.; de Brion, S.; Iglesias, Ò.; et al. Shifted Loops and Coercivity from Field-Imprinted High-Energy Barriers in Ferritin and Ferrihydrite Nanoparticles. Phys. Rev. B 2011, 84, 104427. [Google Scholar] [CrossRef]
- Mamiya, H.; Nakatani, I.; Furubayashi, T. Magnetic Relaxations of Antiferromagnetic Nanoparticles in Magnetic Fields. Phys. Rev. Lett. 2002, 88, 067202. [Google Scholar] [CrossRef] [PubMed]
- Kodama, R.H.; Berkowitz, A.E.; McNiff, E.J., Jr.; Foner, S. Surface Spin Disorder in NiFe2O4 Nanoparticles. Phys. Rev. Lett. 1996, 77, 394–397. [Google Scholar] [CrossRef] [PubMed]
- Kodama, R. Magnetic Nanoparticles. J. Magn. Magn. Mater. 1999, 200, 359–372. [Google Scholar] [CrossRef]
- Safronov, A.P.; Beketov, I.V.; Komogortsev, S.V.; Kurlyandskaya, G.V.; Medvedev, A.I.; Leiman, D.V.; Larrañaga, A.; Bhagat, S.M. Spherical Magnetic Nanoparticles Fabricated by Laser Target Evaporation. AIP Adv. 2013, 3, 052135. [Google Scholar] [CrossRef]
- Soler, M.A.G.; Paterno, L.G. Magnetic Nanomaterials. In Nanostructures; Elsevier: Amsterdam, The Netherlands, 2017; pp. 147–186. [Google Scholar]
- Benguettat-El Mokhtari, I.; Schmool, D.S. Ferromagnetic Resonance in Magnetic Oxide Nanoparticules: A Short Review of Theory and Experiment. Magnetochemistry 2023, 9, 191. [Google Scholar] [CrossRef]
- Kons, C.; Srikanth, H.; Phan, M.-H.; Arena, D.A.; Pereiro, M. Macrospin Model of an Assembly of Magnetically Coupled Core-Shell Nanoparticles. Phys. Rev. B 2022, 106, 104402. [Google Scholar] [CrossRef]
- Guduri, B.R.; Luyt, A.S. Structure and Mechanical Properties of Polycarbonate Modified Clay Nanocomposites. J. Nanosci. Nanotechnol. 2008, 8, 1880–1885. [Google Scholar] [CrossRef]
- Balaev, D.A.; Krasikov, A.A.; Dubrovskii, A.A.; Semenov, S.V.; Bayukov, O.A.; Stolyar, S.V.; Iskhakov, R.S.; Ladygina, V.P.; Ishchenko, L.A. Magnetic Properties and the Mechanism of Formation of the Uncompensated Magnetic Moment of Antiferromagnetic Ferrihydrite Nanoparticles of a Bacterial Origin. J. Exp. Theor. Phys. 2014, 119, 479–487. [Google Scholar] [CrossRef]
- Bedanta, S.; Kleemann, W. Supermagnetism. J. Phys. D Appl. Phys. 2009, 42, 013001. [Google Scholar] [CrossRef]
- Balaev, D.A.; Krasikov, A.A.; Dubrovskii, A.A.; Bayukov, O.A.; Stolyar, S.V.; Iskhakov, R.S.; Ladygina, V.P.; Yaroslavtsev, R.N. The Effect of Low-Temperature Heat Treatment on the Magnetic Properties of Biogenic Ferrihydrite Nanoparticles. Tech. Phys. Lett. 2015, 41, 705–709. [Google Scholar] [CrossRef]
- Balaev, D.A.; Krasikov, A.A.; Dubrovskiy, A.A.; Popkov, S.I.; Stolyar, S.V.; Bayukov, O.A.; Iskhakov, R.S.; Ladygina, V.P.; Yaroslavtsev, R.N. Magnetic Properties of Heat Treated Bacterial Ferrihydrite Nanoparticles. J. Magn. Magn. Mater. 2016, 410, 171–180. [Google Scholar] [CrossRef]
- Balaev, D.A.; Krasikov, A.A.; Dubrovskiy, A.A.; Popkov, S.I.; Stolyar, S.V.; Iskhakov, R.S.; Ladygina, V.P.; Yaroslavtsev, R.N. Exchange Bias in Nano-Ferrihydrite. J. Appl. Phys. 2016, 120, 183903. [Google Scholar] [CrossRef]
- Bruvera, I.J.; Mendoza Zélis, P.; Pilar Calatayud, M.; Goya, G.F.; Sánchez, F.H. Determination of the Blocking Temperature of Magnetic Nanoparticles: The Good, the Bad, and the Ugly. J. Appl. Phys. 2015, 118, 184304. [Google Scholar] [CrossRef]
- Komogortsev, S.V.; Patrusheva, T.N.; Balaev, D.A.; Denisova, E.A.; Ponomarenko, I.V. Cobalt Ferrite Nanoparticles in a Mesoporous Silicon Dioxide Matrix. Tech. Phys. Lett. 2009, 35, 882–884. [Google Scholar] [CrossRef]
- Poperechny, I.S.; Raikher, Y.L.; Stepanov, V.I. Dynamic Hysteresis of a Uniaxial Superparamagnet: Semi-Adiabatic Approximation. Phys. B Condens. Matter 2013, 435, 58–61. [Google Scholar] [CrossRef]
- Komogortsev, S.V.; Balaev, D.A.; Krasikov, A.A.; Stolyar, S.V.; Yaroslavtsev, R.N.; Ladygina, V.P.; Iskhakov, R.S. Magnetic Hysteresis of Blocked Ferrihydrite Nanoparticles. AIP Adv. 2021, 11, 015329. [Google Scholar] [CrossRef]
- Akulov, N.S. Uber Den Verlauf Der Magnetisierungskurve in Starken Feldern. Z. Fur Phys. Phys. 1931, 69, 822–831. [Google Scholar] [CrossRef]
- Czerlinsky, E. Über Magnetische Sättigung. Ann. Phys. 1932, 405, 80–100. [Google Scholar] [CrossRef]
- Brown, W. Theory of the Approach to Magnetic Saturation. Phys. Rev. 1940, 58, 736–743. [Google Scholar] [CrossRef]
- Devi, E.C.; Soibam, I. Law of Approach to Saturation in Mn–Zn Ferrite Nanoparticles. J. Supercond. Nov. Magn. 2018, 32, 1293–1298. [Google Scholar] [CrossRef]
- Devi, E.C.; Soibam, I. Magnetic Properties and Law of Approach to Saturation in Mn-Ni Mixed Nanoferrites. J. Alloys Compd. 2019, 772, 920–924. [Google Scholar] [CrossRef]
- Stolyar, S.V.; Komogortsev, S.V.; Gorbenko, A.S.; Knyazev, Y.V.; Yaroslavtsev, R.N.; Olkhovskiy, I.A.; Neznakhin, D.S.; Tyumentseva, A.V.; Bayukov, O.A.; Iskhakov, R.S. Maghemite Nanoparticles for DNA Extraction: Performance and Blocking Temperature. J. Supercond. Nov. Magn. 2022, 35, 1929–1936. [Google Scholar] [CrossRef]
- Iskhakov, R.S.; Komogortsev, S.V. Magnetic Microstructure of Amorphous, Nanocrystalline, and Nanophase Ferromagnets. Phys. Met. Metallogr. 2011, 112, 666–681. [Google Scholar] [CrossRef]
- Abo, G.S.; Hong, Y.-K.; Park, J.; Lee, J.; Lee, W.; Choi, B.-C. Definition of Magnetic Exchange Length. IEEE Trans. Magn. 2013, 49, 4937–4939. [Google Scholar] [CrossRef]
- Komogortsev, S.V.; Iskhakov, R.S. Law of Approach to Magnetic Saturation in Nanocrystalline and Amorphous Ferromagnets with Improved Transition Behavior between Power-Law Regimes. J. Magn. Magn. Mater. 2017, 440, 213–216. [Google Scholar] [CrossRef]
- Beketov, I.V.; Safronov, A.P.; Medvedev, A.I.; Alonso, J.; Kurlyandskaya, G.V.; Bhagat, S.M. Iron Oxide Nanoparticles Fabricated by Electric Explosion of Wire: Focus on Magnetic Nanofluids. AIP Adv. 2012, 2, 022154. [Google Scholar] [CrossRef]
- Komogortsev, S.V.; Denisova, E.A.; Iskhakov, R.S.; Balaev, A.D.; Chekanova, L.A.; Kalinin, Y.E.; Sitnikov, A. V Multilayer Nanogranular Films (Co40Fe40B20)50(SiO2)50/α-Si:H and (Co40Fe40B20)50(SiO2)50/SiO2: Magnetic Properties. J. Appl. Phys. 2013, 113, 17C105. [Google Scholar] [CrossRef]
- Komogortsev, S.V.; Iskhakov, R.S.; Zimin, A.A.; Filatov, E.Y.; Korenev, S.V.; Shubin, Y.V.; Chizhik, N.A.; Yurkin, G.Y.; Eremin, E.V. The Exchange Interaction Effects on Magnetic Properties of the Nanostructured CoPt Particles. J. Magn. Magn. Mater. 2016, 401, 236–241. [Google Scholar] [CrossRef]
- Stolyar, S.V.; Komogortsev, S.V.; Chekanova, L.A.; Yaroslavtsev, R.N.; Bayukov, O.A.; Velikanov, D.A.; Volochaev, M.N.; Cheremiskina, E.V.; Bairmani, M.S.; Eroshenko, P.E.; et al. Magnetite Nanocrystals with a High Magnetic Anisotropy Constant Due to the Particle Shape. Tech. Phys. Lett. 2019, 45, 878–881. [Google Scholar] [CrossRef]
- Devi, E.C.; Singh, S.D. Tracing the Magnetization Curves: A Review on Their Importance, Strategy, and Outcomes. J. Supercond. Nov. Magn. 2021, 34, 15–25. [Google Scholar] [CrossRef]
- Ignatchenko, V.A.; Iskhakov, R.S.; Popov, G.V. Law of Approach to Ferromagnetic Saturation in Amorphous Ferromagnets. Zh. Eksp. Teor. Fiz. 1982, 82, 1518–1531. [Google Scholar]
- Chudnovsky, E.M.; Saslow, W.M.; Serota, R.A. Ordering in Ferromagnets with Random Anisotropy. Phys. Rev. B 1986, 33, 251–261. [Google Scholar] [CrossRef] [PubMed]
- Chudnovsky, E.M. Magnetic Properties of Amorphous Ferromagnets (Invited). J. Appl. Phys. 1988, 64, 5770. [Google Scholar] [CrossRef]
- Donahue, M.J.; Porter, D.G. OOMMF User’s Guide, Version 1.0; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1999. [Google Scholar]
- Newell, A.J.; Williams, W.; Dunlop, D.J. A Generalization of the Demagnetizing Tensor for Nonuniform Magnetization. J. Geophys. Res. Solid Earth 1993, 98, 9551–9555. [Google Scholar] [CrossRef]
- Aharoni, A. Demagnetizing Factors for Rectangular Ferromagnetic Prisms. J. Appl. Phys. 1998, 83, 3432–3434. [Google Scholar] [CrossRef]
- Coey, J.M.D. Magnetism and Magnetic Materials; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Komogortsev, S.V.; Iskhakov, R.S.; Zimin, A.A.; Filatov, E.Y.; Korenev, S.V.; Shubin, Y.V.; Chizhik, N.A.; Yurkin, G.Y.; Eremin, E.V. Magnetic Anisotropy and Order Parameter in Nanostructured CoPt Particles. Appl. Phys. Lett. 2013, 103, 152404. [Google Scholar] [CrossRef]
- Kurlyandskaya, G.V.; Bhagat, S.M.; Safronov, A.P.; Beketov, I.V.; Larrañaga, A. Spherical Magnetic Nanoparticles Fabricated by Electric Explosion of Wire. AIP Adv. 2011, 1, 042122. [Google Scholar] [CrossRef]
- Denisova, E.A.; Komogortsev, S.V.; Iskhakov, R.S.; Chekanova, L.A.; Balaev, A.D.; Kalinin, Y.E.; Sitnikov, A.V. Magnetic Anisotropy in Multilayer Nanogranular Films (Co40Fe40B20)50(SiO2)50/α-Si:H. J. Magn. Magn. Mater. 2017, 440, 221–224. [Google Scholar] [CrossRef]
- Komogortsev, S.V.; Stolyar, S.V.; Chekanova, L.A.; Yaroslavtsev, R.N.; Bayukov, O.A.; Velikanov, D.A.; Volochaev, M.N.; Eroshenko, P.E.; Iskhakov, R.S. Square Plate Shaped Magnetite Nanocrystals. J. Magn. Magn. Mater. 2021, 527, 167730. [Google Scholar] [CrossRef]
- Usov, N.A.; Grebenshchikov, Y.B. Hysteresis Loops of an Assembly of Superparamagnetic Nanoparticles with Uniaxial Anisotropy. J. Appl. Phys. 2009, 106, 023917. [Google Scholar] [CrossRef]
- Wood, R. Exact Solution for a Stoner–Wohlfarth Particle in an Applied Field and a New Approximation for the Energy Barrier. IEEE Trans. Magn. 2009, 45, 100–103. [Google Scholar] [CrossRef]
- Yasumori, I.; Reinen, D.; Selwood, P.W. Anisotropic Behavior in Superparamagnetic Systems. J. Appl. Phys. 1963, 34, 3544–3549. [Google Scholar] [CrossRef]
- Stolyar, S.V.; Yaroslavtsev, R.N.; Tyumentseva, A.V.; Komogortsev, S.V.; Tyutrina, E.S.; Saitova, A.T.; Gerasimova, Y.V.; Velikanov, D.A.; Rautskii, M.V.; Iskhakov, R.S. Manifestation of Stoichiometry Deviation in Silica-Coated Magnetite Nanoparticles. J. Phys. Chem. C 2022, 126, 7510–7516. [Google Scholar] [CrossRef]
- Vazhenina, I.G.; Stolyar, S.V.; Tyumentseva, A.V.; Volochaev, M.N.; Iskhakov, R.S.; Komogortsev, S.V.; Pyankov, V.F.; Nikolaeva, E.D. Study of Magnetic Iron Oxide Nanoparticles Coated with Silicon Oxide by Ferromagnetic Method. Phys. Solid State 2023, 65, 884. [Google Scholar] [CrossRef]
- Pérez, N.; Guardia, P.; Roca, A.G.; Morales, M.P.; Serna, C.J.; Iglesias, O.; Bartolomé, F.; García, L.M.; Batlle, X.; Labarta, A. Surface Anisotropy Broadening of the Energy Barrier Distribution in Magnetic Nanoparticles. Nanotechnology 2008, 19, 475704. [Google Scholar] [CrossRef] [PubMed]
- Zákutná, D.; Nižňanský, D.; Barnsley, L.C.; Babcock, E.; Salhi, Z.; Feoktystov, A.; Honecker, D.; Disch, S. Field Dependence of Magnetic Disorder in Nanoparticles. Phys. Rev. X 2020, 10, 031019. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).